Rationally Extended Harmonic Oscillator potential, Isospectral Family and the Uncertainity Relations
Abstract
We consider the rationally extended harmonic oscillator potential which is isospectral to the conventional one and whose solutions are associated with the exceptional, - Hermite polynomials and discuss its various important properties for different even codimension of . The uncertainty relations are obtained for different and it is shown that for the ground state, the uncertainity increases as increases. A one parameter family of exactly solvable isospectral potential corresponding to this extended harmonic oscillator potential is obtained. Special cases corresponding to the and , which give the Pursey and the Abhram-Moses potentials respectively, are discussed. The uncertainty relations for the entire isospectral family of potentials for different and are also calculated.
Department of Physics, Model College, Dumka-814101, India.
Department of Physics, S. K. M. University, Dumka-814110, India.
Department of Physics, Savitribai Phule Pune University, Pune-411007, India.
1 Introduction
The idea of Supersymmetric Quantum Mechanics(SQM) [1] is not only useful in solving the quantum mechanical potential problems but has also opened the scope for discovering new exactly solvable potentials. These potentials have applications in diverse areas like inverse scattering [2, 3], soliton theory [4, 5], etc. This sparked a race among researchers to search for a family of isospectral potentials [6, 7, 8, 9]. To accomplish this purpose, several methods were developed like Darboux transformation [10], Darboux Crum Krein Adler Transformation [11], SQM [12, 13], etc. Popular among them was the SQM approach due to its simplicity and it was shown using this approach that for any 1-D potential with atleast one bound state, one can always construct one continuous parameter family of strictly isospectral potentials.
The discovery of the -exceptional orthogonal polynomials (EOPs) [14, 15, 16] paved the path for discovering new rationally extended shape invariant potentials whose eigenfunctions are in terms of these EOPs. Various properties of these potentials have been studied in detail in [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29] and the references therein. After the discovery of the exceptional Hermite polynomials [30], Fellows and Smith [31] discovered rationally extended one dimensional harmonic oscillator potentials. Their work has been further extended using the SQM approach [32].
The one dimensional harmonic oscillator potential is one of the most important potential having numerous applications. However, so far as we are aware off, there has not been much progress in studying the various properties of the rationally extended family of harmonic oscillator (REHO) potentials. The purpose of this paper is to take a step in that direction. Firstly, we calculate the Heisenberg uncertainty relation for the REHO potentials. Further, we follow the idea of SQM [1], and generate a one parameter family of rationally extended strictly isospectral potentials including the corresponding Pursey and the Abrahm-Mosses potentials and obtain their eigenfunctions explicitly in terms of the -Hermite EOPs. We calculate the Heisenberg uncertainty relations for the one parameter family of rationally extended isospectral potentials (including the corresponding Pursey and the Abrahm-Mosses potentials) for different and .
The plan of the paper is as follows: In Sec. , we briefly discuss the formulation of SQM. In Sec. , we summarise the known important results related to the rationally extended harmonic oscillator potentials. A one parameter family of isospectral potentials (including the corresponding Pursey and Abrahm-Mosses potentials) are obtained in Sec. for any even integral . In Sec. , we follow the results discussed in Sec. and Sec. and calculate the Heisenberg uncertainty relations for REHO and their isospectral family of potentials (including the corresponding Pursey and Abrahm-Mosses potentials). Finally, we summarize our results and mention some open possible problems in Sec. .
2 SQM Formalism
In SQM approach, one considers the Hamiltonian (in the units )
| (1) |
where is the factorization energy. By assuming the ground state energy of this Hamiltonian , we factorize in terms of and as
| (2) |
with
| (3) |
Here is known as superpotential which is expressed in term of the ground state eigenfunction as . In this way, another set of Hamiltonian can easily be constructed by reversing the order of the operators and i.e.,
| (4) |
Thus, the partner potentials in term of superpotential are given by
| (5) |
Here a prime denotes a derivative with respect to . The precise relationship between the energies and the eigenfunctions of the partner Hamiltonians are
| (6) |
| (7) |
The ground state eigenfunction is obtained by solving the differential equation,
| (8) |
One parameter family of isospectral potentials are obtained by redefining the form of the superpotential
| (9) |
and by assuming the uniqueness of the partner potential i.e.,
which gives
We then find that on substituting , the above equation satisfies the Bernoulli equation
whose solution is
Here and is an integration constant.
Therefore, the potential which is strictly isospectral to is given by
| (10) |
where either or so as to avoid singularity (For details, see[1, 33]). The normalized ground state eigenfunction for the entire family of potentials is given by
| (11) |
The normalized excited states eigenfunctions can be easily calculated similar to (7) as
| (12) | ||||
and the Hamiltonian is defined similar to (1) as
| (13) | ||||
It is worth reminding that all these strictly isospectral family of potentials have same partner potential .
In the limit there is a loss of a bound state and the corresponding potential is called the Pursey potential . An analogous situation occurs in the limit and the potential is called the Abraham-Moses potential . The normalized eigenfunctions of are given by
| (14) |
Similarly, the normalized eigenfunctions of are given by
| (15) |
The energy eigenvalues of the Pursey and the Abraham-Moses Hamiltonians obtained by substituting equal to and respectively in (13) has the same expressions as that of , i.e.
| (16) |
3 REHO Potential
In this section, we briefly review the results obtained in [31, 32] about the REHO potentials. These authors extended the conventional one-dimensional harmonic oscillator potential () using the idea of SQM and obtained the REHO potentials valid for even co-dimension of and are given by
| (17) |
where is pseudo-hermite polynomials and factorization energy used in the calculation was . The normalized ground state eigenfunction having zero eigenvalue and the excited states eigenfunction for different are
| (18) |
and
| (19) |
respectively. Here and is the Exceptional Hermite Polynomial. Note that . The whole system is the exceptional orthogonal polynomial system, , of co-dimension and is orthogonal and complete with respect to the positive-definite measure . The Hamiltonian defined similar to (1) has the energy eigenvalues given by
| (20) |
It is seen that the difference in energy eigenvalues is units between ground state and first excited state and 2 units between any successive excited states. Therefore energy spectra is equidistant only for . Note that is singular at for odd and therefore is restricted to positive even integers only.
It is worth noting that the complete set of eigenfunctions for the case, i.e. the one dimensional harmonic oscillator, can be reduced to a single formula containing ground state eigenfunction and excited state eigenfunction given by
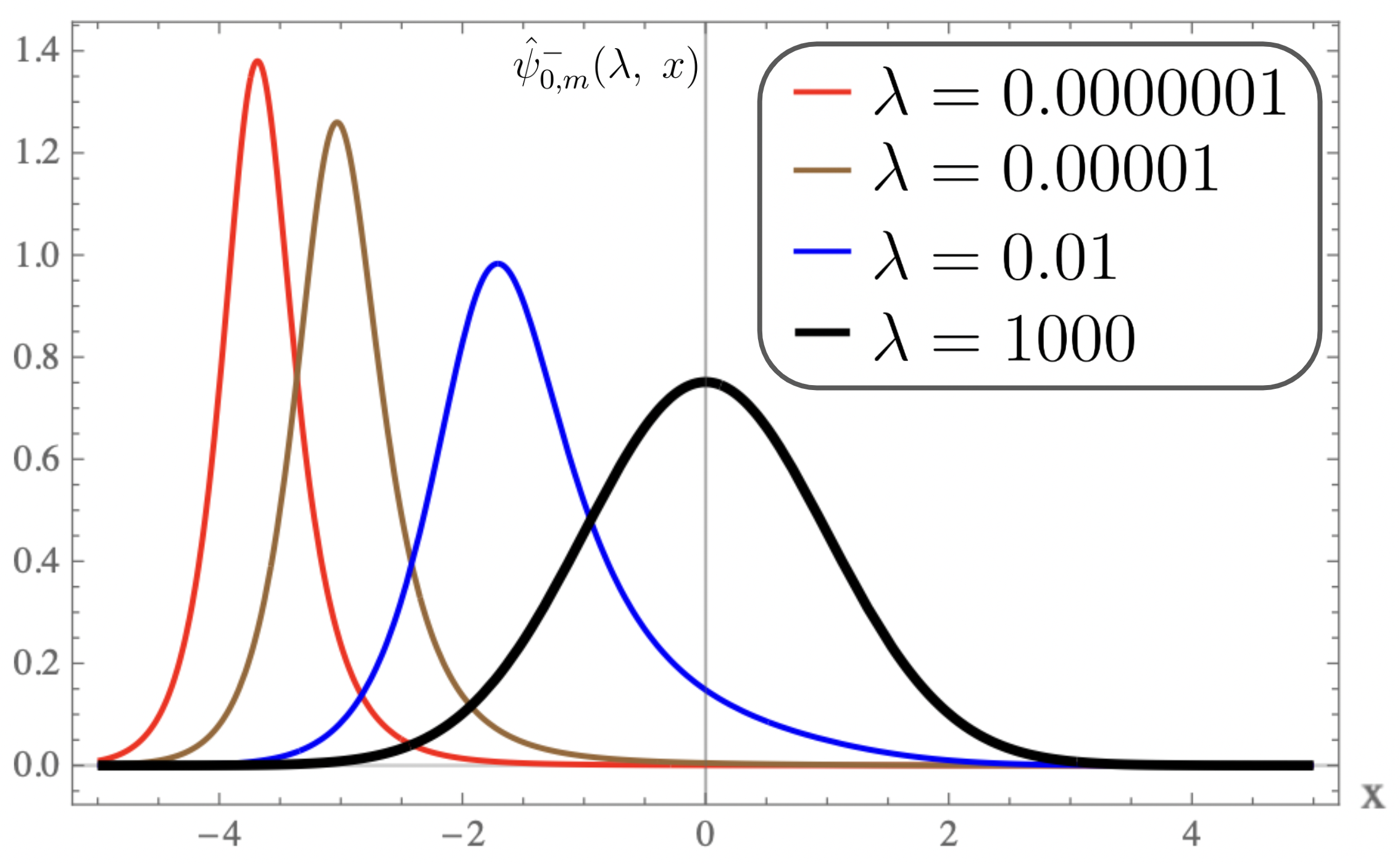
The plot of the ground, first and the second excited state eigenfunctions as well as the potential versus position for are given in Fig-1.a ,Fig-1.b and Fig-1.c respectively. It is interesting to note from these figures that as increases, the eigenfunctions and the potential well becomes sharper. In Table we have given expressions for the potential as well as the ground and the excited state eigenfunctions in case . Expressions for exceptional Hermite polynomials are given in Table in case and .
The superpotential corresponding to the REHO potential is easily obtained from the ground state eigenfunctions of as
| (21) | |||||
The energy eigenvalues of the partner Hamiltonians , defined using (1) and (4), are given by
| (22) | ||||
| (23) |
| m | |||
|---|---|---|---|
| 0 | |||
| 2 | |||
| 4 |



4 One parameter family of REHO potentials
The One parameter () family of strictly isospectral potentials corresponding to are easily obtained using (11-12) as
| (24) |
where the integral is calculated using (18) as
| (25) |
The expressions for and for equal to are given in table-2 and table-3 respectively in terms of the error function defined as
The normalized ground state wave function is obtained using (11), (18) and (25) as
| (26) |
| m | ||
|---|---|---|
| 0 | ||
| 2 | ||
| 4 |
| m | |
|---|---|
| 0 | |
| 2 | |
| 4 |
The normalized excited states eigenfunction of , using (12) are given by
| (27) | ||||
and
The expression of for equal to are tabulated in table-4 . As mentioned above, the spectra of , defined using (13), is strictly isospectral to spectra and is given by Eq. (20).
| m | |
|---|---|
| 0 | |
| 2 | |
| 4 |
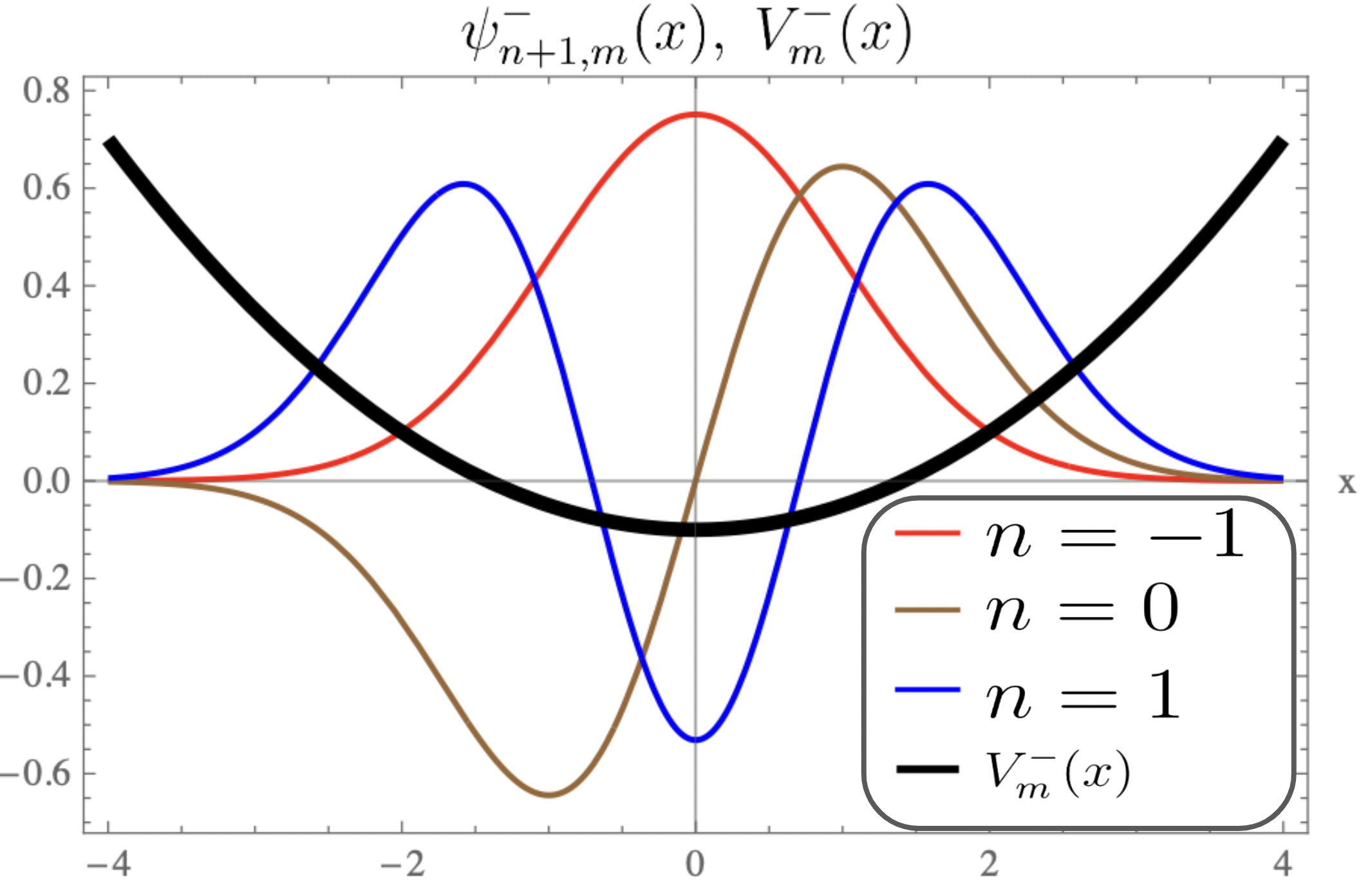
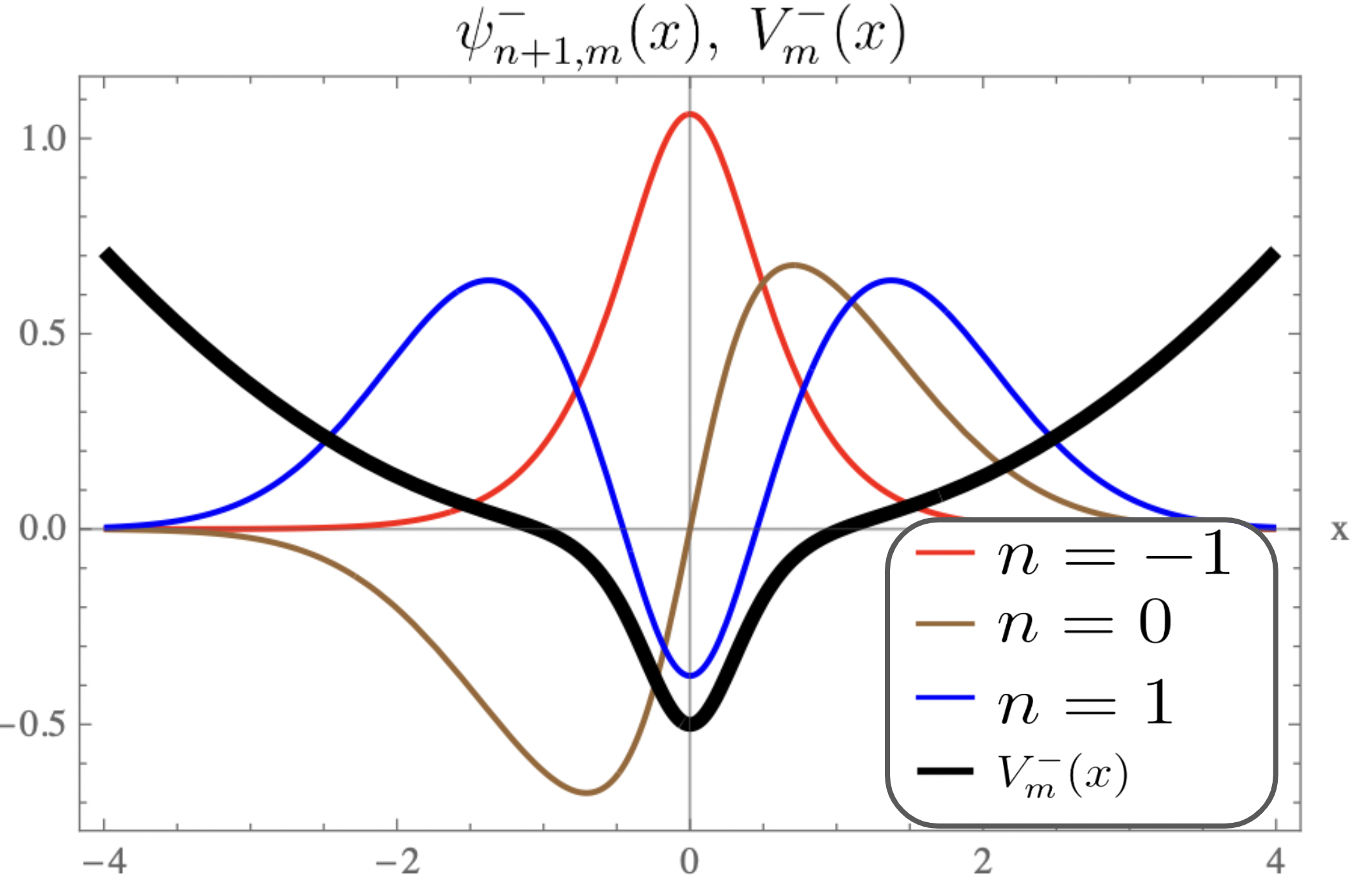
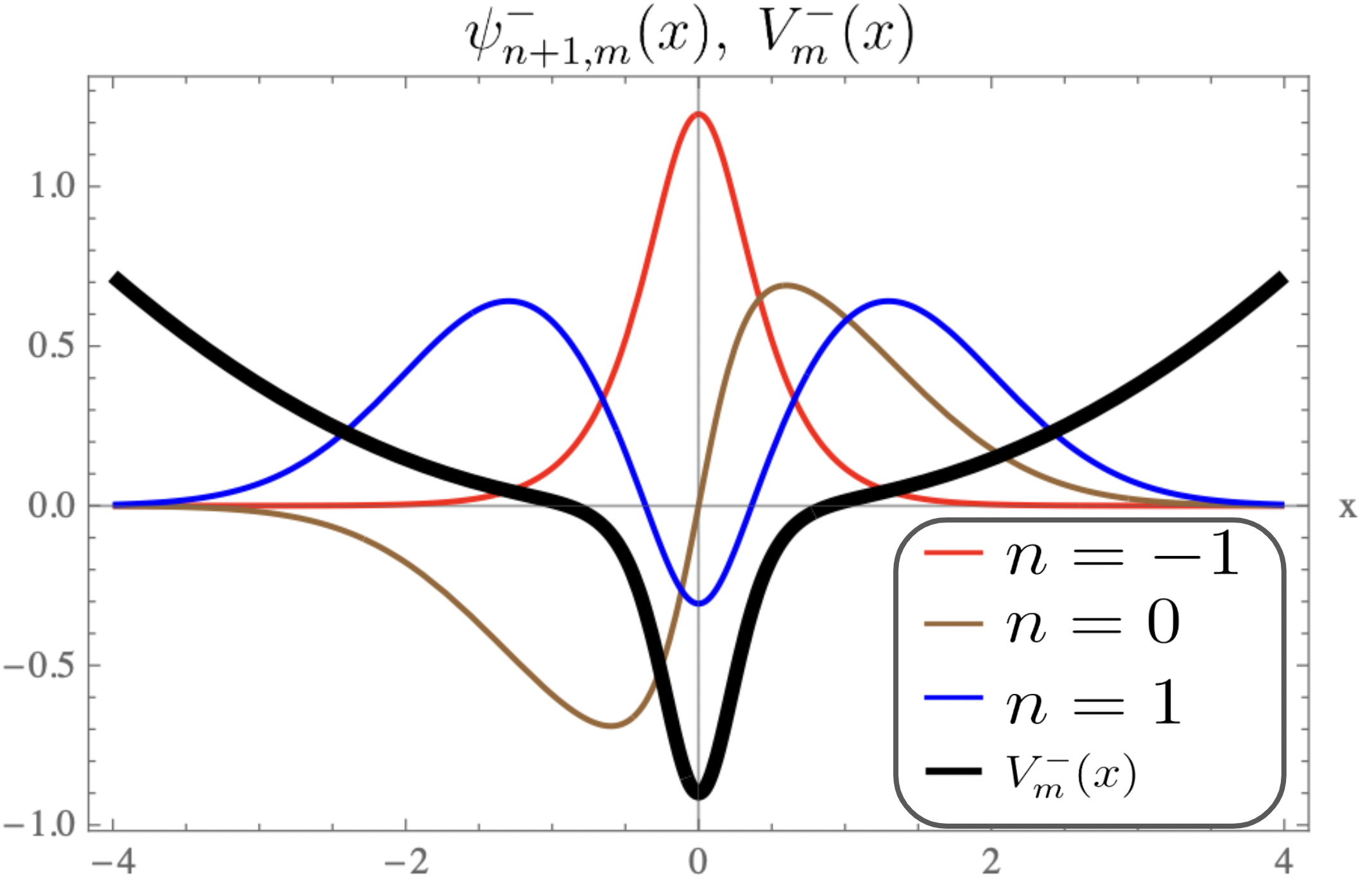
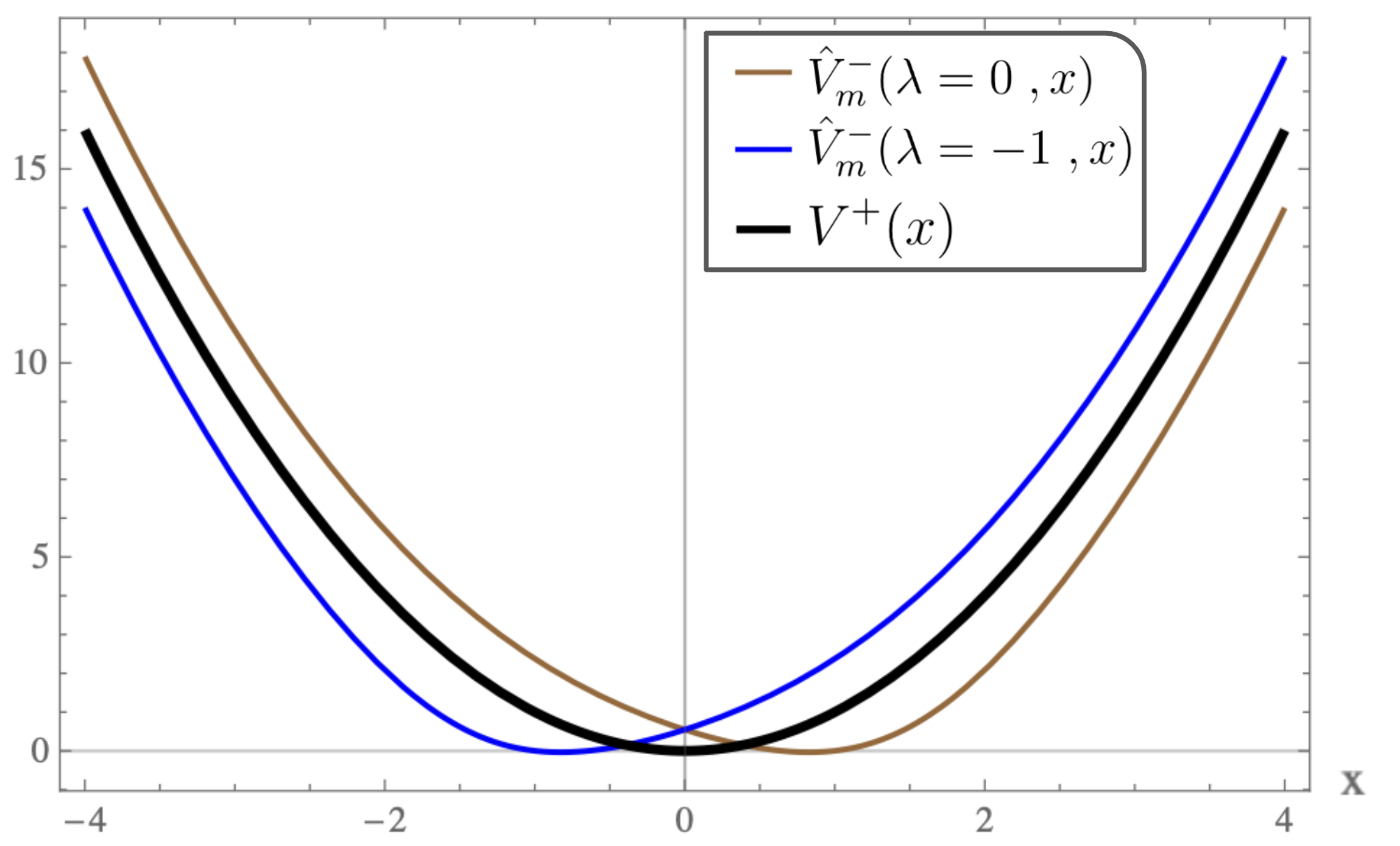
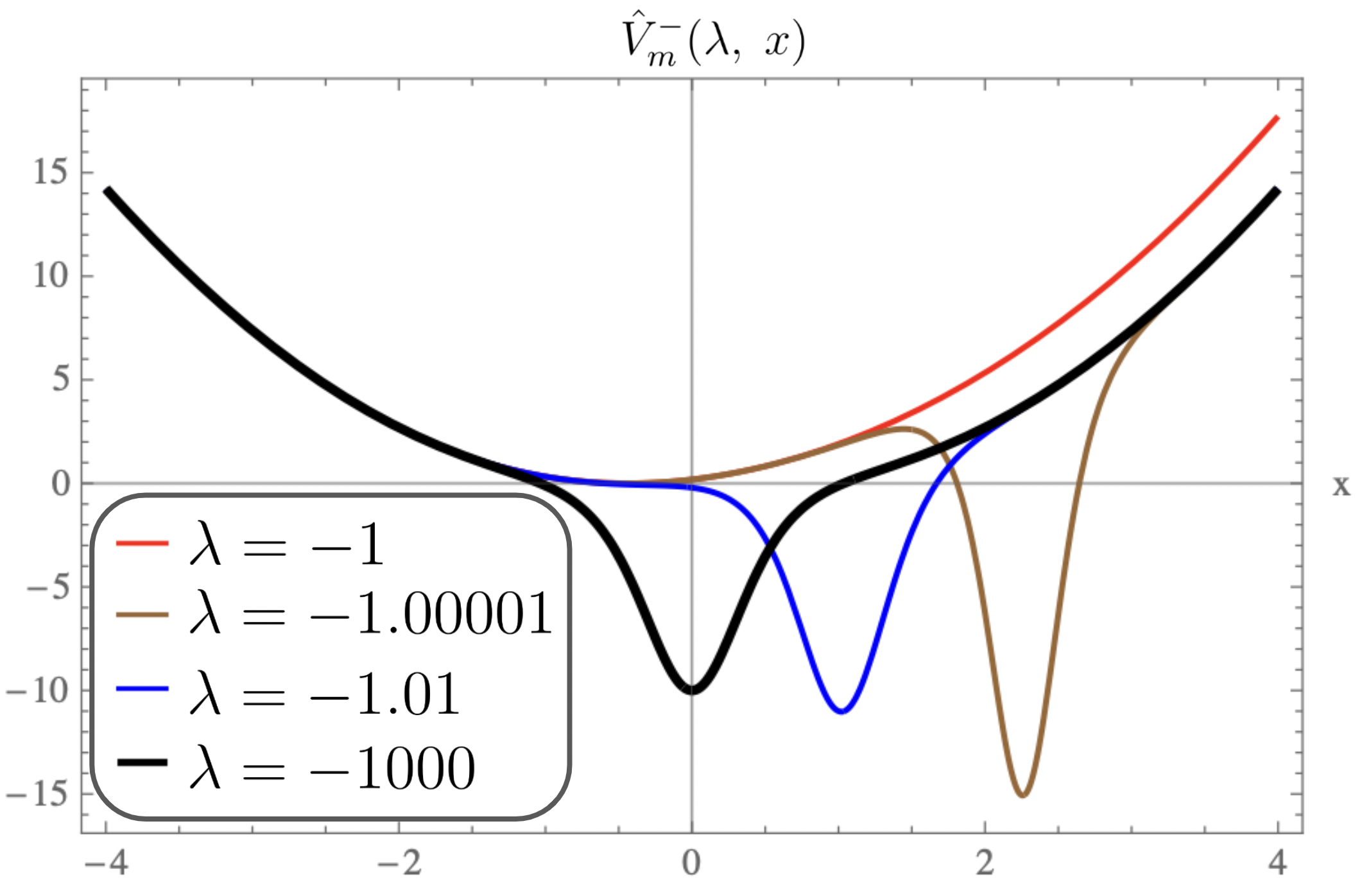
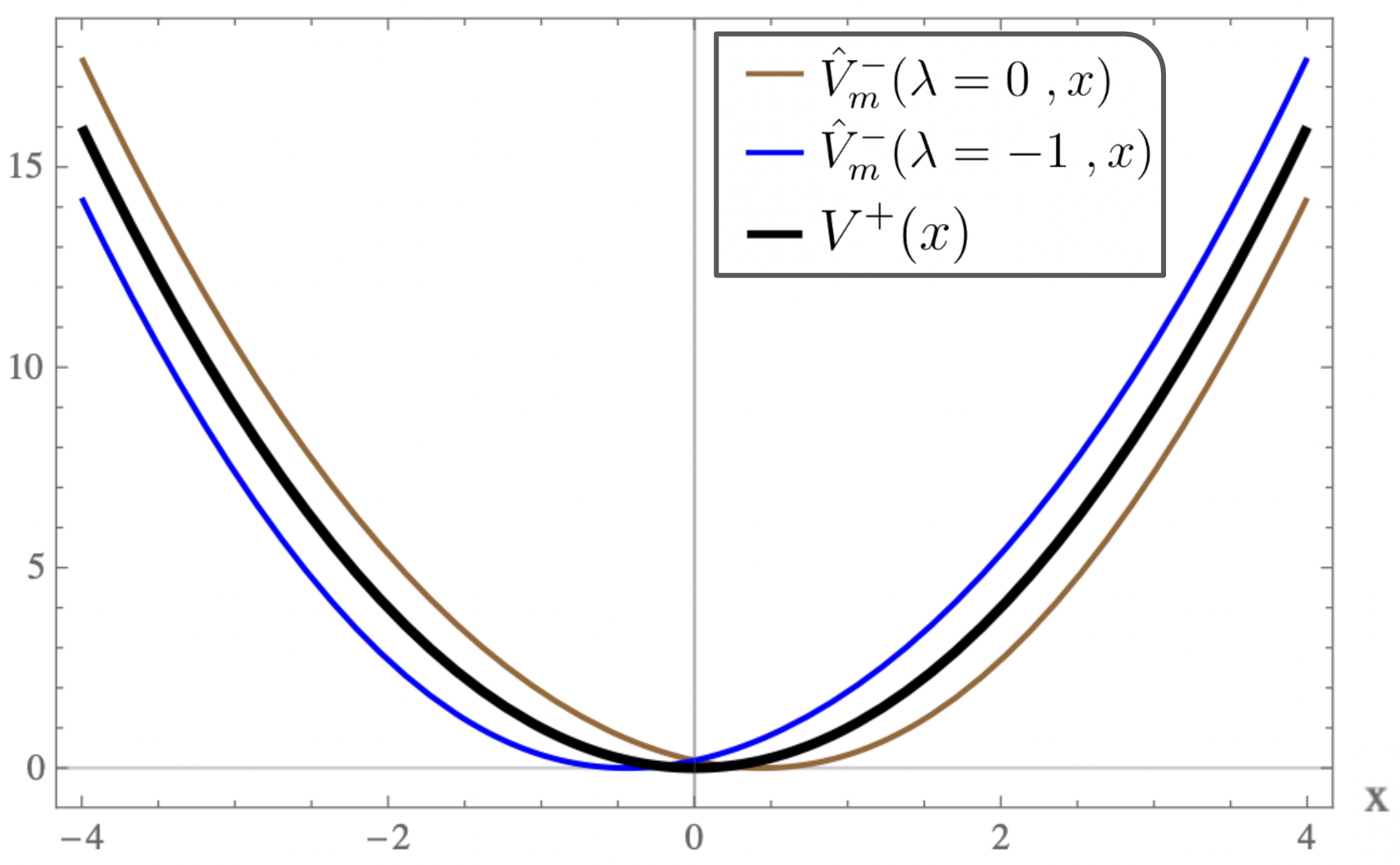
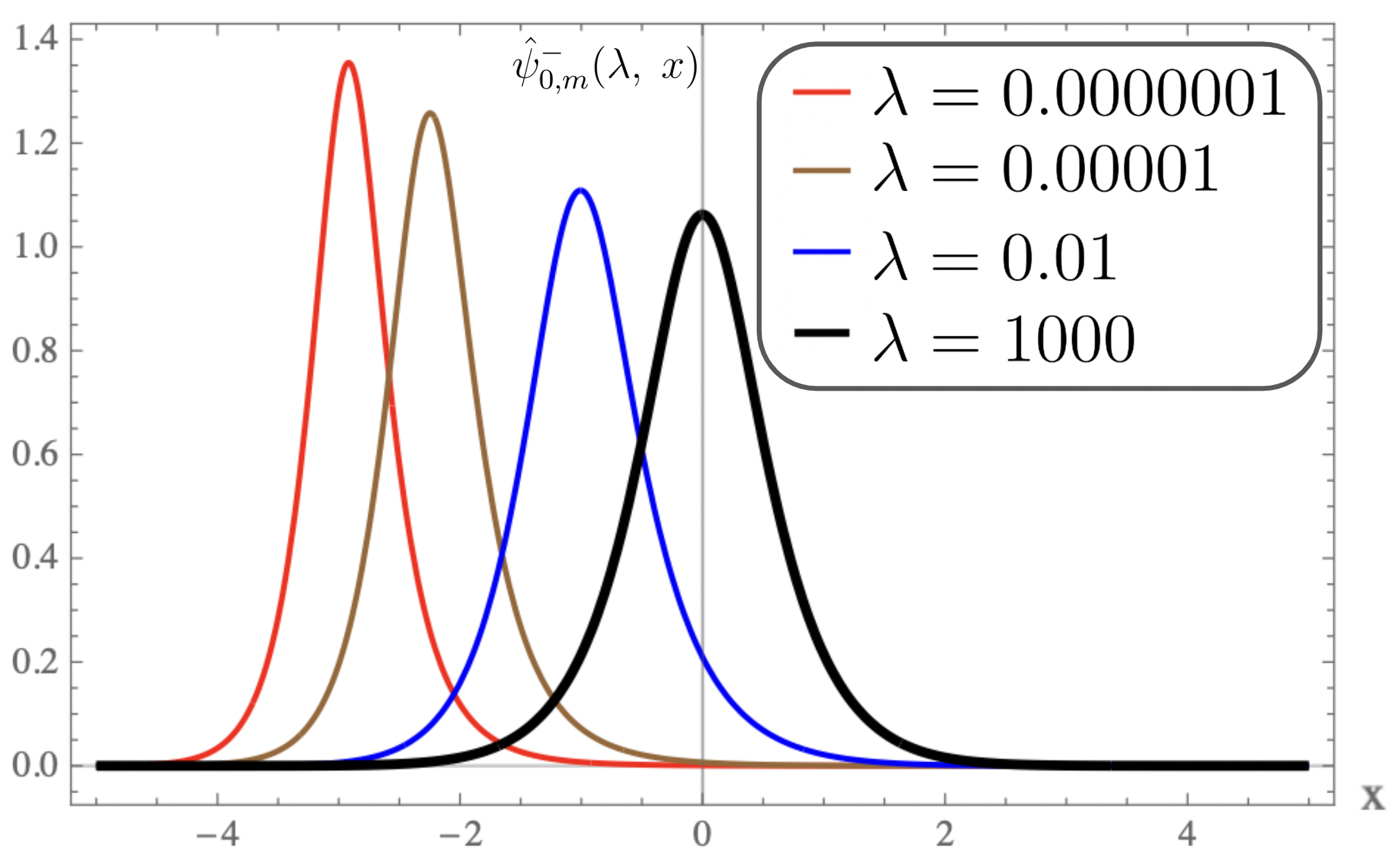
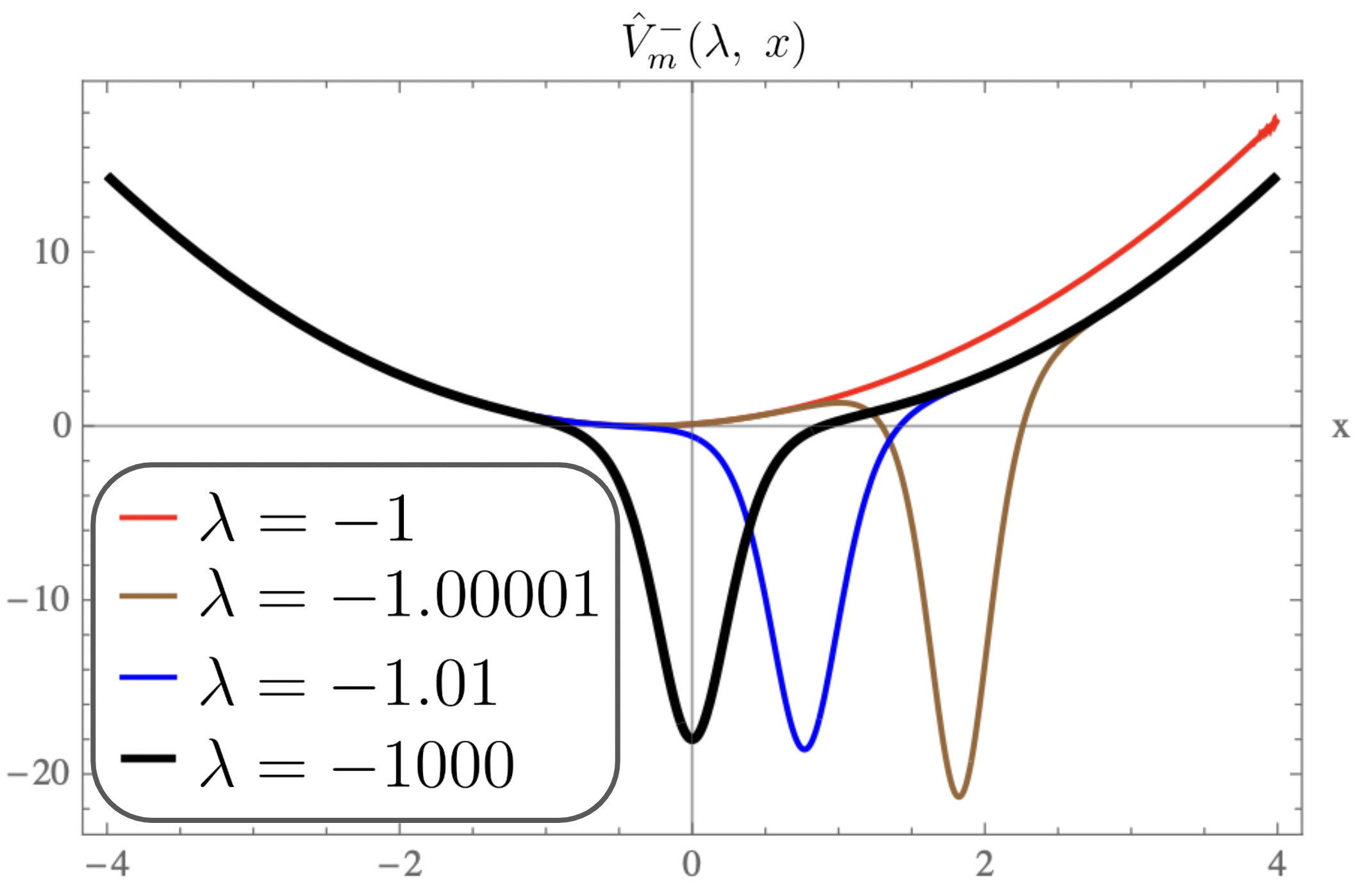
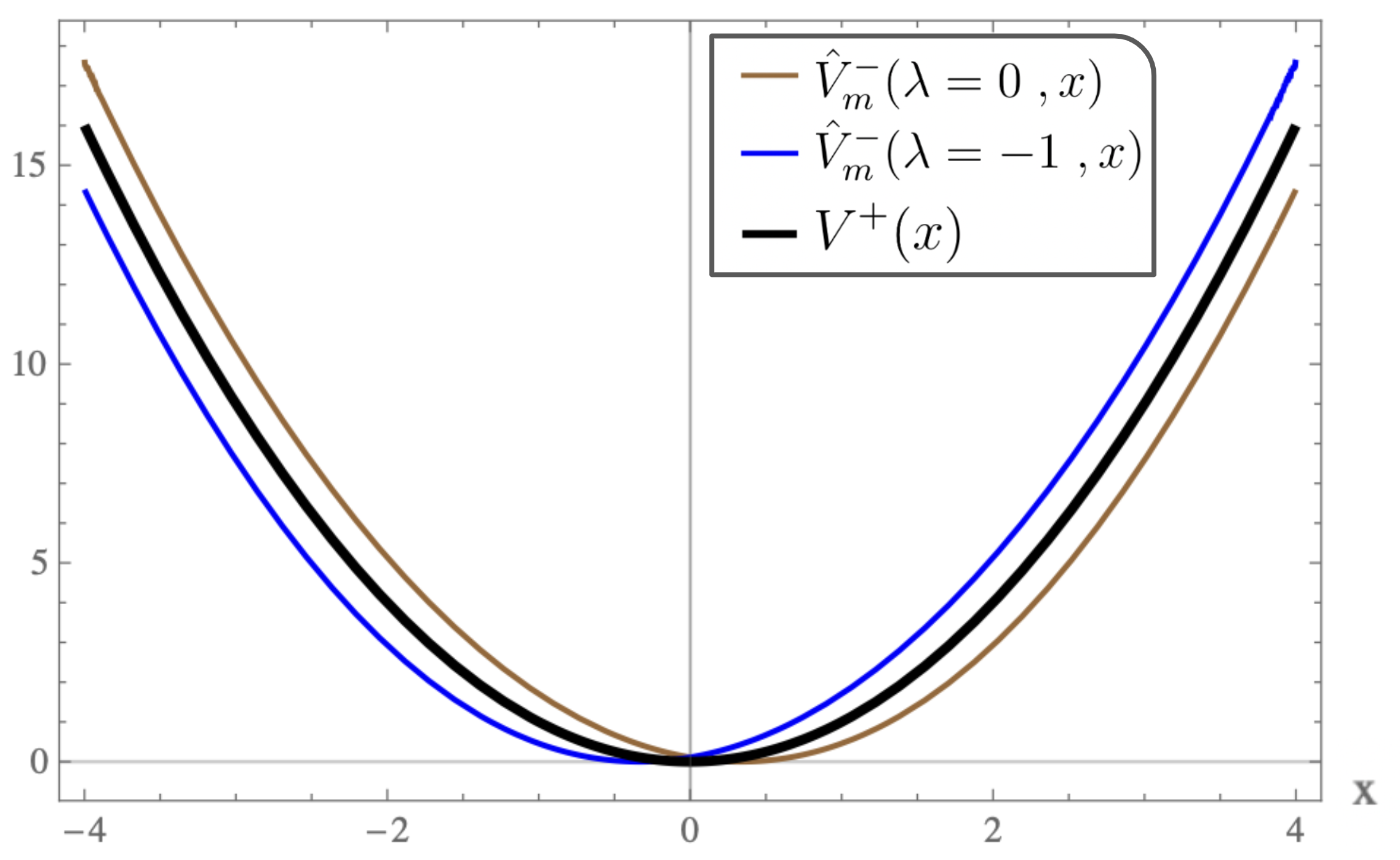
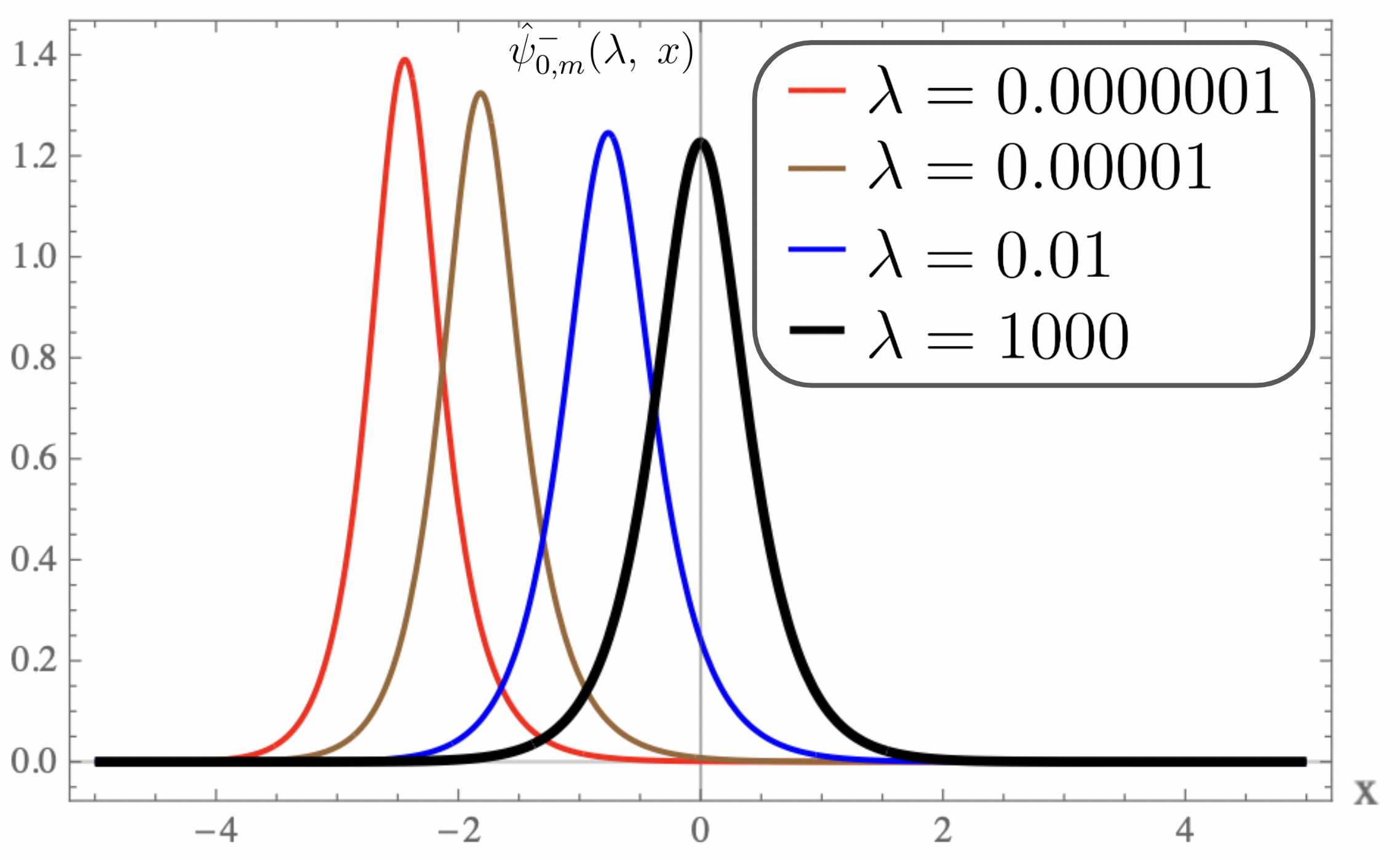
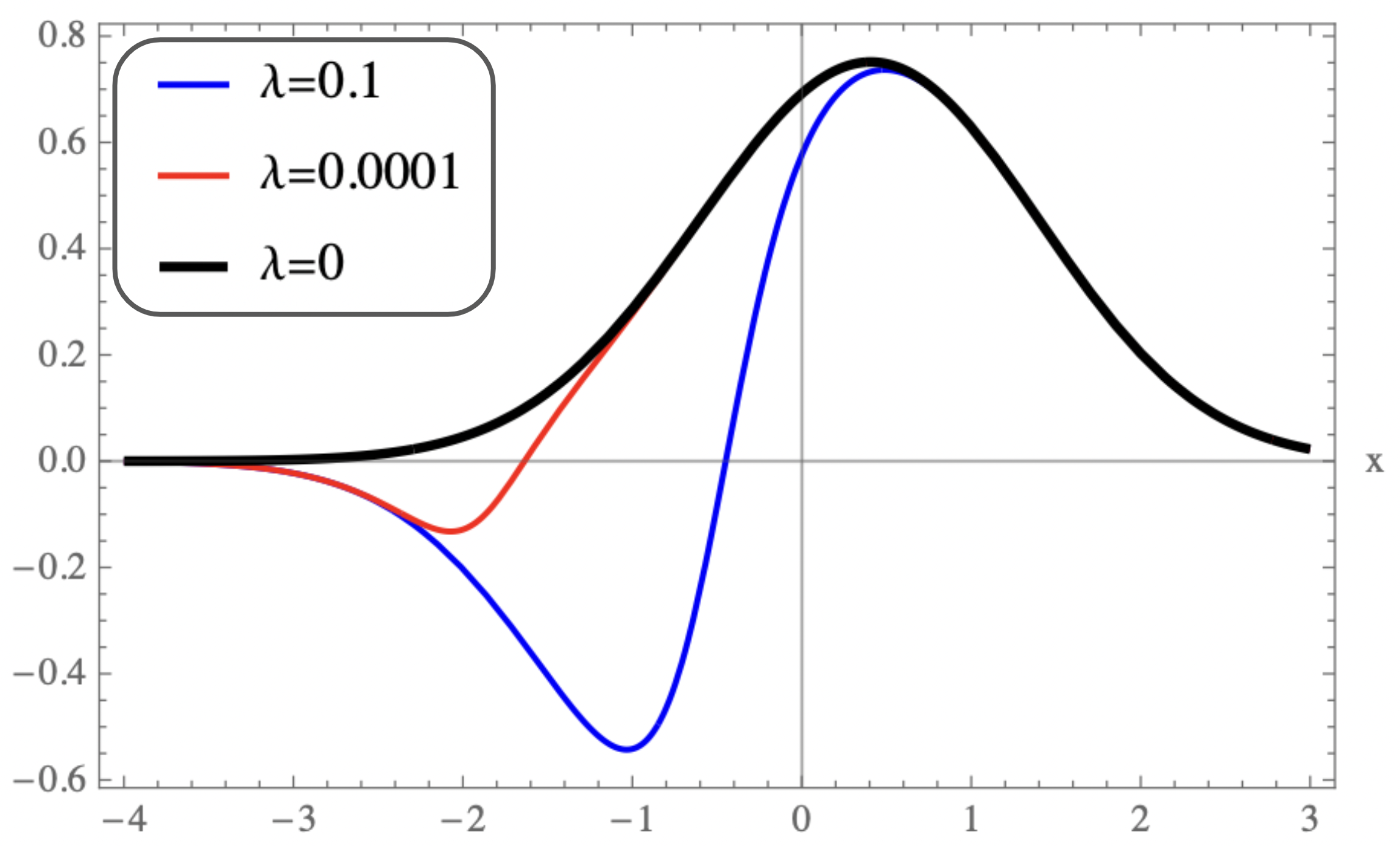
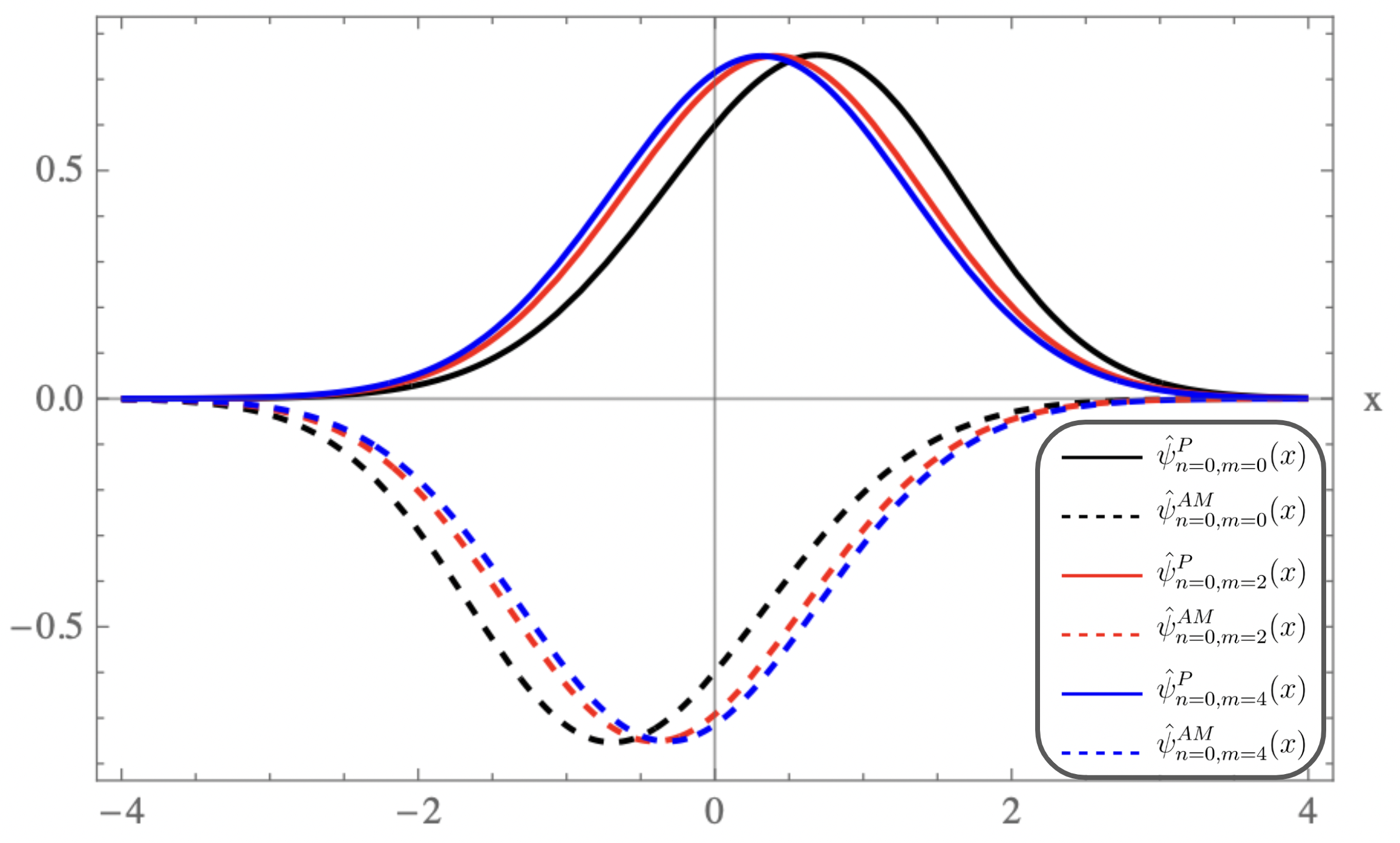
For equal to , the plots of the strictly isospectral potentials for positive and negative as a function of are shown in Fig-(2.a, 3.a, 4.a) and Fig-(2.b, 3.b, 4.b) respectively. Pursey and Abraham-Moses potential plots as a function of are shown in Fig-(2.c, 3.c, 4.c). The ground-state wavefunction plots as a function of for various are shown in Fig-(2.d, 3.d, 4.d). From the figures one observes that the eigen functions and the strictly isospectral potentials become sharper with increasing . In the limit approaching to the potential approaches to . Also notice that the potential starts developing a minimum when decreases from to zero and the attractive potential well shifts towards and finally vanishes when equals zero. There is a loss of bound state and the corresponding potential is called the Pursey potential . An analogous situation occurs in the limit and the potential is called the Abraham-Moses potential .
4.1 The Pursey and The Abraham-Moses Potentials
The Pursey and The Abraham-Moses Potentials are obtained from (27) by substituting and respectively. In this case as mentioned above, one looses a bound state and the spectrum is identical to that of , i.e.
where
The normalized eigenfunctions of are given by
| (28) |
Similarly, the normalized eigenfunctions of is given by
| (29) |
The expression of and for equal to are obtained from table-4 by substituting equal to and respectively.
The ground state wavefunction plot for Pursey and AM potentials for various are shown in figure-5.b and transition in wavefunction shape as approaches zero is shown in figure-5.a.
5 Calculation of Uncertainty
The Heisenberg Uncertainty relation for position, , and momentum, , is defined as
| (30) |
where, the angle bracket, , represents expectation value in a given wavefunction basis.
5.1 Uncertainty relation for REHO potential
For the REHO potentials the expectation value of the position, , and the momentum, , in the ground as well as the excited states is zero as the integrand is an odd function in the calculation of while the expectation value of is zero since the eigenfunctions are real. The uncertainty relation therefore takes the simpler form
The expectation values and hence the uncertainty values can be calculated by using Eqs. (18). It is observed that for but the same is not true for . The uncertainty values for and (i.e. ground, first and second excited states) are shown in table-5.
| m | |||
|---|---|---|---|
| 0 | |||
| 2 | |||
| 4 |
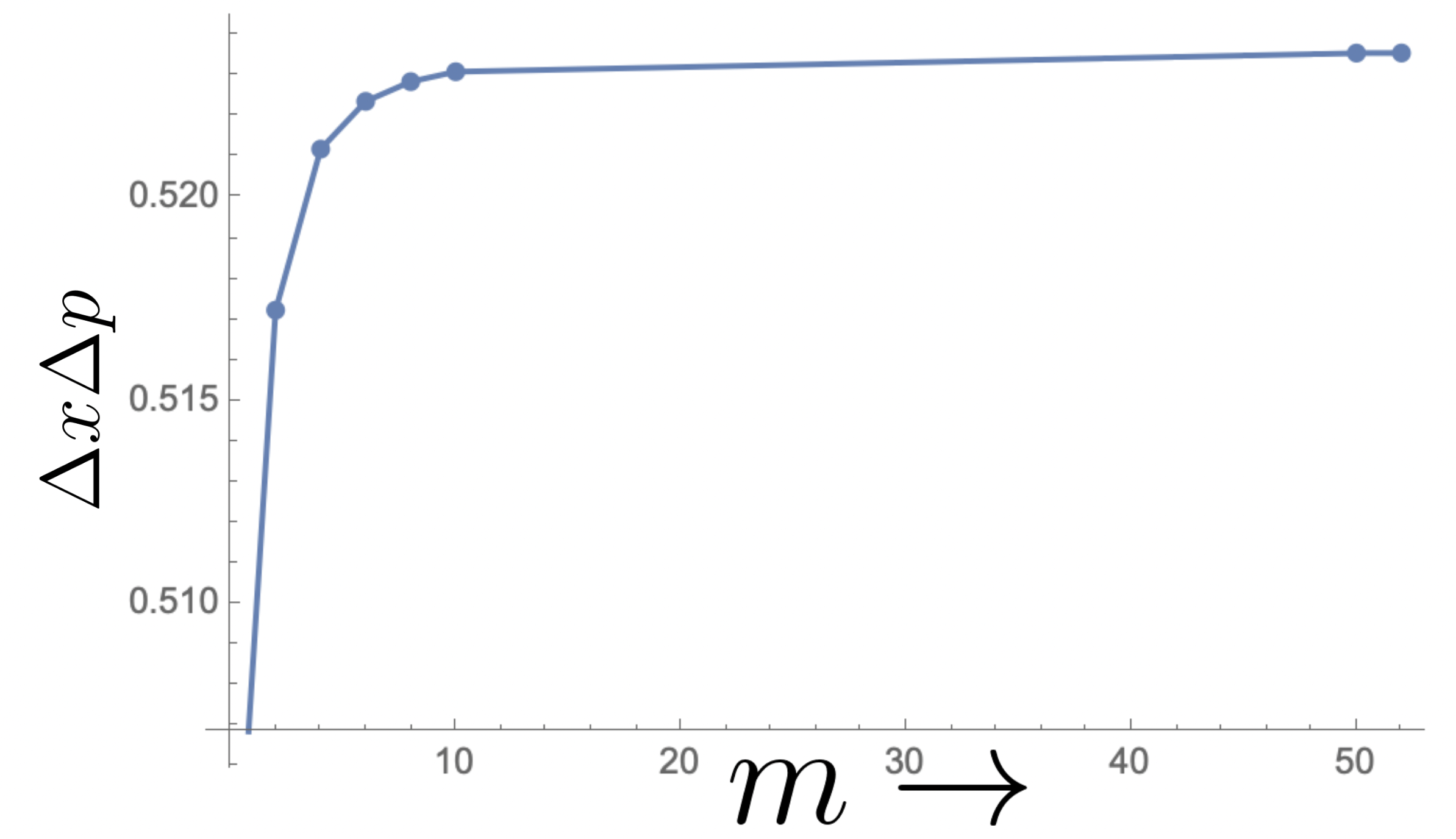
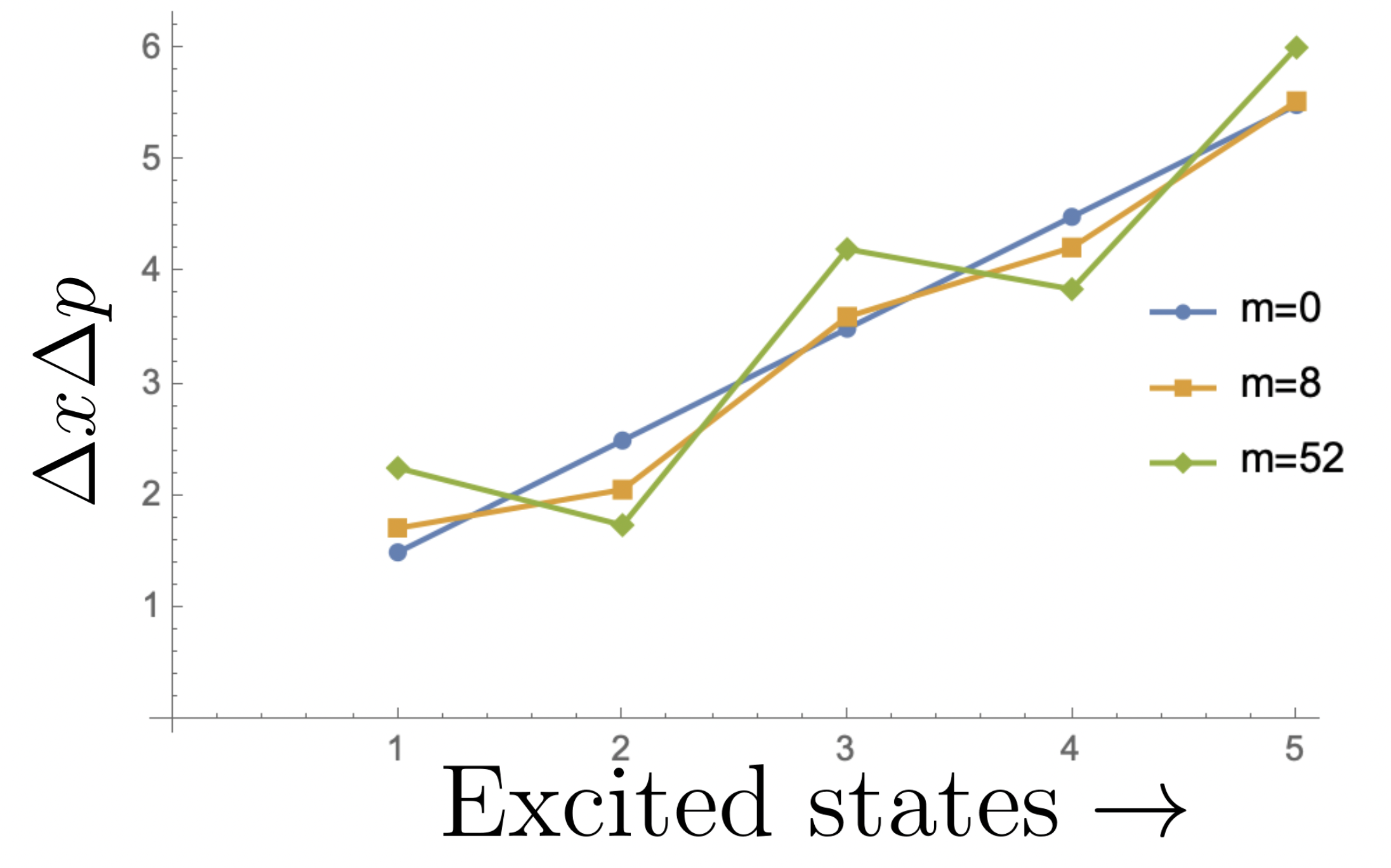
It can be seen from figure-6.a that for the ground state, the uncertainty value increases as increases from and then flattens out around . On the other hand, in the different excited states the Uncertainty values show peculair behaviour. In particular, while it decreases with increasing for any given even excited states but it increases with increasing for any given odd excited states. This peculiar behaviour in the uncertainty may be attributed to the even and odd degree of exceptional Hermite polynomials for a given . The figure-6.b shows the variation of uncertainty with different excite states for equal to 0, 8 and 52.
5.2 Uncertainty relation for one parameter family of REHO potential
The expectation value of momentum, , is again zero as the eigenfunctions are real. The uncertainty in is, therefore, . The expectation values of , for various values of and are given in Appendix A. The uncertainty relation at ground-state for various values of and is given in table-6.
| m/ | ||||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 2 | ||||||
| 4 |
When the values of in the table-6 are replaced by the uncertainty relation remains unchanged and it corresponds to the Abraham Moses potential. The plot of uncertainty versus for and is shown in figure-7.a and 7.b respectively. The peak of uncertainty curve rapidly moves towards origin with increasing .
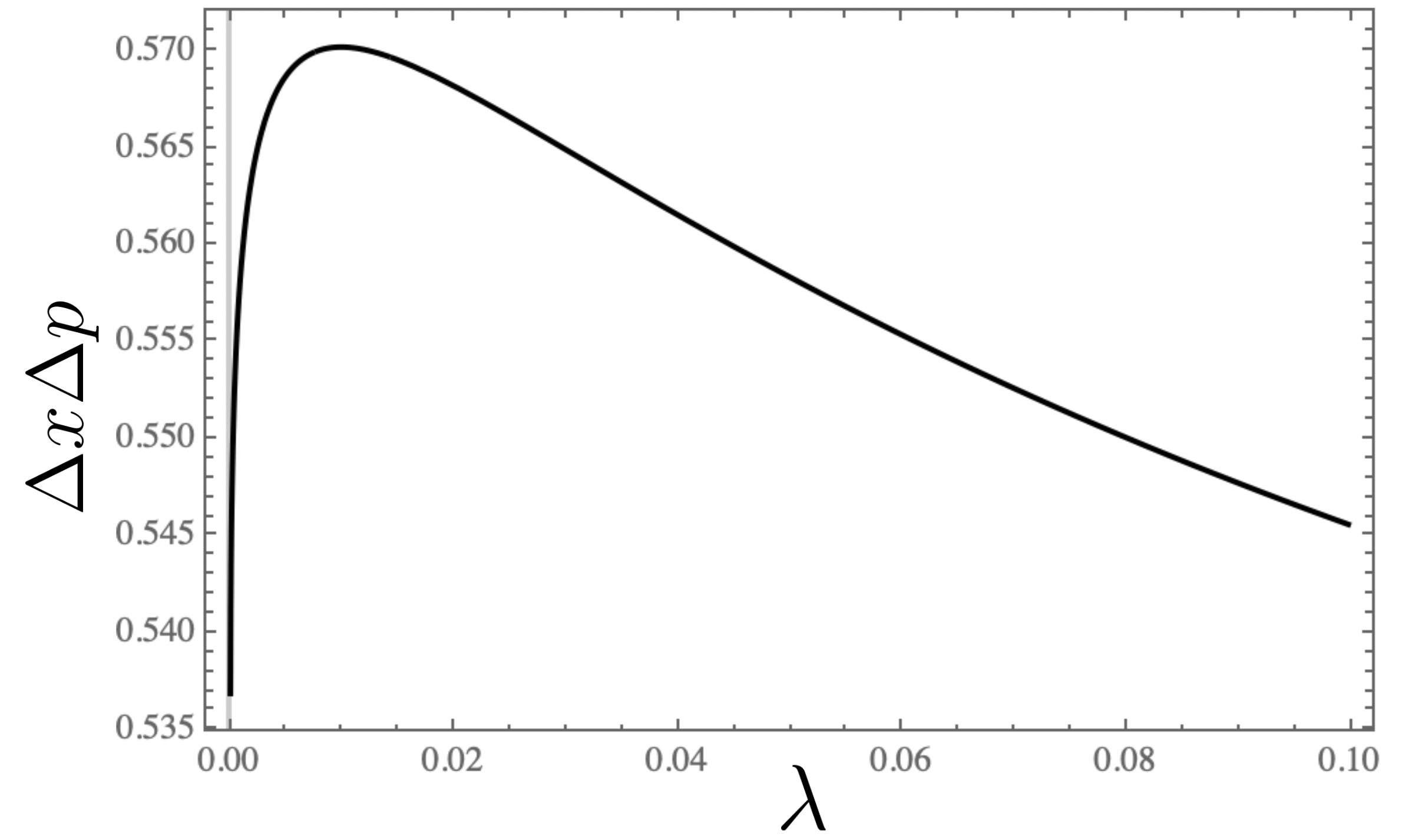
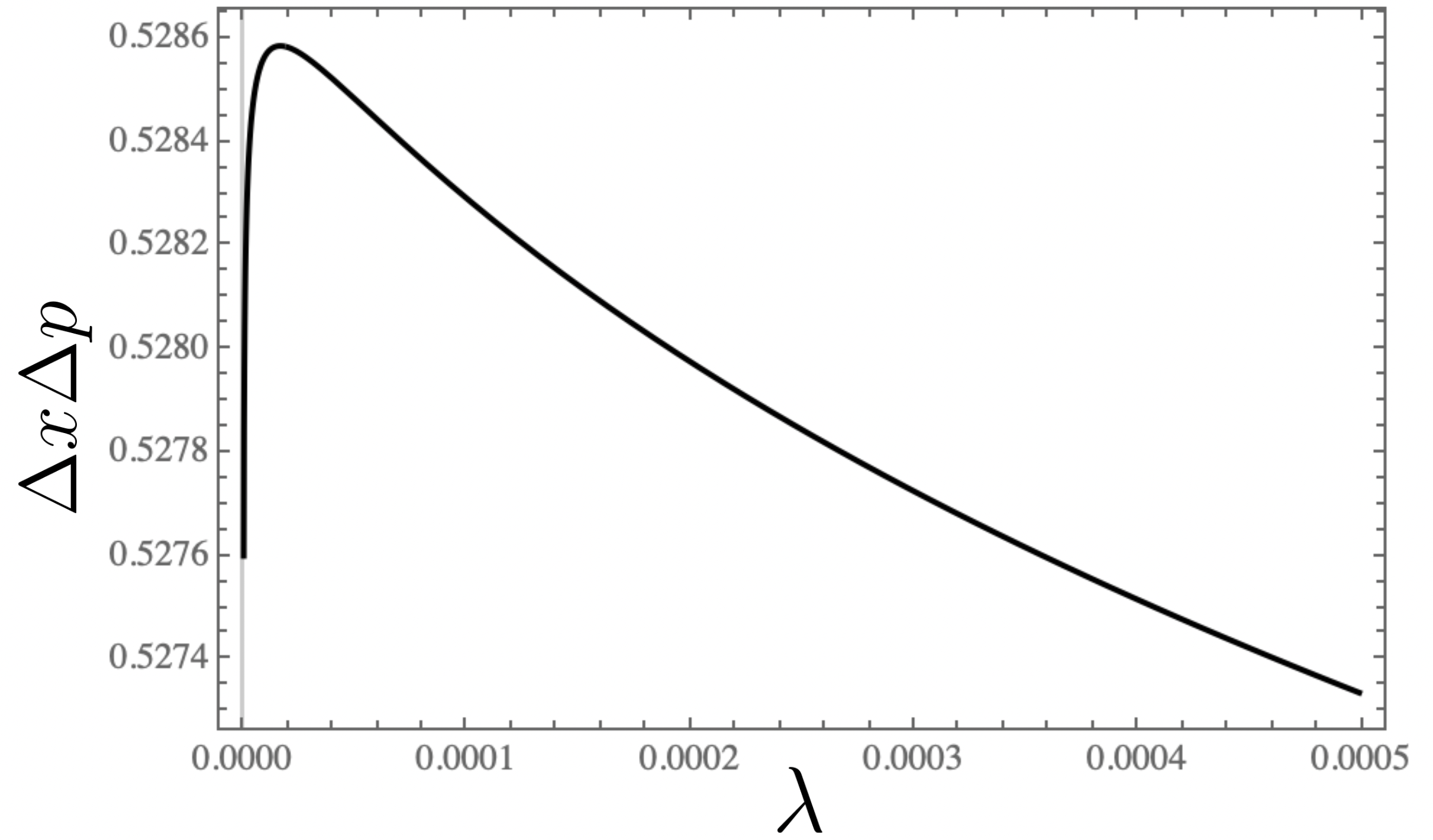
5.2.1 Uncertainty relations for Pursey and Abraham Moses Potentials
The expectation value of and are calculated in Appendix C for various values of . It is interesting to note that the expectation value of is equal and opposite in the case of the Pursey and the AM Potentials while the expectation value of and is the same in both the cases.
| m/n | 0 | 1 | 2 | 3 | 10 |
|---|---|---|---|---|---|
| 0 | |||||
| 2 | |||||
| 4 |
As a result the uncertainty value corresponding to a given is the same for the Pursey and the AM potentials. The uncertainty value for the Pursey and the AM potentials at the ground and the different excited-states is given in table-7. The uncertainty decreases at ground state with increasing and becomes asymptotic to . On contrast it is seen that uncertainty is lesser than QHO () uncertainty for excited states.
6 Summary and discussion
In this manuscript, we consider the rationally extended one dimensional harmonic oscillator potential associated with exceptional -Hermite polynomials. Unlike the one dimensional oscillator, for nonzero , while the energy gap between the excited states is units, the energy gap between the groundstate and first excited state is . Using the idea of SQM, we obtained one parameter () family of strictly isospectral potentials corresponding to the REHO potential as well as the corresponding eigenfunctions. As a special case, as approaches or , we obtained the rationally extended Pursey and the AM potentials respectively as well as their eigenfunctions. Further, we calculated the Heisenberg uncertainty relations for the REHO and as well as the corresponding strictly isopectral one parameter () family of potentials. In addition, we also calculated the uncertainity relation for the corresponding Pursey and AM potentials. In the case of the REHO, we showed that the ground state uncertainity increases as increases. In the case of the strictly isospectral one parameter family of potentials, one finds that the uncertainty relation depends on as well as . Remarkably, we find that for any , the uncertainty relation is the same for the Pursey and the AM potentials.
There are several open problems. For example, In this paper we have only studied the potentials with even codimension and obtained the corresponding strictly isospectral one parameter family. Can one similarly obtain the corresponding one parameter family of potentials in case the codimension is odd. Further, apart from the one dimensional oscillator, are there other rationally extended potentials for which the eigenfunctions can be expressed in terms of exceptional Hermite polynomials? Another obvious question is whether there are exceptional Legendre polynomials and if yes can one discover new potentials whose eigenfunctions can be expressed in terms of exceptional Legendre polynomials? We hope to study some of these problems in coming days.
Acknowledgements
AK is gratefel to Indian National Science Academy (INSA) for awarding INSA
Honarary Scientist position at Savitribai Phule Pune University. One of us (RK) is grateful to Ian Marquette for useful comments.
Appendix A. Expectation value of and for one parameter
family of REHO
The expectation value of and for various values of positive are calculated using (26) as:
When the values of in the above table are replaced by the magnitude of the values of remain unchanged but the sign reverses.
When the values of in the above table are replaced by the expectation values of remains unchanged.
Similarly, the expectation value of can be calculated.
Appendix B. Expectation value of and for Puresey and
Abraham Moses Potentials
The expectation value and uncertainty relation can be calculated from (28) and (29).
The expectation value of and for various values of are as follows:
References
- [1] Fred Cooper, Avinash Khare, and Uday Sukhatme. Supersymmetry and quantum mechanics. Physics Reports, 251(5-6):267–385, 1995.
- [2] ZS Agranovich and Vladimir Aleksandrovich Marchenko. The inverse problem of scattering theory. Courier Dover Publications, 2020.
- [3] Khosrow Chadan and Pierre C Sabatier. Inverse problems in quantum scattering theory. Springer Science & Business Media, 2012.
- [4] George L Lamb Jr. Elements of soliton theory. New York, page 29, 1980.
- [5] Philip G Drazin and Robin Stanley Johnson. Solitons: an introduction, volume 2. Cambridge university press, 1989.
- [6] Michael Martin Nieto. Relationship between supersymmetry and the inverse method in quantum mechanics. Physics Letters B, 145(3-4):208–210, 1984.
- [7] RD Amado. Phase-equivalent supersymmetric quantum-mechanical partners of the coulomb potential. Physical Review A, 37(7):2277, 1988.
- [8] DL Pursey. Isometric operators, isospectral hamiltonians, and supersymmetric quantum mechanics. Physical Review D, 33(8):2267, 1986.
- [9] PB Abraham and HE Moses. Changes in potentials due to changes in the point spectrum: anharmonic oscillators with exact solutions. Physical Review A, 22(4):1333, 1980.
- [10] G Darboux. On a proposition relative to linear equations. arXiv preprint physics/9908003, 1999.
- [11] Satoru Odake and Ryu Sasaki. Krein–adler transformations for shape-invariant potentials and pseudo virtual states. Journal of Physics A: Mathematical and Theoretical, 46(24):245201, 2013.
- [12] Avinash Khare and Uday Sukhatme. Phase-equivalent potentials obtained from supersymmetry. Journal of Physics A: Mathematical and General, 22(14):2847, 1989.
- [13] Wai-Yee Keung, Uday P Sukhatme, Qinmou Wang, and Tom D Imbo. Families of strictly isospectral potentials. Journal of Physics A: Mathematical and General, 22(21):L987, 1989.
- [14] David Gómez-Ullate, Niky Kamran, and Robert Milson. An extended class of orthogonal polynomials defined by a sturm–liouville problem. Journal of Mathematical Analysis and Applications, 359(1):352–367, 2009.
- [15] David Gomez-Ullate, Niky Kamran, and Robert Milson. Exceptional orthogonal polynomials and the darboux transformation. Journal of Physics A: Mathematical and Theoretical, 43(43):434016, 2010.
- [16] David Gomez-Ullate, Niky Kamran, and Robert Milson. On orthogonal polynomials spanning a non-standard flag. Contemp. Math, 563:51–71, 2012.
- [17] Bikashkali Midya and Barnana Roy. Exceptional orthogonal polynomials and exactly solvable potentials in position dependent mass schrödinger hamiltonians. Physics Letters A, 373(45):4117–4122, 2009.
- [18] Choon-Lin Ho. Dirac (-pauli), fokker–planck equations and exceptional laguerre polynomials. Annals of Physics, 326(4):797–807, 2011.
- [19] Rajesh Kumar Yadav, Avinash Khare, and Bhabani Prasad Mandal. The scattering amplitude for a newly found exactly solvable potential. Annals of Physics, 331:313–316, 2013.
- [20] Rajesh Kumar Yadav, Avinash Khare, and Bhabani Prasad Mandal. The scattering amplitude for rationally extended shape invariant eckart potentials. Physics Letters A, 379(3):67–70, 2015.
- [21] C-L Ho, J-C Lee, and R Sasaki. Scattering amplitudes for multi-indexed extensions of solvable potentials. Annals of Physics, 343:115–131, 2014.
- [22] Rajesh Kumar Yadav, Nisha Kumari, Avinash Khare, and Bhabani Prasad Mandal. Group theoretic approach to rationally extended shape invariant potentials. Annals of Physics, 359:46–54, 2015.
- [23] Nisha Kumari, Rajesh Kumar Yadav, Avinash Khare, Bijan Bagchi, and Bhabani Prasad Mandal. Scattering amplitudes for the rationally extended pt symmetric complex potentials. Annals of Physics, 373:163–177, 2016.
- [24] Rajesh Kumar Yadav, Avinash Khare, Bijan Bagchi, Nisha Kumari, and Bhabani Prasad Mandal. Parametric symmetries in exactly solvable real and pt symmetric complex potentials. Journal of Mathematical Physics, 57(6):062106, 2016.
- [25] Nisha Kumari, Rajesh Kumar Yadav, Avinash Khare, and Bhabani Prasad Mandal. A class of exactly solvable rationally extended calogero–wolfes type 3-body problems. Annals of Physics, 385:57–69, 2017.
- [26] Rajesh Kumar Yadav, Avinash Khare, Nisha Kumari, and Bhabani Prasad Mandal. Rationally extended many-body truncated calogero–sutherland model. Annals of Physics, 400:189–197, 2019.
- [27] B Basu-Mallick, Bhabani Prasad Mandal, and Pinaki Roy. Quasi exactly solvable extension of calogero model associated with exceptional orthogonal polynomials. Annals of Physics, 380:206–212, 2017.
- [28] Suman Banerjee, Rajesh Kumar Yadav, Avinash Khare, Nisha Kumari, and Bhabani Prasad Mandal. Solutions of (1+ 1)-dimensional dirac equation associated with exceptional orthogonal polynomials and the parametric symmetry. arXiv preprint arXiv:2211.02557, 2022.
- [29] Arturo Ramos, Bijan Bagchi, Avinash Khare, Nisha Kumari, Bhabani Prasad Mandal, and Rajesh Kumar Yadav. A short note on “group theoretic approach to rationally extended shape invariant potentials”[ann. phys. 359 (2015) 46–54]. Annals of Physics, 382:143–149, 2017.
- [30] David Gómez-Ullate, Yves Grandati, and Robert Milson. Rational extensions of the quantum harmonic oscillator and exceptional hermite polynomials. Journal of Physics A: Mathematical and Theoretical, 47(1):015203, 2013.
- [31] Jonathan M Fellows and Robert A Smith. Factorization solution of a family of quantum nonlinear oscillators. Journal of Physics A: Mathematical and Theoretical, 42(33):335303, 2009.
- [32] Ian Marquette and Christiane Quesne. Two-step rational extensions of the harmonic oscillator: exceptional orthogonal polynomials and ladder operators. Journal of Physics A: Mathematical and Theoretical, 46(15):155201, 2013.
- [33] Rajesh Kumar Yadav, Suman Banerjee, Nisha Kumari, Avinash Khare, and Bhabani Prasad Mandal. One parameter family of rationally extended isospectral potentials. Annals of Physics, 436:168679, 2022.