Reaction rate of a composite core-shell nanoreactor with multiple, spatially distributed embedded nano-catalysts
Abstract
We present a detailed theory for the total reaction rate constant of a composite core-shell nanoreactor, consisting of a central solid core surrounded by a hydrogel layer of variable thickness, where a given number of small catalytic nanoparticles are embedded at prescribed positions and are endowed with a prescribed surface reaction rate constant. Besides the precise geometry of the assembly, our theory accounts explicitly for the diffusion coefficients of the reactants in the hydrogel and in the bulk as well as for their transfer free energy jump upon entering the hydrogel shell. Moreover, we work out an approximate analytical formula for the overall rate constant, which is valid in the physically relevant range of geometrical and chemical parameters. We discuss in depth how the diffusion-controlled part of the rate depends on the essential variables, including the size of the central core. In particular, we derive some simple rules for estimating the number of nanocatalysts per nanoreactor for an efficient catalytic performance in the case of small to intermediate core sizes. Our theoretical treatment promises to provide a very useful and flexible tool for the design of superior performing nanoreactor geometries and with optimized nanoparticle load.
I Introduction
In recent years, metallic nanoparticles have emerged as potent catalysts for various
applications Pushkarev et al. (2012); Zhang et al. (2012). In particular, the discovery that gold becomes
a catalyst when divided to the nanophase has led to an intense research in this
field Haruta (2003); Hutchings and Haruta (2005). In many cases the synthesis and the catalytic applications
must be handled in the liquid phase, mostly in water. Secure handling of nanoparticles in a
liquid phase can be achieved by polymeric carriers that have typical dimensions in the colloidal domain.
Examples thereof include dendrimers Crooks et al. (2001); Noh and Meijboom (2015) or spherical polyelectrolyte
brushes Ballauff (2007). Such systems allow one to generate nanoparticles in aqueous phase
in a well-defined manner and handle them securely in catalytic reactions.
More recently, thermosensitive colloidal microgels have been used as carriers for
metallic nanoparticles in catalysis Lu and Ballauff (2011). Fig. 1 displays the scheme
of such a carrier system that may be regarded as a nanoreactor: a thermosensitive network
composed of cross-linked chains of poly(N-isopropylacrylamide) (PNIPAM) has been attached to a solid
core made of an inert material as, e.g., polystyrene or silica Lu et al. (2006).
Metal nanoparticles are embedded in the network which is fully swollen in cold water.
Raising the temperature above the critical temperature (32∘ C for PNIPAM), a volume transition
takes place within the network and most of the water is expelled Lu and Ballauff (2011).
Lu et al. Lu et al. (2006) have been the first to show that the catalytic activity of
the embedded nanoparticles is decreased when shrinking the network by raising the temperature.
This effect has been explained by an increased diffusional resistance mass transport
within the shrunk network Lu et al. (2006); Lu and Ballauff (2011). A similar model has been advanced by
Carregal-Romero et al. when considering the catalytic activity of a single
gold nanoparticle embedded concentrically in a PNIPAM-network Carregal-Romero et al. (2010).
Recently, we have shown that the mobility of reactants is not the only important factor:
an even larger role is played by the change of polarity of the network when considering
mass transport from bulk to the catalyst(s) through such medium Wu et al. (2012); Angioletti-Uberti et al. (2015).
This theory is based on the well-known seminal paper by Debye Debye (1942) and considers
a single nanoparticle located in the center of a hollow thermosensitive network Angioletti-Uberti et al. (2015).
Here, the substrate that reacts at the surface of the nanoparticle diffuses through a
free-energy landscape created by the hydrogel environment. In other words,
the reactants experience a change in the solvation free energy when entering the gels from bulk solvent,
which can be equally regarded as adsorption free energy or transfer free energy.
For instance, the free energy of a substrate may
be lowered upon entering the network. In this way the number of substrate molecules
in the network will be augmented, so that their increased concentration in the vicinity of the catalyst
will lead to a higher reaction rate. The free-energy change
for the substrate outside and inside the network leads to a Nernst distribution for the substrate’s
concentration within the system. This effect offers a new way to manipulate the catalytic activity and
selectivity of metallic nanoparticles Wu et al. (2012).
In this paper we formulate a more general theory, that is able to account for
the geometry of core-shell nanoreactors featuring many catalysts,
as shown schematically in Fig. 1. Here, a given number of catalytic centers
are encapsulated randomly in a network. We calculate the total rate of the catalytic reaction
for a prescribed geometry of the catalysts, given values of and and specified
diffusion constants for the substrate in the bulk and in the network. The rate constant computed in this way
can be compared to that characterizing an equal number of particles suspended freely in solution.
The present model has been designed to describe the well-studied core-shell systems Lu et al. (2006); Lu and Ballauff (2011),
but is equally adapted to the study of systems where catalytic centers are embedded in homogeneous microgels Shi et al. (2014).
Up to now, most of the experimental work has been done using the reduction of 4-nitrophenol by borohydride ions
in aqueous solution Aditya et al. (2015); Zhao et al. (2015). This reaction can be regarded as a model reaction Herves et al. (2012),
since it can be monitored with high precision thus leading to very accurate kinetic data.
The rate-determining step proceeds at the surface of the nanoparticles and the
mechanism is known Gu et al. (2014). The present theory, however, comprises also the nanoreactors in which enzymes
are used as catalytic centers embedded in the network shell Welsch et al. (2012).
In general, diffusion-influenced reactions (DIR) are ubiquitous in many contexts in physics, chemistry and
biology Calef and Deutch (1983); Rice (1985); Szabo (1989); Zhou et al. (2008).
However, while the mathematical foundations for the description of DIR in simple systems have been laid
nearly a century ago von Smoluchowski (1916); Debye (1942); Collins and Kimball (1949), many important present-day problems,
including the catalytic activity of composite core-shell nanoreactors,
require considering complex geometries and multi-connected reactive boundary systems.
The first attempts to consider DIR featuring many competing sinks date back to the
1970s Deutch et al. (1976); Felderhof and Deutch (1976), while more sophisticated methods have been
developed subsequently to deal with arbitrary systems comprising many partially reactive
boundaries Traytak (1992, 2003); Gordeliy et al. (2009).
Along similar lines, the theory developed in this paper,
based on general results proved in Ref. Traytak (2003),
provides a novel, accurate description of DIR occurring between a small substrate
molecule and the catalytic centers embedded in a large, composite nanoreactor system.
Our theory is fully general, in that it covers the whole spectrum of rate-limiting
steps in catalysis, from reaction-limited to diffusion-limited reactions. While the theory allows
one to compute the reaction rate for an arbitrary catalytic surface turnover rate, closed-form
analytical expression are derived for strongly reaction-limited and diffusion-limited reactions.
In the limit of a dilute random distribution of NPs encapsulated in a thick hydrogel shell,
we find that the overall diffusion-controlled rate constant of our core-shell composites
is described by a Langmuir-like isotherm of the form
| (1) |
where is the number of nanoparticles, is the ratio of the diffusion constants
in the hydrogel ( for inner) and bulk ( for outer), is the ratio of
NP size (radius) to the nanoreactor size and is the Smoluchowski rate constant for
the nanoreactor as a whole, i.e.
the total flux (in units of bulk substrate concentration) of substrate molecules to a stationary
perfectly absorbing sink of size in the bulk. The above expression is valid for
small sizes of the central core. Interestingly, for configurations where the core size becomes of the same
order of the whole composite (thin shell), our theory shows that in general the rate constant is
increased, up to 40 %, depending on the transfer free energy jump and on the
reactant mobility in the shell.
In the limit of slow surface substrate-product conversion rate, i.e. for reaction-limited
kinetics, we find that
| (2) |
where is the intrinsic turnover rate constant that describes the transformation of substrate to product molecules at the nanocatalyst surface (units of inverse concentration times inverse time). This means that when the surface substrate conversion rate constant is weak, the geometrical features of the overall assembly and the mobility of substrate molecules within the hydrogel shell become immaterial. In this case, the crucial control parameter is the transfer free energy jump. The paper is organized as follows. In section II we describe our mathematical model and pose the associated boundary-value problem. In section III, we describe concisely the procedure that leads us to the exact solution of the posed problem (the mathematical details can be found in the appendix). Section IV illustrates an analytic approximation that provides an extremely good description of the exact solution for small core sizes in the physically relevant range of parameters. In particular, we discuss how this formula can be used to derive practical criteria to design nanoreactors with optimized performances. Finally, we wrap up our main results in section V.
II Core-shell model and defining equations
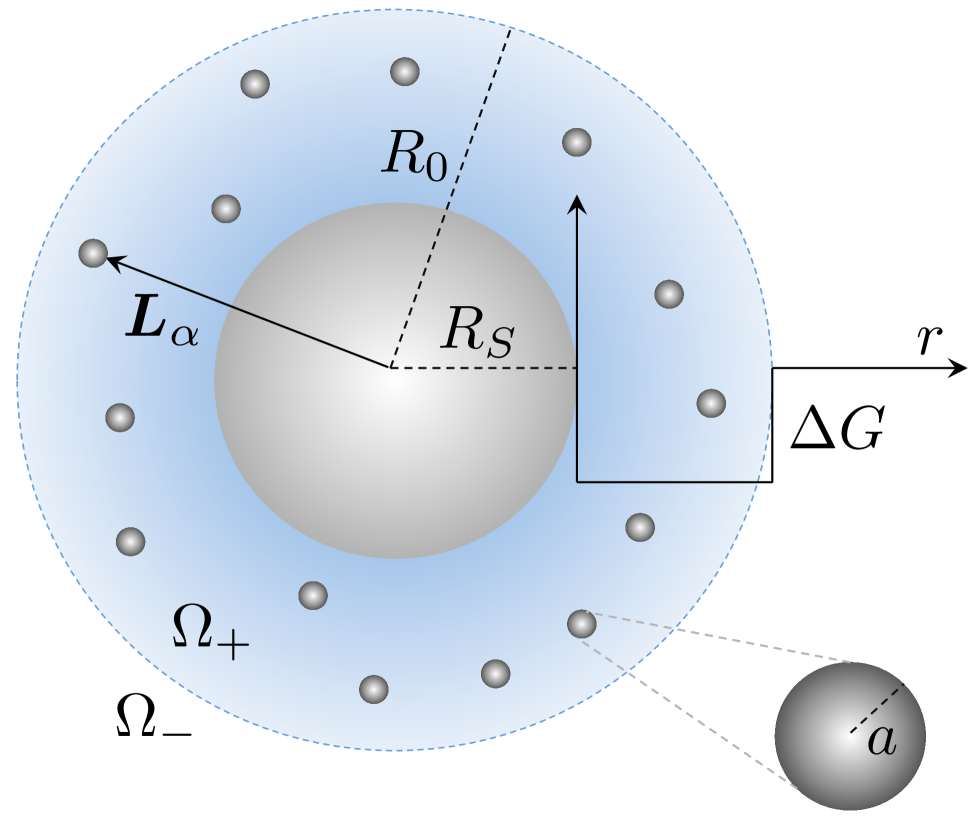
We model a core-shell nanoreactor consisting of a polystyrene (PS) core surrounded by a microgel layer as two concentric spheres centered at the origin of a Cartesian 3 frame, as depicted in Fig. 1. We denote with and the core and shell radius, respectively. The shell is assumed to be a homogeneous continuum, carrying small nano-catalysts (metal nanoparticles or enzymes) that we model as spheres of radius . For the sake of simplicity, and in accordance to our general multi-sink theory Galanti et al. (2016), we label the PS core as the inner sphere with and position vector and denote the position of the nanocatalysts with the vectors , . We want to compute the total reaction rate constant for reactions where a substrate (or ligand) molecule is converted to some product species at the surface of the catalyst spheres. These are endowed with a surface rate constant , which is in general a function of temperature due to underlying thermally activated surfaces processes. Let us denote with the reference frame with the origin at the nanoreactor center and with the reference frames with the origins at the nanospheres centers and the axes parallel to (of course ). This formally defines the following domains
| (3) | ||||
where denotes the interior of the PS core
and ,
, denote the interior of the -th nanosphere.
The reactant diffuses with diffusion coefficients and inside the microgel
shell and in the bulk, respectively. In general one can assume due to obstructed
or hindered diffusion in the microgel Cukier (1984).
II.1 Steady-state boundary-value problem
Let denote the bulk density of reactants and let us introduce the time-dependent normalized density . We assume that the system relaxation time for the diffusive flux of particles (the reactants), , is small enough to neglect time-dependent effects. Hence, in the absence of external forces, the diffusion of reactants with normalized number density is described by the steady-state diffusion equation
| (4) |
with
| (5) |
and which should be solved with the customary bulk boundary condition
| (6) |
It is well known from the general theory of partial differential equations that the classical solution (twice continuously differentiable in and continuous on ) of the stationary diffusion equation (4) does not exist in the whole domain Ladyzhenskaya and Uralt’seva (1968). Therefore one should consider the function
| (7) |
Accordingly, we should impose a condition for the substrate concentration field at the bulk/microgel interface, . It has been demonstrated recently that a key factor controlling the overall reaction rate is the transfer free-energy jump , a quantity that describes the partitioning of the reactant in the microgel versus bulk Angioletti-Uberti et al. (2015). For a single nanocatalyst at the nanoreactor center, a free-energy jump at the solvent-microgel interface can be accounted for through a modified reactant density in the microgel, namely when crossing the bulk/microgel interface. This is also the case for many catalysts in the infinite dilution limit. Here we assume that such description is a valid approximation for realistic nanoreactors, where the nanocatalyst packing fraction is indeed very small, as discussed in depth later. Accordingly, we require
| (8) |
where , being the inverse temperature. Furthermore, the following continuity condition for the local diffusion fluxes should also hold at the bulk/microgel interface
| (9) |
where we have introduced the diffusion anisotropy parameter
| (10) |
Finally, reflecting boundary conditions should hold at the surface of the inert PS core, i.e.
| (11) |
II.2 The reaction rate constant
We are interested in the pseudo-first-order irreversible diffusion-influenced reaction between the nano-catalysts encapsulated in the microgel and reactants freely diffusing in the bulk and in the microgel
| (12) |
where denotes the so-called encounter complex, and are the association and dissociation diffusive rate constants, respectively, and is the surface rate constant of the chemical reaction occurring at the reactive catalysts’ boundaries. Reactions of the kind (12) are customary dealt with by enforcing radiation boundary conditions (also known as Robin boundary conditions) at the reaction surfaces , Collins and Kimball (1949), i.e.
| (13) |
Thus, we can consider that the nanoreactors effectively act as sinks of infinite capacity according to the pseudo-first-order reaction scheme
| (14) |
where the forward diffusion-influenced rate constant (i.e. the equivalent of the measured rate constant Angioletti-Uberti et al. (2015)) is defined by the formula
| (15) |
Using this rate constant one can approximately describe the kinetics of the effective reaction (14) as
| (16) |
where is the volume concentration of nanocatalysts within the microgel and
is the time-dependent effective bulk concentration of ligands.
We stress that our schematization of the problem holds under the excess reactant
condition . Our goal is to compute the rate constant defined in
Eq. (15).
Equation (4) with the boundary
conditions (6), (8), (9), (11) and (13)
completely specify our mathematical problem. It is expedient in the following to
use the dimensionless spatial variables , and for
. Hence, our problem can be cast in the following form
| (17a) | |||
| (17b) | |||
| (17c) | |||
| (17d) | |||
| (17e) | |||
| (17f) | |||
The parameter
| (18) |
gauges the character of the reaction. Here we have introduced the Smoluchowski rate constant for a nanocatalyst embedded in the microgel, . The limit corresponds to considering the boundaries as perfectly absorbing sinks. In this case the reaction (12) becomes diffusion-limited, as the chemical conversion from the encounter complex to the product becomes infinitely fast with respect to the diffusive step leading to the formation of . Otherwise, for , the chemical conversion step is slow enough compared to diffusion, which makes the reaction overall reaction-limited.
III Exact solution of the problem and approximate analytical treatment
We look for solutions for the stationary density of reactants in the bulk and in the microgel as linear combinations of regular and irregular harmonics. Given the multi-connected structure of the boundary manifold , we must consider as many local Cartesian reference frames as there are non-concentric boundaries. Thus, we can look for solutions in the form
| (19a) | |||
| (19b) | |||
where are spherical harmonics, , , for and and are infinite-dimensional sets of unknown coefficients that can be determined by imposing the boundary conditions (17b) and (17d) and the pseudo-continuity conditions at the microgel-solvent interface, eqs (17e) and (17f). This can be done straightforwardly using known addition theorems for spherical harmonics, which results in an infinite-dimensional linear system of equations for the unknown coefficients (see appendix A for the details). Furthermore, making use of known properties of solid spherical harmonics, it is easy to see that the rate constant defined by Eq. (15) is simply given by
| (20) |
As shown in the appendix A, the exact solution to the steady-state problem (17) can be worked out in principle to any desired precision by keeping an appropriate number of multipoles. Remarkably, a simple yet accurate analytical expression can be easily obtained in the monopole approximation (MOA), which corresponds to keeping only the term in the multipole expansions (19) Deutch et al. (1976); Felderhof and Deutch (1976). In particular, it is interesting to compute the rate normalized to the Smoluchowski rate of an isolated sink of the same size as the whole nanoreactor in the bulk, i.e. . We obtain (see appendix B for the details)
| (21) |
where we recall that and . This is the key analytical result derived in this work, that can be readily employed to predict and optimize the geometry and activity of typical core-shell nanoreactors. The quantity stands for the average inverse inter-catalyst separation. This can be computed analytically under the reasonable assumption that spatial correlations in the catalysts configurations are negligible (see appendix B),
| (22) | ||||
where denotes the fraction of the nanoreactor size occupied by the PS core
and is the non-dimensional size of each catalyst.
We see that, since , one has ,
i.e., is of the order of unity,
(taking from experiments Mei et al. (2007)).
In the limit of vanishing surface reactivity of the embedded nano-catalysts
it is immediate to show from eq. (21) that
| (23) |
We see that, if the surface substrate conversion rate constant is weak, this becomes the rate-limiting step for the overall rate of the nanoreactor, irrespective of the geometrical features of the assembly and of the mobility properties of the hydrogel shell. In this case, it becomes crucial to control the transfer free energy jump to tune the rate of the composite nanoreactor. Conversely, if the catalytic action exerted by the metal nanoparticles encapsulated in the microgel is fast with respect to diffusion, i.e. , expression (21) can be simplified by taking the limit . This yields the expression for the fully diffusion-controlled rate
| (24) |
which we will discuss in depth in the following section. Note that for Eq. (24)
coincides with the solution of the Debye-Smoluchowski problem Debye (1942) for a single
perfectly absorbing sink located at the center of the shell, with
.
Formulas (21) and (24) have been derived in the monopole approximation,
which means that any reflecting boundaries in the problem are not taken into account.
Therefore, these should be used to approximate the rate constant of a composite nanoreactor for small
to moderate sizes of the central PS core.
In the following sections, we provide a thorough characterization of the rate constant of
a composite core-shell nanoreactor, computed exactly by solving Eqs. (31),
and we compare it to the approximate MOA analytical expression (24) in the
physically relevant diffusion-limited regime ().
IV The diffusion-controlled regime
We now discuss in more detail the essential features of the diffusion-controlled rate in Eq. (24).
In the monopole approximation, valid for small to intermediate sizes of the central reflecting (inert) core,
the role of the latter only enters
indirectly through the spatial average ,
with .
In the swollen configuration, the central core does not occupy a large fraction of the
overall nanoreactor volume, with (as taken from the experiments reported in
Ref. Mei et al. (2007)). Hence, in this regime
we expect that the exact size of the core should not play a significant role for the
diffusion-controlled rate for relevant values of the physical parameters, i.e.,
(weak) attraction to the hydrogel and decreased internal diffusion .
|
|
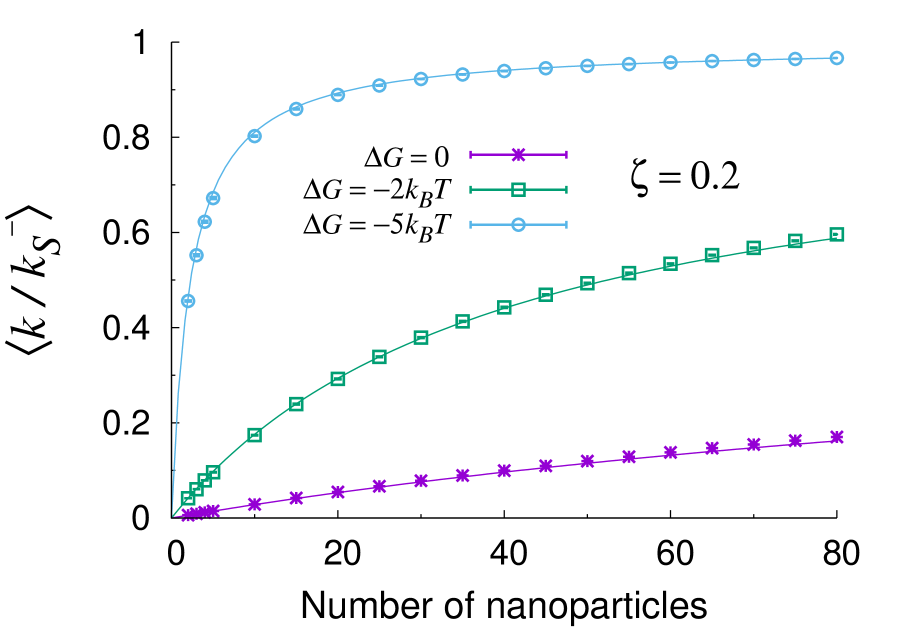
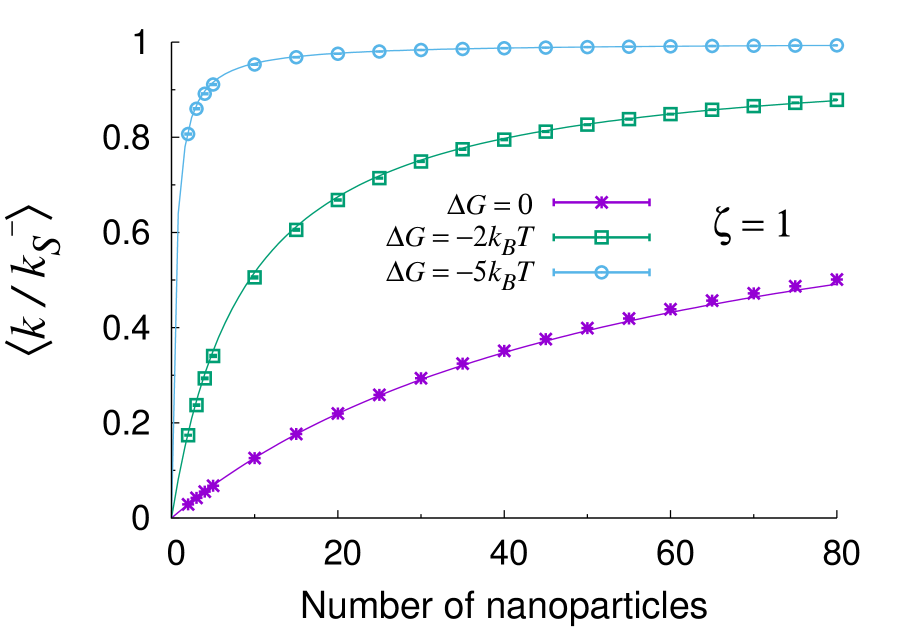
In Fig. 2 we compare the approximate expression (24) to the exact solution of Eqs. (31) for two different mobility ratios and 1.0 and core size (as in previous experiments Mei et al. (2007)). The NP size is held fixed as as also provided from experiments. It is apparent that the analytical treatment is remarkably accurate in these conditions and deviates from the exact solution by less than one percent in the worst cases. This proves that our analytical treatment provides a reliable tool for realistic values of the physico-chemical and geometrical parameters. A comparison of different values of the substrate mobility within the gel (), clearly highlights that all rates are higher when the ligand is more mobile within the gel shell. Concerning the overall form of the curves, one can see that the initial linear rise of the rates is followed by a saturation at large values of . The approach to saturation is slow for small values of , but begins markedly earlier (i.e. for smaller ) if the sorption free energy reaches values as small as a few , the thermal energy. Hence, as discussed already previously, a decisive factor in the design of optimized nanoreactors must be clearly the tuning of the reactant-hydrogel interaction towards attraction. We note that free energy gains of the order of a few seem utterly realistic for small hydrophilic substrates, such as nitrobenzol and nitrophenyl. For comparison, a reasonable upper bound could be estimated as the free energy jump of about 7 kT reported for the sorption of a protein into a hydrophilic network Yigit et al. (2012). These estimates are also consistent with partitioning data of small molecules, such as acetaminophen, into PNIPAM Palasis and Gehrke (1992), where the transfer free energy can be estimated as , where is the partitioning coefficient.
IV.1 Optimizing the number of nanocatalysts
As we see from Eq. (25) the maximum achievable rate is , that is, the Smoluchowski rate of a sink of size equal to that of the total nanoreactor, i.e. the nanoreactor should be big for high activity. In the limit of small NP to nanoreactor size ratio, , Eq. (24) can be simplified to the following form
| (25) |
Let us recall the important parameters, that is, the NP to nanoreactor size ratio ,
the number of NPs , the scaled reactant mobility inside the shell ,
and finally the transfer free energy change for the reactants upon entering the hydrogel.
Clearly, if the mobility vanishes, or the free energy jump
is substantially repulsive, the reaction is significantly slowed down. However, in realistic systems
the mobility will be certainly slowed down to some extent but not vanish. may be even negative
(attractive) if the reactant interacts favorably with the polymer as found for rather hydrophobic reactants and
collapsed PNIPAM-based hydrogels Wu et al. (2012); Angioletti-Uberti et al. (2015).
Since enters Eq. (25) exponentially, substantial effects are expected
following small changes in the interaction. Together with , clearly the number of NPs and their
size ratio with respect to the total nanoreactor size are the key quantities
to tune. To save resources should be small but large enough to warrant a high catalytic activity.
The behavior of Eq. (25) resembles a Langmuir-binding isotherm form.
The rate as a function of initially rises linearly with a slope
and finally saturates to the maximum rate for large
values of . For a single NP, and not too attractive transfer free energy,
we recover essentially the result for a yolk-shell
nanoreactor , where a single NP is embedded in the center of a
spherical hydrogel, apart from a slight modification of the target size, which is not for the
yolk-shell but , the radius of the interior hollow confinement Wu et al. (2012); Angioletti-Uberti et al. (2015).
It is instructive to define an efficieny factor between 0 and 100 ,
that quantifies the desired target efficiency of the nanoreactor.
Solving Eq. (25) for , we find
| (26) |
that is, for a fixed efficiency, the NP number needed to maintain it changes exponentially
with the transfer free energy change.
As a numerical example, let us assume reasonable values of , , and .
To obtain an efficiency of 50 , nanoparticle catalysts would be needed.
If , the number wold drop of a factor to .
For such values of the MOA is an excellent approximation (see Fig. 2),
which makes our treatment self-consistent and sound.
Note that does not scale with the catalyst surface, as one might naively expect,
rather it decreases linearly with the catalyst size.
Formula (26) provides a simple rule of thumb for optimizing the design and
synthesis of core-shell nanoreactors for small to intermediate values of the core size.
As an example, if one aims at 50
efficiency for a relatively neutral hydrogel chemical environment (),
where the mobility of the substrate is not significantly reduced (),
one needs to employ nanoparticles. For that would be .
In the case of a polymer matrix in physical-chemical conditions leading to a reduced
mobility (e.g. ), one would need five times more NPs for ,
but about the same number for . This clearly illustrates
how the performance of a composite core-shell nanoreactor is non-trivially shaped by the combined
action of the physical chemical properties of the hydrogel shell matrix, such as the bulk solvent-microgel
transfer free energy jump and changes in translational mobility of the substrate molecules.
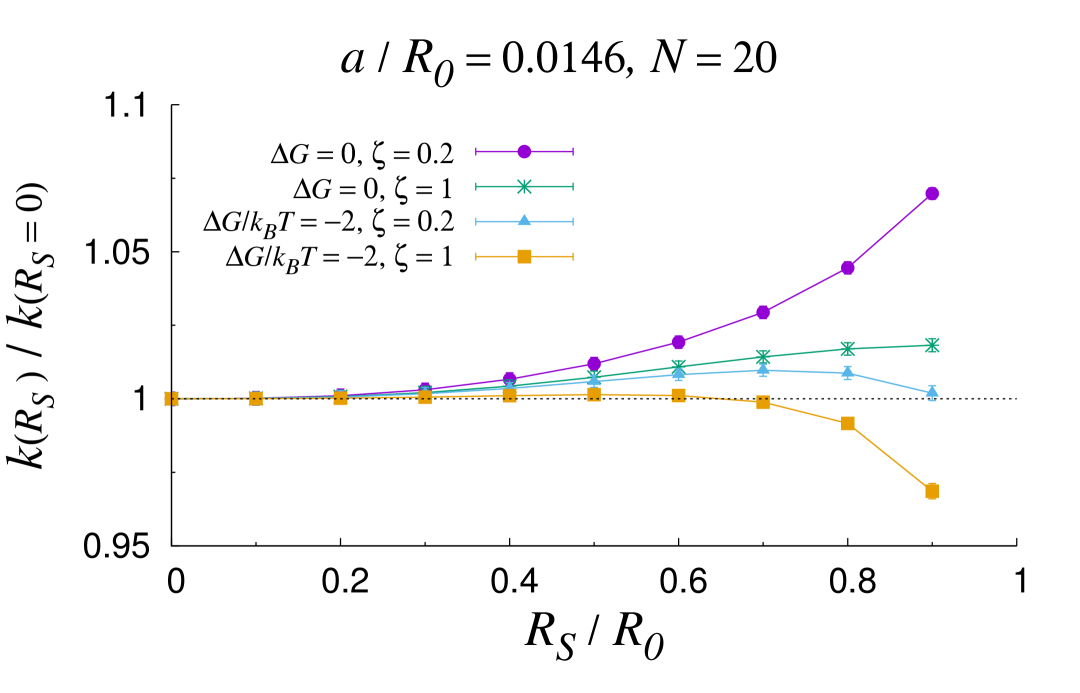
|
|
|
|
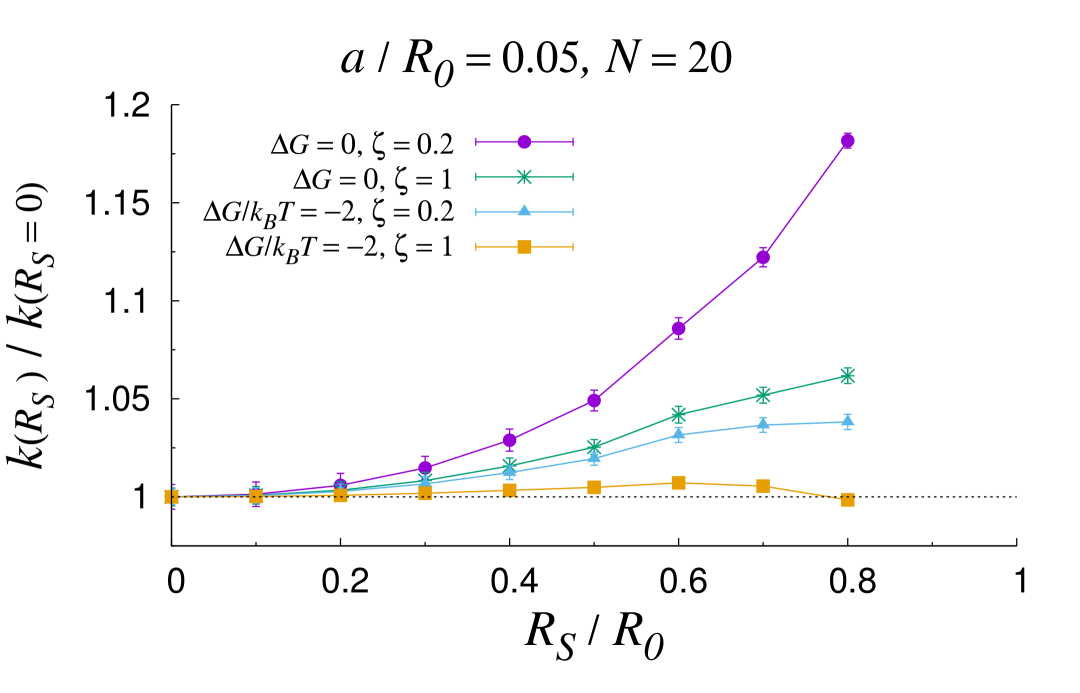
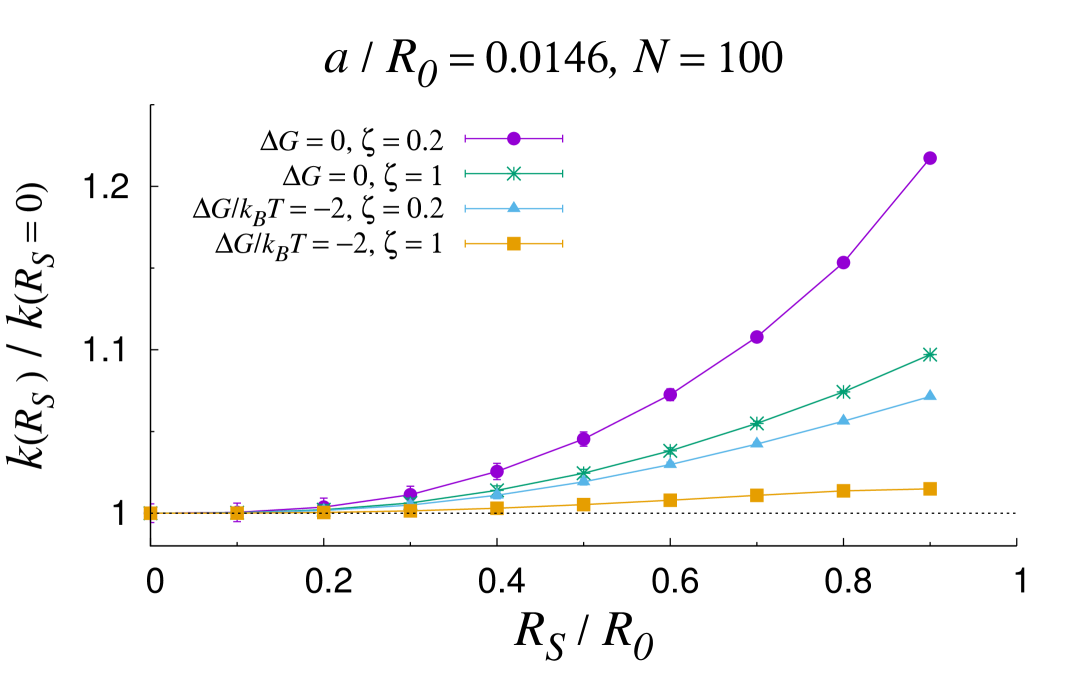
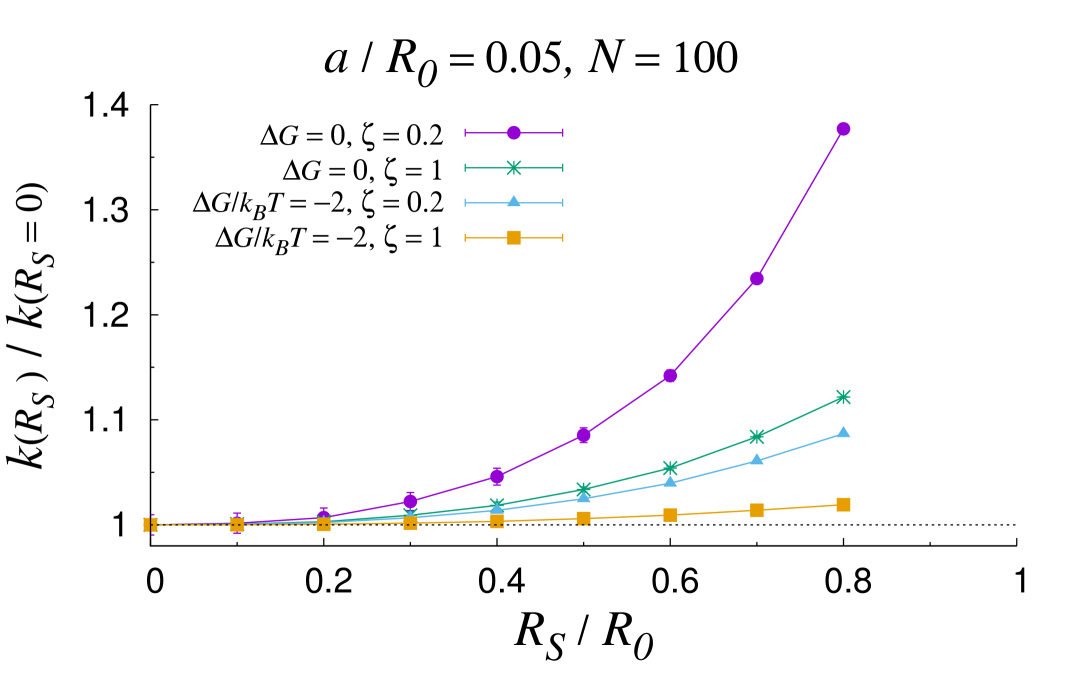
IV.2 The role of the core size
In certain configurations, such as in the shrunk phase of thermosensitive core-shell nanoreactors past the lower critical solution temperature (LCST) Lu and Ballauff (2011), the core size can become comparable to the overall size of the nanoreactor. In these circumstances, the MOA breaks down and the full solution should be used instead. Fig. 3 reports an analysis of the rate constant as the core sized is varied for different values of the geometrical and physico-chemical parameters. As a first observation, the plots confirm and substantiate the discussion laid out in the previous section, as it can be appreciated that the core size does not influence the overall rate until . More generally, one can recognize that the rate constant tends to increase as the shell shrinks (increasing values of ). The only exception is for low and attractive transfer free energy, where a non-monotonic trend is observed (top left panel). This is a typical screening effect Galanti et al. (2015), which originates from the subtle interplay between diffusive interactions among the nanocatalysts and individual screening due the reflecting PS core. It turns out that the transfer free energy is the prime parameter that controls the increase in the rate as the PS core size increases. The more attractive the transfer free energy, the less marked the increase. Interestingly, at fixed values of , the less mobile the substrate in the shell, the more marked the rate boosting effect of the shell shrinking. Importantly, it is apparent from the plots reported in Fig. 3 that the role of the core size is reduced for loading number of the order of a few tens and small size of the nanocatalysts. All in all, these results confirm the complex intertwining of the structural, geometrical and physico-chemical features underlying the overall catalytic activity of core-shell nanoreactors.
V Concluding remarks
In this paper we have developed a detailed theory to compute the total reaction rate of core-shell nanoreactors with multiple catalysts embedded in the shell. The theory is utterly general and allows one to compute the overall reaction rate to any desired accuracy for () given configuration, dimension and surface reactivity of the encapsulated nanocatalysts, () size of the core and the shell, () substrate mobility in the bulk and in the shell and () transfer free-energy jump for substrate molecules. Furthermore, we computed analytical expressions in the monopole approximation that provide an excellent interpolation of the exact solution for small to intermediate sizes of the central core in the physically relevant range of parameters, i.e. small size and high dilution of the nanocatalysts. Our formulas supply ready-to-use simple tools that can be employed to interpret and optimize the activity of experimentally realizable nanoreactor systems. This shall be particularly useful to estimate the optimal number of embedded NPs, that should reflect a compromise between a resource-friendly design and the highest possible catalytic output. Our analytical treatment predicts an optimal number of NPs given by the following expression
| (27) |
where is the desired efficiency, and are the NP and overall nanoreactor
sizes, respectively, and , are the substrate mobility in the shell and in the
bulk, respectively. For realistic values of these parameters, one gets of the
order of hundreds, a value for which the monopole approximation is still in excellent
agreement with the exact solution for core sizes such that .
As discussed already previously, eq. (27) makes it clear that a decisive factor
in the design of optimized hydrogel-based nanoreactors must be the tuning of the reactant-hydrogel
interaction towards attraction () for a specific reaction (or mix of reactions).
Furthermore, as hydrogel that cause strongly reduced substrate mobility also demand more
NPs to achieve high efficiency (), the choice of the shell hydrogel should
be made so as to privilege smooth longer-ranged interactions
(like electrostatic, hydrophobic, or dispersion) with respect to short-ranged ones (like H-bonds),
in order to avoid too sticky interactions that would slow down the reactant mobility
substantially due to activated hopping.
Our analytical treatment breaks down if one
wishes to push the nanoreactor performances towards full efficiency (), where
the loading number of NP increases rapidly, or in the case of larger core
sizes (of the order of the whole spherical assembly). In such cases, the diffusive interaction
between NPs can no longer be neglected, as well as the effect of the inert PS core,
as diffusive and screening interactions
among the different boundaries become important. As a consequence, the full exact solution should be employed
to investigate the behavior of the rate and elaborate an optimal design of the composite
nanoreactor. Interestingly, we have shown that, as a general situation, increasing both the core and the
nanocatalyst sizes either has a rather mild effect on the overall performances, or, more generally,
causes a rate-boosting effect, with an increase of the overall rate constant of up to 40 %
for values of the core size .
Acknowledgments
S. A-U acknowledges financial support from the Beijing Municipal Government Innovation Center for Soft Matter Science and Engineering. J. D. acknowledges funding by the ERC (European Research Council) Consolidator Grant with project number 646659–NANOREACTOR. M. G. and F. P. would like to thank S. D. Traytak for insightful discussions. F. P. and D. F. acknowledge funding by the CNRS (Centre National de la Recherche Scientifique) under the PICS scheme.
Appendix A
In order to determine the unknown coefficients in the expansions (19), we have to express the solution in the local coordinates on every boundary (the spherical surfaces ) and at the microgel-bulk interface , where we impose the pseudo-continuity conditions for the reactant density field. This can be accomplished by using known addition theorems for spherical harmonics Arfken et al. (2005); Caola (2001). After some lengthy algebra, we obtain the following linear equations
| (28a) | |||
| (28b) | |||
| (28c) | |||
where , for and we have introduced characteristic functions . Eqs. (28a), (28b), (28c) hold with and . The matrices read
| (29a) | |||
| (29b) | |||
| (29c) | |||
where (according to this notation ) and
| (30) |
Here, for the sake of coherence, we pose (radius of the PS core) and , for (radius of the nanocatalysts). The system (28a), (28b), (28c) can be expressed more conveniently by subtracting eq. (28c) from eq. (28a), which leads to
| (31a) | |||
| (31b) | |||
If the multipole expansions are truncated at multipoles, the system (31)) comprises equations, which can be easily solved numerically. Once the the coefficients have been determined, the rate constant can be obtained from eq. (15). Recalling the definitions (19) and making use of known properties of solid spherical harmonics, it is easy to see that
| (32) |
The system to be solved has the following structure
To solve this system of equation numerically we employ standard linear algebra packages (LAPACK). The number of multipoles considered to truncate the system was chosen so that the relative accuracy on the rate was less than or equal to , namely .
Appendix B
The monopole approximation of the system (31) for a given configuration of the nanocatalysts can be obtained by truncating the expansion to . The ensuing equations read
| (33) |
with . Recalling the definitions (29a), (29b) and (29c), we have , , , and , so that Eqs. (33) take the following form
| (34) |
Since , the overall rate constant of the nanoreactor can be computed simply as (note that is identically zero as the PS core is modeled as a reflecting sphere). Moreover, we can average the system (34) over the catalyst configurations, in the reasonable hypothesis that spatial correlations between the positions of the catalysts are negligible. This reduces the many-body average to a two-body problem, namely
| (35) | |||||
where . We therefore get from Eqs. (34)
| (36) |
where we have taken as the catalysts are identical. By eliminating the solution (21) is easily recovered as
| (37) |
The diffusion-limited solution (24) follows straightforwardly in the limit .
References
- Pushkarev et al. (2012) V. V. Pushkarev, Z. Zhu, K. An, A. Hervier and G. A. Somorjai, Topics in Catalysis, 2012, 55, 1257–1275.
- Zhang et al. (2012) Y. Zhang, X. Cui, F. Shi and Y. Deng, Chemical Reviews, 2012, 112, 2467–2505.
- Haruta (2003) M. Haruta, Chemical Record, 2003, 3, 75–87.
- Hutchings and Haruta (2005) G. J. Hutchings and M. Haruta, Applied Catalysis A: General, 2005, 291, 2–5.
- Crooks et al. (2001) R. M. Crooks, M. Zhao, L. Sun, V. Chechik and L. K. Yeung, Accounts of Chemical Research, 2001, 34, 181–190.
- Noh and Meijboom (2015) J.-H. Noh and R. Meijboom, Applied Catalysis A: General, 2015, 497, 107–120.
- Ballauff (2007) M. Ballauff, Progress in Polymer Science, 2007, 32, 1135–1151.
- Lu and Ballauff (2011) Y. Lu and M. Ballauff, Progress in Polymer Science (Oxford), 2011, 36, 767–792.
- Lu et al. (2006) Y. Lu, Y. Mei, M. Drechsler and M. Ballauff, Angewandte Chemie - International Edition, 2006, 45, 813–816.
- Carregal-Romero et al. (2010) S. Carregal-Romero, N. J. Buurma, J. Perez-Juste, L. M. Liz-Marzan and P. Herv es, Chem. Mater., 2010, 22, 3051–3059.
- Wu et al. (2012) S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angewandte Chemie - International Edition, 2012, 51, 2229–2233.
- Angioletti-Uberti et al. (2015) S. Angioletti-Uberti, Y. Lu, M. Ballauff and J. Dzubiella, The Journal of Physical Chemistry C, 2015, 119, 15723–15730.
- Debye (1942) P. Debye, Trans. Electrochem. Soc., 1942, 92, 265–272.
- Shi et al. (2014) S. Shi, Q. Wang, T. Wang, S. Ren, Y. Gao and N. Wang, The journal of physical chemistry B, 2014, 118, 7177–86.
- Aditya et al. (2015) T. Aditya, A. Pal and T. Pal, Chemical communications (Cambridge, England), 2015, 51, 9410–31.
- Zhao et al. (2015) P. Zhao, X. Feng, D. Huang, G. Yang and D. Astruc, Coordination Chemistry Reviews, 2015, 287, 114–136.
- Herves et al. (2012) P. Herves, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu, M. Ballauff, P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chemical Society Reviews, 2012, 41, 5577.
- Gu et al. (2014) S. Gu, S. Wunder, Y. Lu, M. Ballauff, R. Fenger, K. Rademann, B. Jaquet and A. Zaccone, The Journal of Physical Chemistry C, 2014, 118, 18618–18625.
- Welsch et al. (2012) N. Welsch, A. L. Becker, J. Dzubiella and M. Ballauff, Soft Matter, 2012, 8, 1428.
- Calef and Deutch (1983) D. F. Calef and J. M. Deutch, Annual Review of Physical Chemistry, 1983, 34, 493–524.
- Rice (1985) Diffusion-limited reactions, ed. S. A. Rice, Elsevier, Amsterdam, 1985, vol. 25.
- Szabo (1989) A. Szabo, The Journal of Physical Chemistry, 1989, 93, 6929–6939.
- Zhou et al. (2008) H. X. Zhou, G. Rivas and A. P. Minton, Annual review of biophysics, 2008, 37, 375–397.
- von Smoluchowski (1916) M. von Smoluchowski, Physik Z, 1916, 17, 557–571.
- Collins and Kimball (1949) F. C. Collins and G. E. Kimball, Journal of Colloid Science, 1949, 4, 425–437.
- Deutch et al. (1976) J. M. Deutch, B. U. Felderhof and M. J. Saxton, The Journal of Chemical Physics, 1976, 64, 4559.
- Felderhof and Deutch (1976) B. U. Felderhof and J. M. Deutch, The Journal of Chemical Physics, 1976, 64, 4551.
- Traytak (1992) S. D. Traytak, Chemical Physics Letters, 1992, 197, 247 – 254.
- Traytak (2003) S. D. Traytak, The Journal of Composite Mechanics And Design, 2003, 9, 495–521.
- Gordeliy et al. (2009) E. Gordeliy, S. L. Crouch and S. G. Mogilevskaya, International Journal for Numerical Methods in Engineering, 2009, 77, 751–775.
- Galanti et al. (2016) M. Galanti, D. Fanelli, S. D. Traytak and F. Piazza, Phys. Chem. Chem. Phys., 2016, 18, 15950–15954.
- Cukier (1984) R. Cukier, Macromolecules, 1984, 17, 252–255.
- Ladyzhenskaya and Uralt’seva (1968) O. A. Ladyzhenskaya and N. N. Uralt’seva, Linear and Quasilinear Elliptic Equations, Academic Press, New York and London, 1968, vol. 46.
- Mei et al. (2007) Y. Mei, Y. Lu, F. Polzer, M. Ballauff and M. Drechsler, Chemistry of Materials, 2007, 19, 1062–1069.
- Yigit et al. (2012) C. Yigit, N. Welsch, M. Ballauff and J. Dzubiella, Langmuir, 2012, 28, 14373–14385.
- Palasis and Gehrke (1992) M. Palasis and S. H. Gehrke, Journal of Controlled Release, 1992, 18, 1–11.
- Galanti et al. (2015) M. Galanti, D. Fanelli and F. Piazza, 2015, 5.
- Arfken et al. (2005) G. Arfken, H. J. Weber and F. E. Harris, Mathematical Methods for Physicists, Sixth Edition: A Comprehensive Guide, Elsevier Academic Press, 2005.
- Caola (2001) M. J. Caola, Journal of Physics A: Mathematical and General, 2001, 11, L23–L25.