Realization of a quantum degenerate mixture of highly magnetic and nonmagnetic atoms

The research field of ultracold atoms has become a vast and rich one. The number of atomic species that have been brought to quantum degeneracy spans across the entire periodic table of elements, reaching from the lightest ones Fried et al. (1998) to very heavy species Takasu et al. (2003), and is by now too large to list them all individually here. In addition to single-species experiments, two-element experiments have also gained considerable attention. Starting with an ultracold Cs-Li mixture Mosk et al. (2001), this field also evolved in many directions, again covering a range from large mass-imbalance Yb-Li mixtures Hansen et al. (2011) to highly magnetic and anisotropic Er-Dy mixtures Trautmann et al. (2018). This diversity is not redundancy but a richness of possibilities, each one looking at the fundamental questions stemming from quantum physics, many-body physics, quantum simulation and quantum computation at slightly angles.

It is in this spirit that we here introduce another member to the family of experimentally realized quantum degenerate mixtures: a mixture of bosonic erbium (¹⁶⁸Er) and bosonic ytterbium (¹⁷⁴Yb). Without going to the extremes of either large mass imbalances or nearly overwhelmingly complicated interspecies interaction potentials, this mixture might be ideal for exploring physical phenomena in-depth and systematically with reasonable computational efforts, as first proposed and theoretically described by Kosicki, Borkowski, and Żuchowski Kosicki et al. (2020). In short, while quantum chaotic behavior could be confirmed experimentally in, e.g., the complex dynamics of highly magnetic and highly anisotropic Er-Er collisions Frisch et al. (2014), it is believed that evidence of quantum chaos may also be found in the significantly simpler Er-Yb collisional system. In that case, one of the collisional partners, Yb, is a comparatively-easy-to-model spin-singlet atom, and the interspecies interactions can be derived from ab initio calculations Kosicki et al. (2020). This greatly helps in identifying the driving mechanisms, such as anisotropic interactions, that contribute to the chaotic behavior. Furthermore, the two species have similarly large masses while also offering various isotopes each for use in the experiments, Er-Yb mixtures offer a unique possibility to study the effects of minute reduced-mass differences on the Feshbach spectra. The expected shifts of the interspecies Feshbach resonance positions should be well controlled and might be sensitive to temporal changes in the proton-to-electron mass ratio Ketterle and Druten (1996).

In addition, this quantum degenerate mixture is unique in that one of its constituents is a highly magnetic atom, ¹⁶⁸Er, with a magnetic moment of $7\,\mu_{B}$ whereas the other one, ¹⁷⁴Yb, is nonmagnetic. This offers the possibility of studying the magnetic-nonmagnetic impurity problem at vanishing interspecies interactions by means of a Feshbach resonance, especially when loaded into an optical lattice. There, the additional existence of narrow and ultranarrow optical transitions for both Er Patscheider et al. (2021) and Yb Yamaguchi et al. (2010) would provide a powerful tool for such investigations.

In the following we will first describe the details of our experiment relevant to the formation of the quantum degenerate ¹⁶⁸Er-¹⁷⁴Yb mixture (Sec. II). We then present the experimental data and our evidence for achieving simultaneous Bose-Einstein condensates (BECs; Sec. III) and conclude with a short discussion of these results (Sec. IV).

The setup of the experiment and the experimental sequence are largely as in our previous works Schäfer et al. (2022), and we will here only highlight the key aspects and changes relevant to the present work. After first loading the ¹⁷⁴Yb magneto-optical trap (MOT) to saturation in $45\,\mathrm{s}$ a rather small amount of ¹⁶⁸Er is added with just $2\,\mathrm{s}$ of loading. Due to the narrow-linewidth nature of the Er MOT the obtained Er sample is automatically spin polarized into the lowest energy $m_{J}=-6$ state Frisch et al. (2014); Schäfer et al. (2022). Both species are then transferred into an optical far-off resonant trap in the horizontal direction (H-FORT) at $1064\,\mathrm{nm}$ where we typically obtain about $3\times 10^{5}$ Er atoms and $4\times 10^{6}$ Yb atoms, both at an estimated temperature of $80\,\mu\mathrm{K}$. This one-order-of-magnitude difference in atom numbers is to facilitate the sympathetic cooling of Er by Yb which this experiment relies on. That is, by forced evaporation of Yb the Yb sample has to not only cool itself down but also remove the energy from the Er sample which is in good thermal contact with Yb by means of frequent elastic collisions. Before evaporation a second FORT beam in the vertical direction (V-FORT) at $1070\,\mathrm{nm}$ is added for increased atom densities and thus evaporation efficiencies in the resulting crossed FORT configuration. In the following forced evaporation step, both FORT powers are gradually reduced over a period of $10\,\mathrm{s}$ as shown in the top panel of Fig. 1.

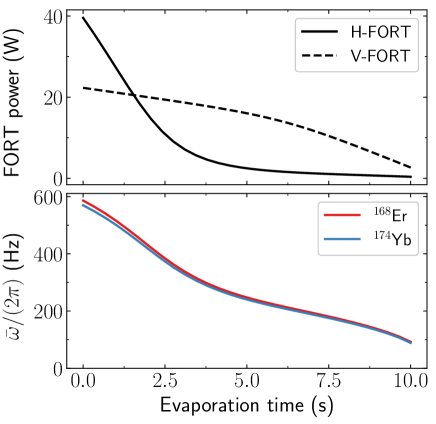
The evaporation ramp shape of each FORT is a spline curve with, in addition to the start and end points, two additional in-between control points. The ramp shapes and their duration have been optimized for optimal evaporation of ¹⁷⁴Yb. During the first $4\,\mathrm{s}$ of evaporation a magnetic bias field of $1.6\,\mathrm{G}$ is applied in the vertical direction that is then reduced to $0.4\,\mathrm{G}$ for the remainder of the evaporation ramp. This choice is to ensure that the initial spin polarization of ¹⁶⁸Er is maintained throughout the evaporation while also having optimal interspecies collisional properties and low Er-Er inelastic collisional losses Frisch et al. (2014).

Due to both the similar masses of ¹⁶⁸Er and ¹⁷⁴Yb and the similar polarizabilities of the two species at the wavelengths of the FORT lasers the resulting traps are quite similar. As expressed in the bottom panel of Fig. 1 the geometric mean trap frequencies start at about $2\pi\times 600\,\mathrm{Hz}$ and then decrease in a nearly linear fashion to about $2\pi\times 100\,\mathrm{Hz}$ after $10\,\mathrm{s}$. The final trap frequencies are about $(\omega_{x},\omega_{y},\omega_{z})=2\pi\times(55,70,190)\,\mathrm{Hz}$ where $\omega_{z}$ is in the vertical direction. From earlier works it is known that the ¹⁷⁴Yb-¹⁷⁴Yb scattering length is $105\,a_{0}$, where $a_{0}$ is the Bohr radius Kitagawa et al. (2008). The ¹⁶⁸Er-¹⁶⁸Er scattering length was measured to be between $150$ and $200\,a_{0}$ where, however, additional effects due to dipole-dipole interactions should also be considered carefully Aikawa et al. (2012). The ¹⁶⁸Er-¹⁷⁴Yb interspecies scattering length is as of yet unknown.

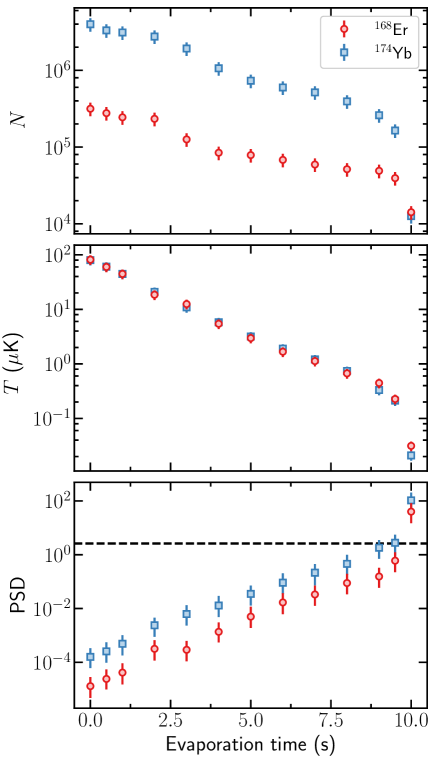
We now address the development of the atom numbers $N$, the temperatures $T$, and the phase-space density (PSD) during the evaporation process, which is shown in Fig. 2. As expected, at the expense of mostly Yb atoms the overall temperature of the mixture decreases. It is important to note the high fidelity with which the temperature of Er follows the temperature of Yb, highlighting the very good thermal contact between the two species and allowing for successful sympathetic cooling of Er. Correspondingly, the PSD increases by more than four orders of magnitude. After about $9.5\,\mathrm{s}$ of evaporation it reaches the critical value of about $2.6$, the onset of quantum degeneracy into a BEC. This is further evidenced by the apparent discontinuity of the observed quantities at $10\,\mathrm{s}$. This change is most probably due to the phase transition from a thermal cloud to a BEC where a Gaussian fit is no longer the appropriate description of the actual density distribution but instead highlights the sudden “compactification” of the sample.

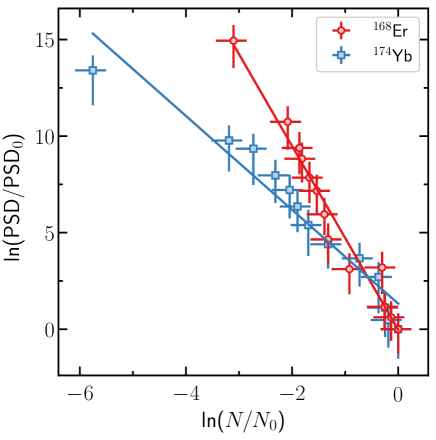
As a measure of the evaporation efficiency we look at the relationship of the $\mathrm{PSD}$, normalized to its initial value $\mathrm{PSD}_{0}$, to the atom numbers $N$, normalized to their initial values $N_{0}$. There, usually a power-law-like behavior is observed, and $\gamma=-d\ln(\mathrm{PSD}/\mathrm{PSD}_{0})/d\ln(N/N_{0})$ serves as a good indicator of evaporation efficiency Ketterle and Druten (1996). In the case at hand (see Fig. 3), one obtains $\gamma=4.8(3)$ for Er and $2.4(2)$ for Yb. Comparing this, e.g., with our earlier results in the evaporation of an Yb-Li mixture Schäfer et al. (2018), we find a similar efficiency for Yb to that found before ($\gamma_{\rm Yb}=2.9$ for Yb-Li) but a reduced evaporation efficiency of the sympathetically cooled species Er as compared with Li ($\gamma_{\rm Li}=6.5$ in Yb-Li). This might in part be due to the reduced effect of gravity on the very light Li resulting in a significantly deeper trap and reduced losses for hotter Li atoms. The sympathetic cooling of Er is not perfect in the sense that a reduction in the Er atom number is also observed. It is rather that in this scenario of similar trap depths for both species and also due to favorable Er-Er collisional properties Aikawa et al. (2012), Yb efficiently supports the cooling process of Er. This is further evidenced by the fact that in our experiment no Er BEC can be achieved by single-species evaporation due to an insufficient number of Er atoms initially loaded into the FORT, while a single-species-evaporated Yb BEC is possible.

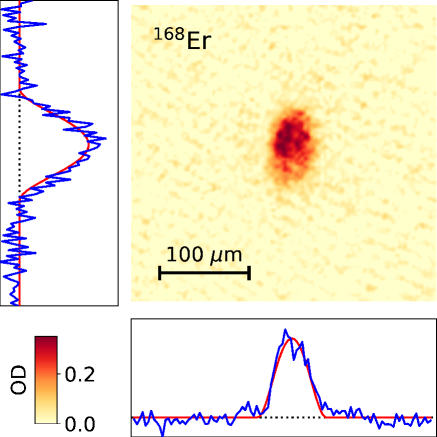
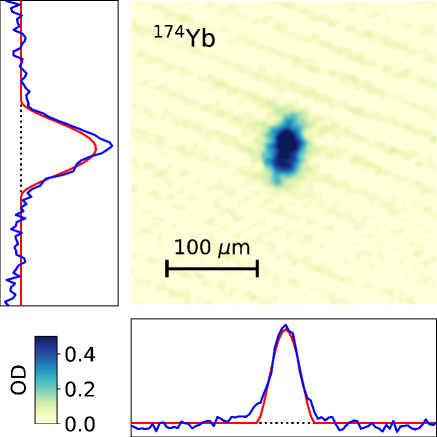
We probe the dual-species BEC after $10\,\mathrm{s}$ of evaporation by standard absorption imaging. Before releasing the sample from the optical trap we keep the FORT lasers at their final values for an additional $500\,\mathrm{ms}$ to allow for final thermalization of the two atom clouds. The trapping lasers are then suddenly switched off, and the atoms are allowed to expand freely. After $22\,\mathrm{ms}$ of expansion time both atomic species are imaged simultaneously in absorption imaging on the strong transitions at $401\,\mathrm{nm}$ for Er and $399\,\mathrm{nm}$ for Yb. The results are shown in Fig. 4. Both clouds are reasonably well described by Thomas-Fermi distributions, indicative of only small contributions from still thermal atoms. Indeed, tentative fits with bimodal distributions (i.e., distributions including Gaussian-shaped thermal contributions) seemed unrealistic, a situation typically experienced in the case of only small thermal contributions. We find no appreciable change in the cloud shapes in the case where one species is removed before releasing the remaining atoms from the trap. This indicates that the Er-Yb interspecies interactions are below the threshold beyond which immiscibility effects are expected Pethick and Smith (2008); Burchianti et al. (2020) and gives us the possibility to estimate an upper bound Riboli and Modugno (2002) for the Er-Yb scattering length, $a_{\rm ErYb}$: Assuming an ¹⁶⁸Er scattering length of $a_{\rm Er}\leq 200\,a_{0}$ and taking the known $a_{\rm Yb}=105\,a_{0}$ it follows that $|a_{\rm ErYb}|<145\,a_{0}$.

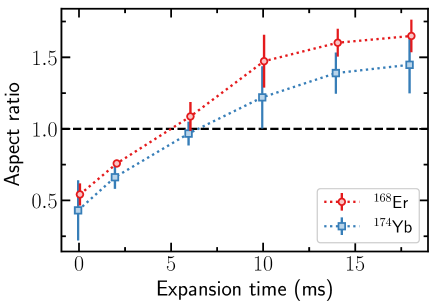
The overall shape of the atom clouds in Fig. 4 is not spherically symmetric as would be expected of thermal samples. Instead they are elongated in the vertical direction. A more systematic investigation of the dependence of these aspect ratios on the expansion time is presented in Fig. 5, where expansion times in the range $0$–$18\,\mathrm{ms}$ are investigated. For both species an inversion of the aspect ratio at about $5$–$6\,\mathrm{ms}$ of expansion time is observed. This agrees reasonably well with a theoretically expected inversion point at about $4\,\mathrm{ms}$ based on the final trapping frequencies Castin and Dum (1996) and further corroborates the quantum degenerate nature of the ultracold mixture of ¹⁶⁸Er and ¹⁷⁴Yb.

Evaluating the stability of the obtained BEC mixture at $0.4\,\mathrm{G}$ we observe lifetimes of the Er BEC in excess of $10\,\mathrm{s}$ while the lifetime of our Yb BEC is generally lower, at about $2\,\mathrm{s}$, which is purely due to technical limitations of our apparatus and not due to the presence of Er. Therefore, for a more qualitative evaluation of the inelastic collisional processes, we investigate the atom loss with a cold but still thermal mixture at about $400\,\mathrm{nK}$. There, we find single-species three-body collision rates Ye et al. (2022) for ¹⁶⁸Er and ¹⁷⁴Yb of $3(1)\times 10^{-28}$ and $1.0(5)\times 10^{-28}\,\mathrm{cm}^{6}\,\mathrm{s}^{-1}$, respectively. The additionally observed interspecies three-body collisional losses are at $1.0(5)\times 10^{-28}\,\mathrm{cm}^{6}\,\mathrm{s}^{-1}$ comparable to the intraspecies losses and well described by Er-Yb-Yb interactions while Er-Er-Yb collisions are not compatible with our observations. These low losses underline the good suitability of ultracold ¹⁶⁸Er-¹⁷⁴Yb mixtures for future experiments.

First and foremost the work presented here confirms that a stable formation of a ¹⁶⁸Er-¹⁷⁴Yb double BEC is not only theoretically desirable but also experimentally feasible. That is by no means an a priori certainty as the expected dense interspecies Feshbach resonance structure might easily have interdicted such a state by strong inelastic collisional losses at the low magnetic fields that are typically used during standard evaporation stages. Along the way, our experiment once again underlines the quite amazing versatility of the heavy Yb not only from a physics standpoint but also in its capability to efficiently cool a variety of other species sympathetically Hansen et al. (2011); Schäfer et al. (2022).

The present work focused on the most commonly used bosonic isotopes of Er and Yb. An extension to different isotope combinations with interesting applications to fundamental research Kosicki et al. (2020) appears straightforward and our experiment is already set up to also work with various bosonic and fermionic isotopes.

It seems obvious that from these encouraging results it is only a few minor steps towards a full investigation of the ¹⁶⁸Er-¹⁷⁴Yb interspecies Feshbach resonance spectrum for at least this isotope combination. In the case of our experiment, in particular, we will, however, need to first make some improvements to (i) increase the atoms numbers in the final ultracold samples and (ii) improve the magnetic field stability of our setup Schäfer et al. (2022). The latter will be necessary to reliably identify also the narrow Feshbach resonances in order to obtain complete Feshbach spectra that are necessary for the envisioned statistical analyses. These instrumental challenges are not insurmountable, and we are therefore confident that our results will further enrich the family of experiment-proven ultracold atomic mixtures to address some of the quantum questions of our times.

This work was supported by the Grant-in-Aid for Scientific Research of JSPS Grants No. JP17H06138, No. 18H05405, and No. 18H05228, JST CREST Grant No. JPMJCR1673 and the Impulsing Paradigm Change through Disruptive Technologies (ImPACT) program by the Cabinet Office, Government of Japan, and MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) Grant No. JPMXS0118069021 and Moonshot Program Grant No. JPMJMS2269.