Recent Developments in DEMIRCI, the RFQ Design Software

Designing an RFQ, consisting of about hundred cells, necessitates correct determination of the time independent part of the electrical K-T potential for each cell given [1]by:

where $r$ and $\theta$ are spherical coordinates for which $z$ represents the beam direction, $V$ is the inter-vane voltage, $k$ is the wave parameter given by $k\equiv 2\pi/\lambda\beta$, with $\lambda$ being the RF wavelength and $\beta$ being the speed of the ion relative to the speed of light. Also, $r_{0}$ is the mean aperture of the vanes, $I_{2m}$ is the modified Bessel function of order $2m$ and the $A_{nm}$ are the multipole coefficients whose values, depending on the vane geometry, should be obtained. The heritage from the very first RFQ studies in LANL can still be found in the industry standard software PARMTEQ’s [3] method to determine the multipole coefficients of the first 8 terms. It is based on data from pre-prepared tables containing image charge calculations using the integral method. Another approach reported in the literature uses a 3 dimensional differential finite element method to obtain the potential distribution across the RFQ length and then does a least squares fit to obtain the multipole coefficients [7]. Since this method is reported to be as accurate as the image charge method and much faster from computation point of view, an independent implementation of this approach is realized in DEMIRCI.

The procedure for finding the 8T coefficients starts with the division of the RFQ to be simulated into a number 20 node bricks as shown in Figure 1. Although the number of segmentations in 3D is user selectable, a good compromise between speed and accuracy is encoded as the default value set: 5x5x6 in $x$, $y$ and $z$ coordinates. Once the meshing is complete, the general stiffness matrix is prepared from individual segments. Finite element method (FEM) is used to formulate the Poisson equation to find the electrostatic potential for each cell. This equation is solved numerically using the conjugate gradient technique for each node and for each cell. The solutions for the nodes within the minimum bore radius are then fitted to the 8T potential function with the least squares method to find the first eight KT potential coefficients at each cell.

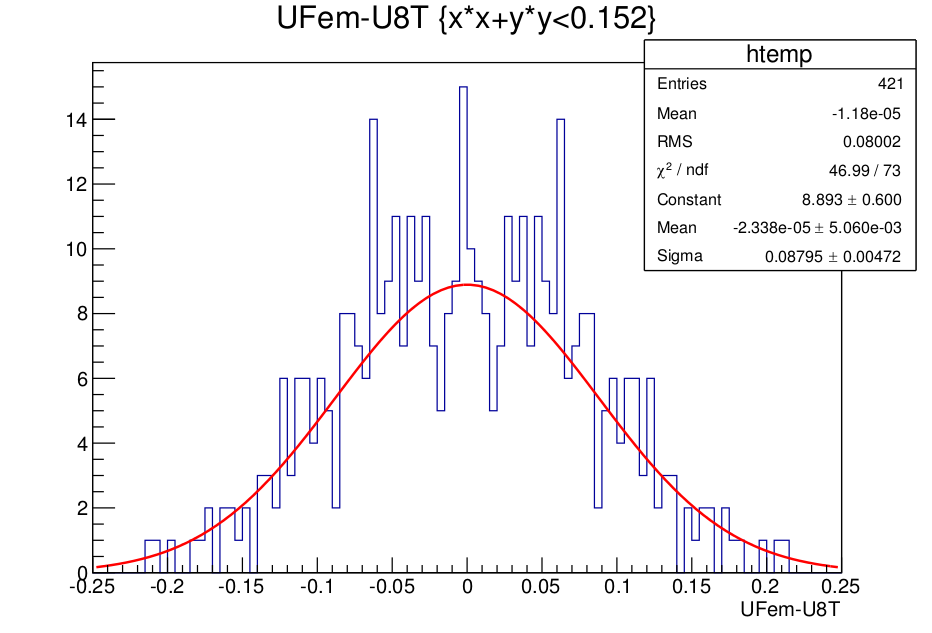
The validity of the method and of the results are checked using two different approaches. Firstly, a similar RFQ 8T coefficient calculation report has been found and the same calculations are repeated in DEMIRCI. The encouraging results of that study are reported elsewhere [8]. As an additional check, FEM solutions on all nodes are compared to fit results for a random cell. The histogram of the difference between the two are shown in Figure 2 together with a gaussian fit. The distribution shows that the error originating from the fitting procedure is about 1/1000. Even if in some long cells, the 8T potential is not adequate for defining the equipotential surface, the error is smoothed out by the fitting procedure and it’s order of magnitude is expected to remain at this level.

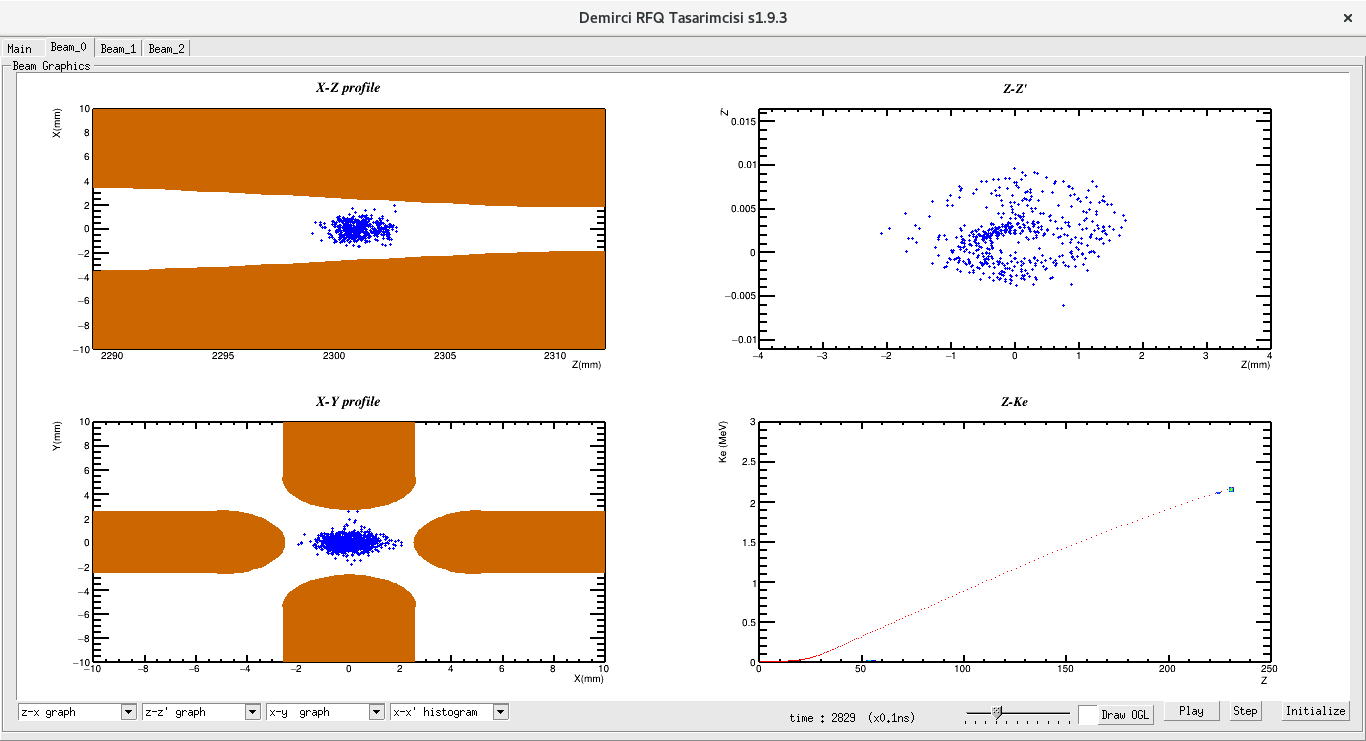
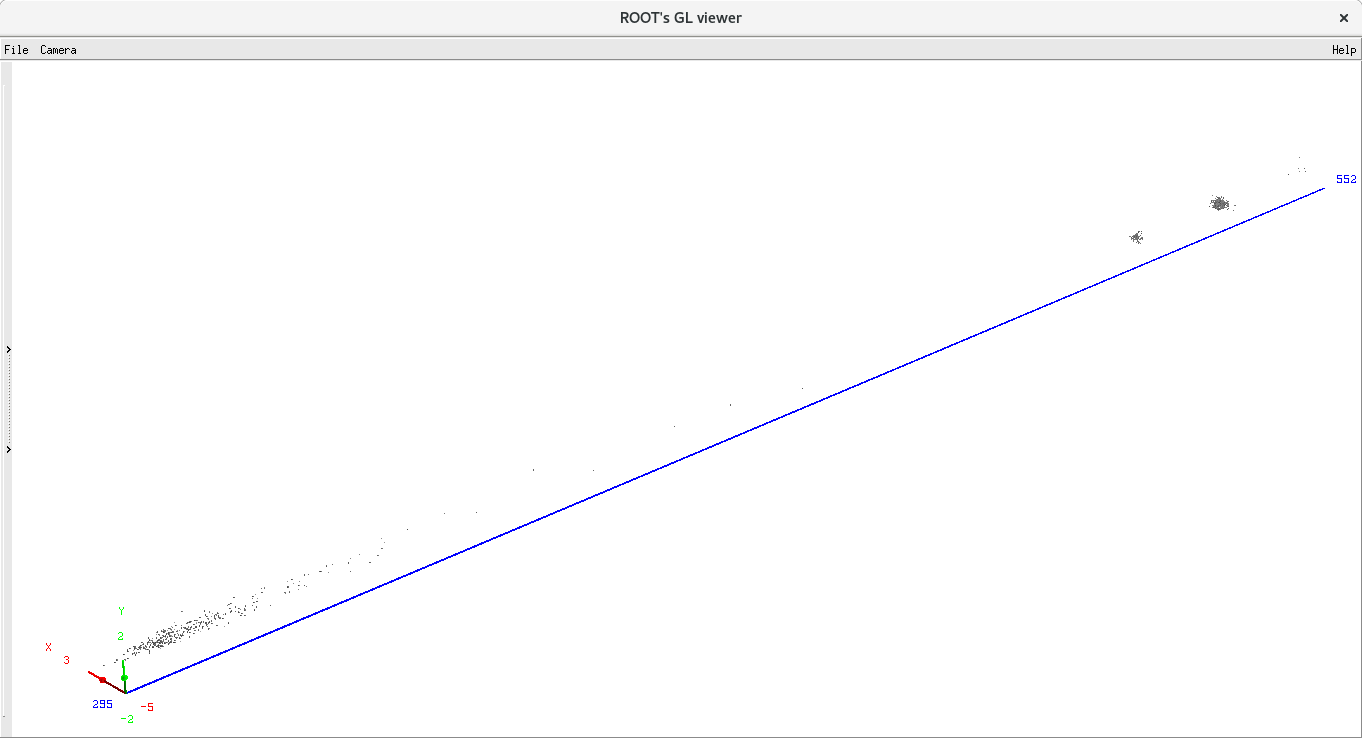
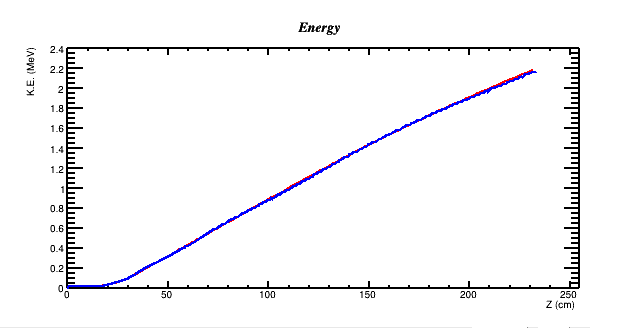
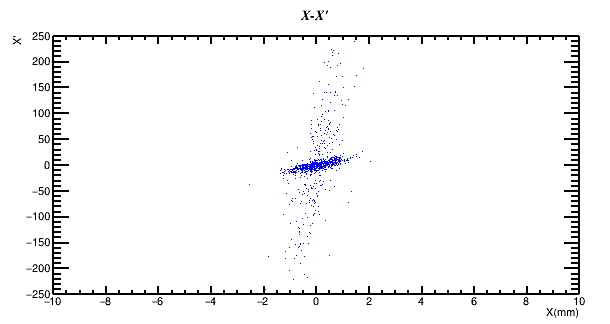
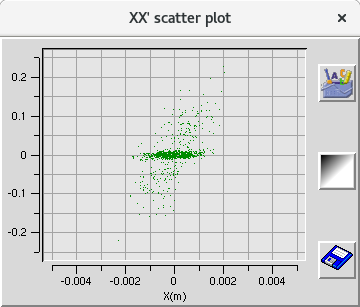
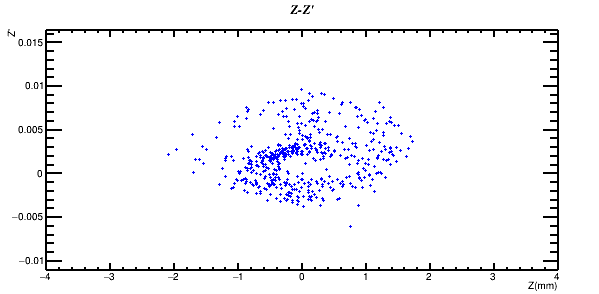
Once all the 8T potential coefficients are calculated, the Beam Dynamics tabs of the DEMIRCI graphical user interface, shown in Figure3, become available to the designer. The designer has three such tabs with four user selectable beam dynamics related plots are available. For the beam dynamics calculations a constant time step (set as 0.1ns, not adjustable by the user) based approach is used for finding all relevant EM fields, particle positions and velocities during the simulation. Synchronous particle energy calculated with these fields closely follows the predicted kinetic energy for our test design as shown in the Figure 5. Another visualization facility available to the designer is the 3D beam view shown in Figure 4. In this particular example, where the synchronous particle is at 520mm from the origin, the bunched and accelerated particles are shown along the $z$ axis.