1 Introduction, Notations, and Main Results
Band-dominated operators.
We study bounded linear operators on the space ℓ 2 := ℓ 2 ( ℤ ) \ell^{2}:=\ell^{2}({\mathbb{Z}}) x = ( x k ) k ∈ ℤ x=(x_{k})_{k\in{\mathbb{Z}}} ‖ x ‖ = ∑ k ∈ ℤ | x k | 2 < ∞ \|x\|=\sqrt{\sum_{k\in{\mathbb{Z}}}|x_{k}|^{2}}<\infty A A ℓ 2 \ell^{2} ( a i j ) i , j ∈ ℤ (a_{ij})_{i,j\in{\mathbb{Z}}} A A band operator if its matrix ( a i j ) (a_{ij}) A A d := max { | i − j | : a i j ≠ 0 } d:=\max\{|i-j|:a_{ij}\neq 0\} bandwidth of A A A A band-dominated operator if it is the limit, in the induced operator norm on ℓ 2 \ell^{2}
Pseudospectra.
Because the spectrum of a non-normal operator A A A A ε {\varepsilon} A A
spec ε A := { λ ∈ ℂ : ‖ ( A − λ I ) − 1 ‖ > 1 / ε } = ⋃ ‖ T ‖ < ε spec ( A + T ) , ε > 0 . {\rm spec}_{\varepsilon}A\ :=\ \{\lambda\in{\mathbb{C}}:\|(A-\lambda I)^{-1}\|>1/{\varepsilon}\}\ =\ \bigcup_{\|T\|<{\varepsilon}}{\rm spec}\,(A+T),\qquad{\varepsilon}>0.
Here we agree upon writing ‖ B − 1 ‖ = ∞ \|B^{-1}\|=\infty B B [28 ] ) shows that spec ε A {\rm spec}_{\varepsilon}A spec A {\rm spec}\,A A A < ε <{\varepsilon} A A spec ε A {\rm spec}_{\varepsilon}A ε {\varepsilon} spec A {\rm spec}\,A [28 ] for many more reasons to study pseudospectra and for more references.
The lower norm.
As a counterpart to the operator norm ‖ A ‖ = sup ‖ x ‖ = 1 ‖ A x ‖ \|A\|=\sup_{\|x\|=1}\|Ax\|
ν ( A ) := inf ‖ x ‖ = 1 ‖ A x ‖ , \nu(A)\ :=\ \inf_{\|x\|=1}\|Ax\|,
that is sometimes (by abuse of notation) called the lower norm of A A ‖ A ‖ \|A\| A A ν ( A ) \nu(A) [19 , p.69f] ) that ν ( A ) > 0 \nu(A)>0 A A
‖ A − 1 ‖ = 1 / min ( ν ( A ) , ν ( A ∗ ) ) \|A^{-1}\|\ =\ 1/\min(\nu(A),\nu(A^{*}))
holds with 1 / 0 := ∞ 1/0:=\infty A A A A ν ( A ) \nu(A) ν ( A ∗ ) \nu(A^{*}) spec ε A {\rm spec}_{\varepsilon}A
spec ε A = { λ ∈ ℂ : min ( ν ( A − λ I ) , ν ( ( A − λ I ) ∗ ) ) < ε } . {\rm spec}_{\varepsilon}A\ =\ \{\lambda\in{\mathbb{C}}:\min\!\big{(}\nu(A-\lambda I),\nu((A-\lambda I)^{*})\big{)}<{\varepsilon}\}. (1)
Approximating the lower norm of band-dominated operators.
For x ∈ ℓ 2 x\in\ell^{2} supp x := { j ∈ ℤ : x j ≠ 0 } {\rm supp\,}x:=\{j\in{\mathbb{Z}}:x_{j}\neq 0\} J ⊂ ℤ J\subset{\mathbb{Z}} diam J := max { | i − j | : i , j ∈ J } {\rm diam\,}J:=\max\{|i-j|:i,j\in J\} [11 ] (also see [13 , 21 ] ) is that the lower norm of a band-dominated operator A A δ > 0 \delta>0 x ∈ ℓ 2 x\in\ell^{2} n ∈ ℕ n\in{\mathbb{N}} δ \delta
ν ( A ) ≤ ‖ A x ‖ ≤ ν ( A ) + δ \nu(A)\ \leq\ \|Ax\|\ \leq\ \nu(A)+\delta (2)
for a particular x ∈ ℓ 2 x\in\ell^{2} ‖ x ‖ = 1 \|x\|=1 diam ( supp x ) < n {\rm diam\,}({\rm supp\,}x)<n supp x {\rm supp\,}x J k n := { k + 1 , … , k + n } J^{n}_{k}:=\{k+1,...,k+n\} k ∈ ℤ k\in{\mathbb{Z}} ‖ A x ‖ \|Ax\| 2 A A ℓ 2 ( J k n ) \ell^{2}(J^{n}_{k}) diam ( supp x ) < n {\rm diam\,}({\rm supp\,}x)<n J k n J^{n}_{k} k ∈ ℤ k\in{\mathbb{Z}} k k k ∈ ℤ k\in{\mathbb{Z}}
ν ( A ) ≤ inf k ∈ ℤ ν ( A | ℓ 2 ( J k n ) ) ≤ ν ( A ) + δ \nu(A)\ \leq\ \inf_{k\in{\mathbb{Z}}}\nu(A|_{\ell^{2}(J^{n}_{k})})\ \leq\ \nu(A)+\delta (3)
If A A A | ℓ 2 ( J k n ) A|_{\ell^{2}(J^{n}_{k})} k + 1 , … , k + n k+1,...,k+n ν ( A | ℓ 2 ( J k n ) ) \nu(A|_{\ell^{2}(J^{n}_{k})}) k ∈ ℤ k\in{\mathbb{Z}} { A | ℓ 2 ( J k n ) : k ∈ ℤ } \{A|_{\ell^{2}(J^{n}_{k})}:k\in{\mathbb{Z}}\} A A
It is clear that the size n n δ \delta 2 3 [11 ] (also see §3 and 4 in [13 ] ) shows, for the particular case of tridiagonal (bandwidth d = 1 d=1 ( a i j ) i , j ∈ ℤ (a_{ij})_{i,j\in{\mathbb{Z}}} δ \delta 1 / n 1/n
δ ≤ 2 ( sup j ∈ ℤ | a j + 1 , j | + sup j ∈ ℤ | a j − 1 , j | ) sin π 2 n + 2 ∈ 𝒪 ( 1 n ) , \delta\ \leq\ 2\left(\sup_{j\in{\mathbb{Z}}}|a_{j+1,j}|+\sup_{j\in{\mathbb{Z}}}|a_{j-1,j}|\right)\sin\frac{\pi}{2n+2}\ \in\ {\mathcal{O}}\left(\frac{1}{n}\right), (4)
The constant turns out to be optimal. We make use of that result by two simple steps of reduction:
( i ) (i)
Given an accuracy η > 0 \eta>0 A A B B ‖ A − B ‖ ≤ η \|A-B\|\leq\eta ν ( ⋅ ) \nu(\cdot)
| ν ( A ) − ν ( B ) | ≤ ‖ A − B ‖ ≤ η , as well as | ν ( A ∗ ) − ν ( B ∗ ) | ≤ ‖ A ∗ − B ∗ ‖ ≤ η . |\nu(A)-\nu(B)|\leq\|A-B\|\leq\eta,\quad\textrm{as well as}\quad|\nu(A^{*})-\nu(B^{*})|\leq\|A^{*}-B^{*}\|\leq\eta. (5)
( i i ) (ii)
Use that the matrix of the band operator B B B B [11 , 13 ] even apply to tridiagonal matrices with operator entries – hence to block-tridiagonal matrices.
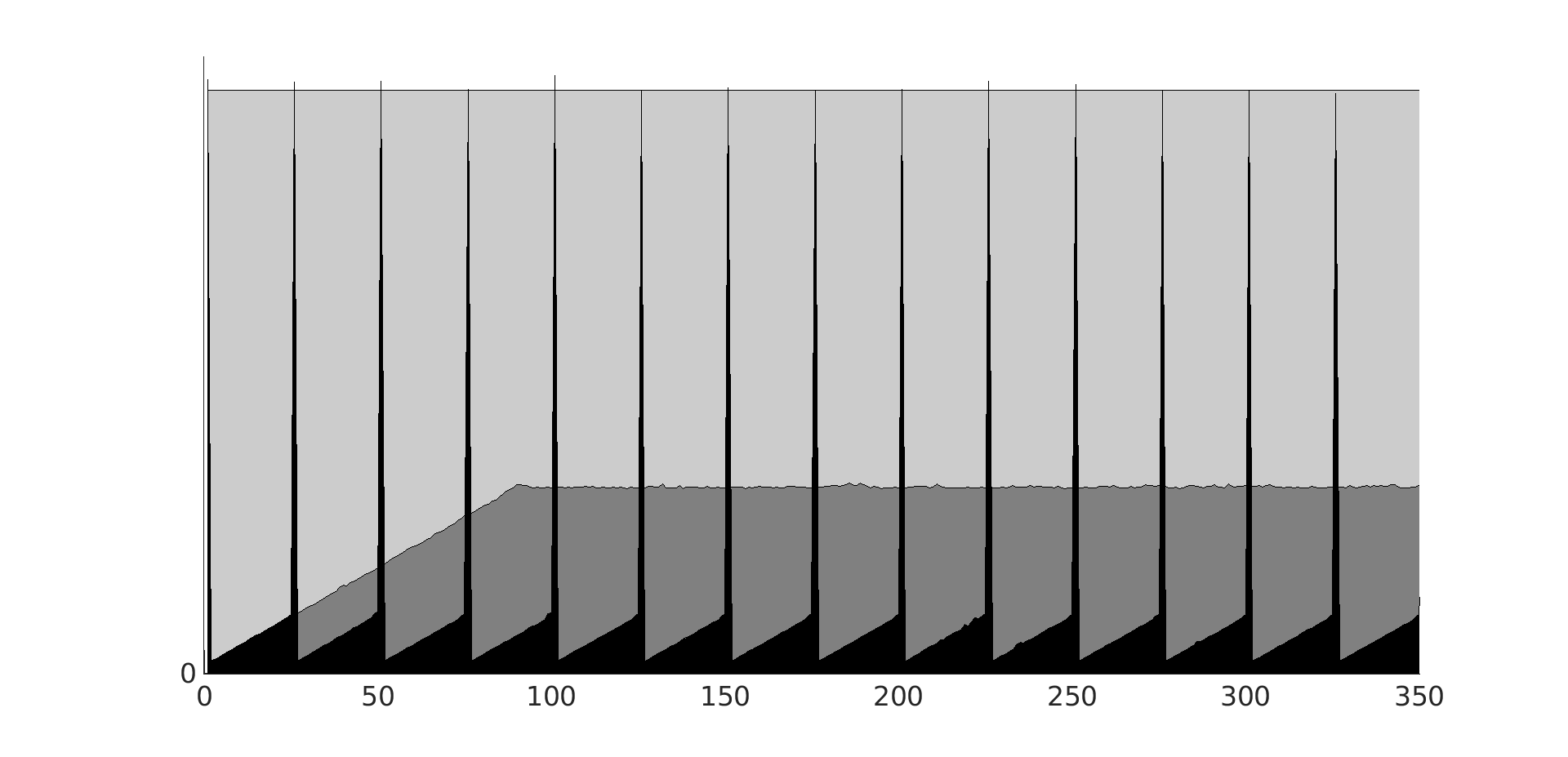
Figure 1.1: Left: A banded matrix (support shown in gray) is turned into block-tridiagonal form with blocks of according size. Right: The dotted blocks equally do the job of turning the banded matrix into block-tridiagonal form. There are b b b × b b\times b
We discuss further details of steps ( i ) (i) ( i i ) (ii) 2
Approximating pseudospectra of band-dominated operators.
From (1
Inequality (3 A ∗ A^{*}
min ( ν ( A ) , ν ( A ∗ ) ) ≤ inf k ∈ ℤ min ( ν ( A | ℓ 2 ( J k n ) ) , ν ( A ∗ | ℓ 2 ( J k n ) ) ) ≤ min ( ν ( A ) , ν ( A ∗ ) ) + δ , \min(\nu(A),\nu(A^{*}))\ \leq\ \inf_{k\in{\mathbb{Z}}}\min\!\big{(}\nu(A|_{\ell^{2}(J^{n}_{k})}),\nu(A^{*}|_{\ell^{2}(J^{n}_{k})})\big{)}\ \leq\ \min(\nu(A),\nu(A^{*}))+\delta,
from which we conclude the implications
inf k ∈ ℤ min ( ν ( A | ℓ 2 ( J k n ) ) , ν ( A ∗ | ℓ 2 ( J k n ) ) ) < ε \displaystyle\inf_{k\in{\mathbb{Z}}}\min\!\big{(}\nu(A|_{\ell^{2}(J^{n}_{k})}),\nu(A^{*}|_{\ell^{2}(J^{n}_{k})})\big{)}<{\varepsilon}\quad ⇒ min ( ν ( A ) , ν ( A ∗ ) ) < ε \displaystyle\Rightarrow\quad\min(\nu(A),\nu(A^{*}))<{\varepsilon}
⇒ inf k ∈ ℤ min ( ν ( A | ℓ 2 ( J k n ) ) , ν ( A ∗ | ℓ 2 ( J k n ) ) ) < ε + δ \displaystyle\Rightarrow\quad\inf_{k\in{\mathbb{Z}}}\min\!\big{(}\nu(A|_{\ell^{2}(J^{n}_{k})}),\nu(A^{*}|_{\ell^{2}(J^{n}_{k})})\big{)}<{\varepsilon}+\delta
for all ε > 0 {\varepsilon}>0
Γ ε n ( A ) ⊂ spec ε A ⊂ Γ ε + δ n ( A ) , \Gamma^{n}_{\varepsilon}(A)\ \subset\ {\rm spec}_{\varepsilon}A\ \subset\ \Gamma^{n}_{{\varepsilon}+\delta}(A), (6)
where
Γ ε n ( A ) := ⋃ k ∈ ℤ { λ ∈ ℂ : min ( ν ( ( A − λ I ) | ℓ 2 ( J k n ) ) , ν ( ( A − λ I ) ∗ | ℓ 2 ( J k n ) ) ) < ε } . \Gamma^{n}_{\varepsilon}(A)\ :=\ \bigcup_{k\in{\mathbb{Z}}}\left\{\lambda\in{\mathbb{C}}:\min\!\big{(}\nu((A-\lambda I)|_{\ell^{2}(J^{n}_{k})}),\nu((A-\lambda I)^{*}|_{\ell^{2}(J^{n}_{k})})\big{)}<{\varepsilon}\right\}. (7)
Concerning the approximation step ( i ) (i) 5
ν ( B ) < ε − η ⇒ ν ( A ) < ε ⇒ ν ( B ) < ε + η , \nu(B)<{\varepsilon}-\eta\qquad\Rightarrow\qquad\nu(A)<{\varepsilon}\qquad\Rightarrow\qquad\nu(B)<{\varepsilon}+\eta,
and the same holds for the adjoints. Subtracting λ I \lambda I A A B B 1
spec ε − η B ⊂ spec ε A ⊂ spec ε + η B , 0 < η < ε , {\rm spec}_{{\varepsilon}-\eta}B\ \subset\ {\rm spec}_{\varepsilon}A\ \subset\ {\rm spec}_{{\varepsilon}+\eta}B,\qquad 0<\eta<{\varepsilon}, (8)
so that upper and lower bounds on certain pseudospectra of B B spec ε A {\rm spec}_{\varepsilon}A 8 η → 0 \eta\to 0
Existing results.
The probably most natural idea to approximate spec ε A {\rm spec}_{\varepsilon}A spec ε A n {\rm spec}_{\varepsilon}A_{n} A n = ( a i j ) i , j = − n n A_{n}=(a_{ij})_{i,j=-n}^{n} A = ( a i j ) i , j ∈ ℤ A=(a_{ij})_{i,j\in{\mathbb{Z}}} n → ∞ n\to\infty [24 , 8 ] , random Jacobi operators
[12 ] ), the sets spec ε A n {\rm spec}_{\varepsilon}A_{n} spec ε A {\rm spec}_{\varepsilon}A spec ε A n {\rm spec}_{\varepsilon}A_{n} spec ε A {\rm spec}_{\varepsilon}A [27 ] , one speaks of spectral pollution).
Even in a simple selfadjoint example such as A = diag ( … , B , B , B , … ) A={\rm diag}(...,B,B,B,...) B = ( 0 1 1 0 ) B={0~1\choose 1~0} spec A = { − 1 , 1 } {\rm spec}\,A=\{-1,1\} spec A n {\rm spec}\,A_{n} { − 1 , 1 } \{-1,1\} { − 1 , 0 , 1 } \{-1,0,1\} n n [17 , 26 ] study
so-called ( N , ε ) (N,{\varepsilon}) 2 N 2^{N} 1 / ε 1/{\varepsilon} [5 ]
the lower norms of rectangular submatrices are suggested for the approximation of the spectrum and the ( N , ε ) (N,{\varepsilon}) [1 , 14 ] and the references therein).
One major problem in approximating ℤ {\mathbb{Z}} { − n , … , n } \{-n,...,n\} n n A A { − n , … , n } \{-n,...,n\} [11 ] (also see §3 and 4 in [13 ] ) – that is very much in the spirit of Gershgorin and that we adopt here – replaces { − n , … , n } \{-n,...,n\} n → ∞ n\to\infty J k n = { k + 1 , … , k + n } J_{k}^{n}=\{k+1,...,k+n\} k ∈ ℤ k\in{\mathbb{Z}} n n k k [11 ] approach is that it comes with sharp and explicit bounds (4 6
What is new here?
The tridiagonal results and the ideas of transferring them to band-dominated operators via ( i ) (i) ( i i ) (ii) [11 ] , therefore not new. But there are two degrees of freedom in the choice of the blocks in step ( i i ) (ii) b ∈ ℕ b\in{\mathbb{N}} d ∈ ℕ d\in{\mathbb{N}} b b b b 1.1
We play with that second degree of freedom, arguing that there is usually no best choice (in terms of sharpness of (6 b b spec ε A {\rm spec}_{\varepsilon}A b b b b b b ν ( A | ℓ 2 ( J k n ) ) \nu(A|_{\ell^{2}(J^{n}_{k})}) ν ( A | ℓ 2 ( J k + 1 n ) ) \nu(A|_{\ell^{2}(J^{n}_{k+1})}) A | ℓ 2 ( J k n ) A|_{\ell^{2}(J^{n}_{k})} A | ℓ 2 ( J k + 1 n ) A|_{\ell^{2}(J^{n}_{k+1})} b b ν ( A | ℓ 2 ( J k n ) ) \nu(A|_{\ell^{2}(J^{n}_{k})}) ν ( A | ℓ 2 ( J k + b n ) ) \nu(A|_{\ell^{2}(J^{n}_{k+b})})
In a nutshell, the smallest singular value of A | ℓ 2 ( J k n ) A|_{\ell^{2}(J^{n}_{k})} R k R_{k} A | ℓ 2 ( J k n ) = Q k R k A|_{\ell^{2}(J^{n}_{k})}=Q_{k}R_{k} Q k Q_{k} k k k + 1 k+1 ν ( A | ℓ 2 ( J k + 1 n ) ) = ν ( R k + 1 ) \nu(A|_{\ell^{2}(J^{n}_{k+1})})=\nu(R_{k+1}) 𝒪 ( n d 2 ) {\mathcal{O}}(nd^{2}) 𝒪 ( n d ) {\mathcal{O}}(nd) b ≈ d b\approx d ν ( A | ℓ 2 ( J k + 2 n ) ) , ν ( A | ℓ 2 ( J k + 3 n ) ) \nu(A|_{\ell^{2}(J^{n}_{k+2})}),\nu(A|_{\ell^{2}(J^{n}_{k+3})})
Contents of the paper.
In Section 2 ( i ) (i) ( i i ) (ii) 3 ν ( A | ℓ 2 ( J k + 1 n ) ) \nu(A|_{\ell^{2}(J^{n}_{k+1})}) ν ( A | ℓ 2 ( J k n ) ) \nu(A|_{\ell^{2}(J^{n}_{k})}) 4
3 The Algorithm
To simplify notation abbreviate, for k ∈ ℤ , n ∈ ℕ k\in{\mathbb{Z}},n\in{\mathbb{N}} λ ∈ ℂ \lambda\in{\mathbb{C}}
A λ k := ( A − λ I ) | ℓ 2 ( J k n ) : ℓ 2 ( J k n ) → ℓ 2 ( J k − d n + 2 d ) ≅ ≅ ℂ n ℂ n + 2 d \displaystyle\begin{array}[]{cccc}A^{k}_{\lambda}:=(A-\lambda I)|_{\ell^{2}(J^{n}_{k})}:&\ell^{2}(J^{n}_{k})&\rightarrow&\ell^{2}(J_{k-d}^{n+2d})\\
&\cong&&\cong\\
&{\mathbb{C}}^{n}&&{\mathbb{C}}^{n+2d}\end{array}
and treat A λ k A^{k}_{\lambda} A ¯ λ k := ( A − λ I ) ∗ | ℓ 2 ( J k n ) \overline{A}^{k}_{\lambda}:=(A-\lambda I)^{*}|_{\ell^{2}(J^{n}_{k})} ν ( A λ k ) \nu(A^{k}_{\lambda}) ν ( A ¯ λ k ) \nu(\overline{A}^{k}_{\lambda}) λ ∈ ℂ \lambda\in{\mathbb{C}} k k σ n ( A λ k ) \sigma_{n}(A^{k}_{\lambda}) σ n ( A ¯ λ k ) \sigma_{n}(\overline{A}^{k}_{\lambda}) [31 ] ) and similar computational problems arise.
A λ k A^{k}_{\lambda} A 0 k A^{k}_{0} A 0 k A^{k}_{0} λ \lambda σ n ( A λ k ) \sigma_{n}(A^{k}_{\lambda}) λ ∈ ℂ \lambda\in{\mathbb{C}} [9 ] on ( A λ k ) − 1 (A_{\lambda}^{k})^{-1} A 0 k A_{0}^{k} λ ∈ ℂ \lambda\in{\mathbb{C}} ( A λ k ) k (A^{k}_{\lambda})_{k} ( A ¯ λ k ) k (\overline{A}^{k}_{\lambda})_{k} λ ∈ ℂ \lambda\in{\mathbb{C}} n ∈ ℕ n\in{\mathbb{N}} A k := A λ k ∈ ℂ ( n + 2 d ) × n A^{k}:=A^{k}_{\lambda}\in{\mathbb{C}}^{(n+2d)\times n} k ∈ ℤ k\in{\mathbb{Z}} A k 0 + 1 , A k 0 + 2 , … , A k 0 + k max A^{k_{0}+1},A^{k_{0}+2},\ldots,A^{k_{0}+k_{\max}} 14 k 0 = 0 k_{0}=0
A i , j k = A i − 1 , j − 1 k + 1 , for all { 1 ≤ k ≤ k max − 1 2 ≤ i ≤ n + 2 d = : m 2 ≤ j ≤ n . A^{k}_{i,j}=A^{k+1}_{i-1,j-1},\;\text{for all }\left\{\begin{array}[]{l}1\leq k\leq k_{\max}-1\\
2\leq i\leq n+2d=:m\\
2\leq j\leq n.\end{array}\right. (18)
Since ν ( A k ) = σ n ( A k ) \nu(A^{k})=\sigma_{n}(A^{k})
{ σ n ( A k ) } 1 ≤ k ≤ k max , \displaystyle\{\sigma_{n}(A^{k})\}_{1\leq k\leq k_{\max}},
where σ n \sigma_{n}
Q k A k = R k = ( R ~ k 0 ) , with R ~ k ∈ ℂ n × n upper triangular , Q k ∈ ℂ m × m unitary \displaystyle Q^{k}A^{k}=R^{k}=\left(\begin{array}[]{c}{\tilde{R}}^{k}\\
\textbf{0}\end{array}\right),\text{ with }\tilde{R}^{k}\in{\mathbb{C}}^{n\times n}\text{ upper triangular},Q^{k}\in{\mathbb{C}}^{m\times m}\text{ unitary} (21)
and applying an inverse Golub-Kahan-Lanczos-Bidiagonalization method ([2 , 15 ] ), from now on abbreviated as GKLB method, to R ~ k \tilde{R}^{k} ( R ~ k ) − 1 {(\tilde{R}^{k})}^{-1} A k A^{k} R ~ k \tilde{R}^{k} R ~ k \tilde{R}^{k} Q k A k = R k Q^{k}A^{k}=R^{k} ( Q k ) H A k = R k (Q^{k})^{H}A^{k}=R^{k} A k A^{k} R ~ k \tilde{R}^{k} R ~ k \tilde{R}^{k} 2 d + 1 2d+1 R ~ k \tilde{R}^{k} 𝒪 ( n d ) {\mathcal{O}}(nd) 21 𝒪 ( n d 2 ) {\mathcal{O}}(nd^{2}) d d Q 1 A 1 = H 1 Q^{1}A^{1}=H^{1} H 1 ∈ ℂ m × n H^{1}\in{\mathbb{C}}^{m\times n} 2 d + 1 2d+1 A 2 , A 3 , … A^{2},A^{3},\ldots A 1 , A 2 , … A^{1},A^{2},\ldots n n 21 A 2 , A 3 , … A^{2},A^{3},\ldots 𝒪 ( n d ) {\mathcal{O}}(nd) 𝒪 ( n d 2 ) {\mathcal{O}}(nd^{2})
Preliminaries.
We will only use Givens rotations acting on consecutive rows and define a rotation on the i i ( i + 1 ) (i+1)
G i : 𝔻 ¯ × 𝔻 ¯ → ℂ m × m ( c , s ) ↦ G i ( c , s ) . \displaystyle\begin{array}[]{llll}G_{i}:&\overline{{\mathbb{D}}}\times\overline{{\mathbb{D}}}&\rightarrow&{\mathbb{C}}^{m\times m}\\
&(c,s)&\mapsto&G_{i}(c,s).\end{array}
and
G i ( c , s ) = i i + 1 ( 1 ⋯ 0 0 ⋯ 0 ) ⋮ ⋱ ⋮ ⋮ ⋮ i 0 ⋯ c s ⋯ 0 i + 1 0 ⋯ − s ¯ c ¯ ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 ⋯ 0 0 ⋯ 1 \displaystyle G_{i}(c,s)=\bordermatrix{&&&i&i+1&&\cr&1&\cdots&0&0&\cdots&0\cr&\vdots&\ddots&\vdots&\vdots&&\vdots\cr i&0&\cdots&c&s&\cdots&0\cr i+1&0&\cdots&-\overline{s}&\overline{c}&\cdots&0\cr&\vdots&&\vdots&\vdots&\ddots&\vdots\cr&0&\cdots&0&0&\cdots&1}
where 𝔻 ¯ := { z ∈ ℂ : | z | ≤ 1 } \overline{{\mathbb{D}}}:=\{z\in{\mathbb{C}}:\,\left|z\right|\leq 1\} c , s c,s [15 , 29 ] .
To simplify notation we will, in most cases, write G i ≡ G i ( c , s ) G_{i}\equiv G_{i}(c,s) c , s c,s c , s c,s [29 , 30 ] :
1 ↱ 2 ↱ ↱ 3 ↱ ↱ 4 ↱ ↱ 5 ↱ 4 3 2 1 \displaystyle\begin{array}[]{c@{\hspace{1mm}}|c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}1\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
2\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
3\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
4\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
5\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\cline{1-5}\cr\hfil\hskip 2.84526pt&4\hfil\hskip 2.84526pt&3\hfil\hskip 2.84526pt&2\hfil\hskip 2.84526pt&1\hfil\hskip 2.84526pt\end{array} (28)
The arrows in (28 28 G 4 G 3 G 2 G 1 G_{4}G_{3}G_{2}G_{1}
↱ ↱ ↱ ↱ [ × × × × × × × × ] = ↱ ↱ ↱ ↱ [ × × × × × × × × ] , but ↱ ↱ ↱ ↱ [ × × × × × × × × ] ≠ ↱ ↱ ↱ ↱ [ × × × × × × × × ] \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right],\text{ but }\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\neq\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right] (61)
We say that a product G i 1 , G i 2 , … , G i l G_{i_{1}},G_{i_{2}},\ldots,G_{i_{l}} descending , respectively ascending , sequence of Givens rotations of length l l i p + 1 = i p − 1 i_{p+1}=i_{p}-1 i p + 1 = i p + 1 i_{p+1}=i_{p}+1 p = 1 , … , l − 1 p=1,\ldots,l-1 28 4 4
Example 3.1
The following Givens rotations can be written as a product of 3 3 4 4 4 4 3 3
( G 4 G 3 G 2 G 1 ) ( G 5 G 4 G 3 G 2 ) ( G 6 G 5 G 4 G 3 ) = \displaystyle(G_{4}G_{3}G_{2}G_{1})(G_{5}G_{4}G_{3}G_{2})(G_{6}G_{5}G_{4}G_{3})= ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ⏟ ( ∗ ) \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}};{2pt/2pt}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}};{2pt/2pt}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&&\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\end{array}=\underbrace{\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}}_{(*)}
= ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = \displaystyle=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}};{2pt/2pt}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}};{2pt/2pt}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}};{2pt/2pt}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&&&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}&&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&&&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&&&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}= ( G 4 G 5 G 6 ) ( G 3 G 4 G 5 ) ( G 2 G 3 G 4 ) ( G 1 G 2 G 3 ) \displaystyle(G_{4}G_{5}G_{6})(G_{3}G_{4}G_{5})(G_{2}G_{3}G_{4})(G_{1}G_{2}G_{3})
Note that the rotations can be written in this compact form since the order of rotations that are in the same column of ( ∗ ) (*) 61 n = 7 n=7 d = 2 d=2 ℂ 11 × 7 {\mathbb{C}}^{11\times 7} { A k } 1 ≤ k ≤ k max \{A^{k}\}_{1\leq k\leq k_{\max}}
Step 1:
We start the first step by computing a QH factorization of A 1 A^{1} 2 d 2d 2 d − 1 2d-1
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 0 ] \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\end{array}\right] (95)
⇓ \displaystyle\Downarrow
Q 1 A 1 = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle Q^{1}A^{1}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × 0 0 0 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] = H 1 . \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\end{array}\right]=H^{1}. (129)
Notice that, since the right hand side is of Hessenberg form, no rotations acting on the first row are required and the first row of Q 1 Q^{1} e 1 T e_{1}^{T} Q 1 Q^{1}
Q 1 = ( 1 0 0 Q ~ 1 ) , Q ~ 1 ∈ ℂ m − 1 × m − 1 \displaystyle Q^{1}=\left(\begin{array}[]{cc}1&\textbf{0}\\
\textbf{0}&\tilde{Q}^{1}\end{array}\right),\;\;\tilde{Q}^{1}\in{\mathbb{C}}^{m-1\times m-1} (132)
The computational effort of this step consists of the computation and application of n ( 2 d − 1 ) n(2d-1) 𝒪 ( n d 2 ) {\mathcal{O}}(nd^{2}) n n H 1 H^{1} 𝒪 ( n d ) {\mathcal{O}}(nd)
Step 2 :
Since A 1 A^{1} A 2 A^{2} A 2 A^{2} A 1 A^{1} 18
C p := ( 0 I p − 1 1 0 ) : ( x 1 ⋮ x p − 1 x p ) ↦ ( x 2 ⋮ x p x 1 ) \displaystyle C_{p}:=\left(\begin{array}[]{cc}\textbf{0}&I_{p-1}\\
1&\textbf{0}\end{array}\right):\left(\begin{array}[]{c}x_{1}\\
\vdots\\
x_{p-1}\\
x_{p}\end{array}\right)\mapsto\left(\begin{array}[]{c}x_{2}\\
\vdots\\
x_{p}\\
x_{1}\end{array}\right)
denote the circulant backward shift of size p p A ^ 2 := C m A 1 C n − 1 \hat{A}^{2}:=C_{m}A^{1}C_{n}^{-1} A 2 A^{2} n − 1 n-1 18 A 1 → A ^ 2 → A 2 A^{1}\rightarrow\hat{A}^{2}\rightarrow A^{2} − - + +
[ − 0 0 0 0 0 0 − × 0 0 0 0 0 − × × 0 0 0 0 − × × × 0 0 0 − × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] ⏟ = A 1 → [ × 0 0 0 0 0 − × × 0 0 0 0 − × × × 0 0 0 − × × × × 0 0 − × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 0 − ] ⏟ = A ^ 2 → [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × + 0 0 0 × × × + 0 0 0 0 × × + 0 0 0 0 0 × + 0 0 0 0 0 0 + ] ⏟ = A 2 \displaystyle\underbrace{\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}-\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
-\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
-\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
-\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
-\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]}_{=A^{1}}\rightarrow\underbrace{\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&-\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&-\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&-\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&-\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&-\hfil\hskip 2.84526pt\end{array}\right]}_{=\hat{A}^{2}}\rightarrow\underbrace{\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\end{array}\right]}_{=A^{2}}
We apply the same transformation to the factorization Q 1 A 1 = H 1 Q^{1}A^{1}=H^{1}
Q 1 A 1 = H 1 ⇒ C m Q 1 C m − 1 ⏟ = : Q ^ 2 C m A 1 C n − 1 ⏟ = A ^ 2 = C m H 1 C n − 1 ⏟ = : H ^ 2 . \displaystyle Q^{1}A^{1}=H^{1}\Rightarrow\underbrace{C_{m}Q^{1}C_{m}^{-1}}_{=:\hat{Q}^{2}}\underbrace{C_{m}A^{1}C_{n}^{-1}}_{=\hat{A}^{2}}=\underbrace{C_{m}H^{1}C_{n}^{-1}}_{=:\hat{H}^{2}}. (133)
Notice that Q ^ 2 \hat{Q}^{2}
Q ^ 2 = C m Q 1 C m − 1 = C m ( 1 0 0 Q ~ 1 ) C m − 1 = ( Q ~ 1 0 0 1 ) . \displaystyle\hat{Q}^{2}=C_{m}Q^{1}C_{m}^{-1}=C_{m}\left(\begin{array}[]{cc}1&\textbf{0}\\
\textbf{0}&\tilde{Q}^{1}\end{array}\right)C_{m}^{-1}=\left(\begin{array}[]{cc}\tilde{Q}^{1}&\textbf{0}\\
\textbf{0}&1\end{array}\right).
The matrix Q ^ 2 \hat{Q}^{2} 133
Q ^ 2 A ^ 2 = ( Q ~ 1 0 0 1 ) ⋅ ( | | | a ^ 1 2 ⋯ a ^ n − 1 2 a ^ n 2 | | | 0 ⋯ 0 a ^ n , n 2 ) = ( | | | Q ~ 1 a ^ 1 2 ⋯ Q ~ 1 a ^ n − 1 2 Q ~ 1 a ^ n 2 | | | 0 ⋯ 0 a ^ n , n 2 ) = H ^ 2 , \displaystyle\hat{Q}^{2}\hat{A}^{2}=\left(\begin{array}[]{c|c}\tilde{Q}^{1}&\textbf{0}\\
\hline\cr\textbf{0}&1\end{array}\right)\cdot\left(\begin{array}[]{clc|c}|&&|&|\\
\hat{a}^{2}_{1}&\cdots&\hat{a}^{2}_{n-1}&\hat{a}^{2}_{n}\\
|&&|&|\\
\hline\cr 0&\cdots&0&\hat{a}^{2}_{n,n}\end{array}\right)=\left(\begin{array}[]{clc|c}|&&|&|\\
\tilde{Q}^{1}\hat{a}^{2}_{1}&\cdots&\tilde{Q}^{1}\hat{a}^{2}_{n-1}&\tilde{Q}^{1}\hat{a}^{2}_{n}\\
|&&|&|\\
\hline\cr 0&\cdots&0&\hat{a}^{2}_{n,n}\end{array}\right)=\hat{H}^{2}, (144)
where a ^ i 2 \hat{a}^{2}_{i} i i A ^ 2 \hat{A}^{2} 133 H ^ 2 \hat{H}^{2} A ^ 2 \hat{A}^{2} A 2 A^{2} 133 144 Q ^ 2 A 2 = : H ~ 2 \hat{Q}^{2}A^{2}=:\tilde{H}^{2} 144 H ^ 2 \hat{H}^{2} H ~ 2 \tilde{H}^{2} A ^ 2 \hat{A}^{2} A 2 A^{2} Q ^ 2 \hat{Q}^{2} A 2 A^{2} 2 d − 1 2d-1 + + Q ^ 2 \hat{Q}^{2} A 2 A^{2}
Q 1 A 1 = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle Q^{1}A^{1}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × 0 0 0 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] = H 1 \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\end{array}\right]=H^{1} (178)
⇓ \displaystyle\Downarrow
Q ^ 2 A 2 = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle\hat{Q}^{2}A^{2}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&{\color[rgb]{.5,.5,.5}\definecolor[named]{pgfstrokecolor}{rgb}{.5,.5,.5}\pgfsys@color@gray@stroke{.5}\pgfsys@color@gray@fill{.5}\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × + 0 0 0 × × × + 0 0 0 0 × × + 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × ] = H ~ 2 \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]=\tilde{H}^{2} (212)
We anticipate that in the next step we would like to apply the same shift again. However, since Q ^ 2 \hat{Q}^{2} 132 Q ^ 2 \hat{Q}^{2} e m T e_{m}^{T} Q ^ 3 \hat{Q}^{3} Q ^ 2 \hat{Q}^{2} 212 ( n − 1 ) (n-1) 𝒪 ( n d ) {\mathcal{O}}(nd) 212 + +
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × 0 0 0 0 0 0 × × × × 0 0 0 + × × × × 0 0 0 + × × × × 0 0 0 + × × × × 0 0 0 + × × × 0 0 0 0 + × × 0 0 0 0 0 + × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × ] . \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&+\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right].
Now we remove the second subdiagonal on the right hand side by adding a descending sequence of Givens rotations from the left:
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad= [ × 0 0 0 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × ] . \displaystyle\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]. (246)
Finally we can reduce the last column of the right hand side thus bringing it into Hessenberg-form. This can be achieved using an ascending sequence of Givens rotations of length 2 d − 1 2d-1
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ⏟ = : Q 2 [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = [ × 0 0 0 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] ⏟ = : H 2 \displaystyle\underbrace{\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}}_{=:Q^{2}}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad=\quad\underbrace{\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\end{array}\right]}_{=:H^{2}} (280)
Notice, that Q 2 Q^{2} 280 Q 1 Q^{1} 129
Step 3:
We start as we have in the second step by shifting the factorization Q 2 A 2 = H 2 Q^{2}A^{2}=H^{2} 212
Q ^ 3 A 3 = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ [ × 0 0 0 0 0 0 × × 0 0 0 0 0 × × × 0 0 0 0 × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × ] = [ × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × × 0 0 0 × × × × 0 0 0 0 × × × 0 0 0 0 0 × × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × 0 0 0 0 0 0 × ] = H ~ 3 \displaystyle\hat{Q}^{3}A^{3}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]\quad=\quad\left[\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\\[-1.42271pt]
0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&0\hfil\hskip 2.84526pt&\times\hfil\hskip 2.84526pt\end{array}\right]=\tilde{H}^{3}
Analogous to step 2 we want to remove all Givens rotations acting on the first row so that we can apply the shift again. This time however we have two descending sequences starting in the first row. We could of course remove both outer-most sequences of Givens-rotations and add them again starting in the second row, but in our illustrative example this would already cost more than simply restarting an entire factorization from scratch. One may argue that for higher values d d 3 3 2 d − 1 2d-1 3.2
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ → ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ , \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}\rightarrow\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}, (303)
i.e. all but one Givens rotation acting on the first row has been moved to the end of the outer-most sequence. Note, that when applying Theorem 3.2 ( c , s ) (c,s) 𝒪 ( n ) {\mathcal{O}}(n)
Step 𝟒 , … , 𝟐 d 4,\ldots,2d :
We repeat the procedure applied in step 3 3 3.2 3 3 3.2 2 d − 1 2d-1 3.2 𝒪 ( n d ) {\mathcal{O}}(nd)
Step 𝟐 d + 𝟏 , … , k 𝐦𝐚𝐱 2d+1,\ldots,k_{\max} :
From now on the entire procedure simply repeats itself.
The whole procedure is summarized in Algorithm 1
Input: A sequence of
d d -banded consecutive matrices
{ A k } k = 1 , … , k max \{A^{k}\}_{k=1,\ldots,k_{\max}} as in (
18 )
Output: A sequence of upper triangular matrices
{ R k } k = 1 , … , k max \{R^{k}\}_{k=1,\ldots,k_{\max}} with bandwidth
d d
1
First step: Compute QH factorization
Q 1 A 1 = H 1 Q^{1}A^{1}=H^{1} using
2 d − 1 2d-1 sequences of Givens rotations as in (
129 );
2
Compute QR factorization
G 1 Q 1 A 1 = R 1 {G}^{1}Q^{1}A^{1}=R^{1} using one more sequence of Givens rotations;
3
for k = 2 , … , k max k=2,\ldots,k_{\max} do
4
Shift factorization
Q k − 1 A k − 1 = H k − 1 → Q ^ k A k = H ~ k Q^{k-1}A^{k-1}=H^{k-1}\rightarrow\hat{Q}^{k}A^{k}=\tilde{H}^{k} as in (
212 );
5
Move rotations acting on the first row to the left-most sequence as in Theorem
3.2 ;
6
Remove the last rotation acting on the first row by replacing the left-most sequence as in (
246 );
7
Bring
H ^ k \hat{H}^{k} to Hessenberg form by removing
2 d − 1 2d-1 entries in the last column as in (
280 );
8
Compute QR factorization
G k Q k A k = R k {G}^{k}Q^{k}A^{k}=R^{k} ;
9
10 end for
Algorithm 1
The reordering of Givens rotations applied in (303
Theorem 3.2
Let l , s , m ∈ ℕ l,s,m\in{\mathbb{N}} l + s ≤ m l+s\leq m
Q = ( G l G l − 1 ⋯ G 1 ) ( G l + 1 G l ⋯ G 1 ) ⋯ ( G l + s − 1 G l + s − 2 ⋯ G 1 ) ∈ ℂ m × m \displaystyle Q=(G_{l}G_{l-1}\cdots G_{1})(G_{l+1}G_{l}\cdots G_{1})\cdots(G_{l+s-1}G_{l+s-2}\cdots G_{1})\in{\mathbb{C}}^{m\times m}
be a product of s s Q Q s s
Q = ( G l + s − 1 G l + s − 2 ⋯ G 1 ) ( G l + 1 G l ⋯ G 2 ) ( G l + 2 G l + 1 ⋯ G 2 ) ⋯ ( G l + s − 1 G l + s − 2 ⋯ G 2 ) \displaystyle Q=(G_{l+s-1}G_{l+s-2}\cdots G_{1})(G_{l+1}G_{l}\cdots G_{2})(G_{l+2}G_{l+1}\cdots G_{2})\cdots(G_{l+s-1}G_{l+s-2}\cdots G_{2})
Q = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ \displaystyle Q=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}
Proof.
We start by noting the so-called shift-through lemma of [29 ] (see Lemma 9.38 there), which states that a product of 3 3 G 2 G 1 G 2 G_{2}G_{1}G_{2} 3 3 G 1 G 2 G 1 G_{1}G_{2}G_{1}
Q = ↱ ↱ ↱ ↱ ↱ ↱ = ↱ ↱ ↱ ↱ ↱ ↱ . \displaystyle Q=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\end{array}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}.
Of course the values c , s c,s
Q = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ . \displaystyle Q=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}.
As described in [3 ] a repeated application of this lemma to 2 2 ( G l G l − 1 ⋯ G 1 ) ( G l + 1 G l ⋯ G 1 ) (G_{l}G_{l-1}\cdots G_{1})(G_{l+1}G_{l}\cdots G_{1}) shift-through lemma of higher length :
( G l ⋯ G 1 ) ( G l + 1 ⋯ G 1 ) = \displaystyle(G_{l}\cdots G_{1})(G_{l+1}\cdots G_{1})= ( G l + 1 ⋯ G 1 ) ( G l + 1 ⋯ G 2 ) \displaystyle(G_{l+1}\cdots G_{1})(G_{l+1}\cdots G_{2})
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}= ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = ⋯ = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}=\cdots=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}
Figuratively speaking we have moved the rotation from the top right to the lower left. If the right sequence is of higher length than the left sequence, the additional Givens rotations will be added to the left sequence in the end, i.e.
( G l G l − 1 ⋯ G 1 ) ( G l + t G l + t − 1 ⋯ G 1 ) = \displaystyle(G_{l}G_{l-1}\cdots G_{1})(G_{l+t}G_{l+t-1}\cdots G_{1})= ( G l + t G l + t − 1 ⋯ G 1 ) ( G l + 1 G l ⋯ G 2 ) \displaystyle(G_{l+t}G_{l+t-1}\cdots G_{1})(G_{l+1}G_{l}\cdots G_{2})
↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ = \displaystyle\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}= ⋯ = ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ ↱ \displaystyle\cdots=\begin{array}[]{c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}c@{\hspace{1mm}}
c@{\hspace{1mm}}c@{\hspace{1mm}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\\[-1.42271pt]
\hfil\hskip 2.84526pt&\raisebox{3.1298pt}[2.84544pt][0.0pt]{\mbox{\rotatebox[origin={c}]{180.0}{\reflectbox{\raisebox{-3.1298pt}[2.84544pt][0.0pt]{\mbox{$\Rsh$}}}}}}\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt&\hfil\hskip 2.84526pt\end{array}
The theorem follows directly from applying the shift-through-lemma of higher length pairwise s − 1 s-1
step time 1 1 2 d 2d k max k_{\max} Figure 3.1: QH-Shift Algorithm without reset: Time per step
As stated before, the number of descending Givens sequences to which Theorem 3.2 1 2 d 2d 3.1 r r r ∈ { 2 , … , 2 d } r\in\{2,...,2d\} 2 , … , r 2,...,r 3.2 r r 4.2
step time 1 1 k max k_{\max} Figure 3.2: QH-Shift Algorithm with one restart after r = 9 r=9