Reduced kinetic model of polyatomic gases
Abstract
Kinetic models of polyatomic gas typically account for the internal degrees of freedom at the level of the two-particle distribution function. However, close to the hydrodynamic limit, the internal (rotational) degrees of freedom tend to be well represented just by rotational kinetic energy density. We account for the rotational energy by augmenting the Ellipsoidal-statistical BGK (ES–BGK) model, an extension of the Bhatnagar–Gross–Krook (BGK) model, at the level of the single-particle distribution function with an advection-diffusion-relaxation equation for the rotational energy. This reduced model respects the theorem and recovers the compressible hydrodynamics for polyatomic gases as its macroscopic limit. As required for a polyatomic gas model, this extension of the ES–BGK model has not only correct specific heat ratio but also allows for three independent tunable transport coefficients: thermal conductivity, shear viscosity, and bulk viscosity. We illustrate the effectiveness of the model via a lattice Boltzmann method implementation.
1 Introduction
The dynamics of a dilute monoatomic gas in terms of the single-particle distribution function is described by the Boltzmann equation (Chapman & Cowling, 1970; Cercignani, 1988). Unlike the continuum Navier–Stokes–Fourier hydrodynamics equation, the Boltzmann equation is a valid description even at highly non-equilibrium states (Mott-Smith, 1951; Liepmann et al., 1962; Cercignani, 1988), encountered in the presence of strong shock waves at high Mach number (ratio of flow speed to sound speed) and in a highly rarefied flow characterized by a large Knudsen number (ratio of the mean free path to characteristic length scale) (Oh et al., 1997; Struchtrup, 2004; Ansumali et al., 2007b). However, any analysis of the integro-differential Boltzmann equation is a formidable task even for the simplest problems. Thus, one often models the Boltzmann dynamics via a simplified collision term that converts the evolution equation to a partial differential equation (Bhatnagar et al., 1954; Lebowitz et al., 1960; Holway Jr, 1966; Shakhov, 1968; Gorban & Karlin, 1994; Levermore, 1996; Andries et al., 2000; Ansumali et al., 2007a; Lebowitz et al., 1960; Singh & Ansumali, 2015; Agrawal et al., 2020). An important example is the BGK model (Bhatnagar et al. 1954), which states that the relaxation of the distribution function towards the Maxwell–Boltzmann (MB) form happens in a time scale corresponding to the mean free time with the assumption that every moment of the distribution function relaxes at the same rate. The BGK model is quite successful in replicating qualitative features of the Boltzmann dynamics (collisional invariants, the zero of the collision, H-theorem, conservation laws, etc). However, the BGK model predicts the Prandtl number of the fluid to be unity, while the value predicted by the Boltzmann equation for monoatomic gas is . Thus, several other variations of the collision model such as ES–BGK model (Holway Jr, 1966; Andries et al., 2000), the quasi-equilibrium models (Gorban & Karlin, 1994; Levermore, 1996), the Shakhov model (Shakhov, 1968), and the Fokker-Plank model (Singh & Ansumali, 2015; Singh et al., 2016) are used as kinetic models with tunable Prandtl number. The ES–BGK model (Holway Jr, 1966; Andries et al., 2000) is an elegant but simple improvement over the BGK model. This model assumes that the distribution function relaxes to an anisotropic Gaussian distribution within mean free time . The anisotropic Gaussian in itself evolves towards the MB distribution with a second time scale. The presence of a second time scale as free parameter ensures that the time scales related to momentum and thermal diffusivity are independent and thus permits one to vary the Prandtl number in the range of to .
Despite their success, the Boltzmann collision kernel and its aforementioned simplifications are limited to monoatomic gases as they do not account for the internal molecular structure. However, many real gases such as nitrogen, oxygen, or methane are polyatomic. At the macroscopic level, the internal molecular structure predominantly manifests in terms of modified specific heat ratio and bulk viscosity , which is crucial for a number of aerodynamic and turbomachinery engineering applications (von Backstrom, 2008; Wu et al., 2015). The specific heat ratio predicted by the Boltzmann equation is that of a monoatomic gas (), whereas that of a diatomic gas is .
Two-particle kinetic theory as an extension of the Boltzmann equation as expected correctly predicts the specific heat ratio for polyatomic gases along with heat conductivity and the bulk viscosity (Wang-Chang & Uhlenbeck, 1951; Wu et al., 2015; Chapman & Cowling, 1970). However, it is often not feasible to do any analysis on the Boltzmann-type equation for polyatomic gases. Therefore, several simplifications to model polyatomic gases have also been proposed. They essentially incorporate the rotational kinetic energy by decomposing the two-particle distribution function into two independent single-particle distribution functions (Morse, 1964; Andries et al., 2000; Tsutahara et al., 2008; Kataoka & Tsutahara, 2004; Watari, 2007; Nie et al., 2008; Larina & Rykov, 2010; Wu et al., 2015; Wang et al., 2017; Bernard et al., 2019). Furthermore, a thermodynamic framework and extensions thereof were developed for modelling highly nonequilibrium phenomena in dense and rarefied polyatomic gases where the Navier–Stokes–Fourier theory is no longer valid (Müller & Ruggeri, 2013; Ruggeri & Sugiyama, 2015; Arima et al., 2012). A few BGK like models have also been proposed for polyatomic gases which accept the Prandtl number as a tunable parameter (Andries et al., 2000; Brull & Schneider, 2009).
Hydrodynamic simulations for a realistic system require the development of reduced-order models to account for rotational degrees of freedom ideally without increasing the phase-space dimensionality. Indeed, the standard approach is to demonstrate that the two-particle distribution function describing the translational and rotational degree of freedom can be approximated by considering two single-particle distribution functions (one each for the translational and rotational degree of freedom) whose dynamics are coupled to each other (Andries et al., 2000). However, recently it was pointed out that a simplified description in terms of single-particle distribution function for the translational degree of freedom and a scalar field variable for rotational kinetic energy is sufficient for modelling the change in specific heat ratio for a dilute diatomic gas in the hydrodynamic limit (Kolluru et al., 2020a). This model supplemented the standard Boltzmann BGK equation with an advection-relaxation equation for the evolution of rotational energy. It preserved the correct conservation laws for diatomic gases in the hydrodynamic limit and satisfied the theorem. However, the model was restricted to diatomic gases and a Prandtl number , limiting its application for heat transfer problems.
We propose a kinetic model of polyatomic gases to tune Prandtl number, specific heat ratio, and bulk viscosity in a physically transparent fashion. To do so, we write a new collision kernel which is a linear combination of the ES–BGK and BGK kernels that are locally relaxing to different temperatures at different timescales. The ratio of the two relaxation timescales is used to tune the Prandtl number. We couple the evolution of the single-particle distribution function (with this modified collision kernel) via an advection-diffusion-relaxation equation for the rotational energy. The rotational contribution to the internal energy alters the specific heat ratio to that of a polyatomic gas and allows to model bulk viscosity contribution arising out of the rotational degree of freedom. Such an extension of the ES–BGK model indeed reproduces the hydrodynamic behaviour of a polyatomic gas and also has a valid theorem. These minimal extensions of the ES–BGK model of monoatomic gas are constructed at a single-particle level for polyatomic gases and are phenomenological by construction. It is commensurate with the top-down modelling approach as developed in the context of the lattice Boltzmann models and aim to be analytically and numerically tractable (Succi, 2001; Ansumali et al., 2007b; Atif et al., 2017). The present model which requires only the solution of an advection-diffusion-relaxation equation along with the Boltzmann ES–BGK equation adds only a minor complexity over analogous monoatomic gas ES–BGK model and can be implemented in the mesoscale framework such as lattice Boltzmann (LB) method quite easily. This approach is distinctly different and is more detailed than the existing approach in the LB models where the effect of rotational degree of freedom is further coarse-grained and the correction needed to model specific heat ratio is directly added as a force term in the BGK collision model (Kataoka & Tsutahara, 2004; Nie et al., 2008; Chen et al., 2010; Huang et al., 2020). In contrast, this model of polyatomic gas enlarges the set of microscopic degrees of freedom and models dynamics of rotational energy in an explicit manner.
The manuscript is organized as follows: A brief kinetic description of monoatomic and polyatomic gases is given in Sections 2 and 3 respectively. In Section 4 we propose an extension to the ES–BGK model for polyatomic gases. The lattice Boltzmann formulation is described in Section 5. The proposed model is numerically validated in Section 6.
2 Kinetic description of a monoatomic gas
The dynamics of dilute monoatomic gases is well-described by the Boltzmann equation in terms of the evolution of the single-particle distribution function , where is the probability of finding a particle within , possessing a velocity in the range at a time . The hydrodynamic variables are density , velocity and total energy . Here onwards, we use a scaled temperature defined in terms of Boltzmann constant and mass of the particle as . The thermodynamic pressure and the scaled temperature are related via the ideal gas equation of state as . These hydrodynamic variables are computed as the moments of the single-particle distribution function
| (1) | ||||
where we define the averaging operator . In the comoving reference frame with fluctuating velocity - , the stress tensor is traceless part of the flux of the momentum tensor and the heat flux is the flux of the energy. Thus,
| (2) |
where the symmetrized traceless part for any second-order tensor is . The stress tensor and heat flux tensor are related to the pressure tensor and energy flux respectively as
| (3) | ||||
We also define third-order moment , with the traceless part and the fourth-order moments divided into contracted part and the trace
| (4) |
| (5) |
In the dilute gas limit, the time evolution of the distribution function is a sequence of free-flight and binary collisions well described by the Boltzmann equation
| (6) | ||||
where the collision kernel models the binary collisions between particles under the assumptions of molecular chaos (Chapman & Cowling, 1970; Cercignani, 1988; McQuarrie, 2000). The nonlinear integro-differential Boltzmann collision kernel is often replaced by simpler models that should recover the following essential features (Cercignani, 1988):
-
(a)
Conservation Laws: As the mass, momentum, and energy density of the particles are conserved during the elastic collision, any collision model must satisfy
(7) Thus, the macroscopic conservation laws obtained by taking appropriate moments (with respect to ) of the Boltzmann equation
(8) are the same as those of the compressible hydrodynamics.
-
(b)
Zero of collision: The collision term is zero if and only if the distribution function attains Maxwell–Boltzmann form, i.e.,
(9) where the Maxwell–Boltzmann distribution is
(10) which ensures that the dynamics is consistent with the equilibrium thermodynamics.
-
(c)
The H Theorem: The Boltzmann equation generalizes the second law of thermodynamics to nonequilibrium situations. Boltzmann defined a nonequilibrium generalization of the entropy known as the function (Cercignani, 1988)
(11) At equilibrium, the thermodynamic entropy is calculated as (Cercignani, 1988)
(12) The evolution of this function is
(13) where is the entropy flux and is the negative of the entropy generation. Boltzmann demonstrated that the entropy generation is positive, hence, the function is nonincreasing in time (Cercignani, 1988). Thus, any consistent approximation for the Boltzmann collision kernel should also satisfy the same condition.
We briefly describe the two most widely used models, the BGK collision model and the ES–BGK model. The Bhatnagar–Gross–Krook (BGK) model, perhaps the simplest and most widely-used model of the Boltzmann collision kernel models the collision as a relaxation of the distribution function towards the equilibrium (Bhatnagar et al., 1954) as
| (14) |
This assumes that the process occurs at a single time scale corresponding to the mean free time. It is trivial to see that this model has the same collisional invariants as the Boltzmann kernel, hence, recovers the same conservation laws (Bhatnagar et al., 1954). The entropy production due to the BGK model is written as
| (15) | ||||
Thus, like the Boltzmann equation, the BGK model also satisfies the theorem. By taking appropriate moments of the Boltzmann BGK equation, we can also see that the evolution of the stress and the heat flux are (Liboff, 2003)
| (16) | ||||
The form of relaxation dynamics shows that the time-scales for the momentum diffusivity and thermal diffusivity are equal for the BGK model. These equations show that, like any equation of Boltzmann type, the dynamics of order moment involves moment and thus form an infinite order moment chain. The hydrodynamic limit is typically analysed via Chapman–Enskog expansion which allows evaluating the dynamic viscosity and thermal conductivity for the model with the specific heat for a monoatomic ideal gas as is (Chapman & Cowling, 1970)
| (17) |
Despite this defect of , the BGK model is extremely successful both as a numerical and an analytical tool for analysis. The ES–BGK model (Holway Jr, 1965) also describes the collision as simple relaxation process but unlike the BGK model, it overcomes the restriction on the Prandtl number. The extra ingredient for ES–BGK model is quasi-equilibrium form of distribution derived by minimizing the H–function (Eq.(11)) under the constraints of an additional condition of fixed stresses, which implies absolute minimization of
| (18) |
The solution to this minimization problem is an anisotropic Gaussian
| (19) |
Like the MB distribution, this has the same conserved moments as that of the single-particle distribution function but this also treats as a conserved variable (Kogan, 1969) i.e.,
| (20) |
On this quasi-equilibrium manifold with stress as variable when the is minimum we have
| (21) |
The ES–BGK model uses the anisotropic Gaussian distribution
| (22) |
where instead of pressure tensor a positive definite matrix
| (23) |
is used with as a free parameter, the range of is dictated by the positive definiteness of . For , is trivially positive as it is a convex combination of two positive definite matrices. The non-trivial range is better understood from the eigenvalue analysis of (Andries et al., 2000). Let the eigenvalues of be and that of positive definite matrix be and thus . In terms of these eigenvalues, the matrix after suitable rotation can be rewritten as
| (24) |
which is a convex combination of diagonal matrices and as
| (25) |
As in the diagonal representation, the non-zero components are the eigenvalues and one obtains the relationship between and as
| (26) | ||||
Thus, the eigenvalues of are non-negative if the range of is restricted to as we also know that . In the ES–BGK model, the collisional relaxation is towards this anisotropic Gaussian distribution which itself attains the form of the Maxwellian at the equilibrium. The collision kernel in explicit form is
| (27) |
where it is evident that corresponds to the limit of the BGK equation and would imply that stress is conserved. For , the model has the same set of conservation laws as the BGK equation. As the stress and heat flux tensors follow the relation
| (28) | ||||
thus, the evolution equations for stress tensor and heat flux are
| (29) | ||||
which shows that the momentum and thermal diffusivities are different in an ES–BGK model and the Prandtl number is a free parameter. In particular, the Chapman-Enskog analysis of this model yields
| (30) |
Thus, the free parameter in the anisotropic Gaussian allows one to vary the Prandtl number from to infinity. At , the Prandtl number predicted by the ES–BGK model is , which matches with the value obtained from the Boltzmann equation, and when , the model is equivalent to the BGK model. The thermal conductivity is fixed only by while the viscosity can be tuned via to obtain the required Prandtl number.
The theorem for this model was first proved by Andries & Perthame (2001) by showing that the entropy production is non-positive. We briefly review the proof of the theorem for the ES-BGK model. The expression for the entropy production is
| (31) |
The proof is built on the property of an arbitrary convex function that
| (32) |
using which we can write
| (33) |
with the last term as in the above equation is non-positive as is by construction the minima of . To prove that , using Eq.(21) we have
| (34) |
Starting from the Brunn-Minkowsky inequality
| (35) |
relating the determinants of two positive matrices and and their convex combinations, we can show that (Horn & Johnson, 2012). This inequality along with Eq.(25) allows us to write
| (36) |
However, from the definitions of , and one can see that
| (37) |
Hence, the total entropy production is non-positive, i.e., .
3 Kinetic description of a polyatomic gas
The rotational degrees of freedom of a polyatomic gas manifest themselves at the continuum level in terms of change in specific heat ratio and a non-zero bulk viscosity due to interaction among the translational component and rotational component of energy. Thus, the rotational degrees of freedom need to be explicitly accounted for in any microscopic or kinetic description. Indeed, typically the kinetic descriptions are in terms of a two-particle distribution function which defines the probability of finding a molecule with a position in the range possessing a velocity in the range with an internal energy due to the additional degrees of freedom (Morse, 1964; Rykov, 1975; Kuščer, 1989). For a polyatomic gas with additional rotational degrees of freedom, the moments of this distribution function give the density, momentum, and total energy (with corresponding to a monoatomic gas)
| (38) | ||||
like its monoatomic counterpart and the operator is defined as
| (39) |
For the reduced-order modeling, the distribution function is often split into two coupled distribution functions and defined as
| (40) | ||||
where is related to the translational energy and with the rotational energy dynamics (Rykov, 1975; Andries et al., 2000). The moments of reduced distribution are then same as the moments of single-particle distribution function
| (41) |
By construction, we have the zeroth moment of as the rotational energy
| (42) |
In other words, the temperature consists of contributions from the translational and rotational temperatures, and they follow the relation
| (43) |
and in thermodynamic equilibrium the equipartition of energy requires . The heat flux for a polyatomic gas is where is the translational heat flux and is an additional heat flux due rotational energy. The rotational heat flux and a stress like quantity (second moment) are defined as
| (44) |
Like the monoatomic gas, the evolution equation for this distribution function with collisional kernel in the Boltzmann form is
| (45) | ||||
which is consistent with the equipartition of energy at equilibrium (Pullin, 1978; Kuščer, 1989). Similar to the monoatomic gas, one defines the BGK collision kernel in terms of the two-particle distribution function for a polyatomic gas as (Brull & Schneider, 2009)
| (46) | ||||
with normalisation factor . Equation (45) with is written as two kinetic equations for the reduced distributions and by multiplying with and and then integrating over the internal energy variable as
| (47) | ||||
This approach, where two reduced distributions are weakly coupled via temperature, recovers all the features of Eq.(46) and is widely adopted for polyatomic gases. Andries et al. (2000) extended this approach via an extended ES–BGK collision kernel as
| (48) |
where with a generalized Gaussian
| (49) |
with and . Similar to the monoatomic ES–BGK model, the parameter is used to tune the Prandtl number, while parameter is used to tune the bulk viscosity coefficient independently. The reduced description which generalizes the ES–BGK model in terms of the and is
| (50) | ||||
A common feature between Eqs. (47) and (50) is that the kinetic equation for translation distribution function is coupled with the kinetic equation for the rotational distribution function via rotational temperature only. At this point, it might be instructive to analyse the moment chains of the BGK and ES–BGK systems. As both the collision kernels conserve mass and momentum, the evolution equations for density and momentum are of the same form as that of monoatomic gas. In particular
| (51) | ||||
where is the modified stress tensor and the velocity evolution is
| (52) |
For polyatomic gases, the energy equation gets an additional contribution from the rotational energy. In both the BGK and ES–BGK models, the evolution equation for translational part of the energy and the rotational part of the energy are of the form
| (53) | ||||
with for the BGK model and for the ES–BGK model. The evolution equation for the total energy is written as the sum of Eqs. (53) as
| (54) |
where the relationship between translational, rotational temperatures (Eq.(43)) is used to show that energy is collisional invariant. From Eqs. (47) and (50), the stress evolution and the translational heat flux evolution equations in explicit form are
| (55) | ||||
with for BGK and for the ES–BGK model. Multiplying rotational energy equation from Eq.(53) with and using Eq.(52) we have
| (56) | ||||
using which the rotational heat flux evolution obtained as first moment of dynamics is
| (57) |
where . The Eqs. (51) and (54) form the compressible Navier–Stokes–Fourier equations for a polyatomic gas. A Chapman-Enskog analysis shows that the Eq.(51) can be written in familiar compressible Navier–Stokes equation form as
| (58) |
with the shear and bulk viscosities
| (59) |
Similarly, an analysis of the translational and rotational heat flux dynamics at leads to with the translational and rotational thermal conductivities respectively. The effective thermal conductivity Thus, the Prandtl number is i.e., for BGK model and for the ES–BGK model.
4 Reduced ES–BGK model for polyatomic gases
In the kinetic theory of gases, one often builds an extended moment system in terms of physically relevant lower-order moments (Grad, 1958). In this spirit of Grad’s moment method, one may ask whether a reduced description for rotational degrees of freedom is feasible. It should be noted that the evolution equation of is only weakly coupled with the evolution of via . An appropriate choice in the current context is a reduced description in terms of lower-order moments of second distribution . For example, the rotational component can be modelled by the evolution of two scalars – rotational energy and its flux (which are the zeroth and the first moment of ). Such a class of reduced-order kinetic models might be better suited for large-scale hydrodynamic simulations. An extended BGK model for diatomic gases was formulated by Kolluru et al. (2020a) wherein the BGK collision model was coupled with the rotational part of energy (zeroth moment of ) which in itself follows an advection-relaxation equation.
We extend this approach by a generalized ES-BGK model for polyatomic gases with tunable Prandtl numbers where the collision term is a linear combination of ES–BGK and the BGK collision kernels. In this model, the ES–BGK term describes relaxation to a temperature over a time whereas the BGK collision kernel describes relaxation to a temperature over a time . The kinetic equation of the unified model along with the evolution equation for the rotational energy is
| (60) | ||||
with the form of heat flux due to internal degrees of freedom as
| (61) |
This model is a minimal extension of the monoatomic ES–BGK model needed for modeling polyatomic gases which also recovers all important features such as the positivity, macroscopic limit, and the theorem. Here, the Prandtl number is a tunable parameter due to the presence of two relaxation time scales, whereas the rotational part of the internal energy alters the specific heat ratio to that of a polyatomic gas. The model satisfies the theorem, thus ensuring convergence to a unique equilibrium state. A few important characteristic of the present model are as follows:
-
•
Conservation Laws: The mass and momentum conservation equations for the proposed model are obtained by taking the zeroth and first moments of evolution (Eq.(60)). The second moment signifying translational energy evolution equation is
(62) which when combined with the rotational energy equation shows that the total energy is conserved. This implies that the evolution equation for slow moments
(63) mass density, momentum density, and total energy density are
(64) Thus, the conservation laws have correct macroscopic form.
-
•
H–Theorem: For polyatomic gases, a part of entropy production should be due to rotational degrees of freedom. In the current model, as internal degrees of freedom are accounted for in a mean-field manner, similar to the Enskog equation one would expect that entropy contribution should only depend on rotational energy (Resibois, 1978). Thus, we write generalized –function for polyatomic gas in Sackur–Tetrode form as a sum of Boltzmann part for monoatomic contribution and rotational part (Huang, 2009)
(65) with being an unknown scale factor to be fixed later. On multiplying Eq.(60) with , and integrating over the velocity space we obtain the evolution of as
(66) where is related to the entropy flux with being the entropy production due to the ES–BGK and the BGK terms respectively. The evolution of the rotational energy (second equation in Eq.(60)) can be rewritten as
(67) Multiplying the above equation with and exploiting continuity we obtain
(68) Thereby, adding Eq.(66) and Eq.(68) and using the form of from Eq.(61) the evolution of is obtained as
(69) where the right hand side is the net entropy production with contributions from the ES–BGK collision, the BGK collision, and the rotational component of the model. Here,
(70) Similar to the standard BGK or ES–BGK case (Andries et al., 2000), the entropy production in this model is non-positive too. This is achieved by choosing and exploiting the relation Eq.(43) to rewrite as
(71) Hence, the proposed model satisfies the theorem.
-
•
Hydrodynamics: In order to derive the hydrodynamic limit and the transport coefficients, the moments are typically categorized into fast and slow moments . The stress tensor and the heat flux constitutes the relevant set of fast moments along with the translational and rotational temperatures as they are not conserved
(72) The base state is obtained from zero of collision from Eq.(60) as
(73) Thus, the fast moment can be expanded around their equilibrium values in a series as
(74) In Chapman–Enskog expansion, the time derivative of any quantity is expanded as
(75) The set of conservation laws (Eqs.(64)) upon substituting the expansion of time derivative provide the definition of time derivative at of slow variables as Euler equations
(76) Thus, pressure evolution at satisfies the adiabatic condition for a polyatomic gas
(77) Similarly, at order we have
(78) The expressions for and can be obtained from the evolution equations of translational temperature (Eq.(109)) and stress tensor (Eq.(111)) respectively as [Details of derivations in Appendix A]
(79) where . Substituting the above expressions in momentum conservation equation, hydrodynamics with shear viscosity and bulk viscosity is
(80) Similarly, translational thermal conductivity for the model is obtained from the translational heat flux evolution (Eq.(112)). A Chapman–Enskog expansion of Eq.(112) by substituting at yields
(81) Thus, the translational thermal conductivity is which means the total thermal conductivity with is . Hence,
(82) The relaxation times and are fixed based on the shear and bulk viscosities respectively and the free parameters and can be adjusted to obtain a target Prandtl number.
5 Discretizing via lattice Boltzmann Method
In this section, we formulate a lattice Boltzmann scheme for solving the proposed model. Firstly, the velocity space is discretized into a discrete velocity set consisting of vectors. These vectors form the links of a lattice that should satisfy appropriate isotropy conditions (Succi, 2001; Atif et al., 2018). In particular, we validate the proposed kinetic model using a 41-velocity crystallographic lattice from Kolluru et al. (2020b), which uses a body-centered cubic (bcc) arrangement of grid points. The bcc lattice contains two simple cubic lattices offset by half the length of grid spacing in all directions for better spatial discretization (Namburi et al., 2016). The discrete velocities and their corresponding weights for this RD3Q41 model are given in Table 1. The kinetic equation (Eq.(60)) in discrete in velocity space for populations is
| (83) | ||||
where
| (84) | ||||
with moments of the discrete populations defined as
| (85) | ||||
| Discrete Velocities() | Weight() |
|---|---|
To have a numerically efficient scheme for the coupled partial differential equations of Eq.(83), it is desirable to have large time steps, i.e., . Upon integrating Eq.(83) along the characteristics and approximating the integral related to collision term via trapezoid rule, we obtain the implicit relation
| (86) |
which is made explicit by a transformation to an auxiliary population . This implies the evolution equation for is
| (87) | ||||
with and . The moments of the auxiliary distribution are related to the moments of discrete populations as
| (88) | ||||
To solve the the second part of Eq.(60) that represents the internal energy, we write
| (89) |
by exploiting the Eqs. (43), (61), and the continuity equation. The above equation is an advection-relaxation-diffusion equation that is solved by the steps detailed below:
-
1.
The relaxation equation
(90) is first solved using the backward Euler method for a half-time step along with the relation in Eq. (43) to obtain
(91) where .
-
2.
The MacCormack scheme (MacCormack, 2003), which uses forward and backward differences for spatial derivatives in the predictor and corrector steps respectively, is used to solve the advection equation
(92) -
3.
The diffusion equation
(93) is then solved using the standard forward time centered space (FTCS) scheme to get .
-
4.
Finally, the second part of relaxation is completed by an advance of by another half time-step leading to the final solution at as
(94)
Note that the choice of the solver for the evolution equation of rotational energy is independent of the lattice Boltzmann solver used for solving . In the next section, we validate the proposed numerical model by simulating a few benchmark problems related to acoustics, hydrodynamics, and heat transfer such as propagation of an acoustic pulse, startup of a simple shear flow, thermal conduction, and viscous heat dissipation.
6 Validation
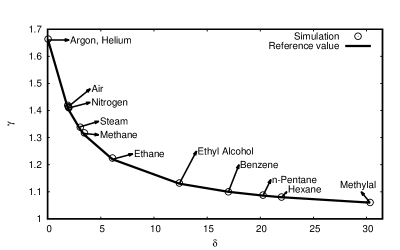
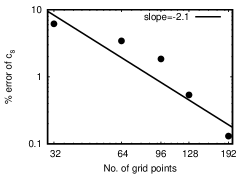
In this section, we validate the model by contrasting simulation result with various benchmark results. As a first example, we consider a periodic domain with lattice points to verify numerical sound speed. We initialize the domain with a pressure fluctuation of the form with . The pressure pulse is expected to reach the same state as the initial condition after one acoustic time period . The -norm of the pressure fluctuation is computed using the current state and initial state which is expected to be minimum when the waves are in-phase. The number of time-steps taken to achieve the least -norm is used to compute and the speed of sound as where is the domain length. The is thus computed from the speed of sound and the lattice temperature. Here, we demonstrate the versatility of the model by simulating several real fluids by imposing the effective rotational degrees of freedom as given in Table 2. We show in Figure 1 that our model accurately recovers the specific heat ratio for various polyatomic gases, even for fractional (effective) rotational degrees of freedom. The proposed model remains accurate even for fractional rotational degrees of freedom, thereby achieving any target specific heat ratio values. In Figure 2, we perform a grid convergence study for air and observe a second order convergence. We perform additional validation studies by restricting our attention to diatomic gases with variable Prandtl number.
| Fluid | Effective- | |
| Argon, Helium | 1.66 | 0.03 |
| Air | 1.403 | 1.96 |
| Nitrogen | 1.404 | 1.95 |
| Steam | 1.33 | 3.06 |
| Methane | 1.31 | 3.45 |
| Ethane | 1.22 | 6.09 |
| Ethyl alcohol | 1.13 | 12.38 |
| Benzene | 1.1 | 17 |
| n-Pentane | 1.086 | 20.26 |
| Hexane | 1.08 | 22 |
| Methylal | 1.06 | 30.33 |
.
Next, we study the absorption of sound in a dissipative compressible medium. The presence of both viscosity and thermal conductivity leads to the dissipation of energy in the sound waves. For an emitted wave, the pressure perturbations far away from the source decays during a finite time is (Landau & Lifshitz, 1987)
| (95) |
where the dimensionless Landau number is (Ansumali et al., 2005)
| (96) |
Here, is the ratio of bulk to shear viscosities and is the Knudsen number. The form of pressure perturbation shows that the wave profile is Gaussian-like at large distances and the width of the wave is proportional to for a fixed domain length .
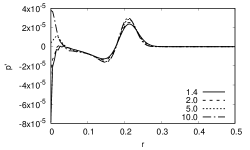
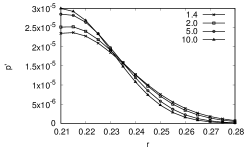
| 1.4 | 2.3302 |
|---|---|
| 2.0 | 2.0311 |
| 5.0 | 1.6124 |
| 10.0 | 1.4729 |
To demonstrate the effectiveness of the LB scheme, we perform a simulation at a fixed value of on a domain of size at Prandtl numbers , , and . We initialize the domain with a normal density perturbation of amplitude at the center of the fluid of uniform density at rest. From Eq.(80) and setting one obtains . Using this above relation and the Landau number is calculated as
| (97) |
The Landau numbers for the chosen set of parameters are listed in Table 3. It is evident that is inversely proportional to which suggests that the width of the Gaussian increases with a decrease in number. The pressure fluctuations far from the source of perturbation after for various Prandtl numbers are plotted in Figure 3, where is the acoustic time scale. It is evident that as expected the width of the wave is inversely proportional to the Prandtl number.
Next, we investigate the propagation of an acoustic pulse in a diatomic gas with where the isentropic speed of sound is . An axisymmetric pressure pulse is initialized at the centre of a domain of size with grid points. The acoustic pulse is of the form
| (98) |
with , , , , and . For low amplitudes of pressure fluctuations and low viscosity, the exact form of the pressure fluctuation is known as the solution of the linearized Euler equations as (Tam & Webb, 1993)
| (99) |
where is the Bessel function of the first kind of zero-order (Abramowitz & Stegun, 1965).
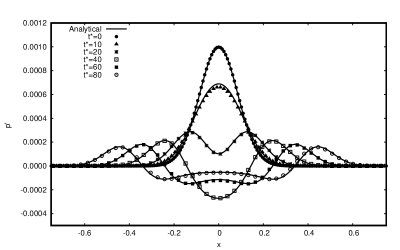
Figure. 4 shows that the pressure fluctuations from the simulation and the exact solution along the centerline of -axis are in agreement.
Next, we simulate the transient hydrodynamics in the startup of a simple shear flow between two flat plates separated by a distance on a grid of size with diffusive wall boundary condition (Ansumali & Karlin, 2002) and periodicity in the other two directions. Here, the top plate is suddenly started with a velocity while the bottom plate remains stationary. The viscous effects play an important role in the development of the flow which is driven by momentum diffusion. Figure 5 contrasts the solutions at various diffusion times obtained from our simulations with the known analytical solution for the velocity (Pozrikidis & Jankowski, 1997)
| (100) |
As expected, the simulation recovers the analytical solution with good accuracy.
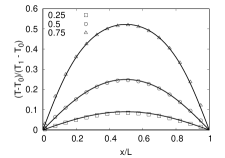
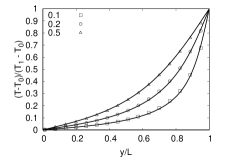
Next, we investigate the effects of thermal conduction by considering a setup consisting of fluid confined in a square cavity of size with points and stationary walls. The top wall maintained at a higher temperature , while the other three walls are maintained at a temperature . Diffusive wall boundary conditions are applied in both directions. The analytical solution for the temperature profile at steady state is (Leal, 2007)
| (101) |
Figure 6 shows that the simulated temperature profiles along lines , and and along , and for a temperature difference of matches well with the analytical solution.
Next, we validate our model for a thermal Couette flow problem to evaluate its capability in simulating viscous heat dissipation at various Prandtl numbers. We study the steady-state of a flow induced by a wall at moving with a constant horizontal velocity and maintained at a constant elevated temperature . The lower wall at is kept stationary at a constant temperature (). The analytical solution for the temperature profile for this setup is (Bird et al., 2015)
| (102) |
where is the temperature difference between the two walls and is the Eckert number that represents the ratio of viscous dissipation to heat conduction with as the specific heat at constant pressure for a diatomic gas.
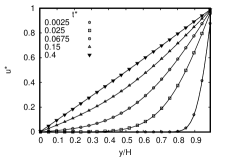
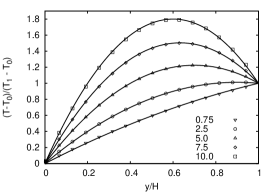
Simulations were performed for , and at Eckert number fixed at unity on a domain with grid points. The walls were maintained at temperatures and and plate velocity is chosen corresponding to a Mach number of . Figure 7 compares the temperature profiles obtained analytically and via simulations and they are found to be in good agreement.
7 Outlook
We have proposed a kinetic model for polyatomic gases with a tunable Prandtl number. This model is based on the ES–BGK model and recovers the compressible hydrodynamic equations of polyatomic gases as its macroscopic limit. It was shown that the transport coefficients of the model can be tuned for simulation of flows at different Prandtl numbers and specific heat ratios. This framework is general enough to deal with a more complex model of internal structures. We also demonstrated that the model respects the theorem. The simplicity of the model makes it suitable for LB and other numerical implementations.
Appendix A Evolution equations
We derive the evolution equations for kinetic energy, internal energy, pressure, stress, heat flux, translational, and rotational temperatures for the proposed model. Using the momentum evolution equation Eq.(64), we obtain the evolution equation for as
| (103) |
Evolution of kinetic energy obtained by taking the trace of the above equation is
| (104) |
Subtracting the above equation from the evolution equation of total energy from Eq.(64), gives the evolution equation for internal energy as
| (105) | ||||
and the evolution equation of pressure as
| (106) | ||||
Using the pressure and continuity equation, the evolution equation for temperature is
| (107) | ||||
From the evolution of kinetic energy (Eq.(104)) and the translational temperature (Eq.(62)), the evolution for translational energy can be evaluated as
| (108) | ||||
Using the continuity equation, the evolution for translational temperature is
| (109) | ||||
For the evolution of the stress tensor , we multiply the kinetic equation (Eq.(60)) with and integrate over the velocity space to obtain
| (110) | ||||
Thereafter, multiplying Eq.(108) with and subtracting from the above equation one obtains evolution of stress tensor as
| (111) |
Similarly, the evolution equation for translational heat flux is obtained by multiplying the kinetic equation (Eq.(60)) with to obtain
| (112) | ||||
References
- Abramowitz & Stegun (1965) Abramowitz, Milton & Stegun, Irene A 1965 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, , vol. 55. Courier Corporation.
- Agrawal et al. (2020) Agrawal, Samarth, Singh, S. K. & Ansumali, S. 2020 Fokker–Planck model for binary mixtures. J. Fluid Mech. 899, A25.
- Andries et al. (2000) Andries, Pierre, Le Tallec, Patrick, Perlat, Jean-Philippe & Perthame, Benoıt 2000 The Gaussian-BGK model of Boltzmann equation with small Prandtl number. Euro. J. Mech. B 19 (6), 813–830.
- Andries & Perthame (2001) Andries, Pierre & Perthame, Benoit 2001 The ES-BGK model equation with correct Prandtl number. In AIP conference proceedings, , vol. 585, pp. 30–36. AIP.
- Ansumali et al. (2007a) Ansumali, S, Arcidiacono, S, Chikatamarla, SS, Prasianakis, NI, Gorban, AN & Karlin, IV 2007a Quasi-equilibrium lattice Boltzmann method. Euro. Phys. J. B 56 (2), 135–139.
- Ansumali et al. (2007b) Ansumali, S, Karlin, IV, Arcidiacono, S, Abbas, A & Prasianakis, NI 2007b Hydrodynamics beyond Navier-Stokes: Exact solution to the lattice Boltzmann hierarchy. Phys. Rev. Lett. 98 (12), 124502.
- Ansumali & Karlin (2002) Ansumali, Santosh & Karlin, Iliya V 2002 Kinetic boundary conditions in the lattice Boltzmann method. Phys. Rev. E 66 (2), 026311.
- Ansumali et al. (2005) Ansumali, Santosh, Karlin, Iliya V & Öttinger, Hans Christian 2005 Thermodynamic theory of incompressible hydrodynamics. Physical review letters 94 (8), 080602.
- Arima et al. (2012) Arima, Takashi, Taniguchi, Shigeru, Ruggeri, Tommaso & Sugiyama, Masaru 2012 Extended thermodynamics of dense gases. Contin. Mech. Thermodyn. 24 (4-6), 271–292.
- Atif et al. (2017) Atif, Mohammad, Kolluru, Praveen Kumar, Thantanapally, Chakradhar & Ansumali, Santosh 2017 Essentially entropic lattice Boltzmann model. Phys. Rev. Lett. 119, 240602.
- Atif et al. (2018) Atif, Mohammad, Namburi, Manjusha & Ansumali, Santosh 2018 Higher-order lattice Boltzmann model for thermohydrodynamics. Phys. Rev. E 98, 053311.
- von Backstrom (2008) von Backstrom, Theodor W 2008 The effect of specific heat ratio on the performance of compressible flow turbo-machines. In ASME Turbo Expo 2008, pp. 2111–2117. ASME.
- Bernard et al. (2019) Bernard, Florian, Iollo, Angelo & Puppo, Gabriella 2019 BGK polyatomic model for rarefied flows. J. Sci. Comput. 78 (3), 1893–1916.
- Bhatnagar et al. (1954) Bhatnagar, Prabhu Lal, Gross, Eugene P & Krook, Max 1954 A model for collision processes in gases. i. small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511.
- Bird et al. (2015) Bird, Robert Byron, Stewart, Warren E, Lightfoot, Edwin N & Klingenberg, Daniel J 2015 Introductory Transport Phenomena, , vol. 1. Wiley New York.
- Brull & Schneider (2009) Brull, Stéphane & Schneider, Jacques 2009 On the ellipsoidal statistical model for polyatomic gases. Contin. Mech. Thermodyn. 20 (8), 489–508.
- Cercignani (1988) Cercignani, Carlo 1988 The Boltzmann equation. In The Boltzmann equation and its applications, pp. 40–103. Springer.
- Chapman & Cowling (1970) Chapman, Sydney & Cowling, Thomas George 1970 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge university press.
- Chen et al. (2010) Chen, Feng, Xu, Aiguo, Zhang, Guangcai, Li, Yingjun & Succi, Sauro 2010 Multiple-relaxation-time lattice boltzmann approach to compressible flows with flexible specific-heat ratio and prandtl number. EPL (Europhysics Letters) 90 (5), 54003.
- Gorban & Karlin (1994) Gorban, Alexander N & Karlin, Iliya V 1994 General approach to constructing models of the Boltzmann equation. Physica A 206 (3-4), 401–420.
- Grad (1958) Grad, Harold 1958 Principles of the kinetic theory of gases. In Thermodynamik der Gase/Thermodynamics of Gases, pp. 205–294. Springer.
- Green & Southard (2019) Green, Don W & Southard, Marylee Z 2019 Perry’s chemical engineers’ handbook. McGraw-Hill Education.
- Holway Jr (1965) Holway Jr, Lowell H 1965 Kinetic theory of shock structure using an ellipsoidal distribution function. Rarefied Gas Dyn. 1, 193.
- Holway Jr (1966) Holway Jr, Lowell H 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9 (9), 1658–1673.
- Horn & Johnson (2012) Horn, Roger A & Johnson, Charles R 2012 Matrix analysis. Cambridge university press.
- Huang (2009) Huang, Kerson 2009 Introduction to statistical physics. Chapman and Hall/CRC.
- Huang et al. (2020) Huang, Rongzong, Lan, Lijuan & Li, Qing 2020 Lattice boltzmann simulations of thermal flows beyond the boussinesq and ideal-gas approximations. Physical Review E 102 (4), 043304.
- Kataoka & Tsutahara (2004) Kataoka, Takeshi & Tsutahara, Michihisa 2004 Lattice boltzmann model for the compressible navier-stokes equations with flexible specific-heat ratio. Physical review E 69 (3), 035701.
- Kogan (1969) Kogan, Mikhail Naumovič 1969 Rarefied Gas Dynamics. Translated from Russian. Plenum Press.
- Kolluru et al. (2020a) Kolluru, Praveen Kumar, Atif, Mohammad & Ansumali, Santosh 2020a Extended BGK model for diatomic gases. J. Comput. Sci. 45, 101179.
- Kolluru et al. (2020b) Kolluru, Praveen Kumar, Atif, Mohammad, Namburi, Manjusha & Ansumali, Santosh 2020b Lattice Boltzmann model for weakly compressible flows. Phys. Rev. E 101 (1), 013309.
- Kuščer (1989) Kuščer, Ivan 1989 A model for rotational energy exchange in polyatomic gases. Physica A 158 (3), 784–800.
- Landau & Lifshitz (1987) Landau, LD & Lifshitz, EM 1987 Fluid mechanics. translated from the russian by jb sykes and wh reid. Course of Theoretical Physics 6.
- Larina & Rykov (2010) Larina, IN & Rykov, VA 2010 Kinetic model of the Boltzmann equation for a diatomic gas with rotational degrees of freedom. Computational Mathematics and Mathematical Physics 50 (12), 2118–2130.
- Leal (2007) Leal, L Gary 2007 Advanced transport phenomena: fluid mechanics and convective transport processes, , vol. 7. Cambridge University Press.
- Lebowitz et al. (1960) Lebowitz, JL, Frisch, HL & Helfand, E 1960 Nonequilibrium distribution functions in a fluid. Phys. Fluids 3 (3), 325–338.
- Levermore (1996) Levermore, C David 1996 Moment closure hierarchies for kinetic theories. J. Stat. Phys. 83 (5-6), 1021–1065.
- Liboff (2003) Liboff, Richard L 2003 Kinetic theory: classical, quantum, and relativistic descriptions. Springer Science & Business Media.
- Liepmann et al. (1962) Liepmann, Hans Wolfgang, Narasimha, R & Chahine, Moustafa T 1962 Structure of a plane shock layer. Phys. Fluids 5 (11), 1313–1324.
- MacCormack (2003) MacCormack, Robert 2003 The effect of viscosity in hypervelocity impact cratering. Journal of spacecraft and rockets 40 (5), 757–763.
- McQuarrie (2000) McQuarrie, D.A. 2000 Statistical Mechanics. University Science Books.
- Morse (1964) Morse, TF 1964 Kinetic model for gases with internal degrees of freedom. Phys. Fluids 7 (2), 159–169.
- Mott-Smith (1951) Mott-Smith, Harold Meade 1951 The solution of the Boltzmann equation for a shock wave. Phys. Rev. 82 (6), 885.
- Müller & Ruggeri (2013) Müller, Ingo & Ruggeri, Tommaso 2013 Rational extended thermodynamics. Springer Science & Business Media.
- Namburi et al. (2016) Namburi, Manjusha, Krithivasan, Siddharth & Ansumali, Santosh 2016 Crystallographic lattice Boltzmann method. Sci. Rep. 6, 27172.
- Nie et al. (2008) Nie, Xiaobo, Shan, Xiaowen & Chen, Hudong 2008 Thermal lattice Boltzmann model for gases with internal degrees of freedom. Phys. Rev. E 77 (3), 035701.
- Oh et al. (1997) Oh, CK, Oran, ES & Sinkovits, RS 1997 Computations of high-speed, high Knudsen number microchannel flows. J. Thermophys. Heat Trans. 11 (4), 497–505.
- Pozrikidis & Jankowski (1997) Pozrikidis, Constantine & Jankowski, D 1997 Introduction to theoretical and computational fluid dynamics, , vol. 675. Oxford university press New York.
- Pullin (1978) Pullin, D.I. 1978 Kinetic models for polyatomic molecules with phenomenological energy exchange. Phys. Fluids 21 (2), 209–216.
- Resibois (1978) Resibois, Pierre 1978 H-theorem for the (modified) nonlinear enskog equation. Journal of Statistical Physics 19 (6), 593–609.
- Ruggeri & Sugiyama (2015) Ruggeri, Tommaso & Sugiyama, Masaru 2015 Rational extended thermodynamics beyond the monatomic gas. Springer.
- Rykov (1975) Rykov, VA 1975 A model kinetic equation for a gas with rotational degrees of freedom. Fluid Dyn. 10 (6), 959–966.
- Shakhov (1968) Shakhov, EM 1968 Generalization of the krook kinetic relaxation equation. Fluid dynamics 3 (5), 95–96.
- Singh & Ansumali (2015) Singh, SK & Ansumali, Santosh 2015 Fokker–Planck model of hydrodynamics. Phys. Rev. E 91 (3), 033303.
- Singh et al. (2016) Singh, SK, Thantanapally, Chakradhar & Ansumali, Santosh 2016 Gaseous microflow modeling using the fokker-planck equation. Physical Review E 94 (6), 063307.
- Struchtrup (2004) Struchtrup, Henning 2004 Stable transport equations for rarefied gases at high orders in the Knudsen number. Phys. Fluids 16 (11), 3921–3934.
- Succi (2001) Succi, Sauro 2001 The lattice Boltzmann equation: for fluid dynamics and beyond. Oxford university press.
- Tam & Webb (1993) Tam, Christopher KW & Webb, Jay C 1993 Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys. 107 (2), 262–281.
- Tsutahara et al. (2008) Tsutahara, Michihisa, Kataoka, Takeshi, Shikata, Kenji & Takada, Naoki 2008 New model and scheme for compressible fluids of the finite difference lattice Boltzmann method and direct simulations of aerodynamic sound. Comput. Fluids 37 (1), 79–89.
- Wang et al. (2017) Wang, Zhao, Yan, Hong, Li, Qibing & Xu, Kun 2017 Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes. J. Comput. Phys. 350, 237–259.
- Wang-Chang & Uhlenbeck (1951) Wang-Chang, CS & Uhlenbeck, GE 1951 Transport phenomena in polyatomic gases. Research Rep. CM-681. University of Michigan Engineering .
- Watari (2007) Watari, Minoru 2007 Finite difference lattice Boltzmann method with arbitrary specific heat ratio applicable to supersonic flow simulations. Physica A 382 (2), 502–522.
- Wu et al. (2015) Wu, Lei, White, Craig, Scanlon, Thomas J, Reese, Jason M & Zhang, Yonghao 2015 A kinetic model of the Boltzmann equation for non-vibrating polyatomic gases. J. Fluid Mech. 763, 24–50.