Reducing spheres of genus-2 Heegaard splitting of
Abstract
The Goeritz group of the standard genus-g Heegaard splitting of the three sphere, , acts on the space of isotopy classes of reducing spheres for this Heegaard splitting. Scharlemann [7] uses this action to prove that is finitely generated. In this article, we give an algorithm to construct any reducing sphere from a standard reducing sphere for a genus-2 Heegaard splitting of the . Using this we give an alternate proof of the finite generation of assuming the finite generation of the stabilizer of the standard reducing sphere.
aSreekrishna Palaparthi, Department of Mathematics, Indian Institute of Technology Guwahati, Assam 781039, India, email : passkrishna@iitg.ac.in
bSwapnendu Panda, Department of Mathematics, Indian Institute of Technology Guwahati, Assam 781039, India, email : p.swapnendu@iitg.ac.in
Keywords : Goeritz Group, Automorphisms of three sphere, Heegaard splittings, Reducing sphere, Mapping class groups.
Mathematics Subject Classification : 57M60, 20F38, 57K30
Acknowledgements: We are thankful to the Department of Mathematics, Indian Institute of Technology Guwahati for its support while carrying out this work. A part of this work intersects with the thesis work of the second author.
1 Introduction
The genus- Goeritz group of , denoted , is the group of isotopy classes of homeomorphisms of which preserve a genus- Heegaard surface of . By a theorem of Waldhausen [9], every Heegaard splitting of of genus greater than is stabilized. So the group can be taken to be the group of isotopy classes of homeomorphisms of which preserve the standard genus- Heegaard splitting of . Scharlemann [7] proved that the genus-2 Goeritz group, , of is finitely generated by four generators. He did so by considering a certain simplicial complex whose vertices are the isotopy classes of reducing spheres of the standard genus- Heegaard splitting of . Akbas [1] used Scharlemann’s complex to give a finite presentation for . Cho [2] independently used a certain disk complex to give a finite presentation for . For , Zupan [10] generalized Scharlemann’s work and defined a reducing sphere complex for genus- Heegaard splittings of and showed that the group is finitely generated if and only if this complex is connected. Freedman and Scharlemann [4] proved that is also finitely generated. They conjectured that the five generators mentioned in Powell [5] generate for all . Much is unknown about for .
The literature on the Goeritz group of shows the importance of describing an arbitrary reducing sphere for reducible Heegaard splittings of , and for reducible Heegaard splittings of 3-manifolds in general. In this article, we look at the set of all the reducing spheres for the genus-2 Heegaard splitting of . We give structure theorems for such spheres. We then give an algorithm to construct any reducing sphere for the standard genus-2 Heegaard splitting of , upto isotopy, from the standard reducing sphere.
The layout of this article is as follows. In section 2, we prove Theorem 2.2 which gives some intersection conditions satisfied by the curve of intersection of a reducing sphere with the standard genus-2 Heegaard surface of . In section 3, we use the fundamental group of a genus-2 handlebody to deduce some conditions which apply to the arcs of intersection of a reducing sphere with a certain component pair of pants of the genus-2 Heegaard surface of . We then use these conditions to prove Theorem 3.6 for such arcs of a reducing sphere. In section 4, we prove Theorem 4.1 which is a key tool to de-construct a given reducing sphere. In section 5, we give an algorithm to de-construct and transform any reducing sphere into the standard reducing sphere. Using this algorithm and assuming that the stabilizer of the standard reducing sphere of the genus-2 Heegaard splitting of is finitely generated, we show that the Goeritz group is finitely generated.
2 Reducing Curves - Intersection Numbers
For preliminaries regarding Heegaard splittings of 3-manifolds, one can consult [6] and for preliminaries on mapping class groups and simple closed curves on surfaces, one can consult Farb and Margalit [3]. We start by considering the standard genus-2 Heegaard splitting of , written and denoted by , where both and are unknotted genus-2 handlebodies embedded in with disjoint interiors glued along their common boundary . The Heegaard surface, , of the above splitting is a closed orientable surface of genus two embedded in . Since is stabilized, one can find a reducing sphere for i.e. a sphere which intersects each of and in an embedded disk with a common boundary circle on . Such a reducing sphere intersects in an essential separating simple closed curve, which we call a reducing curve for . A reducing curve on uniquely determines a reducing sphere, upto isotopy in . Two reducing spheres of are said to be isotopic with respect to , if any of their isotopy in restricts to an isotopy of the corresponding reducing curves on the surface . Likewise, if two reducing curves for are isotopic on , this isotopy can be extended to an isotopy of the corresponding reducing spheres with respect to . This allows one to study reducing curves on in order to study reducing spheres of .
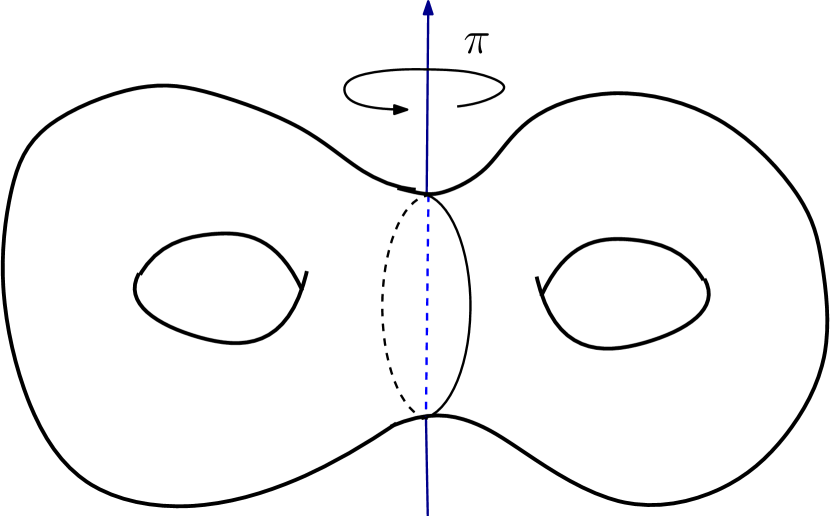
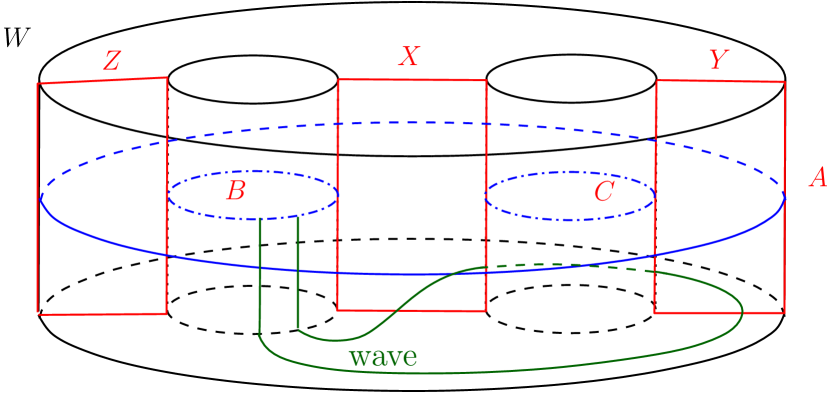
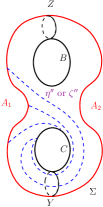
The Heegaard splitting of admits the following four automorphisms, as described in Scharlemann [7], which preserve the structure of . The automorphisms and are the automorphisms of induced by the -rotations of about the axes indicated in Figures 1(a) and 1(c). The automorphism is the half twist of the about the central separating curve as indicated in Figure 1(b).
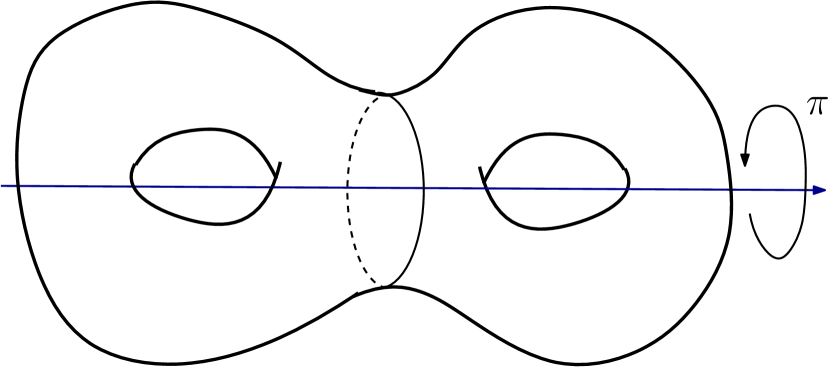

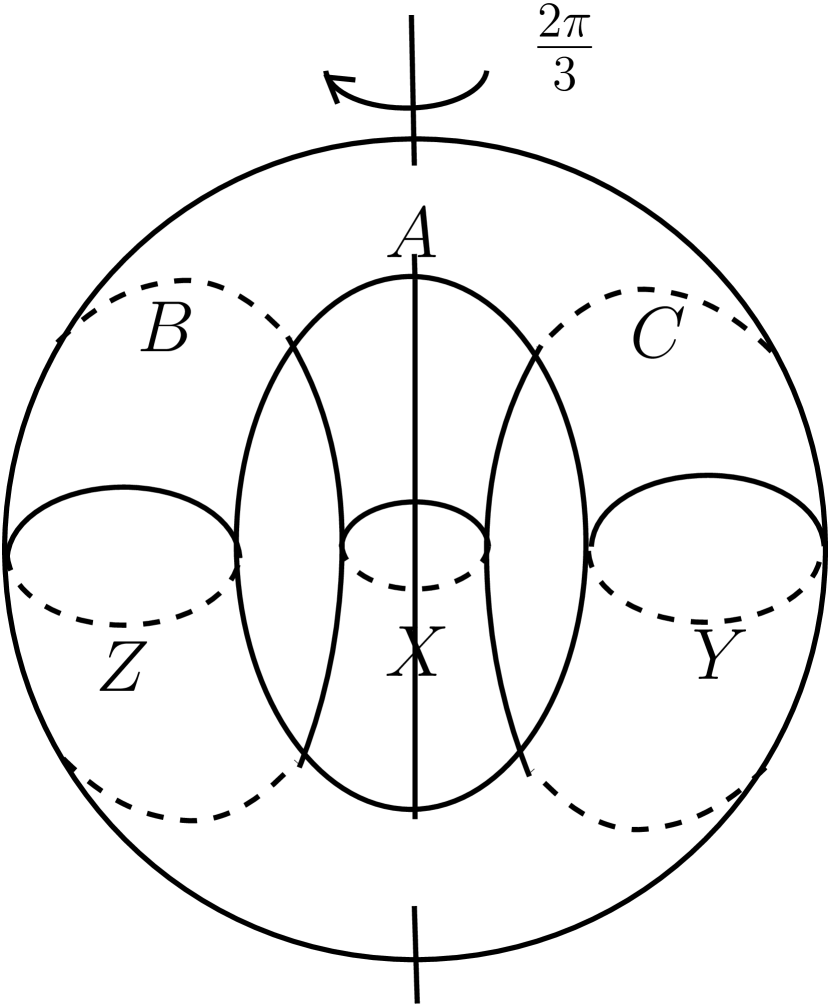
The automorphism is of order three which can be described as follows. Consider a graph on the unit sphere in whose vertices are the north and the south pole and whose edges are three distinct half meridians on the sphere connecting the north pole and the south pole such that the rotation of the sphere by an angle about the axis connecting the north and south pole permutes the three edges cyclically. If is a regular neighborhood in of this graph such that is homeomorphic to the handlebody , then is the order three automorphism which cyclically permutes the 1-handles of by rotation by an angle as shown in Figure 1(d).
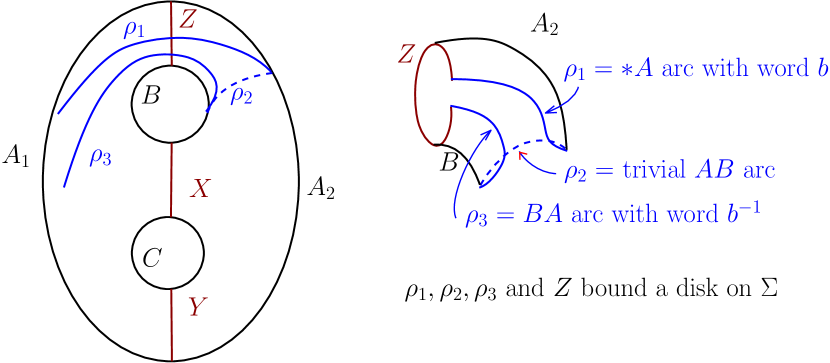
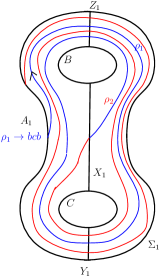
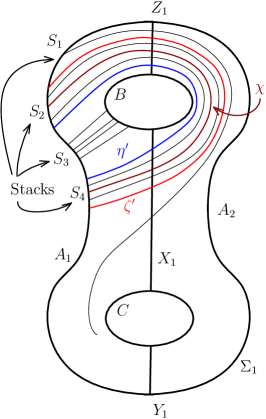
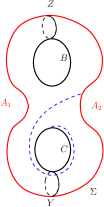
Figure 2 shows an embedding of the Heegaard surface of in . is the reducing sphere whose reducing curve, , is shown in Figure 2. We call as the standard reducing sphere. Consider the non-separating curves on as shown in Figure 2.
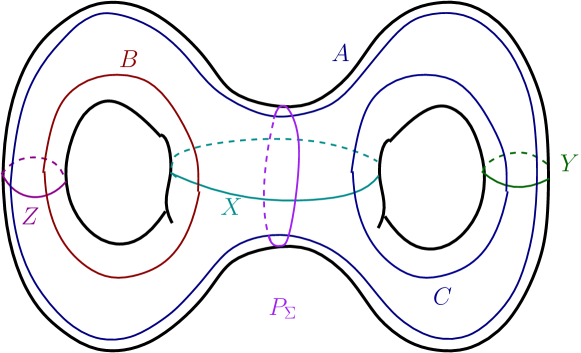
separates into two thrice boundered spheres, call them and . We will refer to the curves in Figure 2 throughout this article.
Any reducing sphere of intersects in the corresponding reducing curve, which we denote by . Such a is an essential separating simple closed curve on which separates into two surfaces, each of which is a surface of genus with one boundary component. Since cannot be null-homotopic on , will intersect both and and will also intersect at least one of or . For any , we assume that intersects and minimally and transversally (refer to Figure 2). or is a collection of simple essential arcs on the thrice boundered spheres or , respectively. For , an arc of type , or a arc, for short, on (or on ) is a connected arc of which is contained in (or in ) and which has its end-points on the curves and . So there are six possible types of arcs of on or namely an arc, a arc, a arc, an arc, an arc and a arc. Some arc types intersect the others. So a reducing curve, , cannot have intersecting arc types.
Table 1 shows arc types which necessarily intersect and hence cannot be components of the same reducing curve on and likewise on :
| X | X | X | ||||
| X | ||||||
| X | ||||||
| X | X | X | ||||
| X | ||||||
| X | X | X |
For an arbitrary reducing sphere , the number of arcs of and of have to be equal, as a mismatch will leave an open end which is impossible for a closed curve. For , let and denote the number of arcs of of type on and , respectively. For instance, denotes the number of arcs of of type on and denotes the number of arcs of on . When the context is clear, we will drop in the subscript. For instance, we will just use , instead of . We define and . Since is a separating curve, and are non-negative even numbers.
The four automorphisms of described above, namely, and affect the numbers and of a reducing sphere of as follows:
-
1.
cyclically permutes and ,
-
2.
permutes and and keeps unchanged,
-
3.
keeps and unchanged and
-
4.
or its inverse increase or decrease , while keeping and unchanged.
Table 2 lists the contribution of each arc type to , and .
| Type of arc | Each arc’s contribution to | ||
| +2 | 0 | 0 | |
| +1 | +1 | 0 | |
| +1 | 0 | +1 | |
| 0 | +2 | 0 | |
| 0 | +1 | +1 | |
| 0 | 0 | +2 | |
Lemma 2.1.
For any reducing sphere , let and denote any distinct non-negative integers in the set . Then .
Proof.
By the order three symmetry of , it suffices to prove the statement for and .
If is isotopic to with respect to , i.e. is isotopic to on then , and the lemma holds.
Now suppose is not isotopic to . Using Table 2 for on we have, , and . If then .
So if one of or is non-zero, then and vice versa which means that has an arc along with one of , or arc which is impossible by table 1. We can also arrive at this contradiction by counting arcs on instead of . Therefore, we should have for .
Therefore, for to be equal to , can only have and type arcs on both and . But, if these are the only type of arcs of , then following starting on any point of , an arc should be followed by a arc and an arc should be followed by a arc and so will intersect in only one orientation. Hence the absolute value of the algebraic intersection number of with , or will be non-zero, contradicting the fact that is a separating curve on . This shows that . ∎
Theorem 2.2.
For any reducing sphere for , we have:
-
(i)
if and only if contains at least one arc on each of and .
-
(ii)
if and only if contains at least one arc on each of and ,
-
(iii)
if and only if contains at least one arc on each of and .
Furthermore, exactly one of the above three holds for .
Proof.
By the order three symmetry of , it suffices to prove statement (i). The other two statements follow. Let or for this proof. As in the proof of Lemma 2.1, , and . So, implies . The strict inequality implies that . Thus implies has an arc on both and .
Conversely, suppose has an arc on . Then, and using Table 1, cannot simultaneously have any of or arcs on . This implies . Then,
This proves statement (i) of the lemma.
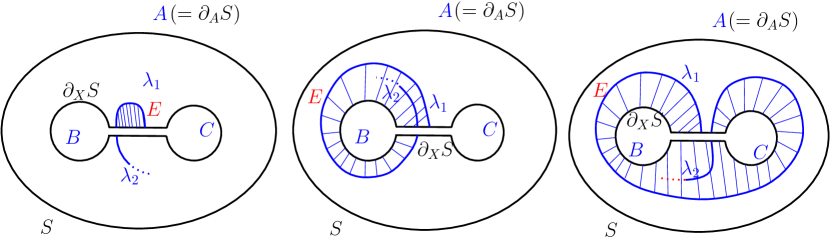
Now we show that exactly one of the three inequalities hold for any . For that, we consider the complement of the case and show that or must hold. By Lemma 2.1 . So the complement of is when . If , by lemma 2.2, cannot have any arc on or on . By the work of Volodin et al. [8], since bounds a disk in the handlebody , must have a ‘wave’ on with respect to or (also refer [1]). In other words, must either have a arc (see figure 3(a)) disjoint from or a arc disjoint from . Likewise, since must also bound a disk in , must also have a ‘wave’ on with respect to or i.e. a arc disjoint from or a arc disjoint from respectively. The ‘wave’ on with respect to when viewed on , is a arc on , since there are no type arcs on or on . The ‘wave’ on with respect to is shown in figure 3(b), 3(c) and 3(d) respectively.



Similarly, the ‘wave’ on with respect to when viewed on , is a arc on since there are no arcs on or on .
Therefore, when , by an isotopy, we can assume that has a or a arc on one of or . Without loss of generality let us assume that this wave is on . By Table 1, can have only one of or arc types on .
Remark 2.3.


The proof of Theorem 2.2 also shows the following:
Corollary 2.4.
(i) If a reducing sphere satisfies , then contains only and type arcs on and on .
(ii) If a reducing sphere satisfies , then contains only and type arcs on and on .
(iii) If a reducing sphere satisfies , then contains only and type arcs on and on .
In any of the above three cases, the number of arcs of any type are equal on and on .
3 Arcs of a reducing curve
We assume the setup of the previous section. By Theorem 2.2, and by invoking the order three symmetry, , of , in order to describe an arbitrary reducing sphere, , of , it is enough to describe a reducing sphere in the case . Also, by Theorem 2.2, the inequality implies the existence of an arc on and an arc on . Further, by Remark 2.3, there must be an arc on or on which is as shown in Figure 4.
So, throughout this section, we assume that a reducing sphere satisfies the inequality and describe how the , and arcs of the corresponding reducing curve can be presented on and on .

Let the two distinct arcs of each of which has one end-point on and another end-point on be denoted by and .
We can arrange the standard embedded genus-2 surface, , in such that: (i) is the intersection of the plane with (ii) the points and lie along the -axis with the -coordinate of points on increasing from to , (iii) no two points of or no two points of have the same -coordinate. We will refer to this arrangement throughout this section. With this arrangement the -coordinate can be thought of as a height function on and likewise on . See Figure 5. Owing to this observation, if and if the height of is greater than the height of , then we say is above or that is below . If such that the height of is between the heights of and then we say that is in between and .
By an isotopy of , we can assume that it does not intersect the points or . Since is finite, there are only finitely many arcs on or on . These arcs are essential on or on as inessential arcs on a thrice boundered sphere are boundary reducible and a boundary reducing disk gives an isotopy of reducing the intersection number of with . Also these arcs do not intersect each other as is a simple curve. Since every essential arc on a thrice-boundered sphere from a boundary component to itself is separating, these arcs are separating arcs of and .
The curve is a finite collection of arcs on and for some natural number . Fix an orientation of and number these arcs sequentially as following the orientation of such that if and only if and . Without loss of generality we assume that for each , is on and is on .
Lemma 3.1.
For , an arc of on intersects exactly once.
Proof.
Let Cut along to get an annulus , which has two boundary components. One boundary component is the curve and the other boundary component is a union of and with two copies of . For brevity, we denote these two boundary components of by and respectively.
If an arc does not intersect , then it is an arc in the annulus with both its endpoints on the same boundary component of and hence is boundary-reducible. The boundary-reducing disk is a bigon as the arc intersects only at its endpoints. Then by the bigon criterion, we have an isotopy of reducing its intersection with contradicting the minimal intersection position of with . So an arc on has to intersect at least once.
Suppose now that an arc, call it , intersects more than once. Orient from one end point on to another and let be the points of intersection of with listed in order when following the orientation of . cuts into its component arcs on . All such component arcs on the annulus run from to itself and hence are boundary reducible. Two boundary-reducing disks of such component arcs of are either disjoint or one is contained in the other, otherwise will have self-intersections. Hence by following a chain of containment of these boundary reducing disks, we can get an innermost disk which does not contain any other disk. We will now show that is a bigon on the surface formed by and .
Let be the boundary reducing disk for an arc on which is a component arc of on . Let considered on join to . on is bounded by and a portion, call it , of the boundary component of . If includes or or both, then following the arc , in the orientation of or in the opposite orientation, beyond , we arrive at yet another component arc of , call it , on which enters . See Figure 6.
Since enters , it is completely contained in . This is because, cannot intersect , or , so it has to intersect which then means that is contained in . Now, as remarked earlier, is also boundary reducible and the boundary reduction disk of to the boundary is completely contained inside , contradicting the assumption that is the innermost disk. This proves that cannot include or or both.
This implies that contains only an arc from . So along with forms a bigon on the surface . So by the bigon criterion there is an isotopy of reducing the intersection with . So if is in minimal intersection position with , then an arc on cannot intersect more than once.
Hence, we conclude that any arc of on intersects in exactly one point.
Likewise, we can repeat the same argument for an arc on and conclude that such an arc intersects in exactly one point. ∎
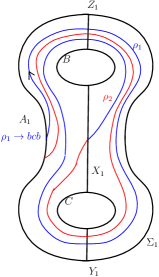
We now use the fundamental group of the handlebody to get more information about the , and arcs of when . In particular we will show that an arc of on or on can wind around the circles or at most once.
Let and be the essential disks in bounded by the curves and respectively. Consider the core curves of the handlebody , dual to the disks and , based at a point lying in the interior of and denote them by and respectively. Note that and are freely isotopic in to and respectively. The element in whose representative is a loop which traces once in the direction shown in Figure 7 will be denoted by and the element which traces once in the direction shown in Figure 7 will be denoted by .
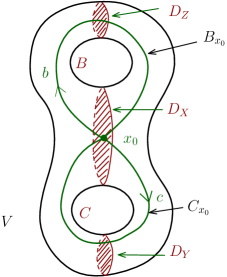
We consider the presentation of the fundamental group of based at and henceforth refer to this presentation simply as . With a slight abuse of notation, we use the same letters to indicate the elements in and the loops in . By this abuse of notation the loop in Figure 7 is also denoted by , for instance.
Now, let be a reducing sphere which is in minimal position with the curves and and which satisfies . Consider some orientation of and view it as a union of oriented arcs as mentioned earlier, where the orientation on , , is the one induced from the orientation of . Let denote an integer in the set throughout the following discussion with addition and subtraction performed modulo when indices are added or subtracted. Each is an , or an arc with a starting point indicated by its orientation. Since is an oriented arc we would distinguish between an arc and a arc, and likewise between an and a arc depending upon the orientation of . Let be an arc contained in the interior of oriented from to the starting point of such that does not intersect or . By , we mean with the reversed orientation. Now, is a loop in based at . This loop, , represents a word in the in the generators and in , which we call the word of .
Also, is freely homotopic to the product loop and correspondingly represents a product word in the generators and in . Since bounds a disk in , the corresponding reduced word must be cyclically trivial. This last requirement imposes restrictions on the arcs ’s which we discuss in the following.
The union of curves divides into four disks, which we call the component hexagons of , owing to the fact that the boundary of each of these disks contain exactly one arc each of the six curves and . In this context, an arc of on a component hexagon of is of the type if it starts on the curve and ends on the curve in the orientation of , where . A sub-arc of is called its initial-arc if it is completely contained in one of the component hexagons of and is of the type where and . Similarly, a sub-arc of is called its terminal-arc if it is completely contained in one of the component hexagons of and is of the type where and . Note that neither the terminal nor the initial arc of of type can have .
Lemma 3.2.
Consider any two component hexagons and of both of which have a side in common or both of which have a side in common. If intersects in an or a arc, then cannot intersect in an or a arc. Likewise, both and cannot simultaneously intersect in a or an arc.
Proof.
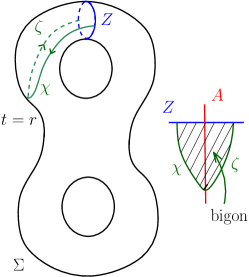


Let be an arc of in with one endpoint on and the other on . Let . If possible let be an arc on with end-points on and and . If , then and bound a bigon with on contradicting the minimal intersection position of with . If is below on , then the continuation arc of on is contained in the disk cut out of by , and and hence is another arc with one endpoint as and the other on . But then, and bound a bigon with on , once again contradicting the minimal intersection position of with . If is below , then the continuation arc of on and together bound a bigon with leading us to a similar contradiction. See Figure 8.
So cannot be above or below on nor can it coincide with and hence does not exist. The proof for the case where is an arc of in with one endpoint on and the other on is similar. ∎
Corollary 3.3.
When the word of a which is an , or a arc of is concatenated with word of , which is an , or an arc the concatenated word cannot have trivial relators of .
Proof.
This is so because a trivial relator at the word interface contradicts Lemma 3.2.
Suppose that is an , or a arc on whose word ends with a letter , and that is an , or an arc on whose word starts with a letter . See Figure 8(a). The terminal-arc of on is a arc and the initial-arc of on is an arc, contradicting Lemma 3.2.
Similarly, if is an arc on with a word which ends with any letter , where and the word of begins with then forms a bigon with or on and this will lead to a contradiction with the minimal position of with and . Since the roles of and can be reversed in the above argument, the corollary is proved. ∎
Corollary 3.4.
If the word of a , which is an arc (on or ), ends in or then the word of , which has to be a arc (on or , respectively) cannot start with or , respectively. Similarly, if the word of a , which is an arc (on or ), ends in or then the word of which has to be a arc (on or , respectively) cannot start with or , respectively.
Proof.
As in the proof of Corollary 3.3 if is an arc on (or on ) whose word ends with a letter or , then will be a arc on (or on ), and its word cannot begin with or respectively, because if it does, then the terminal-arc of and the initial-arc of form a bigon with on leading to a contradiction with the assumption that is in minimal position with . See Figure 9.
Similarly, if is an arc on either (or ), whose word ends with a letter or , then will be a arc on (or ), and its word cannot begin with or respectively, because if it does, then the terminal-arc of and the initial-arc of form a bigon with leading to a contradiction with the assumption that is in minimal position with . ∎
Lemma 3.5.
A concatenated word of a sequence and of arcs of where is an arc cannot contain the trivial relators or . Similarly, a concatenated word of a sequence and of arcs of where is an arc cannot contain the trivial relators or .
Proof.
Corollary 3.3 implies that a trivial relator or cannot occur when the word of is concatenated with the word of a when is an or a arc and is an arc. Corollary 3.4 implies that a trivial relator or cannot occur when the word of is concatenated with the word of a when is an arc and is a arc. So we need to prove that when is an arc whose word is empty word, , the concatenated words of and arc sequence cannot be of the form or of the form where and are some words in and . But if this happens, then as in the proof of Corollary 3.4, the terminal arc of the , the whole of and the initial-arc of form a bigon with as shown in figure 10.
This contradicts the assumption that is in minimal position with . This proves the first statement of the lemma. The proof of the second statement of this lemma is similar. ∎
Now, we describe the words of and arcs. For , let and .
We will first describe the words of arcs on . The same argument applies to words of arcs on . An arc on can be described completely upto isotopy by a sequence of arc types in the component hexagons of because these hexagons are disks. Further, it is possible to give an exhaustive description of these arc sequences owing to the conditions on an arc imposed by Lemma 3.1. Let be a non-negative integer, and be any integer for the following discussion.
Table 3 gives all possible arc sequences of an arc on which starts on and ends on , where , and gives its corresponding word in . Note that the arc types alternate on the two component hexagons of . The first, third, etc. arc-types are on the component hexagon which has as an edge and the second, fourth etc. arc-types are on the component hexagon which has as an edge.
| Start | End | Arc-type sequence and Word |
|---|---|---|
| empty | ||
Figure 11 shows these arc sequences for a sample.
Using this technique, we summarize the reduced word forms in of various arc-types as follows. Let represent some reduced word in . An arc of on or on starting on and ending on has words with three possible reduced forms, viz: empty, , . An arc starting on and ending on has words with three possible reduced forms, viz: empty, , . An arc starting on and ending on has words with the following possible reduced forms: , , , , , . An arc starting on and ending on has words with following possible reduced forms: , , , , , . The and arcs of on or on have reduced word forms based on the word form of its arc, which necessarily exists when . Depending on the beginning letter of the word described by an arc, an arc starting on describes a reduced word of the following forms: , , or . Depending on the beginning letter of the word described by an arc, an arc starting on describes a reduced word of the following forms: , , , . Likewise, an arc starting on describes a reduced word of the following forms: , , , . An arc starting on describes a reduced word of the following forms: , , , . The word forms of a arc are the inverses of the word forms of an arc and the word forms of a arc are the inverses of the word forms of an arc of the corresponding kind.
Since represents the conjugacy class of the trivial reduced word, the following Theorem shows that the variable word in the word-form summary, presented above, has to be trivial.
Theorem 3.6.
The word in of an arc of can have a length at most . Correspondingly, the word of an or arc of can have a word of the form and respectively, for some integer , where can have a length at most .
Proof.
When we concatenate the words of the arcs of on and from to , then the words should reduce to an empty word. Since the words described by various arcs, as summarized above are already in their reduced form, at least one trivial relator, a relator of the form , where could be any of , has to occur at the join of some and . Referring to the summary of word-forms of arcs, if the word in the word of an arc which is of the form is non-trivial, where then a trivial relator does not arise when words of arcs which form the word of are concatenated, leaving us with a conclusion that cannot have arcs with non-trivial words .
Now consider an arc of . Suppose that is a or a arc, whose word is of any of the types described above where is not the empty word.
-
Case 1:
and is an or an arc combination. Suppose first that is an arc and is a arc. In this case, by Corollary 3.3 and Lemma 3.5, for any trivial relator to arise, if at all it does, when words in are concatenated, the words of both and must be empty. But this is impossible as both and are on or on and is a arc which cannot describe an empty word when is not the empty word. So no trivial relator arises when concatenating the words of and . A similar argument shows that no trivial relator arises when concatenating the words of and when is an arc combination.
-
Case 2:
is an arc. Even in this case, by Corollary 3.3, there cannot be a trivial relator when the words of and are concatenated. However, the word of could be empty, in which case it should be an arc from to or an arc from to .
-
Subcase 1:
ends on : In this sub-case, the word of ends with or . Here we refer to the summary of words of arcs. So if the word of is empty it must be an arc from to , and so has to start on and hence has a word starting with either or . As a result there is no trivial relator while concatenating these three words.
-
Subcase 2:
ends on : In this sub-case, the word of ends with or . So if the word of is empty it must be an arc from to , and so has to start on and hence has a word starting with either or . As a result there is no trivial relator while concatenating these three words.
-
Subcase 1:
If is an or an arc whose word is of any of the types described above where is not the empty word, then the corresponding arc combination or an arc combination can never be the empty word by Corollary 3.4.
The arcs for to of are a sequence of arcs, arc combinations and arc combinations. When the corresponding words in are concatenated by following the order of ’s, at-least one of these pieces gives a non-trivial reduced word when is not the empty word and none of the concatenation results in a trivial relator. This shows that the word described by cannot be the empty word resulting in a contradiction to the assumption that bounds a disk in . This shows that the word of any arc on or can only be of the form with an empty and where . Hence the words of arc on or can contain at most two letters. Correspondingly, we infer from the summary of arcs above that the word of an or of an arc of is of the form and respectively, for some integer , where can have a length at most . ∎
Remark 3.7.
An arc with empty word on (or on ) will intersect an arc with two-letter word on (or on ). So cannot contain two arcs on (or on ), one with an empty word and another with a two-letter word.
Remark 3.8.
By the word forms arrived at, preceding the Theorem 3.6, we can further refine the words of and arcs based on whether their -end is on or as follows.
-
•
An arc which starts on can only have a word of the form or and correspondingly a arc which ends on can only have the inverse words or .
-
•
An arc which starts on can only have a word of the form , and correspondingly a arc which ends on can only have the inverse words or .
-
•
An arc which starts on can only have a word of the form , and correspondingly a arc which ends on can only have the inverse words or .
-
•
An arc which starts on can only have a word of the form , and correspondingly a arc which ends on can only have the inverse words or .
When for a reducing sphere , the following proposition gives one more condition which applies to word lengths of arcs.
Proposition 3.9.
Suppose that and that has no arc on or on describing a single letter word in . Then and , cannot simultaneously contain arcs each of which describe a two letter word in .
Proof.
Assume that has no arc on or on describing a single letter word in and assume to the contrary that both and contain an arc which describe a two letter word in . Without loss of generality, assume that contains an arc with end points on and which describes the word in the orientation of . In this case cannot contain an arc describing the same word or the inverse word owing to Lemma 3.2. So, the arc on will have to describe the word or the word depending on whether it starts on or , respectively. We will now show that even this cannot occur. For the purpose of this argument, we note that an arc of has to continue as a arc. So we tie up such arc combinations and call them arcs. We concatenate the words described by the and the arcs involved and call the concatenated and reduced word in as the word of the arc. Likewise we tie up arc combinations and call them arcs. We likewise define the words of arcs. Now, can be seen as a sequence of , and arcs. Further, the concatenation of the words described by these arcs should reduce to the empty word. Now, we gather the possible words described by these arcs when they are traced from to for in Table 4.
In this table 4 an arc starts on means that an arc starts on and on , whereas an arc starts on means that it starts on and on . An arc ends on means that the arc ends on and on whereas it ends on means that the arc ends on and on .
| Ends on | ||||
| Starts on | ||||
Figure 12(a) shows the possible arcs on along with the arc whose word is . Figure 12(b) shows the possible arcs on along with the arc whose word is or depending on how it is traced.

Let be the arc of whose word is . Starting at and following the orientation of , we list the , and arcs of as ’s for some positive integer . The end point of is the starting point of . We first define to be the word of . At the step, for , we define to be the reduced word corresponding to concatenation of with the word of . By induction on , we show that the length of , written , is always more than one. Since represents the word of and should have length zero, we have a contradiction. Initially . ends on . So has its initial arc on and has the possible words from the row against in Table 4. Note that none of the words start with . So the concatenation of with the word of is already reduced and . This can be taken as the base case. Now suppose that, for some integer , the reduced word is formed and for all . The arc ends on any of or and so the will start on or respectively. In the above table, for any of these combinations, we notice that there is no reduction upon concatenation of the words, except possibly when the word of is empty. So, except possibly in the case that the word of is empty, . Let us now consider the remaining case when the word of is empty and suppose that starts on . Then should have ended on . From the Table 4, there is only one possibility for an arc describing the empty word and ending on , namely an arc which starts on , which in turn means that the must have ended on . For all arcs ending on we notice that the ending letter of such arcs is or , unless it is the empty word. So the possible words for , when has an empty word, have no reduction when concatenated with the word of , unless the word of is trivial. So unless the has an empty word, . If has an empty word then from the Table 4, we infer that it must have been an arc starting on . Continuing thus, we see that unless is preceded by a finite sequence of and arcs which end on and , respectively, contributing empty words to , we have that . Even in the case when there are a sequence of and arcs preceeding which end on and , respectively, contributing empty words to , this sequence has to end in finite number of steps as the index starts reducing and when such a sequence ends, the arc immediately preceding this sequence of arcs will contribute a word which ends with or . So there is no reduction on concatenation with the word of . Hence . The argument when starts on or is similar to the case when starts on . So, even in the case that the word of is empty, we see that and so by induction, we conclude that for all when the indexing is taken modulo . This contradicts the fact that must have a trivial word and so . This completes the proof of this theorem. ∎
Using Proposition 3.9, we conclude that when , for a reducing sphere , and when , the word length of arcs on and can have the following possibilities:
-
Case (i):
one of or have an -arc describing a single letter word
-
Case (ii):
neither nor have an -arc describing a single letter word and both and have an -arc with an empty word, and
-
Case (iii):
neither nor have an -arc describing a single letter word and one of or has an -arc describing a two-letter word and the other has an -arc describing an empty word.
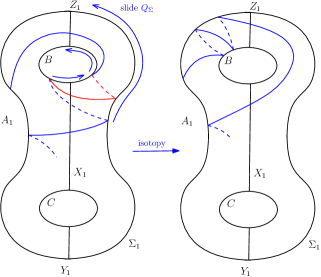
For Case (ii) we can choose an isotopy so that we can convert this case into Case (i) as follows: has to intersect or , else by cutting along , we notice that is a separating curve on a four-boundered sphere and either piece separated by cannot be a torus with one boundary component, which is a contradiction to the fact that is a reducing sphere. So suppose intersects without loss of generality. Since arcs have empty words, an or a arc must intersect in an essential way. A finite sequence of arcs connect this intersecting or a arc to an arc. Sliding the curve past so that the intersection is shifted onto the first arc gives the required isotopy. See Figure 13.
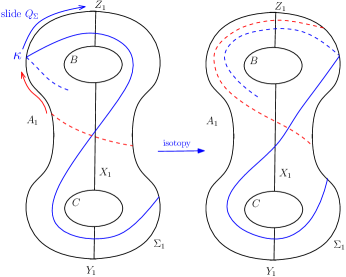
Even for Case (iii) we can choose an isotopy to convert this case into Case (i). Without loss of generality, suppose that has an arc describing the word . Choose such an arc, , which has the topmost coordinate on . Now any arc of on having a -coordinate above the -coordinate of , cannot end on . This can be inferred by looking at the component hexagon of containing as shown in Figure 14. So for any such arc, including , the order of intersection on of first with and then with can be swapped as intersection with and then an intersection with on as shown in Figure 14.
Using these isotopies, whenever for a reducing sphere , we can always assume that there is an arc of on or on which describes a single letter word in .
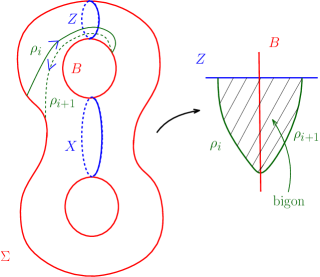
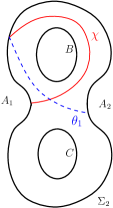
4 Lowering Intersections Using
In this section we study the action of the automorphism , which is as described in the section 1. If is a reducing sphere with and , we show that an application of one of or to decreases its geometric intersection number with . We do so by showing that the geometric intersection number of with one of the curves or shown in Figure 15 is lesser than that with .

Theorem 4.1.
If for a reducing sphere then either or .
Without loss of generality, as remarked at the end of the previous section, we can assume that contains an -arc on or on which describes a single letter word or in . Before we prove this Theorem, we need a few results which give some conditions on and arcs.
Let us assume that has an arc on , call it , which has both its endpoints on and its word is or based on its orientation. Every arc on which satisfies the description of , i.e. which starts and ends on and has the word or will be called an arc parallel to .
Let and be distinct arcs of on parallel to . Let the -coordinates of the endpoints of be and with and the -coordinates of the endpoints of be and with . Then either or . This is because, if the endpoints of and alternate on , then would intersect on . If then we say that is nested inside . Or if , then we say that is nested inside .
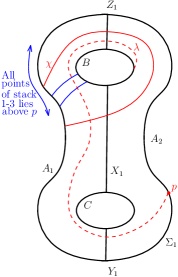
Since cuts an annulus out of containing the circle , all the -ends of the arcs of on have to lie on and between the endpoints of . With the -coordinate as height we classify the points of into five stacks. The first stack of points with the largest -coordinates consists of -ends of arc segments of which lie outside , if any, which connect to and which are not end points of arcs on parallel to . Every arc on which is parallel to has two ends, one with a higher -coordinate and one with a lower -coordinate. The second stack of points consists of those -ends of arcs on parallel to , which have higher -coordinate than their counterparts. The fourth stack of points consists of those -ends of arcs on parallel to which have lower -coordinate than their counterparts. The third stack of points consists of the -ends of arcs of , if any on . The fifth stack of points consists of the -ends of the arc segments of on , if any, which have a -coordinate lower than that of any point in the fourth stack of points and are not the end-points of arcs parallel to . See figure 16.
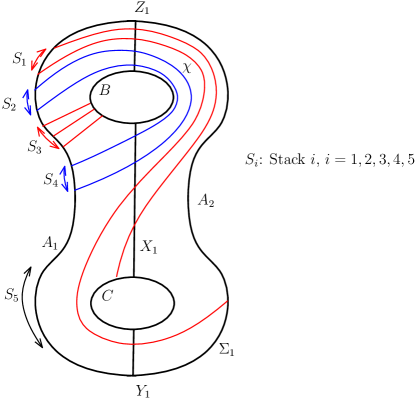
Now without loss of generality, we can assume that is the innermost among all these parallel -arcs on having word or .
Under the above circumstances, we note the following conditions on , and arcs of on .
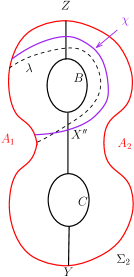
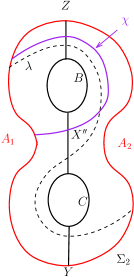
Proposition 4.2.
cannot have an -arc on with both ends on , whose word is either or . Also cannot have an -arc on with word or .
Proposition 4.3.
On , if has an arc with word such that one of its endpoints is on and another is on , then its -end should lie in stack one, two or three barring the point in stack three with the least -coordinate.
Proof.
If possible, suppose has an arc on with word such that one of its endpoints is on and another is on , where its -end in stack four or five or is the point in stack three with the least -coordinate. Then all arcs on having their ends on stacks one, two and three must end on . Including the - end point of in stack one and the - end point of , there are at least points in stack one, two and three on which are to be connected via arcs on to points on , which is impossible. See Figure 18(a). So, such an arc cannot exist.


∎
Proposition 4.4.
If contains an arc of with endpoints on and with the word then such an -end should be in stack three, four or five, barring the topmost point in the third stack with the largest -coordinate.
Proof.
Suppose to the contrary that is such an -arc on with an endpoint on with word and with its endpoint in stack one or two of or the topmost point in stack three on . See Figure 18(b). Then will force every arc of on starting from stacks three, four and five to end on due to Theorem 3.6. Including the - end point of on stack four and the - end point of , there are at least points in stack three four and five on which are to be connected via arcs on to points on , which is impossible. Hence such a cannot exist. ∎
Proposition 4.5.
If an arc of on has its end points on and , then its word has to be of the form for some integer .
Proof.
If possible suppose is an arc on with word and having its end points on and . See Figure 18(c). Note that by Theorem 3.6, this is the only other option for such an arc apart from having a word of the form for some integer .
Due to Lemma 3.2, such a will force all arcs on having one end-point on to start with a word or end with , as the case maybe, and they must have the other end-point on . But, including the -end-points of , there are at-least points on whereas only points on . Therefore, such a cannot exist. ∎
Proposition 4.6.
cannot have an -arc on with word , where
Proof.
The presence of such an arc on along with contradicts Lemma 3.2. ∎
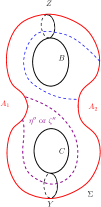
We now define -arcs, and on which are not arcs of and are disjoint from arcs of on and are parallel to as follows. Define to be an arc whose ends on are nested inside the ends of so that -ends of all -arcs on , if any, are between the ends of . Likewise, define to be an arc whose ends on are such that (i) every arc of on parallel to is nested inside , (ii) the -ends of every -arc on is also between the ends of and (iii) the -ends of no other arc of on is between the ends of . Figure 19 shows and .
Define and to be arcs (also not of ) on such that: (i) , , (ii) the word of or is or and (iii) and intersect minimally on where the end points of all arcs on are rigid i.e.cannot be moved while considering their intersection numbers. The simple closed curves or are isotopic to each other on and in turn are isotopic to . We now show that . By construction, . So it is enough to show that either or . We will first show that and .
Taking the restrictions on the possible arcs of on into account, the intersection of such arcs with and are as shown in Figure 20. Likewise, the intersection of possible arcs of on with and are as shown in Figure 21. The intersection of possible arcs of on with and are as shown in Figure 22.
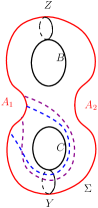
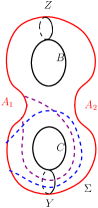
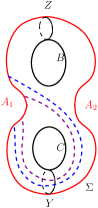
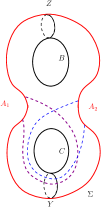
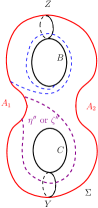
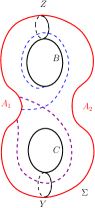
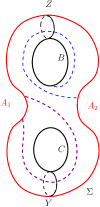
Proposition 4.7.
Every arc of on satisfies and .
Next we show that at least one of the two strict inequalities: or holds, by showing the following.
Lemma 4.8.
There exists an arc of on such that or .
Proof.
Consider the points . Let the arc of on with the point in stack two of as an endpoint be and the arc with the point in stack four of as an endpoint be . By proposition 4.4, cannot be an arc with the word or a arc with the word . We have the following cases.
-
Case 1
Suppose that is an -arc with endpoints on and with the empty word. In this case, is disjoint from and is the required . See Figure 23(a).
(a) 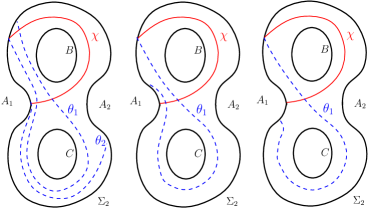
(b) 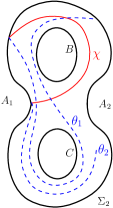
(c) 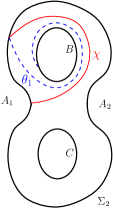
(d) 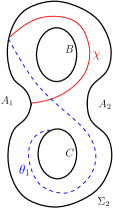
(e) Figure 23: The arc of on -
Case 2
Suppose is an -arc with both its endpoints on with the word or . If the other end point of is in stack one or two, then cuts off an annulus from containing as one boundary component and so , cannot be an arc. So, if the other end point of is in stack one or two then is an arc with the word , or or an arc with the word , (or a arc with the inverse word), and in any case, is disjoint from and is the required . If the other end point of is in stack three then it intersects once, whereas intersects twice. So is the required . Finally, if the other end point of is in stack four or five then it is disjoint from and is the required . See Figure 23(b).
-
Case 3
If is an arc with endpoints on and with the word , then is either an arc with the word or is an arc with the word (or a arc with the inverse word). In any case, is disjoint from and is the required . See Figure 23(c).
-
Case 4
If is an arc with the word , , then it is disjoint from and is the required . See Figure 23(d).
-
Case 5
Suppose that is an -arc or a -arc with the word , . Then, is disjoint from and is the required . See Figure 23(e).
∎
Owing to the symmetry of , all of the above discussion holds even if we replace by any arc on with both endpoints on or both endpoints on describing a single letter word in . For comprehensiveness, Figure 24 shows the eight possibilities for such an arc. We note that, in some cases we might have to use instead of throughout the above discussion for the inequalities to hold.

So the above discussion proves Theorem 4.1.
5 A Reduction Algorithm
We have the following:
Lemma 5.1.
Suppose that for a reducing sphere of . Then , unless in which case is automatically .
Proof.
First we note that all three of and cannot be simultaneously zero because then will be a trivial curve on implying that is not a reducing sphere.
If , we can apply for some integer to to reduce to at which stage we get, , the standard reducing sphere. But then and is invariant under implying , which means .
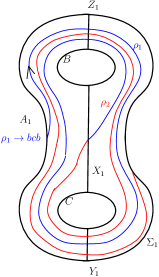
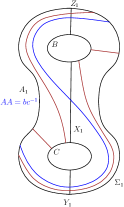
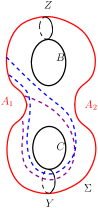
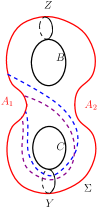
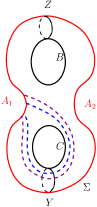
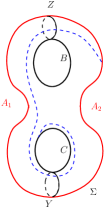
Among the four automorphisms of mentioned in section 2, we note that the non-zero integral powers of are the only ones which change the value of . Lemma 5.1 shows that the lowest possible value of is . Three possibilities for with are: (i) giving the standard reducing sphere , (ii) giving the simple reducing sphere or (iii) giving the simple reducing sphere . The reducing curves of and are shown in Figure 25. We note that and , where is the order three automorphism of described in section 2.



Let be a reducing sphere of . Using automorphisms and , we have the following algorithm which transforms into :
Algorithm 5.2.
Reduction Algorithm:
-
Step 1:
If then or .
If , Exit.
Else: apply or to or , respectively, to get . Exit. -
Step 2:
While , Do
-
Step (i):
If , go to Step (ii), else: let , . If , set to be . If , set to be . Go to Step (ii).
-
Step (ii):
Let , . If , set to be . If , set to be .
-
Step (i):
-
Step 3:
Now, and or .
If , Exit.
Else: apply or to or , respectively, to get . Exit.
Note that in Step (i) within the while-loop in the reduction algorithm for , if , Theorem 2.2 asserts that one of or will hold. Also, in Step (ii) within the while-loop, Theorem 4.1 asserts that one of or holds. So each iteration of the while loop indeed updates to a new reducing sphere such that .
By applying the reduction algorithm to the given reducing sphere , we can obtain . So by applying the automorphisms or in the inverse sequence, as dictated by the reduction algorithm, we can obtain from . Note that this inverse process applies a reduced word, , of automorphisms or to to obtain .
Let , then for some reducing sphere . By using the reducing algorithm, we get a word in the automorphisms or such that , so . This implies that . If we assume that is finitely generated by the automorphisms and , then since is also a finite word generated by and , we have that , an arbitrary element in , can also be written as a word in and their inverses. Hence we can conclude that is finitely generated by .
We conclude this article by asking a question. Let a triple of non-negative integers be called a non-triangular triple if it satisfies one of the inequalities or . From Corollary 2.4, the set of triples of intersection numbers with the curves as in Figure 2 of a given reducing sphere for is a specific subset of the set of non-triangular triples of integers.
Question 5.1.
Describe the set which is in one-to-one correspondence with the set of reducing spheres for the genus-2 Heegaard splitting of .
References
- Akbas [2008] Erol Akbas. A presentation for the automorphisms of the 3-sphere that preserve a genus two Heegaard splitting. Pacific J. Math., 236(2):201–222, 2008.
- Cho [2008] Sangbum Cho. Homeomorphisms of the 3-sphere that preserve a Heegaard splitting of genus two. Proc. Amer. Math. Soc., 136(3):1113–1123, 2008.
- Farb and Margalit [2012] Benson Farb and Dan Margalit. A primer on mapping class groups, volume 49 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 2012.
- Freedman and Scharlemann [2018] Michael Freedman and Martin Scharlemann. Powell moves and the goeritz group, 2018. URL https://arxiv.org/abs/1804.05909.
- Powell [1980] Jerome Powell. Homeomorphisms of leaving a Heegaard surface invariant. Trans. Amer. Math. Soc., 257(1):193–216, 1980.
- Scharlemann [2003] Martin Scharlemann. Heegaard splittings of 3-manifolds. In Low dimensional topology, volume 3 of New Stud. Adv. Math., pages 25–39. Int. Press, Somerville, MA, 2003.
- Scharlemann [2004] Martin Scharlemann. Automorphisms of the 3-sphere that preserve a genus two Heegaard splitting. Bol. Soc. Mat. Mexicana (3), 10(Special Issue):503–514, 2004.
- Volodin et al. [1974] I. A. Volodin, V. E. Kuznecov, and A. T. Fomenko. The problem of the algorithmic discrimination of the standard three-dimensional sphere. Uspehi Mat. Nauk, 29(5(179)):71–168, 1974. Appendix by S. P. Novikov.
- Waldhausen [1968] Friedhelm Waldhausen. Heegaard-Zerlegungen der -Sphäre. Topology, 7:195–203, 1968.
- Zupan [2020] Alexander Zupan. The Powell conjecture and reducing sphere complexes. J. Lond. Math. Soc. (2), 101(1):328–348, 2020.