Reinforcement of superconductivity by quantum critical fluctuations of metamagnetism in UTe2
Abstract
The normal-conducting state of the superconductor UTe2 is studied by entropy analysis for magnetic fields along the -axis, obtained from magnetization using the relation . We observe a strong increase in entropy with magnetic field due to metamagnetic fluctuations (spatially uniform, ). The field dependence is well described by the Hertz-Millis-Moriya theory for quantum criticality of itinerant metamagnetism. Notably, the lower bound of the quantum-critical region coincides well with the position of the minimum in the superconducting transition temperature . Hence, our results suggest that fluctuations reinforce the superconductivity.
Unconventional superconductivity arises from an anomalous normal-conducting (NC) state [1, 2, 3]. The NC states of heavy-fermion, iron-pnictide, and cuprate high- superconductors exhibit non-Fermi liquid behavior with unusual -dependence of resistivity due to quantum fluctuations from magnetic quantum criticality. Extensive studies have established close relationships between superconductivity and magnetic criticality, leading to the widely accepted belief that the superconducting (SC) pairing interaction is provided by such fluctuations. Hence, investigating the NC states of unconventional superconductors is of great importance to gain insights into the SC pairing mechanism.
In this study, our focus is on the recently discovered superconductor, UTe2, which undergoes a superconducting transition at K [4, 5]. The superconductivity has garnered significant attention due to its reinforcement (re-entrance) under high magnetic fields and the presence of multiple superconducting phases [4, 6, 7, 8, 1, 10]. The pairing symmetry has been subject to extensive investigations [11, 12, 13, 14, 15, 16]. Furthermore, considerable effort has been dedicated to improving the crystal quality, leading to a significant enhancement of to over 2 K from the originally reported value [17, 18, 19, 20]. Notably, recent progress has allowed the successful observation of quantum oscillations in high-quality single crystals grown using the molten-salt flux (MSF) method [21, 22].
The reinforcement of superconductivity is observed when the field is applied along the hard -axis, where a sharp metamagnetic (MM) transition takes place around 35 T [23, 24]. There, the superconducting transition temperature is initially suppressed with magnetic field; however, it remarkably enhances above 15,T. As a result, a minimum in () is observed as a function of magnetic field. For certain magnetic field angles between the - and -axes, the magnetic field completely suppresses the superconductivity, but above 40,T, the superconductivity reappears [25, 6]. These reinforcement and reappearance bear resemblance to other uranium ferromagnetic superconductors, URhGe and UCoGe of which the superconductivity may be mediated by ferromagnetic fluctuations [26, 27, 28, 29, 30]. Unlike these superconductors, UTe2 is paramagnetic. The absence of ferromagnetism and the similarity to ferromagnetic superconductors open the intriguing possibility of ferromagnetic quantum fluctuations providing the superconducting pairing interaction. However, the magnetic susceptibility of recently grown high-quality crystals tends to saturate at low temperatures [20], which is consistent with a temperature-independent Knight shift [31]. Instead, magnetic excitations at incommensurate -vectors have been observed by neutron scattering experiments [32, 33]. Therefore, the nature of magnetic fluctuations responsible for the superconductivity remains unknown [34]. A broad anomaly observed in the NC state around 15 K in several thermodynamic, transport, and NMR experiments may be related to the key magnetic fluctuations [35, 36, 9, 31].
In strong magnetic fields along the -axis, fluctuations associated with the MM transition likely play a crucial role. Metamagnetism is identical to ferromagnetism in the sense that they both correspond to a spatially-uniform () magnetic instability, as evidenced by the discontinuity in uniform magnetization, , at the transition field. The only distinction from ferromagnetism lies in its induction by magnetic field. When the critical end point (CEP) of metamagnetism is tuned to zero temperature, the quantum fluctuations lead to the formation of an anomalous metallic state [7, 6]. Even when a system is not precisely tuned to QCEP but is in close proximity with the CEP at a finite temperature, the quantum-critical fluctuations can still induce anomalous state. [7, 40, 6, 2, 3, 43, 44]. In UTe2, an increase in electron mass and longitudinal fluctuations with the field towards the metamagnetism is observed and is proposed to drive the reinforcement of superconductivity [23, 45, 1, 46].
Entropy is a direct thermodynamic measure of fluctuations, as it accumulates at a quantum critical point and exhibits a peak as a function of control parameters, such as magnetic field and pressure [47, 48]. Because unconventional superconducting pairing is believed to be mediated by such quantum critical fluctuations, it is interesting to map entropy in some parameter space. In UTe2, the superconductivity couples to the magnetic field in a very peculiar manner, as evidenced by the non-monotonic behavior of . Therefore, the magnetic field-temperature parameter space is the most interesting to map entropy. To achieve this, we performed high-resolution magnetization measurements for -axis, enabling us to extract the field dependence of entropy in the NC state of UTe2 using a thermodynamic relation, . The consistency with specific heat [1] is checked by comparing and == at low temperatures in Fermi liquid regime, where is the Sommerfeld coefficient. (see Supplementary Material [49]). In this study, we reveal an anomalous increase in fluctuations attributed to metamagnetism in an entropy map. We investigate the nature of these fluctuations by fitting their field dependence with the Hertz-Millis-Moriya theory, which pertains to the quantum criticality of itinerant metamagnetism [7, 6]. The theory, widely recognized as a standard, is frequently employed to describe the anomalous behavior associated with metamagnetic quantum criticality [40, 3, 43, 52, 53].
Magnetization is measured by a vibration-sample magnetometer (VSM) with an accuracy of 210-4 emu in magnetic fields up to 24 T and for temperatures between 2.2 K and 65K, in the High-Field Laboratory for Superconducting Materials at the Institute for Materials Research at Tohoku University. We measured magnetization () at various temperatures with a typical interval of 1 K up to 20 K, 2K up to 40 K and 5 K up to 65 K to obtain a magnetization landscape (see Supplementary Material [49]). From the slope along -axis we have a landscape of field derivative of entropy /=/. Then, / is integrated over to obtain entropy increment from zero field, namely . Note that does not contain entropy at zero field. A large single crystal with a weight of 94 mg, grown by the chemical vapor transport (CVT) method, is used. The SC transition temperature, the residual resistivity ratio and the residual specific heat coefficient divided by the value at the normal-conducting state of the same batch are respectively =1.7 K, RRR=25 and . We note that the properties of the normal-conducting state remain unaffected by the sample quality. Specifically, the characteristics of magnetic fluctuations and the metamagnetic critical field show no variation across crystals of different quality [46, 54]. We will delve into the discussion later, explaining how this robustness in the properties of metamagnetism leads to the independence of , where exhibits a minimum, from variations in the sample quality.
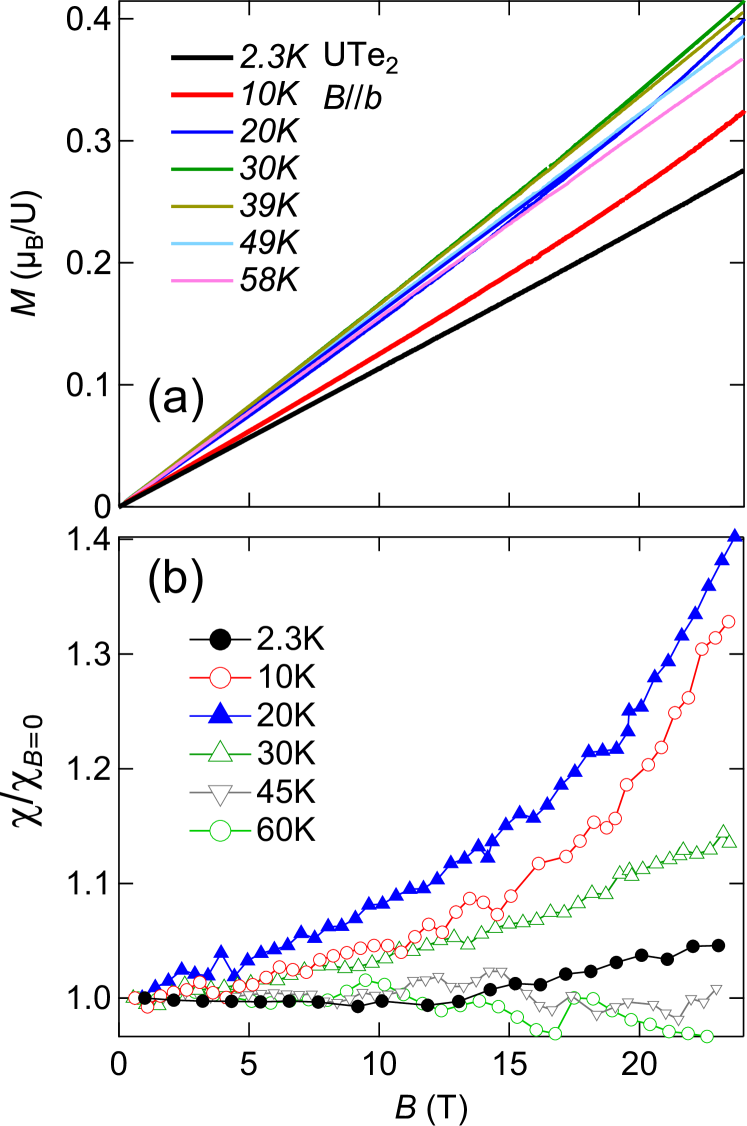
Figure 1(a) shows the magnetization of UTe2 for the field along -axis. Magnetization at 10 and 20 K shows clearly the stronger-than linear field dependence due to metamagnetic fluctuations, which we will discuss later. Note that the magnetization of a paramagnet, such as those described by the Brillouin function, exhibits a downward curvature. As a consequence, the differential magnetic susceptibility () normalized by the zero-field value of a paramagnet is always less than 1 under magnetic fields, . Figure 1(b) displays such a normalized magnetic susceptibility of UTe2 for the field along -axis. Reflecting the non-linear magnetization, at 10 and 20 K increases with magnetic field. The non-linear magnetization (1) is observed up to 30 K, indicating the influence of metamagnetic fluctuations in a wide temperature range. Notably, at 10 and 20 K changes its slope above 15 T. At 2.3 K, is nearly constant below 15 T, but, it deviates from the constant value above 15 T.
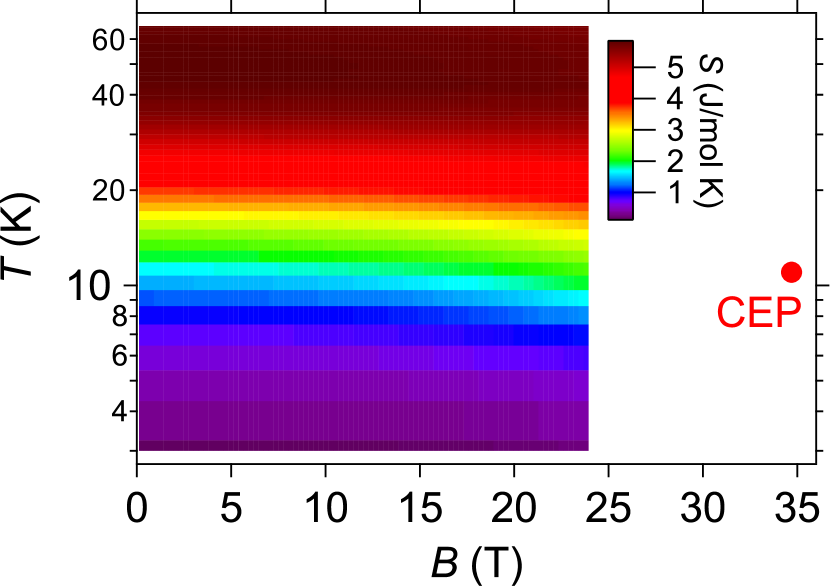
From the () measurements, we obtain magnetic entropy increment , as shown in Fig. 2. For an ideal paramagnet entropy decreases with magnetic field, because magnetic field aligns magnetic moments. In heavy fermion compounds, there is a cross-over across [55]. At high temperatures above paramagnetic behavior is expected, while below entropy depends on subtle field variations of density of states, since in Fermi liquid (FL) =.
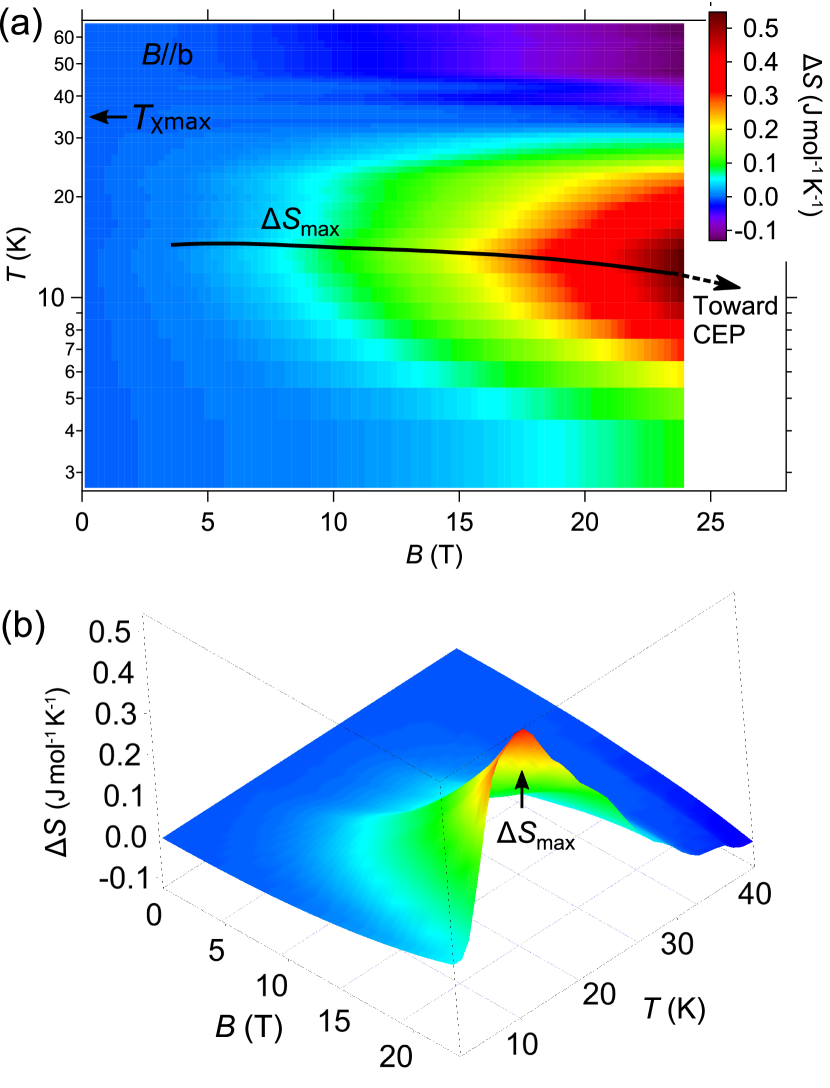
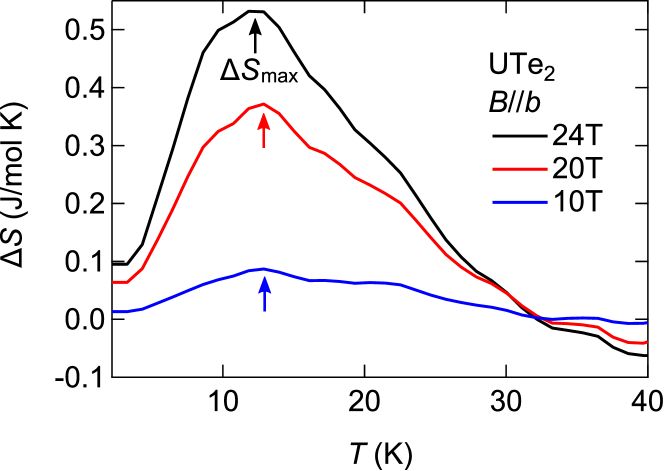
In UTe2, the paramagnetic behavior with decreasing entropy is found at temperatures above 35 K, as shown in Fig. 2. This temperature 35 K corresponds to a maximum of magnetization as a function of temperature, where ==0, in agreement with the reported maximum of magnetic susceptibility around 35 K [4, 24]. Across this temperature changes its sign. Below this temperature decreases with decreasing , therefore entropy increases with magnetic field, =0. Such entropy increase is commonly observed in compounds with MM transitions/cross-overs due to increasing MM fluctuations toward the critical field [2, 3, 5]. In Figs. 2(a,b) we plot a position of , where is the most as a function of temperature.(See also Supplementary Material for the temperature dependence of at different magnetic fields [49].) It shifts to lower temperatures with magnetic field, approaching the CEP of metamagnetism. At lower tempratures below the CEP, the entropy increase with magnetic field weakens. This is attributed to the weakening of magnetic fluctuations caused by the sharpening of metamagnetic transition with decreasing temperature. We note that the entropy increase still remains finite even at low temperatures, as can be seen in Fig.3(a), likely playing a crucial role in the reinforcement of superconductivity. Importantly, as demonstrated by Figure. 2, the entropy increase at low temperatures is caused by the metamagnetism, which represents a instability.
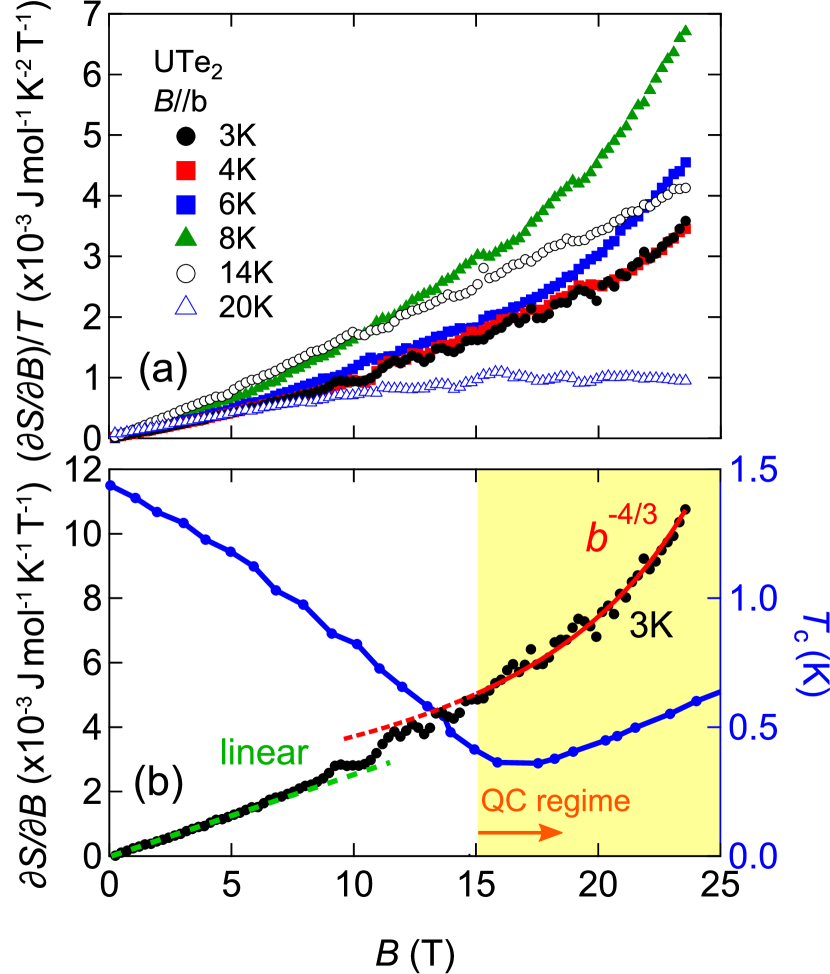
In Fig. 3(a), we plot . In FL state, where , this quantity equals to the field derivative of Sommerfeld coefficient, , which is -independent. The data sets at 3 and 4 K lay on top of each other, indicating formation of FL state below 4 K. They exhibit the upward curvature, indicating an accelerating increase of entropy at high fields. The upward curvature persists up to 8 K and changes to a downward curvature at high temperatures above the line of . Magnetic field derivative of entropy, , at 3 K in the FL regime, is plotted in Fig. 3(b). At low fields it is linear in field, as expected from a symmetry consideration, ()(-) with a leading -linear term. The data gradually deviates from the linear dependence and increases rapidly with a positive curvature at high fields.
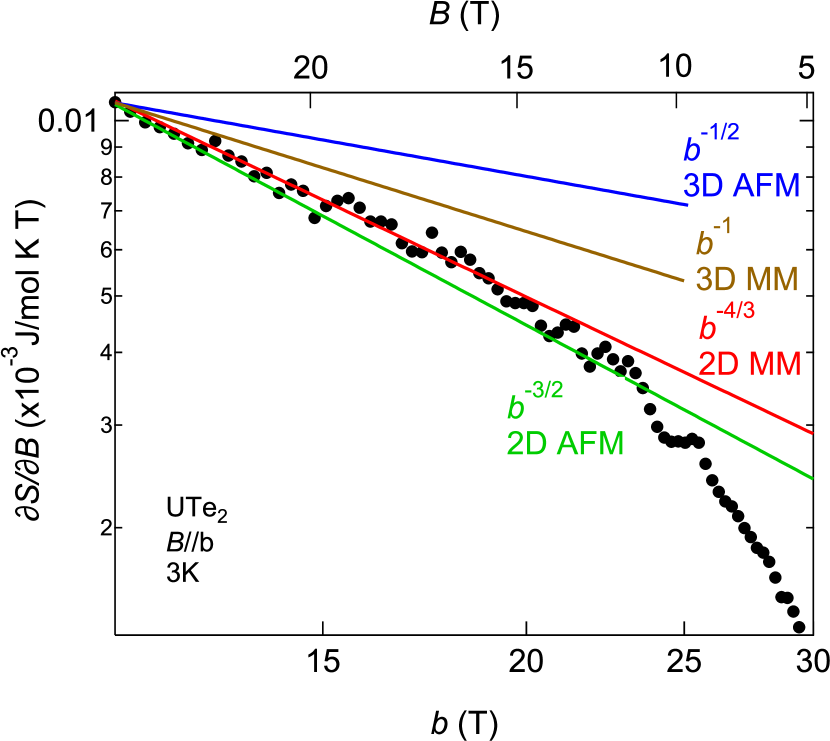
According to the Hertz-Millis-Moriya theory [7, 6], / in the critical regime follows , where =- is the distance to the critical field, , and is the dimensionality. Since Fermi surfaces consist of mainly cylindrical ones [59, 21, 22], =2 is appropriate, resulting in a power-law dependence . By fixing =34.75 T of a recently reported detailed study [1], the data is well described by above 15 T. (See also Supplementary Material for fitting with other cases such as three-dimensional (3D) metamagnetism and antiferromagnetic fluctuations [49].) The best fit, among all the considered models, is achieved with 2D metamagnetism, suggesting that 2D metamagnetic quantum critical fluctuations are dominanting at high magnetic fields. The lower-bound field of 15 T coincides well with the field of () minimum, . Furthermore, above the same field, specific heat [1] also follows the theoretical power-law, in agreement with our result (see Supplementary Material [49]). This indicates that the system at low fields is initially non-critical with the linear-in-field dependence and then crossovers to the two-dimensional quantum critical behavior above 15 T. Given that the theory addresses fluctuations [6], the coincidence between and the lower field boundary of the quantum critical regime hints at the involvement of metamagnetic quantum fluctuations in bolstering the superconducting transition temperature.
While this correlation is suggestive, it should be interpreted with caution until further evidence solidifies this connection, because antiferromagnetic (AFM, ) excitations have been identified in neutron scattering experiments as reported in [32, 33, 34]. A key unresolved question concerns how these AFM fluctuations evolve under magnetic fields. The observation that without zero-field entropy markedly reflects the anomaly associated with the metamagnetism, underscores the predominant role of metamagnetism at magnetic fields. We note that the change in entropy in our study, represented by , accounts for merely 10% of at its peak. This is substantially smaller compared to the entropy increase with temperature at zero magnetic field, which reaches 80% of at 25 K [9]. Consequently, the anomaly due to metamagnetism become less discernible in the absolute entropy, obscured by the dominant zero-field entropy (See Supplementary Material [49]).This could be interpreted as at zero (or low) magnetic fields, AFM contributions being more significant, whereas at high magnetic fields, the influence of metamagnetism prevails. Such a trend aligns well with the fundamental behaviour of AFM coupling, which tends to diminish in the presence of magnetic fields. Furthermore, a recent NMR study highlights dominant ferromagnetic fluctuations along the -axis [60]. While our findings suggest the dominance of fluctuations, further direct investigation into magnetic fluctuations with -resolved experiments, particularly through neutron scattering, is essential for further understanding.
The recent improvements of sample quality have enhanced by 25 % from the originally reported value [20]. Notably, the upper critical field, , is enhanced twice for the field along the magnetic easy -axis, owing to a weak metamagnetism around 8 T [55]. In sharp contrast, () curve for the field along -axis does not change its characteristic shape with a minimum at the . Remarkably, is independent from the sample quality [10]. This is most likely because is determined by metamagnetic fluctuations, which are not influenced from the crystal quality [46]. This assertion is further supported by the fact that the metamagnetic critical field is independent from the sample quality [54].
In this study, we show the accelerated increase of entropy with magnetic field along -axis in UTe2 due to metamagnetic fluctuations. The field dependence in the Fermi liquid regime is well described by Hertz-Millis-Moriya theory for quantum criticality of itinerant metamagnetism. The coincidence between the low-field bound of the quantum-critical fluctuations and indicates that fluctuations boost superconductivity. This is in line with the result for the field along the easy -axis, showing that the weak metamagnetism strongly enhances the upper critical field [55]. Thus, our results show that 0 fluctuations play crucial roles in the spin-triplet superconductivity in UTe2 and promotes further experimental research to more conclusively determine the nature of fluctuations under high magnetic fields.
We thank M. Garst, Y. Yanase, H. Kusunose and T. Takimoto for stimulating discussions. We thank M. Nagai and K. Shirasaki for experimental support. The work was supported by JSPS KAKENHI Grant Numbers, JP16KK0106, JP17K05522, JP17K05529, and JP20K03852 and by the JAEA REIMEI Research Program. This work (A part of high magnetic field experiments) was performed at HFLSM under the IMR-GIMRT program (Proposal Numbers 202012-HMKPB-0012, 202112-HMKPB-0010, 202112-RDKGE-0036 and 202012-RDKGE-0084).
References
- Mathur et al. [1998] N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer, and G. G. Lonzarich, Magnetically mediated superconductivity in heavy fermion compounds, Nature 394, 39 (1998).
- Cooper et al. [2009] R. A. Cooper, Y. Wang, B. Vignolle, O. J. Lipscombe, S. M. Hayden, Y. Tanabe, T. Adachi, Y. Koike, M. Nohara, H. Takagi, C. Proust, and N. E. Hussey, Anomalous criticality in the electrical resistivity of La2-xSrxCuO4, Science 323, 603 (2009), https://www.science.org/doi/pdf/10.1126/science.1165015 .
- Hashimoto et al. [2012] K. Hashimoto, K. Cho, T. Shibauchi, S. Kasahara, Y. Mizukami, R. Katsumata, Y. Tsuruhara, T. Terashima, H. Ikeda, M. A. Tanatar, H. Kitano, N. Salovich, R. W. Giannetta, P. Walmsley, A. Carrington, R. Prozorov, and Y. Matsuda, A sharp peak of the zero-temperature penetration depth at optimal composition in BaFe2(As1-xPx)2, Science 336, 1554 (2012), https://www.science.org/doi/pdf/10.1126/science.1219821 .
- Ran et al. [2019a] S. Ran, C. Eckberg, Q.-P. Ding, Y. Furukawa, T. Metz, S. R. Saha, I.-L. Liu, M. Zic, H. Kim, J. Paglione, and N. P. Butch, Nearly ferromagnetic spin-triplet superconductivity, Science 365, 684 (2019a).
- Aoki et al. [2019a] D. Aoki, A. Nakamura, F. Honda, D. Li, Y. Homma, Y. Shimizu, Y. J. Sato, G. Knebel, J.-P. Brison, A. Pourret, D. Braithwaite, G. Lapertot, Q. Niu, M. Vališka, H. Harima, and J. Flouquet, Unconventional superconductivity in heavy fermion UTe2, Journal of the Physical Society of Japan 88, 043702 (2019a).
- Knebel et al. [2019] G. Knebel, W. Knafo, A. Pourret, Q. Niu, M. Vališka, D. Braithwaite, G. Lapertot, M. Nardone, A. Zitouni, S. Mishra, I. Sheikin, G. Seyfarth, J.-P. Brison, D. Aoki, and J. Flouquet, Field-reentrant superconductivity close to a metamagnetic transition in the heavy-fermion superconductor UTe2, Journal of the Physical Society of Japan 88, 063707 (2019).
- Aoki et al. [2020] D. Aoki, F. Honda, G. Knebel, D. Braithwaite, A. Nakamura, D. Li, Y. Homma, Y. Shimizu, Y. J. Sato, J.-P. Brison, and J. Flouquet, Multiple superconducting phases and unusual enhancement of the upper critical field in UTe2, Journal of the Physical Society of Japan, Journal of the Physical Society of Japan 89, 053705 (2020).
- Kinjo et al. [2023] K. Kinjo, H. Fujibayashi, S. Kitagawa, K. Ishida, Y. Tokunaga, H. Sakai, S. Kambe, A. Nakamura, Y. Shimizu, Y. Homma, D. X. Li, F. Honda, D. Aoki, K. Hiraki, M. Kimata, and T. Sasaki, Change of superconducting character in induced by magnetic field, Phys. Rev. B 107, L060502 (2023).
- Rosuel et al. [2022] A. Rosuel, C. Marcenat, G. Knebel, T. Klein, A. Pourret, N. Marquardt, Q. Niu, S. Rousseau, A. Demuer, G. Seyfarth, G. Lapertot, D. Aoki, D. Braithwaite, J. Flouquet, and J.-P. Brison, Field-induced tuning of the pairing state in a superconductor (2022).
- Sakai et al. [2023] H. Sakai, Y. Tokiwa, P. Opletal, M. Kimata, S. Awaji, T. Sasaki, D. Aoki, S. Kambe, Y. Tokunaga, and Y. Haga, Field induced multiple superconducting phases in along hard magnetic axis (2023).
- Jiao et al. [2020] L. Jiao, S. Howard, S. Ran, Z. Wang, J. O. Rodriguez, M. Sigrist, Z. Wang, N. P. Butch, and V. Madhavan, Chiral superconductivity in heavy-fermion metal UTe2, Nature 579, 523 (2020).
- Kittaka et al. [2020] S. Kittaka, Y. Shimizu, T. Sakakibara, A. Nakamura, D. Li, Y. Homma, F. Honda, D. Aoki, and K. Machida, Orientation of point nodes and nonunitary triplet pairing tuned by the easy-axis magnetization in Ue2, Phys. Rev. Research 2, 032014 (2020).
- Xu et al. [2019] Y. Xu, Y. Sheng, and Y.-f. Yang, Quasi-two-dimensional fermi surfaces and unitary spin-triplet pairing in the heavy fermion superconductor UTe2, Phys. Rev. Lett. 123, 217002 (2019).
- Ishizuka et al. [2019] J. Ishizuka, S. Sumita, A. Daido, and Y. Yanase, Insulator-metal transition and topological superconductivity in UTe2 from a first-principles calculation, Phys. Rev. Lett. 123, 217001 (2019).
- Machida [2021] K. Machida, Nonunitary triplet superconductivity tuned by field-controlled magnetization: Urhge, ucoge, and , Phys. Rev. B 104, 014514 (2021).
- Kanasugi and Yanase [2022] S. Kanasugi and Y. Yanase, Anapole superconductivity from pt-symmetric mixed-parity interband pairing, Communications Physics 5, 39 (2022).
- Haga et al. [2022] Y. Haga, P. Opletal, Y. Tokiwa, E. Yamamoto, Y. Tokunaga, S. Kambe, and H. Sakai, Effect of uranium deficiency on normal and superconducting properties in unconventional superconductor UTe2, Journal of Physics: Condensed Matter 34, 175601 (2022).
- Rosa et al. [2022] P. F. S. Rosa, A. Weiland, S. S. Fender, B. L. Scott, F. Ronning, J. D. Thompson, E. D. Bauer, and S. M. Thomas, Single thermodynamic transition at 2 K in superconducting UTe2 single crystals, Communications Materials 3, 33 (2022).
- Aoki et al. [2022a] D. Aoki, J.-P. Brison, J. Flouquet, K. Ishida, G. Knebel, Y. Tokunaga, and Y. Yanase, Unconventional superconductivity in UTe2, Journal of Physics: Condensed Matter 34, 243002 (2022a).
- Sakai et al. [2022] H. Sakai, P. Opletal, Y. Tokiwa, E. Yamamoto, Y. Tokunaga, S. Kambe, and Y. Haga, Single crystal growth of superconducting by molten salt flux method, Phys. Rev. Mater. 6, 073401 (2022).
- Aoki et al. [2023] D. Aoki, I. Sheikin, A. McCollam, J. Ishizuka, Y. Yanase, G. Lapertot, J. Flouquet, and G. Knebel, de haas–van alphen oscillations for the field along c-axis in UTe2, Journal of the Physical Society of Japan 92, 065002 (2023), https://doi.org/10.7566/JPSJ.92.065002 .
- Eaton et al. [2023] A. G. Eaton, T. I. Weinberger, N. J. M. Popiel, Z. Wu, A. J. Hickey, A. Cabala, J. Pospisil, J. Prokleska, T. Haidamak, G. Bastien, P. Opletal, H. Sakai, Y. Haga, R. Nowell, S. M. Benjamin, V. Sechovsky, G. G. Lonzarich, F. M. Grosche, and M. Valiska, Quasi-2d fermi surface in the anomalous superconductor UTe2 (2023), arXiv:2302.04758 [cond-mat.supr-con] .
- Knafo et al. [2019] W. Knafo, M. Vališka, D. Braithwaite, G. Lapertot, G. Knebel, A. Pourret, J.-P. Brison, J. Flouquet, and D. Aoki, Magnetic-field-induced phenomena in the paramagnetic superconductor UTe2, Journal of the Physical Society of Japan 88, 063705 (2019).
- Miyake et al. [2019] A. Miyake, Y. Shimizu, Y. J. Sato, D. Li, A. Nakamura, Y. Homma, F. Honda, J. Flouquet, M. Tokunaga, and D. Aoki, Metamagnetic transition in heavy fermion superconductor UTe2, Journal of the Physical Society of Japan 88, 063706 (2019).
- Ran et al. [2019b] S. Ran, I.-L. Liu, Y. S. Eo, D. J. Campbell, P. M. Neves, W. T. Fuhrman, S. R. Saha, C. Eckberg, H. Kim, D. Graf, F. Balakirev, J. Singleton, J. Paglione, and N. P. Butch, Extreme magnetic field-boosted superconductivity, Nature Physics 15, 1250 (2019b).
- Aoki et al. [2019b] D. Aoki, K. Ishida, and J. Flouquet, Review of u-based ferromagnetic superconductors: Comparison between UGe2, URhGe, and UCoGe, Journal of the Physical Society of Japan 88, 022001 (2019b), https://doi.org/10.7566/JPSJ.88.022001 .
- Aoki et al. [2001] D. Aoki, A. Huxley, E. Ressouche, D. Braithwaite, J. Flouquet, J.-P. Brison, E. Lhotel, and C. Paulsen, Coexistence of superconductivity and ferromagnetism in urhge, Nature 413, 613 (2001).
- Huy et al. [2007] N. T. Huy, A. Gasparini, D. E. de Nijs, Y. Huang, J. C. P. Klaasse, T. Gortenmulder, A. de Visser, A. Hamann, T. Görlach, and H. v. Löhneysen, Superconductivity on the border of weak itinerant ferromagnetism in ucoge, Phys. Rev. Lett. 99, 067006 (2007).
- Hattori et al. [2012] T. Hattori, Y. Ihara, Y. Nakai, K. Ishida, Y. Tada, S. Fujimoto, N. Kawakami, E. Osaki, K. Deguchi, N. K. Sato, and I. Satoh, Superconductivity induced by longitudinal ferromagnetic fluctuations in ucoge, Phys. Rev. Lett. 108, 066403 (2012).
- Tokunaga et al. [2015] Y. Tokunaga, D. Aoki, H. Mayaffre, S. Krämer, M.-H. Julien, C. Berthier, M. Horvatić, H. Sakai, S. Kambe, and S. Araki, Reentrant superconductivity driven by quantum tricritical fluctuations in urhge: Evidence from 59Co nmr in URh0.9Co0.1Ge, Phys. Rev. Lett. 114, 216401 (2015).
- Tokunaga et al. [2022] Y. Tokunaga, H. Sakai, S. Kambe, Y. Haga, Y. Tokiwa, P. Opletal, H. Fujibayashi, K. Kinjo, S. Kitagawa, K. Ishida, A. Nakamura, Y. Shimizu, Y. Homma, D. Li, F. Honda, and D. Aoki, Slow electronic dynamics in the paramagnetic state of UTe2, Journal of the Physical Society of Japan 91, 023707 (2022).
- Duan et al. [2021] C. Duan, R. E. Baumbach, A. Podlesnyak, Y. Deng, C. Moir, A. J. Breindel, M. B. Maple, E. M. Nica, Q. Si, and P. Dai, Resonance from antiferromagnetic spin fluctuations for superconductivity in UTe2, Nature 600, 636 (2021).
- Knafo et al. [2021a] W. Knafo, G. Knebel, P. Steffens, K. Kaneko, A. Rosuel, J.-P. Brison, J. Flouquet, D. Aoki, G. Lapertot, and S. Raymond, Low-dimensional antiferromagnetic fluctuations in the heavy-fermion paramagnetic ladder compound UTe2, Phys. Rev. B 104, L100409 (2021a).
- Butch et al. [2022] N. P. Butch, S. Ran, S. R. Saha, P. M. Neves, M. P. Zic, J. Paglione, S. Gladchenko, Q. Ye, and J. A. Rodriguez-Rivera, Symmetry of magnetic correlations in spin-triplet superconductor UTe2, npj Quantum Materials 7, 39 (2022).
- Tokunaga et al. [2019] Y. Tokunaga, H. Sakai, S. Kambe, T. Hattori, N. Higa, G. Nakamine, S. Kitagawa, K. Ishida, A. Nakamura, Y. Shimizu, Y. Homma, D. Li, F. Honda, and D. Aoki, 125te-nmr study on a single crystal of heavy fermion superconductor UTe2, J. Phys. Soc. Jpn. 88, 073701 (2019).
- Eo et al. [2021] Y. S. Eo, S. R. Saha, H. Kim, S. Ran, J. A. Horn, H. Hodovanets, J. Collini, W. T. Fuhrman, A. H. Nevidomskyy, N. P. Butch, M. S. Fuhrer, and J. Paglione, Anomalous c-axis transport response of UTe2 (2021).
- Willa et al. [2021] K. Willa, F. Hardy, D. Aoki, D. Li, P. Wiecki, G. Lapertot, and C. Meingast, Thermodynamic signatures of short-range magnetic correlations in UTe2, Phys. Rev. B 104, 205107 (2021).
- Millis et al. [2002] A. J. Millis, A. J. Schofield, G. G. Lonzarich, and S. A. Grigera, Metamagnetic quantum criticality in metals, Phys. Rev. Lett. 88, 217204 (2002).
- Zacharias and Garst [2013] M. Zacharias and M. Garst, Quantum criticality in itinerant metamagnets, Phys. Rev. B 87, 075119 (2013).
- Gegenwart et al. [2006] P. Gegenwart, F. Weickert, M. Garst, R. S. Perry, and Y. Maeno, Metamagnetic quantum criticality in studied by thermal expansion, Phys. Rev. Lett. 96, 136402 (2006).
- Rost et al. [2009] A. W. Rost, R. S. Perry, J.-F. Mercure, A. P. Mackenzie, and S. A. Grigera, Entropy landscape of phase formation associated with quantum criticality in Sr3Ru2O7, Science 325, 1360 (2009), http://www.sciencemag.org/content/325/5946/1360.full.pdf .
- Tokiwa et al. [2013] Y. Tokiwa, M. Garst, P. Gegenwart, S. L. Bud’ko, and P. C. Canfield, Quantum bicriticality in the heavy-fermion metamagnet YbAgGe, Phys. Rev. Lett. 111, 116401 (2013).
- Aoki et al. [2011] D. Aoki, T. Combier, V. Taufour, T. D. Matsuda, G. Knebel, H. Kotegawa, and J. Flouquet, Ferromagnetic quantum critical endpoint in ucoal, Journal of the Physical Society of Japan 80, 094711 (2011), https://doi.org/10.1143/JPSJ.80.094711 .
- Kotegawa et al. [2011] H. Kotegawa, V. Taufour, D. Aoki, G. Knebel, and J. Flouquet, Evolution toward quantum critical end point in uge2, Journal of the Physical Society of Japan 80, 083703 (2011), https://doi.org/10.1143/JPSJ.80.083703 .
- Knafo et al. [2021b] W. Knafo, M. Nardone, M. Vališka, A. Zitouni, G. Lapertot, D. Aoki, G. Knebel, and D. Braithwaite, Comparison of two superconducting phases induced by a magnetic field in UTe2, Communications Physics 4, 40 (2021b).
- Tokunaga et al. [2023] Y. Tokunaga, H. Sakai, S. Kambe, P. Opletal, Y. Tokiwa, Y. Haga, S. Kitagawa, K. Ishida, D. Aoki, G. Knebel, G. Lapertot, S. Krämer, and M. Horvatić, Longitudinal spin fluctuations driving field-reinforced superconductivity in , Phys. Rev. Lett. 131, 226503 (2023).
- Garst and Rosch [2005] M. Garst and A. Rosch, Sign change of the gruneisen parameter and magnetocaloric effect near quantum critical points., Phys. Rev. B 72, 205129 (2005).
- Wu et al. [2011] J. Wu, L. Zhu, and Q. Si, Entropy accumulation near quantum critical points: effects beyond hyperscaling, Journal of Physics: Conference Series 273, 012019 (2011).
- [49] See Supplemental Material at [URL] for additional data and analyses, including: a consistency check through the comparison of with , which are expected to be equal in the Fermi liquid state at low temperatures; the magnetization landscape in the - parameter space; variations of under magnetic fields as a function of temperature; fits of and specific heat data to various theoretical models; and a color contour plot of the absolute entropy in the - parameter space. The Supplemental Material also contains Refs. [4, Zhu].
- Zhu et al. [2003] L. Zhu, M. Garst, A. Rosch, and Q. Si, Universally diverging Grüneisen parameter and the magnetocaloric effect close to quantum critical points, Phys. Rev. Lett. 91, 066404 (2003).
- Tokiwa et al. [2015] Y. Tokiwa, C. Stingl, M.-S. Kim, T. Takabatake, and P. Gegenwart, Characteristic signatures of quantum criticality driven by geometrical frustration, Science Advances 1, 10.1126/sciadv.1500001 (2015).
- Weickert et al. [2010] F. Weickert, M. Brando, F. Steglich, P. Gegenwart, and M. Garst, Universal signatures of the metamagnetic quantum critical endpoint: Application to , Phys. Rev. B 81, 134438 (2010).
- Michor et al. [2004] H. Michor, M. El-Hagary, M. D. Mea, M. W. Pieper, M. Reissner, G. Hilscher, S. Khmelevskyi, P. Mohn, G. Schneider, G. Giester, and P. Rogl, Itinerant electron metamagnetism in , Phys. Rev. B 69, 081404 (2004).
- Wu et al. [2023] Z. Wu, T. I. Weinberger, J. Chen, A. Cabala, D. V. Chichinadze, D. Shaffer, J. Pospisil, J. Prokleska, T. Haidamak, G. Bastien, V. Sechovsky, A. J. Hickey, M. J. Mancera-Ugarte, S. Benjamin, D. E. Graf, Y. Skourski, G. G. Lonzarich, M. Valiska, F. M. Grosche, and A. G. Eaton, Enhanced triplet superconductivity in next generation ultraclean ute2 (2023), arXiv:2305.19033 [cond-mat.supr-con] .
- Tokiwa et al. [2022] Y. Tokiwa, P. Opletal, H. Sakai, K. Kubo, E. Yamamoto, S. Kambe, M. Kimata, S. Awaji, T. Sasaki, D. Aoki, Y. Tokunaga, and Y. Haga, Stabilization of superconductivity by metamagnetism in an easy-axis magnetic field on ute2 (2022).
- Ikeda et al. [2006] S. Ikeda, H. Sakai, D. Aoki, Y. Homma, E. Yamamoto, A. Nakamura, Y. Shiokawa, Y. Haga, and Y. Ōnuki, Single crystal growth and magnetic properties of UTe2, Journal of the Physical Society of Japan 75, 116 (2006).
- Li et al. [2021] D. Li, A. Nakamura, F. Honda, Y. J. Sato, Y. Homma, Y. Shimizu, J. Ishizuka, Y. Yanase, G. Knebel, J. Flouquet, and D. Aoki, Magnetic properties under pressure in novel spin-triplet superconductor UTe2, Journal of the Physical Society of Japan 90, 073703 (2021), https://doi.org/10.7566/JPSJ.90.073703 .
- Tokiwa et al. [2016] Y. Tokiwa, M. Mchalwat, R. S. Perry, and P. Gegenwart, Multiple metamagnetic quantum criticality in Sr3Ru2O7, Phys. Rev. Lett. 116, 226402 (2016).
- Aoki et al. [2022b] D. Aoki, H. Sakai, P. Opletal, Y. Tokiwa, J. Ishizuka, Y. Yanase, H. Harima, A. Nakamura, D. Li, Y. Homma, Y. Shimizu, G. Knebel, J. Flouquet, and Y. Haga, First observation of de haas-van alphen effect and fermi surfaces in unconventional superconductor UTe2 (2022b).
- Fujibayashi et al. [2023] H. Fujibayashi, K. Kinjo, G. Nakamine, S. Kitagawa, K. Ishida, Y. Tokunaga, H. Sakai, S. Kambe, A. Nakamura, Y. Shimizu, Y. Homma, D. Li, F. Honda, and D. Aoki, Low-temperature magnetic fluctuations investigated by 125te-nmr on the uranium-based superconductor ute2, Journal of the Physical Society of Japan 92, 053702 (2023), https://doi.org/10.7566/JPSJ.92.053702 .
Supplemental Materials for ”Reinforcement of superconductivity by quantum critical fluctuations of metamagnetism in UTe2”
I Consistency with specific heat
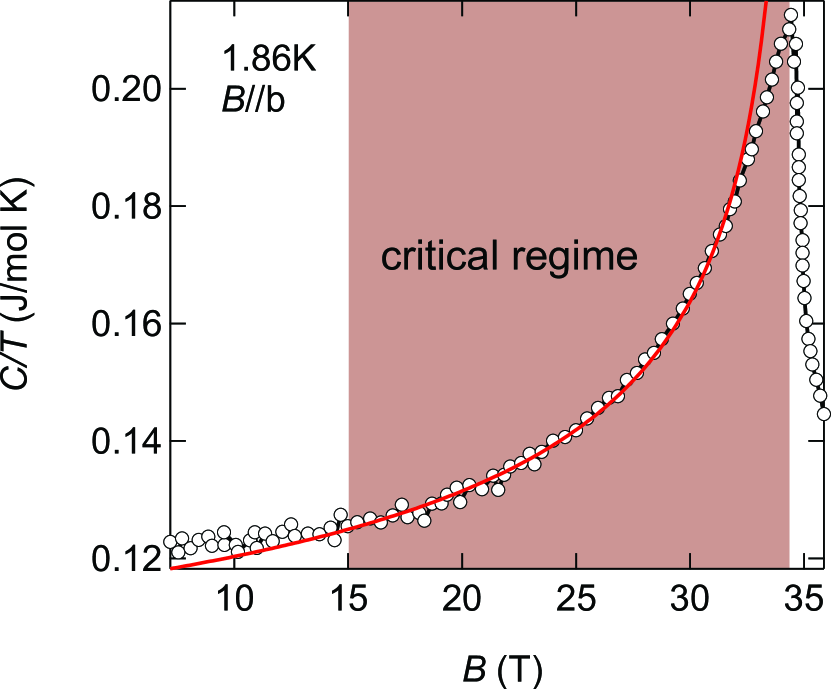
Figure SS7(a) compares specific heat divided by temperature, , at 1.86 K [1] and at 3 K. At low temperatures in Fermi liquid regime, the two quantities are equal, because ==. The two data sets compares well, despite the difference in measurement methods, sample quality and temperature. The discrepancies can also be attributed to the potential misalignment of the samples to the field direction, which can affect the metamagnetic behaviour. Figure SS7(b) demonstrates that when data are scaled, it closely matches the behaviour of , implying a shared functional form between the two. This comparison supports our conclusion that both data sets can be consistently explained by the same model.
II Metamagnetic quantum critical behavior in specific heat
Figure SS5 shows specific heat divided by temperature of UTe2 for the field along the -axis, taken from Ref. [1]. The strong enhancement toward metamagnetic field, 34.75 T, is reminiscent of the other examples of itinerant metamagnet, such as Sr3Ru2O7, YbAgGe, CeRhSn and UCoAl [2, 3, 4, 5]. This is due to fluctuations caused by metamagnetic quantum critical endpoint (QCEP) [6]. Exactly at QCEP / diverges. The critical contribution in / in the diverging regime is /, where =- is the distance to the critical field, , and is the dimensionality. Since Fermi surfaces consist of mainly cylinders, we assume =2. We fix =34.75 T, as reported [1]. In Fig. S5 we show a fitting result with /=+, where and are fitting parameters. The data follows the theoretical power-law field dependence from 15 T to 32 T. The deviation above 32 T is caused by the fact that the system still has some distance to QCEP. Only a system with a QCEP exhibits a divergence of / and otherwise it deviates downwards [6]. We note that the data starts to follow the exponent from 15 T, in agreement with the entropy increment shown in the main text.
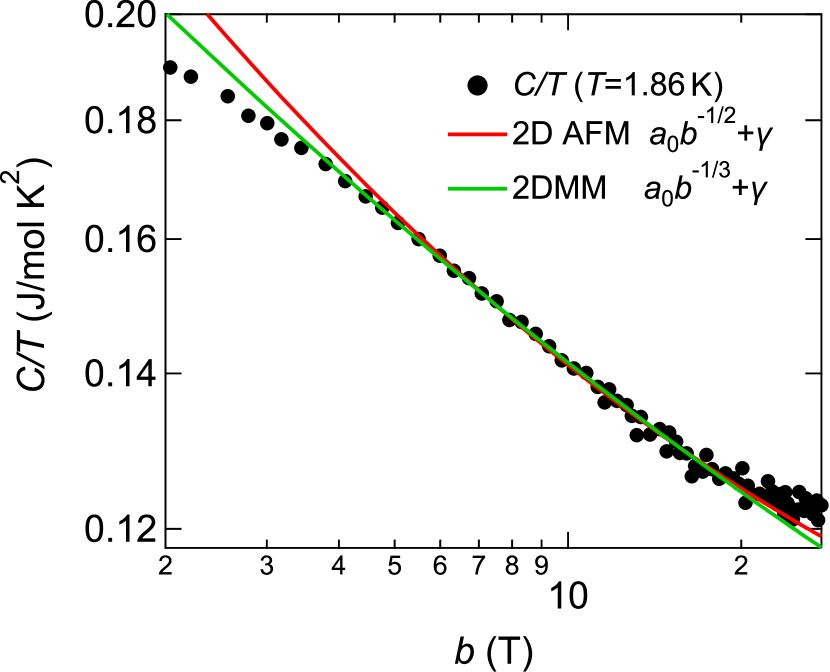
Figure SS6 displays the data as a function of [1]. This data is analyzed using theoretical models for two-dimensional antiferromagnetic (2D AFM) and two-dimensional metamagnetic (2D MM) quantum criticality. Due to the presence of a constant term, distinguishing between the models based solely on their slopes is challenging. Nonetheless, the 2D MM model demonstrates a wider range of fitting, which further suggests that metamagnetic fluctuations are likely responsible for the observed anomalous increase in .

References
- Rosuel et al. [2022] A. Rosuel, C. Marcenat, G. Knebel, T. Klein, A. Pourret, N. Marquardt, Q. Niu, S. Rousseau, A. Demuer, G. Seyfarth, G. Lapertot, D. Aoki, D. Braithwaite, J. Flouquet, and J.-P. Brison, Field-induced tuning of the pairing state in a superconductor (2022).
- Rost et al. [2009] A. W. Rost, R. S. Perry, J.-F. Mercure, A. P. Mackenzie, and S. A. Grigera, Entropy landscape of phase formation associated with quantum criticality in Sr3Ru2O7, Science 325, 1360 (2009), http://www.sciencemag.org/content/325/5946/1360.full.pdf .
- Tokiwa et al. [2013] Y. Tokiwa, M. Garst, P. Gegenwart, S. L. Bud’ko, and P. C. Canfield, Quantum bicriticality in the heavy-fermion metamagnet YbAgGe, Phys. Rev. Lett. 111, 116401 (2013).
- Tokiwa et al. [2015] Y. Tokiwa, C. Stingl, M.-S. Kim, T. Takabatake, and P. Gegenwart, Characteristic signatures of quantum criticality driven by geometrical frustration, Science Advances 1, 10.1126/sciadv.1500001 (2015).
- Tokiwa et al. [2016] Y. Tokiwa, M. Mchalwat, R. S. Perry, and P. Gegenwart, Multiple metamagnetic quantum criticality in Sr3Ru2O7, Phys. Rev. Lett. 116, 226402 (2016).
- Zacharias and Garst [2013] M. Zacharias and M. Garst, Quantum criticality in itinerant metamagnets, Phys. Rev. B 87, 075119 (2013).
- Millis et al. [2002] A. J. Millis, A. J. Schofield, G. G. Lonzarich, and S. A. Grigera, Metamagnetic quantum criticality in metals, Phys. Rev. Lett. 88, 217204 (2002).
- Zhu et al. [2003] L. Zhu, M. Garst, A. Rosch, and Q. Si, Universally diverging Grüneisen parameter and the magnetocaloric effect close to quantum critical points, Phys. Rev. Lett. 91, 066404 (2003).
- Willa et al. [2021] K. Willa, F. Hardy, D. Aoki, D. Li, P. Wiecki, G. Lapertot, and C. Meingast, Thermodynamic signatures of short-range magnetic correlations in UTe2, Phys. Rev. B 104, 205107 (2021).