Repeated Padding for Sequential Recommendation
Abstract.
Sequential recommendation aims to provide users with personalized suggestions based on their historical interactions. When training sequential models, padding is a widely adopted technique for two main reasons: 1) The vast majority of models can only handle fixed-length sequences; 2) Batch-based training needs to ensure that the sequences in each batch have the same length. The special value 0 is usually used as the padding content, which does not contain the actual information and is ignored in the model calculations. This common-sense padding strategy leads us to a problem that has never been explored in the recommendation field: Can we utilize this idle input space by padding other content to improve model performance and training efficiency further?
In this paper, we propose a simple yet effective padding method called Repeated Padding (RepPad). Specifically, we use the original interaction sequences as the padding content and fill it to the padding positions during model training. This operation can be performed a finite number of times or repeated until the input sequences’ length reaches the maximum limit. Our RepPad can be considered as a sequence-level data augmentation strategy. Unlike most existing works, our method contains no trainable parameters or hyperparameters and is a plug-and-play data augmentation operation. Extensive experiments on various categories of sequential models and five real-world datasets demonstrate the effectiveness and efficiency of our approach. The average recommendation performance improvement is up to 60.3% on GRU4Rec and 24.3% on SASRec. We also provide in-depth analysis and explanation of what makes RepPad effective from multiple perspectives. Our datasets and codes are available at https://github.com/KingGugu/RepPad.
1. Introduction
Sequential recommendation (SR) focuses on characterizing users’ dynamic preferences in their historical sequences to predict the next user-item interaction(s). In the last few years, various sequential models have been proposed to model the transition pattern from the previous item to the next in user sequences. Pioneering works employed Markov Chains (Rendle et al., 2010; Shani et al., 2005) and session-based KNN (He and McAuley, 2016; Hu et al., 2020) to model sequential data. Later, CNN-based (Yuan et al., 2019; Tang and Wang, 2018) and RNN-based (Hidasi et al., 2015a; Liu et al., 2016; Qu et al., 2022) models were proposed to capture the dependencies among items within a sequence or across different sequences. More recently, the powerful capability of Transformers (Vaswani et al., 2017; Devlin et al., 2018) in encoding sequences has been adopted for applications in SR. Transformer-based SR models (Kang and McAuley, 2018; Sun et al., 2019; Li et al., 2020; Dang et al., 2023b, a) encode sequences by learning item importance and behavior relevance via self-attention mechanisms.
Although numerous models with different architectures have been proposed, padding has never been explored as a necessary technique for training sequential models. The vast majority of sequence models can only support inputting fixed-length sequences to define the model architecture and process model calculations. In addition, during training, the Batch Processing techniques require all sequences in each batch to be the same length. Therefore, the maximum sequence length is usually used as a specified hyperparameter before the model training. During training, interceptions are performed for long sequences, and padding is performed for short sequences. Due to user habits and the long-tail effect, only a few users have long interaction sequences, while most users have very short ones (Jiang et al., 2021). When padding a sequence, the special value 0 is usually treated as content. It does not contain meaningful information and is not involved in model calculations. This universally observed convention and custom leads us to the question: Can we utilize this idle input space by padding other content to improve model performance and training efficiency further?
Motivated by the question above, we propose a simple yet effective padding strategy called Repeated Padding (RepPad for short) in this paper. Unlike the traditional padding strategy, we iteratively pad the original whole interaction sequence. This operation can be performed a limited number of times or repeated until the sequence length reaches a preset maximum limit. To avoid the situation where the head of the sequence is used to predict the tail, we add a delimiter between each padding. We aim to utilize these input spaces that are not involved in model training but occupying positions to improve model performance and training efficiency.
From another perspective, RepPad is a sequence-level data augmentation method. The training of recommendation models relies heavily on large-scale labeled data. Data sparsity has been one of the major problems faced by recommender systems (Jing et al., 2023). Earlier works use random data augmentation methods to increase the size of the training dataset directly, such as Dropout (Tan et al., 2016a) and Slide Windows (Tang and Wang, 2018). Besides, some researchers utilize counterfactual thinking (Wang et al., 2021), bidirectional Transformer (Jiang et al., 2021; Liu et al., 2021b), or diffusion model (Liu et al., 2023) to augment sequence data. Inspired by recent developments of Contrastive Learning (CL) (Jing et al., 2023; Yu et al., 2023; Zhao et al., 2023a, b), many effective data augmentation operators have been proposed (Xie et al., 2022; Liu et al., 2021a; Dang et al., 2023b; Qin et al., 2023; Tian et al., 2023). These models typically leverage shared encoders to encode original and augmented sequences. The representations of the original sequences are used for the main recommendation task, and the representations of the augmented sequence are used as the input for contrastive learning (Liu et al., 2021a). These methods also use the special value 0 as the padding content when dealing with sequences whose length is less than a specified value. However, adding additional sequence data to the original dataset makes the training process more time-consuming. Our RepPad utilizes the idle padding space to perform repeated padding before the sequences are fed into the model. There is no additional increase in the number of sequences that need to be involved in training.
In the discussion section, we analyze the advantages of RepPad over existing methods and present possible drawbacks. Different from elaborate data augmentation operators or the methods that require training, our method requires no training process and introduces no additional hyper-parameters or trainable parameters. It is independent of the backbone network and is a data augmentation plugin. We implement RepPad on various representative models based on different architectures. Extensive experimental results demonstrate the effectiveness and efficiency of our method. It also achieves satisfactory improvements over existing data augmentation methods. Furthermore, we explore the performance of different variants of RepPad. To explore what makes RepPad effective, we provide in-depth analyses from the perspectives of loss convergence and gradient stability.
In summary, our work makes the following contributions:
-
•
We propose a simple yet effective padding paradigm called Repeated Padding. It does not contain any parameters and is a plug-and-play data augmentation method.
-
•
Comprehensive experiments on multiple datasets, various types of sequential models, and augmentation methods demonstrate the effectiveness and efficiency of RepPad.
-
•
We provide analysis and insights of why RepPad is effective from the perspectives of loss convergence and gradient stability. To our knowledge, this is the first work to explore the padding strategy in the recommendation field.
2. Methodology
In this section, we formally present the problem of sequential recommendation. After that, we introduce the current widely used padding strategy and briefly describe the sequence data augmentation. More data augmentation methods will be introduced in section 4, Related Work. Finally, we present our proposed RepPad.
2.1. Problem Formulation
Suppose we have user and item sets denoted by symbols and , respectively. Each user is associated with a sequence of interacted items in chronological order , where indicate the item that user has interacted with at time step and is the sequence length. The sequential recommendation task can be formulated as follows. Given the sequences of interacted items , our task is to accurately predict the most possible item that user will interact with at time step , formulated as follows:
| (1) |
This equation can be interpreted as calculating the probability of all candidate items and selecting the highest one for recommendation.
2.2. Padding in Sequential Recommendation
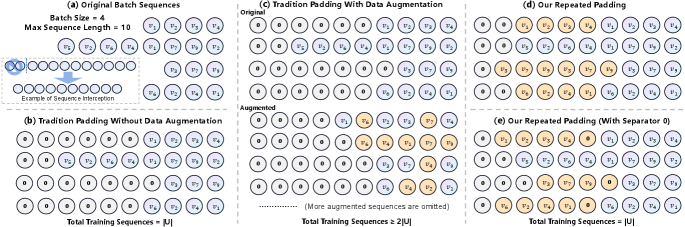
Padding is a common technique when training sequential models. The Batch Processing requires that the sequences in each batch have the same length. In addition, common CNN- or Transformer-based models can only handle fixed-length sequences and require model initialization and operations based on fixed sequence lengths. So, before training a recommendation model, we usually specify a maximum sequence length . For sequences with an original length of more than , the most recent items are usually chosen because they represent the user’s recent preferences. As shown in Figure1 (a) and (b), original sequences of length less than are padded with the special value 0 to reach the length . The special value 0 contains no actual information and does not participate in model calculations. The above process can be formulated as follows:
| (2) |
where indicates padding the 0 to the left side of the sequence until its length is , and indicates intercepting the nearest interactions. The is the final input to the model where . Typically, the total number of sequences involved in model training is , i.e., one sequence for each user.
2.3. Sequence Data Augmentation
To alleviate the data sparsity problem, data augmentation is often used to augment the original data to increase the number of sequence involved in model training. Given an original sequence , a data augmentation operation makes minor but appropriate changes to to generate a new sequence . Both and are used for model training or self-supervised learning. For example, as shown in Figure1 (c), for an original sequence , we intercept a portion of the consecutive sequence to generate a new sequence data . For original sequence , we inert an item between and to generate sequence data . In each epoch, each sequence will be augmented at least once, so the total number of sequences involved in model training will be at least 2. The original and augmented sequences also need to apply function Eq. (2) before being fed into the model.
2.4. Ours: Repeated Padding
As illustrated in Figure 1 (b) and (c), a large amount of free space is filled with 0 regardless of whether data augmentation is performed. Also, due to the long-tail effect, the interaction sequences of the vast majority of users are usually short. Therefore, our idea is to utilize these free spaces further to improve the efficiency of model training and recommendation performance.
| The Value of | Interpretation |
| No repeated padding and use original sequence. | |
| Repeated padding a fixed number of times. | |
| Padding until the remaining space is insufficient. | |
| Randomly select between 0 and maximum value. | |
| Randomly select between 1 and maximum value. |
| Methods | Augmentation Type | No Hyper-Parameters | No Training | Model Agnostic | Total Training Sequences |
| Only Augmentation (Tan et al., 2016a; Tang and Wang, 2018) | Random or Elaborate Operators | ✘ | ✔ | ✔ | 2 |
| Augmentation with CL (Xie et al., 2022; Liu et al., 2021a; Dang et al., 2023b; Qin et al., 2023; Tian et al., 2023) | Operators or Synthesis Modules | ✘ | ✘ | ✔ | 3 |
| CASR (Wang et al., 2021) | Counterfactual Thinking | ✘ | ✘ | ✔ | 2 |
| ASReP (Liu et al., 2021b), BiCAT (Jiang et al., 2021) | Bidirectional Transformers | ✘ | ✘ | ✘ | |
| L2Aug (Wang et al., 2022) | Synthesis Modules | ✘ | ✘ | ✔ | |
| DiffuASR (Liu et al., 2023) | Diffusion Models | ✘ | ✘ | ✔ | 4 |
| RepPad (Ours) | Repeated Padding | ✔ | ✔ | ✔ |
In order to achieve this objective, we propose a simple but effective padding strategy called Repeated Padding (RepPad). Specifically, we utilize the original sequence as padding content instead of the special value 0. As shown in Figure 1 (d), give the original sequence , and we pad the original sequence once on the left and get the padded sequence . This operation can be formulated as:
| (3) |
where is padding times and indicates sequence concatenation. This operation can be performed only once or repeated several times until there is not enough space left to hold the original sequence. In other words, can be pre-specified or calculated based on the original sequence length and the maximum sequence length . For example, when the maximum sequence length is 10, the remaining length of 2 is insufficient to accommodate the original sequence of length 4, so it still needs to apply function Eq. (2). The final input sequence . In addition, given the original sequence , the padding operation can be performed up to 3 times, and the final sequence .
However, there is a problem with the above padding strategy: there may be cases where the end of the original sequence is used to predict the head. Using as training data, there will be cases where is used to predict . To solve this problem, we add the special value 0 between each repeated padding to prevent this from happening. This operation can be formulated as:
| (4) |
As shown in Figure 1 (e), given original sequence , the final sequence after Eq. (4) and (2) is . We give the possible values of and their interpretation in Table 1.
Our method has no trainable parameters or hyper-parameters that need to be manually tuned. It is a model-agnostic plug-and-play data augmentation approach. In the Experiments section, we will explore and analyze several variants of RepPad, including different times of padding and whether to add the delimiter 0. The best-performing variant is The best-performing variant is randomly selected in the range from one to the maximum number of times. Our method is very easy to implement, and we present its Python procedure in Algorithm 1. So far, we have introduced the basic idea of our RepPad. It is worth emphasizing that the repeated padding sequences still need to apply function Eq. (2) operation before they can be fed into the model:
| (5) |
2.5. Discussions
2.5.1. Comparison with Existing Methods.
The advantages of our approach are as follows: (i) No increase in number of sequences: From Figure 1, we can observe that our approach performs data augmentation without increasing the amount of data for training. While previous approaches can be considered as extending the length of the dataset vertically, our approach utilizes the free space horizontally. For traditional data augmentation methods, the amount of data involved in training will be at least 2. For sequential recommendation models that leverage both data augmentation and contrastive learning, each sequence is augmented at least twice, and with the addition of the original sequence, the number of model sequences involved in training is at least 3. (ii) No Hyper-parameters: These existing augmentation methods or augmentation operators (Slide Window, Dropout, Crop, Insert, Mask, Substitute, Reorder, and so on.) typically contain at least one hyper-parameter for each that must be manually tuned based on the dataset. However, our approach does not involve any hyperparameters that need to be tuned carefully. (iii) No Training Cost and Model Agnostic: Some researchers propose to use bidirectional Transformers (Liu et al., 2021b; Jiang et al., 2021) or diffusion models (Liu et al., 2023) for data augmentation. These methods require training of data augmentation modules in addition to training of backbone recommendation networks and have limitations on the type of backbone network. In contrast, our method does not contain any parameters, does not require a training process, and can be adapted to most sequential models. We present a summary comparison between PepPad and existing methods in Table 2. It should be emphasized that our focus is on sequence-level data augmentation, which is also the most mainstream practice in data augmentation in the field of sequential recommendation. Augmentation at the embedding (Qiu et al., 2022) and model (Hao et al., 2023) levels are not involved in our discussion.
2.5.2. Possible Limitations.
Our approach intends to maximize the use of idle input space. Intuitively, RepPad is more effective on short-sequence datasets and may be ineffective on long-sequence datasets. This is because for long-sequence datasets, most users have sequence lengths that close to or exceed the given maximum sequence length, and thus, there will be no space left for padding. We will verify our conjecture in the experimental section.
3. Experiments
3.1. Experiment Setup
3.2. Datasets
The experiments are conducted on six datasets:
-
•
Toys, Beauty, Sports, and Home: Four datasets obtained from Amazon (McAuley et al., 2015) and correspond to the ”Toys and Games”, ”Beauty”, ”Sports and Outdoors”, and ”Home” categories, respectively.
-
•
Yelp111https://www.yelp.com/dataset: It is the second version of the Yelp dataset released in 2020. We utilize the records after January 1st, 2019.
-
•
MovieLens-1M222https://grouplens.org/datasets/movielens/ (ML-1M for short): This dataset comprises rating behaviors gathered from a movie review website.
The Amazon and Yelp datasets contain mainly short user sequences. The MovieLens-1M contains mainly long user sequences. Following (Liu et al., 2021a; Dang et al., 2023a; Tian et al., 2023), we reduce the data by extracting the 5-core. The maximum sequence length is set to 200 for the MovieLens-1M dataset and 50 for other datasets. The detailed statistics are summarized in Table 3.
| Dataset | Toys | Beauty | Sports | Yelp | Home | ML-1M |
| # Users | 19,412 | 22,363 | 35,958 | 30,431 | 66,519 | 6,040 |
| # Items | 11,924 | 12,101 | 18,357 | 20,033 | 28,237 | 3,706 |
| # Inter | 167,597 | 198,502 | 296,337 | 316,354 | 551,682 | 1,000,209 |
| # AvgLen | 8.6 | 8.9 | 8.3 | 10.4 | 8.3 | 165.6 |
| Sparsity | 99.93% | 99.92% | 99.95% | 99.95% | 99.97% | 95.53% |
3.3. Baselines
In order to conduct a comprehensive evaluation of the effectiveness and superiority of RepPad, the baselines consist of three main categories:
First. The first category is eight representative sequential recommendation models, which are used to evaluate whether RepPad is effective in improving the model’s performance.
- •
- •
-
•
MLP-based models: FMLP-Rec (Zhou et al., 2022) is an all-MLP model with learnable filters for sequential recommendation tasks.
-
•
Transformer-based models: SASRec (Kang and McAuley, 2018) leverages the multi-head attention mechanism to perform sequential recommendation. LightSANs (Fan et al., 2021) proposes the low-rank decomposed self-attention networks to overcome quadratic complexity and vulnerability to over-parameterization. STOSA (Fan et al., 2022) embeds each item as a stochastic Gaussian distribution and devises a Wasserstein Self-Attention module to characterize item-item relationships.
Second. The second category is the widely used stochastic data augmentation methods, which do not require training but include several hyper-parameters that need to be manually tuned.
-
•
Random (Ran) (Liu et al., 2023): This method augments each sequence by randomly selecting items from the whole item set .
-
•
Slide Window (SW) (Tan et al., 2016b): It adopts slide windows to intercept multiple new subsequences from the original sequence.
-
•
Random-seq (Ran-S) (Liu et al., 2023): It selects items from the original sequence randomly as the augmentation items.
-
•
CMR (Xie et al., 2022): This work proposes three sequence data augmentation operators with contrastive learning. In this category, we only use the three operators including Crop, Mask, and Reorder.
-
•
CMRSI (Liu et al., 2021a): Based on CMR, this work proposes two additional operators with contrastive learning. We adopt five operators including Crop, Mask, Reorder, Substitute, and Insert.
Third. The third category is representative of training-required data augmentation models, which usually include trainable parameters and hyper-parameters that need to be manually tuned.
-
•
ASReP (Liu et al., 2021b): This method employs a reversely pre-trained transformer to generate pseudo-prior items for short sequences. Then, fine-tune the pre-trained transformer to predict the next item.
-
•
DiffuASR (Liu et al., 2023): It adopts the diffusion model for sequence generation. Besides, two guide strategies are designed to control the model to generate the items corresponding to the raw data.
-
•
CL4SRec (Xie et al., 2022): This method leverages random data augmentation and utilizes contrastive learning to extract self-supervised signals from the original data.
We do not include method L2Aug (Wang et al., 2022) and CASR (Wang et al., 2021) since they do not provide open-source codes for reliable reproduction.
3.4. Evaluation Metrics
Following (Liu et al., 2021a; Dang et al., 2023a; Tian et al., 2023), we adopt the leave-one-out strategy, wherein the last item of each user sequence serves as the test data, the items preceding it as validation data, and the remaining data as training data. We rank the prediction over the whole item set rather than negative sampling, otherwise leading to biased discoveries (Krichene and Rendle, 2020). The evaluation metrics include Hit Ratio@K (denoted by HR@K), and Normalized Discounted Cumulative Gain@K (NDCG@K). We report results with K . Generally, greater values imply better ranking accuracy.
3.5. Implementation Details
For all baselines, we adopt the implementation provided by the authors. We set the embedding size to 64 and the batch size to 256. To ensure fair comparisons, we carefully set and tune all other hyper-parameters of each method as reported and suggested in the original papers. We use the Adam (Kingma and Ba, 2014) optimizer with the learning rate 0.001, , . For all methods, we adopt early stopping on the validation set if the performance does not improve for 20 epochs and report results on the test set.
| Dataset | Metric | GRU4Rec (Hidasi et al., 2015b) | w/ RP | Improve | NARM (Li et al., 2017) | w/ RP | Improve | Caser (Tang and Wang, 2018) | w/ RP | Improve | NextItNet (Yuan et al., 2019) | w/ RP | Improve |
| Toys | Hit@5 | 0.0134 | 0.0276 | 105.97% | 0.0275 | 0.0286 | 4.00% | 0.0132 | 0.0152 | 15.15% | 0.0229 | 0.0273 | 19.21% |
| Hit@10 | 0.0256 | 0.0434 | 69.53% | 0.0401 | 0.0415 | 3.49% | 0.0231 | 0.0246 | 6.49% | 0.0391 | 0.0452 | 15.60% | |
| Hit@20 | 0.0432 | 0.0652 | 50.93% | 0.0598 | 0.0589 | -1.51% | 0.0364 | 0.0380 | 4.40% | 0.0539 | 0.0613 | 13.73% | |
| NDCG@5 | 0.0083 | 0.0179 | 115.66% | 0.0179 | 0.0188 | 5.03% | 0.0079 | 0.0096 | 21.52% | 0.0128 | 0.0153 | 19.53% | |
| NDCG@10 | 0.0121 | 0.0229 | 89.26% | 0.0220 | 0.0233 | 5.91% | 0.0111 | 0.0126 | 13.51% | 0.0172 | 0.0201 | 16.86% | |
| NDCG@20 | 0.0166 | 0.0284 | 71.08% | 0.0269 | 0.0276 | 2.60% | 0.0149 | 0.0160 | 7.38% | 0.0217 | 0.0251 | 15.67% | |
| Beauty | Hit@5 | 0.0182 | 0.0286 | 57.14% | 0.0213 | 0.0244 | 14.55% | 0.0149 | 0.0199 | 33.56% | 0.0223 | 0.0263 | 17.94% |
| Hit@10 | 0.0327 | 0.0468 | 43.12% | 0.0367 | 0.0400 | 8.99% | 0.0261 | 0.0330 | 26.44% | 0.0393 | 0.0442 | 12.47% | |
| Hit@20 | 0.0551 | 0.0732 | 32.85% | 0.0617 | 0.0659 | 6.81% | 0.0457 | 0.0511 | 11.82% | 0.0633 | 0.0725 | 14.53% | |
| NDCG@5 | 0.0116 | 0.0175 | 50.86% | 0.0131 | 0.0152 | 16.03% | 0.0090 | 0.0127 | 41.11% | 0.0135 | 0.0151 | 11.85% | |
| NDCG@10 | 0.0162 | 0.0234 | 44.44% | 0.0180 | 0.0202 | 12.22% | 0.0126 | 0.0169 | 34.13% | 0.0191 | 0.0221 | 15.71% | |
| NDCG@20 | 0.0219 | 0.0300 | 36.99% | 0.0243 | 0.0258 | 6.17% | 0.0175 | 0.0214 | 22.29% | 0.0251 | 0.0280 | 11.55% | |
| Sports | Hit@5 | 0.0078 | 0.0114 | 46.15% | 0.0126 | 0.0140 | 11.11% | 0.0081 | 0.0092 | 13.58% | 0.0104 | 0.0112 | 7.69% |
| Hit@10 | 0.0143 | 0.0204 | 42.66% | 0.0218 | 0.0238 | 9.17% | 0.0146 | 0.0160 | 9.59% | 0.0195 | 0.0215 | 10.26% | |
| Hit@20 | 0.0249 | 0.0338 | 35.74% | 0.0361 | 0.0385 | 6.65% | 0.0257 | 0.0265 | 3.11% | 0.0338 | 0.0368 | 8.88% | |
| NDCG@5 | 0.0044 | 0.0073 | 65.91% | 0.0076 | 0.0088 | 15.79% | 0.0048 | 0.0056 | 16.67% | 0.0064 | 0.0074 | 15.63% | |
| NDCG@10 | 0.0065 | 0.0100 | 53.85% | 0.0106 | 0.0120 | 13.21% | 0.0069 | 0.0078 | 13.04% | 0.0093 | 0.0103 | 10.75% | |
| NDCG@20 | 0.0091 | 0.0134 | 47.25% | 0.0142 | 0.0157 | 10.56% | 0.0096 | 0.0105 | 9.38% | 0.0129 | 0.0139 | 7.75% | |
| Yelp | Hit@5 | 0.0092 | 0.0119 | 29.35% | 0.0140 | 0.0159 | 13.57% | 0.0131 | 0.0144 | 9.92% | 0.0109 | 0.0121 | 11.01% |
| Hit@10 | 0.0172 | 0.0223 | 29.65% | 0.0255 | 0.0277 | 8.63% | 0.0238 | 0.0252 | 5.88% | 0.0218 | 0.0240 | 10.09% | |
| Hit@20 | 0.0314 | 0.0407 | 29.62% | 0.0443 | 0.0482 | 8.80% | 0.0414 | 0.0435 | 5.07% | 0.0400 | 0.0433 | 8.25% | |
| NDCG@5 | 0.0057 | 0.0072 | 26.32% | 0.0084 | 0.0098 | 16.67% | 0.0084 | 0.0089 | 5.95% | 0.0075 | 0.0081 | 8.00% | |
| NDCG@10 | 0.0083 | 0.0105 | 26.51% | 0.0120 | 0.0136 | 13.33% | 0.0118 | 0.0127 | 7.63% | 0.0106 | 0.0117 | 10.38% | |
| NDCG@20 | 0.0118 | 0.0151 | 27.97% | 0.0167 | 0.0188 | 12.57% | 0.0162 | 0.0173 | 6.79% | 0.0149 | 0.0162 | 8.72% | |
| Home | Hit@5 | 0.0030 | 0.0063 | 110.00% | 0.0059 | 0.0073 | 23.73% | 0.0035 | 0.0044 | 25.71% | 0.0039 | 0.0043 | 10.26% |
| Hit@10 | 0.0057 | 0.0108 | 89.47% | 0.0109 | 0.0125 | 14.68% | 0.0066 | 0.0075 | 13.64% | 0.0074 | 0.0085 | 14.86% | |
| Hit@20 | 0.0106 | 0.0182 | 71.70% | 0.0185 | 0.0205 | 10.81% | 0.0125 | 0.0136 | 8.80% | 0.0137 | 0.0151 | 10.22% | |
| NDCG@5 | 0.0018 | 0.0040 | 122.22% | 0.0037 | 0.0048 | 29.73% | 0.0022 | 0.0026 | 18.18% | 0.0025 | 0.0029 | 16.00% | |
| NDCG@10 | 0.0027 | 0.0054 | 100.00% | 0.0053 | 0.0065 | 22.64% | 0.0031 | 0.0039 | 25.81% | 0.0037 | 0.0042 | 13.51% | |
| NDCG@20 | 0.0039 | 0.0073 | 87.18% | 0.0072 | 0.0085 | 18.06% | 0.0046 | 0.0050 | 8.70% | 0.0051 | 0.0059 | 15.69% | |
| Dataset | Metric | SASRec (Kang and McAuley, 2018) | w/ RP | Improve | LightSANs (Fan et al., 2021) | w/ RP | Improve | FMLP-Rec (Zhou et al., 2022) | w/ RP | Improve | STOSA (Fan et al., 2022) | w/ RP | Improve |
| Toys | Hit@5 | 0.0472 | 0.0587 | 24.36% | 0.0376 | 0.0388 | 3.19% | 0.0418 | 0.0463 | 10.77% | 0.0486 | 0.0611 | 25.72% |
| Hit@10 | 0.0716 | 0.0843 | 17.74% | 0.0505 | 0.0564 | 11.68% | 0.0570 | 0.0632 | 10.88% | 0.0699 | 0.0865 | 23.75% | |
| Hit@20 | 0.0965 | 0.1142 | 18.34% | 0.0656 | 0.0770 | 17.38% | 0.0759 | 0.0852 | 12.25% | 0.0976 | 0.1196 | 22.54% | |
| NDCG@5 | 0.0317 | 0.0393 | 23.97% | 0.0265 | 0.0260 | -1.89% | 0.0289 | 0.0314 | 8.65% | 0.0330 | 0.0416 | 26.06% | |
| NDCG@10 | 0.0396 | 0.0476 | 20.20% | 0.0307 | 0.0316 | 2.93% | 0.0338 | 0.0368 | 8.88% | 0.0398 | 0.0498 | 25.13% | |
| NDCG@20 | 0.0471 | 0.0551 | 16.99% | 0.0345 | 0.0368 | 6.67% | 0.0386 | 0.0423 | 9.59% | 0.0467 | 0.0581 | 24.41% | |
| Beauty | Hit@5 | 0.0409 | 0.0477 | 16.63% | 0.0312 | 0.0328 | 5.13% | 0.0387 | 0.0439 | 13.44% | 0.0387 | 0.0468 | 20.93% |
| Hit@10 | 0.0637 | 0.0726 | 13.97% | 0.0469 | 0.0485 | 3.41% | 0.0566 | 0.0648 | 14.49% | 0.0613 | 0.0708 | 15.50% | |
| Hit@20 | 0.0942 | 0.1034 | 9.77% | 0.0709 | 0.0741 | 4.51% | 0.0814 | 0.0905 | 11.18% | 0.0909 | 0.1047 | 15.18% | |
| NDCG@5 | 0.0257 | 0.0310 | 20.62% | 0.0201 | 0.0217 | 7.96% | 0.0260 | 0.0286 | 10.00% | 0.0248 | 0.0313 | 26.21% | |
| NDCG@10 | 0.0331 | 0.0390 | 17.82% | 0.0255 | 0.0267 | 4.71% | 0.0317 | 0.0353 | 11.36% | 0.0320 | 0.0390 | 21.88% | |
| NDCG@20 | 0.0408 | 0.0468 | 14.71% | 0.0319 | 0.0323 | 1.25% | 0.0380 | 0.0418 | 10.00% | 0.0394 | 0.0476 | 20.81% | |
| Sports | Hit@5 | 0.0187 | 0.0237 | 26.74% | 0.0130 | 0.0150 | 15.38% | 0.0149 | 0.0201 | 34.90% | 0.0218 | 0.0271 | 24.31% |
| Hit@10 | 0.0299 | 0.0369 | 23.41% | 0.0208 | 0.0231 | 11.06% | 0.0238 | 0.0294 | 23.53% | 0.0325 | 0.0429 | 32.00% | |
| Hit@20 | 0.0447 | 0.0553 | 23.71% | 0.0327 | 0.0352 | 7.65% | 0.0345 | 0.0439 | 27.25% | 0.0482 | 0.0640 | 32.78% | |
| NDCG@5 | 0.0124 | 0.0154 | 24.19% | 0.0087 | 0.0097 | 11.49% | 0.0097 | 0.0132 | 36.08% | 0.0146 | 0.0174 | 19.18% | |
| NDCG@10 | 0.0160 | 0.0196 | 22.50% | 0.0112 | 0.0122 | 8.93% | 0.0126 | 0.0162 | 28.57% | 0.0181 | 0.0225 | 24.31% | |
| NDCG@20 | 0.0197 | 0.0242 | 22.84% | 0.0142 | 0.0153 | 7.75% | 0.0153 | 0.0199 | 30.07% | 0.0220 | 0.0277 | 25.91% | |
| Yelp | Hit@5 | 0.0168 | 0.0210 | 25.00% | 0.0120 | 0.0159 | 32.50% | 0.0121 | 0.0154 | 27.27% | 0.0164 | 0.0216 | 31.71% |
| Hit@10 | 0.0282 | 0.0359 | 27.30% | 0.0207 | 0.0267 | 28.99% | 0.0209 | 0.0258 | 23.44% | 0.0283 | 0.0367 | 29.68% | |
| Hit@20 | 0.0443 | 0.0587 | 32.51% | 0.0346 | 0.0429 | 23.99% | 0.0356 | 0.0425 | 19.38% | 0.0471 | 0.0593 | 25.90% | |
| NDCG@5 | 0.0106 | 0.0129 | 21.70% | 0.0073 | 0.0099 | 35.62% | 0.0070 | 0.0099 | 41.43% | 0.0103 | 0.0134 | 30.10% | |
| NDCG@10 | 0.0142 | 0.0177 | 24.65% | 0.0101 | 0.0134 | 32.67% | 0.0098 | 0.0133 | 35.71% | 0.0141 | 0.0183 | 29.79% | |
| NDCG@20 | 0.0183 | 0.0234 | 27.87% | 0.0136 | 0.0175 | 28.68% | 0.0135 | 0.0175 | 29.63% | 0.0189 | 0.0240 | 26.98% | |
| Home | Hit@5 | 0.0096 | 0.0130 | 35.42% | 0.0059 | 0.0065 | 10.17% | 0.0079 | 0.0085 | 7.59% | 0.0115 | 0.0138 | 20.00% |
| Hit@10 | 0.0155 | 0.0204 | 31.61% | 0.0100 | 0.0098 | -2.00% | 0.0125 | 0.0128 | 2.40% | 0.0171 | 0.0196 | 14.62% | |
| Hit@20 | 0.0244 | 0.0311 | 27.46% | 0.0173 | 0.0185 | 6.94% | 0.0193 | 0.0191 | -1.04% | 0.0262 | 0.0312 | 19.08% | |
| NDCG@5 | 0.0061 | 0.0087 | 42.62% | 0.0034 | 0.0039 | 14.71% | 0.0051 | 0.0055 | 7.84% | 0.0072 | 0.0077 | 6.94% | |
| NDCG@10 | 0.0083 | 0.0116 | 39.76% | 0.0047 | 0.0050 | 6.38% | 0.0066 | 0.0069 | 4.55% | 0.0092 | 0.0101 | 9.78% | |
| NDCG@20 | 0.0101 | 0.0137 | 35.64% | 0.0064 | 0.0067 | 4.69% | 0.0083 | 0.0085 | 2.41% | 0.0115 | 0.0130 | 13.04% |
| Dataset | Metric | GRU4Rec (Hidasi et al., 2015b) | w/ RP | Improve | NARM (Li et al., 2017) | w/ RP | Improve | Caser (Tang and Wang, 2018) | w/ RP | Improve | NextItNet (Yuan et al., 2019) | w/ RP | Improve |
| ML-1M | Hit@5 | 0.1104 | 0.1407 | 27.45% | 0.0493 | 0.0541 | 9.74% | 0.0465 | 0.0495 | 6.45% | 0.0922 | 0.1008 | 9.33% |
| Hit@10 | 0.1841 | 0.2200 | 19.50% | 0.0868 | 0.0879 | 1.27% | 0.0823 | 0.0841 | 2.19% | 0.1491 | 0.1623 | 8.85% | |
| Hit@20 | 0.2849 | 0.3300 | 15.83% | 0.1459 | 0.1470 | 0.75% | 0.1416 | 0.1429 | 0.92% | 0.2354 | 0.2519 | 7.01% | |
| NDCG@5 | 0.0704 | 0.0914 | 29.83% | 0.0297 | 0.0349 | 17.51% | 0.0277 | 0.0304 | 9.75% | 0.0620 | 0.0643 | 3.71% | |
| NDCG@10 | 0.0941 | 0.1168 | 24.12% | 0.0417 | 0.0457 | 9.59% | 0.0398 | 0.0414 | 4.02% | 0.0815 | 0.0866 | 6.26% | |
| NDCG@20 | 0.1195 | 0.1446 | 21.00% | 0.0565 | 0.0606 | 7.26% | 0.0541 | 0.0562 | 3.88% | 0.0963 | 0.1025 | 6.44% | |
| Metric | SASRec (Kang and McAuley, 2018) | w/ RP | Improve | LightSANs (Fan et al., 2021) | w/ RP | Improve | FMLP-Rec (Zhou et al., 2022) | w/ RP | Improve | STOSA (Fan et al., 2022) | w/ RP | Improve | |
| Hit@5 | 0.1748 | 0.1674 | -4.23% | 0.1179 | 0.1096 | -7.04% | 0.1045 | 0.1109 | 6.12% | 0.1750 | 0.1720 | -1.71% | |
| Hit@10 | 0.2624 | 0.2608 | -0.61% | 0.1873 | 0.1758 | -6.14% | 0.1667 | 0.1639 | -1.68% | 0.2720 | 0.2596 | -4.56% | |
| Hit@20 | 0.3762 | 0.3780 | 0.48% | 0.2765 | 0.2647 | -4.27% | 0.2454 | 0.2445 | -0.37% | 0.3809 | 0.3747 | -1.63% | |
| NDCG@5 | 0.1171 | 0.1096 | -6.40% | 0.0770 | 0.0712 | -7.53% | 0.0670 | 0.0719 | 7.31% | 0.1157 | 0.1131 | -2.25% | |
| NDCG@10 | 0.1450 | 0.1396 | -3.72% | 0.0993 | 0.0924 | -6.95% | 0.0871 | 0.0889 | 2.07% | 0.1467 | 0.1413 | -3.68% | |
| NDCG@20 | 0.1737 | 0.1693 | -2.53% | 0.1218 | 0.1153 | -5.34% | 0.1069 | 0.1092 | 2.15% | 0.1742 | 0.1703 | -2.24% |
| GRU4Rec | SASRec | |||||||||||||||||
| Dataset | Metric | Original | Ran | SW | Ran-S | CMR | CMRSI | RepPad | Dataset | Metric | Original | Ran | SW | Ran-S | CMR | CMRSI | RepPad | |
| Toys | Hit@10 | 0.0256 | 0.0306 | 0.0342 | 0.0363 | 0.0361 | 0.0411 | 0.0434 | Toys | Hit@10 | 0.0716 | 0.0600 | 0.0522 | 0.0660 | 0.0634 | 0.0713 | 0.0843 | |
| Hit@20 | 0.0432 | 0.0491 | 0.0557 | 0.0594 | 0.0585 | 0.0629 | 0.0652 | Hit@20 | 0.0965 | 0.0875 | 0.0807 | 0.0950 | 0.0952 | 0.1039 | 0.1142 | |||
| NDCG@10 | 0.0121 | 0.0158 | 0.0169 | 0.0192 | 0.0181 | 0.0203 | 0.0229 | NDCG@10 | 0.0396 | 0.0321 | 0.0292 | 0.0366 | 0.0347 | 0.0400 | 0.0476 | |||
| NDCG@20 | 0.0166 | 0.0205 | 0.0223 | 0.0248 | 0.0238 | 0.0267 | 0.0284 | NDCG@20 | 0.0471 | 0.0390 | 0.0363 | 0.0439 | 0.0428 | 0.0482 | 0.0551 | |||
| Beauty | Hit@10 | 0.0327 | 0.0370 | 0.0365 | 0.0419 | 0.0398 | 0.0463 | 0.0468 | Beauty | Hit@10 | 0.0637 | 0.0553 | 0.0542 | 0.0563 | 0.0562 | 0.0603 | 0.0726 | |
| Hit@20 | 0.0551 | 0.0581 | 0.0604 | 0.0650 | 0.0673 | 0.0712 | 0.0732 | Hit@20 | 0.0942 | 0.0850 | 0.0846 | 0.0882 | 0.0876 | 0.0940 | 0.1034 | |||
| NDCG@10 | 0.0162 | 0.0191 | 0.0176 | 0.0203 | 0.0196 | 0.0224 | 0.0234 | NDCG@10 | 0.0331 | 0.0285 | 0.0270 | 0.0289 | 0.0290 | 0.0316 | 0.0390 | |||
| NDCG@20 | 0.0219 | 0.0241 | 0.0236 | 0.0255 | 0.0266 | 0.0290 | 0.0300 | NDCG@20 | 0.0408 | 0.0359 | 0.0346 | 0.0369 | 0.0639 | 0.0401 | 0.0468 | |||
| Sports | Hit@10 | 0.0143 | 0.0163 | 0.0165 | 0.0194 | 0.0186 | 0.0176 | 0.0204 | Sports | Hit@10 | 0.0299 | 0.0330 | 0.0315 | 0.0308 | 0.0332 | 0.0318 | 0.0369 | |
| Hit@20 | 0.0249 | 0.0267 | 0.0301 | 0.0319 | 0.0309 | 0.0296 | 0.0338 | Hit@20 | 0.0447 | 0.0520 | 0.0496 | 0.0514 | 0.0530 | 0.0504 | 0.0553 | |||
| NDCG@10 | 0.0065 | 0.0080 | 0.0078 | 0.0096 | 0.0093 | 0.0088 | 0.0100 | NDCG@10 | 0.0160 | 0.0177 | 0.0165 | 0.0154 | 0.0173 | 0.0173 | 0.0196 | |||
| NDCG@20 | 0.0091 | 0.0106 | 0.0112 | 0.0127 | 0.0124 | 0.0117 | 0.0134 | NDCG@20 | 0.0197 | 0.0225 | 0.0211 | 0.0206 | 0.0223 | 0.0212 | 0.0242 | |||
| Yelp | Hit@10 | 0.0172 | 0.0184 | 0.0195 | 0.0210 | 0.0203 | 0.0214 | 0.0223 | Yelp | Hit@10 | 0.0282 | 0.0316 | 0.0279 | 0.0364 | 0.0278 | 0.0310 | 0.0359 | |
| Hit@20 | 0.0314 | 0.0347 | 0.0349 | 0.0380 | 0.0375 | 0.0389 | 0.0407 | Hit@20 | 0.0443 | 0.0516 | 0.0483 | 0.0620 | 0.0480 | 0.0523 | 0.0587 | |||
| NDCG@10 | 0.0083 | 0.0085 | 0.0090 | 0.0096 | 0.0103 | 0.0101 | 0.0105 | NDCG@10 | 0.0142 | 0.0162 | 0.0137 | 0.0184 | 0.0136 | 0.0156 | 0.0177 | |||
| NDCG@20 | 0.0118 | 0.0126 | 0.0133 | 0.0142 | 0.0139 | 0.0147 | 0.0151 | NDCG@20 | 0.0183 | 0.0212 | 0.0189 | 0.0248 | 0.0187 | 0.0210 | 0.0234 | |||
| Home | Hit@10 | 0.0057 | 0.0064 | 0.0072 | 0.0087 | 0.0078 | 0.0094 | 0.0108 | Home | H@10 | 0.0155 | 0.0156 | 0.0166 | 0.0208 | 0.0167 | 0.0173 | 0.0204 | |
| H@20 | 0.0106 | 0.0120 | 0.0141 | 0.0151 | 0.0149 | 0.0159 | 0.0182 | H@20 | 0.0244 | 0.0247 | 0.0270 | 0.0336 | 0.0275 | 0.0276 | 0.0311 | |||
| N@10 | 0.0027 | 0.0030 | 0.0034 | 0.0042 | 0.0037 | 0.0044 | 0.0054 | N@10 | 0.0083 | 0.0086 | 0.0089 | 0.0110 | 0.0092 | 0.0099 | 0.0109 | |||
| N@20 | 0.0039 | 0.0045 | 0.0051 | 0.0059 | 0.0054 | 0.0060 | 0.0073 | N@20 | 0.0101 | 0.0105 | 0.0111 | 0.0141 | 0.0113 | 0.0122 | 0.0137 | |||
3.6. Overall Improvements
The experimental results of original sequential recommendation models and adding our RepPad are presented in Table 4 and Table 5. These tables show that our method can significantly improve the performance of recommendation models on short-sequence datasets, but our method may become ineffective for long-sequence datasets. These results validate our conjecture in Section 2.5.2.
(1) As a whole, the RNN- and CNN-based models perform comparably. NARM is usually the best performer, which verifies the effectiveness of combining attention mechanisms and RNN architectures. The Transformer-based models perform better overall, especially SASRec and STOSA. This shows the ability of the Transformer architecture to model user sequence patterns. FMLP-Rec performs slightly less well, which we believe may be related to the fact that the pure MLP architecture cannot accurately capture the fine-grained relationship between each user interaction and historical behavior as the Transformer does.
(2) As demonstrated in Table 4, after adding our RepPad to the original model, the performance of all models is significantly improved. The average recommendation performance improvement is up to 60.3% on GRU4Rec, 24.3% on SASRec, and 22.8% on STOSA. In particular, Our method gives GRU4Rec a boost of up to 110.00% Hit@5 and 122.22% for NDCG@5 on the Home dataset. The above experimental results validate the effectiveness of our method on short-sequence datasets. It also shows that RepPad can be applied to various types of sequential models. Considering that in real-world scenarios, the vast majority of user history records are short sequences (Liu et al., 2021b; Jiang et al., 2021), our approach has great potential for application.
(3) From Table 5, we can observe that RepPad can only achieve less improvement on some models for the long-sequence dataset and even cause performance degradation on some methods. These results verify our conjecture in Section 2.5.2. Even though we have set the maximum sequence length to 200 for long-sequence datasets, most user sequences still do not have enough space left for repeated padding. At the same time, repeated padding may interfere with the model’s ability to capture long-term user preferences and impair recommendation performance. We also note that the Transformer-based model still outperforms other types of models overall, further demonstrating the power of its architecture.
| Dataset | Metric | Original | ASReP | DiffuASR | CL4SRec | RepPad |
| Toys | Hit@10 | 0.0716 | 0.0755 | 0.0783 | 0.0804 | 0.0843 |
| Hit@20 | 0.0965 | 0.1021 | 0.1085 | 0.1052 | 0.1142 | |
| NDCG@10 | 0.0396 | 0.0423 | 0.0453 | 0.0447 | 0.0476 | |
| NDCG@20 | 0.0471 | 0.0506 | 0.0535 | 0.0520 | 0.0551 | |
| Beauty | Hit@10 | 0.0637 | 0.0664 | 0.0679 | 0.0686 | 0.0726 |
| Hit@20 | 0.0942 | 0.0959 | 0.0966 | 0.0982 | 0.1034 | |
| NDCG@10 | 0.0331 | 0.0351 | 0.0372 | 0.0366 | 0.0390 | |
| NDCG@20 | 0.0408 | 0.0422 | 0.0454 | 0.0449 | 0.0468 | |
| Sports | Hit@10 | 0.0299 | 0.0324 | 0.0375 | 0.0339 | 0.0369 |
| Hit@20 | 0.0447 | 0.0503 | 0.0566 | 0.0521 | 0.0553 | |
| NDCG@10 | 0.0160 | 0.0166 | 0.0169 | 0.0172 | 0.0196 | |
| NDCG@20 | 0.0197 | 0.0201 | 0.0214 | 0.0225 | 0.0231 | |
| Yelp | Hit@10 | 0.0282 | 0.0323 | 0.0345 | 0.0385 | 0.0359 |
| Hit@20 | 0.0443 | 0.0539 | 0.0566 | 0.0621 | 0.0587 | |
| NDCG@10 | 0.0142 | 0.0153 | 0.0169 | 0.0182 | 0.0177 | |
| NDCG@20 | 0.0183 | 0.0207 | 0.0228 | 0.0251 | 0.0234 | |
| Home | Hit@10 | 0.0155 | 0.0176 | 0.0198 | 0.0220 | 0.0204 |
| Hit@20 | 0.0244 | 0.0285 | 0.0301 | 0.0329 | 0.0311 | |
| NDCG@10 | 0.0083 | 0.0098 | 0.0113 | 0.0122 | 0.0116 | |
| NDCG@20 | 0.0101 | 0.0121 | 0.0144 | 0.0149 | 0.0137 |
3.7. Compare with Other Methods
In this subsection, we compare RepPad with different data augmentation methods. For the heuristic methods, we choose the two representative models, SASRec and GRU4Rec, as the backbone network. For methods that require training, we chose the most versatile SASRec since different methods have different restrictions on the type of backbone network.
From Table 6, we observe that RepPad outperforms existing heuristic data augmentation methods in most cases. CMRSI performs the best among the baselines, thanks to the five well-designed data augmentation operators that help discover more preference information while mitigating data sparsity. Ran-S also achieves competitive performance in some examples due to its augmentation using items in the original sequence. We also observe that in some cases, the model performance degraded after using data augmentation methods, which may be related to the fact that these methods introduce too much noise that destroys the integrity of the original sequence. RepPad utilizes the free data space and uses the original sequences for padding, which improves model performance while retaining the user’s complete preference knowledge. From Table 7, RepPad still achieves satisfactory results in the face of data augmentation methods that require training. Among the baseline methods, DiffuASR and CL4SRec leverage the diffusion model and sequence-level augmentation with contrastive learning to achieve competitive performance in some cases. Surprisingly, RepPad achieves the best or second-best performance in all cases without including any parameters and training process.
Overall, RepPad proved its superiority by achieving highly competitive results without including any parameters or training processes. Also, our approach is not limited by the backbone network and can be seamlessly inserted into most existing sequential recommendation models.
3.8. Ablation Study
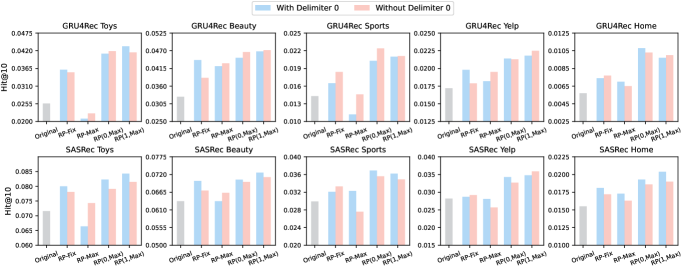
In this section, we conduct an ablation study to explore the different variants of RepPad. Based on the padding times in Table 1 and whether or not to add the delimiter 0, we compare the performance of the following variants: 1) RP-Fix: Performing repeated padding with a fixed number of times, we report the best results for times in range . 2) RP-Max: Performing repeated padding until the remaining space is insufficient (i.e., maximum padding times). 3) RP(0, Max): When performing repeated padding each time, randomly select between 0 and the maximum number of times. 4) RP(1, Max): When performing repeated padding each time, randomly select between 1 and the maximum number of times. Figure 2 presents the results. We report the performance of each of the four variants with and without adding the delimiter 0.
For performance between different variants, in most results, the performance of RP(0, Max) and RP(1, Max) can come with considerable improvements. RP-Fix and RP-Max bring limited performance improvement compared to RP(0, Max) and RP(1, Max). For PR-Fix, RepPad is executed with a fixed number of times, so it does not utilize the idle input space. For RP-Max, we observe that it not only does not bring improvement in some cases but also leads to a significant decrease in model performance. If every sequence performs RepPad to the maximum number of times, it may make the representation learned by the model unbalanced. Because the repeated padding time tends to be large for short sequences, multiple iterations of short behavioral sequences may interfere with the model’s ability for long-sequence and long-term preferences modeling, which in turn impairs recommendation performance. For RP(0, Max) and RP(1, Max), they avoid the imbalance problem caused by RP-Max while utilizing the free input space. Meanwhile, RP(1, Max) performs better than RP(0, Max), indicating that executing RepPad at least once is essential.
For whether or not to add the delimiter 0, we observe that this factor is related to the type of recommendation model. For GRU4Rec, there are more examples of better performance when no delimiter is added. In contrast, for SASRec, there are more examples that models perform better when the delimiter is added. In other words, RNN-based models are less susceptible to the interference of ”predicting the tail with the head”. The self-attention module of Transformer-based models pays attention to the effect of each historical interaction on the following action, so the negative effect of ”predicting the tail with the head” can be minimized by adding the delimiter 0. We leave the theoretical explanation of this phenomenon to the future work.
| Dataset | SASRec | GRU4Rec | ||
| Method | Epoch Time | Method | Epoch Time | |
| Beauty | Original | 2.389 | Original | 0.960 |
| w/ CMRSI | 4.561 (+2.172) | w/ CMRSI | 2.547 (+1.587) | |
| w/ CL4SRec | 3.954 (+1.565) | w/ CL4SRec | 1.748 (+0.778) | |
| w/ RP-Fix | 2.483 (+0.094) | w/ RP-Fix | 1.049 (+0.089) | |
| w/ RP(1, Max) | 2.768 (+0.379) | w/ RP(1, Max) | 1.308 (+0.384) | |
| Sports | Original | 3.133 | Original | 1.422 |
| w/ CMRSI | 6.400 (+3.267) | w/ CMRSI | 3.853 (+2.431) | |
| w/ CL4SRec | 5.479 (+2.346) | w/ CL4SRec | 2.620 (+1.198) | |
| w/ RP-Fix | 3.219 (+0.086) | w/ RP-Fix | 1.548 (+0.126) | |
| w/ RP(1, Max) | 3.740 (+0.607) | w/ RP(1, Max) | 1.998 (+0.576) | |
4. Why RepPad Works
4.1. Loss Convergence and Training Efficiency
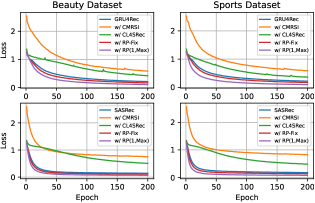
In Figure 3, we illustrate the loss convergence of different methods during training. We also compare the epoch time consumption of different methods in Table 8. From the figures and tables, we can observe that RepPad’s losses converge slightly faster than the original model. For CMRSI, the heuristic data augmentation introduces more different training sequences along with more noise, resulting in more epochs for the model to converge. The contrastive learning task of CL4SRec also imposes additional computational overhead and convergence burden. Also, RepPad only adds a small amount of epoch elapsed time compared to the original model. While CMSRI and CL4SRec add extra training sequences and auxiliary tasks, resulting in a substantial increase in training elapsed time. Comparing RP-Fix and RP(1, Max), the former can only be performed repeated padding a fixed and smaller number of times. At the same time, the latter randomly chooses between one time and the maximum number of times, which slightly increases the elapsed time but improves the speed of loss convergence and model performance.
4.2. Gradient Stability
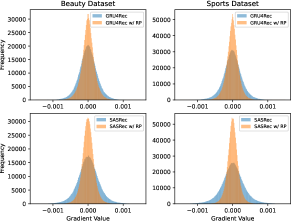
Research has shown that more stable or smooth gradients are more helpful for model training (Li et al., 2019; Reddi et al., 2019; Xu et al., 2019), thus improving model robustness and performance. In Figure 4, we illustrate the average gradient of item embeddings throughout the training process with and without our RepPad. We show the frequency of the gradient values as histograms. We can observe that the average gradient values are more centralized with the addition of our method. While the gradient is more likely to have large or small values during the original model training, RepPad mitigates this phenomenon, making the gradient more stable during the training process. Smooth updating of the gradient allows training to converge stably and improves the model’s recommendation performance
4.3. Summary and Insights
RepPad can make the gradient update of the model more stable without increasing the total number of training sequences. Unlike existing methods, our method augments short sequences to a length comparable to that of long sequences in a nearly lossless manner. Existing methods inevitably generate noise or compromise the integrity of the original data when perform augmentation. From another perspective, RepPad enables the model to focus fairly on short and long sequences, giving more attention to long-tail items and users. In this way, the model can better learn the representation of cold-start users and items. We also speculate that RepPad acts as some kind of regularization, which mitigates the negative effects of the uneven distribution of original dataset.
5. Related Works
5.1. Sequential Recommendation
Sequential recommendation (SR) is an emerging topic in the field of recommender systems (Qu et al., 2022). An early solution is to treat the item sequence as a Markov Chain (Rendle et al., 2010; Shani et al., 2005; He and McAuley, 2016), where the next item to predict is closely related to the latest few interactions. The limitation lies in the inability to learn the dependency in a relatively large time step. Hence, a better solution based on recurrent neural networks (RNNs) (Schuster and Paliwal, 1997) emerges since it can capture long- and short-term preferences. A pioneering work GRU4Rec (Hidasi et al., 2015a) introduced RNN into the field of recommender systems. It trained a Gated Recurrent Unit (GRU) architecture to model the evolution of user interests. Following this idea, CmnRec (Qu et al., 2022) proposed to divide proximal information units into chunks, whereby the number of memory operations can be significantly reduced. More recently, transformer-based approaches have attracted much attention because of their convenience for parallelization and carefully designed self-attention architecture (Vaswani et al., 2017; Devlin et al., 2018). SASRec (Kang and McAuley, 2018) employed unidirectional Transformers to fulfill the next-item prediction task in the sequential recommendation. Some works further optimized the Transformer’s architecture to make it more suitable for recommendation scenarios, such as reducing computational complexity (Fan et al., 2021) and stochastic self-attention (Fan et al., 2022). Furthermore, FMLP-Rec (Zhou et al., 2022) proposes an all-MLP architecture with learnable filters to enhance recommendation performance.
5.2. Data Augmentation for SR
Data augmentation has been established as a standard technique to train more robust models in many domains. In recommender systems, Slide Windows is an early work (Tan et al., 2016b), which modified the original click sequence by splitting it into many sub-sequences or randomly discarding a certain number of items. Inspired by counterfactual thinking, CASR (Wang et al., 2021) revised the sequence of user behaviors by substituting some previously purchased items with other unknown items. Some researchers proposed to leverage bi-directional transformers (Liu et al., 2021b; Jiang et al., 2021) and diffusion models (Liu et al., 2023) for sequence data augmentation. With the rise of self-supervised techniques (e.g., contrastive learning), many researchers used it as an auxiliary task to further improve model performance (Qin et al., 2023; Xie et al., 2022). For example, CL4SRec (Xie et al., 2020) developed three data augmentation operators for pre-training recommendation tasks equipped with a contrastive learning framework. Based on CL4SRec, CoSeRec (Liu et al., 2021a) integrated item similarity information for data augmentation with a contrastive learning objective, aiming to maximize the agreement of augmented sequences. Unlike existing methods, we are the first to explore the use of idle padding space for data augmentation. In terms of simplicity and applicability, our method does not contain any parameters or training processes and can be plugged into most existing sequential models.
6. Conclusion
In this work, we start from the commonly used padding strategy, aiming to utilize the idle input space to further improve the model performance and training efficiency. Based on this idea, we propose RepPad, which leverages the original sequence as padding content instead of the special value 0. The RepPad can be considered as a sequence-level data augmentation method. Compared with existing methods, our method does not contain any parameters or training processes, and it is a data augmentation plugin with high applicability. Extensive experiments demonstrate the superiority of RepPad. It improves the performance of various sequential models and outperforms existing data enhancement methods. We also provide multiple perspectives and insights into what makes RepPad effective. For future work, we hope to provide theoretical underpinnings for RepPad or explore more appropriate padding strategies. We are also interested in combining RepPad with other data augmentation methods.
Acknowledgements.
This work is partially supported by the National Natural Science Foundation of China under Grant No. 62032013, the Science and technology projects in Liaoning Province (No. 2023JH3/10200005), and the Fundamental Research Funds for the Central Universities under Grant No. N2317002.References
- (1)
- Dang et al. (2023a) Yizhou Dang, Enneng Yang, Guibing Guo, Linying Jiang, Xingwei Wang, Xiaoxiao Xu, Qinghui Sun, and Hong Liu. 2023a. TiCoSeRec: Augmenting Data to Uniform Sequences by Time Intervals for Effective Recommendation. TKDE (2023).
- Dang et al. (2023b) Yizhou Dang, Enneng Yang, Guibing Guo, Linying Jiang, Xingwei Wang, Xiaoxiao Xu, Qinghui Sun, and Hong Liu. 2023b. Uniform sequence better: Time interval aware data augmentation for sequential recommendation. In AAAI, Vol. 37. 4225–4232.
- Devlin et al. (2018) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018).
- Fan et al. (2021) Xinyan Fan, Zheng Liu, Jianxun Lian, Wayne Xin Zhao, Xing Xie, and Ji-Rong Wen. 2021. Lighter and better: low-rank decomposed self-attention networks for next-item recommendation. In SIGIR. 1733–1737.
- Fan et al. (2022) Ziwei Fan, Zhiwei Liu, Yu Wang, Alice Wang, Zahra Nazari, Lei Zheng, Hao Peng, and Philip S Yu. 2022. Sequential recommendation via stochastic self-attention. In WWW. 2036–2047.
- Hao et al. (2023) Yongjing Hao, Pengpeng Zhao, Xuefeng Xian, Guanfeng Liu, Lei Zhao, Yanchi Liu, Victor S Sheng, and Xiaofang Zhou. 2023. Learnable Model Augmentation Contrastive Learning for Sequential Recommendation. TKDE (2023).
- He and McAuley (2016) Ruining He and Julian McAuley. 2016. Fusing similarity models with markov chains for sparse sequential recommendation. In ICDM. IEEE, 191–200.
- Hidasi et al. (2015a) Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. 2015a. Session-based recommendations with recurrent neural networks. arXiv preprint arXiv:1511.06939 (2015).
- Hidasi et al. (2015b) Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. 2015b. Session-based recommendations with recurrent neural networks. arXiv preprint arXiv:1511.06939 (2015).
- Hu et al. (2020) Haoji Hu, Xiangnan He, Jinyang Gao, and Zhi-Li Zhang. 2020. Modeling personalized item frequency information for next-basket recommendation. In SIGIR. 1071–1080.
- Jiang et al. (2021) Juyong Jiang, Yingtao Luo, Jae Boum Kim, Kai Zhang, and Sunghun Kim. 2021. Sequential recommendation with bidirectional chronological augmentation of transformer. arXiv preprint arXiv:2112.06460 (2021).
- Jing et al. (2023) Mengyuan Jing, Yanmin Zhu, Tianzi Zang, and Ke Wang. 2023. Contrastive Self-supervised Learning in Recommender Systems: A Survey. arXiv preprint arXiv:2303.09902 (2023).
- Kang and McAuley (2018) Wang-Cheng Kang and Julian McAuley. 2018. Self-attentive sequential recommendation. In ICDM. IEEE, 197–206.
- Kingma and Ba (2014) Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
- Krichene and Rendle (2020) Walid Krichene and Steffen Rendle. 2020. On sampled metrics for item recommendation. In KDD. 1748–1757.
- Li et al. (2017) Jing Li, Pengjie Ren, Zhumin Chen, Zhaochun Ren, Tao Lian, and Jun Ma. 2017. Neural attentive session-based recommendation. In CIKM. 1419–1428.
- Li et al. (2020) Jiacheng Li, Yujie Wang, and Julian McAuley. 2020. Time interval aware self-attention for sequential recommendation. In WSDM. 322–330.
- Li et al. (2019) Xiang Li, Shuo Chen, Xiaolin Hu, and Jian Yang. 2019. Understanding the disharmony between dropout and batch normalization by variance shift. In CVPR. 2682–2690.
- Liu et al. (2016) Qiang Liu, Shu Wu, Diyi Wang, Zhaokang Li, and Liang Wang. 2016. Context-aware sequential recommendation. In ICDM. IEEE, 1053–1058.
- Liu et al. (2023) Qidong Liu, Fan Yan, Xiangyu Zhao, Zhaocheng Du, Huifeng Guo, Ruiming Tang, and Feng Tian. 2023. Diffusion augmentation for sequential recommendation. In CIKM. 1576–1586.
- Liu et al. (2021a) Zhiwei Liu, Yongjun Chen, Jia Li, Philip S Yu, Julian McAuley, and Caiming Xiong. 2021a. Contrastive self-supervised sequential recommendation with robust augmentation. arXiv preprint arXiv:2108.06479 (2021).
- Liu et al. (2021b) Zhiwei Liu, Ziwei Fan, Yu Wang, and Philip S Yu. 2021b. Augmenting sequential recommendation with pseudo-prior items via reversely pre-training transformer. In SIGIR. 1608–1612.
- McAuley et al. (2015) Julian McAuley, Rahul Pandey, and Jure Leskovec. 2015. Inferring networks of substitutable and complementary products. In KDD. 785–794.
- Qin et al. (2023) Xiuyuan Qin, Huanhuan Yuan, Pengpeng Zhao, Guanfeng Liu, Fuzhen Zhuang, and Victor S Sheng. 2023. Intent Contrastive Learning with Cross Subsequences for Sequential Recommendation. arXiv preprint arXiv:2310.14318 (2023).
- Qiu et al. (2022) Ruihong Qiu, Zi Huang, Hongzhi Yin, and Zijian Wang. 2022. Contrastive learning for representation degeneration problem in sequential recommendation. In WSDM. 813–823.
- Qu et al. (2022) Shilin Qu, Fajie Yuan, Guibing Guo, Liguang Zhang, and Wei Wei. 2022. CmnRec: Sequential Recommendations with Chunk-accelerated Memory Network. TKDE (2022).
- Reddi et al. (2019) Sashank J Reddi, Satyen Kale, and Sanjiv Kumar. 2019. On the convergence of adam and beyond. arXiv preprint arXiv:1904.09237 (2019).
- Rendle et al. (2010) Steffen Rendle, Christoph Freudenthaler, and Lars Schmidt-Thieme. 2010. Factorizing personalized markov chains for next-basket recommendation. In WWW. 811–820.
- Schuster and Paliwal (1997) Mike Schuster and Kuldip K Paliwal. 1997. Bidirectional recurrent neural networks. TSP 45, 11 (1997), 2673–2681.
- Shani et al. (2005) Guy Shani, David Heckerman, Ronen I Brafman, and Craig Boutilier. 2005. An MDP-based recommender system. JMLR 6, 9 (2005).
- Sun et al. (2019) Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, and Peng Jiang. 2019. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In CIKM. 1441–1450.
- Tan et al. (2016a) Yong Kiam Tan, Xinxing Xu, and Yong Liu. 2016a. Improved recurrent neural networks for session-based recommendations. In DLRS. 17–22.
- Tan et al. (2016b) Yong Kiam Tan, Xinxing Xu, and Yong Liu. 2016b. Improved recurrent neural networks for session-based recommendations. In DLRS. 17–22.
- Tang and Wang (2018) Jiaxi Tang and Ke Wang. 2018. Personalized top-n sequential recommendation via convolutional sequence embedding. In WSDM. 565–573.
- Tian et al. (2023) Changxin Tian, Binbin Hu, Wayne Xin Zhao, Zhiqiang Zhang, and Jun Zhou. 2023. Periodicity May Be Emanative: Hierarchical Contrastive Learning for Sequential Recommendation. In CIKM. 2442–2451.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. NIPS 30 (2017).
- Wang et al. (2022) Jianling Wang, Ya Le, Bo Chang, Yuyan Wang, Ed H Chi, and Minmin Chen. 2022. Learning to Augment for Casual User Recommendation. In WWW. 2183–2194.
- Wang et al. (2021) Zhenlei Wang, Jingsen Zhang, Hongteng Xu, Xu Chen, Yongfeng Zhang, Wayne Xin Zhao, and Ji-Rong Wen. 2021. Counterfactual data-augmented sequential recommendation. In SIGIR. 347–356.
- Xie et al. (2020) Xu Xie, Fei Sun, Zhaoyang Liu, Shiwen Wu, Jinyang Gao, Bolin Ding, and Bin Cui. 2020. Contrastive learning for sequential recommendation. arXiv preprint arXiv:2010.14395 (2020).
- Xie et al. (2022) Xu Xie, Fei Sun, Zhaoyang Liu, Shiwen Wu, Jinyang Gao, Jiandong Zhang, Bolin Ding, and Bin Cui. 2022. Contrastive learning for sequential recommendation. In ICDE. IEEE, 1259–1273.
- Xu et al. (2019) Jingjing Xu, Xu Sun, Zhiyuan Zhang, Guangxiang Zhao, and Junyang Lin. 2019. Understanding and improving layer normalization. NIPS 32 (2019).
- Yu et al. (2023) Junliang Yu, Hongzhi Yin, Xin Xia, Tong Chen, Jundong Li, and Zi Huang. 2023. Self-supervised learning for recommender systems: A survey. TKDE (2023).
- Yuan et al. (2019) Fajie Yuan, Alexandros Karatzoglou, Ioannis Arapakis, Joemon M Jose, and Xiangnan He. 2019. A simple convolutional generative network for next item recommendation. In WSDM. 582–590.
- Zhao et al. (2023a) Chuang Zhao, Hongke Zhao, Ming He, Jian Zhang, and Jianping Fan. 2023a. Cross-domain recommendation via user interest alignment. In Proceedings of the ACM Web Conference 2023. 887–896.
- Zhao et al. (2023b) Chuang Zhao, Hongke Zhao, Xiaomeng Li, Ming He, Jiahui Wang, and Jianping Fan. 2023b. Cross-Domain Recommendation via Progressive Structural Alignment. IEEE Transactions on Knowledge and Data Engineering (2023).
- Zhou et al. (2022) Kun Zhou, Hui Yu, Wayne Xin Zhao, and Ji-Rong Wen. 2022. Filter-enhanced MLP is all you need for sequential recommendation. In WWW. 2388–2399.