Rethinking the Capacity of Graph Neural Networks for Branching Strategy

While the capacity of GNNs for general graph tasks, such as node and link prediction or function approximation on graphs, has been extensively studied [xu2019powerful, maron2019universality, chen2019equivalence, keriven2019universal, sato2019approximation, Loukas2020What, azizian2020expressive, geerts2022expressiveness, zhang2023rethinking], their capacities in approximating SB remains largely unexplored. The closest studies [chen2022representing-lp, chen2022representing-milp] have explored GNNs’ ability to represent properties of linear programs (LPs) and MILPs, such as feasibility, boundedness, or optimal solutions, but have not specifically focused on branching strategies. Recognizing this gap, our paper makes the following contributions:

• •

  In the context of L2B using GNNs, we first focus on the most widely used type: message-passing GNNs (MP-GNNs). Our study reveals that MP-GNNs can reliably predict SB results, but only for a specific class of MILPs that we introduce as message-passing-tractable (MP-tractable). We prove that for any distribution of MP-tractable MILPs, there exists an MP-GNN capable of accurately predicting their SB results. This finding establishes a theoretical basis for the widespread use of MP-GNNs to approximate SB results in current research.

• •

  Through a counter-example, we demonstrate that MP-GNNs are incapable of predicting SB results beyond the class of MP-tractable MILPs. The counter-example consists of two MILPs with distinct SB results to which all MP-GNNs, however, yield identical branching predictions.

• •

  For general MILPs, we explore the capabilities of second-order folklore GNNs (2-FGNNs), a type of higher-order GNN with enhanced expressive power. Our results show that 2-FGNNs can reliably answer question (1.1) positively, effectively replicating SB results across any distribution of MILP problems, surpassing the capabilities of standard MP-GNNs.

Overall, as a series of works have empirically shown that learning an MP-GNN as a fast approximation of SB significantly benefits the performance of an MILP solver on specific data sets [khalil2016learning, alvarez2017machine, balcan2018learning, gasse2019exact, gupta2020hybrid, zarpellon2021parameterizing, gupta2022lookback, lin2022learning, yang2022learning], our goal is to determine whether there is room, in theory, to further understand and improve the GNNs’ performance on this task.

Here we present an approach to represent MILP as a bipartite graph, termed the MILP-graph. This conceptualization was initially proposed by [gasse2019exact] and has quickly become a prevalent model in ML for MILP-related tasks. The MILP-graph is defined as a tuple $G=(V,W,A,F_{V},F_{W})$, where the components are specified as follows: $V=\{1,2,\dots,m\}$ and $W=\{1,2,\dots,n\}$ are sets of nodes representing the constraints and variables, respectively. An edge $(i,j)$ connects node $i\in V$ to node $j\in W$ if the corresponding entry $A_{ij}$ in the coefficient matrix of (2.1) is non-zero, with $A_{ij}$ serving as the edge weight. $F_{V}$ are features/attributes of constraints, with features $v_{i}=(b_{i},\circ_{i})$ attached to node $i\in V$. $F_{W}$ are features/attributes of variables, with features $w_{j}=(c_{j},\ell_{j},u_{j},\delta_{I}(j))$ attached to node $j\in W$, where $\delta_{I}(j)\in\{0,1\}$ indicates whether the variable $x_{j}$ is integer-constrained.

We define $\mathcal{N}_{W}(i)=:\{j\in W:A_{ij}\neq 0\}\subset W$ as the neighbors of $i\in V$ and similarly define $\mathcal{N}_{V}(j)=:\{i\in V:A_{ij}\neq 0\}\subset V$. This graphical representation completely describes a MILP’s information, allowing us to interchangeably refer to a MILP and its graph throughout this paper. An illustrative example is presented in Figure 1. We also introduce a space of MILP-graphs:

Message-passing graph neural networks (MP-GNNs) are a class of GNNs that operate on graph-structured data, by passing messages between nodes in a graph to aggregate information from their local neighborhoods. In our context, the input is an aforementioned MILP-graph $G=(V,W,A,F_{V},F_{W})$, and each node in $W$ is associated with a real-number output. We use the standard MP-GNNs for MILPs in the literature [gasse2019exact, chen2022representing-milp].

Specifically, the initial layer assigns features $s_{i}^{0},t_{j}^{0}$ for each node as

• •

  $s_{i}^{0}=p^{0}(v_{i})$ for each constraint $i\in V$, and $t_{j}^{0}=q^{0}(w_{j})$ for each variable $j\in W$.

Then message-passing layers $l=1,2,\dots,L$ update the features via

• •

  $s_{i}^{l}=p^{l}\big{(}s_{i}^{l-1},\sum_{j\in\mathcal{N}_{W}(i)}f^{l}(t_{j}^{l-1},A_{ij})\big{)}$ for each constraint $i\in V$, and

• •

  $t_{j}^{l}=q^{l}\big{(}t_{j}^{l-1},\sum_{i\in\mathcal{N}_{V}(j)}g^{l}(s_{i}^{l-1},A_{ij})\big{)}$ for each variable $j\in W$.

Finally, the output layer produces a read-number output $y_{j}$ for each node $j\in W$:

• •

  $y_{j}=r\big{(}\sum_{i\in V}s_{i}^{L},\sum_{j\in W}t_{j}^{L},t_{j}^{L}\big{)}$.

In practice, functions $\{p^{l},q^{l},f^{l},g^{l}\}_{l=1}^{L},r,p^{0},q^{0}$ are learnable and usually parameterized with multi-linear perceptrons (MLPs). In our theoretical analysis, we assume for simplicity that those functions are continuous on given domains. The space of MP-GNNs is introduced as follows.

Overall, any MP-GNN $F\in\mathcal{F}_{\textup{MP-GNN}}$ maps a MILP-graph $G$ to a $n$-dim vector: $y=F(G)\in\mathbb{R}^{n}$.

Second-order folklore graph neural networks (2-FGNNs) are an extension of MP-GNNs designed to overcome some of the capacity limitations. It is proved in [xu2019powerful] the expressive power of MP-GNNs can be measured by the Weisfeiler-Lehman test (WL test [weisfeiler1968reduction]). To enhance the ability to identify more complex graph patterns, [morris2019weisfeiler] developed high-order GNNs, inspired by high-order WL tests [cai1992optimal]. Since then, there has been growing literature about high-order GNNs and other variants including high-order folklore GNNs [maron2019provably, geerts2020expressive, geerts2020walk, azizian2020expressive, zhao2022practical, geerts2022expressiveness]. Instead of operating on individual nodes of the given graph, 2-FGNNs operate on pairs of nodes (regardless of whether two nodes in the pair are neighbors or not) and the neighbors of those pairs. We say two node pairs are neighbors if they share a common node. Let $G=(V,W,A,F_{V},F_{W})$ be the input graph. The initial layer performs:

• •

  $s_{ij}^{0}=p^{0}(v_{i},w_{j},A_{ij})$ for each constraint $i\in V$ and each variable $j\in W$, and

• •

  $t_{j_{1}j_{2}}^{0}=q^{0}(w_{j_{1}},w_{j_{2}},\delta_{j_{1}j_{2}})$ for variables $j_{1},j_{2}\in W$,

where $\delta_{j_{1}j_{2}}=1$ if $j_{1}=j_{2}$ and $\delta_{j_{1}j_{2}}=0$ otherwise. For internal layers $l=1,2,\dots,L$, compute

• •

  $s_{ij}^{l}=p^{l}\big{(}s_{ij}^{l-1},\sum_{j_{1}\in W}f^{l}(t_{j_{1}j}^{l-1},s_{ij_{1}}^{l-1})\big{)}$ for all $i\in V,j\in W$, and

• •

  $t_{j_{1}j_{2}}^{l}=q^{l}\big{(}t_{j_{1}j_{2}}^{l-1},\sum_{i\in V}g^{l}(s_{ij_{2}}^{l-1},s_{ij_{1}}^{l-1})\big{)}$ for all $j_{1},j_{2}\in W$.

The final layer produces the output $y_{j}$ for each node $j\in W$:

• •

  $y_{j}=r\big{(}\sum_{i\in V}s_{ij}^{L},\sum_{j_{1}\in W}t_{j_{1}j}^{L}\big{)}$.

Similar to MP-GNNs, the functions within 2-FGNNs, including $\{p^{l},q^{l},f^{l},g^{l}\}_{l=1}^{L},r,p^{0},q^{0}$, are also learnable and typically parameterized with MLPs. The space of 2-FGNNs is defined with:

Any $2$-FGNN, $F\in\mathcal{F}_{\textup{2-FGNN}}$, maps a MILP-graph $G$ to a $n$-dim vector: $y=F(G)$. While MP-GNNs and 2-FGNNs share the same input-output structure, their internal structures differ, leading to distinct expressive powers.

SB is notably effective in reducing the size of the BnB search space. This size is measured by the size of the BnB tree. Here, a “tree” refers to a hierarchical structure of “nodes”, each representing a decision point or a subdivision of the problem. The tree’s size corresponds to the number of these nodes. For instance, consider the instance “neos-3761878-oglio” from MIPLIB [gleixner2021miplib]. When solved using SCIP [BolusaniEtal2024OO, BolusaniEtal2024ZR] under standard configurations, the BnB tree size is $851$, and it takes $61.04$ seconds to attain optimality. However, disabling SB, along with all branching rules dependent on SB, results in an increased BnB tree size to $35548$ and an increased runtime to $531.0$ seconds.

SB itself is computationally expensive. In the above experiment under standard settings, SB consumes an average of $70.40\%$ of the total runtime, $42.97$ out of $61.04$ seconds in total.

Therefore, there is a clear need of approximating SB with efficient ML models. Ideally, if we can substantially reduce the SB calculation time from $42.97$ seconds to a negligible duration while maintaining its effectiveness, the remaining runtime of $61.04-42.97=18.07$ seconds would become significantly more efficient.

To move forward, we introduce some basic concepts related to SB.

SB begins by identifying candidate variables for branching, typically those with non-integer values in the solution to the linear relaxation but which are required to be integers. Each candidate is then assigned a SB score, a non-negative real number determined by creating two linear relaxations and calculating the objective improvement. A higher SB score indicates the variable has a higher priority to be chosen for branching. Variables that do not qualify as branching candidates are assigned a zero score. Compiling these scores for each variable results in an $n$-dimensional SB score vector, denoted as $\textup{SB}(G)=(\textup{SB}(G)_{1},\textup{SB}(G)_{2},\dots,\textup{SB}(G)_{n})$.

Consequently, the task of approximating SB with GNNs can be described with a mathematical language: finding an $F\in\mathcal{F}_{\textup{MP-GNN}}$ or $F\in\mathcal{F}_{\textup{2-FGNN}}$ such that $F(G)\approx\textup{SB}(G)$. Formally, it is:

To provide clarity, we present a formal definition of SB scores:

We only define the SB score for MILP problems with feasible and bounded LP relaxations; otherwise the optimal solution $x^{*}_{\textup{LP}}(G)$ does not exist. If the LP relaxation of $G$ admits multiple optimal solutions, then the strong branching score $\textup{SB}(G)$ depends on the choice of the particular optimal solution. To guarantee that the SB score is uniquely defined, in Definition 3.2, we use the optimal solution with the smallest $\ell_{2}$-norm, which is unique.

While the strong branching score discussed here primarily pertains to root SB, it is equally relevant to SB at leaf nodes within the BnB framework. By interpreting the MILP-graph $G$ in Definition 3.2 as representing the subproblems encountered during the BnB process, we can extend our findings to strong branching decisions at any point in the BnB tree. Here, root SB refers to the initial branching decisions made at the root of the BnB tree, while leaf nodes represent subsequent branching points deeper in the tree, where similar SB strategies can be applied.

Although this paper primarily focuses on the product SB scores (where the SB score is defined as the product of objective value changes when branching up and down), our analysis can extend to other forms of SB scores in [dey2024theoretical]. (Refer to Appendix D.1)

We train an MP-GNN and a 2-FGNN with $L=2$, where we replace the functions $f^{l}(t_{j}^{l-1},A_{ij})$ and $g^{l}(s_{i}^{l-1},A_{ij})$ in the MP-GNN by $A_{ij}f^{l}(t_{j}^{l-1})$ and $A_{ij}g^{l}(s_{i}^{l-1})$ to guarantee that they take the value $0$ whenever $A_{ij}=0$. For both GNNs, $p^{0},q^{0}$ are parameterized as linear transformations followed by a non-linear activation function; $\{p^{l},q^{l},f^{l},g^{l}\}_{l=1}^{L}$ are parameterized as 3-layer multi-layer perceptrons (MLPs) with respective learnable parameters; and the output mapping $r$ is parameterized as a 2-layer MLP. All layers map their input to a 1024-dimensional vector and use the ReLU activation function. With $\theta$ denoting the set of all learnable parameters of a network, we train both MP-GNN and 2-FGNN to fit the SB scores of the MILP dataset $\mathcal{G}$, by minimizing $\frac{1}{2}\sum_{G\in\mathcal{G}}\|F_{\theta}(G)-\textup{SB}(G)\|^{2}$ with respect to $\theta$, using Adam [kingma2014adam]. The networks and training scheme is implemented with Python and TensorFlow [abadi2016tensorflow]. The numerical experiments are conducted on a single NVIDIA Tesla V100 GPU for two datasets:

• •

  We randomly generate $100$ MILP instances, with 6 constraints and 20 variables, that are MP-tractable with probability $1$. SB scores are collected using SCIP [scip]. More details about instance generation are provided in Appendix E.

• •

  We train the MP-GNN and 2-FGNN to fit the SB scores of (4.1) and (4.2), i.e., the dataset only consists of two instances that are not MP-tractable.

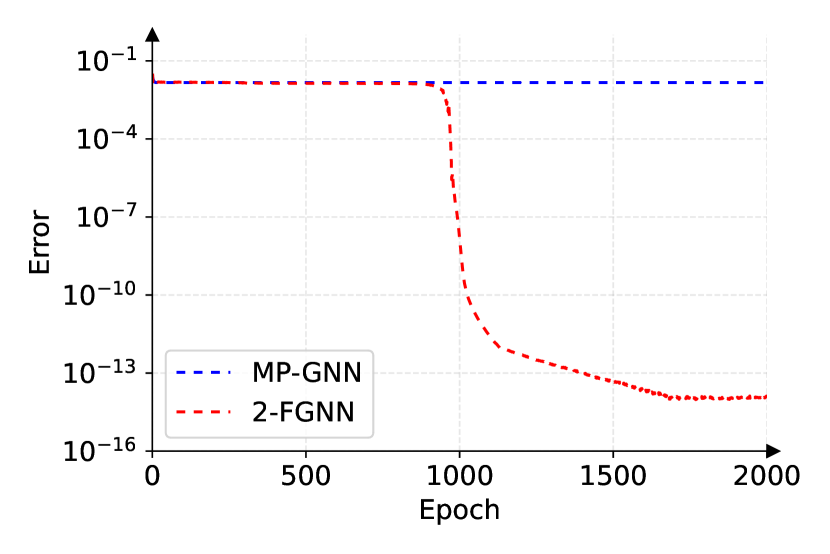
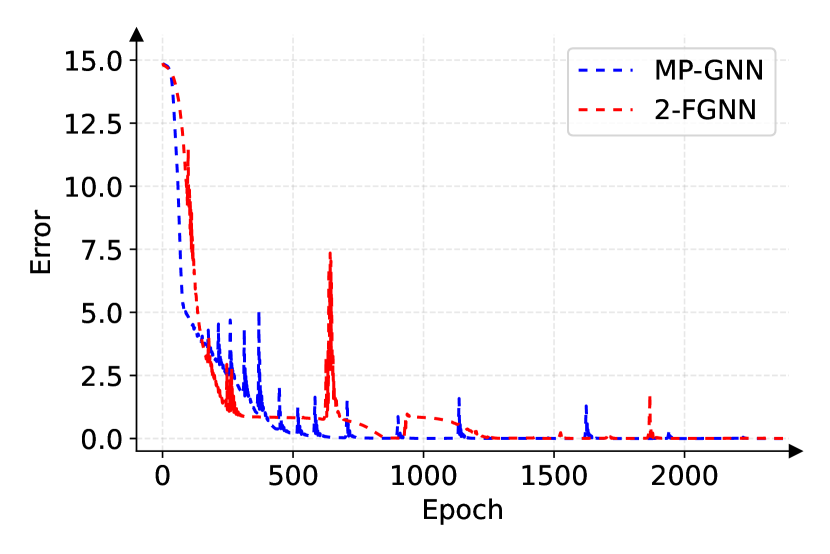
The numerical results are displayed in Figure 3. One can see from Figure 3(a) that both MP-GNN and 2-FGNN can approximate the SB scores over the dataset of random MILP instances very well, which validates Theorem 4.4 and Theorem 4.7. As illustrated in Figure 3(b), 2-FGNN can perfectly fit the SB scores of (4.1) and (4.2) simultaneously while MP-GNN can not, which is consistent with Theorem 4.5 and Theorem 4.7 and serves as a numerical verification of the capacity differences between MP-GNN and 2-FGNN for SB prediction. The detailed exploration of training and performance evaluations of GNNs is deferred to future work to maintain a focused investigation on the theoretical capabilities of GNNs in this paper.

In Figure 3(b), the behavior of MP-GNN remains unchanged regardless of the number of parameters used, as guaranteed by Theorem 4.5. This error is intrinsically due to the structure of MP-intractable MILPs and cannot be reduced by adding parameters. Conversely, 2-FGNN can achieve near-zero loss with sufficient parameters, as guaranteed by Theorem 4.7 and confirmed by our numerical experiments. To further verify this, we tested 2-FGNN with embedding sizes from 64 to 2,048. All models reached near-zero errors, though epoch counts varied, as shown in Table 1. The results suggest that larger embeddings improve model capacity to fit counterexamples. The gains level off beyond an embedding size of 1,024 due to increased training complexity.

While our study primarily focuses on theory and numerous empirical studies have shown the effectiveness of GNNs in branching strategies (as noted in Section 1), we conducted experiments on larger instances to further assess the scalability of this approach. We trained an MP-GNN on 100 large-scale set covering problems, each with 1,000 variables and 2,000 constraints, generated following the methodology in [gasse2019exact]. The MP-GNN achieved a training loss of $1.94\times 10^{-4}$, calculated as the average $\ell_{2}$ norm of errors across all training instances.