Rheology of dense suspensions under shear rotation

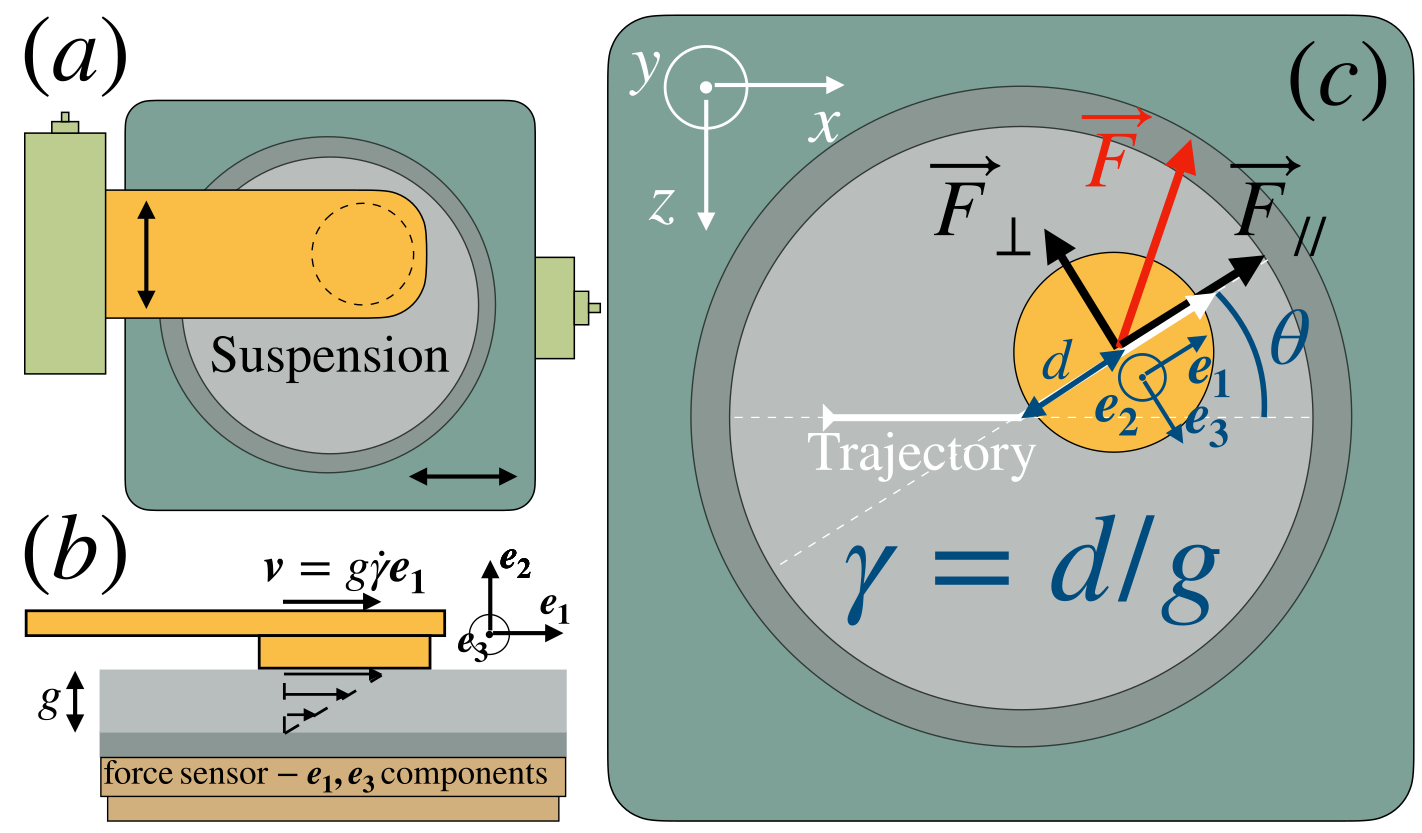
We designed a cross rheometer [38, 39], sketched in Fig. 1, made with two parallel plates mounted on two motorized linear stages of 25mm stroke (Newport MFA-CC) acting in perpendicular directions, allowing for arbitrary relative parallel motion and therefore arbitrary simple shear with velocity gradient orthogonal to the plates. We apply a simple shear (Fig. 1(b)) with velocity gradient $\bm{L}=\dot{\gamma}\bm{e}_{1}\bm{e}_{2}$ (with $\bm{e}_{1}$, $\bm{e}_{2}$ and $\bm{e}_{3}$ respectively the flow, gradient and vorticity directions), from which we define the strain-rate tensor $\bm{E}=\dot{\gamma}\hat{\bm{E}}\equiv(\bm{L}+\bm{L}^{\mathrm{T}})/2$. The shear rate $\dot{\gamma}$ is related to the velocity of the top plane relative to the bottom plane $\bm{v}=\dot{\gamma}g\bm{e}_{1}$, $g=$1\text{\,}\mathrm{mm}$$ being the gap width between the two plates.

A force sensor (AMTI HE6x6-1) measures the tangential force $\vec{F}=\vec{F}_{\parallel}+\vec{F}_{\perp}$ exerted on the lower plate (and thus by the upper plate on the suspension), with $\vec{F}_{\parallel}$ and $\vec{F}_{\perp}$ respectively along $\bm{e}_{1}$ and $\bm{e}_{3}$ (Fig. 1(b)-(c)). We define the shear viscosity $\eta_{12}\equiv\bm{\Sigma}:\bm{e}_{\mathrm{1}}\bm{e}_{\mathrm{2}}/\dot{\gamma}=\vec{F}_{\parallel}\cdot\bm{e}_{1}/(S\dot{\gamma})$, with $S$ the area of the upper plate, as well as the “orthogonal” shear viscosity $\eta_{32}\equiv\bm{\Sigma}:\bm{e}_{\mathrm{3}}\bm{e}_{\mathrm{2}}/\dot{\gamma}=\vec{F}_{\perp}\cdot\bm{e}_{3}/(S\dot{\gamma})$. Both have opposite $\theta$-parities: $\eta_{12}$ is even, $\eta_{12}(\gamma,\theta)=\eta_{12}(\gamma,-\theta)$, while $\eta_{32}$ is odd, $\eta_{32}(\gamma,\theta)=-\eta_{32}(\gamma,-\theta)$ (in particular this enforces that $\eta_{32}(\gamma,0)$ and $\eta_{32}(\gamma,\pi)$ vanish).

A preshear is first applied over 10 strain units, which is enough to reach steady state, followed by a shear rotation where we rotate the flow direction $\bm{e}_{1}$ and vorticity direction $\bm{e}_{3}$ by an angle $\theta\in[-\pi,\pi]$ around the gradient direction $\bm{e}_{2}$ (thick white line in Fig. 1(c)). The imposed shear rate is set at $\dot{\gamma}=0.4\,\mathrm{s}^{-1}$ for all presented experimental data.

The viscosities $\eta_{12}(\gamma,\theta)$ and $\eta_{32}(\gamma,\theta)$ are recorded via a Data Acquisition System (USB-1608FS-PLUS, MCCDAQ) as a function of the subsequent strain $\gamma<10$. The strain resolution is $\approx$3\text{\times}{10}^{-3}$$, the lowest available strain is $\approx$1\text{\times}{10}^{-2}$$, and $\theta$ is sampled every $\pi/18$.

The suspension particles are polystyrene spheres with a diameter of $40\text{\,}\mathrm{\SIUnitSymbolMicro m}$ (Microbeads TS40). They are dispersed in poly(ethylene glycol-ran-propylene glycol) (Sigma-Aldrich, viscosity $\eta_{0}=$38.4\text{\,}\mathrm{Pa}\text{\,}\mathrm{s}$$ at $25\text{\,}\mathrm{\SIUnitSymbolCelsius}$, $M_{\mathrm{n}}\approx$12\,000$$) for suspensions at $\phi=0.45$ or silicone oil (M1000, Roth, $\eta_{0}=$0.98\text{\,}\mathrm{Pa}\text{\,}\mathrm{s}$$ at $25\text{\,}\mathrm{\SIUnitSymbolCelsius}$) at $\phi=0.55$ and $0.57$.

We perform the same protocol in DEM simulations of a suspension of $N=2000$ frictional particles subject to lubrication and contact forces in a tri-periodic configuration, using a method described in [39, 31]. The suspension is bidisperse (with a size ratio $1:1.4$) and the friction coefficient is $\mu_{\mathrm{p}}=0.5$, in order to match the viscosity values observed experimentally.

We also compare our results to the predictions of the GW model, a model capturing the features of shear reversal [36, 40]. A detailed derivation and discussion of the underlying assumptions of the GW model can be found in [37]. The GW model considers the strain evolution of a fabric tensor $\langle\bm{n}\bm{n}\rangle$ where $\bm{n}$ is the unit separation vector between pairs of particles in a near interaction via contact or lubrication forces

The top line of Eq. (1) describes that particle pairs rotate like dumbbells with the velocity gradient $\hat{\bm{L}}=\bm{L}/\dot{\gamma}$ and the bottom line describes the association and dissociation of particle pairs due to the compressive part $\hat{\bm{E}}_{\mathrm{c}}$ and the extensive part $\hat{\bm{E}_{\mathrm{e}}}$ of the strain rate tensor $\hat{\bm{E}}$ which pushes particles together and pulls them apart, respectively. The pair association (and dissociation) rate $\beta$ is a tuneable parameter. The tensor $\langle\bm{nnnn}\rangle$ is approximated in terms of $\langle\bm{n}\bm{n}\rangle$ with the Hinch & Leal closure [41]. Furthermore, the GW model decomposes the stress $\bm{\Sigma}=\bm{\Sigma}^{\mathrm{H}}+\bm{\Sigma}^{\mathrm{C}}+2\eta_{0}\bm{E}$ in contributions from hydrodynamics, $\bm{\Sigma}^{\mathrm{H}}$, and contacts, $\bm{\Sigma}^{\mathrm{C}}$,

where $\alpha_{0}$ and $\chi_{0}$ are tuneable parameters. $\bm{\Sigma}^{\mathrm{H}}$ diverges when $\phi$ approaches the random close packing volume fraction $\phi_{\mathrm{RCP}}=0.65$ and $\bm{\Sigma}^{\mathrm{C}}$ diverges when the ‘jamming coordinate’ $\xi=-\langle\bm{n}\bm{n}\rangle:\bm{E}_{\mathrm{c}}|\bm{E}_{\mathrm{c}}|^{-1}$, a proxy for the coordination number, approaches the jamming value $\xi_{\mathrm{J}}$. By demanding that, in steady shear flow, $\bm{\Sigma}^{\mathrm{C}}$ diverges when $\phi$ approaches the friction-dependent jamming volume fraction $\phi_{\mathrm{J}}=0.58$, we have previously shown that: $\xi_{\mathrm{J}}=\phi_{\mathrm{J}}\left(213\beta^{2}-234\beta+2080\right)\left[15\left(9\beta^{2}+54\beta+416\right)\right]^{-1}$ [37]. In the SI we argue our choices for $\alpha_{0}=2.4$, $\chi_{0}=2.3$ and $\beta=7$.

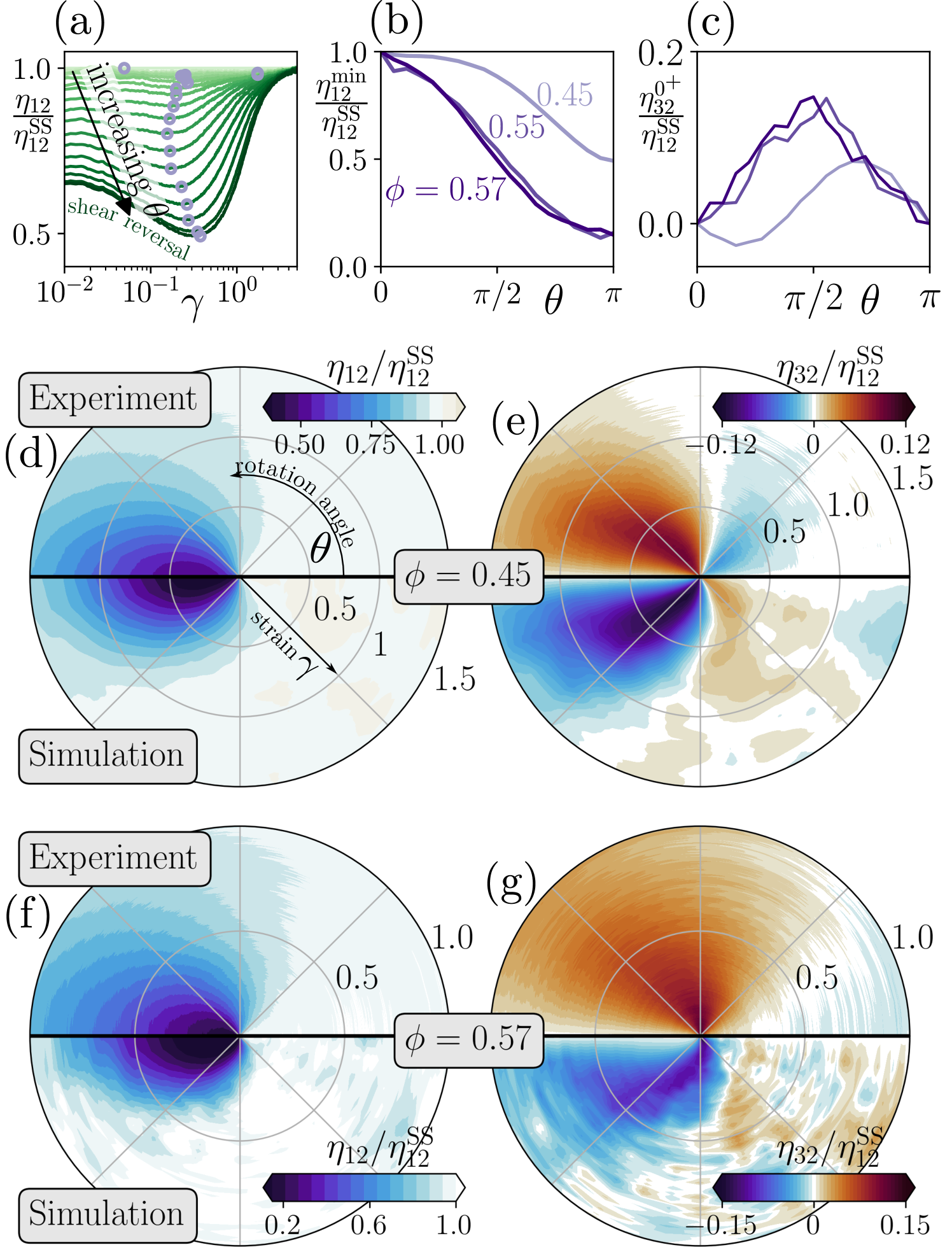
In Fig. 2(a), we show the viscosity $\eta_{12}(\gamma,\theta)$ measured in experiments, for a moderately dense suspension at $\phi=0.45$. It decreases at low strain values, then passes through a minimum before increasing back to its steady-state value. The minimum is located at a strain $\gamma_{\mathrm{min}}$ weakly dependent on $\theta$, from $\gamma_{\mathrm{min}}\approx 0.15$ for $\theta\approx\pi/2$ to $\gamma_{\mathrm{min}}\approx 0.35$ for shear reversal ($\theta=\pi$). As shown in Fig. 2(b), the minimum value $\eta_{12}^{\mathrm{min}}$ gradually decreases when $\theta$ increases, to reach its lowest value for shear reversal. Once normalized by the steady-state value $\eta_{12}^{\mathrm{SS}}$, $\eta_{12}^{\mathrm{min}}/\eta_{12}^{\mathrm{SS}}$ for a given $\theta$ decreases when $\phi$ increases, as is already known for shear reversal [25]. Interestingly, for the lowest $\phi=0.45$, $\eta_{12}^{\mathrm{min}}\approx\eta_{12}^{\mathrm{SS}}$ for $\theta\lesssim\pi/4$: the suspension seems oblivious to the shear rotation at small angles. We will see that this is not quite true when considering $\eta_{32}$.

We compare these data with the DEM ones in a radial representation $\eta_{12}(\gamma,\theta)$ in Fig. 2(d), with experiments in the top half and numerics in the bottom half. The agreement is good, besides simulations predicting a quicker relaxation to steady state than actually observed.

We turn in Fig. 2(e) to $\eta_{32}$, again comparing experiments in the top half and numerics in the bottom half. Both datasets are in excellent agreement and reveal a structure mixing first and second order odd circular harmonics (respectively $\propto\sin\theta$ and $\propto\sin 2\theta$) with similar amplitudes. For $0<\theta\lesssim\pi/2$, we find $\eta_{32}<0$ for $\gamma\lesssim 1$, i.e. the suspension exerts on the top plate a “restoring” force in the direction of decreasing $\theta$ values. In a force control setup where one sets the upper plate force $\vec{F}_{\parallel}$ rather than its displacement, the suspension would thus be stable with respect to shear rotations, by rotating the velocity of the top plate towards lower $\theta$ values. By contrast, for $\pi/2\lesssim\theta<\pi$, we find $\eta_{32}>0$ for $\gamma\lesssim 2$, which can be interpreted as the suspension tending to rotate the trajectory of the top plate towards larger $\theta$ values.

In Fig. 2(f),(g), we show $\eta_{12}$ and $\eta_{32}$ for $\phi=0.57$. Both experimental and numerical data show that the relaxation to steady state is quicker than at $\phi=0.45$, with a smaller $\eta_{12}^{\mathrm{min}}/\eta_{12}^{\mathrm{SS}}$ value [25, 27]. More importantly, the first harmonic of $\eta_{32}$ dominates. For $0<\theta<\pi$, we find $\eta_{32}>0$: the suspension always tends to push the top plate to move towards larger $\theta$ values, that is, the response is no longer stabilizing for small shear rotations. In Fig. 2(c), we highlight this qualitative change by showing the $\theta$ dependence of the values just after rotation $\eta_{32}^{0^{+}}$.

Our simulations also show that the fabric evolution after shear rotation does not mimic the full stress response but only its contact contribution [39]. Notably, the fabric evolution does not exhibit any qualitative change upon increase of $\phi$ that we could correlate to the change of behavior of $\eta_{32}$.

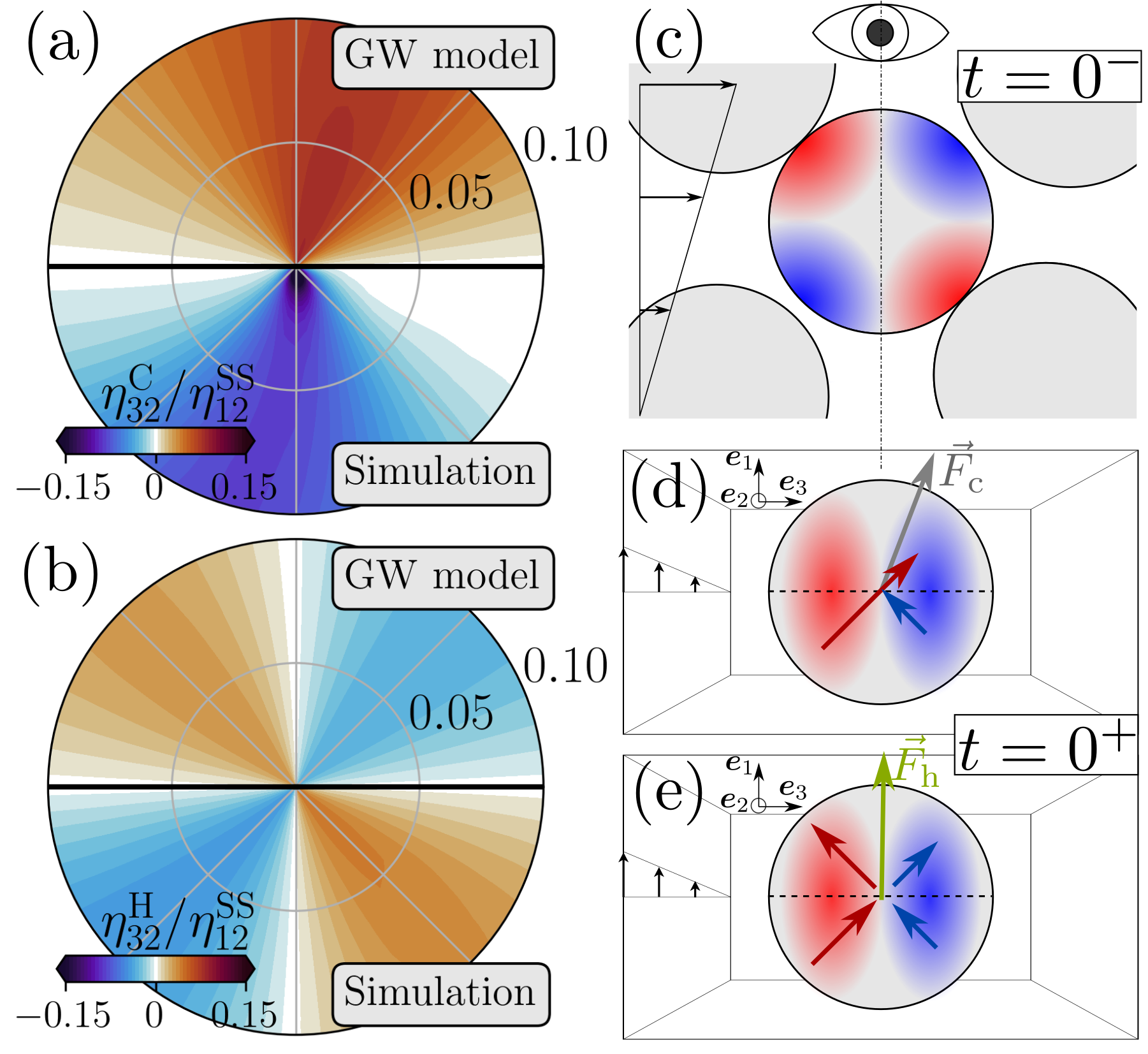
To understand the origin of the $\eta_{32}$ behavior, we interrogate the GW model and its predictions for the contact and hydrodynamic contributions to the stress response. As shown in Fig. 3(a), the contact contribution $\eta^{\mathrm{C}}_{32}$ has a dominant first harmonic, with $\eta^{\mathrm{C}}_{32}>0$ for $0<\theta<\pi$. The large second harmonic of $\eta_{32}$ is instead due to the hydrodynamic component $\eta^{\mathrm{H}}_{32}$ (Fig. 3(b)), which at $\phi=0.45$ still accounts for a substantial part of the total stress [32]. This is confirmed by numerical simulations, which compare well to the predictions of the model.

The difference between contact and hydrodynamic contributions can be qualitatively understood. In Fig. 3(c), we sketch in the shear plane a particle during preshear. It shows a fore-aft asymmetry: it has more near interactions (lubricated and in contact) in the compressional quadrants (in red) than in the elongational one (in blue). The same particle is seen from the gradient direction $\bm{e}_{2}$ right after a shear rotation with $\theta=\pi/2$ in Fig. 3(d),(e). After rotation, the fore-aft asymmetry accumulated in preshear is a “left-right” asymmetry, and fore-aft symmetry is temporarily restored. Post-rotation contact stresses (Fig. 3(d)) stem from contacts in the post-rotation compressional quadrant, below the dashed line, and due to the left-right asymmetry, are dominated by contacts that carry over from the pre-rotation in the intersect of pre- and post-rotation compressional quadrants. Contact forces $\vec{F}_{\mathrm{C}}$ in this overlap region (red vector) are such that $\bm{e}_{3}\cdot\vec{F}_{\mathrm{C}}>0$, giving a positive contribution to $\eta_{32}$. By contrast, in Fig. 3(d), all interactions contribute hydrodynamic forces, and the fore-aft symmetry ensures that the hydrodynamic contribution from the post-rotation elongational and compressional quadrants share the same $\bm{e}_{1}$ component, but have opposite $\bm{e}_{3}$ component. This results in a net-zero hydrodynamic contribution to $\eta_{32}$.

Whereas this reasoning can be extended to show that $\eta^{\mathrm{C}}_{32}>0$ for $\theta\in]0,\pi[$, the sign of $\eta^{\mathrm{H}}_{32}$ for $\theta\neq\pi/2$ depends on aspects of the distribution of near interactions that cannot be deduced from symmetry considerations. The GW model however gives us a quantitative picture alongside a microstructural insight. Calling $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}$ the steady-state fabric in pre-shear, we get the following contributions to $\eta_{32}$ at $\gamma=0^{+}$ [39]

with

For the contact contribution, the first harmonic dominates for the values of $\phi$ and $\beta$ investigated. It is such that $\eta^{\mathrm{C}}_{32}>0$ for $0<\theta<\pi$. By contrast, the hydrodynamic contribution only has a second harmonic. Therefore, when $\alpha(\phi)/\chi(\xi)$ is large enough, the four-lobed hydrodynamic response dominates, which happens at moderate $\phi$. However, since contact stresses diverge for $\phi\to\phi_{\mathrm{J}}$ while hydrodynamic stresses diverge for $\phi\to\phi_{\mathrm{RCP}}>\phi_{\mathrm{J}}$, the two-lobed contact response takes over when $\phi$ moves closer to $\phi_{J}$.

The sign of $\eta^{\mathrm{H}}_{32}$ is not obvious, as it is set by $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{xx}-\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{zz}$. With our value of $\beta=7$, we always find $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{xx}-\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{zz}<0$ in the GW model. For small $\theta$ values, it therefore “stabilizes” the microstructure, as $\operatorname{sgn}\eta^{\mathrm{H}}_{32}=-\operatorname{sgn}\theta$: it provides a restoring force acting against the rotation of the flow direction. In simulations, $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{xx}-\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{zz}$ is measured tiny [27]. To test the GW model predictions, from our DEM simulations we compute $\langle\bm{n}\bm{n}\rangle$ based on particle pairs separated by at most a gap of $\epsilon_{\mathrm{c}}=0.05$ times the average radius of the pair. We find $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{xx}-\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{zz}<0$, albeit decreasing in amplitude when $\phi$ increases. Interestingly, the value of $\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{xx}-\langle\bm{n}\bm{n}\rangle^{\mathrm{ss}}_{zz}$ becomes positive for small enough $\epsilon_{\mathrm{c}}$, which highlights how subtle the hydrodynamic stabilization is.

We performed shear rotations experimentally, numerically, and in a constitutive model, measuring both the shear viscosity $\eta_{12}$ and the orthogonal viscosity $\eta_{32}$ which is not measurable in a conventional rotational rheometer. It revealed a rich phenomenology. The shear viscosity exhibits a dip (except at small $\theta$ for the smallest $\phi$ explored here, $\phi=0.45$) on strain scales of order unity or less, and its amplitude increases upon increase of $|\theta|$ or $\phi$. Remarkably, we find that $\eta_{32}\neq 0$ during the post-rotation transient, with $|\eta_{32}|$ reaching up to $50\text{\,}\mathrm{\char 37\relax}$ of $\eta_{12}$ at $\phi=0.57$, and $10\text{\,}\mathrm{\char 37\relax}$ of $\eta_{12}^{\mathrm{SS}}$. The qualitative angular structure of $\eta_{32}(\gamma,\theta)$ depends on $\phi$, which is explained by the predominance of either hydrodynamic or contact stresses. For $\phi=0.45$, the second harmonic of $\eta(\gamma,\theta)$ is large as hydrodynamic stresses are significant, while for $\phi=0.57$ it is small as contact stresses dominate. Consequently, for small $\theta$, $\eta_{32}$ produces a force that acts to reduce (stabilize) $\theta$ at smaller $\phi$ while it increases (destabilizes) $\theta$ at larger $\phi$.

In an actual non-uniform or unsteady flow where strain axes rotation occur over a strain $\gamma_{\mathrm{unsteady}}$, we can define a Deborah-like number $\mathrm{De}=\gamma_{\mathrm{min}}/\gamma_{\mathrm{unsteady}}$ [42, 43], such that one should expect to observe the transient effects described here when $\mathrm{De}\gtrsim 1$. The decrease of $\eta_{12}$ under shear rotations has already been used to suggest energy-saving flow strategies [16, 17, 19], however the behavior of $\eta_{32}$ has so far been overlooked. Whereas in this work we impose the deformation and measure $\eta_{32}$, in many cases one imposes the force or stress. A finite $\eta_{32}$ may lead to non-trivial trajectories, e.g. during the pulling or the sedimentation of an object in a dense suspension, especially if the suspension is not stable against shear rotations.

We have focused on a subset of the possible flow changes in a complex geometry. One would also need to characterize changes from simple shear to extensional flows and non-uniform flows, which are known to induce migration phenomena [44]. While characterizing all flow histories relevant for applications (or even a carefully selected subset) is a major task, our results show that it would certainly reveal non-trivial yet possibly important stress responses. The GW model captures the salient features of the stress response under shear rotation and in non-uniform flows [45], and could also prove an efficient design tool in this endeavour.

Work funded in part by the European Research Council under the Horizon 2020 Programme, ERC grant agreement number 740269.