Rigidity results for large displacement quotients of mapping class groups

Giorgio Mangioni (Giorgio Mangioni) Maxwell Institute and Department of Mathematics, Heriot-Watt University, Edinburgh, UK gm2070@hw.ac.uk

Abstract.

We consider quotients of mapping class groups of orientable, finite type surfaces by subgroups whose action on the curve graph has large displacement. This class includes quotients by the normal closure of a pseudo-Anosov element, the mapping class group itself, and in view of forthcoming work of Abbott-Berlyne-Ng-Rasmussen also random quotients. First, we show that every automorphism of the corresponding quotient of the curve graph is induced by a mapping class, thus generalising Ivanov’s Theorem about automorphisms of the curve graph. Then we use this to prove quasi-isometric rigidity under additional assumptions, satisfied by all aforementioned quotients. In the process, we clarify a proof of quasi-isometric rigidity of mapping class groups by Behrstock, Hagen, and Sisto. Finally, we show that the outer automorphisms groups of our quotients, as well as their abstract commensurators, are “the smallest possible”.

Introduction

In recent years there has been a growing interest in studying quotients and subgroups of mapping class groups of orientable, finite type surfaces, in order to establish the analogues of Ivanov’s theorem about automorphisms of the curve graph and its consequences (see e.g. [BM19, McL19] for a wide class of normal subgroups, and, among others, [MS23] for quotients by large enough powers of Dehn Twists).

In this paper, we address the problem for a class of quotients which we call large displacement quotients. The defining property, articulated in Definition 1.2, is that every non-trivial element in the kernel acts with large displacement on the curve graph of the surface, that is, the distance between any vertex and its image is bounded from below by a large enough constant, which we call the minimum displacement. An example of such behaviour is the quotient by the normal closure of some power of a pseudo-Anosov element, which was studied in e.g. [DGO17] to answer questions about the existence of normal free subgroups of $\mathcal{MCG}^{\pm}(S)$ . Furthermore, the definition applies to the mapping class group itself, seen as the quotient by the trivial subgroup.

We have three main results, which we think of as rigidity properties of our quotients. The first one is a generalisation of a celebrated theorem of Ivanov-Korkmaz [Iva97, Kor99], and morally tells us that all properties of a large displacement quotient are already encoded in the action on the corresponding quotient of the curve graph. Here $\mathcal{MCG}^{\pm}(S)$ denotes the extended mapping class group, where we allow orientation-reversing mapping classes.

Theorem 1.

Let $S$ be a surface of complexity at least $3$ which is not $S_{2,0}$ , and let $N\unlhd\mathcal{MCG}^{\pm}(S)$ be a normal subgroup. If the minimum displacement of $N$ is large enough, then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ , induced by the action of $\mathcal{MCG}^{\pm}(S)/N$ on $\mathcal{C}S/N$ , is an isomorphism.

The bound on the minimum displacement is made precise in Theorem 2.1. A similar result holds for some surfaces of low complexity too, but in these cases the map might only be surjective with finite kernel (see Subsection 2.1 for the details).

In the second half of the paper, we restrict our attention to those large displacement quotients admitting a hierarchically hyperbolic group (HHG) structure, in the sense of [BHS19]. We also require the structure to be “inherited” from the standard HHG structure of the mapping class group, in a sense that is clarified in Convention 3.2. Roughly, we ask that the domain set of the HHG structure consists almost exclusively of all $N$ -orbits of surfaces, that the top-level coordinate space coincides with $\mathcal{C}S/N$ , and that the coordinate space of the orbit of a subsurface $U\subsetneq S$ is quasi-isometric to the curve graph of $U$ . The class of quotients admitting such a HHG structure, which we call “surface-inherited”, includes:

•

the mapping class group itself (by e.g. [BHS19, Theorem 11.1]);
•

the quotient by the normal closure of a power of a pseudo-Anosov element (by [BHS17a, Corollary F]);
•

more generally, quotients by “deep enough” subgroups of hierarchically hyperbolically embedded subgroups, in the sense of [BHS17a, Definition 6.1] (see Lemma 3.5 for details);
•

in view of forthcoming work of Abbott-Berlyne-Ng-Rasmussen, also random quotients of $\mathcal{MCG}^{\pm}(S)$ .

For such quotients, we can state our second main result, which is quasi-isometric rigidity. Recall that two groups $G$ and $H$ are weakly commensurable if there exist two finite normal subgroups $L\unlhd H$ and $M\unlhd G$ such that the quotients $H/L$ and $G/M$ have two finite index subgroups that are isomorphic.

Theorem 2.

Let $S$ be a surface of complexity at least $2$ which is not a torus with two punctures, and let $N\unlhd\mathcal{MCG}^{\pm}(S)$ be a normal subgroup. If the minimum displacement of $N$ is large enough, and if $\mathcal{MCG}^{\pm}(S)/N$ has a surface-inherited HHG structure, then $\mathcal{MCG}^{\pm}(S)/N$ is quasi-isometrically rigid, meaning that if a finitely generated group $G$ and $\mathcal{MCG}^{\pm}(S)/N$ are quasi-isometric then they are weakly commensurable.

Since $\mathcal{MCG}^{\pm}(S)$ itself is a large displacement quotient, we also recover quasi-isometric rigidity of mapping class groups, first proven in [BKMM12].

Finally, combining quasi-isometric rigidity and results on automorphisms of acylindrically hyperbolic groups from [AMS16], we are able to deduce the following, which can be regarded as a form of algebraic rigidity and is a generalisation of a result of Ivanov for mapping class groups [Iva97]:

Theorem 3 (Algebraic rigidity).

(1)

The map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{MCG}^{\pm}(S)/N)$ , which maps every element to the corresponding inner automorphism, is an isomorphism. In particular, $\text{Out}(\mathcal{MCG}^{\pm}(S)/N)$ is trivial.
(2)

The abstract commensurator of $\mathcal{MCG}^{\pm}(S)/N$ coincides with $\mathcal{MCG}^{\pm}(S)/N$ itself. In particular, any isomorphism between finite index subgroups of $\mathcal{MCG}^{\pm}(S)/N$ is the restriction of an inner automorphism.

Sketch of proofs

Combinatorial rigidity

To show that any automorphism $\overline{\phi}:\,\mathcal{C}S/N\to\mathcal{C}S/N$ is induced by some element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ we proceed as follows. First, we find an automorphism $\phi:\mathcal{C}S\to\mathcal{C}S$ which “lifts” $\overline{\phi}$ , i.e. that makes the following diagram commute, where $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ is the quotient map:

The key observation is that, if we regard both $\mathcal{C}S$ and $\mathcal{C}S/N$ as simplicial complexes, then $\pi$ is a covering map (see Lemma 2.2). Moreover, by a result of Harer [Har86], $\mathcal{C}S$ is simply connected whenever $S$ has large enough complexity, and we can lift $\overline{\phi}$ by standard arguments of covering theory. Then one can apply a result of Ivanov-Korkmaz [Iva97, Kor99] to show that the lift $\phi$ is induced by a mapping class $g\in\mathcal{MCG}^{\pm}(S)$ , and therefore its image $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ induces $\overline{\phi}$ .

Quasi-isometric rigidity

We follow a general strategy, developed by Jason Behrstock, Mark Hagen, and Alessandro Sisto in [BHS21], to prove quasi-isometric rigidity of certain HHG. The key idea from that paper is that any self-quasi-isometry $f$ of a HHG, satisfying some additional assumptions, induces an automorphism of a certain graph, which should be thought of as encoding the intersection patterns of maximal quasiflats (that is, quasi-isometric embeddings of $\mathbb{R}^{n}$ of maximum dimension). In the case of $\mathcal{MCG}^{\pm}(S)/N$ , such graph is precisely the quotient of the curve graph, since maximal quasiflats of $\mathcal{MCG}^{\pm}(S)/N$ morally correspond to subgroups generated by maximal families of commuting Dehn Twists. But then, by the combinatorial rigidity results from Section 2, the automorphism of $\mathcal{C}S/N$ is induced by some element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ , and with a little more effort one can show that $f$ coarsely coincides with the left multiplication by $\overline{g}$ .

In [BHS21], the main result to extract combinatorial data from a self-quasi-isometry of a HHG is [BHS21, Theorem 5.7], which is then used in [BHS21, Theorem 5.10] to give a new proof of quasi-isometric rigidity of mapping class groups. Unfortunately, as pointed out by Jason Behrstock after that paper was published, [BHS21, Theorem 5.7] does not apply to mapping class groups. Indeed, if $U$ is a subsurface of complexity $1$ , then any maximal collection of pairwise disjoint subsurfaces that contains $U$ must also contain the boundary annuli of $U$ . Hence, mapping class groups do not satisfy [BHS21, Assumption 2], which roughly states that such a $U$ should be the only subsurface shared by two maximal collections of pairwise disjoint subsurfaces.

Behrstock, Hagen, and Sisto, worked out a modification of their Assumptions which allows them to prove a version of [BHS21, Theorem 5.7] which applies to the mapping class group. Rather than writing their argument separately, they instead opted to allow me to incorporate a version of those assumptions into this work, and I am extremely grateful for this possibility. Then the proof of [BHS21, Theorem 5.10] runs verbatim once one replaces [BHS21, Theorem 5.7] with our Lemma 3.18, whose Assumptions (A) - (F) are satisfied by both $\mathcal{MCG}^{\pm}(S)$ and our quotients (see Lemma 3.20).

We stress that [BHS21, Theorem 5.7] is true as stated, and it is also used in [DDLS21] to study quasi-isometric rigidity of extensions of Veech groups.

Algebraic rigidity

Given an isomorphism $\phi:\,H\to H^{\prime}$ between finite-index subgroups of $\mathcal{MCG}^{\pm}(S)/N$ , one can consider the element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ whose left-multiplication coarsely coincides with $\phi$ , seen as a self-quasi-isometry of $\mathcal{MCG}^{\pm}(S)/N$ , and then try to prove that the conjugation by $\overline{g}$ restricts to the given isomorphism on $H$ . We do just that in Theorem 4.1, using tools from [AMS16] for acylindrical group actions on hyperbolic spaces. We can use such tools since, by [BHS17b, Corollary 14.4], $\mathcal{MCG}^{\pm}(S)/N$ acts acylindrically on the top-level coordinate space of the HHG structure, which coincides with $\mathcal{C}S/N$ for those quotients satisfying Convention 3.2. Notice that finite normal subgroups could cause the outer automorphism group to be finite rather than trivial, so the key technical results we need is that $\mathcal{MCG}^{\pm}(S)/N$ does not contain non-trivial finite normal subgroups, Lemma 4.7.

Comparison with quotients by large powers of Dehn twists

Very similar results hold for quotients of the form $\mathcal{MCG}^{\pm}(S)/DT_{K}$ , where $DT_{K}$ is the normal subgroup generated by all $K$ -th powers of Dehn Twists. Such quotients can be regarded as “Dehn filling quotients” of mapping class groups, as pointed out and explored in [DHS21] and then in [BHMS20], where they are proven to be hierarchically hyperbolic. Moreover, in view of [MS23], they enjoy the same combinatorial, quasi-isometric, and algebraic rigidity properties as our quotients (at least when $S$ is a punctured sphere, and conjecturally also in the general case). While the proofs there also rely on lifting, the quotient map $\mathcal{C}S\to\mathcal{C}S/DT_{K}$ is not a covering map, and indeed it is quite far from being locally injective; therefore lifting properties follow from different technologies, involving results from [Dah18] about rotating families and the existence of finite rigid sets as defined in [AL13]. Moreover, in this paper quasi-isometric rigidity relies on the fact that Dehn twist flats survive in the quotient, while they disappear in the quotient by $DT_{K}$ for any choice of $K$ . In particular, quasi-isometries of $\mathcal{MCG}^{\pm}(S)/DT_{K}$ induce automorphisms of a graph which is not $\mathcal{C}S/DT_{K}$ , and then one has to relate these two graphs with further combinatorial considerations.

Questions

The following question was asked by Jason Behrstock, during an exchange on a first draft of this paper:

Question 1.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ ) or a $S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ be a large displacement quotient with a surface-inherited HHG structure. Does there exist $D\geq 0$ such that, if the minimum displacement is at least $D$ , any injection from a finite index subgroup $H\leq\mathcal{MCG}^{\pm}(S)/N$ to $\mathcal{MCG}^{\pm}(S)/N$ is induced by an inner automorphism?

This would be a strengthening of our Theorem 3, where we also require the image of the injection to have finite index. Indeed, our proof needs this further assumption, since we want to apply Theorem 2 in order to find a candidate element of $\mathcal{MCG}^{\pm}(S)/N$ , and an isomorphism between subgroups is a quasi-isometry of $\mathcal{MCG}^{\pm}(S)/N$ if and only if both its domain and image are of finite index.

Question 1 would also be a generalisation of the analogue results for mapping class groups, proved by Irmak in [Irm06a, Irm04, Irm06b] and then extended by Behrstock-Margalit in [BM06]. The main strategy of all these papers is articulated in two steps:

•

First, one proves that any superinjective map of $\mathcal{C}S$ (that is, any self-map preserving adjacency and non-adjacency between vertices) is induced by an element of $\mathcal{MCG}^{\pm}(S)$ . This is a generalisation of Ivanov’s combinatorial rigidity theorem, since a simplicial isomorphism is clearly superinjective.
•

Then one shows that any injection from a finite-index subgroup of $\mathcal{MCG}^{\pm}(S)$ into $\mathcal{MCG}^{\pm}(S)$ maps powers of Dehn Twists to powers of Dehn Twists, preserving commutation and non-commutation. Therefore the injection induces a superinjective map of $\mathcal{C}S$ , and one finds a candidate element of $\mathcal{MCG}^{\pm}(S)$ whose conjugation restricts to the given injection.

Therefore, if we want to repeat the same argument for our quotients, we need to answer the following:

Question 2.

In the setting of Question 1, is any superinjective map of $\mathcal{C}S/N$ induced by an element of $\mathcal{MCG}^{\pm}(S)/N$ ?

This would be a generalisation of Theorem 1, which I believe to be true. One could try to lift a superinjective map of $\mathcal{C}S/N$ to a superinjective map of $\mathcal{C}S$ , and then conclude by the results of Irmak and Behrstock-Margalit.

Question 3.

In the setting of Question 1, does the injection $H\to\mathcal{MCG}^{\pm}(S)/N$ map powers of Dehn Twists to powers of Dehn Twist?

Irmak proof is ultimately a refined version of Ivanov’s characterisation of Dehn Twists from [Iva88], in terms of the centres of their centralisers in $\mathcal{MCG}^{\pm}(S)$ , which might extend to our quotients. I believe this is one more reason to try to understand better centralisers in hierarchically hyperbolic groups.

Outline of the paper

In Section 1 we gather some examples of the quotients $\mathcal{MCG}^{\pm}(S)/N$ by subgroups with large displacement, and we develop the lifting tools that are used throughout the paper.

In Section 2 we prove combinatorial rigidity for the general case, which is Theorem 2.1, and for some low-complexity surfaces, see Subsection 2.1. This establishes Theorem 1.

Section 3 is devoted to the proof of Theorem 2. First, we show that a self-quasi-isometry of a hierarchically hyperbolic space, satisfying certain properties (which are Assumption (A) - (F)), induce an automorphism of a certain graph, which encodes the intersections of certain maximal quasiflats (see Lemma 3.18). Then in Subsection 3.5 we relate such graph to $\mathcal{C}S/N$ , and in the proof of Theorem 3.8 we use the combinatorial rigidity results from Section 2 to produce an element of $\mathcal{MCG}^{\pm}(S)/N$ whose left-multiplication is within finite distance from the quasi-isometry.

We conclude the paper with Section 4, where we use quasi-isometric rigidity and some tools from [AMS16] about acylindrical actions on hyperbolic spaces to show that any automorphism between finite index subgroups of $\mathcal{MCG}^{\pm}(S)/N$ is the restriction of the conjugation by a unique element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ (see Theorem 4.1 for the existence of such an element, and Lemma 4.8 for the uniqueness). Therefore, the outer automorphism group of $\mathcal{MCG}^{\pm}(S)/N$ , as well as its abstract commensurator, are the smallest possible, as clarified in Corollaries 4.9 and 4.10. This proves the two parts of Theorem 3.

Acknowledgements

I would like to thank Jason Behrstock, Mark Hagen, and Alessandro Sisto for sharing with me their previous attempts to find a different set of assumptions under which the conclusion of [BHS21, Theorem 5.7] holds, and for suggesting many corrections to the first draft of this paper. I am especially grateful to my supervisor Alessandro Sisto for his constant support. I am also grateful to Piotr Przytycki for suggesting a way to shorten the proof of Theorem 2.8. Finally, I thank Carolyn Abbott, Daniel Berlyne, Thomas Ng, and Alexander Rasmussen for fruitful discussions.

1. Large displacement quotients

Let $S$ be a surface of finite type, that is, a surface obtained from a closed, connected, oriented surface after removing a finite number of points, called punctures. When we want to emphasise the genus $g$ and the number of punctures $b$ we will use the notation $S_{g,b}$ , and we will denote by $\zeta(S)=3g+b-3$ the complexity of $S_{g,b}$ . Let $\mathcal{C}S$ be the curve graph of $S$ , whose vertices are (isotopy classes of) curves and adjacency corresponds to disjointness. Whenever it will not cause ambiguity, we will always say “curve” to mean its isotopy class. Finally, let $\mathcal{MCG}^{\pm}(S)$ be the extended mapping class group of $S$ , where we allow orientation-reversing mapping classes. If $x\in\mathcal{C}S^{(0)}$ is a curve and $f\in\mathcal{MCG}^{\pm}(S)$ is a mapping class, we will denote the image of $x$ under $f$ simply by $fx$ .

Let us introduce which quotients of $\mathcal{MCG}^{\pm}(S)$ we are considering.

Definition 1.1 (Minimum displacement).

The minimum displacement of a mapping class $f\in\mathcal{MCG}^{\pm}(S)$ is defined as $\min_{x\in\mathcal{C}S^{(0)}}\mathrm{d}_{\mathcal{C}S}(x,fx)$ . Similarly, the minimum displacement of a subgroup $N\leq\mathcal{MCG}^{\pm}(S)$ is defined as

\min_{f\in N-\{1\}}\min_{x\in\mathcal{C}S^{(0)}}\mathrm{d}_{\mathcal{C}S}(x,fx),

where $1\in\mathcal{MCG}^{\pm}(S)$ is the identity.

Definition 1.2 (Large displacement quotient).

Let $N\unlhd\mathcal{MCG}^{\pm}(S)$ be a normal subgroup, and let $D\in\mathbb{N}_{>0}$ . We will say that the quotient group $\mathcal{MCG}^{\pm}(S)/N$ is a $D$ -large displacement quotient if the minimum displacement of $N$ is at least $D$ .

Here are some examples of this behaviour.

Example 1.3.

Definition 1.2 applies to the trivial subgroup $N=\{1\}$ , thus $\mathcal{MCG}^{\pm}(S)$ itself is a $D$ -large displacement quotient for every $D\in\mathbb{N}_{>0}$ .

Example 1.4.

Let $f\in\mathcal{MCG}^{\pm}(S)$ be a pseudo-Anosov element. For every $D\in\mathbb{N}_{>0}$ one can find some large enough $K\in\mathbb{N}_{>0}$ such that $f^{K}$ has minimum displacement at least $D$ . Moreover, up to choosing a larger $K$ , the quotient by the normal closure $N=\langle\langle f^{K}\rangle\rangle$ is a $D$ -large displacement quotient. We will give a proof in Corollary 3.6, after we have developed some more notation.

1.1. Isometric projections

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. Since $N$ acts on $\mathcal{C}S$ by simplicial automorphisms, we can consider the quotient $\mathcal{C}S/N$ by this action. Here we gather some properties of $\mathcal{C}S/N$ and the projection map $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ , which hold whenever $D$ is large enough:

Lemma 1.5.

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 3$ then $\mathcal{C}S/N$ is a simplicial graph.

Proof.

By definition of quotient by a simplicial action, there is an edge in $\mathcal{C}S/N$ between two vertices $\overline{x},\overline{y}\in\mathcal{C}S/N^{(0)}$ if they admit two adjacent representatives in $\mathcal{C}S$ . First notice that, by the assumption on the minimum displacement, two vertices in the same $N$ -orbit cannot be adjacent, hence no edge of $\mathcal{C}S/N$ connects a vertex to itself. Moreover, we claim that no two vertices $\overline{x},\overline{y}$ are connected by more than one edge. Indeed, if there were two edges between them, we could find two edges $\{x,y\}$ and $\{x^{\prime},y^{\prime}\}$ between representatives of $\overline{x}$ and $\overline{y}$ , respectively. We can further assume that $y=y^{\prime}$ , up to replacing $\{x^{\prime},y^{\prime}\}$ with one of its $N$ -translates. But then $x$ and $x^{\prime}$ would be $N$ -translate within distance at most $2$ , contradicting the fact that the minimum displacement is at least $3$ . ∎

Definition 1.6.

Let $\overline{X}$ be a subgraph of $\mathcal{C}S/N$ . We say that a subgraph $X$ of $\mathcal{C}S$ is a lift of $\overline{X}$ if the projection map $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ restricts to an isometry between $X$ and $\overline{X}$ .

Lemma 1.7 (Isometric lifts and projections).

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 8$ then the following facts hold for the projection $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ :

•

$\pi$ is $1$ -Lipschitz;
•

For every combinatorial path $\overline{\Gamma}\subset\mathcal{C}S/N$ there exists a combinatorial path $\Gamma\subset\mathcal{C}S$ such that $\pi(\Gamma)=\overline{\Gamma}$ , and moreover if $\overline{\Gamma}$ is geodesic then so is $\Gamma$ ;
•

For every $x\in\mathcal{C}S^{(0)}$ , $\pi$ restricts to an isometry between the closed ball of radius $2$ centred at $x$ , which we denote by $B(x,2)$ , and the closed ball of radius $2$ centred at its projection $\overline{x}$ , which we denote by $\overline{B}(\overline{x},2)$ ;
•

Every subgraph $\overline{X}$ of $\mathcal{C}S/N$ which is contained in a closed ball of radius $2$ admits a unique $N$ -orbit of lifts.

It is possible that our bound on $D$ can be sharpened. However this is irrelevant, since in all notable applications one is always allowed to replace $N$ with a suitable finite-index subgroup, in order to make the minimum displacement larger.

Proof.

The quotient map is $1$ -Lipschitz since the action of $N$ on $\mathcal{C}S$ is simplicial. In order to find a combinatorial path $\Gamma\subset\mathcal{C}S$ which projects to a given path $\overline{\Gamma}\subset\mathcal{C}S/N$ it suffices to lift one edge at a time, given a lift of its starting point, and again this can be done since the action is simplicial. Notice that, by construction, $\Gamma$ has the same length of $\overline{\Gamma}$ . Moreover, suppose that $\overline{\Gamma}$ is a geodesic between its endpoints $\overline{x},\overline{y}$ , which lift to the endpoints $x,y$ of $\Gamma$ . Then, denoting by $\ell(\Gamma)$ the length of $\Gamma$ , and similarly for $\overline{\Gamma}$ , we get

\mathrm{d}_{\mathcal{C}S}(x,y)\leq\ell(\Gamma)=\ell(\overline{\Gamma})=\mathrm{d}_{\mathcal{C}S/N}(\overline{x},\overline{y})\leq\mathrm{d}_{\mathcal{C}S}(x,y),

where we used that $\overline{\Gamma}$ realises the distance between $\overline{x}$ and $\overline{y}$ , and that the projection map is $1$ -Lipschitz. But then the inequalities above are all equalities, and in particular $\Gamma$ realises the distance between its endpoints, i.e., it is a geodesic path.

Now, let $x\in\mathcal{C}S^{(0)}$ and let $\overline{x}$ be its projection. Combining the previous points we have that $\pi(B(x,2))=\overline{B}(\overline{x},2)$ , so we are left to show that, for every $y,z\in B(x,2)$ , we have that $\mathrm{d}_{\mathcal{C}S/N}(\overline{y},\overline{z})=\mathrm{d}_{\mathcal{C}S}(y,z)$ , where $\overline{y}$ and $\overline{z}$ are the respective projections. If by contradiction this was not the case, then we could pick any geodesic $\overline{\Gamma}$ between $\overline{y}$ and $\overline{z}$ . Notice that, since $y,z\in B(x,2)$ and $\pi$ is $1$ -Lipschitz, we have that $\mathrm{d}_{\mathcal{C}S/N}(\overline{y},\overline{z})\leq 4$ , thus $\overline{\Gamma}$ must have length at most $3$ . Now lift $\overline{\Gamma}$ to a geodesic path $\Gamma$ starting at $y$ and ending at some $z^{\prime}$ in the same orbit of $z$ . But then $z$ and $z^{\prime}$ would be within distance at most $7$ , contradicting the assumption on the minimum displacement.

For the last statement, every subgraph $\overline{X}$ which is contained in a closed $2$ -ball admits a lift, by applying the local inverse of $\pi$ . Given any two lifts $X,X^{\prime}$ , let $x\in X$ and $x^{\prime}\in X^{\prime}$ be two points with the same projection, so that there exists an element $n\in N$ such that $x^{\prime}=nx$ . Now pick another pair $y\in X$ and $y^{\prime}\in X^{\prime}$ with the same projection. Since $y^{\prime}$ and $ny$ are within distance at most $4$ , by the assumption on the minimum displacement we must have that $y^{\prime}=ny$ . Hence $nX=X^{\prime}$ , that is, all lifts belong to the same $N$ -orbit. ∎

1.2. Orbits of subsurfaces

We conclude the Section with a study of how $N$ acts on the subsurfaces of $S$ . We first recall a definition from [BKMM12, Section 2.1.3]:

Definition 1.8.

A subsurface $U\subset S$ is essential if it is the disjoint union of some components of the complement of a collection of disjoint simple closed curves, so that no component is a pair of pants and no two annuli components are isotopic.

Let $\mathfrak{S}$ be the collection of (isotopy classes of) essential subsurfaces. Whenever it will not cause ambiguity, we will always say “subsurface” to mean its isotopy class. Moreover, if $U\in\mathfrak{S}$ is an annulus, then it is the regular neighbourhood of some curve $x\in\mathcal{C}S^{(0)}$ , which we call the core of $U$ .

Two subsurfaces $U,V\in\mathfrak{S}$ are nested (resp. orthogonal), and we write $U\sqsubseteq V$ (resp. $U\bot V$ ) if $U$ is contained in $V$ (resp. if they are disjoint). If $U,V$ are neither $\sqsubseteq$ -related nor orthogonal, then they are transverse and we write $U\pitchfork V$ .

Now let $\overline{\mathfrak{S}}=\mathfrak{S}/N$ be the collection of $N$ -orbits of subsurfaces. We will denote the equivalence class of a subsurface $U\in\mathfrak{S}$ by $\overline{U}$ , and similarly if $\mathcal{U}=\{U_{i}\}_{i\in I}$ is a collection of subsurfaces we will set $\overline{\mathcal{U}}=\{\overline{U}_{i}\}_{i\in I}$ . Two classes $\overline{U},\overline{V}\in\overline{\mathfrak{S}}$ are nested (resp. orthogonal), and we write $\overline{U}\sqsubseteq\overline{V}$ (resp. $\overline{U}\bot\overline{V}$ ) if there exists at least one pair of representatives $U,V$ such that $U\sqsubseteq V$ (resp. $U\bot V$ ). Notice that we are not requiring that all pairs of representatives are nested (resp. orthogonal), and indeed this is almost never the case. If $\overline{U},\overline{V}$ are neither $\sqsubseteq$ -related nor orthogonal, then they are transverse and we write $\overline{U}\pitchfork\overline{V}$ .

Lemma 1.9.

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 2$ then nesting and orthogonality in $\overline{\mathfrak{S}}$ are mutually exclusive, meaning that if $\overline{U}\sqsubseteq\overline{V}\in\overline{\mathfrak{S}}$ then $\overline{U}\not\bot\overline{V}$ .

Proof.

Let $U,V$ be two representatives such that $U\sqsubseteq V$ , and let $x$ be a curve which lies in $U$ . By the assumption on the minimum displacement, for every $n\in N-\{1\}$ the curve $nx$ , which lies in $nU$ , must intersect $x$ . This means that any representative for $\overline{U}$ cannot be disjoint from $x$ , and therefore from $V$ .

Now let $U^{\prime}\in\overline{U}$ and $V^{\prime}\in\overline{V}$ be any two representatives, and let $n^{\prime}\in N$ such that $n^{\prime}V=V^{\prime}$ . Then the pair $(U^{\prime},V^{\prime})$ is the image under $n^{\prime}$ of $((n^{\prime})^{-1}U,V)$ , and by the previous argument we know that the latter two subsurfaces intersect. Hence $U^{\prime}$ intersects $V^{\prime}$ , that is, any representative for $\overline{V}$ is not disjoint from any representative for $\overline{U}$ . ∎

Lemma 1.10.

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient for some $D\geq 4$ and let $\overline{U}_{1},\ldots,\overline{U}_{k}\in\overline{\mathfrak{S}}$ be a collection of pairwise orthogonal elements. Then there exist representatives $U_{1},\ldots,U_{k}\in\mathfrak{S}$ which are pairwise orthogonal.

Notice that this lemma is not at all obvious: we just know that every two elements of the collection admit disjoint representatives, but this does not mean, a priori, that this conditions can all be satisfied simultaneously.

Proof.

The proof is by induction on $k$ , the base case $k=2$ being true by how we defined orthogonality. Thus let $k>2$ and let $U_{1},U_{2}$ be disjoint representatives for $\overline{U}_{1},\overline{U}_{2}$ . Moreover, let $U_{3}\in\overline{U}_{3}$ be such that $U_{3}\bot U_{1}$ (such representative exists since we know that $\overline{U}_{1},\overline{U}_{3}$ admit disjoint representatives, and up to the $N$ -action we can assume that the representative for $\overline{U}_{1}$ is $U_{1}$ ). Similarly, there exists $n\in N$ such that $nU_{3}\bot U_{2}$ .

Now fix a curve $x\in U_{1}$ . First notice that every curve $y$ lying on $U_{3}$ is disjoint from $x$ . Moreover, $ny$ is disjoint from all curves on $U_{2}$ , which are in turn disjoint from $x$ . Hence $\mathrm{d}_{\mathcal{C}S}(y,ny)\leq 3$ , and by the assumption on the minimum displacement we must have that $n=1$ . Thus $U_{3}$ is disjoint from both $U_{1}$ and $U_{2}$ . If we repeat the procedure we can find representatives $U_{i}\in\overline{U}_{i}$ for every $i=3,\ldots,k$ which are disjoint from both $U_{1}$ and $U_{2}$ . Hence we can replace $U_{1}$ and $U_{2}$ with the subsurface $U_{1}\sqcup U_{2}$ , and now the conclusion follows by induction. ∎

2. Combinatorial rigidity

For the rest of the paper, $\mathcal{MCG}^{\pm}(S)/N$ will be a $D$ -large displacement quotient for some constant $D\geq 8$ , so that all results from Subsections 1.1 and 1.2 hold. The $\mathcal{MCG}^{\pm}(S)$ -action on $\mathcal{C}S$ induces an action of $\mathcal{MCG}^{\pm}(S)/N$ on $\mathcal{C}S/N$ , defined as follows: for every equivalence classes $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ and $\overline{x}\in\mathcal{C}S/N$ we can choose representatives $g$ and $x$ and set $\overline{g}\cdot\overline{x}=\overline{gx}$ . Using that $N$ is a normal subgroup, one can see that the definition is well-posed. Moreover, the action is by simplicial automorphism, since it preserves adjacency. Thus we have a group homomorphism $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ , where $\text{Aut}(\mathcal{C}S/N)$ is the group of simplicial automorphisms of $\mathcal{C}S/N$ .

The goal of this Section is to prove the following, which is Theorem 1 from the Introduction. For the sake of simplicity, we will first state the result for surfaces of complexity at least $3$ which are not $S_{2,0}$ , postponing low-complexity cases to Subsection 2.1.

Theorem 2.1 (Combinatorial rigidity).

Let $S$ be a surface of complexity at least $3$ which is not $S_{2,0}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 8$ then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ , induced by the natural action, is an isomorphism.

For this Section only, it is convenient to see $\mathcal{C}S$ and $\mathcal{C}S/N$ as simplicial complexes, that is, we consider the flag simplicial complexes whose $1$ -skeleton are the curve graph and its quotient, respectively. By a result of Harer [Har86], if $S$ has complexity at least $3$ then $\mathcal{C}S$ is simply connected. We can show that $\mathcal{C}S$ is actually the universal cover of $\mathcal{C}S/N$ :

Lemma 2.2.

Let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 8$ then the projection $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ is a covering map.

Proof.

Just notice that, for every point $p\in\mathcal{C}S$ , there exists an open neighbourhood $U$ whose preimage is the disjoint union of open subsets which are homeomorphic to $U$ via $\pi$ . Indeed, for every $p\in\mathcal{C}S$ , choose a clique $\Delta$ that contains $p$ , and let $x$ be any of its vertices. Then we can choose $U$ to be the interior of the subcomplex spanned by $B(x,2)$ , as a consequence of Lemma 1.7. ∎

Proof of Theorem 2.1.

We first argue that the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ is surjective, i.e. that, given an automorphism $\overline{\phi}\in\text{Aut}(\mathcal{C}S/N)$ , we can find an element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ which induces $\overline{\phi}$ . Since $\pi:\,\mathcal{C}S\to\mathcal{C}S/N$ is the universal cover, there exists a continuous map $\phi:\,\mathcal{C}S\to\mathcal{C}S$ that makes the following diagram commute:

Recall that $\phi$ is defined as follows: fix a vertex $x_{0}\in\mathcal{C}S$ and a lift $x_{1}$ of $\overline{\phi}(\pi(x_{0}))$ . Then for every $x\in\mathcal{C}S$ pick any path $\Gamma$ from $x_{0}$ to $x$ , and set $\phi(x)$ as the endpoint of the lift of $\overline{\phi}(\pi(\Gamma))$ starting at $x_{0}$ . In particular, if two vertices $x,y\in\mathcal{C}S^{(0)}$ are adjacent, then their images $\phi(x),\phi(y)$ will either be adjacent or coincide. Moreover, the second happens precisely when $\pi(x)=\pi(y)$ , and by the assumption on the minimum displacement this cannot happen for adjacent vertices.

Hence, at the level of the $1$ -skeleton, $\phi$ is a simplicial map, and it is actually an automorphism since we can repeat the same argument replacing $\overline{\phi}$ with its inverse $\overline{\phi}^{-1}$ . Hence, by Ivanov’s Theorem [Iva97, Kor99] there is an element $g\in\mathcal{MCG}^{\pm}(S)$ which induces $\phi$ , and therefore its image $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ induces $\overline{\phi}$ .

Now we turn to injectivity. If an element $g\in\mathcal{MCG}^{\pm}(S)$ induces the identity on $\mathcal{C}S/N$ when passing to the quotient, then the $g$ -action on $\mathcal{C}S$ is a covering automorphism. Now, the group of covering automorphisms is the group $N$ itself, since by Definition 1.2 the $N$ -action on $\mathcal{C}S$ is properly discontinuous. Thus there exists an element $n\in N$ such that the composition $gn$ fixes every curve of $\mathcal{C}S$ , and since $S$ has complexity at least $3$ and is not an $S_{2,0}$ we have that $gn$ must be the identity (see e.g. the discussion in [FM12, Section 3.4]). ∎

2.1. Some low-complexity cases

In this Subsection we establish an analogue of Theorem 2.1 for some surfaces of low complexity. Let us first consider the cases when $S$ is either $S_{0,4}$ , $S_{1,0}$ or $S_{1,1}$ . Then the curve graph has a slightly different definition: we connect two (isotopy classes of) curves if and only if they realise the minimal intersection number among all pairs of curves on the surface, which is $1$ for $S_{1,0}$ and $S_{1,1}$ and $2$ for $S_{0,4}$ . The resulting simplicial complex is the Farey complex (see e.g. [Min96] for a proof), which is a triangulation of the compactification of the hyperbolic plane and therefore is simply connected. Moreover, the definition of a $D$ -large displacement quotient and the relative Lemmas from Section 1 did not assume any property on the nature of the vertices of $\mathcal{C}S$ , thus they still hold in our context. Then one gets the following:

Theorem 2.3.

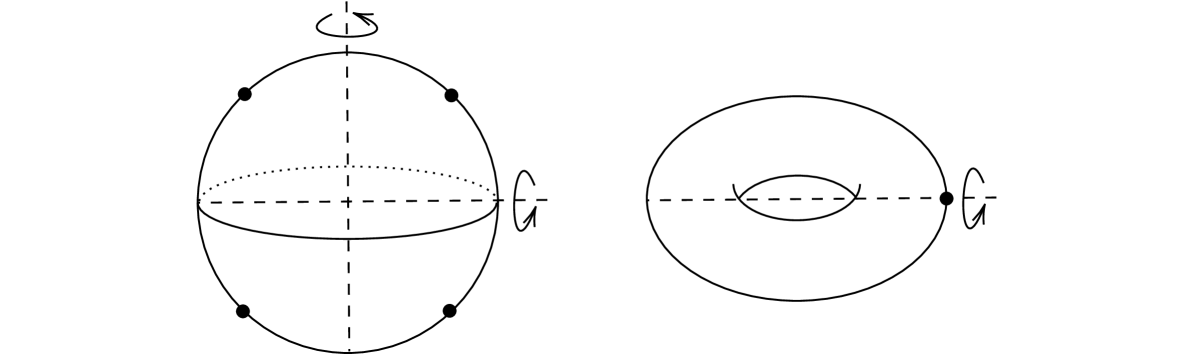
Let $S$ be either $S_{0,4}$ , $S_{1,0}$ or $S_{1,1}$ , let $D\geq 8$ and let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. Then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ is surjective and has finite kernel $\overline{K}$ , generated by the images of the hyperelliptic involutions in Figure 1.

Proof.

For the surjectivity part, we can run the exact same proof of Theorem 2.1, which only uses that the covering space $\mathcal{C}S$ is simply connected. Moreover, the injectivity part of that proof implies that, if $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ acts trivially on $\mathcal{C}S/N$ , then it is the image of an element $g\in\mathcal{MCG}^{\pm}(S)$ which acts trivially on $\mathcal{C}S$ . Such $g$ must then lie in the finite subgroup generated by the hyperelliptic involutions in Figure 1 (again, this follows from e.g. [FM12, Section 3.4]). ∎

With the exact same procedure, one can get the following:

Theorem 2.4.

Let $S=S_{2,0}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 8$ then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ is surjective, and the kernel is the $\mathbb{Z}/2\mathbb{Z}$ subgroup generated by the image of the hyperelliptic involution in Figure 1.

Refer to caption — Figure 1. The dots represent the punctures. Rotations by $\pi$ about the indicated axes fix all curves on the surfaces.

Finally, leaving aside the case $S=S_{1,2}$ , which is more involved since the natural map $\mathcal{MCG}(S_{1,2})\to\text{Aut}(\mathcal{C}S_{1,2})$ is not surjective (see the main result of [Luo00]), we are left to deal with the case $S=S_{0,5}$ . The curve complex $\mathcal{C}S$ has dimension $1$ and is not simply connected. However, we shall see that we can repeat the same procedure as in Theorem 2.1 if we show that the polyhedral complex, obtained from $\mathcal{C}(S_{0,5})$ by gluing a cell to every $5$ -cycle, is simply connected. The latter is an unpublished result of Piotr Przytycki, which I thank for explaining its proof to me.

First, by an arc we mean the isotopy class, relative to the punctures, of a map $\gamma:\,[0,1]\to S_{0,5}$ mapping each endpoint of the interval to a puncture. For every surface $S$ with at least $2$ punctures, let $\mathcal{A}^{2}(S)$ be the simplicial complex whose vertices are all arcs $\gamma:\,[0,1]\to S_{0,5}$ whose endpoints are distinct punctures, and where a collection of arcs span a simplex if their interiors are pairwise disjoint.

Lemma 2.5.

If $S$ has at least two punctures, $\mathcal{A}^{2}(S)$ is simply-connected.

The same proof will yield that $\mathcal{A}^{2}(S)$ is contractible, though we will not need it.

Proof.

This fact is proven as [Sch20, Claim 3.17], but we spell out the details for clarity. Let $\gamma:\,\mathbb{S}^{1}\to\mathcal{A}^{2}(S)$ be a simplicial loop, and fix an arc $x_{0}\in\gamma$ . If every other arc $y\in\gamma$ is disjoint from $x_{0}$ , then we can connect $x_{0}$ to $y$ , and this defines an extension of $\gamma$ to some triangulation of the disk $D^{2}$ .

Thus, suppose that $\Sigma(\gamma)=\sum_{y\in\gamma}i(x,y)>0$ , where $i(x,y)$ is the number of intersection of two representatives of $x$ and $y$ in minimal position. Fix and endpoint $p_{0}$ of $x_{0}$ , and let $y_{0}\in\gamma$ be the first arc one meets when travelling along $x_{0}$ starting from $p_{0}$ . Let $t$ be the path along $x_{0}$ from $p_{0}$ to the first intersection to $y_{0}$ , and let $z$ and $z^{\prime}$ be the essential arcs obtained as the boundaries of a regular neighbourhood of $t\cup y_{0}$ . Since $y_{0}$ has distinct endpoints, one of its endpoints is not $p_{0}$ , and therefore one of the new arcs, say $z$ , has distinct endpoints. Notice moreover that $z$ is disjoint from $y_{0}$ , and if $y_{1}\in\gamma$ was disjoint from $y_{0}$ then it is also disjoint from $z$ , because we choose $y_{0}$ to have the closest intersection to $p_{0}$ . Thus, we can replace $y_{0}$ with $z$ and obtain a loop $\gamma^{\prime}$ , which is homotopic to $\gamma$ but is such that $\Sigma(\gamma^{\prime})<\Sigma(\gamma)$ . Then we conclude by induction on $\Sigma(\gamma)$ . ∎

Definition 2.6.

Let $S=S_{0,5}$ . By a pentagon we mean a $5$ -cycle $P\subset\mathcal{C}S$ . Let $\mathcal{C}S_{P}$ be the polyhedral complex obtained from $\mathcal{C}S$ by gluing a $2$ -cell to every pentagon.

Lemma 2.7 (Przytycki).

The complex $\mathcal{C}S_{P}$ is simply connected.

Proof.

First, notice that $\mathcal{C}S$ can be seen as a non-complete subgraph of $\mathcal{A}^{2}(S)$ , by mapping every curve $y$ to the unique arc $a(y)$ in the twice-punctured disk that $y$ cuts out on $S$ . The map $a:\,\mathcal{C}S\to\mathcal{A}^{2}(S)$ is bijective at the level of vertices, but not at the level of edges since in $\mathcal{A}^{2}(S)$ we allow two arcs to have the same endpoints. Notice moreover that, if the union of five arcs is a pentagon on $S$ (meaning that there is a cyclic ordering such that each arc intersects only the previous and the following, and only at a single endpoint), then the preimages under $a$ of these arcs form a pentagon, in the sense of Definition 2.6.

Now let $\gamma:\,\mathbb{S}^{1}\to\mathcal{C}S_{P}$ be a simplicial loop, whose image lies in the $1$ -skeleton $\mathcal{C}S_{P}^{(1)}=\mathcal{C}S$ . The image $a(\gamma)\subset\mathcal{A}^{2}(S)$ can be filled with triangles, since $\mathcal{A}^{2}(S)$ is simply connected. Let $x_{0},x_{1},x_{2}\in\mathcal{A}^{2}(S)$ be the vertices of such a triangle $T$ . If $x_{i}$ and $x_{j}$ have disjoint endpoints, then the corresponding curves $a^{-1}(x_{i})$ and $a^{-1}(x_{j})$ are disjoint, so that they are connected by an edge in $\mathcal{C}S$ . Otherwise, there exists a unique arc $\varepsilon_{ij}\in\mathcal{A}^{2}(S)$ such that $a^{-1}(\varepsilon_{ij})$ is disjoint from both $a^{-1}(x_{i})$ and $a^{-1}(x_{j})$ , as in Figure 2 (it is the only arc with distinct endpoints in the complement of $x_{i}\cup x_{j}$ ).

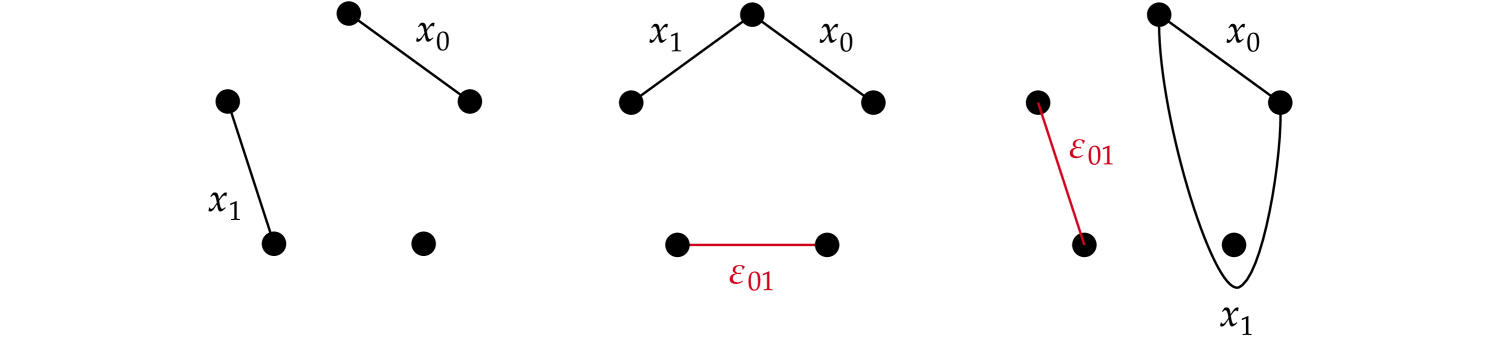
Now by construction, the curves

a^{-1}\left(\{x_{i}\}_{i=0,1,2}\cup\{\varepsilon_{ij}\}_{0\leq i<j\leq 2}\right)

form a loop $\delta$ in $\mathcal{C}S$ . Therefore we are left to prove that $\delta$ can be filled with finitely many pentagons.

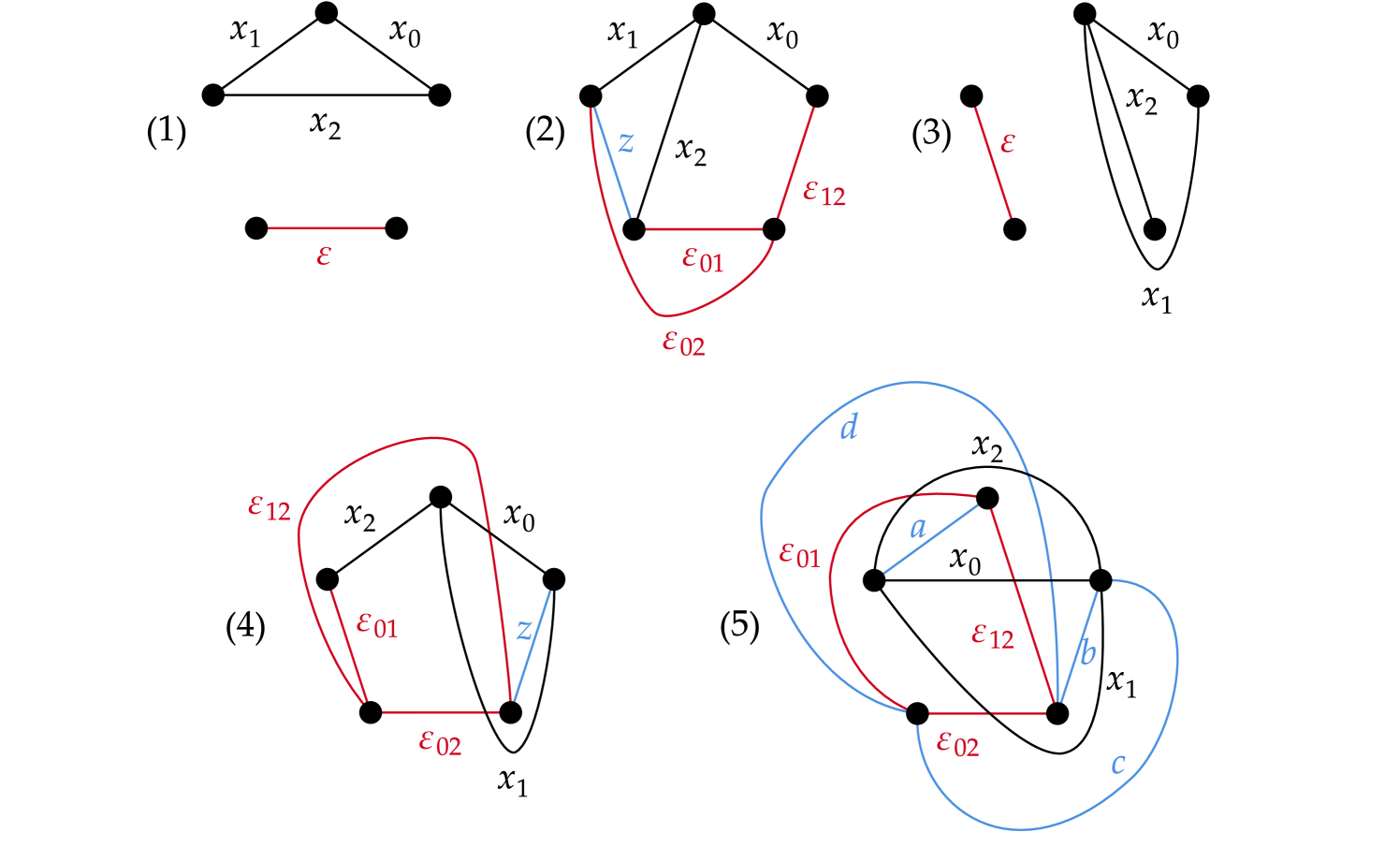
If there is a pair of arcs, say, $x_{0}$ , $x_{1}$ , which have distinct endpoints, then $x_{2}$ must share an endpoint with each of them. This shows that $\delta$ has precisely $5$ vertices, and therefore is filled by a pentagon in $\mathcal{C}S_{P}$ . Otherwise, suppose that all pairs $x_{i}$ , $x_{j}$ share an endpoint, that is, $\delta$ has six vertices. There are five possible cases, as in Figure 3.

Let us analyse all of them separately.

(1)

The $\varepsilon$ -arcs coincide, thus $\delta=a^{-1}\left(\{x_{i}\}_{i=0,1,2}\cup\{\varepsilon\}\right)$ is a tripod.
(2)

Add the arc $z$ in the Figure. Now $\{x_{0},x_{1},z,\varepsilon_{01},\varepsilon_{12}\}$ form a pentagon, as well as $\{x_{0},x_{2},z,\varepsilon_{02},\varepsilon_{12}\}$ . Therefore we can fill $\delta$ with the preimage under $a$ of these arcs, which is a union of two pentagons joined along two edges.
(3)

The $\varepsilon$ -arcs coincide, so we are in the same situation as case 1.
(4)

Similarly to case 2, adding $z$ creates two pentagons.
(5)

This time we need four auxiliary curves, in order to form four pentagons $P_{1}=\{x_{0},a,\varepsilon_{01},\varepsilon_{12},b\}$ , $P_{2}=\{x_{2},a,\varepsilon_{12},\varepsilon_{02},c\}$ , $P_{3}=\{x_{1},a,\varepsilon_{12},d,c\}$ and $P_{4}=\{x_{1},a,\varepsilon_{01},d,b\}$ .

∎

Now we are ready to prove quasi-isometric rigidity for $\mathcal{C}(S_{0,5})/N$ :

Theorem 2.8.

Let $S=S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ be a $D$ -large displacement quotient. If $D\geq 8$ then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ is an isomorphism.

Proof of Theorem 2.8.

Notice first that pentagons in $\mathcal{C}S/N$ can be lifted and pentagons in $\mathcal{C}S$ can be projected isometrically, as a consequence of Lemma 1.7. Thus we can consider the quotient $\mathcal{C}S_{P}/N$ , which is again a polygonal complex. Moreover, any automorphism $\overline{\phi}:\,\mathcal{C}S/N\to\mathcal{C}S/N$ maps pentagons to pentagons, and therefore extends to an automorphism of $\mathcal{C}S_{P}/N$ . Now we can argue as in Theorem 2.1, this time using the covering $\mathcal{C}S_{P}\to\mathcal{C}S_{P}/N$ , to show that the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{C}S/N)$ is an isomorphism (again, injectivity follows from [FM12, Section 3.4]). ∎

3. Quasi-isometric rigidity

This section is devoted to the proof of Theorem 2 from the Introduction, that is quasi-isometric rigidity of certain large displacement quotients, which admit a particular hierarchically hyperbolic group (HHG) structure (see Theorem 3.8 for the exact statement). The idea is to show that, from any self-quasi-isometry $f$ of a HHG satisfying some additional assumptions, one can extract an automorphism of a certain graph, which in our case will coincide with $\mathcal{C}S/N$ . Then we will be able to apply the combinatorial rigidity results from Section 2 to produce a candidate element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ , and with a little more effort we will show that $f$ coarsely coincides with the left multiplication by $\overline{g}$ . Once again, I am grateful to Jason Behrstock, Mark Hagen, and Alessandro Sisto for their contribution, in particular to the proof of Lemma 3.15.

3.1. Background on hierarchical hyperbolicity

First, we recall the intuition behind some notions from the world of hierarchically hyperbolic spaces and groups, first introduced by Behrstock, Hagen, and Sisto in [BHS17b]. We refer to [BHS19] for the details of the definitions.

3.1.1. HHS and HHG

A hierarchically hyperbolic space (HHS for short) is a metric space $X$ that comes with certain additional data, most importantly a family of uniformly hyperbolic spaces $\{\mathcal{C}Y\}_{Y\in\mathfrak{S}}$ , called coordinate spaces, and uniformly coarsely Lipschitz maps $\pi_{Y}:X\to\mathcal{C}Y$ , which shall be thought of as coordinates for points in $X$ . For mapping class groups, these are curve graphs of subsurfaces and maps coming from subsurface projections. Moreover, the domain set $\mathfrak{S}$ , that is, the set which indexes the family of coordinate spaces, has a partial ordering $\sqsubseteq$ , called nesting, with a unique maximal element, and an equivalence relation $\bot$ , called orthogonality. For mapping class groups, these are containment and disjointness of subsurfaces (up to isotopy). When two domains $U,V$ of $\mathfrak{S}$ are not $\sqsubseteq$ - nor $\bot$ -related, one says that they are transverse, and one writes $U\pitchfork V$ . Finally, whenever $U\not\bot V$ there is a projection $\rho^{U}_{V}:\,\mathcal{C}U\to\mathcal{C}V$ , which for mapping class group is again defined using subsurface projection.

An action of a finitely generated group $G$ on a hierarchically hyperbolic space $(X,\mathfrak{S})$ is the data of:

•

an action $G\circlearrowleft X$ by isometries;
•

an action $G\circlearrowleft\mathfrak{S}$ , preserving nesting and orthogonality;
•

for every $g\in G$ and every $Y\in\mathfrak{S}$ , an isometry $g_{Y}:\,\mathcal{C}Y\to\mathcal{C}g(Y)$ .

Moreover, one requires that the two actions are compatible, meaning that for every $g\in G$ and every non-orthogonal domains $U,V\in\mathfrak{S}$ the following diagrams commute:

We will often slightly abuse notation and drop the subscript for the isometries $g_{U}$ . If the action on $X$ is metrically proper and cobounded, and the action on $\mathfrak{S}$ is cofinite, then $G$ is a hierarchically hyperbolic group (HHG for short), and any quasi-isometry between $G$ and $X$ given by the Milnor-Švarc lemma can be used to endow $G$ with the HHS structure of $X$ .

For later purposes, we point out that hierarchically hyperbolic groups are examples of asymphoric HHS, in the sense of [BHS21, Definition 1.14], though we will not need the actual definition of this property.

3.1.2. Product, flats, orthants

The idea of orthogonality is that it corresponds to products, in the following sense. Given any $U\in\mathfrak{S}$ , there is a corresponding space $F_{U}$ associated to it, which is quasi-isometrically embedded in $X$ ( $F_{U}$ is a HHS itself with domain set $\mathfrak{S}_{U}=\{Y\in\mathfrak{S}:Y\sqsubseteq U\}$ , and in mapping class groups these essentially correspond to mapping class groups of subsurfaces). Given a maximal set $\{U_{i}\}$ of pairwise orthogonal elements of $\mathfrak{S}$ , there is a corresponding standard product region $P_{\{U_{i}\}}$ which is quasi-isometric to the product of the $F_{U_{i}}$ (think of a Dehn twist flat as, coarsely, a product of annular curve graphs).

Moreover, inside $X$ and the $F_{U}$ s there are special (uniform) quasi-geodesics, called hierarchy paths, which are those that project monotonically (with uniform constants) to all $\mathcal{C}Y$ . Similarly, there are hierarchy rays and hierarchy lines (which are quasigeodesic rays and lines, respectively). Given a product region $P_{\{U_{i}\}}$ and hierarchy lines (resp., rays) in some of the $F_{U_{i}}$ , the product region contains a product of those (where for the indices $i$ for which a line/ray has not been assigned one chooses a point in $F_{U_{i}}$ instead). This is what we will refer to as standard $k$ -flats (resp., orthants), where $k$ is the number of lines/rays. The support of a standard $k$ -flat (resp., orthant) is the set of $U_{i}$ for which a line/ray has been assigned. Related to this, a complete support set is a subset $\{U_{i}\}_{i=1}^{\nu}\subseteq\mathfrak{S}$ of pairwise orthogonal domains with all $\mathcal{C}U_{i}$ unbounded, and with maximal possible cardinality $\nu$ among sets with these properties. This definition is relevant here as $\nu$ , which is called the rank of $X$ , is then the maximal dimension of standard orthants (if the $\mathcal{C}U_{i}$ are not only unbounded, but also have non-empty Gromov boundary, as will be the case for us). Moreover, in this case points in the Gromov boundary $\partial C(U_{i})$ each determine a hierarchy ray, and similarly pairs of points determine hierarchy lines. In particular, for every complete support set $\{U_{i}\}_{i=1}^{\nu}$ and for every choice of distinct points $p_{i}^{\pm}\in\partial\mathcal{C}U_{i}$ there exists an associated standard $\nu$ -flat $\mathfrak{F}_{\{(U_{i},p_{i}^{\pm})\}}$ , which is the product of the hierarchy lines in $F_{U_{i}}$ whose projections to $\mathcal{C}U_{i}$ have endpoints $p_{i}^{\pm}$ . We will refer to standard $\nu$ -flats (resp. standard $\nu$ -orthants) simply as standard flats (resp. standard orthants).

The following Lemma, which follows from carefully inspecting the proofs of [BHS21, Lemmas 4.11 and 4.12], describes the (coarse) intersection of standard flats and orthants. Recall that, given subsets $A,B$ of a metric space $X$ , the coarse intersection $A\tilde{\cap}B$ , if well-defined, is a subspace of $X$ within bounded Hausdorff distance of all intersections $N_{R}(A)\cap N_{R}(B)$ of their $R$ -neighbourhoods, for $R$ sufficiently large.

Lemma 3.1 (Coarse intersection of standard orthants and flats).

Let $(X,\mathfrak{S})$ be an asymphoric HHS of rank $\nu$ .

•

Let $\mathcal{O},\mathcal{O}^{\prime}$ be standard orthants in $X$ with supports $\{U_{i}\}_{i=1}^{\nu}$ and $\{V_{i}\}_{i=1}^{\nu}$ . Then $\mathcal{O}\tilde{\cap}\mathcal{O}^{\prime}$ is well-defined, and coarsely coincides with a standard $k$ –orthant whose support is contained in $\{U_{i}\}_{i=1}^{\nu}\cap\{V_{i}\}_{i=1}^{\nu}$ .
•

Let $\mathcal{F},\mathcal{F}^{\prime}$ be standard orthants in $X$ with supports $\{U_{i}\}_{i=1}^{\nu}$ and $\{V_{i}\}_{i=1}^{\nu}$ . Then $\mathcal{F}\tilde{\cap}\mathcal{F}^{\prime}$ is well-defined, and coarsely coincides with a product $\prod_{T}\ell_{T}$ , where $T$ varies in $\{U_{i}\}_{i=1}^{\nu}\cap\{V_{i}\}_{i=1}^{\nu}$ and every $\ell_{T}$ is either a point, a standard $1$ -orthant or a standard $1$ -flat supported on $T$ .

3.2. HHG structures inherited from the surface

From now on, we will further restrict our attention to those large displacement quotients admitting a HHG structure whose “interesting” domains are orbits of subsurfaces:

Convention 3.2 (Surface-inherited HHG structure).

$\mathcal{MCG}^{\pm}(S)/N$ is a $D$ -large displacement quotient for some $D\geq 8$ , and it admits a HHG structure with the following properties:

•

The domain set is $\mathfrak{T}=\overline{\mathfrak{S}}\sqcup\mathfrak{T}^{\prime}$ , where $\overline{\mathfrak{S}}=\mathfrak{S}/N$ is the collection of $N$ -orbits of essential subsurfaces.
•

Two domains $\overline{U},\overline{V}\in\overline{\mathfrak{S}}$ are nested (resp. orthogonal) if and only if they admit representatives $U,V\in\mathfrak{S}$ which are nested (resp. orthogonal).
•

The $\sqsubseteq$ -maximal element of $\mathfrak{T}$ is (the $N$ -orbit of) the whole surface $S$ , and its coordinate space, which we refer to as the top-level coordinate space, is $\mathcal{MCG}^{\pm}(S)/N$ -equivariantly quasi-isometric to $\mathcal{C}S/N$ . In particular, $\mathcal{C}S/N$ is hyperbolic.
•

Whenever $\overline{U}\in\overline{\mathfrak{S}}$ is not the $\sqsubseteq$ -maximal element, the coordinate space associated to $\overline{U}$ is $\left(\bigcup_{U\in\overline{U}}\mathcal{C}U\right)/N$ . Furthermore, the quotient projection $\bigcup_{U\in\overline{U}}\mathcal{C}U\to\mathcal{C}\overline{U}$ restricts to a quasi-isometry $\mathcal{C}U\to\mathcal{C}\overline{U}$ , for any representative $U\in\overline{U}$ . Here $\mathcal{C}U$ is the usual curve graph of $U$ , unless $U$ has complexity $1$ and $\mathcal{C}U$ is isomorphic to the Farey complex, or $U$ is an annulus and $\mathcal{C}U$ is its annular curve graph.
•

There exists a constant $E$ such that, for every $T\in\mathfrak{T}^{\prime}$ , either $\mathrm{diam}(\mathcal{C}T)\leq E$ or $T$ is not orthogonal to any other element of $\mathfrak{T}$ .

Here are some examples of quotients with a surface-inherited structure.

Example 3.3.

$\mathcal{MCG}^{\pm}(S)$ itself has a HHG structure whose domain set coincides with $\mathfrak{S}$ and whose coordinate spaces are curve graphs of subsurfaces (see e.g. [BHS19, Theorem 11.1]).

Example 3.4 (Hierarchically hyperbolically embedded subgroups).

Let $H$ be a finitely generated subgroup of $\mathcal{MCG}^{\pm}(S)$ which is hierarchically hyperbolically embedded, as defined in [BHS17a, Definition 6.1] building on the notion of hyperbolically embedded subgroups from [DGO17, Definition 2.1]. Lemma 3.5 describes conditions on a subgroup $M\leq H$ ensuring that the quotient by the normal closure of $M$ satisfies Convention 3.2.

Lemma 3.5.

Let $H\leq\mathcal{MCG}^{\pm}(S)$ be a finitely generated subgroup which is hierarchically hyperbolically embedded. There exists a finite set $F\subset H-\{1\}$ such that, if a normal subgroup $M\unlhd H$ avoids $F$ and $H/M$ is hyperbolic, then the quotient $\mathcal{MCG}^{\pm}(S)/N$ by the normal closure of $M$ satisfies Convention 3.2.

Proof.

Consider any Cayley graph for $H$ , with respect to any finite set of generators. As noted in [BHS17a, Remark 6.3], the orbit maps of $H$ to $\mathcal{C}S$ are quasi-isometric embeddings (actually, the image is also quasi-convex). Hence there exists $R\geq 0$ such that, denoted by $B(1,R)$ the ball of radius $R$ centred at the identity of $H$ , if $M\cap B(1,R)=\{1\}$ then $M$ acts on $\mathcal{C}S$ with minimum displacement at least $8$ . This in turn means that, for $M$ - to act with large minimum displacement, it suffices that it avoids finitely many elements, since balls in a Cayley graph of a finitely generated group are finite.

Now we claim that, if $M$ avoids a possibly bigger finite set, then its normal closure $N$ acts on $\mathcal{C}S$ with minimum displacement at least $8$ as well. This follows from results of [DGO17] on hyperbolically embedded subgroups, but we can give a proof based on the machinery from [CM22]. There the authors take as input our setting and output a projection complex, which we shall think of as the data of:

•

a graph $\mathcal{P}$ , whose vertices correspond in our case to orbits of the form $gH(x_{0})\subset\mathcal{C}S$ for all $g\in\mathcal{MCG}^{\pm}(S)$ and for a fixed basepoint $x_{0}\in\mathcal{C}S^{(0)}$ ;
•

a notion of projection between vertices of $\mathcal{P}$ , which for us is given by projections onto the quasi-convex subsets $gH(x_{0})\subset\mathcal{C}S$ ;
•

an action $N\circlearrowleft\mathcal{P}$ , such that the stabiliser of $gH(x_{0})$ is precisely $gMg^{-1}$ (this follows from [DGO17, Theorem 2.14], where $N$ is described as an infinite free product of conjugates of $M$ ).

An example of the construction of the projection complex for the case when $M$ is generated by a pseudo-Anosov mapping class can be found in [CM22, Section 8.1].

Now, for every $x\in\mathcal{C}S^{(0)}$ there exists $g\in\mathcal{MCG}^{\pm}(S)$ such that the orbit $gH(x_{0})$ is uniformly close to $x$ , since $\bigcup_{g\in\mathcal{MCG}^{\pm}(S)}gH=\mathcal{MCG}^{\pm}(S)$ and the action of $\mathcal{MCG}^{\pm}(S)$ on the curve graph is cofinite. Now let $n\in N-\{1\}$ , and we want to say that $\mathrm{d}_{\mathcal{C}S}(x,nx)\geq 8$ . Notice that we can think of $gH(x_{0})$ and $ngH(x_{0})$ as vertices of $\mathcal{P}$ . Therefore, by [CM22, Proposition 3.2] one of the following must hold:

•

$n$ fixes $gH(x_{0})$ , and therefore it belongs to $gMg^{-1}$ . In particular, $n$ has minimum displacement at least $8$ , since we already know that every non-trivial element in $M$ does and minimum displacement is preserved under conjugation.
•

$n$ fixes $ngH(x_{0})$ , and for the same reason it has minimum displacement at least $8$ .
•

There exists a third vertex of $\mathcal{P}$ , that is, a third orbit $g^{\prime}H(x_{0})$ , on which $gH(x_{0})$ and $ngH(x_{0})$ have distant projection. Now, the projection of $x$ is close to the projection of $gH(x_{0})$ , and similarly $nx$ projects close to $ngH(x_{0})$ . Therefore $x$ and $nx$ have distant projections to $g^{\prime}H(x_{0})$ , and in turn this means that $x$ and $nx$ are far from each other in $\mathcal{C}S$ .

Now, [BHS17a, Theorem 6.2] states that, if $M$ avoids a (possibly larger) finite set and $H/M$ is hyperbolic, then $\mathcal{MCG}^{\pm}(S)/N$ admits a hierarchically hyperbolic structure with the following properties:

•

The index set is $\mathfrak{T}=\overline{\mathfrak{S}}\cup\{NgH\}_{g\in\mathcal{MCG}^{\pm}(S)}$ ;
•

Orthogonality and nesting in $\overline{\mathfrak{S}}$ correspond to orthogonality and nesting between representatives;
•

If $\overline{U}\in\overline{\mathfrak{S}}$ is not the maximal element, then $\mathcal{C}\overline{U}$ is quasi-isometric to $\mathcal{C}U$ via the projection map, for any representative $U$ for $\overline{U}$ ;
•

If $T\in\mathfrak{T}$ is of the form $NgH$ then $T$ has no orthogonal, and $\mathcal{C}T$ is isometric to $H/M$ ;
•

The top-level coordinate space is obtained from $\mathcal{C}S/N$ after coning off every $H/M$ -orbit.

Thus all requirements of Convention 3.2 are satisfied, except for the quasi-isometry type of the top-level coordinate space. Now one can apply the procedure from [ABD21, Theorem 3.7] to remove the domains without orthogonals, and get a new structure $(\mathcal{MCG}^{\pm}(S)/N,\mathfrak{R})$ such that:

•

The new index set coincides with the maximal element, together with all elements $\mathfrak{T}$ admitting an orthogonal domain with unbounded coordinate space. Hence $\mathfrak{R}=\overline{\mathfrak{S}}$ ;
•

Orthogonality and nesting are inherited from the original structure;
•

If $\overline{U}\in\overline{\mathfrak{S}}$ is not the maximal element, then $\mathcal{C}\overline{U}$ is unchanged;
•

The top-level coordinate space is the space $\widehat{X}$ obtained from $\mathcal{MCG}^{\pm}(S)/N$ after coning off the factors $F_{\overline{U}}$ for every non-maximal $\overline{U}\in\overline{\mathfrak{S}}$ . These factors correspond to the stabilisers of the action of $\mathcal{MCG}^{\pm}(S)/N$ on $\mathcal{C}S/N$ . Therefore, by a version of the Milnor-Švarc Lemma described in e.g. [CC07, Theorem 5.1], $\mathcal{C}S/N$ is quasi-isometric to $\widehat{X}$ .

Therefore the new structure satisfies Convention 3.2. ∎

Now we can finally prove that the quotient by a high enough power of a pseudo-Anosov element is a large displacement quotient:

Corollary 3.6.

Let $f\in\mathcal{MCG}^{\pm}(S)$ be pseudo-Anosov element. There exists $K_{0}\in\mathbb{N}$ such that, if $K\in\mathbb{Z}-\{0\}$ is a multiple of $K_{0}$ , then the quotient $\mathcal{MCG}^{\pm}(S)/N$ by the normal closure of $f^{K}$ satisfies Convention 3.2, and in particular is a $D$ -large displacement for some $D\geq 8$ .

Proof.

The elementary closure $E(f)$ of a pseudo-Anosov element $f\in\mathcal{MCG}^{\pm}(S)$ , that is, the unique maximal virtually-cyclic subgroup containing $f$ , is hierarchically hyperbolically embedded (this ultimately follows from [DGO17, Theorem 6.50]). Moreover, by inspection of the proof of [DGO17, Lemma 6.5], the cyclic group $\langle f\rangle$ generated by $f$ has finite index in $E(f)$ , therefore there exists $K_{0}$ such that $\langle f^{K_{0}}\rangle$ is normal in $E(f)$ . We can further assume that $\langle f^{K_{0}}\rangle$ avoids the finite set $F\subset E(f)$ given by Lemma 3.5. Hence, the hypothesis of Lemma 3.5 are satisfied by $\langle f^{K}\rangle$ whenever $K$ is a non-trivial multiple of $K_{0}$ . ∎

For later purposes, we also notice that the existence of a surface-inherited HHG structure implies that $\mathcal{C}/N$ is unbounded, though in all known examples this is already true for less artificial reasons:

Lemma 3.7.

Let $S$ be either a surface of complexity at least $2$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then $\mathcal{C}S/N$ is unbounded.

Proof.

By [PS23, Theorem 3.2], with holds for any HHG, there exists a maximal family $\{T_{1},\ldots,T_{k}\}\subset\mathfrak{T}$ of pairwise orthogonal domains with unbounded coordinate spaces, such that any other domain $R\in\mathfrak{T}$ with unbounded coordinate space is nested in one of the $T_{i}$ . If one of the $T_{i}$ is the $\sqsubseteq$ -maximal element then we are done, because then its coordinate space, which by Convention 3.2 is quasi-isometric to $\mathcal{C}S/N$ , must be unbounded.

Otherwise, pick an annulus $U$ , and let $V$ be the subsurface obtained from $S-U$ after removing all connected components which are pants. Since the complexity is at least $2$ , $V$ is actually an element of $\mathfrak{S}$ , which is nested only inside $S$ and itself. Moreover, if we denote its $N$ -orbit by $\overline{V}$ , then $\mathcal{C}\overline{V}$ is quasi-isometric to $\mathcal{C}V$ and is therefore unbounded. Thus, without loss of generality $\overline{V}\sqsubseteq T_{1}$ , and since $T_{1}$ is not the maximal element, we must have that $T_{1}=\overline{V}$ . In particular, since any other $T_{i}$ is orthogonal to $T_{1}$ , the collection $\{T_{1},\ldots,T_{k}\}$ can consist only of $\overline{V}$ and $\overline{U}$ .

Now it is enough to produce an annulus $W$ whose $N$ -orbit $\overline{W}$ is not nested in either $\overline{V}$ or $\overline{U}$ , and this will lead to a contradiction because $\mathcal{C}\overline{W}$ is unbounded by our Convention. Let $x$ be the core of $U$ , which is also the boundary of $V$ inside $S$ , pick a curve $y\in\mathcal{C}S^{(0)}$ at distance $2$ from $x$ , and let $W$ be the annulus with core $y$ . Then all $N$ -translates of $x$ must be at distance at least $2$ from $y$ , by the assumption on the minimum displacement, and this means that all $N$ -translates of $W$ must cross $U$ . In particular $\overline{W}$ cannot be nested in either $\overline{U}$ or $\overline{V}$ . ∎

3.3. Statement of the results

The goal of this Section is to prove that, if $\mathcal{MCG}^{\pm}(S)/N$ satisfies Convention 3.2, then it is quasi-isometrically rigid in the following sense. Recall that two groups $G$ and $H$ are said to be weakly commensurable if there exist two finite normal subgroups $L\unlhd H$ and $M\unlhd G$ such that the quotients $H/L$ and $G/M$ have two finite index subgroups that are isomorphic.

Theorem 3.8 (Quasi-isometric rigidity).

Let $S$ be a surface of complexity at least $2$ which is not a torus with two punctures, and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then $MCG/N$ is quasi-isometrically rigid, meaning that if a finitely generated group $G$ and $\mathcal{MCG}^{\pm}(S)/N$ are quasi-isometric then they are weakly commensurable.

As we will see, the assumption on the topological type of $S$ is needed to ensure that every automorphism of $\mathcal{C}S/N$ is induced by a mapping class, as a consequence of Theorems 2.1, 2.4 and 2.8. Moreover, we require the complexity to be at least $2$ , so that in $\mathcal{MCG}^{\pm}(S)/N$ we can find “Dehn Twist flats”, that is, standard flats supported on the orbits of pairwise disjoint annuli, of dimension at least $2$ . See Lemma 3.20 for more details.

Since $\mathcal{MCG}^{\pm}(S)$ itself is a $D$ -large displacement quotient for every choice of $D$ , as pointed out in Example 1.3, we also recover quasi-isometric rigidity of mapping class groups:

Corollary 3.9 (QI-rigidity of $\mathcal{MCG}^{\pm}(S)$ ).

Let $S$ be a surface of complexity at least $2$ which is not a torus with two punctures. Then $\mathcal{MCG}^{\pm}(S)$ is quasi-isometrically rigid, meaning that if a finitely generated group $G$ and $\mathcal{MCG}^{\pm}(S)$ are quasi-isometric then they are weakly commensurable.

Moreover, in view of Lemma 3.5 we get the following:

Corollary 3.10.

Let $S$ be a surface of complexity at least $2$ which is not a torus with two punctures. Let $H\leq\mathcal{MCG}^{\pm}(S)$ be a hierarchically hyperbolically embedded subgroup, let $M\leq H$ and let $N$ be the normal closure of $M$ . There exists a finite set $F\subset H-\{1\}$ such that, if $M$ avoids $F$ and $H/M$ is hyperbolic, then $\mathcal{MCG}^{\pm}(S)/N$ is quasi-isometrically rigid, meaning that if a finitely generated group $G$ and $\mathcal{MCG}^{\pm}(S)/N$ are quasi-isometric then they are weakly commensurable.

3.4. Quasi-isometries induce maps on hinges

For this Subsection only, we will work in the general framework of an asymphoric HHS $(X,\mathfrak{S})$ of rank $\nu$ . We will show that, if $X$ satisfies some additional properties (see Assumptions (A) - (F)), then any self-quasi-isometry of $X$ induces an automorphism of a certain graph, which we shall think of as encoding certain standard flats and their intersections.

Recall that a complete support set is a collection $\{U_{1}\}_{i=1}^{\nu}\subset\mathfrak{S}$ of pairwise orthogonal domains with unbounded coordinate spaces, with maximal cardinality $\nu$ among all such collections.

Definition 3.11 ([BHS21, Definition 5.2]).

A hinge is a pair $(U,p)$ where $U$ belongs to a complete support set and $p\in\partial CU$ . We say that $U$ is the support of $(U,p)$ . Let $\bf{Hinge}(\mathfrak{S})$ be the set of hinges.

As in [BHS21, Definition 5.3], one can associate to a hinge $\sigma=(U,p)$ a standard $1$ -orthant, denoted $\mathfrak{h}_{\sigma}$ . This is a hierarchy ray whose projection to $\mathcal{C}U$ is a quasigeodesic ray asymptotic to $p$ , and whose projections to all other coordinate spaces are uniformly bounded. Another property of $\mathfrak{h}_{\sigma}$ , stated in [BHS21, Remark 5.4], is that if $\sigma\neq\sigma^{\prime}$ are two different hinges then $\mathrm{d}_{Haus}(\mathfrak{h}_{\sigma},\mathfrak{h}_{\sigma^{\prime}})=\infty$ .

Let us introduce the first set of hypothesis on $(X,\mathfrak{S})$ .

Assumption A.

For every $U$ which belongs to a complete support set, the Gromov boundary $\partial\mathcal{C}U$ of its coordinate space consists of at least $2$ points.

Definition 3.12 (Good domain).

A domain $U\in\mathfrak{S}$ is good if there exist two complete support sets whose intersection is $\{U\}$ . Let $\mathfrak{S}_{G}$ be the set of good domains, and let $\mathbf{Hinge}_{G}(\mathfrak{S})$ be the set of hinges supported on good domains.

Assumption B.

For every $U,V\in\mathfrak{S}_{G}$ which are orthogonal, there exist two support sets whose intersection is $\{U,V\}$ .

Assumption C.

For every $U\in\mathfrak{S}$ which belongs to a complete support set, there exists a (possibly empty) collection of good domains $\{V_{1},\ldots,V_{n}\}$ and two complete support sets whose intersection is $\{U,V_{1},\ldots,V_{n}\}$ .

Remark 3.13.

Let $f:\,X\to X$ be a quasi-isometry. With the same arguments as in the first half of the proof of [BHS21, Theorem 5.7], one can define a map $f_{Hin}:\,\mathbf{Hinge}_{G}(\mathfrak{S})\to\mathbf{Hinge}(\mathfrak{S})$ by mapping $\sigma\in\mathbf{Hinge}_{G}(\mathfrak{S})$ to the unique hinge $\sigma^{\prime}\in\mathbf{Hinge}(\mathfrak{S})$ such that $\mathrm{d}_{\text{Haus}}(f(\mathfrak{h}_{\sigma}),\mathfrak{h}_{\sigma^{\prime}})<+\infty$ . Moreover, by inspection of the construction one sees that $\sigma^{\prime}$ is itself good, since $\mathfrak{h}_{\sigma^{\prime}}$ arises as the coarse intersection of two standard orthants (whose supports must therefore coincide only on the support of $\sigma^{\prime}$ by Lemma 3.1). Hence $f_{Hin}$ maps $\mathbf{Hinge}_{G}(\mathfrak{S})$ to itself, and therefore is a bijection whose inverse is the map $g_{Hin}$ , induced by any quasi-inverse $g$ for $f$ .

Definition 3.14.

We say that two hinges are co-supported if they are supported on the same domain, i.e. if the union of their hinge rays is (coarsely) a 1-dimensional standard flat. We say that two hinges are orthogonal if they are supported on orthogonal domains.

Lemma 3.15 (Behrstock, Hagen, Sisto).

Under Assumptions (A) - (C), if two good hinges $\sigma,\sigma^{\prime}\in\mathbf{Hinge}_{G}(\mathfrak{S})$ are orthogonal then $f_{Hin}(\sigma)$ and $f_{Hin}(\sigma^{\prime})$ are either orthogonal or co-supported.

Proof.

Let $\sigma=(U,p)$ and $\sigma^{\prime}=(U^{\prime},p^{\prime})$ . By Assumption (B) there exist two standard flats $\mathcal{F}_{1},\mathcal{F}_{2}$ whose coarse intersection is a standard 2-flat containing $\mathfrak{h}_{\sigma}$ and $\mathfrak{h}_{\sigma^{\prime}}$ . Let $\mathcal{O}$ be the orthant spanned by $\mathfrak{h}_{\sigma}$ and $\mathfrak{h}_{\sigma^{\prime}}$ in this standard 2-flat.

As a consequence of the Quasiflats Theorem [BHS21, Theorem A] and of Lemma 3.1, $f(\mathcal{F}_{1})\tilde{\cap}f(\mathcal{F}_{2})$ is a union of standard 2-orthants, whose “boundary” 1-orthants, which we call coordinate rays, can be ordered cyclically. Moreover, $f(\mathfrak{h}_{\sigma})$ must arise as some coordinate ray, since it coarsely coincides with some hinge $\mathfrak{h}_{f_{Hin}(\sigma)}$ , and if a hinge is contained in a standard 2-orthant then it must be one of its boundary 1-orthants by [BHS21, Lemma 4.11]. The same is true for $f(\mathfrak{h}_{\sigma^{\prime}})$ .

Now, if $f(\mathfrak{h}_{\sigma})$ and $f(\mathfrak{h}_{\sigma^{\prime}})$ are adjacent in the cyclic ordering, then they belong to a common 2-orthant, and therefore they are orthogonal. Thus suppose that there is a coordinate ray $r\in f(\mathcal{O})$ between $f(\mathfrak{h}_{\sigma})$ and $f(\mathfrak{h}_{\sigma^{\prime}})$ , and let $V\in\mathfrak{S}$ be its support.

If $V$ is good then we can proceed as in the proof of [BHS21, Theorem 5.7] to get a contradiction. Indeed, in this case $f^{-1}(r)$ must coincide with some hinge ray $\mathfrak{h}_{\sigma^{\prime\prime}}$ , which belongs to $\mathcal{O}$ but lies at infinite Hausdorff distance from both $\mathfrak{h}_{\sigma}$ and $\mathfrak{h}_{\sigma^{\prime}}$ , and this contradicts [BHS21, Lemma 4.11].

Then we can assume that no ray between $f(\mathfrak{h}_{\sigma})$ and $f(\mathfrak{h}_{\sigma^{\prime}})$ is supported on a good domain, and in particular that $V$ is not good. By Assumption (C) there exists a collection of good domains $\{V_{1},\ldots,V_{n}\}$ and two complete support sets whose intersection is $\{V,V_{1},\ldots,V_{n}\}$ .

Hence, there exist two standard flats $\mathcal{G}_{1},\mathcal{G}_{2}$ whose intersection is a flat supported on $\{V,V_{1},\ldots,V_{n}\}$ and containing $r$ . Now consider $Y=\mathcal{G}_{1}\tilde{\cap}\mathcal{G}_{2}\tilde{\cap}f(\mathcal{F}_{1})\tilde{\cap}f(\mathcal{F}_{2})$ . This coarse intersection is well-defined, since both $f(\mathcal{F}_{1})$ and $f(\mathcal{F}_{2})$ are finite unions of standard orthants by the Quasiflat Theorem, and the coarse intersection of standard orthants and flats is well-defined by Lemma 3.1. Moreover, let $Z=f^{-1}(Y)$ , which is a union of standard 1- and 2-orthants supported on $\{U,U^{\prime}\}$ (again, this follows from combining the Quasiflat Theorem, applied to $f^{-1}(\mathcal{G}_{1})$ and $f^{-1}(\mathcal{G}_{2})$ , and Lemma 3.1). Now, $Z$ contains the ray $f^{-1}(r)$ , which lies inside $\mathcal{O}$ but cannot coarsely coincide with $\mathfrak{h}_{\sigma}$ nor with $\mathfrak{h}_{\sigma^{\prime}}$ , since their image lie at infinite Hausdorff distance. Therefore, $Z$ must contain the whole 2-orthant $\mathcal{O}$ . In turn, this means that $Y$ must contain all 2-orthants of $f(\mathcal{F}_{1})\tilde{\cap}f(\mathcal{F}_{2})$ which lie between $f(\mathfrak{h}_{\sigma})$ and $f(\mathfrak{h}_{\sigma^{\prime}})$ in the cyclic ordering, and moreover the support of every such 2-orthant must be contained in $\{V,V_{1},\ldots,V_{n}\}$ .

Now, since $f(\mathfrak{h}_{\sigma})$ and $f(\mathfrak{h}_{\sigma^{\prime}})$ are boundary 1-orthants of some 2-orthants of $Y$ , their supports must belong to $\{V,V_{1},\ldots,V_{n}\}$ , and therefore they are either orthogonal or co-supported. ∎

For the rest of the Section, we will work under the following additional assumptions:

Assumption D.

If $U\in\mathfrak{S}_{G}$ is a good domain, then $|\partial\mathcal{C}U|=2$ .

Assumption E.

For every two good domains $U\neq V\in\mathfrak{S}_{G}$ there exists a good domain $W\in\mathfrak{S}_{G}$ which is orthogonal to $U$ but not to $V$ . In other words, every good domain is uniquely determined by the set of good domains which are orthogonal to it.

Lemma 3.16.

Under Assumptions (A) - (E), if $\sigma,\sigma^{\prime}\in\mathbf{Hinge}_{G}(\mathfrak{S})$ are co-supported then $f_{Hin}(\sigma)$ and $f_{Hin}(\sigma^{\prime})$ are either orthogonal or co-supported.

Proof.

Let $\sigma,\sigma^{\prime}\in\mathbf{Hinge}_{G}(\mathfrak{S})$ be two co-supported good hinges. For every good hinge $\theta$ which is orthogonal to $f_{Hin}(\sigma)$ we can consider its preimage $(f_{Hin})^{-1}(\theta)$ . By Lemma 3.15, which also applies to $(f_{Hin})^{-1}$ (again, because it coincides with the map $g_{Hin}$ for any quasi-inverse $g$ for $f$ ), we have that $(f_{Hin})^{-1}(\theta)$ and $\sigma$ are either orthogonal or co-supported. Moreover, by Assumption (D) the unique hinge which has the same support of $\sigma$ is $\sigma^{\prime}$ , thus $(f_{Hin})^{-1}(\theta)$ is orthogonal to $\sigma$ and therefore also to $\sigma^{\prime}$ . Then again Lemma 3.15 tells us that $\theta$ and $f_{Hin}(\sigma^{\prime})$ are either co-supported or orthogonal.

We can repeat the argument for every good hinge $\theta$ which is orthogonal to $f_{Hin}(\sigma)$ , and we get that either $f_{Hin}(\sigma^{\prime})$ has the same support of some $\theta$ , and therefore is orthogonal to $f_{Hin}(\sigma)$ , or $f_{Hin}(\sigma)$ and $f_{Hin}(\sigma^{\prime})$ are orthogonal to the same hinges, and therefore they are co-supported by Assumption (E). ∎

To conclude the proof, we also need good domains to satisfy the following strengthening of Definition 3.12, which roughly says that good hinges arise as intersection of “good” standard orthants:

Definition 3.17 (Very good domain).

A domain $U\in\mathfrak{S}$ is very good if there exist two complete support sets, made of good domains, whose intersection is $\{U\}$ .

Assumption F.

Good domains are very good.

Lemma 3.18.

Under Assumptions (A) - (F), $f_{Hin}$ induces an automorphism $f_{G}$ of the graph $(\mathfrak{S}_{G},\bot)$ , whose vertex set is $\mathfrak{S}_{G}$ and where adjacency corresponds to orthogonality.

Proof.

We can give $\mathbf{Hinge}_{G}(\mathfrak{S})$ a simplicial graph structure, by saying that two hinges are adjacent if and only if they are orthogonal or co-supported. Combining Remark 3.13, Lemma 3.15, and Lemma 3.16, we obtain that $f$ induces a simplicial automorphism of $\mathbf{Hinge}_{G}(\mathfrak{S})$ . With a slight abuse of notation, we will keep denoting such automorphism as $f_{Hin}$ , since at the level of vertices it maps every good hinge $\sigma$ to $f_{Hin}(\sigma)$ .

Now notice that any maximal clique of $\mathbf{Hinge}_{G}(\mathfrak{S})$ is the (infinite) subgraph spanned by all hinges supported on some complete support set, made of good domains. Moreover, we claim that two good hinges $\sigma$ and $\sigma^{\prime}$ are co-supported if and only if they belong to the same maximal cliques. Indeed, if two hinges are co-supported then they clearly belong to the same maximal cliques; conversely, if $\sigma$ and $\sigma^{\prime}$ are supported on $U\neq V$ , respectively, then one of the following holds:

•

$U\pitchfork V$ , and therefore $\sigma$ and $\sigma^{\prime}$ cannot belong to the same maximal cliques since they are not adjacent in $\mathbf{Hinge}_{G}(\mathfrak{S})$ ;
•

$U\bot V$ , and in view of Assumption (F) we can find a complete support set, made of good domains, which contains $U$ but not $V$ .

Since we just showed that being co-supported is a purely combinatorial property, it must be preserved by the automorphism $f_{Hin}$ . Moreover, the same argument works for the inverse $(f_{Hin})^{-1}$ , hence two good hinges $\sigma,\sigma^{\prime}\in\mathbf{Hinge}_{G}(\mathfrak{S})$ are co-supported if and only if $f_{Hin}(\sigma)$ and $f_{Hin}(\sigma^{\prime})$ are co-supported. This also implies that two good hinges $\sigma,\sigma^{\prime}\in\mathbf{Hinge}_{G}(\mathfrak{S})$ are orthogonal if and only if $f_{Hin}(\sigma)$ and $f_{Hin}(\sigma^{\prime})$ are orthogonal.

Now, $f_{Hin}$ induces an automorphism $f_{G}$ of $(\mathfrak{S}_{G},\bot)$ as follows. For every $U\in\mathfrak{S}$ choose a hinge $\sigma$ supported on $U$ , and set $f_{G}(U)$ as the support of $f_{Hin}(\sigma)$ . This map is well-defined since $f_{Hin}$ maps co-supported hinges to co-supported hinges, and it preserves orthogonality since $f_{Hin}$ does. ∎

The last Lemma gives a uniform bound between the image of a maximal flat, supported on good domains, and the maximal flat supported on the image of the supports. In the case of $\mathcal{MCG}^{\pm}(S)/N$ , this will tell us that the quasi-isometry permutes “Dehn twist flats”, up to uniformly bounded distance.

Lemma 3.19 (Flats go to flats).

Let $(X,\mathfrak{S})$ be an asymphoric HHS of rank $\nu$ , satisfying Assumptions (A) - (F). For every $L\geq 0$ there exists $C\geq 0$ such that the following holds. Let $f:\,X\to X$ be a $(L,L)$ -quasi-isometry. Let $\{U_{i}\}_{i=1}^{\nu}$ be a complete support set, made of good domains, and let $\mathcal{F}_{\{U_{i}\}}$ be the standard flat it supports. Similarly, let $\mathcal{F}_{\{f_{G}(U_{i})\}}$ the standard flat supported on $\{f_{G}(U_{i})\}_{i=1}^{\nu}$ . Then $\mathrm{d}_{Haus}\left(f\left(\mathcal{F}_{\{U_{i}\}}\right),\mathcal{F}_{\{f_{G}(U_{i})\}}\right)\leq C$ .

Proof.

One can argue as in [BHS21, Lemma 5.9], whose proof only relies on asymphoricity of $X$ and the fact that $f_{Hin}$ maps hinges on the same support to hinges on the same support. ∎

3.5. Application to large displacement quotients

Now let $S$ be a surface of complexity at least $2$ . It is easy to see that, if $U\in\mathfrak{S}$ belongs to a complete support set for $\mathcal{MCG}^{\pm}(S)$ , then $U$ is either an annulus, a $S_{0,4}$ or a $S_{1,1}$ . Moreover, if $U$ has complexity one then every complete support set containing $U$ must also contain all its boundary annuli, thus $U$ is not good; on the other hand, annuli are very good, since every annulus can be obtained as intersection of two pants decompositions, that is, two collections of pairwise disjoint annuli. Finally, the rank of $\mathcal{MCG}^{\pm}(S)$ is precisely the complexity of $S$ .

The next lemma shows that, if $\mathcal{MCG}^{\pm}(S)/N$ satisfies Convention 3.2, then it fits the framework of Subsection 3.4:

Lemma 3.20.

Let $S$ be a surface of complexity at least $2$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then good domains correspond to $N$ -orbits of annuli, and Assumptions (A) - (F) hold.

Proof.

First, let $\{U_{i}\}_{i=1}^{\zeta(S)}$ be a complete support set for $\mathcal{MCG}^{\pm}(S)$ . The set of all curves lying on $\bigcup_{i=1}^{\zeta(S)}U_{i}$ has diameter at most $2$ inside $\mathcal{C}S$ , hence the subsurfaces must belong to pairwise distinct orbits $\{\overline{U}_{i}\}_{i=1}^{\zeta(S)}$ by the assumption on the minimum displacement. Moreover, $\{\overline{U}_{i}\}_{i=1}^{\zeta(S)}$ are again pairwise orthogonal, by how orthogonality in $\mathfrak{T}$ is defined, and have unbounded coordinate spaces, since by assumption $\mathcal{C}\overline{U}_{i}$ is quasi-isometric to $\mathcal{C}U_{i}$ . Hence the projection of a complete support set for $\mathcal{MCG}^{\pm}(S)$ is a support set for $\mathcal{MCG}^{\pm}(S)/N$ with the same number of domains, and in particular the rank $\nu$ of $\mathcal{MCG}^{\pm}(S)/N$ is at least ${\zeta(S)}$ .

Conversely, let $\mathcal{T}=\{T_{1},\ldots,T_{\nu}\}\subset\mathfrak{T}$ be a complete support set. If $T_{i}\in\mathcal{T}$ belonged to $\mathfrak{T}-\overline{\mathfrak{S}}$ then $\mathcal{T}$ would only consist of $T_{i}$ , because elements of $\mathfrak{T}-\overline{\mathfrak{S}}$ with unbounded coordinate spaces have no orthogonals by Convention 3.2. Then $\mathcal{T}$ could not be complete, since $\nu\geq{\zeta(S)}\geq 2$ . Hence, for every $i=1,\ldots,\nu$ , we have that $T_{i}=\overline{U}_{i}$ , and by Lemma 1.10 we can find pairwise disjoint representatives $U_{i}\in\overline{U}_{i}$ . Thus $\nu$ is at most $\zeta(S)$ , and if we combine this with the previous inequality we get $\nu=\zeta(S)$ . We just proved that every complete support set for $\mathcal{MCG}^{\pm}(S)/N$ is of the form $\{\overline{U}_{i}\}_{i=1}^{\zeta(S)}$ , for some complete support set $\{U_{i}\}_{i=1}^{\zeta(S)}$ for $\mathcal{MCG}^{\pm}(S)$ .

Now, we claim that $\overline{U}\in\overline{\mathfrak{S}}$ is a good domain if and only if it is the orbit of an annulus. Indeed, if $\overline{U}$ is the orbit of an annulus $U$ we can find two pants decompositions $\mathcal{U}$ and $\mathcal{V}$ whose intersection is $\{U\}$ . Since all curves in $\mathcal{U}\cup\mathcal{V}$ lie in the ball of radius $1$ centred at $U$ inside $\mathcal{C}S$ , the assumption on the large displacement implies that any two domains in $\mathcal{U}\cup\mathcal{V}$ lie in different $N$ -orbits. Hence $\overline{\mathcal{U}}\cap\overline{\mathcal{V}}=\{\overline{U}\}$ . On the other hand, if $\overline{U}$ is the class of a subsurface $U$ of complexity one, then every complete support set $\overline{\mathcal{U}}$ containing $\overline{U}$ lifts to a complete support set containing $U$ , which must also contain the boundary annuli of $U$ . Hence $\overline{\mathcal{U}}$ must contain the $N$ -orbit of the boundary annuli of $U$ .

We conclude the proof by checking the Assumptions:

(A) Whenever $\overline{U}$ belongs to a complete support set, $\mathcal{C}\overline{U}$ is isometric to $\mathcal{C}U$ for any of its representatives $U$ , and in particular has at least two points at infinity.

(B) For every two $\overline{U}$ , $\overline{V}$ which lift to disjoint annuli $U,V$ , we can find two pants decompositions $\mathcal{U}$ and $\mathcal{V}$ whose intersection is $\{U,V\}$ . Moreover, any two annuli in $\mathcal{U}\cup\mathcal{V}$ belong to different $N$ -orbits, because their core curves are disjoint, so $\{\overline{U},\overline{V}\}$ is the intersection of $\overline{\mathcal{U}}$ and $\overline{\mathcal{V}}$ .

(C) Let $\overline{U}$ belong to a complete support set. If $\overline{U}$ is not good, we can pick one of its lift $U$ and find two complete support sets $\mathcal{U}$ and $\mathcal{V}$ whose intersection is $\{U,V_{1},\ldots,V_{n}\}$ , where $\{V_{1},\ldots,V_{n}\}$ are the boundary annuli of $U$ . Now, all curves in $\mathcal{U}\cup\mathcal{V}$ lie in the ball of radius $1$ centred at any curve $x$ which lies in $U$ . Therefore, by the assumption on the large displacement, any two domains in $\mathcal{U}\cup\mathcal{V}$ must belong to different $N$ -orbits, and in turn this means that $\{\overline{U},\overline{V}_{1},\ldots,\overline{V}_{n}\}$ is the intersection of $\overline{\mathcal{U}}$ and $\overline{\mathcal{V}}$ .

(D) If $\overline{U}$ is good then $\mathcal{C}\overline{U}$ is quasi-isometric to an annular curve graph, hence $|\partial\mathcal{C}\overline{U}|=2$ .

(E) It is enough to prove that, if $\overline{x},\overline{y}\in\mathcal{C}S/N^{(0)}$ have the same link inside $\mathcal{C}S/N$ , i.e., if they are adjacent to the same vertices, then they coincide. Indeed, the subgraph spanned by $\{\overline{x},\overline{y}\}\cup\text{Lk}_{\mathcal{C}S/N}(\overline{x})$ has diameter at most $2$ , and therefore can be lifted by Lemma 3.16. Thus we get two lifts $x,y$ such that $\text{Lk}_{\mathcal{C}S}(x)$ is the lift of $\text{Lk}_{\mathcal{C}S/N}(\overline{x})$ , and therefore coincides with $\text{Lk}_{\mathcal{C}S}(y)$ . Now we are left to prove that, if two curves $x,y$ have the same link in $\mathcal{C}S$ , then they must coincide. Now, if the curves are disjoint then $x\in\text{Lk}(y)-\text{Lk}(x)$ , and we are done. Otherwise, let $S^{\prime}$ be a component of $S-{x}$ which is not a pair of pants (here we are using that $S$ has complexity at least $2$ ), and let $z$ be the subsurface projection of $y$ inside $S^{\prime}$ . By applying a partial pseudo-Anosov of $S^{\prime}$ to $z$ we can find a curve $z^{\prime}$ inside $S$ which crosses $z$ , and therefore also $y$ .

(F) As we saw before, every $\overline{U}$ which is the orbit of an annulus arises as the intersection of two complete support sets which come from two pants decompositions. Therefore good domains are very good. ∎

Now, good domains correspond to orbits of annuli, and orthogonality corresponds to having disjoint representatives. Hence, as a consequence of Lemma 3.18 we get:

Corollary 3.21.

Let $S$ be a surface of complexity at least $2$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Every quasi-isometry $f:\,\mathcal{MCG}/N\mapsto\mathcal{MCG}/N$ induces an automorphism $f_{\mathcal{C}S/N}$ of $\mathcal{C}S/N$ .

Now we are finally ready to prove quasi-isometric rigidity:

Proof of Theorem 3.8.

Let $S$ be a surface of complexity at least $2$ which is not a $S_{1,2}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. By [MS23, Lemma 9.15], which follows from standard arguments (see e.g. [Sch95, Section 10.4]), to prove quasi-isometric rigidity of $\mathcal{MCG}^{\pm}(S)/N$ it is enough to verify that, for every $L\geq 0$ , there exists $R\geq 0$ such that:

(a)

Every $(L,L)$ -self-quasi-isometry of $\mathcal{MCG}^{\pm}(S)/N$ lies within distance $R$ from the left multiplication by some element of $\mathcal{MCG}^{\pm}(S)/N$ ;
(b)

If a $(L,L)$ -self-quasi-isometry of $\mathcal{MCG}^{\pm}(S)/N$ lies within finite distance from the identity, then it lies within distance $R$ from the identity.

a Let $f:\,\mathcal{MCG}^{\pm}(S)/N\to\mathcal{MCG}^{\pm}(S)/N$ be a $(L,L)$ -quasi-isometry, and let $f_{\mathcal{C}S/N}$ be the induced automorphism of $\mathcal{C}S/N$ . By either Theorem 2.1, Theorem 2.4 or Theorem 2.8, according to the homeomorphism type of $S$ , we get that $f_{\mathcal{C}S/N}$ is induced by some element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ . Moreover, by Lemma 3.19 there exist a constant $C$ such that, whenever $\{\overline{U}_{i}\}_{i=1}^{\nu}$ is a maximal collection of pairwise orthogonal orbits of annuli, $f$ maps the standard flat $\mathcal{F}_{\{\overline{U}_{i}\}}$ within Hausdorff distance at most $C$ from $\mathcal{F}_{\{f_{\mathcal{C}S/N}(\overline{U}_{i})\}}=\mathcal{F}_{\{\overline{g}(\overline{U}_{i})\}}$ , which in turn is within Hausdorff distance at most $C$ from $\overline{g}\left(\mathcal{F}_{\{\overline{U}_{i}\}}\right)$ . Therefore $\mathrm{d}_{Haus}\left(f(\mathcal{F}_{\{\overline{U}_{i}\}}),\overline{g}(\mathcal{F}_{\{\overline{U}_{i}\}})\right)\leq 2C$ .

Now, to show that $f$ and $\overline{g}$ uniformly coarsely coincide it is enough to say that, for every point $x\in\mathcal{MCG}^{\pm}(S)/N$ , there exist two standard flats $\mathcal{F},\mathcal{F}^{\prime}$ , supported on orbits of annuli, whose coarse intersection is within finite Hausdorff distance from $x$ , and all constants do not depend on $x$ . Indeed, if this is the case then $f$ and $\overline{g}$ should uniformly coarsely agree on the coarse intersection $\mathcal{F}\tilde{\cap}\mathcal{F}^{\prime}$ , and therefore on $x$ . In turn, since $\mathcal{MCG}^{\pm}(S)/N$ acts transitively on itself and maps orbits of annuli to orbits of annuli, it is enough to exhibit a pair $\mathcal{F},\mathcal{F}^{\prime}$ of standard flats, supported on orbits of annuli, whose coarse intersection is bounded.

As a consequence of Lemma 3.1, if $\mathcal{F}$ is supported on $\{\overline{U}_{i}\}_{i=1}^{\nu}$ , $\mathcal{F}^{\prime}$ is supported on $\{\overline{V}_{i}\}_{i=1}^{\nu}$ , and $\{\overline{U}_{i}\}_{i=1}^{\nu}\cap\{\overline{V}_{i}\}_{i=1}^{\nu}=\emptyset$ , then the coarse intersection is bounded. Thus, we are left to find two collections $\{\overline{U}_{i}\}_{i=1}^{\nu}$ and $\{\overline{V}_{i}\}_{i=1}^{\nu}$ of pairwise orthogonal orbits of annuli whose intersection is empty. By Lemma 1.7, it is enough to find two pants decompositions $\{U_{i}\}_{i=1}^{\nu}$ and $\{V_{i}\}_{i=1}^{\nu}$ such that $\{U_{i}\}_{i=1}^{\nu}\cap\{V_{i}\}_{i=1}^{\nu}=\emptyset$ and the subgraph of $\mathcal{C}S$ spanned by the core curves of $\{U_{i}\}_{i=1}^{\nu}\cup\{V_{i}\}_{i=1}^{\nu}$ has diameter at most $2$ . This is easy: just pick any pants decomposition $\{U_{i}\}_{i=1}^{\nu}$ , and then replace every $U_{i}$ with an annulus $V_{i}$ which only intersects $U_{i}$ . This proves Item a.

b Let $f:\,\mathcal{MCG}^{\pm}(S)/N\to\mathcal{MCG}^{\pm}(S)/N$ be a $(L,L)$ -quasi-isometry which lies within finite distance from the identity. By Item a we know that $f$ lies within distance $R$ from the left multiplication by some $\overline{g}$ , which depends only on the induced map $f_{\mathcal{C}S/N}$ . In turn $f_{\mathcal{C}S/N}$ is induced by $f_{Hin}$ , thus if we show that this map is the identity then $\overline{g}$ can be chosen to be the identity, and the corollary follows. Now, for every good hinge $\sigma$ , $f_{Hin}(\sigma)$ was defined in Remark 3.13 as the unique hinge such that $d_{Haus}(h_{f_{Hin}(\sigma)},f(h_{\sigma}))<\infty$ . But then, since $d_{Haus}(f(h_{\sigma}),h_{\sigma})<\infty$ we must have that $f_{Hin}(\sigma)=\sigma$ , that is, $f_{Hin}$ is the identity. ∎

4. Algebraic rigidity

We end the paper by showing that, whenever $\mathcal{MCG}^{\pm}(S)/N$ satisfies Convention 3.2, then the automorphism group of $\mathcal{MCG}^{\pm}(S)/N$ and its abstract commensurator are both isomorphic to $\mathcal{MCG}^{\pm}(S)/N$ itself, via the action of $\mathcal{MCG}^{\pm}(S)/N$ on itself by conjugation. This is Theorem 3 from the introduction, which is covered by Corollaries 4.9 and 4.10 below. The main result of this Section is the following:

Theorem 4.1.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ ) or a $S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then any isomorphism $\phi:\,H\to H^{\prime}$ between finite index subgroups of $\mathcal{MCG}^{\pm}(S)/N$ is the restriction of an inner automorphism.

We first recall some definitions and a theorem from [AMS16].

Definition 4.2.

Two elements $h$ and $g$ of a group $G$ are commensurable, and we write $h\stackrel{{\scriptstyle G}}{{\approx}}g$ , if there exist $m,n\in\mathbb{Z}\setminus\{0\}$ , $k\in G$ such that $kg^{m}k^{-1}=h^{n}$ (that is, if they have non-trivial conjugate powers).

Definition 4.3.

If a group $G$ acts by isometries on a hyperbolic space $\mathcal{S}$ , an element $g\in G$ is loxodromic if for some $x\in\mathcal{S}$ the map $\mathbb{Z}\to\mathcal{S}$ , $n\mapsto g^{n}(x)$ is a quasi-isometric embedding. In the same setting, an element $g\in G$ is weakly properly discontinuous, or WPD, if for every $\varepsilon>0$ and any $x\in\mathcal{S}$ there exists $N_{0}=N_{0}(\varepsilon,x)$ such that whenever $N\geq N_{0}$ we have

\left|\left\{h\in G|\max\left\{d_{S}\left(x,h(x)\right),d_{S}\left(g^{N}(x),hg^{N}(x)\right)\right\}\leq\varepsilon\right\}\right|<\infty

We denote by $\mathcal{L}_{WPD}$ the set of loxodromic WPD elements.

The following result is a special case of [AMS16, Theorem 7.1]. Roughly speaking, the theorem says that if $H$ is a subgroup of $G$ and both act “interestingly enough” on some hyperbolic space, then any homomorphism $\phi:H\to G$ is either (the restriction of) an inner automorphism or it maps some loxodromic WPD to an element which is not commensurable to it.

Theorem 4.4.

Let $G$ be a group acting coboundedly and by isometries on a hyperbolic space $\mathcal{S}$ , with loxodromic WPD elements. Let $H\leq G$ be a non-virtually-cyclic subgroup such that $H\cap\mathcal{L}_{WPD}\neq\emptyset$ , and let $E_{G}(H)$ be the unique maximal finite subgroup of $G$ normalised by $H$ , whose existence is proven in [AMS16, Lemma 5.6]. Let $\phi:\,H\to G$ be a homomorphism such that whenever $h\in H\cap\mathcal{L}_{WPD}$ then $\phi(h)\stackrel{{\scriptstyle G}}{{\approx}}h$ . If $E_{G}(H)=\{1\}$ then $\phi$ is the restriction of an inner automorphism.

Our proof of Theorem 4.1 will be very similar to that of [MS23, Theorem 10.1], from which we now abstract a general statement, both for clarity and for later purpose. Recall that a finitely generated group is acylindrically hyperbolic if it is not virtually-cyclic and it acts coboundedly and by isometries on a hyperbolic space $\mathcal{S}$ , with loxodromic WPD elements.

Theorem 4.5 (Algebraic rigidity from quasi-isometric rigidity).

Let $G$ be an acylindrically hyperbolic group. Suppose that $G$ has no non-trivial finite normal subgroups, and that every self-quasi-isometry of $G$ is within bounded distance from the left multiplication by some element of $G$ . Then any isomorphism between finite index subgroups of $G$ is the restriction of an inner automorphism.

Proof.

We just need to verify that the hypotheses of Theorem 4.4 are satisfied for any isomorphism $\phi:\,H\to H^{\prime}$ between subgroups of finite index of $G$ . By definition of acylindrical hyperbolicity, the hypotheses on the action are satisfied. Moreover, $G$ is not virtually-cyclic, and so also $H$ is not because its index is finite.

Next, we show that $\phi$ has the required commensurating property, that is, for every $h\in H\cap\mathcal{L}_{WPD}$ we have that $\phi(h)\stackrel{{\scriptstyle G}}{{\approx}}h$ . Indeed, $\phi$ can be extended to a quasi-isometry $\Phi:\,G\to G$ (for example, by precomposing $\phi$ with any closest-point projection $G\to H$ ). Hence we can find an element $g\in G$ whose left-multiplication is uniformly close to $\Phi$ . From here, one can argue as in [MS23, Lemma 10.5], which only uses some basic properties of Cayley graphs of finitely generated groups, to prove that $\phi(h)\stackrel{{\scriptstyle G}}{{\approx}}h$ whenever $h\in H$ has infinite order, and in particular whenever $h$ is loxodromic WPD.

We are left to prove that $E_{G}(H)=\{1\}$ . In view of Lemma [MS23, Lemma 10.6], which holds for any acylindrically hyperbolic group, this follows from the fact that $E_{G}(G)=\{1\}$ , i.e. that $G$ has no non-trivial finite normal subgroups. ∎

Thus to prove Theorem 4.1 we reduced ourselves to verify the hypotheses of Theorem 4.5 when $G$ is $\mathcal{MCG}^{\pm}(S)/N$ , and $S$ is as in Theorem 4.1. We know that $\mathcal{MCG}^{\pm}(S)/N$ is quasi-isometrically rigid, by Theorem 3.8, so just need to show that it is acylindrically hyperbolic (Lemma 4.6) and that it has no non-trivial finite normal subgroups (Lemma 4.7). For the first result, we can actually make milder requirements on the topological type of $S$ :

Lemma 4.6.

Let $S$ be either a surface of complexity at least $2$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then $\mathcal{MCG}^{\pm}(S)/N$ is acylindrically hyperbolic.

Proof.

First of all, $\mathcal{MCG}^{\pm}(S)/N$ is non-virtually-cyclic. Indeed, if $x,y\in\mathcal{C}S^{(0)}$ are disjoint curves, then the $\mathbb{Z}^{2}$ subgroup generated by the Dehn twists $T_{x}$ and $T_{y}$ around $x$ and $y$ , respectively, intersects $N$ trivially, since it fixes $x$ and therefore its minimum displacement is zero. Therefore $\langle T_{x},T_{y}\rangle$ injects in $\mathcal{MCG}^{\pm}(S)/N$ , which is therefore non-virtually-cyclic.

Now, $\mathcal{MCG}^{\pm}(S)/N$ acts coboundedly on $\mathcal{C}S/N$ , because the action is induced by the cobounded action of $\mathcal{MCG}^{\pm}(S)$ over $\mathcal{C}S$ . Moreover, our Convention 3.2 says that $\mathcal{C}S/N$ is hyperbolic and $\mathcal{MCG}^{\pm}(S)/N$ -equivariantly quasi-isometric to the main coordinate space of the HHG structure. Therefore, by [BHS17b, Corollary 14.4] the action admits loxodromic WPD elements provided that $\mathcal{C}S/N$ is unbounded, as we noticed in Lemma 3.7. ∎

Lemma 4.7.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ ) or a $S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then $\mathcal{MCG}^{\pm}(S)/N$ has no non-trivial finite normal subgroup.

Proof.

Let $K\leq\mathcal{MCG}^{\pm}(S)/N$ be a finite normal subgroup, and by contradiction let $\overline{f}\in K$ be a non-trivial element. If $\overline{f}$ acts trivially on $\mathcal{C}S/N$ then $\overline{f}$ is the identity, by the injectivity part of either Theorem 2.1 or Theorem 2.8. Thus let $\overline{x}\in\mathcal{C}S/N^{(0)}$ be a vertex which is not fixed by $\overline{f}$ . Let $x\in\mathcal{C}S^{(0)}$ be a representative for $\overline{x}$ , let $f\in\mathcal{MCG}^{\pm}(S)$ be a representative for $\overline{f}$ , let $T_{x}\in\mathcal{MCG}^{\pm}(S)$ be the Dehn Twist around $x$ , and let $\overline{T_{x}}\in\mathcal{MCG}^{\pm}(S)/N$ be its image in the quotient. Since $K$ is finite, we can find $m\in\mathbb{N}_{>0}$ such that $\overline{f}=(\overline{T_{x}})^{-m}\overline{f}(\overline{T_{x}})^{m}$ . Hence, denoting by $T_{f(x)}$ the Dehn twist around $f(x)$ , and by $\overline{1}\in\mathcal{MCG}^{\pm}(S)/N$ the identity element of the quotient, we have

\overline{1}=(\overline{T_{x}})^{-m}\left(\overline{f}(\overline{T_{x}})^{m}\overline{f}^{-1}\right)=(\overline{T_{x}})^{-m}(\overline{T_{f(x)}})^{m},

where we used how Dehn twists behave under conjugation. In other words, we have that $T_{x}^{-m}T_{f(x)}^{m}\in N$ .

Now, if $\overline{x}$ and $\overline{f}(\overline{x})$ are adjacent in $\mathcal{C}S/N$ , then we could have chosen representatives $x$ and $f$ such that $x$ and $f(x)$ are disjoint curves. Then $T_{x}^{-m}T_{f(x)}^{m}$ cannot be an element of $N$ , since it does not have positive displacement.

Hence suppose that $\overline{x}$ and $\overline{f}(\overline{x})$ are not adjacent in $\mathcal{C}S/N$ . Let $U\in\mathfrak{S}$ be the annulus with core curve $x$ , let $\overline{U}\in\overline{\mathfrak{S}}$ be its $N$ -orbit and let $\rho_{\overline{U}}:\,\mathcal{C}S/N\to\mathcal{C}\overline{U}$ be the projection given by the HHG structure. Notice that $\overline{T_{x}}$ acts on $\mathcal{C}\overline{U}$ , since $T_{x}$ fixes $x$ .

Now, $(\overline{T_{x}})^{-m}(\overline{T_{f(x)}})^{m}=\overline{1}$ , so it must act as the identity on $\mathcal{C}S/N$ , and in particular it must fix $\overline{f}(\overline{x})$ . Hence, when we project to $\mathcal{C}\overline{U}$ we get

\rho_{\mathcal{C}\overline{U}}\left(\overline{f}(\overline{x})\right)=\rho_{\mathcal{C}\overline{U}}\left((\overline{T_{x}})^{-m}(\overline{T_{f(x)}})^{m}\overline{f}(\overline{x})\right)=\rho_{\mathcal{C}\overline{U}}\left((\overline{T_{x}})^{-m}(\overline{f}(\overline{x})\right),

where we used that $T_{f(x)}$ fixes $f(x)$ . Moreover

\rho_{\mathcal{C}\overline{U}}\left((\overline{T_{x}})^{-m}(\overline{f}(\overline{x})\right)=(\overline{T_{x}})^{-m}\rho_{\mathcal{C}\left((\overline{T_{x}})^{-m}(\overline{U})\right)}\left(\overline{f}(\overline{x})\right)=(\overline{T_{x}})^{-m}\rho_{\mathcal{C}\overline{U}}\left(\overline{f}(\overline{x})\right),

where we used that projections in a HHG are equivariant with respect to the action of the group. Hence, the action of $(\overline{T_{x}})^{-m}$ on $\mathcal{C}\overline{U}$ must fix the element $\rho_{\mathcal{C}\overline{U}}\left(\overline{f}(\overline{x})\right)$ .

However, the action of $\overline{T_{x}}$ on $\mathcal{C}\overline{U}$ was defined via the action of $T_{x}$ on $\mathcal{C}U$ , so that the following diagram commutes:

Here the vertical arrows are the restriction to $\mathcal{C}U$ of the quotient projection

\bigcup_{U^{\prime}\in\overline{U}}\mathcal{C}U^{\prime}\to\mathcal{C}\overline{U}=\left(\bigcup_{U^{\prime}\in\overline{U}}\mathcal{C}U^{\prime}\right)/N.

Such restriction is a quasi-isometry by Convention 3.2. Hence, no power of $\overline{T_{x}}$ can fix a point in $\mathcal{C}\overline{U}$ , since the action of the Dehn twist $T_{x}$ on its annular curve graph $\mathcal{C}U$ is loxodromic. ∎

As a by-product of Theorem 4.1, we get that any automorphism of $\mathcal{MCG}^{\pm}(S)/N$ is the conjugation by some element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ . The following lemma states that such $\overline{g}$ is also unique:

Lemma 4.8.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ ) or $S=S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then $\mathcal{MCG}^{\pm}(S)/N$ is centerless.

Proof.

By either Theorem 2.1 or Theorem 2.8, it is enough to show that $\overline{g}$ acts as the identity on $\mathcal{C}S/N$ . Notice that $\overline{g}$ commutes with the image of the Dehn twist $\overline{T_{x}}$ for any curve $x\in\mathcal{C}S^{(0)}$ . In particular, by how Dehn twists behave under conjugation, we have that $\overline{T_{x}}=\overline{T_{g(x)}}$ , where $g\in\mathcal{MCG}^{\pm}(S)$ is any representative for $\overline{g}$ . Now one can argue as in the proof of Theorem 4.1 to get that $\overline{g}(\overline{x})=\overline{x}$ , and the conclusion follows. ∎

Combining Theorem 4.1 and Lemma 4.8 we get:

Corollary 4.9.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ ) or $S=S_{0,5}$ , and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Aut}(\mathcal{MCG}^{\pm}(S)/N)$ , which maps an element $\overline{g}\in\mathcal{MCG}^{\pm}(S)/N$ to the conjugation by $\overline{g}$ , is an isomorphism. Therefore $\text{Out}(\mathcal{MCG}^{\pm}(S)/N)$ is trivial.

Finally, we recall the definition of the abstract commensurator of a group $G$ . Consider the set of all isomorphisms $H\to H^{\prime}$ between finite-index subgroups of $G$ . Let $\text{Comm}(G)$ be the quotient of this set by the following equivalence relation: two isomorphisms are identified if they coincide on a finite index subgroup of $G$ . Then $\text{Comm}(G)$ can be endowed with a group structure, induced by the composition. Our final result shows that $\text{Comm}(\mathcal{MCG}^{\pm}(S)/N)$ is “the smallest possible”:

Corollary 4.10.

Let $S$ be either a surface of complexity at least $3$ (excluding the case $S=S_{2,0}$ , or $S=S_{0,5}$ and let $\mathcal{MCG}^{\pm}(S)/N$ satisfy Convention 3.2. Then the map $\mathcal{MCG}^{\pm}(S)/N\to\text{Comm}(\mathcal{MCG}^{\pm}(S)/N)$ , which maps an element $\overline{g}$ to the conjugation by $\overline{g}$ , is an isomorphism.

Proof.

The map is surjective by Theorem 4.1. Moreover, if the conjugation by $\overline{g}$ coincides with the identity on a finite-index subgroup $H$ , then $\overline{g}$ commutes with the $m$ -th power of the image of any Dehn twist, where $m$ only depends on the index of $H$ in $\mathcal{MCG}^{\pm}(S)/N$ . Then one can argue as in the proof of Lemma 4.8 to get that $\overline{g}$ acts as the identity on $\mathcal{C}S/N$ , and therefore $\overline{g}=\overline{1}$ by either Theorem 2.1 or Theorem 2.8. ∎

References

[ABD21] Carolyn Abbott, Jason Behrstock, and Matthew Gentry Durham. Largest acylindrical actions and stability in hierarchically hyperbolic groups. Trans. Amer. Math. Soc. Ser. B, 8:66–104, 2021. With an appendix by Daniel Berlyne and Jacob Russell.
[AL13] Javier Aramayona and Christopher J. Leininger. Finite rigid sets in curve complexes. J. Topol. Anal., 5(2):183–203, 2013.
[AMS16] Yago Antolín, Ashot Minasyan, and Alessandro Sisto. Commensurating endomorphisms of acylindrically hyperbolic groups and applications. Groups Geom. Dyn., 10(4):1149–1210, 2016.
[BHMS20] Jason Behrstock, Mark Hagen, Alexandre Martin, and Alessandro Sisto. A combinatorial take on hierarchical hyperbolicity and applications to quotients of mapping class groups, 2020.
[BHS17a] Jason Behrstock, Mark F. Hagen, and Alessandro Sisto. Asymptotic dimension and small-cancellation for hierarchically hyperbolic spaces and groups. Proc. Lond. Math. Soc. (3), 114(5):890–926, 2017.
[BHS17b] Jason Behrstock, Mark F. Hagen, and Alessandro Sisto. Hierarchically hyperbolic spaces, I: Curve complexes for cubical groups. Geom. Topol., 21(3):1731–1804, 2017.
[BHS19] Jason Behrstock, Mark F. Hagen, and Alessandro Sisto. Hierarchically hyperbolic spaces II: Combination theorems and the distance formula. Pacific J. Math., 299(2):257–338, 2019.
[BHS21] Jason Behrstock, Mark F. Hagen, and Alessandro Sisto. Quasiflats in hierarchically hyperbolic spaces. Duke Math. J., 170(5):909–996, 2021.
[BKMM12] Jason Behrstock, Bruce Kleiner, Yair Minsky, and Lee Mosher. Geometry and rigidity of mapping class groups. Geom. Topol., 16(2):781–888, 2012.
[BM06] Jason Behrstock and Dan Margalit. Curve complexes and finite index subgroups of mapping class groups. Geom. Dedicata, 118:71–85, 2006.
[BM19] Tara E. Brendle and Dan Margalit. Normal subgroups of mapping class groups and the metaconjecture of Ivanov. J. Amer. Math. Soc., 32(4):1009–1070, 2019.
[CC07] Ruth Charney and John Crisp. Relative hyperbolicity and Artin groups. Geom. Dedicata, 129:1–13, 2007.
[CM22] Matt Clay and Johanna Mangahas. Hyperbolic quotients of projection complexes. Groups Geom. Dyn., 16(1):225–246, 2022.
[Dah18] François Dahmani. The normal closure of big Dehn twists and plate spinning with rotating families. Geom. Topol., 22(7):4113–4144, 2018.
[DDLS21] Spencer Dowdall, Matthew G. Durham, Christopher J. Leininger, and Alessandro Sisto. Extensions of veech groups ii: Hierarchical hyperbolicity and quasi-isometric rigidity, 2021.
[DGO17] F. Dahmani, V. Guirardel, and D. Osin. Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces. Mem. Amer. Math. Soc., 245(1156):v+152, 2017.
[DHS21] François Dahmani, Mark Hagen, and Alessandro Sisto. Dehn filling Dehn twists. Proc. Roy. Soc. Edinburgh Sect. A, 151(1):28–51, 2021.
[FM12] Benson Farb and Dan Margalit. A primer on mapping class groups, volume 49 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 2012.
[Har86] John L. Harer. The virtual cohomological dimension of the mapping class group of an orientable surface. Invent. Math., 84(1):157–176, 1986.
[Irm04] Elmas Irmak. Superinjective simplicial maps of complexes of curves and injective homomorphisms of subgroups of mapping class groups. Topology, 43(3):513–541, 2004.
[Irm06a] Elmas Irmak. Complexes of nonseparating curves and mapping class groups. Michigan Math. J., 54(1):81–110, 2006.
[Irm06b] Elmas Irmak. Superinjective simplicial maps of complexes of curves and injective homomorphisms of subgroups of mapping class groups. II. Topology Appl., 153(8):1309–1340, 2006.
[Iva88] N. V. Ivanov. Automorphisms of Teichmüller modular groups. In Topology and geometry—Rohlin Seminar, volume 1346 of Lecture Notes in Math., pages 199–270. Springer, Berlin, 1988.
[Iva97] Nikolai V. Ivanov. Automorphisms of complexes of curves and of Teichmüller spaces. In Progress in knot theory and related topics, volume 56 of Travaux en Cours, pages 113–120. Hermann, Paris, 1997.
[Kor99] Mustafa Korkmaz. Automorphisms of complexes of curves on punctured spheres and on punctured tori. Topology Appl., 95(2):85–111, 1999.
[Luo00] Feng Luo. Automorphisms of the complex of curves. Topology, 39(2):283–298, 2000.
[McL19] Alan McLeay. Geometric normal subgroups in mapping class groups of punctured surfaces. New York J. Math., 25:839–888, 2019.
[Min96] Yair N. Minsky. A geometric approach to the complex of curves on a surface. In Topology and Teichmüller spaces (Katinkulta, 1995), pages 149–158. World Sci. Publ., River Edge, NJ, 1996.
[MS23] Giorgio Mangioni and Alessandro Sisto. Rigidity of mapping class groups mod powers of twists, 2023.
[PS23] Harry Petyt and Davide Spriano. Unbounded domains in hierarchically hyperbolic groups. Groups Geom. Dyn., 17(2):479–500, 2023.
[Sch95] Richard Evan Schwartz. The quasi-isometry classification of rank one lattices. Inst. Hautes Études Sci. Publ. Math., 82:133–168 (1996), 1995.
[Sch20] Saul Schleimer. Notes on the complex of curves, 2020.

Rigidity results for large displacement quotients of mapping class groups

Abstract.

Introduction

Theorem 1.

Theorem 2.

Theorem 3 (Algebraic rigidity).

Sketch of proofs

Combinatorial rigidity

Quasi-isometric rigidity

Algebraic rigidity

Comparison with quotients by large powers of Dehn twists

Questions

Question 1.

Question 2.

Question 3.

Outline of the paper

Acknowledgements

1. Large displacement quotients

Definition 1.1 (Minimum displacement).

Definition 1.2 (Large displacement quotient).

Example 1.3.

Example 1.4.

1.1. Isometric projections

Lemma 1.5.

Proof.

Definition 1.6.

Lemma 1.7 (Isometric lifts and projections).

Proof.

1.2. Orbits of subsurfaces

Definition 1.8.

Lemma 1.9.

Proof.

Lemma 1.10.

Proof.

2. Combinatorial rigidity

Theorem 2.1 (Combinatorial rigidity).

Lemma 2.2.

Proof.

Proof of Theorem 2.1.

2.1. Some low-complexity cases

Theorem 2.3.

Proof.

Theorem 2.4.

Lemma 2.5.

Proof.

Definition 2.6.

Lemma 2.7 (Przytycki).

Proof.

Theorem 2.8.

Proof of Theorem 2.8.

3. Quasi-isometric rigidity

3.1. Background on hierarchical hyperbolicity

3.1.1. HHS and HHG

3.1.2. Product, flats, orthants

Lemma 3.1 (Coarse intersection of standard orthants and flats).

3.2. HHG structures inherited from the surface

Convention 3.2 (Surface-inherited HHG structure).

Example 3.3.

Example 3.4 (Hierarchically hyperbolically embedded subgroups).

Lemma 3.5.

Proof.

Corollary 3.6.

Proof.

Lemma 3.7.

Proof.

3.3. Statement of the results

Theorem 3.8 (Quasi-isometric rigidity).

Corollary 3.9 (QI-rigidity of ℳ​𝒞​𝒢±​(S)\mathcal{MCG}^{\pm}(S)).

Corollary 3.10.

3.4. Quasi-isometries induce maps on hinges

Definition 3.11 ([BHS21, Definition 5.2]).

Assumption A.

Definition 3.12 (Good domain).

Assumption B.

Assumption C.

Remark 3.13.

Definition 3.14.

Lemma 3.15 (Behrstock, Hagen, Sisto).

Proof.

Assumption D.

Corollary 3.9 (QI-rigidity of $\mathcal{MCG}^{\pm}(S)$ ).