Risk Bounds for Mixture Density Estimation on Compact Domains via the $h$-Lifted Kullback–Leibler Divergence

We are particularly interested in oracle bounds of the form

$${\mathrm{\mathbf{E}}}\left\{\ell\left(f,f_{k,n}\right)\right\}-\ell\left(f,\mathcal{C}\right)\leq\rho\left(k,n\right),$$

(2)

where $\left(p,q\right)\mapsto\ell\left(p,q\right)\in\mathbb{R}_{\geq 0}$ is a loss function on pairs of density functions. We define the density-to-class loss

$$\ell\left(f,\mathcal{C}\right)=\inf_{q\in\mathcal{C}}\ell\left(f,q\right),\ \mathcal{C}=\mathrm{cl}\left(\bigcup_{k\in\mathbb{N}}\mathrm{co}_{k}\left(\mathcal{P}\right)\right),$$

where $\mathrm{cl}(\cdot)$ is the closure. Here, we identify $\left(k,n\right)\mapsto\rho\left(k,n\right)$ as a characterization of the rate at which the left-hand side of (2) converges to zero as $k$ and $n$ increase. Our present work follows the research of Li & Barron (1999), Rakhlin et al. (2005) and Klemelä (2007) (see also Klemelä 2009, Ch. 19). In Li & Barron (1999) and Rakhlin et al. (2005), the authors consider the case where $\ell\left(p,q\right)$ is taken to be the Kullback–Leibler (KL) divergence

$$\mathrm{KL}\left(p\,||\,q\right)=\int p\log\frac{p}{q}\mathrm{d}\mu$$

and $f_{k,n}=f_{k}\left(\cdot;{\psi}_{k,n}\right)$ is a maximum likelihood estimator (MLE), where

$${\psi}_{k,n}\in\underset{\psi_{k}\in\mathcal{S}_{k}\times\Theta^{k}}{\operatorname*{arg\,max\,}}\frac{1}{n}\sum_{i=1}^{n}\log f_{k}\left(X_{i};\psi_{k}\right),$$

is a function of $\mathbf{X}_{n}$, with $\mathcal{S}_{k}$ denoting the probability simplex in $\mathbb{R}^{k}$.

Under the assumption that $f,f_{k}\geq a$, for some $a>0$ and each $k\in\left[n\right]$ (i.e., strict positivity), Li & Barron (1999) obtained the bound

$${\mathrm{\mathbf{E}}}\left\{\mathrm{KL}\left(f\,||\,f_{k,n}\right)\right\}-\mathrm{KL}\left(f\,||\,\mathcal{C}\right)\leq c_{1}\frac{1}{k}+c_{2}\frac{k\log\left(c_{3}n\right)}{n},$$

for constants $c_{1},c_{2},c_{3}>0$, which was then improved by Rakhlin et al. (2005) who obtained the bound

$${\mathrm{\mathbf{E}}}\left\{\mathrm{KL}\left(f\,||\,f_{k,n}\right)\right\}-\mathrm{KL}\left(f\,||\,\mathcal{C}\right)\leq c_{1}\frac{1}{k}+c_{2}\frac{1}{\sqrt{n}},$$

for constants $c_{1},c_{2}>0$ (constants $(c_{j})_{j\in\mathbb{N}}$ are typically different between expressions).

Alternatively, Klemelä (2007) takes $\ell\left(p,q\right)$ to be the squared $L_{2}\left(\mu\right)$ norm distance (i.e., the least-squares loss):

$$\ell\left(p,q\right)=\lVert p-q\rVert_{2,\mu}^{2},$$

where $\lVert p\rVert_{2,\mu}^{2}=\int_{\mathcal{X}}\lvert p\rvert^{2}\mathrm{d}\mu$, for each $p\in L_{2}\left(\mu\right)$, and choose $f_{k,n}$ as minimizers of the $L_{2}\left(\mu\right)$ empirical risk, i.e., $f_{k,n}=f_{k}\left(\cdot;{\psi}_{k,n}\right)$, where

$$\psi_{k,n}\in\underset{\psi_{k}\in\mathcal{S}_{k}\times\Theta^{k}}{\operatorname*{arg\,min\,}}-\frac{2}{n}\sum_{i=1}^{n}f_{k}\left(\cdot;\psi_{k}\right)+\left\|f_{k}\left(\cdot;\psi_{k}\right)\right\|_{2,\mu}^{2}.$$

(3)

Here, Klemelä (2007) establish the bound

$${\mathrm{\mathbf{E}}}\left\|f-{f}_{k,n}\right\|_{2,\mu}^{2}-\inf_{q\in\mathcal{C}}\left\|f-q\right\|_{2,\mu}^{2}\leq c_{1}\frac{1}{k}+c_{2}\frac{1}{\sqrt{n}},$$

$c_{1},c_{2}>0$, without the lower bound assumption on $f,f_{k}$ above, even permitting $\mathcal{X}$ to be unbounded. Via the main results of Naito & Eguchi (2013), the bound above can be generalized to the $U$-divergences, which includes the special $L_{2}(\mu)$ norm distance as a special case.

On the one hand, the sequence of MLEs required for the results of Li & Barron (1999) and Rakhlin et al. (2005) are typically computable, for example, via the usual expectation–maximization approach (cf. McLachlan & Peel 2004, Ch. 2). This contrasts with the computation of least-squares density estimators of form (3), which requires evaluations of the typically intractable integral expressions $\left\|f_{k}\left(\cdot;\psi_{k}\right)\right\|_{2}^{2}$. However, the least-squares approach of Klemelä (2007) permits the analysis using families $\mathcal{P}$ of usual interest, such as normal distributions and beta distributions, the latter of which being compactly supported but having densities that cannot be bounded away from zero without restrictions, and thus do not satisfy the regularity conditions of Li & Barron (1999) and Rakhlin et al. (2005).

We propose the following $h$-lifted KL divergence, as a generalization of the standard KL divergence to address the computationally tractable estimation of density functions which do not satisfy the regularity conditions of Li & Barron (1999) and Rakhlin et al. (2005). The use of the $h$-lifted KL divergence has the possibility to advance theories based on the standard KL divergence in statistical machine learning. To this end, let $h:\mathcal{X}\rightarrow\mathbb{R}_{\geq 0}$ be a function in $L_{1}(\mu)$, and define the $h$-lifted KL divergence by:

$$\mathrm{KL}_{h}\left(p\,||\,q\right)=\int_{\mathcal{X}}\left\{p+h\right\}\log\frac{p+h}{q+h}\mathrm{d}\mu.$$

(4)

In the sequel, we shall show that $\mathrm{KL}_{h}$ is a Bregman divergence on the space of probability density functions, as per Csiszár (1995).

Assume that $h$ is a probability density function, and let $\mathbf{Y}_{n}=\left(Y_{i}\right)_{i\in\left[n\right]}$ be a an i.i.d. sample, independent of $\mathbf{X}_{n}$, where each $Y_{i}:\Omega\rightarrow\mathcal{X}$ is a random variable with probability measure on $(\mathcal{X},\mathfrak{F})$, characterized by the density $h$ with respect to $\mu$. Then, for each $k$ and $n$, let $f_{k,n}$ be defined via the maximum $h$-lifted likelihood estimator ($h$-MLLE; see Appendix B for further discussion) $f_{k,n}=f_{k}\left(\cdot;{\psi}_{k,n}\right)$, where

$${\psi}_{k,n}\in\underset{\psi_{k}\in\mathcal{S}_{k}\times\Theta^{k}}{\operatorname*{arg\,max\,}}~{}\frac{1}{n}\sum_{i=1}^{n}\left(\log\left\{f_{k}\left(X_{i};\psi_{k}\right)+h\left(X_{i}\right)\right\}+\log\left\{f_{k}\left(Y_{i};\psi_{k}\right)+h\left(Y_{i}\right)\right\}\right).$$

(5)

The primary aim of this work is to show that

$${\mathrm{\mathbf{E}}}\left\{\mathrm{KL}_{h}\left(f\,||\,f_{k,n}\right)\right\}-\mathrm{KL}_{h}\left(f\,||\,\mathcal{C}\right)\leq c_{1}\frac{1}{k}+c_{2}\frac{1}{\sqrt{n}}$$

(6)

for some constants $c_{1},c_{2}>0$, without requiring the strict positivity assumption that $f,f_{k}\geq a>0$.

This result is a compromise between the works of Li & Barron (1999) and Rakhlin et al. (2005), and Klemelä (2007), as it applies to a broader space of component densities $\mathcal{P}$, and because the required $h$-MLLEs (5) can be efficiently computed via minorization–maximization (MM) algorithms (see e.g., Lange 2016). We shall discuss this assertion in Section 4.

Our work largely follows the approach of Li & Barron (1999), which was extended upon by Rakhlin et al. (2005) and Klemelä (2007). All three texts use approaches based on the availability of greedy algorithms for maximizing convex functions with convex functional domains. In this work, we shall make use of the proof techniques of Zhang (2003). Related results in this direction can be found in DeVore & Temlyakov (2016) and Temlyakov (2016). Making the same boundedness assumption as Rakhlin et al. (2005), Dalalyan & Sebbar (2018) obtain refined oracle inequalities under the additional assumption that the class $\mathcal{P}$ is finite. Numerical implementations of greedy algorithms for estimating finite mixtures of Gaussian densities were studied by Vlassis & Likas (2002) and Verbeek et al. (2003).

The $h$-MLLE as an optimization objective can be compared to other similar modified likelihood estimators, such as the $L_{q}$ likelihood of Ferrari & Yang (2010) and Qin & Priebe (2013), the $\beta$-likelihood of Basu et al. (1998) and Fujisawa & Eguchi (2006), penalized likelihood estimators, such as maximum a posteriori estimators of Bayesian models, or $f$-separable Bregman distortion measures of Kobayashi & Watanabe (2024; 2021).

The practical computation of the $h$-MLLEs, (5), is made possible via the MM algorithm framework of Lange (2016), see also Hunter & Lange (2004), Wu & Lange (2010), and Nguyen (2017) for further details. Such algorithms have well-studied global convergence properties and can be modified for mini-batch and stochastic settings (see, e.g., Razaviyayn et al., 2013 and Nguyen et al., 2022a).

A related and popular setting of investigations is that of model selection, where the objects of interest are single-index sequences $\left(f_{k_{n},n}\right)_{n\in\mathbb{N}}$, and where the aim is to obtain finite-sample bounds for losses of the form $\ell\left(f_{k_{n},n},f\right)$, where each $k_{n}\in\mathbb{N}$ is a data dependent function, often obtained by optimizing some penalized loss criterion, as described in Massart (2007), Koltchinskii (2011, Ch. 6), and Giraud (2021, Ch. 2). In the context of finite mixtures, examples of such analyses can be found in the works of Maugis & Michel (2011) and Maugis-Rabusseau & Michel (2013). A comprehensive bibliography of model selection results for finite mixtures and related statistical models can be found in Nguyen et al. (2022c).

The manuscript is organized as follows. In Section 2, we formally define the $h$-lifted KL divergence as a Bregman divergence and establish several of its properties. In Section 3, we present new risk bounds for the $h$-lifted KL divergence of the form (2). In Section 4, we discuss the computation of the $h$-lifted likelihood estimator in the form of (5), followed by empirical results illustrating the convergence of (2) with respect to both $k$ and $n$. Additional insights and technical results are provided in the Appendices at the end of the manuscript.

Let $\phi:\mathcal{I}\to\operatorname*{\mathbb{R}}$, $\mathcal{I}=(0,\infty)$ be a strictly convex function that is continuously differentiable. The Bregman divergence between scalars $d_{\phi}:\mathcal{I}\times\mathcal{I}\to\mathbb{R}_{\geq 0}$ generated by the function $\phi$ is given by:

$$d_{\phi}(p,q)=\phi(p)-\phi(q)-\phi^{\prime}(q)(p-q),$$

where $\phi^{\prime}(q)$ denotes the derivative of $\phi$ at $q$.

Bregman divergences possess several useful properties, including the following list:

1. 1.

   Non-negativity: $d_{\phi}(p,q)\geq 0$ for all $p,q\in\mathcal{I}$ with equality if and only if $p=q$;

2. 2.

   Asymmetry: $d_{\phi}(p,q)\neq d_{\phi}(q,p)$ in general;

3. 3.

   Convexity: $d_{\phi}(p,q)$ is convex in $p$ for every fixed $q\in\mathcal{I}$.

4. 4.

   Linearity: $d_{c_{1}\phi_{1}+c_{2}\phi_{2}}(p,q)=c_{1}d_{\phi_{1}}(p,q)+c_{2}d_{\phi_{2}}(p,q)$ for $c_{1},c_{2}\geq 0$.

The properties for Bregman divergences between scalars can be extended to density functions and other functional spaces, as established in Frigyik et al. (2008) and Stummer & Vajda (2012), for example. We also direct the interested reader to the works of Pardo (2006), Basu et al. (2011), and Amari (2016).

The class of $h$-lifted KL divergences constitute a generalization of the usual KL divergence and are a subset of the Bregman divergences over the space of density functions that are considered by Csiszár (1995). Namely, let $\mathcal{P}$ be a convex set of probability densities with respect to the measure $\mu$ on $\mathcal{X}$. The Bregman divergence $D_{\phi}:\mathcal{P}\times\mathcal{P}\to[0,\infty)$ between densities $p,q\in\mathcal{P}$ can be constructed as follows:

$$D_{\phi}(p\,||\,q)=\int_{\mathcal{X}}d_{\phi}\left(p(x),q(x)\right)\mathrm{d}\mu(x).$$

The $h$-lifted KL divergence $\mathrm{KL}_{h}$ as a Bregman divergence is generated by the function $\phi(u)=(u+h)\log(u+h)-(u+h)+1$. This assertion is demonstrated in Appendix C.1.

One solution for computing (5) is to employ an MM algorithm. To do so, we first write the objective of (5) as

$$L_{h,n}\left(\psi_{k}\right)=\frac{1}{n}\sum_{i=1}^{n}\left(\log\left\{\sum_{j=1}^{k}\pi_{j}\varphi\left(X_{i};\theta_{j}\right)+h\left(X_{i}\right)\right\}+\log\left\{\sum_{j=1}^{k}\pi_{j}\varphi\left(Y_{i};\theta_{j}\right)+h\left(Y_{i}\right)\right\}\right),$$

where $\psi_{k}\in\Psi_{k}=\mathcal{S}_{k}\times\Theta^{k}$. We then require the definition of a minorizer $Q_{n}$ for $L_{h,n}$ on the space $\Psi_{k}$, where $Q_{n}:\Psi_{k}\times\Psi_{k}\rightarrow\mathbb{R}$ is a function with the properties:

1. (i)

   $Q_{n}\left(\psi_{k},\psi_{k}\right)=L_{h,n}\left(\psi_{k}\right)$, and

2. (ii)

   $Q_{n}\left(\psi_{k},\chi_{k}\right)\leq L_{h,n}\left(\psi_{k}\right)$,

for each $\psi_{k},\chi_{k}\in\Psi_{k}$. In this context, given a fixed $\chi_{k}$, the minorizer $Q_{n}\left(\cdot,\chi_{k}\right)$ should possess properties that simplify it compared to the original objective $L_{h,n}$. These properties should make the minorizer more tractable and might include features such as parametric separability, differentiability, convexity, among others.

In order to build an appropriate minorizer for $L_{h,n}$, we make use of the so-called Jensen’s inequality minorizer, as detailed in Lange (2016, Sec. 4.3), applied to the logarithm function. This construction results in a minorizer of the form

	$\displaystyle Q_{n}\left(\psi_{k},\chi_{k}\right)$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{k}\left\{\tau_{j}\left(X_{i};\chi_{k}\right)\log\pi_{j}+\tau_{j}\left(X_{i};\chi_{k}\right)\log\varphi\left(X_{i};\theta_{j}\right)\right\}$
			$\displaystyle+\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{k}\left\{\tau_{j}\left(Y_{i};\chi_{k}\right)\log\pi_{j}+\tau_{j}\left(Y_{i};\chi_{k}\right)\log\varphi\left(Y_{i};\theta_{j}\right)\right\}$
			$\displaystyle+\frac{1}{n}\sum_{i=1}^{n}\left\{\gamma\left(X_{i};\chi_{k}\right)\log h\left(X_{i}\right)+\gamma\left(Y_{i};\chi_{k}\right)\log h\left(Y_{i}\right)\right\}$
			$\displaystyle-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{k}\left\{\tau_{j}\left(X_{i};\chi_{k}\right)\log\tau_{j}\left(X_{i};\chi_{k}\right)+\tau_{j}\left(Y_{i};\chi_{k}\right)\log\tau_{j}\left(Y_{i};\chi_{k}\right)\right\}$
			$\displaystyle-\frac{1}{n}\sum_{i=1}^{n}\left\{\gamma\left(X_{i};\chi_{k}\right)\log\gamma\left(X_{i};\chi_{k}\right)+\gamma\left(Y_{i};\chi_{k}\right)\log\gamma\left(Y_{i};\chi_{k}\right)\right\}$

where

$$\gamma\left(X_{i};\psi_{k}\right)=h\left(X_{i}\right)/\left\{\sum_{j=1}^{k}\pi_{j}\varphi\left(X_{i};\theta_{j}\right)+h\left(X_{i}\right)\right\}$$

and

$$\tau_{j}\left(X_{i};\psi_{k}\right)=\pi_{j}\varphi\left(X_{i};\theta_{j}\right)/\left\{\sum_{j=1}^{k}\pi_{j}\varphi\left(X_{i};\theta_{j}\right)+h\left(X_{i}\right)\right\}.$$

Observe that $Q_{n}\left(\cdot,\chi_{k}\right)$ now takes the form of a sum-of-logarithms, as opposed to the more challenging log-of-sum form of $L_{h,n}$. This change produces a functional separation of the elements of $\psi_{k}$.

Using $Q_{n}$, we then define the MM algorithm via the parameter sequence $\left(\psi_{k}^{\left(s\right)}\right)_{s\in\mathbb{N}}$, where

$$\psi_{k}^{\left(s\right)}=\underset{\psi_{k}\in\Psi_{k}}{\operatorname*{arg\,max\,}}~{}Q_{n}\left(\psi_{k},\psi_{k}^{\left(s-1\right)}\right),$$

(9)

for each $s>0$, and where $\psi_{k}^{\left(0\right)}$ is user chosen and is typically referred to as the initialization of the algorithm. Notice that for each $s$, (9) is a simpler optimization problem than (5). Writing $\psi_{k}^{\left(s\right)}=\left(\pi_{1}^{\left(s\right)},\dots,\pi_{k}^{\left(s\right)},\theta_{1}^{\left(s\right)},\dots,\theta_{k}^{\left(s\right)}\right)$, we observe that (9) simplifies to the separated expressions:

$$\pi_{j}^{\left(s\right)}=\frac{\sum_{i=1}^{n}\left\{\tau_{j}\left(X_{i};\psi_{k}^{\left(s-1\right)}\right)+\tau_{j}\left(Y_{i};\psi_{k}^{\left(s-1\right)}\right)\right\}}{\sum_{i=1}^{n}\sum_{l=1}^{k}\left\{\tau_{l}\left(X_{i};\psi_{k}^{\left(s-1\right)}\right)+\tau_{l}\left(Y_{i};\psi_{k}^{\left(s-1\right)}\right)\right\}}$$

and

$$\theta_{j}^{\left(s\right)}=\underset{\theta_{j}\in\Theta}{\operatorname*{arg\,max\,}}\frac{1}{n}\sum_{i=1}^{n}\left\{\tau_{j}\left(X_{i};\psi_{k}^{\left(s-1\right)}\right)\log\varphi\left(X_{i};\theta_{j}\right)+\tau_{j}\left(Y_{i};\psi_{k}^{\left(s-1\right)}\right)\log\varphi\left(Y_{i};\theta_{j}\right)\right\},$$

for each $j\in\left[k\right]$.

A noteworthy property of the MM sequence $\left(\psi_{k}^{\left(s\right)}\right)_{s\in\mathbb{N}}$ is that it generates an increasing sequence of objective values, due to the chain of inequalities

$$L_{h,n}\left(\psi_{k}^{\left(s-1\right)}\right)=Q_{n}\left(\psi_{k}^{\left(s-1\right)},\psi_{k}^{\left(s-1\right)}\right)\leq Q_{n}\left(\psi_{k}^{\left(s\right)},\psi_{k}^{\left(s-1\right)}\right)\leq L_{h,n}\left(\psi_{k}^{\left(s\right)}\right),$$

where the equality is due to property (i) of $Q_{n}$, the first in equality is due to the definition of $\psi_{k}^{\left(s\right)}$, and the second inequality is due to property (ii) of $Q_{n}$. This provides a kind of stability and regularity to the sequence $\left(L_{h,n}\left(\psi_{k}^{\left(s\right)}\right)\right)_{s\in\mathbb{N}}$.

Of course, we can provide stronger guarantees under additional assumptions. Namely, assume that (iii) $\Psi_{k}\subset\varPsi_{k}$, where $\varPsi_{k}$ is an open set in a finite dimensional Euclidean space on which $L_{h,n}$ and $Q_{n}\left(\cdot,\chi_{k}\right)$ is differentiable, for each $\chi_{k}\in\Psi_{k}$. Then, under assumptions (i)–(iii) regarding $L_{h,n}$ and $Q_{n}$, and due to the compactness of $\Psi_{k}$ and the continuity of $Q_{n}$ on $\Psi_{k}\times\Psi_{k}$, Razaviyayn et al. (2013, Cor. 1) implies that $\left(\psi_{k}^{\left(s\right)}\right)_{s\in\mathbb{N}}$ converges to the set of stationary points of $L_{h,n}$ in the sense that

$$\lim_{s\rightarrow\infty}\inf_{\psi_{k}^{*}\in\Psi_{k}^{*}}\left\|\psi_{k}^{\left(s\right)}-\psi_{k}^{*}\right\|_{2}=0,\text{ where }\Psi_{k}^{*}=\left\{\psi_{k}^{*}\in\Psi_{k}:\left.\frac{\partial L_{h,n}}{\partial\psi_{k}}\right|_{\psi_{k}=\psi_{k}^{*}}=0\right\}.$$

More concisely, we say that the sequence $\left(\psi_{k}^{\left(s\right)}\right)_{s\in\mathbb{N}}$ globally converges to the set of stationary points $\Psi_{k}^{*}$.

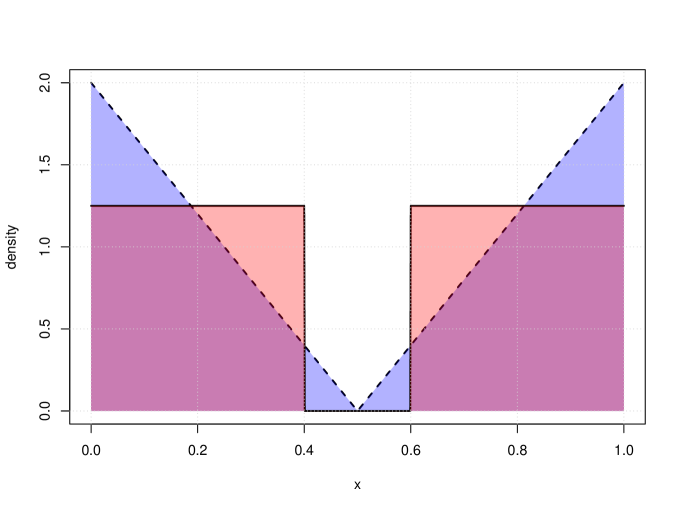
Towards the task of demonstrating empirical evidence of the rates in Theorem 5, we consider the family of beta distributions on the unit interval $\mathcal{X}=\left[0,1\right]$ as our base class (i.e., (7)) to estimate a pair of target densities

$$f_{1}\left(x\right)=\frac{1}{2}\chi_{\left[0,2/5\right]}\left(x\right)+\frac{1}{2}\chi_{\left[3/5,1\right]}\left(x\right),$$

and

$$f_{2}\left(x\right)=\chi_{\left[0,1\right]}\left(x\right)\begin{cases}2-4x&\text{if }x\leq 1/2,\\ -2+4x&\text{if }x>1/2,\end{cases}$$

where $\chi_{\mathcal{A}}$ is the characteristic function that takes value $1$ if $x\in\mathcal{A}$ and $0$, otherwise. Note that neither $f_{1}$ nor $f_{2}$ are in $\mathcal{C}$. In particular, $f_{1}\left(x\right)=0$ when $x\in\left(\frac{2}{5},\frac{3}{5}\right)$, and $f_{2}(x)=0$ when $x=1/2$, and hence neither densities are bounded away from 0, on $\mathcal{X}$. Thus, the theory of Rakhlin et al. (2005) cannot be applied to provide bounds for the expected KL divergence between MLEs of beta mixtures and the pair of targets. We visualize $f_{1}$ and $f_{2}$ in Figure 1.

To observe the rate of decrease of the $h$-lifted KL divergence between the targets and respective sequences of $h$-MLLEs, we conduct two experiments E1 and E2. In E1, our target density is set to $f_{1}$ and $h_{1}=\beta\left(\cdot;1/2,1/2\right)$. For each $n\in\left\{2^{10},\dots,2^{15}\right\}$ and $k\in\left\{2,\dots,8\right\}$, we independently simulate $\mathbf{X}_{n}$ and $\mathbf{Y}_{n}$ with each $X_{i}$ and $Y_{i}$ ($i\in\left[n\right]$), i.i.d., from the distributions characterized by $f_{1}$ and $h_{1}$, respectively. In E2, we target $f_{2}$ with $h$-MLLEs over the same ranges of $k$ and $n$, but with $h_{2}=\beta\left(\cdot;1,1\right)$–the density of the uniform distribution. For each $k$ and $n$, we simulate $\mathbf{X}_{n}$ and $\mathbf{Y}_{n}$, respectively, from distributions characterized by $f_{2}$ and $h_{2}$.

In both experiments, we simulate $r=50$ replicates of each $\left(k,n\right)$-scenario and compute the corresponding $h$-MLLEs, $\left(f_{k,n,l}\right)_{l\in[r]}$, using the previously described MM algorithm. For each $l\in\left[r\right]$, we compute the corresponding negative log $h$-lifted likelihood between the target $f$ and $f_{k,n,l}$:

$$K_{k,n,l}=-\int_{\mathcal{X}}\left(f+h\right)\log\left(f_{k,n,l}+h\right)\mathrm{d}\mu$$

to assess the rates, and note that

$$\mathrm{KL}_{h}\left(f\,||\,f_{k,n,l}\right)=\int_{\mathcal{X}}\left(f+h\right)\log\left(f+h\right)\mathrm{d}\mu+K_{k,n,l},$$

where the prior term is a constant with respect to $k$ and $n$.

To analyze the sample of $7\times 6\times 50=2100$ observations of relationship between the values $\left(K_{k,n,l}\right)_{l\in[r]}$ and the corresponding values of $k$ and $n$, we use non-linear least squares (Amemiya, 1985, Sec. 4.3) to fit the regression relationship

$${\operatorname*{{\mathrm{\mathbf{E}}}}}\left[K_{k,n,l}\right]=a_{0}+\frac{a_{1}}{\left(k+2\right)^{b_{1}}}+\frac{a_{2}}{n^{b_{2}}}.$$

(10)

We obtain $95\%$ asymptotic confidence intervals for the estimates of the regression parameters $a_{0}$, $a_{1}$, $a_{2}$, $b_{1}$, $b_{2}\in\mathbb{R}$, under the assumption of potential mis-specification of (10), by using the sandwich estimator for the asymptotic covariance matrix (cf. White 1982).

We report the estimates along with $95\%$ asymptotic confidence intervals for the parameters of (10) for E1 and E2 in Table 1. Plots of the average negative log $h$-lifted likelihood values by sample sizes $n$ and numbers of components $k$ are provided in Figure 2.

From Table 1, we observe that $\operatorname*{{\mathrm{\mathbf{E}}}}\left[K_{k,n,l}\right]$ decreases with both $n$ and $k$ in both simulations, and that the rates at which the averages decrease are faster than anticipated by Theorem 5, with respect to both $n$ and $k$. We can visually confirm the decreases in the estimate of $\operatorname*{{\mathrm{\mathbf{E}}}}\left[K_{k,n,l}\right]$ via Figure 2. In both E1 and E2, the rate of decrease over the assessed range of $n$ is approximately proportional to $1/n$, as opposed to the anticipated rate of $1/\sqrt{n}$, whereas the rate of decrease in $k$ is far larger, at approximately $1/k^{1.87}$ for E1 and $1/k^{4.36}$ for E2.

These observations provide empirical evidence towards the fact that the rate of decrease of $\operatorname*{{\mathrm{\mathbf{E}}}}\left[K_{k,n,l}\right]$ is at least $1/k$ and $1/\sqrt{n}$, respectively, for $k$ and $n$, at least over the simulation scenarios. These fast rates of fit over small values of $n$ and $k$ may be indicative of a diminishing returns of fit phenomenon, as discussed in Cadez & Smyth (2000) or the so-called elbow phenomenon (see, e.g., Ritter 2014, Sec. 4.2), whereupon the rate of decrease in average loss for small values of $k$ is fast and becomes slower as $k$ increases, converging to some asymptotic rate. This is also the reason why we do not include the outcomes when $k=1$, as the drop in $\operatorname*{{\mathrm{\mathbf{E}}}}\left[K_{k,n,l}\right]$ between $k=1$ and $k=2$ is so dramatic that it makes our simulated data ill-fitted by any model of form (10). As such, we do not view Theorem 5 as being pessimistic in light of these phenomena, as it applies uniformly over all values of $k$ and $n$.