Risk Consistency of Cross-Validation with Lasso-Type Procedures
Abstract
The lasso and related sparsity inducing algorithms have been the target of substantial theoretical and applied research. Correspondingly, many results are known about their behavior for a fixed or optimally chosen tuning parameter specified up to unknown constants. In practice, however, this oracle tuning parameter is inaccessible so one must use the data to select one. Common statistical practice is to use a variant of cross-validation for this task. However, little is known about the theoretical properties of the resulting predictions with such data-dependent methods. We consider the high-dimensional setting with random design wherein the number of predictors grows with the number of observations . Under typical assumptions on the data generating process, similar to those in the literature, we recover oracle rates up to a log factor when choosing the tuning parameter with cross-validation. Under weaker conditions, when the true model is not necessarily linear, we show that the lasso remains risk consistent relative to its linear oracle. We also generalize these results to the group lasso and square-root lasso and investigate the predictive and model selection performance of cross-validation via simulation. Key words and phrases: Linear oracle; Model selection; Persistence; Regularization
1 Introduction
Following its introduction in the statistical (Tibshirani, 1996) and signal processing (Chen, Donoho, and Saunders, 1998) communities, -regularized linear regression has become a fixture as both a data analysis tool and as a subject for deep theoretical investigations. In particular, for a response vector , design matrix , and tuning parameter , we consider the lasso problem of finding
| (1) |
for any , where and indicate the Euclidean and -norms respectively. An equivalent but less computationally convenient specification of the lasso problem given by Equation (1) is the constrained optimization version:
| (2) |
where . By convexity, for each (or ), there is always at least one solution to these optimization problems. While it is true that the solution is not necessarily unique if rank, this detail is unimportant for our purposes, and we abuse notation slightly by referring to as ‘the’ lasso solution.
These two optimization problems are equivalent mathematically, but they differ substantially in practice. Though the constrained optimization problem (Equation (2)) can be solved via quadratic programming, most algorithms use the Lagrangian formulation (Equation (1)). In this paper, we address both estimators as each is more amenable to theoretical treatment in different contexts.
The literature contains numerous results regarding the statistical properties of the lasso, and, while it is beyond the scope of this paper to give a complete literature review, we highlight some of these results here. Early results about the asymptotic distribution of the lasso solution are shown in Knight and Fu (2000) under the assumption that the sample covariance matrix has a nonnegative definite limit and is fixed. Many authors (e.g. Donoho, Elad, and Temlyakov, 2006; Meinshausen and Bühlmann, 2006; Meinshausen and Yu, 2009; Wainwright, 2009; Zhao and Yu, 2006; Zou, 2006) have investigated model selection properties of the lasso—showing that when the best predicting model is linear and sparse, the lasso will tend to asymptotically recover those predictors. The literature has considered this setting under various “irrepresentability” conditions which ensure that the relevant predictors are not too highly correlated with irrelevant ones. Bickel, Ritov, and Tsybakov (2009) analyze the lasso and the Dantzig selector (Candès and Tao, 2007) under restricted eigenvalue conditions with an oracle tuning parameter. Finally, Belloni, Chernozhukov, and Wang (2014) develop results for a related method, the square-root lasso, with heteroscedastic noise and oracle tuning parameter.
Theoretical results such as these and others, depend critically on the choice of tuning parameters and are typically of the form: if , then possesses some desired behavior (correct model selection, risk consistency, sign consistency, et cetera). However comforting results of this type are, this theoretical guidance says little about the properties of the lasso when the tuning parameter is chosen in a data-dependent way.
In this paper, we show that the lasso under random design with cross-validated tuning parameter is indeed risk consistent under some conditions on the joint distribution of the design matrix and the response vector . Additionally, we demonstrate that our framework can be used to show similar results for other lasso-type methods. Our results build on the previous theory presented in Homrighausen and McDonald (2014) and Homrighausen and McDonald (2013). Homrighausen and McDonald (2014) proves risk consistency for cross-validation under strong conditions on the data generating process, most notably , and on the cross-validation procedure (requiring leave-one-out CV). The results in this paper differ from those in Homrighausen and McDonald (2013) in a number of ways. The current paper examines the Lagrangian formulation of the lasso problem under typical conditions, weakens the conditions on an upper bound for , provides more refined results via concentration inequalities, examines the influence of , and includes related results for the group lasso and the square-root lasso.
1.1 Overview of results
The criterion we focus on for this paper is risk consistency, (alternatively known as persistence). That is, we investigate the difference between the prediction risk of the lasso estimator with tuning parameter estimated by cross-validation and the risk of the best linear oracle predictor (with oracle tuning parameter). Risk consistency of lasso has previously been studied by Greenshtein and Ritov (2004); Bunea, Tsybakov, and Wegkamp (2007); van de Geer (2008) and Bartlett, Mendelson, and Neeman (2012). Their results, in contrast to ours, assume that the tuning parameter is selected in an oracle fashion.
We present two main results which make progressively stronger assumptions on the data generating process and use both forms of the lasso estimator. The first imposes strong conditions on the design matrix, assumes the linear model is true, and that this linear model is sparse. The second is more general and allows the true model to be neither linear nor correctly specified. For this reason, our focus is on risk consistency rather than estimation of a “true” parameter or correct identification of a “true” sparsity pattern. Additionally, well-known results of Shao (1993) imply that cross-validation leads to inconsistent model selection in general, suggesting that results for sparse recovery may not exist. Although prediction is an important goal, one is often interested in variable selection for more interpretable models or follow-up experiments. In light of the negative results in Shao (1993), we are unable to offer theoretical results which promise consistent model selection by cross validation, but simulations in Section 4 suggest that it performs well nevertheless. Both the estimation and sparse recovery settings are frequently studied in the literature assuming the tuning parameter is the oracle and that the data generating model is linear (e.g. Bunea, Tsybakov, and Wegkamp, 2007; Candès and Plan, 2009; Donoho, Elad, and Temlyakov, 2006; Leng, Lin, and Wahba, 2006; Meinshausen and Bühlmann, 2006; Meinshausen and Yu, 2009).
In the first case, when the truth is linear, we examine the Lagrangian formulation in Equation (1). In this scenario, we prove convergence rates which differ only by a factor relative to those achievable with the oracle tuning parameter (e.g. Negahban, Ravikumar, Wainwright, and Yu, 2012; Bühlmann and van de Geer, 2011; Bunea, Tsybakov, and Wegkamp, 2007). That is, for an -sparse linear model with restricted isometry conditions on the covariance of the design, the risk of the cross-validated estimator approaches the oracle risk at a rate of . Under more general conditions, we follow the approach of Greenshtein and Ritov (2004) and examine the constrained optimization form in Equation (2). Using our methods, we require that the set of candidate predictors, , satisfies where is a sequence which approaches infinity and characterizes the tail behavior of the data. This is essentially as quickly as one could hope relative to Greenshtein and Ritov (2004) under our more general assumptions on the design matrix. We note however that, using empirical process techniques, Bartlett, Mendelson, and Neeman (2012) have been able to improve the rate shown in Greenshtein and Ritov (2004) to for sub-Gaussian design and oracle tuning parameter.
1.2 Tuning parameter selection methods and outline of the paper
There are several proposed data-dependent techniques for choosing or . Kato (2009) and Tibshirani and Taylor (2012) investigate estimating the “degrees of freedom” of a lasso solution. With an unbiased estimator of the degrees of freedom, the tuning parameter can be selected by minimizing the empirical risk penalized by a function of this estimator. Note that this approach requires an estimate of the variance, which is nontrivial when (Giraud, Huet, and Verzelen, 2012; Homrighausen and McDonald, 2016). Another risk estimator is the adapted Bayesian information criterion proposed by Wang and Leng (2007) which uses a plug-in estimator based on the second-order Taylor’s expansion of the risk. Arlot and Massart (2009) and Saumard (2011) consider “slope heuristics” as a method for penalty selection with Gaussian noise, paying particular attention to the regressogram estimator in the first case and piecewise polynomials with fixed in the second. Finally, Sun and Zhang (2012) present an algorithm to jointly estimate the regression coefficients and the noise level. This results in a data-driven value for the tuning parameter which possesses oracle properties under some regularity conditions.
However, many authors (e.g. Efron et al., 2004; Friedman et al., 2010; Greenshtein and Ritov, 2004; Tibshirani, 1996, 2011; Zou et al., 2007 and as discussed by van de Geer and Bühlmann, 2011, Section 2.4.1) recommend selecting or in the lasso problem by minimizing a -fold cross-validation estimator of the risk (see Section 2 for the precise definition). Cross-validation is generally well-studied in a number of contexts, especially model selection and risk estimation. In the context of model selection, Arlot and Celisse (2010) give a detailed survey of the literature emphasizing the relationship between the sizes of the validation set and the training set as well as discussing the positive bias of cross-validation as a risk estimator.
Some results supporting the use of cross-validation for statistical methods other than lasso are known. For instance, Stone (1974, 1977) outlines various conditions under which cross-validated methods can result in good predictions. More recently, Dudoit and van der Laan (2005) find finite sample bounds for various cross-validation procedures. These results do not address the lasso nor parameter spaces with increasing dimensions, and furthermore, apply to choosing the best estimator from a finite collection of candidate estimators. Lecué and Mitchell (2012) provide oracle inequalities related to using cross-validation with lasso, however, it treats the problem as aggregating a dictionary of lasso estimators with different tuning parameters, and the results are stated for fixed rather than the high-dimensional setting investigated here. Most recently, Flynn, Hurvich, and Simonoff (2013) investigate numerous methods for tuning parameter selection in penalized regression, but the theoretical results hold only when and not for cross-validation. In particular, the authors state “to our knowledge the asymptotic properties of []-fold CV have not been fully established in the context of penalized regression” (Flynn, Hurvich, and Simonoff, 2013, p. 1033).
Rather than cross-validation, one may use information criteria such as AIC (Akaike, 1974) or BIC (Schwarz, 1978). These techniques are frequently advocated in the literature (for example Bühlmann and van de Geer, 2011; Wang et al., 2007; Tibshirani, 1996; Fan and Li, 2001), but the classical asymptotic arguments underlying these methods apply only for fixed and rely on maximum likelihood estimates (or Bayesian posteriors) for all parameters including the noise. The theory in the high-dimensional setting supporting these methods is less complete. Recent work has developed new information criteria with supporting asymptotic results uf but is still allowed to increase. For example, the criterion developed by Wang et al. (2009) selects the correct model asymptotically even if as long as . If is allowed to increase more quickly than , theoretical results assume is known to get around the difficult task of high-dimensional variance estimation (Chen and Chen, 2012; Zhang and Shen, 2010; Kim et al., 2012; Fan and Tang, 2013).
In Section 2, we outline the mathematical setup for the lasso prediction problem and discuss some empirical concerns. Section 3 contains the main result and associated conditions. Section 4 compares different choices of for cross-validation via simulation, while Section 5 summarizes our contribution and presents some avenues for further research.
2 Notation and definitions
2.1 Preliminaries
Suppose we observe data consisting of predictor variables, , and response variables, , where are independent and identically distributed for and the distribution is in some class to be specified. Here, we use the notation to allow the number of predictor variables to change with . Similarly, we index the distribution to emphasize its dependence on . For simplicity, in what follows, we omit the subscript when there is little risk of confusion.
We consider the problem of estimating a linear functional for predicting , when is a new, independent random variable from the same distribution as the data and . For now, we do not assume a linear model, only the usual regression framework where with and independent and is some unknown function. We will use zero-based indexing for so that . To measure performance, we use the -risk of the predictor :
| (3) |
Note that this is a conditional expectation: for any estimator ,
| (4) |
and the expectation is taken only over the new data and not over any observables which may be used to choose .
Using the independent observations , we can form the response vector and the design matrix . Then, given a vector , we write the squared-error empirical risk function as
| (5) |
Analogously to Equation (5), we write the -fold cross-validation estimator of the risk with respect to the tuning parameter , which we abbreviate to CV-risk or just CV, as
| (6) |
Here, is a set of validation sets, is the estimator in Equation (2) with the observations in the validation set removed, and indicates the cardinality of . Notice in particular that the cross-validation estimator of the risk is a function of rather than a single predictor —it uses different predictors at a fixed , averaging over their performance on the respective held-out sets. Over the course of the paper, we will freely exchange for in this definition.
Lastly, we define the CV-risk minimizing choice of tuning parameter to be
| (7) |
In our setting, we will take (or ) as an interval subset of the nonnegative real numbers which needs to be defined by the data-analyst. The choice of is an important part of the performance of and requires some explanation. First, we provide some insight into the computational load of using CV-risk to find .
2.2 Computations
In practice, CV-risk is known to be time consuming and somewhat unstable due to the randomness associated with forming . For a fixed , suppose is found for the entire lasso path via the lars (Efron et al., 2004) algorithm, which can be computed in the same computational complexity as a least squares fit. To fix ideas, suppose , which means lars has computational complexity . Hence, as the feature matrix with rows removed has approximately rows, can be computed for all in time. Repeating this times means the computational complexity for forming over all is . If is a fixed fraction of , CV-risk has computational complexity of order , which is a factor of slower than a single lasso fit.
Though more expensive on a single processor, CV-risk is readily parallelizable over the folds and therefore (ignoring communication costs between processors) CV-risk could actually be faster to compute than (and hence ) as
. This advantage is of course lost if we ultimately compute . However, this computational advantage would be maintained if we instead report
| (8) |
where is the lasso estimate trained on the observations in with the tuning parameter chosen by minimizing the empirical risk using the test observations in . For , for example, this would provide a 25% reduction in computation time. The properties of this approximation is an interesting avenue for further investigation.
2.3 Choosing the sets and
The data analyst must be able to solve the optimization problem in Equation (7). For , we must choose a lower bound: . This implies we must choose as a function of the data. While it is tempting to allow , this results in numerical and practical implementation issues if rank and is unnecessary as the theory will show. However, the lower bound will have a nontrivial impact on the quality of the recovery, as choosing a value too large may eliminate the best solutions. We will see in the next section that under some assumptions on the data generating process, we can safely choose a particular that allows order coefficients to be selected without compromising the quality of the estimator.
In the case of , an upper bound must be selected for any grid-search optimization procedure. As we will impose much weaker conditions on the data generating process, choosing such an upper bound is more complicated. Note that, by Equation (2), must be in the -ball with radius . This constraint is only binding (Osborne, Presnell, and Turlach, 2000) if
where is a least-squares solution and . Observe that if and otherwise has dimension , which would imply is not unique. Both of these statements assume that the columns of contain a linearly independent set of size . See Tibshirani (2013) for the more general situation. In either case, if , then is equal to a least-squares solution. Based on this argument and the fact that , it is tempting to define the upper bound to be , where is the least-squares solution when is given by the Moore-Penrose inverse. However, this upper bound has at least two problems. First, although theoretically well-defined, as with setting , it suffers from numerical and practical implementation issues if rank. The second problem is that it grows much too fast, at least order , therefore potentially including solutions which will have low bias but very high variance.
Instead, we define an upper bound based on a rudimentary variance estimator where is an increasing sequence of constants. Hence, we consider the optimization interval to be . We defer fixing a particular sequence until the next section. As our main results demonstrate, this choice of is enough to ensure that a risk consistent sequence of tuning parameters can be selected.
Remark 1.
We emphasize here that using a cross-validated tuning parameter involves more than simply allowing the tuning parameter to be selected in a data-dependent manner. In order to meaningfully analyze tuning parameter selection, we allow the search set and the tuning parameter to be chosen based on the data.
Remark 2.
The computational implementation of CV for an interval (or ) deserves some discussion. Two widely used algorithms for lasso are glmnet (Friedman et al., 2010), which uses coordinate descent, and lars (Efron et al., 2004), which leverages the piece-wise linearity of the lasso solution as varies (the lasso path). The package glmnet is much faster than lars, however, glmnet examines a grid of values, , say, and approximates the solution at each with increasing accuracy depending on the number of iterations. On the other hand, lars evaluates the entire solution path exactly, such that it is theoretically possible to choose any via numerical optimization. However, optimizing Equation (7) with standard solvers can be difficult due to a possible lack of convexity. In both cases, the extremes of the interval will affect the quality of the solution.
3 Main results
In this section, we present results for both forms of the lasso estimator in Equations (1) and (2) under more and less restrictive assumptions, respectively. First, we define the types of random variables which we allow. To quantify the tail behavior of our data, we appeal to the notion of an Orlicz norm.
Definition 1.
For any random variable and function that is nondecreasing, convex, and , define the -Orlicz norm
For any integer , we are interested in both the usual -norm given by and the norm given by choosing and represented notationally as . Note that if , then for sufficiently large , there are constants such that
In the particular case of the -Orlicz norm, if it holds that and where is the Gamma function. Additionally, and .
Before outlining our results, we define the following set of distributions.
Definition 2.
Let and be a constant independent of . Then define
that is, all centered cross products of a random variable have uniformly finite -Orlicz norm, independent of . Define the analogous set which contains the measures such that almost surely for each .
Remark 3.
To make subsequent expressions as a function of make sense, interpret for any , and .
While is a measure on indexing with is more natural than indexing with given that our results include increasing with . Section 3 is a common moment condition (Greenshtein and Ritov, 2004; Nardi and Rinaldo, 2008; Bartlett, Mendelson, and Neeman, 2012) for showing risk consistency of lasso-type methods in high dimensional settings.
To simplify our exposition, we make the following condition about the size of the validation sets for CV.
Condition 1.
The sequence of validation sets is such that, as , , for some sequence .
This condition is intended to rule out some pathological cases of unbalanced validation sets, but standard CV methods satisfy it. For example, with -fold cross-validation, we can take , which is the integer part of . For design random variables and oracle prediction function , define .
3.1 Persistence when is linear
If we are willing to impose strong conditions on , as in Bunea, Tsybakov, and Wegkamp (2007) and Meinshausen (2007), then we can obtain cross-validated lasso estimators which achieve nearly oracle rates.
If we assume that , then we can write the risk of an estimator as
where . We write the excess risk as and prove a convergence rate for . In this case, targeting the excess risk is the same as estimating the conditional expectation of , but if is not linear (as in Section 3.2), the excess risk remains a meaningful way of assessing prediction behavior.
Theorem 3.
Assume the following conditions:
-
M1:
There exists a constant independent of such that almost surely for all .
-
M2:
and .
-
M3:
-
M4:
such that and are diagonally dominant at level ; that is for all .
-
M5:
, which is independent of .
-
M6:
.
-
M7:
.
Then,
These conditions and the result warrant a few comments. First, note that condition M4 implies that is positive semi-definite. Second, as is fixed, M6 and M7 ensure so that will eventually allow models with covariates. Thus, the procedure is asymptotically consistent for model selection (Meinshausen, 2007). Finally, note that is random due to the term . Here, we emphasize that is a function of the data: the conditional expectation of a new test random variable given the observed data used to choose both and as in Equation (4).
While the conditions of Theorem 3 are strong, they are typical of those used to prove persistence of the lasso estimator with oracle tuning parameter (for the case of fixed design, see Negahban et al., 2012). For instance, Bunea et al. (2007) prove an oracle rate for the lasso of with . Under similar conditions, our result with cross-validated tuning parameter requires a larger (resulting in smaller models) and a slower convergence rate to the oracle by a factor . A reasonable choice of suggested by Theorem 3 is .
Proof of Theorem 3.
We have that, for all ,
by the proof of Theorem 7 in Meinshausen (2007). Note that is defined in Equation (5). Furthermore, the second term on the right hand side goes to 0 by that result. Now note that
By Corollary 1 in Bunea, Tsybakov, and Wegkamp (2007), for any , we have that
Setting proportional to is enough for the upper bound to go to zero as yielding the result. ∎
3.2 Persistence when is not linear
In order to derive results under more general conditions, we move to the linear oracle estimation framework. For any , define the oracle estimator with respect to as
Suppose is an estimator, such as by cross-validation. Then we can decompose the risk of an estimator as follows:
where is the risk of the mean function . Because the data generating process is not necessarily linear, we study the performance of an estimator via the excess risk of relative to , which we define as
| (9) |
Here, depends on the cross-validated tuning parameter as well as the oracle set through . Focusing on Equation (9), allows for meaningful theory when the approximation error does not necessarily converge to zero as grows. This is particularly important here, as we do not assume that the conditional expectation of given is linear. As , the approximation error decreases and hence we desire to take for some increasing sequence . As discussed in the introduction, Greenshtein and Ritov (2004) show that if , then converges in probability to zero. Bartlett, Mendelson, and Neeman (2012) increase the size of this search set allowing while still having
Theorem 4.
Remark 4.
The sets account for cases wherein results in suboptimal sets . If is such that grows too quickly with non-negligible probability, then cross-validation may result in low-bias but high variance solutions. On the other hand, if is too small, then we will rule out possible estimators with lower risk. Here calibrates a high-probability upper bound on based on and the choice of while ensures that will be large enough to include low risk estimators.
Remark 5.
Usually in the oracle estimation framework, and so the excess risk is necessarily nonnegative because the oracle predictor, , is selected as the risk minimizer over . In that case, Equation (10) would correspond to convergence in probability. As we are examining the case where the optimization set is estimated, may be negative. However, we are only interested in bounding the case where is positive, i.e. the case where the estimator is worse than the oracle.
Define . It follows that We state the following corollary to Theorem 4, which outlines the conditions under which we can do asymptotically at least as well at predicting a new observation as the oracle linear model. That is, when the right hand side of Equation (10) goes to zero.
Corollary 5.
Under the conditions of Theorem 4, if and , where is any sequence which tends toward infinity and , we have that for large enough and ,
In particular, .
Remark 6.
The rate at which can be taken to zero quantifies the decay of the size of the ‘bad’ set where is large. For the corollary, both and . Therefore, it is necessary for and hence, must go to zero at a slower rate than .
Remark 7.
As increases, which corresponds to putting less mass on the tails of the centered interactions of the components of , the faster the oracle set given by can grow. That, is the weaker the -sparsity assumption of the linear oracle. When , the random variables have no tails and we get the fastest rate of growth for ; that is, .
The parameter controls the minimum size of the validation versus training sets that comprise cross-validation. It must be true that is strictly less than . To get the best guarantee, should increase as fast as possible. Hence, our results advocate a cross-validation scheme where the validation and training sets are asymptotically balanced, i.e. . This should be compared with the results in Shao (1993), which state that for model selection consistency, one should have . However, Shao (1993) presents results for model selection while we focus on prediction error. Similarly, Dudoit and van der Laan (2005) provide oracle inequalities for cross-validation and also advocate for the validation set to grow as fast as possible. Note that for -fold cross-validation, so that .
Additionally, the rates and deserve comment. It is instructive to compare this choice of with , a standard estimate of the noise variance in high dimensions (e.g. van de Geer and Bühlmann, 2011, p. 104). If , then is an overestimate of the variance due to the presence of the regression function . Our results state that we must choose to increase slower than , thereby increasing this overestimation and enlarging the potential search set . While depends on several parameters, , , and are known to the analyst. Also, the choice of depends on how much approximation error the analyst is willing to make. The term is required to slow the growth of just slightly. While this shrinks the size of the set relative to that used by Greenshtein and Ritov (2004), potentially eliminating some better solutions, effectively quantifies their requirement , making explicit the need for to grow more slowly than . As such, if we set and set , we reaquire the rate shown by Greenshtein and Ritov (2004), where Section 3.2 implies that both and .
While the entire proof is contained in the supplementary material, we provide a brief sketch here.
Proof sketch of Theorem 4 and Section 3.2.
In order to control the behavior of , we require a number of steps.
- 1.
-
2.
By standard rules of probability, it is enough to control each term (I) through (IV) on the intersection as long as and are both small.
-
3.
For each of the terms, we rewrite the difference in risks as a difference of quadratic forms involving the covariance matrices of the random variables and the extended coefficients. For example, where and , and where . Thus, we have, for example,
-
4.
After some algebraic manipulation and an application of Hölder’s inequality, we can rewrite these differences as the product of the squared -norm of the coefficient vector and the expected value of the -norm of the difference between an empirical and expected covariance. For example
-
5.
Finally, the -norm of the coefficient vector is bounded by due to the constraint in Equation (2) while by Nemirovski’s inequality and some intermediate lemmas.
-
6.
To move to the corollary, we use the Orlicz condition on to show that and are both small with high probability. This ensures that and for any sequences and which satisfy , .
∎
We note here that our results generalize to other -estimators which use an -constraint. In particular, relative to the set of coefficients with , an empirical estimator with cross-validated tuning parameter has prediction risk which converges to the prediction risk of the oracle.
Corollary 6.
Consider the group lasso (Yuan and Lin, 2006)
and the square-root lasso (Belloni, Chernozhukov, and Wang, 2014)
Let and be as in Section 3.2. Then, for large enough, , and , we have
4 Simulations
So far, though we have given some indication about the asymptotic order of , we haven’t provided any guidance for the choice of with a fixed and . In this section, we investigate the predictive and model selection performance of -fold cross-validation for a range of .
We consider three criteria: prediction risk, sensitivity, and specificity. For prediction risk, we approximate by the empirical risk of 500 test observations. For sensitivity and specificity, define the active set of a coefficient vector to be , along with and to be the active sets of and , respectively. Then sensitivity = and specificity = , where counts the number of elements in a set and indicates the complement of a set .
4.1 Simulation details
Conditions:
For these simulations, we consider a wide range of possible conditions by varying the correlation in the design, ; the number of parameters, ; the sparsity, ; and the signal-to-noise ratio, SNR. In all cases, we let , , and set the measurement error variance . Lastly, we run each simulation condition combination 100 times. For these simulations, we assume that there exists a such that the regression function in order to make model selection meaningful.
The design matrices are produced in two steps. First, for and , forming the matrix . Second, correlations are introduced by defining a matrix D that has all off diagonal elements equal to and diagonal elements equal to one. Then, we redefine . For these simulations, we consider correlations .
For sparsity, we take and generate the non-zero elements of from a Laplace distribution with parameter 1. We let . Also, to compensate for the random amount of signal in each observation, we vary the signal-to-noise ratio, defined to be We consider and . Note that as the SNR increases the observations go from a high-noise and low-signal regime to a low-noise and high-signal one. Lastly, we consider two different noise distributions, and . Here indicates a distribution with 3 degrees of freedom and the term makes the variance equal to 1. Finally, we take , the last case being leave-one-out CV.
4.2 Simulation results
Though we have run all of the above simulations, to save space we have only included plots from a select number of simulation conditions that are the most informative. For prediction risk, all considered ’s result in remarkably similar prediction risks. In Figure 1, for , SNR = 1, and , we see that taking or results in slightly smaller prediction risks. This is comforting as both of these values of are used frequently by default and they are the least computationally demanding.
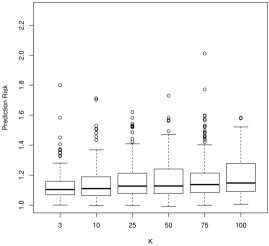
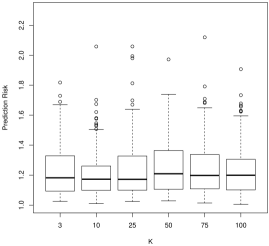
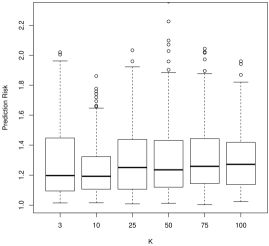
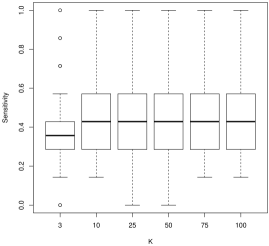
For model selection, there is a more nuanced story. For sensitivity, which describes how often we would correctly identify a coefficient as nonzero, larger values of tend to work better. For instance, in Figure 2, we see that is often decidedly worse than larger , followed by . As is often the case, this conclusion presents a trade-off with the results for specificity (Figure 3): smaller values of tend to work better. In general, tends to have more nonzero entries as increases holding all else constant. As the correlation parameter or the signal to noise (SNR) increases, all values of have approximately the same performance.

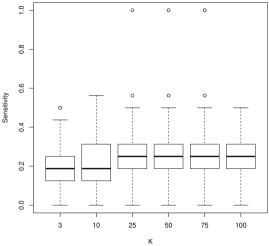
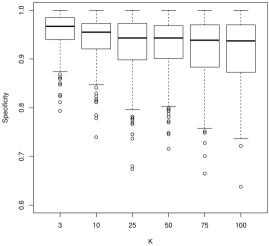
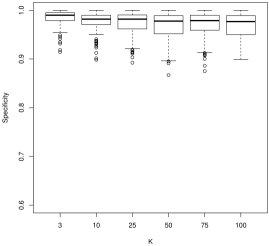
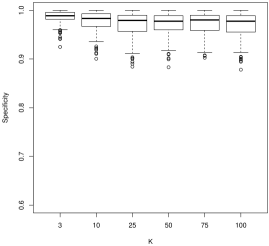
5 Discussion
A common practice in data analysis is to attempt to estimate a coefficient vector via lasso with its regularization parameter chosen via cross-validation. Unfortunately, no definitive theoretical results existed as to the effect of choosing the tuning parameter in this data-dependent way in the high-dimensional random design setting.
We have demonstrated that the lasso, group lasso, and square-root lasso with tuning parameters chosen by cross-validation are risk consistent relative to the linear oracle predictor. Under strong conditions on the joint distribution (as in related literature), our results differ from the standard convergence rates by a factor of . Imposing more mild conditions on the joint distribution of the data, we can achieve the same rate of convergence to the risk of the linear oracle predictor with a data-dependent tuning parameter as with the optimal, yet inaccessible, oracle tuning parameter. Together, these results show that if the data analyst is interested in using lasso for prediction, choosing the tuning parameter via cross-validation is still a good procedure. In practice, our results justify data-driven sets and over which we can safely select tuning parameters. For -fold CV, when is linear, our theory suggests taking while for arbitrary, a reasonable choice assuming is .
This work reveals some interesting open questions. First, our most general results do not apply for leave-one-out cross-validation as for all and hence the upper-bounds become trivial. Leave-one-out cross-validation is more computationally demanding than -fold cross-validation, but is still used in practice. These results also do not give any prescription for choosing other than that it should be . Our simulation study indicates that all ranging from 3 to have approximately the same prediction ability. For model selection, larger tends to produce more nonzero coefficients and hence has better sensitivity but poorer specificity.
As there are many other methods for choosing the tuning parameter in the lasso problem, a direct comparison of the behavior of the lasso estimator with tuning parameter chosen via cross-validation versus a degrees-of-freedom-based method is of substantial interest and should be investigated. Also, our results depend strongly on the upper bound for or the lower bound for . However, in most cases, we will never need to use tuning parameters this extreme. So it makes sense to attempt to find more subtle theory to provide greater intuition for the behavior of lasso under cross-validation.
Acknowledgements
The authors gratefully acknowledge support from the National Science Foundation (DH, DMS–1407543; DJM, DMS–1407439) and the Institute of New Economic Thinking (DH and DJM, INO14-00020). Additionally, the authors would like the thank Cosma Shalizi and Ryan Tibshirani for reading preliminary versions of this manuscript and also Larry Wasserman for the inspiration and encouragement.
References
- Akaike (1974) Hirotugu Akaike. A new look at the statistical model identification. Automatic Control, IEEE Transactions on, 19(6):716–723, 1974.
- Arlot and Celisse (2010) Sylvain Arlot and Alain Celisse. A survey of cross-validation procedures for model selection. Statistics Surveys, 4:40–79, 2010.
- Arlot and Massart (2009) Sylvain Arlot and Pascal Massart. Data-driven calibration of penalties for least-squares regression. The Journal of Machine Learning Research, 10:245–279, 2009.
- Bartlett et al. (2012) Peter L. Bartlett, Shahar Mendelson, and Joseph Neeman. -regularized linear regression: Persistence and oracle inequalities. Probability Theory and Related Fields, 154(1-2):193–224, 2012.
- Belloni et al. (2014) Alexandre Belloni, Victor Chernozhukov, and Lie Wang. Pivotal estimation via square-root lasso in nonparametric regression. The Annals of Statistics, 42(2):757–788, 2014.
- Bickel et al. (2009) Peter J. Bickel, Ya’acov Ritov, and Alexandre B. Tsybakov. Simultaneous analysis of lasso and Dantzig selector. The Annals of Statistics, pages 1705–1732, 2009.
- Bühlmann and van de Geer (2011) Peter Bühlmann and Sara van de Geer. Statistics for high-dimensional data: Methods, theory and applications. Springer, New York, 2011.
- Bunea et al. (2007) Florentina Bunea, Alexandre B. Tsybakov, and Marten H. Wegkamp. Sparsity oracle inequalities for the lasso. Electronic Journal of Statistics, 1:169–194, 2007.
- Candès and Plan (2009) Emmanuel J. Candès and Yaniv Plan. Near-ideal model selection by minimization. The Annals of Statistics, 37(5A):2145–2177, 2009.
- Candès and Tao (2007) Emmanuel J. Candès and Terence Tao. The Dantzig selector: Statistical estimation when is much larger than . The Annals of Statistics, 35(6):2313–2351, 2007.
- Chen and Chen (2012) Jiahua Chen and Zehua Chen. Extended bic for small-n-large-p sparse glm. Statistica Sinica, 22(2):555, 2012.
- Chen et al. (1998) Scott Shaobing Chen, David L. Donoho, and Michael A. Saunders. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing, 20(1):33–61, 1998.
- Donoho et al. (2006) David. L. Donoho, Michael Elad, and Vladimir Temlyakov. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Transactions on Information Theory, 52(1):6–18, 2006.
- Dudoit and van der Laan (2005) Sandrine Dudoit and Mark J. van der Laan. Asymptotics of cross-validation risk estimation in estimator selection and performance assessment. Statistical Methodology, pages 131–154, 2005.
- Dümbgen et al. (2010) Lutz Dümbgen, Sara A. van de Geer, Mark C. Veraar, and Jon A. Wellner. Nemirovski’s inequalities revisited. American Mathematical Monthly, 117(2):138–160, 2010.
- Efron et al. (2004) Bradley Efron, Trevor Hastie, Ian Johnstone, and Robert Tibshirani. Least angle regression. The Annals of Statistics, 32(2):407–499, 2004.
- Fan and Li (2001) Jianqing Fan and Runze Li. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American statistical Association, 96(456):1348–1360, 2001.
- Fan and Tang (2013) Yingying Fan and Cheng Yong Tang. Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 75(3):531–552, 2013.
- Flynn et al. (2013) Cheryl J. Flynn, Clifford M. Hurvich, and Jeffrey S. Simonoff. Efficiency for regularization parameter selection in penalized likelihood estimation of misspecified models. Journal of the American Statistical Association, 108:1031–1043, 2013.
- Friedman et al. (2010) Jerome Friedman, Trevor Hastie, and Robert Tibshirani. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1):1–22, 2010.
- Giraud et al. (2012) Christophe Giraud, Sylvie Huet, and Nicolas Verzelen. High-dimensional regression with unknown variance. Statistical Science, 27(4):500–518, 2012.
- Greenshtein and Ritov (2004) Eitan Greenshtein and Ya’acov Ritov. Persistence in high-dimensional linear predictor selection and the virtue of overparametrization. Bernoulli, 10(6):971–988, 2004.
- Homrighausen and McDonald (2013) Darren Homrighausen and Daniel J. McDonald. The lasso, persistence, and cross-validation. In Proceedings of The 30th International Conference on Machine Learning, pages 1031–1039, 2013.
- Homrighausen and McDonald (2014) Darren Homrighausen and Daniel J. McDonald. Leave-one-out cross-validation is risk consistent for lasso. Machine Learning, 97(1-2):65–78, 2014.
- Homrighausen and McDonald (2016) Darren Warren Homrighausen and Daniel J. McDonald. Risk estimation for high-dimensional lasso regression, 2016. URL http://arxiv.org/abs/1602.01522.
- Kato (2009) Kengo Kato. On the degrees of freedom in shrinkage estimation. Journal of Multivariate Analysis, 100(7):1338–1352, 2009.
- Kim et al. (2012) Yongdai Kim, Sunghoon Kwon, and Hosik Choi. Consistent model selection criteria on high dimensions. The Journal of Machine Learning Research, 13(1):1037–1057, 2012.
- Knight and Fu (2000) Keith Knight and Wenjiang Fu. Asymptotics for lasso-type estimators. Annals of Statistics, 28(5):1356–1378, 2000.
- Lecué and Mitchell (2012) Guillaume Lecué and Charles Mitchell. Oracle inequalities for cross-validation type procedures. Electronic Journal of Statistics, 6:1803–18374, 2012.
- Leng et al. (2006) Chenlei Leng, Yi Lin, and Grace Wahba. A note on the lasso and related procedures in model selection. Statistica Sinica, 16(4):1273–1284, 2006.
- Meinshausen (2007) Nicolai Meinshausen. Relaxed lasso. Computational Statistics & Data Analysis, 52(1):374–393, 2007.
- Meinshausen and Bühlmann (2006) Nicolai Meinshausen and Peter Bühlmann. High-dimensional graphs and variable selection with the lasso. The Annals of Statistics, 34(3):1436–1462, 2006.
- Meinshausen and Yu (2009) Nicolai Meinshausen and Bin Yu. Lasso-type recovery of sparse representations for high-dimensional data. The Annals of Statistics, 37(1):246–270, 2009.
- Nardi and Rinaldo (2008) Yuval Nardi and Alessandro Rinaldo. On the asymptotic properties of the group lasso estimator for linear models. Electronic Journal of Statistics, 2:605–633, 2008.
- Negahban et al. (2012) Sahand Negahban, Pradeep Ravikumar, Martin J Wainwright, and Bin Yu. A unified framework for high-dimensional analysis of -estimators with decomposable regularizers. Statistical Science, 27:538–337, 2012.
- Osborne et al. (2000) Michael R. Osborne, Brett Presnell, and Berwin A. Turlach. On the lasso and its dual. Journal of Computational and Graphical statistics, 9(2):319–337, 2000.
- Saumard (2011) Adrien Saumard. The slope heuristics in heteroscedastic regression, 2011. URL http://arxiv.org/abs/1104.1050.
- Schwarz (1978) G. Schwarz. Estimating the dimension of a model. The Annals of Statistics, 6:461–464, 1978.
- Shao (1993) Jun Shao. Linear model selection by cross-validation. Journal of the American Statistical Association, 88:486–494, 1993.
- Stone (1974) M. Stone. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society. Series B (Methodological), 36(2):111–147, 1974.
- Stone (1977) M. Stone. Asymptotics for and against cross-validation. Biometrika, 64(1):29–35, 1977.
- Sun and Zhang (2012) Tingni Sun and Cun-Hui Zhang. Scaled sparse linear regression. Biometrika, 99(4):879–898, 2012.
- Tibshirani (1996) Robert Tibshirani. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 58(1):267–288, 1996.
- Tibshirani (2011) Robert Tibshirani. Regression shrinkage and selection via the lasso: A retrospective. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(3):273–282, 2011.
- Tibshirani (2013) Ryan J. Tibshirani. The lasso problem and uniqueness. Electronic Journal of Statistics, 7:1456–1490, 2013.
- Tibshirani and Taylor (2012) Ryan J. Tibshirani and Jonathan Taylor. Degrees of freedom in lasso problems. Annals of Statistics, 40:1198–1232, 2012.
- van de Geer (2008) Sara A. van de Geer. High-dimensional generalized linear models and the lasso. The Annals of Statistics, 36(2):614–645, 2008.
- van de Geer and Bühlmann (2011) Sara A. van de Geer and Peter Bühlmann. Statistics for High-Dimensional Data. Springer Verlag, 2011.
- van der Vaart and Wellner (1996) Aad W. van der Vaart and Jon A. Wellner. Weak Convergence and Empirical Processes. Springer, New York, 1996.
- Vershynin (2012) Roman Vershynin. Introduction to the non-asymptotic analysis of random matrices. In Yonina C. Eldar and Gitta Kutyniok, editors, Compressed Sensing: Theory and Applications, pages 210–268. Cambridge University Press, 2012.
- Wainwright (2009) Martin J. Wainwright. Sharp thresholds for high-dimensional and noisy sparsity recovery using -constrained quadratic programming (lasso). IEEE Transactions on Information Theory, 55(5):2183–2202, 2009.
- Wang and Leng (2007) Hansheng Wang and Chenlei Leng. Unified LASSO estimation by least squares approximation. Journal of the American Statistical Association, 102(479):1039–1048, 2007.
- Wang et al. (2007) Hansheng Wang, Runze Li, and Chih-Ling Tsai. Tuning parameter selectors for the smoothly clipped absolute deviation method. Biometrika, 94(3):553–568, 2007.
- Wang et al. (2009) Hansheng Wang, Bo Li, and Chenlei Leng. Shrinkage tuning parameter selection with a diverging number of parameters. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71(3):671–683, 2009.
- Yuan and Lin (2006) Ming Yuan and Yi Lin. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(1):49–67, 2006.
- Zhang and Shen (2010) Yongli Zhang and Xiaotong Shen. Model selection procedure for high-dimensional data. Statistical Analysis and Data Mining: The ASA Data Science Journal, 3(5):350–358, 2010.
- Zhao and Yu (2006) Peng Zhao and Bin Yu. On model selection consistency of lasso. The Journal of Machine Learning Research, 7:2541–2563, 2006.
- Zou (2006) Hui Zou. The adaptive lasso and its oracle properties. Journal of the American Statistical Association, 101(476):1418–1429, 2006.
- Zou et al. (2007) Hui Zou, Trevor Hastie, and Robert Tibshirani. On the degrees of freedom of the lasso. The Annals of Statistics, 35(5):2173–2192, 2007.
Appendix A Appendix
To show Theorem 4, we need a few preliminary results. We will show how to rewrite the risk as a quadratic form in Section A.1. In Section A.2, we state a concentration of measure result and some standard properties of Orlicz norms. In Section A.3 we prove some useful preliminary lemmas. Lastly, in Section A.4 we prove the main theorem and corollaries.
A.1 Squared-error loss and quadratic forms
We can rewrite the various formulas for the risk from Section 2 as quadratic forms. Define the parameter to be , with associated estimator . We can rewrite Equation (3) as
| (11) |
where . Analogously, Equation (5) has the following form
where . Lastly, we rewrite Equation (6) as
| (12) |
where , , and
with .
A.2 Background Results
We use the following results in our proofs. First is a special case of Nemirovski’s inequality. See Dümbgen, van de Geer, Veraar, and Wellner (2010) for more general formulations.
Lemma 7 (Nemirovski’s inequality).
Let be independent random vectors in , for with and . Then, for any validation set and distribution for the ’s,
Also, we need the following results about the Orlicz norms.
Lemma 8 (van der Vaart and Wellner 1996).
For any -Orlicz norm with and sequence of -valued random variables
where is a constant that depends only on .
Lemma 9 (Corollary 5.17 in Vershynin 2012).
Let be iid centered random variables and let . Then for every ,
where .
A.3 Supporting Lemmas
Several times in our proof of the main results we need to bound a quadratic form given by a symmetric matrix and an estimator indexed by a tuning parameter. To this end, we state the following lemma.
Lemma 10.
Suppose and . Then
where is the entry-wise max norm.
We use Section A.2 to find the rate of convergence for the sample covariance matrix to the population covariance.
Lemma 11.
Let be an index set and let be its number of elements. If , then there exists a constant , depending only on , such that
where it is understood that .
Proof.
(Section A.3) Let be the vectorized version of the zero-mean matrix . Then, by Jensen’s inequality
Using Section A.2 with and writing we find
Note that is the Orlicz norm induced by the measure and the third inequality follows by Section A.2. ∎
Corollary 12.
By the definition of ,
where is an absolute constant and .
Proof.
A.4 Proof of Main Results
Theorem 4.
Let be any two sets. Then we can make the following decomposition:
| (13) |
Also,
| (14) |
where we use the notation . Now, for any , by the definition of , and thus .
Final predictor and cross-validation risk :
Using the notation introduced in Section A.1, note that by equations (11) and (12)
Likewise,
The last inequality follows as is chosen to minimize , and so for any ,
| (16) |
Cross-validation risk and empirical risk :
Due to the discussion following Equation (14), it is sufficient to bound instead. Recall that
Then,
where the inequality follows by Section A.3 and the fact that is chosen to minimize , which implies
| (18) |
As before,
We can use a straight-forward adaptation of Section A.3 to show that
Therefore,
| (19) |
Empirical risk and expected risk
The proof of these results is given by Greenshtein and Ritov (2004). We include a somewhat different proof for completeness. Observe
Using Section A.3 (See Section A.1 for notation)
Therefore,
| (20) |
The proof follows by combining Equation (13) with Equation (15) and using the bounds from Equations (17), (19), and (20).
Lastly, there are the various constants incurred in the course of this proof. In Section A.2, the constant can be chosen arbitrarily small based on inspecting the proof of Lemma 2.2.2 in van der Vaart and Wellner (1996). As this constant premultiplies every term in and , we can without loss of generality set the constant equal to one. For instance, in Section A.3, the constant is upper bounded by . This constant can be taken arbitrarily small by choosing small enough. ∎
Lemma 13.
Define the set where is the normalizing rate defined in Section 3.2 and . Then, .
Proof.
Lemma 14.
Define the set If , then, for all ,
Proof.
Section 3.2.
For the , the result is nearly immediate as we are considering the same constraint set and the same search space for the tuning parameter . However, in Equations (16) and (18), we rely on the empirical minimizer. The analogous results here are and respectively, but this implies that (16) and (18) hold.
For the group lasso with , we have so that Section A.4 still applies with as before. We note that in this case, the oracle group linear model is restricted to the ball rather than the larger set . ∎