Rmote Sensing Image Change Detection
With Graph Interaction
Abstract
Modern remote sensing image change detection (CD) has witnessed substantial advancements by harnessing the potent feature extraction capabilities of CNNs and Transforms. Yet, prevailing change detection techniques consistently prioritize extracting semantic features related to significant alterations, overlooking the viability of directly interacting with bitemporal image features.In this letter, we propose a bitemporal image graph Interaction network for remote sensing change detection, namely BGINet-CD. More specifically, by leveraging the concept of non-local operations and mapping the features obtained from the backbone network to the graph structure space, we propose a unified self-focus mechanism for bitemporal images. This approach enhances the information coupling between the two temporal images while effectively suppressing task-irrelevant interference.Based on a streamlined backbone architecture, namely ResNet18, our model demonstrates superior performance compared to other state-of-the-art methods (SOTA) on the GZ CD dataset. Moreover, the model exhibits an enhanced trade-off between accuracy and computational efficiency, further improving its overall effectiveness.
Index Terms:
Change detection, deep learning, Graph convolutional, remote sensing (RS) images.I Introduction
THE change detection is an important research topic in remote sensing, as it aims to identify changes that occur between two images acquired at different times in the same geographical location. With the growing availability and utilization of remote sensing satellites, change detection has found widespread application in various fields. It is commonly used for monitoring urban sprawl[11], assessing damage caused by natural disasters[10], and conducting surveys of urban and rural areas[9].Multi-temporal remote sensing images often contain a variety of interferences due to different imaging conditions and shooting times. These interferences include spectral differences caused by varying light intensity and seasonal changes, as well as differences in shooting angles that result in varying shapes of buildings within the scene. Consequently, these factors can introduce pseudo-change during the detection process.
A strong model should accurately identify unrelated disturbances in diachronic images and distinguish natural changes from complex uncorrelated ones[2]. Existing methods for change detection can be broadly categorized into two main groups: traditional change detection methods and deepl learning methods. Traditional change detection methods encompass various approaches, including algebraic operation-based, transform-based, and classification-based methods. Algebraic operation-based methods involve direct pixel-wise comparison in multi-temporal images and the selection of an appropriate threshold to classify pixels as changed or unchanged. Image transformation techniques, such as principal component analysis (PCA)[3] and change vector analysis[4], are also commonly used. On the other hand, machine learning-based methods, such as support vector machines, random forests, and kernel regression, have emerged as alternative approaches in recent years.
Deep learning-based approaches have gained prominence due to their powerful nonlinear feature extraction capabilities. These approaches have witnessed the proposal of several attention mechanisms, such as spatial attention[8], channel attention[7], and self-attention[12], aimed at obtaining improved feature representations. Chen et al. effectively modeled the context in the visual space-time domain by visually representing the high-level concept of interest change[2]. Fang et al. addressed the exact spatial location loss from continuous sampling by combining DenseNet and NestedUnet[5]. Additionally, Chen et al. proposed a novel edge loss that enhances the network’s attention to details like boundary regions and small regions[6].
Although the methods above have shown promising results, none have explored the possibility of feature interaction between bi-temporal images prior to extracting different features. Drawing inspiration from non-local operations and DMINet [13], we have proposed a bi-temporal image graph Interaction network(BGINet) to facilitate feature interaction between bi-temporal images. This approach enhances the information coupling between bi-temporal images by extracting bi-temporal features using a backbone network and routing them through a graph interaction module, effectively suppressing uncorrelated changes.
To demonstrate the effectiveness of our method, we have utilized a simple backbone network (ResNet18) in BGINet-CD. Initially, the features obtained from the backbone network are subjected to soft clustering, with each cluster being mapped to a vertex in the graph space. The Graph Interaction Module (GIM) captures the coupling relationship between the bi-temporal images, thus enhancing the information coupling. Finally, the clusters are reprojected to their original spatial coordinates.
The contributions of this letter are mainly as follows:
-
1.
We propose BGINet-CD, a graph convolutional neural network for remote sensing change detection, which effectively enhances the information coupling between diachronic images.
-
2.
The introduction of the GIM module enables the capture of the coupling relationship between biphasic images, enhancing information coupling and suppressing uncorrelated changes.
-
3.
We conducted quantitative and qualitative experiments on two datasets, our experiments demonstrated that our proposed BGINet-CD achieves a desirable balance between accuracy and efficiency, achieving state-of-the-art performance on the GZ dataset.Code is available at https://github.com/JackLiu-97/BGINet.git.
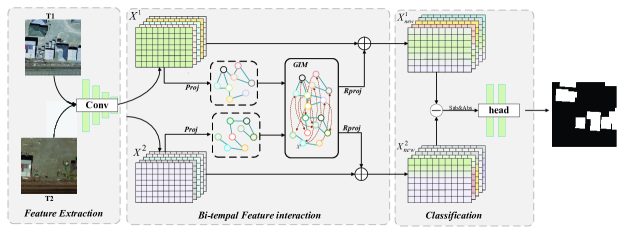
II Proposed Method
II-A Overall Architecture
Figure 1 illustrates the architecture of the proposed BGINet. The network comprises two main components: a generic feature extractor and a Bitemporal Graph Interaction Module. To ensure model efficiency, we utilize the first three stages of ResNet-18 [15] as the generic feature extractor. The Graph Interaction Module (GIM) branch takes the bitemporal generic features extracted by the feature extractor as input and maps them into a graph structure. Inspired by nonlocal operations, we incorporate self-attentiveness in the graph space to efficiently capture remote dependencies between bitemporal features. The evolved bitemporal features are then integrated with the original features. Finally, a 1 × 1 convolutional layer with a sigmoid activation function is applied to obtain the final difference map, which serves as an indicator of change.
II-B Graph Interaction Module (GIM)
Here, we detail the Graph Interaction Module (GIM). As shown in Figure 2, GIM are composed of three operations, namely, graph projection, graph interaction, and graph reprojection. Given bitemporal 2D feature map , , , denotes the d-dimensional feature at of bitemporal. The graph embedding can be denoted as or , where , is a set of nodes, , is the feature matrix, and , is the affinity matrix between the nodes.
1) Graph Projection: To establish a correspondence between maps and , we perform a feature mapping to obtain graphs and . In this mapping, pixels with similar features are assigned to the same vertex in the graph. For simplicity, let’s consider the feature mapping of the time phase as an example. Following the approach in [14], we parameterize two matrices and , where represents the number of vertices, which can be pre-specified.
Each row of serves as the anchor point for vertex . To compute the soft assignment of feature vector to , we use the following equation:
| (1) |
In this equation, is the row vector of and is constrained to the range using a sigmoid function. The numerator measures the similarity between the feature vector and the anchor point, while the denominator normalizes the assignment across all vertices. Next, we encode the vertex feature matrix using the corresponding pixel features. For vertex , we compute , which represents the weighted average of the residuals between feature vectors and . Then, we normalize to obtain , the unit vector that forms the row vector of the feature matrix of graph :
| (2) |
Finally, the graph affinity matrix is computed using the equation:
| (3) |
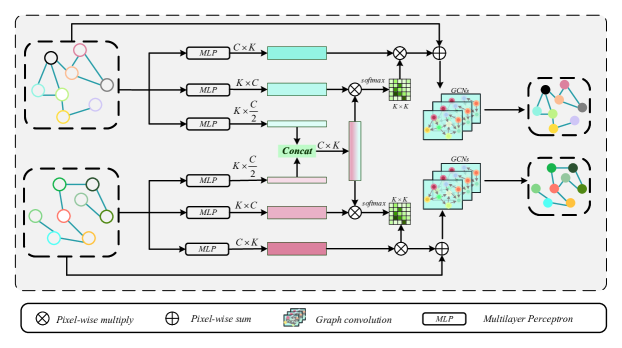
2) Graph Interaction: The proposed GIM receiver map embeddings , and as inputs form the feature mapping of time phase and time phase, respectively, and models the between graph interaction and guides the inter-graph message passing from to and to . This goal leads us to take inspiration from non-local operations and DMINet [51] and compute inter-graph dependencies with a concern mechanism. This operation of ours significantly reduces the number and computational complexity of parameters and achieves better results
GIM models the betweengraph interaction and guides the inter-graph message passing from to or from to As shown in Figure3,we use different multi-layer perceptrons (MLPs) to transform to the query graph ,key graph and value graph transform to the query graph ,key graph and value .Next, we unify , as:
| (4) |
Then, the similarity matrix and is calculated by a matrix multiplication as:
| (5) | |||
| (6) |
where . After that, we can transfer semantic information from to and to by
| (7) | |||
| (8) |
After performing inter-graph interaction, we conduct the intra-graph reasoning by taking and as inputs to obtain enhanced graph representations.
| (9) | |||
| (10) |
3) Graph Reprojection: To map the enhanced graph representations back to the original coordinate space, we revisit the assignments from the graph projection step.
| (11) | |||
| (12) |
III Experiments and Results
III-A Experimental Dataset and Parameter Setting
The WHU Building Change Detection Dataset[16]:The data consists of two aerial images of two different time phases and the exact location, which contains 12796 buildings in 20.5 km2 with a resolution of 0.2 m and a size of 32570x15354. We crop the images to 256x256 size and randomly divide the training, validation, and test sets: 6096/762/762.
Guangzhou Dataset(GZ-CD)[17]: The dataset was collected from 2006-2019, covering the suburbs of Guangzhou, China, and to facilitate the generation of image pairs, the Google Earth service of BIGEMAP software was used to collect 19 seasonally varying VHR image pairs with a spatial resolution of 0.55 m and a size range of 1006x1168 pixels to 4936x5224.We crop the images to 256x256 size and randomly divide the training, validation, and test sets: 2876/353/374.
In the experiment, the number of vertices is set to 32. We utilize the AdamW optimizer with weight decay 1e-4 and a polynomial schedule, where the initial learning rate is set to 0.0004. The total number of iterations is set to 100. The GPU used for the experiment is an NVIDIA V100.In this experiment, we employ the joint loss function consisting of Focal loss and Dice loss. For Focal loss, we set the parameters and to 2.0 and 0.2, respectively.The overall loss function is formulated as follows:
| (13) |
Here, represents the sigmoid activation function. We denote the model prediction as , and and as the coefficients of the Focal loss and Dice loss, respectively. In this experiment, we set and to 0.5 and 1, respectively.
III-B Experimental Results and Comparison
Our comparison experiments evaluate the trade-off between accuracy, number of parameters, and floating-point operations (FLOP). The quantitative results for the two datasets are presented in Table I and Table II, respectively. The best-performing model in each column is highlighted in bold, while the second-best model is underlined. The tables provide a comprehensive view of the performance metrics, allowing us to analyze the accuracy and efficiency of different models
| Model | Precision (%) | Recall (%) | F1-score | Params (m) |
| FC-EF[19] | 91.19 | 85.30 | 88.15 | 1.1 |
| FC-Siam-conc[19] | 69.04 | 84.93 | 76.17 | 1.55 |
| FC-Siam-diff[19] | 60.66 | 91.24 | 72.87 | 1.35 |
| STANet[18] | 91.73 | 73.39 | 81.54 | 12.18 |
| SNUNet | 75.23 | 89.12 | 81.59 | 12.04 |
| BIT | 87.44 | 90.24 | 88.82 | 3.55 |
| DMINet | 93.84 | 86.25 | 88.69 | 6.24 |
| BGINEt | 91.84 | 90.22 | 91.02 | 2.88 |
| Model | Precision (%) | Recall (%) | F1-score | Params (m) |
| FC-EF[19] | 85.92 | 78.43 | 82.00 | 1.1 |
| FC-Siam-conc[19] | 87.63 | 83.50 | 85.52 | 1.55 |
| FC-Siam-diff[19] | 90.47 | 79.45 | 84.60 | 1.35 |
| STANet[18] | 88.40 | 78.84 | 83.35 | 12.18 |
| SNUNet | 89.61 | 84.40 | 86.92 | 12.04 |
| BIT | 86.38 | 88.60 | 87.48 | 3.55 |
| DMINet | 89.31 | 83.901 | 86.52 | 6.24 |
| BGINEt | 88.52 | 88.00 | 88.25 | 2.88 |
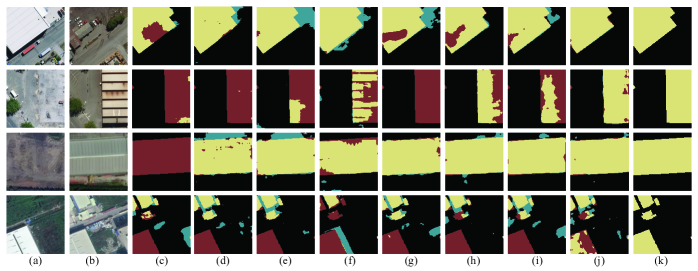
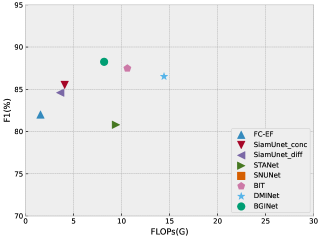
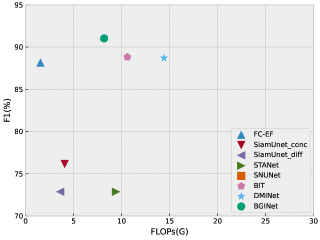
In Fig. 3 and Fig. 4, we present a tradeoff analysis between the F1 score and computational cost for various classical remote sensing image change detection methods and recently proposed methods (e.g., STANet, BIT, DMINet, etc.). These figures provide valuable insights into different approaches’ performance and computational requirements.The results indicate that while the aforementioned methods demonstrate good performance, they often have a significant computational overhead. On the other hand, baseline models like FC-EF require minimal computational resources but fall short in accuracy. Our proposed method, however, achieves a favorable balance between accuracy and computational overhead.By examining the figures, it is evident that our method outperforms the baseline models in terms of accuracy while still maintaining a manageable computational cost. This highlights the effectiveness and efficiency of our approach in remote sensing image change detection tasks.
| Model | Precision (%) | Recall (%) | F1-score |
| 87.47 | 85.37 | 86.41 | |
| 88.52 | 88.00 | 88.25 | |
| 85.70 | 92.20 | 88.80 | |
| 91.84 | 90.22 | 91.02 |
III-C Ablation Experiment
To validate the effectiveness of our proposed BGINet, we conducted ablation experiments on network knots using two publicly available datasets. The results of these experiments are presented in Table 3. As a baseline model, we selected resnet18 and utilized only the first three stages of the network. Upon introducing GIM (Graph Interaction Module) on the GZ-CD dataset, we observed improved precision, recall, and F1 scores by , respectively. On the WHU dataset, although there was a decrease in the recall by , we observed improvements in precision and F1 scores by and , respectively. These findings highlight the positive impact of our proposed BGINet, particularly when integrated with GIM, in enhancing the performance of remote sensing image change detection. The ablation experiments demonstrate the introduced graph interaction module’s significance and contribution to improving precision, recall, and overall F1 score on both datasets. Overall, the results affirm the effectiveness of our approach and its potential for advancing the field of remote sensing image change detection.
IV Conclusion
In this letter, we introduce a novel method for improving change detection accuracy in dual-temporal images. By mapping the image features into the graph space and utilizing the Graph Interaction Module (GIM), we enable effective feature interaction and mitigate the influence of pseudo-change. Our proposed approach achieves a lightweight implementation, offering a favorable tradeoff between accuracy, number of parameters, and computational complexity. Experimental results on two publicly available datasets demonstrate the effectiveness of our model, with our approach achieving state-of-the-art performance on the GZ-CD dataset.
References
- [1] M. Liu, Z. Chai, H. Deng, and R. Liu, “A cnn-transformer network with multiscale context aggregation for fine-grained cropland change detection,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 15, pp. 4297–4306, 2022, doi:10.1109/JSTARS.2022.3177235.
- [2] H. Chen, Z. Qi, and Z. Shi, “Remote sensing image change detection with transformers,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–14, 2022, doi:10.1109/TGRS.2021.3095166.
- [3] T. Celik, “Unsupervised change detection in satellite images using principal component analysis and -means clustering,” IEEE Geoscience and Remote Sensing Letters, vol. 6, no. 4, pp. 772–776, 2009, doi:10.1109/LGRS.2009.2025059.
- [4] N. Zerrouki, F. Harrou, and Y. Sun, “Statistical monitoring of changes to land cover,” IEEE Geoscience and Remote Sensing Letters, vol. 15, no. 6, pp. 927–931, 2018, doi:10.1109/LGRS.2018.2817522.
- [5] S. Fang, K. Li, J. Shao, and Z. Li, “Snunet-cd: A densely connected siamese network for change detection of vhr images,” IEEE Geoscience and Remote Sensing Letters, vol. 19, pp. 1–5, 2022, doi:10.1109/LGRS.2021.3056416.
- [6] H. Chen, F. Pu, R. Yang, R. Tang, and X. Xu, “Rdp-net: Region detail preserving network for change detection,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–10, 2022, doi:10.1109/TGRS.2022.3227098.
- [7] J. Hu, L. Shen, and G. Sun, “Squeeze-and-excitation networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 7132–7141.
- [8] S. Woo, J. Park, J.-Y. Lee, and I. S. Kweon, “Cbam: Convolutional block attention module,” in Proceedings of the European conference on computer vision (ECCV), 2018, pp. 3–19.
- [9] M. Liu, Z. Chai, H. Deng, and R. Liu, “A cnn-transformer network with multiscale context aggregation for fine-grained cropland change detection,” IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 15, pp. 4297–4306, 2022, doi:10.1109/JSTARS.2022.3177235.
- [10] A. Abuelgasim, W. Ross, S. Gopal, and C. Woodcock, “Change detection using adaptive fuzzy neural networks: Environmental damage assessment after the gulf war,” Remote Sensing of Environment, 1999.
- [11] A. Frick and S. Tervooren, “A framework for the long-term monitoring of urban green volume based on multi-temporal and multi-sensoral remote sensing data,” Journal of geovisualization and spatial analysis, vol. 3, no. 1, p. 6, 2019.
- [12] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” Advances in neural information processing systems, vol. 30, 2017.
- [13] Y. Feng, J. Jiang, H. Xu, and J. Zheng, “Change detection on remote sensing images using dual-branch multilevel intertemporal network,” IEEE Transactions on Geoscience and Remote Sensing, vol. 61, pp. 1–15, 2023.
- [14] Y. Li and A. Gupta, “Beyond grids: Learning graph representations for visual recognition,” in Neural Information Processing Systems, 2018.
- [15] K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- [16] S. Ji, S. Wei, and M. Lu, “Fully convolutional networks for multisource building extraction from an open aerial and satellite imagery data set,” IEEE Transactions on geoscience and remote sensing, vol. 57, no. 1, pp. 574–586, 2018.
- [17] D. Peng, L. Bruzzone, Y. Zhang, H. Guan, H. Ding, and X. Huang, “Semicdnet: A semisupervised convolutional neural network for change detection in high resolution remote-sensing images,” IEEE Transactions on Geoscience and Remote Sensing, vol. 59, no. 7, pp. 5891–5906, 2021, doi:10.1109/TGRS.2020.3011913.
- [18] H. Chen and Z. Shi, “A spatial-temporal attention-based method and a new dataset for remote sensing image change detection,” Remote Sensing, vol. 12, no. 10, 2020, doi:10.3390/rs12101662. [Online]. Available: https://www.mdpi.com/2072-4292/12/10/1662
- [19] R. Caye Daudt, B. Le Saux, and A. Boulch, “Fully convolutional siamese networks for change detection,” in 2018 25th IEEE International Conference on Image Processing (ICIP), 2018, pp. 4063–4067, doi:10.1109/ICIP.2018.8451652.