Robust Change Detection Based on Neural Descriptor Fields
Abstract
The ability to reason about changes in the environment is crucial for robots operating over extended periods of time. Agents are expected to capture changes during operation so that actions can be followed to ensure a smooth progression of the working session. However, varying viewing angles and accumulated localization errors make it easy for robots to falsely detect changes in the surrounding world due to low observation overlap and drifted object associations. In this paper, based on the recently proposed category-level Neural Descriptor Fields (NDFs), we develop an object-level online change detection approach that is robust to partially overlapping observations and noisy localization results. Utilizing the shape completion capability and -equivariance of NDFs, we represent objects with compact shape codes encoding full object shapes from partial observations. The objects are then organized in a spatial tree structure based on object centers recovered from NDFs for fast queries of object neighborhoods. By associating objects via shape code similarity and comparing local object-neighbor spatial layout, our proposed approach demonstrates robustness to low observation overlap and localization noises. We conduct experiments on both synthetic and real-world sequences and achieve improved change detection results compared to multiple baseline methods. Project webpage: http://yilundu.github.io/ndf_change
I Introduction
The ability to perform robust long-term operations is critical for many robotics applications such as room scanning and household cleaning. As these tasks usually involve frequent visits to the same environment over extended periods of time, during which the environment may experience changes, robots are expected to understand these newly-emerged scene differences, e.g., the introduction and removal of a coffee mug, as they may impact the proper subsequent actions to be taken during operation.
An intuitive way to conduct change detection is to perform scene differencing between current observations and scenes reconstructed from previous sessions. Using various scene representations such as point clouds and Truncated Signed Distance Fields (TSDF), previous works detect changed areas in the environment through global point-wise or voxel-wise differencing on two scenes reconstructed and pre-aligned post hoc from sequential data [1, 2, 3]. These methods, which treat the environment as an unordered collection of points or voxels, demand high inter-session viewpoint overlap and are susceptible to noisy sensor data and localization errors. Considering the fact that changes take place at the object level, recent works [4, 5] explore the use of semantic consistency for local object-level verification on top of the common global point- or voxel-wise scene comparison scheme. Having demonstrated improved robustness to localization errors, they are nevertheless prone to failure with noisy reconstruction input and little observation overlap, both of which are frequently encountered during online change detection tasks.
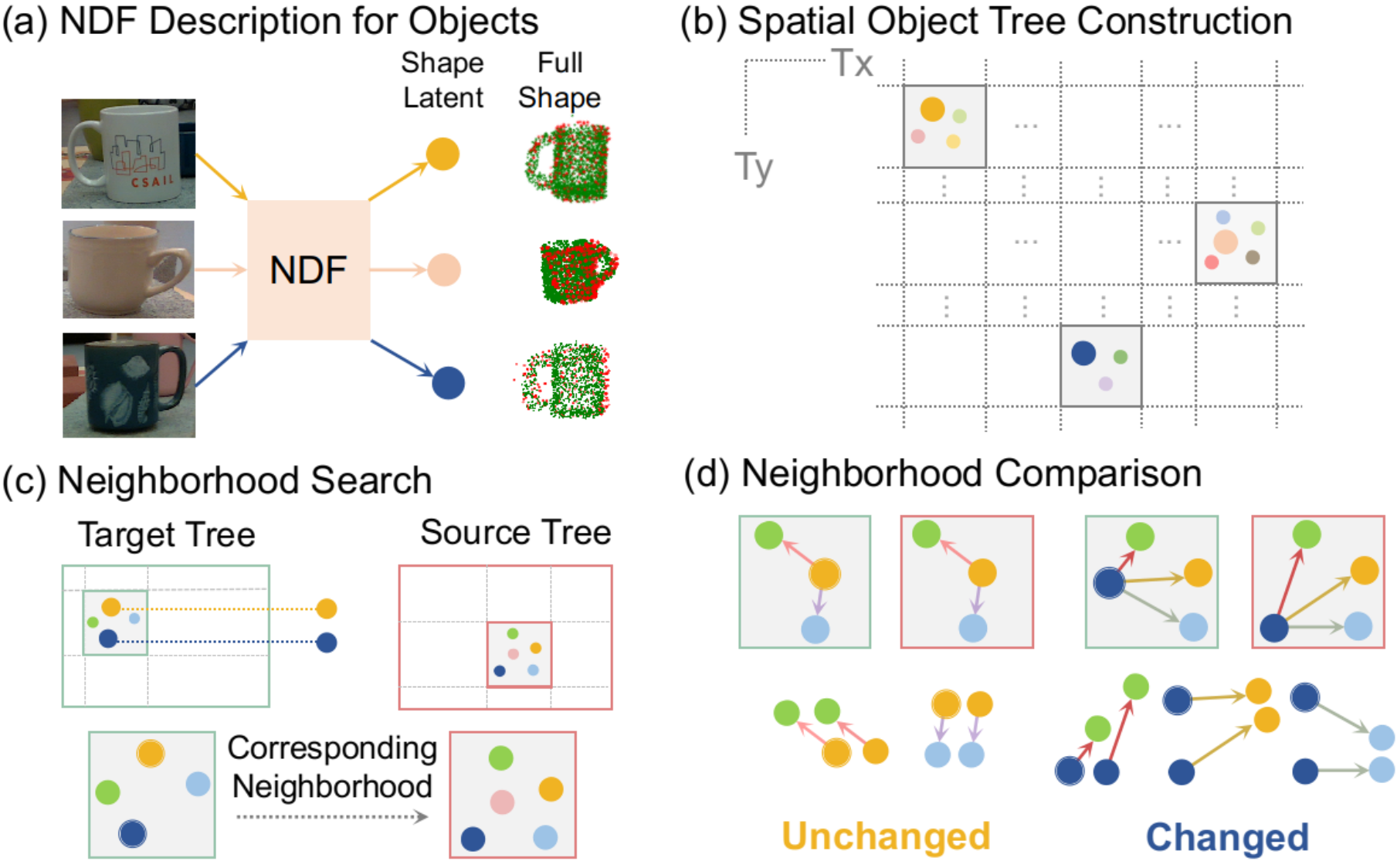
It is therefore highly desirable to seek approaches that yield consistent representations of the object surmounting viewing angle limitations, where we then adopt the recently proposed Neural Descriptor Fields (NDFs) [6]. NDFs have been developed as a category-level, -equivariant object representation for object manipulation tasks. By encoding object as a continuous -equivariant function, NDFs are able to reconstruct the full object shape through a compact shape encoding and further recover object centers (translation). Considering that NDFs are formulated to only ensure identical shape codes given rotated point clouds that are otherwise identical, we augment its shape completion capability by enforcing a new shape similarity loss with partial object observations as inputs, making it encode consistent full object shape and positions across different viewing angles.
Following the object-level interpretation of the world via NDFs-derived object representations, in this paper, we propose an object change detection approach (see Fig. 1) for mobile robots, targeting the most common online operating scenarios with high viewing angle variation, potential localization errors, and no pre-alignment tools available. Based on the -equivariance property and category-level shape completion ability of NDFs, we represent the object with a compact full shape code obtained from partial observations, and organize the objects in a spatial tree structure in terms of object centers recovered from NDFs for fast query of object neighborhoods. By associating objects through shape code similarity and decomposing the global differencing scheme into local object-neighbor layout comparison, our approach shows improved robustness to little observation overlap and localization errors. Our main contributions are as follows:
-
1.
First, we explore the use of NDFs for category-generalizable shape consistent object representation across different viewing angles.
-
2.
Next, we propose an online change detection approach based on NDF-derived object representations and local object layout comparison.
-
3.
Finally, we demonstrate the effectiveness of the proposed approach on both synthetic and real-world testing sequences featuring novel same-category object instances not seen during training time.
II Related Work
II-A Change Detection
Previous works conduct change detection based on inputs in various 2D and 3D environment representations. Given 2D image inputs, Derner et al. [7] build a visual database and compare classical 2D feature descriptors extracted from greyscale images for query and reference feature matching. For works with 3D representations, Finman et al. [1] discover new objects as changed parts of multiple depth point clouds while Herbst et al. detect changes through movement of surfaces [8]. Ambrus et al. [2] compute a meta-room static reference map based on point clouds, and discover new objects from changes via spatial clustering. Fehr et al. [3] propose a multi-layer TSDF grid structure and perform volumeric differencing for object discovery and class recognition. Langer et al. [4] combine semantic information and supporting plane information to discover objects newly introduced to the scene. Schmid et al. [5] propose a multi-TSDF panoptic mapping approach and conduct online change detection based on TSDF value comparison.
Most previous works focus on point-wise or voxel-wise differencing on pre-aligned reconstructions in an offline fashion, demanding high observation overlap and decent localization results. They therefore do not always satisfy the need for online change detection under various viewing angles, as commonly encountered during mobile robot operation.
II-B Neural Implicit Representations
Neural implicit representations have been proposed as a continuous, differentiable, and parameterized representation of 3D geometry [9, 10, 11], appearance [12, 13], and tactile properties [14] of both objects and scenes. Neural implicit representations represent shapes as continuous functions, enabling the principled incorporation of symmetries, such as equivariance [15, 6], as well as the construction of latent spaces that encode class information as well as 3D correspondences [16]. Owing to their continuous parameterized nature, several works have applied [6, 17] them to robotics tasks as intermediate object representations directly inferable from raw perception. Simenov et al. [6] show that symmetries incorporated from such a representation can generalize demonstrations of objects to novel poses, while [17, 18, 19] demonstrate their ability to be integrated with online robotic mapping tasks.
In this paper, we explore how the -equivariance of NDFs [6] enables them to represent objects from partial observations and thus allows for robust online change detection with disparate viewing angles and localization noises.
III Category-level Object Representation for Partial Observations
We base our object representation on the recently proposed Neural Descriptor Fields (NDFs) [6], a function that encodes both object shape and pose through a category-level -equivariant latent representation.
III-A Neural Descriptor Fields
NDFs consist of an encoder function , which maps a partial object point cloud into a global latent code , and a decoder function, , which maps an input point to its predicted occupancy value:
| (1) | ||||
The encoder function is constructed such that by zero-centering the input , the inferred global latent code is represented as a vector of points that is equivariant with respect to rotations of the input point cloud . This means that if a point cloud is rotated by , the inferred latent will be equivalently rotated by , as ensured via the Vector Neuron encoder layers [15]. By subtracting from the point cloud center of as the translation, we then make an -equivariant shape occupancy predictor for different points on and off .
NDFs are trained with partial object point clouds recovered from semantic-segmented RGB-D images and corresponding 3D occupancy voxelgrids of objects’ complete geometry. During training, the full model is trained to predict the complete 3D occupancy of an object using the standard cross-entropy classification loss :
| (2) |
where is a point sampled from the object occupancy grid and is the ground truth occupancy value at point .
By feeding with a query point cloud , which is obtained via uniform sampling within a large bounding box centered around , the full shape point cloud of the object can be reconstructed in terms of the predicted occupancy values:
| (3) |
where is the occupancy threshold to mark a point location as occupied.
III-B Shape Consistency
Thanks to the -equivariance of , a shape code invariant of view direction, , can then be extracted from its rotation invariant portion:
| (4) |
Ideally, the shape code, serving as a compact representation of the full object shape, should be consistently close among partial observations of the same shape from various viewing perspectives, while discriminatively far apart across observations of different shapes. While NDFs enable identical shape codes given identical point clouds that are rotated, shape consistency across partial inputs of the same shape is not inherently guaranteed.
To enforce to be a discriminative yet consistent representation for shapes seen from various viewing angles, as commonly seen during mobile robot operation, we further formulate a shape similarity loss, , fashioned after the idea of the triplet loss with [anchor, positives, negatives] for person re-identification tasks [20]. Taking a partial point cloud from object shape as the anchor , we assign it with a positive sample as the point cloud obtained from another perspective of the same object, and any other partial observations of a different object as the negative sample . With the distance metric chosen as the cosine similarity, then tends to pull the shape codes of and closer, while pushing those of and further apart:
| (5) |
Moreover, to ensure that always finds the more informative triplet, we adopt the batch hard way for triplet forming [20], i.e., using the most dissimilar and the most similar within each batch to guide training.
We hence populate each training batch with randomly generated observations of pairs of different (but likely repetitive) object shapes, which ensures that at least two observations exist for each object within the batch. Every sample within the batch is then treated as an anchor, and paired batch-wise for the most dissimilar positive and the most similar negative samples. Hence the final batch-hard shape similarity loss is formulated as:
| (6) | ||||
where is the number of objects whose observations are included in the current batch, the number of samples of object and the th observation of object within batch.
The final training objective is therefore formulated as the weighted combination of the cross entropy loss and the shape similarity loss as:
| (7) |
where is the weighting coefficient set as 0.01.
III-C Training in Simulation
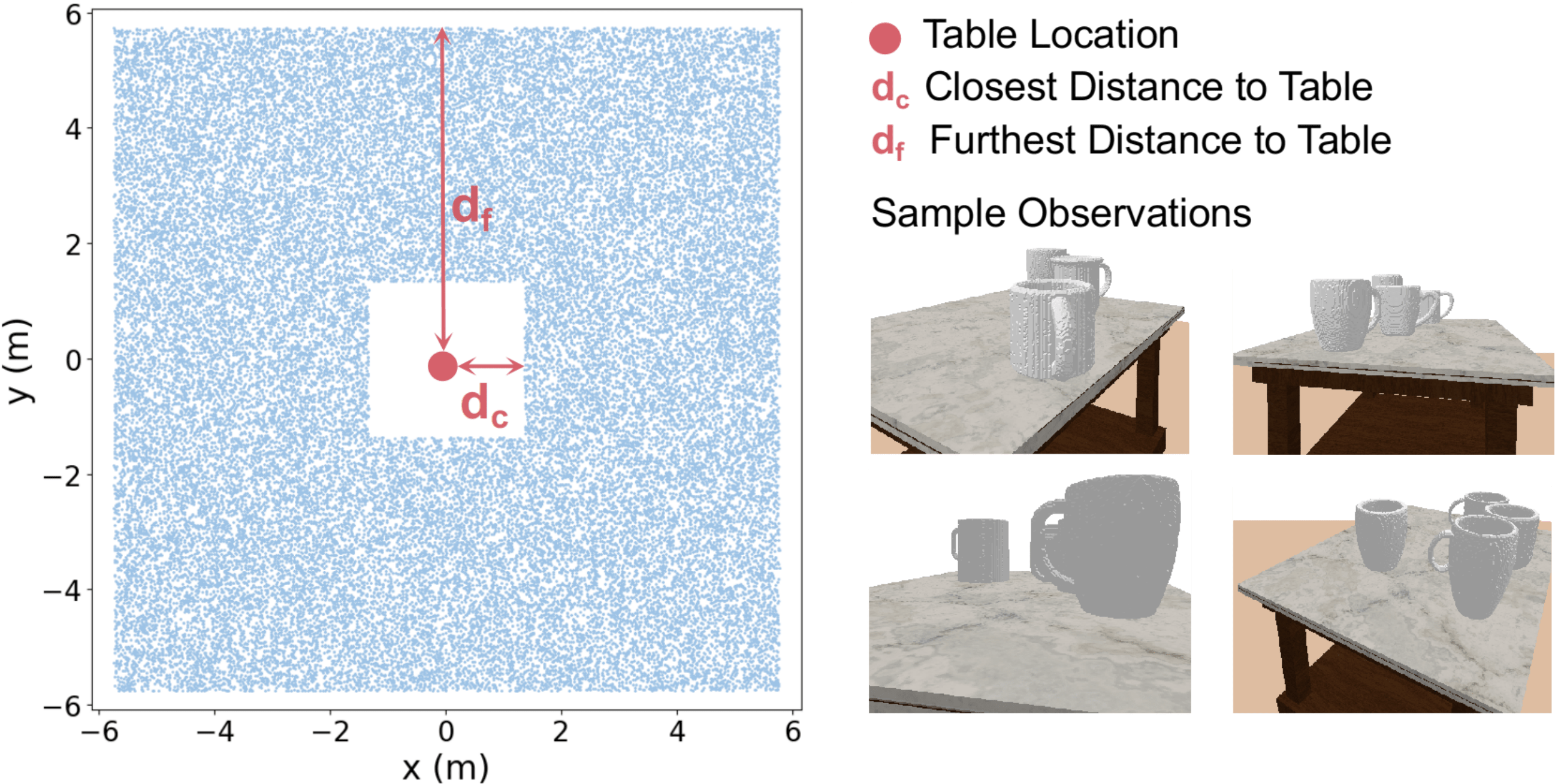
To overcome the data availability issue, we train our category-level shape-consistent NDFs fully in simulation using depth images rendered with Pybullet [21]. To consider the commonly encountered variation in viewing angles, observation distances, and occlusions during operation, for each training sample, we place a randomly-posed object on the table, along with 2-4 randomly drawn objects around it to create occlusion. The camera locations are sampled in a hollow rectangular region with the table at the center, thus accounting for both nearby and longer distance observations seen in real-world operations (see Fig. 2).
III-D Object Representation
We hence base our object representation on the shape code in (4) and the object center (translation) recovered from NDFs as , where is simply the predicted center of the reconstructed full point cloud in (3):
| (8) |
By converting into the world frame with the given camera pose, the object is characterized by for its full shape and for its global location. With the shape completion ability of NDFs, the current object representation is expected to provide a compact as well as robust way to distinguish object instances, even under varying viewing angles during robot motion.
IV NDF-based Object Change Detection
Inspired by the idea that local relative comparison is less sensitive to global localization drift than its global counterpart [4], we organize the observed object instances in a spatial object tree based on the predicted object centers, allowing for the convenient query of object neighborhoods. By comparing local neighboring object layout, we improve the method’s robustness to localization drift by avoiding direct comparison on the absolute values of localization results.
IV-A Spatial Object Tree Construction
To enable the online execution of our approach, we construct and maintain a spatial object tree in the world coordinate to organize the incoming data stream.
Built on top of the coordinate interval tree proposed in [22], our object tree comprises two translation interval trees, , in the and direction, respectively, which are initialized and updated simultaneously in the same fashion each time a new object measurement arrives. Considering that adjacent objects are located mostly on the same plane, for our case, it suffices to maintain trees only in the and direction for neighborhood query (while an extension to the direction should be straightforward).
Tree Construction. Consider for instance. divides the plane into several equi-distant interval slices in the direction (Fig. 1(b)), where each instantiated interval of fixed length is represented by a node . Each node stores a set of object instances whose translation component follows . The and are determined by the first that initializes this new node as . The new node is then inserted in the tree such that the upper interval limit of a left child is always smaller than the lower interval limit of its parent node , i.e., and similarly for the right child , we have .
Intra-tree Update. We associate the incoming object measurement with existing object instances in the tree through spatial proximity and the shape cosine similarity used in (5). We first traverse through and to locate the corresponding coordinate interval nodes and that and land in, respectively. By finding the intersection of the objects within and , we obtain the neighborhood that should be adjacent to as . The measurement is then successfully associated with an object instance in the neighborhood when:
| (9) |
where and are the maximum distance threshold and minimum shape similarity threshold for valid association. We then replace the old shape code and the recovered object center of the object with as an update if the average occupancy value of the reconstructed full shape point cloud for (calculated in (3)) is higher than that of .
IV-B NDF-based Change Detection
Given two sequences as the source and the target, we construct the source object tree in advance and perform object change detection during construction of the target tree .
Sequence Registration. We wish to apply our approach in an online mobile operating scenario where post-alignment tools or motion capture systems are not always readily available. Therefore, we first conduct a rough alignment between the target and the source sequence at the beginning of the target traverse, in the hope that target objects can correctly locate the corresponding neighborhood patch in the source so as to enable valid neighboring object comparison.
With all the shape codes of the source objects easily obtainable from , after intra-tree update for , we determine each corresponding source object for the current target object as the one sharing the highest shape code similarity among all the objects (if exist) whose shape similarity with is above (similar to (9) amid intra-tree measurement-object association).
After pairs of object correspondences have been accumulated, we apply Single Value Decomposition (SVD) with RANSAC onto the object center pairs and obtain the relative transform between the two sequences. This considers the potential inclusion of changed object instances, while assuming that they only take up a small portion of the environment to allow for alignment when the target sequence starts. Here, we set to account for transform accuracy versus timing to start change detection.
Change Detection. Rather than examining object-wise correspondences through spatial proximity and shape similarity (as in (9)), we draw support from neighboring objects and detect changes through the relative spatial layout consistency of the object within its target neighborhood and that of its corresponding neighborhood (if exists) in the source.
When an object measurement arrives, we update the by finding/instantiating the associated object instance . Considering the online operation setting, change detection is then performed on that has not been marked as changed before.
Given along with its neighborhood in the target, we find the projected location in with and query the corresponding source neighborhood . Potential object matches are found based on shape code similarity between and each in .
The most straightforward change cases are that either is empty or no matched is found in the source neighborhood, as both indicate newly added objects to new locations or else new shapes.
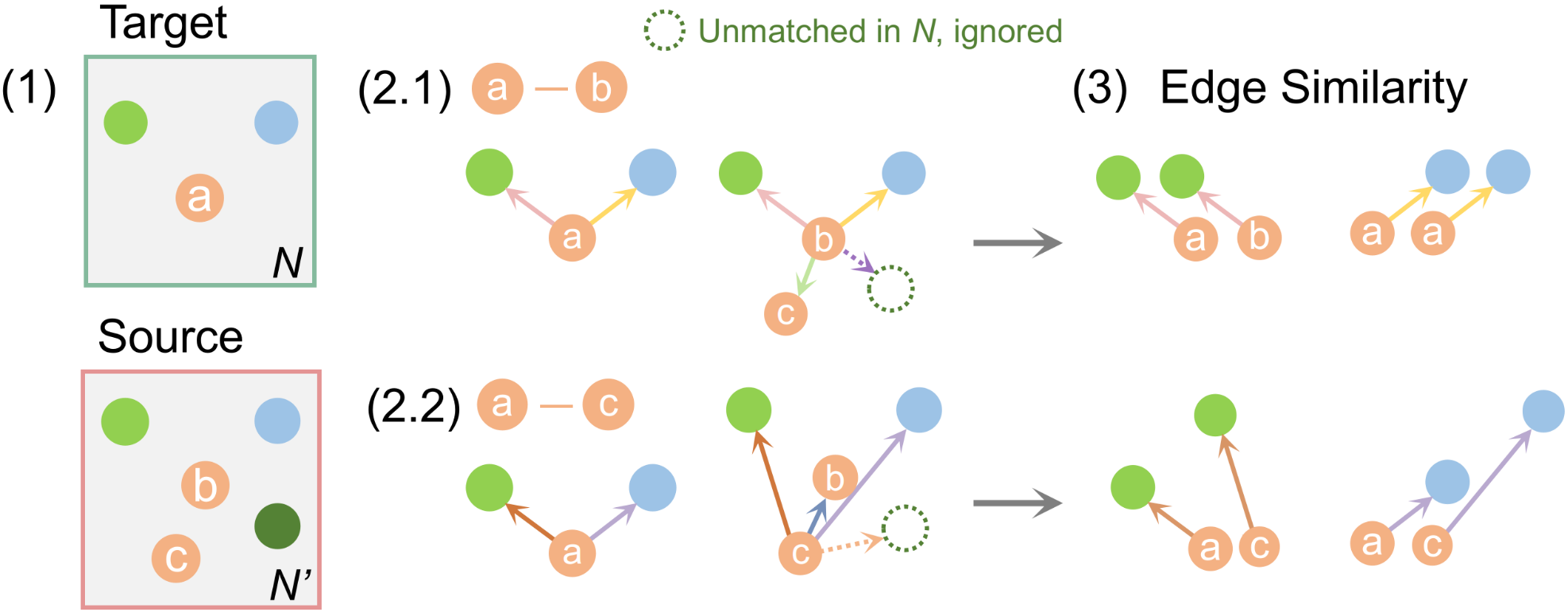
Then with object matches found within , we conduct local neighborhood comparison for each matched pair (see Fig. 3 for a concrete example). This also serves as a validation step for rejecting false positives in dealing with noise-corrupted localization. When object position changes at a scale similar to cross-session localization errors, it can be hard to determine if the absolute object center difference between is brought by actual changes (e.g., object moves within the plane) or merely localization/projection drift, while the latter can be validated through the relatively more stable inter-object spatial layout.
For each of the matched pairs, neighborhood comparison is accomplished via object graph matching.
A local object graph for object in neighborhood is constructed as a directed graph with vertices as all the objects in , , and directed edges as the object center difference pointing from to its neighbors, . Considering the limited number of objects within a neighborhood (size set similar to a tabletop), the relatively small graph size makes it possible for edge-wise matching. We find corresponding edges and through vertex shape matching. Similar edges, indicating unchanged inter-object layout, is determined by the Euclidean distance between them:
| (10) |
If at least one pair of edges is found to be closer than , i.e., at least one out of the few neighboring objects remains the same, the local object layout is marked as consistent. This implies an unchanged object, and vice versa. Note that in the rarer case when either or is the only object in the neighborhood, we revert back to the object-wise comparison in terms of spatial proximity and shape similarity.
Lastly, for detecting objects removed from the source, during target streaming we label each source object as observed if it ever participates in shape matching with any target objects, then removed objects can be found after the target sequence finishes as those observed but never matched with a target object.
V Experiments and Results
Targeting robust online change detection in the face of little observation overlap and localization errors, we would like to answer two questions: (1) Can we use the shape-consistent NDF-based representation as a valid category-level object representation that robustly generalizes to unseen object instances under partial observations? (2) Can our change detection approach perform well on sequences with little observation overlap and demonstrate robustness to localization errors? We evaluate our approach on both synthetic and real-world sequences consisting of various mug instances, where mugs are added, removed, and switched places between sequences.
V-A Datasets
To better examine the effectiveness of our category-level object representation and the change detection approach built on top of it, we choose to have our testing sequences composed of objects from the same category. We hence design two pairs of testing sequences, in simulation and in real world, respectively, featuring coffee mugs of diverse shapes observed from distinct viewing angles. Considering the extensive multi-category results reported in relevant works [6, 23], we argue that the effectiveness of our approach should be extendable to the multi-category case by incorporating more object categories into the training data.

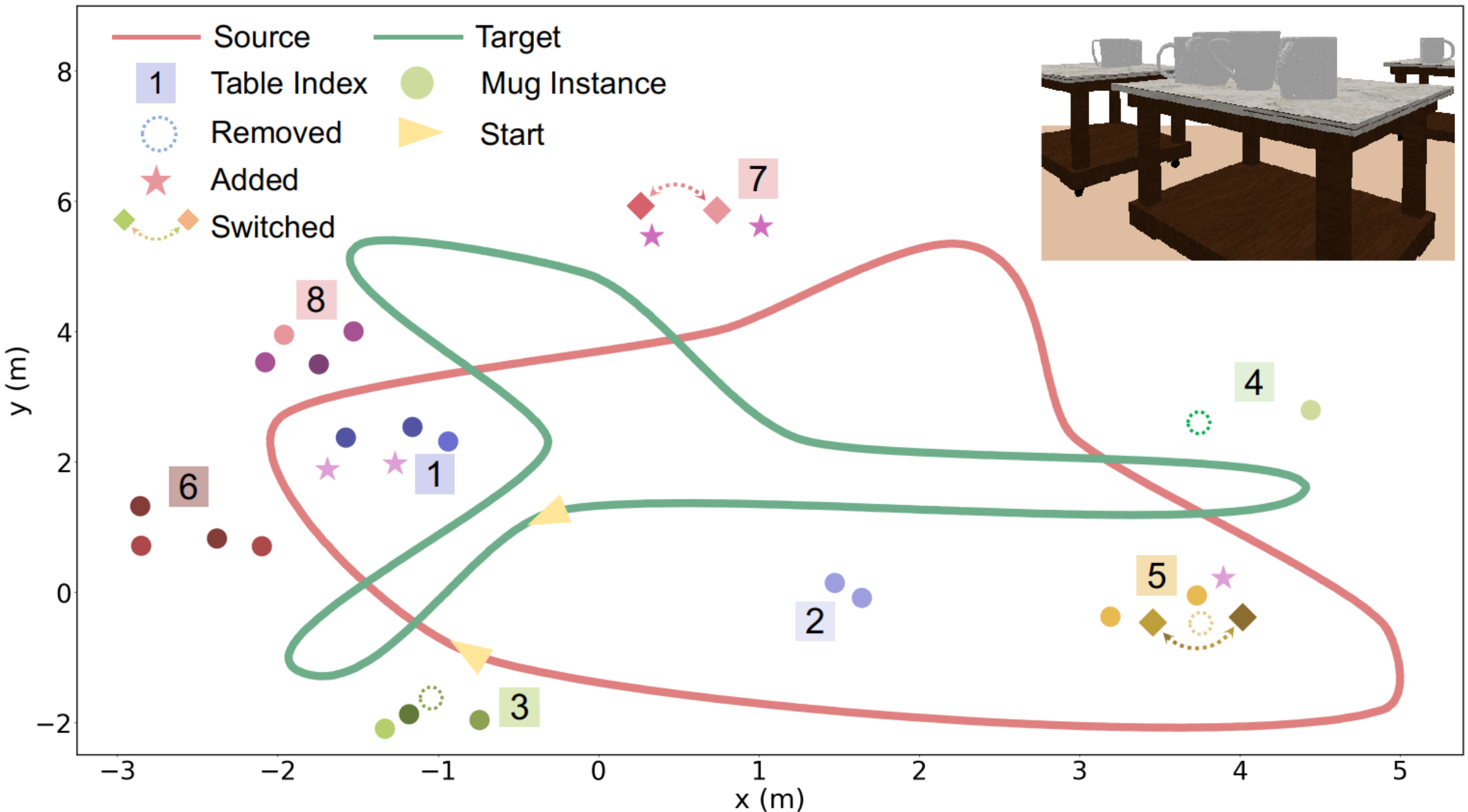
Synthetic Sequences. We set up an environment in Pybullet with 35-40 instances of 20 ShapeNet [24] mugs models scattered around eight tables and obtain RGB-D images along with segmentation masks from two preset camera trajectories. The mug models are unseen by NDFs during training. Each table supports 3-5 mugs with mugs newly added, removed, or switched locations, creating in total 12 changes between the two sessions. The two camera trajectories are designed such that the camera always faces towards the nearest table, prompting less observation overlap between sequences around table 1,2, and 5 (see Fig. 4).
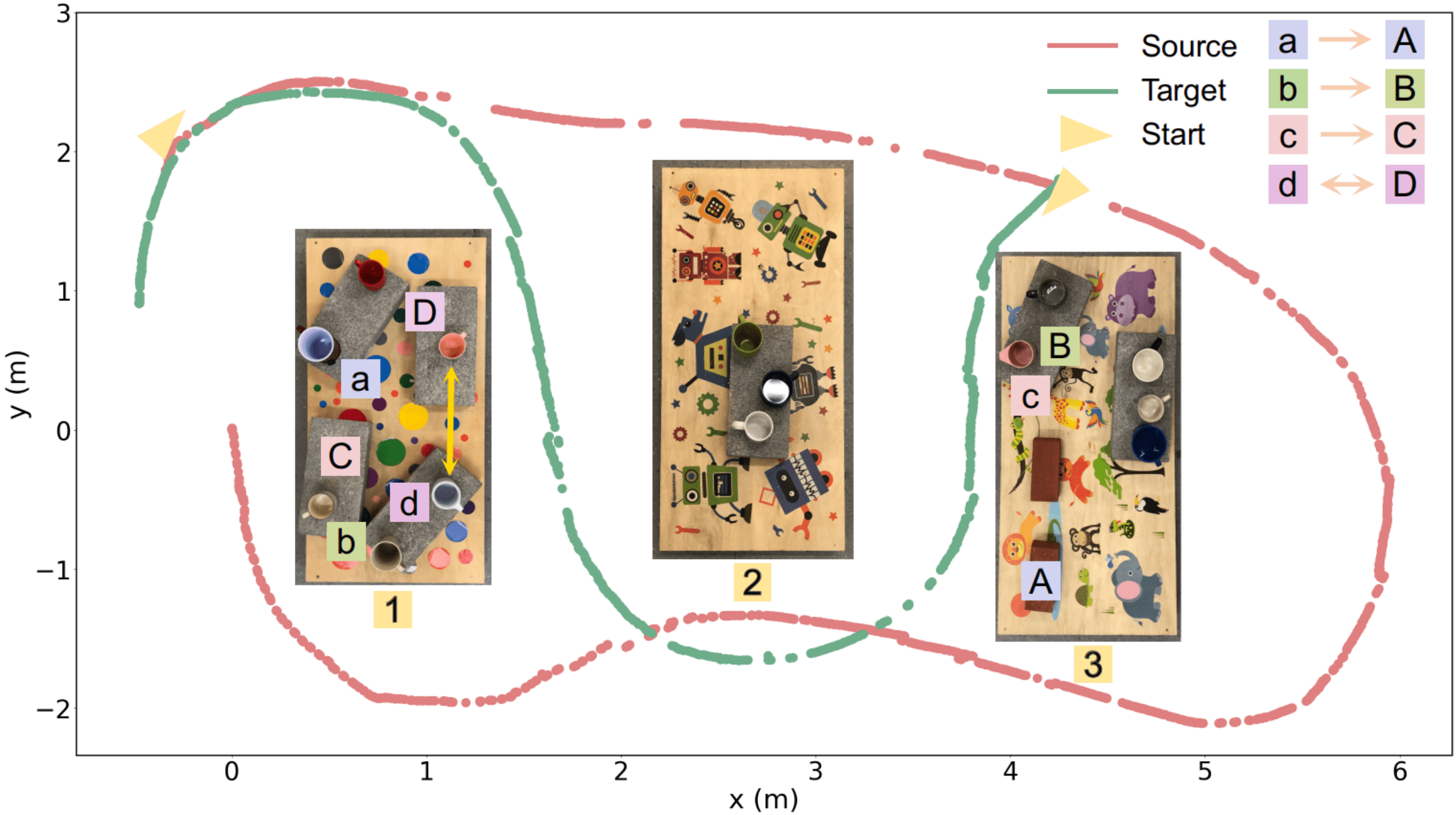
Real-world Sequences. We collect two sequences featuring 14 mugs of diverse shapes randomly placed on three rectangular tables. We mount an Intel RealSense L515 camera onto a Jackal robot close to mugs’ height and collect RGB-D data with the trajectories shown in Fig. 5. The camera trajectories are recovered using ORB-SLAM3 [25]. Since the camera is mounted facing sideways, while the camera circles around table 1, 2, 3 in the source, it only weaves through table 1 and 3 in the target, thereby creating observation disparity on mugs along the inner side of table 1 and 3.
V-B Metrics
We adopt the commonly used precision and recall rate at the object level, i.e., the number of objects, for evaluation. We report the number of correctly detected changes (true positives, TP), falsely detected changes (false positives, FP), and undetected changes (false negatives, FN). Precision and recall rate are computed as and .
V-C Implementation Details
To train NDFs using an occupancy network, we set the camera-table distances as 0.2 m and 5 m and generate 50,000 RGB-D partial observations with 94 ShapeNet [24] mug models following the sample generation strategy in III-C. Partial object point clouds are obtained by extracting corresponding depth points in the camera frame indicated by the segmentation masks on RGB images. We build our model upon the network implementation provided by [6] and train it on two NVIDIA RTX 3090 GPUs using a learning rate of with the Adam optimizer. The length of the interval tree is set to be 1.2 m and 1.6 m for the synthetic and real-world sequence, respectively, intending to group most objects on the same table plane. For parameters in IV, we set 0.9, 0.02 m, and 0.03 m.
V-D Generalization to Unseen Instances
To demonstrate the robust generalization of the shape-consistent NDFs to unseen object instances under various viewing angles, in Fig. 6, we render the reconstructed 3D shapes of five mugs drawn from the synthetic and real-world testing sequences. The three views are selected in the hope of representing some of the most typical perspectives when observing a mug, e.g., handles visible in different directions and handle obscured. We can conclude that despite the variety of the selected mug shapes, the shape-consistent NDFs still demonstrate satisfactory performance in encoding and completing the full shape under varying viewing angles, justifying the adoption of NDF-derived object representation in our change detection task.
This can be attributed to the fact that by learning purely from geometric structures embedded in the partial point clouds, NDFs are able to transfer this structural knowledge to unseen instances regardless of object color and texture. We also include cases with occlusion and shape ambiguity. For occluded observations, as shown in the first two columns of “View 2” and “View 3” , we can still see decent reconstruction results by virtue of the occlusion scenes incorporated in the training data. For the case of shape ambiguity, i.e., the handle is obscured in the second and last column of “View 2”, the major body parts of the mugs are still reconstructed reasonably well. While the handle location was incorrectly predicted, such mistakes only result in negligible errors to object center recovery.
V-E Results on Change Detection
We further present the change detection results on the two sets of testing sequences based on our proposed approach and compare them to two baselines.
The first baseline is the typical nearest neighboring point search (NN) commonly used for offline scene differencing [4, 2]. Given two spatially aligned observations and , the change point set of w.r.t is found as . We adapt it to the object-level and define that an object is changed if a certain proportion of its target point cloud finds no neighbors in the source. To make the results interpretable to online object-level change detection evaluation, we mark an object as changed the first time during data streaming it is detected as changed, as during real-world operation, corresponding actions will be taken right after changes are detected and usually no correction can be made for false positives.
The second baseline is the recently proposed panoptic multi-TSDFs (PMT) mapping method by Schimd et al. [5], which represents panoptic entities as TSDF submaps and captures online object-level scene changes based on voxel-wise weight counting informed by TSDF value differences. After tuning the default parameters for better performance, we count the total number of changed objects based on the number of conflicting submaps determined by the baseline.
Since both baselines require pre-aligned sequences, we feed the baselines with ground truth camera poses from Pybullet and those aligned by ORB-SLAM3, respectively. For NN, the reference partial point cloud of each source object is fused from the whole sequence of the source depth images. Data associations between the target partial mug observations and the source point clouds are determined by the instance ID in Pybullet for synthetic sequences and manual labeling based on the panoptic masks produced by Detectron2 [26] (used in PMT) for real-world sequences.
All results are obtained on a laptop with an Intel Core i7-9750H CPU and an Nvidia GeForce RTX 2070 GPU. The network inference speed for NDF is around 0.019 s per frame, and the change detection operation with an expanding spatial tree executes at an average speed of 0.023 s per frame given the magnitude of the object number in our experiment setting (up to 40 mugs). These result in an overall speed of 24 FPS for the complete pipeline, thus showing no obvious latency for online operation.
Results on Synthetic Sequences. We present the change detection results of the three methods in Table. I. Here for NN, we set 0.002 m and 0.3. We apply a 6 DoF random transform to the target camera poses when running our approach so as to simulate the unavailability of motion capture systems during common mobile robot operations.
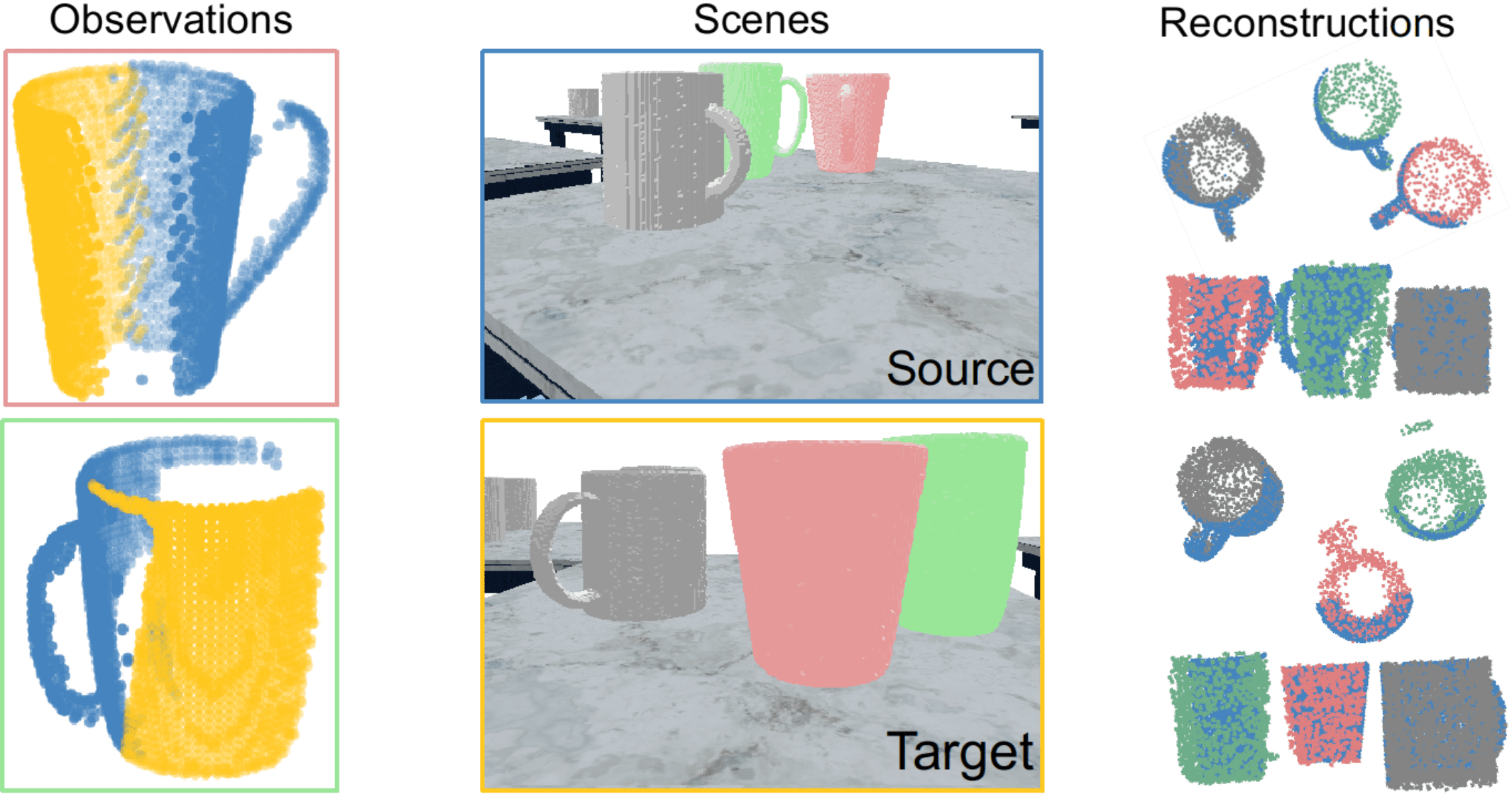
We can see that our method accurately detects all the changes without any false positives. On the one hand, NN and PMT respectively ignore four and one changes for the two pairs of mugs switching positions at table 5 and 7, as the similar viewing angles of these mugs during the source and target traverse induce high overlap between the target and source point clouds, thereby confounding the baselines by the existence of neighboring points and similar local geometry.
On the other, both baselines falsely mark the four mugs on table 1 and 2 as changed, which is due to the remarkable viewing angle difference on these four mugs between the source and target trajectory. As explained in Fig. 7, the two mugs highlighted in red and green are observed in almost opposite directions, which then leads to little/no overlap between the two partial point clouds (blue and yellow). Therefore, few neighboring points can be found between the source and target observations, while at the same time leads to drastic differences in the resulted TSDF values. In contrast, our method is capable of encoding the full mug shape with a compact shape code from the partial observations and hence produces no false positives.
Results on Real-world Sequences. We report change detection results of the three methods on the real sequence in Table. II and present the reconstructions obtained from PMT and our method (for mugs) in Fig. 8. For fair comparison, we obtain the mug point clouds for all the three methods using the panoptic mask adopted in PMT, which are generated by Detectron2 [26] and preprocessed by DBSCAN [27]. Here, the parameters of NN are set as 0.002 m and 0.4 considering the noises in the real-world point clouds. Due to localization drift between two sessions, for PMT, the final number of changed objects are counted after manual merging of the few submaps instantiated for the same object. In order to mimic the real operating scenarios, the camera poses to our approach are obtained through running ORB-SLAM3 separately on the two traverses.

| Approach | TP | FP | FN | Precision | Recall |
|---|---|---|---|---|---|
| NN | 8 | 4 | 4 | 66.7% | 66.7% |
| PMT | 11 | 4 | 1 | 73.3% | 91.7% |
| Ours | 12 | 0 | 0 | 100% | 100% |
| Approach | TP | FP | FN | Precision | Recall |
|---|---|---|---|---|---|
| NN | 3 | 3 | 2 | 50% | 60% |
| PMT | 5 | 3 | 0 | 62.5% | 100% |
| Ours | 5 | 1 | 0 | 83.3% | 100% |
When confronted with noisy point cloud inputs and localization results, despite the reconstruction failure of the beige mug on table 1 and the blue mug on table 2 (as shown Fig. 8(a)) due to poor point cloud and panoptic mask quality, our method still maintains better detection efficacy in terms of both precision and recall rate. From Fig. 8(b), we see that the confusion brought by disparate viewing angles persists, as both NN and PMT wrongly mark the black and blue mug on table 3 (highlighted in green) as changed. This matches the PMT reconstruction results shown in the second column, as the two mugs have just one side partially reconstructed during each session. Furthermore, another false detection emerges as the dark blue mug on table 3 (highlighted in yellow in Fig. 8(a)), which results from the larger localization error at the starting point of the target trajectory. Our method reduces its reliance on the absolute accuracy of camera pose estimation by conducting local neighborhood layout matching, i.e., the relative spatial relationship among neighboring mugs, thereby successfully recognizing the mug through its unchanged relative positions with its neighbors.
Limitation and Extension. The proposed approach works well under the assumption that the changed objects do not take up a predominant portion of all the objects in the scene, which is a common case for doing frequent visits of the same environment whose changes occur incrementally. For scenes with drastic changes between the two scans, our approach may not work well with the absence of a consistent local layout to refer to. Our approach can be further extended to detect objects that only rotate but do not move by utilizing the equivariance of NDFs, i.e., computing an extra transform between the two ’s after the shape-similarity-based registration step. This situation was not included in the experiment as it is rare for changed daily objects to have pure rotation but no translation.
VI Conclusion and Future Work
In this paper, we propose an online object-level change detection approach based on an NDF-derived object representation, demonstrating improved robustness to viewing angle disparity and localization drift. For future work, we would like to test the approach’s scalability to larger scenes if incorporated as part of an object-level SLAM system targeting long-term operation, and further explore the potential of using NDFs for providing object pose constraints to help improve camera localization.
References
- [1] Ross Finman, Thomas Whelan, Michael Kaess and John J Leonard “Toward lifelong object segmentation from change detection in dense rgb-d maps” In 2013 European Conference on Mobile Robots, 2013, pp. 178–185 IEEE
- [2] Rareş Ambruş, Nils Bore, John Folkesson and Patric Jensfelt “Meta-rooms: Building and maintaining long term spatial models in a dynamic world” In 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2014, pp. 1854–1861 IEEE
- [3] Marius Fehr et al. “TSDF-based change detection for consistent long-term dense reconstruction and dynamic object discovery” In 2017 IEEE International Conference on Robotics and automation (ICRA), 2017, pp. 5237–5244 IEEE
- [4] Edith Langer, Timothy Patten and Markus Vincze “Robust and efficient object change detection by combining global semantic information and local geometric verification” In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020, pp. 8453–8460 IEEE
- [5] Lukas Schmid et al. “Panoptic Multi-TSDFs: a Flexible Representation for Online Multi-resolution Volumetric Mapping and Long-term Dynamic Scene Consistency” In 2022 IEEE International Conference on Robotics and Automation (ICRA), 2022
- [6] Anthony Simeonov et al. “Neural Descriptor Fields: SE(3)-Equivariant Object Representations for Manipulation” In 2022 International Conference on Robotics and Automation (ICRA), 2022, pp. 6394–6400 DOI: 10.1109/ICRA46639.2022.9812146
- [7] Erik Derner et al. “Change detection using weighted features for image-based localization” In Robotics and Autonomous Systems 135, 2021, pp. 103676 DOI: https://doi.org/10.1016/j.robot.2020.103676
- [8] Evan Herbst, Peter Henry, Xiaofeng Ren and Dieter Fox “Toward object discovery and modeling via 3-D scene comparison” In 2011 IEEE International Conference on Robotics and Automation, 2011, pp. 2623–2629 DOI: 10.1109/ICRA.2011.5980542
- [9] Michael Niemeyer, Lars Mescheder, Michael Oechsle and Andreas Geiger “Occupancy Flow: 4D Reconstruction by Learning Particle Dynamics” In Proc. ICCV, 2019
- [10] Jeong Joon Park et al. “DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation” In Proc. CVPR, 2019
- [11] Songyou Peng et al. “Convolutional occupancy networks” In European Conference on Computer Vision, 2020, pp. 523–540 Springer
- [12] Vincent Sitzmann, Michael Zollhöfer and Gordon Wetzstein “Scene Representation Networks: Continuous 3D-Structure-Aware Neural Scene Representations” In Proc. NeurIPS 2019, 2019
- [13] Ben Mildenhall et al. “NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis” In Proc. ECCV, 2020
- [14] Ruohan Gao et al. “ObjectFolder: A Dataset of Objects with Implicit Visual, Auditory, and Tactile Representations” In CoRL, 2021
- [15] Congyue Deng et al. “Vector Neurons: A General Framework for SO(3)-Equivariant Networks” In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021, pp. 12200–12209
- [16] Yu Deng, Jiaolong Yang and Xin Tong “Deformed implicit field: Modeling 3d shapes with learned dense correspondence” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 10286–10296
- [17] Edgar Sucar, Kentaro Wada and Andrew Davison “NodeSLAM: Neural object descriptors for multi-view shape reconstruction” In 2020 International Conference on 3D Vision (3DV), 2020, pp. 949–958 IEEE
- [18] Stefan Lionar et al. “Neuralblox: Real-time neural representation fusion for robust volumetric mapping” In 2021 International Conference on 3D Vision (3DV), 2021, pp. 1279–1289 IEEE
- [19] Jiahui Huang, Shi-Sheng Huang, Haoxuan Song and Shi-Min Hu “Di-fusion: Online implicit 3d reconstruction with deep priors” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 8932–8941
- [20] Alexander Hermans, Lucas Beyer and Bastian Leibe “In defense of the triplet loss for person re-identification” In arXiv preprint arXiv:1703.07737, 2017
- [21] Erwin Coumans and Yunfei Bai “Pybullet, a python module for physics simulation for games, robotics and machine learning” In GitHub repository, 2016
- [22] Jiazhao Zhang, Chenyang Zhu, Lintao Zheng and Kai Xu “Fusion-aware point convolution for online semantic 3d scene segmentation” In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 4534–4543
- [23] Lars Mescheder et al. “Occupancy Networks: Learning 3D Reconstruction in Function Space” In Proc. CVPR, 2019
- [24] Angel X Chang et al. “Shapenet: An information-rich 3d model repository” In arXiv preprint arXiv:1512.03012, 2015
- [25] Carlos Campos et al. “Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam” In IEEE Transactions on Robotics 37.6 IEEE, 2021, pp. 1874–1890
- [26] Yuxin Wu et al. “Detectron2”, 2019
- [27] Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu “A density-based algorithm for discovering clusters in large spatial databases with noise.” In kdd 96.34, 1996, pp. 226–231