Robust Fractional order PI Controller for Switching Systems
Abstract
This paper is concerned with the robust design for a class of switching systems from a fractional order control (FOC) perspective. In particular, the tuning of the robust fractional order PI (RFPI) controller is proposed based on phase margin and cross over frequency specifications, ensuring the quadratic stability of the system, i.e., the third design specification is given by the stability condition. The quadratic stability is analyzed using a frequency-domain method equivalent to the common Lyapunov one. Two examples are given to show the effectiveness of the proposed controller.
keywords:
Fractional order PI controller, Robust Control, Switching systems, Stability, Common Lyapunov method., ,
1 Introduction
In recent years, the study of switched systems has received a growing attention. Switched systems are a class of hybrid dynamical systems consisting of a family of continuous (or discrete) time subsystems and a rule that orchestrates the switching between them (see e.g. Liberzon (2003), Daafouz et al. (2002)). The widespread application of such systems is motivated by increasing performance requirements, and by the fact that high performance control systems can be realized by switching between relatively simple LTI systems. However, the potential gain of switched systems is offset by the fact that the switching action introduces behaviour in the overall system that is not present in any of the composite subsystems. A survey of main problems in stability and design of switched systems was reported in Liberzon and Morse (1999), Sun and Ge (2005a), Sun and Ge (2005b). There are many methodologies and approaches developed in the switched systems theory in order to mitigate some problems encountered in practice (refer to Dong (2011) and the references therein for a current review). However, despite much effort, relatively little work can be found in the literature from a robustness viewpoint.
Fractional order control (FOC), that is, the generalization to non-integer-orders of traditional controllers or control schemes, and its applications, are becoming an important research field since it translates into more tuning parameters or, in other words, more adjustable time and frequency responses of the control system, allowing the fulfillment of robust performances. Robust design of fractional order controllers was investigated in several papers (see e.g. Ladaci et al. (2009), Feliu-Batlle et al. (2009), Feliu-Batlle et al. (2007), Ahn et al. (2007), Monje et al. (2004)). Nevertheless, its application to switching systems has not been paid much attention, expecting to open a new perspective in the field.
Given this context, the objective of this paper is to examine stability issues and robust design of switching systems based on fundamentals of FOC.
The remaining of this paper is organized as follows. Section 2 provides some important theorems for quadratic stability of switching systems in the frequency domain, as well as an introduction to fractional order PI controllers. In Section 3, the studied problem is stated. Section 4 addresses the robust design of fractional order PI controllers for such class of systems. An application example is given in Section 5 to show the goodness of the proposed controller. Finally, Section 6 draws the conclusions of this paper.
2 Preliminaries
In this section, the quadratic stability of switching systems will be studied. A brief introduction of fractional order PI controllers is also given.
2.1 Quadratic stability of switching systems
The quadratic stability of switching systems is studied using the method introduced in Kunze and Karimi (2011) in the frequency domain which is a link between quadratic stability using Lyapunov theory and strictly positive realness (SPR) properties. Thus, it shows the link between time-domain conditions and frequency-domain conditions in order to obtain quadratic stability.
Consider a switched hybrid system as
| (1) |
where denotes the convex combination and is the switching subsystem. According to Pardalos and Rosen (1987), (1) can be alternatively written as:
| (2) |
Theorem 1 (Boyd et al. (1994))
A system described by (2) is quadratically stable if and only if there exists a matrix , , such that
Denoting
and
a stable polynomial of order corresponding to the system is as follows:
| (3) |
Then the relation between SPRness and the quadratic stability can be stated in the following theorem.
Theorem 2 (Kunze and Karimi (2011))
Consider and , two stable polynomials of order , corresponding to the systems and , respectively, then the following statements are equivalent:
-
1.
and are SPR.
-
2.
.
-
3.
and are quadratically stable, which means that such that , .
2.2 Fractional order PID controllers
Fractional calculus (FC) is a more generalized form of calculus. Unlike the integer order calculus, where operations are centered mainly at the integers, FC considers every real number. It owes its origin to a question of whether the meaning of a derivative to an integer order could be extended to still be valid when is not an integer. This question was first raised by L’Hopital on September 30th, 1695. Nowadays, the theoretical and practical interest of fractional order operators is well-established, as well as its applicability to several areas of science and engineering, especially related to automatic control and robotics.
The widespread use of PID controllers has motivated many researchers to look for better design methods or alternative controllers for many years. As reported in Chen et al. (2009), more than percent of the control loops are PID-type. The generalization of the PID controller to non-integer order, namely PIλDμ, was proposed by Podlubny (1999), whose transfer function, in general form, is given by:
| (4) |
where and are the non-integer orders of the integrator and differentiator terms, respectively (). Intuitively, with non-integer order controllers, there are more flexibilities in adjusting the gain and phase characteristics than using integer order ones, i.e., fractional order controllers take advantage of the fractional orders introduced in the control action in order to perform a more effective control. The better performance of this type of controllers in comparison with the integer ones was demonstrated in many works (e.g. refer to the pioneering study Podlubny (1999)). A review of fractional order controllers can be found in Monje et al. (2010), Val rio and S da Costa (2010), Chen et al. (2009), Monje et al. (2008).
In this paper, we will focus on the fractional order PI controller of the form:
| (5) |
where is the controller order, .
3 PROBLEM FORMULATION
In this section, a more precise problem statement for the class of systems under consideration is given.
It is well known a switching system can be potentially destabilized by an appropriate choice of switching signal, even if the switching is between a number of Hurwitz-stable closed-loops systems. Even in the case where the switching is between systems with identical transfer functions, it is sometimes possible to destabilize the switching system by means of switching (Leith et al. (2003)). Likewise, the concept of robustness with respect to parameter variations is well defined for LTI systems. However, this issue is somewhat more difficult to quantify for switched linear systems. In particular, robustness may be defined with respect to a number of design parameters, including, not only the parameters of the closed-loop system matrices, but also with respect to switching signal.
Let us illustrate the importance of designing a robust controller for switching systems by means of a particular example. Consider a switching system given by the following second order transfer function:
| (6) |
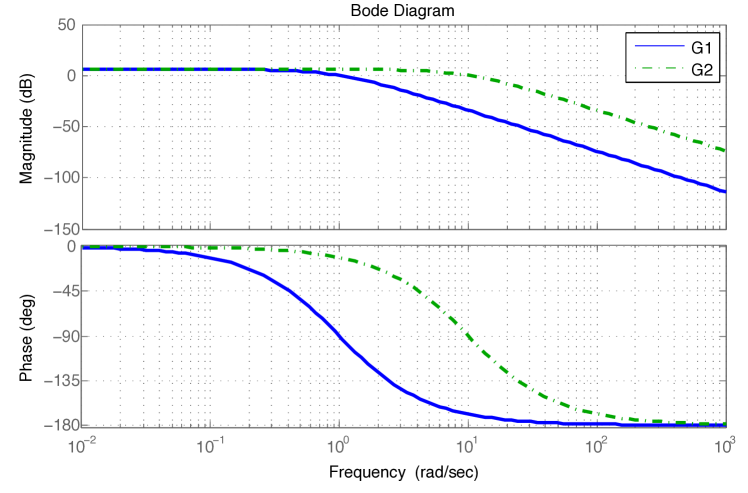
with and . One can state than only the time constant of the system changes. As can be observed in Fig. 1, both subsystems has the same phase margin of 90 . Applying Theorem 2 to the closed-loop system, we have:
| (7) |
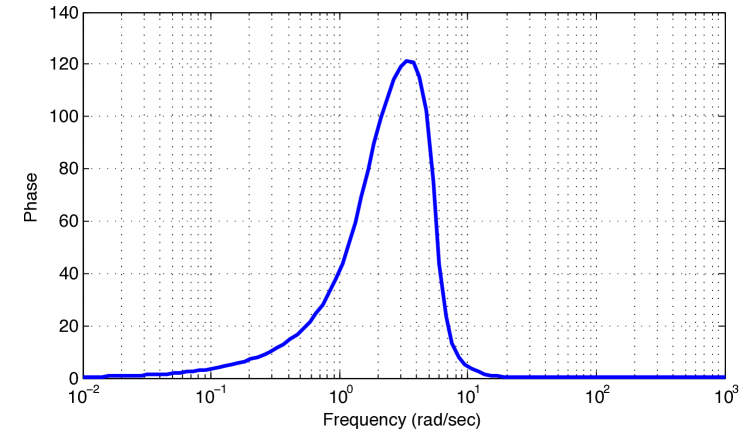
Figure 2 depicts (7) graphically. Therefore, it is obvious that the system is not quadratically stable.
4 Robust Control Design for Switching Systems
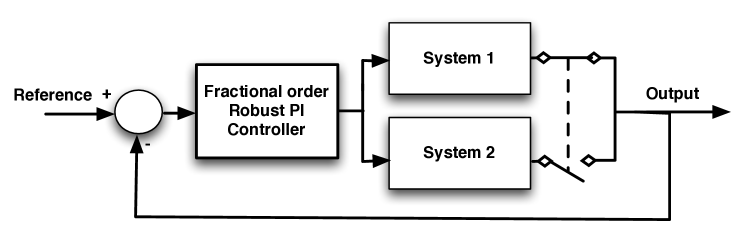
In this section, a method for designing a robust fractional order PI controller for a class of switching systems is proposed. For ease of the controller design we consider a system given by (2) with , but the design procedure can be applied for more than two switching. A scheme of the control approach is shown in Fig. 3. Next, the transfer function of each subsystem will be referred to as and , respectively. Therefore, the aim of this paper is the robust stabilization of a general system , by applying a fractional order PI controller of the form (5) –will be referred as to RFPI in the text–, i.e., cancelling the effect of switching on the system stability.
Let assume that the phase margin and gain crossover frequency are denoted as and , respectively. Thus, the three specification to be fulfilled are:
-
1.
Phase margin specification:
(8) -
2.
Gain crossover frequency specification:
(9) -
3.
Quadratic stability specification:
(10) where and are characteristic polynomials of each closed-loop system. In order to apply this condition to design the fractional order PI controller, CRONE approximation of fractional order integral is used. One can use any other approximation for fractional order integral.
To determine the controller parameters, the set of nonlinear equations (8)-(10) has to be solved. To do so, the optimization toolbox of Matlab can be used to reach out the better solution with the minimum error. More precisely, the function FMINCON is able to find the constrained minimum of a function of several variables. It solves problems of the form subject to: , , , where is the function to minimize; and represent the nonlinear inequalities and equalities, respectively (non-linear constraints); is the minimum we are looking for; and and define a set of lower and upper bounds on the design variables, .
5 Examples
This section gives two examples of application of the proposed method for designing robust fractional order PI controllers for switching systems. Specifically, two cases will be considered next: the velocity control of a car, described by a first order model, and the control of a second order system.
Example 1
In HosseinNia et al. (2012) and HosseinNia et al. (2011), the authors proposed a hybrid model of the car taking into account its different dynamics when accelerating and braking. In this respect, its throttle and brake dynamics can be given, respectively, as follows:
| (11) |
and
| (12) |
For the comfort of car’s occupants, phase margin and crossover frequency has to be chosen around and rad/s, respectively, in order to obtain a smooth closed-loop response, i.e., with a value of overshoot close to . Solving the set of equations (8)-(10) for the previous specifications, the PI controller is given by:
| (13) |
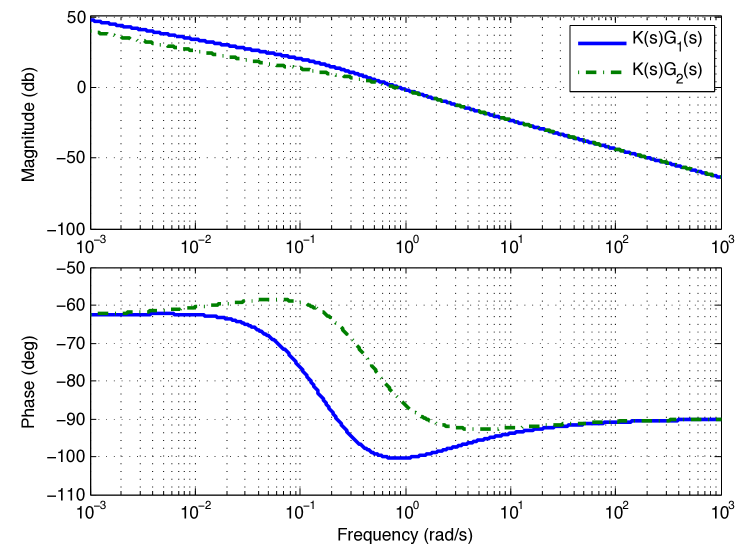
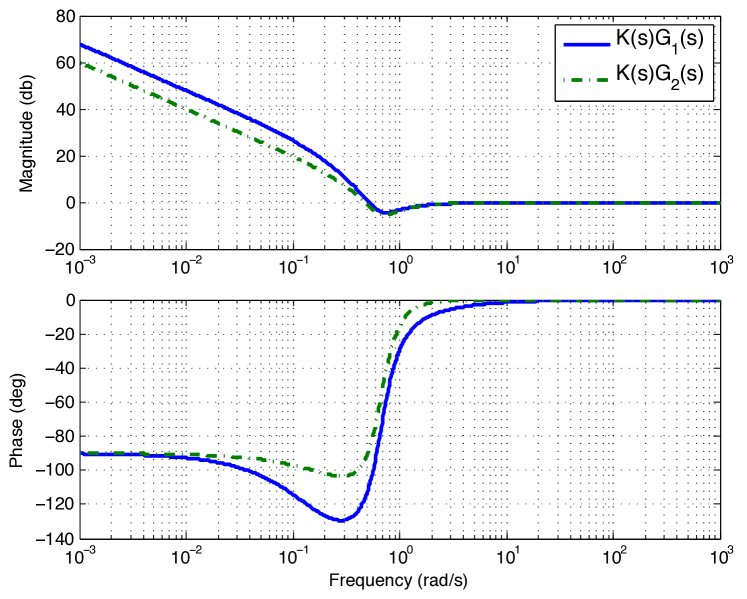
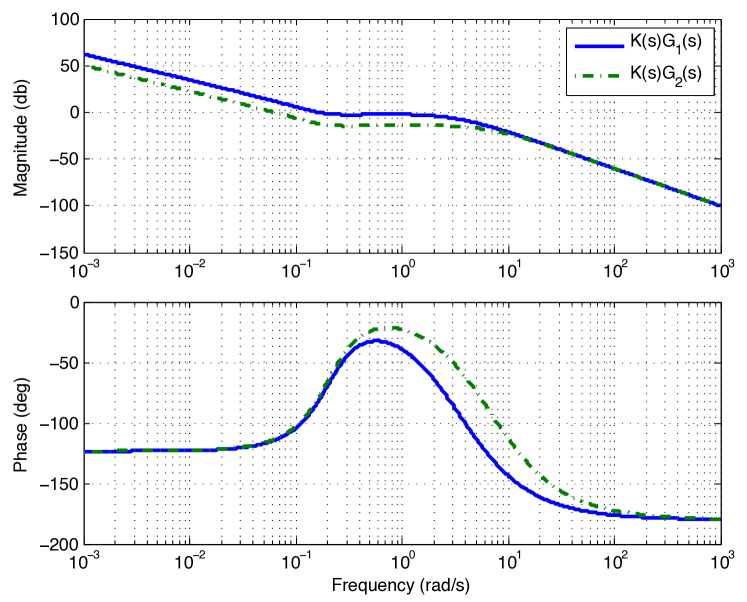
Figure 4 shows the frequency response of the controlled system. As can be seen, the design specifications are fulfilled for both subsystems –the phase margin obtained after optimization problem is even higher than deg.
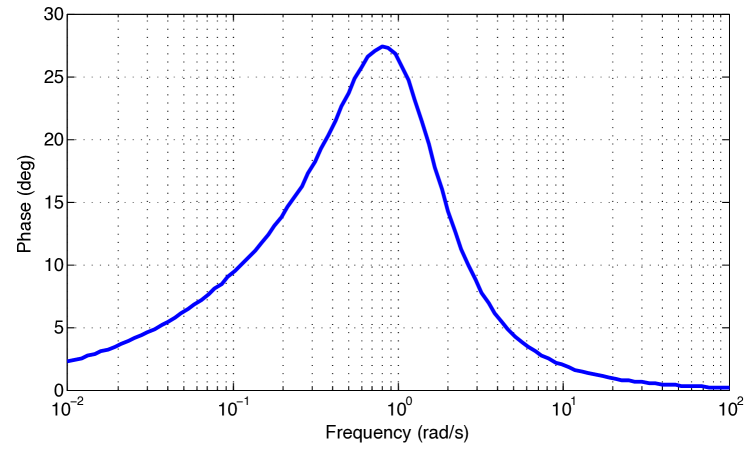
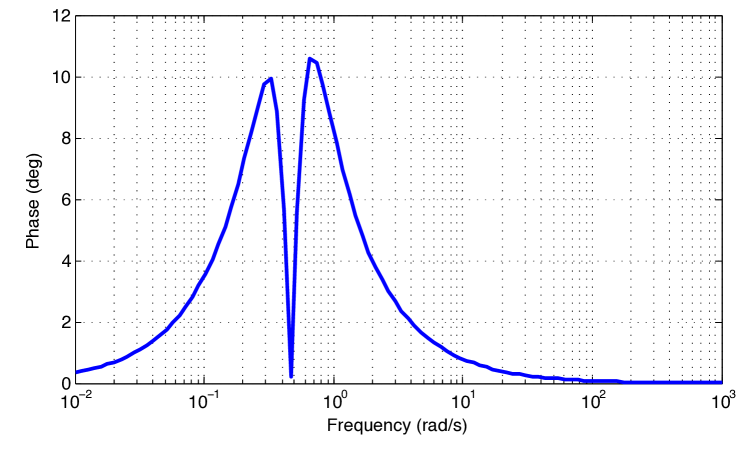
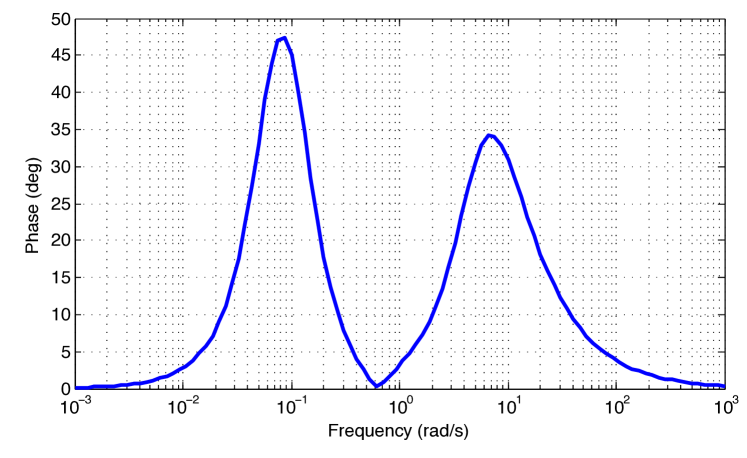
The phase difference between the two characteristic polynomials of the closed-loop controlled subsystems is shown in Fig. 5. It is observed that the maximum phase difference is deg –less than deg–, so the controlled system is quadratically stable.
For comparison purposes, a three-parameter controller, specifically, a traditional PID controller of the form
| (14) |
is designed for the same specifications (8)-(10). Applying the optimization method, the PID parameters are: , and . Figures 6 and 7 show the bode diagram of each closed-loop subsystem when applying the PID and phase difference between the two characteristic polynomials of the closed-loop controlled subsystems, respectively. The phase margin for both subsystems and the maximum of the phase difference are about and deg, respectively, so the design specifications are fulfilled. Comparing the Bode plots of both controlled system when applying RFPI and PID, i.e., Fig. (4) and (6), one can observe that the system controlled by PID has constant magnitude for high frequency, which may cause the system sensitive to high frequency noises and, consequently, instability.
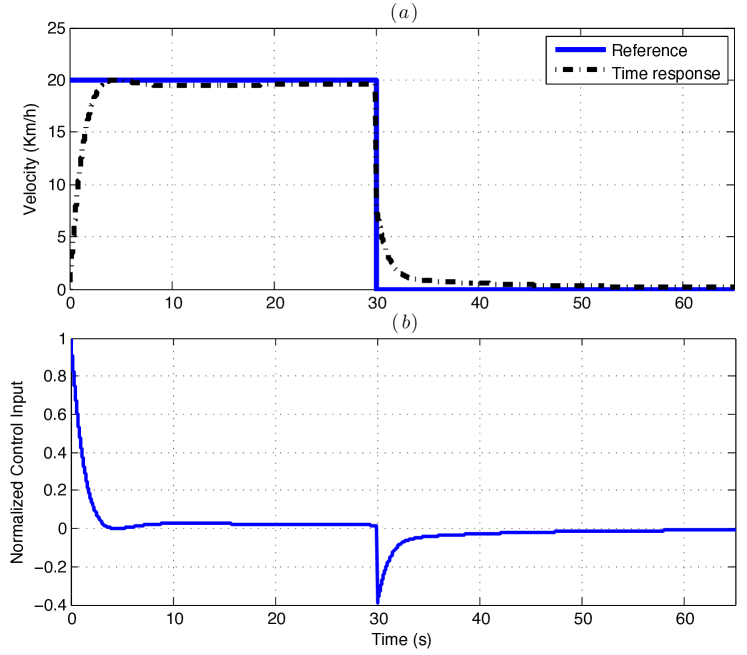
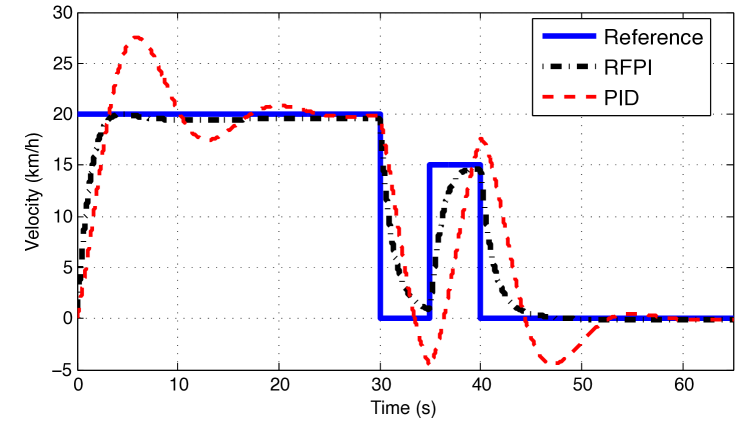
To show the system performance in time domain, a maneuver which simulates the car acceleration to km/h and, after that, the braking to km/h –stop completely– is depicted in Fig. 8 in (a) and the normalized control action when using the RFPI in (b). In addition, for arbitrary switching, including a comparison of its velocity for the RFPI and PID cases is depicted in Fig. 9. As observed in this figure, the car has an adequate performance for both the throttle and the brake actions when applying the RFPI controller (dashdotted black line), achieving the reference velocity in a suitable time and without overshoot in both cases. On the contrary, the response when using the PID (dashed red line) is significantly poor –has considerable overshoot–. Likewise, as shown in Fig. 8 (b), throttle and brake actions for the RFPI case are low, which will be referred to soft actions. As a result, it can be said that the occupants’ comfort is guaranteed when applying the proposed controller. It is important to remark that the control action when applying the PID was omitted due to the bad behavior of the system obtained by this controller. It should be mentioned that in the real application the car will not have negative velocity, and in this case when the velocity reach zero the car will stop.
Example 2
This example considers a second order switched system given by:
| (15) | |||
| (16) |
The design specifications for the RFPI controller are as follows: deg, rad/s and rad/s. After the optimization process, the RFPI obtained is:
| (17) |
The Bode plots of the controlled system is depicted in Fig. 10. As observed, the phase margins are deg and deg, which fulfill the design specifications. The phase difference between the two characteristic polynomials of the closed-loop controlled system is plotted in Fig. 11. It can be seen that the maximum value of phase difference is deg, then the system is quadratically stable.
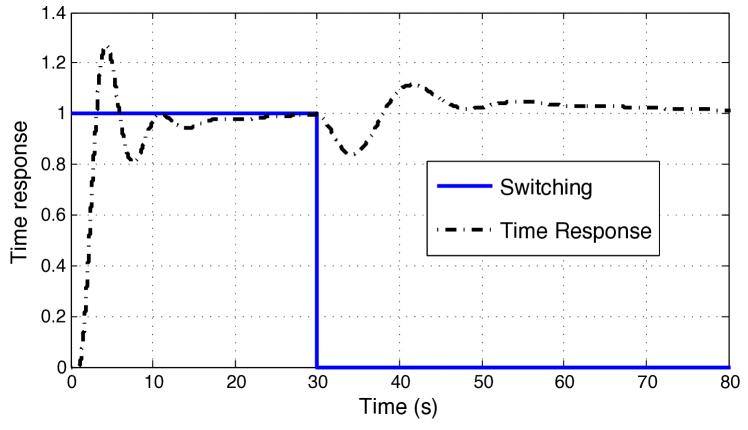
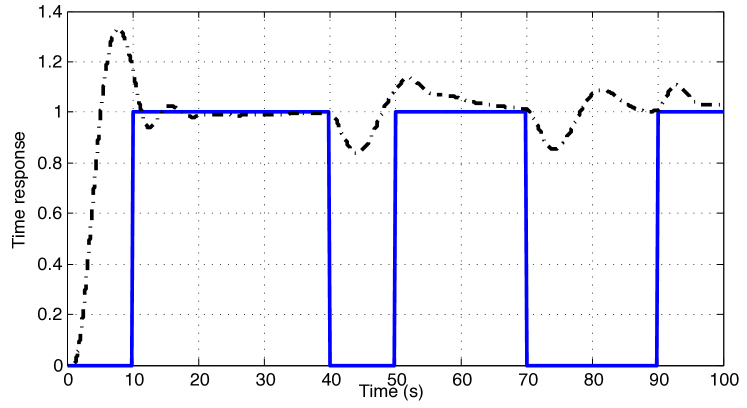
In order to demonstrate the goodness of the designed RFPI controller against switching, two situations will be simulated next: arbitrary and fast arbitrary switching. The step responses are shown in Fig. 12 and 13, respectively. Switching signal is set to or , which indicates the subsystem or subsystem is activated, respectively. One can see that the system responses go through an adaptation when the system switches, but achieving the reference and keeping stable for both switching situations.
6 Conclusion
This paper addresses the design of a robust fractional order PI (RFPI) controller for switching systems in frequency domain. To this respect, RFPI is tuned based on phase margin and cross over frequency specifications, ensuring the quadratic stability of the system, i.e., the third specification is given by the stability condition. Two examples for switching systems with subsystems are given to show the effectiveness of the proposed controller. In particular, the speed control of the car is considered, in which the car has different dynamics for accelerating and braking actions. The other example refers to a second order switched system. In both examples, the goodness of the RFPI controller is demonstrated against arbitrary switching. Especially, it is worth mentioning the relevant system performance when applying RFPI in comparison with the obtained by a traditional PID controller, which was also designed to fulfill similar frequency-domain specifications.
Our future efforts will focus on the generalization of the RFPI design for switching systems with subsystems and its experimental validation.
References
- Ahn et al. [2007] Ahn, H., Chen, Y., and Podlubny, I. (2007). Robust stability test of a class of linear time-invariant interval fractional-order system using Lyapunov inequality. Applied Mathematics and Computation, 187(1), 27–34.
- Boyd et al. [1994] Boyd, S., Ghaoui, L.E., Feron, E., and Balakrishnan, V. (1994). Linear Matrix Inequalities in System and Control Theory. SIAM.
- Chen et al. [2009] Chen, Y.Q., Petras, I., and Xue, D. (2009). Fractional order control - a tutorial. In Proceedings of the 2009 American Control Conference (ACC’09), 1397 –1411. 10.1109/ACC.2009.5160719.
- Daafouz et al. [2002] Daafouz, J., Riedinger, P., and Iung, C. (2002). Stability analysis and control synthesis for switched systems: A switched Lyapunov function approach. IEEE Transactions on Automatic Control, 47(11), 1883 – 1887.
- Dong [2011] Dong, Y. (2011). Robust stability analysis for uncertain switched discrete-time systems. Journal of Applied Mathematics, 2011, 20 pages. doi:10.1155/2011/523020.
- Feliu-Batlle et al. [2007] Feliu-Batlle, V., Rivas-Pérez, R., and Sánchez-Rodríguez, L. (2007). Fractional robust control of main irrigation canals with variable dynamic parameters. Control Engineering Practice, 15(6), 673–685.
- Feliu-Batlle et al. [2009] Feliu-Batlle, V., Rivas-Pérez, R., Sánchez-Rodríguez, L., and Ruiz-Torija, M.A. (2009). Robust fractional-order PI controller implemented on a laboratory hydraulic canal. Journal of Hydraulic Engineering, 135(4), 271–282.
- HosseinNia et al. [2012] HosseinNia, S.H., Tejado, I., Vinagre, B.M., Milanés, V., and Villagrá, J. (2012). Experimental application of hybrid fractional order adaptive cruise control at low speed. Submitted to IET Control Theory and Applications.
- HosseinNia et al. [2011] HosseinNia, S., Tejado, I., Vinagre, B., Milanes, V., and Villagra, J. (2011). Low speed control of an autonomous vehicle using a hybrid fractional order controller. In 2nd International Conference on Control Instrumentation and Automation (ICCIA). Iran.
- Kunze and Karimi [2011] Kunze, M. and Karimi, A. (2011). Frequency-domain controller design for switched systems. submitted to Automatica.
- Ladaci et al. [2009] Ladaci, S., Charef, A., and Louiseau, J.J. (2009). Robust fractional adaptive control based on the strictly positive realness condition. Int. J. Appl. Math. Comput. Sci., 19(1).
- Leith et al. [2003] Leith, D., Shorten, R., Leithead, W., Mason, O., and Curran, P. (2003). Issues in the design of switched linear control systems: A benchmark study. International Journal of Adaptive Control and Signal Processing, 17(2), 103 –118.
- Liberzon [2003] Liberzon, D. (2003). Switching in Systems and Control. Birkäuser.
- Liberzon and Morse [1999] Liberzon, D. and Morse, A.S. (1999). Basic problems in stability and design of switched systems. IEEE Control Systems Magazine, 19, 59–70.
- Monje et al. [2004] Monje, C.A., Vinagre, B.M., Chen, Y.Q., and Feliu, V. (2004). On fractional controllers: Some tuning rules for robustness to plant uncertainties. Nonlinear Dynamics, 38(1-4), 369–381.
- Monje et al. [2010] Monje, C., Chen, Y., Vinagre, B., Xue, D., and Feliu, V. (2010). Fractional-order Systems and Controls. Fundamentals and Applications. Springer.
- Monje et al. [2008] Monje, C., Vinagre, B., Feliu, V., and Chen, Y. (2008). Tuning and auto-tuning of fractional order controllers for industry applications. Control Engineering Practice, 16(7), 798– –812. DOI: 10.1016/j.conengprac.2007.08.006. URL http://www.sciencedirect.com/science/article/B6V2H-4PYJDYF-1/2/b1e7bb7beb49cdbbc890aad6a00b936a.
- Pardalos and Rosen [1987] Pardalos, P. and Rosen, J. (1987). Constrained global optimization: Algorithms and applications. Lecture Notes in Computer Science, 268.
- Podlubny [1999] Podlubny, I. (1999). Fractional-order systems and piλdμ-controllers. IEEE Trans. Automatic Control, 44(1)(208—214).
- Sun and Ge [2005a] Sun, Z. and Ge, S.S. (2005a). Analysis and synthesis of switched linear control systems. Automatica, 41(2), 181–195.
- Sun and Ge [2005b] Sun, Z. and Ge, S.S. (2005b). Switched Linear Systems: Control and Design. Springer.
- Val rio and S da Costa [2010] Val rio, D. and S da Costa, J. (2010). A review of tuning methods for fractional pids. In Proceedings of the 4th IFAC Workshop on Fractional Differentiation and Its Applications (FDA’10).