Robust Macroscopic Schrödinger’s Cat on a Nucleus
Abstract
We propose a scheme to generate spin cat states, i.e., superpositions of maximally separated quasiclassical states on a single high-dimensional nuclear spin in a solid-state device. We exploit a strong quadrupolar nonlinearity to drive the nucleus significantly faster than usual gate sequences, achieving collapses and revivals two orders of magnitude faster than the dephasing timescale. Furthermore, these states are engineered without entanglement with an ancilla, hence, are robust against error propagation. With our multitone control, we can realize arbitrary high-spin rotations within an experimentally feasible regime, as well as transform a spin coherent state to a spin cat state using only phase modulation, opening the possibility of storing and manipulating high-fidelity cat states.
I Introduction
A Schrödinger cat state [1, 2, 3] is an equal superposition of two distinct “classical” states of a system [4, 5, 6], that is a probe for fundamental aspects of quantum physics, including the measurement problem [7], macro-realism [8, 9], quantum-classical transition [10], and non-locality [11]. Cat states also serve as important resources for quantum error correction [12, 13, 14, 15], quantum sensing [16, 17, 18], and quantum communication [19, 20]. Thus, practical realization of cat states is of interest for both foundational and technological applications.
In continuous-variable systems, cat states are generated using nonlinearity induced by light-matter interactions in the Jaynes-Cummings model [21, 22], e.g., a harmonic oscillator coupled to a superconducting qubit [23, 24, 25] or an atom in an optical cavity [26]. However, errors occurring in the qubit can propagate to the cavity, corrupting such nonclassical states [25]. Alternatively, Greenberger-Horne-Zeilinger (GHZ) states, which are spin cat states (SCSs) for permutationally symmetric systems, can be realized by entangling multiple qubits [27, 28, 29, 30], but such SCSs are fragile—with their decoherence rate proportional to the square of the number of qubits [31].
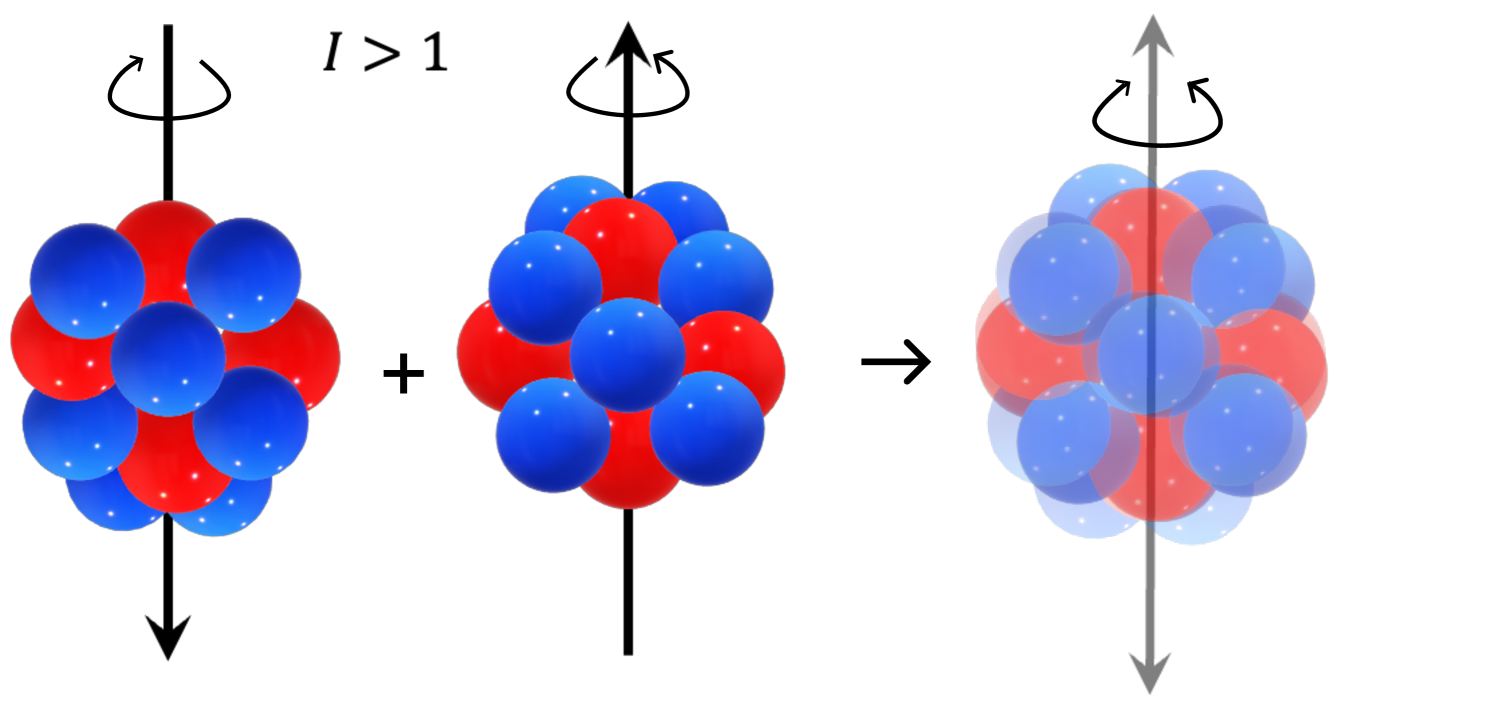
We propose a new platform to generate cat states deterministically, on-demand and without post selection using a nucleus, which is controlled without entanglement with an ancilla, hence, is robust against error propagation, unlike continuous-variable systems [12, 23, 24, 25, 26]. Here, we consider SCSs (implying macroscopic to differentiate them from “kitten” states [32]) on a nuclear spin, e.g., shown in Fig. 1, but, more generally, a superposition of any two maximally separated quasi-classical states, which are minimum uncertainty states that follow a classical evolution under a linear drive [5, 6]. We are motivated by recent experiments on high-spin nuclei (spin ) in a solid-state device [33, 34] accompanied by an enhanced electric field-driven quadrupole interaction, two orders of magnitude faster than the dephasing timescale, that could achieve ultrafast non-linear dynamics.
A highly coherent nuclear spin could open the possibility of robust generation and long-lived storage of SCSs. So far, quadrupole interaction has only been utilized for realizing spin squeezed states (SQSs), that too, on an ensemble of nuclear spins [35, 36]. However, individual addressing of high-spin systems is important for applications like quantum information processing and error correction [15]. We present two key results: i) a scheme to go beyond squeezed states towards generating SCSs and ii) an experimentally feasible control protocol for storing and manipulating SCSs on an individual nucleus.
II Setup
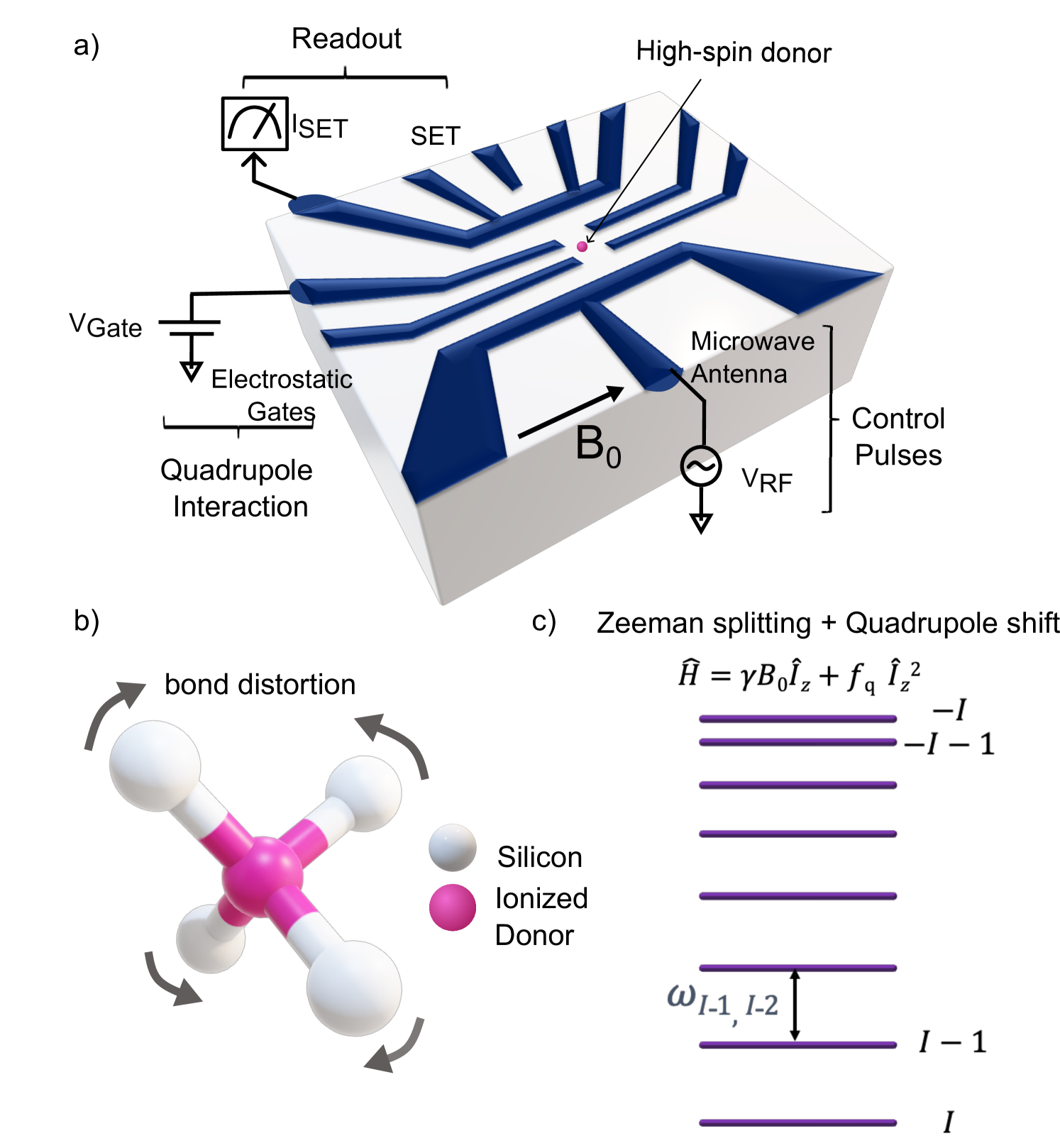
We consider a high-spin donor (Group-V element with a high-spin nucleus) implanted in a nanoelectronic device based on enriched 28Si (or any other spinless Group-IV atoms), as described in [33]. The chip is affixed to a dilution refrigerator maintained at a low temperature ( K) and placed inside a superconducting coil that produces a static magnetic field T. As shown in Fig. 2(a), the chip includes electrostatic gates to control the electrochemical potential of the donor, a microwave antenna to supply electromagnetic pulses, and a single electron transistor (SET) for reading out the donor spin state [37].
An implanted Group-V donor contains five electrons in its outermost shell, four of which form bonds with neighboring Si atoms and the remaining electron can be removed by ionizing the donor using electrostatic gates. The quantum state of the nuclear spin is initialized using flip-flop drive [38], where an electron and nuclear spin pair is flipped together in opposite directions. The donor atom is subject to a static potential, and a target nuclear-spin eigenstate can be achieved by applying a combination of flip-flop pulses and electron spin-resonance pulses that move population from higher and lower nuclear spin states towards a target state [34]. Then, the electrostatic potential is increased to ionize the donor atom by removing the electron and only the nuclear spin is manipulated using RF pulses. [39]. The readout process using electron spin resonance can be made dependent on the nuclear spin state, thus achieving nuclear readout via spin dependent tunneling of the electron [40, 33].
The differential thermal expansion between the silicon substrate and the electrostatic gates induce lattice strain in the chip [33], thereby distorting the bonds between the donor atom and neighboring Si atoms, as shown in Fig. 2(b). The electric-field gradient (EFG) generated from distortion of the bonds results in a quadrupole interaction of the high-spin nucleus, which has a non-zero quadrupole moment due to its asymmetric nuclear charge distribution. For a spatially varying potential , the EFG tensor comprises elements which is real, traceless and symmetric. Thus, can be diagonalized in a principal axis system , , , such that , and the EFG is characterized by the asymmetry parameter for . For a nucleus with electric quadrupole moment , the quadrupole interaction is
| (1) |
where is the quadrupole coupling strength, e the elementary charge, the reduced Planck’s constant, the nuclear spin operator vector and invariant .
In addition to the quadrupole interaction, we manipulate the nuclear spin state using a static magnetic dipole interaction due to and time dependent perturbation driven by magnetic field with time-dependence (). For a nucleus with gyromagnetic ratio , the nuclear spin dynamics are described by
| (2) |
The degenerate levels of a nuclear spin undergo Zeeman splitting due to which creates an equal spacing between the energy levels. The electric quadrupole interaction causes an unequal shift of the levels such that the transition frequency between two consecutive levels and , for , is unique, as shown in Fig. 2(c). We represent spin states as , where , and RF pulses drive transitions which follow the selection rule . For numerical simulations [41], we use the example of a spin- 123Sb donor [33, 34], with Zeeman splitting MHz, kHz and perturbation strength Hz.
III One-Axis Twisting
Quadrupole interaction is equivalent to one-axis twisting (OAT) due to if , two-axis counter twisting (TACT) due to and if [36, 42], and partial TACT otherwise. Generally, TACT is preferred over OAT as TACT generates faster squeezing in comparison to OAT and can help produce SQSs for metrology [43]. However, TACT cannot produce SCSs, and, in general, quadrupolar non-linear evolution with cannot go beyond SQSs on a nuclear spin [35].
We devise a way to convert TACT to OAT by adding a large linear term to the quadrupole interaction, induced here by the Zeeman coupling. The resulting dynamics depend on the orientation of the EFG and strength of magnetic field . When the Zeeman splitting is much larger than quadrupole coupling, i.e. , the component perpendicular to does not affect the nuclear spin because quadrupolar transitions () are prevented by the large energy difference. In this regime, only the component of the quadrupole interaction parallel to generates non-linear rotation, which effectively results in OAT, regardless of the value of . In contrast to TACT, our scheme allows generation of SCSs for any orientation of the quadrupolar axes of symmetry with respect to linear interaction along the axis. For numerical simulations in this work, we set , , , and EFG to be symmetric about axis, i.e. , but, our results can be generalized to other configurations.
Despite the femtometer scale of a nucleus, nuclear-SCSs are macroscopic with their size, quantified by the relative quantum Fisher information [44, 45], scaling linearly with . The size or degree of superposition of a nuclear-spin state for measurement operator is
| (3) |
i.e., proportional to the variance of the observable. For an appropriate , the variance is for bimodal SCSs and we calculate the size of a nuclear SCS to be , which denotes the maximum quantum Fisher information of the system and is equivalent to a GHZ state [46] made of entangled qubits [47]. A nuclear SCS with dimensions, e.g., a spin- SCS with 8 dimensions is equivalent to a qubit GHZ state with permutation symmetry, and not a qubit state, and can have macroscopicity up to for a 209Bi donor.
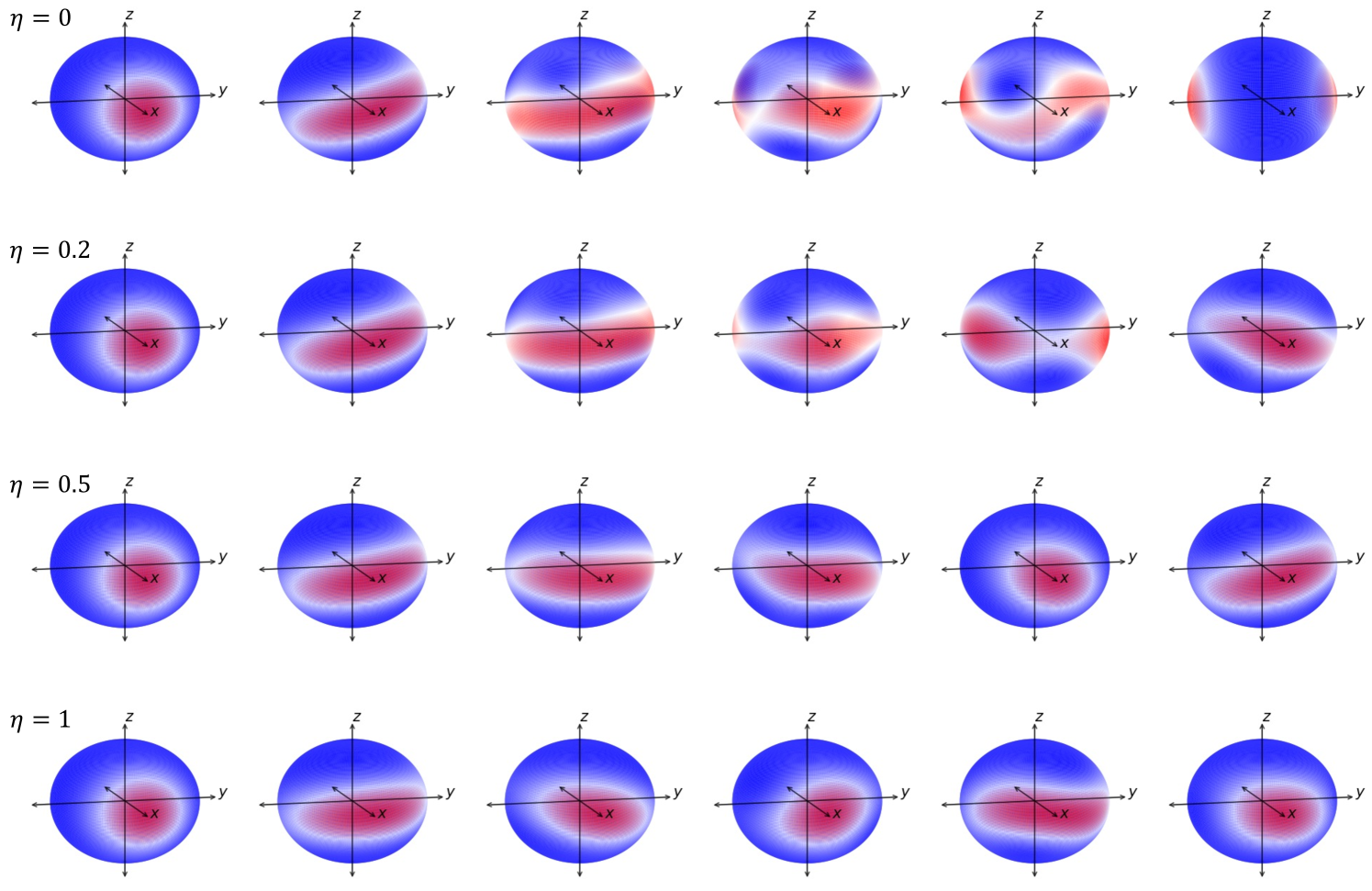
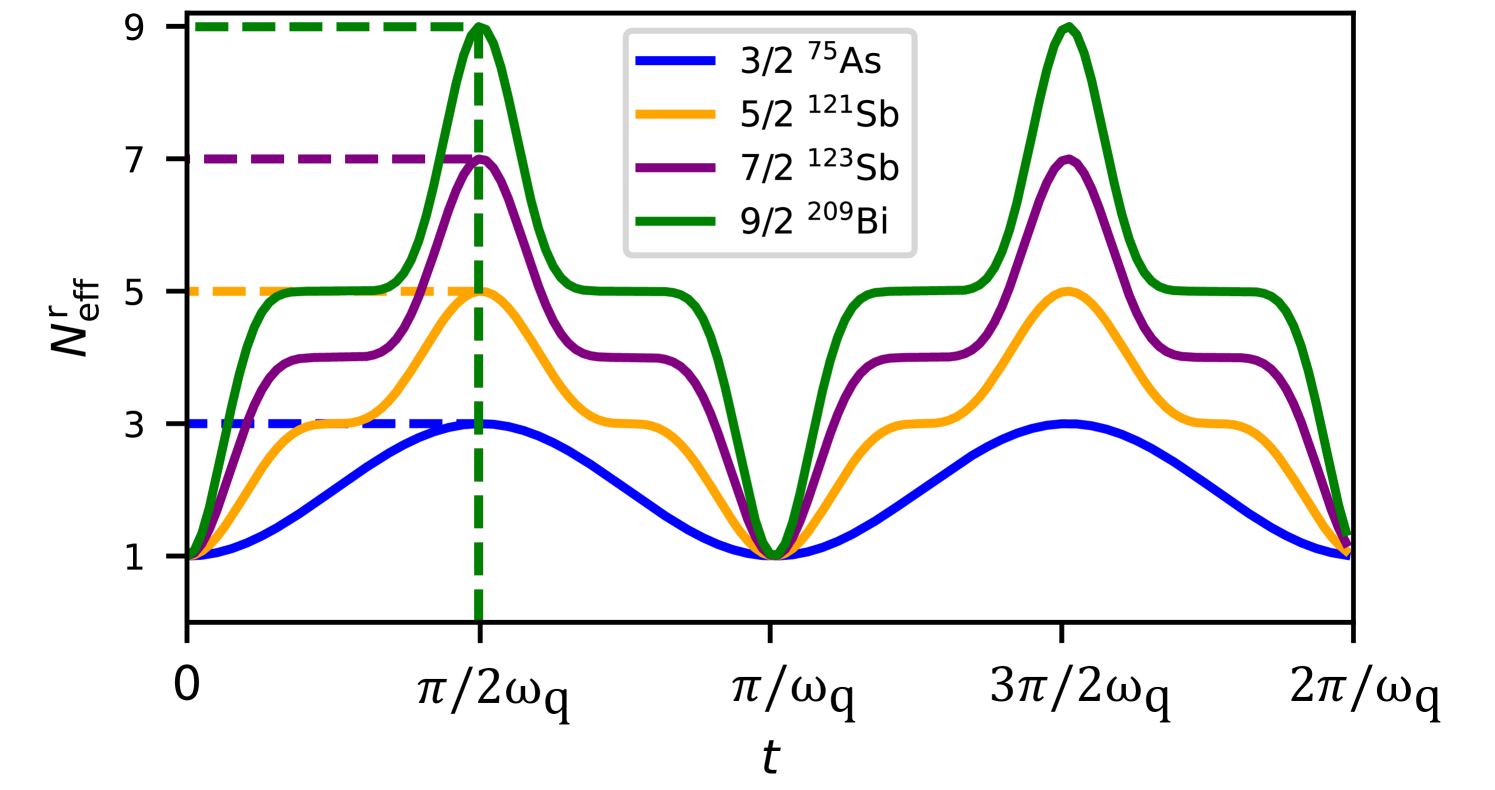
The degree of superposition (Eq. (3)) increases and decreases periodically during OAT, as shown in Fig. 3. for a spin coherent state on the axis of the Bloch sphere at , increases as the spin state squeezes, then reaches the flat-top of the “mesa” where it interferes with itself and finally increases again (“hill”) as two distinct components form resulting in a SCS at . Under further evolution, the SCS returns to a coherent state at , which again squeezes to a SCS at , and so on. This periodic process of collapse-and-revival of the SCS has a time period of and is a signature of coherence [47]. From the plots for different values of nuclear spin in Fig. 3, we note the macroscopicity of the SCSs through the linear scaling of their size .
IV Control Scheme
External control of a high-spin nucleus is required for initialization, manipulation and detection of nuclear-SCSs. For initialization, the eigenstate , which is also a coherent state, should first be rotated to reside on the axis of the Bloch sphere. Then, OAT results in a SCS on the axis for a half-integer nuclear spin, but, for donors in solid-state devices, nuclear-spin initialization and measurement is limited to the eigenstates of . Observing nuclear SCSs could be possible with angular momentum operations, which are trivial when [42, 48] or with a tunable non-linearity [49]. However, quantum control is needed as, experimentally, Hz kHz such that a RF pulse can only selectively drive a particular nuclear spin transition leading to Givens rotations, and the quadrupole coupling cannot be turned on-and-off.
For applying global SU(2) rotations with an always-on non-linearity and low drive strength, we use a multi-tone (MT) pulse that is a superposition of tones of equal amplitudes, corresponding to the nearest neighbor sub-spaces with transition frequencies represented by frequency vector . Each tone has a global phase and a pulse envelope switched on at a time is described by the amplitude . Here, tunes the axis of rotation on the Bloch sphere while preserving the relative phase between different energy levels. The frequency of SU(2) rotations is generalized from the Rabi frequency for a two-level nuclear spin, to a high-spin nucleus by dividing the Rabi frequency by the number of tones , i.e. . Applying this pulse for time rotates the nuclear spin by angle given by . In contrast to other schemes that employ numerical techniques with multi-tone control [50, 51], we derive exact expressions for phase-locked pulses, which can enable novel experimental applications such as full-state tomography and interferometry with a high-spin nucleus.
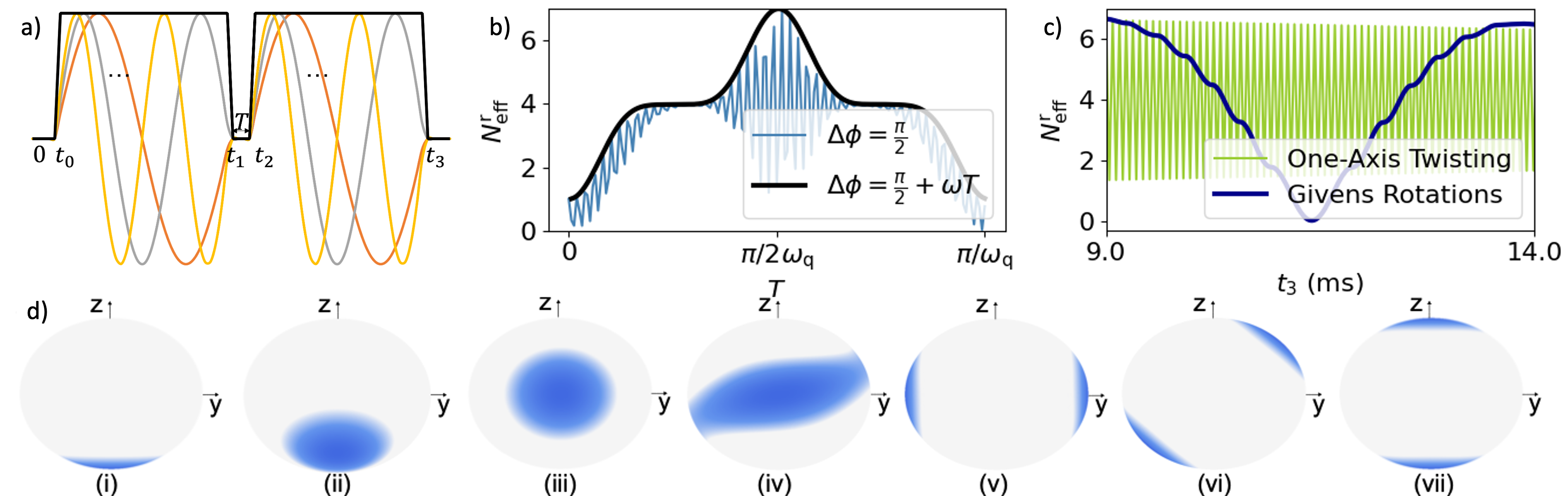
Figure 4(a) shows our Ramsey-like control sequence to realize SCSs, where a square-shaped MT RF pulse is applied to the initial state between time and . Then the pulse is switched off for time , and again applied between and , with the amplitude
| (4) |
for the top-hat function. Here, the global rotation of would take time and setting the phase difference between the first and the second global rotations accounts for the angle between a coherent state and the resulting SCS on the equator. The resulting dynamics are shown in Fig. 4(d), where we note that SCSs along any axis can be realized using global rotations (Fig. 4(d)(vi)). The quadrupole coupling cannot be turned off and these states squeeze during rotations. A SCS can be stored for long times by aligning it to the fixed points on the axis (Fig. 4(d)(vii)).
For a spin- 123Sb nucleus, Fig. 4(b) shows the change in , for , as is varied, similar to Fig. 3. When , we observe a rapid variation of with a frequency of , because nuclear-spin states generated by OAT undergo Larmor precession and when the axis of rotation corresponds with the axis of the SCS, the second global rotation is unable to move the state. To remedy this immobility, we assign a -dependent shift to the phase difference: in (IV), which is equivalent to a rotating-frame transformation, and results in the periodic collapses-and-revivals of a SCS solely due to OAT, which would enable efficient experimental detection.
V Virtual Phase Control
In this section, we show that cat-state generation is possible with just phase modulation of multi-tone pulses in the generalized rotating frame of reference. First, we note that, in the limit of large Zeeman interaction , we can neglect non-commuting terms, such as of the quadrupole interaction (1) so that the non-linear evolution is only described in terms of the strength of quadrupole tensor, , parallel to the magnetic field . Under this approximation and using the notation , the effective Hamiltonian is
| (5) |
where , , and are respectively the frequency, amplitude and phase of the component of the multi-tone control. The eigenstates of the nuclear spin have energy
| (6) |
for .
Now we transform the Hamiltonian to the generalized rotating frame, defined by the diagonal matrix [50]
| (7) |
and obtain
| (8) |
where
| (9) |
We note that global rotations are applied by setting and ; for example, using is equivalent to
| (10) |
and is equivalent to .
One-axis twisting can be realized by virtually updating the phases of a multi-tone pulse. To see this, we note that that the effective quadrupolar operator applied for duration generates the operation , which results in a non-linear phase shift between the different eigenstates of a nuclear-spin Hamiltonian. Using the dummy variable for integers in the interval , a state
| (11) |
is transformed as
| (12) |
where is the resulting phase shift on the energy eigenstate .
Now, we can factor out the global phase and instead of freely evolving a state under one-axis twisting, apply equivalent phase updates,
| (13) |
to the subsequent multi-tone pulse. Such virtual phase updates would have same effect as free non-linear evolution and would result in cat state formation when . Thus, in the generalized rotating frame, we can start with the initial state , apply a global rotation with , followed by a second by a global rotation with
| (14) |
realizing cat states by only phase modulation of multi-tone pulses.
VI Decoherence
Cat states with a lifetime of several milliseconds can be achieved using silicon-based chips with an implanted spin- 123Sb donor atom, that have a nuclear spin coherence time ms for two-level transitions inferred from experiments on nuclear electric resonance [33]. SCSs along the -axis would have a reduced coherence time, lower by a factor of , due to the large separation between the two components, resulting in a coherence time of ms for 123Sb. Even for a modest driving strength Hz, a -global rotation would take ms. Thus, our approach, using two MT pulses and OAT, can yield highly coherent SCSs in less than 9 ms—within the dephasing time on current hardware. Faster Rabi frequencies are easily achieved for nuclear magnetic resonance (NMR) methods [40, 34], that could reduce the time needed for MT pulses and lead to faster generation and detection of nuclear SCSs.
We compare the performance of OAT to an intuitively appealing gate sequence for creating SCSs, achieved by sequential Givens rotations [52]. Starting with , we apply a -pulse of frequency to form the superposition , with unit norm implied. Then, we apply a sequence of -pulses to create the SCS . For observing a collapse of the SCS, repeating the same sequence evolves the SCS into the coherent state , opposite to the initial state . In total, pulses would be needed for each collapse-and-revival using Givens rotations, that would take ms for a with Rabi frequency Hz, in contrast to OAT which takes just s when kHz.
We simulate our scheme under decoherence from a magnetic field fluctuating at rate , modeled using Lindblad operator , and an electric field fluctuating at rate , modeled using . Figure 4(c) shows vs evolution time beyond 9 ms (approximate time to form the first SCS). We note that OAT is two orders of magnitude faster than both Givens rotations and the dephasing timescale, opening the possibility of realizing hundreds of SCS collapses-and-revivals by using a strong non-linearity relative to decoherence, which makes our SCS robust, in contrast to alternative platforms [53]. Additionally, SCSs generated by Givens rotations lie on the axis, where the dephasing rate of the cat state increases with the nuclear spin increases; in comparison, cat states produced by one-axis twisting lie on the equator, perpendicular to the dephasing axis, and are highly protected against decoherence.
VII Conclusion
In summary, Schrödinger cat states are important for investigating foundations of quantum mechanics as well as for applications such as quantum error correction but are fragile and hard to realize. We propose a new platform for realizing macroscopic spin cat states by converting quadrupolar two-axis counter twisting to one-axis twisting on a high-spin donor in a solid-state device. Our scheme can deterministically generate spin cat states on-demand without post-selection and is two orders of magnitude faster than the dephasing timescale, resulting in highly coherent states. We show that, in the generalized rotating frame, a spin coherent state can be converted to a cat states by only phase modulation of multi-tone pulses. Unlike continuous-variable systems, we generate cat states without entanglement with an ancilla, which renders robustness against error propagation [25] and opens the possibility of storing long-lived nuclear-spin cat states. Furthermore, our cat states can be experimentally realized on a single nucleus, which could lead to novel applications in quantum information processing.
Acknowledgements.
We thank Dipankar Home for useful discussion on macroscopicity of nuclear cat states. P.G. and B.C.S. acknowledge support from NSERC. Work at UNSW was funded by an Australian Research Council (DP210103769). A.V. and X.Y. acknowledge support from the Sydney Quantum Academy.References
- Schrödinger [1935] E. Schrödinger, Die gegenwärtige Situation in der Quantenmechanik, Naturwissenschaften 23, 807 (1935).
- Yurke and Stoler [1986] B. Yurke and D. Stoler, Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion, Phys. Rev. Lett. 57, 13 (1986).
- Sanders [1989] B. C. Sanders, Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement, Phys. Rev. A 40, 2417 (1989).
- Glauber [1963] R. J. Glauber, Coherent and incoherent states of the radiation field, Phys. Rev. 131, 2766 (1963).
- Perelomov [1986] A. Perelomov, Generalized Coherent States and Their Applications (Springer, Berlin, 1986).
- Perelomov [1972] A. M. Perelomov, Coherent states for arbitrary Lie group, Commun. Math. Phys. 26, 222 (1972).
- Schlosshauer [2005] M. Schlosshauer, Decoherence, the measurement problem, and interpretations of quantum mechanics, Rev. Mod. Phys. 76, 1267 (2005).
- Leggett [1980] A. J. Leggett, Macroscopic Quantum Systems and the Quantum Theory of Measurement, Prog. Theor. Phys. Suppl. 69, 80 (1980).
- Leggett [2002] A. J. Leggett, Testing the limits of quantum mechanics: motivation, state of play, prospects, J. Phys. Condens. Matter 14, R415 (2002).
- Bassi et al. [2013] A. Bassi, K. Lochan, S. Satin, T. P. Singh, and H. Ulbricht, Models of wave-function collapse, underlying theories, and experimental tests, Rev. Mod. Phys. 85, 471 (2013).
- Wódkiewicz [2000] K. Wódkiewicz, Nonlocality of the Schrödinger cat, New J. Phys. 2, 21 (2000).
- Ofek et al. [2016] N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, Extending the lifetime of a quantum bit with error correction in superconducting circuits, Nature 536, 441 (2016).
- Puri et al. [2019] S. Puri, A. Grimm, P. Campagne-Ibarcq, A. Eickbusch, K. Noh, G. Roberts, L. Jiang, M. Mirrahimi, M. H. Devoret, and S. M. Girvin, Stabilized cat in a driven nonlinear cavity: a fault-tolerant error syndrome detector, Phys. Rev. X 9, 041009 (2019).
- Puri et al. [2020] S. Puri, L. St-Jean, J. A. Gross, A. Grimm, N. E. Frattini, P. S. Iyer, A. Krishna, S. Touzard, L. Jiang, A. Blais, S. T. Flammia, and S. M. Girvin, Bias-preserving gates with stabilized cat qubits, Sci. Adv. 6, eaay5901 (2020).
- Gross [2021] J. A. Gross, Designing codes around interactions: the case of a spin, Phys. Rev. Lett. 127, 010504 (2021).
- Simmons et al. [2010] S. Simmons, J. A. Jones, S. D. Karlen, A. Ardavan, and J. J. L. Morton, Magnetic field sensors using 13-spin cat states, Phys. Rev. A 82, 022330 (2010).
- Facon et al. [2016] A. Facon, E.-K. Dietsche, D. Grosso, S. Haroche, J.-M. Raimond, M. Brune, and S. Gleyzes, A sensitive electrometer based on a Rydberg atom in a Schrödinger-cat state, Nature 535, 262 (2016).
- Giovannetti et al. [2006] V. Giovannetti, S. Lloyd, and L. Maccone, Quantum metrology, Phys. Rev. Lett. 96, 010401 (2006).
- Karimipour et al. [2002] V. Karimipour, A. Bahraminasab, and S. Bagherinezhad, Entanglement swapping of generalized cat states and secret sharing, Phys. Rev. A 65, 042320 (2002).
- Brask et al. [2010] J. B. Brask, I. Rigas, E. S. Polzik, U. L. Andersen, and A. S. Sørensen, Hybrid long-distance entanglement distribution protocol, Phys. Rev. Lett. 105, 160501 (2010).
- Fink et al. [2008] J. M. Fink, M. Göppl, M. Baur, R. Bianchetti, P. J. Leek, A. Blais, and A. Wallraff, Climbing the Jaynes–Cummings ladder and observing its nonlinearity in a cavity QED system, Nature 454, 315 (2008).
- Lee et al. [2017] J. Lee, M. J. Martin, Y.-Y. Jau, T. Keating, I. H. Deutsch, and G. W. Biedermann, Demonstration of the Jaynes-Cummings ladder with Rydberg-dressed atoms, Phys. Rev. A 95, 041801(R) (2017).
- Grimm et al. [2020] A. Grimm, N. E. Frattini, S. Puri, S. O. Mundhada, S. Touzard, M. Mirrahimi, S. M. Girvin, S. Shankar, and M. H. Devoret, Stabilization and operation of a Kerr-cat qubit, Nature 584, 205 (2020).
- Heeres et al. [2017] R. W. Heeres, P. Reinhold, N. Ofek, L. Frunzio, L. Jiang, M. H. Devoret, and R. J. Schoelkopf, Implementing a universal gate set on a logical qubit encoded in an oscillator, Nat. Commun. 8, 94 (2017).
- Rosenblum et al. [2018] S. Rosenblum, P. Reinhold, M. Mirrahimi, L. Jiang, L. Frunzio, and R. J. Schoelkopf, Fault-tolerant detection of a quantum error, Science 361, 266 (2018).
- Hacker et al. [2019] B. Hacker, S. Welte, S. Daiss, A. Shaukat, S. Ritter, L. Li, and G. Rempe, Deterministic creation of entangled atom–light Schrödinger-cat states, Nat. Photon. 13, 110 (2019).
- Omran et al. [2019] A. Omran, H. Levine, A. Keesling, G. Semeghini, T. T. Wang, S. Ebadi, H. Bernien, A. S. Zibrov, H. Pichler, S. Choi, J. Cui, M. Rossignolo, P. Rembold, S. Montangero, T. Calarco, M. Endres, M. Greiner, V. Vuletifá, and M. D. Lukin, Generation and manipulation of Schrödinger cat states in Rydberg atom arrays, Science 365, 570 (2019).
- Rauschenbeutel et al. [2000] A. Rauschenbeutel, G. Nogues, S. Osnaghi, P. Bertet, M. Brune, J.-M. Raimond, and S. Haroche, Step-by-step engineered multiparticle entanglement, Science 288, 2024 (2000).
- Song et al. [2017] C. Song, K. Xu, W. Liu, C. P. Yang, S. B. Zheng, H. Deng, Q. Xie, K. Huang, Q. Guo, L. Zhang, P. Zhang, D. Xu, D. Zheng, X. Zhu, H. Wang, Y. Chen, C. Lu, S. Han, and J. W. Pan, 10-qubit entanglement and parallel logic operations with a superconducting circuit, Phys. Rev. Lett. 119, 180511 (2017).
- Song et al. [2019] C. Song, K. Xu, H. Li, Y.-R. Zhang, X. Zhang, W. Liu, Q. Guo, Z. Wang, W. Ren, J. Hao, H. Feng, H. Fan, D. Zheng, D.-W. Wang, H. Wang, and S.-Y. Zhu, Generation of multicomponent atomic Schrödinger cat states of up to 20 qubits, Science 365, 574 (2019).
- Monz et al. [2011] T. Monz, P. Schindler, J. T. Barreiro, M. Chwalla, D. Nigg, W. A. Coish, M. Harlander, W. Hänsel, M. Hennrich, and R. Blatt, 14-qubit entanglement: creation and coherence, Phys. Rev. Lett. 106, 130506 (2011).
- Ourjoumtsev et al. [2006] A. Ourjoumtsev, R. Tualle-Brouri, J. Laurat, and P. Grangier, Generating optical schrödinger kittens for quantum information processing, Science 312, 83 (2006).
- Asaad et al. [2020] S. Asaad, V. Mourik, B. Joecker, M. A. I. Johnson, A. D. Baczewski, H. R. Firgau, M. T. Ma̧dzik, V. Schmitt, J. J. Pla, F. E. Hudson, K. M. Itoh, J. C. McCallum, A. S. Dzurak, A. Laucht, and A. Morello, Coherent electrical control of a single high-spin nucleus in silicon, Nature 579, 205 (2020).
- de Fuentes et al. [2023] I. F. de Fuentes, T. Botzem, M. A. I. Johnson, A. Vaartjes, S. Asaad, V. Mourik, F. E. Hudson, K. M. Itoh, B. C. Johnson, A. M. Jakob, J. C. McCallum, D. N. Jamieson, A. S. Dzurak, and A. Morello, Navigating the 16-dimensional Hilbert space of a high-spin donor qudit with electric and magnetic fields (2023), arXiv:2306.07453 [quant-ph] .
- Auccaise et al. [2015] R. Auccaise, A. G. Araujo-Ferreira, R. S. Sarthour, I. S. Oliveira, T. J. Bonagamba, and I. Roditi, Spin squeezing in a quadrupolar nuclei NMR system, Phys. Rev. Lett. 114, 043604 (2015).
- Aksu Korkmaz and Bulutay [2016] Y. Aksu Korkmaz and C. Bulutay, Nuclear spin squeezing via electric quadrupole interaction, Phys. Rev. A 93, 013812 (2016).
- Morello et al. [2020] A. Morello, J. J. Pla, P. Bertet, and D. N. Jamieson, Donor spins in silicon for quantum technologies, Adv. Quantum Technol. 3, 2000005 (2020).
- Savytskyy et al. [2023] R. Savytskyy, T. Botzem, I. Fernandez de Fuentes, B. Joecker, J. J. Pla, F. E. Hudson, K. M. Itoh, A. M. Jakob, B. C. Johnson, D. N. Jamieson, et al., An electrically driven single-atom “flip-flop” qubit, Sci. Adv. 9, eadd9408 (2023).
- Dehollain et al. [2012] J. P. Dehollain, J. J. Pla, E. Siew, K. Y. Tan, A. S. Dzurak, and A. Morello, Nanoscale broadband transmission lines for spin qubit control, Nanotechnol. 24, 015202 (2012).
- Pla et al. [2013] J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. Morton, F. A. Zwanenburg, D. N. Jamieson, A. S. Dzurak, and A. Morello, High-fidelity readout and control of a nuclear spin qubit in silicon, Nature 496, 334 (2013).
- Johansson et al. [2013] J. Johansson, P. Nation, and F. Nori, QuTiP 2: a Python framework for the dynamics of open quantum systems, Comput. Phys. Commun. 184, 1234 (2013).
- Bulutay [2017] C. Bulutay, Cat-state generation and stabilization for a nuclear spin through electric quadrupole interaction, Phys. Rev. A 96, 012312 (2017).
- Liu et al. [2011] Y. C. Liu, Z. F. Xu, G. R. Jin, and L. You, Spin squeezing: transforming one-axis twisting into two-axis twisting, Phys. Rev. Lett. 107, 013601 (2011).
- Fröwis and Dür [2012] F. Fröwis and W. Dür, Measures of macroscopicity for quantum spin systems, New J. Phys. 14, 093039 (2012).
- Fröwis et al. [2018] F. Fröwis, P. Sekatski, W. Dür, N. Gisin, and N. Sangouard, Macroscopic quantum states: measures, fragility, and implementations, Rev. Mod. Phys. 90, 025004 (2018).
- Greenberger et al. [1989] D. M. Greenberger, M. A. Horne, and A. Zeilinger, Going beyond Bell’s theorem, in Bell’s Theorem, Quantum Theory and Conceptions of the Universe, Fundamental Theories of Physics, Vol. 37, edited by M. Kafatos (Springer Netherlands, Dordrecht, 1989) pp. 69–72.
- Chalopin et al. [2018] T. Chalopin, C. Bouazza, A. Evrard, V. Makhalov, D. Dreon, J. Dalibard, L. A. Sidorenkov, and S. Nascimbene, Quantum-enhanced sensing using non-classical spin states of a highly magnetic atom, Nat. Commun. 9, 4955 (2018).
- Omanakuttan et al. [2021] S. Omanakuttan, A. Mitra, M. J. Martin, and I. H. Deutsch, Quantum optimal control of ten-level nuclear spin qudits in , Phys. Rev. A 104, L060401 (2021).
- Pezzè et al. [2018] L. Pezzè, A. Smerzi, M. K. Oberthaler, R. Schmied, and P. Treutlein, Quantum metrology with nonclassical states of atomic ensembles, Rev. Mod. Phys. 90, 035005 (2018).
- Leuenberger and Loss [2003] M. N. Leuenberger and D. Loss, Grover algorithm for large nuclear spins in semiconductors, Phys. Rev. B 68, 165317 (2003).
- Godfrin et al. [2017] C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer, and F. Balestro, Operating quantum states in single magnetic molecules: implementation of Grover’s quantum algorithm, Phys. Rev. Lett. 119, 187702 (2017).
- Cybenko [2001] G. Cybenko, Reducing quantum computations to elementary unitary operations, Comput. Sci. Eng. 3, 27 (2001).
- Kirchmair et al. [2013] G. Kirchmair, B. Vlastakis, Z. Leghtas, S. E. Nigg, H. Paik, E. Ginossar, M. Mirrahimi, L. Frunzio, S. M. Girvin, and R. J. Schoelkopf, Observation of quantum state collapse and revival due to the single-photon kerr effect, Nature 495, 205 (2013).
- Morello et al. [2010] A. Morello, J. J. Pla, F. A. Zwanenburg, K. W. Chan, K. Y. Tan, H. Huebl, M. Möttönen, C. D. Nugroho, C. Yang, J. A. van Donkelaar, A. D. C. Alves, D. N. Jamieson, C. C. Escott, L. C. L. Hollenberg, R. G. Clark, and A. S. Dzurak, Single-shot readout of an electron spin in silicon, Nature 467, 687 (2010).
- Wang et al. [2020] Y. Wang, Z. Hu, B. C. Sanders, and S. Kais, Qudits and high-dimensional quantum computing, Front. Phys. 8 (2020).
- Huelga et al. [1997] S. F. Huelga, C. Macchiavello, T. Pellizzari, A. K. Ekert, M. B. Plenio, and J. I. Cirac, Improvement of frequency standards with quantum entanglement, Phys. Rev. Lett. 79, 3865 (1997).
Appendix A Dynamics
A.1 Quadrupole interaction
Our system is described by the Hamiltonian
| (15) |
where is the nuclear gyromagnetic ratio, is the strength of the static magnetic field oriented along axis, is the strength of perturbative magnetic field and the time-dependent pulse amplitude. The quadrupole moment tensor components are
| (16) |
with the electric quadrupole moment, which characterizes the spherical asymmetry of the nuclear charge distribution, e the elementary charge, the reduced Planck’s constant, and the electric field gradient. The quadrupole moment tensor ((16)) is real, traceless and symmetric; thus, a set of principal axes of symmetry (PAS) exist for which the quadrupole moment tensor can be diagonalized.
The quadrupole term in the Hamiltonian can be expressed in the PAS as
| (17) |
where is the asymmetry parameter for , and . The orientation of the PAS with respect to the lab frame of reference can be expressed using Euler angles as
| (18) |
| (19) |
| (20) |
Together with , the three Euler angles completely specify the symmetric and traceless quadrupole tensor for a given nucleus.
The EFG depends on several factors including microscopic interactions within the crystal lattice, the position of the donor, the magnitude of the applied electric field and the fabrication process of the device. In general, it is hard to pre-determine the EFG orientation or quadrupole splitting; however, finite-elements modelling can be used to estimate the strength of quadrupole interaction. In recent experiments [33, 34], a quadrupole splitting of up to kHz was observed.
A.2 Macroscopicity
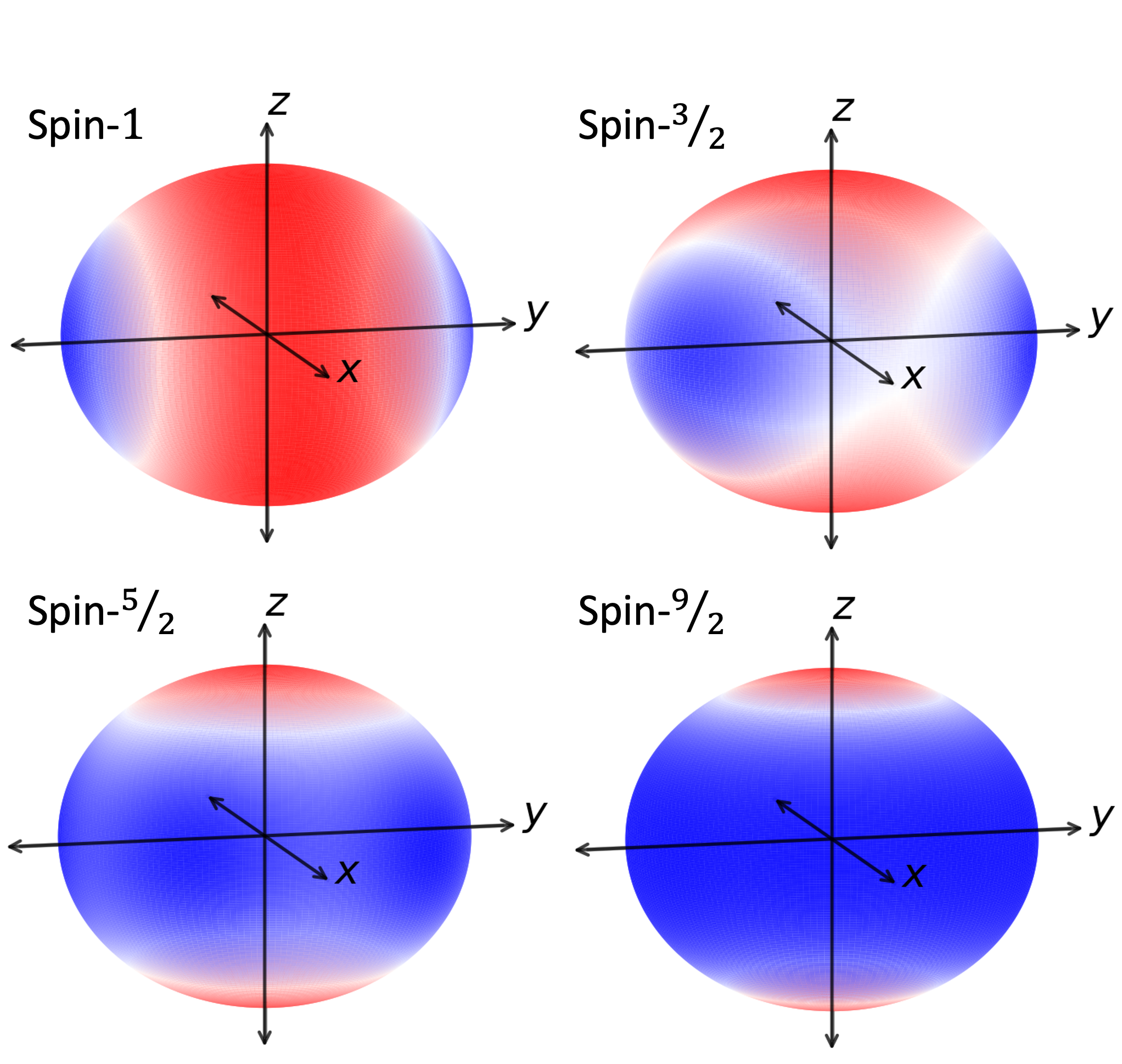
Figure 5 shows the Husimi Q-function plots of superpositions of maximally separated coherent states along the axis of the Bloch sphere. We note that spin- case lacks bi-modality and cannot form cat states. Spin- case forms spin kitten states and higher spins () are required for forming cat states (implying macroscopic).
Appendix B Experimental Control
B.1 Initialization and readout
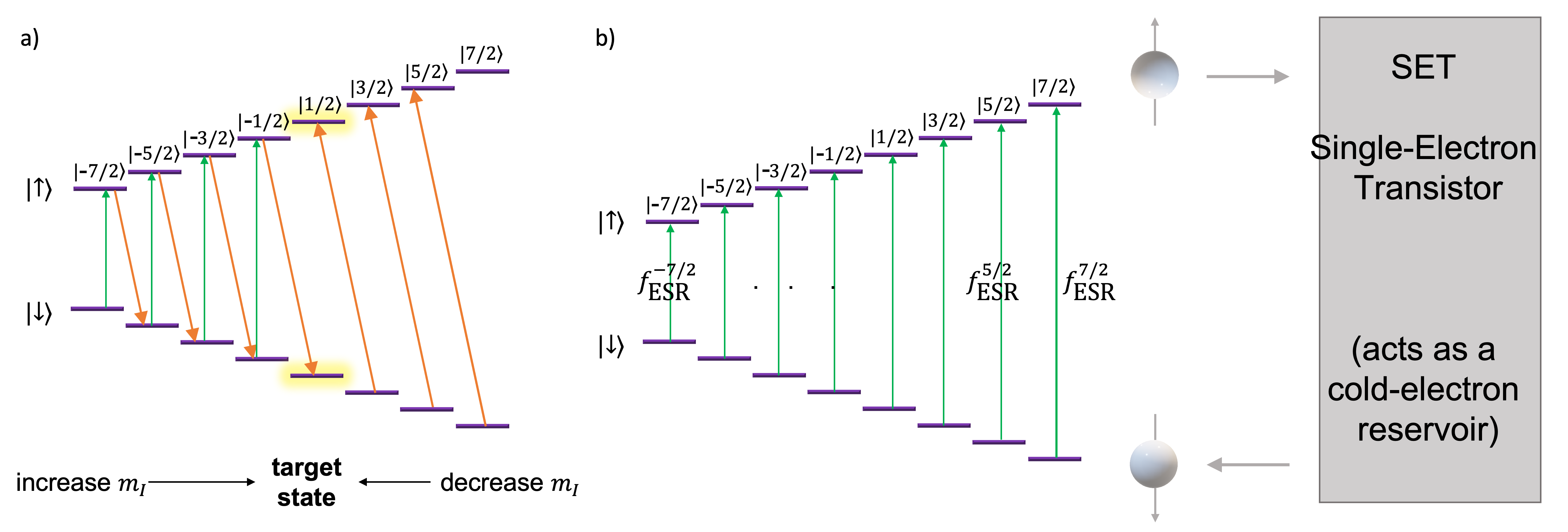
The nuclear spin of the donor atom can be coherently controlled through electromagnetic interaction using the electrostatic gates and microwave antenna fabricated on the chip. The donor atom is subjected to a static potential, with the nuclear spin coupled to an electron spin, and initialization of the nuclear spin is done via electron-nuclear hyperfine coupling. A typical experiment uses flip-flop driving [38], in which an electron spin is flipped and a nuclear spin is flopped in opposite directions and high-power chirp pulses, corresponding to different transitions, are applied sequentially. As shown in Fig. 6 (a), to reach a target state in the energy ladder, first, the nuclear spin is pumped down from all higher-lying energy levels using flip-flop transitions (orange). Then, the nuclear spin state is pumped up from all the lower-lying energy levels using a combination electron-spin resonance pulses (green) and flip-flop pulses (orange).
The initialization and readout schemes benefit from the coupling of a nuclear spin to an electron spin, which enables fast initialization of the nuclear spin to any energy eigenstate , of which are spin coherent states. We use the ground state as the initial state in our scheme. After initialization, the electrostatic potential is increased to ionize the donor atom by removing the electron and only the nuclear spin is manipulated using RF pulses [39]. When the nuclear spin reaches the desired final state, the donor atom is de-ionized such that the nuclear spin again couples to an electron. As shown in Fig. 6 (b), the nuclear-spin state is read out using single-shot detection with pulsed electron spin resonance and spin-dependent tunneling of the electron to the SET, which acts as a cold-electron reservoir [54].
.
B.2 Control
We manipulate the nucleus using RF magnetic pulses that cause NMR transitions with selection rule . The quadrupole interaction shifts the energy levels of a nuclear spin qudit, as shown in Fig. 2 of the main text, which allows selectively addressed transitions by tuning the frequency of Rabi pulses, applied through the time-dependent perturbation in Eq. (15). At off-resonant drives, the probability of a Rabi flip is given by,
| (21) |
where is the drive strength (15), with the difference between the detuning of the drive from the transition frequency. With quadrupole interaction kHz achieved in experiments [33, 34] and drive strength kHz, frequency difference between two transitions , thus, . Thus, cross talks are highly suppressed. Additionally, the quadrupole interaction generates fast collapse and revivals due to non-linear evolution having time-period of a few microseconds, which can be resolved by pulses applied using an Arbitrary Waveform Generator (AWG) with a resolution of 1 ns. While lower-order non-linearity would slow down SCS generation, higher-order non-linearity, for example in the GHz range, would generate OAT at a rate faster than the resolution of an AWG.
Appendix C Decoherence
C.1 Master equation for a high-spin nucleus
We model decoherence using a Lindblad master equation of the form
| (22) |
where is the density matrix of the nuclear spin, is the decay rate due to magnetic field fluctuations, modeled using Lindblad operator and is the decay rate due to electric field fluctuations, modeled using Lindblad operator . Here, we take the electric field fluctuation only in the direction, i.e. parallel to the Zeeman splitting, because other components of the electric quadrupole interaction are washed out, as described above.
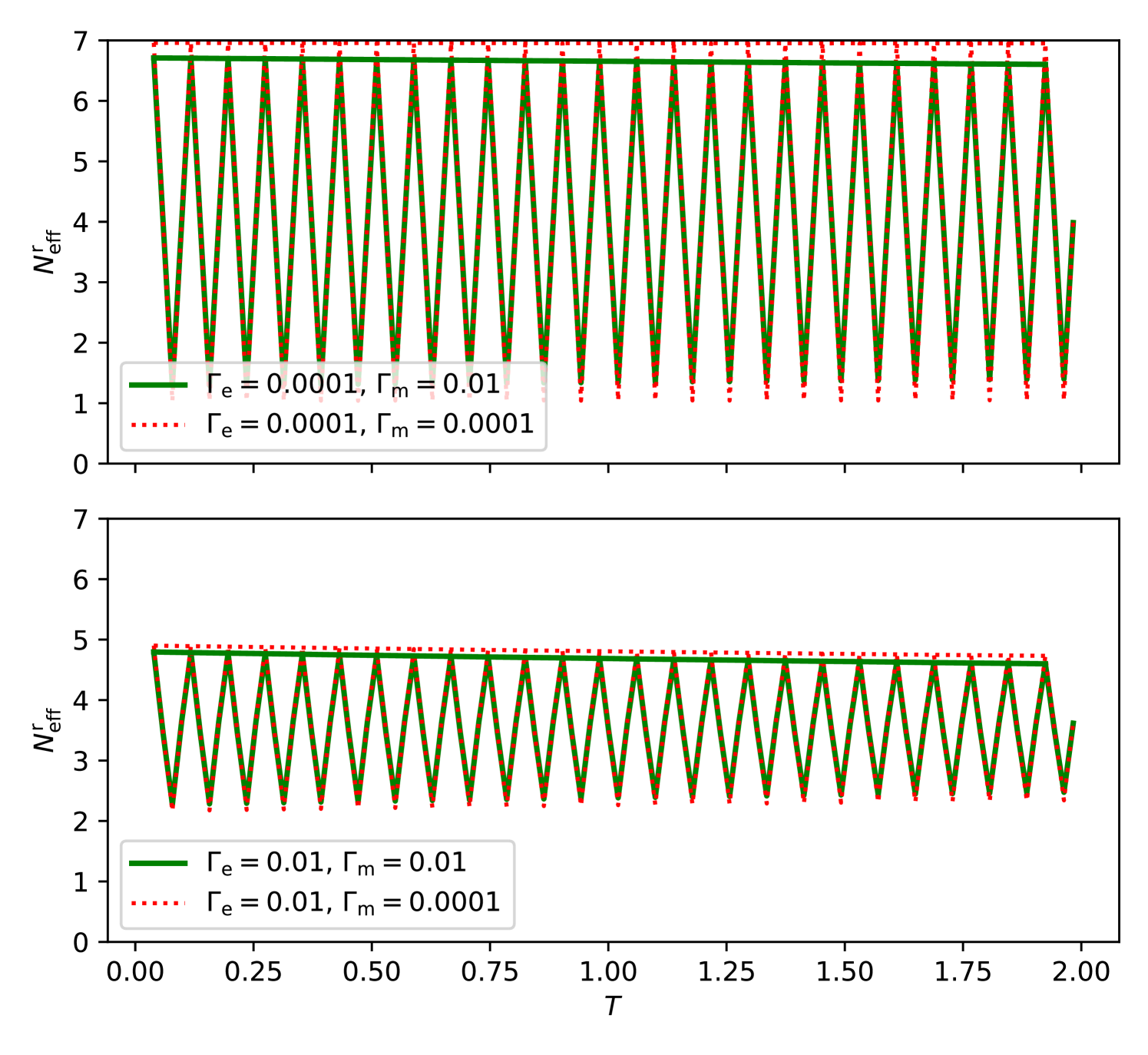
We simulate the cat-state collapse-and-revival control scheme for various values of and , shown in Fig. 7. Here, magnetic fluctuations slowly dephase the nuclear spin and the coherence of the SCS decreases during collapse-and-revivals. On the other hand, electric field fluctuations have a more drastic effect on SCSs generated by quadrupole interaction, resulting in an overall decrease of the variance, i.e. macroscopicity of the SCSs.
C.2 Coherence time of a qudit SCS
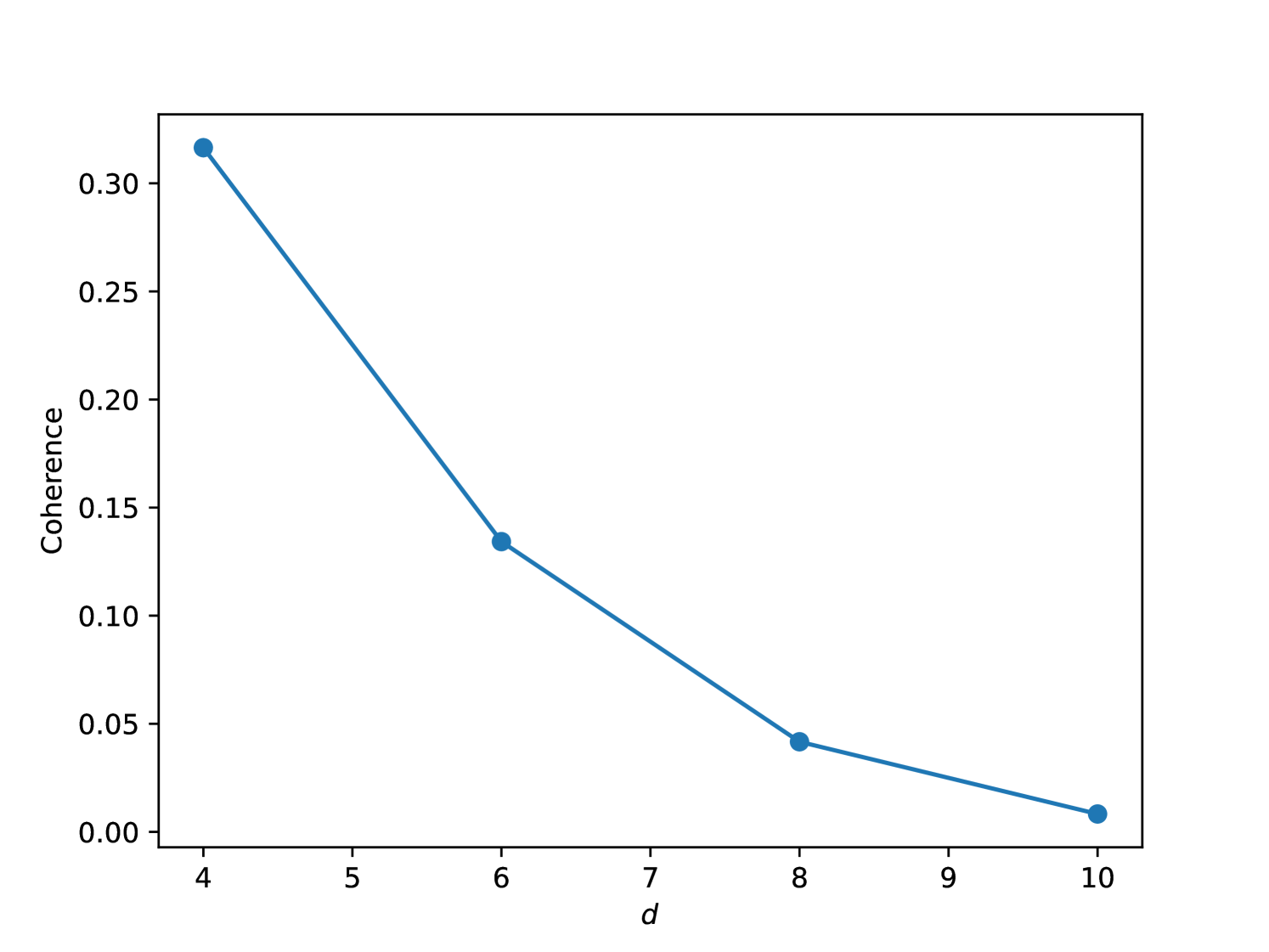
We study the scaling of the coherence of a SCS with respect to the Hilbert space dimension of a qudit [55] and consider dephasing purely due to magnetic field fluctuations, of the state for different values of . The density matrix of such a state consists only of four elements: two diagonal elements corresponding to the population in and two off-diagonal components that quantify the coherence of the superposition state. In Fig. 8, we plot the magnitude of the off-diagonal component after a fixed time of 1 ms under an amplified dephasing at rate of kHz (). We note that coherence decreases with the dimension of the nuclear spin and results in a linear decrease in coherence time as the dimension of a qudit increases. Such a trade-off between lifetime and the macroscopicity of a SCS is similarly found in other systems such as harmonic oscillators and maximally entangled GHZ states [56]. However, compared to other systems, a nuclear spin, with naturally long coherence times, can help increase the lifetime of practically achievable SCSs.
Appendix D Converting two-axis counter twisting to one-axis twisting
D.1 Two-axis counter twisting
Substituting in Eq. (17), the quadrupole interaction can be described as
| (23) |
which is equivalent to one-axis twisting (OAT) when , two-axis counter twisting (TACT) when , and partial TACT otherwise. Under TACT, the nuclear spin is simultaneously twisted about two axes, which increases the squeezing speed and the nuclear spin returns to a coherent state faster than in the case of OAT (as can be noted in Fig. 9 for ). During this, the spin does not spread over the equator of the Bloch sphere due to counter twisting, which prevents interference and cat-state formation.
The quadrupole interaction can only generate squeezed states for , as can be seen in Fig. 9. For small , partial TACT can create cat-like states, as shown for in Fig. 9; however, its two components are not spin coherent states and the separation between them is smaller than that for a macroscopic SCS. In practice, there is little to no control over the in-situ EFG generated by the lattice distortions, and depends on several experimental factors. Thus, quadrupole interaction alone cannot be used for realizing SCSs.
D.2 Adding a linear interaction
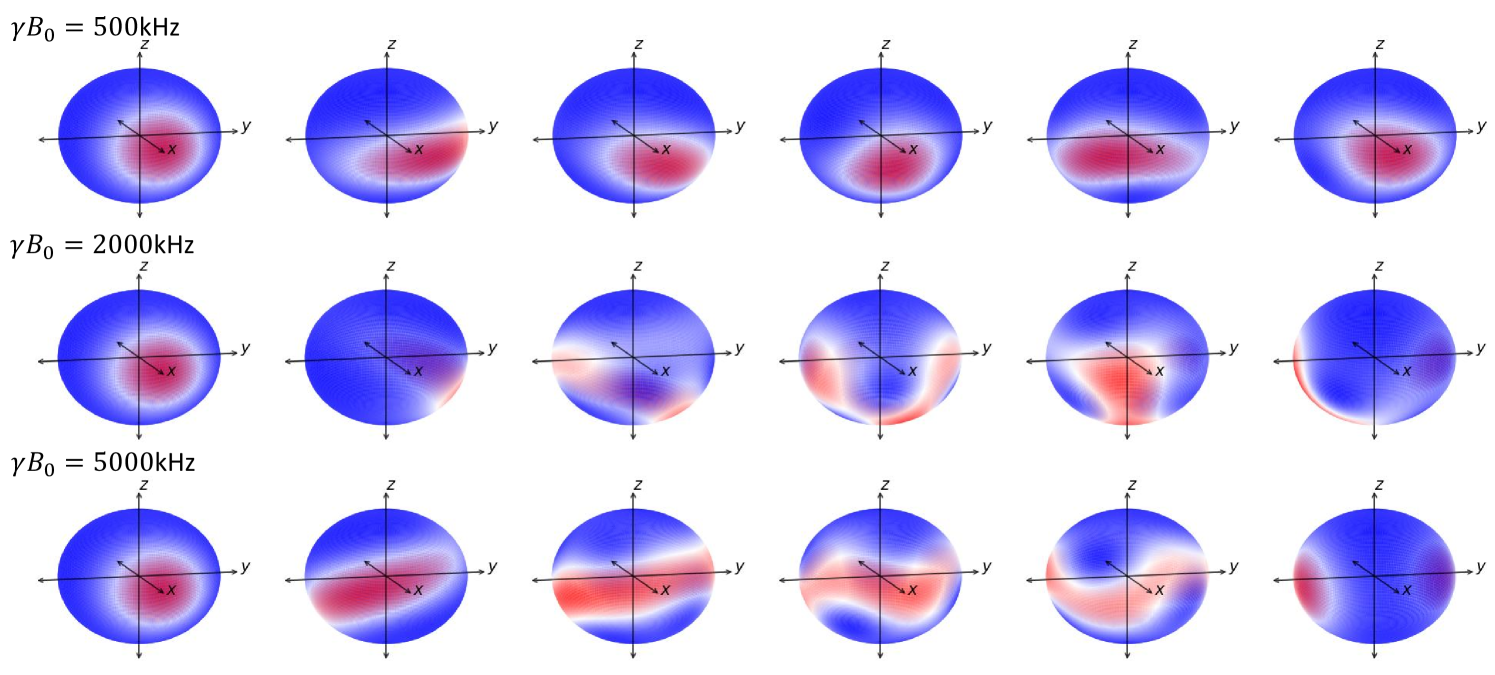
We convert TACT to OAT by adding a large linear term, introduced here by the Zeeman interaction, that “washes out” TACT. To understand this, we note that spin squeezing is caused by non-linear transitions induced by and , and, for the simple case of , causes non-linear phase shifts and causes quadrupolar transitions between different energy eigenstates with . TACT can be converted to OAT if -induced quadrupolar transitions can be prevented. This is achieved when the Zeeman splitting is much larger than quadrupole coupling, i.e. , and non-linear transitions induced by the relatively small term are prevented by the large energy level splitting. In such a case, only the component of the quadrupole interaction parallel to Zeeman interaction generates squeezing, which results in an effective one-axis twisting, regardless of the value of . Figure 10 shows nuclear spin squeezing under different strengths of quadrupole interaction, where we note that SCSs are formed only for a very large value of .
D.3 Effect of quadrupolar orientation
Above, we analyzed the special case of ; however, the conversion of TACT to OAT holds for any set of Euler angles and our scheme can create SCSs in-situ for any configuration of the nuclear quadrupolar interaction. In the presence of a large Zeeman interaction, effective spin squeezing is only caused by (15) and any other non-linear effect is washed-out. is always non-zero except when the principal axis is perpendicular to the Zeeman interaction, i.e. (20) and the asymmetry parameter , resulting in a quadrupole interaction similar to . In this corner case of OAT, an initial nuclear spin coherent state can form a spin SCS without any additional control.