Robust photon-mediated entangling gates between quantum dot spin qubits

We can model the effects of quasistatic charge noise on our cross-resonance gate by substituting $\epsilon_{i}\to\epsilon_{i}+\delta\epsilon_{i}$ and $t_{ci}\to t_{ci}+\delta t_{ci}$ for the detunings and tunnel couplings respectively, where $\delta\epsilon_{i}$ and $\delta t_{ci}$ are Gaussian-distributed random variables with standard deviations $\sigma_{\epsilon}$ and $\sigma_{t}$, respectively. In terms of the low-energy dynamics, the effect of these substitutions is random shifts in the qubit splittings $\omega_{i}$, drive strengths $\Omega_{i}^{x}$, and effective qubit-qubit interaction $J$. The noisy lab-frame Hamiltonian is

	$\displaystyle H(t)$	$\displaystyle=\frac{1}{2}\quantity(\omega_{1}+\delta\omega_{1})\sigma_{1}^{z}+\frac{1}{2}\quantity(\omega_{2}+\delta\omega_{2})\sigma_{2}^{z}-\quantity(J+\delta J)\sigma_{1}^{x}\sigma_{2}^{x}$
		$\displaystyle\hskip 8.53581pt+\cos(\omega_{2}t)\quantity(\quantity(\Omega_{1}^{z}+\delta\Omega_{1}^{z})\sigma_{1}^{z}+\quantity(\Omega_{1}^{x}+\delta\Omega_{1}^{x})\sigma_{1}^{x}).$

As in the noiseless case, we move into the frame rotating with the drive and diagonalize single-qubit terms. Then, discarding all of the same rapidly-oscillating terms as before, we arrive at the noisy DDF Hamiltonian

$$H_{DDF}=\frac{1}{2}\quantity(\eta+\delta\eta)\sigma_{1}^{z}+\frac{1}{2}\delta\omega_{2}\sigma_{2}^{z}-\frac{1}{2}\quantity(\tilde{J}-\delta\tilde{J})\sigma_{1}^{z}\sigma_{2}^{x}.$$

(2)

Note that, because of variations $\delta\omega_{1}$ and $\delta\Omega_{x}$, this is actually not the same DDF as in the noiseless case, but is related to it by an additional $\sigma_{1}^{y}$ rotation of angle $\delta\chi$.

We can compute the average fidelity $\bar{F}$ of the noisy gate $U^{(1)}_{\phi}=\mathcal{T}\exp(-i\int_{0}^{\phi/\tilde{J}}H_{DDF}(t^{\prime})\differential{t^{\prime}})$ relative to the noiseless gate. Expanding to lowest order in each of the shifted parameters, the average gate fidelity for a cross-resonance CNOT ($\phi=\pi/2$) is

$$\bar{F}\approx 1-\frac{\pi^{2}}{20}\quantity(\frac{\delta\eta}{\tilde{J}})^{2}-\frac{2}{5}\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{2}-\frac{\pi^{2}}{20}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})^{2}-\frac{2}{5}\delta\chi^{2}.$$

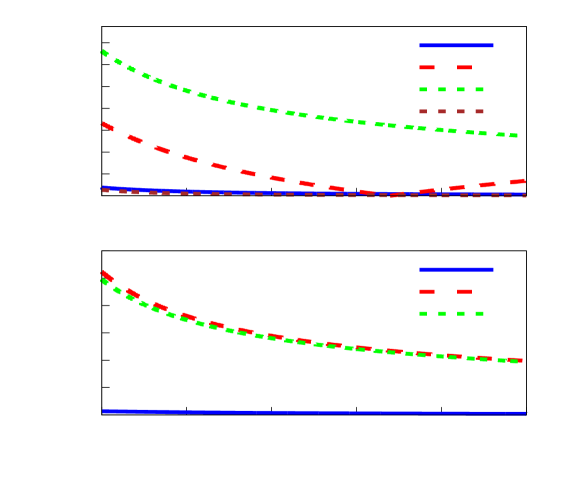
The sensitivities of various cross-resonance gate parameters to charge noise are plotted in Fig. 2a for some realistic system parameters. In this regime, we see that $\eta$ and $\omega_{2}$ are much more sensitive to electrical fluctuations than $\chi$ or $\tilde{J}$. For this reason, we neglect errors due to $\delta\tilde{J}$ and $\delta\chi$, and focus our efforts instead on correcting the larger errors. Notably, there is a sweet spot at which $\eta$ is first-order insensitive to charge noise fluctuations. This can be understood from competing effects of $\delta\omega_{1}$ and $\delta\Omega_{1}^{x}$. For $2t_{c1}>\omega_{1}^{z}$, spin-charge hybridization decreases $\omega_{1}$. Thus, when fluctuations increase spin-charge hybridization, $\delta\omega_{1}<0$. Meanwhile, the drive strength felt by the qubit increases, so $\Omega_{1}^{x}\delta\Omega_{1}^{x}>0$. By choosing $\Delta>0$ and using an appropriate drive amplitude, then, we can engineer a situation in which $\delta\eta\approx\frac{1}{\eta}\quantity(\Delta\delta\omega_{1}+\Omega_{1}^{x}\delta\Omega_{1}^{x})=0$.

The noisy 2-qubit Hamiltonian in Eq. (2) belongs to an $\mathfrak{su}(2)\oplus\mathfrak{u}(1)$ subalgebra of $\mathfrak{su}(4)$, with $\mathfrak{su}(2)$ generators $\{\sigma_{1}^{z}\sigma_{2}^{x},\sigma_{1}^{z}\sigma_{2}^{y},\sigma_{2}^{z}\}$, all of which commute with the $\mathfrak{u}(1)$ generator $\sigma_{1}^{z}$. While the $\delta\eta$ error commutes with the $\sigma_{1}^{z}\sigma_{2}^{x}$ generator and can be eliminated with a simple $\pi$-pulse (as we discuss below), the $\delta\omega_{2}$ error anticommutes with it, and requires more nontrivial error correction.

One option for suppressing the $\delta\omega_{2}$ error, inspired by techniques used in superconducting qubits [32, 33], is the addition of a microwave-frequency drive applied to the target qubit concurrently with the cross-resonance drive applied to the control qubit (Fig. 3a). By driving the target qubit at its own transition frequency and in-phase with the cross-resonance drive, we introduce a large $(\Omega_{2}^{x}+\delta\Omega_{2}^{x})\sigma_{2}^{x}$ term to the noisy $H_{DDF}$. As this new term commutes with our desired $\sigma_{1}^{z}\sigma_{2}^{x}$ generator, but anticommutes with $\sigma_{2}^{z}$, this additional driving actively suppresses the $\delta\omega_{2}$ error without interfering with entanglement generation. This comes at the expense of introducing a new $\delta\Omega_{2}^{x}$ error. However, this can be eliminated, along with the $\delta\eta$ error, by a $\pi$ rotation about the $\sigma_{i}^{y}$ axis on each qubit. The entire gate sequence, with simultaneous drive on both qubits and single-qubit echo pulses, we refer to as “2Qecho,” and is shown in Fig. 3b. For $\Omega_{2}^{x}\gg\tilde{J}$, the average gate fidelity to lowest order in the presence of this cancellation pulse is

$$\bar{F}_{\text{2Qecho}}\approx 1-\frac{2}{5}\quantity(\frac{\delta\omega_{2}}{\Omega_{2}^{x}})^{2}-\frac{\pi^{2}}{20}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})^{2}-\frac{2}{5}\delta\chi^{2}.$$

Below in Sec. IV.3, we test the efficacy of this approach using full numerical simulations. Before we examine these results, however, we first introduce alternative approaches to suppressing noise errors.

While driving the target qubit concurrently with the cross-resonance drive is an effective strategy for suppressing the $\delta\omega_{2}$ error, it requires simultaneous microwave drive of both the target and control qubits, which may be impractical for some devices. As an alternative, we can use the isomorphism that exists between the $\mathfrak{su}(2)$ subalgebra of our Hamiltonian and the ordinary $\mathfrak{su}(2)$ algebra for single-qubit operations to adapt to our purposes the fastest pulse sequence that can eliminate a single-qubit drift error [26]. While Ref. [26] assumed the ability to directly change the sign of the desired generator term, we can achieve the same effect by applying $\pi$ rotations about the $\sigma_{1}^{z}$ axis on the control qubit. Defining $\psi(\phi)\equiv\arccos(\cos(\phi/2)/2)$, we can correct the $\delta\omega_{2}$ error to lowest order for arbitrary $\phi$ with the gate sequence

	$\displaystyle U_{\phi}^{\text{1Qpartial}}$	$\displaystyle=U_{\psi(\phi)-\phi/2}^{(1)}\sigma_{2}^{z}U_{2\psi(\phi)+\pi}^{(1)}\sigma_{2}^{z}U_{\psi(\phi)-\phi/2}^{(1)}$
		$\displaystyle\approx e^{-i\frac{\zeta(\phi)}{2}\sigma_{1}^{z}}e^{-i\frac{\phi+\pi}{2}\sigma_{1}^{z}\sigma_{2}^{x}}$
		$\displaystyle\hskip 7.11317pt+\mathcal{O}\quantity(\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{2})+\mathcal{O}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})+\mathcal{O}\quantity(\delta\chi)$

where $\zeta(\phi)=\quantity(4\psi(\phi)+\pi-\phi)(\eta+\delta\eta)/\tilde{J}$. If we stop here and set $\phi=\pi/2$, we get a CNOT equivalent which is first-order insensitive to $\delta\omega_{2}$ errors and which never requires simultaneous drive of both qubits. In fact, using virtual gates, it should be possible to realize this gate sequence without applying any drive at all to the target qubit. This sequence, which we call “1Qpartial,” is shown in Fig. 3c. The average gate fidelity relative to the noiseless case, to lowest order, is

	$\displaystyle\bar{F}_{\text{1Qpartial}}$	$\displaystyle\approx 1-8.21\quantity(\frac{\delta\eta}{\tilde{J}})^{2}-\frac{9\pi^{2}}{20}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})^{2}$
		$\displaystyle\hskip 7.11317pt-\frac{2}{5}\delta\chi^{2}-5.99\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{2}\frac{\delta\tilde{J}}{\tilde{J}}-2.02\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{4}.$

Neglecting single-qubit gate times, which are small relative to the two-qubit gates, this gate sequence increases the total gate time by a factor of $\frac{8}{\pi}\psi(\pi/2)+1\approx 4.08$ compared to the uncorrected CNOT.

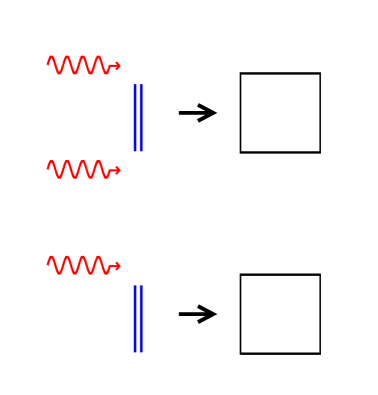
Just as in 2Qecho, the remaining $\delta\eta$ error can be completely eliminated using $\pi$ rotations about the $\sigma_{i}^{y}$ axis on each qubit:

	$\displaystyle U_{\phi}^{\text{1Qfull}}$	$\displaystyle=U_{\phi/2}^{\text{1Qpartial}}\sigma_{1}^{y}\sigma_{2}^{y}U_{\phi/2}^{\text{1Qpartial}}\sigma_{1}^{y}\sigma_{2}^{y}$
		$\displaystyle\approx e^{-i\frac{\phi}{2}\sigma_{1}^{z}\sigma_{2}^{x}}+\mathcal{O}\quantity(\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{2})+\mathcal{O}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})+\mathcal{O}\quantity(\delta\chi).$

The full nested gate sequence, which we call “1Qfull,” is shown in Fig. 3d. Although 1Qfull does require driving both qubits to realize single-qubit gates, it still does not require driving both qubits simultaneously at any point. Note that, because they commute with $\sigma_{1}^{y}$, all single-qubit gates can be applied in the doubly-rotating frame using EDSR regardless of the $\chi$ rotation. In principle, single-qubit EDSR gates will also suffer some gate infidelity as a result of charge noise, reducing the fidelity of the corrected gate sequence. However, single-qubit $\pi$-pulse EDSR gate fidelities exceeding $99.9\%$ have been reported for single-electron DQD qubits [3], so we choose here to neglect this additional error source.

Once again setting $\phi=\pi/2$, we obtain a robust CNOT equivalent with average gate fidelity

	$\displaystyle\bar{F}_{\text{1Qfull}}$	$\displaystyle\approx 1-\frac{5\pi^{2}}{4}\quantity(\frac{\delta\tilde{J}}{\tilde{J}})^{2}-\frac{2}{5}\delta\chi^{2}$
		$\displaystyle\hskip 7.11317pt-20.41\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{2}\frac{\delta\tilde{J}}{\tilde{J}}-8.44\quantity(\frac{\delta\omega_{2}}{\tilde{J}})^{4}.$

This additional step of correcting $\delta\eta$ errors yields a gate which is insensitive to charge noise to lowest order. However, the total time required for 1Qfull is increased by a factor $\frac{16}{\pi}\psi(\pi/4)+3\approx 8.55$ compared to the uncorrected CNOT, neglecting single-qubit gate times, and the effect of the $\delta\omega_{2}$ error has been amplified relative to 1Qpartial. For this reason, especially in the presence of accumulating error due to decoherence, it might be preferable to take advantage of the $\delta\eta=0$ sweet spot and only correct the $\delta\omega_{2}$ error. This tradeoff is examined more closely in Sec. IV.3, where we also provide a side-by-side comparison of the 2Qecho, 1Qpartial, and 1Qfull sequences.

Much of the same analysis can be applied to the iSWAP gate discussed in Refs. [21, 22]. Starting with the noisy, undriven 2-qubit effective Hamiltonian with $\omega_{1}=\omega_{2}=\omega$,

$$H=\frac{1}{2}\quantity(\omega+\delta\omega_{1})\sigma_{1}^{z}+\frac{1}{2}\quantity(\omega+\delta\omega_{2})\sigma_{2}^{z}-\quantity(J+\delta J)\sigma_{1}^{x}\sigma_{2}^{x},$$

we move to the rotating frame for both qubits and make the RWA. In the doubly-rotating frame, we have

	$\displaystyle H_{DF}$	$\displaystyle=\frac{1}{2}\delta\omega_{1}\sigma_{1}^{z}+\frac{1}{2}\delta\omega_{2}\sigma_{2}^{z}-\frac{1}{2}\quantity(J+\delta J)\quantity(\sigma_{1}^{x}\sigma_{2}^{x}+\sigma_{1}^{y}\sigma_{2}^{y})$
		$\displaystyle=\frac{1}{2}\delta\omega_{+}\frac{\sigma_{1}^{z}+\sigma_{2}^{z}}{2}+\frac{1}{2}\delta\omega_{-}\frac{\sigma_{1}^{z}-\sigma_{2}^{z}}{2}$
		$\displaystyle\hskip 7.11317pt-\quantity(J+\delta J)\frac{\sigma_{1}^{x}\sigma_{2}^{x}+\sigma_{1}^{y}\sigma_{2}^{y}}{2},$

where $\delta\omega_{\pm}=\delta\omega_{1}\pm\delta\omega_{2}$. The gate generated by this Hamiltonian, $U_{\phi}=\exp(-i\frac{\phi}{2J}H_{DF})$, thus implements a noisy iSWAP local equivalent for $\phi=\pi$. The average gate fidelity relative to a noiseless iSWAP gate is

$$\bar{F}\approx 1-\frac{\pi^{2}}{10}\quantity(\frac{\delta J}{J})^{2}-\frac{1}{10}\quantity(\frac{\delta\omega_{-}}{J})^{2}-\frac{\pi^{2}}{40}\quantity(\frac{\delta\omega_{+}}{J})^{2}.$$

The sensitivities of the iSWAP Hamiltonian parameters to charge noise are shown in Fig. 2b. Similar to the cross-resonance gate, we find that the $\omega_{i}$ are much more sensitive than $J$, so we neglect the $\delta J$ error (though such errors could in principle be corrected with a more complicated gate sequence [34]).

Thus again we have a Hamiltonian in an $\mathfrak{su}(2)\oplus\mathfrak{u}(1)$ subalgebra of $\mathfrak{su}(4)$, now with $\mathfrak{su}(2)$ generators $\{\quantity(\sigma_{1}^{x}\sigma_{2}^{x}+\sigma_{1}^{y}\sigma_{2}^{y})/2,\quantity(\sigma_{1}^{x}\sigma_{2}^{y}-\sigma_{1}^{y}\sigma_{2}^{x})/2,\quantity(\sigma_{1}^{z}-\sigma_{2}^{z})/2\}$, all of which commute with the $\mathfrak{u}(1)$ generator $\quantity(\sigma_{1}^{z}+\sigma_{2}^{z})/2$. And again, we have commuting ($\delta\omega_{+}$) and non-commuting ($\delta\omega_{-}$) error terms which we would like to eliminate. In fact, we can use the exact same nested gate sequence as for the cross-resonance gate to suppress these errors as well. Simply substituting this new $U_{\phi}$ for $U_{\phi}^{(1)}$ in the $U_{\phi}^{\text{1Qfull}}$ gate sequence in Fig. 3d and setting $\phi=\pi$ yields a robust iSWAP gate which has substantially reduced sensitivity to charge noise. The fidelity of this corrected iSWAP, to lowest order, is

$$\bar{F}_{\text{1Qfull}}\approx 1-\frac{9\pi^{2}}{10}\quantity(\frac{\delta J}{J})^{2}-3.00\frac{\delta J}{J}\quantity(\frac{\delta\omega_{-}}{J})^{2}-0.25\quantity(\frac{\delta\omega_{-}}{J})^{4}.$$

Unlike the cross-resonance gate, there is no sweet spot at which the commuting error vanishes, nor can we simply suppress the non-commuting error by driving the qubits, so we must use 1Qfull to obtain a gate which corrects the largest charge noise errors. However, because the iSWAP is a $\pi$ rotation, the gate time penalty is not as severe, with 1Qfull only increasing the total gate time by a factor of $\frac{8}{\pi}\psi(\pi/2)+1\approx 4.08$ compared to the uncorrected noisy iSWAP, neglecting single-qubit gate times.

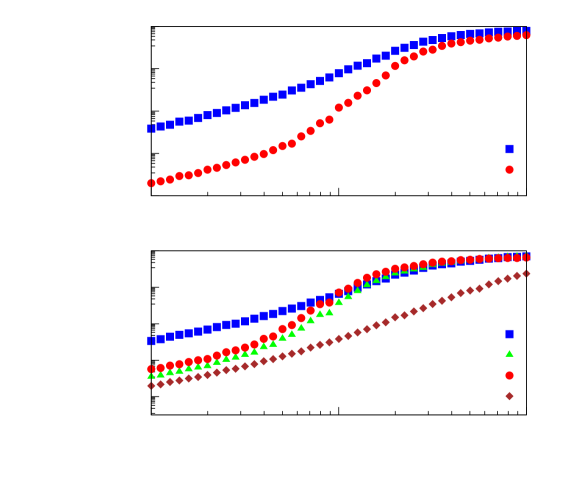
To investigate the effectiveness of our corrected gate sequences, we numerically compute the average gate fidelity of our corrected iSWAP and cross-resonance sequences at various quasistatic noise amplitudes. For the iSWAP (Fig. 4a), we find that our corrected gate sequence always outperforms the uncorrected gate, at least in the absence of decohering interactions, with the improvement becoming more pronounced at smaller values of charge noise. We can roughly estimate the impact of decoherence by noting that, at short times, gate fidelity goes as $\exp(-t^{2}/T_{2}^{2})$. As 1Qfull increases gate time by a factor of nearly 4 for the iSWAP, the relative penalty incurred by 1Qfull due to decoherence is then roughly $\exp(-15t_{\text{iSWAP}}^{2}/T_{2}^{2})$, where $t_{\text{iSWAP}}$ is the duration of the uncorrected iSWAP. This suggests that our gate sequence still retains its advantage if it is feasible to realize $t_{\text{iSWAP}}/T_{2}\lesssim 10^{-2}$.

For the cross-resonance CNOT (Fig. 4b), 2Qecho outperforms all other gate sequences at all levels of charge noise. As 2Qecho does not require increasing gate time beyond the addition of relatively short single-qubit gates, it also incurs no additional penalty due to decoherence. Meanwhile, 1Qfull and 1Qpartial do offer substantial fidelity improvements at sufficiently low charge noise, but no meaningful improvement is offered by either at these system parameters for $\sigma_{\epsilon}\gtrsim$100\text{\,}\mathrm{MHz}$$ or $\sigma_{t}\gtrsim$1\text{\,}\mathrm{MHz}$$. Previous experimental work in Si DQDs found detuning noise on the order of $200\text{\,}\mathrm{MHz}$ [35], suggesting that 1Qfull and 1Qpartial may offer a substantial advantage with moderate improvements over current charge noise levels, provided that gate times can be made sufficiently short relative to $T_{2}$. Notably, because we chose our cross-resonance pulse amplitude to tune the system to the $\delta\eta=0$ sweet spot, 1Qpartial actually outperforms 1Qfull here. Considering also the additional penalty incurred by 1Qfull due to increased gate time, this demonstrates the considerable advantage of forgoing 1Qfull for 1Qpartial executed at the sweet spot.