Robust photon transmission in nonlinear parity-time-symmetric cavities

Considerable progress has been made in parity-time (PT)- symmetric optics to explore intriguing properties makris08 ; klaiman ; kottos ; suchkov ; lv15 , which has been investigated both theoretically bender ; klaiman08 ; jin10 ; hassan15 and experimentally ruter ; peng ; sun14 . PT symmetric system, despite being non-Hermiticity, has been found novel phenomenons, such as PT symmetry breaking ruter ; peng , and nonreciprocal reflectionless transmission feng2013 . Even through the Hermiticity of the quantum observables was never in doubt, a wide class of non-Hermitian Hamiltonians with PT symmetry have motivated discussions on several fronts in physics, including cavity optomechanics jing ; fan ; peng12 , quantum field theories bender04 , PT-symmetric lattice longhi ; zhen15 , and open quantum system rotter ; dembowski . A variety of optical structures provide a alternative platform for testing various theoretical proposals on non-Hermitian PT-symmetric quantum mechanic chang14 .

PT-symmetric systems are invariant under under simultaneous parity-flip and time-flip operations ganainy07 ; chong11 . In optical systems, PT symmetry can be established by incorporating gain and loss in coupled resonators. A linear PT-symmetric system with balanced gain and loss can exhibit a real eigenvalue spectrum and present unusual properties jin17 ; guo09 . If the gain-loss contrast exceeds a certain threshold, the PT symmetry can be spontaneously broken and the spectrum is no longer entirely real, exhibiting an exceptional point. When the gain induces large nonlinear saturation under high pumping and no longer matches the loss, the linear PT symmetry of the coupled cavities breaks down. Theoretically, the nonlinear gain saturation can causes the system to reach a steady state that still contains the PT symmetry characteristics fan17 ; hassan ; ge . Can such nonlinear gain saturation effects be harnessed to enhance the photon transmission in coupled cavities? Photons transmission, such reflection and transmission as a consequence of the nonlinear PT symmetry motivates us to achieve an optimal photon transfer scheme.

We focus on how PT symmetry relates to the nonlinear gain and loss system leads to a robust photon transfer in two coupled cavities. Different from the linear PT-symmetric system with fixed value of gain, we consider a nonlinear PT-symmetric system with a nonlinear gain depending on intracavity photons. An analysis based on quantum Langevin equations is presented to study the steady-state dynamics. It is observed that the eigenfrequency self-adjusts to the nonlinear gain saturation, and the saturated gain in the steady state automatically satisfies PT symmetry. As a consequence of the PT symmetry with nonlinear gain saturation, the photons transfer efficiency obtained is robust independent on the coupling strength, exhibiting an improvement over a conventional transfer scheme, in which the input light frequency is required to adjusted as the coupling strength to maintain optimal efficiency.

To explore the photon transfer scheme in coupled cavities, we consider an input cavity coupling to an output cavity. The Hamiltonian is described by

where $a_{i}^{\dagger}$ ($a_{i}$) is the creation (annihilation) operator of the cavity $i$ with the frequency $\omega_{i}$, $\kappa$ is the coupling strength between two cavities.

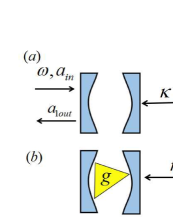
Fig. 1(a) shows a conventional scheme of photon transfer in two coupled cavities. A pump light field $a_{in}$ of a frequency $\omega$ transfers photons to the input cavity at a rate $\gamma_{1}$, and the output cavity out-puts photons at a rate $\gamma_{2}$ due to the leakage of photons. The intrinsic loss rate of each cavity is $\gamma_{0}$.

The dynamics of the photon transfer process undergoes dissipation due to leakage of photons. It can be described by the quantum Langevin equations for the Heisenberg operators $a_{1}$ and $a_{2}$,

where $f_{1}(t)=\sqrt{2\gamma_{1}}a_{in}(t)$ is the quantum Langevin force originating from the input light field $a_{in}(t)$. For simplicity, the force term $f_{2}(t)$ is neglected.

To solve above equations in frequency space, we employ a transforming operator as $a(\omega)=\int_{-\infty}^{+\infty}e^{i\omega t}a(t)dt$ of $a(t)$. The input-output relations are given by

where $a_{1out}$ and $a_{2out}$ are the reflected and output operators of cavities, respectively. For an input light field at frequency $\omega$, the transmission function $T(\omega)$ of the output cavity is obtained as

and the response function $R(\omega)$ of the input cavity for the reflection is

where $\Delta_{1(2)}=-\omega+\omega_{1(2)}$. The corresponding photon transfer efficiency from output cavity is given by

which, for a symmetric case ($\gamma_{1}=\gamma_{2}=\gamma_{0}$ and $\omega_{1}=\omega_{2}=\omega_{0}$), becomes

with the detuning frequency $\Delta=-\omega+\omega_{0}$. In the conventional photon transport process, it involves reflections $R(\omega)$, which plays a role in the photon transport from the input cavity.

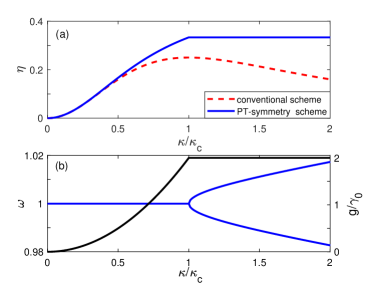
Fig. 2(a) shows the transfer efficiency of photons with a resonance frequency $\omega=\omega_{0}$. It behaves non-monotonically dependent on the coupling strength $\kappa$. The type of the conventional photon transfer is not robust against coupling strength in the operating conditions. To maximize the transfer efficiency $\eta$, it is required $\omega=\omega_{0}\pm\sqrt{\kappa^{2}-4\gamma_{0}^{2}}$ for $\kappa\geqslant 2\gamma_{0}$ by minimizing the module of the denominator in Eq.(9). One can tune the input frequency according to the coupling strength $\kappa$ to achieve the optimal value of $\eta$.

Different from the conventional scheme, the PT-symmetric scheme circumvent photon reflections. The linear PT-symmetric system of two coupled resonators with balanced gain and loss was previously investigated, in which a gain can be induced by pumping erbium ions in the gain resonatorchang14 ; jing . Here, we consider the lasing of the gain medium provides the nonlinear gain theoretically, which depends on the intracavity photons fan17 ; hassan . Fig. 1(b) illustrates a nonlinear saturable gain element into the input cavity for amplification of photons generation and a nonlinear loss in the output cavity. The nonlinear gain rate $g$ and loss rate $\gamma$ depend on the intracavity average photons $\langle a_{1(2)}^{\dagger}a_{1(2)}\rangle=|\alpha_{1(2)}|^{2}$, which are expressed as

with the unsaturated gain and loss rates $g_{0}$ and $f_{0}$, respectively.

The Heisenberg operators $a_{1}$ and $a_{2}$ obey

Since the nonlinear gain $g$ depends on the mean photons in the input cavity, we explore the stable state with a saturable gain by solving the above equations analytically.

PT-symmetric regime.–A enhancement of the nonlinear gain and loss generates large steady-state amplitudes in two cavities. We use the mean-field description for the operators $\alpha_{i}=\langle a_{i}\rangle=\alpha_{i0}e^{-i\omega t}$ lv16 ; lv , where $\alpha_{i0}$ is the steady-state amplitude of the cavity mode. According to Eqs.(11) and (12), the steady-state amplitudes is given by the following equations

where the saturated gain and loss are $g_{s}=g_{0}/(1+|\alpha_{10}|^{2})$, and $f_{s}=f_{0}/(1+|\alpha_{20}|^{2})$, respectively. The above equations suggest the relation $\alpha_{02}=\rho e^{i\phi}\alpha_{01}$ with a phase shift $\phi$ and the modal ratio $\rho\in{Re}^{+}$. It leads to the equation for the eigen-frequencies

To obtain a real $\omega$, it is required $g_{s}/2\gamma_{0}-f_{s}/2\gamma_{0}=1$. Then it is reasonable to give $g_{s}=2\gamma_{0}\cosh^{2}\eta$ and $f_{s}=2\gamma_{0}\sinh^{2}\eta$ with a positive real quantity $\eta$. It leads to the relations for the mean photons

Then the eigenfrequencies in Eq. (III) reduces to $(\omega-\omega_{0})^{2}=\kappa^{2}-\gamma_{0}^{2}\cosh^{2}(2\eta)$. By substituting into Eqs. (13) and (14), one obtains $\rho=\pm 1$ and $\tanh\eta=\sqrt{f_{0}/g_{0}}$.

The saturated gain and loss are obtained as

Therefore, the stable state is in the PT-symmetric phase with the balanced gain and loss

The eigenfrequencies are obtained as

which is real for $\kappa>k_{c}=\gamma_{0}(g_{0}+f_{0})/(g_{0}-f_{0})$. By setting $g_{s}=3\gamma_{0}$ and $f_{s}=\gamma_{0}$ with $g_{0}=3f_{0}$, the eigenfrequencies reduce into

with the PT-symmetry $g_{\mathtt{PT}}=\gamma_{\mathtt{PT}}=2\gamma_{0}$. The eigenfrequencies are consistent with the optimal frequency to maximize the transfer efficiency in Eq. (9) in the conventional scheme. In contrast to the conventional scheme with frequency tuning, the advantage of the PT-symmetric scheme lies in the self-selected eigenfrequencies without any active tunings.

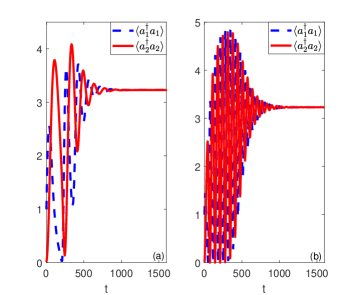
Fig. 2 (b) show the saturated gain and the self-adjusting eigen-frequency $\omega$ in the steady state. We observe a bifurcation in the real part of the frequency at the critical coupling strength $\kappa_{c}$, exhibiting a PT symmetry-breaking transition. In the strong coupling regime $\kappa>k_{c}$, the system have two modes with eigenfrequencies $\omega=\omega_{0}\pm\sqrt{\kappa^{2}-4\gamma_{0}^{2}}$. The corresponding saturated gain in Eq. (19) is a constant independent on the coupling strength, and can balance out the loss, $g_{\mathtt{PT}}=\gamma_{\mathtt{PT}}$. It demonstrate that the system posses the PT symmetry in the strong coupling regime $\kappa>k_{c}$.

The steady state in the PT-symmetric phase is given by

with $\sin\phi=\pm\gamma_{0}/\kappa$. One can easily obtain the mean photons in the steady state for the input and output cavities, which have the same value,

Fig. 3 shows the time evolution of the mean photons obtained by solving Eqs.(11) and (12) numerically for different coupling strength $\kappa$. It is observed that in the steady state $\langle a_{2}^{\dagger}a_{2}\rangle$ equals to $\langle a_{1}^{\dagger}a_{1}\rangle$, which is consistent with the analytical results in Eq. (23). In the steady state, the mean photons $\langle a_{1(2)}^{\dagger}a_{1(2)}\rangle$ for $\kappa/\kappa_{c}=2$ is the same as that for $\kappa/\kappa_{c}=4$, which is independent on the coupling strength.

With the input and output relations $\hat{a}_{in}=\sqrt{2g_{s}}\hat{a}_{1},\hat{a}_{2out}=\sqrt{2f_{s}}\hat{a}_{2}$, the photon transfer efficiency is obtained as

where $g_{s}$ and $f_{s}$ are the saturated gain and loss in Eq. (18). So the efficiency is independent on the coupling strength $\kappa$ in the PT-symmetric regime.

Fig. 2(a) shows the transfer efficiency in the strong coupling regime $\kappa>k_{c}$. The efficiency $\eta$ is robust against the variation of the coupling strength $\kappa$. And $\eta$ is larger than that obtained by the conventional transfer scheme, which varies dependent on the coupling strength for a fixed input frequency. Since the eigen-frequency in the non-linear PT-symmetric scheme can self-adjust to the variation of the the coupling strength for an optimal transfer efficiency. It exhibits an improvement over the conventional scheme due to the robust efficiency induced by the saturated gain and self-adjusting frequency in the steady state.

PT-broken regime.– In the PT-broken regime for a weak coupling strength $\kappa<\kappa_{c}$, the real eigenfrequency is given by $\omega=\omega_{0}$ from Eq. (21). The mean-field approximation for the stationary solutions is assumed to be $\alpha_{i}=\langle a_{i}\rangle=\alpha_{i0}$. The equations of motion in the steady state can be given in the interacting representation

By solving the above equations, one obtains the saturated gain

The corresponding gain and loss in the stable state are obtained by setting $f_{s}=\gamma_{0}$

Obviously, it exhibits the PT symmetry broken, because the saturated gain does not match the loss $g_{\mathtt{b}}\neq\gamma_{\mathtt{b}}$. Our results are consistent with the saturated gain in wireless power transfer system with magnetic resonators fan17 .

The ratio of mean photons in the input and output cavity is obtained analytically as

where $\alpha_{20}/\alpha_{10}=-i\kappa/(2\gamma_{0})$ is obtained from Eq.(25). Obviously, the ratio depends on the coupling strength $\kappa$, which is different from that in Eq.(23) in the PT-symmetry regime. Since the ration is smaller than $1$, giving $\kappa^{2}/4\gamma_{0}^{2}\leq 1$, it leads to the PT-broken regime $\kappa<\kappa_{c}$ with the critical value $\kappa_{c}=2\gamma_{0}$.

One obtains the photon transfer efficiency

Fig. 2(a) shows the transfer efficiency in the PT-broken regime for $\kappa<\kappa_{c}$. $\eta$ increases as the coupling strength $\kappa$ increases. Fig. 2(b) shows that the saturated gain in Eq. (28) is proportional to $\kappa^{2}$. It is different the photon transfer efficiency and the saturated gain in the PT-symmetric regime for $\kappa>\kappa_{c}$, which is robust independent on the coupling strength.

We have studied theoretically a nonlinear PT-symmetric scheme for photon transfer in two coupled cavities by introducing a nonlinear gain and loss. The gain induces nonlinearity dependent on the intracavity photons, which is different from the linear PT-symmetric system with the balanced gain and loss. We obtain the analytical solution to the steady state, which agree well with the numerical ones. The nonlinear saturated gain and loss in the steady state satisfy the PT symmetry automatically. And the eigen-frequency self-adjusts to the nonlinear saturated gain, and exhibits a bifurcation at the critical coupling strength. Consequence, we obtain the robust photon transmission efficiency independent on the coupling strength, exhibiting an improvement over the conventional scheme. In contrast to the conventional scheme of the photon transfer involving the photon reflections, in which the transfer efficiency depends on the coupling strength and input frequency tuning, the nonlinear saturated gain guarantees the stable state with the PT-symmetry and a self-selected frequency, which do not require active tuning to maintain optimal efficiency. The proposal of the nonlinear PT-symmetric system with nonlinear gain and loss provides a powerful platform for investigating intriguing properties prior to those in linear PT-symmetric systems, especially for compound photonic system.