Robust production planning with budgeted cumulative demand uncertainty
Abstract
This paper deals with a problem of production planning, which is a version of the capacitated single-item lot sizing problem with backordering under demand uncertainty, modeled by uncertain cumulative demands. The well-known interval budgeted uncertainty representation is assumed. Two of its variants are considered. The first one is the discrete budgeted uncertainty, in which at most a specified number of cumulative demands can deviate from their nominal values at the same time. The second variant is the continuous budgeted uncertainty, in which the sum of the deviations of cumulative demands from their nominal values, at the same time, is at most a bound on the total deviation provided. For both cases, in order to choose a production plan that hedges against the cumulative demand uncertainty, the robust minmax criterion is used. Polynomial algorithms for evaluating the impact of uncertainty in the demand on a given production plan in terms of its cost, called the adversarial problem, and for finding robust production plans under the discrete budgeted uncertainty are constructed. Hence, in this case, the problems under consideration are not much computationally harder than their deterministic counterparts. For the continuous budgeted uncertainty, it is shown that the adversarial problem and the problem of computing a robust production plan along with its worst-case cost are NP-hard. In the case, when uncertainty intervals are non-overlapping, they can be solved in pseudopolynomial time and admit fully polynomial time approximation schemes. In the general case, a decomposition algorithm for finding a robust plan is proposed.
Keywords: robustness and sensitivity analysis; production planning; demand uncertainty; robust optimization
1 Introduction
Production planning under uncertainty is a fundamental and important managerial decision making problem in various industries, among others, agriculture, manufacturing, food and entertainment ones (see, e.g., [26]). Uncertainty arises due to the versatility of a market and the bullwhip effect that increases uncertainty through a supply chain (see [29]). In consequence, it induces supply chain risks such as backordering and obsolete inventory, accordingly, there is a need to face uncertainty in planning processes, in order to manage these risks.
Nowadays most companies use the manufacturing resource planning (MRP II) for a manufacturing planning and control, which is composed of three levels [6]: the strategic level (production plan/resource plan), the tactical level (master production schedule/ rough-cut capacity plan and material requirement planning/capacity requirements plan) and the operational level (production activity control/capacity control). In this paper we will be concerned with the study of an impact of uncertainty in models that are applicable to a production planning in the strategic level and/or a master production scheduling in the first level of the tactical one. More specifically, we will look more closely at a capacitated lot sizing problem with backordering under uncertainty. In the literature on production planning (see, e.g., [5, 16, 34, 36, 43]) three different sources of uncertainty such as: demand, process and supply are distinguished. For the aforementioned strategic/tactical planning processes taking demand uncertainty into account plays a crucial role. Therefore, in this paper, we focus on uncertainty in the demand. Namely, we deal with a version of the capacitated lot sizing problem with backordering under uncertainty in the demand.
Various models of demand uncertainty in lot sizing problems have been discussed in the literature so far, each of which has its pros and cons. Typically, uncertainty in demands (parameters) is modeled by specifying a set of all possible realizations of the demands (parameters), called scenarios. In stochastic models, demands are random variables with known probability distributions that induce a probability distribution in set and the expected solution performance is commonly optimized [39, 31, 24, 40]. In fuzzy (possibilistic) models, demands are modeled by fuzzy intervals, regarded as possibility distributions, describing the sets of more or less plausible values of demands. These fuzzy intervals induce a possibility distribution in scenario set and some criteria based on possibility measure are optimized [20, 33, 41].
When no historical data or no information about plausible demand values are available, required to draw probability or possibility distributions for demands, an alternative way to handle demand uncertainty is a robust model. There are two common methods of defining scenario (uncertainty) set in this model, namely the discrete and interval uncertainty representations. Under the discrete uncertainty representation, set is defined by explicitly listing all possible realizations of demand scenarios. While, under the interval uncertainty representation, a closed interval is assigned to each demand, which means that it will take some value within this interval, but it is not possible to predict which one. Thus is the Cartesian product of the intervals. In order to choose a solution, the minmax or minmax regret criteria are usually applied. As the result, a solution minimizing its cost or opportunity loss under a worst scenario which may occur is computed (see, e.g., [28]). Under the discrete uncertainty representation of demands the minmax version of a capacitated lot sizing problem turned out to be NP-hard even for two demand scenarios but can be solved in pseudopolynomial time, if the number of scenarios is constant [28]. When the number of scenarios is a part of the input, the is strongly NP-hard and no algorithm for solving it is know. A situation is computationally much better for the interval representation of demands. It was shown in [20] that the minmax version of the lot sizing problems with backorders can be efficiently solved. Indeed, the problem of computing a robust production plan with no capacity limits can be solved in time, where is the number of periods. For its capacitated version an effective iterative algorithm based on Benders’ decomposition [8] was provided. At each iteration of the algorithm a worst-case scenario for a feasible production plan is computed by a dynamic programming algorithm. Such a problem of evaluating a given production plan in terms of its worst-case cost is called the adversarial problem. The minmax regret version of two-stage uncapacitated lot sizing problems, studied in [45], can be solved in time.
The minmax (regret) approach, commonly used in robust optimization, can lead to very conservative solutions. In [9, 10] a budgeted uncertainty representation was proposed, which addresses this drawback under the interval uncertainty representation. It allows decision maker to flexibly control the level of conservatism of solutions computed by specifying a parameter , called a budget or protection level. The intuition behind this was that it is unlikely that all parameters can deviate from their nominal values at the same time. The first application of the budgeted uncertainty representation to lot sizing problems under demand uncertainty was proposed [11], where the resulting true minmax counterparts were approximated by linear programing problem (LP) and a mixed integer programing one (MIP). It is worth pointing out that the authors in [11] assumed a budgeted model, in which is an upper bound on the total scaled deviation of the demands (parameters) from their nominal values under any demand scenario. Along the same line as in [11], the robust optimization was adapted to periodic inventory control and production planning with uncertain product returns and demand in [42], to lot sizing combined with cutting stock problems under uncertain cost and demand in [4], and to a production planning under make-to-stock policies in [1]. In [2, 7, 12, 38] the minmax lot sizing problems under demand uncertainty were solved exactly by algorithms being variants of Benders’ decomposition. They consist in iterative inclusion of rows and columns, resulting from solving an adversarial problem (see also [44]). Hence their effectiveness heavily relies on the computational complexity of adversarial problems. In [12] the adversarial problems, related to computing basestock levels for a specific lot sizing problem, were solved by a dynamic programing algorithm and by a MIP formulation. MIPs also model adversarial problems corresponding to lot sizing problems under demand uncertainty in [7, 38]. While in [2] a more general problem under parameter uncertainty containing, among others, a capacitated lot sizing problem under demand uncertainty, was examined and its corresponding adversarial problem was solved by a dynamic programing algorithm and by a fully polynomial approximation scheme (FPTAS). Therefore, a pseudopolynomial algorithm and an FPTAS were proposed for a robust version of the original general problem under consideration.
In most of the literature devoted to robust lot sizing problems the interval uncertainty representation is used to model uncertainty in demands (see, e.g., [1, 4, 2, 7, 12, 20, 38, 42, 45]). This is not surprising, as it is one of the simplest and most natural ways of handling the uncertainty. In majority of papers the demand uncertainty is interpreted as the uncertainty in actual demands in periods. In this case, however, the uncertainty cumulates in the subsequent periods due to the interval addition, which may be unrealistic in applications. In [22] the uncertainty in cumulative demands was modeled, which resolves this problem. Indeed, it is able to take uncertain demands in periods as well as dependencies between the periods into account [21].
In this paper a capacitated lot sizing problem with backordering under the cumulative demand uncertainty is discussed. The uncertainty in cumulative demands is modeled by using two variants of the interval budgeted uncertainty. In the first one, called the discrete budgeted uncertainty [9, 10], at most a specified number of cumulative demands can deviate from their nominal values at the same time. In the second variant, called the continuous budgeted uncertainty [35], the total deviation of cumulative demands from their nominal values, at the same time, is at most . The latter variant is similar to that considered in [11], where the total scaled deviation is upper bounded by , but it is different from the computational point of view. To the best of our knowledge, the above lot sizing problem with uncertain cumulative demands under the discrete and continuous budgeted uncertainty has not been investigated in the literature so far.
Our contribution: The purpose of this paper is not to motivate the robust approach in lot sizing problems (this was well done in other papers), but rather to provide a complexity characterization, containing both positive and negative results for the problem under consideration. For both variants of the budgeted uncertainty, we analyze the adversarial problem, denoted by Adv, and the problem of finding a minmax (robust) production plan along with its worst-case cost, denoted by MinMax. We first consider the restrictive case, in which the cumulative demand intervals are non-overlapping (it is actually possible for the master production scheduling) and we study then the general case in which the intervals can overlap. Under the discrete budgeted uncertainty, we provide polynomial algorithms for the Adv problem and polynomial linear programming based methods for the MinMax problem in the non-overlapping case. We then extend these results to the general case by showing a characterization of optimal cumulative demand scenarios for Adv. In consequence, under the discrete budgeted model the Adv and MinMax problems can be solved efficiently. Under the continuous budgeted uncertainty the situation is different. In particular, we prove that the Adv problem and, in consequence, the MinMax one are NP-hard even in the non-overlapping case. For the non-overlapping case, we construct pseudopolynomial algorithms for the Adv problem and propose a pseudopolynomial ellipsoidal algorithm and a linear programming program with pseudopolynomial number of constraints and variables for the MinMax problem. Moreover, we show that both problems admit an FPTAS. In the general case, the Adv and MinMax problems still remain NP-hard. Unfortunately, in this case there is no easy characterization of vertex cumulative demand scenarios. Accordingly, we propose a MIP based approach for Adv and an exact solution algorithm, being a variant of Benders’ decomposition, for MinMax.
This paper is organized as follows. In Section 2 we formulate a deterministic capacitated lot sizing problem with backordering and present a model of the cumulative demand uncertainty, i.e. the discrete and continuous budgeted uncertainty representations, together with the Adv and MinMax problems corresponding to the lot sizing problem. In Sections 3 and 4 we study the problem under both budgeted uncertainty representations providing positive and negative results. We finish the paper with some conclusions in Section 5.
2 Problem formulation
In this section we first recall a formulation of the deterministic capacitated single-item lot sizing problem with backordering. Then we assume that demands are subject to uncertainty and present a model of uncertainty, called the budgeted uncertainty representation. In order to choose a robust production plan we apply the minmax criterion, commonly used in robust optimization.
2.1 Deterministic production planning problem
We are given periods, a demand in each period , ( denotes the set ), production, inventory and backordering costs and a selling price, denoted by , , and , respectively, which do not depend on period . Let be a production amount in period , . We assume that the production amounts , called the production plan, can be under some linear constraints. Namely, let be a set of production plans, specified by linear constraints, for instance:
where , and , are prescribed capacity and cumulative capacity limits, respectively. Accordingly, we wish to find a feasible production plan , subject to the conditions of satisfying each demand and the capacity limits, which minimizes the total production, storage and backordering costs minus the benefit from selling the product.
Set and , i.e. and stand for the cumulative demand up to period and the cumulative production up to period , respectively. We do not examine additional production processes, for example with setup times and costs, which lead to NP-hard problems even for special cases (see, e.g., [17, 14]). The problem under consideration is a version of the capacitated single-item lot sizing problem with backordering (see, e.g., [13, 37]). It can be represented by the following linear program:
| (1) | |||||
| s.t. | (2) | ||||
| (3) | |||||
| (4) | |||||
| (5) | |||||
| (6) | |||||
where , and are inventory level, backordering level and sales of the product at the end of period , respectively. We assume that the initial inventory and backorder levels are equal to 0. There is an optimal solution to (1)-(6) which satisfies for each , so inventory storage from period to period and backordering from period to period are not performed simultaneously. Indeed, if and , then we can modify the solution so that or without violating the constraints (2)-(3) and increasing the objective value. Using this observation, we can rewrite (1)-(6) in the following equivalent compact form, which is more convenient to analyze:
| (7) |
Define
Hence, after considering two cases, namely and , for each , problem (7) can be represented as follows
| (8) |
From now on, we will refer to (8) instead of (1)-(6). Observe that is nonincreasing function of , is nondecreasing function of . Furthermore, the function is convex in and , since both functions and are linear in and .
2.2 Robust production planning problem
We now admit that demands in problem (8) are subject to uncertainty. In practice, a knowledge about uncertainty in a demand is often expressed as , where is a possible deviation from a nominal demand value. This means that the actual demand will take some value within the interval determined by , but it is not possible to predict at present which one. In consequence, a simple and natural interval uncertainty representation is induced.
A demand has a twofold interpretation, namely an actual demand in period or a cumulative demand up to period , . The former interpretation is often considered in the literature. However, in this case the deviations cumulate in subsequent periods, due to the interval addition, , , where is the nominal value of the demand in period . This may be unrealistic in practice, because the deviation for cumulative demand in period becomes (see Figure 1a). Therefore, in this paper we use a model of uncertainty in the cumulative demands rather than in actual demands, expressed by symmetric intervals , , prescribed, where is the nominal value of the cumulative demand up to period (see Figure 1b). Such a model is able to take the uncertain demands in periods into account ( lies in ) as well as dependencies between periods. We allow different deviations for each period. Accordingly, the value of cumulative demand is only known to belong to the interval , , where is the maximum deviation of the cumulative demand from its nominal value . Each feasible vector of cumulative demands, called scenario, must satisfy the following two reasonable constraints: for every and for every . Since the vector of nominal cumulative demands should be feasible, we also assume that , . Notice that scenario induces a vector of actual demands in periods , i.e. , , .
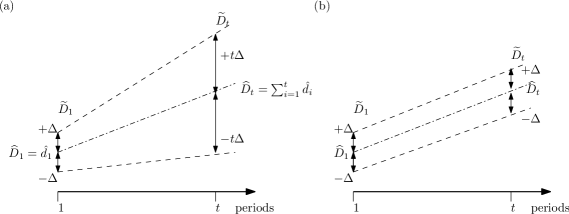
In this paper we study the following two special cases of the interval, symmetric uncertainty representations, that are common in robust optimization, in which scenario sets are defined in the following way (see, e.g., [9, 10, 35]):
| (9) | ||||
| (10) |
The first representation (9) is called the discrete budgeted uncertainty, where , and the second one (10) is called the continuous budgeted uncertainty, where . The parameters and , called budgets or protection levels, control the amount of uncertainty in and , respectively. If , then all cumulative demands take their nominal values (there is only one scenario). On the other hand, for sufficiently large and the uncertainty sets and are the Cartesian products of , , which yields the interval uncertainty representation discussed in [28].
In order to compute a robust production plan, we adopt the minmax approach (see, e.g., [28]), in which we seek a plan minimizing the maximal total cost over all cumulative demand scenarios. This leads to the following minmax problem:
| (11) |
where , i.e. to the one of computing an optimal production plan of (11) along with its worst-case cost . Indeed, is a robust choice, because we are sure that it optimizes against all scenarios in in which the amount of uncertainty allocated by an adversary to cumulative demands is upper bounded by a budget provided. Furthermore, the budget enables to control the level of robustness of a production plan computed. More specifically, an optimal production plan to the MinMax problem under optimizes against all scenarios, in which at most cumulative demands take values different from their nominal ones at the same time. Moreover, by changing the value of , from to , one can flexibly control the level of robustness of the plan computed. An optimal production plan to the MinMax problem under optimizes against all scenarios in in which the total deviation of the cumulative demands from their nominal values, at the same time, is at most a bound on the total variability . In this case one can also flexibly control the level of robustness of the plan computed by changing the value of from to a big number, say .
The MinMax problem contains the inner adversarial problem, i.e.
| (12) |
The Adv problem consists in finding a cumulative demand scenario that maximizes the cost of a given production plan over scenario set . In other words, an adversary maliciously wants to increase the cost of .
Throughout this paper, we study the Adv and MinMax problems under two standing assumptions about cumulative demand uncertainty intervals , . Under the first one, the intervals are non-overlapping, i.e. , . This assumption is realistic, in particular at the tactical level of planning, for instance in the master production scheduling (MPS) (see, e.g. [6]), where the lengths of periods are big enough (for example, they are equal to one month). This restriction leads to more efficient methods of solving the problems under consideration. Notice that it allows us to drop the constraints , , in the definition of scenario sets and . Under the second assumption, called the general case, we impose no restrictions on the interval bounds, i.e. they can now overlap.
3 Discrete budgeted uncertainty
In this section we consider the problem with uncertainty set defined as (9). We will discuss the Adv and the MinMax problems, i.e. the problems of evaluating a given production plan and computing the robust production plan, respectively. We provide polynomial algorithms for solving both problems.
3.1 Non-overlapping case
In this section we consider the non-overlapping case, i.e we assume that for each . We first focus on the Adv problem, i.e the inner one of MinMax.
Lemma 1.
Proof.
The objective (13) is a convex function with respect to . Hence, it attains the maximum value at a vertex of the convex polytope (14)-(15) (see, e.g., [32]). Moreover, since the matrix of constraints (14) and (15) is totally unimodular and , an optimal solution to (13)-(15) is integral and has exactly components equal to 1.
Let be an optimal solution of the Adv problem. This solution can be expressed by a feasible solution to (13)-(15). Indeed, , , . Obviously , since . The value of the objective function of (12) for can be bounded from above by the value of (13) for and, in consequence, by the value of (13) for . Let us form the cumulative demand scenario , that corresponds to , by setting
| (16) |
Since for each (by the assumption that we consider the non-overlapping case), we get and thus . We see at once that the optimal value of (13) for is equal to the value of the objective function of (12) for . By the optimality of , this value is bounded from above by the value of the objective function of (12) for . Hence is an optimal solution to (12) as well, which proves the lemma. ∎
From Lemma 1 and the integrality of , it follows that an optimal solution to (12) is such that for every . Accordingly, we can provide an algorithm for finding an optimal solution to (13)-(15). An easy computation shows that the objective function (13) can be rewritten as follows:
| (17) |
where
are fixed coefficients. The first sum in (17) is constant. Therefore, in order to solve Adv, we need to solve the following problem:
| (18) | ||||
| s.t. | (19) | |||
| (20) |
Problem (18)-(20) can be solved in time. Indeed, we first find, in time (see, e.g., [27]), the th largest coefficient, denoted by , such that , where is a permutation of . Then having we can choose coefficients , , and set . Having the optimal solution , we can construct the corresponding scenario as in the proof of Lemma 1 (see (16)). Hence, we get the following theorem.
Theorem 1.
The Adv problem under , for the non-overlapping case, can be solved in time.
We now show how to solve the MinMax problem for the non-overlapping case in polynomial time. We will first reformulate Adv as a linear programming problem with respect to . Then, the linearity will be preserved by adding linear constraints for . Writing the dual to (18)-(20), we obtain:
| (21) | |||||
| s.t. | (22) | ||||
| (23) | |||||
| (24) | |||||
where and are dual variables. Using (21)-(24), equality (17), and the definition of , we can rewrite (13)-(15) as:
| (25) | |||||
| s.t. | (26) | ||||
| (27) | |||||
| (28) | |||||
| (29) | |||||
| (30) | |||||
| (31) | |||||
where constraints (26)-(27) specify the maximum operators in the first sum of (17) and the remaining constraints model (22)-(24) and the coefficients , . We now prove that (25)-(31) solves the Adv problem.
Proof.
It is enough to show that there is an optimal solution to (25)-(31) such that for each . Let us fix and consider the term in the objective function. In an optimal solution, we have
| (32) |
where . Suppose and . We can then fix , for some , so that . Accordingly, we modify using (32), preserving the feasibility of (25)-(31) . The new value of is increased by at most . In consequence, the objective value (25) does not increase. ∎
Adding linear constraints , , and to (25)-(31) and using the fact that and are linear with respect to yield a linear program for the MinMax problem. This leads to the following theorem.
Theorem 2.
The MinMax problem under , for the non-overlapping case, can be solved in polynomial time.
3.2 General case
In this section we drop the assumption that the cumulative demand intervals are non-overlapping. We first consider the Adv problem. The following lemma is the key to constructing algorithms in this section, namely it shows that it is enough to consider only values of the cumulative demand in each interval.
Lemma 3.
There is an optimal solution to the Adv problem such that
| (33) |
Proof.
Scenario set is not convex. However, it can be decomposed into a union of convex sets in the following way. Let and define
| (34) |
where . Obviously, is a convex polytope. Furthermore, it is easy to check that . The objective function in (12) is convex with respect to and attains the maximum value at a vertex of a convex polytope (see, e.g., [32]). Hence, and from the fact that , there exists and, consequently, the convex polytope , whose vertex is an optimal solution to the Adv problem.
To simplify notation, let us write , if ; and , if . The constraints , , imply the polytope does not change if we narrow the intervals so that
| (35) |
From now on, we assume that the modified bounds and fulfill (35). Observe that after the narrowing, we get .
Assume that is a vertex of and so , . Suppose that for some . Let , , be subsequence of , such that and . We now claim that or , in consequence or , which completes the proof.
Suppose, contrary to our claim, that the first and the last components of the subsequence are such that and . Observe that , because otherwise , which contradicts (35). Similarly, . Therefore, and . We thus have
Let be such that for each and for . Since for each , there is sufficiently small, but positive , such that and . Hence is a strict convex combination of two solutions from and is not a vertex solution. ∎
Equality (33) means that, in order to solve Adv, it is enough to examine only values for every cumulative demand , . This fact allows us to transform, in polynomial time, the Adv problem to a version of the following restricted longest path problem (RLP for short). We are given a layered directed acyclic graph . Two nodes and are distinguished as the source node (no arc enters to ) and the sink node (no arc leaves ). Two attributes are associated with each arc , namely is the length (cost) and is the weight of and a bound on the total weights of paths. In the RLP problem we seek a path in from to whose total weight is at most () and the length (cost) of () is maximal.
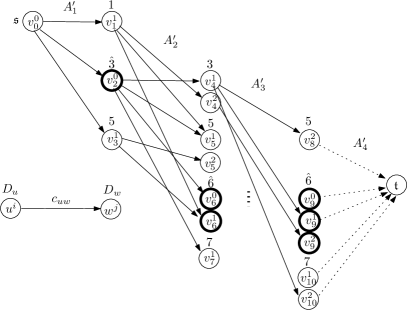
Given an instance of the Adv problem, the corresponding instance of RLP is constructed as follows. We first build a layered directed acyclic graph . The node set is partitioned into disjoint layers in which and contain the source and the sink node, respectively. Each node , , corresponds to exactly one possible value of the th component of a cumulative demand vertex scenario (see (33)), denoted by , , . We also partition the arc set into disjoint subsets, . Arc if and ; if and ; and arc , , if , and . Set . Finally two attributes are associated with each arc : and , whose values are determined as follows:
| (36) |
The second atribute is equal to 1 if the value of differs from the nominal value , and 0 otherwise, . The transformation can be done in time, since has arcs. An example is shown in Figure 2. At the nodes, other than and , the possible values of the cumulative demands are shown. Observe that . Hence , and . We can further assume that , due to the constraint .

Proposition 1.
A cumulative demand scenario with the cost of is optimal for an instance of the Adv problem if and only if there is an optimal - path with the length (cost) of for the constructed instance of the RLP problem.
Proof.
Suppose that with the cost of is an optimal cumulative demand scenario for an instance of Adv for . By Lemma 3, without loss of generality, we can assume that is a vertex of for some . Thus , , (see (33)). From the construction of and the definition of it follows that corresponds to an - path in , say , which satisfies the budget constraint and with the length of . We claim that is an optimal path for RLP in . Suppose, contrary to our claim, that there exists a feasible - path in of length (cost) greater than . By the construction of , the first arcs of correspond to scenario such that , , and . Obviously, has the same cost as . Since , for some and in consequence . This contradicts the optimality of over set .
Assume that is an optimal - path with the length (cost) of in . Similarly, from the construction of and the feasibility of it follows that its first arcs correspond to scenario from for some and from . The cost of is equal to the cost of . Furthermore, (33) and again the construction of show that each vertex scenario of for every corresponds to a feasible - path in with the same cost, that is not better than due to the optimality of . Lemma 3 now leads to the optimality of for an instance of Adv. ∎
In general, the restricted longest (shortest) path problem is weakly NP-hard, even for series-parallel graphs (see, e.g., [18]). However, it can be solved in pseudopolynomial time in directed acyclic graphs, if the bound and the weights , , (see, e.g., [25]). Fortunately, in our case and has arcs. We are thus led to the following theorem.
Theorem 3.
The Adv problem for can be solved in time.
We now deal with the problem of computing an optimal production plan. Our goal is to construct a linear programming formulation for the MinMax problem. Unfortunately, a direct approach based on the network flow theory leads to a linear program with the associated polytope that has not the integrality property (see [15]), i.e the one being the intersection of the path polytope defined as the convex hull of the characteristic vectors of - paths in and the half-space defined by the budged constraint , even if is bounded by an integer and the weights , . In consequence, such a restricted longest path problem in cannot be solved as the flow based linear program. However, using the fact that , we will transform in polynomial time our RLP problem to the longest path problem in acyclic graphs, for which a compact linear program can be built. The idea consists in transforming into by splitting each node of , different from , into at most nodes labeled as . Each arc with the attributes (see (36)) induces the set of arcs , , in with the same costs . The nodes from the th layer are connected to by arcs with 0 cost. We remove from all nodes which are not connected to or , obtaining a reduced graph ’. The resulting graph , for the graph presented in Figure 2, is shown in Figure 3.
Graph has nodes and arcs. Since , its size is polynomial in the input size of the MinMax problem. We now use the dual linear programming formulation of the longest path problem in . Let us associate unrestricted variable with each node of other than and unrestricted variable with node . The corresponding linear programming formulation for the longest path problem in (and for Adv) is a follows:
Using the definition of (see (36)), and adding linear constraints , , and , we can rewrite this program as follows:
| (37) |
Formulation (37) is a linear programming formulation for the MinMax problem, with variables and constraints. We thus get the following result:
Theorem 4.
The MinMax problem under in the general case is polynomially solvable.
4 Continuous budgeted uncertainty
In this section we discuss the MinMax and Adv problem under the continuous budgeted cumulative demand uncertainty defined in (10). Similarly as in Section 3, we first study the non-overlapping case and we consider then the general one. We provide negative and positive complexity results for the Adv and MinMax problems.
4.1 Non-overlapping case
We start by analyzing the properties of the Adv problem.
Lemma 4.
The Adv problem under , for the non-overlapping case, boils down to the following problem:
| (38) | ||||
| s.t. | (39) | |||
| (40) |
Proof.
The existence of an optimal vertex solution to (38)-(40) follows from the convexity of the objective function (38) (see, e.g., [32]). Let be an optimal solution of the Adv problem. Since , , where , , such that . Thus is a feasible solution to (39)-(40). The value of the objective function of (12) for can be bounded from above by the value of (38) for , and so by the value of (38) for . On the other hand, the cumulative demand scenario corresponding to can be built as follows:
| (41) |
and by the optimality of , the value of the objective function of (12) for , which equal to the value of (38) for , is bounded from above by the value of (12) for . Therefore is also an optimal solution to (12) and the lemma follows. ∎
Lemma 4 now shows that solving the Adv problem is equivalent to solving (38)-(40). An optimal solution to Adv can be formed according to (41). The following problem is an equivalent reformulation of (38)-(40):
| (42) | ||||
| s.t. | (43) | |||
| (44) |
where
and
is a linear or piecewise linear nonnegative convex function in , , (see Figure 4). Observe that is constant. Thus in order to solve the Adv problem we need to solve the inner optimization problem of (42)-(44), i.e.
| (45) | ||||
| s.t. | (46) | |||
| (47) |
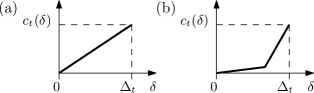
The above problem is a special case of a continuous knapsack problem with separable convex utilities that is weakly NP-hard in general (see [30]). In (45)-(47) the separable convex utilities have the simpler forms, piecewise linear ones, depicted in Figure 4. The next lemma shows that (45)-(47) is also weakly NP-hard even for the restricted separable convex utilities shown in Figure 4b and so Adv is weakly NP-hard (the proof is similar in spirit to that in [30]).
Theorem 5.
The Adv problem under , for the non-overlapping case, is weakly NP-hard.
Proof.
Consider the following weakly NP-hard Subset Sum problem (see, e.g., [18]), in which we are given a collection of positive integers and an integer . We ask if there is a subset such that .
We first show a polynomial time reduction from Subset Sum to (45)-(47). We are given an instance of the Subset-Sum and a corresponding instance of is built by setting the following parameters: the number of periods ; the costs , , ; the selling price ; the nominal value of cumulative demand for every , where ; the upper bound for every ; the cumulative production for every ; the budget . Therefore , , is a piecewise linear convex utility function, . Now the problem (45)-(47) has the following form:
| (48) | ||||
| s.t. | (49) | |||
| (50) |
Note that if and only if and for . Thus, by the constraint (49), the optimal value of (48) is bounded from above by . Accordingly, it is easily seen that if and only if the instance of Subset Sum is positive. Indeed, if and only if for each , the equality holds, which means that the answer to Subset Sum is yes. This completes the proof is (45)-(47) is weakly NP-hard. Furthermore, a trivial verification shows that (48)-(50) is an instance of (38)-(40. Hence, the Adv problem under is weakly NP-hard as well. ∎
Before proposing a pseudopolynomial algorithm for the Adv problem, we show the integrality property of an optimal solution to (45)-(47) or equivalently to (38)-(40). The following lemma is a key one.
Proof.
Substituting into , where , , we can rewrite (45)-(47) as:
| s.t. | |||
The constraint matrix of the resulting problem is totally unimodular. Hence, be the assumption , , each vertex solution is integral, i.e. , (see, e.g., [27]). Moreover, since the objective function is convex, it attains its maximum value at a vertex solution (see, e.g., [32]) that is integral. Thus an original optimal solution is integral as well and the lemma follows. ∎
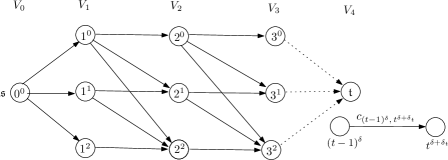
Now we ready to give a pseudopolynomial transformation of problem (38)-(40) to a longest path problem in a layered directed acyclic graph . We are given an instance of (38)-(40), where , . Graph is build as follows: the set is partitioned into disjoint layers , in which each layer corresponding to period , , has nodes denoted by ; sets and contain two distinguished nodes, and . The notation , , means that units of the available uncertainty have been allocated by an adversary to the cumulative demands in periods from to . Each node , (including the source node in ) has at most arcs that go to nodes in layer , namely arc exists and it is included to the set of arcs if , where . Moreover, we associate with such arc the cost in the following way (see also (38)):
| (51) |
Notice that the costs are constant, because is fixed. We finish with connecting each node from with the sink node by the arc of zero cost. The transformation can be done in time, where . An example for , and , , is shown in Figure 5.
Proposition 2.
Proof.
A trivial verification shows that each path from to in (its first arcs) models an integral feasible solution to (38)-(40) and vise a versa if , (see Lemma 5). Indeed, consider any - path in , by the construction of , its form is as follows: , where , , and its arcs , since , . Thus the total amount of uncertainty to cumulative demands along this path (along its first arcs) is at most , i.e. . Furthermore, it follows from (51) that the cost of this path is equal to the value of the objective function (38) for . Accordingly, the costs of an optimal solution to (38)-(40) and the length of a longest path in are the same, equal to . ∎
From Lemma 4 and Proposition 2 it follows that solving the Adv problem boils down to finding a longest path from to in built, which can be done in (see, e.g., [3]). Taking into account the running time required to construct and finding a longest path in we obtain the following theorem:
Theorem 6.
Suppose that , . Then the Adv problem under , for the non-overlapping case, can be solved in time.
There are some polynomially solvable cases of the Adv problem (problem (38)-(40)). The first one is obvious, namely, when is bounded by a polynomial of the problem size (notice that ). The second case is the uniform one, i.e. bounds for every , and then the inner problem (45)-(47) can be solved in time [30]. The last case, when , in the objective function (45), is linear (see Figure 4a) for every . Then the problem (45)-(47) becomes a continuous knapsack problem with separable linear utilities that can be solved in time (see, e.g., [27]).
It turns out that if , , then the Adv problem has a fully polynomial approximation scheme (FPTAS)111A maximization (resp. minimization) problem has an FPTAS if for each and every its instance the inequality (resp. ) holds, where is the optimal cost of and is the cost returned by an approximation algorithm whose running time is polynomial in both and the size of . It is assumed that the cost of each possible solution of the problem is nonnegative.. Indeed, the existence of the FPTAS follows from the fact that problem (45)-(47) with the integral property is a special case of the nonlinear knapsack problem with a separable nondecreasing objective function, a separable nondecreasing packing (budget) constraint and integer variables that admits an FPTAS (see [23]).
Corollary 1.
Suppose that , . Then the Adv problem under , for the non-overlapping case, admits an FPTAS.
Proof.
Let be an optimal solution to (42)-(44) (equivalently to the Adv problem) and be a solution to (45)-(47) returned by an FPTAS proposed in [23]. Obviously, the running time of the FPTAS for (42)-(44 is the same as the one for (45)-(47). We only need to show that the inequality holds for every . There is no loss of generality in assuming . Hence and from the fact that is an approximate solution to (45)-(47), we get . ∎
We now deal with the MinMax problem. Theorem 5 immediately yields the following corollary.
Corollary 2.
The MinMax problem under , for the non-overlapping case, is weakly NP-hard.
We now provide some positive results for the MinMax problem. We propose an ellipsoid algorithm based approach, adapted from [2], where a similar class of robust problems (with a different scenario set) has been studied. The MinMax problem (see (11)) can be formulated as the following convex programing model:
| (52) | |||||
| s.t. | (53) | ||||
| (54) | |||||
where is a convex function (recall that ). Thus the above program has infinitely many convex constraints of the form (53) and together with the linear constraints (54) that describe a convex set. One can solve (52)-(54) by the ellipsoid algorithm (see, e.g., [19]). By the equivalence of optimization and separation (see, e.g., [19]), we need only a separation oracle for the convex set determined by the constraints (53) and (54), i.e. a procedure, which for given , either decide that or return a separating hyperplane between and . Write , where is a convex set corresponding to constraints (53). Clearly, checking if or forming a separating hyperplane, if , that boils down to detecting a violated constraint by , can be trivially done in polynomial time, since is explicitly given by a polynomial number of linear constraints. While either deciding that or forming a separating hyperplane relies on solving the Adv problem for a . Indeed, if then . Otherwise, a separating hyperplane is of the form: , where if and , otherwise. The overall running time of the algorithm for solving (52)-(54) depends on the running time of an algorithm for the Adv problem applied, since the ellipsoid algorithm performs a polynomial number of operations and calls to our separation oracle. On account of the above remark and by Theorem 6, we get the following result:
Theorem 7.
Suppose that , . Then the MinMax problem under , for the non-overlapping case, can be solved in a pseudopolynomial time.
Accordingly, for all the polynomial solvable cases of the Adv problem, aforementioned in this section, one can obtain polynomial algorithms for the MinMax problem. An alternative approach to solve the MinMax problem is a linear programming formulation with pseudopolynomial number of constraints and variables, which is a constructive proof of Theorem 7. Assuming that , , we can reduce problem (38)-(40), that corresponds to Adv, to finding a longest path in layered weighted graph (see Proposition 2). We can use the same reasoning as in the previous section and build the following linear programming problem for MinMax:
| (55) | |||||
| s.t. | (56) | ||||
| (57) | |||||
| (58) | |||||
| (59) | |||||
where is unrestricted variable associated with node and is unrestricted variable associated with node of . The number of constraints and variables in (55)-(59) is . Now adding linear constraints , , and to (55)-(59) gives a linear program for the MinMax problem with a pseudopolynomial number of constraints and variables. It is worth pointing out that all the polynomially solvable cases of the Adv problem, presented in this section, can be modeled by linear programs with polynomial numbers of constraints and variables and thus they apply to MinMax one as well.
We now show that there exists an FPTAS for the MinMax problem. It turns out that the formulation (52)-(54) admits an FPTAS if there exits an FPTAS for for a given (the Adv problem). This result can easily be adapted from [2, Lemma 3.5]. Corollary 1 now implies:
Corollary 3.
Suppose that , . Then the MinMax problem under , for the non-overlapping case, admits an FPTAS.
4.2 General case
We now drop the assumption . Theorem 5 and Corollary 2 now implie the following hardness results for both problems under consideration.
Corollary 4.
The Adv and MinMax problems for in the general case are weakly NP-hard.
From an algorithmic point of view, the situation for the general case is more difficult Recall, that for the non-overlapping case the model for the Adv problem has the integrality property (see Lemma 5), which allowed us to build pseudopolynomial algorithms. Now, in order to ensure that , we have to add additional constraints , and the resulting model for the Adv problem takes the following form:
| (60) | |||||
| s.t. | (61) | ||||
| (62) | |||||
| (63) | |||||
The constraints (61)-(63) ensure that the cumulative demand scenario , induced by , belongs to . These constraints determine a convex polytope. Since the objective function is convex, its maximum value is attained at a vertex of this convex polytope. However, we show an instance of the Adv problem which has no optimal solutions being integer, when , . Let , , , , , , , , , , , and . Now the model (60)-(63) has the following form:
| (64) |
An easy computation shows that , and is an optimal vertex solution to (64) and there is no optimal integer solution.
One can easily construct a mixed integer programming (MIP) counterpart of (60)-(63) for the Adv problem, by linearizing (60) and (61), namely
| (65) | |||||
| s.t. | (66) | ||||
| (67) | |||||
| (68) | |||||
| (69) | |||||
| (70) | |||||
| (71) | |||||
| (72) | |||||
| (73) | |||||
where , , are suitably chosen large numbers. Unfortunately (65)-(73) cannot be extended to a compact MIP for the MinMax problem by using dualization.
In order to cope with the MinMax problem we construct a decomposition algorithm that can be seen as a version of Benders’ decomposition (similar algorithms have been previously used in [2, 7, 12, 20, 38, 44]). The idea consists in solving a certain restricted MinMax problem iteratively, which provides exact or approximate solution. At each iteration an approximate production plan is computed. It is then evaluated by solving the Adv problem and the lower and upper bounds on the cost of an optimal production plan for the original MinMax problem are improved. Consider the following linear programming program, called the master problem with :
| (74) | |||||
| s.t. | (75) | ||||
| (76) | |||||
| (77) | |||||
| (78) | |||||
| (79) | |||||
The constraints (75)-(77) are the linearization of (53). Thus (74)-(79) is a relaxation of the MinMax problem (for we get the MinMax one). An optimal solution to (74)-(79) is an approximate plan for MinMax and its quality is evaluated by solving the MIP model (65)-(73). In this way we get lower an upper bound on the optimal cost. The formal description of the above decomposition procedure is presented in the form of Algorithm 1.
Without loss of generality we can assume that is a finite set containing only vertex scenarios, since the Adv problem attains its optimum at vertex scenarios. This assumption ensures the convergence of Algorithm 1 in a finite number iterations. More precisely, Algorithm 1 terminates after at most iterations [44, Proposition 2]. However, in practice, the decomposition based algorithms perform quite small number iterations (see, e.g., [7, 12, 20, 38, 44]).
5 Conclusions
In this paper we have discussed a capacitated production planning under uncertainty. More specifically, we have studied a version of the capacitated single-item lot sizing problem with backordering under the budgeted cumulative demand uncertainty. We have considered two variants of the interval budgeted uncertainty representation and used the minmax criterion to choose a best robust production plan. For both variants, we have examined the problem of evaluating a given production plan in terms of its worst-case cost (the Adv problem) and the problem of finding a robust production plan along with its worst-case cost (the MinMax one). Under the discrete budgeted uncertainty, we have provided polynomial algorithms for the Adv problem and polynomial linear programming based methods for the MinMax problem in the non-overlapping case as well as in the general case. We have shown in this way that introducing uncertainty under the discrete budgeted model does not make the problems much computationally harder than their deterministic counterparts. Under the continuous budgeted uncertainty the problems under consideration have different properties than under the discrete budgeted one. In particular, the Adv problem and in consequence the MinMax one have turned to be weakly NP-hard even in the non-overlapping case. For the non-overlapping case we have constructed pseudopolynomial algorithms for the Adv problem and proposed a pseudopolynomial ellipsoidal algorithm and a linear programming program with a pseudopolynomial number of constraints and variables for the MinMax problem. Furthermore, we have shown that both problems admit an FPTAS. In the general case the problems still remain weakly NP-hard and, unfortunately, there is no easy characterization of vertex cumulative demand scenarios, namely the integral property does not hold. We recall that this property has allowed us to build the pseudopolynomial methods in the non-overlapping case. Accordingly, we have proposed a MIP model for the Adv problem and a constraint generation algorithm for the MinMax problem in the general case.
There is still a number of open questions concerning the examined problems, in particular, under the continuous budgeted uncertainty in the general case. The Adv and MinMax problems are weakly NP-hard. Thus a full-fledged complexity analysis of the problems has to be carried out, i.e. it is interesting to check the existence pseudopolynomial algorithms, FPTASs or approximation algorithms for them. Furthermore, proposing a compact MIP model for the MinMax problem is an interesting open problem.
Acknowledgements
Romain Guillaume was partially supported by the project caasc ANR-18-CE10-0012 of the French National Agency for Research. Adam Kasperski and Paweł Zieliński were supported by the National Science Centre, Poland, grant 2017/25/B/ST6/00486.
References
- [1] A. Agra, M. Poss, and M. Santos. Optimizing make-to-stock policies through a robust lot-sizing model. International Journal of Production Economics, 200:302–310, 2018.
- [2] A. Agra, M. C. Santos, D. Nace, and M. Poss. A dynamic programming approach for a class of robust optimization problems. SIAM Journal on Optimization, 26:1799–1823, 2016.
- [3] R. K. Ahuja, T. L. Magnanti, and J. B. Orlin. Network Flows: theory, algorithms, and applications. Prentice Hall, Englewood Cliffs, New Jersey, 1993.
- [4] D. J. Alem and R. Morabito. Production planning in furniture settings via robust optimization. Computers & Operations Research, 39:139–150, 2012.
- [5] M. A. Aloulou, A. Dolgui, and M. Y. Kovalyov. A bibliography of non-deterministic lot-sizing models. International Journal of Production Research, 52:2293–2310,, 2014.
- [6] J. R. T. Arnold, S. N. Chapman, and L. M. Clive. Introduction to Materials Management. Prentice Hall, 7-th edition, 2011.
- [7] Ö. N. Attila, A. Agra, K. Akartunali, and A. Arulselvan. A decomposition algorithm for robust lot sizing problem with remanufacturing option. In O. Gervasi, B. Murgante, S. Misra, G. Borruso, C. M. Torre, A. M. A. C. Rocha, D. Taniar, B. O. Apduhan, E. N. Stankova, and A. Cuzzocrea, editors, Computational Science and Its Applications - ICCSA 2017, Part II, volume 10405 of Lecture Notes in Computer Science, pages 684–695. Springer, 2017.
- [8] J. F. Benders. Partitioning procedures for solving mixed-variables programming problems. Numerische Mathematik, 4:238–252, 1962.
- [9] D. Bertsimas and M. Sim. Robust discrete optimization and network flows. Mathematical Programming, 98:49–71, 2003.
- [10] D. Bertsimas and M. Sim. The price of robustness. Operations research, 52:35–53, 2004.
- [11] D. Bertsimas and A. Thiele. A robust optimization approach to inventory theory. Operations Research, 54:150–168, 2006.
- [12] D. Bienstock and N. Özbay. Computing robust basestock levels. Discrete Optimization, 5:389–414, 2008.
- [13] N. Brahimi, N. Absi, S. Dauzère-Pérès, and A. Nordli. Single-item dynamic lot-sizing problems: An updated survey. European Journal of Operational Research, 263:838–863, 2017.
- [14] W. H. Chen and J. M. Thizy. Analysis of relaxations for the multi-item capacitated lot-sizing problem. Annals of Operations Research, 26:29–72, 1990.
- [15] G. Dahl and B. Realfsen. The cardinality-constrained shortest path problem in 2-graphs. Networks, 36:1–8, 2000.
- [16] A. Dolgui and C. Prodhon. Supply planning under uncertainties in MRP environments: A state of the art. Annual Reviews in Control, 31:269–279, 2007.
- [17] M. Florian, K. J. Lenstra, and A. H. G. Rinnooy Kan. Deterministic Production Planning: Algorithms and Complexity. Management Science, 26:669–679, 1980.
- [18] M. R. Garey and D. S. Johnson. Computers and Intractability. A Guide to the Theory of NP-Completeness. W. H. Freeman and Company, 1979.
- [19] M. Grötschel, L. Lovász, and A. Schrijver. Geometric Algorithms and Combinatorial Optimization. Springer-Verlag, 1993.
- [20] R. Guillaume, P. Kobylański, and P. Zieliński. A robust lot sizing problem with ill-known demands. Fuzzy Sets and Systems, 206:39–57, 2012.
- [21] R. Guillaume, C. Thierry, and B. Grabot. Modelling of ill-known requirements and integration in production planning. Production Planning and Control, 22:336–352, 2011.
- [22] R. Guillaume, C. Thierry, and P. Zieliński. Robust material requirement planning with cumulative demand under uncertainty. International Journal of Production Research, 55:6824–6845, 2017.
- [23] N. Halman, D. Klabjan, C. Li, J. B. Orlin, and D. Simchi-Levi. Fully Polynomial Time Approximation Schemes for Stochastic Dynamic Programs. SIAM Journal on Discrete Mathematics, 28:1725–1796, 2014.
- [24] N. Halman, D. Klabjan, M. Mostagir, J. B. Orlin, and D. Simchi-Levi. A fully polynomial-time approximation scheme for single-item stochastic inventory control with discrete demand. Mathematics of Operations Research, 34:674–685, 2009.
- [25] R. Hassin. Approximation Schemes for the Restricted Shortest Path Problem. Mathematics of Operations Research, 17:36–42, 1992.
- [26] A. Jamalnia, J.-B. Yang, A. Feili, D.-L. Xu, and G. Jamali. Aggregate production planning under uncertainty: a comprehensive literature survey and future research directions. The International Journal of Advanced Manufacturing Technology, 102:159–181, 2019.
- [27] B. Korte and J. Vygen. Combinatorial Optimization: Theory and Algorithms, Algorithms and Combinatorics. Springer-Verlag, 2012.
- [28] P. Kouvelis and G. Yu. Robust Discrete Optimization and its Applications. Kluwer Academic Publishers, 1997.
- [29] H. L. Lee, V. Padmanabhan, and S. Whang. Information Distortion in a Supply Chain: The Bullwhip Effect. Management Science, 43:546–558, 1997.
- [30] R. Levi, G. Perakis, and G. Romero. A continuous knapsack problem with separable convex utilities: Approximation algorithms and applications. Operations Research Letters, 42:367–373, 2014.
- [31] R. Levi, R. Roundy, and D. B. Shmoys. Provably near-optimal sampling-based policies for stochastic inventory control models. Mathematical Methods of Operations Research, 32:821–839, 2007.
- [32] B. Martos. Nonlinear programming theory and methods. Akadémiai Kiadó, Budapest, 1975.
- [33] J. Mula, D. Peidro, and R. Poler. The effectiveness of a fuzzy mathematical programming approach for supply chain production planning with fuzzy demand. International Journal of Production Economics, 128:136–143, 2010.
- [34] J. Mula, R. Poler, J. Garcia-Sabater, and F. C. Lario. Models for production planning under uncertainty: A review. International Journal of Production Economics, 103:271–285, 2006.
- [35] E. Nasrabadi and J. B. Orlin. Robust optimization with incremental recourse. CoRR, abs/1312.4075, 2013.
- [36] D. Peidro, J. Mula, R. Poler, and F. C. Lario. Quantitative models for supply chain planning under uncertainty: a review. The International Journal of Advanced Manufacturing Technology, 43:400–420, 2009.
- [37] Y. Pochet and L. A. Wolsey. Production Planning by Mixed Integer Programming. Springer-Verlag, 2006.
- [38] M. C. Santos, A. Agra, and M. Poss. Robust inventory theory with perishable products. Annals of Operations Research, 289:473–494, 2020.
- [39] C. R. Sox. Dynamic lot sizing with random demand and non-stationary costs. Operations Research Letters, 20(4):155–164, 1997.
- [40] H. Tempelmeier. Stochastic lot sizing problems. In J. M. Smith and B. Tan, editors, Handbook of Stochastic Models and Analysis of Manufacturing System Operations, pages 313–344. Springer New York, 2013.
- [41] R.-C. Wang and T.-F. Liang. Applying possibilistic linear programming to aggregate production planning. International Journal of Production Economics, 98:328–341, 2005.
- [42] C. Wei, Y. Li, and X. Cai. Robust optimal policies of production and inventory with uncertain returns and demand. International Journal of Production Economics, 134:357–367, 2011.
- [43] J. H. Yeung, W. C. K. Wong, and L. Ma. Parameters affecting the effectiveness of MRP systems: A review. International Journal of Production Research, 36:313–332, 1998.
- [44] B. Zeng and L. Zhao. Solving two-stage robust optimization problems using a column and constraint generation method. Operation Research Letters, 41:457–461, 2013.
- [45] M. Zhang. Two-stage minimax regret robust uncapacitated lot-sizing problems with demand uncertainty. Operations Research Letters, 39:342–345, 2011.