Robust Unsupervised Cross-Lingual Word Embedding
using Domain Flow Interpolation
Abstract
This paper investigates an unsupervised approach towards deriving a universal, cross-lingual word embedding space, where words with similar semantics from different languages are close to one another. Previous adversarial approaches have shown promising results in inducing cross-lingual word embedding without parallel data. However, the training stage shows instability for distant language pairs. Instead of mapping the source language space directly to the target language space, we propose to make use of a sequence of intermediate spaces for smooth bridging. Each intermediate space may be conceived as a pseudo-language space and is introduced via simple linear interpolation. This approach is modeled after domain flow in computer vision, but with a modified objective function. Experiments on intrinsic Bilingual Dictionary Induction tasks show that the proposed approach can improve the robustness of adversarial models with comparable and even better precision. Further experiments on the downstream task of Cross-Lingual Natural Language Inference show that the proposed model achieves significant performance improvement for distant language pairs in downstream tasks compared to state-of-the-art adversarial and non-adversarial models.
1 Introduction
Learning cross-lingual word embedding (CLWE) is a fundamental step towards deriving a universal embedding space in which words with similar semantics from different languages are close to one another. CLWE has also shown effectiveness in knowledge transfer between languages for many natural language processing tasks, including Named Entity Recognition (Guo et al., 2015), Machine Translation (Gu et al., 2018), and Information Retrieval (Vulic and Moens, 2015).
Inspired by Mikolov et al. (2013), recent CLWE models have been dominated by mapping-based methods (Ruder et al., 2019; Glavas et al., 2019; Vulic et al., 2019). They map monolingual word embeddings into a shared space via linear mappings, assuming that different word embedding spaces are nearly isomorphic. By leveraging a seed dictionary of 5000 word pairs, Mikolov et al. (2013) induces CLWEs by solving a least-squares problem. Subsequent works (Xing et al., 2015; Artetxe et al., 2016; Smith et al., 2017; Joulin et al., 2018) propose to improve the model by normalizing the embedding vectors, imposing an orthogonality constraint on the linear mapping, and modifying the objective function. Following work has shown that reliable projections can be learned from weak supervision by utilizing shared numeralsArtetxe et al. (2017), cognates Smith et al. (2017), or identical strings Søgaard et al. (2018).
Moreover, several fully unsupervised approaches have been recently proposed to induce CLWEs by adversarial training (Zhang et al., 2017a; Zhang et al., 2017b; Lample et al., 2018). State-of-the-art unsupervised adversarial approaches (Lample et al., 2018) have achieved very promising results and even outperform supervised approaches in some cases. However, the main drawback of adversarial approaches lies in their instability on distant language pairs Søgaard et al. (2018), inspiring the proposition of non-adversarial approaches (Hoshen and Wolf, 2018; Artetxe et al., 2018b). In particular, Artetxe et al. (2018b) (VecMap) have shown strong robustness on several language pairs. However, it still fails on 87 out of 210 distant language pairs (Vulic et al., 2019).
Subsequently, Li et al. (2020) proposed Iterative Dimension Reduction to improve the robustness of VecMap. On the other hand, Mohiuddin and Joty (2019) revisited adversarial models and add two regularization terms that yield improved results. However, the problem of instability still remains. For instance, our experiments show that the improved version(Mohiuddin and Joty, 2019) still fails in inducing reliable English-to-Japanese and English-to-Chinese CLWE space.
In this paper, we focus on the challenging task of unsupervised CLWE on distant language pairs. Due to the high precision achieved by adversarial models, we revisit adversarial models and propose to improve their robustness. We adopt the network architecture from Mohiuddin and Joty (2019) but treat the unsupervised CLWE task as a domain adaptation problem. Our approach is inspired by the idea of domain flow in computer vision that has been shown to be effective for domain adaptation tasks. Gong et al. (2019) introduced intermediate domains to generate images of intermediate styles. They added an intermediate domain variable on the input of the generator via conditional instance normalization. The intermediate domains can smoothly bridge the gap between source and target domains to ease the domain adaptation task. Inspired by this idea, we adapt domain flow for our task by introducing intermediate domains via simple linear interpolations. Specifically, rather than mapping the source language space directly to the target language space, we map the source language space to intermediate ones. Each intermediate space may be conceived as a pseudo-language space and is introduced as a linear interpolation of the source and target language space. We then engage the intermediate space approaching the target language space gradually. Consequently, the gap between the source language space and the target space could be smoothly bridged by the sequence of intermediate spaces. We have also modified the objective functions of the original domain flow for our task.
We evaluate the proposed model on both intrinsic and downstream tasks. Experiments on intrinsic Bilingual Dictionary Induction (BLI) tasks show that our method can significantly improve the robustness of adversarial models. Simultaneously, it could achieve comparable or even better precision compared with the state-of-the-art adversarial and non-adversarial models. Although BLI is a standard evaluation task for CLWEs, the performance on the BDI task might not correlate with performance in downstream tasks(Glavas et al., 2019). Following previous works (Glavas et al., 2019; Doval et al., 2020; Ormazabal et al., 2021), we choose Cross-Lingual Natural Language Inference (XNLI), a language understanding task, as the downstream task to further evaluate the proposed model. Experiments on the XNLI task show that the proposed model achieves higher accuracy on distant language pairs compared to baselines, which validates the importance of robustness of CLWE models in downstream tasks and demonstrates the effectiveness of the proposed model.
2 Proposed Model
Our model is implemented based on the network structure from Mohiuddin and Joty (2019), which implements a cycleGAN on the latent word representations transformed by autoencoders. In our model, the source language space corresponds to the source domain and the target language space corresponds to the target domain .
2.1 Introducing Intermediate Domains
Let and denote the intermediate domain as , similar to Gong et al. (2019). corresponds to the source domain , and corresponds to the target domain . By varying from 0 to 1, we can obtain a sequence of intermediate domains from to , referred to as domain flow. There are many possible paths from to and we expect to be the shortest one.
Moreover, given any z, we expect the distance between and to be proportional to the distance between and by z, or equivalently,
| (1) |
Thus finding the shortest path from to , i.e., the sequence of , leads to minimizing the following loss:
| (2) |
2.2 Implementation of Generators
Suppose x is sampled from the source domain and y is sampled from the target domain .
The generator in our model transfers data from the source domain to an intermediate domain instead of the target domain. Denote , then is a mapping from to .
To ensure the generator to be a linear transformation, we consider our generator as
| (3) |
In this setup, and . We adopt as a simple scale multiplication on a matrix, i.e.,
| (4) |
where is the final transformation matrix that we are interested in. Finally, our intermediate mappings become
| (5) |
These intermediate mappings are simple linear interpolations between the data from source domain and that from the pseudo target domain . The generator can be defined similarly.
2.3 The Domain Flow Model
The discriminator is used to distinguish and , and is used to distinguish and . Using the adversarial loss as the distribution distance measure, we obtain the adversarial losses between and as
| (6) |
Similarly, the adversarial losses between and can be written as
| (7) |
Deploying the above losses as and in Eq. (2), we can derive the following loss
| (8) |
Consider the other direction from to , we can define similar loss . Then the total adversarial loss is
| (9) |
Modification of Adversarial Loss
In the loss discussed above, is trained to assign a high value (i.e. 1) to x and assign a low value (i.e. 0) to , and similar for . But when is small, is close to the data from source domain and it will be too aggressive if we train the discriminator to assign 0 to it. In our model, we train the discriminator to assign instead of 0 to . When , and the discriminator is trained to assign 1 to it. and are trained to fool the discriminator , trying to make close to 1 and close to .
Besides the adversarial loss, the cycle consistency loss in the cycle GAN here is defined as:
| (10) |
Based on the model structure from Mohiuddin and Joty (2019), we deploy the domain flow on the latent space obtained from two autoencoders, i.e., replace and with and in above losses. An additional reconstruction loss in the autoencoders is defined as:
| (11) |
Then the total loss is
| (12) |
where and are two hyperparameters.
Choice of
In our model, is sampled from a beta distribution , where is the Beta function, is fixed to be 1, and is set as a function of the training iterations. Specifically, , where is the current iteration and is the total number of iterations. In this setting, tends to be more likely to be small values at the beginning, and gradually shift to larger values during training. In practice, we set in the last several epochs to fine-tune the model. For the case of running 10 epochs using our proposed model, the intermediate domain variable z is fixed to be 1 in the last 3 epochs, trying to fine-tune our proposed model. For other cases, i.e., when running 20 and 30 epochs, z is fixed to be 1 in the last 5 epochs.
3 Bilingual Lexicon Induction
3.1 Experimental Setup
| Languages | Language Family | Morphology Type | Wikipedia Size | ISO 639-1 |
|---|---|---|---|---|
| English | Indo-European | isolating | 6.46M | en |
| German | Indo-European | fusional | 2.67M | de |
| French | Indo-European | fusional | 2.40M | fr |
| Russian | Indo-European | fusional | 1.80M | ru |
| Spanish | Indo-European | fusional | 1.75M | es |
| Italian | Indo-European | fusional | 1.74M | it |
| Japanese | Japonic | agglutinative | 1.31M | ja |
| Chinese | Sino-Tibetan | isolating | 1.25M | zh |
| Arabic | Afro-Asiatic | fusional | 1.16M | ar |
| Finnish | Uralic | agglutinative | 0.52M | fi |
| Turkish | Turkic | agglutinative | 0.47M | tr |
| Malay | Austronesian | agglutinative | 0.36M | ms |
| Hebrew | Afro-Asiatic | fusional | 0.31M | he |
| Bulgarian | Indo-European | isolating | 0.28M | bg |
| Hindi | Indo-European | fusional | 0.15M | hi |
Bilingual Lexical Induction (BLI) has become the de facto standard evaluation for mapping-based CLWEs (Ruder et al., 2019; Glavas et al., 2019; Vulic et al., 2019). Given a shared CLWE space and a list of source language words, the task is to retrieve their target translations based on their word vectors. The lightweight nature of BLI allows us to conduct a comprehensive evaluation across a large number of language pairs. We adopt Cross-domain Similarity Local Scaling (CSLS) from Lample et al. (2018) for the nearest neighbor retrieval. Following a standard evaluation practice (Mikolov et al., 2013; Lample et al., 2018; Mohiuddin and Joty, 2019), we evaluate the performance of induced CLWEs with the Precision at k (P@k) metric, which measures the percentage of ground-truth translations that are among the top k ranked candidates.
Monolingual Embeddings
Following prior works (Lample et al., 2018; Søgaard et al., 2018; Glavas et al., 2019; Mohiuddin and Joty, 2019), we use 300-dimensional fastText embeddings (Bojanowski et al., 2017) 111https://fasttext.cc/docs/en/pretrained-vectors.html trained on Wikipedia monolingual corpus. All vocabularies are truncated to the 200K most frequent words.
Evaluation Dictionary
For the BLI task, we evaluate our model on two datasets. The first one is from Lample et al. (2018), which contains 110 bilingual dictionaries.222https://github.com/facebookresearch/MUSE#ground-truth-bilingual-dictionaries The other one is from Dinu and Baroni (2015) and its extension by Artetxe et al. (2018a), which consists of gold dictionaries for 4 language pairs. This dataset is refered to as Dinu-Artetxe in later sections.
Selection of Languages
From the 110 bilingual test dictionaries of Lample et al. (2018), we select test language pairs based on the following goals: a) for a direct comparison with recent works, we aim to cover both close and distant language pairs that are discussed in recent works; and b) for analyzing a large set of language pairs, we aim to ensure the coverage of different language properties and training data size. The resulting 15 languages (including English) are listed in Table 1333Since the training corpus size of fastText embeddings is not available, the Wikipedia Size in Table 1 is chosen as the number of wikipedia articles listed in https://en.wikipedia.org/wiki/List_of_Wikipedias#Details_table. It may differ from the actual size of fastText training corpus but the relative size among languages should not be far away from this.. We run BLI evaluations for language pairs of English and the rest 14 languages in both directions. The first five languages other than English in Table 1 belong to the same language family as English and have large monolingual corpora, which are categorized as "close" languages to English. The remaining languages are then categorized as "distant" to English since they belong to different language family from English or have much smaller monolingual corpora. For the Dinu-Artetxe dataset, we select all its 4 language pairs, i.e., English-German (en-de), English-Spanish (en-es), English-Italian (en-it), and English-Finnish (en-fi).
| models | en-de | de-en | en-fr | fr-en | en-ru | ru-en | en-es | es-en | en-it | it-en |
|---|---|---|---|---|---|---|---|---|---|---|
| MUSE | 75.26 | 72.53 | 82.21 | 82.36 | 40.65 | 58.46 | 82.60 | 83.40 | 77.87 | 77.30 |
| VecMap | 75.33 | 74.00 | 82.20 | 83.73 | 47.13 | 64.13 | 82.33 | 84.33 | 78.67 | 79.40 |
| AutoEnc | 75.77 | 73.87 | 82.55 | 83.33 | 47.29 | 64.48 | 82.25 | 84.21 | 79.06 | 80.20 |
| Our model | 75.78 | 74.83 | 82.53 | 83.51 | 47.55 | 65.08 | 82.36 | 84.43 | 79.10 | 80.20 |
Baselines
We compare our model with the well-known unsupervised models of Lample et al. (2018) (MUSE)444https://github.com/facebookresearch/MUSE and Artetxe et al. (2018b) (VecMap)555https://github.com/artetxem/vecmap. We implemented our proposed method of domain flow based on Mohiuddin and Joty (2019)666https://ntunlpsg.github.io/project/unsup-word-translation/, which is denoted as AutoEnc in this paper. Results of all baselines are obtained by rerunning the public codes with the default settings on our machine. More experimental details are presented in Appendix A.777We have not compared with Li et al. (2020) since its code is not publicly available.
3.2 Results and Discussion
Results of Precision on Lample et al. (2018) Dataset
We report the average precision at 1 (across the successful runs out of 10 runs) on Lample et al. (2018) dataset in Table 2, Table 3, and Table 4. The P@1 of close language pairs is shown in Table 2 and that of distant language pairs is Table 3 and Table 4. The detailed results including P@5, P@10 are presented in Appendix B. As shown in Table 2, the proposed model performs on par with that of the unsupervised baselines in close language pairs. As shown in Table 3 and Table 4, the proposed model gets comparable results with the baselines on distant language pairs en-bg and en-ms and achieves higher precision on en-he, en-tr, en-hi, en-fi, and en-ar. For more distant language pairs en-ja and en-zh, AutoEnc fails for all 10 runs.888Kindly note that we obtained one successful run for en-zh and 2 for en-ja when we changed the default SGD optimizer of the released code to Adam, with the learning rate of 0.001, and trained 50 epochs with epoch size of 100,000 for 20 times. Even for the most robust system VecMap, it still fails on en-zh. Our results show that the proposed model offers enhanced robustness that is able to complete these two difficult cases and exceed the performance of all baselines.
| models | en-he | he-en | en-tr | tr-en | en-bg | bg-en | en-hi | hi-en | en-fi | fi-en |
|---|---|---|---|---|---|---|---|---|---|---|
| MUSE | 36.26 | 54.07 | 45.40 | 59.65 | 41.97 | 56.29 | 30.40 | 39.55 | 42.70 | 59.30 |
| VecMap | 41.20 | 52.80 | 48.06 | 59.64 | 44.46 | 57.80 | 35.33 | 37.57 | 46.13 | 62.27 |
| AutoEnc | 43.71 | 57.76 | 49.31 | 61.01 | 46.62 | 61.01 | 35.74 | 46.58 | 44.65 | 62.59 |
| Our model | 44.67 | 58.01 | 50.45 | 61.19 | 46.77 | 60.85 | 36.88 | 49.17 | 48.28 | 64.66 |
| models | en-ar | ar-en | en-ms | ms-en | en-ja | ja-en | en-zh | zh-en |
|---|---|---|---|---|---|---|---|---|
| MUSE | 32.00 | 0 | 0.67 | 0.67 | 0 | 5.31 | 0.67 | 0 |
| VecMap | 34.79 | 49.26 | 48.40 | 38.80 | 37.56 | 26.12 | 0 | 0 |
| AutoEnc | 36.27 | 53.27 | 53.42 | 48.53 | 0 | 0 | 0 | 0 |
| Our model | 36.33 | 53.60 | 52.64 | 51.22 | 46.67 | 31.11 | 41.45 | 32.62 |
Results of Precision on Dinu-Artetxe Dataset
We report the average precision at 1 on Dinu-Artetxe dataset in Table 5. Similar conclusion can be drawn. Specifically, the proposed model gets comparable results with baselines for close language pairs en-de, en-es, and en-it. Moreover, the proposed model achieves higher precision on distant-language pair en-fi.
| models | en-de | en-es | en-it | en-fi |
|---|---|---|---|---|
| MUSE | 65.57 | 67.89 | 67.45 | 30.76 |
| VecMap | 65.73 | 69.31 | 68.71 | 37.95 |
| AutoEnc | 65.76 | 69.25 | 68.76 | 36.38 |
| Our model | 66.01 | 69.53 | 68.78 | 38.35 |
Results on Robustness
We reference Artetxe et al. (2018b) to define that a system ‘succeeds’ when it attains a precision above 5% and ‘fails’ otherwise. The precision in above sections is averaged over all successful runs. Indeed, the baselines do not always succeed even in the case where a positive precision is reported. For instance, using the default setting (5 epochs with epoch size of 1,000,000) and running the codes 10 times, AutoEnc model succeeds 7 runs on en-he, 7 runs on en-ar, and 5 runs on en-hi. Even worse, out of 10 runs, the baseline MUSE only succeeds 6 runs on en-he, 7 runs on en-ar, and 2 runs on en-hi. To show the effectiveness of the proposed domain flow in improving the robustness of adversarial models, we compare the proposed model with AutoEnc on distant language pairs of en-he, en-tr, en-bg, en-hi, en-fi, en-ar and en-ms.999En-ja and en-zh are not compared since Table 4 has shown that AutoEnc can never succeed in these two language pairs. Specifically, using an epoch size of 100,000 and various numbers of epochs, we count the successful runs of the proposed model and AutoEnc out of 10 runs. The results are shown in Table 6. As shown in Table 6, our model succeeds with a much higher probability (cf AutoEnc) for all the 3 language pairs, as well as succeeds 100% if it is given 30 epochs. Note that the default setting of AutoEnc is equivalent to 50 epochs. AutoEnc can not achieve 100% success under this setting. However, for the proposed approach, 30 epochs are sufficient for all the 7 distant language pairs.
| of epochs | models | en-he | en-tr | en-bg | en-hi | en-fi | en-ar | en-ms |
|---|---|---|---|---|---|---|---|---|
| 10 | AutoEnc | 2 | 7 | 8 | 6 | 2 | 3 | 0 |
| Ours | 6 | 9 | 10 | 9 | 6 | 8 | 9 | |
| 20 | AutoEnc | 6 | 7 | 8 | 7 | 4 | 6 | 2 |
| Ours | 8 | 10 | 10 | 8 | 10 | 10 | 10 | |
| 30 | AutoEnc | 7 | 7 | 9 | 7 | 4 | 7 | 4 |
| Ours | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
Visualization on Smoothing Training
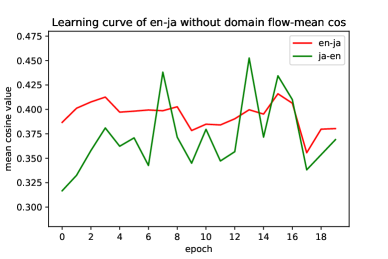
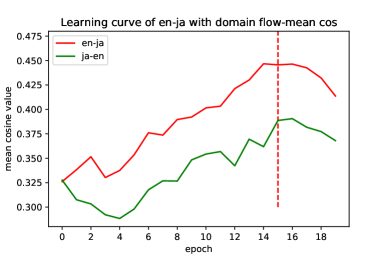
We use the unsupervised validation criterion proposed by Lample et al. (2018), which is the mean cosine value in a pseudo dictionary (details in Appendix C), to show the learning curves of en-ja in Figure 1. We observe that the training procedure of AutoEnc is very unstable. However, the mean cosine value of the proposed model can increase smoothly (z=1 in the last 5 epochs, i.e., applying 5 training iterations of AutoEnc to do fine-tuning). This suggests that the proposed model can learn cross-lingual mappings along a smoother trajectory than AutoEnc. This demonstrates the advantage of introducing intermediate domains to smoothly bridge the gap between the source and target domains, thus improving the robustness of unsupervised models.
4 Cross-Lingual Natural Language Inference
Moving beyond the BLI evaluation, we evaluate our model on a language understanding downstream task, Cross-Lingual Natural Language Inference (XNLI). Given a pair of sentences, the Natural Language Inference (NLI) task is to detect entailment, contradiction and neutral relations between them. We test our model on a zero-shot cross-lingual transfer setting where an NLI model is trained on English corpus and then tested on a second language (L2). Following Glavas et al. (2019), we train a well-known robust neural NLI model, Enhanced Sequential Inference Model (ESIM; Chen et al., 2017) on the English MultiNLI corpus (Williams et al., 2018).101010https://cims.nyu.edu/~sbowman/multinli/ The English word embeddings are from the induced CLWE space and are kept fixed during training. The trained ESIM model is then evaluated on the L2 portion of the XNLI (Conneau et al., 2018)111111https://github.com/facebookresearch/XNLI by changing the embedding layer to L2 embeddings from the induced CLWE space. The test languages are the intersection of the selected 14 languages in Table 1 and the available languages in XNLI dataset, which include 9 languages, i.e., German(de), French(fr), Russian(ru), Spanish(es), Chinese(zh), Arabic(ar), Turkish(tr), Bulgarian(bg), and Hindi (hi).
4.1 Results and Discussion
We report the average XNLI accuracy scores (from 3 NLI model training) in Table 7 and Table 8. The accuracy values in Table 7 are obtained by evaluating the L2 portion of XNLI using the fully trained English NLI model. We also evaluate the XNLI accuracy of L2 using the English NLI model checkpoint from every training epoch. We observe that while the test accuracy of English on MNLI is always increasing with more training epochs, the XNLI accuracy of L2 increases in the first few epochs and then decreases. The phenomenon may come from the overfitting of English NLI model. Thus we also report the highest XNLI accuracy value of L2 in Table 8 by evaluating the L2 portion of XNLI on every checkpoint and selecting the highest one. Following Glavas et al. (2019), we use asterisks to denote language pairs for which the given CLWE models sometimes could not yield successful runs in BLI task.
| models | de | ru | es | fr | ar | tr | bg | hi | zh |
|---|---|---|---|---|---|---|---|---|---|
| MUSE | 56.53 | 47.33 | 48.75 | 41.40 | 45.36* | 50.18 | 47.10* | 34.04* | 34.06* |
| VecMap | 51.38 | 45.46 | 40.51 | 36.61 | 41.13 | 44.74 | 41.60 | 37.43 | 33.89* |
| AutoEnc | 56.21 | 49.73 | 50.45 | 40.83 | 43.80* | 51.56 | 48.83* | 34.91* | 33.67* |
| Our model | 56.33 | 49.00 | 49.32 | 42.50 | 51.64 | 52.28 | 51.82 | 43.47 | 45.44 |
| models | de | ru | es | fr | ar | tr | bg | hi | zh |
|---|---|---|---|---|---|---|---|---|---|
| MUSE | 58.65 | 48.81 | 49.87 | 42.82 | 47.07* | 51.78 | 49.27* | 34.65* | 34.89* |
| VecMap | 52.46 | 46.35 | 41.45 | 38.13 | 43.54 | 45.50 | 44.58 | 43.83 | 34.61* |
| AutoEnc | 60.23 | 51.36 | 51.63 | 42.94 | 46.27* | 53.92 | 50.46* | 39.47* | 34.67* |
| Our model | 59.73 | 51.50 | 51.36 | 46.40 | 55.13 | 54.18 | 54.92 | 46.11 | 50.76 |
As shown in Table 7 and Table 8, the proposed model gets comparable results on close languages de, ru, and es. For all other languages, the proposed model outperforms all the baselines. Moreover, the performance of the proposed model gives marked improvements over all baselines for the languages where CLWE models yield failed runs in BLI task. When testing in zh, the XNLI accuracy values of all baselines are close to 33.33%, which means their predictions are almost like random guessing. Furthermore, the test XNLI accuracy values for NLI models trained from "failed" CLWEs are all close to 33.33% , which degrades the overall accuracy of ar, bg, and hi (shown in Table 7 and Table 8). This observation validates the importance of successful runs in BLI for downstream XNLI task and the high accuracy of the proposed model demonstrate its effectiveness in improving the robustness of adversarial models.
5 Related Work
Adversarial Approaches
Adversarial training has shown great success in inducing unsupervised CLWEs. This was first proposed by Barone (2016), who initially utilized an adversarial autoencoder to learn CLWEs. Despite encouraging results, his model is not competitive with approaches using bilingual seeds. Based on a similar model structure, Zhang et al. (2017a) improve the adversarial training with orthogonal parameterization and cycle consistency. They incorporate additional techniques like noise injection to aid training and report competitive results on the BLI task. Their follow-up work (Zhang et al., 2017b) propose to view word embedding spaces as distributions and to minimize their earth mover’s distance. Lample et al. (2018) report impressive results on a large BLI dataset by adversarial training and an iterative refinement process. Mohiuddin and Joty (2019) revisit the adversarial training and focus on mitigating the robustness issue by adding cycle consistency loss and learning cross-lingual mapping in a latent space encoder by autoencoders.
Projecting Embeddings into Intermediate Spaces
The idea of projecting word embedding spaces into intermediate spaces has been explored in other works. Jawanpuria et al. (2019) propose to decouple the cross-lingual mappings into language-specific rotations, to align embeddings in a latent common space, and a language-independent similarity metric, i.e., Mahalanobis metric, to measure the similarity of words in the latent common space. Doval et al. (2018) apply an additional transformation to refine the already aligned word embeddings, which moves cross-lingual synonyms towards a middle point between them. Kementchedjhieva et al. (2018) propose to project two languages onto a third latent space via generalized procrustes analysis. Different from us, their work focus on weakly supervised settings and they consider no constraint on the third latent space. However, we focus on the unsupervised case and the third space in our model is forced to approach the target space gradually staring from the source space. Heyman et al. (2019) utilize a similar idea to induce multilingual word embeddings. To learn a shared multilingual embedding space for a variable number of languages, they propose to incrementally add new languages to the current multilingual space. They find that it is beneficial to project close languages first and then more distant languages. Different from our work, their model is based on real languages and requires to construct a language order for the incremental learning. In contrast, our model utilizes a sequence of pseudo-languages and no additional engineering work on language order is required.
Motivation for unsupervised CLWE
Despite the success of fully unsupervised CLWE approaches, some recent works have questioned the motivations behind them. Søgaard et al. (2018) challenge the basic assumption of unsupervised CLWE approaches that monolingual word embedding graphs are approximately isomorphic. They further show the well-known adversarial approach, MUSE (Lample et al., 2018), performs poorly on morphologically rich languages and adding a weak supervision signal from identical words enables more robust induction. Vulic et al. (2019) show that the most robust non-adversarial approach, VecMap (Artetxe et al., 2018b), still fails on 87 out of 210 distant language pairs. Artetxe et al. (2020) argue that a scenario without any parallel data and abundant monolingual data is unrealistic in practice. However, Søgaard et al. (2018) shows that unsupervised approaches can sometimes outperform the supervised approaches (last row in their Table 2). Vulic et al. (2019) point out that techniques learned from unsupervised approaches can also benefit supervised and weakly supervised approaches. Artetxe et al. (2020) analyze the scientific value of unsupervised approaches. According to the literature, it is still an open problem which approach is better. The main drawback of unsupervised approaches lies in their instability. The research value of unsupervised approaches may exceed that of supervised approaches if we can solve the instability problem. 121212Additional discussions on CLWE and multilingual pre-trained language models are in Appendix D.
6 Conclusion
This paper proposes an approach for improving the robustness of unsupervised cross-lingual word embeddings by leveraging the idea of domain flow from computer vision. Experimental results on BLI tasks demonstrate that the proposed approach can achieve comparable precision on close language pairs and effectively enhance the robustness of adversarial models on distant language pairs, achieving a smooth learning curve. The experiments on XNLI tasks further validate importance of successful runs in BLI and the effectiveness of the proposed model.
References
- Artetxe et al. (2016) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2016. Learning principled bilingual mappings of word embeddings while preserving monolingual invariance. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, EMNLP 2016, Austin, Texas, USA, November 1-4, 2016, pages 2289–2294. The Association for Computational Linguistics.
- Artetxe et al. (2017) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2017. Learning bilingual word embeddings with (almost) no bilingual data. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, Canada, July 30 - August 4, Volume 1: Long Papers, pages 451–462. Association for Computational Linguistics.
- Artetxe et al. (2018a) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2018a. Generalizing and improving bilingual word embedding mappings with a multi-step framework of linear transformations. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, Louisiana, USA, February 2-7, 2018, pages 5012–5019. AAAI Press.
- Artetxe et al. (2018b) Mikel Artetxe, Gorka Labaka, and Eneko Agirre. 2018b. A robust self-learning method for fully unsupervised cross-lingual mappings of word embeddings. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, ACL 2018, Melbourne, Australia, July 15-20, 2018, Volume 1: Long Papers, pages 789–798. Association for Computational Linguistics.
- Artetxe et al. (2020) Mikel Artetxe, Sebastian Ruder, Dani Yogatama, Gorka Labaka, and Eneko Agirre. 2020. A call for more rigor in unsupervised cross-lingual learning. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, ACL 2020, Online, July 5-10, 2020, pages 7375–7388. Association for Computational Linguistics.
- Barone (2016) Antonio Valerio Miceli Barone. 2016. Towards cross-lingual distributed representations without parallel text trained with adversarial autoencoders. In Proceedings of the 1st Workshop on Representation Learning for NLP, Rep4NLP@ACL 2016, Berlin, Germany, August 11, 2016, pages 121–126. Association for Computational Linguistics.
- Bojanowski et al. (2017) Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomás Mikolov. 2017. Enriching word vectors with subword information. Transactions of the Association for Computational Linguistics, 5:135–146.
- Chen et al. (2017) Qian Chen, Xiaodan Zhu, Zhen-Hua Ling, Si Wei, Hui Jiang, and Diana Inkpen. 2017. Enhanced LSTM for natural language inference. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, Canada, July 30 - August 4, Volume 1: Long Papers, pages 1657–1668. Association for Computational Linguistics.
- Chronopoulou et al. (2021) Alexandra Chronopoulou, Dario Stojanovski, and Alexander Fraser. 2021. Improving the lexical ability of pretrained language models for unsupervised neural machine translation. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2021, Online, June 6-11, 2021, pages 173–180. Association for Computational Linguistics.
- Conneau et al. (2020) Alexis Conneau, Kartikay Khandelwal, Naman Goyal, Vishrav Chaudhary, Guillaume Wenzek, Francisco Guzmán, Edouard Grave, Myle Ott, Luke Zettlemoyer, and Veselin Stoyanov. 2020. Unsupervised cross-lingual representation learning at scale. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, ACL 2020, Online, July 5-10, 2020, pages 8440–8451. Association for Computational Linguistics.
- Conneau and Lample (2019) Alexis Conneau and Guillaume Lample. 2019. Cross-lingual language model pretraining. In Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, December 8-14, 2019, Vancouver, BC, Canada, pages 7057–7067.
- Conneau et al. (2018) Alexis Conneau, Ruty Rinott, Guillaume Lample, Adina Williams, Samuel R. Bowman, Holger Schwenk, and Veselin Stoyanov. 2018. XNLI: evaluating cross-lingual sentence representations. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, October 31 - November 4, 2018, pages 2475–2485. Association for Computational Linguistics.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 4171–4186. Association for Computational Linguistics.
- Dinu and Baroni (2015) Georgiana Dinu and Marco Baroni. 2015. Improving zero-shot learning by mitigating the hubness problem. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Workshop Track Proceedings.
- Doval et al. (2018) Yerai Doval, José Camacho-Collados, Luis Espinosa Anke, and Steven Schockaert. 2018. Improving cross-lingual word embeddings by meeting in the middle. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, October 31 - November 4, 2018, pages 294–304. Association for Computational Linguistics.
- Doval et al. (2020) Yerai Doval, José Camacho-Collados, Luis Espinosa Anke, and Steven Schockaert. 2020. On the robustness of unsupervised and semi-supervised cross-lingual word embedding learning. In Proceedings of The 12th Language Resources and Evaluation Conference, LREC 2020, Marseille, France, May 11-16, 2020, pages 4013–4023. European Language Resources Association.
- Glavas et al. (2019) Goran Glavas, Robert Litschko, Sebastian Ruder, and Ivan Vulic. 2019. How to (properly) evaluate cross-lingual word embeddings: On strong baselines, comparative analyses, and some misconceptions. In Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, pages 710–721. Association for Computational Linguistics.
- Gong et al. (2019) Rui Gong, Wen Li, Yuhua Chen, and Luc Van Gool. 2019. DLOW: domain flow for adaptation and generalization. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 2477–2486. Computer Vision Foundation / IEEE.
- Goodfellow et al. (2014) Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron C. Courville, and Yoshua Bengio. 2014. Generative adversarial nets. In Advances in Neural Information Processing Systems 27: Annual Conference on Neural Information Processing Systems 2014, December 8-13 2014, Montreal, Quebec, Canada, pages 2672–2680.
- Gu et al. (2018) Jiatao Gu, Hany Hassan, Jacob Devlin, and Victor O. K. Li. 2018. Universal neural machine translation for extremely low resource languages. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2018, New Orleans, Louisiana, USA, June 1-6, 2018, Volume 1 (Long Papers), pages 344–354. Association for Computational Linguistics.
- Guo et al. (2015) Jiang Guo, Wanxiang Che, David Yarowsky, Haifeng Wang, and Ting Liu. 2015. Cross-lingual dependency parsing based on distributed representations. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing of the Asian Federation of Natural Language Processing, ACL 2015, July 26-31, 2015, Beijing, China, Volume 1: Long Papers, pages 1234–1244. The Association for Computer Linguistics.
- Heyman et al. (2019) Geert Heyman, Bregt Verreet, Ivan Vulic, and Marie-Francine Moens. 2019. Learning unsupervised multilingual word embeddings with incremental multilingual hubs. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 1890–1902. Association for Computational Linguistics.
- Hoshen and Wolf (2018) Yedid Hoshen and Lior Wolf. 2018. Non-adversarial unsupervised word translation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, October 31 - November 4, 2018, pages 469–478. Association for Computational Linguistics.
- Jawanpuria et al. (2019) Pratik Jawanpuria, Arjun Balgovind, Anoop Kunchukuttan, and Bamdev Mishra. 2019. Learning multilingual word embeddings in latent metric space: A geometric approach. Trans. Assoc. Comput. Linguistics, 7:107–120.
- Joulin et al. (2018) Armand Joulin, Piotr Bojanowski, Tomás Mikolov, Hervé Jégou, and Edouard Grave. 2018. Loss in translation: Learning bilingual word mapping with a retrieval criterion. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, October 31 - November 4, 2018, pages 2979–2984. Association for Computational Linguistics.
- Kementchedjhieva et al. (2018) Yova Kementchedjhieva, Sebastian Ruder, Ryan Cotterell, and Anders Søgaard. 2018. Generalizing procrustes analysis for better bilingual dictionary induction. In Proceedings of the 22nd Conference on Computational Natural Language Learning, CoNLL 2018, Brussels, Belgium, October 31 - November 1, 2018, pages 211–220. Association for Computational Linguistics.
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A method for stochastic optimization. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings.
- Lample et al. (2018) Guillaume Lample, Alexis Conneau, Marc’Aurelio Ranzato, Ludovic Denoyer, and Hervé Jégou. 2018. Word translation without parallel data. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net.
- Li et al. (2020) Yanyang Li, Yingfeng Luo, Ye Lin, Quan Du, Huizhen Wang, Shujian Huang, Tong Xiao, and Jingbo Zhu. 2020. A simple and effective approach to robust unsupervised bilingual dictionary induction. In Proceedings of the 28th International Conference on Computational Linguistics, COLING 2020, Barcelona, Spain (Online), December 8-13, 2020, pages 5990–6001. International Committee on Computational Linguistics.
- Mikolov et al. (2013) Tomás Mikolov, Quoc V. Le, and Ilya Sutskever. 2013. Exploiting similarities among languages for machine translation. CoRR, abs/1309.4168.
- Mohiuddin and Joty (2019) Tasnim Mohiuddin and Shafiq R. Joty. 2019. Revisiting adversarial autoencoder for unsupervised word translation with cycle consistency and improved training. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 3857–3867. Association for Computational Linguistics.
- Ormazabal et al. (2021) Aitor Ormazabal, Mikel Artetxe, Aitor Soroa, Gorka Labaka, and Eneko Agirre. 2021. Beyond offline mapping: Learning cross-lingual word embeddings through context anchoring. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, ACL/IJCNLP 2021, (Volume 1: Long Papers), Virtual Event, August 1-6, 2021, pages 6479–6489. Association for Computational Linguistics.
- Ouyang et al. (2021) Xuan Ouyang, Shuohuan Wang, Chao Pang, Yu Sun, Hao Tian, Hua Wu, and Haifeng Wang. 2021. ERNIE-M: enhanced multilingual representation by aligning cross-lingual semantics with monolingual corpora. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, EMNLP 2021, Virtual Event / Punta Cana, Dominican Republic, 7-11 November, 2021, pages 27–38. Association for Computational Linguistics.
- Ruder et al. (2019) Sebastian Ruder, Ivan Vulic, and Anders Søgaard. 2019. A survey of cross-lingual word embedding models. Journal of Artificial Intelligence Research, 65:569–631.
- Smith et al. (2017) Samuel L. Smith, David H. P. Turban, Steven Hamblin, and Nils Y. Hammerla. 2017. Offline bilingual word vectors, orthogonal transformations and the inverted softmax. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net.
- Søgaard et al. (2018) Anders Søgaard, Sebastian Ruder, and Ivan Vulic. 2018. On the limitations of unsupervised bilingual dictionary induction. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, ACL 2018, Melbourne, Australia, July 15-20, 2018, Volume 1: Long Papers, pages 778–788. Association for Computational Linguistics.
- Vernikos and Popescu-Belis (2021) Giorgos Vernikos and Andrei Popescu-Belis. 2021. Subword mapping and anchoring across languages. In Findings of the Association for Computational Linguistics: EMNLP 2021, Virtual Event / Punta Cana, Dominican Republic, 16-20 November, 2021, pages 2633–2647. Association for Computational Linguistics.
- Vulic et al. (2019) Ivan Vulic, Goran Glavas, Roi Reichart, and Anna Korhonen. 2019. Do we really need fully unsupervised cross-lingual embeddings? In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP 2019, Hong Kong, China, November 3-7, 2019, pages 4406–4417. Association for Computational Linguistics.
- Vulic and Moens (2015) Ivan Vulic and Marie-Francine Moens. 2015. Monolingual and cross-lingual information retrieval models based on (bilingual) word embeddings. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago, Chile, August 9-13, 2015, pages 363–372. ACM.
- Williams et al. (2018) Adina Williams, Nikita Nangia, and Samuel R. Bowman. 2018. A broad-coverage challenge corpus for sentence understanding through inference. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2018, New Orleans, Louisiana, USA, June 1-6, 2018, Volume 1 (Long Papers), pages 1112–1122. Association for Computational Linguistics.
- Xing et al. (2015) Chao Xing, Dong Wang, Chao Liu, and Yiye Lin. 2015. Normalized word embedding and orthogonal transform for bilingual word translation. In NAACL HLT 2015, The 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, Colorado, USA, May 31 - June 5, 2015, pages 1006–1011. The Association for Computational Linguistics.
- Zhang et al. (2017a) Meng Zhang, Yang Liu, Huanbo Luan, and Maosong Sun. 2017a. Adversarial training for unsupervised bilingual lexicon induction. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, Canada, July 30 - August 4, Volume 1: Long Papers, pages 1959–1970. Association for Computational Linguistics.
- Zhang et al. (2017b) Meng Zhang, Yang Liu, Huanbo Luan, and Maosong Sun. 2017b. Earth mover’s distance minimization for unsupervised bilingual lexicon induction. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, EMNLP 2017, Copenhagen, Denmark, September 9-11, 2017, pages 1934–1945. Association for Computational Linguistics.
Appendix A A Experimental Details
All experiments are conducted on a single GPU of Tesla V100 DGXS 32GB.
Parameter and Optimizer Settings
In our setting, and are set to be 5 and 1, respectively. The dimension of the hidden space from autoencoders is set to be 350. We use the Adam optimizer (Kingma and Ba, 2015) with the learning rate of 0.001 and the batch size of 32 to train our model. The epoch size is chosen as 100,000. Note that in the default setting of MUSE and AutoEnc, the epoch size is chosen as 1,000,000 and the optimizer is chosen as the SGD with the learning rate of 0.1.
Fine-tuning Steps
After the initial mapping is derived from the adversarial training, some fine-tuning steps are used to refine it, just like what Lample et al. (2018) and Mohiuddin and Joty (2019) did in their work. That is, using the self-learning scheme to update the mappings and dictionaries alternatively and apply symmetric re-weighting (Artetxe et al., 2018a) on the transformed word embeddings. Then Cross-domain Similarity Local Scaling (Lample et al., 2018) is used to retrieve the word translation.
Appendix B B Detailed BLI Results
The detailed BLI precision results on Lample et al. (2018) dataset are shown in Table 10 and the results on Dinu-Artetxe dataset are shown in Table 9. In Table 10 and Table 9, ’ refers to the direction from English to other languages and ’’ refers to the direction from other languages to English.
| language | models | |||
|---|---|---|---|---|
| pairs | P@1 | P@5 | P@10 | |
| de | MUSE | 65.57 | 79.61 | 83.23 |
| VecMap | 65.73 | 79.73 | 83.37 | |
| AutoEnc | 65.76 | 79.85 | 82.98 | |
| Ours | 66.01 | 80.05 | 83.14 | |
| es | MUSE | 67.89 | 81.74 | 84.73 |
| VecMap | 69.31 | 82.11 | 85.33 | |
| AutoEnc | 69.25 | 82.46 | 85.25 | |
| Ours | 69.53 | 82.66 | 85.51 | |
| it | MUSE | 67.45 | 81.83 | 85.69 |
| VecMap | 68.71 | 83.60 | 86.04 | |
| AutoEnc | 68.76 | 83.22 | 86.00 | |
| Ours | 68.78 | 83.35 | 86.06 | |
| fi | MUSE | 30.76 | 49.57 | 57.47 |
| VecMap | 37.95 | 58.22 | 65.23 | |
| AutoEnc | 36.38 | 57.60 | 64.24 | |
| Ours | 38.35 | 58.56 | 65.25 | |
| language | models | ||||||
|---|---|---|---|---|---|---|---|
| pairs | P@1 | P@5 | P@10 | P@1 | P@5 | P@10 | |
| de | MUSE | 74.70 | 88.80 | 91.56 | 72.49 | 85.45 | 88.36 |
| VecMap | 75.33 | 89.66 | 92.26 | 74.00 | 85.73 | 88.53 | |
| AutoEnc | 75.72 | 89.50 | 92.18 | 74.35 | 85.67 | 88.77 | |
| Ours | 75.79 | 89.51 | 91.78 | 74.75 | 85.89 | 88.96 | |
| fr | MUSE | 82.21 | 90.53 | 92.78 | 82.36 | 91.34 | 93.08 |
| VecMap | 82.20 | 91.13 | 93.20 | 83.73 | 91.80 | 93.33 | |
| AutoEnc | 82.55 | 91.27 | 93.03 | 83.33 | 91.34 | 93.38 | |
| Ours | 82.53 | 91.17 | 93.05 | 83.51 | 91.47 | 93.41 | |
| ru | MUSE | 40.65 | 68.78 | 75.53 | 58.46 | 75.65 | 79.76 |
| VecMap | 47.13 | 70.20 | 75.93 | 64.13 | 77.33 | 81.20 | |
| AutoEnc | 47.29 | 73.41 | 78.91 | 64.48 | 77.40 | 81.11 | |
| Ours | 47.55 | 73.83 | 79.36 | 65.08 | 77.75 | 81.45 | |
| es | MUSE | 82.36 | 91.17 | 93.60 | 84.02 | 91.90 | 93.54 |
| VecMap | 82.33 | 91.33 | 92.91 | 84.33 | 92.26 | 93.86 | |
| AutoEnc | 82.25 | 90.70 | 92.96 | 84.31 | 92.48 | 94.34 | |
| Ours | 82.36 | 90.80 | 92.95 | 84.43 | 92.42 | 94.37 | |
| it | MUSE | 77.87 | 88.57 | 91.00 | 77.30 | 88.07 | 90.27 |
| VecMap | 78.67 | 89.26 | 91.40 | 79.40 | 88.00 | 90.06 | |
| AutoEnc | 78.97 | 89.13 | 91.60 | 80.10 | 88.36 | 90.46 | |
| Ours | 79.04 | 89.11 | 91.69 | 80.31 | 88.29 | 90.47 | |
| he | MUSE | 38.07 | 60.47 | 67.20 | 52.33 | 6q8.09 | 72.16 |
| VecMap | 41.20 | 62.06 | 69.00 | 52.80 | 66.96 | 72.16 | |
| AutoEnc | 43.71 | 65.39 | 70.36 | 57.76 | 70.21 | 73.50 | |
| Ours | 44.67 | 65.60 | 70.60 | 58.01 | 70.35 | 73.71 | |
| tr | MUSE | 45.40 | 64.80 | 72.16 | 59.65 | 73.93 | 78.21 |
| VecMap | 48.06 | 66.33 | 72.00 | 59.64 | 72.51 | 75.78 | |
| AutoEnc | 49.31 | 69.33 | 74.79 | 61.01 | 73.36 | 76.37 | |
| Ours | 50.45 | 70.50 | 75.73 | 61.19 | 74.08 | 77.18 | |
| bg | MUSE | 41.97 | 63.75 | 70.49 | 56.29 | 72.17 | 76.74 |
| VecMap | 44.46 | 64.13 | 68.87 | 57.80 | 71.33 | 74.93 | |
| AutoEnc | 46.62 | 67.63 | 73.85 | 61.01 | 75.03 | 78.76 | |
| Ours | 46.77 | 68.60 | 74.53 | 60.85 | 74.42 | 78.17 | |
| hi | MUSE | 30.40 | 47.07 | 52.64 | 39.55 | 57.97 | 63.13 |
| VecMap | 35.33 | 49.86 | 53.80 | 37.57 | 52.17 | 55.86 | |
| AutoEnc | 35.74 | 50.68 | 56.57 | 46.58 | 62.49 | 66.63 | |
| Ours | 36.88 | 52.69 | 58.62 | 49.27 | 65.82 | 70.10 | |
| fi | MUSE | 42.70 | 67.13 | 74.10 | 59.30 | 74.20 | 78.40 |
| VecMap | 46.13 | 70.26 | 76.33 | 62.27 | 76.46 | 80.20 | |
| AutoEnc | 44.65 | 63.05 | 74.33 | 62.59 | 75.87 | 79.43 | |
| Ours | 48.28 | 72.11 | 78.20 | 64.66 | 77.16 | 80.87 | |
| ar | MUSE | 30.94 | 50.34 | 58.20 | 44.48 | 60.94 | 65.91 |
| VecMap | 34.79 | 55.80 | 62.60 | 49.26 | 65.06 | 68.14 | |
| AutoEnc | 36.28 | 56.84 | 64.15 | 53.28 | 67.65 | 71.24 | |
| Ours | 36.79 | 58.27 | 66.17 | 54.42 | 69.31 | 72.64 | |
| ms | VecMap | 50.27 | 64.40 | 69.06 | 47.10 | 61.64 | 65.04 |
| AutoEnc | 53.42 | 68.66 | 73.95 | 48.53 | 62.61 | 66.77 | |
| Ours | 52.64 | 67.91 | 72.98 | 51.22 | 66.12 | 70.32 | |
| ja | VecMap | 37.56 | 53.39 | 59.08 | 26.12 | 35.29 | 38.87 |
| Ours | 46.67 | 62.59 | 67.15 | 31.11 | 44.87 | 49.19 | |
| zh | Ours | 41.45 | 59.75 | 65.24 | 32.62 | 51.53 | 57.89 |
Appendix C C Unsupervised Validation Criterion
We apply the unsupervised validation criterion proposed by Lample et al. (2018) to select the best model. Specifically, we consider 10,000 most frequent source words and find their nearest neighbors in the target space via the current mapping. We maintain a pseudo dictionary that consists of the words with their translations if the translations are also among the 10,000 most frequent words in the target language space. Then among these pseudo translation pairs, the average cosine similarity is calculated as the validation criterion, i.e., we save the model with the largest average cosine similarity. This average cosine value is empirically highly correlated with the mapping quality Lample et al. (2018).
Appendix D D Related Work on CLWE and Multilingual Pre-trained Language Models
Multilingual pre-trained language models (MPLMs) have shown impressing results on cross-lingual tasks by pre-training a single model to handle multiple languages (Devlin et al., 2019; Conneau and Lample, 2019; Conneau et al., 2020; Ouyang et al., 2021). The shared information among multiple languages is implicitly explored by the overlapped subword vocabulary. Recent works have shown that CLWE is effective to improve the cross-lingual transferability of MPLMs. Chronopoulou et al. (2021) utilize the mapped CLWEs to initialize the embedding layer of multilingual pre-trained language models and achieve a little improvement on the unsupervised machine translation task. Vernikos and Popescu-Belis (2021) transfer a pretrained Language Model from one language () to another language () by initializing the embedding layer in as the embeddings of aligned words in . They observe performance improvement in the zero-shot XNLI task and the machine translation task. The research of CLWE may benefit recent MPLMs and we leave it for future work.