Robustness and Games Against Nature in Molecular Programming

We now review the definition of CRNs. We fix a countably infinite set $\mathbf{S}$ whose elements are called species. We informally regard each species as an abstract type of molecule.

A reaction over a finite set $S\subseteq\mathbf{S}$ is an ordered triple

$$\rho=(\mathbf{r},\mathbf{p},k)\in\mathbb{N}^{S}\times\mathbb{N}^{S}\times(0,\infty),$$

where $\mathbf{r}\neq\mathbf{p}$ and $\mathbb{N}^{S}$ is the set of functions from $S$ into $\mathbb{N}$. Given such a reaction $\rho$, we call $\mathbf{r}(\rho)=\mathbf{r}$ the reactant vector of $\rho$, $\mathbf{p}(\rho)=\mathbf{p}$ the product vector of $\rho$, and $k(\rho)=k$ the rate constant of $\rho$. (Since $S$ is finite, it is natural to regard elements of $\mathbb{N}^{S}$ as vectors.) The species in the support $\operatorname{supp}(\mathbf{r})=\{X\in S\mid\mathbf{r}(X)>0\}$ are the reactants of $\rho$, and the species in $\operatorname{supp}(\mathbf{p})$ are the products of $\rho$.

We usually write reactions in a more chemistry-like notation. For example, if $S=\{X,Y,C\}$, then we write

$$X+C\overset{k}{\to}2Y+C$$

for the reaction $(\mathbf{r},\mathbf{p},k)$, where $\mathbf{r}(X)=1$, $\mathbf{r}(Y)=0$, $\mathbf{r}(C)=1$, $\mathbf{p}(X)=0$, $\mathbf{p}(Y)=2$, and $\mathbf{p}(C)=1$. A species $C$ satisfying $\mathbf{r}(\rho)(C)=\mathbf{p}(\rho)(C)>0$, as in this example, is called a catalyst of the reaction $\rho$. The net effect of a reaction $\rho$ is the vector $\Delta\rho=\mathbf{p}(\rho)-\mathbf{r}(\rho)\in\mathbb{Z}^{S}$. The arity of a reaction $\rho$ is

$$\operatorname{arity}(\rho)=\sum_{Y\in S}\mathbf{r}(\rho)(Y),$$

i.e., its total number of reactants. A chemical reaction network (CRN) is an ordered pair $N=(S,R)$, where $S\subseteq\mathbf{S}$ is finite and $R$ is a finite set of reactions over $S$.

In this paper we assign each CRN $N=(S,R)$ the operational meaning given by the stochastic mass action semantics (also called the stochastic mass action kinetics) introduced by Gillespie [13]. In this semantics a state of $N$ is a vector $\mathbf{x}\in\mathbb{N}^{S}$. For each $Y\in S$, the component $\mathbf{x}(Y)$ of $\mathbf{x}$ is the count of species $Y$ in the state $\mathbf{x}$. A reaction $\rho$ is applicable to state $\mathbf{x}$ if $\mathbf{r}(\rho)\leq\mathbf{x}$, i.e., all the reactants of $\rho$ are present in $\mathbf{x}$. If $\rho$ is applicable to $\mathbf{x}$, then the result of applying $\rho$ to $\mathbf{x}$ is the state $\rho(\mathbf{x})=\mathbf{x}+\Delta\rho\in\mathbb{N}^{S}$.

The (stochastic mass action) rate of a reaction $\rho$ in a state $\mathbf{x}\in\mathbb{N}^{S}$ and volume $V>0$ of solution, which we denote by $\operatorname{rate}_{\mathbf{x}}(\rho)$, was defined and justified by Gillespie [13]. Here we give a single example. Let $\rho$ be a reaction

$$3Y+Z\to\textrm{RHS}.$$

(The right-hand side RHS does not affect the rate of a reaction.) For brevity, write $y=\mathbf{x}(Y)$ and $z=\mathbf{x}(Z)$. If $\rho$ is applicable to $\mathbf{x}$ (i.e., if $y\geq 3$ and $z\geq 1$), then

	$\displaystyle\operatorname{rate}_{\mathbf{x}}(\rho)$	$\displaystyle=k\cdot V^{1-\operatorname{arity}(\rho)}\cdot y\cdot(y-1)\cdot(y-2)\cdot z$
		$\displaystyle=ky(y-1)(y-2)z/V^{3}.$

Under stochastic mass-action semantics, a CRN $N=(S,R)$ functions as a continuous-time Markov chain [22] with state space $\mathbb{N}^{S}$ and, for each $\mathbf{x},\mathbf{y}\in\mathbb{N}^{S}$, transition rate

$$\operatorname{rate}(\mathbf{x},\mathbf{y})=\sum_{\rho(\mathbf{x})=\mathbf{y}}\operatorname{rate}_{\mathbf{x}}(\rho).$$

The CRN $N$ is initialized to some state or distribution over states. When it enters a state $\mathbf{x}$, it stays there for a random, real-valued sojourn time $t\in(0,\infty]$ before instantaneously executing some reaction $\rho$ and jumping to the state $\rho(\mathbf{x})$. A trajectory of $N$ is thus a sequence $\tau=((\mathbf{x}_{0},t_{0}),(\mathbf{x}_{1},t_{1}),\ldots)$ of ordered pairs $(\mathbf{x}_{i},t_{i})$, where $\mathbf{x}_{i}$ is a state of $N$ and $t_{i}$ is the associated sojourn time. The trajectory $\tau$ is finite if it reaches a state to which no reaction is applicable. Otherwise, the trajectory is infinite.

We measure the robustness of a CRN $N_{1}$ to a profile $(N_{2},N_{3},\ldots,N_{n})$ of other players’ CRNs by comparing player 1’s expected utility playing $N_{1}$ against those CRNs to its expected utility playing $N_{1}$ against trivial CRNs. Formally, for any $\alpha\in[0,1]$, a CRN $N_{1}\in\mathbf{N}_{1}$ is $\alpha$-robust to $(N_{2},N_{3},\ldots,N_{n})$ in game $\mathcal{G}$ under $\xi$ if

$$U_{1}((N_{1},N_{2},\ldots,N_{n}),\xi)\geq\alpha U_{1}((N_{1},(\emptyset,\emptyset),\ldots,(\emptyset,\emptyset)),\xi^{\prime}),$$

where $\xi^{\prime}=(\xi_{1},\epsilon,\epsilon,\ldots,\epsilon)$ and $\epsilon$ is the trivial distribution that assigns probability 1 to the empty vector. This means that the participation of other players using these strategies can decrease player 1’s expected utility by at most a factor of $\alpha$.

The very general CRN games that we have defined allow essentially unrestricted interactions among the players’ CRNs. For many purposes, including those of this paper, it is more appropriate to restrict these interactions to those mediated by catalysts.

A catalytic game is one in which each player’s set of species can be written as $\mathbf{S}_{i}=\mathbf{A}_{i}\cup\mathbf{C}_{i}$ such that

1. 1.

   $\mathbf{A}_{i}$ and $\mathbf{A}_{j}$ are disjoint for all $j\neq i$, and

2. 2.

   for all $C\in\mathbf{C}_{i}$ and $\rho\in\mathbf{R}_{i}$, we have $\Delta\rho(C)=0$.

In such a game, each player can affect other players only by altering the counts of their catalysts, and hence only by altering the rates of their reactions.

In this preliminary report, we use a game against nature to investigate the robustness of a simple chemical reaction network that computes approximate majority.

The task in approximate majority is to design a chemical reaction network $N$ with two designated species $X$ and $Y$ and the following objective. Let $x(t)$ and $y(t)$ be the counts of $X$ and $Y$, respectively, at time $t$. First, the total population $x(t)+y(t)$ should be constant as $t$ varies. Moreover, if $x(0)$ and $y(0)$ differ by a non-negligible amount, then whichever is larger should eventually “take over.” That is, if $x(0)\gg y(0)$, then we should with high probability have $x(t)=x(0)+y(0)$ (and hence $y(t)=0$) for all sufficiently large $t$. Similarly, if $y(0)\gg x(0)$, then we should with high probability have $y(t)=x(0)+y(0)$ for all sufficiently large $t$. If $x(0)$ is very close to $y(0)$, then we want one of these “takeovers” to occur with high probability, but it may be either species that takes over.

We investigate the robustness of the approximate majority CRN

$$R:\begin{array}[]{l}2X+Y\overset{1}{\to}3X\\ X+2Y\overset{1}{\to}3Y\end{array}$$

of Condon, Hajiaghayi, Kirkpatrick and Manuch [5]. In order to do this in a catalytic game, we replace $R$ with the catalyzed CRN

$$R^{\prime}:\begin{array}[]{l}2X+Y+A\overset{1}{\to}3X+A\\ X+2Y+B\overset{1}{\to}3Y+B.\end{array}$$

The crucial thing to note here is that, if $x$, $y$, $a$, and $b$ are the counts of $X$, $Y$, $A$, and $B$ at some time, then the rates (“clock speeds”) of the reactions in $R$ at this time are $x(x-1)y$ and $xy(y-1)$, respectively, while the rates of the reactions in $R^{\prime}$ are $ax(x-1)y$ and $bxy(y-1)$, respectively. If $a$ and $b$ are equal and constant, then $R^{\prime}$ is merely a uniformly sped-up version of $R$. However, if $a$ and $b$ vary randomly, then the relative rates of the reactions in $R^{\prime}$ also vary randomly (i.e., the ratio of these rates varies randomly).

In order to test the robustness of $R$ to random perturbations of the relative rates of their reactions we thus play the CRN $R^{\prime}$ against a random “nature” that varies the initially equal counts $a$ and $b$ randomly. We model this behavior by the simple CRN

$$N_{k}:\begin{array}[]{l}A\overset{k}{\to}B\\ B\overset{k}{\to}A\end{array},$$

which is “calibrated” by the rate constant $k\in(0,\infty)$.

We assessed the robustness of the approximate majority CRN $R$ by comparing the performance of the catalyzed CRN $R^{\prime}$ in isolation with its performance in the presence of the CRN $N_{k}$ representing nature randomly perturbing rate constants. We frame this as a game where the utility of the approximate majority player is given by its success frequency.

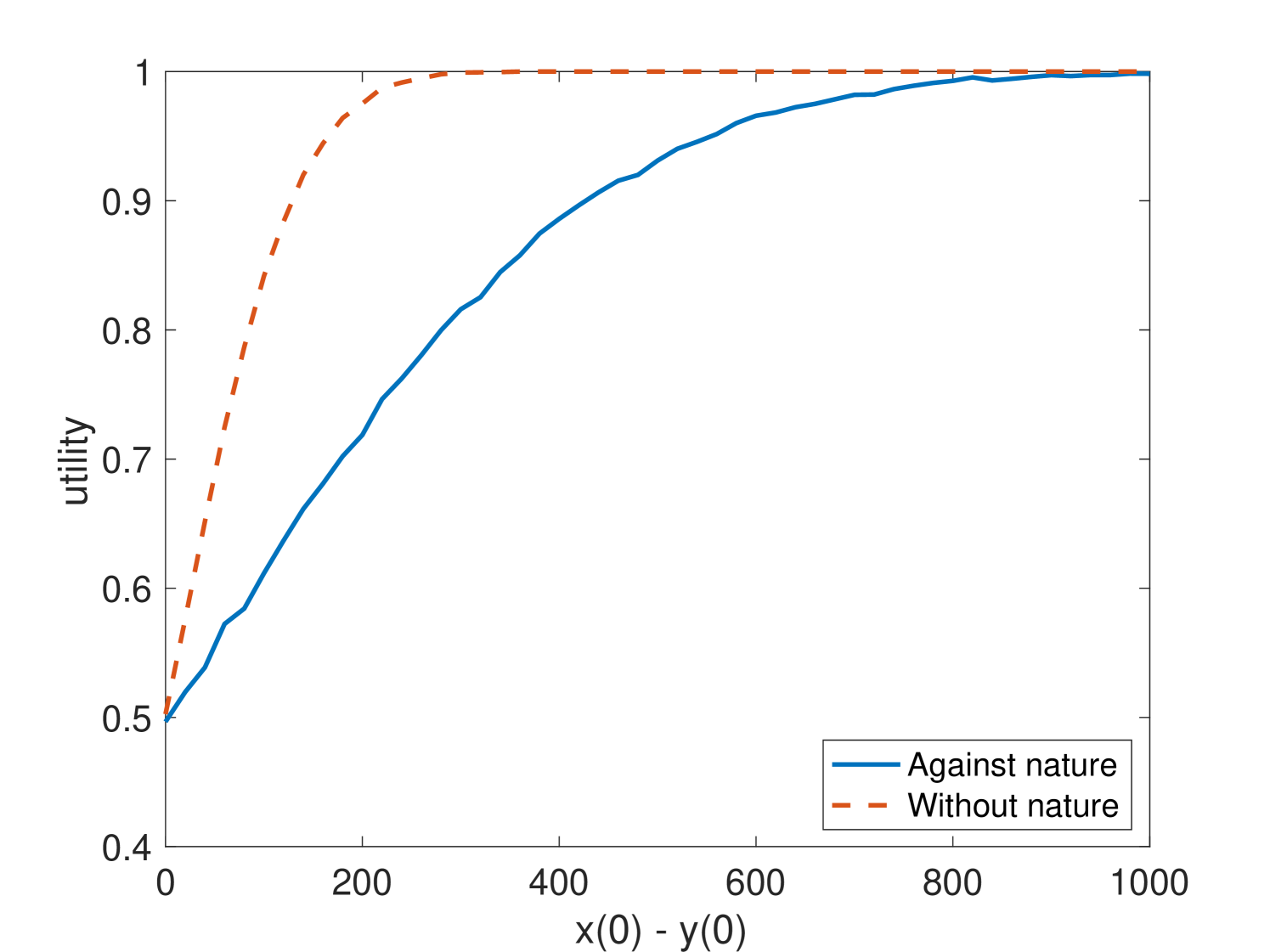
We first created models in MATLAB using SimBiology software tools for the catalyzed approximate majority CRN $R^{\prime}$ and the nature CRN $N_{k}$ described above. With initial populations $a(0)=b(0)=100$ and combined initial population $x+y=10,000$, we varied the difference $x(0)-y(0)$ from 0 to 1,000 by intervals of 10. With these initial conditions, we ran $R^{\prime}$ in the presence of $N_{k}$ with $k=10^{9}$. We ran 10,000 trials for each set of initial conditions. Each trial converged within $10^{-8}$ time units, meaning that either $x(10^{-8})$ or $y(10^{-8})$ was 0. The design of the CRN $R^{\prime}$ guarantees that, once one population has taken over, no further reactions can occur.

As Fig. 1 shows, the random perturbations of $a$ and $b$ did reduce the success probability of the approximate majority algorithm for some values of $x(0)-y(0)$. For example, when $x(0)=5,120$ and $y(0)=4,880$, $R^{\prime}$ was $99\%$ successful in a vacuum but only $76\%$ successful in the presence of nature. However, even with the random perturbations, the success frequency in the presence of nature was always greater than $70\%$ of the success frequency in the absence of nature. This suggests that the CRN $R^{\prime}$ is at least $0.7$-robust to $N_{10^{9}}$ in this game under arbitrary distributions of initial states with $a=b=100$ and $x+y=10,000$.