Role of Atoms in Atomic Gravitational-Wave Detectors
Abstract
Recently, it has been proposed that space-based atomic sensors may be used to detect gravitational waves. These proposals describe the sensors either as clocks or as atom interferometers. Here, we seek to explore the fundamental similarities and differences between the two types of proposals. We present a framework in which the fundamental mechanism for sensitivity is identical for clock and atom interferometer proposals, with the key difference being whether or not the atoms are tightly confined by an external potential. With this interpretation in mind, we propose two major enhancements to detectors using confined atoms, which allow for an enhanced sensitivity analogous to large-momentum-transfer (LMT) used in atom interferometry (though with no transfer of momentum to the atoms), and a way to extend the useful coherence time of the sensor beyond the atom’s excited state lifetime.
I Introduction
The recent observation of gravitational waves (GWs) Abbott et al. (2016a, b) has established gravitational wave detection as an exciting new observational tool for cosmological phenomena. Terrestrial optical interferometers are sensitive to gravitational radiation at frequencies above roughly 10 Hz Harry et al. . In order to extend these techniques to lower frequencies where there are expected to be an abundance of signals, space-based optical interferometers such as the Laser Interferometer Space Antenna (LISA) have been proposed, and are currently under technological development Seoane et al. (2013); Armano et al. (2017).
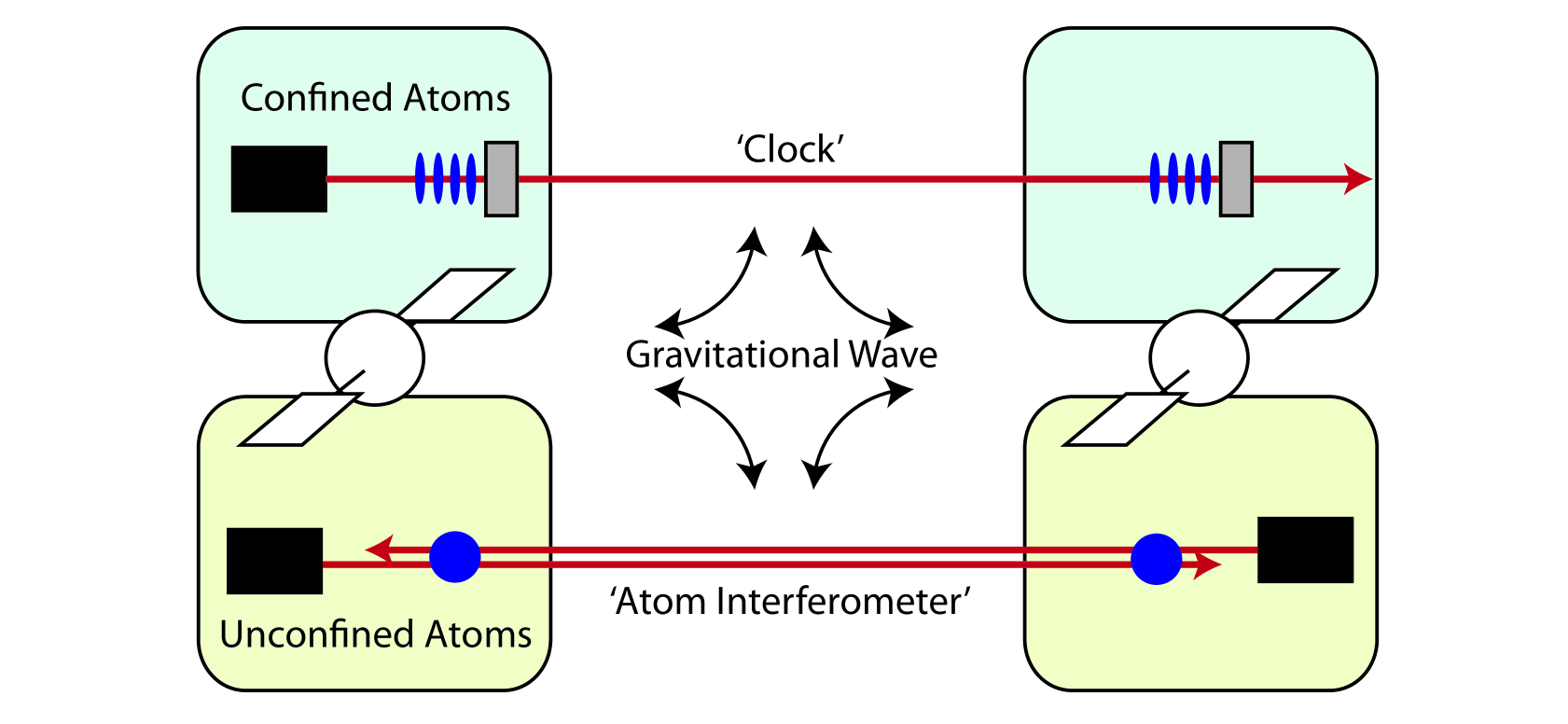
More recently, space-based gravitational wave detectors based on optical transitions in cold atoms have been proposed as an alternative architecture Loeb and Maoz ; Dimopoulos et al. (2009a); Yu and Tinto (2011); Kolkowitz et al. (2016); Vutha (2015); Hollberg et al. (2017); Graham et al. (2013); Hogan and Kasevich (2016); Graham et al. (2016). These proposals rely on a combination of optical and atomic coherence to provide sensitivity to gravitational waves. While optical interferometers require three satellites to cancel laser phase noise, these proposals require only two. We will focus here on two categories of the atom-based proposals: those described as “atom interferometers” (AI) typified by Graham et al. (2013), and those described as “optical lattice clocks” Kolkowitz et al. (2016). These two types of proposal are illustrated in Fig. 1.
AI-type proposals based on two-photon Raman transitions have also been proposed as a means of detecting gravitational waves, both in space-based and ground-based applications Dimopoulos et al. (2009b); Canuel et al. (2014); Chaibi et al. (2016). However, these proposals are not inherently insensitive to laser phase noise, and thus require noise cancellation techniques similar to a purely optical interferometer, such as the use of three interferometers. AI detectors based on two-photon Raman transitions may prove to be powerful tools for detecting gravitational waves, but here will focus exclusively on proposals that leverage long-lived optical atomic coherence on a single detection baseline with intrinsic insensitivity to laser phase noise.
In both clock and AI type proposals, two ensembles of atoms with a long-lived optically excited state are prepared in two satellites separated by a large distance. Laser pulses transmitted between the two satellites interact with the atoms in order to imprint the effects of a passing gravitational wave onto atomic observables. In both cases, the atoms are in a freely falling reference frame. In AI proposals, this is accomplished by simply preparing the atoms in a high vacuum environment. In clocks, the atoms are tightly trapped in an optical lattice formed by reflecting a laser off of a freely falling mirror that serves as an inertial reference, as in the proposed LISA interferometer Armano et al. (2017). In AI proposals, the interaction between the atoms and the laser leads to recoil momentum kicks imparted to the atoms, while in clock proposals the photon momentum is absorbed by the much more massive inertial reference.
In the clock community, gravitational wave detection has been described as a frequency measurement of Doppler shifts that result from the stretching of space between the satellites Kolkowitz et al. (2016); Vutha (2015). In the AI community, the stretching of space has been described as causing a phase shift between the laser phase and the atomic coherence Graham et al. (2016). A key element of AI proposals is enhanced sensitivity to gravity waves through the use of Large Momentum Transfer (LMT) pulses in which the atoms acquire many photon recoil momentum kicks. In contrast, the tight confinement of the atoms relative to the inertial reference mass in an optical lattice clock causes the photon recoil to be suppressed. This difference in particular, as well as the language used to describe the devices, would seem to indicate that the two sensors are somehow fundamentally different.
In sections II and III we provide a comparison of these two sensors to show that the fundamental mechanism for sensitivity is in fact the same for the clock and AI type detectors. In both types of sensors, laser pulses that couple a ground and long-lived optically excited state imprint their local phase onto an internal quantum superposition state of each atom. The atoms primarily act as a highly coherent phase memory that keeps track of these phase imprints and allows them to be read out through atomic observables.
By viewing clock-like detectors as phase memories, rather than simply as clocks whose sole capability is to measure frequency, we show in section IV that they support the implementation of LMT-like protocols with enhanced sensitivity even when negligible momentum is transferred to the atom. We further show in section V that the relevant phase information can actually be stored in stable ground states that evolve phases at acoustic rather than optical frequencies. This enables useful coherent evolution times beyond the lifetime of the optically excited state.
II Optical Path Length Changes due to Gravitational Waves
For both types of proposals, the important effect of a gravitational wave is its modification of the optical path length between the two satellites. We will describe the effects of a gravitational wave at angular frequency by replacing the gravitational wave with a phase modulator that fills the space between the two satellites (e.g. an electro-optic modulator or EOM) sinusoidally driven at frequency . The drive applied to the modulator leads to a phase shift on laser light that is launched from one satellite and detected at the other satellite. The light is launched from the first satellite at time , but arrives at the second satellite where it is detected at time , where is the nominal delay or transit time between satellites.
The total phase shift for a pulse launched at time is calculated by integrating along the optical path. We can define a net effective path length for the pulse where the small change in optical path length is
| (1) |
We have made the approximation that the gravitational wave’s strain is very small In this expression, is the speed of light in the undriven modulator, is the wavenumber of the laser light, and is the laser wavelength.
III Detecting Changes in Optical Path Length
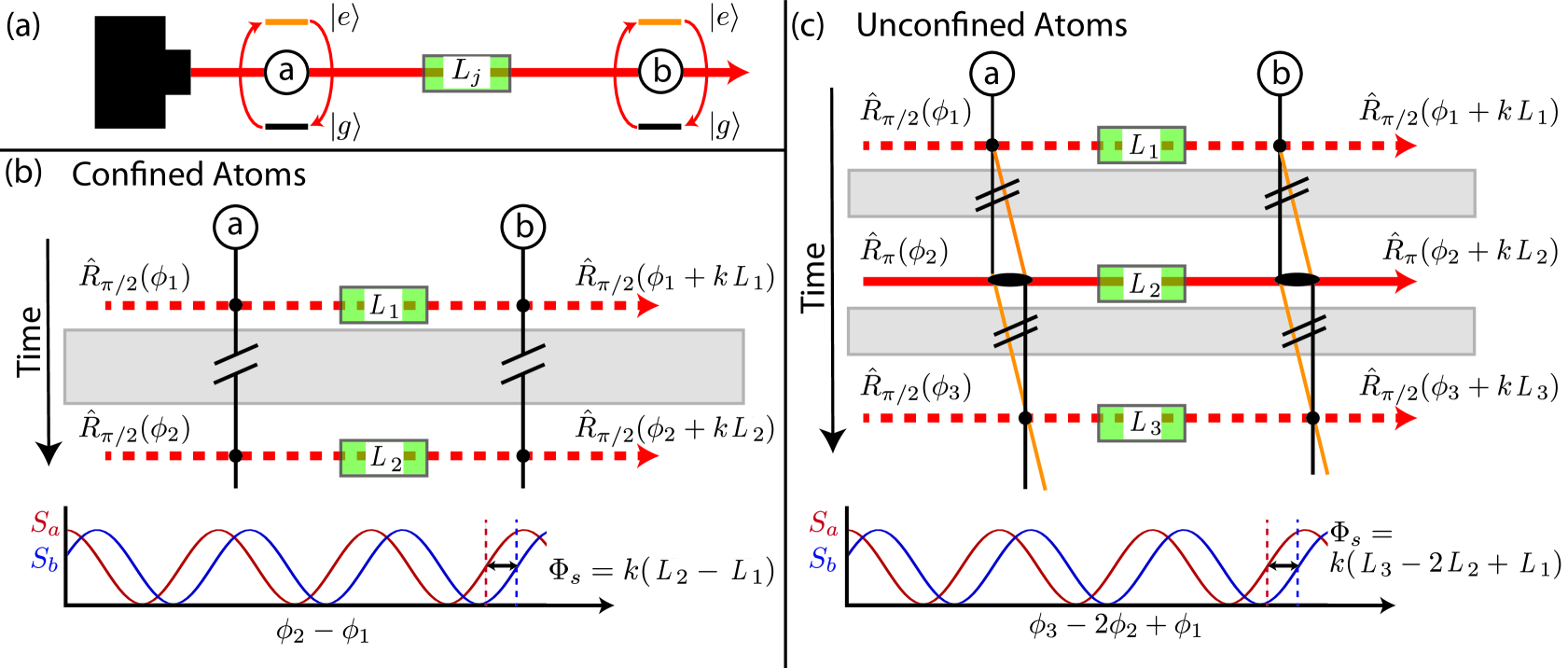
The goal of this section is to understand how AI and clock-like sensors can be used to precisely estimate changes in the optical path length . In our model, shown in Fig. 2, we consider two atoms labeled and that are separated by distance . The atoms may either be cooled in free space (atom interferometers) or tightly confined (clocks). The atoms have a long-lived optical transition, such as those in alkaline-earth and similar atoms (for example, Sr and Yb atoms). A laser located near atom launches pulses of light that interact with both atoms with equal intensity.
The laser pulses interact with the atoms by applying so-called and pulses between ground and excited states. We will assume that the coupling or Rabi frequency is much larger than the atomic decay rate from and any relevant Doppler shifts due to atomic motion. We will also assume for simplicity that the laser frequency is exactly equal to the atomic transition frequency. These assumptions rule out some of the capabilities of atom interferometers (such as addressing atoms that have experienced different recoils independently), but retains the basic mechanism for sensitivity. The effect of the laser pulses on the atoms written in a rotating frame at the atomic transition frequency can then be expressed using the operators:
| (2) |
| (3) |
These operators act on the basis states :
| (4) |
| (5) |
that are a product of an internal state label or , and an external state wavefunction . Here represents the distance from a fixed plane where the laser’s phase is defined as . The effect of these interactions is both to transfer amplitude between the internal states of the atoms and also to imprint the laser’s local phase upon the transferred portion of the atom’s wave function. The fact that may differ from indicates the possibility of entanglement between the internal and external degrees of freedom of the atom.
For simplicity, we account for laser frequency noise by allowing the laser phases to vary between pulses, but taking the actual laser frequency to be fixed at the atomic transition frequency such that is constant Rel .
First, we consider the effect of these rotations for a clock-like sensor in which the atoms are confined to much less than the laser wavelength (known as the Lamb Dicke regime.) In this limit, we can think of the term as imprinting a spatially constant phase onto the atom, whose value is determined by the location of the atom along the laser’s path. For example, a pulse applied to an atom tightly confined in a trap centered at position and in the ground state transfers the atom to the state . The external state wave-function is to very good approximation unmodified by the pulse, but its internal wavefunction has acquired a net phase .
In contrast, in AI sensors the atoms are not confined and a change in the internal state is accompanied by a change in the external state. In particular, one cannot neglect the variation of the optical phase factor over the spatial extent of the atomic wavefunction. For concreteness, a pulse applied to an unconfined atom centered at and in the ground state transfers the atom to the state . As written, the internal portion of the wavefunction appears identical to that of the confined case, but now the external wavefunction has a spatially varying phase corresponding to one photon’s worth of momentum recoil.
A change in the optical path length between the atom and the laser producing the -pulse manifests in the confined case as and in the unconfined case as . The sensitivity to changes in path lengths from gravitational waves is due to the imprinting of an additional phase , which is the same whether the atoms are confined or not. In the case of AI sensors one must add additional pulses to become insensitive to the terms associated with the photon recoil.
III.1 Clock-like Detectors
A clock-like gravitational wave detector with confined atoms could be used to detect the gravitational wave phase shift using a basic Ramsey sequence Kolkowitz et al. (2016), pictured in Fig. 2b. A change in the optical path length leads to a modification of the laser phase experienced by atom of . The phase experienced by atom is unmodified by the change in optical path length. In this sequence, the role of atom is then simply to record any variation of the phase of the laser itself due to technical sources of noise so that this laser phase noise can be subtracted out from the final measurement.
Stepping through the Ramsey measurement, atoms in both locations are initially prepared in . At time , the laser drives the first pulse with phase . we keep track of this phase only to demonstrate insensitivity to its value. The rotation applied to atom is . When the same pulse arrives at atom it creates a rotation . At a later time , a second pulse is applied to atom with a laser phase : . The same pulse of light travels to atom to drive a pulse .
The final signal that is detected is the difference in the probability for finding the atom in its excited and ground states. For atom this observable can be parameterized as and for atom as . For the above Ramsey sequence, the signal phases are given and , The gravitational wave signal is given by extracting the difference of the phase of these two signals Foster et al. (2002)
| (6) |
The key result is that the technical laser phase noise is canceled by having been recorded on both atoms and only the gravitational wave’s signal remains.
III.2 Atom Interferometer Detectors
In an atom interferometer, the atoms are unconfined and a slightly more complicated sequence is needed. The initial pulse entangles internal and external degrees of freedom of the atom by imparting a momentum kick to the portion of the atomic wavefunction transferred to . If this momentum kick is not reversed, the portions of the atomic wavefunction will not be spatially overlapped to interfere at the time of the second pulse. The simplest solution is to add a pulse in the middle of the sequence (Fig. 2c). More complex sequences, with enhanced performance in different regimes are presented in Graham et al. (2013, 2016), though the core mechanism for sensitivity is the same as this simple version.
Stepping through the simplest AI sequence, the first pulse, pulse and second pulse are launched from the laser at times , , and , respectively. When the three pulses arrive at atom they will have experienced optical path length differences , , and .
The signal that is extracted is the same as above, and depends only on the optical path lengths as
| (7) |
where the random fluctuations in laser phase , , and are again cancelled because they are common to both atoms. A similar analysis for the atom interferometer is presented in Yu and Tinto (2011).
IV Enhanced sensitivity analogous to large-momentum-transfer
We now propose a mechanism by which the signal recorded by the clock-like sensor can be enhanced. In atom interferometry in general, and AI based GW detectors in particular Graham et al. (2013), large momentum transfer (LMT) is a crucial tool used to enhance the size of measured signals. Our enhancement mechanism is very similar to LMT, but is applied to confined atoms, so no momentum is actually transferred to the atoms. Instead, by allowing for multiple interactions between the lasers and atoms, a phase is repeatedly written in to the atomic coherence in a constructive manner to enhance the signal size .
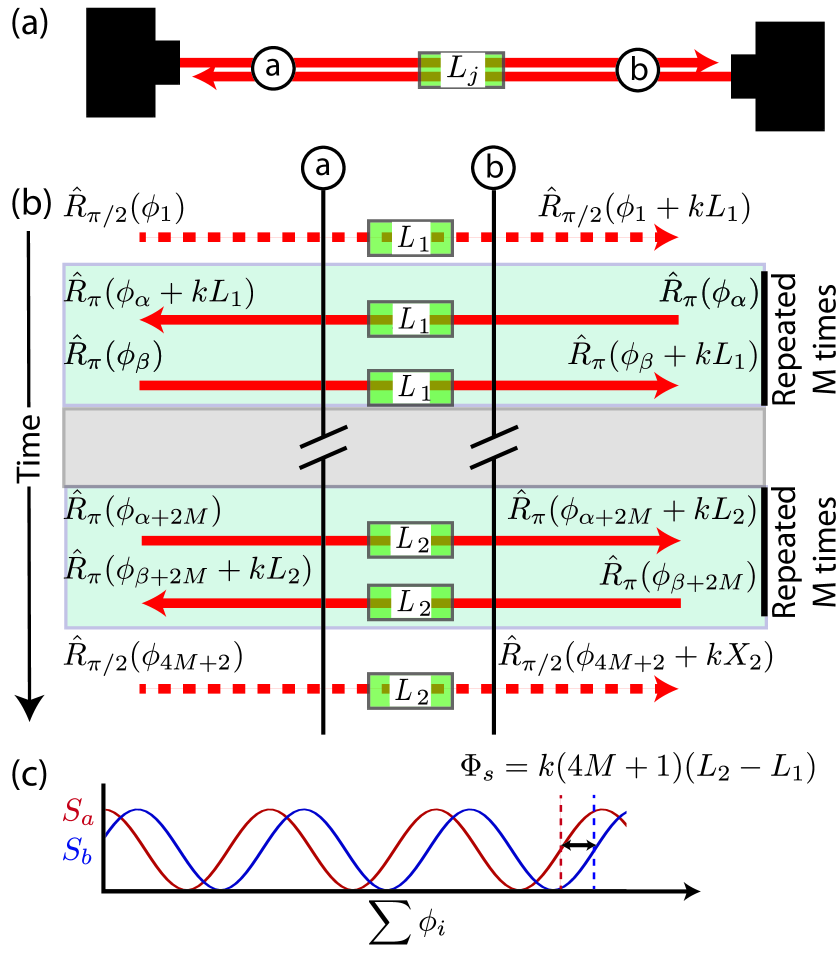
The key to this enhancement sequence is to apply the laser pulses from alternating sides (as is proposed for LMT protocols for single-photon transitions with unconfined atoms Graham et al. (2013); Hogan and Kasevich (2016); Graham et al. (2016)) using one laser near atom and one laser near atom , as illustrated in Fig. 3. Because the sign of the laser phase shift imprinted on the atoms is opposite in sign when the atoms are driven from to versus to , if the same laser were used to try to imprint its phase multiple times, it would simply unwrite the phase that it had just written in. By interleaving pulses from a second laser, which does not encode the same gravitational wave phase shift as the first, we can ensure that the phase shift corresponding to the GW is always written in with the same sign. The phases of the laser pulses are always referenced to a plane near the laser from which they originate so that there is negligible GW contribution to this phase.
For simplicity, we treat the case where a set of pulses is applied in quick succession at the beginning of the measurement sequence, with launch times roughly equal to and with optical path length changes all equal to . During a subsequent free evolution period , much longer than the time over which the rotations were applied, the optical path length may change. At time , a second set of rotations is quickly applied with launch times all roughly equal to such that all pulses experience an optical path length change equal to (a discussion of the effects of time delays is included in the appendix).
Consider the first group of pulses. From the perspective of one of the two atoms, the laser pulse that arrives from the distant laser encodes in its phase the change in path length. This phase is then imprinted on the atomic superposition with a different sign between the portion that was transferred from to versus to such that the difference phase is . The next laser pulse that is launched from the locally situated laser resets the two portions of the atomic superposition to their original internal states. It imprints a phase shift of its own, but this phase does not encode information about the change in optical path length , and the laser’s phase noise cancels in the final differential signal phase . Because the two portions of the atomic superposition have been reset to their original internal states, a subsequent rotation from the distant laser will imprint a phase encoding the same path length difference that adds constructively with the previously imprinted phase so that the total imprinted phase on the atom is now .
If we apply pairs of rotations after the first pulse and pairs of rotations before the last pulse (i.e. total launched pulses), with each pair containing a rotation originating from both the left and right sides, the differential phase shift between the two output channels is enhanced by a factor of relative to the simple Ramsey sequence presented above so that now
| (8) |
In the regime we consider here, even a single pair of LMT pulses (i.e. total -pulses), improves the estimate of by a factor of 25 in variance. As a result, the same precision can be achieved with a reduction in required resources such as atom number or averaging time by a factor of 25. Alternatively, one could achieve the same sensitivity to gravitational waves with a 5 times shorter satellite separation or evolution time for reduced technical complexity or enhanced bandwidth for detecting gravitational waves, respectively.
This enhanced protocol is insensitive to laser phase noise for the same reason that the simple protocols presented in section III are: each laser pulse interacts with both interferometers, so any phase noise on the laser cancels in the differential signal.
Previous proposals for detectors using confined Kolkowitz et al. (2016) and unconfined Graham et al. (2016) atoms include so-called dynamical decoupling (DD) sequences. A DD sequence would amount to applying a pulse from the same laser every time at which the magnitude of the optical path length change is maximal. Because the sign of alternates between pulses, the resulting imprinted phase shifts add constructively. This is conceptually similar to our LMT-like enhancement mechanism, except that we can switch the sign of the phase shift by alternating which laser applies the pulse instead of waiting for the sign of the GW to switch.
Dynamical decoupling is useful when the evolution time greatly exceeds the GW period . In this regime, the enhancement in signal scales as . This reflects the fact that the phase shifts from cycles of the gravitational wave may be added constructively. There is no constraint on delay time .
LMT-type sequences are useful when the period of the GW and total evolution time are long compared to the pulse transit time . This is necessary in order to send multiple pulses back and forth between the two satellites before the path length changes caused by the gravitational wave switches sign. The full signal response versus gravitational wave frequency is considered in the appendix. The main result is that one can build a long baseline experiment and set using a straightforward Ramsey sequence, or one can use LMT-type sequences to dramatically shorten the baseline such that is the same but now . In either case, the sensitivities are comparable. LMT-like enhancement allows one to address technical constraints that might be relaxed by operating with shorter baselines, at the expense of potentially introducing technical errors associated with the additional laser pulses.
Finally, as analyzed in Graham et al. (2016), LMT can be combined with DD when both and . Doing so amounts to varying from which satellite the pulses are sent.
V Evolution times longer than the excited state lifetime
We now present a further enhancement that can be realized by treating the atoms as a phase memory, rather than a clock. In a typical clock, the atoms are considered to be a two-state system. Because external degrees of freedom ideally remain unchanged, clocks lack additional quantum labels to specify other states. Any pulse that interacts with one ‘arm’ of the clock interferometer () also interacts with the other (): the quantum mechanical amplitudes may be swapped between ground and excited states, but the portion of the wave-function in the ground state cannot be manipulated without also modifying the portion of the wave function in the excited state. In an AI, the external degrees of freedom of the atom provide additional labels that allow the two arms to be manipulated independently.
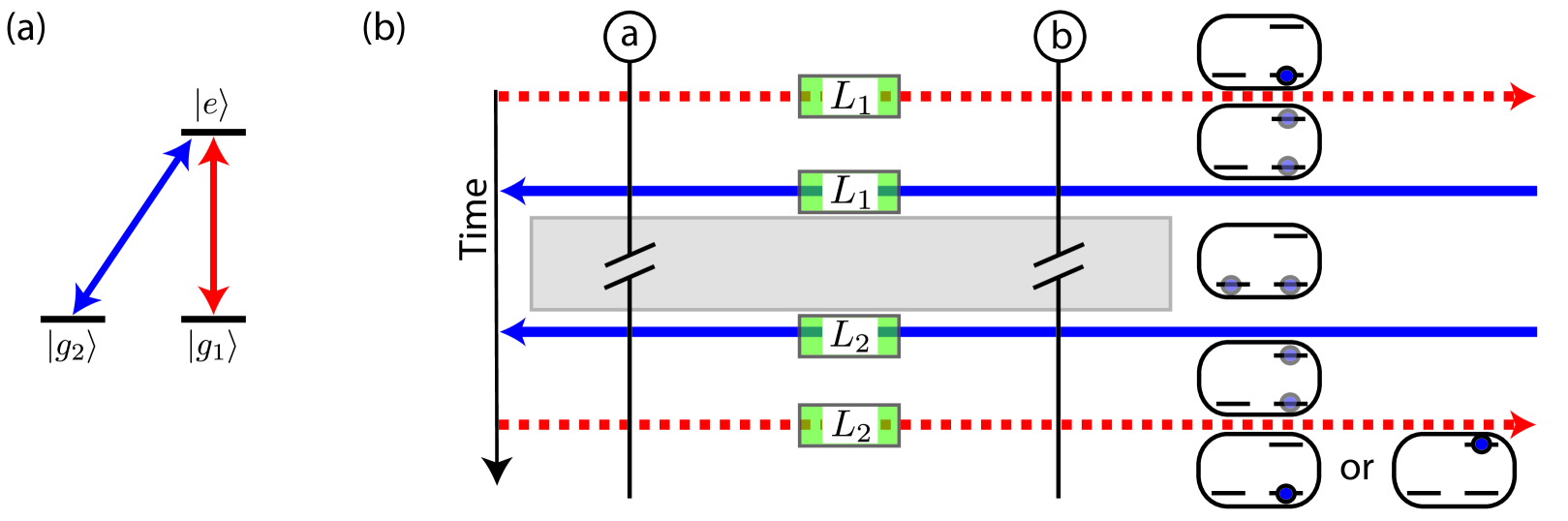
While in clock type proposals, a fraction of the atomic wave-function must always be in the excited state to achieve sensitivity, AI type detection sequences may include useful periods where both arms of the interferometer are in the ground state Graham et al. (2013), allowing for evolution times greater than the excited state lifetime. This technique is particularly useful for enhancing the signal in the regime where the period of the GW exceeds the lifetime of the excited state.
In a recoil-free GW detector, additional internal states of the atoms can provide additional quantum labels that allow for the independent manipulation of only one arm of the interferometer. Here, we consider an atomic species like 171Yb with nuclear spin . There are two ground states with nuclear spin projections that we we will label as and . For our purposes, we care about a single excited state , as shown in Fig. 4a. A small magnetic field is applied to define a quantization axis. Transitions may be driven between either and or and by applying laser light with different polarizations or frequencies.
An experimental sequence for such a protocol is shown in Fig. 4b. A superposition is prepared by driving a pulse originating from the left between and . A pulse originating from the right then transfers the population of to . The atoms remain in this configuration while the path length is allowed to change during an evolution time , which we take to be much larger than the delay time . The pulse sequence is then reversed and the change in path length is read out via a population measurement. The resulting signal is , again with no contribution from laser phase noise. Memory storage in ground states could be combined with LMT-type enhancement by inserting pulses on the to transition in between the pulses on the to transition and the initial and final pulses to realize further enhancement.
Because the atoms are in superpositions of ground states, there is no spontaneous emission during . Instead, the relative phase that would normally exist between and is now stored between and during the evolution period . In addition to extending the evolution time beyond the spontaneous-decay limited coherence time of the atoms, this technique of shelving the atoms in ground states provides insensitivity to collisional effects that may limit the atomic density or coherence time achievable in practice. Inelastic collisions between excited state atoms, which contribute to atom loss in dense systems, would be eliminated by storing the atoms in the ground states Lisdat et al. (2009); Bishof et al. (2011). Because elastic collisional properties of alkaline-earth-like atoms are independent of nuclear spin state Zhang et al. (2014); Scazza et al. (2014), mean-field shifts due to elastic collisions are common to the two ground states and will not lead to noise or dephasing. Other bias errors in clocks such as black-body, electrostatic, and lattice polarizability and hyperpolarizability shifts would also be suppressed. As in the AI case, this technique is applicable when the evolution time would otherwise be limited to much less than the gravitational wave period .
The key result is that it is not necessary for the phase memory to exist in a frame accumulating phase at an optical frequency. It is only necessary that the interactions with the laser pulses happen between optical transitions, but these interactions can in principle represent a small fraction of the total evolution time.
This protocol may appear similar to those that use two-photon Raman transitions in that the atoms occupy two ground states during a long evolution time. However, Raman transitions require a laser pulse from each satellite to interact with an atomic ensemble at the same time in order to perform a rotation without populating the short-lived excited state. As with single-photon transitions, each laser pulse must also interact with both interferometers in order to obtain a signal that is insensitive to laser phase noise. These two requirements lead to a conflict for detectors that use Raman transitions: to our knowledge, there is no protocol based on a two-satellite configuration in which each rotation is performed by simultaneously incident pulses from both satellites, and in which each pulse leads to the desired rotation in both interferometers. Because the use of single-photon transitions as discussed here allows population to be stored in the excited state for a time of order or longer, the laser pulses from the two satellites need not be simultaneously incident on the atoms, enabling phase-noise insensitive protocols that do not appear to be possible with Raman transitions.
VI Conclusion
Gravitational waves create phase shifts on optical pulses, which we would like to detect as sensitively as possible. At the most basic level, one would like to store an optical pulse of light sent at time with phase shift until a second pulse of light arrives with a different phase shift at time , then compare the phases of the two pulses. Note that this is a related mechanism to that employed by purely optical GW detectors, which compare the phase shifts experienced by light travelling on two different paths that experience opposite GW-induced phase shifts, rather than light that that travelled along the same path at two different times. By providing a highly coherent phase memory with which the two pulses may interact, the atoms allow one to make time-separated phase comparisons of the two pulses in a manner that is insensitive to laser phase noise. This capability eliminates the need in atomic detectors for a third satellite that is required in purely optical interferometers.
Further, multiple pulses can be made to constructively imprint their phases onto the atoms by properly alternating their launch direction (LMT) or by synchronizing their launch times with the frequency of the gravitational wave one wishes to detect (DD). From a fundamental perspective, the ability to achieve LMT-type signal enhancement does not appear to require the transfer of momentum to the atoms or that the two lasers originate from different directions (although the latter is required for cancellation of technical sources of noise). In certain regimes, LMT allows the signal size to be increased such that the uncertainty in the estimate of the optical phase of interest can be greatly reduced to well below the atomic standard quantum limit rad on atomic phase resolution.
For gravitational wave detection, we do not need to measure the absolute frequency of a laser relative to an atomic transition frequency, as one would do in a clock. As we have shown, this allows for the construction of a ground state shelving protocol with reduced sensitivities to perturbations and evolution times greater than the optical transition lifetime.
Ultimately, the decision to use confined or unconfined atoms will depend on a myriad of technical considerations that we have no business weighing in on. From a fundamental perspective, both methods have the same mechanism for sensitivity: atom interferometers and clocks both sense changes in phase that result from changes in optical path length between the two satellites. This interpretation should help distinguish to what degree differing expected sensitivities for future proposals are due to the choice of sensor architecture versus the specific parameters considered.
VII ACKNOWLEDGMENTS
We thank Shimon Kolkowitz, Jason Hogan and Peter Graham for important discussions and input. All authors acknowledge financial support from DARPA QuASAR, ARO, NSF PFC, and NIST. J.R.K.C. acknowledges financial support from NSF GRFP. This work is supported by the National Science Foundation under Grant Number 1125844.
VIII Appendix: Accounting for Time Delays
In the main text, we considered an LMT pulse sequence in which the time delay is much shorter than both the evolution time and gravitational wave period . Rather than launching a series of LMT pulses at the beginning and at the end, one could in principle launch a continuous series of alternating -pulses during the entire period of time between the pulses. For continuous LMT, we find that the signal size averaged over all phases of the gravitational wave is (to good approximation) given by:
| (9) |
where is the laser angular frequency. When , the sensitivity falls of rapidly as . However, in the limit the scaling changes to
| (10) |
For comparison, if the spacing of the satellites is increased until , then one cannot use LMT and the Ramsey sequence yields an averaged signal:
| (11) |
The oscillations in the signal versus differ by a factor of 2 and the envelope of the signal size is larger by a factor of 2 for LMT. Most importantly, approximately the same signal can be obtained using continuous LMT with of order pulses and an approximately times shorter satellite satellite spacing. It is likely that decreasing the spacing of the satellites will be advantageous for technical reasons, for instance, it allows for reduced requirements on laser power and pointing stability.
References
- Abbott et al. (2016a) B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Observation of gravitational waves from a binary black hole merger,” Phys. Rev. Lett. 116, 061102 (2016a).
- Abbott et al. (2016b) B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Gw151226: Observation of gravitational waves from a 22-solar-mass binary black hole coalescence,” Phys. Rev. Lett. 116, 241103 (2016b).
- (3) Gregory M Harry et al. (LIGO Scientific Collaboration), “Advanced ligo: the next generation of gravitational wave detectors,” .
- Seoane et al. (2013) Pau Amaro Seoane et al. (eLISA), “The Gravitational Universe,” (2013), arXiv:1305.5720 [astro-ph.CO] .
- Armano et al. (2017) M. Armano et al. (LISA Pathfinder Collaboration), “Charge-induced force noise on free-falling test masses: Results from lisa pathfinder,” Phys. Rev. Lett. 118, 171101 (2017).
- (6) A. Loeb and D. Maoz, “Using Atomic Clocks to Detect Gravitational Waves,” ArXiv e-prints: 1501.00996 (2015) arXiv:1501.00996 .
- Dimopoulos et al. (2009a) Savas Dimopoulos, Peter W. Graham, Jason M. Hogan, Mark A. Kasevich, and Surjeet Rajendran, “Gravitational wave detection with atom interferometry,” Physics Letters B 678, 37 – 40 (2009a).
- Yu and Tinto (2011) Nan Yu and Massimo Tinto, “Gravitational wave detection with single-laser atom interferometers,” General Relativity and Gravitation 43, 1943–1952 (2011).
- Kolkowitz et al. (2016) Shimon Kolkowitz, Igor Pikovski, Nicholas Langellier, Mikhail D Lukin, Ronald L Walsworth, and Jun Ye, “Gravitational wave detection with optical lattice atomic clocks,” Physical Review D 94, 124043 (2016).
- Vutha (2015) Amar Vutha, “Optical frequency standards for gravitational wave detection using satellite doppler velocimetry,” New Journal of Physics 17, 063030 (2015).
- Hollberg et al. (2017) L Hollberg, EH Cornell, and A Abdelrahmann, “Optical atomic phase reference and timing,” Phil. Trans. R. Soc. A 375, 20160241 (2017).
- Graham et al. (2013) Peter W Graham, Jason M Hogan, Mark A Kasevich, and Surjeet Rajendran, “New method for gravitational wave detection with atomic sensors,” Physical review letters 110, 171102 (2013).
- Hogan and Kasevich (2016) Jason M Hogan and Mark A Kasevich, “Atom-interferometric gravitational-wave detection using heterodyne laser links,” Physical Review A 94, 033632 (2016).
- Graham et al. (2016) Peter W Graham, Jason M Hogan, Mark A Kasevich, and Surjeet Rajendran, “Resonant mode for gravitational wave detectors based on atom interferometry,” Physical Review D 94, 104022 (2016).
- Dimopoulos et al. (2009b) Savas Dimopoulos, Peter W Graham, Jason M Hogan, Mark A Kasevich, and Surjeet Rajendran, “Gravitational wave detection with atom interferometry,” Physics Letters B 678, 37–40 (2009b).
- Canuel et al. (2014) B Canuel, L Amand, A Bertoldi, W Chaibi, R Geiger, J Gillot, A Landragin, M Merzougui, I Riou, SP Schmid, et al., “The matter-wave laser interferometer gravitation antenna (miga): New perspectives for fundamental physics and geosciences,” in E3S Web of Conferences, Vol. 4 (EDP Sciences, 2014) p. 01004.
- Chaibi et al. (2016) W. Chaibi, R. Geiger, B. Canuel, A. Bertoldi, A. Landragin, and P. Bouyer, “Low frequency gravitational wave detection with ground-based atom interferometer arrays,” Phys. Rev. D 93, 021101 (2016).
- (18) “One can relax this assumption by accounting for an additional phase that results from the laser’s detuning from atomic resonance and cancels the effect of associated changes in the wave-vector . this leads to the laser frequency noise insensitivity demonstrated in previous proposals Kolkowitz et al. (2016); Graham et al. (2013), but doing this careful accounting does not alter the main results here,” .
- Foster et al. (2002) GT Foster, JB Fixler, JM McGuirk, and MA Kasevich, “Method of phase extraction between coupled atom interferometers using ellipse-specific fitting,” Optics letters 27, 951–953 (2002).
- Lisdat et al. (2009) Ch. Lisdat, J. S. R. Vellore Winfred, T. Middelmann, F. Riehle, and U. Sterr, “Collisional losses, decoherence, and frequency shifts in optical lattice clocks with bosons,” Phys. Rev. Lett. 103, 090801 (2009).
- Bishof et al. (2011) Michael Bishof, Michael J Martin, Matthew D Swallows, Craig Benko, Yige Lin, Goulven Quéméner, Ana Maria Rey, and Jun Ye, “Inelastic collisions and density-dependent excitation suppression in a 87 sr optical lattice clock,” Physical Review A 84, 052716 (2011).
- Zhang et al. (2014) X. Zhang, M. Bishof, S. L. Bromley, C. V. Kraus, M. S. Safronova, P. Zoller, A. M. Rey, and J. Ye, “Spectroscopic observation of su(n)-symmetric interactions in sr orbital magnetism,” Science 345, 1467–1473 (2014).
- Scazza et al. (2014) Francesco Scazza, Christian Hofrichter, Moritz Höfer, PC De Groot, Immanuel Bloch, and Simon Fölling, “Observation of two-orbital spin-exchange interactions with ultracold su (n)-symmetric fermions,” Nature Physics 10, 779–784 (2014).