Rotating Drops with Helicoidal Symmetry
Abstract.
We consider helicoidal immersions in whose axis of symmetry is the -axis that are solutions of the equation where is the mean curvature of the surface, is the distance form the point in the surface to the -axis and is a real number. We refer to these surfaces as helicoidal rotating drops. We prove the existence of properly immersed solutions that contain the -axis. We also show the existence of several families of embedded examples. We describe the set of possible solutions and we show that most of these solutions are not properly immerse and are dense in the region bounded by two concentric cylinders. We show that all properly immersed solutions, besides being invariant under a one parameter helicoidal group, they are invariant under a cyclic group of rotations of the variables and .
The second variation of energy for the volume constrained problem with Dirichlet boundary conditions is also studied.
2000 Mathematics Subject Classification:
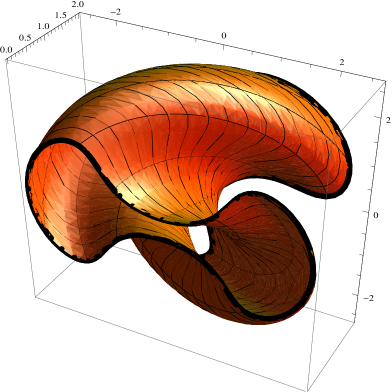
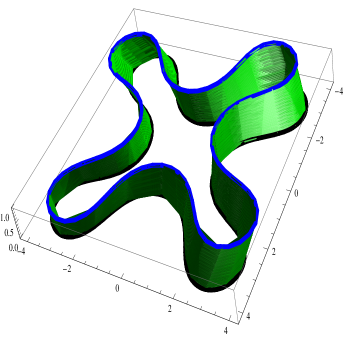
53C42, 53C10![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/5b6ffedf-cbf6-4992-b848-737332f238af/x1.png)
1. Introduction
In this paper we study the equilibrium shape of a rotating liquid drop or liquid film, which is invariant under a helicoidal motion of the three dimensional Euclidean space. The subject of rotating drops has been studied by many authors, including Chandrasekhar [2], Brown and Scriven [1], Solonikov [8] and many others. Our main objective here is to use a new construction, recently developed by the second author [4], to construct an abundant supply of examples. This construction is closely related to the Delaunay’s classical construction of the axially symmetric constant mean curvature surfaces whose generating curves are produced by rolling a conic section. A special case of the type of surface which we study here, occurs when the rotating drop is a cylinder over a plane curve. We treat that case in detail in [7].
If a rigid object is moved from one position in space to another, this repositioning can be realized via a helicoidal motion of . If then, this motion is successively repeated, one arrives at a configuration which is invariant under a helicoidal motion. The simple idea that helicoidal motions give all repeated motions of a rigid object, known in the physical sciences as Pauling’s Theorem, is behind many of the occurrences of helicoidal symmetry in nature, since it allows for extensive growth with a minimal amount of information.
We will consider the equilibrium shape of a liquid drop rotating with a constant angular velocity about a vertical axis. The surface of the drop, which we denote by , is represented as a smooth surface. The bulk of the drop is assumed to be occupied by an imcomressible liquid of a constant mass density while the drop is surrounded by a fluid of constant mass density . Since the drop is liquid, its free surface energy is proportional to its surface area and we take the constant of proportionality to be one. The rotation contributes a second energy term of the form , where is difference of moments of inertia about the vertical axis,
This term represents twice the rotational kinetic energy.
The total energy is thus of the form
| (1.1) |
where denotes the volume of the drop and is a Lagrange multiplier. Let , then by introducing a constant , we can write the functional in the form
where is the three dimensional region occupied by the bulk of the drop, and .
Since we want to consider both embedded and immersed surfaces, we will precisely define the last two terms in the energy in the following way. First define vector fields on by
If denotes the divergence operator on , then it is easily checked that and hold. We, then define
The definitions are valid so long as is immersed and oriented.
We will next derive the first variation of the functional given above. Let be a variation of , where is a smooth function, is the unit normal to the surface and is a tangent vector field along . The first variation formula for the area gives,
We will show in the appendix that
| (1.2) |
where is a vector field satisfying on , and it is well known that the first variation of volume is
| (1.3) |
By combining the last three formulas, we arrive at
| (1.4) | |||||
Regardless of the boundary conditions, a necessary condition for an equilibrium is that in the interior of , there holds
| (1.5) |
If we assume that the surface has free boundary contained in a supporting surface having outward unit normal , then the admissible variations must satisfy the condition on . In order that the boundary integral in (1.4) vanishes for all admissible variations, we must have that parallel to along the boundary which means that the surface meets the supporting surface in a right angle.
We now assume that an equilibrium surface , i.e. a surface satisfying (1.5) is invariant under a helicoidal motion:
| (1.6) |
and we will derive a conservation law which characterizes the equilibrium surfaces. We do not assume that the angular velocity which determines the pitch of the helicoidal surface is the same as the angular velocity appearing above,
Let denote the compact region in bounded on the sides by two integral curves and of the Killing field and bounded below and above by the horizontal planes and . Then, is a compact surface with oriented boundary where and are congruent arcs in the planes , , respectively. By the calculations in the appendix, we have, using (1.5)
| (1.7) |
If we take the variation with then, since generates a translation, the first variation will vanish. Consequently, we obtain
| (1.8) |
Note that the integration over the 1-chain yields zero since the two arcs are congruent and are traversed in opposite directions. On , , we have .
where is the support function of the surface. Setting , We can conclude from this that the integral
is independent of . Also, it is easily checked that the integrand is, in fact, constant on each helix and we obtain the result that
| (1.9) |
Proposition 1.1.
Let be a helicoidal surface. A necessary and sufficient condition that is a critical point for the functional is that (1.9) holds.
Proof.
The necessity was shown above, we now show that the condition is sufficient. We can assume that the helicoidal symmetry group of the surface fixes the vertical axis.
Any helicoidal surface arises as the orbit of a planar “ generating curve” under a helicoidal motion. We let be the arc length coordinate of and we let denote a coordinate for the helices which are the orbits of points in . Local calculations which can be found in [4], show that the mean curvature and the third component of the normal are functions of alone. Also, it is clear that the function only depends on .
It is easy to see that if vanishes on any arc of , then this arc is necessarily circular. It is clear that the orbit of a circular arc satisfying 1.9 is a critical surface for the functional . Now consider a connected arc on which (say) holds almost everywhere. If (1.5) does not hold on , we can assume, by replacing with a sub-arc if necessary, that holds almost everywhere on also. Let denote the compact domain consisting of the orbit of the arc , for . The boundary of consists of two helices , together with two arcs , both congruent to .
We take the first variation of with the variation field being the constant vector . Since is the generator of a one parameter family of isometries, this first variation vanishes. We express the first variation as in (1.4). Since (1.9) holds, the contributions to the boundary integral is zero since it is given by the right hand side of vanishes and the integrals over and cancel each other since these arcs are congruent and are traversed in opposite directions. We then obtain from the calculations given above, that
which is a contradiction since the integrand is positive almost everywhere on .
∎
This result can easily be modified for axially symmetric surfaces. In that case, the Killing field used is simply and the helices are replaced by circles and the equation (1.9) still holds.
2. TreamillSled coordinates analysis
We will be considering immersions of the form
with the curve parametrized by arc-length. We will refer to the curve as the profile curve of the surface since the surface given as the image of is the orbit of under the helicoidal motion (1.6). For defined by
We define the TreadmillSled coordinates and by
| (2.1) |
The Gauss map of the immersion can be computed as
and so by a direct calculation, we obtain . Finally, using that , we see from (1.9), that the immersion represents a rotating helicoidal drop if and only if there holds
| (2.2) |
After direct computation shows that the equation reduces to
| (2.3) |
From the definition of , and we get that and . Using Equation (2.3) we conclude that and must satisfy
| (2.4) | |||||
| (2.5) |
This system of ordinary differential equations for and provides a different proof of the fact that the must be constant. Since we can check that
Remark 2.1.
The level sets of are symmetric with respect to the -axis, therefore in order to understand the level set of , it is enough to understand those points in the level set with .
In order to study the level sets of the function we change the variables and for the variables and where
Doing this change, we get that the equation reduces to
In fact, this equation is exactly the one appearing in (1.9).
Therefore,
By Remark 2.1, it is enough to consider those points with . Since we get that
where
| (2.6) |
Remark 2.2.
Since is a polynomial in of degree 4 with negative leading coefficient when and is a polynomial of degree two when , we get that the values of for which is positive are bounded. Since , we conclude that the profile curve of any helicoidal rotating drop is bounded.
Definition 1.
Let and be two non negative values that satisfies and for all . We define by
Remark 2.3.
As pointed out before, all the level sets of the function are bounded. We have that the map parametrizes half of the level set .
Definition 2.
In the case the level set is a regular closed curve or union of regular closed curves, we define a fundamental piece of the profile curve as a simple connected part of the profile curve such that the parametrized curve given by equations (2.1) correspond to exactly one closed curve in the level set of
Remark 2.4.
From the definition of TreadmillSled given in [4], we obtain that the profile curve of the solutions of the helicoidal rotational drop equation are characterized by the property that their treadmillSled are the level sets of . In other words, using the notation of [4], we have that where is a parametrization of a connected component of the level set of and is the profile curve of the helicoidal rotating drop. We will see that, for a few exceptional examples, the profile curve is a bounded complete curve having a circle as a limit cycle. For the non exceptional examples we can define an initial and final point of the fundamental piece and we have that the whole profile curve is the union of rotated fundamental pieces. We also have that if and and is the variation of the angle between and where and are the initial and final points of a fundamental piece, then, the profile curve is properly immersed if is a rational number, otherwise the profile curve is dense in the set .
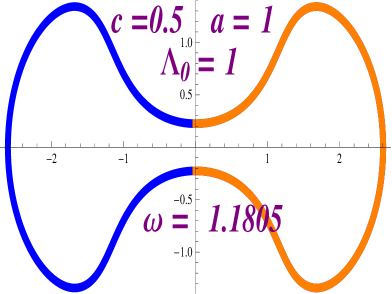


We compute the variation in terms of the parameter . We assume that is the profile curve of a helicoidal rotational drop. Recall that we are assuming that that is the arc-length parameter for the curve . If , then we have that for some function , holds. By the chain rule we have that
| (2.7) |
and we also have that if denotes the polar angle of the profile curve, this is, if satisfies the equation , then
| (2.8) |
Since the map parametrizes half of the TreadmillSled of the fundamental piece of the profile curve, we obtain the following expression for function defined in Remark 2.4
| (2.9) |
Remark 2.5.
If we have a helicoidal rotational drop and we multiply every point by a positive fixed number , this is, if we consider the surface , then this new surface satisfies the equation of the rotating drop for some other values of and . We also have that if we change the orientation of the profile curve of a surface that satisfies the equation of the rotating drop with values , and , then the reparametrized surface satisfies the equation with values , and . With these two observations in mind, we have that in order to consider all the helicoidal rotational drops, up to parametrizations, rigid motions and dilations, it is enough to consider two cases: Case I, and and Case II, and is any real number.
2.1. Case I: and
In this case the polynomial reduces to
Recall that we are interested in finding two positive consecutive roots of the polynomial . Notice that when is a negative large number then the polynomial has no roots and when is a positive large number then the polynomial has more than one root. In every case and the limit when of is negative infinity. The following lemma was proven in [7] and provides the number of possible roots of in terms of the values of .
Lemma 2.6.
For any , the polynomial has exactly two positive real roots. When , is the only real root of and when , has not real roots.
Now we will compute the limit of when goes to . We will use the following lemma from [5]
Lemma 2.7.
Let and be smooth functions such that and where . If , and are sequences such that converges to , and converges to with , and and for all , then
Notice that helicoidal rotating drops are defined when takes value from to . When the only root of the polynomial is . If we apply Lemma 2.7 with and to the integral given in (2.9), we obtained that
| (2.10) |
Remark 2.8.
Recall that whenever holds for some pair of integers and , then the entire profile curve is properly immersed and it is invariant under the group .
Remark 2.9.
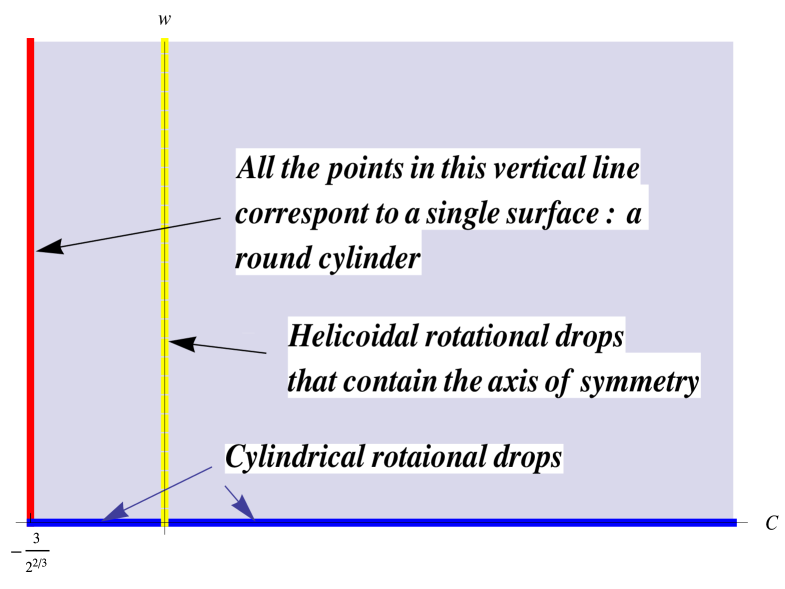
Up to dilations and rigid motions, the moduli space for all helicoidal rotating drops with is the region in the plane
Moreover, for any , the surface associated with the point is a round cylinder of radius , because it can be easily checked that when , then, for any , the level set reduces to the point
2.2. Case II:
First note that the case corresponds to helicoidal surface with constant mean curvature. These surfaces were studied using similar techniques in [4] and for this reason we will assume here that . In this case the polynomial reduces to
| (2.11) |
Recall that we are interested in finding two positive consecutive roots of the polynomial . The roots of the polynomial given in (2.11) were analyzed in [7]. In order to describe the roots of we need to define the following functions.
Definition 3.
Let , and define , and by
We also define the functions , and by
The following lemma was proven in [7] and provides the number of roots of depending on the values and .
Lemma 2.10.
Let , and be as in Definition 3 and for define
and
Recall that the domain of is the same domain of . That is, the domain of is and the domain of and is the interval . For any and any , the polynomial has non negative real roots whose multiplicities are given in the following table.
| range of | range of | number of distinct real roots of |
| 2 | ||
| , , | ||
| (****) | ||
| (***) | ||
| , | ||
| (*) | ||
| (**) | ||
(*) In this case the roots are with multiplicity and with multiplicity one.
(**) In this case the only real root is with multiplicity .
(***) In this case the first root has multiplicity 2.
(****) In this case the second root has multiplicity 2.
Now that we have discussed the roots of the polynomial we can describe the moduli space of all helicoidal rotating drops with .
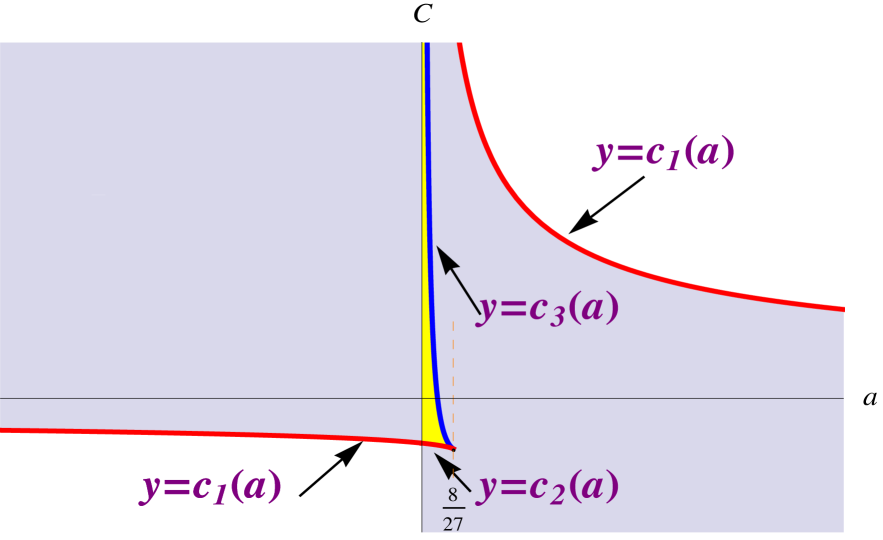
Theorem 2.11.
Let and let be the function defined in (2.9). Let
Under the convention that a point represents a helicoidal rotating drop if the TreadmillSled of its profile curve is contained in the level set , we have:
i.) Every point in the interior of represents a helicoidal rotating drop with its fundamental piece having finite length. The TreadmillSled of the profile curve of these surfaces are parametrized by defined for values of between the only two roots of the polynomial .
ii.) Every point in represents two helicoidal rotating drops, both having fundamental pieces of finite length. The TreadmillSleds of the profile curves of these surfaces are parametrized by defined for those values of that lie between the first and second root of the polynomial and the third and fourth root of the polynomial respectively.
iii.) Every point in the set represents a circular helicoidal rotating drop. This cylinder is the same for all values of .
iv.) Every point in the set represents two helicoidal rotating drops: a circular cylinder and a non circular cylinder with bounded length of its fundamental piece. The circular cylinder is the same for all values of .
v.) Every point in the set represents three helicoidal rotating drops. One is a circular cylinder, which is the same for all values of . The second one has a TreadmillSled parametrized by defined for those values of that lie between the first and second root of the polynomial . Recall that the second root has multiplicity . The third surface has a TreadmillSled parametrized by defined for those values of that lie between the second and third root of the polynomial . The second and third surfaces are not properly immersed and their profile curves have a circle as a limit cycle and they have infinite winding number with respect to a point interior to this circle. Solutions similar to these second or third types will be called helicoidal drops of exceptional type.
vi.) Points of the form represent two helicoidal rotating drops: a circular cylinder, which is the same for all values of , and one helicoidal drop of exceptional type.
vii.) Up to a rigid motion, every helicoidal drop falls into one of the cases above.
viii.) Every helicoidal drop that is not exceptional is either properly immersed (when is a rational number) or it is dense in the region bound by two round cylinders (when is an irrational number).
Proof.
We already know that the TreadmillSled of the profile curve of any helicoidal rotating drop satisfies the equation
We also know that, up to rigid motions, the TreadmillSled of a curve determines the curve, see [4]. Since any level set of can be parametrized using the map given in Definition 1, and every parametrization of a level set of is defined for values of where the polynomial is positive, it then follows from Lemma 2.10 that every helicoidal rotating drop can be represented as one of the cases i, ii, iii, iv, v and vi. It is worth recalling, see Remark 2.3, that the parametrization only covers half of the level set of the map . Each one of these level sets is symmetric with respect to the axis, and the parametrization covers the half on the right.
Notice that when the profile curve is a circle, the level set reduces to a point. When the profile curve is a circle we will take the parametrization to be defined just in a point, a root with multiplicity 2 of the polynomial .
When case (i) occurs, has only two simple roots and with . We can check that the derivative of at is positive while the derivative of at is negative, so the length of the fundamental piece, according to Equation (2.7), reduces to which converges. Therefore the length of the fundamental piece is finite.
For values of , and that fall into case (ii), the polynomial q has 4 roots and it is positive from to and from to . Also, the level set of has two connected components. Half of each connected components of can be parametrized using the map . One half of the connected component of uses the domain for and the half of the other connected component of uses the domain for . The proof that the length of the fundamental piece of each surface is finite follows as in the proof in case (i).
For values of that satisfies the case (iii), the polynomial has only one root with multiplicity two. We take . A direct calculation shows that if , then and if we consider the profile curve , then , and . Using the definition of and the fact that , we can check that the expression reduces to , which was our goal in order to show that the point represents a round cylinder. Similarly, a direct verification shows that if , then and if we consider the profile curve , then , and . Using the definition of and the fact that , we can check that the expression reduces to . Since is independent of we have that these cylinders are independent of the value of . This finish the proof of part (iii).
For values of that fall into case (iv), the polynomial has three roots , where has multiplicity two and and are simple. The polynomial is positive for values of between and . In this case the level set is the union of the point and a closed curve. If we consider the cylinder or radius oriented by the inward pointing normal, then, a direct computation shows that its mean curvature is . Therefore this circular cylinder is a helicoidal rotating drop for the given parameters. Note that this cylinder is independent of . The TreamillSled of the profile curve of the other rotating drop is the level closed curve component of ; half of this part can be parametrized by the map with domain those values of between and .
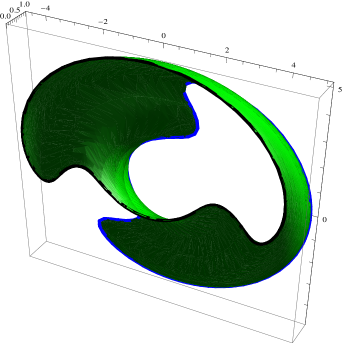
For values of in case (v), the polynomial has only three roots , where has multiplicity two and and are simple. The polynomial is positive for values of between and and for values of between and . In this case the level set is connected but it self-intersects at the point . Any part of a curve that crosses the -axis non-horizontally cannot be the TreadmillSled of a regular curve (see Proposition 2.11 in [6]). Therefore the correct way to view the level set in this case is not as a connected closed curve that self intersects but as the union of two curves and a point. Figure 2.4 shows one of these level sets.
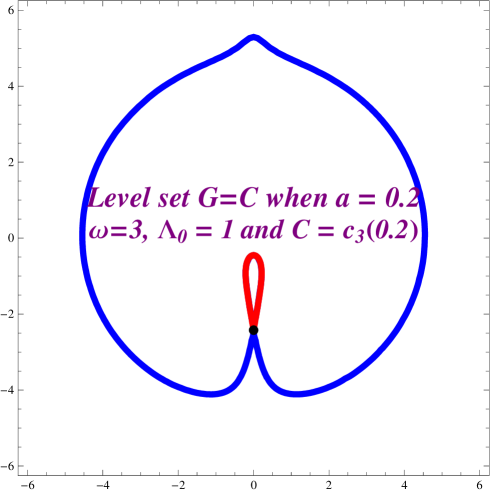
.
One can check that the circular cylinder with radius , oriented by the inward pointing normal satisfies the , therefore this circular cylinder is a helicoidal rotating drop for the given parameters. The TreadmillSled associated with the profile curve of this round cylinder reduces to the point . The set minus the point has two connected components. One of these connected components can be parametrized using the map with values of between and and the other using the map with values of between and . Each of these connected components is the TreamillSled of the fundamental curve for a rotating helicoidal drop whose length is unbounded. Specifically, their lengths are given respectively by the divergent integrals and . Moreover, using the definition of TreadmillSled, we notice that the function giving the distance to the origin of the profile curve, , agrees with the function distance to the origin of the level set given by . Therefore as aproaches , goes to and the function approaches . Since polar angle of the profile curve can be calculated by integrating the expression in (2.8), we conclude that also goes to as approaches . We conclude that the profile curve has a circle of radius as a limit cycle and it has infinite winding number with respect to a point interior to this circle.
For values of that satisfies the case (vi) the polynomial has only two roots where has multiplicity three and is simple. The polynomial is positive for values of between and . In this case the level set is connected but it has a singularity at the . We can check that the circular cylinder with radius oriented by the inward pointing normal satisfies the , therefore this circular cylinder is a helicoidal rotating drop. The TreadmillSled associated of the profile curve of this round cylinder reduces to the point . The set minus the point is connected and half of it can be parametrized using the map with values of between and . This part of the set is the TreamillSled of the fundamental curve of a rotating helicoidal drop whose length is not bounded.
Since we know that the profile curve of every rotating helicoidal drop satisfies the integral equation and cases (i)-(vi) cover all the possible level sets for the level sets of then every rotating helicoidal drop fall into one of the first 6 cases of this proposition. This proves (vii).
In order to prove (viii) we notice that when a helicoidal rotating drop is not exceptional, it has a fundamental piece with finite length whose TreadmillSled is a closed regular curve (a connected component of the set ). By the properties of the TreadmillSled operator (in particular the one that states that the TreadmillSled inverse is unique up to rotations about the origin), we have the the whole profile curve is a union of rotations of the fundamental piece. The angle of rotation is given by . We therefore have that the profile curve is invariant under the group of rotations
| (2.12) |
It is clear that if is a rational number then the group is finite and the helicoidal surface is properly immerse. Moreover, if is not a rational number, then the group is not finite and the helicoidal drop is dense in the region bounded by the two cylinders of radius and . A more detailed explanation of this last statement can be found in [4].
∎
2.3. Embedded and properly embedded examples
In this subsection we will find some embedded examples and we will show their profile curves. As pointed out before, when the helicoidal drop is not exceptional, its profile curve is a union rotations of fundamental pieces that ends up being invariant under the group define in (2.12). It is not difficult to see that a necessary condition for the helicoidal drop to be embedded is that for some integer . We will show that this condition is not sufficient. In order to catch the potentially embedded examples we need to understand the function . As a very elementary technique to solve the equation we will use the intermediate value theorem. We know that for any , there is a first (or last) value of , , for which the function is defined. We will compute the limit of when goes to using Lemma 2.7. The graphs shown in this paper were generated using the software Mathematica 8 .
2.4. Embedded examples with and
From Lemma 2.6 we know that the polynomial has two positive root if and only if . A direct application of Lemma 2.7 shows:
Proposition 2.12.
If , and for any , and denote the two roots of the polynomial , then
holds.
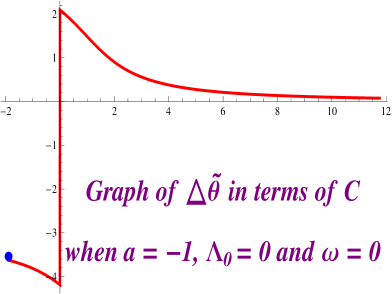
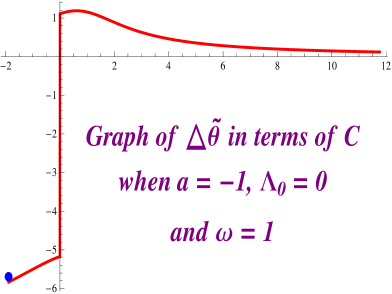

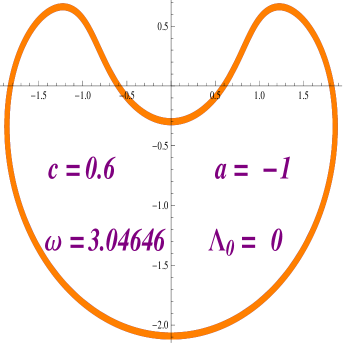
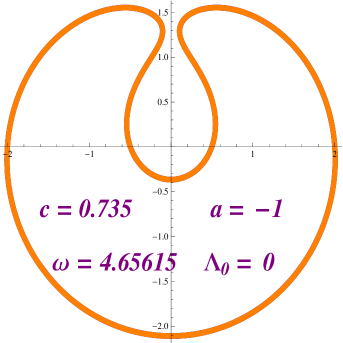



2.5. Embedded examples with and
We now show some embedded examples in this case. Again the Intermediate Value Theorem is used to numerically solve the equation . A direct application of Lemma 2.7 shows:
Proposition 2.13.
Let and be the expressions given in Definition 3 and let , and be the expression defined in Lemma 2.10. For let us defined the following two bounds.
a.) If then . Here and are the first two roots of the polynomial
b.) If then . Here and are the first two roots of the polynomial
c.) If then . Here and are the first two roots of the polynomial .
Proof.
Since , in every case, when approaches the limit value, the two roots approach (i=1 or 2), which is a root of with multiplicity . Therefore Lemma 2.7 applies and the proposition follows. Notice that the value in Lemma 2.7 is given by
∎
Remark 2.14.
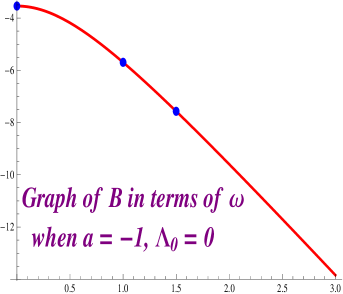
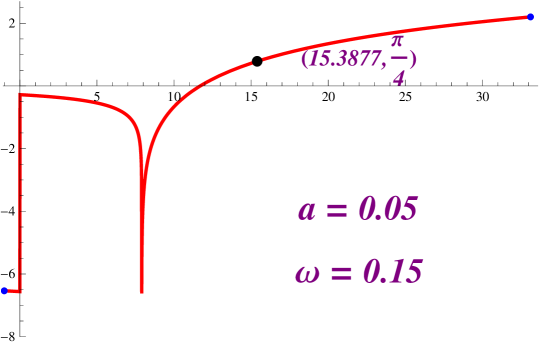
When the domain of the function starts at and the limit of the function when is . Moreover, this function has a vertical asymptote at , and then it has a jump discontinuity at . Finally, this function is define for all values of smaller than and the limit of when is

Taking a look at Figure 2.8 we notice that, when and , we have that for any integer , the equation has a solution. We have numerically solved this equation for and . Figures 2.9 and 2.10 provides a picture of the profile curves of the properly immerse examples.

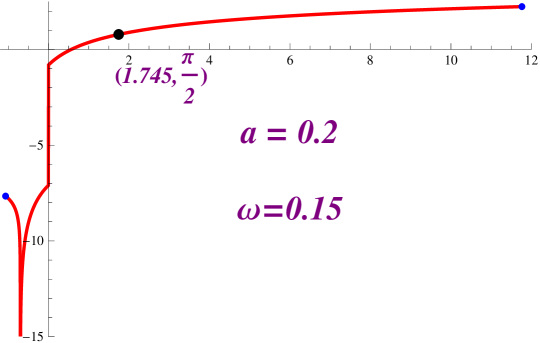

We have that if we decrease the value of while keeping the value of constant, we can again solve the equation but this time the helicoidal rotational drop is embedded. See Figure 2.11.

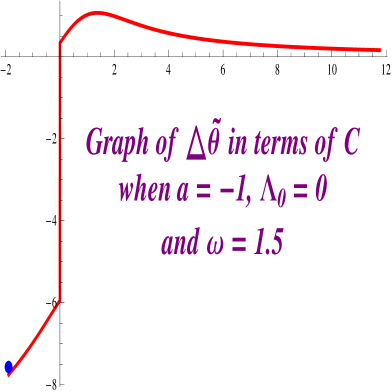
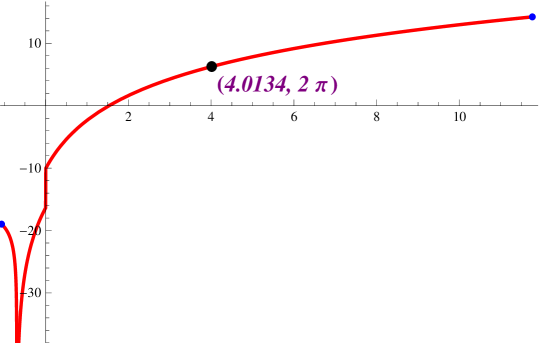
Finally we would like to show that if we increase then it is possible to solve the equation , (see Figure 2.12) .
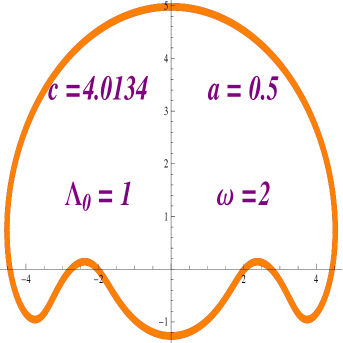
3. Second variation
For any sufficiently smooth surface, we define an invariant . The first variation formula (1.4) restricted to compactly supported variations can then be expressed
where . We assume that the surface is in equilibrium so that holds. The second variation is thus
A well known formula for the pointwise variation of the mean curvature is
| (3.1) |
where . Also
where . Combining this with (3.1), we have
| (3.2) |
where . Since we are assuming constant, the second term above vanishes and the second variation formula for variations vanishing on then reads
| (3.3) |
This formula can be found in [3]. As usual, an equilibrium surface will be called stable if the second variation is non negative for all compactly supported variations satisfying the additional condition
| (3.4) |
This is just the first order condition which is necessary and sufficient for the variation to be volume preserving.
For a part of the surface of the form this can be written
where denotes the Gaussian curvature. Choosing , gives
In addition, for this choice of , we have on the boundary and the mean value of on is zero.
Lemma 3.1.
There holds
and hence
Proof.
From calculations found in [4], one finds
since the last integrand is the derivative of a function of . ∎
Proposition 3.2.
A necessary condition for the stability of for the fixed boundary problem is that
| (3.6) |
holds. Equivalently, this can be expressed as
| (3.7) |
Proof.
We choose in the second variation formula. For this choice of , we have on the boundary and the mean value of on is zero. The result then follows directly from (3) and the previous lemma. ∎
The bound (3.6) gives a condition on the maximum height of a stable helicoidal surface in terms of the geometry of the generating curve.
There is no possible way to obtain a positive lower bound for the right hand side of (3.6). For a round cylinder of radius , the equation becomes , so for arbitrary , we can simply define by this equation so and hence the cylinder will be an equilibrium surface. For a cylinder, the potential in the second variation formula is
so for the potential is non positive and the cylinder is stable for arbitrary heights.
We will now give an upper bound for the height of a stable helicoidal equilibrium surface which is valid for any such surface which is not a cylinder over a planar curve. This upper bound will only depend on the generating curve. In [7], this estimate is modified so that it applies to non circular cylindrical equilibrium surfaces as well.
Theorem 3.3.
For a helicoidal surface which is not a round cylinder, a necessary condition for the stability of the part the surface between horizontal planes separated by a distance is that
| (3.8) |
holds. The result also holds true if , i.e. if the surface has constant mean curvature.
Remark. In [7] a similar estimate is given for cylindrical surfaces which are not round cylinders.
Proof.
To begin, note that the the third component of the normal satisfies since vertical translation is a symmetry of the normal. Also, this function will vanish identically if and only if the surface is a cylinder.
4. Appendix
We assume that is contained in a three dimensional region and that is contained in a supporting surface which is part of . We assume that there is a (not necessarily connected) domain such that bounds a subregion . The volume of will be denoted by .
Let be a solution of in with on where is the outward pointing normal to . This boundary value problem is undertermined and is solvable provided is not closed.
We subject the surface to a variation which keeps on . Then along and
We have
A well known formula relating the Laplacian on a submanifold to the Laplacian on the ambient space gives . Therefore we obtain
However, all of , and are perpendicular to on , so the line integral above vanishes.
To obtain (1.2), we let be a vector field on satisfying and along . This boundary value problem is undertermined and is solvable provided is not closed. Then by the Divergence Theorem
Again, all of , and are perpendicular to along so the line integral will vanish.
If the pair used above are replaced by another pail satisfying the same equations: and , then by the Divergence Theorem
for constants and . Thus these replacements will not affect the variational formulas for these integrals.
References
- [1] Brown, R.A., Scriven, L.E., The Shape and Stability of Rotating Liquid Drops, Proc. R. Soc. Lond. A 30 June 1980 vol. 371 no. 1746 331-357
- [2] Chandrasekhar, S. The Stability of a Rotating Liquid Drop Proc. R. Soc. Lond. A 25 May 1965 vol. 286 no. 1404 1-26.
- [3] López, Rafael, Stationary rotating surfaces in Euclidean space, Calculus of Variations in Partial Differential Equations, 39, numbers 3-4, (2010), 333-359.
- [4] Perdomo, O. A dynamical interpretation of cmc Twizzlers surfaces, Pacific J. Math. 258 (March 2012) No. 2, 459-585.
- [5] Perdomo, O. Embedded constant mean curvature hypersurfaces of spheres, Asian J. Math. 14 (March 2010) No. 1, 73-108.
- [6] Perdomo, O. Hellicoidal minimal surfaces in , To appear in the Ilinois J. of Math.
- [7] Palmer, B. and Perdomo, O. Equilibrium Shapes of Cylindrical Rotating Liquid Drops. Preprint.
- [8] Solonikov, V., A., Instability of axially symmetric equilibrium figures of a rotating, viscous, incompressible liquid, Journal of Mathematical Sciences July 2006, Volume 136, Issue 2, pp 3812-3825.