Safe Human-Robot Collaborative Transportation via
Trust-Driven Role Adaptation

Let the environment be contained within a set $\mathcal{X}$. In this work, we assume that the obstacles in the environment are static, although the proposed framework can be extended to dynamic obstacles. At any time step $t$, let the set of obstacle constraints known to the human and the robot (detected at $t$ and stored until $t$) be denoted by $\mathcal{C}_{h,t}$ and $\mathcal{C}_{r,t}$, respectively. We denote:

$\displaystyle\mathcal{C}_{r,t}\cup\mathcal{C}_{h,t}=\mathcal{O}_{t},~{}\forall t\leq T,$

where $T\gg 0$ is the task duration limit and $\mathcal{O}_{t}$ is the set of obstacle constraints to be avoided at $t$ during the task. The approach proposed in this paper focuses on the challenging situation where no agent has the full information of all the detected obstacles in $\mathcal{O}_{t}$, i.e., $\mathcal{C}_{h,t}\subset\mathcal{O}_{t}$ and $\mathcal{C}_{r,t}\subset\mathcal{O}_{t}$.

We model both the human and the robot transporting a three dimensional rigid object. Let $(\vec{I}_{I},\vec{J}_{I},\vec{K}_{I})$ and $(\vec{I}_{B},\vec{J}_{B},\vec{K}_{B})$ be the orthogonal unit bases vectors defining the inertial and the transported object fixed coordinate frames, respectively. Let $(X,Y,Z)$ be the position of the center of mass of the transported object in the inertial frame, $\vec{v}$ be the velocity of the center of mass relative to the inertial frame, expressed in the body-frame as

$\displaystyle\vec{v}=v_{x}\vec{I}_{B}+v_{y}\vec{J}_{B}+v_{z}\vec{K}_{B}.$

(1)

Furthermore, let the Euler angles $E=\begin{bmatrix}\psi&\theta&\phi\end{bmatrix}^{\top}$ be the roll, pitch, yaw angles describing the orientation of the body w.r.t. the inertial frame, and $\vec{\omega}_{B/I}$ be the angular velocity of the body-fixed frame w.r.t. the inertial frame, expressed in the body-fixed frame as

$\displaystyle\vec{w}_{B/I}=w_{x}\vec{I}_{B}+\omega_{y}\vec{J}_{B}+\omega_{z}\vec{K}_{B}.$

(2)

We denote $\dot{E}=W^{-1}\begin{bmatrix}\omega_{x}&\omega_{y}&\omega_{z}\end{bmatrix}^{\top}$, with matrix

$\displaystyle W^{-1}=\frac{1}{\cos\theta}\begin{bmatrix}0&\sin\phi&\cos\phi\\ 0&\cos\phi\cos\theta&-\sin\phi\cos\theta\\ \cos\theta&\sin\phi\sin\theta&\cos\phi\sin\theta\end{bmatrix}.$

Let $(F_{x},F_{y},F_{z})$ be the force components along the inertial axes applied at the body’s center of mass, $(\tau_{x},\tau_{y},\tau_{z})$ are the torques about the body fixed axes, and $J$ be the moment of inertia of the body expressed in the body frame, given by $J=\mathrm{diag}(J_{x},J_{y},J_{z})$. Then the equations of motion of the object transported are written as follows:

		$\displaystyle\begin{bmatrix}\dot{X}&\dot{Y}&\dot{Z}\end{bmatrix}^{\top}=Q_{B/\mathbb{I}}\begin{bmatrix}v_{x}&v_{y}&v_{z}\end{bmatrix}^{\top},$		(3)
		$\displaystyle\begin{bmatrix}\dot{\psi}&\dot{\theta}&\dot{\phi}\end{bmatrix}^{\top}=W^{-1}\begin{bmatrix}\omega_{x}&\omega_{y}&\omega_{z}\end{bmatrix}^{\top},$
		$\displaystyle\begin{bmatrix}\dot{v}_{x}&\dot{v}_{y}&\dot{v}_{z}\end{bmatrix}^{\top}=\frac{1}{M}\begin{bmatrix}F_{x}&F_{y}&F_{z}\end{bmatrix}^{\top}-\Omega\begin{bmatrix}v_{x}&v_{y}&v_{z}\end{bmatrix}^{\top},$
		$\displaystyle\begin{bmatrix}\dot{\omega}_{x}&\dot{\omega}_{y}&\dot{\omega}_{z}\end{bmatrix}^{\top}=J^{-1}\begin{bmatrix}\tau_{x}&\tau_{y}&\tau_{z}\end{bmatrix}^{\top}$
		$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}-J^{-1}\Omega J\begin{bmatrix}\omega_{x}&\omega_{y}&\omega_{z}\end{bmatrix}^{\top},$

with $M$ being the mass of the body and the angular velocity and rotation matrices given by

	$\displaystyle\Omega=\begin{bmatrix}0&-\omega_{z}&\omega_{y}\\ \omega_{z}&0&-\omega_{x}\\ -\omega_{y}&\omega_{x}&0\end{bmatrix},~{}\textnormal{and}$
	$\displaystyle Q_{B/I}=\begin{bmatrix}c\theta c\phi&c\phi s\theta s\phi-c\phi s\psi&s\phi s\psi+c\phi c\psi s\theta\\ c\theta s\psi&c\phi c\psi+s\theta s\phi s\psi&c\phi s\theta s\psi-c\psi s\phi\\ s\theta&c\theta s\phi&c\theta c\phi\end{bmatrix},$

respectively, where $\sin$ and $\cos$ have been abbreviated. Using (3), the state-space equation for the transported object is compactly written as:

$\displaystyle\dot{S}(t)$

$\displaystyle=f_{c}(S(t),u(t)),$

(4)

with states and inputs at time $t$ given by:

	$\displaystyle S(t)=[X(t),Y(t),Z(t),\psi(t),\theta(t),\phi(t),v_{x}(t),v_{y}(t),v_{z}(t),$
	$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}\omega_{x}(t),\omega_{y}(t),\omega_{z}(t)]^{\top},$
	$\displaystyle u(t)=[F_{x}(t),F_{y}(t),F_{z}(t),\tau_{x}(t),\tau_{y}(t),\tau_{z}(t)]^{\top}.$

We discretize (4) with the sampling time of $T_{s}$ of the robot to obtain its discrete time version:

$\displaystyle S_{t+T_{s}}=f(S_{t},u_{t}).$

(5)

Given any input $u_{t}$ to the center of mass of the object, we decouple it into the corresponding human inputs $u^{h}_{t}$ and robot inputs $u^{r}_{t}$, such that $u_{t}=u^{h}_{t}+u^{r}_{t}$. We consider constraints on the inputs of the robot and the human given by $u^{h}_{t}\in\mathcal{U}^{h}$ and $u^{r}_{t}\in\mathcal{U}^{r}$ for all $t\geq 0$. The set $\mathcal{U}^{h}$ can be learned from human demonstrations’ data.

The constrained finite time optimal control problem that the robot solves at time step $t$ with a horizon of $N\ll T$ is given by:

	$\displaystyle\min_{U_{t}}$	$\displaystyle\sum\limits_{k=1}^{N}[(S_{t+kT_{s}|t}-S_{\mathrm{tar}})^{\top}Q_{s}(S_{t+kT_{s}|t}-S_{\mathrm{tar}})+\cdots$		(6)
		$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}~{}+u_{t+(k-1)T_{s}|t}^{\top}Q_{i}u_{t+(k-1)T_{s}|t}]+\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$
		$\displaystyle\text{s.t.,}~{}~{}~{}~{}~{}{S}_{t+kT_{s}|t}=f(S_{t+(k-1)T_{s}|t},u_{t+(k-1)T_{s}|t}),$
		$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}\mathcal{B}(S_{t+kT_{s}|t})\in\mathcal{X}\setminus\mathcal{C}_{r,t},~{}u_{t+(k-1)T_{s}|t}\in\mathcal{U}^{r}\oplus\mathcal{U}^{h},$
		$\displaystyle~{}~{}~{}~{}~{}~{}~{}~{}~{}\forall k\in\{1,2,\dots,N\},~{}S_{t|t}={S}_{t},$

where $\mathcal{B}(\cdot)$ is a set of positions defining the transported object, $U_{t}=\{u_{t|t},\dots,u_{t+(N-1)T_{s}|t}\}$, $S_{\mathrm{tar}}$ is the target state, $Q_{s},Q_{i}\succcurlyeq 0$ are the weight matrices, and inferred obstacle zone penalty $\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$ is defined in Section III-D. Once an optimal input $u^{\star}_{t}$ is computed, the robot utilizes the following assumption to estimate the human’s inputs.

The fraction $p$ can be roughly estimated from collected trial data where the human limits to playing a complying role in the task¹¹1If the human actively leads the task, potentially forcing/opposing robot’s actions, human inputs may be drastically different from its approximate (7).. Thus, the robot’s estimate of the human policy inherently considers that the human is trying to minimize their felt forces and torque in the task to assist the robot, while reacting to the surrounding obstacles in $\mathcal{C}_{r,t}$ in a way which is consistent with the MPC planned trajectory by the robot. Utilizing Assumption 1, the robot computes its actions at $t$ as:

$\displaystyle u^{\star,r}_{t}=u^{\star}_{t}-\hat{u}^{h}_{t}.$

(8)

Since the robot does not perfectly know the human’s intentions and the configuration of obstacles in the vicinity of the human, it does not apply its computed MPC input $u^{\star,r}_{t}$ to system (4) directly. Instead, it checks the deviation of its estimated human inputs from the actual closed-loop inputs applied by the human. The latter can be measured using force and torque sensors on the robot. As the applied human inputs at the current time step are not available for this computation, the robot approximates²²2For sample period $T_{s}\ll 1$, this can constitute a reasonable approximation. this deviation by:

$\displaystyle\Delta u^{h}_{t}\approx\hat{u}^{h}_{t}-u^{h}_{t-T_{s}}.$

The trust value $\alpha_{t}$ is then computed as:

$\displaystyle\alpha_{t}=1-\min\{1,\frac{\|\Delta u^{h}_{t}\|}{\delta_{\mathrm{thr}}}\},$

(9)

where $\delta_{\mathrm{thr}}$ is a chosen threshold deviation. The robot uses this trust value to apply a weighted combination of its computed MPC inputs $u^{\star,r}_{t}$, and inputs proportional to $u^{h}_{t-T_{s}}$ as detailed later in equation (LABEL:eq:mpc_pol_formulation). This trust-driven combination of inputs is motivated by works such as [22, 23, 24]. The robot additionally deploys a safe stopping policy, in case the computed trust value is below a chosen threshold, and it nears obstacles potentially unknown to the human. These two modes of the robot’s policy are detailed in the next section.

At time step $t$, we denote the inertial position coordinates of the robot’s seen point on the object closest to any obstacle in $\mathcal{C}_{r,t}$ as $R_{t}$. After finding a solution to (6) and computing $u^{\star,r}_{t}$ using (8), the robot utilizes (9) and applies its closed-loop input computed as follows:

$\displaystyle u^{r}_{t}=\begin{cases}\mathrm{proj}_{\mathcal{U}^{r}}(\alpha_{t}u^{\star,r}_{t}+K_{1}(1-\alpha_{t})u^{h}_{t-T_{s}}),~{}\textnormal{if (SS) not true,}\\ \mathrm{proj}_{\mathcal{U}^{r}}(-K_{2}\frac{\dot{R}_{t}}{Ts}),~{}\textnormal{otherwise,}\\ \end{cases}$

(10)

to system (5) in closed-loop with chosen gains $K_{1},K_{2}>0$, where $\mathrm{proj}_{\mathcal{A}}(x)$ denotes the Euclidean projection of $x$ onto set $\mathcal{A}$, and the robot’s safe stop policy triggering condition (SS) is given by:

$\displaystyle\textnormal{(SS)}:\alpha_{t}\!<\frac{1}{2},~{}\min_{o\in\mathcal{C}_{r,t}}\|R_{t}-o\|\leq d_{\mathrm{thr}},\dot{R}_{t}\cdot(o-R_{t})>v_{\mathrm{thr}},$

(11)

with distance and velocity thresholds $d_{\mathrm{thr}}>0$ and $v_{\mathrm{thr}}>0$. That is, when point $R_{t}$ approaches any obstacle $o$ at a high velocity under a low trust $\alpha_{t}<\frac{1}{2}$, the robot actively tries to decelerate the the object and bring it to a halt. From policy (LABEL:eq:mpc_pol_formulation), we make the following observations:

1. 1.

   A large trust value (e.g., $\alpha_{t}$ closer to 1), corresponds to the case when the robot’s estimates of the human’s inputs align with the actual human’s inputs. This means that the human is taking on a follower role, trusting on the robot’s actions. The robot trusts the computed inputs $u^{\star,r}_{t}$ from the MPC problem (6) and takes the leader’s role in the task.

2. 2.

   A small trust value (e.g., $\alpha_{t}$ close to 0) corresponds to the case when the robot’s predictions of the human’s inputs do not align with the actual human’s inputs. This means that the human is taking on the leader’s role, either reacting to obstacles nearby or actively leading the task. The robot does not trust the computed inputs $u^{\star,r}_{t}$ from the MPC problem (6) and takes the follower’s role (unless the safe stop policy condition is triggered).

Policy (LABEL:eq:mpc_pol_formulation) is motivated by [12], and qualitatively has the properties of joint impedance and admittance, similar to [25]. We see that satisfying condition 1 increases the efficacy of the robot’s solution to (6), i.e., $u^{\star,r}_{t}$. To that end, we add the inferred obstacle zone penalty $\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$ to (6), adapting the cost to be optimized by inferring information on potential obstacles at the human’s vicinity. This is elaborated next.

At time step $t$, we denote the inertial position coordinates of the human by $H_{t}$. We also denote the first three force components of the human input $u^{h}_{t}$ by $u^{h}_{f,t}$. Motivated by the obstacle learning work of [26], we add the extra term $\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$ to the cost in (6) at every time step. This term is to be chosen when $\alpha_{t}<\frac{1}{2}$, and the human applies forces along directions which are more than a user specified threshold $\nu_{\mathrm{thr}}$ radians apart from its expected ones. We then choose the term $\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$ as follows:

$\displaystyle\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})=\begin{cases}\sum_{i=1}^{n}\frac{1}{\|(S_{t}-H_{t}+K_{3}u^{h}_{f,t-T_{s}}+o_{i})\|},~{}\textnormal{if (IO)},\\ 0,~{}\textnormal{otherwise},\end{cases}$

(12)

with $n$ choices of the random parameter $0<o_{i}\ll 1$ (introduces noise in the direction vector), control gain $K_{3}>0$, and condition (IO) being

$\displaystyle\textnormal{(IO)}:\alpha_{t}<\frac{1}{2},~{}|\arccos(\frac{\hat{u}^{h}_{f,t}\cdot u^{h}_{f,t-T_{s}}}{\|\hat{u}^{h}_{f,t}\|\|u^{h}_{f,t-T_{s}}\|})|>\nu_{\mathrm{thr}}.$

Intuitively, we assume that if the human unexpectedly pushes against the robot, they are attempting to avoid some obstacle unknown to the robot. The robot uses these force measurements and generates $n$ virtual obstacle points that are placed relative to the human’s location at a distance scaled by the negative force vector, plus some noise. These virtual obstacle points are the robot’s estimates of potential obstacles in the human’s vicinity, due to which the human’s input $u^{h}_{t-T_{s}}$ is significantly different from the estimate $\hat{u}^{h}_{t}$. Introducing the penalty $\mathcal{I}_{\mathcal{O}}(S_{t},u^{h}_{t-T_{s}})$ can improve the MPC planner (6), increasing the value of $\alpha_{t}$ and enabling more effective role of the robot in the task.

For this section, two obstacles are placed between the agents and the target, as shown in the rendered experiment space in Fig. 2b. We first show the benefits of using the trust-driven policy mode, where the robot utilizes the trust value $\alpha_{t}$ to apply a weighted combination of its MPC inputs and the human’s inputs to the system. The baseline for comparison is a pure MPC policy, with the robot solving MPC problem (6) and applying its optimal input (8), being agnostic to the responses of the human.

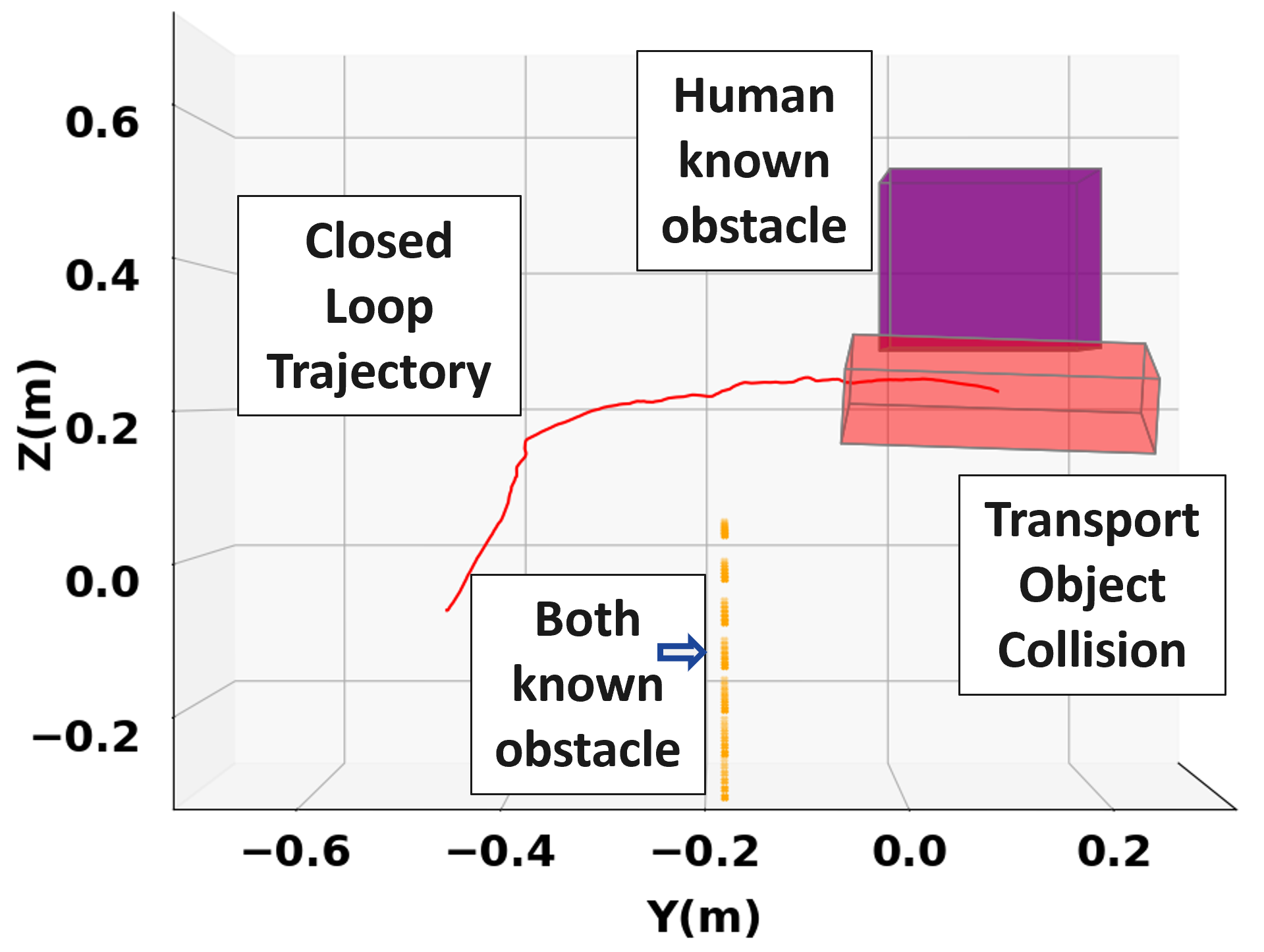
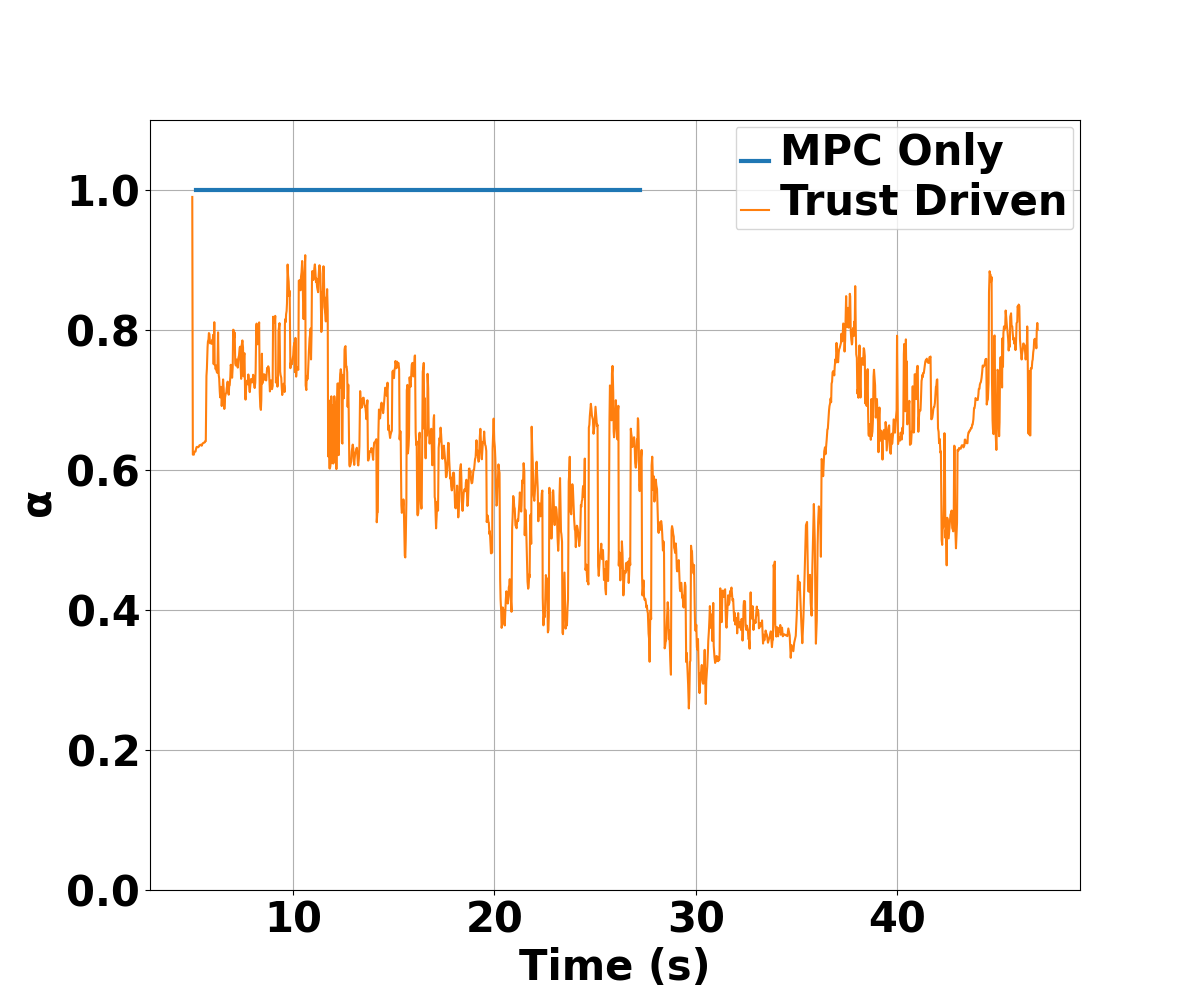
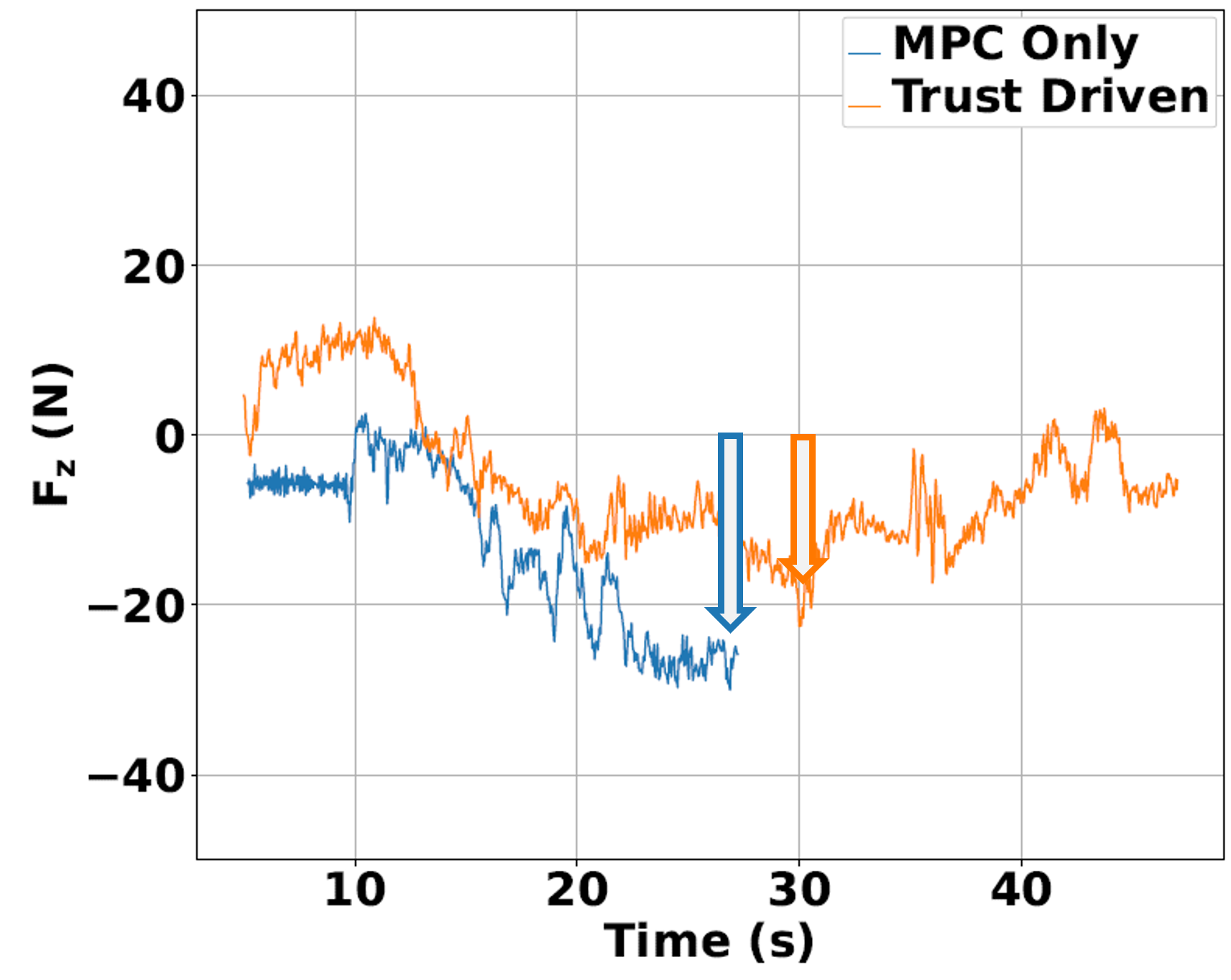
In the considered scenario in Fig. 2, the purple box obstacle located between $Z\in[0.35m,0.57m]$ is known only by the human. Both agents are aware of the dotted wall obstacle at $Y=-0.2$ m. In Fig. 2a, the robot is operating with the pure MPC baseline policy, agnostic to the human’s actions. As a consequence, the planned trajectory by the robot results in the human colliding with this obstacle, as seen in Fig. 2a. Resisting force values by the human in Fig. 2d indicate the human’s opposition to the robot’s actions. On the other hand, with our proposed trust-driven policy mode, the robot is cognizant of the human’s intentions. The evolution of $\alpha_{t}$ as the human navigates in the proximity of the box obstacle is shown in Fig. 2c. When the transport object nears the obstacle (around 30 sec), the robot distrusts its estimate of the human policy with a computed $\alpha_{t}\approx 0.3$ and applies more of the measured human input in  (LABEL:eq:mpc_pol_formulation). Collision is averted as a consequence, as seen in Fig. 2b. Lower force magnitudes in Fig. 2d further indicate that the human’s resistance to robot’s actions during this collision avoidance is lowered, as the robot lowers the contribution of its MPC inputs in (LABEL:eq:mpc_pol_formulation) with a low value of $\alpha_{t}$.

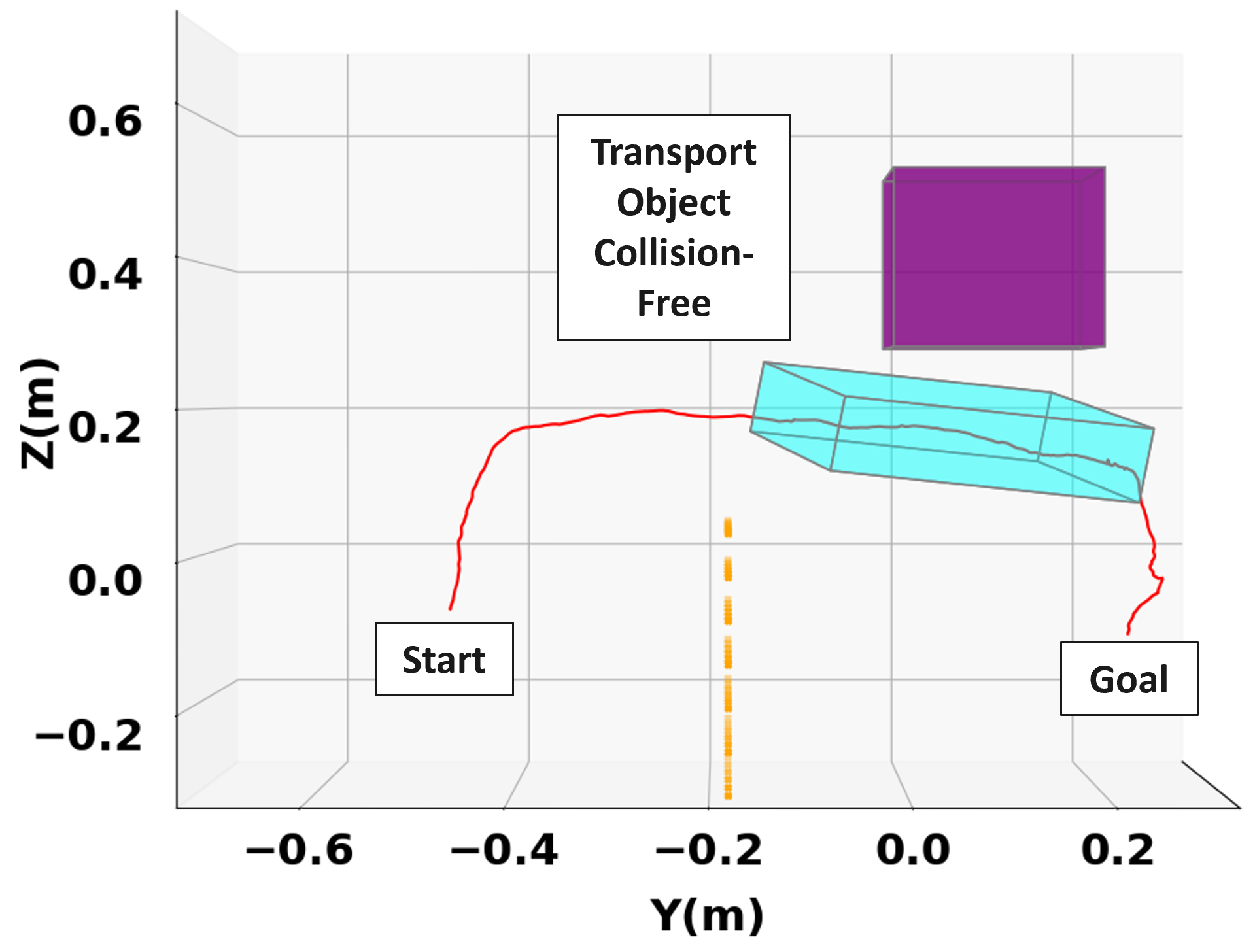
To highlight the safety benefits of adding the safe stop policy mode in (LABEL:eq:mpc_pol_formulation), we consider the scenario shown in Fig. 3. For this scenario, only one simulated obstacle wall at $Y=-0.2$ m is in the experiment space which the human does not see. The human decides to drive the transport object towards the goal via the shortest path without being aware that it is leading towards the wall.

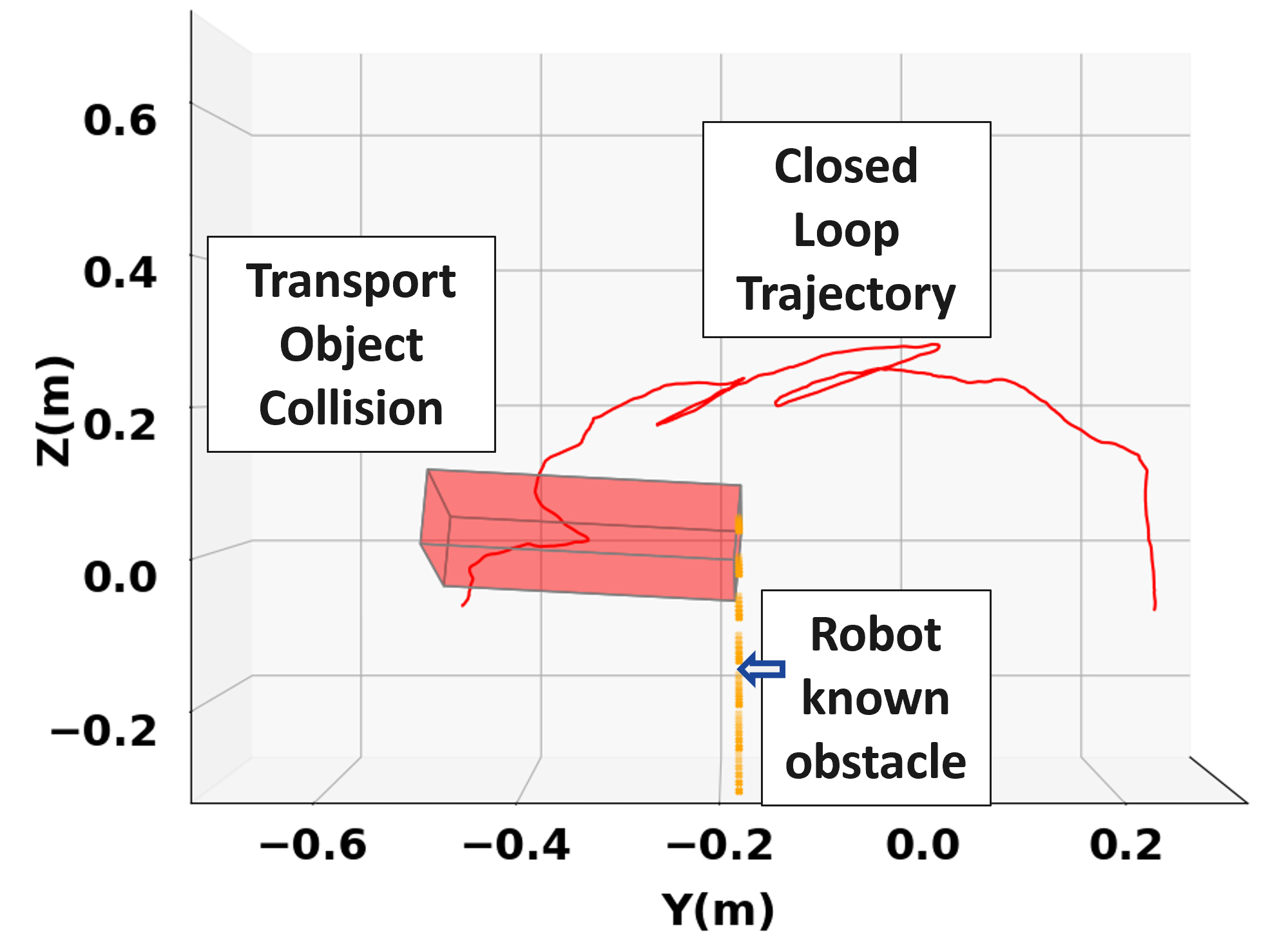
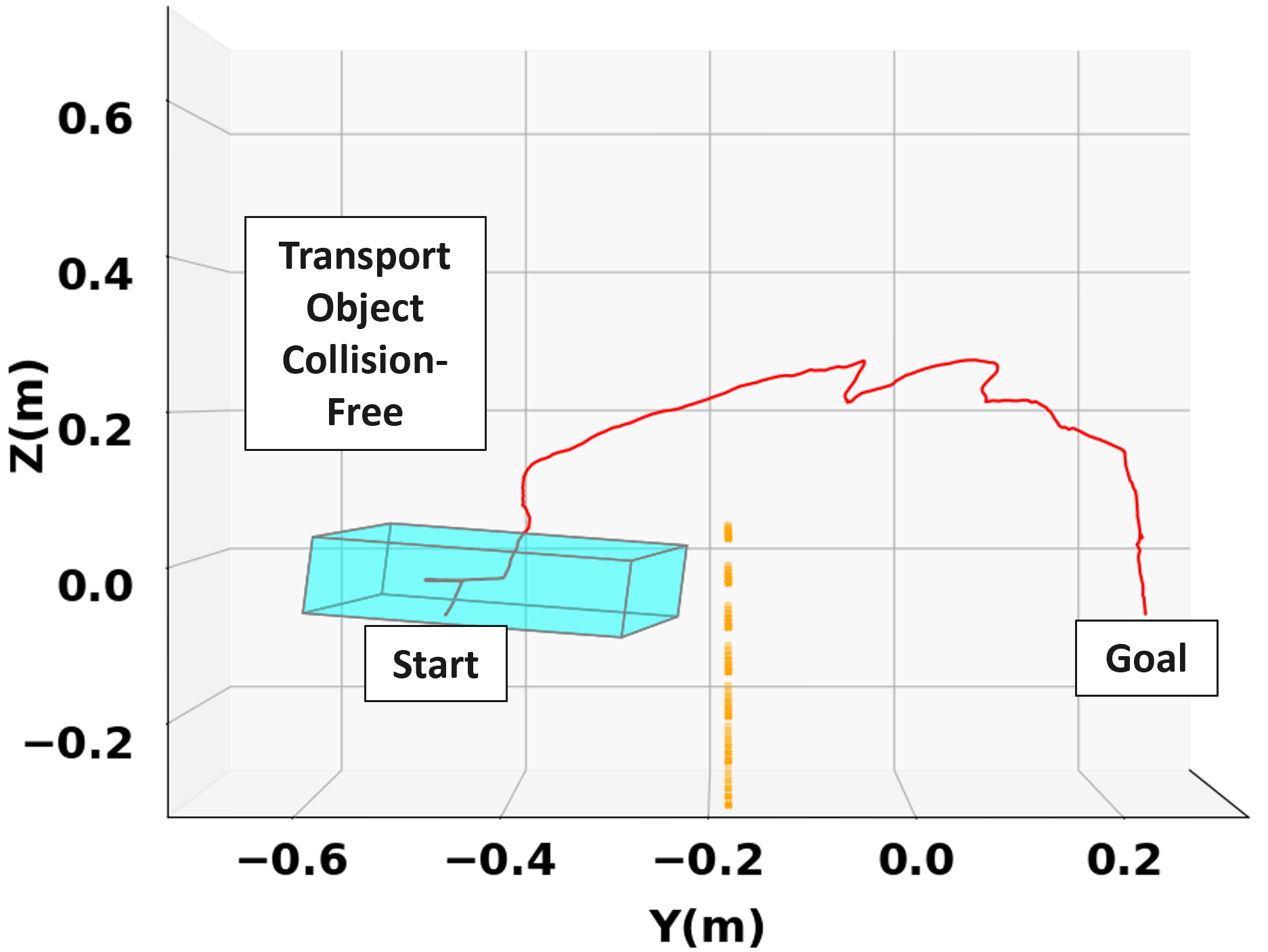
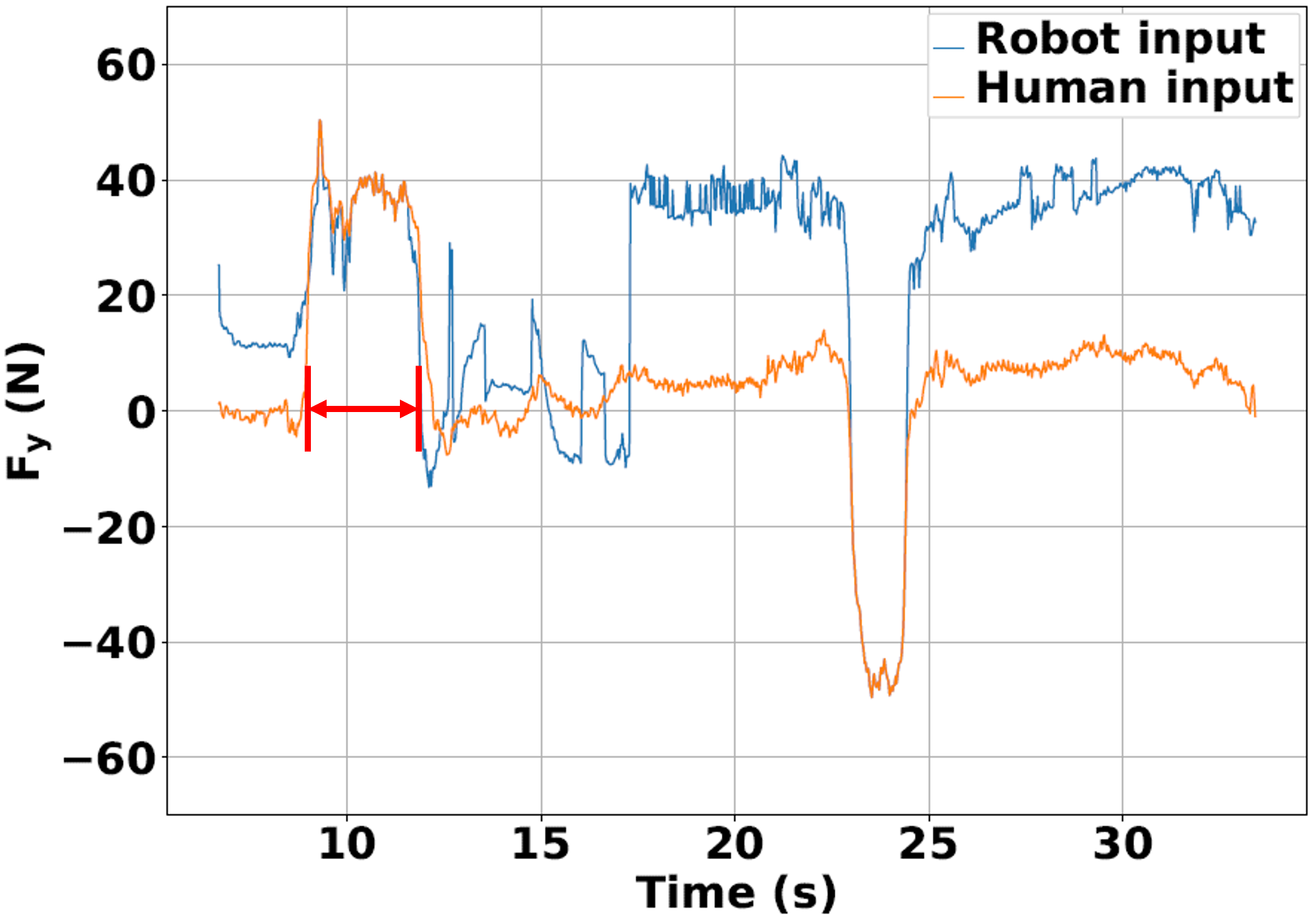
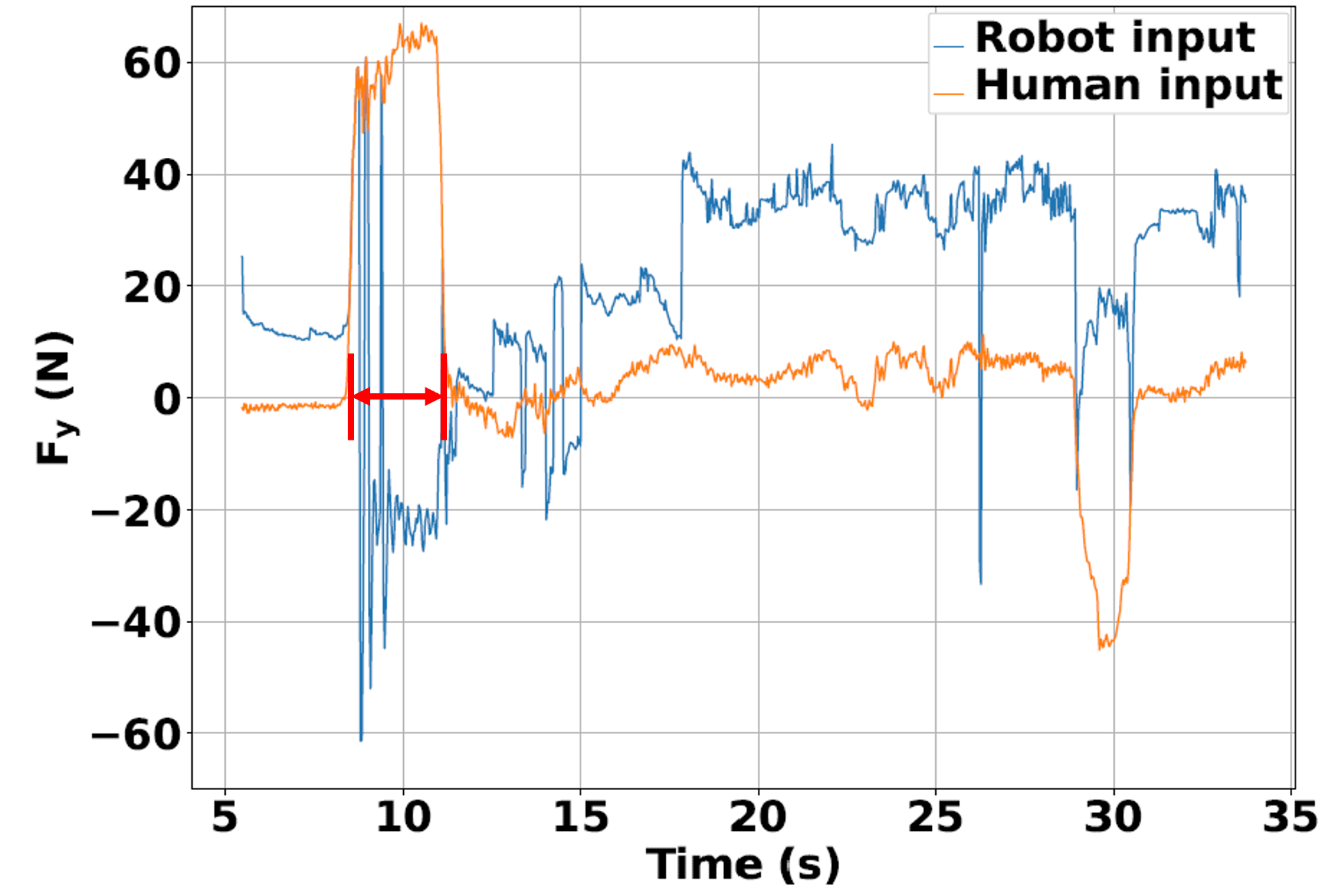
Without activating the safe stop policy backup, the robot’s inputs continue to comply with the inputs from the human, as shown in the force plots in Fig. 3c. As a result, the transported object collides with the obstacle wall, as seen in Fig. 3a. On the other hand, in Fig. 3b we see that utilizing the safe stop policy mode manages to prevent this collision and maintain safety in the transportation task. This safety retaining effect of the safe stop mode can be explained from Fig. 3d, where next to the obstacle wall when condition (SS) is triggered (around 10 sec), we no longer see the robot’s applied forces complying with the human’s forces. Instead, the robot applies a decelerating safe stop input, which results in the collision avoidance. The task is completed successfully.

In order to generalize the validity of the above results beyond the considered example, we carried out the transportation task and analyzed the closed loop behaviors of the proposed controller with 100 configurations of randomized start, goal and obstacle positions. In some cases, the obstacles are purely simulated for faster testing purposes. The detailed results are shown in Table II where we use three metrics to compare the 100 trials. A Collision-Free Success is a trial where the transport object is brought to the target state without hitting obstacles. Peak Human Force is the largest magnitude of force applied by the human throughout a given trial. The Duration of Intervening Forces is the length of time in which the human has applied more than 30N in a given trial.

Table II shows that the proposed approach results in a 37% increase in the number of Collision-Free Successes. Moreover, the average value of the Peak Human Force lowers by 14.9% with the proposed approach, indicating decreased opposition of the human during the task. The results show that the average Duration of Intervening Forces shortens by 61.8% with our approach. The robot cedes some of the control authority to the human as the trust value decreases. This occurs when the human does something unexpected to the robot. On the other hand, with the pure MPC approach, the robot attempts to follow its optimal trajectory even in the case where a collision with an object known only by the human is imminent. Thus, the human needs to continuously apply the intervening force for longer periods of time when no trust value is used.