Safe Perception-Based Control under Stochastic Sensor
Uncertainty using Conformal Prediction

Perception-based control has received much attention lately [1, 2, 3, 4]. System states are usually not directly observable and can only be estimated from complex and noisy sensors, e.g., cameras or LiDAR. Learning-enabled perception maps can be utilized to estimate the system’s state from such high-dimensional measurements. However, these estimates are usually imperfect and may lead to estimation errors, which are detrimental to the system safety.

The above observation calls for perception-based control with safety guarantees as it is crucial for many autonomous and robotic systems like self-driving cars. Recent work has been devoted to addressing these safety concerns while applying perception-based control using perception maps, see, e.g.,  [5, 6, 7, 3, 8]. These work, however, either assume simple or no sensor noise models, consider specific perception maps, or lack end-to-end safety guarantees. In realistic settings, stochastic sensor noise may be unknown and follow skewed and complex distributions that do not resemble a Gaussian distribution, as is often assumed. Additionally, perception maps can be complex, e.g., deep neural networks, making it difficult to quantify estimation uncertainty.

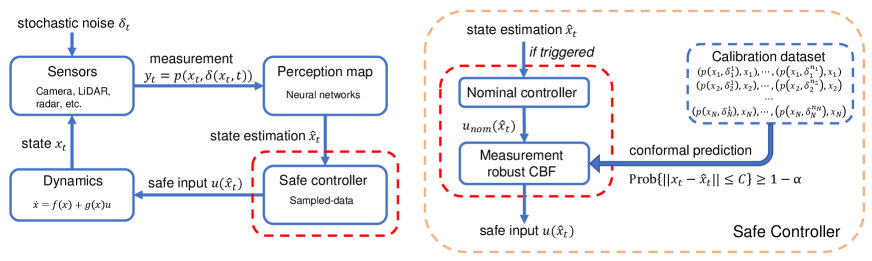
In this paper, we study perception-based control under stochastic sensor noise that follows arbitrary and unknown distributions. To provide rigorous safety guarantees, we have to account for estimation uncertainty caused by i) imperfect learning-enabled perception maps, and ii) noisy sensor measurements. As shown in Figure 1, to perform safety-critical control, we first leverage conformal prediction [9], a statistical tool for uncertainty quantification, to obtain state estimation regions that are valid with high probability. We then integrate these uncertain state estimation regions into the control design inspired by the notion of measurement robust control barrier functions from [5]. Specifically, we design a sampled-data controller using idea from self-triggered control to ensure safety for continuous-time systems while avoiding the use of stochastic calculus.

To summarize, we make the following contributions:

• •

  We use conformal prediction to quantify state estimation uncertainty of complex learning-enabled perception maps under arbitrary sensor and noise models;

• •

  We use these uncertainty quantifications to design a sampled-data controller for continuous-time systems. We provide probabilistic safety guarantees which, to our knowledge, is the first work to do so in such a setting;

• •

  We demonstrate the effectiveness of our framework in the LiDAR-enabled F1/10th vehicle simulations.

Perception-based control: Control from high-dimensional sensor measurements such as cameras or LiDAR has lately gained attention. While empirical success has been reported, e.g., [1, 2, 10, 11], there is a need for designing safe-by-construction perception-enabled systems. Resilience of perception-enabled systems to sensor attacks has been studied in [12, 13], while control algorithms that provably generalize to novel environments are proposed in [14, 15]. In another direction, the authors in [16] plan trajectories that actively reduce estimation uncertainty.

Control barrier functions under estimation uncertainty: Control barrier functions (CBFs) have been widely used for autonomous systems since system safety can be guaranteed [17, 18, 19, 20, 21]. For example, an effective data-driven approach for synthesizing safety controllers for unknown dynamic systems using CBFs is proposed in [22]. Perception maps are first presented in combination with measurement-robust control barrier functions in [5, 8] when true system states are not available but only imprecise measurements. In these works, the perception error is quantified for the specific choice of the Nadarya-Watson regressor. Our approach is agnostic to the perception map and, importantly, allows to consider arbitrary stochastic sensor noise which poses challenges for continuous-time control. Measurement robust control barrier functions are learned in different variations in [23, 24, 6]. Perception maps are further used to design sampled-data controllers [25, 26, 27] without explicit uncertainty quantification of the sensor and perception maps.

The works in [28, 29] consider state observers, e.g., extended Kalman filters, for barrier function-based control of stochastic systems. On the technical level, our approach is different as we avoid dealing with It$\hat{o}$ calculus using sampled-data control. Similarly, bounded state observers were considered in [30, 31]. However, state observer-based approaches are generally difficult to use in perception-systems as models of high-dimensional sensors are difficult to obtain. The authors in [32] address this challenge by combining perception maps and state observers. However, the authors assume a bound on the sensor noise and do not explicitly consider the effect of stochastic noise distributions.

Uncertainty quantification of perception maps is vital. In similar spirit to our paper, [7, 33] use (self-)supervised learning for uncertainty quantification of vision-based systems. While success is empirically demonstrated, no formal guarantees are provided as we pursue in this paper.

Conformal prediction for control: Conformal prediction is a statistical method that provides probabilistic guarantees on prediction errors of machine learning models. It has been applied in computer vision [34, 35], protein design [36], and system verification [37, 38]. Recently, there are works that use conformal prediction for safe planning in dynamic environments, e.g., [39, 40]. However, conformal prediction is only used for quantifying the prediction and not perception uncertainty, as we do in this work. To our knowledge, our work is the first to integrate uncertainty quantification from conformal prediction into perception-based control.

We denote by $\mathbb{R}$, $\mathbb{N}$, and $\mathbb{R}^{n}$ the set of real numbers, natural numbers, and real vectors, respectively. Let $\beta$: $\mathbb{R}\rightarrow\mathbb{R}$ denote an extended class $\mathcal{K}_{\infty}$ function, i.e., a strictly increasing function with $\beta(0)=0$. For a vector $v\in\mathbb{R}^{n}$, let $\|v\|$ denote its Euclidean norm.

Addressing Problem 1 is challenging for two reasons. First, the perception map $\hat{q}$ may not be exact, e.g., even in the disturbance-free case, it may not hold that $\hat{q}(p(x,0))=x$. Second, even if we have accurate state estimates in the disturbance-free case, i.e., when $\hat{q}(p(x,0))$ is close to $x$, this does not imply that we have the same estimation accuracy with disturbances, i.e., $\hat{q}(p(x,\delta))$ may not necessarily be close to $x$. Our setting is thus distinctively different from existing approaches and requires uncertainty quantification of the noisy error between $\hat{x}(t)$ and $x(t)$.

To demonstrate our proposed safe perception-based control law, we consider navigating an F1/10th autonomous vehicle in a structured environment [48], which is shown in Figure 2. The vehicle system has the state $x=[p_{x},p_{y},\theta]$, where $[p_{x},p_{y}]$ denotes its position and $\theta$ denotes its orientation. We have $[\dot{p}_{x},\dot{p}_{y}]=[u_{x},u_{y}]$, where $u_{x}$ and $u_{y}$ are control inputs denoting velocities, and $\theta=\arctan(u_{y}/u_{x})$. The control input constraint is $(u_{x},u_{y})\in[-1,1]\times[-1,1]$. Thus, the assumption that there exists an upper bound $\bar{F}$ for dynamics holds for this system.

Observation model: The vehicle is equipped with a 2D LiDAR scanner from which it obtains LiDAR measurements as its observations. Specifically, the measurement include 64 LiDAR rays uniformly ranging from $-\frac{3\pi}{4}$ to $\frac{3\pi}{4}$ relative to the vehicle’s heading direction. To model the uncertainty of measurements, unknown noise conforming to exponential distribution is added to each ray:

where $y^{k}$ is the ground truth for ray $k$, $y^{k}_{n}$ is the corrupted observed ray $k$, and $\lambda$ is the parameter of exponential distribution, where the noise $\delta$ is drawn from. In our experiments, we let $\lambda:=2/3$.

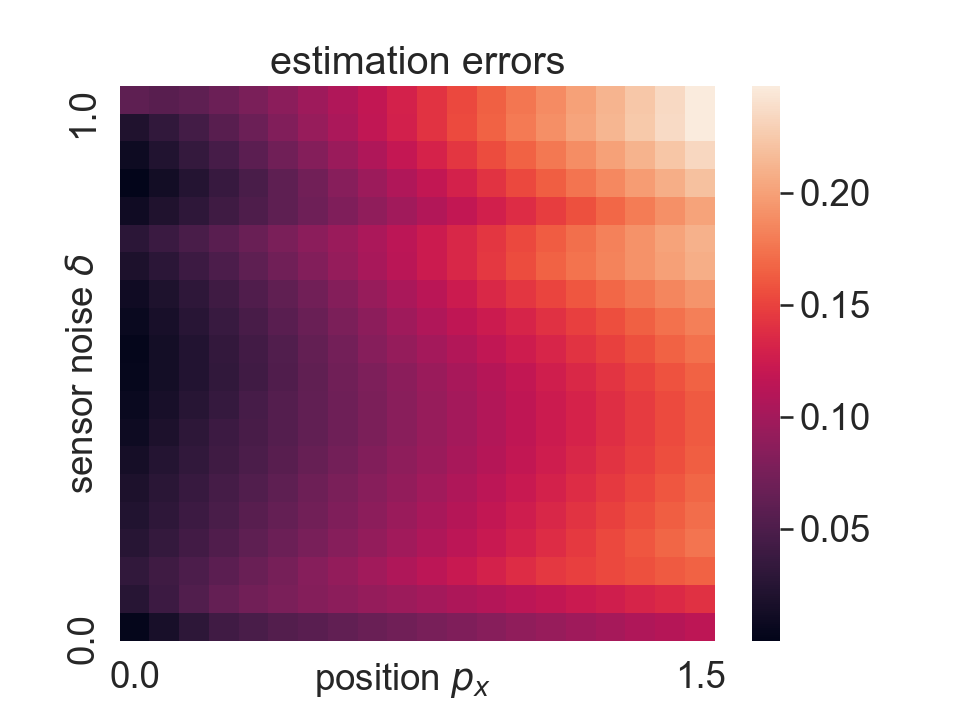
Perception map: We trained a feedforward neural network to estimate the state of the vehicle. The input is the 64-dimensional LiDAR measurement and output is the vehicle’s state. The training dataset $D_{train}$ contains $4\times 10^{5}$ data points, and the calibration dataset $D_{cal}$ for conformal prediction contains $1.25\times 10^{4}$ data points. For illustration, under a fixed heading $\theta$ and longitudinal position $p_{y}$, the errors $e(x)$ of the learned perception map with respect to sensor noise $\delta$ and horizontal position $p_{x}$ is shown in Figure 3.

Barrier functions: To prevent collision with the walls, when the vehicle is traversing the long hallway, the CBF is chosen as $h(x)=\min\{h_{1}(x),h_{2}(x)\}$, where $h_{1}(x)=p_{x}$ and $h_{2}(x)=1.5-p_{x}$. Then we have the safe set $\mathcal{C}=\{x\in\mathbb{R}^{3}|h(x)\geq 0\}$. CBFs can be similarly defined when the vehicle is operating in the corner. To demonstrate the effectiveness of our method, we compare the following two cases in simulations:

1. 1.

   Measurement robust CBF: as shown in Theorem 1, we choose the parameters pair $(a(y),b(y))=((\mathcal{L}_{L_{f}h}+\mathcal{L}_{\beta\circ h})\Delta,\mathcal{L}_{L_{g}h}\Delta)$ to ensure robust safety.

2. 2.

   Vanilla CBF: we choose the parameters pair $(a(y),b(y))=(0,0)$, which essentially reduces to the vanilla non-robust CBF [17]. However, the perceived state is from perceptual estimation rather than real state, so this CBF cannot provide any safety guarantee.

Note that we obtain necessary Lipschitz constants using sampling-based estimation method in simulations.

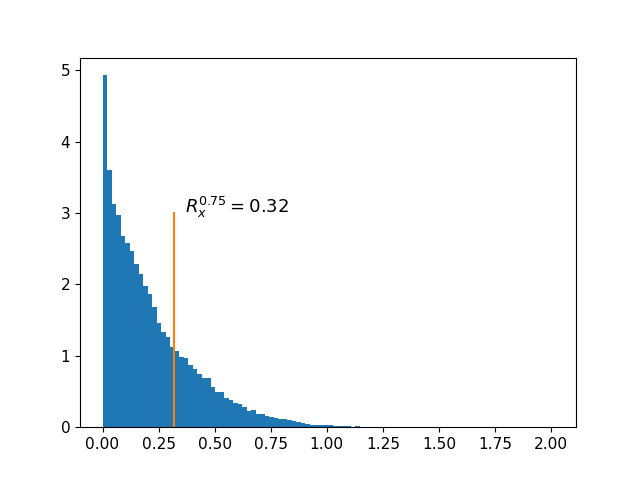
Uncertainty and results: The vehicle is expected to track along the hallway and make a successful turn in the corner as shown in Figure 2. The nominal controller is a PID controller. We set the coverage error $\alpha=0.25$, so we desire $P(\|x_{t}-\hat{x}_{t}\|\leq\epsilon^{\prime})\geq 1-\alpha=75\%$. Based on calibration of conformal prediction and Proposition 1, we calculate that $\epsilon^{\prime}=0.34$, and we choose $\Delta=0.35>\epsilon^{\prime}$. The nonconformity score histogram is presented in Figure 4, in which the $75\%$ quantile value is $R_{x}^{0.75}=0.32<\epsilon^{\prime}$, so our Proposition 1 holds in practice. As presented in Figure 5(b), the safety rate of sampled-data measurement robust CBF is $93\%$, which is significantly higher than vanilla non-robust CBF case ($16\%$).

In this paper, we consider the safe perception-based control problem under stochastic sensor noise. We use conformal prediction to quantify the state estimation uncertainty, and then integrate this uncertainty into the design of sampled-data safe controller. We obtain probabilistic safety guarantees for continuous-time systems. Note that, in this work, the perception map only depends on current observation, which might limit its accuracy in some cases. We plan to incorporate history observations into perception maps in the future. Also, we are interested in providing a more sample-efficient scheme while constructing calibration dataset.

Proof of Proposition 1: First, note that

due to Lipschitz continuity of $p$ and $\hat{q}$. Since, for any $x\in\mathcal{X}$, there exists a $x_{i}\in\bar{\mathcal{X}}$ such that $\|x-x_{i}\|\leq\epsilon$, we know that

Thus, we can bound the state estimation error $e(x,t)$ with probabability at least $1-\alpha$ as

Particularly, note that the last inequality holds since $\text{Prob}(\|\hat{x}_{i}-x_{i}\|\leq\bar{E}_{x_{i}})\geq 1-\alpha$ for each $x_{i}\in\bar{\mathcal{X}}$. Finally, we have that $\text{Prob}\big{(}e(x,t)\leq\sup_{j}\bar{E}_{x_{j}}+(\mathcal{L}_{p}\mathcal{L}_{\hat{q}}+1)\epsilon\big{)}\geq 1-\alpha$.

Proof of Lemma 2: First, recall the system dynamics:

By integrating the above ODE, we have that

Then, for any $t\in[t_{i},t_{i+1})$, it holds w.p. $1-\alpha$ that

where we used that Prob$(\|x(t_{i})-\hat{x}(t_{i})\|\leq\sup_{j}\bar{E}_{x_{j}}+(\mathcal{L}_{p}\mathcal{L}_{\hat{q}}+1)\epsilon)\geq 1-\alpha$ according to Proposition 1. Thus, we have that $\text{Prob}\Big{(}\|x(t)-\hat{x}(t_{i})\|\leq\Delta,\forall t\in[t_{i},t_{i+1})\Big{)}\geq 1-\alpha.$

Proof of Theorem 1: Let us first define

For any $t\in[t_{i},t_{i+1})$, we can now upper bound the absolute difference between $c(\hat{x}(t_{i}),u(t_{i}))$ and $c(x(t),u(t))$ as

Since $c(\hat{x}(t_{i}),u(t_{i}))\geq(\mathcal{L}_{L_{f}h}+\mathcal{L}_{L_{g}h}\|u(t_{i})\|+\mathcal{L}_{\beta\circ h})\cdot\Delta$, we can quickly obtain $c(x(t),u(t))\geq c(\hat{x}(t_{i}),u(t_{i}))-(\mathcal{L}_{L_{f}h}+\mathcal{L}_{L_{g}h}\|u(t_{i})\|+\mathcal{L}_{\beta\circ h})\cdot\Delta\geq 0$ using the absolute difference bound we derived above, which implies $h(x(t))\geq 0$, $\forall t\in[t_{i},t_{i+1})$. Also, $\|x(t)-\hat{x}(t_{i})\|\leq\Delta$ holds with the probability $1-\alpha$, so we finally obtain that $\text{Prob}\Big{(}h(x(t))\geq 0,\forall t\in[t_{i},t_{i+1})\Big{)}\geq 1-\alpha$. This ends the proof.

Proof of Proposition 2: We first prove that

which can be obtained by the following derivations:

Note that the third equality holds due to the continuity of $h(x)$, i.e., if $\lim_{t\rightarrow t_{m-1}}h(x(t))\geq 0$, then we have that $h(x(t_{m-1}))\geq 0$, which implies that the event $x(t)\in\mathcal{C},\forall t\in[t_{0},t_{m-1})$ and the event $x(t)\in\mathcal{C},\forall t\in[t_{0},t_{m-1}]$ are essentially the same event. Finally, we can recursively decompose the probability over time interval $[0,T)$: