Safe Projections of Binary Data Sets
Abstract
Selectivity estimation of a boolean query based on frequent itemsets can be solved by describing the problem by a linear program. However, the number of variables in the equations is exponential, rendering the approach tractable only for small-dimensional cases. One natural approach would be to project the data to the variables occurring in the query. This can, however, change the outcome of the linear program.
We introduce the concept of safe sets: projecting the data to a safe set does not change the outcome of the linear program. We characterise safe sets using graph theoretic concepts and give an algorithm for finding minimal safe sets containing given attributes. We describe a heuristic algorithm for finding almost-safe sets given a size restriction, and show empirically that these sets outperform the trivial projection.
We also show a connection between safe sets and Markov Random Fields and use it to further reduce the number of variables in the linear program, given some regularity assumptions on the frequent itemsets.
Keywords:
Itemsets Boolean Query Estimation Linear ProgrammingMSC:
68R10 90C05CR:
G.31 Introduction
Consider the following problem: given a large, sparse matrix that holds boolean values, and a boolean formula on the columns of the matrix, approximate the probability that the formula is true for a random row of the matrix. A straightforward exact solution is to evaluate the formula on each row. Now consider the same problem using instead of the original matrix a family of frequent itemsets, i.e., sets of columns where true values co-occur in a large fraction of all rows [1, 2]. An optimal solution is obtained by applying linear programming in the space of probability distributions [11, 19, 3], but since a distribution has exponentially many components, the number of variables in the linear program is also large and this makes the approach infeasible. However, if the target formula refers to a small subset of the columns, it may be possible to remove most of the other columns without degrading the solution; somewhat surprisingly, it is not safe to remove all columns that do not appear in the formula. In this paper we investigate the question of which columns may be safely removed. Let us clarify this scenario with the following simple example.
Example 1
Assume that we have three attributes, say , , and , and a data set having five transactions
Let us consider five itemsets, namely , , , , and . The frequency of an itemset is the fraction of transactions in which all the attributes appearing in the itemset occur simultaneously. This gives us the frequencies , , , , and . Let . Let us now assume that we want to estimate the frequency of the formula . Consider now a distribution defined on these three attributes. We assume that the distribution satisfies the frequencies, that is, , , etc. We want to find a distribution minimising/maximising . To convert this problem into a linear program we consider as a real vector having elements. To guarantee that is indeed a distribution we must require that sum to and that . The requirements that must satisfy the frequencies can be expressed in a form for a certain . In addition, can be expressed as for a certain . Thus we have transform the original problem into a linear program
Solving this program (and also the max-version of the program) gives us an interval for possible frequencies of . This interval has the following property: A rational frequency if and only if there is a data set having the frequencies and having as the fraction of the transactions satisfying the formula . If we, however, delete the attribute from the data set and evaluate the boundaries using only the frequencies and , we obtain a different interval .
The problem is motivated by data mining, where fast methods for computing frequent itemsets are a recurring research theme [10]. A potential new application for the problem is privacy-preserving data mining, where the data is not made available except indirectly, through some statistics. The idea of using itemsets as a surrogate for data stems from [16], where inclusion-exclusion is used to approximate boolean queries. Another approach is to assume a model for the data, such as maximum entropy [21]. The linear programming approach requires no model assumptions.
The boolean query scenario can be seen as a special case for the following minimisation problem: Let be the number of attributes. Given a family of itemsets, frequencies for , and some function that maps any distribution defined on a set to a real number find a distribution satisfying the frequencies and minimising . To reduce the dimension we assume that depends only on a small subset, say , of items, that is, if is a distribution defined on and is marginalised to , then we can write . The projection is done by removing all the itemsets from that have attributes outside .
The question is, then, how the projection to alters the solution of the minimisation problem. Clearly, the solution remains the same if we can always extend a distribution defined on satisfying the projected family of itemsets to a distribution defined on all items and satisfying all itemsets in . We describe sufficient and necessary conditions for this extension property. This is done in terms of a certain graph extracted from the family . We call the set safe if it satisfies the extension property.
If the set is not safe, then we can find a safe set containing . We will describe an efficient polynomial-time algorithm for finding a safe set containing and having the minimal number of items. We will also show that this set is unique. We will also provide a heuristic algorithm for finding a restricted safe set having at maximum elements. This set is not necessarily a safe set and the solution to the minimisation problem may change. However, we believe that it is the best solution we can obtain using only elements.
The rest of the paper is organised as follows: Some preliminaries are described in Section 2. The concept of a safe set is presented in Section 3 and the construction algorithm is given in Section 4. In Section 5 we explain in more details the boolean query scenario. In Section 6 we study the connection between safe sets and MRFs. Section 7 is devoted to restricted safe sets. We present empirical tests in Section 8 and conclude the paper with Section 9. Proofs for the theorems are given in Appendix.
2 Preliminaries
We begin by giving some basic definitions. A – database is a pair , where is a set of items and is a data set, that is, a multiset of subsets of .
A subset of items is called an itemset. We define an itemset indicator function such that
Throughout the paper we will use the following notation: We denote a random binary vector of length by . Given an itemset we define to be the binary vector of length obtained from by taking only the elements corresponding to .
The frequency of the itemset taken with respect of , denoted by , is the mean of taken with respect , that is, . For more information on itemsets, see e.g. [1].
An antimonotonic family of itemsets is a collection of itemsets such that for each each subset of also belongs to . We define straightforwardly the itemset indicator function and the frequency for families of itemsets.
If we assume that is an ordered family, then we can treat as an ordinary function , where is the number of elements in . Also it makes sense to consider the frequencies as a vector (rather than a set). We will often use to denote this vector. We say that a distribution defined on satisfies the frequencies , if .
Given a set of items , we define a projection operator in the following way: A data set is obtained from by deleting the attributes outside . A projected family of itemsets is obtained from by deleting the itemsets that have attributes outside . The projected frequency vector is defined similarly. In addition, if we are given a distribution defined on , we define a distribution to be the marginalisation of to . Given a distribution over we say that is an extension of if .
3 Safe Projection
In this section we define a safe set and describe how such sets can be characterised using certain graphs.
We assume that we are given a set of items and an antimonotonic family of itemsets and a frequency vector for . We define to be the set of all probability distributions defined on the set . We assume that we are given a function mapping a distribution to a real number. Let us consider the following problem:
| (1) |
That is, we are looking for the minimum value of among the distributions satisfying the frequencies . Generally speaking, this is a very difficult problem. Each distribution in has entries and for large even the evaluation of may become infeasible. This forces us to make some assumptions on . We assume that there is a relatively small set such that does not depend on the attributes outside . In other words, we can define by a function such that for all . Similarly, we define to be the set of all distributions defined on the set . We will now consider the following projected problem:
Let us denote the minimising distribution of Problem P by and the minimising distribution of Problem PC by . It is easy to see that . In order to guarantee that , we need to show that is safe as defined below.
Definition 1
Given an antimonotonic family and frequencies for , a set is -safe if for any distribution satisfying the frequencies , there exists an extension satisfying the frequencies . If is safe for all , we say that it is safe.
Example 2
Let us continue Example 1. We saw that the outcome of the linear program changes if we delete the attribute . Let us now show that the set is not a safe set. Let be a distribution defined on the set such that , , , and . Obviously, this distribution satisfies the frequencies and . However, we cannot extend this distribution to such that all the frequencies are to be satisfied. Thus, is not a safe set.
We will now describe a sufficient condition for safeness. We define a dependency graph such that the vertices of are the items and the edges correspond to the itemsets in having two items . The edges are undirected. Assume that we are given a subset of items and select . A path from to is a graph path such that and only . We define a frontier of with respect of to be the set of the last items of all paths from to
Note that , if and are connected by a path not going through . The following theorem gives a sufficient condition for safeness.
Theorem 3.1
Let be an antimonotonic family of itemsets. Let be a set of items such that for each the frontier of is in , that is, . It follows that is a safe set.
The vague intuition behind Theorem 3.1 is the following: has influence on only through . If , then the distributions marginalised to are fixed by the frequencies. This means that has no influence on and hence it can be removed.
We saw in Examples 1 and 2 that the projection changes the outcome if the projection set is not safe. This holds also in the general case:
Theorem 3.2
Let be an antimonotonic family of itemsets. Let be a set of items such that there exists whose frontier is not in , that is, . Then there are frequencies for such that is not -safe.
Safeness implies that we can extend every satisfying distribution in Problem PC to a satisfying distribution in Problem P. This implies that the optimal values of the problems are equal:
Theorem 3.3
Let be an antimonotonic family of itemsets. If is a safe set, then the minimum value of Problem P is equal to the minimum value of Problem PC for any query function and for any frequencies for .
If the condition of being safe does not hold, that is, there is a distribution that cannot be extended, then we can define a query resulting if the input distribution is , and otherwise. This construction proves the following theorem:
Theorem 3.4
Let be an antimonotonic family of itemsets. If is not a safe set, then there is a function and frequencies for such that the minimum value of Problem P is strictly larger than the minimum value of Problem PC.
Example 3
Assume that we have attributes, namely, , and an antimonotonic family whose maximal itemsets are , , , , , , and . The dependency graph is given in Fig. 1.
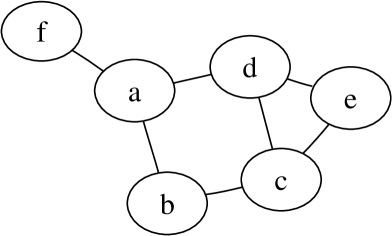
Let . This set is not a safe set since . On the other hand the set is safe since and .
The proof of Theorem 3.1 reveals also an interesting fact:
Theorem 3.5
Let be an antimonotonic family of itemsets and let be frequencies for . Let be a safe set. Let be the maximum entropy distribution defined on and satisfying . Let be the maximum entropy distribution defined on and satisfying the projected frequencies . Then is marginalised to .
The theorem tells us that if we want to obtain the maximum entropy distribution marginalised to and if the set is safe, then we can remove the items outside . This is useful since finding maximum entropy using Iterative Fitting Procedure requires exponential amount of time [7, 12]. Using maximum entropy for estimating the frequencies of itemsets has been shown to be an effective method in practice [21]. In addition, if we estimate the frequencies of several boolean formulae using maximum entropy distribution marginalised to safe sets, then the frequencies are consistent. By this we mean that the frequencies are all evaluated from the same distribution, namely .
4 Constructing a Safe Set
Assume that we are given a function that depends only on a set , not necessarily safe. In this section we consider a problem of finding a safe set such that for a given . Since there are usually several safe sets that include , for example, the set of all attributes is always a safe set, we want to find a safe set having the minimal number of attributes. In this section we will describe an algorithm for finding such a safe set. We will also show that this particular safe set is unique.
The idea behind the algorithm is to augment until the safeness condition is satisfied. However, the order in which we add the items into matters. Thus we need to order the items. To do this we need to define a few concepts: A neighbourhood of an item of radius is the set of the items reachable from by a graph path of length at most , that is,
| (2) |
In addition, we define a restricted neighbourhood which is similar to except that now we require that only the last element of the path in Eq. 2 can belong to . Note that and that the equality holds for sufficiently large .
The rank of an item with respect of , denoted by , is a vector of length such that is the number of elements in to whom the shortest path from has the length , that is,
We can compare ranks using the bibliographic order. In other words, if we let and , then if and only if there is an integer such that and for all .
We are now ready to describe our search algorithm. The idea is to search the items that violate the assumption in Theorem 3.1. If there are several candidates, then items having the maximal rank are selected. Due to efficiency reasons, we do not look for violations by calculating . Instead, we check whether . This is sufficient because
This is true because and is antimonotonic. The process is described in full detail in Algorithm 1.
We will refer to the safe set Algorithm 1 produces as . We will now show that is the smallest possible, that is,
The following theorem shows that in Algorithm 1 we add only necessary items into during each iteration.
Theorem 4.1
Corollary 1
A safe set containing containing the minimal number of items is unique. Also, this set is contained in each safe set containing .
Corollary 2
Algorithm 1 produces the optimal safe set.
Example 4
Let us continue Example 3. Assume that our initial set is . We note that . Therefore, is not a safe set. The ranks are and (the trailing zeros are removed). It follows that the rank of is larger than the rank of and therefore is added into during Algorithm 1. The resulting set is the minimal safe set containing .
5 Frequencies of Boolean Formulae.
A boolean formula maps a binary vector to a binary value. Given a family of itemsets and frequencies for we define a frequency interval, denoted by , to be
that is, a set of possible frequencies coming from the distribution satisfying given frequencies. For example, if the formula is of form , then we are approximating the frequency of a possibly unknown itemset.
Note that this set is truly an interval and its boundaries can be found using the optimisation problem given in Eq. 1. It has been shown that finding the boundaries can be reduced to a linear programming [11, 19, 3]. However, the problem is exponential in and therefore it is crucial to reduce the dimension. Let us assume that the boolean formula depends only on the variables coming from some set, say . We can now use Algorithm 1 to find a safe set including and thus to reduce the dimension.
Example 5
Let us continue Example 3. We assign the following frequencies to the itemsets: where , , , and the frequencies of the rest itemsets in are equal to . We consider the formula . In this case depends only on . If we project directly to , then the frequency is equal to .
The minimal safe set containing is . Since it follows that is equivalent to . This implies that the frequency of must be equal to .
There exists many problems similar to ours: A well-studied problem is called PSAT in which we are given a CNF-formula and probabilities for each clause asking whether there is a distribution satisfying these probabilities. This problem is NP-complete [9]. A reduction technique for the minimisation problem where the constraints and the query are allowed to be conditional is given in [14]. However, this technique will not work in our case since we are working only with unconditional queries. A general problem where we are allowed to have first-order logic conditional sentences as the constraints/queries is studied in [15]. This problem is shown to be NP-complete. Though these problems are of more general form they can be emulated with itemsets [4]. However, we should note that in the general case this construction does not result an antimonotonic family.
There are many alternative ways of approximating boolean queries based on statistics: For example, the use of wavelets has been investigated in [17]. Query estimation using histograms was studied in [18] (though this approach does not work for binary data). We can also consider assigning some probability model to data such as Chow-Liu tree model or mixture model (see e.g. [22, 21, 6]). Finally, if is an itemset and we know all the proper subsets of and is safe, then to estimate the frequency of we can use inclusion-exclusion formulae given in [5].
6 Safe Sets and Junction Trees
Theorem 3.1 suggests that there is a connection between safe sets and Markov Random Fields (see e.g. [13] for more information on MRF). In this section we will describe how the minimal safe sets can be obtained from junction trees. We will demonstrate through a counter-example that this connection cannot be used directly. We will also show that we can use junction trees to reformulate the optimisation problem and possibly reduce the computational burden.
6.1 Safe Sets and Separators
Let us assume that the dependency graph obtained from a family of itemsets is triangulated, that is, the graph does not contain chordless circuits of size or larger. In this case we say that is triangulated. For simplicity, we assume that the dependency graph is connected. We need some concepts from Markov Random Field theory (see e.g. [13]): The clique graph is a graph having cliques of as vertices and two vertices are connected if the corresponding cliques share a mutual item. Note that this graph is connected. A spanning tree of the clique graph is called a junction tree if it has a running intersection property. By this we mean that if two cliques contain the same item, then each clique along the path in the junction tree also contains the same item. An edge between two cliques is called a separator, and we associate with each separator the set of items mutual to both cliques.
We also make some further assumptions concerning the family : Let be the set of items of some clique of the dependency graph. We assume that every proper subset of is in . If satisfies this property for each clique, then we say that is clique-safe. We do not need to have because there is no node having an entire clique as a frontier.
Let us now investigate how safe sets and junction trees are connected. First, fix some junction tree, say , obtained from . Assume that we are given a set of items, not necessarily safe. For each item we select some clique such that (same clique can be associated with several items). Let and consider the path in from to . We call the separators along such paths inner separators. The other separators are called outer separators. We always choose cliques such that the number of inner separators is the smallest possible. This does not necessarily make the choice of the cliques unique, but the set of inner separators is always unique. We also define an inner clique to be a clique incident to some inner separator. We refer to the other cliques as outer cliques.
Example 6
Let us assume that we have items, namely . The dependency graph, its clique graph, and the possible junction trees are given in Figure 2.
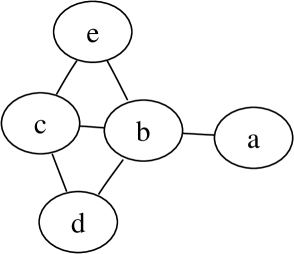
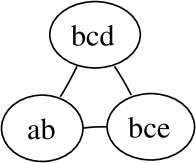
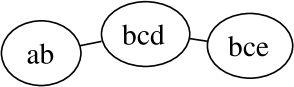
Let . Then the inner separator in the upper junction tree is the left edge. In the lower junction tree both edges are inner separators.
The following three theorems describe the relation between the safe sets containing and the inner separators.
Theorem 6.1
Let be an antimonotonic, triangulated and clique-safe family of itemsets. Let be a junction tree. Let be a set containing and all the items from the inner separators of . Then is a safe set.
The following corollary follows from Corollary 1.
Corollary 3
Let be an antimonotonic, triangulated and clique-safe family of itemsets. Let be a junction tree. The minimal safe set containing may contain (in addition to the set ) only items from the inner separators of .
Theorem 6.2
Let be an antimonotonic, triangulated and clique-safe family of itemsets. There exists a junction tree such that the minimal safe set is precisely the set and the items from the inner separators of .
Theorem 6.2 raises the following question: Is there a tree, not depending on , such that the minimal safe set is precisely the set and the items from the inner separators. Unfortunately, this is not the case as the following example shows.
6.2 Reformulation of the Optimisation Problem Using Junction Trees
We have seen that a optimisation problem can be reduced to a problem having variables, where is a safe set. However, it may be the case that is very large. For example, imagine that the dependency graph is a single path and we are interested in finding the frequency for . Then the safe set contains the entire path. In this section we will try to reduce the computational burden even further.
The main benefit of MRF is that we are able to represent the distribution as a fraction of certain distributions. We can use this factorisation to encode the constraints. A small drawback is that we may not be able to express easily the distribution defined on , the set of which the query depends. This happens when is not contained in any clique. This can be remedied by adding edges to the dependency graph.
Let us make the previous discussion more rigorous. Let be a query function and let be the set of attributes of which depends. Let be the minimal safe set containing . Project the items outside and let be the connectivity graph obtained from . We add some additional edges to . First, we make the set fully connected. Second, we triangulate the graph. Let be a junction tree of the resulting graph.
Since is fully connected, there is a clique such that . For each clique in we define to be a distribution defined on . Similarly, for each separator we define to be a distribution defined on . Denote by the collection of separators of a clique .
| (3) |
The following theorem states that the above formulation is correct:
Theorem 6.3
The problem in Eq. 3 solves correctly the optimisation problem.
Note that we can remove all by combining the constraining equations. Thus we have replaced the original optimisation problem having variables with a problem having variables. The number of cliques in is bounded by , the number of attributes in the safe set. To see this select any leaf clique . This clique must contain a variable that is not contained in any other clique because otherwise is contained in its parent clique. We remove and repeat this procedure. Since there are only attributes, there can be only cliques. Let be the size of the maximal clique. Then the number of variables is bounded by . If is small, then solving the problem is much easier than the original formulation.
Example 8
Assume that we have a family of itemsets whose dependency graph is a path and that we want to evaluate the boundaries for a formula . We cannot neglect any variable inside the path, hence we have a linear program having variables.
By adding the edge to we obtain a cycle. To triangulate the graph we add the edges for . The junction tree in consists of cliques of the form , where . The reformulation of the linear program gives us a program containing only variables.
7 Restricted Safe Sets
Given a set Algorithm 1 constructs the minimal safe set . However, the set may still be too large. In this section we will study a scenario where we require that the set should have items, at maximum. Even if such a safe set may not exist we will try to construct such that the solution of the original minimisation problem described in Eq. 1 does not alter. As a solution we will describe a heuristic algorithm that uses the information available from the frequencies.
First, let us note that in the definition of a safe set we require that we can extend the distribution for any frequencies. In other words, we assume that the frequencies are the worst possible. This is also seen in Algorithm 1 since the algorithm does not use any information available from the frequencies.
Let us now consider how we can use the frequencies. Assume that we are given a family of itemsets and frequencies for . Let be some (not necessarily a safe) set. Let be some item violating the safeness condition. Assume that each path from to has an edge having the following property: Let , , and be the frequencies of the itemsets , , and , respectively. We assume that and that the itemset is not contained in any larger itemset in . We denote the set of such edges by .
Let be the set of items reachable from by paths not using the edges in . Note that the set has the same property than . We argue that we can remove the set . This is true since if we are given a distribution defined on , then we can extend this distribution, for example, by setting , where is the maximum entropy distribution defined on . Note that if we remove the edges , then Algorithm 1 will not include .
Let us now consider how we can use this situation in practice. Assume that we are given a function which assign to each edge a non-negative weight. This weight represents the correlation of the edge and should be if the independence assumption holds. Assume that we are given an item violating the safeness condition but we cannot afford adding into . Define to be the subgraph containing , the frontier and all the intermediate nodes along the paths from to . We consider finding a set of edges that would cut from its frontier and have the minimal cost . This is a well-known min-cut problem and it can be solved efficiently (see e.g. [20]). We can now use this in our algorithm in the following way: We build the minimal safe set containing the set . For each added item we construct a cut with a minimal cost. If the safe set is larger than a constant , we select from the cuts the one having the smallest weight. During this selection we neglect the items that were added before the constraint was exceeded. We remove the edges and the corresponding itemsets and restart the construction. The algorithm is given in full detail in Algorithm 2.
Example 9
We continue Example 5. As a weight function for the edges we use the mutual information. This gives us and . The rest of the weights are . Let . We set the upper bound for the size of the safe set to be . The minimal safe set is . The min cuts are and . The corresponding weights are and . Thus by cutting the edges we obtain the set . The frequency interval for the formula is which is the same as in Example 5.
8 Empirical Tests
We performed empirical tests to assess the practical relevance of the restricted safe sets, comparing it to the (possibly) unsafe trivial projection. We mined itemset families from two data sets, and estimated boolean queries using both the safe projection and the trivial projection. The first data set, which we call Paleo111Paleo was constructed from NOW public release 030717 available from [8]., describes fossil findings: the attributes correspond to genera of mammals, the transactions to excavation sites. The Paleo data is sparse, and the genera and sites exhibit strong correlations. The second data set, which we call Mushroom, was obtained from the FIMI repository222http://fimi.cs.helsinki.fi. The data is relatively dense.
First we used the Apriori [2] algorithm to retrieve some families of itemsets. A problem with Apriori was that the obtained itemsets were concentrated on the attributes having high frequency. A random query conducted on such a family will be safe with high probability — such a query is trivial to solve. More interesting families would the ones having almost all variables interacting with each other, that is, their dependency graphs have only a small number of isolated nodes. Hence we modified APriori: Let be the set containing all items and for each let be the frequency of . Let be the smallest frequency and define . Let be an itemset and let be its frequency. Define . We modify Apriori such that the itemset is in the output if and only if the ratio is larger than given threshold . Note that this family is antimonotonic and so Apriori can be used. By this modification we are trying to give sparse items a fair chance and in our tests the relative frequencies did produce more scattered families.
For each family of itemsets we evaluated random boolean queries. We varied the size of the queries between and . At first, such queries seem too simple but our initial experiments showed that these queries do result large safe sets. A few examples are given in Figure 3. In most of the queries the trivial projection is safe but there are also very large safe sets. Needless to say that we are forced to use restricted safe sets.
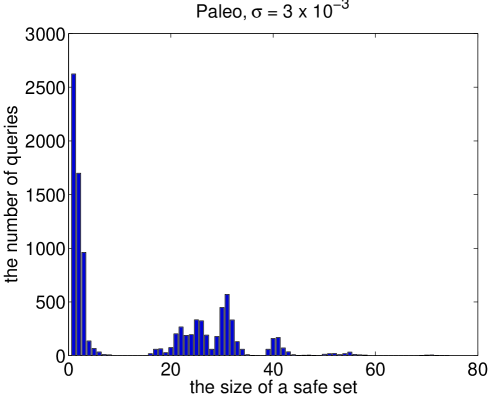
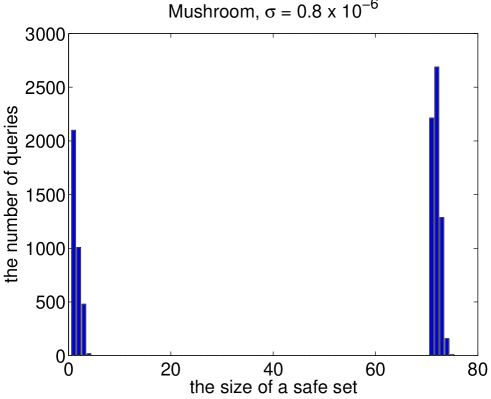
Given a query we calculated two intervals and where contains the attributes of and is the restricted safe set obtained from using Algorithm 2. In other words, is obtained by using the trivial projection and is obtained by projecting to the restricted safe set. As parameters for Algorithm 2 we set the upper bound and the weight function to be the mutual information.
We divided queries into two classes. A class Trivial contained the queries in which the trivial projection and the restricted safe set were equal. The rest of the queries were labelled as Complex. We also defined a class All that contained all the queries.
As a measure of goodness for a frequency interval we considered the difference between the upper and the lower bound. Clearly , so if we define a ratio , then it is always guaranteed that . Note that the ratio for the queries in Trivial is always .
The ratios were divided into appropriate bins. The results obtained from Paleo data are shown in the contingency table given in Tables 1 and 2 and the results for Mushroom data are given in Tables 3 and 4.
| Class | |||||||
|---|---|---|---|---|---|---|---|
| Complex | |||||||
| Trivial | |||||||
| Class | |||||
|---|---|---|---|---|---|
| Complex | |||||
| All | |||||
| Class | |||||
|---|---|---|---|---|---|
| Complex | |||||
| Trivial | |||||
| Class | |||
|---|---|---|---|
| Complex | |||
| All | |||
By examining Tables 1 and 2 we conclude the following: If we conduct a random query of form , then in of the cases the frequency intervals are equal . However, if we limit ourselves to the cases where the projections differ (the class Complex), then the frequency interval is equal only in about of the cases. In addition, the probability of being equal to increases as the threshold grows.
The same observations apply to the results for Mushroom data (Tables 3 and 4): In of the cases the frequency intervals are equal , but if we consider only the cases where projections differ, then the percentage drops to . The percentages are slightly smaller than those obtained from Paleo data and also there are relatively many queries whose ratios are very small.
The computational burden of a trivial query is equivalent for both trivial projection and restricted safe set. Hence, we examine complex queries in which there is an actual difference in the computational burden. The results suggest that in abt. of the complex queries the restricted safe sets produced tighter interval.
9 Conclusions
We started our study by considering the following problem: Given a family of itemsets, frequencies for , and a boolean formula find the bounds of the frequency of the formula. This can be solved by linear programming but the problem is that the program has an exponential number of variables. This can be remedied by neglecting the variables not occurring in the boolean formula and thus reducing the dimension. The downside is that the solution may change.
In the paper we defined a concept of safeness: Given an antimonotonic family of itemsets a set of attributes is safe if the projection to does not change the solution of a query regardless of the query function and the given frequencies for . We characterised this concept by using graph theory. We also provided an efficient algorithm for finding the minimal safe set containing some given set.
We should point out that while our examples and experiments were focused on conjunctive queries, our theorems work with a query function of any shape
If the family of itemsets satisfies certain requirements, that is, it is triangulated and clique-safe, then we can obtain safe sets from junction trees. We also show that the factorisation obtained from a junction tree can be used to reduce the computational burden of the optimisation problem.
In addition, we provided a heuristic algorithm for finding restricted safe sets. The algorithm tries to construct a set of items such that the optimisation problem does not change for some given itemset frequencies.
We ask ourselves: In practice, should we use the safe sets rather than the trivial projections? The advantage is that the (restricted) safe sets always produce outcome at least as good as the trivial approach. The downside is the additional computational burden. Our tests indicate that if a user makes a random query then in abt. of the cases the bounds are equal in both approaches. However, this comparison is unfair because there is a large number of queries where the projection sets are equal. To get the better picture we divide the queries into two classes Trivial and Complex, the first containing the queries such that the projections sets are equal, and the second containing the remaining queries. In the first class there is no improvement in the outcome but there is no additional computational burden (checking that the set is safe is cheap comparing to the linear programming). If a query was in Complex, then in of the cases projecting on restricted safe sets did produce more tight bounds.
Acknowledgements.
The author wishes to thank Heikki Mannila and Jouni Seppänen for their helpful comments.References
- [1] Rakesh Agrawal, Tomasz Imielinski, and Arun N. Swami. Mining association rules between sets of items in large databases. In Peter Buneman and Sushil Jajodia, editors, Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, pages 207–216, Washington, D.C., 26–28 1993.
- [2] Rakesh Agrawal, Heikki Mannila, Ramakrishnan Srikant, Hannu Toivonen, and Aino Inkeri Verkamo. Fast discovery of association rules. In U.M. Fayyad, G. Piatetsky-Shapiro, P. Smyth, and R. Uthurusamy, editors, Advances in Knowledge Discovery and Data Mining, pages 307–328. AAAI Press/The MIT Press, 1996.
- [3] Artur Bykowski, Jouni K. Seppänen, and Jaakko Hollmén. Model-independent bounding of the supports of Boolean formulae in binary data. In Pier Luca Lanzi and Rosa Meo, editors, Database Support for Data Mining Applications: Discovering Knowledge with Inductive Queries, LNCS 2682, pages 234–249. Springer Verlag, 2004.
- [4] Toon Calders. Computational complexity of itemset frequency satisfiability. In Proceedings of the 23nd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database System, 2004.
- [5] Toon Calders and Bart Goethals. Mining all non-derivable frequent itemsets. In Proceedings of the 6th European Conference on Principles and Practice of Knowledge Discovery in Databases, 2002.
- [6] C. K. Chow and C. N. Liu. Approximating discrete probability distributions with dependence trees. IEEE Transactions on Information Theory, 14(3):462–467, May 1968.
- [7] J. Darroch and D. Ratchli. Generalized iterative scaling for log-linear models. The Annals of Mathematical Statistics, 43(5):1470–1480, 1972.
- [8] Mikael Forselius. Neogene of the old world database of fossil mammals (NOW). University of Helsinki, http://www.helsinki.fi/science/now/, 2005.
- [9] George Georgakopoulos, Dimitris Kavvadias, and Christos H. Papadimitriou. Probabilistic satisfiability. Journal of Complexity, 4(1):1–11, March 1988.
- [10] Bart Goethals and Mohammed Javeed Zaki, editors. FIMI ’03, Frequent Itemset Mining Implementations, Proceedings of the ICDM 2003 Workshop on Frequent Itemset Mining Implementations, 19 December 2003, Melbourne, Florida, USA, volume 90 of CEUR Workshop Proceedings, 2003.
- [11] Theodore Hailperin. Best possible inequalities for the probability of a logical function of events. The American Mathematical Monthly, 72(4):343–359, Apr. 1965.
- [12] Radim Jiroušek and Stanislav Přeušil. On the effective implementation of the iterative proportional fitting procedure. Computational Statistics and Data Analysis, 19:177–189, 1995.
- [13] Michael I. Jordan, editor. Learning in graphical models. MIT Press, 1999.
- [14] Thomas Lukasiewicz. Efficient global probabilistic deduction from taxonomic and probabilistic knowledge-bases over conjunctive events. In Proceedings of the sixth international conference on Information and knowledge management, pages 75–82, 1997.
- [15] Thomas Lukasiewicz. Probabilistic logic programming with conditional constraints. ACM Transactions on Computational Logic (TOCL), 2(3):289–339, July 2001.
- [16] Heikki Mannila and Hannu Toivonen. Multiple uses of frequent sets and condensed representations (extended abstract). In Knowledge Discovery and Data Mining, pages 189–194, 1996.
- [17] Yossi Matias, Jeffrey Scott Vitter, and Min Wang. Wavelet-based histograms for selectivity estimation. In Proceedings of ACM SIGMOD International Conference on Management of Data, pages 448–459, 1998.
- [18] M. Muralikrishna and David DeWitt. Equi-depth histograms for estimating selectivity factors for multi-dimensional queries. In Proceedings of ACM SIGMOD International Conference on Management of Data, pages 28–36, 1988.
- [19] Nils Nilsson. Probabilistic logic. Artificial Intelligence, 28(1):71–87, 1986.
- [20] Christos Papadimitriou and Kenneth Steiglitz. Combinatorial Optimization Algorithms and Complexity. Dover, 2nd edition, 1998.
- [21] Dmitry Pavlov, Heikki Mannila, and Padhraic Smyth. Beyond independence: Probabilistic models for query approximation on binary transaction data. IEEE Transactions on Knowledge and Data Engineering, 15(6):1409–1421, 2003.
- [22] Dmitry Pavlov and Padhraic Smyth. Probabilistic query models for transaction data. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining, pages 164–173, 2001.
Appendix A Appendix
This section contains the proofs for the theorems presented in the paper.
A.1 Proof of Theorem 3.1
Let be any consistent frequencies for . Let . To prove the theorem we will show that any distribution defined on items and satisfying the frequencies can be extended to a distribution defined on the set and satisfying the frequencies .
Let . Partition into connected blocks such that if and only if there is a path from to such that . Note that the items coming from the same have the same frontier. Therefore, is well-defined. We denote by .
Let be the maximum entropy distribution defined on the items and satisfying . Note that there is no chord containing elements from and from at the same time. This implies that we can write as
Let be any distribution defined on and satisfying the frequencies . Note that , and hence we can extend to the set by defining
To complete the proof we will need to prove that satisfies the frequencies . Select any itemset . There are two possible cases: Either , which implies that and since satisfies it follows that also satisfies .
The other case is that has elements outside . Note that can have elements in only one , say, . This in turn implies that cannot have elements in , that is, . Note that . Since satisfies , satisfies . This completes the theorem.
A.2 Proof of Theorem 3.2
Assume that we are given a family of itemsets and a set such that there exists such that . Select to be some subset of the frontier such that and each proper subset of is contained in . We can also assume that paths from to are of length . This is done by setting the intermediate attributes lying on the paths to be equivalent with . We can also set the rest of the attributes to be equivalent with . Therefore, we can redefine , the underlying set of attributes to consist only of and , and to be
Let be the frequencies for the itemset family such that
| (4) |
where is a constant (to be determined later).
Define to be the number of elements in . Let be the number of ones in the random bit vector . Let us now consider the following three distributions defined on :
Note that all three distributions satisfy the first condition in Eq. 4. Note also that depends only on the number of ones in . We will slightly abuse the notation and denote , where is a random vector having ones.
Assume that we have extended to satisfying . We can assume that depends only on the number of ones in and the value of . Define , where is a random vector having ones. Note that
If we select any attribute , then
If we now consider the conditions given in Eq. 4 and require that and also require that is the largest possible, then we get the following three optimisation problems:
| (5) |
If we can show that the statement
is false, then by setting in Eq. 4 we obtain such frequencies that at least one of the distributions cannot be extended to . We will prove our claim by assuming otherwise and showing that the assumption leads to a contradiction.
Note that . This implies that the maximal solution has the unique form
| (6) |
Define series . Note that is a feasible solution for Problem P2 in Eq. 5. Moreover, since we assume that , it follows that produces the optimal solution . Therefore, . This implies that and have the forms
| (7) |
| (8) |
Assume now that is odd. The conditions of Problems P1 and P3 imply that
By applying Eqs. 6– 8 to this equation we obtain, depending on , either the identity
or
Both of these identities are false since the series having the term is always larger. This proves our claim for the cases where is odd.
A.3 Proof of Theorem 3.5
Denote by the entropy of a distribution . We know that . Assume now that is a distribution satisfying the frequencies . Let us extend as we did in the proof of Theorem 3.1:
The entropy of this distribution is of the form , where
is a constant not depending on . This characterisation is valid because . If we let , it follows that
If we now let , it follows that and this implies that . Thus . The distribution maximising entropy is unique, thus .
A.4 Proof of Theorem 4.1
Assume that there is such that . Let be as it is defined in Algorithm 1. Let be the shortest path from to and define to be the first item on belonging to . There are two possible cases: Either which implies that , or is blocked by some other element in . If , then the safeness condition is violated. Therefore, there exists such that .
We will prove that outranks , that is, . It is easy to see that it is sufficient to prove that . In order to do this note that . Therefore, because of the antimonotonic property of , there is an edge from to each . This implies that there is a path from to such that , that is, the length of is smaller or equal than the length of . Also note, that since lies on , there exists a path from to such that . This implies that .
Also, note that , where is the search radius defined in Algorithm 1. This implies that is discovered during the search phase, that is, is one of the violating nodes.
To complete the proof we need to show that is a neighbour of . Since is a neighbour of , there is such that there is an edge between and . This implies that . Since there is an edge between and , it follows that is neighbour of .
A.5 Proof of Theorem 6.1
Let be some item belonging to some inner clique but not belonging in any inner separator. The clique is unique and the only reachable items of from are the inner separators incident to . Since is a clique, it follows from the clique-safeness assumption that the frontier of is included in .
Let now be any item that is not included in any inner clique. There exists a unique inner clique such that all the paths from to go through this clique. This implies that the frontier of is again the inner separators incident to .
A.6 Proof of Theorem 6.2
We will prove that if we have an item coming from some inner separator and not included in the minimal safe set, then we can alter the junction tree such that the item is no longer included in the inner separators. For the sake of clarity, we illustrate an example of the modification process in Figure 4.
Let be the dependency graph and the current junction tree. Let be the minimal safe set containing and let be an item coming from some inner separator. Let us consider paths (in ) from to its frontier. For the sake of clarity, we prove only the case where the paths from to are of length . The proof for the general case is similar.
Let be the collection of inner separators containing . Let be the collection of (inner) cliques incident to the inner separators included in . The pair defines a subtree of . Let be the set of inner separators incident to some clique in but not included in . Note that each item coming from the inner separators included in must be included in because otherwise we have violated the assumption that the paths from to its frontier are of length .
The frontier of consists of the items of the inner separators in and of possibly some items from the set . By the assumption the frontier is in and thus it is fully connected. It follows that there is a clique containing the frontier. If , a clique from closest to also contains the frontier. Hence we can assume .
Select a separator . Let be the clique incident to . We modify the tree by cutting the edge and reattaching to . The procedure is performed to each separator in . The obtained tree satisfies the running intersection property since contains the items coming from each inner separators included in . If the frontier contained any items included in , then contains these items. It is easy to see that each clique in , except for the clique , becomes outer. Therefore, is no longer included in any inner separator.
A.7 Proof of Theorem 6.3
Let be the optimal distribution. Then by marginalising we can obtain , and which produce the same solution for the reduced problem.
To prove the other direction let , and be the optimal distributions for the reduced problem. Since the running intersection property holds, we can define the joint distribution by . It is straightforward to see that satisfies the frequencies. This proves the statement.