Salsa Fresca: Angular Embeddings and Pre-Training
for ML Attacks on Learning With Errors
Abstract
Learning with Errors (LWE) is a hard math problem underlying recently standardized post-quantum cryptography (PQC) systems for key exchange and digital signatures (Chen et al., 2022). Prior work (Wenger et al., 2022; Li et al., 2023a, b) proposed new machine learning (ML)-based attacks on LWE problems with small, sparse secrets, but these attacks require millions of LWE samples to train on and take days to recover secrets. We propose three key methods—better preprocessing, angular embeddings and model pre-training—to improve these attacks, speeding up preprocessing by and improving model sample efficiency by . We demonstrate for the first time that pre-training improves and reduces the cost of ML attacks on LWE. Our architecture improvements enable scaling to larger-dimension LWE problems: this work is the first instance of ML attacks recovering sparse binary secrets in dimension , the smallest dimension used in practice for homomorphic encryption applications of LWE where sparse binary secrets are proposed (Lauter et al., 2011).
1 Introduction
Lattice-based cryptography was recently standardized by the US National Institute of Standards and Technology (NIST) in the 5-year post-quantum cryptography (PQC) competition (Chen et al., 2022). Lattice-based schemes are believed to be resistant to attacks by both classical and quantum computers. Given their importance for the future of information security, verifying the security of these schemes is critical, especially when special parameter choices are made such as secrets which are binary or ternary, and sparse. Both the NIST standardized schemes and homomorphic encryption (HE) rely on the hardness of the “Learning with Errors” (Regev, 2005, LWE) problem. NIST schemes standardize small secrets (binomial), and the HE standard includes binary and ternary secrets (Albrecht, 2017), with sparse versions used in practice.
The LWE problem is defined as follows: in dimension , the secret is a vector of length with integer entries modulo . Let be a uniformly random matrix with rows, and an error vector sampled from a narrow Gaussian (see Table 2 for notation summary). The goal is to find given and , where
| (1) |
The hardness of this problem depends on the parameter choices: , , and the secret and error distributions.
Many HE implementations use sparse, small secrets to improve efficiency and functionality, where all but entries of are zero (so is the Hamming weight of ). The non-zero elements have a limited range of values: for binary secrets, and for ternary secrets. Sparse binary or ternary secrets allow for fast computations, since they replace the -dimensional scalar product by sums. However, binary and ternary secrets might be less secure.
| highest | LWE () matrices needed | preprocessing time (hrs/CPU/matrix) | training time (hrs) | total time (hrs) | ||
| 1955 | ||||||
| 1302 | ||||||
| 977 |
Most attacks on LWE rely on lattice reduction techniques, such as LLL or BKZ (Lenstra et al., 1982; Schnorr, 1987; Chen & Nguyen, 2011), which recover by finding short vectors in a lattice constructed from and (Ajtai, 1996; Chen et al., 2020). BKZ attacks scale poorly to large dimension and small moduli (Albrecht et al., 2015).
ML-based attacks on LWE were first proposed in Wenger et al. (2022); Li et al. (2023a, b), inspired by viewing LWE as a linear regression problem on a discrete torus. These attacks train small transformer models (Vaswani et al., 2017) to extract a secret from eavesdropped LWE samples (, ), using lattice-reduction for preprocessing. Although Li et al. (2023b) solves medium-to-hard small sparse LWE instances, for example, dimension , the approach is bottlenecked by preprocessing and larger dimensions used in HE schemes, such as .
In this work, we introduce several improvements to Li et al.’s ML attack, enabling secret recovery for harder LWE problems in less time. Our main contributions are:
- •
-
•
An encoder-only transformer architecture, coupled with an angular embedding for model inputs. This reduces the model’s logical and computational complexity and halves the input sequence length, significantly improving model performance (see §4).
-
•
The first use of pre-training for LWE to improve sample efficiency for ML attacks, further reducing preprocessing cost by (see §5).
Overall, these improvements in both preprocessing and modeling allow us to recover secrets for harder instances of LWE, i.e. higher dimension and lower modulus in less time and with fewer computing resources. A summary of our main results can be found in Table 1.
| Symbol | Description |
| LWE matrix/vector pair, with . | |
| An LWE vector/integer pair, one row of . | |
| Modulus of the LWE problem. | |
| The (unknown) true secret. | |
| Number of nonzero bits in secret. | |
| Error vector, drawn from distribution | |
| Standard deviation of the . | |
| Problem dimension (the dimension of and ) | |
| The total number of LWE samples available | |
| LWE samples in each subset during reduction | |
| Candidate secret, not necessarily correct | |
| Matrix computed to reduce the coordinates of . | |
| Preprocessing reduction factor; the ratio |
2 Context and Attack Overview
Wenger et al. (2022); Li et al. (2023a, b) demonstrated the feasibility of ML-based attacks on LWE. Li et al.’s attack has 2 parts: 1) data preprocessing using lattice reduction techniques; 2) model training interleaved with regular calls to a secret recovery routine, which uses the trained model as a cryptographic distinguisher to guess the secret. In this section we provide an overview of ML-based attacks in prior work to put our contributions in context.
2.1 Attack Part 1: LWE data preprocessing
The attack assumes that initial LWE samples () (rows of ()) with the same secret are available. Sampling of the initial samples without replacement, matrices and associated -dimensional vectors are constructed.
The preprocessing step strives to reduce the norm of the rows of by applying a carefully selected integer linear operator . Because is linear with integer entries, the transformed pairs are also LWE pairs with the same secret, albeit larger error. In practice, is found by performing lattice reduction on the matrix , and finding linear operators such that the norms of are small. This achieves a reduction of the norms of the entries of , but also increases the error in the calculation of , making secret recovery more difficult. Although ML models can learn from noisy data, too much noise will make the distribution of uniform on and inhibit learning. The parameter controls the trade-off between norm reduction and error increase. Reduction strength is measured by , where denotes the mean of the standard deviations of the rows of and .
Li et al. (2023a) use BKZ (Schnorr, 1987) for lattice reduction. Li et al. (2023b) improves the reduction time by via a modified definition of the matrix and by interleaving BKZ2.0 (Chen & Nguyen, 2011) and polish (Charton et al., 2024) (see Appendix C).
This preprocessing step produces many () pairs that can be used to train models. Individual rows of and associated elements of , denoted as reduced LWE samples () with some abuse of notation, are used for model training. Both the subsampling of samples from the original LWE samples and the reduction step are done repeatedly and in parallel to produce 4 million reduced LWE samples, providing the data needed to train the model.
2.2 Attack Part 2: Model training and secret recovery
With million reduced LWE samples (), a transformer is trained to predict from . For simplicity, and without loss of generality, we will say the transformer learns to predict from . Li et al. train encoder-decoder transformers (Vaswani et al., 2017) with shared layers (Dehghani et al., 2019). Inputs and outputs consist of integers that are split into two tokens per integer by representing them in a large base with and binning the lower digit to keep the vocabulary small as increases. Training is supervised and minimizes a cross-entropy loss.
The key intuition behind ML-attacks on LWE is that to predict from , the model must have learned the secret . We extract the secret from the model by comparing model predictions for two vectors and which only differ on one entry. We expect the difference between the model’s predictions for and to be small (of the same magnitude as the error) if the corresponding bit of is zero, and large if it is non-zero. Repeating the process on all positions yields a guess for the secret.
For ternary secrets, Li et al. (2023b) introduce a two-bit distinguisher, which leverages the fact that if secret bits and have the same value, adding a constant to inputs at both these indices should induce similar predictions. Thus, if is the basis vector and is a random integer, we expect model predictions for and to be the same if . After using this pairwise method to determine whether the non-zero secret bits have the same value, Li et al. classify them into two groups. With only two ways to assign and to the groups of non-zero secret bits, this produces two secret guesses.
Wenger et al. (2022) tests a secret guess by computing the residuals over the initial LWE sample. If is correct, the standard deviation of the residuals will be close to . Otherwise, it will be close to the standard deviation of a uniform distribution over : .
For a given dimension, modulus and secret Hamming weight, the performance of ML attacks vary from one secret to the next. Li et al. (2023b) observes that the difficulty of recovering a given secret from a set of reduced LWE samples () depends on the distribution of the scalar products . If a large proportion of these products remain in the interval (assuming centering) even without a modulo operation, the problem is similar enough to linear regression that the ML attack will usually recover the secret. Li et al. introduce the statistic NoMod: the proportion of scalar products in the training set having this property. They demonstrate that large NoMod strongly correlates with likely secret recoveries for the ML-attack.
2.3 Improving upon prior work
Li et al. (2023b) recover binary and ternary secrets, for and LWE problems with Hamming weight , in about days, using 4,000 CPUs and one GPU (see their Table 1). Most of the computing resources are needed in the preprocessing stage: reducing one matrix takes about days, and matrices must be reduced to build a training set of million examples. This suggests two directions for improving the attack performance. First, by introducing fast alternatives to BKZ2.0, we could shorten the time required to reduce one matrix. Second, we could minimize the number of samples needed to train the models, which would reduce the number of CPUs needed for the preprocessing stage.
Another crucial goal is scaling to larger dimensions . The smallest standardized dimension for LWE in the HE Standard (Albrecht et al., 2021) is . At present, ML attacks are limited by their preprocessing time and the length of the input sequences they use. The attention mechanisms used in transformers is quadratic in the length of the sequence, and Li et al. (2023b) encodes dimensional inputs with tokens. More efficient encoding would cut down on transformer processing speed and memory consumption quadratically.
2.4 Parameters and settings in our work
Before presenting our innovations and results, we briefly discuss the LWE settings considered in our work. LWE problems are parameterized by the modulus , the secret dimension , the secret distribution (sparse binary/ternary) and the hamming weight of the secret (the number of non-zero entries). Table 3 specifies the LWE problem settings we attack. Proposals for LWE parameter settings in homomorphic encryption suggest using with sparse secrets (as low as ), albeit with smaller than we consider (Curtis & Player, 2019; Albrecht, 2017). Thus, it is important to show that ML attacks can work in practice for dimension if we hope to attack sparse secrets in real-world settings.
| 512 | 41 | |
| 768 | 35 | |
| 1024 | 50 |
3 Data Preprocessing
Prior work primarily used BKZ2.0 in the preprocessing/lattice reduction step. While effective, BKZ2.0 is slow for large values of . We found that for matrices it could not finish a single loop in days on an Intel Xeon Gold 6230 CPU, eventually timing out.
Our preprocessing pipeline. Our improved preprocessing incorporates a new reduction algorithm Flatter111https://github.com/keeganryan/flatter, which promises similar reduction guarantees to LLL with much-reduced compute time (Ryan & Heninger, 2023), allowing us to preprocess LWE matrices in dimension up to . We interleave Flatter and BKZ2.0 and switch between them after loops of one results in . Following Li et al. (2023b), we run polish after each Flatter and BKZ2.0 loop concludes. We initialize our Flatter and BKZ2.0 runs with block size 18 and , which provided the best empirical trade-off between time and reduction quality (see Appendix C for additional details), and make reduction parameters stricter as reduction progresses—up to block size 22 for BKZ2.0 and for Flatter.
| CPU hours matrix | ||||
| (Li et al., 2023b) | Ours | |||
| 512 | 41 | 0.41 | 13.1 | |
| 768 | 35 | 0.71 | N/A | 12.4 |
| 1024 | 50 | 0.70 | N/A | 26.0 |
| 1 | 3 | 5 | 7 | 10 | 13 | |
| 0.685 | 0.688 | 0.688 | 0.694 | 0.698 | 0.706 | |
| / | 0.341 | 0.170 | 0.118 | 0.106 | 0.075 | 0.068 |
Preprocessing performance.
Table 4 records the reduction achieved for each pair and the time required, compared with Li et al. (2023b). Recall that measures the reduction in the standard deviation of relative to its original uniform random distribution; lower is better. Reduction in standard deviation strongly correlates with reduction in vector norm, but for consistency with Li et al. (2023b) we use standard deviation.
We record reduction time as CPU hours matrix, the amount of time it takes our algorithm to reduce one LWE matrix using one CPU. We parallelize our reduction across many CPUs. For , our methods improve reduction time by a factor of , and scale easily to problems. Overall, we find that Flatter improves the time (and consequently resources required) for preprocessing, but does not improve the overall reduction quality.
Error penalty . We run all reduction experiments with penalty . Table 5 demonstrates the tradeoff between reduction quality and reduction error, as measured by , for , problems. Empirically, we find that is sufficiently low to recover secrets from LWE problems with .
Experimental setup. In practice, we do not preprocess a different set of pairs for each secret recovery experiment because preprocessing is so expensive. Instead, we use a single set of preprocessed rows combined with an arbitrary secret to produce different pairs for training. We first generate a secret and calculate for the original pairs. Then, we apply the many different produced by preprocessing to and to produce many pairs with reduced norm. This technique enables analyzing attack performance across many dimensions (varying , model parameters, etc.) in a reasonable amount of time. Preprocessing a new dataset for each experiment would make evaluation at scale near-impossible.
4 Model Architecture
Previous ML attacks on LWE use a encoder-decoder transformer (Vaswani et al., 2017). A bidirectional encoder processes the input and an auto-regressive decoder generates the output. Integers in both input and output sequences were tokenized as two digits in a large base smaller than . We propose a simpler and faster encoder-only model and introduce an angular embedding for integers modulo .
4.1 Encoder-only model
Encoder-decoder models were originally introduced for machine translation, because their outputs can be longer than their inputs. However, they are complex and slow at inference, because the decoder must run once for each output token. For LWE, outputs (one integer) are always shorter than inputs (a vector of integers). Li et al. (2023b) observe that an encoder-only model, a 4-layer bidirectional transformer based on DeBERTa (He et al., 2020), achieves comparable performance with their encoder-decoder model.
Here, we experiment with simpler encoder-only models without DeBERTa’s disentangled attention mechanism with to layers. Their outputs are max-pooled across the sequence dimension, and decoded by a linear layer for each output digit (Figure 1). We minimize a cross-entropy loss. This simpler architecture improves training speed by .

4.2 Angular embedding
Most transformers process sequences of tokens from a fixed vocabulary, encoded in by a learned embedding. Typical vocabulary sizes vary from K in Llama2 (Touvron et al., 2023), to K in Jurassic-1 (Lieber et al., 2021). The larger the vocabulary, the more data needed to learn the embeddings. LWE inputs and outputs are integers from . For and : encoding integers with one token creates a too-large vocabulary. To avoid this, Li et al. (2023a, b) encode integers with two tokens by representing them in base with small and binning the low digit so the overall vocabulary has K tokens.
This approach has two limitations. First, input sequences are tokens long, which slows training as grows, because transformers’ attention mechanism scales quadratically in sequence length. Second, all vocabulary tokens are learned independently and the inductive bias of number continuity is lost. Prior work on modular arithmetic (Power et al., 2022; Liu et al., 2022) shows that trained integer embeddings for these problems move towards a circle, e.g. with the embedding of close to and .
To address these shortcomings, we introduce an angular embedding which strives to better represent the problem’s modular structure in embedding space, while encoding integers with only one token. An integer is first converted to an angle by the transformation , and then to the point . All input integers (in ) are therefore represented as points on the 2-dimensional unit circle, which is then embedded as an ellipse in , via a learned linear projection . Model outputs, obtained by max-pooling the encoder output sequence, are decoded as points in by another linear projection . The training loss is the distance between the model prediction and the point representing on the unit circle.
4.3 Experiments
Here, we compare our new architecture with previous work, and assess its performance on larger instances of LWE ( and ). All comparisons with prior work are performed on LWE instances with and for binary and ternary secrets, using the same pre-processing techniques as Li et al. (2023b).
Encoder-only models vs prior designs. In Table 6, we compare our encoder-only model (with and without the angular embedding) with the encoder-decoder and the DeBERTa models from Li et al. (2023b). The encoder-only and encoder-decoder models are trained for 72 hours on one 32GB V100 GPU. The DeBERTa model, which requires more computing resources, is trained for 72 hours on four 32GB V100 GPUs. Our encoder-only model, using the same vocabulary embedding as prior work, processes samples faster than the encoder-decoder architecture and is faster than the DeBERTa architecture. With the angular embedding, training is faster, because input sequences are half as long, which accelerates attention calculations. Our models also outperform prior designs in terms of secret recovery: previous models recover binary secrets with Hamming weight and ternary secrets with Hamming weight . Encoder-only models with an angular embedding recover binary and ternary secrets with Hamming weights up to . §D.1 in the Appendix provides detailed results.
| Architecture | Samples/ Sec | Largest Binary | Largest Ternary |
| Encoder-Decoder | |||
| Encoder (DeBERTa) | |||
| Encoder (Vocab.) | |||
| Encoder (Angular) |
Impact of model size. Table 7 compares encoder-only models of different sizes (using angular embeddings). All models are run for up to hours on one 32GB V100 GPU on . We observe that larger models yield little benefit in terms of secret recovery rate, and small models are significantly faster (both in terms of training and recovery). Additional results are in Appendix D.2. We use 4 layers with embedding dimension 512 for later experiments because it recovers the most secrets () the fastest.
| Layers | Emb. Dim. | Params | Samples/S | Recovered | Hours |
| 2 | 128 | M | 2560 | 23% | 18.9 |
| 4 | 256 | M | 1114 | 22% | 19.6 |
| 4 | 512 | M | 700 | 25% | 26.2 |
| 6 | 512 | M | 465 | 25% | 28.1 |
| 8 | 512 | M | 356 | 24% | 30.3 |
Embedding ablation. Next, we compare our new angular embedding scheme to the vocabulary embeddings. The better embedding should recover both more secrets and more difficult ones (as measured by Hamming weight and NoMod; see §2.2 for a description of NoMod). To measure this, we run attacks on identical datasets, with unique secrets per . One set of models uses the angular embedding, while the other uses the vocabulary embedding from Li et al. (2023b).

To check if angular embedding outperforms vocabulary embedding, we measure the attacked secrets’ NoMod. We expect the better embedding to recover secrets with lower NoMod and higher Hamming weights (e.g. harder secrets). As Figure 2 and Table 6 demonstrate, this is indeed the case. Angular embeddings recover secrets with NoMod vs. for vocabulary embedding (see Table 29 in Appendix F for raw numbers). Furthermore, angular embedding models recover more secrets than those with vocabulary embeddings ( vs. ) and succeed on higher secrets ( vs. ). We conclude that an angular embedding is superior to a vocabulary embedding because it recovers harder secrets.
Scaling . Finally, we use our proposed architecture improvements to scale . The long input sequence length in prior work made scaling attacks to difficult, due to both memory footprint and slow model processing speed. In contrast, our more efficient model and angular embedding scheme (§4.1,§4.2) enable us to attack and secrets. Table 8 shows that we can recover up to for both and settings, with hours of training on a single 32GB V100 GPU. In §5.1 we show recovery of for using a more sample-efficient training strategy. We run identical experiments using prior work’s encoder-decoder model, but fail to recover any secrets with in the same computational budget. Our proposed model improvements lead to the first successful ML attack that scales to real-world values of : proposed real-world use cases for LWE-based cryptosystems recommend using dimensions and (Avanzi et al., 2021; Albrecht et al., 2021; Curtis & Player, 2019), although they also recommend smaller and harder secret distributions than we currently consider.
| Samples/ Sec | Hours to recovery for different values | |||||
| , , | , , | , | - | |||
| , , , , , , | , , , | - | ||||
5 Training Methods
The final limitation we address is the million preprocessed LWE samples for model training. Recall that each training sample is a row of a reduced LWE matrix , so producing million training samples requires reducing LWE matrices. Even with the preprocessing improvements highlighted in §3, for , this means preprocessing between and matrices at the cost of hours per CPU per matrix. 222 We bound the number of reduced matrices needed because some rows of reduction matrices are , discarded after preprocessing. Between and nonzero rows of are kept, so we must reduce between and matrices. To further reduce total attack time, we propose training with fewer samples and pre-training models.
5.1 Training with Fewer Samples
We first consider simply reducing training dataset size and seeing if the attack succeeds. Li et al. always use M training examples. To test if this many is needed for secret recovery, we subsample datasets of size = [K, K, M, M] from the original M examples preprocessed via the techniques in §3. We train models to attack LWE problems with binary secrets and . Each attack is given 3 days on a single V100 32GB GPU.
| Training samples | Total # | Best | Mean Hours |
| 300K | 1 | 32 | |
| 1M | 18 | 44 | |
| 3M | 21 | 44 | |
| 4M | 22 | 44 |
Table 9 shows that our attack still succeeds, even when as few as K samples are used. We recover approximately the same number of secrets with M samples as with M, and both settings achieve the same best recovery. Using M rather than M training samples reduces our preprocessing time by 75%. We run similar experiments for and , and find that we can recover up to secrets for with only M training samples. Those results are in Tables 18, 18, 20 and 20 in Section E.1.
5.2 Model Pre-Training
To further improve sample efficiency, we introduce the first use of pre-training in LWE. Pre-training models has improved sample efficiency in language (Devlin et al., 2019; Brown et al., 2020) and vision (Kolesnikov et al., 2020); we hypothesize similar improvements are likely for LWE. Thus, we frame secret recovery as a downstream task and pre-train a transformer to improve sample efficiency when recovering new secrets, further reducing preprocessing costs.
Formally, an attacker would like to pre-train a model parameterized by on samples such that the pre-trained parameters are a better-than-random initialization for recovering a secret from new samples . Although pre-training to get may require significant compute, can initialize models for many different secret recoveries, amortizing the initial cost.
Pre-training setup. First, we generate and reduce a new dataset of million samples with which we pre-train a model. The -initialized model will then train on the samples used in §5.1, leading to a fair comparison between a randomly-initialized model and a -initialized model. Pre-training on the true attack dataset is unfair and unrealistic, since we assume the attacker will train before acquiring the real LWE samples they wish to attack.
The pre-trained weights should be a good initialization for recovering many different secrets. Thus, we use many different secrets with the 4M rows . In typical recovery, we have 4M rows and 4M targets . In the pre-training setting, however, we generate 150 different secrets so that each has 150 different possible targets. So the model can distinguish targets, we introduce 150 special vocabulary tokens , one for each secret . We concatenate the appropriate token to row paired with . Thus, from 4M rows , we produce 600M triplets . The model learns to predict from a row and an integer token .333 is embedded using a learned vocabulary.
We hypothesize that including many different pairs produced from different secrets will induce strong generalization capabilities. When we train the -initialized model on new data with an unseen secret , we indicate that there is a new secret by adding a new token to the model vocabulary that serves the same function as above. We randomly initialize the new token embedding, but initialize the remaining model parameters with those of . Then we train and extract secrets as in §2.2.

Experiments. For pre-training data, we use M rows reduced to , generated from a new set of LWE () samples. We use binary and ternary secrets with Hamming weights from to , with different secrets for each weight, for a total of secrets and M triplets for pre-training. We pre-train an encoder-only transformer with angular embeddings for 3 days on 8x 32GB V100 GPUs with a global batch size of 1200. The model sees M total examples, less than one epoch. We do not run the distinguisher step during pre-training because we are not interested in recovering these secrets.
We use the weights as the initialization and repeat §5.1’s experiments. We use three different checkpoints from pre-training as to evaluate the effect of different pre-training amounts: K, K and K pre-training steps.
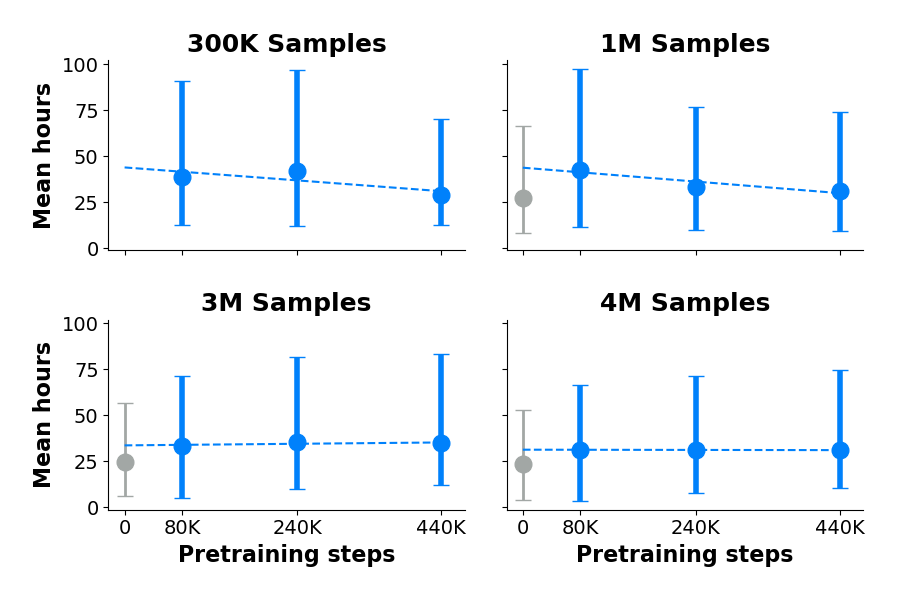
Results. Figure 3 demonstrates that pre-training improves sample efficiency during secret recovery. We record the minimum number of samples required to recover each secret for each checkpoint. Then we average these minimums among secrets recovered by all checkpoints (including the randomly initialized model) to fairly compare them. We find that 80K steps improves sample efficiency, dropping from 1.7M to 409K mean samples required. However, further pre-training does not further improve sample efficiency.
Recall that using fewer samples harms recovery speed (see Table 9). Figure 4 shows trends for recovery speed for pre-trained and randomly initialized models for different numbers of training samples. We find that any pre-training slows down recovery, but further pre-training might minimize this slowdown. Appendix E has complete results.
6 Related Work
Using machine learning for cryptanalysis. An increasing number of cryptanalytic attacks in recent years have incorporated ML models. Often, models are used to strengthen existing cryptanalysis approaches, such as side channel or differential analysis (Chen & Yu, 2021). Of particular interest is recent work that successfully used ML algorithms to aid side-channel analysis of Kyber, a NIST-standardized PQC method (Dubrova et al., 2022). Other ML-based cryptanalysis schemes train models on plaintext/ciphertext pairs or similar data, enabling direct recovery of cryptographic secrets. Such approaches have been studied against a variety of cryptosystems, including hash functions (Goncharov, 2019), block ciphers (Gohr, 2019; Benamira et al., 2021; Chen & Yu, 2021; Alani, 2012; So, 2020; Kimura et al., 2021; Baek & Kim, 2020), and substitution ciphers (Ahmadzadeh et al., 2021; Srivastava & Bhatia, 2018; Aldarrab & May, 2020; Greydanus, 2017). The three ML-based LWE attacks upon which this work builds, Salsa (Wenger et al., 2022), Picante (Li et al., 2023a), and Verde (Li et al., 2023b), also take this approach.
AI for Math. The use of neural networks for arithmetic was first considered by Siu & Roychowdhury (1992), and recurrent networks by Zaremba et al. (2015), Kalchbrenner et al. (2015) and Kaiser & Sutskever (2015). Transformers have been used to solve problems in symbolic and numerical mathematics, integration(Lample & Charton, 2020), linear algebra (Charton, 2022), arithmetic (Charton, 2024) and theorem proving (Polu & Sutskever, 2020). With the advent of large language models, recent research has focused on training or fine-tuning language models on math word problems: problems of mathematics expressed in natural language (Meng & Rumshisky, 2019; Griffith & Kalita, 2021; Lee et al., 2023). The limitations of these approaches were discussed by Nogueira et al. (2021) and Dziri et al. (2023). Modular arithmetic was first considered by Power et al. (2022) and Wenger et al. (2022). Its difficulty was discussed by Palamas (2017) and Gromov (2023).
7 Discussion & Future Work
Our contributions are spread across multiple fronts: faster preprocessing ( fewer CPU hours), simpler architecture ( more samples/sec), better token embeddings ( faster training) and the first use of pre-training for LWE ( fewer samples). These lead to fewer CPU hours spent preprocessing and more samples/sec for for LWE problems, and lead to the first ML attack on LWE for and . Although we have made substantial progress in pushing the boundaries of machine learning-based attacks on LWE, much future work remains in both building on this pre-training work and improving models’ capacity to learn modular arithmetic.
Pre-training. Pre-training improves sample efficiency after 80K steps; however, further improvements to pre-training should be explored. First, our experiments used just one set of M combined with multiple secrets. To encourage generalization to new , pre-training data should include different original s. Second, our transformer only has M parameters, and may be too small to benefit from pre-training. Third, pre-training data does not have to come from a sniffed set of samples. Rather than use expensive preprocessed data, we could simulate reduction and generate random rows synthetically that look like .
ML for modular arithmetic. NoMod experiments consistently show that more training data which does not wrap around the modulus leads to more successful secret recovery (see Figure 2 and Li et al. (2023b)). This explains why a smaller modulus is harder for ML approaches to attack, and indicates that models are not yet learning modular arithmetic (Wenger et al., 2022). Further progress on models learning modular arithmetic problems will likely help to achieve secret recovery for smaller and larger .
Acknowledgements
We thank Mark Tygert for his always insightful comments and Mohamed Malhou for running experiments.
8 Impact Statement
The main ethical concern related to this work is the possibility of our attack compromising currently-deployed PQC system. However, at present, our proposed attack does not threaten current standardized systems. If our attack scales to higher and lower settings, then its impact is significant, as it would necessitate changing PQC encryption standards. For reproducability of these results, our code will be open sourced after publication and is available to reviewers upon request.
References
- Ahmadzadeh et al. (2021) Ahmadzadeh, E., Kim, H., Jeong, O., and Moon, I. A Novel Dynamic Attack on Classical Ciphers Using an Attention-Based LSTM Encoder-Decoder Model. IEEE Access, 2021.
- Ajtai (1996) Ajtai, M. Generating hard instances of lattice problems. In Proc. of the ACM symposium on Theory of Computing, 1996.
- Alani (2012) Alani, M. M. Neuro-cryptanalysis of DES and triple-DES. In Proc. of NeurIPS, 2012.
- Albrecht et al. (2021) Albrecht, M., Chase, M., Chen, H., et al. Homomorphic encryption standard. In Protecting Privacy through Homomorphic Encryption, pp. 31–62. 2021. https://eprint.iacr.org/2019/939.
- Albrecht (2017) Albrecht, M. R. On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL. In Proc. of EUROCRYPT, 2017. ISBN 978-3-319-56614-6.
- Albrecht et al. (2015) Albrecht, M. R., Player, R., and Scott, S. On the concrete hardness of learning with errors. Journal of Mathematical Cryptology, 9(3):169–203, 2015.
- Albrecht et al. (2017) Albrecht, M. R., Göpfert, F., Virdia, F., and Wunderer, T. Revisiting the expected cost of solving usvp and applications to lwe. In Proc. of ASIACRYPT, 2017.
- Aldarrab & May (2020) Aldarrab, N. and May, J. Can sequence-to-sequence models crack substitution ciphers? arXiv preprint arXiv:2012.15229, 2020.
- Avanzi et al. (2021) Avanzi, R., Bos, J., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V., Schanck, J. M., Schwabe, P., Seiler, G., and Stehlé, D. CRYSTALS-Kyber (version 3.02) – Submission to round 3 of the NIST post-quantum project. 2021. Available at https://pq-crystals.org/.
- Baek & Kim (2020) Baek, S. and Kim, K. Recent advances of neural attacks against block ciphers. In Proc. of SCIS, 2020.
- Benamira et al. (2021) Benamira, A., Gerault, D., Peyrin, T., and Tan, Q. Q. A deeper look at machine learning-based cryptanalysis. In Proc. of Annual International Conference on the Theory and Applications of Cryptographic Techniques, 2021.
- Brown et al. (2020) Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., et al. Language models are few-shot learners. Proc. of NeurIPS, 2020.
- Charton (2022) Charton, F. Linear algebra with transformers. Transactions in Machine Learning Research, 2022.
- Charton (2024) Charton, F. Can transformers learn the greatest common divisor? arXiv:2308.15594, 2024.
- Charton et al. (2024) Charton, F., Lauter, K., Li, C., and Tygert, M. An efficient algorithm for integer lattice reduction. SIAM Journal on Matrix Analysis and Applications, 45(1), 2024.
- Chen et al. (2020) Chen, H., Chua, L., Lauter, K., and Song, Y. On the Concrete Security of LWE with Small Secret. Cryptology ePrint Archive, Paper 2020/539, 2020. URL https://eprint.iacr.org/2020/539.
- Chen et al. (2022) Chen, L., Moody, D., Liu, Y.-K., et al. PQC Standardization Process: Announcing Four Candidates to be Standardized, Plus Fourth Round Candidates. US Department of Commerce, NIST, 2022. https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4.
- Chen & Nguyen (2011) Chen, Y. and Nguyen, P. Q. BKZ 2.0: Better Lattice Security Estimates. In Proc. of ASIACRYPT, 2011.
- Chen & Yu (2021) Chen, Y. and Yu, H. Bridging Machine Learning and Cryptanalysis via EDLCT. Cryptology ePrint Archive, 2021. https://eprint.iacr.org/2021/705.
- Curtis & Player (2019) Curtis, B. R. and Player, R. On the feasibility and impact of standardising sparse-secret LWE parameter sets for homomorphic encryption. In Proc. of the ACM Workshop on Encrypted Computing & Applied Homomorphic Cryptography, 2019.
- Dehghani et al. (2019) Dehghani, M., Gouws, S., Vinyals, O., Uszkoreit, J., and Kaiser, Ł. Universal transformers. In Proc. of ICLR, 2019.
- Devlin et al. (2019) Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics, 2019. URL https://aclanthology.org/N19-1423.
- Dubrova et al. (2022) Dubrova, E., Ngo, K., and Gärtner, J. Breaking a fifth-order masked implementation of crystals-kyber by copy-paste. Cryptology ePrint Archive, 2022. https://eprint.iacr.org/2022/1713.
- Dziri et al. (2023) Dziri, N., Lu, X., Sclar, M., Li, X. L., et al. Faith and fate: Limits of transformers on compositionality. arXiv preprint arXiv:2305.18654, 2023.
- Gohr (2019) Gohr, A. Improving attacks on round-reduced speck32/64 using deep learning. In Proc. of Annual International Cryptology Conference, 2019.
- Goncharov (2019) Goncharov, S. V. Using fuzzy bits and neural networks to partially invert few rounds of some cryptographic hash functions. arXiv preprint arXiv:1901.02438, 2019.
- Greydanus (2017) Greydanus, S. Learning the enigma with recurrent neural networks. arXiv preprint arXiv:1708.07576, 2017.
- Griffith & Kalita (2021) Griffith, K. and Kalita, J. Solving Arithmetic Word Problems with Transformers and Preprocessing of Problem Text. arXiv preprint arXiv:2106.00893, 2021.
- Gromov (2023) Gromov, A. Grokking modular arithmetic. arXiv preprint arXiv:2301.02679, 2023.
- He et al. (2020) He, P., Liu, X., Gao, J., and Chen, W. Deberta: Decoding-enhanced bert with disentangled attention. arXiv preprint arXiv:2006.03654, 2020.
- Kaiser & Sutskever (2015) Kaiser, Ł. and Sutskever, I. Neural GPUs learn algorithms. arXiv preprint arXiv:1511.08228, 2015.
- Kalchbrenner et al. (2015) Kalchbrenner, N., Danihelka, I., and Graves, A. Grid long short-term memory. arXiv preprint arxiv:1507.01526, 2015.
- Kimura et al. (2021) Kimura, H., Emura, K., Isobe, T., Ito, R., Ogawa, K., and Ohigashi, T. Output Prediction Attacks on SPN Block Ciphers using Deep Learning. Cryptology ePrint Archive, 2021. URL https://eprint.iacr.org/2021/401.
- Kolesnikov et al. (2020) Kolesnikov, A., Beyer, L., Zhai, X., Puigcerver, J., Yung, J., Gelly, S., and Houlsby, N. Big transfer (bit): General visual representation learning. In Proc. of ECCV, 2020.
- Lample & Charton (2020) Lample, G. and Charton, F. Deep learning for symbolic mathematics. In Proc. of ICLR, 2020.
- Lauter et al. (2011) Lauter, K., Naehrig, M., and Vaikuntanathan, V. Can homomorphic encryption be practical? Proceedings of the 3rd ACM workshop on Cloud computing security workshop, pp. 113–124, 2011.
- Lee et al. (2023) Lee, N., Sreenivasan, K., Lee, J. D., Lee, K., and Papailiopoulos, D. Teaching arithmetic to small transformers. arXiv preprint arXiv:2307.03381, 2023.
- Lenstra et al. (1982) Lenstra, H., Lenstra, A., and Lovász, L. Factoring polynomials with rational coefficients. Mathematische Annalen, 261:515–534, 1982.
- Li et al. (2023a) Li, C. Y., Sotáková, J., Wenger, E., Malhou, M., Garcelon, E., Charton, F., and Lauter, K. Salsa Picante: A Machine Learning Attack on LWE with Binary Secrets. In Proc. of ACM CCS, 2023a.
- Li et al. (2023b) Li, C. Y., Wenger, E., Allen-Zhu, Z., Charton, F., and Lauter, K. E. SALSA VERDE: a machine learning attack on LWE with sparse small secrets. In Proc. of NeurIPS, 2023b.
- Lieber et al. (2021) Lieber, O., Sharir, O., Lenz, B., and Shoham, Y. Jurassic-1: Technical details and evaluation. White Paper. AI21 Labs, 1:9, 2021.
- Liu et al. (2022) Liu, Z., Kitouni, O., Nolte, N. S., Michaud, E., Tegmark, M., and Williams, M. Towards understanding grokking: An effective theory of representation learning. Proc. of NeurIPS, 2022.
- Meng & Rumshisky (2019) Meng, Y. and Rumshisky, A. Solving math word problems with double-decoder transformer. arXiv preprint arXiv:1908.10924, 2019.
- Micciancio & Voulgaris (2010) Micciancio, D. and Voulgaris, P. Faster exponential time algorithms for the shortest vector problem. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, 2010.
- Nogueira et al. (2021) Nogueira, R., Jiang, Z., and Lin, J. Investigating the limitations of transformers with simple arithmetic tasks. arXiv preprint arXiv:2102.13019, 2021.
- Palamas (2017) Palamas, T. Investigating the ability of neural networks to learn simple modular arithmetic. 2017. https://project-archive.inf.ed.ac.uk/msc/20172390/msc_proj.pdf.
- Polu & Sutskever (2020) Polu, S. and Sutskever, I. Generative language modeling for automated theorem proving. arXiv preprint arXiv:2009.03393, 2020.
- Power et al. (2022) Power, A., Burda, Y., Edwards, H., Babuschkin, I., and Misra, V. Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets. arXiv preprint arXiv:2201.02177, 2022.
- Regev (2005) Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proc. of the ACM Symposium on Theory of Computing, 2005.
- Ryan & Heninger (2023) Ryan, K. and Heninger, N. Fast practical lattice reduction through iterated compression. Cryptology ePrint Archive, 2023. URL https://eprint.iacr.org/2023/237.pdf.
- Schnorr (1987) Schnorr, C.-P. A hierarchy of polynomial time lattice basis reduction algorithms. Theoretical Computer Science, 1987. URL https://www.sciencedirect.com/science/article/pii/0304397587900648.
- Siu & Roychowdhury (1992) Siu, K.-Y. and Roychowdhury, V. Optimal depth neural networks for multiplication and related problems. In Proc. of NeurIPS, 1992.
- So (2020) So, J. Deep learning-based cryptanalysis of lightweight block ciphers. Security and Communication Networks, 2020.
- Srivastava & Bhatia (2018) Srivastava, S. and Bhatia, A. On the Learning Capabilities of Recurrent Neural Networks: A Cryptographic Perspective. In Proc. of ICBK, 2018.
- The FPLLL development team (2023) The FPLLL development team. fplll, a lattice reduction library, Version: 5.4.4. Available at https://github.com/fplll/fplll, 2023.
- Touvron et al. (2023) Touvron, H., Martin, L., Stone, K., Albert, P., Almahairi, A., Babaei, Y., et al. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288, 2023.
- Vaswani et al. (2017) Vaswani, A., Shazeer, N., Parmar, N., et al. Attention is all you need. In Proc. of NeurIPS, 2017.
- Wenger et al. (2022) Wenger, E., Chen, M., Charton, F., and Lauter, K. Salsa: Attacking lattice cryptography with transformers. In Proc. of NeurIPS, 2022.
- Zaremba et al. (2015) Zaremba, W., Mikolov, T., Joulin, A., and Fergus, R. Learning simple algorithms from examples. arXiv preprint arXiv:1511.07275, 2015.
Appendix A Appendix
We provide details, additional experimental results, and analysis ommitted in the main text:
-
1.
Appendix B: Attack parameters
-
2.
Appendix C: Lattice reduction background
-
3.
Appendix D: Additional model results (Section 4)
-
4.
Appendix E: Additional training results (Section 5)
-
5.
Appendix F: Further NoMod analysis
Appendix B Parameters for our attack
For training all models, we use a learning rate of , weight decay of , 3000 warmup steps, and an embedding dimension of 512. We use encoder layers, and attention heads for all encoder-only model experiments, except the architecture ablation in Table 7. We use the following primes: for , for , and for . The rest of the parameters used for the experiments are in Table 10.
| LWE parameters | Preprocessing settings | Model training settings | |||||||||
| Base | Bucket size | Batch size | |||||||||
| 512 | 41 | 18 | 22 | 0.04 | 0.025 | 0.96 | 0.9 | 137438953471 | 134217728 | 256 | |
| 768 | 35 | 18 | 22 | 0.04 | 0.025 | 0.96 | 0.9 | 1893812477 | 378762 | 128 | |
| 1024 | 50 | 18 | 22 | 0.04 | 0.025 | 0.96 | 0.9 | 25325715601611 | 5065143120 | 128 | |
Appendix C Additional background on lattice reduction algorithms
Lattice reduction algorithms reduce the length of lattice vectors, and are a building block in most known attacks on lattice-based cryptosystems. If a short enough vector can be found, it can be used to recover LWE secrets via the dual, decoding, or uSVP attack (Micciancio & Voulgaris, 2010; Albrecht et al., 2017, 2021). The original lattice reduction algorithm, LLL (Lenstra et al., 1982), runs in time polynomial in the dimension of the lattice, but is only guaranteed to find an exponentially bad approximation to the shortest vector. In other words the quality of the reduction is poor. LLL iterates through the ordered basis vectors of a lattice, projecting vectors onto each other pairwise and swapping vectors until a shorter, re-ordered, nearly orthogonal basis is returned.
To improve the quality of the reduction, the BKZ (Schnorr, 1987) algorithm generalizes LLL by projecting basis vectors onto -dimensional subspaces, where is the “blocksize”. (LLL has blocksize .) As approaches , the quality of the reduced basis improves, but the running time is exponential in , so is not practical for large block size. Experiments in (Chen et al., 2020) with running BKZto attack LWE instances found that block size and was infeasible in practice. Both BKZ and LLL are implemented in the fplll library (The FPLLL development team, 2023), along with an improved version of BKZ: BKZ2.0 (Chen & Nguyen, 2011). Charton et al. proposed an alternative lattice reduction algorithm similar to LLL. In practice we use it as a polishing step after each BKZ loop concludes. It “polishes” by iteratively orthogonalizing the vectors, provably decreasing norms with each run.
A newer alternative to LLL is flatter (Ryan & Heninger, 2023), which provides reduction guarantees analogous to LLL but runs faster due to better precision management. flatter runs on sublattices, and leverages clever techniques for reducing numerical precision as the reduction proceeds, enabling it to run much faster than other reduction implementations. Experiments in the original paper show flatter running orders of magnitude faster than other methods on high-dimensional () lattice problems. The implementation of flatter444https://github.com/keeganryan/flatter has a few tunable parameters, notably , which characterizes the strength of the desired reduction in terms of lattice “drop”, a bespoke method developed by (Ryan & Heninger, 2023) that mimics the Lovász condition in traditional LLL (Lenstra et al., 1982). In our runs of flatter, we set initially and decrease it to after the lattice is somewhat reduced, following the adaptive reduction approach of (Li et al., 2023b).
Appendix D Additional Results for §4
D.1 Architecture Comparison
Tables 11, 12, (for binary secrets) and Tables 13, and 14 (for ternary secrets) expand on the results in Table 6 by showing how three different model architectures perform on binary and ternary secrets with different Hamming weights. We see that the encoder-only model architecture with angular embedding improves secret recovery compared to the encoder-decoder model and the encoder-only model with two-token embedding. Notably, the encoder-only model with angular embedding is able to recover secrets up to for both binary and ternary secrets, which is a big improvement compared to previous work.
| Architecture | h | |||||||||
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | |
| Encoder-Decoder | 1/10 | 1/10 | 1/10 | |||||||
| Encoder (Vocabulary) | 0/10 | 0/7 | 2/10 | 0/10 | 0/8 | 0/10 | 1/10 | 0/9 | 0/8 | 0/8 |
| Encoder (Angular) | 2/10 | 0/7 | 3/10 | 2/10 | 1/8 | 1/10 | 2/10 | 1/9 | 1/8 | 2/8 |
| Architecture | h | |||||||||
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | |
| Encoder-Decoder | 10.0 | - | 20.0 | - | - | - | 17.5 | - | - | - |
| Encoder (Vocabulary) | - | - | 19.8 | - | - | - | 22.0 | - | - | - |
| Encoder (Angular) | 33.0 | - | 37.0 | 33.2 | 29.1 | 26.7 | 29.8 | 57.1 | 31.6 | 28.8 |
| Architecture | h | |||||||||
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | |
| Encoder-Decoder | - | 1/10 | - | - | - | - | - | - | - | - |
| Encoder (Vocabulary) | 0/9 | 1/8 | 0/9 | 0/9 | 1/10 | 0/8 | 0/7 | 0/7 | 0/10 | 1/9 |
| Encoder (Angular) | 0/9 | 1/8 | 0/9 | 0/9 | 1/10 | 0/8 | 0/7 | 0/7 | 0/10 | 1/9 |
| Architecture | h | |||||||||
| 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | |
| Encoder-Decoder | - | 27.5 | - | - | - | - | - | - | - | - |
| Encoder (Vocabulary) | - | 24.8 | - | - | 28.2 | - | - | - | - | 34.4 |
| Encoder (Angular) | - | 57.6 | - | - | 47.4 | - | - | - | - | 70.3 |
D.2 Architecture Ablation
Here, we present additional results from the architecture ablation experiments summarized in Table 7. The results in Table 15 and Table 16 show the number of successful recoveries and average time to recovery with varying architectures across different Hamming weights. We see that increasing transformer depth (number of layers) tends to improve recovery but also increases average recovery time. Increasing the embedding dimension from 256 to 512 with 4 layers improves secret recovery. Thus, we choose 4 layers with a hidden dimension of 512 as it recovers the most secrets (25%) the fastest (26.2 mean hours).
| Layers | Emb Dim | h | |||||||||
| 49 | 51 | 53 | 55 | 57 | 59 | 61 | 63 | 65 | 67 | ||
| 2 | 128 | 2/9 | 4/10 | 5/10 | 3/9 | 2/10 | 2/8 | 1/9 | 3/10 | 1/9 | 0/10 |
| 4 | 256 | 2/9 | 4/10 | 5/10 | 3/9 | 2/10 | 2/8 | 1/9 | 2/10 | 1/9 | 0/10 |
| 4 | 512 | 3/9 | 4/10 | 5/10 | 4/9 | 2/10 | 2/8 | 1/9 | 3/10 | 1/9 | 0/10 |
| 6 | 512 | 3/9 | 4/10 | 5/10 | 3/9 | 2/10 | 2/8 | 2/9 | 3/10 | 1/9 | 0/10 |
| 8 | 512 | 3/9 | 4/10 | 5/10 | 4/9 | 2/10 | 2/8 | 1/9 | 2/10 | 1/9 | 0/10 |
| Layers | Emb Dim | h | |||||||||
| 49 | 51 | 53 | 55 | 57 | 59 | 61 | 63 | 65 | 67 | ||
| 2 | 128 | 8.7 | 10.0 | 8.3 | 14.0 | 11.0 | 5.5 | 11.5 | 17.9 | 18.9 | - |
| 4 | 256 | 30.9 | 11.0 | 12.3 | 30.3 | 39.9 | 10.4 | 20.6 | 13.3 | 19.6 | - |
| 4 | 512 | 27.2 | 15.4 | 18.2 | 35.2 | 35.4 | 17.3 | 24.3 | 32.2 | 26.2 | - |
| 6 | 512 | 44.1 | 18.8 | 20.7 | 34.2 | 30.5 | 19.4 | 47.9 | 32.1 | 28.1 | - |
| 8 | 512 | 46.4 | 22.5 | 24.0 | 44.6 | 34.6 | 23.8 | 28.0 | 29.0 | 30.3 | - |
Appendix E Additional Results for §5
E.1 Training with Fewer Samples
Here, we present additional results from scaling to 768 and 1024 (without pre-training) as summarized in Table 8. Tables 18 and 18 show the results for the , case with binary secrets. Similarly, Tables 20 and 20 show the results for the , case with binary secrets.
| # Samples | ||||
| 5 | 7 | 9 | 11 | |
| K | 1 | - | - | - |
| K | 1 | 1 | - | - |
| M | 4 | 3 | 2 | - |
| M | 2 | 3 | 1 | - |
| M | 3 | 3 | 2 | - |
| # Samples | ||||
| 5 | 7 | 9 | 11 | |
| K | 1.4 | - | - | - |
| K | 0.7 | 12.3 | - | - |
| M | 27.9 | 24.5 | 39.2 | - |
| M | 17.8 | 13.0 | 44.2 | - |
| M | 13.5 | 18.5 | 21.8 | - |
| # Samples | ||||||
| 5 | 7 | 9 | 11 | 13 | 15 | |
| K | 3 | - | - | - | - | - |
| K | 6 | 3 | - | - | - | - |
| M | 6 | 4 | 1 | - | 1 | - |
| M | 6 | 4 | 1 | 1 | - | - |
| M | 7 | 5 | 1 | - | - | - |
| # Samples | ||||||
| 5 | 7 | 9 | 11 | 13 | 15 | |
| K | 11.6 | - | - | - | - | - |
| K | 14.8 | 17.7 | - | - | - | - |
| M | 15.7 | 29.2 | 36.1 | - | 47.4 | - |
| M | 14.8 | 14.0 | 29.6 | 39.8 | - | - |
| M | 19.9 | 10.6 | 21.3 | - | - | - |
E.2 Model Pre-Training
In this section, we expand upon the pre-training results summarized in Figures 3 and 4. For each pre-training checkpoint, we measure number of successful recoveries out of 10 trials per and the average time in hours to successful secret recovery for to . We also vary the number of samples from K to M to see which setup is most sample efficient. In all of these experiments, and are fixed, , with binary secrets. The results are presented as follows: no pre-training baseline (Tables 21 and 22), 80K steps pre-training (Tables 23 and 24), 240K steps pre-training (Tables 25 and 26), and 440K steps pre-training (Tables 27 and 28).
Based on these results, we conclude that some pre-training helps to recover secrets with less samples, but more pre-training is not necessarily better. We also see that more pre-training increases the average time to successful secret recovery.
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| K | - | - | 1 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| M | - | - | 3 | 2 | 1 | - | 3 | 1 | 2 | 1 | 1 | 1 | - | - | 2 | - |
| M | 1 | - | 4 | 3 | 1 | - | 2 | 1 | 3 | 1 | 1 | 2 | - | - | 2 | - |
| M | 1 | - | 4 | 3 | 1 | 1 | 3 | 1 | 3 | 1 | 1 | 1 | - | - | 2 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| K | - | - | 30.3 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| M | - | - | 21.1 | 36.9 | 36.3 | - | 27.5 | 21.9 | 23.9 | 16.5 | 50.7 | 52.9 | - | - | 36.8 | - |
| M | 14.4 | - | 21.8 | 27.6 | 41.8 | - | 19.8 | 25.5 | 22.7 | 18.1 | 39.5 | 44.3 | - | - | 37.8 | - |
| M | 17.2 | - | 22.8 | 26.5 | 29.1 | 69.7 | 22.7 | 22.7 | 20.9 | 21.4 | 29.0 | 25.7 | - | - | 40.5 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | 1 | - | 2 | 2 | - | - | 1 | - | 1 | 1 | - | - | - | - | 2 | - |
| M | 1 | - | 3 | 2 | 1 | - | 1 | - | 1 | 1 | 1 | - | - | - | 1 | - |
| M | 1 | - | 3 | 2 | 1 | - | 1 | - | 1 | 1 | 1 | - | - | - | 2 | - |
| M | 1 | - | 3 | 2 | - | - | 1 | - | 1 | 1 | 1 | - | - | - | 1 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | 29.2 | 32.1 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | 57.7 | - | 47.6 | 26.9 | - | - | 31.7 | - | 62.6 | 55.6 | - | - | - | - | 50.9 | - |
| M | 53.4 | - | 37.0 | 25.6 | 61.7 | - | 25.1 | - | 65.9 | 30.0 | 44.8 | - | - | - | 51.4 | - |
| M | 34.4 | - | 41.8 | 25.1 | 57.5 | - | 26.2 | - | 45.1 | 23.6 | 38.4 | - | - | - | 39.7 | - |
| M | 35.1 | - | 30.9 | 33.0 | - | - | 35.2 | - | 36.5 | 21.8 | 26.8 | - | - | - | 32.1 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | - | 1 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | 1 | - | 2 | 2 | - | - | 2 | - | 2 | 1 | - | - | - | - | - | - |
| M | 1 | - | 2 | 2 | 1 | - | 1 | - | 1 | 1 | 1 | - | - | - | 1 | - |
| M | 1 | - | 2 | 2 | - | - | 2 | - | 2 | 1 | 1 | - | - | - | 1 | - |
| M | 1 | - | 2 | 2 | 1 | - | 2 | - | 1 | 1 | 1 | - | - | - | 1 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | - | 21.0 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | 49.3 | - | 30.8 | 23.3 | - | - | 50.5 | - | 64.2 | 37.9 | - | - | - | - | - | - |
| M | 49.4 | - | 29.5 | 23.4 | 50.8 | - | 20.1 | - | 24.8 | 24.2 | 51.9 | - | - | - | 61.9 | - |
| M | 48.9 | - | 38.2 | 19.7 | - | - | 38.5 | - | 50.9 | 20.2 | 57.7 | - | - | - | 47.4 | - |
| M | 42.4 | - | 34.9 | 19.5 | 55.8 | - | 29.0 | - | 24.1 | 18.3 | 54.0 | - | - | - | 52.4 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | - | - | 1 | 2 | - | - | 1 | 1 | 1 | 1 | - | - | - | - | 1 | - |
| M | 1 | - | - | 2 | - | - | 1 | - | 2 | 1 | 1 | - | - | - | 1 | - |
| M | 1 | - | 1 | 2 | - | - | 1 | - | 1 | 1 | 1 | - | - | - | 2 | - |
| M | 1 | - | 1 | 2 | - | - | 2 | - | 1 | 1 | 1 | - | - | - | 2 | - |
| # Samples | ||||||||||||||||
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| K | - | - | 33.3 | 20.0 | - | - | - | - | - | - | - | - | - | - | - | - |
| K | - | - | 39.8 | 12.9 | - | - | 29.0 | 60.5 | 36.2 | 49.1 | - | - | - | - | 59.1 | - |
| M | 56.9 | - | - | 16.6 | - | - | 18.6 | - | 43.6 | 24.9 | 36.4 | - | - | - | 53.4 | - |
| M | 50.9 | - | 32.3 | 12.2 | - | - | 25.2 | - | 22.3 | 18.9 | 42.4 | - | - | - | 60.8 | - |
| M | 58.3 | - | 30.0 | 13.5 | - | - | 34.6 | - | 19.7 | 22.3 | 45.7 | - | - | - | 59.7 | - |
Appendix F Results of NoMod Analysis
As another performance metric for our approach, we measure the NoMod factor for the secrets/datasets we attack. Li et al. computed NoMod as follows: given a training dataset of LWE pairs (, ) represented in the range and known secret , compute . If , we know that the computation of did not cause to “wrap around” modulus . The NoMod factor of a dataset is the percentage of (, ) pairs for which .
Although NoMod is not usable in a real world attack, since it requires a priori knowledge of , it is a useful metric for understanding attack success in a lab environment. Li et al. derived an empirical result stating that attacks should be successful when the NoMod factor of a dataset is . The NoMod analysis indicates that models trained in those experiments were only learning secrets from datasets in which the majority of values do not “wrap around” . If models could be trained to learn modular arithmetic better, this might ease the NoMod condition for success.
One of the main goals of introducing the angular embedding is to introduce some inductive bias into the model training process. Specifically, teaching models that and are close in the embedding space may enable them to better learn the modular arithmetic task at the heart of LWE. Here, we examine the NoMod factor of various datasets to see if the angular embedding does provide such inductive bias. If it did, we would expect that models with angular embeddings would recover secrets from datsets with NoMod . Table 29 lists NoMod percentages and successful secret recoveries for the angular and tokenization schemes described in §4.2.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 57 | 45 | 49 | 52 | 41 | 51 | 46 | 51 | 57 | 60 | 49 |
| 58 | 48 | 48 | 48 | 48 | 38 | 43 | 52 | 52 | 45 | 48 |
| 59 | 43 | 46 | 56 | 50 | 66 | 63 | 35 | 46 | 41 | 40 |
| 60 | 48 | 48 | 52 | 59 | 50 | 58 | 48 | 49 | 51 | 54 |
| 61 | 60 | 49 | 43 | 41 | 56 | 42 | 42 | 41 | 41 | 50 |
| 62 | 45 | 42 | 45 | 54 | 55 | 43 | 61 | 56 | 54 | 42 |
| 63 | 56 | 60 | 55 | 54 | 63 | 47 | 54 | 51 | 45 | 43 |
| 64 | 44 | 46 | 41 | 41 | 41 | 47 | 45 | 43 | 41 | 55 |
| 65 | 45 | 51 | 48 | 60 | 45 | 48 | 41 | 48 | 45 | 50 |
| 66 | 45 | 51 | 39 | 64 | 45 | 47 | 43 | 60 | 48 | 55 |
| 67 | 43 | 47 | 48 | 49 | 40 | 47 | 48 | 51 | 50 | 46 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 5 | 61 | 61 | 52 | 61 | 93 | 68 | 66 | 61 | 56 | 62 |
| 7 | 52 | 61 | 56 | 77 | 52 | 68 | 56 | 67 | 56 | 61 |
| 9 | 52 | 55 | 46 | 49 | 52 | 48 | 56 | 60 | 60 | 70 |
| 11 | 55 | 42 | 44 | 55 | 46 | 46 | 54 | 55 | 60 | 51 |
| 13 | 46 | 45 | 60 | 48 | 43 | 43 | 55 | 48 | 60 | 43 |
| 15 | 41 | 38 | 48 | 43 | 40 | 43 | 45 | 43 | 43 | 59 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 5 | 62 | 66 | 70 | 69 | 81 | 81 | 81 | 53 | 69 | 94 |
| 7 | 62 | 47 | 80 | 80 | 69 | 56 | 57 | 52 | 57 | 69 |
| 9 | 56 | 69 | 52 | 49 | 52 | 53 | 56 | 57 | 46 | 52 |
| 11 | 44 | 52 | 52 | 62 | 61 | 62 | 56 | 56 | 52 | 49 |
| 13 | 51 | 46 | 56 | 40 | 46 | 52 | 44 | 49 | 68 | 53 |
| 15 | 61 | 46 | 40 | 45 | 46 | 41 | 38 | 47 | 48 | 44 |