Scaling Law of Quantum Confinement in Single-Walled Carbon Nanotubes
Abstract
Quantum confinement significantly influences the excited states of sub-10 nm single-walled carbon nanotubes (SWCNTs), crucial for advancements in transistor technology and the development of novel opto-electronic materials such as fluorescent ultrashort nanotubes (FUNs). However, the length dependence of this effect in ultrashort SWCNTs is not yet fully understood in the context of the SWCNT exciton states. Here, we conduct excited state calculations using time-dependent density functional theory (TD-DFT) on geometry-optimized models of ultrashort SWCNTs and FUNs, which consist of ultrashort SWCNTs with defects. Our results reveal a length-dependent scaling law of the exciton energy that can be understood through a geometric, dimensional argument, and which departs from the length scaling of a 1D particle-in-a-box. We find that this scaling law applies to ultrashort (6,5) and (6,6) SWCNTs, as well as models of (6,5) FUNs. In contrast, the defect-induced transition, which is redshifted from the optical gap transition, shows little dependence on the nanotube length, even in the shortest possible SWCNTs. We attribute this relative lack of length dependence to orbital localization around the quantum defect that is installed near the SWCNT edge. Our results illustrate the complex interplay of defects and quantum confinement effects in ultrashort SWCNTs and provide a foundation for further explorations of these nanoscale phenomena.
pacs:
61.48.De,36.40.Cg,73.21.La,73.21.-b,78.67.-n,78.67.ChI Introduction
Ultrashort SWCNTs, particularly those shorter than the exciton diffusion length (< 90 nm [1]) and approaching the sub-10 nm regime, are central components for devices such as carbon nanotube transistors [2, 3, 4, 5, 6, 7, 8, 9], as well as light emission sources for near-IR sensing, imaging, and single-photon based quantum information applications enabled by defect-induced fluorescence[10, 11, 12, 13, 14, 15]. Understanding the length dependence of excited state energies in ultrashort SWCNTs is necessary for interpreting experiments involving electrical transport, photon emission and absorption measurements. In the case of optical experiments, the energies of the exciton states are most relevant as these states are chiefly responsible for the optical properties of SWCNTs[16]. Significant finite-size effects, such as those observed in quantum dots due to quantum confinement, also occur in SWCNTs. Numerous studies have investigated finite-size (i.e. length) effects in SWCNTs, both experimentally[17, 18, 19, 20, 21, 22] and theoretically[23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38]. Despite this, our understanding of such length effects on the optical properties of SWCNTs has been limited to relatively long nanotubes. The quantum confinement effect in sub-10 nm SWCNTs is crucial to explore because the greatest blueshifts should occur in this range due to their inverse length dependence, such as can be seen[22] employing the typical 1D particle-in-a-box picture in which . However, an equation that captures the length dependent energy shift of the exciton transitions in ultrashort SWCNTs, similar to the Brus equation[39] for spherical quantum dots, remains elusive.
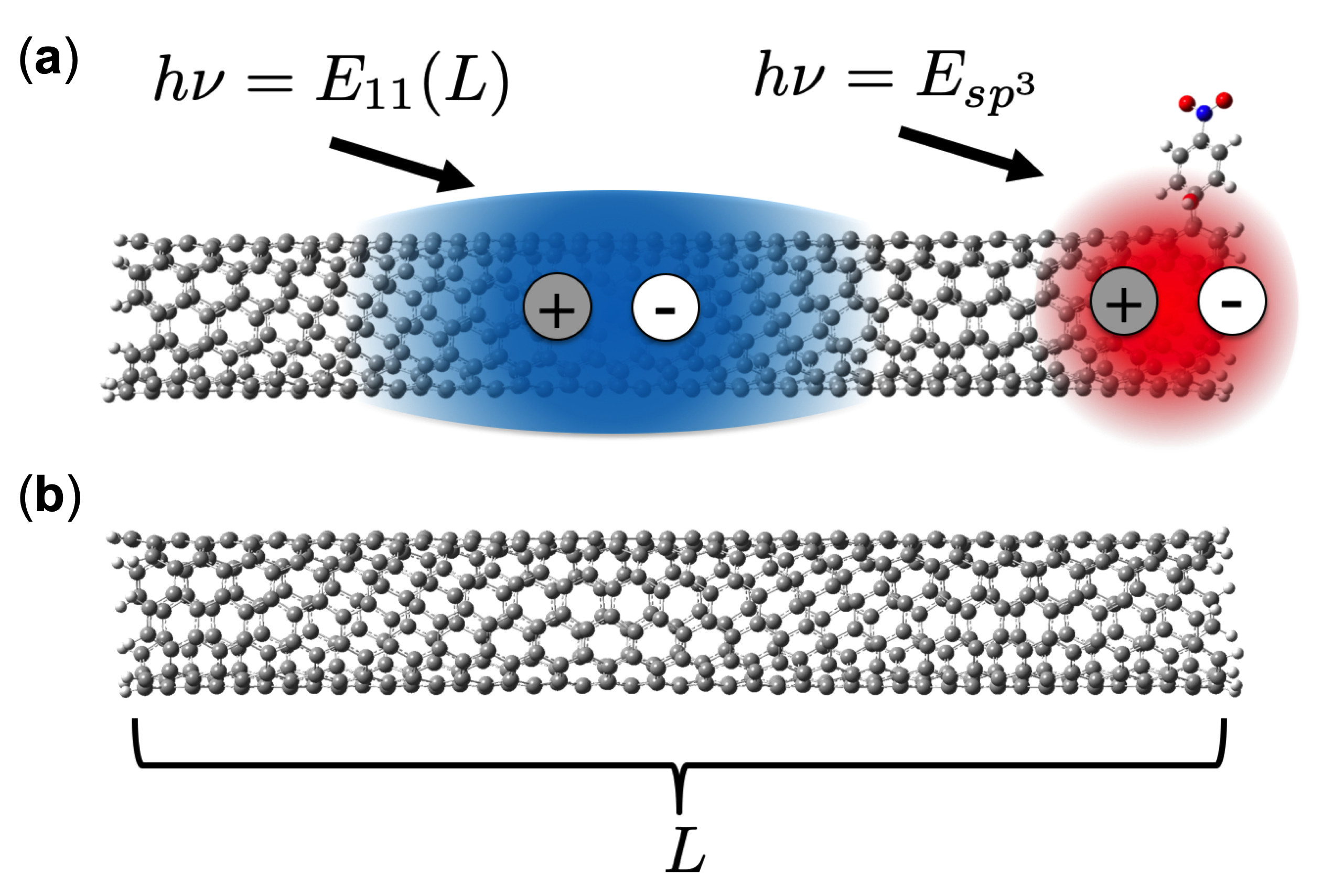
The difficulty arises from the challenge of obtaining and manipulating individualized ultrashort SWCNT samples with precisely controlled lengths to measure resulting blueshifts in the excitonic transitions. Further complications arise as photoluminescence (PL) is typically quenched in ultrashort SWCNTs [40, 12], which restricts their use as near-IR light sources. However, two recent advances in SWCNT chemistry have made it possible to probe the PL of SWCNTs in the ultrashort regime, renewing interest in ultrashort SWCNTs as near-IR emitters. The first advance is the application of SWCNT defect chemistry[10], known to significantly enhance the PL of SWCNTs, to ultrashort SWCNTs to create fluorescent ultrashort nanotubes (FUNs). In FUNs, defects placed near the edges of ultrashort SWCNTs activate the normally quenched PL of excitons, in addition to creating bright defect exciton PL[12]. A simplified model of a FUN is shown in Fig. 1a, which consists of a SWCNT with an defect pair near one edge. The second advance is an improved technique for creating FUNs called defect-induced chemical etching (DICE)[13], which is enabled by -functionalization of SWCNTs. This technique uses hydrogen peroxide to produce clean cuts at the defect sites, leaving the luminescent defects behind at the edges of the thus shortened nanotubes. This method provides a mechanism for molecular tunability of the length distributions of FUNs based on the linear defect density of the initially functionalized SWCNTs, since the expected average lengths of the cut FUNs should be . In principle, the DICE method allows for precise access to fluorescent ultrashort SWCNTs.
Inspired by these developments, we revisit the question of the length dependence of the exciton energy in the context of ultrashort SWCNTs and FUNs. Existing theoretical studies typically investigate the confinement effect by considering the impact of finite lengths on the ground-state electronic structure, usually through either a tight-binding or DFT-based approach [23, 24, 26, 29, 30, 34, 35]. While this provides valuable insight into the electronic structure of ultrashort SWCNTs, what is necessary for studying the confinement energy scaling in these systems is an excited state approach that incorporates electron-hole interactions, as the optical resonances in SWCNTs are excitonic in nature[16].
Time-dependent density functional theory (TD-DFT) offers a promising method for calculating the excited electronic states of molecular SWCNT models across a wide range of lengths, from the smallest definable segments to models that approximate the infinite-length limit. TD-DFT methods using the B3LYP approximation to the exchange-correlation energy have successfully provided insights into low-lying exciton states in SWCNT models with lengths nm[41, 42]. At these lengths the calculated absorption spectra qualitatively reflect the infinite-length limit, and in pristine (6,5) SWCNTs the excited state can be identified as the bright exciton when using the B3LYP approximation. However, previous TD-DFT studies[28, 37, 38] examining confinement effects on absorption spectra in ultrashort SWCNTs did not identify a clear length dependence of the lowest bright exciton energy.
Here, we present TD-DFT calculations of the exciton state in pristine (6,5) SWCNTs. The calculations are performed on molecular models of (6,5) SWCNTs spanning lengths from roughly 0.25–10 nm. An example model is shown in Fig. 1b, depicting a finite-length (6,5) SWCNT of length nm.
Our results show a scaling law for the energy length dependence in ultrashort SWCNTs:
| (1) |
This law differs from the conventional 1D particle-in-a-box picture sometimes applied to understand the effect of quantum confinement on excitons in SWCNTs[22], and contrasts with the confinement effect in spherical quantum dots[39]. To explain this unexpected length dependence, we make a dimensional argument that combines the strong Coulomb interaction between an electron and hole in SWCNTs and the nanotube geometry hosting the excited electron-hole pair.
We show that our scaling law also applies to the bright, low-energy excited states that have been previously seen in ultrashort (6,6) SWCNTs [38]. We also connect the scaling law to models of (6,5) FUNs with edge- defects, where we see both the as well as a redshifted defect-localized transition that we label . The observation of an defect-induced transition redshifted from the mirrors what is observed in experimental probes of the excited states of FUNs via PL [12, 13].
The presence of our scaling law in both semiconducting and metallic chiralities, as well as in SWCNTs with defects, suggests a broad applicability of the dimensional argument to ultrashort SWCNT systems. As demonstrated by Li et. al.[13], the DICE chemistry provides the ability to synthesize FUNs with chemically controlled lengths, which constitute a promising class of SWCNT quantum dot molecules. These materials will be useful for a variety of applications ranging from bioimaging to quantum information science, as well as for the measurement of length-dependent properties of ultrashort SWCNTs, e.g. the length-dependence of the energy seen in our calculations here.
II Methods
All TD-DFT calculations in this paper were performed with Gaussian 16 computational chemical software[43]. The molecular models used in this study were generated in a manner inspired by pioneering applications of the Clar theory of polycyclic hydrocarbons to SWCNTs[44, 45, 46, 47]. The Clar model approach is advantageous for studying molecular models of SWCNTs compared to using unit cells[46], particularly for chiral nanotubes such as (6,5) SWCNTs, where the Clar cell is roughly a quarter of a nanometer long compared to the unit cell that is about 4 nm long. The length of any of our finite SWCNT models can be expressed as (in cu) or (in nm), where is essentially dimensionless as it is an integer used to control the number of screw-axis operations used to generate the models, and is a chirality-specific natural length scale of the models. For the (6,5) and (6,6) chiralities studied in this work, nm and nm.
For the molecular models of (6,5) FUNs, the defect installed near the edge of the SWCNTs can be denoted as (4-nitrobenzene, OH, ortho-90)[38]. All results presented on FUNs in this paper are referring to these models with a single defect pair near one edge of an ultrashort (6,5) SWCNT, which serve as idealized examples of FUNs. Additional details of the methods used in this study are provided in the Supplemental Materials, including details of our computations, coordinates for example models, a schematic depiction of the screw axis operation used to generate the SWCNT models, as well as the defect orientation in the FUN models (Fig. LABEL:supp-model_schematic).
III Results and Discussion
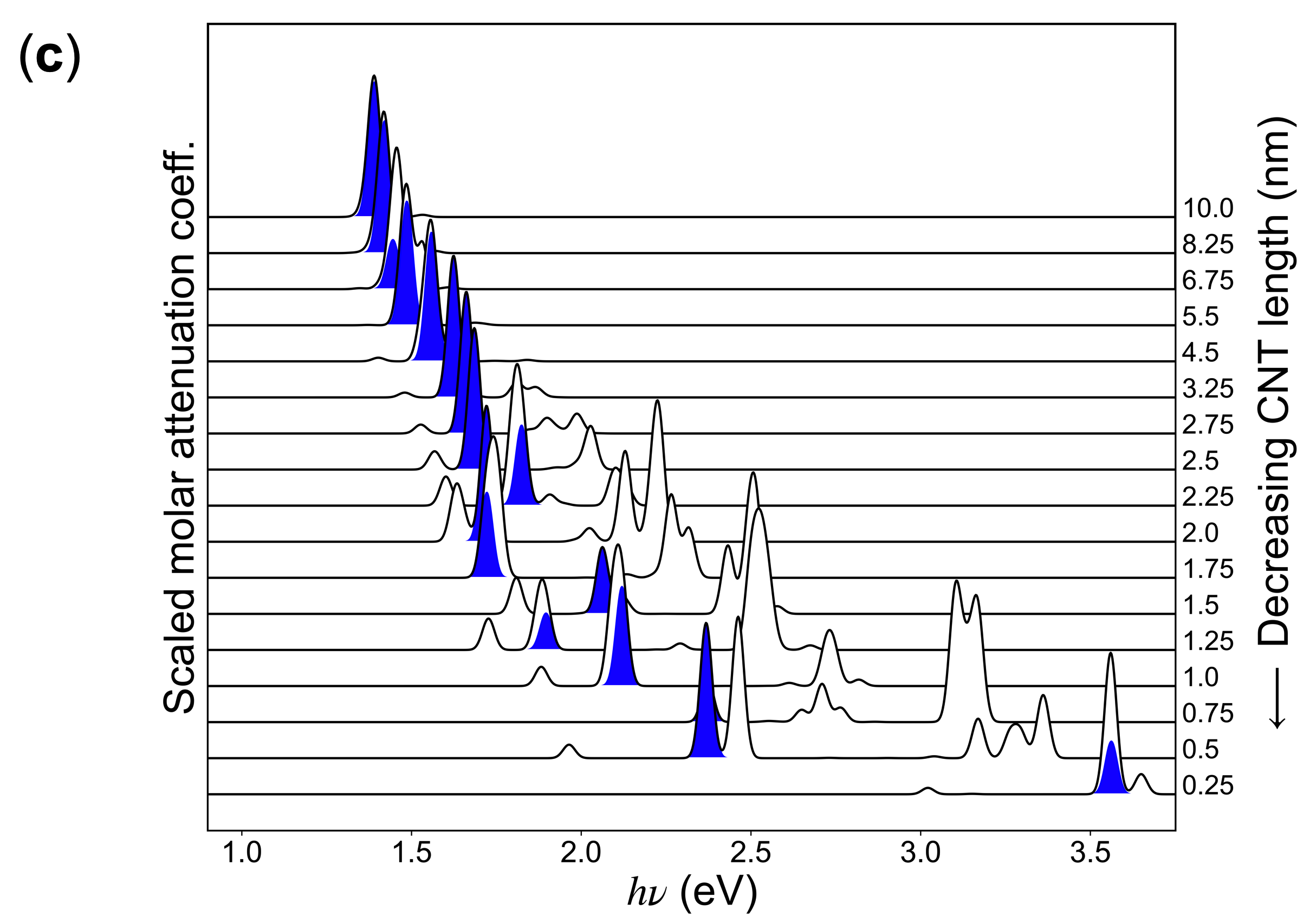
We used the first 15 excited states of the geometry-optimized models calculated by TD-DFT to construct the electronic absorption spectra with the excited state energies and oscillator strengths. The absorption spectra for all pristine (6,5) SWCNTs studied here are displayed in Fig. 1c, where we see the effect of quantum confinement blueshifting the excited state energies as the length is decreased. We analyzed these spectra to identify the transitions for different lengths. In pristine (6,5) SWCNTs with nm, the excited state can be identified as the bright transition[41]. For models longer than approximately 2.5 nm ( cu), the transition is straightforward to identify by inspecting the absorption spectra, as there is only one significant peak, the state. In models shorter than 2.5 nm, this peak splits into multiple transitions, making the assignment less clear.
In order to assign the in SWCNTs shorter than 2.5 nm, we perform a natural transition orbital (NTO) analysis[48] of the excited state in the 10 nm (6,5) SWCNT. Natural transition orbitals provide an orbital description of excited states that is more intuitive than using Kohn-Sham molecular orbitals. We find that in the 10 nm (6,5) SWCNT, the exhibits the waveform shown in Fig. LABEL:supp-NTO_wave. Typically, two relevant NTO pairs (electron-hole) are involved in the transitions, usually with similar contributions to the excited state. The most important NTO pair consists of and , the hole and electron orbitals respectively, with contribution . The second most important pair consists of and , with contribution (typically ). Using Gaussian’s built-in routines, we form an NTO wave by pointwise multiplication, which amounts to evaluating the 2-body wavefunction at the electron-hole relative coordinate of zero, giving as a function of the center of mass coordinate :
| (2) |
Plotting for the 10 nm case in Fig. LABEL:supp-NTO_wave, we see dumbbell-shaped lobes of positive sign on the carbon atoms of the graphitic sidewall of the SWCNT and similar lobes of negative sign on the carbon atoms. The NTO wave’s sign alternates between positive and negative around a C6 ring of the SWCNT sidewall, and along armchair or zigzag chains in the wall, forming helices in accord with the chirality. This ideal waveform is distorted to varying degrees in SWCNTs of different lengths but is still exhibited clearly.
Some lengths of (6,5) SWCNTs exhibit states that are anomalous in terms of the NTO analysis and do not strictly follow this signature waveform. While we think that these states are the best candidates for the in their respective models, we exclude these anomalous states from the dataset used for fitting, as indicated in Fig. 2. The results of the NTO analysis are presented for all (6,5) SWCNT lengths in the Supplemental Materials. All selected peaks are highlighted in the absorption spectra shown in Fig. 1c and referred to as in this paper.
In Fig. 2, we plot the selected peak energies for pristine (6,5) SWCNTs as a function of the scaled length , with the length of the SWCNT in nanometers and the length scale chosen as nm. The quantum confinement effect is clearly seen as cu, which corresponds to the Clar cell used to generate the models, as described in the Supplemental Materials. We note that the exciton size implied by the onset of the substantial blueshift is on the order of 2 nm, with shorter lengths rapidly causing a change in greater than 2%. This length is similar to previous theoretical estimations of the exciton Bohr radii in small-diameter SWCNTs[49, 50, 51]. It is also important to note that this is similar to an early measurement of the electron-hole correlation length[52], a measure of the exciton size. A more recent measurement of the correlation length places it closer to 13 nm[53], and using our best fit parameters we find that the percent change in between and for lengths greater than 13 nm is negligible (). In other words, the vast majority of blueshift occurs in SWCNTs with lengths nm.
As a finite SWCNT can be thought of as a type of quantum dot, it is instructive to consider a simple approach[54, 39] used to understand the confinement blueshift in the original colloidal quantum dots. These dots are spheres characterized by a radius , and the -dependence111The overall -dependence in the third term of Eq. (3) goes as as the dependence is averaged out within the brackets. of the shift in the lowest excited state energy relative to the bulk value () can be approximately modeled as
| (3) |
In this expression, is the reduced effective mass of the electron and hole, and the charges are placed in a dielectric sphere of constant relative permittivity surrounded by another dielectric of constant . The coefficients in the sum follow , with . The brackets denote an expectation value with respect to the first -wave basis function , where is the radial coordinate of either the hole or electron. The three contributions are a kinetic term, a Coulomb attraction of the electron-hole pair, and a polarization term due to a difference in the dielectric constants of the nanostructure and its surroundings. When , all the .
Taking Eq. (3) as a heuristic, we can analyze the expected contributions to the confinement blueshifts in ultrashort SWCNTs. For the spherical quantum dots studied with this approach in[54, 39], the kinetic energy term provides the dominant contribution for small , and the confinement causes a blueshift that goes as , i.e. a particle-in-a-box type dependence. Making an analogy between spherical quantum dots, the size of which is controlled by the radius , and finite SWCNTs, the size of which is controlled by the length , we can let in Eq. (3) and compare the resulting length dependence of the blueshift to the TD-DFT calculated values of in (6,5) SWCNTs, plotted in Fig. 2. We see that the length dependence does not follow scaling, as expected for a 1D particle-in-a-box. Neither does capture the overall trend, nor a combination of the two. Both of these functions increase too rapidly as they approach zero and decay too rapidly to zero as increases.
Using the scaled lengths , we make a conjecture that the length dependence of the blueshift goes as . This scaling is plotted as a solid black line in Fig. 2, and we see that it fits the overall trend. We can understand this length dependence in the following way. The Coulomb interaction between electron and hole is strong in SWCNTs due to their quasi-1D nature, as reflected in the large exciton binding energies measured in these systems[16]. A contribution akin to the Coulomb terms in Eq. (3) should provide the majority of the blueshift.
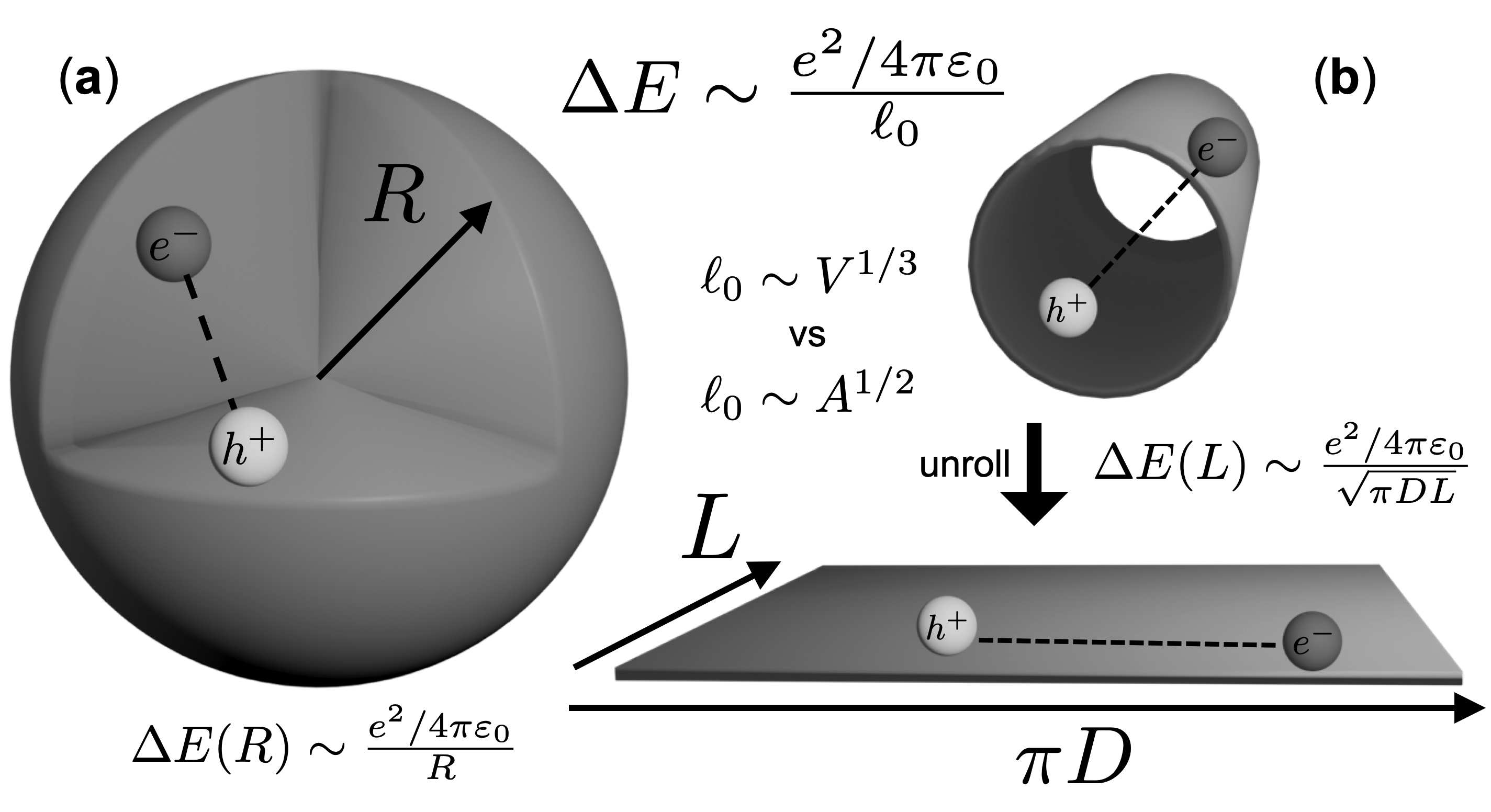
Dimensionally, this major contribution to the energy shift should go as , for some length scale characteristic of the confining geometry. The geometry of a SWCNT containing the exciton is that of an atomically thin cylindrical shell with an area determined by two independent length scales, the length and (chirality-specific) diameter , as . Then setting , we have
| (4) |
yielding the inverse square root dependence of the blueshift on the SWCNT length for a fixed diameter.
This dimensional argument, schematically depicted in Fig. 3, can also apply to the case of the spherical quantum dots. In this case, the exciton lives in a three-dimensional spherical volume characterized by the single length scale . Here, , which recovers the proper -scaling for the electrostatic terms in Eq. (3). Another way to think about the preceding argument is that if the nanostructure geometry is defined by independent length scales , then each length scale should enter into the expression on equivalent footing, and a geometry-induced shift stemming from a Coulomb interaction should go as .
To understand how well the length dependence suggested by Eq. (4) fits our calculated transitions, we can write the scaling law using the scaled lengths :
| (5) |
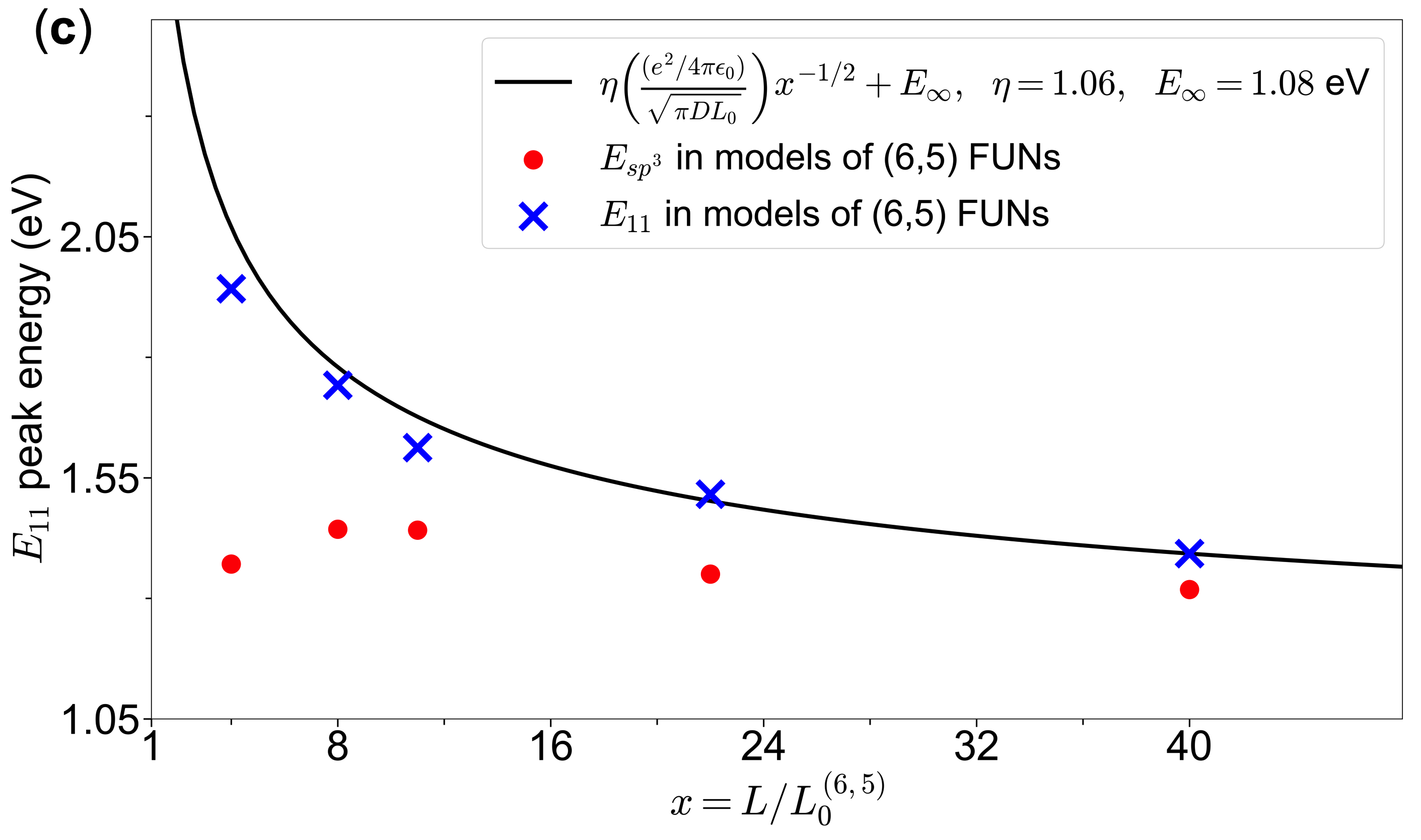
Here the free parameters are the infinite-length limit and the dimensionless pre-factor . The dimensionful scale in the brackets is close to 1.9 eV for (6,5) SWCNTs, using with a carbon-carbon bond length of Å[57] and our chosen length scale . From Fig. 2, the best fit gives , indicating that the dimensional argument predicts the shift within a factor of order unity. The geometry of the SWCNT combined with the strong Coulomb interaction between the electron and hole leads to a length dependence in the of (6,5) SWCNTs distinct from that expected for a 1D particle-in-a-box.
Furthermore, we can apply the scaling law (5) to the shifts in previously reported[38] TD-DFT calculated excited states in ultrashort metallic (6,6) SWCNTs. These states are not the state in the (6,6) SWCNTs, but rather optical transitions allowed by the finite length of armchair nanotubes [28, 38]. We refer to these transitions as . The calculations previously reported[38] are recreated here using a 3-21g basis set instead of a 6-31g, which does not change the qualitative trend. Additional models with , 6, and 83 cu are included, which correspond to approximate lengths of 0.5, 0.75, and 10 nm using the length scale nm. The peak energies are plotted in Fig. LABEL:supp-scaling_law_6-6_cnts and we find that the inverse square root length scaling fits the energies well, producing the zero-frequency long-length limit[28] better than the inverse length or inverse square fits ( eV), and with a pre-factor still of order unity ().
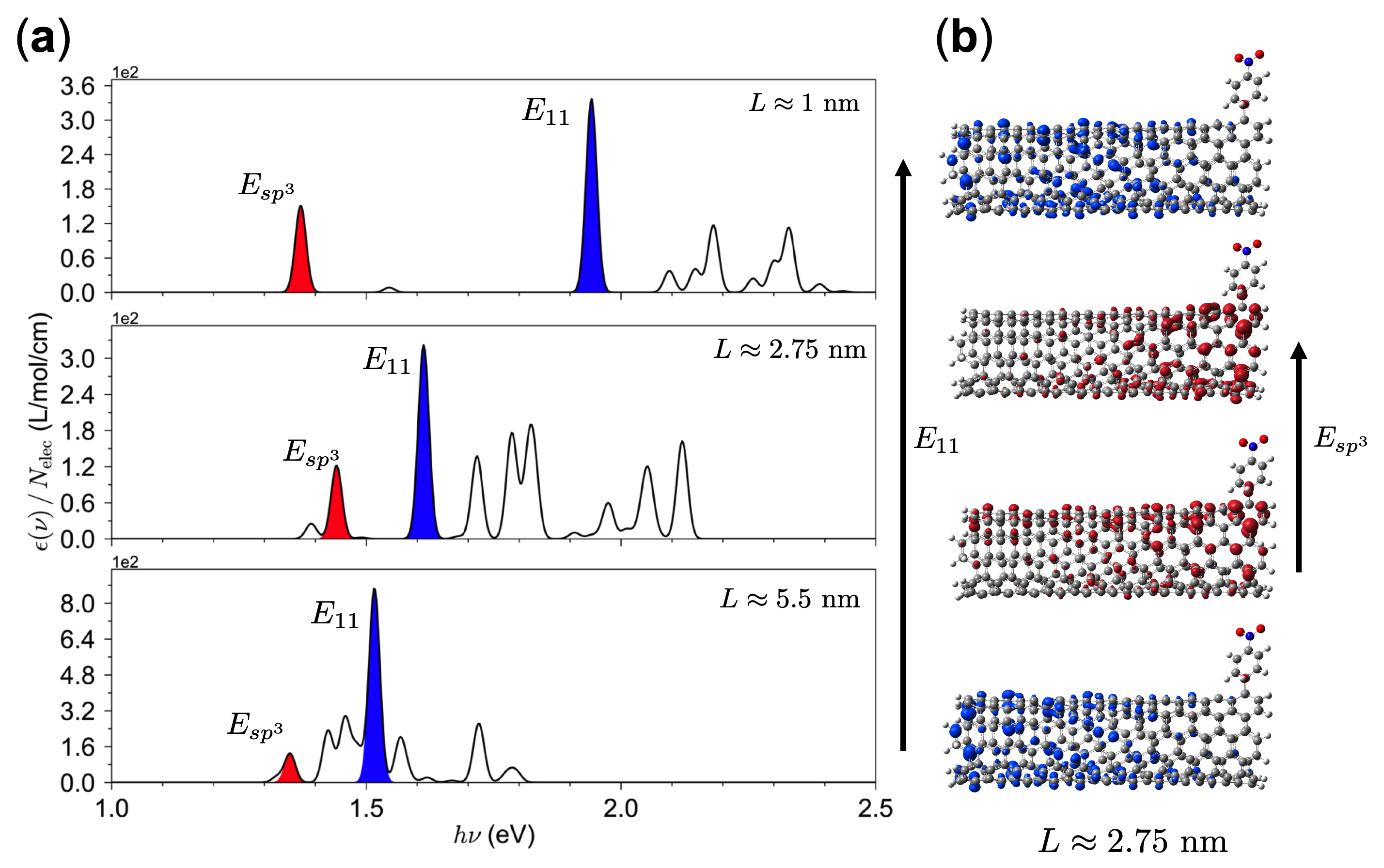
Finally, we connect this scaling law to models of FUNs. In Fig. 4a, we plot calculated absorption spectra of select FUN models ranging in length from 1 to 5.5 nm. By comparing with the corresponding pristine spectra, we identify the transition in the FUNs. Additionally, we find that the edge defects introduce redshifted transitions in a manner similar to previous TD-DFT calculations on finite SWCNTs with defects[38, 42]. These transitions, labeled , appear in different length FUNs. The NTO description of these excited states demonstates their localization at the edge defect, an example of which is shown in Fig. 4b for the cu FUN. The presence of redshifted, edge-localized excited states is reminiscent of transitions seen in PL spectra of FUNs[12, 13].
Figure 4c shows the and peak values for the FUNs plotted against the scaling law Eq. (5) using the fit parameters extracted from the pristine (6,5) models. It is clear that the trend persists in the FUNs, while the state has little dependence on length due to its localized nature around the defect. There are intriguing prospects for systematic access to the ultrashort regime using the DICE method, which would enable an experimental test of the inverse square root length dependence of seen in our calculations here.
IV Conclusion
In conclusion, our calculations of the quantum confinement shift of the lowest exciton energy in ultrashort SWCNTs using the B3LYP approximation of TD-DFT reveal that the blueshift of the scales with length as . This length dependence departs from the expected 1D particle-in-a-box scaling. The onset of significant blueshift occurs when the length of the SWCNT approaches the exciton Bohr radius. We find this scaling in pristine ultrashort (6,5) and (6,6) SWCNTs, as well as in (6,5) models of FUNs that have an defect pair installed near one edge. In the FUNs, we also find defect states whose energies have minor dependence on the length, owing to the edge defect localized nature of these excited states. The appearance of the scaling in both semiconducting and metallic chiralities, as well as in SWCNTs with defects, suggests a broad applicability of the observed scaling to ultrashort SWCNT systems.
Acknowledgements.
This material is based upon work supported in part by the National Science Foundation under award No. 1839165. The authors would like to thank Jacek Kłos, Jacob Fortner, Michael Winer, Andy Sheng and Alexandra Brozena for valuable discussions during the development of this work. We would also like to acknowledge the Alexander Family for their generous support through the Alexander Family Fellowship for students of the Chemical Physics Program at the University of Maryland. Furthermore, we acknowledge the high-performance computing team running the Zaratan Cluster at the University of Maryland, without which this research could not have been completed.References
- Cognet et al. [2007] L. Cognet, D. A. Tsyboulski, J.-D. R. Rocha, C. D. Doyle, J. M. Tour, and R. B. Weisman, “Stepwise quenching of exciton fluorescence in carbon nanotubes by single-molecule reactions,” Science 316, 1465–1468 (2007), https://www.science.org/doi/pdf/10.1126/science.1141316 .
- Cao et al. [2005] J. Cao, Q. Wang, D. Wang, and H. Dai, “Suspended carbon nanotube quantum wires with two gates,” Small 1, 138–141 (2005), https://onlinelibrary.wiley.com/doi/pdf/10.1002/smll.200400015 .
- Franklin and Chen [2010] A. D. Franklin and Z. Chen, “Length scaling of carbon nanotube transistors,” Nature Nanotechnology 5, 858–862 (2010).
- Franklin et al. [2012] A. D. Franklin, M. Luisier, S.-J. Han, G. Tulevski, C. M. Breslin, L. Gignac, M. S. Lundstrom, and W. Haensch, “Sub-10 nm carbon nanotube transistor,” Nano Letters 12, 758–762 (2012), pMID: 22260387, https://doi.org/10.1021/nl203701g .
- Cao et al. [2015] Q. Cao, S.-J. Han, J. Tersoff, A. D. Franklin, Y. Zhu, Z. Zhang, G. S. Tulevski, J. Tang, and W. Haensch, “End-bonded contacts for carbon nanotube transistors with low, size-independent resistance,” Science 350, 68–72 (2015), https://www.science.org/doi/pdf/10.1126/science.aac8006 .
- Qiu et al. [2017] C. Qiu, Z. Zhang, M. Xiao, Y. Yang, D. Zhong, and L.-M. Peng, “Scaling carbon nanotube complementary transistors to 5-nm gate lengths,” Science 355, 271–276 (2017), https://www.science.org/doi/pdf/10.1126/science.aaj1628 .
- Cao et al. [2017] Q. Cao, J. Tersoff, D. B. Farmer, Y. Zhu, and S.-J. Han, “Carbon nanotube transistors scaled to a 40-nanometer footprint,” Science 356, 1369–1372 (2017), https://www.science.org/doi/pdf/10.1126/science.aan2476 .
- Janissek et al. [2021] A. Janissek, J. Lenz, F. d. Giudice, M. Gaulke, F. Pyatkov, S. Dehm, F. Hennrich, L. Wei, Y. Chen, A. Fediai, M. Kappes, W. Wenzel, R. Krupke, and R. T. Weitz, “Ionic liquid gating of single-walled carbon nanotube devices with ultrashort channel length down to 10 nm,” Applied Physics Letters 118, 063101 (2021), https://pubs.aip.org/aip/apl/article-pdf/doi/10.1063/5.0034792/14544471/063101_1_online.pdf .
- Franklin, Hersam, and Wong [2022] A. D. Franklin, M. C. Hersam, and H.-S. P. Wong, “Carbon nanotube transistors: Making electronics from molecules,” Science 378, 726–732 (2022), https://www.science.org/doi/pdf/10.1126/science.abp8278 .
- Piao et al. [2013] Y. Piao, B. Meany, L. R. Powell, N. Valley, H. Kwon, G. C. Schatz, and Y. Wang, “Brightening of carbon nanotube photoluminescence through the incorporation of sp3 defects,” Nature Chemistry 5, 840–845 (2013).
- He et al. [2017] X. He, N. F. Hartmann, X. Ma, Y. Kim, R. Ihly, J. L. Blackburn, W. Gao, J. Kono, Y. Yomogida, A. Hirano, T. Tanaka, H. Kataura, H. Htoon, and S. K. Doorn, “Tunable room-temperature single-photon emission at telecom wavelengths from sp3 defects in carbon nanotubes,” Nature Photonics 11, 577 EP – (2017).
- Danné et al. [2018] N. Danné, M. Kim, A. G. Godin, H. Kwon, Z. Gao, X. Wu, N. F. Hartmann, S. K. Doorn, B. Lounis, Y. Wang, and L. Cognet, “Ultrashort carbon nanotubes that fluoresce brightly in the near-infrared,” ACS Nano 12, 6059–6065 (2018), pMID: 29889499, https://doi.org/10.1021/acsnano.8b02307 .
- Li et al. [2019] Y. Li, X. Wu, M. Kim, J. Fortner, H. Qu, and Y. Wang, “Fluorescent ultrashort nanotubes from defect-induced chemical cutting,” Chemistry of Materials 31, 4536–4544 (2019), https://doi.org/10.1021/acs.chemmater.9b01196 .
- Brozena et al. [2019] A. H. Brozena, M. Kim, L. R. Powell, and Y. Wang, “Controlling the optical properties of carbon nanotubes with organic colour-centre quantum defects,” Nature Reviews Chemistry 3, 375–392 (2019).
- Borel et al. [2023] A. Borel, T. Habrant-Claude, F. Rapisarda, J. Reichel, S. K. Doorn, C. Voisin, and Y. Chassagneux, “Telecom band single-photon source using a grafted carbon nanotube coupled to a fiber fabry–perot cavity in the purcell regime,” ACS Photonics 10, 2839–2845 (2023), https://doi.org/10.1021/acsphotonics.3c00541 .
- Wang et al. [2005] F. Wang, G. Dukovic, L. E. Brus, and T. F. Heinz, “The optical resonances in carbon nanotubes arise from excitons,” Science 308 (2005), 10.1126/science.1110265.
- Venema et al. [1999] L. C. Venema, J. W. G. Wildöer, J. W. Janssen, S. J. Tans, H. L. J. T. Tuinstra, L. P. Kouwenhoven, and C. Dekker, “Imaging electron wave functions of quantized energy levels in carbon nanotubes,” Science 283, 52–55 (1999), https://www.science.org/doi/pdf/10.1126/science.283.5398.52 .
- Heller et al. [2004] D. A. Heller, R. M. Mayrhofer, S. Baik, Y. V. Grinkova, M. L. Usrey, and M. S. Strano, “Concomitant length and diameter separation of single-walled carbon nanotubes,” Journal of the American Chemical Society 126, 14567–14573 (2004), pMID: 15521777, https://doi.org/10.1021/ja046450z .
- Fagan et al. [2007] J. A. Fagan, J. R. Simpson, B. J. Bauer, S. H. De Paoli Lacerda, M. L. Becker, J. Chun, K. B. Migler, A. R. Hight Walker, and E. K. Hobbie, “Length-dependent optical effects in single-wall carbon nanotubes,” Journal of the American Chemical Society 129, 10607–10612 (2007), pMID: 17672462, https://doi.org/10.1021/ja073115c .
- Sun et al. [2008] X. Sun, S. Zaric, D. Daranciang, K. Welsher, Y. Lu, X. Li, and H. Dai, “Optical properties of ultrashort semiconducting single-walled carbon nanotube capsules down to sub-10 nm,” Journal of the American Chemical Society 130, 6551–6555 (2008), pMID: 18426207, https://doi.org/10.1021/ja8006929 .
- Morimoto et al. [2014] T. Morimoto, S.-K. Joung, T. Saito, D. N. Futaba, K. Hata, and T. Okazaki, “Length-dependent plasmon resonance in single-walled carbon nanotubes,” ACS Nano 8, 9897–9904 (2014), pMID: 25283493, https://doi.org/10.1021/nn505430s .
- Gao et al. [2015] Z. Gao, L. Oudjedi, R. Faes, F. Moroté, C. Jaillet, P. Poulin, B. Lounis, and L. Cognet, “Optical detection of individual ultra-short carbon nanotubes enables their length characterization down to 10 nm,” Scientific Reports 5, 17093 (2015).
- Zhu et al. [1998] H.-Y. Zhu, D. Klein, T. Schmalz, A. Rubio, and N. March, “Geometric boundary effects on the electronic properties of finite carbon nanotubes,” Journal of Physics and Chemistry of Solids 59, 417–423 (1998).
- Rochefort, Salahub, and Avouris [1999] A. Rochefort, D. R. Salahub, and P. Avouris, “Effects of finite length on the electronic structure of carbon nanotubes,” The Journal of Physical Chemistry B 103, 641–646 (1999), https://doi.org/10.1021/jp983725m .
- Saito et al. [1999] R. Saito, T. Takeya, T. Kimura, G. Dresselhaus, and M. S. Dresselhaus, “Finite-size effect on the raman spectra of carbon nanotubes,” Phys. Rev. B 59, 2388–2392 (1999).
- Wu et al. [2000] J. Wu, W. Duan, B.-L. Gu, J.-Z. Yu, and Y. Kawazoe, “Finite size effects in carbon nanotubes,” Applied Physics Letters 77, 2554–2556 (2000), https://pubs.aip.org/aip/apl/article-pdf/77/16/2554/18553033/2554_1_online.pdf .
- Compernolle, Chibotaru, and Ceulemans [2003] S. Compernolle, L. Chibotaru, and A. Ceulemans, “Eigenstates and transmission coefficients of finite-sized carbon nanotubes,” The Journal of Chemical Physics 119, 2854–2873 (2003), https://pubs.aip.org/aip/jcp/article-pdf/119/5/2854/19321349/2854_1_online.pdf .
- Zhou et al. [2004] Z. Zhou, M. Steigerwald, M. Hybertsen, L. Brus, and R. A. Friesner, “Electronic structure of tubular aromatic molecules derived from the metallic (5,5) armchair single wall carbon nanotube,” Journal of the American Chemical Society 126, 3597–3607 (2004), pMID: 15025489, https://doi.org/10.1021/ja039294p .
- Lu et al. [2004] D. Lu, Y. Li, S. V. Rotkin, U. Ravaioli, and K. Schulten, “Finite-size effect and wall polarization in a carbon nanotube channel,” Nano Letters 4, 2383–2387 (2004), https://doi.org/10.1021/nl0485511 .
- Chen et al. [2004] R. Chen, C. Chang, F. Shyu, J. Hwang, and M. Lin, “Optical excitations of finite carbon nanotubes,” Carbon 42, 531–535 (2004).
- Yumura et al. [2004a] T. Yumura, K. Hirahara, S. Bandow, K. Yoshizawa, and S. Iijima, “A theoretical study on the geometrical features of finite-length carbon nanotubes capped with fullerene hemisphere,” Chemical Physics Letters 386, 38–43 (2004a).
- Yumura et al. [2004b] T. Yumura, S. Bandow, K. Yoshizawa, and S. Iijima, “The role of fullerene hemispheres in determining structural features of finite-length carbon nanotubes,” The Journal of Physical Chemistry B 108, 11426–11434 (2004b), https://doi.org/10.1021/jp0491010 .
- Bettinger [2004] H. F. Bettinger, “Effects of finite carbon nanotube length on sidewall addition of fluorine atom and methylene,” Organic Letters 6, 731–734 (2004), pMID: 14986961, https://doi.org/10.1021/ol0363974 .
- Yumura et al. [2006] T. Yumura, D. Nozaki, K. Hirahara, S. Bandow, S. Iijima, and K. Yoshizawa, “Quantum-size effects in capped and uncapped carbon nanotubes,” Annu. Rep. Prog. Chem., Sect. C: Phys. Chem. 102, 71–91 (2006).
- Okada [2007] S. Okada, “Electronic structure of finite-length carbon nanotubes: Crossover from fullerenes to nanotubes,” Nano 02, 51–57 (2007), https://doi.org/10.1142/S1793292007000349 .
- Rajan et al. [2008] A. Rajan, M. S. Strano, D. A. Heller, T. Hertel, and K. Schulten, “Length-dependent optical effects in single walled carbon nanotubes,” The Journal of Physical Chemistry B 112, 6211–6213 (2008), pMID: 18327930, https://doi.org/10.1021/jp077144l .
- Silva et al. [2016] J. Silva, M. J. T. Oliveira, S. Lanceros-Mendez, and F. Nogueira, “Finite-size effects in the absorption spectra of a single-wall carbon nanotube,” The Journal of Physical Chemistry C 120, 18268–18274 (2016), https://doi.org/10.1021/acs.jpcc.6b05277 .
- Eller et al. [2022] B. Eller, J. Fortner, J. Kłos, Y. Wang, and C. W. Clark, “Can armchair nanotubes host organic color centers?” Journal of Physics: Condensed Matter 34, 464004 (2022).
- Brus [1984] L. E. Brus, “Electron–electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state,” The Journal of Chemical Physics 80, 4403–4409 (1984), https://pubs.aip.org/aip/jcp/article-pdf/80/9/4403/9721014/4403_1_online.pdf .
- Cherukuri, Tsyboulski, and Weisman [2012] T. K. Cherukuri, D. A. Tsyboulski, and R. B. Weisman, “Length- and defect-dependent fluorescence efficiencies of individual single-walled carbon nanotubes,” ACS Nano 6, 843–850 (2012), pMID: 22128755, https://doi.org/10.1021/nn2043516 .
- Kilina et al. [2009] S. Kilina, E. Badaeva, A. Piryatinski, S. Tretiak, A. Saxena, and A. R. Bishop, “Bright and dark excitons in semiconductor carbon nanotubes: insights from electronic structure calculations,” Phys. Chem. Chem. Phys. 11, 4113–4123 (2009).
- Kilina, Ramirez, and Tretiak [2012] S. Kilina, J. Ramirez, and S. Tretiak, “Brightening of the lowest exciton in carbon nanotubes via chemical functionalization,” Nano Lett. 12 (2012), 10.1021/nl300165w.
- Frisch et al. [2016] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, “Gaussian˜16 Revision B.01,” (2016), gaussian Inc. Wallingford CT.
- Matsuo, Tahara, and Nakamura [2003] Y. Matsuo, K. Tahara, and E. Nakamura, “Theoretical studies on structures and aromaticity of finite-length armchair carbon nanotubes,” Organic Letters 5, 3181–3184 (2003), pMID: 12943382, https://doi.org/10.1021/ol0349514 .
- Ormsby and King [2004] J. L. Ormsby and B. T. King, “Clar valence bond representation of -bonding in carbon nanotubes,” The Journal of Organic Chemistry 69, 4287–4291 (2004), pMID: 15202881, https://doi.org/10.1021/jo035589+ .
- Baldoni, Sgamellotti, and Mercuri [2007] M. Baldoni, A. Sgamellotti, and F. Mercuri, “Finite-length models of carbon nanotubes based on clar sextet theory,” Organic Letters 9, 4267–4270 (2007), pMID: 17854196, https://doi.org/10.1021/ol7018289 .
- Balaban and Klein [2009] A. T. Balaban and D. J. Klein, “Claromatic carbon nanostructures,” The Journal of Physical Chemistry C 113, 19123–19133 (2009), https://doi.org/10.1021/jp9082618 .
- Martin [2003] R. L. Martin, “Natural transition orbitals,” The Journal of Chemical Physics 118, 4775–4777 (2003), https://pubs.aip.org/aip/jcp/article-pdf/118/11/4775/19210043/4775_1_online.pdf .
- Perebeinos, Tersoff, and Avouris [2004] V. Perebeinos, J. Tersoff, and P. Avouris, “Scaling of excitons in carbon nanotubes,” Phys. Rev. Lett. 92, 257402 (2004).
- Spataru et al. [2004] C. D. Spataru, S. Ismail-Beigi, L. X. Benedict, and S. G. Louie, “Excitonic effects and optical spectra of single-walled carbon nanotubes,” Phys. Rev. Lett. 92, 077402 (2004).
- Capaz et al. [2006] R. B. Capaz, C. D. Spataru, S. Ismail-Beigi, and S. G. Louie, “Diameter and chirality dependence of exciton properties in carbon nanotubes,” Phys. Rev. B 74 (2006), 10.1103/PhysRevB.74.121401.
- Lüer et al. [2009] L. Lüer, S. Hoseinkhani, D. Polli, J. Crochet, T. Hertel, and G. Lanzani, “Size and mobility of excitons in (6, 5) carbon nanotubes,” Nature Physics 5, 54–58 (2009).
- Mann and Hertel [2016] C. Mann and T. Hertel, “13 nm exciton size in (6,5) single-wall carbon nanotubes,” The Journal of Physical Chemistry Letters 7, 2276–2280 (2016), pMID: 27249311, https://doi.org/10.1021/acs.jpclett.6b00797 .
- Brus [1983] L. E. Brus, “A simple model for the ionization potential, electron affinity, and aqueous redox potentials of small semiconductor crystallites,” The Journal of Chemical Physics 79, 5566–5571 (1983), https://pubs.aip.org/aip/jcp/article-pdf/79/11/5566/18946007/5566_1_online.pdf .
- Note [1] The overall -dependence in the third term of Eq. (3) goes as as the dependence is averaged out within the brackets.
- Bachrach and Stück [2010] S. M. Bachrach and D. Stück, “Dft study of cycloparaphenylenes and heteroatom-substituted nanohoops,” The Journal of Organic Chemistry 75, 6595–6604 (2010), pMID: 20828116, https://doi.org/10.1021/jo101371m .
- Saito, Dresselhaus, and Dresselhaus [1998] R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes (Imperial College Press, 1998).