eurm10 \checkfontmsam10
Scaling of high-wavenumber energy spectra in the unit aspect-ratio rotating Boussinesq system
Abstract
Phenomenological and numerical studies of the small scale spectra of energy are presented for high Reynolds number rotating Boussinesq flows in unit aspect-ratio domains. We introduce a non-dimensional parameter , where the wavevector has vertical component and horizontal component , is the Coriolis frequency and is the Brunt-Väisälä frequency. While requiring that and are such that the potential vorticity is nearly linear in the dynamical variables, we deduce that for , the potential enstrophy suppresses the transfer of horizontal kinetic energy into large modes while forcing it to become independent of , scaling as . For , the potential enstrophy suppresses the transfer of potential energy into the large modes while forcing it to become independent of , scaling as . The usual scaling exponent is adjusted down to based on a heuristic argument which links the downscale fluxes of potential enstrophy and energy by their ratio. Spectra computed from high-resolution simulations of the Boussinesq equations with isotropic low-wavenumber forcing are used to explore such anisotropic constraints on the energy and provide a posteriori justification for the joint flux ansatz used to obtain the scaling exponent. In simulations for which , the asymptotic regime of is achieved and the horizontal kinetic energy is shown to become independent of and scale as . This collapse results in a uniform scaling for all and hence a uniform scaling of the energy in the spherical wavenumber, indicating extremely efficient net downscale transfer of energy. In simulations for which , the trend towards the asymptotic regime of is observed although the potential energy does not become entirely independent of as predicted. In simulations with where rotation and stratification are equally strong, both and regimes may be recovered depending on the aspect-ratio of the wavevector, , which is also the cotangent of the wavevector angle to the vertical. The dependence of the spectra on results, on average, in shallower scaling exponent values between and in both and implying an effectively more isotropic downscale distribution of energy in this limit. In all cases the empirical evidence points to both energy and potential enstrophy being jointly transferred downscale with the spectral scaling of the the former constrained by the latter.
1 Introduction
The Boussinesq approximation for hydrodynamic flow is the cornerstone for many applications in which a suitable model for scalar transport is needed. It is physically realistic in that it postulates that the fluctuations of the scalar are small compared to its background value and is computationally tenable for linear stratification profiles and simple boundary conditions. The Boussinesq approximation in the rotating frame forms the parent system for the derivation of further simplifications such as the shallow-water, hydrostatic and quasi-geostrophic (QG) models which are standard approximations in geophysical regimes which include rotation and stratification of the flow.
The Boussinesq system for a stably stratified flow in a rotating frame is given by:
| (1) | |||||
| (2) | |||||
| (3) |
where is the velocity, is its vertical component, is the effective pressure and is an external input or force. The total density is given by such that where is the constant background, is constant and larger than zero for stable stratification in the vertical -coordinate, is the density fluctuation. The density in normalized to which has the dimensions of velocity. The Coriolis parameter where is the constant rotation rate about the -axis, the Brunt-Väisälä frequency , is the kinematic viscosity and is the mass diffusivity coefficient. We assume periodic or infinite boundary conditions with Prandtl number . The relevant non-dimensional parameters for this system are the Rossby number and the Froude number , where is the non-linear frequency given input rate of energy Smith & Waleffe (2002). Thus and are the ratios of rotation and stratification timescales respectively to the nonlinear timescale.
There are three overlapping ideas from turbulence theory which we will exploit in this analysis of the Boussinesq equations. First from Kolmogorov (1941) the notion of a universal range of scales governed by the dynamics of the flux of a conserved quantity. Second, the analysis of Kraichnan (1971) on the inertial ranges of two-dimensional flows based on the constraint imposed by the joint conservation of both energy and enstrophy. Kraichnan thus deduced the scaling, up to logarithmic correction, of the energy in wavenumbers larger than the forcing wavenumber and scaling for wavenumbers smaller than . Finally Charney (1971) used Kraichnan’s ideas to show that similar constraints are placed on the quasi-geostrophic system due to the joint conservation of potential enstrophy and energy. Charney showed that in the quasi-geostrophic system, energy must flow upscale and potential enstrophy downscale, with predictable scaling exponents of the energy spectrum in the two ranges.
The general principle then, is that for a given (inviscidly) conserved quantity in a system there is a range of scales over which the flux of that quantity is a constant. The larger the system and the more separation there is between the source (forcing) and the sink (dissipation, boundaries), the more extended this universal ’inertial’ range of scales becomes. Once this is established, it is fairly standard procedure to deduce phenomenologically what the distribution of such quantities must be in spectral space.
In the inviscid and unforced (, ), Boussinesq system the potential vorticity is a local (Lagrangian) invariant, as is its square the potential enstrophy , while the total energy is a global invariant. That is,
At any point , is the kinetic energy, is the potential energy of the density fluctuations. The absolute vorticity and the relative (or local) vorticity . PV may be written in terms of as
| (4) |
The constant part does not participate in the dynamics and we will therefore neglect it from now on. In what follows we will assume that and such that Prandtl number , and the force is confined to the lowest modes. Thus we assume a conventional ‘inertial-range’ of turbulent scales wherein the transfer of conserved quantities dominates over both their dissipation and forcing. Note that the global potential vorticity is zero for unbounded flows. While the potential enstrophy is also Lagrangian invariant, we will use its global conservation properties in our analysis.
This set of invariants is analogous to those for 2-d turbulence where the vorticity is Lagrangian invariant and energy and enstrophy are globally conserved. It therefore seems reasonable to expect that an analysis similar to that of Kraichnan for 2D turbulence would yield similarly useful results. The raw Boussinesq system does not permit an exact relationship between energy and potential enstrophy as in the case of 2d turbulence. One notices that the potential enstrophy is, in general, a quartic quantity, while the energy is quadratic. However, when and are sufficiently large, PV linearizes in the dynamical variables and reduces in fourier space to:
| (5) |
where denotes fourier coefficients, the total wavevector = , the horizontal wavevector component has length , the vertical wavevector component has length and is the horizontal velocity vector with magnitude . We assume that the vertical velocity in the leading order, consistent with empirical observations, and use incompressibility to obtain the last equality of Eq. (5). We will next show how in the formal limits where PV is linear, asymptotically exact relationships can be extracted between potential enstrophy and components of the total energy.
First we briefly review the theoretical results that have been obtained in the limits in which PV linearizes. For strong rotation and stratification, Embid & Majda (1998) and Babin et al. (2000) showed that the limit as is QG after the inertia gravity waves are averaged out. The scalings predicted in Charney (1971) are recovered, namely scaling of the energy for , and scaling for where is the forcing wavenumber and is the typical dissipation wavenumber. Embid & Majda (1998) also showed that the limiting dynamics for with finite includes the so- called vertically sheared horizontal flows (VSHF). In both these cases, one can obtain a set of closed reduced equations for the linear PV dynamics from which all other quantities of interest can be derived. There is as yet no equivalent rigorous theoretical result for the unit-aspect ratio strongly rotating case with finite , since in that limit the scalar equation 2, which is independent of , vanishes in the leading order. This is a key reason why a (closed) reduced QG-like set of equations for this limit in the unit aspect-ratio domain has not been derived. Julien et al. (2006) showed that if an additional small parameter is introduced, namely the aspect-ratio of the domain, then reduced equations are possible for the vanishing limit as well.
In recent theoretical work we predicted that the potential enstrophy associated with the Boussinesq rotating system exhibits universal statistical properties in the so-called ‘inertial range’ of scales (Kurien et al. (2006)) in physical space for the same limiting regimes of the Rossby and Froude numbers described above. Formally, keeping lowest-order terms in a perturbation expansion in powers of , universal statistics are found when the potential vorticity is linear in the dynamical variables and . In those cases, the associated von Kármán-Howarth equation von Kármán & Howarth (1938) for the two-point correlation of yields a simple scaling law for the third-order velocity-potential-vorticity correlation
| (6) |
where is a physical separation scale, subscript denotes the component along , and is the mean dissipation rate of potential enstrophy . The -law (6) assumes that the two-point statistics of potential vorticity have a universal small-scale statistically isotropic component for statistically steady state flows. A related result was subsequently derived for the strict QG case (beginning with the evolution equation for ) Lindborg (2007) relating the third-order moments of potential vorticity difference and horizontal velocity difference across scale to potential enstrophy flux, assuming axisymmetry of the small-scales, and restricted to components of the velocity that are in the horizontal plane (given that vertical velocity is strictly zero for pure QG). The numerical experiments to verify 6 are currently underway and will be presented in a separate work.
There have been key numerical studies of the theoretical limits described above of which we here review the most relevant to our present study. The limit of strong rotation and stratification including the case was examined by Bartello (1995) in a paper which studied geostrophic adjustment as a process in which wave-vortical-wave interactions acted as catalyst for highly efficient downscale transfer of energy downscale. Smith & Waleffe (2002) demonstrated the generation of slow large scales in strongly stratified turbulence with small scale forcing and the dominance of the (VSHF) wave modes in the low wavenumbers. Waite & Bartello (2004) and Lindborg (2006) explored the effect of vortical forcing in stratified turbulence without rotation, thus highlighting the difference that 2D vs. 3D forcing can make in the evolution of the spectra. Sukhatme & L.M. (2008) showed that fairly small departures from can have measurable effect on the scaling of the spectra for moderately low-resolution simulations. Waite & Bartello (2006a, b) and demonstrated the transition to QG from stratified turbulence as is decreased for fixed small . Remmel et al. (2009) proposed a novel non-perturbative model to add non-QG effects to a flow and demonstrate the importance of resolving the small scales (waves) in order to obtain even gross large-scale features such as the energy growth accurately.
We will here study rotating Boussinesq turbulence both heuristically and using data from high-resolution simulations for and chosen such that the potential vorticity is nearly linear, and potential enstrophy is nearly quadratic. In our approach we retain the type of physically sound arguments used by Kolmogorov, Kraichnan and Charney, namely a focus on conserved quantities (in the inviscid, non-diffusive system), existence of inertial ranges where the downscale flux of a conserved quantity (in our case potential enstrophy) governs the dynamics and consequent spectral scaling of other related quantities (energy), and the notion of a statistically universal range of small scales.
2 Spectral relationships between potential enstrophy and energy
We begin by assuming that velocity fluctuations and density fluctuations are about the same order. We can construct spectral relationships between the quadratic potential enstrophy and either the horizontal kinetic energy or the potential energy based on the parameter , which by definition resembles a local Burger number in spectra space. From Eq. 5, for ,
| stratification dominates the PV | (7) | ||||
| and potential enstrophy | (8) | ||||
| giving the constraint | (9) |
Eq. (9) is interpreted to mean that for wavevectors with large , that is the ‘wide’ wavevectors, the potential enstrophy dominates the downscale (horizontal scales smaller than ) dynamics and consequently suppresses the transfer of horizontal kinetic energy into those modes. This is analogous to the relation in 2d turbulence
| (10) |
wherein the enstrophy suppresses the downscale transfer of kinetic energy for sufficiently high wavenumber , and in turn forces the inverse cascade of energy.
In the opposite limit one can show that,
| rotation dominates the PV | (11) | ||||
| and potential enstrophy | (12) | ||||
| giving the constraint | (13) |
which is interpreted to mean that potential enstrophy suppresses the transfer of potential energy into the wavevectors with large , that is the ‘tall’ wavemodes. In physical space this may be loosely interpreted to mean that potential energy transfer into the small vertical scales is vertical scales.
More generally, for fixed there is a transition regime when if the wavenumber regime is large enough. Thus, in an idealized infinite wavenumber flow, for fixed there will be some regime of wavevectors such that for which and horizontal kinetic energy is suppressed in according to Eq. 16, and a regime of wavevectors such that for which and potential energy is suppressed according to Eq. 17. The transition regime is defined by a cone in wavevector space with angle to the vertical such that . All wavenumbers inside the cone would behave according to and all those outside would behave according to . In our simulations in finite sized boxes, we study three extreme cases: where the cone is extremely narrow (small angle) so that most wavevectors lie outside the cone giving , where the cone is very broad (large angle) so that most wavevectors lie inside the cone and and finally where the cone-angle is 45 to the vertical and both and regimes exist.
There are several noteworthy differences between the relations Eq. (9) and (13) derived above and the 2d relation Eq. (10). The latter relates two (inviscidly) conserved quantities in spectral space, while the former relates the spectrum of a conserved quantity () with that of one () that is not conserved in general. The 2d turbulence constraint forces enstrophy downscale and energy upscale. In rotating Boussinesq, for , when the horizontal kinetic energy is suppressed in the large , there is no corresponding constraint in for either the kinetic or potential energies; conversely for which potential energy is suppressed in , there is no corresponding constraint in . Therefore there is always the possibility of a downscale transfer of energy in the unconstrained wavevector component. That is, a dual cascade of potential enstrophy and energy is possible downscale. In addition, Eq. (10) is isotropic in wavenumber in that it depends on the total spherical wavenumber while our new relations Eqs. (9) and (13) are highly anisotropic in wavenumber. As we will show from the data, the spectra indeed indicate that energy is transferred downscale in all cases albeit in a highly anisotropic manner.
2.1 A scaling phenomenology
Following Kraichnan and Charney one can naively postulate a scaling exponent for the horizontal kinetic energy and potential energy. Assuming the potential enstrophy flux governs the downscale dynamics, the energy scaling in the high wavenumber regime must depend only on the potential enstrophy dissipation rate and the wavevector (component) magnitude. Dimensional analysis then results, for the two limits:
| (14) | |||||
| (15) |
where is a prefactor which in principle should depend on the ratio of rotation to stratification since and are not separately conserved. In this study we focus on the scaling in wavenumber and leave the study of the prefactor to a future work. Analysis of high-resolution data (see numerical results below and prior work in Kurien et al. (2008)) showed that the actual scaling exponent was much steeper than , prompting a refinement of the above scaling estimates as follows.
We first suppose that part of the downscale energy transfer in both limits is not entirely suppressed. In the case where we predict that suppressed for large , it may be that or is free to transfer into modes with large . And in the case with suppressed for large , it may be that or is free to fill modes with large . Thus there may be a partial flux of the total energy (kinetic plus potential) to high horizontal or vertical wavenumber leading to the postulate that the spectral distribution of energy must depend on both and energy dissipation in the small scales, where the subscript denotes downscale energy. We will show a posteriori that our data supports such a hypothesis. A simple way to include the dependence on energy dissipation is to postulate that the energy scaling depends on the ratio and on the wavevector component. Then dimensional analysis yields:
| (16) | |||||
| (17) |
Irrespectively of the exact value of the scaling exponent for the steep decay, for the spectral horizontal kinetic energy distribution becomes independent of , while for the spectral potential energy distribution becomes independent of . Notice also that this estimate requires that remains finite in the inviscid , non-diffusive limit. One could presumably add corrections to mollify the blow-up for small and respectively along the lines of the log-correction derived by Kraichnan (1971). This issue of scaling correction will not be addressed in this paper except to say that steeper than -3 scaling implies even stronger non-local transfers than 2d turbulence as discussed by Kraichnan (1971)). As we will show in the sections below, our modified assumptions about energy transfer downscale are supported by the results of our simulations, and the scaling exponents measured from our data for the appropriate regimes are remarkably close to .
Bellet et al. (2004) studies mode-angle dependence of the total energy spectrum of rapidly rotating turbulence flow, using closure models for the anisotropic rotating equations for wave turbulence. The flows they study do not have stratification or any advected scalar and thus have no potential vorticity. Therefore, our present analysis, which does in effect study spectra as function of mode-angle via , cannot be carried over to deduce similar constraints. What we will present poses several departures from Bellet et al. (2004). First, we address, in principle, a very broad parameter space of finite and at high Reynolds numbers via the parameter . We also, for the first time, show that potential enstrophy conservation imposes constraints on the energy distribution in parameter regimes other than strict QG. And finally we propose a way to understand how a conserved quantity (potential enstrophy) may affect the spectral distribution of a non-conserved quantity (horizontal kinetic energy or potential energy) and furthermore propose a consistent argument to estimate the resulting spectral scaling exponents.
3 Numerical simulations and results
We perform pseudo-spectral calculations of the Boussinesq equations with rotation on grids of points and points in unit aspect-ratio domains. The computational domain has length to a side, with wavenumbers in integer multiples of . The time-stepping is 4th-order Runge-Kutta with resolution of the smallest wave frequencies with five timesteps per wave period. In the simulations at , the diffusion of both momentum and density (scalar) is modeled by hyperviscosity of laplacian to the 8th-power in order to extend the inertial scaling ranges. The Reynolds number in these cases is not computed explicitly but the hyperviscosity coefficient is chosen to resolve the total energy in the largest shell Chasnov (1994); Smith & Waleffe (2002) thus ensuring adequately turbulent flow for a given resolution. The simulations at were run with regular Navier-Stokes viscosity. The energy input rate and respectively for the smaller and larger resolutions, and and are varied by varying the rotation and stratification rates for fixed energy input rate which determines the nonlinear timescale. The forcing is incompressible and equipartitioned between the three velocity components and . This is equivalent to forcing the two wavemodes and the one vortical modes equally, thus providing an optimally unbiased calculation. The forcing is also stochastic and the phases of each mode change sufficiently rapidly that the forced modes are statistically isotropic. The forcing spectrum is peaked at , for large scale forcing. The simulations are dealiased according to the isotropic two-thirds dealiasing rule. Lower resolution runs at and (see Kurien et al. (2008)) were also performed in earlier studies, but are not reported here.
We seek to verify our predictions for three particular “extreme” regimes in , (see Table 1). The first is strongly stratified with moderate rotation, (runs 1 and 4); the second regime has strongly rotating with moderate stratification, (runs 2 and 5); and finally the regime which fixes large, (run 3) so that the dependence of potential vorticity on the ratio is reduced to a dependence on the cotangent alone, of the angle of the wavevector with respect to the vertical. Presumably, for sufficiently long inertial ranges any combination of , , and such that or , while maintaining near-linear PV, may be similarly investigated. As discussed in Bartello (1995), strict potential enstrophy conservation is not possible in a truncated inviscid spectral scheme due to the lack of conservation of Lagrangian invariants by individual triads. The best we can expect with this method in the viscous case is that truncation errors are swamped by viscosity thus giving conserved fluxes in the inertial range. We mention this fact because we will be using the notion of potential enstrophy conservation in this study. The spectral method itself is routinely used to compute flows very similar to those we study here and and we proceed while remaining aware of the caveats.
For each case in the Table, we will present the calculations to check specific predictions of the phenomenology proposed, namely the anisotropic suppression of horizontal kinetic energy and potential energy in the different regimes, and the scaling exponents predicted in these regimes by Eqs. (16) and (17). The spectra as a function of are defined as follows:
| (18) |
where is any of , or . We will present the horizontal kinetic energy and potential energy spectra (a) as a function of for various values of fixed , (b) as a function of , summed over , (c) as a function of for various values of fixed , and (d) as a function of , summed over . The (a)-(d) above correspond to subplots (a)-(d) in the sets of figures to follow. In each subplot, horizontal kinetic energy is plotted on top and potential energy on the bottom. We will also show the more conventional decomposition of the energy in contributions from the linear eigenmodes of the Boussinesq system. There are two inertial-gravity wave-eigenmodes with non-zero frequency and zero PV which contribute to the wave (or ageostrophic) energy spectrum. The remaining eigenmode has zero frequency and linear PV and contributes to the vortical (or geostrophic) energy spectrum. We will attempt to relate the mode-angle representation to the usual wave-vortical decomposition. Since this paper is largely an exploration of spectral scaling in the large wavenumbers, we will, for clarity’s sake, use the hyperviscous simulations data with their extended ranges to compute scaling exponents. The Navier-Stokes cases (runs 4,5) show no appreciable differences from their hyperviscous counterparts except for shortened scaling ranges, as is to be expected. Wherever appropriate, and when it does not result in a proliferation of figures, we will also present the data from the simulations with Navier-Stokes viscosity.
| run | grid | diffusion | () | () | ||
|---|---|---|---|---|---|---|
| 1 | hyper | 0.5 | 4 | 14 (0.48) | 3000 (0.0023) | |
| 2 | hyper | 0.5 | 4 | 3000 (0.0023) | 14 (0.048) | |
| 3 | hyper | 0.5 | 4 | 3000 (0.0023) | 3000 (0.0023) | |
| 4 | NS | 1 | 4 | 8.58 (1) | 8580 (0.001) | |
| 5 | NS | 1 | 4 | 4290 (0.002) | 8.58 (1) |
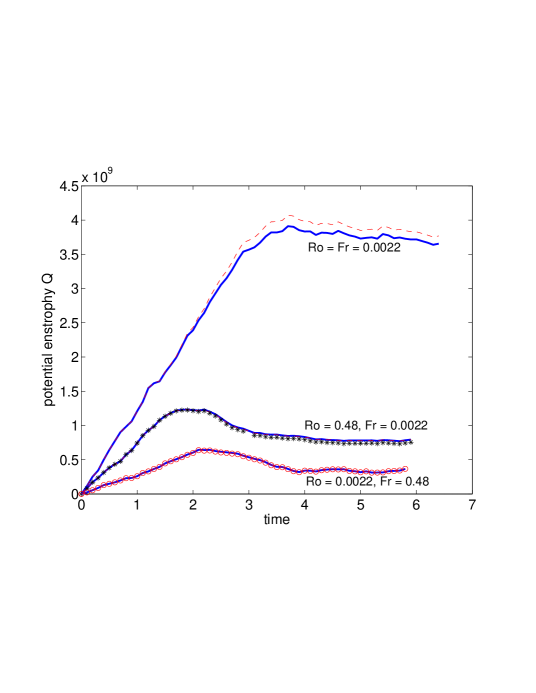
First we show in Fig. 1 that in each of the three cases, the global potential enstrophy (solid line) is captured by one half of the square of the corresponding linear PV, to within 3% or better agreement. potential enstrophy, after a period of spin-up and over-shoot, settles to a constant, indicating statistically steady state for this quantity, the mean rate of input of potential enstrophy balancing the mean rate of dissipation. We are thus able to stablish the time-frame over which the small scales, governed by potential enstrophy dynamics, have achieved statistically steady state. The small scale spectra of energy that we are interested in, achieve a statistically steady state. The total energy meanwhile (not shown) continues to grow since it can transfer upscale, where in our case, there is no sink to drain the energy. The calculation of all statistical quantities in what follows occurs over the time-frame where the mean potential enstrophy is constant, , over about 25 frames.
3.1 Strong stratification, moderate rotation
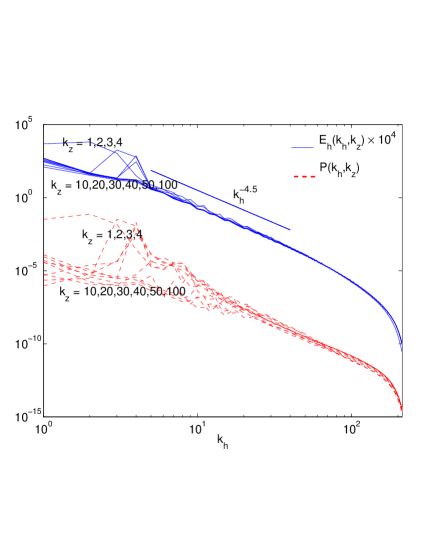
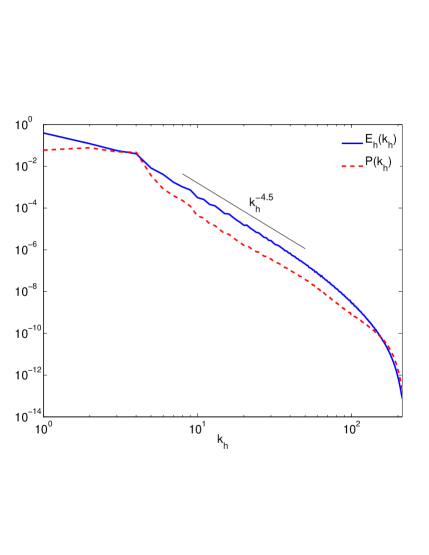
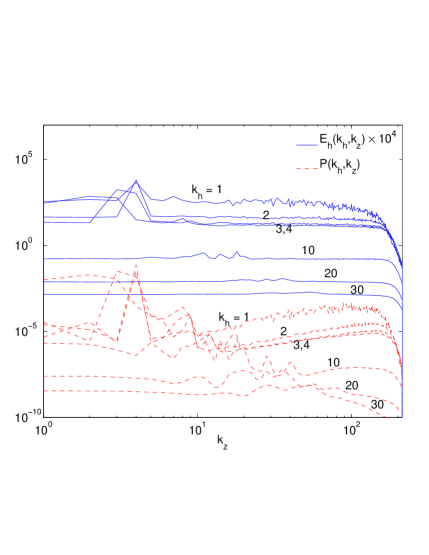
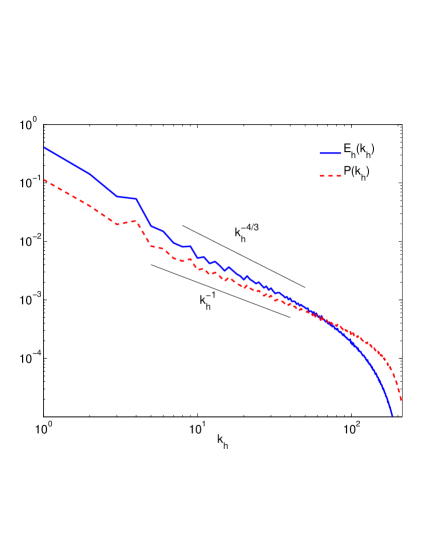
This case is studied using data from runs 1 and 4 of Table 1. We are in the limit since nearly all wavevectors lie outside the narrow cone with vertical angle . Therefore, irrespective of and the spectral scaling of should become independent of as given by Eq. 16. Fig. (2(a)) (top) and shows that collapses to a function of alone over the wide range , and scales very close to . In fact, the collapse is so complete that the converse plotting of as a function of in Fig. (2(c)) for various fixed , gives a series of plateaus, indicating no dependence at all in the inertial range for any particular . The corresponding plots for shows that it nominally follows the scaling of as a function of (Figs. 2(a)), yielding -averaged scaling of (Fig. 2(b))). However the converse plotting of (Fig. 2(c)) shows that it does not become completely independent of even though, when summed over (Fig. 2(d)), its scaling becomes close to as predicted in this limit for . Thus appears to mimic the scaling of as a function of , but not as a function of .
We now make a more conventional representation of the spectra by plotting the energy contained separately in the wave and vortical modes as a function of the spherical wavenumber .
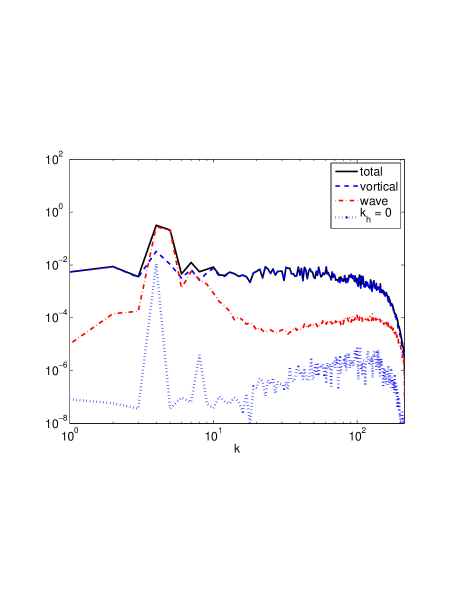
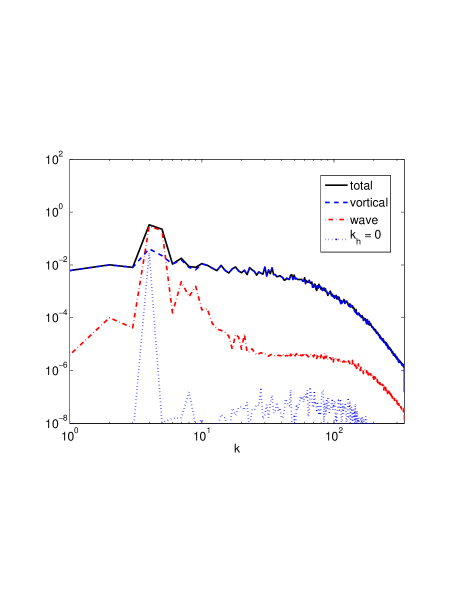
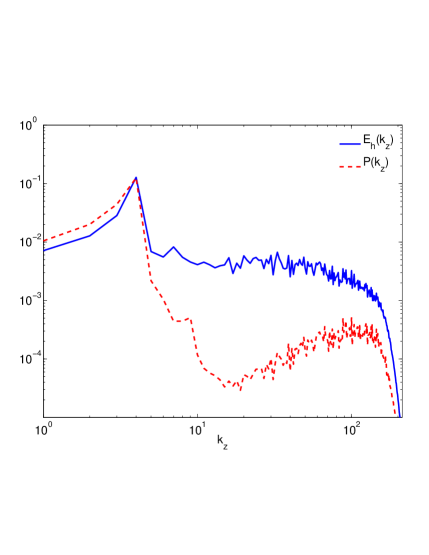
Figure 3 shows that almost the entire downscale energy is captured by the vortical modes. The narrow upscale range is also filled by the vortical modes. The total energy (vortical energy) distribution is nearly a constant as a function of . The wave energy is subdominant everywhere except in the forced modes, indicating that the wave energy does not move efficiently out of those modes in this strongly stratified regime. This figure is to be compared with Fig. 2(d) to see that for the vortical modes mimic the horizontal kinetic energy and that the independence of the latter from translates to a constant spectral distribution over as well, given that the dependence of on is rapidly very decaying (Fig. 2(b)). To the best of our knowledge, this is the first observation and explanation of the asymptotic high wavenumber energy spectrum for strongly stratified flow with finite rotation, with isotropic forcing in the low-wavenumbers (large scales). Waite & Bartello (2004) observed scaling for the total energy spectrum and the vortical mode energy spectrum in flows with rather low stratification , zero rotation and forced in the vortical modes only. They also observed saturation in of the total energy spectrum. In the light of the analysis in the present work, it would appear they achieve something like the regime and linear , not with large , but with large achieved by forcing vortical modes only. Their paper Waite & Bartello (2006b) which studies similar parameter regimes in while varying does show scaling of the vortical mode energy for but does not recover the steep decay. As we have pointed out above, the exact decay exponent does not matter as long as it is a decay and is independent of , leading to the scaling. Our analysis goes a step further in proposing an explanation of why there is suppression in and and not in due to the very particular constraints imposed on energy by the potential enstrophy, leading to independence from . We have also conclusively shown that the asymptotic small regime for the small scales can be achieved with unbiased isotropic forcing and in the presence of finite rotation.
There is also a stark difference from the vertically sheared horizontal flows (VSHF) ( modes) expected to be included in this limit when the forcing is at high wavenumbers (small scales). In our data the modes contain a very small percentage of the total energy (see Fig. 3) and the vortical (PV) modes contain most of the energy, whereas the opposite is true for the low wavenumbers in the case where the forcing is in the high wavenumbers (Smith & Waleffe (2002); Embid & Majda (1998)).
3.2 Strong rotation, moderate stratification, ,
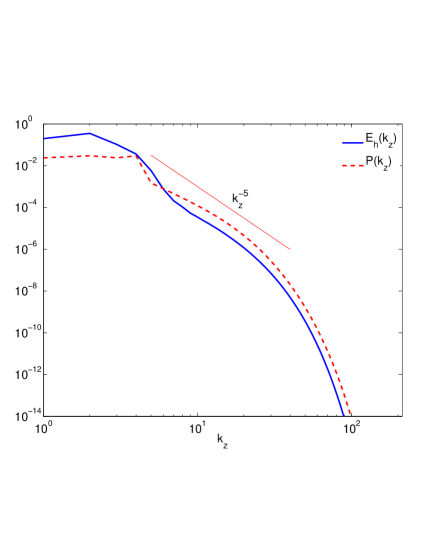
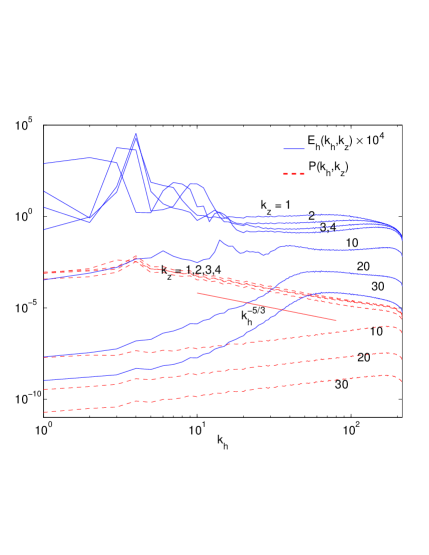
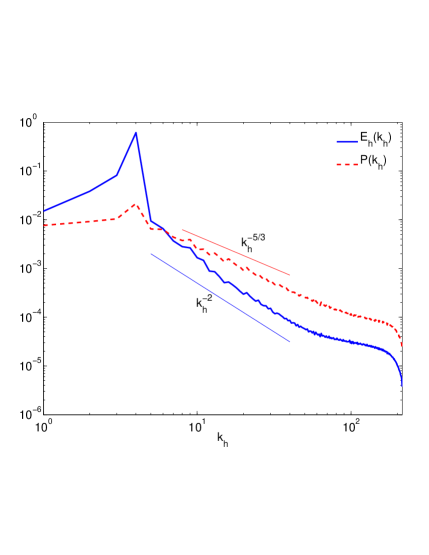
For run 2 of our simulations with moderate stratification and strong rotation, and we expect to observe Eq. (17). In Fig. 4 we see that although the scaling of in for all shows some degree of agreement, the curves themselves have not collapsed. This is also shown by the converse plotting of for various functions of in Fig. 4. However we note that the trend as decreases is for the potential energy curves to collapse to functions of alone. Thus may not be sufficiently small to see the limiting small-scale dynamics for , . And this despite the fact that potential enstrophy has converged to the stratification dependent quadratic component as seen in Fig. 1. Thus it appears, at least empirically, that for the small scales, the asymptotic regime of strong stratification is easier to achieve than that of strong rotation. This would seem related to the fact that the limit for finite is not amenable to a reduced set of equations since in that limit the scalar evolution equation vanishes in the leading order.
Figures 4 and 4 show that the -summed spectra scale between and and the -summed quantities scale approximately as . Thus, on average both horizontal kinetic and potential energies are suppressed in the large modes while both are free to fill the large modes. Again this justifies the ansatz that the scaling depends on , with downscale fluxes of both potential enstrophy and energy fluxes playing a role in the final development of the high wavenumber spectra.
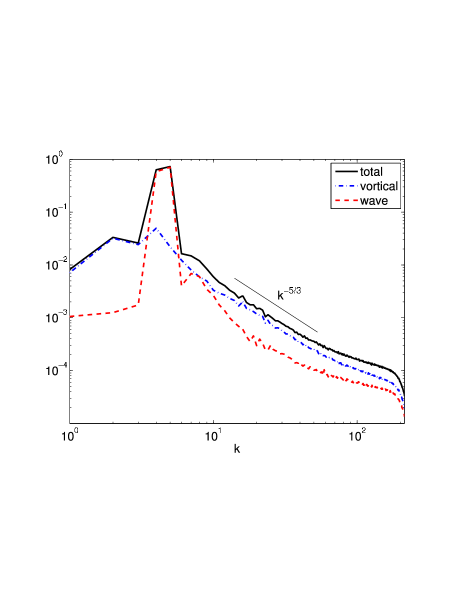
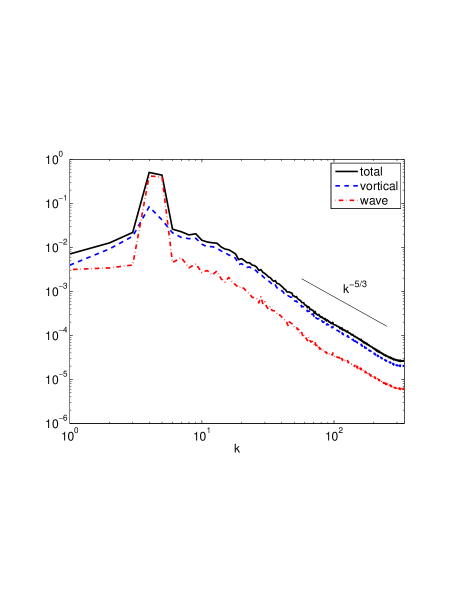
The conventional representation of wave and vortical mode spectra, Fig. 5 shows that in this regime, the vortical modes once again dominate the contribution to the total energy at all wavenumbers except around the forced wavenumbers, where the wave-mode contribution dominates. At high wavenumbers, the vortical modes scale more or less as . When compared with Fig. 4 this may be interpreted as the vortical modes being dominated by the potential energy, which persists strongly into the large modes while decaying rapidly in the large modes. Thus in the aggregate the scaling dominates in the spherically averaged spectra as well. On the right of Fig. 5 shows the same decomposition for the run 5 in the strongly rotating regime which shows qualitative agreement with the hyperviscous case, comparable scalings and hence providing some confidence that in these cases hyperviscosity does not bias our interpretation with undesirable artifacts.
The point of similarity between the strongly stratified versus the strongly rotating limits is that in both cases the vortical modes dominate the high wavenumbers or small scales. However, in the former the vortical modes carry the horizontal kinetic energy whereas in the latter the vortical modes carry the potential energy. This is very different from QG wherein the vortical mode energy decays as in the high wavenumbers. Note also the difference from the equally strongly rotating and stratified case (see below) which, as is well known (see Bartello (1995)), carries most of the high wavenumber energy in the wave modes which scale as .
3.3 Equally strong rotation and stratification,
In the special case of the dependence of PV on reduces to a dependence on the cotangent of the wavevector angle. As , the -dependent part prevails while for , the -dependent part takes over. That is, the cone in -space separating and makes a 45o angle to the vertical allowing equal numbers of modes in both regimes.
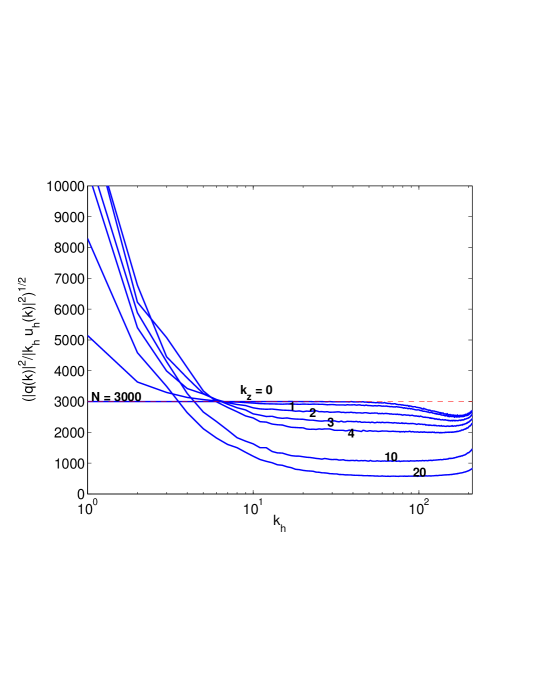
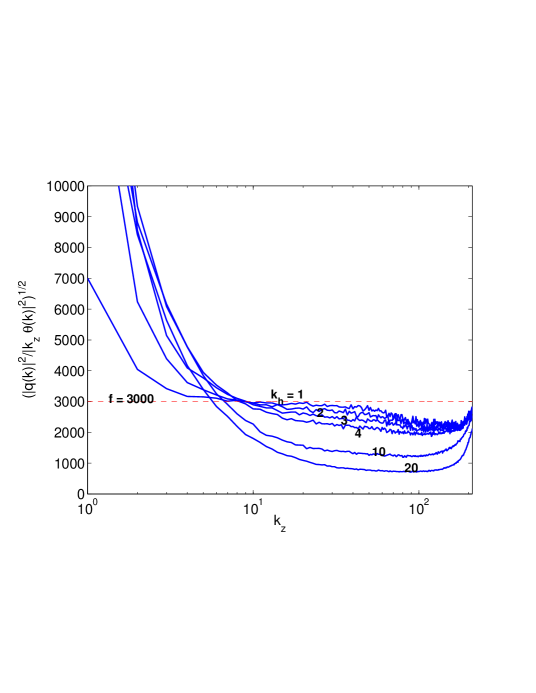
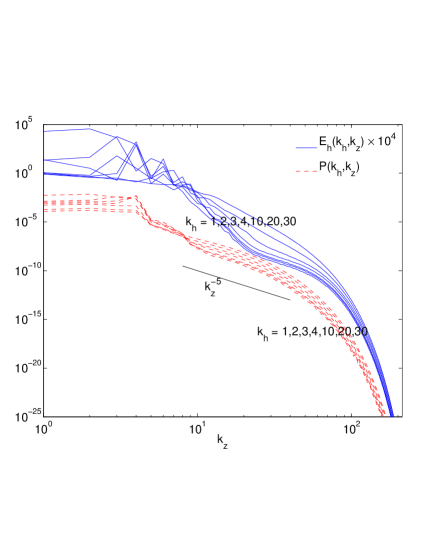
Using run 3, we show that as the value of (Fig. 6, left panel), while as the value of (Fig. 6, right panel). Since there is thus an average over the annulus of horizontal wavenumbers contained in the curves on the left panel of Fig. 6 are smoother than those on the right. The special case of has been omitted for clarity on the right panel as it is noisy (less averaging), while the case on the left poses no such problems. This figure clearly shows the dependence of on the mode-angle with respect to the vertical as expected by Eq. (5) for large.
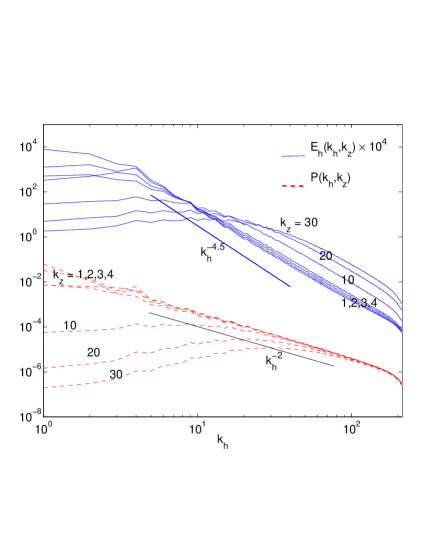
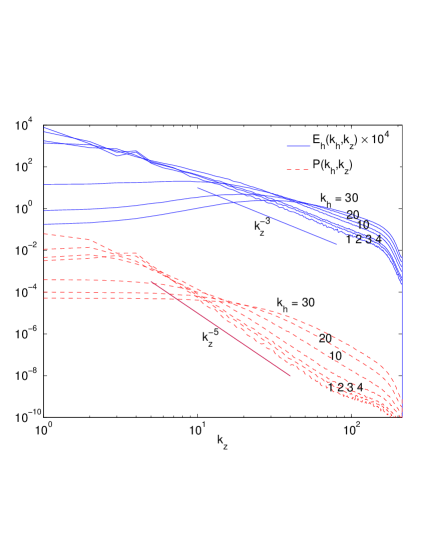
Next we consider the effect on the scaling of energy spectra as predicted in Eqs. (16,17). Fig. 7(a) shows and as a function of for various fixed . For , the spectrum for a particular changes over from basically flat to slowly increasing for small to close to decay when . This is in agreement with the deduction that horizontal kinetic energy is suppressed in the small aspect ratio modes by the dominance of potential enstrophy in those modes, and consequently scales according to Eq.(16). Note that there is a cross-over range below which the energy decreases as increases, and above which the energy increases as increases. In Fig. 7(a) the spectra for potential energy for which we do not have a prediction in this limit of aspect ratio, when plotted in the same manner as above, also shows aspect-ratio dependence for but with much shallower scaling, the line is shown for comparison. There is no cross-over range for and there appears to be much less suppression of potential energy for modes such that .
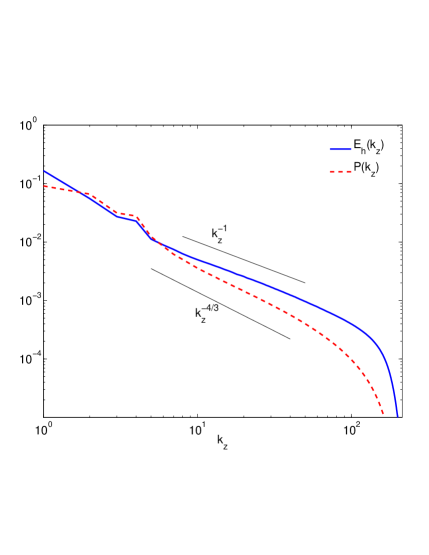
In Fig. 7(b) we show summed over all (top) and similarly (bottom). Interestingly, these scale approximately as and respectively, which is much shallower than the observed or for , and even shallower than . Thus, while for a given the horizontal energy is suppressed for , the average over indicates net transfer to large of both and .
To verify the prediction Eq. (17) for the large aspect-ratio modes we examine the scaling of as a function of for various fixed (Fig. 7(c)). Here again the spectrum is nearly a plateau with a turnover to as . Note again the cross-over range below which potential energy decreases as increases, and above which the potential energy increases as increases. plotted in the same way also shows some aspect ratio dependence but with much shallower scaling indicating that is not suppressed in the wavevectors with .
In Kurien et al. (2008) we presented the spectral scaling results for the case for runs at and all other parameters very similar, except that in that case only the momentum was forced. In that paper, we did not have an estimate for steeper than scaling exponent. The resulting spectra behaved very similarly to what we have presented in Fig. 7 so far as scaling exponents are considered. The overall magnitude of the potential energy spectra are much higher in the scalar-forced case presented here, as is to be expected. Thus the detailed forcing seems not to affect the results as far as the scaling exponents go.
To conclude this discussion for the strongly rotating and stratified case, the suppression of in the small aspect ratio modes with does not result in potential energy being suppressed in the same way. Conversely, the suppression of in the large aspect ratio modes with , does not result in the horizontal kinetic energy being suppressed in those modes. However, on summing over all [] because of the strong aspect-ratio dependence, [] scales with exponent between and . Thus a mode-by-mode suppression of horizontal energy in the small aspect-ratio modes and of the potential energy in the large aspect-ratio modes, nevertheless results in a net transfer of these energies into the high wavenumbers on average, along with the downscale transfer of potential enstrophy. We thus obtain a posteriori justification in our ansatz of dependence (Eqs. (16) and (17)) for the functional form of and .
This example also goes to show how one-dimensional spectra in either the or wave-component may obscure underlying dependencies on aspect-ratio of the modes and hide the subtle ways by which the energy populates the high wavenumbers on average. This possibility was noted in Bellet et al. (2004) who studied purely rotating flow, with no PV, and noticed a dependence of the spectra on the mode-angle as well.
4 Flow visualizations
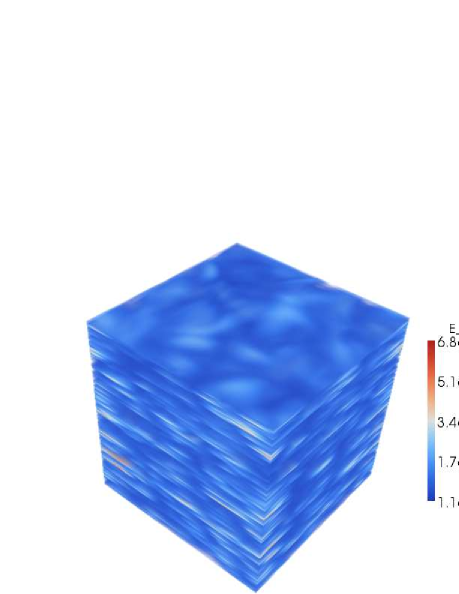
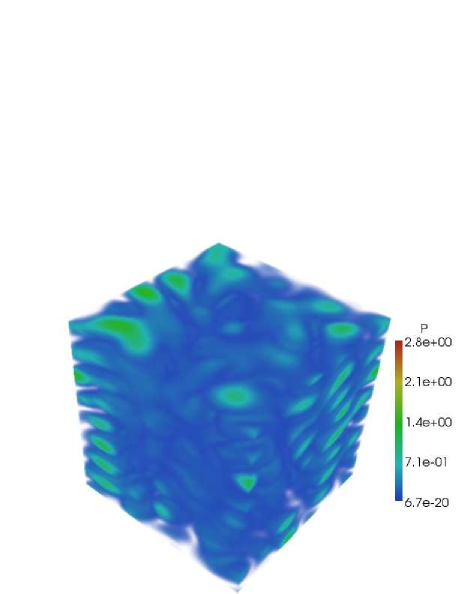
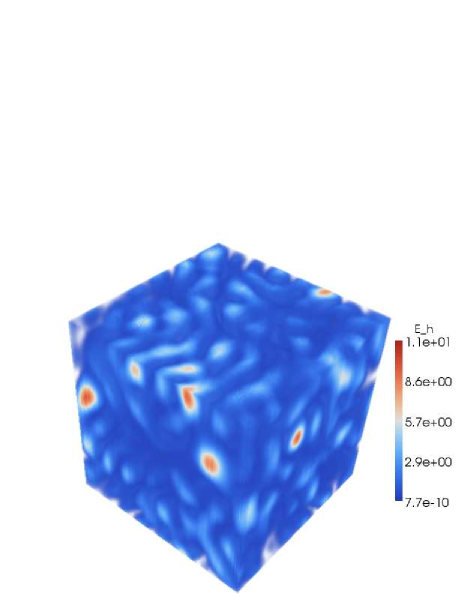
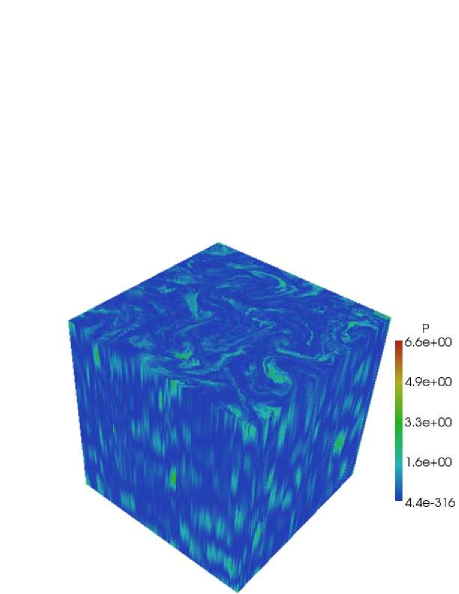

To give a qualitative picture of the quantities of interest, we present volume rendering of snapshots of the fully developed flow for the horizontal kinetic energy and the potential energy in Fig. 9. It must be noted that it is not clear what correspondence the spectra have to the structures in the physical space visualizations of the flow. The spectra are related to the physical space correlations as fourier transform pairs. A particular distribution of a field in physical space does not indicate a unique spectral distribution in fourier. The visualizations presented here should be treated as qualitative impressions of the flow structures. Nevertheless, we will point out consistencies between what is observed in the spectra with what is observed in visualizing the corresponding physical space quantities.
When stratification dominates over rotation the horizontal kinetic energy exhibits flat horizontal structures at all values (Fig.9) which appear to have very little extent in the vertical direction. This is consistent with both Eq. 16 and the discussion and plots in section 3.1 which confirm complete independence from . These structure are quite different from VSHF since the modes have a very small contribution in this regime. The potential energy for this flow (Fig. 9) appears to exhibit some tendency towards horizontally oriented blobs but retains more three-dimensionally coherent structures at the larger values, indicating that the potential energy distribution follows the distribution of horizontal kinetic energy to a degree, consistent with Fig. 2(b) but still retains some dependence on for small (large vertical scales) consistent with Fig. (2(d)).
Conversely, when rotation dominates over stratification, Fig. 9 shows that the potential energy exhibits structures that are strongly oriented in the vertical direction at all values with very little extent in the horizontal, consistent with Eq. (17). The horizontal kinetic energy also shows vertically coherent structures Fig. 9 but also shows high-valued larger blobs with more horizontal extent showing that also retains some horizontal scale dependence.
In the case of equal rotation and stratification (Figs. 9, 9), horizontal kinetic energy and potential energy look rather isotropically distributed with no preferred direction, in agreement with the spectra in Figs. 7(b) and 7(d) which show relatively shallow (ranging between -1 and -4/3) scaling in both and on average.
To summarize, equal rotation and stratification does not show any preferential direction for the energy isosurfaces, consistent with nearly the same shallow scaling in and (Figs. 7(b), 7(d)). Stratification dominated flows align the energy isosurfaces in the horizontal direction while rotation dominated flow align the energy isosurfaces along the vertical. The strongly stratified data are more in agreement with our asymptotic predictions than the strongly rotating data; the latter observation could indicate that even stronger rotation is required to see the asymptotic behavior.
5 Discussion and Conclusions
The small scale, high wavenumber spectra of rotating Boussinesq have never before been studied at such asymptotically low values of and using high-resolution simulations with unbiased isotropic forcing and dissipation. The rigorous theoretical results for the by Embid & Majda (1998) and the corresponding simulations of Smith & Waleffe (2002) extract the wave-modes as the VSHF contribution to the large scales. In our study of the small scales in this limit, which we have checked have negligible contribution of the modes (see Fig. 3), the vortical modes display a constant spectrum for , apparently dominated by the behavior of the horizontal kinetic energy (see Fig. 2(d)). This appears to be a consequence of one of the key new results of this work, namely that the horizontal kinetic energy becomes independent of (constant in) for any (see Eq. 16 and Fig. 2(c)) for . This uniform spectral distribution implies a very efficient downscale transfer, with energy contained predominantly by the vortical modes. The exact value of the steep scaling exponent in is not as important for this result as the fact that the spectrum becomes independent of (constant in) while decaying sufficiently quickly in such that the spectrum becomes independent of spherical wavenumber as well (Fig. 3).
The strongly rotating case with finite stratification (runs 2 and 5) were expected to achieve the limiting behavior of Eq. 17 with collapse of the spectral curves for all as a function of . While we see the correct trend in this direction, the curves in Fig. 4 show that the collapse is not complete. We are thus lead to believe that will need to be driven even lower and the resolution increased to see the collapse. We can postulate that, for sufficiently small , the potential energy curves for various will collapse to the same function of , corresponding to Eq. 17. Then, potential energy as a function of would be flat, governed by the flat spectrum in and strongly decaying spectrum in . Again the exact exponent of the decay law would not affect this general conclusion.
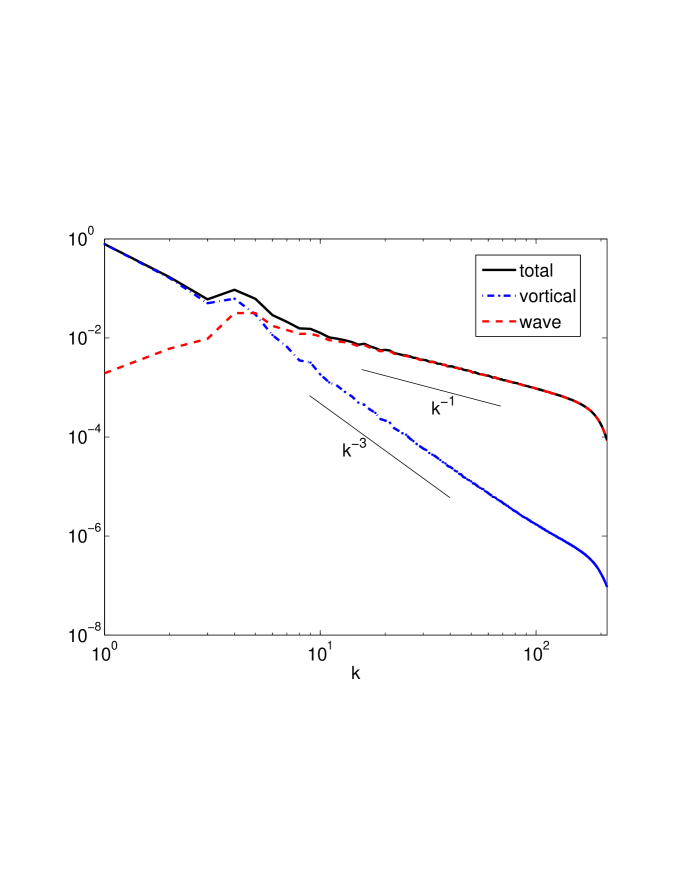
The equally strongly rotating and stratified case (run 3) show how underlying anisotropic scalings of the spectra, depending on the cotangent of the mode-angle , can be masked by summing over one or other of the wavevector components, as is commonly done. In Fig. 7(b) we show that the sum over all of the horizontal kinetic energy shallow with scaling . Thus the average over all smears out the effect of suppression by potential enstrophy and results in a much shallower scaling that the dependent scaling. The net effect is that energy fills the high-wavenumbers with almost the same shallow scaling in and (Fig. 7(b) and 7(d)). In Fig. 8 the wave-vortical mode decomposition of the spectra shows that the total downscale energy scales as and is dominated by wave modes. This is a well-known result and the scaling is identical to that of the passive scalar since the wave-modes are passively advected in this limit. What we further establish from this analysis is that the shallow spectrum is set up in spite of the underlying steeper, anisotropic, -dependent spectra in and .
We have made an attempt at a physically consistent phenomenology that results in a steeper than -3 scaling of the spectra within this framework. The scaling that arises out of the assumption that the ratio , where is the net flux of the energy downscale, plays a role in the downscale dynamics seems justified a posteriori. The analysis and verification of such an ansatz requires a detailed study of the fluxes and dissipation of both potential enstrophy and energy and is the subject of a separate work. As we have said before, the main conclusions of this paper hold irrespective of the specific scaling exponent for the decay of energy in the and .
The prediction for steep decay in according to Eq. (16) arises from the constraint that potential enstrophy places on the horizontal kinetic energy in for . While there is no explicit constraint on the potential energy, the data analysis in this regime reveals that potential energy scales very similarly to the horizontal kinetic energy as a function of , indicating that it too is suppressed in . Thus the total energy, where the contribution from the vertical component of the velocity is measured to be very small, appears to be suppressed in the large modes. The observed shallow scaling in of both horizontal kinetic and potential energies, suggests that the total energy is allowed to transfer into the large modes. Similarly, for , the suppression of potential energy in is mirrored to a large degree by the horizontal kinetic energy. These observations indicate that the exchange between kinetic and potential energies is local in wavenumber in both and regimes.
Recent work explored the connection between hyperviscosity, Galerkin truncation and the energy bottleneck Frisch et al. (2008) in Navier-Stokes turbulence without rotation or stratification. In that paper it was proposed that high values of hyperviscosity result in a partial thermalization of the high wavenumbers which manifests as energy ‘bottleneck’ phenomenon which contaminates the inertial range. In the present studies of rotating and stratified turbulence, the only substantial difference between the hyperviscous and the comparable runs with regular NS viscosity is the consistently less extended scaling ranges of the latter runs, which is to be expected. Therefore we use the hyperviscous runs to extract scaling exponents while checking against the NS runs to make sure that bottleneck-type artifacts are not introduced. It appears that for rotating and stratified flow and for the value of hyperviscous power used, the bottleneck-type artifacts, if any are minimal, and do not affect the purposes of this study.
While we have discussed three extreme parameter regimes, this discussion encompasses all values of thus allowing us to analyze arbitrary in the limit of linear (or near linear) PV. In an idealized infinite domain where , for any fixed the regime is achieved when while the regime is achieved when . The transition between regimes occurs for or when . Thus we observe that this type of analysis could be very relevant to geophysical flow regimes where and values are not as extreme but where the scaling ranges are much longer.
Acknowledgements.
The author is grateful for the hospitality of the Courant Institute (Climate Atmosphere Ocean Science program) for a year-long visit in 2008-2009 during which much of the work for this paper was completed. The author thanks Leslie Smith for numerous valuable discussions related to this work and for comments on an early draft of the paper. Early comments and suggestions by Oliver Buhler, Andrew Majda and Shafer Smith are gratefully acknowledged. Mark Taylor provided generous assistance with the Boussinesq code and its optimal scaling on the Argonne BG/P machine. This research used resources of the Argonne Leadership Computing Facility at Argonne National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract DE- AC02-06CH11357. Partial funding was provided by the DOE Office of Science, ASCR program in Applied Mathematics.References
- Babin et al. (2000) Babin, A., Mahalov, A. & Nicolaenko, B. 2000 Fast singular oscillating limits and global regularity for the 3d primitive equations of geophysics. Math. Modelling and Num. Analysis 34, 201–222.
- Bartello (1995) Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.
- Bellet et al. (2004) Bellet, F., Godeferd, F., Scott, J. & Cambon, C. 2004 Wave-turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.
- Charney (1971) Charney, J. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.
- Chasnov (1994) Chasnov, J. R. 1994 Similarity states of passive scalar transport in isotropic turbulence. Physics of Fluids 6 (2), 1036 – 1051.
- Embid & Majda (1998) Embid, P. & Majda, A. 1998 Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astrophys. Fluid Dyn. 87, 1–50.
- Frisch et al. (2008) Frisch, U., Kurien, S., Pandit, R., Pauls, W., Ray, S. S., Wirth, A. & Zhu, J.-Z. 2008 Hyperviscosity, galerkin-truncation and bottlenecks in turbulence. Phys. Rev. Lett. 101, 144501.
- Julien et al. (2006) Julien, K., Knobloch, E., Milliff, R. & Werne, J. 2006 Generalized quasi-geostrophy for spatially anisotropic rotationally constrained flows. J. Fluid Mech. 555, 233 – 74.
- von Kármán & Howarth (1938) von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 66, 192.
- Kolmogorov (1941) Kolmogorov, A. 1941 On degeneration (decay) of isotropic turbulence in an incompressible viscous liquid. Dokl. Akad. Nauk SSSR 31, 538–540.
- Kraichnan (1971) Kraichnan, R. 1971 Inertial-range transfer in two and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.
- Kurien (2008) Kurien, S. 2008 Numerical study of potential enstrophy inertial ranges in rotating and stratified flows. in preparation .
- Kurien et al. (2006) Kurien, S., Smith, L. & Wingate, B. 2006 On the two-point correlation of potential vorticity in rotating and stratified turbulence. Journal of Fluid Mechanics 555, 131 – 40.
- Kurien et al. (2008) Kurien, S., Wingate, B. & Taylor, M. 2008 Anisotropic constraints on energy distribution in rotating and stratified flows. Europhys. Lett. 84, 24003.
- Lindborg (2006) Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. Journal of Fluid Mechanics 550, 207 – 42.
- Lindborg (2007) Lindborg, E. 2007 Third-order structure function relations for quasi-geostrophic turbulence. Journal of Fluid Mechanics 572, 255 – 60.
- Remmel et al. (2009) Remmel, M., Sukhatme, J. & Smith, L. 2009 Nonlinear inertia-gravity wave-mode interactions in three-dimen sional rotating stratified flows. to appear in Comm. Math. Sc. .
- Smith & Waleffe (2002) Smith, L. & Waleffe, F. 2002 Generation of slow, large scales in forced rotating, stratified turbulence. J. Fluid Mech. 451, 145–168.
- Sukhatme & L.M. (2008) Sukhatme, J. & L.M., S. 2008 Vortical and wave modeds in 3d rotating stratified flows: Random large scale forcing. Geophys. Astrophys. Fluid Dyn. 102, 437.
- Waite & Bartello (2004) Waite, M. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.
- Waite & Bartello (2006a) Waite, M. & Bartello, P. 2006a Stratified turbulence generated by internal gravity waves. J. Fluid Mech. 546, 313–339.
- Waite & Bartello (2006b) Waite, M. & Bartello, P. 2006b The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.