Searching for Designs in-between

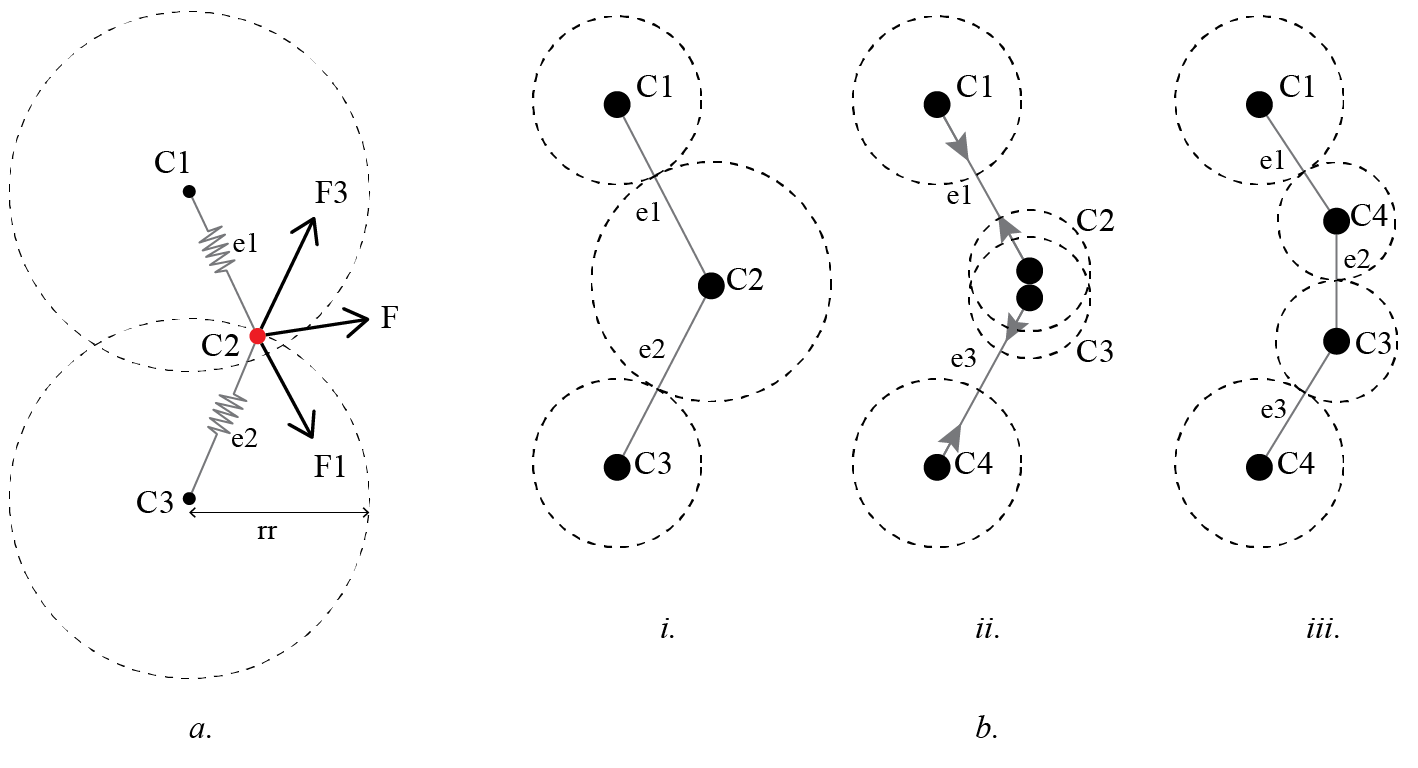
Our generative system operates on the metaphor of colonies of organisms, that develop over time in discrete timesteps. Each organism in a colony is defined as an array of cells $(C_{1},C_{2}\ldots C_{n})$ connected by edges $(e_{1},e_{2}\ldots e_{n})$, where $e_{i}=(C_{i},C_{i+1})$ and $e_{n}=(C_{n},C_{1})$, forming closed loops.

Colonies develop in a synthetic environment – a simulated viscous medium of uniform density. Sources of nutrients are randomly distributed across the environment. Each source has a limited amount of nutrition units, which are released, one at the time, every timestep, and diffused over their neighbouring area. Once nutrients have been released they progressively loose nutritional value over time. Once the source of nutrients is fully depleted, it disappears, giving rise to a new source randomly positioned within the development environment.

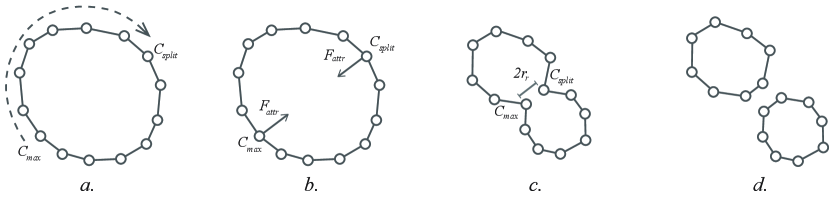
The dynamics of a colony are determined by how its components interact with each other and with the environment. The behaviours of cells and edges - acquiring nutrients, attracting/repelling neighbouring cells (2a), and reproducing (Figure 2b) – determine the shape of organisms as they develop. As a consequence organisms expand, contract, move, change shape and split into multiple organisms, forming a larger colony (Figure 3). The characteristics of these behaviours are defined by the genetic composition of the colony, detailed in Section 2.2.

The genetic information (genome) of a colony consists of the following five alleles:

• •

  Metabolic rate ($\eta$), determines how efficient the cells in a colony are at transforming nutrients into energy. A more efficient metabolism comes at the cost of a higher energy consumption.

• •

  Cell drag coefficient ($\nu$) represents the surface drag per unit area of cells. Cells with low drag move quickly, making stable configurations more unlikely.

• •

  Energy Capacity ($\varepsilon_{max}$) represents the maximum amount of energy a cell can store. As capacity increases, so does the mass of the cells, along with the amount of energy required for movement and metabolism.

• •

  Edge spring coefficient ($k$) determines the stiffness of the edges connecting adjacent cells. High $k$ results in rigid organisms. On the contrary, low k results in organisms that move with fluidity, which leads to stretched edges making the transmission of energy between cells less efficient.

• •

  Energy ratio ($\rho$) determines the relative size of new organisms after one of them splits into two.

We developed three proof of concept fitness functions, each of which attempts to address a different type of design objective: technical, spatial and aesthetic.

The general aim of this research was to develop a system that enables designers to explore diverse landscapes of designs using a combination of domain knowledge and intuition, in search of functional alternatives with novel/unexpected features.

We approximate the desired characteristics with our fitness functions (see Section 3.1). However, due to the uncertain nature of some design goals – especially those related to perceptual attributes, like aesthetic complexity – we regard optimisation processes as instrumental for exploration, rather than tools for the efficiently searching for the best alternative. This is why we used a hybrid, two-stage exploration strategy that combines a powerful optimisation algorithm with a method that introduces some intuitive aspects of creative exploration.

The first stage of our experiments involved the progressive transformation of the genome vector ($\eta,\nu,\varepsilon_{max},k,\rho$) using CMA-ES. We did $5$ evolutionary runs of $150$ generations each, using a population of $\lambda=40$ individuals at each generation. From each population, a set of $2$ parents was selected to define the distribution for the sampling of the new population. For the generation of individual objects we set the environment size to $(600\times 600)$ units. Each object was initialised as a colony of $4$ organisms, located on the midpoints of the diagonal lines connecting the centre of the environment and its vertices. Colonies were developed for 200 timesteps (with 100 timesteps of warmup), resulting in objects 200 layers high. For each evolutionary run the environment was initialised with a different random seed, in order to obtain variation in form via the random distribution of nutrient sources. For the second stage of the experiments two individuals generated on identical environments were selected based on their aesthetic characteristics and fitness. These individuals were used to run a linear interpolation between genome vectors, generating $99$ in-between new individuals which were then evaluated for fitness, as well as by visual inspection.

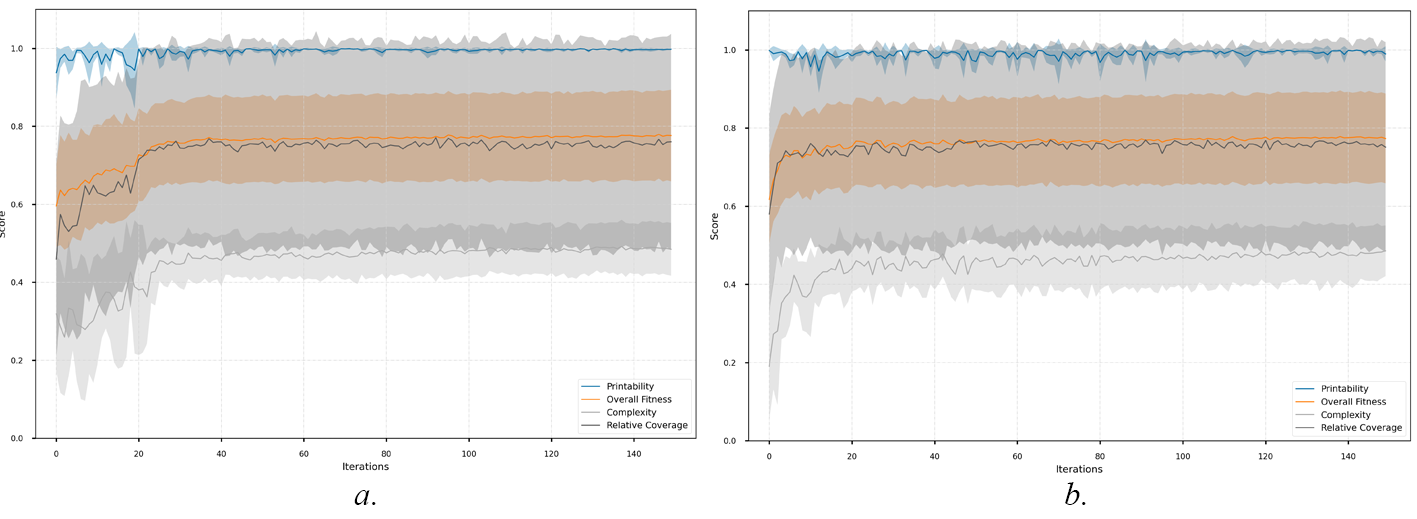
The first stage of experiments tested the ability of the CMA-ES algorithm to find designs with specific characteristics. Figure 4 shows the results when optimising for overall fitness (averaging printability, complexity and relative coverage) (a), and when optimising for relative coverage (b). Even though both graphs show similar results, it is possible to make interesting observations. For instance, in (a) printability (blue) quickly reaches its optimum value and exhibits little variance, whereas complexity (light grey) and relative coverage (dark grey) exhibit a fairly dramatic relative increase and follow remarkably similar trajectories, but do not reach high values. This suggests that once the system finds a highly printable alternative, it becomes difficult for it to find objects that perform well in other metrics. However, an assessment of graph (b) indicates that the system struggles to reach high scores for relative coverage in general.

To further understand the characteristics of the objects that the system can generate, we digitally render the highest performing individual for each generation. We then manually select the ones that exhibit interesting characteristics or are highly fit. Figure 5 shows an example obtained from one of the runs in which we optimised for relative coverage. The pavilion-like shape of the object exhibits a set of complex structures capable of supporting a canopy that covers about $60\%$ of the environment. However, a printability $P<1.0$ renders the object unprintable.

The object shown in Figure 6, in contrast, exhibits simple geometry, low relative coverage and high printability, allowing for a successful 3D print (to which we added a laser-cut canopy for reference). The lack of formal complexity is not necessarily negative, as from an aesthetic point of view the object appears structurally robust and its components are easily discernible. This is why we selected it as the second end point for the interpolation procedure.

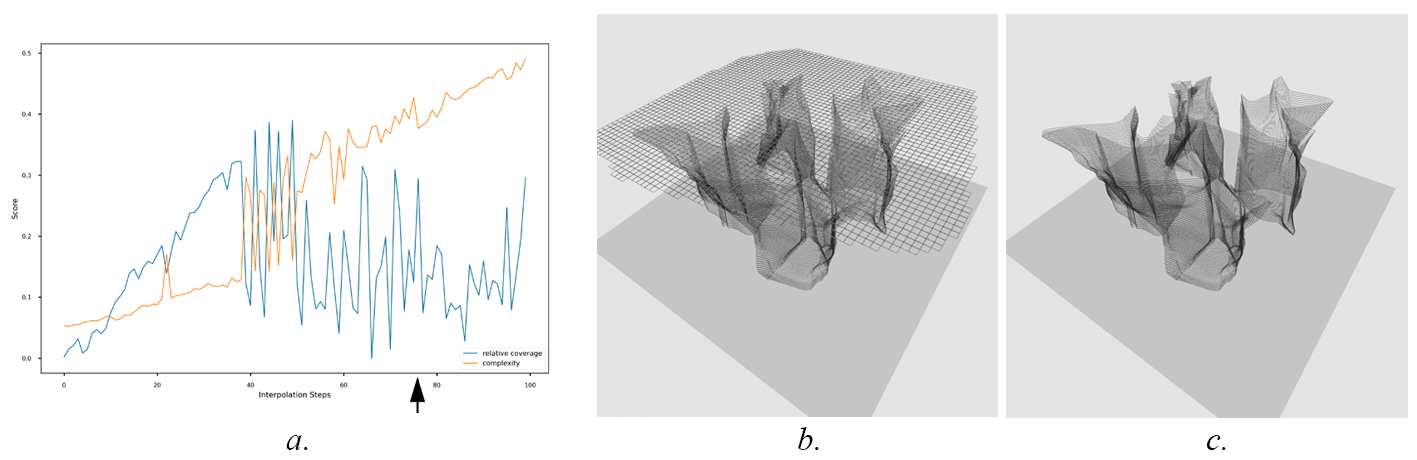
Figure 7 shows the outcomes of the exploration stage. In the graph (a) it is possible to observe unexpected behaviours of the fitness values for complexity and relative coverage as we interpolate between objects. The overall trend shows complexity increasing as coverage decreases. However the random value spikes and drops between steps 40 and 50 suggest that the fitness landscape is not smooth, making it harder for the optimisation algorithm to find the overall best solutions. Nevertheless, this can be fertile ground for creative opportunities, as the user of our system may encounter unexpected attributes in objects found in those areas of the landscape. For instance, the object depicted in (b) and (c) – iteration 78 – exhibits similar characteristics to the object in Figure 5, yet, on closer inspection, it is also possible to see that its contours are smoother, which indicates that some features of the object in Figure 6 have been captured to produce an object in-between.