Huaijin Pihjpi@zju.edu.cn1
\addauthorHuiyu Wanghwang157@jhu.edu2
\addauthorYingwei Liyingwei.li@jhu.edu2
\addauthorZizhang Li zzli@zju.edu.cn1
\addauthorAlan Yuillealan.l.yuille@gmail.com2
\addinstitution
Zhejiang University
Zhejiang, China
\addinstitution
Johns Hopkins University
Baltimore, USA
TrioNet
Searching for TrioNet: Combining Convolution with Local and Global Self-Attention
Abstract
Recently, self-attention operators have shown superior performance as a stand-alone building block for vision models. However, existing self-attention models are often hand-designed, modified from CNNs, and obtained by stacking one operator only. A wider range of architecture space which combines different self-attention operators and convolution is rarely explored. In this paper, we explore this novel architecture space with weight-sharing Neural Architecture Search (NAS) algorithms. The result architecture is named TrioNet for combining convolution, local self-attention, and global (axial) self-attention operators. In order to effectively search in this huge architecture space, we propose Hierarchical Sampling for better training of the supernet. In addition, we propose a novel weight-sharing strategy, Multi-head Sharing, specifically for multi-head self-attention operators. Our searched TrioNet that combines self-attention and convolution outperforms all stand-alone models with fewer FLOPs on ImageNet classification where self-attention performs better than convolution. Furthermore, on various small datasets, we observe inferior performance for self-attention models, but our TrioNet is still able to match the best operator, convolution in this case. Our code is available at https://github.com/phj128/TrioNet.
1 Introduction
Convolution is one of the most commonly used operators for computer vision applications [He et al.(2016)He, Zhang, Ren, and Sun, Ren et al.(2015)Ren, He, Girshick, and Sun, He et al.(2017)He, Gkioxari, Dollár, and Girshick]. However, recent studies [Hu et al.(2019)Hu, Zhang, Xie, and Lin, Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens, Zhao et al.(2020)Zhao, Jia, and Koltun, Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen, Dosovitskiy et al.(2021)Dosovitskiy, Beyer, Kolesnikov, Weissenborn, Zhai, Unterthiner, Dehghani, Minderer, Heigold, Gelly, Uszkoreit, and Houlsby] suggest that the convolution operator is unnecessary for computer vision tasks, and that the self-attention module [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin] might be a better alternative. For example, Axial-DeepLab [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] built stand-alone self-attention models for image classification and segmentation. Although these attention-based models show promising results to take the place of convolution-based models, these attention-based models are all human-designed [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens, Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen], making it challenging to achieve optimal results on new dataset, tasks, or computation budgets.
Given a target dataset, task, and computation budget, Neural Architecture Search (NAS) [Zoph and Le(2017), Zoph et al.(2018)Zoph, Vasudevan, Shlens, and Le, Real et al.(2019)Real, Aggarwal, Huang, and Le, Liu et al.(2019b)Liu, Simonyan, and Yang, Liu et al.(2018)Liu, Simonyan, Vinyals, Fernando, and Kavukcuoglu, Pham et al.(2018)Pham, Guan, Zoph, Le, and Dean, Wu et al.(2019)Wu, Dai, Zhang, Wang, Sun, Wu, Tian, Vajda, Jia, and Keutzer, Tan and Le(2019)] is an efficient technology to automatically find desirable architectures with marginal human labor. Due to its effectiveness, previous works [Zoph and Le(2017), Liu et al.(2019b)Liu, Simonyan, and Yang, Pham et al.(2018)Pham, Guan, Zoph, Le, and Dean, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] have successfully applied NAS to different computer vision tasks, including object detection [Wang et al.(2020c)Wang, Gao, Chen, Wang, Tian, and Shen, Ghiasi et al.(2019)Ghiasi, Lin, Pang, and Le], semantic segmentation [Liu et al.(2019a)Liu, Chen, Schroff, Adam, Hua, Yuille, and Fei-Fei], medical image analysis [Zhu et al.(2019b)Zhu, Liu, Yang, Yuille, and Xu], and video understanding [Wang et al.(2020e)Wang, Lin, Sheng, Yan, and Shao]. However, most of the searched models for these computer vision tasks are built upon convolutional neural network (CNN) backbones [Howard et al.(2017)Howard, Zhu, Chen, Kalenichenko, Wang, Weyand, Andreetto, and Adam, Sandler et al.(2018)Sandler, Howard, Zhu, Zhmoginov, and Chen, Howard et al.(2019)Howard, Sandler, Chu, Chen, Chen, Tan, Wang, Zhu, Pang, Vasudevan, et al.].
Previous convolution-based NAS methods usually consider attention modules as plugins [Li et al.(2020)Li, Jin, Mei, Lian, Yang, Xie, Yu, Zhou, Bai, and Yuille]. During the search procedure, the search algorithm needs to decide whether an attention module should be appended after each convolution layer. This strategy results in the searched network architecture majorly consisting of convolution operators, causing a failure to discover the potentially stronger attention-based models.
Therefore, in this paper, we study how to search for combined vision models which could be fully convolutional or fully self-attentional [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens, Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen]. Specifically, we search for TrioNets where all three operators (local-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens], axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen], and convolution) are considered equally important and compete with each other. Therefore, self-attention is no longer an extra plugin but a primary operator in our search space. Seemingly including the self-attention module into the search space could achieve our goal, we observe it is difficult to apply the commonly used weight-sharing NAS methods [Cai et al.(2019)Cai, Zhu, and Han, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] due to two issues.
One issue is that self-attention modules and convolution blocks make our search space much more complicated and imbalanced than convolution-only spaces [Cai et al.(2019)Cai, Zhu, and Han, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le]. For instance, convolution usually contains kernel size and width to search while self-attention have more options like query, key and value channels, spatial extent and multi-head numbers. The self-attention operators correspond to much larger search spaces than convolution, with the same network depth. This imbalance of self-attention and convolution’s search space makes the training of supernets intractable. Therefore, we propose Hierarchical Sampling, which samples the operator first uniformly before sampling other architecture options. This sampling rule suits our setting better because it ensures an equal chance for each operator to be trained in the supernet, alleviating the bias of search space size.
The other issue is that the multi-head design of attention operators poses a new challenge for weight-sharing [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] NAS algorithms. Current weight-sharing strategy [Stamoulis et al.(2019)Stamoulis, Ding, Wang, Lymberopoulos, Priyantha, Liu, and Marculescu, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] always shares the first few channels of a full weight matrix to construct the weight for small models. However, in self-attention modules, the channels are split into multi-head groups to capture different dependencies [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin]. The current weight-sharing strategy ignores the multi-head structure in the weights and allocates the same channel to different heads depending on the sampled multi-head groups and channels, forcing the same channel to capture different types of dependencies at the same time. We hypothesize and verify by experiments that such weight-sharing is harmful to the training of supernets. Instead, we share our model weights only if they belong to the same head in multi-head self-attention. This dedicated strategy is named Multi-Head Sharing strategy.
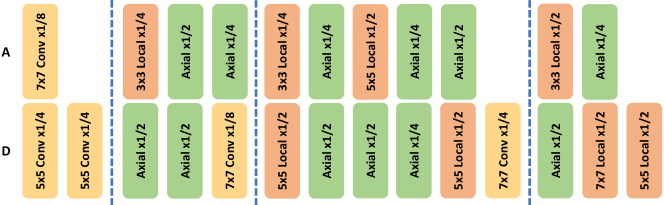
We evaluate our TrioNet on ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton] dataset and various small datasets [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei, Maji et al.(2013)Maji, Rahtu, Kannala, Blaschko, and Vedaldi, Welinder et al.(2010)Welinder, Branson, Mita, Wah, Schroff, Belongie, and Perona, Fei-Fei et al.(2004)Fei-Fei, Fergus, and Perona, Nilsback and Zisserman(2008)]. The TrioNet architectures found on ImageNet are shown in Fig. 1. We observe that TrioNets outperform stand-alone convolution [He et al.(2016)He, Zhang, Ren, and Sun], local-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] models with fewer FLOPs on ImageNet where self-attention performs better than convolution. On small datasets where self-attention models perform inferior to convolution, our TrioNet is still able to matche the best operator with fewer FLOPs on average.
To summarize, our contributions are four-fold: (1) We regard self-attention and convolution as equally important basic operators and propose a new search space that contains both stand-alone self-attention models and convolution models. (2) In order to train a supernet on our highly imbalanced search space, we adopt Hierarchical Sampling rules to balance the training of convolution and self-attention operators. (3) A Multi-Head Sharing strategy is specifically designed for sharing weights in multi-head self-attention operators. (4) Our searched TrioNet reduces computation costs and improves results on ImageNet classification, compared with hand-designed stand-alone networks. The same phenomenon is observed when TrioNets are searched on small datasets as well.
2 Related work
Self-attention.
Self-attention was firstly proposed for NLP tasks [Bahdanau et al.(2015)Bahdanau, Cho, and Bengio, Wu et al.(2016)Wu, Schuster, Chen, Le, Norouzi, Macherey, Krikun, Cao, Gao, Macherey, et al., Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin]. People then successfully apply self-attention module to many computer vision tasks [Wang et al.(2018)Wang, Girshick, Gupta, and He, Bello et al.(2019)Bello, Zoph, Vaswani, Shlens, and Le, Chen et al.(2018)Chen, Kalantidis, Li, Yan, and Feng, Huang et al.(2019)Huang, Wang, Huang, Huang, Wei, and Liu, Zhu et al.(2019a)Zhu, Xu, Bai, Huang, and Bai, Cao et al.(2019)Cao, Xu, Lin, Wei, and Hu]. More recently, it has been shown that self-attention can be used to replace convolution in vision models. Hu et al\bmvaOneDot [Hu et al.(2019)Hu, Zhang, Xie, and Lin] and Local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] build the whole model with self-attention restricted to a local patch. SAN [Zhao et al.(2020)Zhao, Jia, and Koltun] explores a boarder self-attention formulation. Axial-DeepLab [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] extends local self-attention to global self-attention with axial self-attention blocks. Later, ViT [Dosovitskiy et al.(2021)Dosovitskiy, Beyer, Kolesnikov, Weissenborn, Zhai, Unterthiner, Dehghani, Minderer, Heigold, Gelly, Uszkoreit, and Houlsby] approaches image classification with the original NLP transformer architecture. Variants [Wu et al.(2021)Wu, Xiao, Codella, Liu, Dai, Yuan, and Zhang, Han et al.(2021)Han, Xiao, Wu, Guo, Xu, and Wang, Liu et al.(2021)Liu, Lin, Cao, Hu, Wei, Zhang, Lin, and Guo, Yuan et al.(2021)Yuan, Chen, Wang, Yu, Shi, Tay, Feng, and Yan] of ViT propose a few hand-designed ways of applying local constraints to the global self-attention in ViT. In this paper, we automatically search for an architecture in a combined space that includes convolution, local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens], and axial global self-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen].
Neural Architecture Search.
Neural Architecture Search (NAS) was proposed to automate architecture design [Zoph and Le(2017)]. Early NAS methods usually sample many architectures and train them from scratch for picking up a good architecture, leading to large computational overhead [Zoph and Le(2017), Zoph et al.(2018)Zoph, Vasudevan, Shlens, and Le, Real et al.(2019)Real, Aggarwal, Huang, and Le, Liu et al.(2018)Liu, Simonyan, Vinyals, Fernando, and Kavukcuoglu, Tan and Le(2019), Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le, Sahni et al.(2021)Sahni, Varshini, Khare, and Tumanov]. More recently, people develop an one-shot pipeline by training a single over-parameterized network and sampling architectures within it to avoid the expensive train-from-scratch procedure [Bender et al.(2018)Bender, jan Kindermans, Zoph, Vasudevan, and Le, Brock et al.(2018)Brock, Lim, Ritchie, and Weston, Liu et al.(2019b)Liu, Simonyan, and Yang, Pham et al.(2018)Pham, Guan, Zoph, Le, and Dean, Cai et al.(2019)Cai, Zhu, and Han, Yu and Huang(2019a), Hu et al.(2020)Hu, Xie, Zheng, Liu, Shi, Liu, and Lin, Guo et al.(2020)Guo, Zhang, Mu, Heng, Liu, Wei, and Sun, Chu et al.(2021)Chu, Zhang, and Xu]. However, the search space of these methods is restricted in the MobileNet-like space [Howard et al.(2017)Howard, Zhu, Chen, Kalenichenko, Wang, Weyand, Andreetto, and Adam, Sandler et al.(2018)Sandler, Howard, Zhu, Zhmoginov, and Chen, Howard et al.(2019)Howard, Sandler, Chu, Chen, Chen, Tan, Wang, Zhu, Pang, Vasudevan, et al.]. There are also some attempts to search for self-attention vision models [Li et al.(2020)Li, Jin, Mei, Lian, Yang, Xie, Yu, Zhou, Bai, and Yuille, Wang et al.(2020d)Wang, Xiong, Neumann, Piergiovanni, Ryoo, Angelova, Kitani, and Hua, Li et al.(2021)Li, Tang, Wang, Peng, Wang, Liang, and Chang]. These works mainly focus on the single block design [Wang et al.(2020d)Wang, Xiong, Neumann, Piergiovanni, Ryoo, Angelova, Kitani, and Hua] and positions [Li et al.(2020)Li, Jin, Mei, Lian, Yang, Xie, Yu, Zhou, Bai, and Yuille], or searches in a small space [Li et al.(2021)Li, Tang, Wang, Peng, Wang, Liang, and Chang]. In this paper, self-attention and convolution are considered equally in our search space.
3 Method
In this section, we first define our operator-level search space that contains both convolution and self-attention. Next, we discuss our one-shot architecture-level search algorithm that trains a supernet. Finally, we present our proposed Hierarchical Sampling (HS) and Multi-Head Sharing (MHS) that helps training the supernet.
3.1 Operator-Level Search Space
Convolution is usually the default and the only operator for a NAS space [Zoph and Le(2017), Tan and Le(2019), Cai et al.(2019)Cai, Zhu, and Han, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le]. In this paper, however, we introduce self-attention operators into our operator-level space and search for the optimal combination of convolution and self-attention operators [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin]. Specifically, we include efficient self-attention operators that can be used as a stand-alone operator for a network. We use axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] instead of fully connected 2D self-attention [Dosovitskiy et al.(2021)Dosovitskiy, Beyer, Kolesnikov, Weissenborn, Zhai, Unterthiner, Dehghani, Minderer, Heigold, Gelly, Uszkoreit, and Houlsby] as an instantiation of global self-attention for computational efficiency.
Local Self-Attention.
Local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] limits its receptive field to a local window. Given an input feature map with height , width , and channels , the output at position , , is computed by pooling over the projected input as:
| (1) |
where is the local square region centered around location . Queries , keys , values are all linear projections of the input . . are all learnable matrices. The relative positional encodings are also learnable vectors and the inner product measures the compatibility from location to location . In practice, this single-head attention in Equ. (1) is extended to multi-head attention to capture a mixture of affinities [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin]. In particular, multi-head attention is computed by applying single-head attentions in parallel on (with different learnable matrices for the -th head), and then obtaining the final output by concatenating the results from each head, i.e\bmvaOneDot, .
The choice of local window size significantly affects model performance and computational cost. Besides, it is not clear how many local self-attention layers should be used for each stage or how to select a window size for each individual layer. For these reasons, we include local self-attention in our search space to find a good configuration.
Axial Self-Attention.
Axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen, Huang et al.(2019)Huang, Wang, Huang, Huang, Wei, and Liu, Ho et al.(2019)Ho, Kalchbrenner, Weissenborn, and Salimans] captures global relations by factorizing a 2D self-attention into two consecutive 1D self-attention operators, one on the height-axis, followed by one on the width axis Both of the axial-attention layers adopt the multi-head attention mechanism, as described above. Note that we do not use the PS-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] or BN [Ioffe and Szegedy(2015)] layers for fair comparison with local-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and faster implementation.
Despite capturing global contexts, axial-attention is less effective to model local relations if two local pixels do not belong to the same axis. In this case, combining axial-attention with convolution or local-attention is plausible. So we study the combination in this paper by including axial-attention into our operator-level search space.
3.2 Architecture-Level Search Space
| Operator | Convolution | Local Attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] | Axial Attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] |
|---|---|---|---|
| Expansion rates | 1/8, 1/4 | 1/4, 1/2 | 1/4, 1/2 |
| Kernel size | 3, 5, 7 | 3, 5, 7 | - |
| Query (key) channel rates | - | 1/2, 1 | 1/2, 1 |
| Value channels rates | - | 1/2, 1 | 1/2, 1 |
| Number of heads | - | 4, 8 | 4, 8 |
| Total choices (cardinality) | 6 | 48 | 16 |
Similar to hand-designed self-attention models, Local-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and Axial-DeepLab [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen], we employ a ResNet-like [He et al.(2016)He, Zhang, Ren, and Sun] model family to construct our architecture-level search space. Specifically, we replace all 33 convolutions by our operator-level search space that contains convolution, local-attention, and axial-attention.
Tab. 1 summarizes our search space for each block. Different from a cell-level search space in the NAS literature [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le], our spatial operators are not shared in each residual block. As a result, our search space allows a flexible combination of different operators at each layer. This space also includes pure convolutional [He et al.(2016)He, Zhang, Ren, and Sun], pure local-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens], and pure axial-attention[Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] ResNets. Our search space contains roughly models in total, 3.6 M times larger than that of OFA [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han] ().
3.3 Searching Pipeline
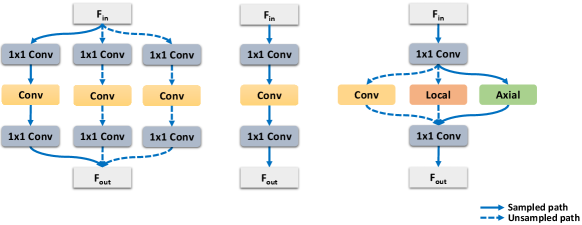
Given this search space, we employ the one-shot NAS pipeline [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le], where the entire search space is built as a weight-sharing supernet. The typical strategy [Cai et al.(2019)Cai, Zhu, and Han, Stamoulis et al.(2019)Stamoulis, Ding, Wang, Lymberopoulos, Priyantha, Liu, and Marculescu] of most one-shot NAS works is shown in Fig. 2 a). A MobileNet-like [Howard et al.(2017)Howard, Zhu, Chen, Kalenichenko, Wang, Weyand, Andreetto, and Adam, Sandler et al.(2018)Sandler, Howard, Zhu, Zhmoginov, and Chen, Howard et al.(2019)Howard, Sandler, Chu, Chen, Chen, Tan, Wang, Zhu, Pang, Vasudevan, et al.] supernet is built with blocks that contain several parallel candidates with different channels and receptive fields. Consequently, the supernet needs a lot of parameters to hold the large search space, making it inapplicable to our huge search space (Tab. 1). OFA and BigNAS [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] propose to share candidate weights in a single block, as shown in Fig. 2 b). This allows a much larger search space with manageable parameters but it still limited one operator only. In our case, different spatial operators can not share all the parameters.
Based on these works [Cai et al.(2019)Cai, Zhu, and Han, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le], we make a step forward. We insert local- [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and axial- [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] attention into the single block parallel with the spatial convolution as the primary spatial operator. These parallel spatial operators share the same projection layers and increase the flexibility of the supernet without introducing many parameters. Like [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le], we can formulate the problem as
| (2) |
where denotes that the selection of the parameters from the weights of the supernet with architecture configuration , is the sampling distribution of and denotes the loss on the training dataset. After training the supernet, an evolutionary algorithm is used to obtain the optimal model on the evolutionary search validation dataset with the goal as
| (3) |
Finally, we retrain the searched model from scratch on the whole training set and validate it on the validation set.
Next, we discuss two issues of the default supernet training pipeline and our solutions.
3.4 Hierarchical Sampling
Previous work [Wang et al.(2020a)Wang, Wu, Liu, Cai, Zhu, Gan, and Han] trains supernets by sampling candidates uniformly. However, as shown in Tab. 1, our search space candidates are highly biased towards the local-attention operator, leading to an imbalanced training of the operators and worse performance of the searched model. Therefore, we propose Hierarchical Sampling (HS). For each block, we first sample the spatial operator uniformly. Given the operator, we then randomly sample a candidate from the operator space. We can formulate this as
| (4) |
where the architecture can be expressed as operators configuration sampled from Tab. 1 (the first row) and weights configuration sampled from Tab. 1 (from the second to the sixth row) with uniform distribution . In this way, we ensure an equal sampling chance for all operators.
In addition, we notice that the training is biased towards middle-sized models. We attributes this to the fact that the search space is full of middle-sized models and thus random sampling trains mostly middle-sized models. To address this issue, we use Sandwich rule [Yu and Huang(2019b), Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] that samples the smallest candidate, the biggest candidate and 2 random candidates. Sandwich rule is adopted in our Hierarchical Sampling after the operator for each block is selected.
3.5 Multi-Head Sharing
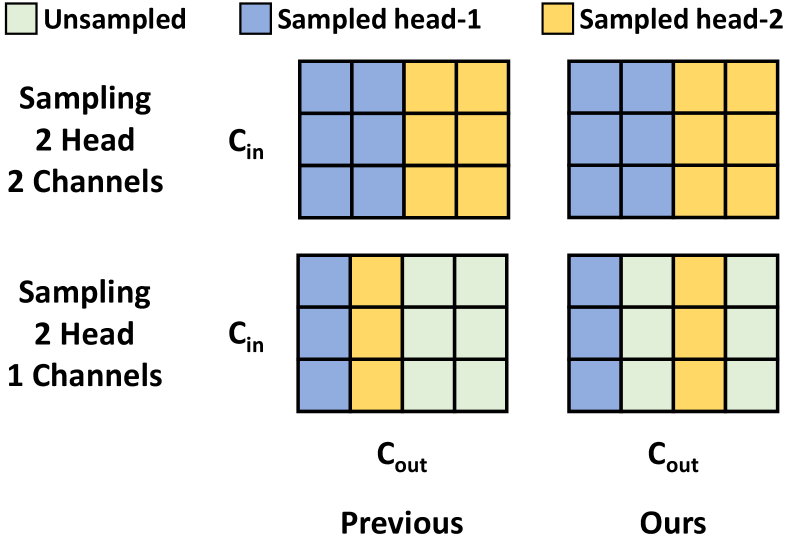
The weight-sharing strategy for convolution has been well studied. Previous works [Stamoulis et al.(2019)Stamoulis, Ding, Wang, Lymberopoulos, Priyantha, Liu, and Marculescu, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le, Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Bender et al.(2020)Bender, Liu, Chen, Chu, Cheng, Kindermans, and Le] share common parts of a convolution weight for different kernel sizes and channels. However, this strategy cannot be simply applied to our search space with multi-head self-attention operators. The varying number of heads makes sharing channels more complicated than convolution. In multi-head attention, the channels are split into multi-head groups to capture different dependencies [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin]. Thus, as shown in Fig. 3, the default weight-sharing strategy allocates the same channels for different multi-head groups, which is harmful to the supernet training. To deal with this issue, we propose Multi-Head Sharing (MHS). As shown in Fig. 3, we take into account the multi-head structure and first split all output channels into number-of-head groups. Then, we share channel weights only if they belong to the same head in multi-head self-attention. We show the selection procedure with PyTorch-like [Paszke et al.(2019)Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein, Antiga, et al.] pseudo code in Alg. 1. In this way, we ensure that different channel groups do not interfere with each other.
# w: weight matrix, c_in: in channels
# c_out: max out channels, s_c_out: sampled out channels, n: multi-head number
h_c = s_c_out / n
w = w.reshape(n, -1, c_in)
w = w[:, :h_c, :] # h_c, n, c_in
w = w.reshape(s_c_out, c_in)
return w
4 Experiments
Our main experiments are conducted on ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton] dataset. We also provide detailed ablation studies on the proposed Hierarchical Sampling and Multi-Head Sharing. Finally, we evaluate the adaptation of our searching algorithm on various small classification datasets.
4.1 ImageNet Classification
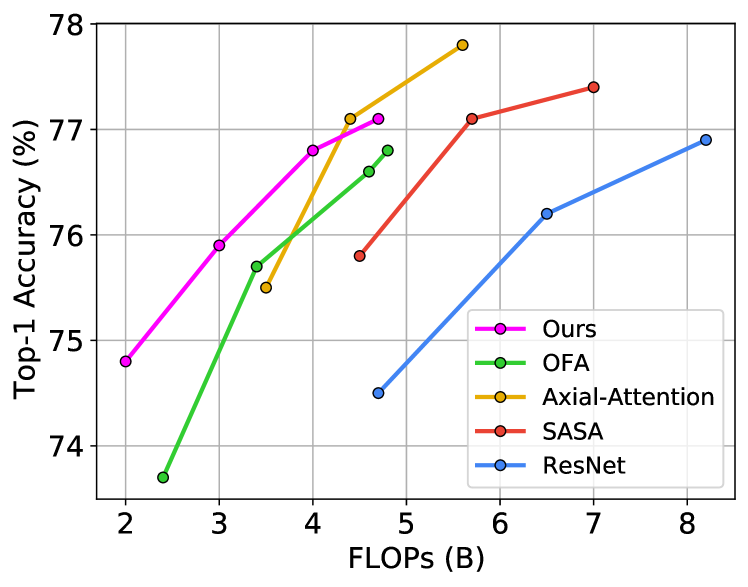
Tab. 4.2 shows the main results of our searched models with different FLOPs constraints. The searched models are compared with stand-alone convolution [He et al.(2016)He, Zhang, Ren, and Sun], stand-alone local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and stand-alone axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] models. As shown in Fig. 4.2, with 2B FLOPs budget, our TrioNet-A achieves 74.8% accuracy and outperforms ResNet with 57.4% less computation. With 3B FLOPs budget, our TrioNet-B achieves 75.9% accuracy, which outperforms stand-alone local self-attention and axial-attention respectively with 33.3% and 14.3% fewer FLOPs. These results show that our searched TrioNet is able to outperform all hand-designed single-operator networks in terms of computation efficiency. In addition to our main focus in the low computation regime, we also evaluate models in the high computation regime. With 4B and 4.7B FLOPs budgets, our TrioNet-C and TrioNet-D achieve comparable performance-FLOPs trade-offs with stand-alone axial-attention and still outperforms fully convolution [He et al.(2016)He, Zhang, Ren, and Sun] or local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] methods with fewer FLOPs. Compared with OFA [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han] under the same training settings as ours, TrioNet outperforms OFA with 1.1%, 0.2%, 0.2% and 0.3% accuracy with 16.7%, 11.8%, 13.0% and 2.1% less computation. Note that the larger models (TrioNet-C and TrioNet-D) are already close to the limit of our architecture space, which might lead to performance degrade. If large models instead of lightweight models are desired, our TrioNet searching pipeline can be directly extended to a high computation search space as well.
4.2 Ablation Studies
In this subsection, we provide more insights by ablating each of our proposed components separately. The experiments are also performed on ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton]. We monitor the training process of the supernets by directly evaluating the largest possible model for each operator.
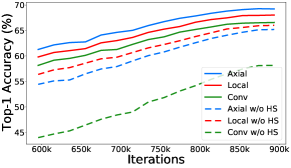
Hierarchical Sampling.
Fig. 5 a) visualizes the supernet training curves with and without our proposed Hierarchical Sampling. We observe that sampling all candidates uniformly hurts convolution models a lot due to the low probability of convolution being sampled. However, with our proposed Hierarchical Sampling, all the model results are improved. It is worth mentioning that with our Hierarchical Sampling strategy, the local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] models are improved too, even if they are not sampled as often as the case without Hierarchical Sampling. We hypothesize that the comparable performances of all three parallel candidates help the optimization of all operators.
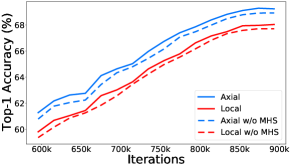
Multi-Head Sharing.
Fig. 5 b) compares the training process of the supernet with and without our proposed Multi-Head Sharing. We observe that our Multi-Head Sharing strategy helps large multi-head self-attention models achieve higher accuracy. Similar curves are observed for small models as well, though the curves are omitted in the figure. In addition to the training curves of the supernet, we also analyze the searched model results. As shown in Tab. 3, adopting Multi-Head Sharing in the supernet training improves the searched architecture by 1.5%, from 75.4% to 76.9%.
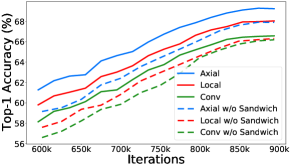
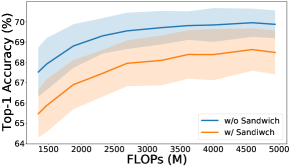
Sandwich rule.
Fig. 6 a) plots the training curves with and without Sandwich rule [Yu and Huang(2019b), Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le]. It shows that Sandwich rule helps the training of large models by a large margin for all operators. Fig. 6 b) shows the distribution of the sub-models selected from the supernet under different strategies. It can be observed that some middle-sized models are comparable with the biggest models because they are trained more and gain a lot from the large models optimization [Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le]. However, this accuracy partial order cannot reflect the training from scratch accuracy, and the searched model accuracy in Tab. 3 also shows this. With Sandwich rule, the sampling distribution is changed and the ranking of these models are kept.
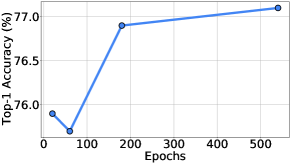
Number of epochs.
Weight-sharing NAS methods require a long supernet training schedule because the candidates need to be well-trained before they can accurately reflect how good each candidate is. Similarly, we evaluate how our TrioNet searching algorithm scales with longer training schedules. As shown in Fig. 7 a), our searched models does not perform well with 20 epochs and 60 epochs, probably because the candidates have not been well-trained with such a short schedule. However, we do not observe a huge difference between 180 epochs and 540 epochs, probably because our supernet saturates with our simple ResNet-like training recipe and the weak data augmentation used.
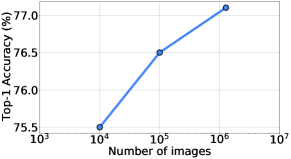
Amount of data.
Our TrioNet searching algorithm is also tested with different amount of data. To achieve this goal, we train the supernets with 10k, 100k images and the full training dataset (we still remove the evolutionary search set). Then, the searched architectures are still trained from scratch on the full training set. In this way, we evaluate only the contribution of data on the searching algorithm, or the quality of the searched architecture, which is decoupled with the amount of data used to the searched models from scratch. Fig. 7 b) shows that the searching on only 10k images gives a poor architecture, and our searching algorithm scales well, i.e\bmvaOneDot, finds better architectures, with more data consumed.
|
 |
|---|---|
| (a) Effect of Hierarchical Sampling. | (b) Effect of Multi-Head Sharing. |
|
 |
|---|---|
| (a) Better large models. | (b) Worse middle-sized models. |
Summary.
| Settings | Sandwich | HS | MHS | Epochs | FLOPs (B) | Acc (%) |
|---|---|---|---|---|---|---|
| Random model | - | - | - | - | 4.8 | 74.7 |
| w/o Sandwich | ✓ | ✓ | 180 | 3.6 | 74.9 | |
| w/o HS | ✓ | ✓ | 180 | 3.5 | 75.6 | |
| w/o MHS | ✓ | ✓ | 180 | 5.1 | 75.4 | |
| Ours | ✓ | ✓ | ✓ | 180 | 5.2 | 76.9 |
| Ours w/ more epochs | ✓ | ✓ | ✓ | 540 | 4.7 | 77.1 |
Tab. 3 summarizes the searched model accuracies of our ablated settings. We notice that without Sandwich rules [Yu and Huang(2019b), Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le], the searched model only achieves 74.9% accuracy with 3.6B FLOPs, which is a middle-sized model. This indicates that the sandwich rules prevent our searching from biasing towards middle-sized models. Besides, our proposed Hierarchical Sampling shows 1.3% performance gain on the searched model and Multi-Head Sharing strategy promotes the searched model with 1.5% accuracy improvement. Furthermore, we also test a random model with the comparable size as the searched model, which only gets 74.7% accuracy. Our NAS pipeline achieves 2.4% improvement compared with the random model.
|
 |
|---|---|
| (a) Varying number of epochs | (b) Varying number of images |
4.3 Results on Small Datasets
The goal of NAS is to automate the architecture design on the target data, task, and computation budget. From this perspective, we adapt our TrioNet NAS algorithm to other datasets beyond ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton], in order to evaluate if the algorithm is able to find a good architecture on the target datasets. These adaptation experiments are performed on five small datasets: Stanford Cars [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei], FGVC Aircraft [Maji et al.(2013)Maji, Rahtu, Kannala, Blaschko, and Vedaldi], CUB [Welinder et al.(2010)Welinder, Branson, Mita, Wah, Schroff, Belongie, and Perona], Caltech-101 [Fei-Fei et al.(2004)Fei-Fei, Fergus, and Perona] and 102 Flowers [Nilsback and Zisserman(2008)].
Overall Performance.
| Dataset | ResNet-18 | Local-26 | Axial-26 | TrioNet | ||||
|---|---|---|---|---|---|---|---|---|
| FLOPs | Acc | FLOPs | Acc | FLOPs | Acc | FLOPs | Acc | |
| (B) | (%) | (B) | (%) | (B) | (%) | (B) | (%) | |
| Stanford Cars | 3.6 | 86.8 | 4.5 | 84.4 | 3.5 | 78.2 | 3.7 | 88.5 |
| FGVC Aircraft | 3.6 | 79.8 | 4.5 | 82.4 | 3.5 | 74.4 | 2.9 | 82.1 |
| CUB | 3.6 | 69.3 | 4.5 | 65.2 | 3.5 | 58.9 | 2.4 | 68.4 |
| Caltech-101 | 3.6 | 75.3 | 4.5 | 71.4 | 3.5 | 66.1 | 2.4 | 72.2 |
| 102 Flowers | 3.6 | 91.4 | 4.5 | 87.7 | 3.5 | 81.9 | 3.6 | 90.3 |
| Average | 3.6 | 80.5 | 4.5 | 78.2 | 3.5 | 71.9 | 3.0 | 80.3 |
| Settings | ResNet-18 | Local-26 | Axial-26 | TrioNet w/ supernet weights | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Survival Prob | 1.00 | 0.80 | 0.33 | 1.00 | 0.80 | 0.33 | 1.00 | 0.80 | 0.33 | - |
| Stanford Cars | 86.8 | 85.7 | 81.5 | 84.4 | 83.5 | 82.7 | 78.2 | 81.7 | 79.7 | 87.7 |
| FGVC Aircraft | 79.8 | 78.6 | 73.8 | 82.4 | 75.8 | 72.9 | 74.4 | 74.0 | 74.6 | 80.5 |
Tab. 4 shows the results of our TrioNet models searched directly on various small datasets [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei, Maji et al.(2013)Maji, Rahtu, Kannala, Blaschko, and Vedaldi, Welinder et al.(2010)Welinder, Branson, Mita, Wah, Schroff, Belongie, and Perona, Fei-Fei et al.(2004)Fei-Fei, Fergus, and Perona, Nilsback and Zisserman(2008)] and finetuned from supernet weights, as well as the accuracies of baseline models. Empirically, we notice that axial-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen], which outperforms ResNet [He et al.(2016)He, Zhang, Ren, and Sun] by a large margin on ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton], performs poorly on these small datasets with a big gap to ResNet (8.6% accuracy on average), probably because the global axial-attention uses less induction bias than convolution or local-attention. However, in this challenging case, our TrioNet finds a better architecture than the hand-designed local self-attention [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] and axial self-attention [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] methods. On these datasets, TrioNet is able to match the performance of the best operator, convolution in this case, with 20% fewer FLOPs. This result, together with our ImageNet classification result, suggests that TrioNet robustly finds a good architecture no matter what operator the target data prefers.
Regularization Effect.
Our sampling-based supernet training, where we sample an operator and then sample a candidate in the supernet, is similar to stochastic depth [Huang et al.(2016)Huang, Sun, Liu, Sedra, and Weinberger] with a survival probability of 0.33 for each operator. Therefore, we compare our TrioNet (weights directly copied from the supernet) with stand-alone models of various survival probability on Stanford Cars [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei] and FGVC Aircraft [Maji et al.(2013)Maji, Rahtu, Kannala, Blaschko, and Vedaldi], as shown in Tab. 5. We notice that most stand-alone models perform worse with stochastic depth [Huang et al.(2016)Huang, Sun, Liu, Sedra, and Weinberger]. However, our TrioNet with its weights directly sampled from the supernet still outperforms these stand-alone models on Stanford Cars [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei]. This suggests that the joint training of different operators is contributing to the performance as a better regularizer than stochastic depth [Huang et al.(2016)Huang, Sun, Liu, Sedra, and Weinberger].
4.4 Results on Segmentation Tasks
| Backbone | Semantic Segmentation | Panoptic Segmentation | ||||
|---|---|---|---|---|---|---|
| FLOPs | FLOPs | |||||
| ResNet-50 [He et al.(2016)He, Zhang, Ren, and Sun] | 66.4B | 71.2 | 97.1B | 31.1 | 31.8 | 29.9 |
| Axial-26 [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] | 33.9B | 67.5 | 60.4B | 30.6 | 30.9 | 30.2 |
| TrioNet-B | 29.6B | 69.3 | 52.3B | 31.8 | 32.4 | 30.8 |
In this section, we evaluate TrioNet on semantic segmentation [Long et al.(2015)Long, Shelhamer, and Darrell, Chen et al.(2015)Chen, Papandreou, Kokkinos, Murphy, and Yuille] and panoptic segmentation [Kirillov et al.(2019)Kirillov, He, Girshick, Rother, and Dollár] tasks. The ImageNet pretrained models are employed. For semantic segmentation, we apply DeepLabV3 [Chen et al.(2017)Chen, Papandreou, Schroff, and Adam] on PASCAL VOC datasets [Everingham et al.(2010)Everingham, Van Gool, Williams, Winn, and Zisserman]. For panoptic segmentation, we perform the experiments on COCO datasets [Lin et al.(2014)Lin, Maire, Belongie, Hays, Perona, Ramanan, Dollár, and Zitnick] with Panoptic-DeepLab [Cheng et al.(2020)Cheng, Collins, Zhu, Liu, Huang, Adam, and Chen] under a short training schedule. All experiments only replace the backbone with TrioNet-B.
Results.
Tab. 6 shows the semantic segmentation and panoptic segmentation results. Using TrioNet-B as the backbone outperforms Axial-26 [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] by 1.8% mIoU on semantic segmentation with 12.7% less computation. On panoptic segmentation, TrioNet-B outperforms Axial-26 [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] by 1.2% with 13.4% fewer FLOPs.
5 Conclusion
In this paper, we design an algorithm to automatically discover optimal deep neural network architectures in a space that includes fully self-attention models [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens, Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen]. We found it is not trivial to extend the conventional NAS strategy [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] directly because of the difference between convolution and self-attention operators. We therefore specifically redesign the searching algorithm to make it effective to search for self-attention vision models. Despite our observation is from studying the self-attention module, we believe this is readily to extend to searching for other components such as normalization modules [Ioffe and Szegedy(2015)].
References
- [Bahdanau et al.(2015)Bahdanau, Cho, and Bengio] Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate. In ICLR, 2015.
- [Bello et al.(2019)Bello, Zoph, Vaswani, Shlens, and Le] Irwan Bello, Barret Zoph, Ashish Vaswani, Jonathon Shlens, and Quoc V Le. Attention augmented convolutional networks. In ICCV, 2019.
- [Bender et al.(2020)Bender, Liu, Chen, Chu, Cheng, Kindermans, and Le] Gabriel Bender, Hanxiao Liu, B. Chen, Grace Chu, S. Cheng, Pieter-Jan Kindermans, and Quoc V. Le. Can weight sharing outperform random architecture search? an investigation with tunas. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 14311–14320, 2020.
- [Bender et al.(2018)Bender, jan Kindermans, Zoph, Vasudevan, and Le] Gabriel M. Bender, Pieter jan Kindermans, Barret Zoph, Vijay Vasudevan, and Quoc Le. Understanding and simplifying one-shot architecture search. 2018. URL http://proceedings.mlr.press/v80/bender18a/bender18a.pdf.
- [Brock et al.(2018)Brock, Lim, Ritchie, and Weston] Andrew Brock, Theo Lim, J.M. Ritchie, and Nick Weston. SMASH: One-shot model architecture search through hypernetworks. In International Conference on Learning Representations, 2018. URL https://openreview.net/forum?id=rydeCEhs-.
- [Cai et al.(2019)Cai, Zhu, and Han] Han Cai, Ligeng Zhu, and Song Han. ProxylessNAS: Direct neural architecture search on target task and hardware. In International Conference on Learning Representations, 2019. URL https://openreview.net/forum?id=HylVB3AqYm.
- [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han] Han Cai, Chuang Gan, Tianzhe Wang, Zhekai Zhang, and Song Han. Once-for-all: Train one network and specialize it for efficient deployment. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=HylxE1HKwS.
- [Cao et al.(2019)Cao, Xu, Lin, Wei, and Hu] Yue Cao, J. Xu, Stephen Lin, Fangyun Wei, and H. Hu. Gcnet: Non-local networks meet squeeze-excitation networks and beyond. 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), pages 1971–1980, 2019.
- [Chen et al.(2015)Chen, Papandreou, Kokkinos, Murphy, and Yuille] Liang-Chieh Chen, George Papandreou, Iasonas Kokkinos, Kevin Murphy, and Alan L Yuille. Semantic image segmentation with deep convolutional nets and fully connected crfs. In ICLR, 2015.
- [Chen et al.(2017)Chen, Papandreou, Schroff, and Adam] Liang-Chieh Chen, George Papandreou, Florian Schroff, and Hartwig Adam. Rethinking atrous convolution for semantic image segmentation. arXiv:1706.05587, 2017.
- [Chen et al.(2018)Chen, Kalantidis, Li, Yan, and Feng] Yunpeng Chen, Yannis Kalantidis, Jianshu Li, Shuicheng Yan, and Jiashi Feng. A^ 2-nets: Double attention networks. In NeurIPS, 2018.
- [Cheng et al.(2020)Cheng, Collins, Zhu, Liu, Huang, Adam, and Chen] Bowen Cheng, Maxwell D Collins, Yukun Zhu, Ting Liu, Thomas S Huang, Hartwig Adam, and Liang-Chieh Chen. Panoptic-DeepLab: A Simple, Strong, and Fast Baseline for Bottom-Up Panoptic Segmentation. In CVPR, 2020.
- [Chu et al.(2021)Chu, Zhang, and Xu] Xiangxiang Chu, Bo Zhang, and Ruijun Xu. Fairnas: Rethinking evaluation fairness of weight sharing neural architecture search. In International Conference on Computer Vision, 2021.
- [Dosovitskiy et al.(2021)Dosovitskiy, Beyer, Kolesnikov, Weissenborn, Zhai, Unterthiner, Dehghani, Minderer, Heigold, Gelly, Uszkoreit, and Houlsby] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An image is worth 16x16 words: Transformers for image recognition at scale. In International Conference on Learning Representations, 2021. URL https://openreview.net/forum?id=YicbFdNTTy.
- [Everingham et al.(2010)Everingham, Van Gool, Williams, Winn, and Zisserman] M. Everingham, L. Van Gool, C. K. I. Williams, J. Winn, and A. Zisserman. The pascal visual object classes (voc) challenge. International Journal of Computer Vision, 88(2):303–338, June 2010.
- [Fei-Fei et al.(2004)Fei-Fei, Fergus, and Perona] Li Fei-Fei, R. Fergus, and P. Perona. Learning generative visual models from few training examples: An incremental bayesian approach tested on 101 object categories. 2004 Conference on Computer Vision and Pattern Recognition Workshop, pages 178–178, 2004.
- [Ghiasi et al.(2019)Ghiasi, Lin, Pang, and Le] Golnaz Ghiasi, Tsung-Yi Lin, Ruoming Pang, and Quoc V. Le. Nas-fpn: Learning scalable feature pyramid architecture for object detection. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 7029–7038, 2019.
- [Goyal et al.(2017)Goyal, Dollár, Girshick, Noordhuis, Wesolowski, Kyrola, Tulloch, Jia, and He] Priya Goyal, Piotr Dollár, Ross Girshick, Pieter Noordhuis, Lukasz Wesolowski, Aapo Kyrola, Andrew Tulloch, Yangqing Jia, and Kaiming He. Accurate, large minibatch sgd: Training imagenet in 1 hour. arXiv:1706.02677, 2017.
- [Guo et al.(2020)Guo, Zhang, Mu, Heng, Liu, Wei, and Sun] Zichao Guo, X. Zhang, Haoyuan Mu, Wen Heng, Z. Liu, Y. Wei, and Jian Sun. Single path one-shot neural architecture search with uniform sampling. In ECCV, 2020.
- [Han et al.(2021)Han, Xiao, Wu, Guo, Xu, and Wang] Kai Han, An Xiao, E. Wu, Jianyuan Guo, Chunjing Xu, and Yunhe Wang. Transformer in transformer. ArXiv, abs/2103.00112, 2021.
- [He et al.(2016)He, Zhang, Ren, and Sun] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
- [He et al.(2017)He, Gkioxari, Dollár, and Girshick] Kaiming He, Georgia Gkioxari, Piotr Dollár, and Ross Girshick. Mask r-cnn. In ICCV, 2017.
- [Ho et al.(2019)Ho, Kalchbrenner, Weissenborn, and Salimans] Jonathan Ho, Nal Kalchbrenner, Dirk Weissenborn, and Tim Salimans. Axial attention in multidimensional transformers. arXiv:1912.12180, 2019.
- [Howard et al.(2019)Howard, Sandler, Chu, Chen, Chen, Tan, Wang, Zhu, Pang, Vasudevan, et al.] Andrew Howard, Mark Sandler, Grace Chu, Liang-Chieh Chen, Bo Chen, Mingxing Tan, Weijun Wang, Yukun Zhu, Ruoming Pang, Vijay Vasudevan, et al. Searching for mobilenetv3. In ICCV, 2019.
- [Howard et al.(2017)Howard, Zhu, Chen, Kalenichenko, Wang, Weyand, Andreetto, and Adam] Andrew G Howard, Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv:1704.04861, 2017.
- [Hu et al.(2019)Hu, Zhang, Xie, and Lin] Han Hu, Zheng Zhang, Zhenda Xie, and Stephen Lin. Local relation networks for image recognition. In ICCV, 2019.
- [Hu et al.(2020)Hu, Xie, Zheng, Liu, Shi, Liu, and Lin] Shoukang Hu, S. Xie, Hehui Zheng, C. Liu, Jianping Shi, Xunying Liu, and D. Lin. Dsnas: Direct neural architecture search without parameter retraining. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 12081–12089, 2020.
- [Huang et al.(2016)Huang, Sun, Liu, Sedra, and Weinberger] Gao Huang, Yu Sun, Zhuang Liu, Daniel Sedra, and Kilian Q Weinberger. Deep networks with stochastic depth. In ECCV, 2016.
- [Huang et al.(2019)Huang, Wang, Huang, Huang, Wei, and Liu] Zilong Huang, Xinggang Wang, Lichao Huang, Chang Huang, Yunchao Wei, and Wenyu Liu. Ccnet: Criss-cross attention for semantic segmentation. In ICCV, 2019.
- [Ioffe and Szegedy(2015)] Sergey Ioffe and Christian Szegedy. Batch normalization: accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
- [Kingma and Ba(2014)] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
- [Kirillov et al.(2019)Kirillov, He, Girshick, Rother, and Dollár] Alexander Kirillov, Kaiming He, Ross Girshick, Carsten Rother, and Piotr Dollár. Panoptic segmentation. In CVPR, 2019.
- [Krause et al.(2013)Krause, Deng, Stark, and Fei-Fei] J. Krause, Jun Deng, Michael Stark, and Li Fei-Fei. Collecting a large-scale dataset of fine-grained cars. 2013.
- [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In NeurIPS, 2012.
- [Li et al.(2021)Li, Tang, Wang, Peng, Wang, Liang, and Chang] Changlin Li, Tao Tang, Guangrun Wang, Jiefeng Peng, Bing Wang, Xiaodan Liang, and Xiaojun Chang. Bossnas: Exploring hybrid cnn-transformers with block-wisely self-supervised neural architecture search. ArXiv, abs/2103.12424, 2021.
- [Li et al.(2020)Li, Jin, Mei, Lian, Yang, Xie, Yu, Zhou, Bai, and Yuille] Yingwei Li, X. Jin, Jieru Mei, Xiaochen Lian, Linjie Yang, Cihang Xie, Qihang Yu, Yuyin Zhou, S. Bai, and A. Yuille. Neural architecture search for lightweight non-local networks. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10294–10303, 2020.
- [Lin et al.(2014)Lin, Maire, Belongie, Hays, Perona, Ramanan, Dollár, and Zitnick] Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In ECCV, 2014.
- [Liu et al.(2019a)Liu, Chen, Schroff, Adam, Hua, Yuille, and Fei-Fei] Chenxi Liu, Liang-Chieh Chen, Florian Schroff, Hartwig Adam, Wei Hua, A. Yuille, and Li Fei-Fei. Auto-deeplab: Hierarchical neural architecture search for semantic image segmentation. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 82–92, 2019a.
- [Liu et al.(2018)Liu, Simonyan, Vinyals, Fernando, and Kavukcuoglu] Hanxiao Liu, Karen Simonyan, Oriol Vinyals, Chrisantha Fernando, and Koray Kavukcuoglu. Hierarchical representations for efficient architecture search. In International Conference on Learning Representations, 2018. URL https://openreview.net/forum?id=BJQRKzbA-.
- [Liu et al.(2019b)Liu, Simonyan, and Yang] Hanxiao Liu, Karen Simonyan, and Yiming Yang. DARTS: Differentiable architecture search. In International Conference on Learning Representations, 2019b. URL https://openreview.net/forum?id=S1eYHoC5FX.
- [Liu et al.(2021)Liu, Lin, Cao, Hu, Wei, Zhang, Lin, and Guo] Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and B. Guo. Swin transformer: Hierarchical vision transformer using shifted windows. ArXiv, abs/2103.14030, 2021.
- [Long et al.(2015)Long, Shelhamer, and Darrell] Jonathan Long, Evan Shelhamer, and Trevor Darrell. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3431–3440, 2015.
- [Maji et al.(2013)Maji, Rahtu, Kannala, Blaschko, and Vedaldi] Subhransu Maji, Esa Rahtu, Juho Kannala, Matthew B. Blaschko, and A. Vedaldi. Fine-grained visual classification of aircraft. ArXiv, abs/1306.5151, 2013.
- [Nilsback and Zisserman(2008)] Maria-Elena Nilsback and Andrew Zisserman. Automated flower classification over a large number of classes. 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing, pages 722–729, 2008.
- [Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens] Niki Parmar, Prajit Ramachandran, Ashish Vaswani, Irwan Bello, Anselm Levskaya, and Jon Shlens. Stand-alone self-attention in vision models. In NeurIPS, 2019.
- [Paszke et al.(2019)Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein, Antiga, et al.] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32:8026–8037, 2019.
- [Pham et al.(2018)Pham, Guan, Zoph, Le, and Dean] Hieu Pham, Melody Y. Guan, Barret Zoph, Quoc V. Le, and J. Dean. Efficient neural architecture search via parameter sharing. In ICML, 2018.
- [Real et al.(2019)Real, Aggarwal, Huang, and Le] Esteban Real, A. Aggarwal, Y. Huang, and Quoc V. Le. Regularized evolution for image classifier architecture search. In AAAI, 2019.
- [Ren et al.(2015)Ren, He, Girshick, and Sun] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. Faster r-cnn: Towards real-time object detection with region proposal networks. In NeurIPS, 2015.
- [Sahni et al.(2021)Sahni, Varshini, Khare, and Tumanov] Manas Sahni, Shreya Varshini, Alind Khare, and Alexey Tumanov. Comp{ofa} – compound once-for-all networks for faster multi-platform deployment. In International Conference on Learning Representations, 2021. URL https://openreview.net/forum?id=IgIk8RRT-Z.
- [Sandler et al.(2018)Sandler, Howard, Zhu, Zhmoginov, and Chen] Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, and Liang-Chieh Chen. Mobilenetv2: Inverted residuals and linear bottlenecks. In CVPR, 2018.
- [Srivastava et al.(2014)Srivastava, Hinton, Krizhevsky, Sutskever, and Salakhutdinov] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929–1958, 2014. URL http://jmlr.org/papers/v15/srivastava14a.html.
- [Stamoulis et al.(2019)Stamoulis, Ding, Wang, Lymberopoulos, Priyantha, Liu, and Marculescu] Dimitrios Stamoulis, Ruizhou Ding, Di Wang, D. Lymberopoulos, B. Priyantha, J. Liu, and Diana Marculescu. Single-path nas: Designing hardware-efficient convnets in less than 4 hours. In ECML/PKDD, 2019.
- [Szegedy et al.(2016)Szegedy, Vanhoucke, Ioffe, Shlens, and Wojna] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. In CVPR, 2016.
- [Tan and Le(2019)] Mingxing Tan and Quoc Le. EfficientNet: Rethinking model scaling for convolutional neural networks. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pages 6105–6114. PMLR, 09–15 Jun 2019. URL http://proceedings.mlr.press/v97/tan19a.html.
- [Vaswani et al.(2017)Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, and Polosukhin] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS, 2017.
- [Wang et al.(2020a)Wang, Wu, Liu, Cai, Zhu, Gan, and Han] Hanrui Wang, Zhanghao Wu, Zhijian Liu, Han Cai, Ligeng Zhu, Chuang Gan, and Song Han. HAT: Hardware-aware transformers for efficient natural language processing. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 7675–7688, Online, July 2020a. Association for Computational Linguistics. 10.18653/v1/2020.acl-main.686. URL https://www.aclweb.org/anthology/2020.acl-main.686.
- [Wang et al.(2020b)Wang, Zhu, Green, Adam, Yuille, and Chen] Huiyu Wang, Yukun Zhu, Bradley Green, Hartwig Adam, Alan Yuille, and Liang-Chieh Chen. Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentation. In ECCV, 2020b.
- [Wang et al.(2020c)Wang, Gao, Chen, Wang, Tian, and Shen] Ning Wang, Y. Gao, Hao Chen, P. Wang, Zhi Tian, and Chunhua Shen. Nas-fcos: Fast neural architecture search for object detection. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 11940–11948, 2020c.
- [Wang et al.(2020d)Wang, Xiong, Neumann, Piergiovanni, Ryoo, Angelova, Kitani, and Hua] Xiaofang Wang, Xuehan Xiong, Maxim Neumann, A. Piergiovanni, M. Ryoo, A. Angelova, Kris M. Kitani, and Wei Hua. Attentionnas: Spatiotemporal attention cell search for video classification. ArXiv, abs/2007.12034, 2020d.
- [Wang et al.(2018)Wang, Girshick, Gupta, and He] Xiaolong Wang, Ross Girshick, Abhinav Gupta, and Kaiming He. Non-local neural networks. In CVPR, 2018.
- [Wang et al.(2020e)Wang, Lin, Sheng, Yan, and Shao] Zihao Wang, Chen Lin, Lu Sheng, Junjie Yan, and Jing Shao. Pv-nas: Practical neural architecture search for video recognition. ArXiv, abs/2011.00826, 2020e.
- [Welinder et al.(2010)Welinder, Branson, Mita, Wah, Schroff, Belongie, and Perona] P. Welinder, S. Branson, T. Mita, C. Wah, F. Schroff, S. Belongie, and P. Perona. Caltech-UCSD Birds 200. Technical Report CNS-TR-2010-001, California Institute of Technology, 2010.
- [Wu et al.(2019)Wu, Dai, Zhang, Wang, Sun, Wu, Tian, Vajda, Jia, and Keutzer] Bichen Wu, Xiaoliang Dai, Peizhao Zhang, Yanghan Wang, Fei Sun, Yiming Wu, Yuandong Tian, Peter Vajda, Yangqing Jia, and Kurt Keutzer. Fbnet: Hardware-aware efficient convnet design via differentiable neural architecture search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10734–10742, 2019.
- [Wu et al.(2021)Wu, Xiao, Codella, Liu, Dai, Yuan, and Zhang] Haiping Wu, Bin Xiao, N. Codella, Mengchen Liu, X. Dai, Lu Yuan, and Lei Zhang. Cvt: Introducing convolutions to vision transformers. ArXiv, abs/2103.15808, 2021.
- [Wu et al.(2016)Wu, Schuster, Chen, Le, Norouzi, Macherey, Krikun, Cao, Gao, Macherey, et al.] Yonghui Wu, Mike Schuster, Zhifeng Chen, Quoc V Le, Mohammad Norouzi, Wolfgang Macherey, Maxim Krikun, Yuan Cao, Qin Gao, Klaus Macherey, et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv:1609.08144, 2016.
- [Yu and Huang(2019a)] J. Yu and T. Huang. Network slimming by slimmable networks: Towards one-shot architecture search for channel numbers. ArXiv, abs/1903.11728, 2019a.
- [Yu and Huang(2019b)] J. Yu and Thomas S. Huang. Universally slimmable networks and improved training techniques. 2019 IEEE/CVF International Conference on Computer Vision (ICCV), pages 1803–1811, 2019b.
- [Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] Jiahui Yu, Pengchong Jin, Hanxiao Liu, Gabriel Bender, Pieter-Jan Kindermans, Mingxing Tan, T. Huang, Xiaodan Song, and Quoc V. Le. Bignas: Scaling up neural architecture search with big single-stage models. In ECCV, 2020.
- [Yuan et al.(2021)Yuan, Chen, Wang, Yu, Shi, Tay, Feng, and Yan] L. Yuan, Y. Chen, Tao Wang, Weihao Yu, Yujun Shi, Francis E. H. Tay, Jiashi Feng, and S. Yan. Tokens-to-token vit: Training vision transformers from scratch on imagenet. ArXiv, abs/2101.11986, 2021.
- [Zhao et al.(2020)Zhao, Jia, and Koltun] Hengshuang Zhao, Jiaya Jia, and V. Koltun. Exploring self-attention for image recognition. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 10073–10082, 2020.
- [Zhu et al.(2019a)Zhu, Xu, Bai, Huang, and Bai] Zhen Zhu, Mengde Xu, Song Bai, Tengteng Huang, and Xiang Bai. Asymmetric non-local neural networks for semantic segmentation. In CVPR, 2019a.
- [Zhu et al.(2019b)Zhu, Liu, Yang, Yuille, and Xu] Zhuotun Zhu, Chenxi Liu, Dong Yang, A. Yuille, and Daguang Xu. V-nas: Neural architecture search for volumetric medical image segmentation. 2019 International Conference on 3D Vision (3DV), pages 240–248, 2019b.
- [Zoph and Le(2017)] Barret Zoph and Quoc V. Le. Neural architecture search with reinforcement learning. 2017. URL https://arxiv.org/abs/1611.01578.
- [Zoph et al.(2018)Zoph, Vasudevan, Shlens, and Le] Barret Zoph, Vijay Vasudevan, Jonathon Shlens, and Quoc V. Le. Learning transferable architectures for scalable image recognition. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8697–8710, 2018.
Appendix A Implementation Details
Search Space
Our search space contains four stages with blocks in total. The selected number of blocks is for the first stage, for the second, for the third and for the last stage. The other choices are shown in Tab. 1 in the main paper.
ImageNet
Following the typical weight-sharing strategy, the original ImageNet training set is split into two subsets: 10k images for evolutionary search validation and the rest for training the supernet [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han]. We report our results on the original validation set.
In our first stage of training, we apply SGD optimizer with learning rate , Nesterov momentum and the weight decay , which is only added to the largest model. Label smoothing [Szegedy et al.(2016)Szegedy, Vanhoucke, Ioffe, Shlens, and Wojna] is also adopted. We do not use dropout [Srivastava et al.(2014)Srivastava, Hinton, Krizhevsky, Sutskever, and Salakhutdinov] or color jitter since this training procedure is already strongly regularized. We train our supernet for epochs, where contains warmup epochs, with batchsize per gpu and in total. We use [Goyal et al.(2017)Goyal, Dollár, Girshick, Noordhuis, Wesolowski, Kyrola, Tulloch, Jia, and He] in the final BN [Ioffe and Szegedy(2015)] layer for each residual block to stabilize the training procedure.
After searching, we train the searched model from scratch. We change the training epochs to , and keep other hyper-parameters not changed.
For OFA [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han] retraining, we apply the same training procedure on the models provided by their codebase. We employ the provided models with MACCs 0.6B, 0.9B, 1.2B and 1.8B (FLOPs are 1.2B, 1.8B, 2.4B and 3.6B). By using our setting that image input size is and convert the stem as conv stem [He et al.(2016)He, Zhang, Ren, and Sun, Parmar et al.(2019)Parmar, Ramachandran, Vaswani, Bello, Levskaya, and Shlens], these models FLOPs become 2.4B, 3.4B, 4.6B and 4.8B.
Small Datasets.
We modify our ImageNet recipe by training 60k iterations with weight decay , dropout 0.1, attention-dropout 0.1, and strong color jittering since the datasets are small and easy to overfit. For each dataset, 500 of the training images are selected for evolutionary search. After training the supernet and the evolutionary search, we directly sample the weights [Cai et al.(2020)Cai, Gan, Wang, Zhang, and Han, Yu et al.(2020)Yu, Jin, Liu, Bender, Kindermans, Tan, Huang, Song, and Le] from the supernet and finetune the searched model for 1k iterations with a base learning rate with batchsize 128. We do not employ ImageNet [Krizhevsky et al.(2012)Krizhevsky, Sutskever, and Hinton] pretraining in order to test the adaptation of our searching algorithm directly on the target data, instead of testing the transfer performance of the found architecture.
Segmentation
For semantic segmentation on PASCAL VOC datasets [Everingham et al.(2010)Everingham, Van Gool, Williams, Winn, and Zisserman], we use SGD optimizer with learning rate , momentum and weight decay . Models are trained with batchsize for iterations and the input image size is . We use output stride and do not apply dilated operators in the backbone. For panoptic segmentation on COCO datasets, we apply Adam optimizer [Kingma and Ba(2014)] with learning rate and without weight decay. Models are trained with batchsize for iterations and the input images size is .