Seer: Facilitating Structured Reasoning and Explanation via Reinforcement Learning
Abstract
Elucidating the reasoning process with structured explanations from question to answer is crucial, as it significantly enhances the interpretability, traceability, and trustworthiness of question-answering (QA) systems. However, structured explanations demand models to perform intricately structured reasoning, which poses great challenges. Most existing methods focus on single-step reasoning through supervised learning, ignoring logical dependencies between steps. Moreover, existing reinforcement learning (RL) based methods overlook the structured relationships, underutilizing the potential of RL in structured reasoning. In this paper, we propose Seer, a novel method that maximizes a structure-based return to facilitate structured reasoning and explanation. Our proposed structure-based return precisely describes the hierarchical and branching structure inherent in structured reasoning, effectively capturing the intricate relationships between different reasoning steps. In addition, we introduce a fine-grained reward function to meticulously delineate diverse reasoning steps. Extensive experiments show that Seer significantly outperforms state-of-the-art methods, achieving an absolute improvement of 6.9% over RL-based methods on EntailmentBank, a 4.4% average improvement on STREET benchmark, and exhibiting outstanding efficiency and cross-dataset generalization performance. Our code is available at https://github.com/Chen-GX/SEER.
1 Introduction
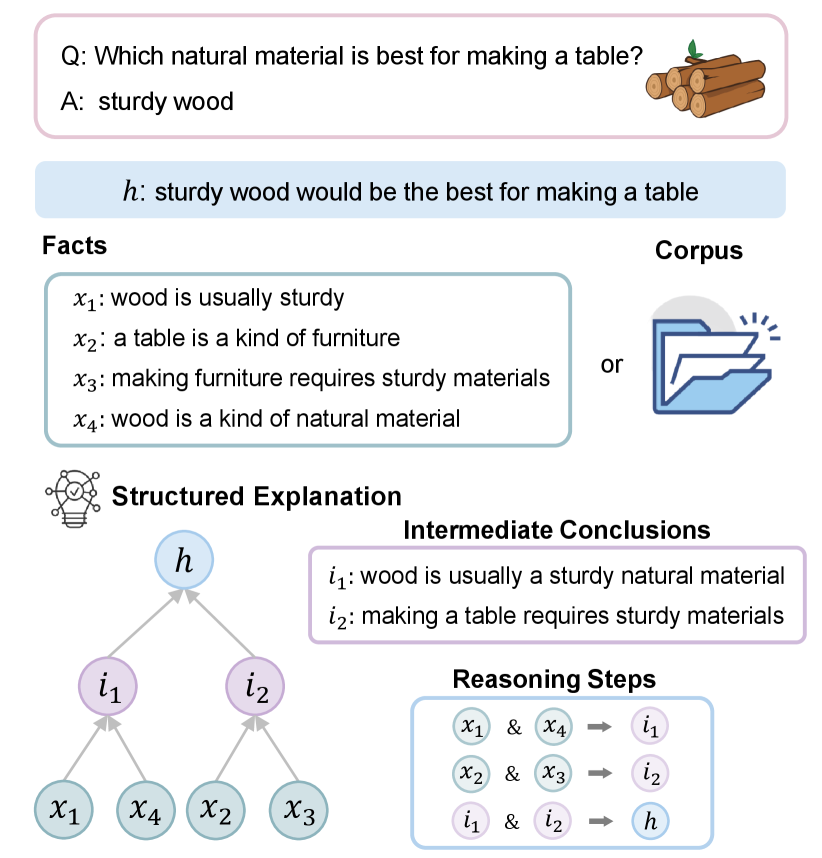
Navigating machines to understand and articulate the thought process from posing a question to arriving at an answer has been a long-term pursuit in the AI community (McCarthy, 1959; Yu et al., 2023). Current QA explainable systems adeptly furnish brief supporting evidence (Rajani et al., 2019; DeYoung et al., 2020). However, they often fail to clarify the reasoning process from prior knowledge to the derived answer. By elucidating the reasoning process of answers generation from the language models, we can greatly improve interpretability, trustworthiness, and debuggability (Dalvi et al., 2021; Ribeiro et al., 2023). As illustrated in Figure 1, when generating answers for the question "Which natural material is best for making a table?", the reasoning process with structured explanations, such as entailment trees (Dalvi et al., 2021) or reasoning graphs (Ribeiro et al., 2023), explains why "sturdy wood" is the best answer.
| Method | Training Emphasis | Runtime | Return |
|---|---|---|---|
| RLET | multi-step reasoning | 9.34s | chained |
| FAME | single-step reasoning | 30.77s | / |
| Ours | structured reasoning | 3.91s | structured |
Deriving such complex structured explanations poses a great challenge. Previous methods (Dalvi et al., 2021; Tafjord et al., 2021) consider structured explanations as linearized sequences and generate the entire reasoning process in one go. However, these methods lack controllability and may hallucinate unreliable reasoning steps. To address these concerns, recent studies (Hong et al., 2022; Neves Ribeiro et al., 2022; Yang et al., 2022) decompose structured explanations and focus on single-step reasoning via supervised learning. Nevertheless, this kind of approach may not always yield optimal results as they fail to consider the interdependencies between different steps. FAME (Hong et al., 2023) attempts to compensate for these shortcomings by leveraging Monte-Carlo planning (Kocsis and Szepesvári, 2006), which significantly increases the running time and inadvertently explores numerous ineffective steps (as shown in Table 1). Furthermore, FAME still concentrates on isolated single-step reasoning, which lacks support for structured reasoning. As a general framework for solving sequential decision-making problems, reinforcement learning (RL) is employed in RLET (Liu et al., 2022) to enhance multi-step reasoning. However, RLET defines the return (a.k.a. cumulative reward) using the standard chain structure, thus lacking the ability to represent the tree (Dalvi et al., 2021) or graph (Ribeiro et al., 2023) logical structures inherent in structured reasoning. As a result, the potential of RL for structured reasoning is not fully exploited.
To address the above issues, we propose Seer, a novel method that facilitates Structured rEasoning and Explanation via Reinforcement learning. In structured reasoning, we observe that the logical dependencies between different steps no longer follow a chained trajectory but instead adhere to the inherent tree or graph structure. Therefore, we propose the structure-based return to precisely describe a tree or graph logical structure, effectively capturing the complex interdependencies between different steps. Additionally, we refine the reward function to meticulously delineate diverse reasoning steps, specifically targeting redundant ones that do not contribute to the final structured explanations. Through experiments in Sec. 5.4, we find that redundant steps represent the exploration in the environment, and appropriate penalization contributes to improved reasoning performance.
Our contributions are summarized as follows:
We propose Seer, a novel RL-based method that facilitates structured reasoning and explanation. To our knowledge, Seer is the first general framework that accommodates scenarios of chained, tree-based, and graph-based structured reasoning.
We propose the structure-based return to address the intricate interdependencies among different reasoning steps, effectively stimulating the potential of RL in structured reasoning.
We conduct extensive experiments to demonstrate the superiority of Seer over state-of-the-art methods. Our method facilitates the effectiveness and efficiency of structured reasoning and exhibits outstanding cross-dataset generalization performance.
2 Related Work
2.1 Explanation for Question Answering
Extensive research has delved into various forms of interpretability in QA systems (Thayaparan et al., 2020; Wiegreffe and Marasovic, 2021; Lamm et al., 2021; Chen et al., 2023). Different from the free-form texts susceptible to hallucinations (Rajani et al., 2019; Wei et al., 2022) or the rationales that only provide supporting evidence (DeYoung et al., 2020; Valentino et al., 2021), the structured explanations, such as the entailment trees (Dalvi et al., 2021) and reasoning graphs (Ribeiro et al., 2023), offer a novel way to generate explanations. These structured methods utilize tree or graph formats to clearly outline what information is used and how it is combined to reach the answer. Despite the remarkable interpretability, the intricately structured reasoning also poses significant challenges (Yu et al., 2023; Xu et al., 2023).
2.2 Natural Language Reasoning
Natural language reasoning, a process that integrates multiple knowledge to derive new conclusions, has attracted significant attention (Saha et al., 2020; Tafjord et al., 2021; Sanyal et al., 2022; Chen et al., 2024). Among these, the entailment trees and reasoning graphs, which involve structured reasoning and reasoning path generation tasks, present considerable challenges (Yu et al., 2023). Dalvi et al. (2021) attempt to transform structured reasoning into a linearized sequence to fit generative models, which may generate hallucinations and invalid reasoning. To alleviate this issue, recent studies (Neves Ribeiro et al., 2022; Hong et al., 2022; Neves Ribeiro et al., 2022; Hong et al., 2023) perform premises selection and reasoning in a step-by-step manner. Nevertheless, these methods decompose structured reasoning and solely leverage isolated single-step supervision to train models. This kind of approach neglects the interdependencies between different steps, which may not always yield optimal results. Therefore, in light of the advancements of RL in various reasoning tasks (Poesia et al., 2021; Le et al., 2022), RLET (Liu et al., 2022) attempts to incorporate RL into the entailment trees. However, it has to enumerate all potential actions, which is unacceptable for practical scenarios. Furthermore, RLET still defines returns in chained trajectories to facilitate multi-step reasoning, which is not suitable for tree/graph-based structured reasoning. In contrast, our Seer showcases superior adaptability to chained, tree-based, and graph-based structured reasoning via the structure-based return, which significantly enhances both the reasoning performance and efficiency.
3 Method
3.1 Task Formulation
As illustrated in Figure 1, the input of the task comprises a set of facts and a hypothesis . The output of the task is the reasoning steps in a structured form, such as an entailment tree or a reasoning graph111Although the reasoning graph (Ribeiro et al., 2023) is a more general structure, to be consistent with the majority of previous work, we use the entailment tree (Dalvi et al., 2021) as an example to formalize the task and illustrate our method. Our proposed method is also applicable to the task described in the form of a reasoning graph.. The entailment tree consists of tree-structured reasoning, whose leaf nodes are selected from the relevant facts () and intermediate nodes represent the derived intermediate conclusions (). We represent the annotated ground-truth entailment tree as , with its leaf nodes signifying .
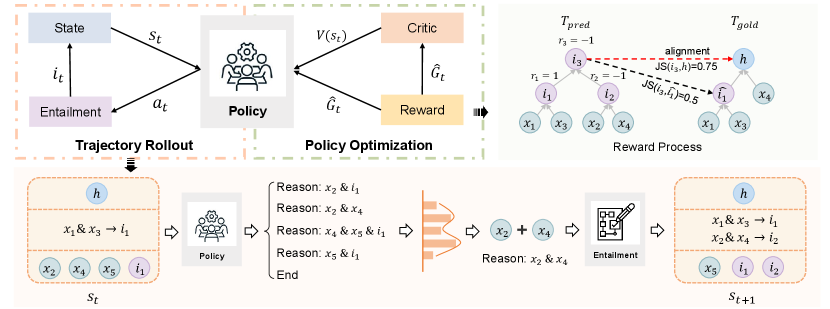
3.2 Overview
We model the structured reasoning as a reinforcement learning (RL) task, the goal of which is to learn the optimal reasoning policy. Figure 2 illustrates the overall framework of Seer, which mainly includes trajectory rollout and policy optimization. For trajectory rollout, we generate trajectories based on the current policy, and each trajectory is produced iteratively until the stopping criteria are satisfied (Appendix C.1). For policy optimization, we assign rewards to the collected trajectories and update both the policy and critic using the structure-based return. Algorithm 1 (Appendix A) outlines our proposed method for further reference.
3.3 Fine-grained Component of Seer
State
At reasoning step , we define the state as a combination of the hypothesis , existing reasoning steps and candidate sentences . contains the reasoning steps so far, and is the set of sentences that can be selected as premises. Each sentence in is either unused facts or intermediate conclusions generated by previous steps, i.e., , where is the set of used sentences. For the initial state, .
Action
Given the state , we consider two types of actions : (1) "Reason: <premises>": the entailment module is invoked to generate a new intermediate conclusion based on the given <premises>. Here, <premises> are selected from . Then, the state is updated as follows: , , and . (2) "End": This action signifies the end of the reasoning process and returns the trajectory .
Policy
The action type "Reason: <premises>" induces a large action space, since premises can be any combination of sentences from the candidate set . To enumerate the probabilities of all potential actions and then sample an action to execute, previous studies (Liu et al., 2022; Hong et al., 2022) limit combinations to pairwise premises, such that the action space is reduced to , where is the size of the set . However, such a simplification incurs some potential drawbacks. First, as the number of candidate sentences increases, the number of potential actions grows exponentially. This renders them impractical for complex reasoning tasks with limited computational resources. Second, by restricting combinations to pairs only, the interdependencies among multiple premises are ignored, which may limit the effectiveness and richness of the derived conclusions.
To address this issue, we adopt a generative model to represent the policy , which can directly sample from the action space . Using the generative model essentially expands the action space where the combinations of premises can be arbitrary. This enables the policy to extensively explore better actions during RL training, not limited to paired premises. Further, to speed up RL training, we first generate the top- actions using policy :
| (1) |
where the input is a linearized state (i.e., the concatenation of , , and ). Then, we proceed with re-normalization to form an appropriate probability distribution over the top- actions, and sample from it to select the action to be performed in the current reasoning step, that is,
| (2) |
| (3) |
Entailment Module
If the action is "Reason: <premises>", we invoke the entailment module to derive the intermediate conclusion to obtain the next state. The entailment module is also a generative model with its input being <premises>. Following Hong et al. (2022); Liu et al. (2022), we fine-tune the entailment model in a supervised manner and freeze the parameters during the reinforcement learning process, as shown in Figure 2.
Reward
To evaluate the correctness of the entailment tree, Dalvi et al. (2021) proposed an alignment algorithm based on Jaccard similarity to align each intermediate node of the predicted tree with . However, different from the fully supervised learning methods, we observe that during the RL process, the policy explores different actions to identify the optimal reasoning process, inevitably attempting some redundant steps that do not contribute to reaching the final hypothesis. Existing RL-based work (Liu et al., 2022) simply treats redundant steps with the same penalty as erroneous steps. This simplification may negatively affect the learning process which discourages necessary exploration in the action space. Furthermore, it lacks detailed feedback to guide the policy toward optimal policy, as it fails to differentiate between innocuous actions (redundant steps) and incorrect actions (erroneous steps).
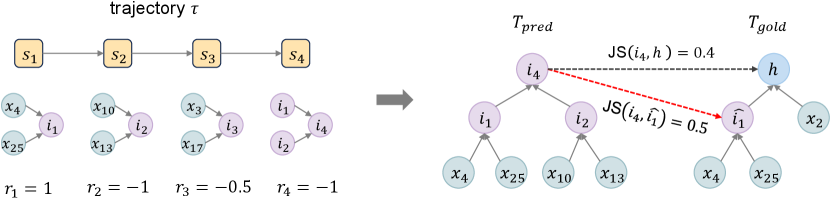
To this end, we propose a fine-grained reward function that assigns different reward values for correct steps, erroneous steps, and redundant steps, as shown in Equation 4. For a trajectory , we assume that the last intermediate conclusion is our predicted hypothesis since the policy deems it should End here. Then, we backtrack to construct the predicted entailment tree (see Appendix C.6 for more details). Note that there might be some steps not participating in , which are regarded as redundant steps. Then, as illustrated in Figure 5, we consider steps that perfectly match via the alignment algorithm (Dalvi et al., 2021) as correct steps and regard others as erroneous steps.
| (4) |
Critic
To enhance training stability, we introduce the critic to estimate the state-value function . The input of is a linearized state, and its output is a scalar representing the return (i.e., cumulative reward) when starting from state . In the simplest case, the return is the chained sum of the rewards. Accordingly, one-step temporal difference (TD) (Sutton, 1988) is often used to estimate , which is updated by the TD-target:
| (5) |
where is the discount factor. However, in structured reasoning, reasoning steps typically adhere to inherent tree (Dalvi et al., 2021) or graph (Ribeiro et al., 2023) structures, with the chained structure being merely a special case. Thus, Equation 5 just describes the chained multi-step reasoning, which may not effectively capture the intricate logical dependencies between steps in structured reasoning.
Therefore, we propose the structure-based return, where the TD-target is expressed in a more general formulation:
| (6) |
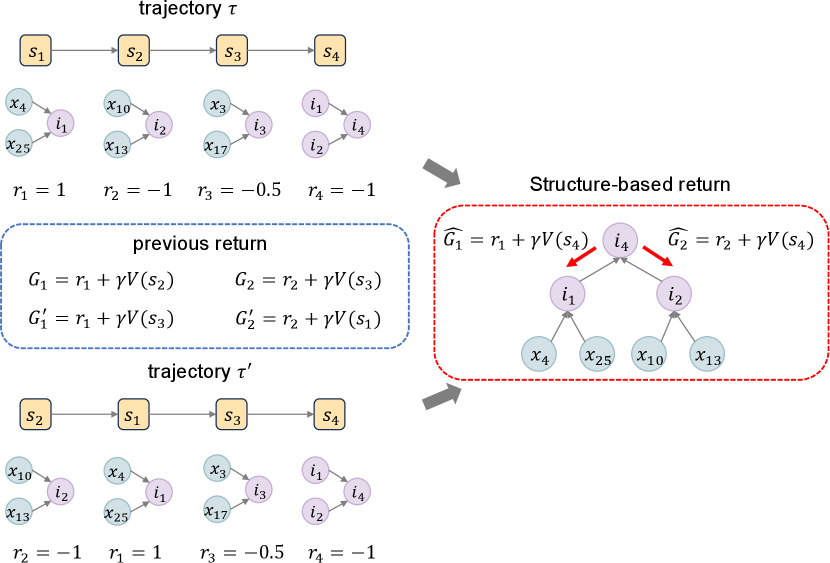
where represents the parent node of state in the entailment tree or reasoning graph. When , . It can be seen that our structure-based return (Equation 6) adapts to structured reasoning involving chained, tree-based and graph-based structured scenarios. Especially, entailment tree is a special case of the reasoning graph, in which each state typically has only one parent node, and thus Equation 6 degenerates into . Furthermore, as shown in Figure 6 (Appendix E), for equivalent trajectories and , previous method (Liu et al., 2022) would assign different returns for state and , even though they represent the same tree in the end. Conversely, our method, by precisely delineating the intricate interdependencies between reasoning steps, consistently allocates the same return to any equivalent trajectories, thereby enhancing both stability and effectiveness.
3.4 Optimization
Our objective is to enhance the structured reasoning capabilities of the policy through RL. To alleviate issues of training instability and sample inefficiency in RL (Zhou et al., 2023; Roit et al., 2023), we employ the proximal policy optimization (PPO) algorithm (Schulman et al., 2017) to train the policy (parameterized by ), as follows:
| (7) |
where represents the probabilities normalized by Equation 2, and are parameters of the new and old policies, is a hyperparameter defining the clipping range, is the entropy exploration coefficient, and is the entropy bonus, which encourages sufficient exploration:
| (8) |
Futhermore, is the estimate of the advantage function for state , defined as follows:
| (9) |
To accurately evaluate return and guide the policy towards better updates, we train the critic by minimizing the difference between its prediction and the TD-target:
| (10) |
Supervised Warm-up
Incorporating the supervised warm-up strategy before RL offers a relatively stable initial policy, which facilitates faster adaptation to the environment, particularly for complex reasoning tasks (Ramamurthy et al., 2023; Wu et al., 2023). Therefore, we convert the structured reasoning into single-step supervised data to warm up the policy as follows:
| (11) |
where is the golden action at .
4 Experiments
4.1 Datasets
Tree-structured reasoning
We conduct experiments on EntailmentBank (Dalvi et al., 2021), the first dataset that supports structured explanation with entailment trees. Following (Hong et al., 2023), we also conduct experiments on EntailmentBankQA (Tafjord et al., 2022), whose objective is to reach the answer based on the entailment tree.
Graph-structured reasoning
4.2 Baselines
For EntailmentBank, we compare with single-pass methods, such as EntailmentWriter (Dalvi et al., 2021), and step-by-step methods including METGEN (Hong et al., 2022), IRGR (Neves Ribeiro et al., 2022), RLET (Liu et al., 2022), NLProofs (Yang et al., 2022) and FAME (Hong et al., 2023). For EntailmentBankQA, we compare with Selection-Inference (SI) (Creswell and Shanahan, 2022) and FAME (Hong et al., 2023). For the STREET benchmark, we compare with the method proposed in (Ribeiro et al., 2023). Furthermore, we conduct comparisons with GPT-4 (OpenAI, 2023) equipped with Chain-of-Thought (CoT) (Wei et al., 2022), Tree of Thought (ToT) (Yao et al., 2023a) and ReAct (Yao et al., 2023b).
4.3 Implementation Details
For a fair comparison222Previous studies have consistently utilized T5-large as the base model. Despite the existence of more advanced generative models (Du et al., 2022; Touvron et al., 2023), using T5-large enables us to maintain a fair comparison., the policy is built with a T5-large model (Raffel et al., 2020), while the critic is the encoder of T5-large combined with a MLP ( as the activation function). For a supervised warm-up, we set a learning rate of 1e-5, a batch size of 16, and train the model for 20 epochs. For RL training, we set learning rate 2e-6 for both policy and critic, discounter factor as 0.95, batch size as 3, buffer size as 12, buffer training epochs as 2, as 0.2, and as 1e-4. More implementation details can be found in Appendix C.
4.4 Evaluation Metrics
For EntailmentBank, we evaluate with the following dimensions: Leaves, Steps, Intermediates, and Overall AllCorrect. For STREET benchmark, we evaluate the reasoning graphs with two dimensions: Answer Accuracy and Reasoning Graph Accuracy. Note that Overall AllCorrect and Reasoning Graph Accuracy are extremely strict metrics, where any deviations will result in a score of 0. More metrics details can be found in Appendix D.
| Task | Method | Leaves | Steps | Intermediates | Overall | |||
|---|---|---|---|---|---|---|---|---|
| F1 | AllCorrect | F1 | AllCorrect | F1 | AllCorrect | AllCorrect | ||
| Task1 | EntailmentWriter | 98.7 | 84.1 | 50.0 | 38.5 | 67.6 | 35.9 | 34.4 |
| METGEN | 100.0 | 100.0 | 57.9 | 42.1 | 71.3 | 39.2 | 37.0 | |
| IRGR | 97.6 | 89.4 | 50.2 | 36.8 | 62.1 | 31.8 | 32.4 | |
| RLET | 100.0 | 100.0 | 54.6 | 40.7 | 66.9 | 36.3 | 34.8 | |
| NLProofS | 97.8 | 90.1 | 55.6 | 42.3 | 72.4 | 40.6 | 38.9 | |
| Seer (Ours) | 100.0 | 100.0 | 67.6 | 52.6 | 70.3 | 42.6 | 40.6 | |
| Task2 | EntailmentWriter | 83.2 | 35.0 | 39.5 | 24.7 | 62.2 | 28.2 | 23.2 |
| METGEN | 83.7 | 48.6 | 41.7 | 30.4 | 62.7 | 32.7 | 28.0 | |
| IRGR | 69.9 | 23.8 | 30.5 | 22.3 | 47.7 | 26.5 | 21.8 | |
| RLET | 81.0 | 39.0 | 38.5 | 28.4 | 56.3 | 28.6 | 25.7 | |
| NLProofS | 90.3 | 58.8 | 47.2 | 34.4 | 70.2 | 37.8 | 33.3 | |
| Seer (Ours) | 86.4 | 53.5 | 56.8 | 39.7 | 66.3 | 38.3 | 34.7 | |
| Task3 | EntailmentWriter | 35.7 | 2.9 | 6.1 | 2.4 | 33.4 | 7.7 | 2.4 |
| METGEN | 34.8 | 8.7 | 9.8 | 8.6 | 36.7 | 20.4 | 8.6 | |
| IRGR | 45.6 | 11.8 | 16.1 | 11.4 | 38.8 | 20.9 | 11.5 | |
| RLET | 38.3 | 9.1 | 11.5 | 7.1 | 34.2 | 12.1 | 6.9 | |
| NLProofS | 43.2 | 8.2 | 11.2 | 6.9 | 42.9 | 17.3 | 6.9 | |
| FAME | 43.4 | 13.8 | 16.6 | 12.4 | 40.6 | 19.9 | 11.9 | |
| GPT4-CoT | 44.1 | 12.1 | 15.4 | 10.8 | 43.1 | 20.6 | 10.8 | |
| GPT4-ToT | 43.3 | 12.0 | 15.8 | 11.0 | 43.9 | 20.0 | 11.0 | |
| GPT4-ReAct | 45.8 | 12.9 | 14.1 | 10.5 | 43.5 | 21.5 | 10.5 | |
| Seer (Ours) | 47.1 | 13.8 | 17.4 | 12.9 | 45.1 | 18.8 | 12.9 | |
5 Result Analysis
5.1 Structured Reasoning
EntailmentBank
As shown in Table 2, our Seer outperforms all baseline methods on the most strict metric, "Overall AllCorrect", across all three tasks. Specifically, our method achieves an absolute improvement of 1.7%/1.4%/1.0% in Task 1/2/3 compared to the strongest baseline. The steps dimension, i.e., premises selection, is the core of EntailmentBank333A comprehensive error analysis is detailed in Appendix G., contributing to enhancing the accuracy of both leaves and intermediates dimensions, thereby improving the overall AllCorrect metric. (1) Compared to SOTA supervised methods, such as NLProofs and FAME, our method exhibits significant advantages in the steps dimension. This demonstrates that focusing solely on isolated single-step reasoning through supervised learning may yield suboptimal solutions in intricate structured reasoning tasks, even though employing advanced planning algorithms, such as Monte-Carlo planning in FAME. (2) Compared to the SOTA RL-based method, our method outperforms RLET by 5.8%/9.0%/6.0% in Task 1/2/3. Our method employs a generative model as the policy to circumvent the issue of enumerating actions, facilitating the policy’s understanding of structured reasoning tasks (generating potential actions by itself). Moreover, our proposed structure-based return more effectively captures the tree-structured logical dependencies between steps and can assign stable returns for equivalent trajectories, which significantly improves reasoning abilities. Subsequent ablation studies will further demonstrate this. (3) Compared to GPT-4 with CoT, ToT, and ReAct, our method achieves an absolute improvement of 1.9% in Task 3. Although GPT-4 exhibits outstanding reasoning capabilities surpassing many other baselines, its performance relies on a vast number of parameters. Details about the prompts of GPT-4 can be found in Appendix F.
| Method | Task 1 | Task 2 |
|---|---|---|
| SI+Halter | 72.4 | 55.9 |
| SI+Halter+Search | 83.2 | 72.9 |
| FAME | 91.5 | 78.2 |
| Seer (Ours) | 92.7 | 85.6 |
EntailmentBankQA
Following Creswell and Shanahan (2022), we introduce the halter module to generate answers based on and substitute hypothesis with question and option during the reasoning process. As illustrated in Table 3, our method surpasses FAME by an absolute margin of 1.2%/7.4% in Task 1/2. While both FAME and SI are supervised methods, FAME significantly outperforms SI by enhancing the model’s reasoning and exploration capabilities through Monte-Carlo planning. However, our method enhances the structured reasoning capabilities of the policy rather than focusing solely on single-step reasoning, which can significantly improve the quality of the entailment tree to aid in answering, especially in complex reasoning environments.
| Method | SCONE | GSM8K | AQUA-RAT | AR-LSAT |
|---|---|---|---|---|
| Answer Accuracy | ||||
| STREET | 69.6 | 10.4 | 28.7 | 28.0 |
| GPT4 † | 66.0 | 94.0 | 78.0 | 32.0 |
| SEER (Ours) | 72.4 | 21.4 | 37.6 | 33.5 |
| Reasoning Graph Accuracy | ||||
| STREET | 60.0 | 0.7 | 0.0 | 0.0 |
| GPT4 † | 32.0 | 10.0 | 4.0 | 2.0 |
| SEER (Ours) | 64.8 | 13.4 | 8.1 | 7.2 |
STREET
As shown in Table 4, compared to GPT-4, our method has achieved absolute improvements of 4.8%/3.4%/4.1%/5.2% across various datasets, although the Reasoning Graph Accuracy is a very strict metric (Ribeiro et al., 2023). While GPT-4 excels at answering questions (far surpassing other methods), its parameter is thousands of times greater than other methods. Moreover, during the reasoning process, GPT-4 is prone to hallucinations (Rawte et al., 2023), resulting in poor performance in structured reasoning, particularly evident in the "Reasoning Graph Accuracy" metric. Since SCONE contains sufficient data as well as similar QA and reasoning patterns, we observe that the STREET method would outperform GPT-4 on SCONE. However, by obtaining high-quality reasoning graphs, our method achieves absolute improvements of 2.8%/11.0%/8.9%/5.5% compared to the STREET method, significantly improving answer accuracy and trustworthiness. In reasoning graphs, a state may have multiple parent nodes. Our structure-based return (Equation 6) still precisely describes the cumulative reward for each state, thereby facilitating reasoning performance in graph-structured reasoning.
5.2 Cross-dataset Performance
| Method | eQASC | eOBQA | ||
|---|---|---|---|---|
| P@1 | NDCG | P@1 | NDCG | |
| EntailmentWriter | 52.48 | 73.14 | 69.07 | 89.05 |
| EntailmentWriter-Iter | 52.56 | 73.28 | 72.15 | 90.19 |
| METGEN | 55.81 | 74.19 | 74.89 | 90.50 |
| FAME | 53.36 | 79.64 | 73.09 | 89.32 |
| GPT-4 | 54.00 | 88.82 | 85.36 | 91.19 |
| Seer (Ours) | 60.33 | 89.76 | 77.50 | 94.62 |
To evaluate the generalization performance, we conduct cross-dataset experiments on eQASC and eOBQA444More details about the setting of eQASC and eOBQA can be found in Appendix B. (Jhamtani and Clark, 2020). We apply the policy of Task 2 for selection without training on eQASC or eOBQA. As illustrated in Table 5, our method exhibits significant superiority in cross-dataset generalization. Compared to supervised methods, our Seer, following the inherent structural nature of entailment trees, can better capture the logical dependencies between reasoning steps, which can effectively promote the generalization ability of the policy. The experimental results further validate the effectiveness of our method.
5.3 Ablation Studies
| Method | Leaves | Steps | Intermediates | Overall |
|---|---|---|---|---|
| Seer (Ours) | 13.8 | 12.9 | 18.8 | 12.9 |
| w/o redundant | 13.2 | 12.6 | 18.5 | 12.3 |
| w/o structure-based return | 12.9 | 11.7 | 18.5 | 11.1 |
| w/o RL | 10.2 | 9.4 | 17.1 | 9.1 |
To evaluate the contribution of each component, we conduct extensive ablation studies. As shown in Table 6, we investigate three different variations of Seer in Task 3 of EntailmentBank: (1) w/o redundant neglects redundant steps by assigning a reward of -1. (2) w/o structure-based return removes the structure-based return and calculates it using the chained sum of rewards (Equation 5). (3) w/o RL removes the RL phase, relying solely on supervised warm-up. We discover that overlooking redundant steps may potentially inhibit the exploration of policy, leading to a performance decline. In addition, the results shown in Table 6 also demonstrate that removing the structure-based return severely affects the performance. It not only adequately addresses the equivalent trajectory problems, but also elegantly captures the logical relationships inherent in entailment trees, which is crucial for structured reasoning. Furthermore, it can be seen that removing the RL phase reduces performance by 3.8% of Overall Allcorrect, which is a significant impact for this strict metric. This indicates that relying solely on supervised learning may overlook the logical relationships in structured reasoning, thereby falling into suboptimal solutions.
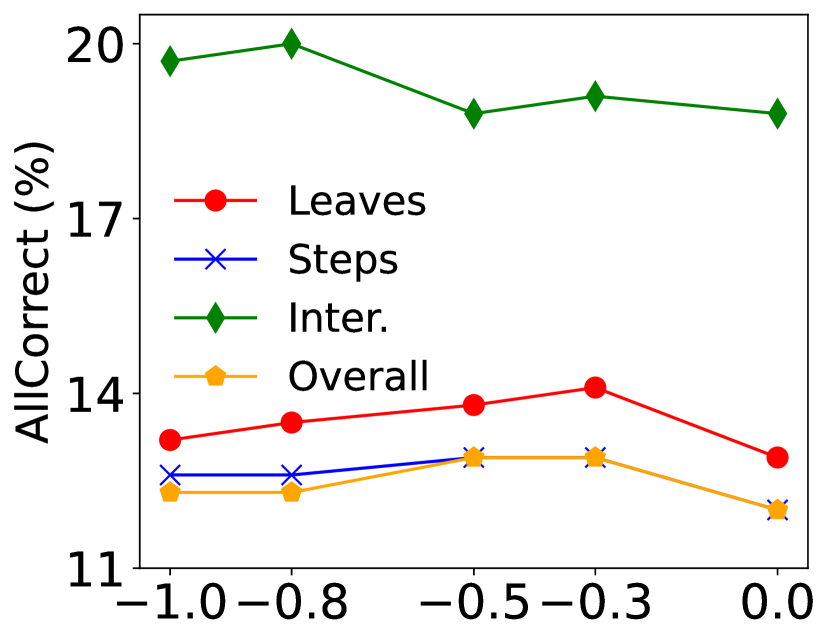
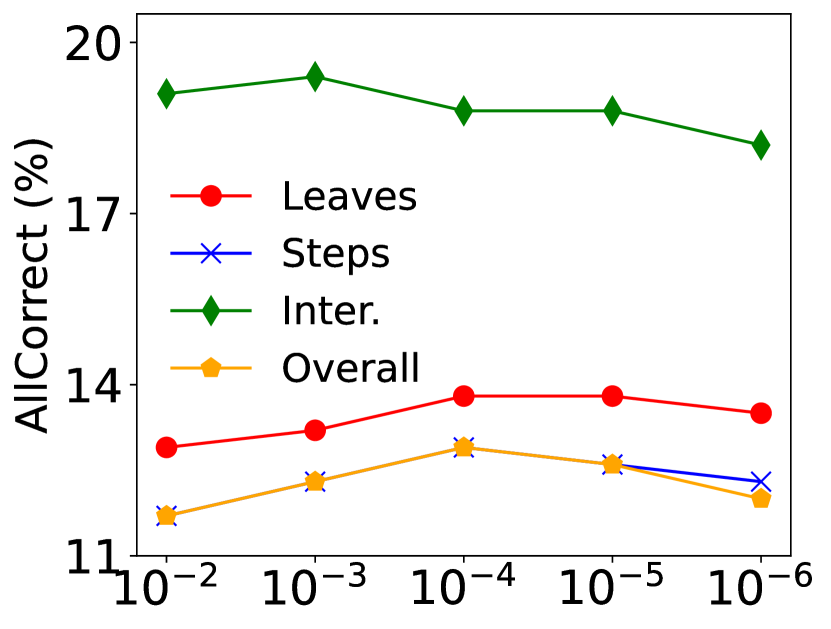
5.4 Parameter Sensitivity Analysis
As illustrated in Figure 3, we further investigate the impact of and on the performance in Task 3. We observe that compared to treating redundant and erroneous steps equally (), not penalizing () may have more detrimental effects, which allows for unrestricted exploration. Moreover, a suitable (the coefficient of entropy bonus) is crucial for performance enhancement, as it encourages the policy to break away from the "stereotypes" of supervised warm-up.
6 Conclusions
We propose Seer, a novel approach that facilitates structured reasoning and explanation via RL. To our knowledge, Seer is the first general framework capable of enhancing chained, tree-based, and graph-based structured reasoning. Our structure-based return precisely delineates the hierarchical and branching structure inherent in structured reasoning, effectively facilitating reasoning ability. Furthermore, Seer employs a generative model to represent the policy and refines the reward function, ingeniously circumventing the limitations of existing works. Comprehensive experimental results demonstrate that Seer significantly outperforms state-of-the-art methods and exhibits outstanding cross-dataset generalization performance.
Limitations
Although our method has achieved excellent performance in structured reasoning and explanation, there remains one issue that deserves further exploration for future work: how to perform structured reasoning in the context of multimodal data. This includes combining content from images, tables, or audio data, a form of multimodal structured reasoning that is increasingly prevalent and demanding in real-world scenarios. In future work, we plan to extend our Seer to accommodate multimodal scenarios.
Ethics Statement
This work focuses primarily on structured reasoning and explanation problems, and its contributions are entirely methodological. Therefore, this work does not have direct negative social impacts. For the experiments, we have open-sourced the code and utilized openly available datasets commonly used in previous research, without any sensitive information to our knowledge. The authors of this work adhere to the ACL ethical guidelines, and the application of this work does not present any apparent issues that may lead to ethical risks.
Acknowledgements
This work is supported by the National Key R&D Program of China (NO.2022ZD0160102). Chao Yang is supported by the Shanghai Post-doctoral Excellent Program (Grant No. 2022234).
References
- Akyurek et al. (2023) Afra Feyza Akyurek, Ekin Akyurek, Ashwin Kalyan, Peter Clark, Derry Tanti Wijaya, and Niket Tandon. 2023. RL4F: Generating natural language feedback with reinforcement learning for repairing model outputs. In ACL.
- Bellman (1957) Richard Bellman. 1957. A markovian decision process. Journal of mathematics and mechanics.
- Chen et al. (2024) Guoxin Chen, Minpeng Liao, Chengxi Li, and Kai Fan. 2024. Alphamath almost zero: process supervision without process.
- Chen et al. (2023) Guoxin Chen, Yiming Qian, Bowen Wang, and Liangzhi Li. 2023. MPrompt: Exploring multi-level prompt tuning for machine reading comprehension. In Findings of EMNLP.
- Clark et al. (2018) Peter Clark, Isaac Cowhey, Oren Etzioni, Tushar Khot, Ashish Sabharwal, Carissa Schoenick, and Oyvind Tafjord. 2018. Think you have solved question answering? try arc, the AI2 reasoning challenge. CoRR.
- Cobbe et al. (2021) Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, et al. 2021. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
- Creswell and Shanahan (2022) Antonia Creswell and Murray Shanahan. 2022. Faithful reasoning using large language models. CoRR.
- Dalvi et al. (2021) Bhavana Dalvi, Peter Jansen, Oyvind Tafjord, Zhengnan Xie, Hannah Smith, Leighanna Pipatanangkura, and Peter Clark. 2021. Explaining answers with entailment trees. In EMNLP.
- DeYoung et al. (2020) Jay DeYoung, Sarthak Jain, Nazneen Fatema Rajani, Eric Lehman, Caiming Xiong, Richard Socher, and Byron C. Wallace. 2020. ERASER: A benchmark to evaluate rationalized NLP models. In ACL.
- Du et al. (2022) Zhengxiao Du, Yujie Qian, Xiao Liu, Ming Ding, Jiezhong Qiu, Zhilin Yang, and Jie Tang. 2022. GLM: General language model pretraining with autoregressive blank infilling. In ACL.
- He et al. (2023) Pengcheng He, Jianfeng Gao, and Weizhu Chen. 2023. Debertav3: Improving deberta using electra-style pre-training with gradient-disentangled embedding sharing. In ICLR.
- Hoffmann et al. (2022) Jordan Hoffmann, Sebastian Borgeaud, Arthur Mensch, Elena Buchatskaya, Trevor Cai, Eliza Rutherford, Diego de Las Casas, Lisa Anne Hendricks, Johannes Welbl, Aidan Clark, Tom Hennigan, Eric Noland, Katie Millican, George van den Driessche, Bogdan Damoc, Aurelia Guy, Simon Osindero, Karen Simonyan, Erich Elsen, Jack W. Rae, Oriol Vinyals, and Laurent Sifre. 2022. Training compute-optimal large language models. CoRR.
- Hong et al. (2022) Ruixin Hong, Hongming Zhang, Xintong Yu, and Changshui Zhang. 2022. METGEN: A module-based entailment tree generation framework for answer explanation. In Findings of NAACL.
- Hong et al. (2023) Ruixin Hong, Hongming Zhang, Hong Zhao, Dong Yu, and Changshui Zhang. 2023. Faithful question answering with Monte-Carlo planning. In ACL.
- Jhamtani and Clark (2020) Harsh Jhamtani and Peter Clark. 2020. Learning to explain: Datasets and models for identifying valid reasoning chains in multihop question-answering. In EMNLP.
- Khot et al. (2020) Tushar Khot, Peter Clark, Michal Guerquin, Peter Jansen, and Ashish Sabharwal. 2020. Qasc: A dataset for question answering via sentence composition. AAAI.
- Kocsis and Szepesvári (2006) Levente Kocsis and Csaba Szepesvári. 2006. Bandit based monte-carlo planning. In ECML. Springer.
- Lamm et al. (2021) Matthew Lamm, Jennimaria Palomaki, Chris Alberti, Daniel Andor, Eunsol Choi, Livio Baldini Soares, and Michael Collins. 2021. Qed: A framework and dataset for explanations in question answering. Transactions of the Association for computational Linguistics.
- Le et al. (2022) Hung Le, Yue Wang, Akhilesh Deepak Gotmare, Silvio Savarese, and Steven Chu Hong Hoi. 2022. Coderl: Mastering code generation through pretrained models and deep reinforcement learning. In NeurIPS.
- Ling et al. (2017) Wang Ling, Dani Yogatama, Chris Dyer, and Phil Blunsom. 2017. Program induction by rationale generation: Learning to solve and explain algebraic word problems. In ACL.
- Liu et al. (2022) Tengxiao Liu, Qipeng Guo, Xiangkun Hu, Yue Zhang, Xipeng Qiu, and Zheng Zhang. 2022. RLET: A reinforcement learning based approach for explainable QA with entailment trees. In EMNLP.
- Liu et al. (2023) Yajiao Liu, Xin Jiang, Yichun Yin, Yasheng Wang, Fei Mi, Qun Liu, Xiang Wan, and Benyou Wang. 2023. One cannot stand for everyone! leveraging multiple user simulators to train task-oriented dialogue systems. In ACL.
- Long et al. (2016) Reginald Long, Panupong Pasupat, and Percy Liang. 2016. Simpler context-dependent logical forms via model projections. In ACL.
- McCarthy (1959) John McCarthy. 1959. Programs with common sense.
- Mihaylov et al. (2018) Todor Mihaylov, Peter Clark, Tushar Khot, and Ashish Sabharwal. 2018. Can a suit of armor conduct electricity? a new dataset for open book question answering. In EMNLP.
- Neves Ribeiro et al. (2022) Danilo Neves Ribeiro, Shen Wang, Xiaofei Ma, Rui Dong, Xiaokai Wei, Henghui Zhu, Xinchi Chen, Peng Xu, Zhiheng Huang, Andrew Arnold, and Dan Roth. 2022. Entailment tree explanations via iterative retrieval-generation reasoner. In Findings of NAACL.
- OpenAI (2023) OpenAI. 2023. GPT-4 technical report.
- Poesia et al. (2021) Gabriel Poesia, WenXin Dong, and Noah Goodman. 2021. Contrastive reinforcement learning of symbolic reasoning domains. In NeurIPS.
- Raffel et al. (2020) Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. 2020. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res.
- Rajani et al. (2019) Nazneen Fatema Rajani, Bryan McCann, Caiming Xiong, and Richard Socher. 2019. Explain yourself! leveraging language models for commonsense reasoning. In ACL.
- Ramamurthy et al. (2023) Rajkumar Ramamurthy, Prithviraj Ammanabrolu, Kianté Brantley, Jack Hessel, Rafet Sifa, Christian Bauckhage, Hannaneh Hajishirzi, and Yejin Choi. 2023. Is reinforcement learning (not) for natural language processing: Benchmarks, baselines, and building blocks for natural language policy optimization. In ICLR.
- Rawte et al. (2023) Vipula Rawte, Amit P. Sheth, and Amitava Das. 2023. A survey of hallucination in large foundation models. CoRR.
- Reimers and Gurevych (2019) Nils Reimers and Iryna Gurevych. 2019. Sentence-bert: Sentence embeddings using siamese bert-networks. In EMNLP.
- Ribeiro et al. (2023) Danilo Neves Ribeiro, Shen Wang, Xiaofei Ma, Henghui Zhu, Rui Dong, Deguang Kong, Juliette Burger, Anjelica Ramos, Zhiheng Huang, William Yang Wang, George Karypis, Bing Xiang, and Dan Roth. 2023. STREET: A multi-task structured reasoning and explanation benchmark. In ICLR.
- Roit et al. (2023) Paul Roit, Johan Ferret, Lior Shani, Roee Aharoni, Geoffrey Cideron, Robert Dadashi, Matthieu Geist, Sertan Girgin, Leonard Hussenot, Orgad Keller, Nikola Momchev, Sabela Ramos Garea, Piotr Stanczyk, Nino Vieillard, Olivier Bachem, Gal Elidan, Avinatan Hassidim, Olivier Pietquin, and Idan Szpektor. 2023. Factually consistent summarization via reinforcement learning with textual entailment feedback. In ACL.
- Saha et al. (2020) Swarnadeep Saha, Sayan Ghosh, Shashank Srivastava, and Mohit Bansal. 2020. PRover: Proof generation for interpretable reasoning over rules. In EMNLP.
- Sanyal et al. (2022) Soumya Sanyal, Harman Singh, and Xiang Ren. 2022. FaiRR: Faithful and robust deductive reasoning over natural language. In ACL.
- Schulman et al. (2017) John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
- Sellam et al. (2020) Thibault Sellam, Dipanjan Das, and Ankur Parikh. 2020. BLEURT: Learning robust metrics for text generation. In ACL.
- Sutton (1988) Richard S Sutton. 1988. Learning to predict by the methods of temporal differences. Machine learning.
- Tafjord et al. (2021) Oyvind Tafjord, Bhavana Dalvi, and Peter Clark. 2021. ProofWriter: Generating implications, proofs, and abductive statements over natural language. In Findings of ACL-IJCNLP.
- Tafjord et al. (2022) Oyvind Tafjord, Bhavana Dalvi Mishra, and Peter Clark. 2022. Entailer: Answering questions with faithful and truthful chains of reasoning. In EMNLP.
- Thayaparan et al. (2020) Mokanarangan Thayaparan, Marco Valentino, and André Freitas. 2020. A survey on explainability in machine reading comprehension. CoRR.
- Touvron et al. (2023) Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
- Valentino et al. (2021) Marco Valentino, Mokanarangan Thayaparan, and André Freitas. 2021. Unification-based reconstruction of multi-hop explanations for science questions. In EACL.
- Wei et al. (2022) Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, brian ichter, Fei Xia, Ed Chi, Quoc V Le, and Denny Zhou. 2022. Chain-of-thought prompting elicits reasoning in large language models. In NeurIPS.
- Wiegreffe and Marasovic (2021) Sarah Wiegreffe and Ana Marasovic. 2021. Teach me to explain: A review of datasets for explainable natural language processing. In NeurIPS.
- Wu et al. (2023) Anne Wu, Kiante Brantley, Noriyuki Kojima, and Yoav Artzi. 2023. lilGym: Natural language visual reasoning with reinforcement learning. In ACL.
- Xie et al. (2020) Zhengnan Xie, Sebastian Thiem, Jaycie Martin, Elizabeth Wainwright, Steven Marmorstein, and Peter Jansen. 2020. WorldTree v2: A corpus of science-domain structured explanations and inference patterns supporting multi-hop inference. In LREC.
- Xu et al. (2023) Fangzhi Xu, Qika Lin, Jiawei Han, Tianzhe Zhao, Jun Liu, and Erik Cambria. 2023. Are large language models really good logical reasoners? a comprehensive evaluation from deductive, inductive and abductive views. arXiv preprint arXiv:2306.09841.
- Yang et al. (2022) Kaiyu Yang, Jia Deng, and Danqi Chen. 2022. Generating natural language proofs with verifier-guided search. In EMNLP.
- Yao et al. (2023a) Shunyu Yao, Dian Yu, Jeffrey Zhao, Izhak Shafran, Thomas L. Griffiths, Yuan Cao, and Karthik Narasimhan. 2023a. Tree of Thoughts: Deliberate problem solving with large language models.
- Yao et al. (2023b) Shunyu Yao, Jeffrey Zhao, Dian Yu, Nan Du, Izhak Shafran, Karthik R. Narasimhan, and Yuan Cao. 2023b. React: Synergizing reasoning and acting in language models. In ICLR.
- Yu et al. (2023) Fei Yu, Hongbo Zhang, and Benyou Wang. 2023. Nature language reasoning, a survey. arXiv preprint arXiv:2303.14725.
- Zhong et al. (2021) Wanjun Zhong, Siyuan Wang, Duyu Tang, Zenan Xu, Daya Guo, Jiahai Wang, Jian Yin, Ming Zhou, and Nan Duan. 2021. Ar-lsat: Investigating analytical reasoning of text. arXiv preprint arXiv:2104.06598.
- Zhou et al. (2023) Jinfeng Zhou, Zhuang Chen, Bo Wang, and Minlie Huang. 2023. Facilitating multi-turn emotional support conversation with positive emotion elicitation: A reinforcement learning approach. In ACL.
Appendix A Algorithm Details
Algorithm 1 describes the overall training process of our proposed Seer in detail, which primarily consists of two phases: supervised warm-up and reinforcement learning (RL). In the supervised warm-up phase, the structured reasoning is first decomposed into single-step reasoning data (Line 2). Then, we employs supervised learning to guide the policy to quickly adapt to the complex reasoning environments (Lines 3-6). This is particularly beneficial when the number of parameters in the policy is relatively small (Akyurek et al., 2023; Liu et al., 2023). In the RL phase, we initially populate the replay buffer through the policy (Lines 9-13). Then, we update the parameters of the policy and the critic using the buffer data. To improve sample efficiency, updates are performed for each replay buffer (Lines 14-18).
For the inference process, we only need to use the policy (without the critic) for structured reasoning. Specifically, as illustrated in the trajectory rollout of Figure 2, we update the state by the policy and the entailment module. Then, we end the reasoning process until the stopping criteria are satisfied. Finally, we backtrack to construct the entire structured explanation, taking the last intermediate conclusion as the hypothesis for entailment tree (or the answer for the STREET benchmark).
Appendix B Datasets Details
| Task Name | Task Domain | # Questions | # Reasoning Steps | Reasoning Type | Answer Type |
|---|---|---|---|---|---|
| EntailmentBank | Science | 1,840 | 5,881 | Tree-structured | / |
| EntailmentBankQA (ARC) | Science | 1,840 | 5,881 | Tree-structured | 4-Way MC |
| SCONE | Processes | 14,574 | 130,482 | Graph-structured | State Pred. |
| GSM8K | Math | 1,030 | 4,666 | Graph-structured | Number |
| AQUA-RAT | Math | 1,152 | 7,179 | Graph-structured | 5-Way MC |
| AR-LSAT | Logic | 500 | 2,885 | Graph-structured | 5-Way MC |
Datasets of Structured Reasoning
Table 7 describes the statistics of datasets in detail. In the answer types, “K-Way MC” stands for multiple choice answer with K options.
EntailmentBank (Dalvi et al., 2021) comprises 1,840 expert-annotated entailment trees with an average of 7.6 nodes spanning across 3.2 entailment steps. The facts are derived from the WorldTree V2 corpus (Xie et al., 2020). Based on different facts , there are three progressively more challenging tasks: Task1 (no-distractor), Task2 (distractor) and Task3 (full-corpus). For GPT-4, we employ all the data in Task 3 from EntailmentBank to evaluate its performance. EntailmentBank was originally designed for post-hoc tree reconstruction tasks instead of QA, Tafjord et al. (2022) converted it into EntailmentBankQA where the task is to choose the correct answer given multiple choice options rather than deriving hypothesis .
To construct the STREET benchmark, Ribeiro et al. (2023) standardized many QA datasets, such as ARC (Clark et al., 2018), SCONE (Long et al., 2016), GSM8K (Cobbe et al., 2021), AQUA-RAT (Ling et al., 2017) and AR-LSAT (Zhong et al., 2021), in the graph-structured explanation format, where the tasks are converted into answering the question based on the predicted reasoning graphs. Please note that ARC in STREET is congruent with Task 1 of EntailmentBankQA (Ribeiro et al., 2023), hence, we do not repeat the experiment for this task in Table 4. Due to the high cost of GPT-4, we randomly sample 50 instances from each dataset in the STREET benchmark to evaluate GPT-4’s performance.
Datasets of Cross-dataset Experiments
To evaluate the generalization performance of our method, following Hong et al. (2022), we conduct cross-dataset experiments on eQASC and eOBQA (Jhamtani and Clark, 2020), which collect one-step entailment trees for questions from QASC (Khot et al., 2020) and OpenBookQA (Mihaylov et al., 2018), respectively. The goal of this task is to select valid one-step trees from the candidate set and evaluate the results with P@1 and NDCG metrics (Hong et al., 2022). Questions with no valid tree are filtered. The candidate sets for eQASC and eOBQA are composed of 10 and 3 sentences respectively.
Appendix C Implementation Details
C.1 Stopping criteria
For a fair comparison, we use the T5-large model to represent the policy. However, we observe that T5-large tends to perform "Reason" actions more frequently, which is caused by the smaller number of model parameters and the issue of having only a few "End" instances. Moreover, unlike GPT-4, T5-large is less able to recognize when a hypothesis has been inferred and when to stop. Therefore, we attach two extra stopping criteria in addition to the "End" action: (1) The semantic similarity between the intermediate conclusion and the hypothesis exceeds a predefined threshold, i.e., BLEURT(, ) > 1. (2) Exceeding the maximum number of reasoning steps (set to 20 in this paper).
C.2 Alignment algorithm
Following (Dalvi et al., 2021), we evaluate the intermediate steps based on Jaccard similarity. Specifically, the intermediate nodes in are aligned with the intermediate nodes in that have the maximum Jaccard similarity. If the Jaccard similarity between the intermediate node in and all intermediate nodes in is zero, it is aligned with "NULL". Note that only the intermediate node that is perfectly matched with a node in , i.e., the Jaccard similarity is 1, is considered as a correct step. Figure 5 provides a detailed illustration of this process. The alignment process is similar in the reasoning graphs (Ribeiro et al., 2023).
C.3 Retriever for Task 3
In Task 3 of EntailmentBank, first, it is necessary to retrieve relevant sentences from the corpus (Dalvi et al., 2021). The research focus of this paper is to enhance the structured reasoning ability of the policy. Therefore, we directly adopt the retriever and its associated parameters proposed in previous work (Hong et al., 2023), which is based on the all-mpnet-base-v2 model (Reimers and Gurevych, 2019). For a fair comparison, we retrieve the top 25 most relevant sentences as for Task 3.
C.4 Entailment Module
The entailment module is also based on the T5-large model, taking premises as input and generating intermediate conclusions. Our primary focus is to enhance the structured reasoning ability of the policy through RL, therefore, we directly employ the entailment module that has already been trained in previous work (Hong et al., 2023), which also aids in a fair comparison.
C.5 Halter Module
In EntailmentBankQA, we employ the Halter module (Creswell and Shanahan, 2022) to answer questions based on the predicted entailment trees. In this paper, the Halter module is built upon the T5-large model. The module is trained with a learning rate of 1e-5 and a batch size of 16.
C.6 Entailment Tree Construction
To evaluate the correctness of each reasoning step, we have to reconstruct the trajectory into an entailment tree and compare it with . Figure 5 illustrates this reconstruction process. We consider the last intermediate conclusion as the hypothesis and then construct the predicted entailment tree based on the reasoning relationship of each step. The reconstruction process is similar in the reasoning graphs (Ribeiro et al., 2023).
C.7 Running time
In our experimental setting, the average training time per entailment tree in Seer is 6.98 seconds, and the average inference time per entailment tree in Seer is 3.91 seconds. As reported in their papers, the inference time per entailment tree in RLET (Liu et al., 2022) and FAME (Hong et al., 2023) are 9.34 seconds and 30.77 seconds, respectively. FAME leverages Monte-Carlo planning, necessitating the exploration of numerous nodes to enhance the reasoning capability of the policy, thus requiring considerable computational time. Our proposed Seer significantly surpasses FAME in terms of both efficiency and effectiveness.
C.8 Experiment Environments
All experiments were conducted on Ubuntu 22.04 equipped with NVIDIA A100 GPUs. Our code mainly depends on python 3.10555https://www.python.org/ and PyTorch 2.0.1666https://pytorch.org/. The pre-trained language models are derived from HuggingFace Transformers777https://huggingface.co/.
C.9 Details of Reasoning Graphs
For the reasoning graphs in the STREET Benchmark, the implementation details are slightly different from the entailment trees. In the reasoning graphs, reasoning steps may possess multiple parent nodes, and a fact () or intermediate conclusion () may be utilized multiple times (Ribeiro et al., 2023). Therefore, in the reasoning graph, we refrain from incorporating previously used premises into , instead continually expanding the candidate sentence set through newly derived intermediate conclusions. In other words, the state in the reasoning graphs is updated according to the following rules: , , and .
C.10 Other Implementation Details
For GPT-4, we set the temperature to 0.7. For Tree of Thought, we set candidates at each step, and then vote to select the optimal action. Details regarding the prompts of CoT, ToT, and ReAct can be found in Appendix F. For all baselines, we obtain the optimal results based on experimental results or hyperparameter settings derived from the original papers. For our method, we initialize the critic with the encoder of the warm-up policy to expedite the convergence of the critic and facilitate policy updates. The hidden layer dimension of the MLP in the critic is set to 512.
Appendix D Metrics Details
For EntailmentBank, we follow (Dalvi et al., 2021) and evaluate the entailment tree using three dimensions:
Leaves: To evaluate the leaf nodes of , we compute F1 by comparing with .
Steps: To evaluate the structural correctness of each step, we compare all steps between and and then compute F1. A predicted step is considered structurally correct if its premises (e.g., , ) exactly match the gold premises.
Intermediates: To evaluate the intermediate conclusions, we compare the aligned intermediate conclusions and then compute F1. A predicted intermediate conclusion is deemed correct if the BLEURT score (Sellam et al., 2020) exceeds 0.28.
For each dimension, the AllCorrect score is 1 if F1 is 1, otherwise 0. Given the above scores, we employ the Overall AllCorrect metric to comprehensively evaluate , which takes a value of 1 if and only if all leaves, steps, and intermediates are correct. Note that this is an extremely strict metric, where any deviations in will result in a score of 0.
For the STREET benchmark, we follow (Ribeiro et al., 2023) and adopt two metrics, namely, the answer to the question and the quality of the reasoning graphs, to evaluate different methods.
Answer Accuracy: This metric measures the ability to correctly answer questions. The answer accuracy serves as an upper bound for other metrics, as any reasoning graph generated with incorrect answers is also labeled as incorrect.
Reasoning Graph Accuracy: This metric compares the predicted reasoning graph and the golden reasoning graph from the aspects of the graph structure and the content of intermediate conclusions. Please note that this is a stringent metric, with minor deviations from the golden reasoning graph resulting in the prediction being incorrect.
Appendix E Illustrations and Case Study of Seer
Given a hypothesis and initial facts , we first obtain the trajectory through the reasoning process, as shown in Figure 4. The state update follows the Markov decision process (Bellman, 1957), meaning the current state only depends on the previous state. Figure 4 is an erroneous reasoning example to better illustrate the following steps. Then, we convert the trajectory into an entailment tree and align it with to assign reward for each intermediate conclusion (as presented in Figure 5). Furthermore, Figure 6 elucidates the issue of equivalent trajectories, and previous work can not accurately describe the logical relationship between different states in entailment trees.

Appendix F Prompts for GPT-4




Figures 7 and 8 show the Chain-of-Thought (CoT) (Wei et al., 2022) and ReAct (Yao et al., 2023b) prompts for GPT-4, and figures 9 and 10 show the prompts of thought generator and state evaluator in Tree of Thought (ToT) (Yao et al., 2023a), respectively. We provide a detailed introduction to the task definition and guide the model to respond in the required format. We randomly selected three examples for in-context learning. For a fair comparison, we use the same examples for CoT and ReAct, attributing similar thoughts to them. ReAct divides the dialogue into two rounds, "Thought" and "Action", to query GPT-4. For ToT, following (Yao et al., 2023a), we generate candidate actions using a thought generator and subsequently select and execute the optimal action through a state evaluator. Due to its exceptional reasoning capabilities and self-evaluation strategy, ToT achieves superior results compared to CoT and ReAct, as shown in Table 2. However, ToT requires higher costs in comparison to CoT and ReAct.
Appendix G Error Analysis
We conduct a comprehensive error analysis on Task2 and Task3 of EntailmentBank.
G.1 Error Analysis of Task2
We randomly sample 50 entailment trees where Seer made incorrect reasoning. We find the following four types of errors.
(1) Reasoning Step Error (62%). This is the main source of errors and predominantly depends on whether the policy can select the correct premise. We observe that a small portion of the errors (accounting for 12.9% of this error type) use all the gold leaves, but have errors in the combination order. Compared to other reasoning step errors, the policy identified the correct premise. For example, the gold steps are "; " and the error steps predicted by Seer are "; ".
(2) Early Termination Error (18%). We observe that the reasoning process may terminate prematurely and the existing entailment steps are all correct. On one hand, T5-large outputs “End” prematurely, unlike GPT-4 which can accurately judge when to stop. On the other hand, the entailment module might erroneously infer a hypothesis, leading to premature termination.
(3) Intermediate Conclusion Error (10%). This error type is different from the above error (where the entailment module prematurely infers a hypothesis). Intermediate conclusion error denotes errors triggered by incorrect entailment in the intermediate conclusions, despite having correct leaves and steps. For a fair comparison, we used the entailment module that has already been trained in previous work Hong et al. (2023). It is noted that the reasoning part, which is the focus of our paper, is completely correct in this type of error, and this type of error can be mitigated by training a better entailment module.
(4) Imperfect Evaluation (10%). We discover that some trees deemed as invalid are valid in fact, indicating that current automated metrics underestimate the validity of the trees. The most common reason is that there are multiple valid ways to construct an entailment tree. For example, consider the structure of a gold tree: "" may be predicted as: "; ".
G.2 Error Analysis of Task3
Task 3 requires retrieving an initial set of facts from the corpus. Therefore, in addition to the errors in Task 2 described above, we found that Task 3 has its own unique set of errors.
(1) Missing Gold Leaves Error (58%). Missing gold leaves error refers to the case where the gold leaves are not included in the facts retrieved from the corpus. This case will inevitably lead to an error in the predicted entailment tree, regardless of how powerful the policy is. The bottleneck of this error lies in the retrieval model. For a fair comparison, we directly use the retrieval model provided in previous work (Hong et al., 2023).
(2) Reasoning Errors (42%). The four error types described in G.1 account for 42% in Task3.
We also discovered that the reasoning graph contains similar error types as found in entailment trees, as they both belong to structured reasoning.