Self-triggered Consensus of Multi-agent Systems with Quantized Relative State Measurements

Masashi Wakaiki Graduate School of System Informatics, Kobe University, Nada, Kobe, Hyogo 657-8501, Japan wakaiki@ruby.kobe-u.ac.jp

Abstract.

This paper addresses the consensus problem of first-order continuous-time multi-agent systems over undirected graphs. Each agent samples relative state measurements in a self-triggered fashion and transmits the sum of the measurements to its neighbors. Moreover, we use finite-level dynamic quantizers and apply the zooming-in technique. The proposed joint design method for quantization and self-triggered sampling achieves asymptotic consensus, and inter-event times are strictly positive. Sampling times are determined explicitly with iterative procedures including the computation of the Lambert $W$ -function. A simulation example is provided to illustrate the effectiveness of the proposed method.

This work was supported by JSPS KAKENHI Grant Number JP20K14362.

1. Introduction

With the recent development of information and communication technologies, multi-agent systems have received considerable attention. Cooperative control of multi-agent systems can be applied to various areas such as multi-vehicle formulation [1] and distributed sensor networks [2]. A basic coordination problem of multi-agent systems is consensus, whose aim is to reach an agreement on the states of all agents. A theoretical framework for consensus problems has been introduced in the seminal work [3], and substantial progress has been made since then; see the survey papers [4, 5] and the references therein.

In practice, digital devices are used in multi-agent systems. Conventional approaches to implementing digital platforms involve periodic sampling. However, periodic sampling can lead to unnecessary control updates and state measurements, which are undesirable for resource-constrained multi-agent systems. Event-triggered control [6, 7, 8] and self-triggered control [9, 10, 11] are promising alternatives to traditional periodic control. In both event-triggered and self-triggered control systems, data transmissions and control updates occur only when needed. Event-triggering mechanisms use current measurements and check triggering conditions continuously or periodically. On the other hand, self-triggering mechanisms avoid such frequent monitoring by calculating the next sampling time when data are obtained. Various methods have been developed for event-triggered consensus and self-triggered consensus; see, e.g., [12, 13, 14, 15, 16]. Comprehensive surveys on this topic are available in [17, 18]. Some specifically relevant studies are cited below.

The bandwidth of communication channels and the accuracy of sensors may be limited in multi-agent systems. In such situations, only imperfect information is available to the agents. We also face the theoretical question of how much accuracy in information is necessary for consensus. From both practical and theoretical point of view, quantized consensus has been studied extensively. For continuous-time multi-agent systems, infinite-level static quantization is often considered under the situation where quantized measurements are obtained continuously; see, e.g., [19, 20, 21, 22, 23, 24, 25]. Event-triggering mechanisms and self-triggering mechanisms have been proposed for continuous-time multi-agent systems with infinite-level static quantizers in [26, 27, 28, 29, 30, 31, 32, 33, 34, 35]. Self-triggered consensus with ternary controllers has been also studied in [36, 37]. For event-triggered consensus under unknown input delays, finite-level dynamic quantizers have been developed in [38], where the quantization error goes to zero as the agent state converges to the origin.

For discrete-time multi-agent systems, finite-level dynamic quantizers to achieve asymptotic consensus have been designed in [39, 40, 41, 42, 43]. This type of dynamic quantization has been also used for periodic sampled-data consensus [44], event-triggered consensus [45, 46, 47, 48, 49], and consensus under denial-of-service attacks [50]. Moreover, an event-triggered average consensus protocol has been proposed for discrete-time multi-agent systems with integer-valued states in [51], and it has been extended to the privacy-preserving case in [52].

In this paper, we consider first-order continuous-time multi-agent systems over undirected graphs. Our goal is to jointly design a finite-level dynamic quantizer and a self-triggering mechanism for asymptotic consensus. We focus on the situation where relative states, not absolute states, are sampled as, e.g., in [16, 19, 22, 30, 29, 24, 31, 32, 34]. We assume that each agent’s sensor has a scaling parameter to adjust the maximum measurement range and the accuracy. For example, if indirect time-of-flight sensors [53] are installed in agents, then the modulation frequency of light signals determines the maximum range and the accuracy. In the case of cameras, they can be changed by adjusting the focal length; see Section 11.2 of [54] for a mathematical model of cameras.

In the proposed self-triggered framework, the agents send the sum of the relative state measurements to all their neighbors as in the self-triggered consensus algorithm presented in [14]. In other words, each agent communicates with its neighbors only at the sampling times of itself and its neighbors. The sum is transmitted so that the neighbors compute the next sampling times, not the inputs. After receiving it, the neighbors update the next sampling times. Since the measurements are already quantized when they are sampled, the sum can be transmitted without error, even over channels with finite capacity.

The main contributions of this paper are summarized as follows:

1. We propose a joint algorithm for finite-level dynamic quantization and self-triggered sampling of the relative states. We also provide a sufficient condition for the consensus of the quantized self-triggered multi-agent system. This sufficient condition represents a quantitative trade-off between data accuracy and sampling frequency. Such a trade-off can be a useful guideline for sensing performance, power consumption, and channel capacity.

2. In the proposed method, the inter-event times, i.e., the sampling intervals of each agent, are strictly positive, and hence Zeno behavior does not occur. In addition, the agents can compute sampling times using an explicit formula with the Lambert $W$ -function (see, e.g., [55] for the Lambert $W$ -function). Consequently, the proposed self-triggering mechanism is simple and efficient in computation.

We now compare our results with previous studies. The finite-level dynamic quantizers developed in [39, 40, 41, 42, 43] and their aforementioned extensions require the absolute states. More specifically, they quantize the error between the absolute state and its estimate for communication over finite-capacity channels. In this framework, the agents have to estimate the states of all their neighbors for decoding. In contrast, we develop finite-level dynamic quantizers for relative state measurements. As in the existing studies above, we also employ the zooming-in technique introduced for single-loop systems in [56, 57]. However, due to the above-mentioned difference in what is quantized, the quantizer we study has several notable features. For example, the proposed algorithm can be applied to GPS-denied environments. Moreover, the estimation of neighbor states is not needed, which reduces the computational burden on the agents.

A finite-level quantizer may be saturated, i.e., it does not guarantee the accuracy of quantized data in general if the original data is outside of the quantization region. To achieve asymptotic consensus, we need to update the scaling parameter of the quantizer so that the relative state measurement is within the quantization region and the quantization error goes to zero asymptotically. In [29, 32, 34], infinite-level static quantizers have been used for quantized self-triggered consensus of first-order multi-agent systems. Hence the issue of quantizer saturation has not been addressed there. In [29], infinite-level uniform quantization has been considered, and consequently only consensus to a bounded region around the average of the agent states has been achieved. The quantized self-triggered control algorithm proposed in [32, 34] achieves asymptotic consensus with the help of infinite-level logarithmic quantizers, but sampling times have to belong to the set $\{t=kh:\text{$k$ is a nonnegative integer}\}$ with some $h>0$ , which makes it easy to exclude Zeno behavior. Table 1 summarizes the comparison between this study and several relevant studies.

The difficulty of this study is that the following three conditions must be satisfied:

•

avoiding quantizer saturation;
•

decreasing the quantization error asymptotically; and
•

guaranteeing that the inter-event times are strictly positive.

To address this difficulty, we introduce a new semi-norm ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}$ for the analysis of multi-agent systems. The semi-norm is constructed from the maximum norm and is suitable for handling errors of individual agents due to quantization and self-triggered sampling. Moreover, the Laplacian matrix $L\in\mathbb{R}^{N\times N}$ of the multi-agent system has the following semi-contractivity property: There exists a constant $\gamma>0$ such that

{|\kern-1.07639pt|\kern-1.07639pt|e^{-Lt}v|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq e^{-\gamma t}{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}

for all $v\in\mathbb{R}^{N}$ and $t\geq 0$ ; see [58, 59] for the semi-contraction theory. The semi-contractivity property facilitates the analysis of state trajectories under self-triggered sampling and consequently leads to a simple design of the scaling parameter for finite-level dynamic quantization.

Table 1. Comparison between this study and several relevant studies.

	Triggering mechanism	Measurement	Quantization	Agent dynamics
This study	Self-trigger	Relative state	Finite-level & dynamic	First-order
[38, 46, 47, 48, 49]	Event-trigger	Absolute state	Finite-level & dynamic	High-order
[29, 32, 34]	Self-trigger	Relative state	Infinite-level & static	First-order

The rest of this paper is organized as follows. In Section 2, we introduce the system model. In Section 3, we provide some preliminaries on the semi-norm and sampling times. Section 4 contains the main result, which gives a sufficient condition for consensus. In Section 5, we explain how the agents compute sampling times in a self-triggered fashion. A simulation example is given in Section 6, and Section 7 concludes this paper.

Notation: We denote the set of nonnegative integers by $\mathbb{N}_{0}$ . We define $\inf\emptyset\coloneqq\infty$ . Let $M,N\in\mathbb{N}$ . We denote the transpose of $A\in\mathbb{R}^{M\times N}$ by $A^{\top}$ . For a vector $v\in\mathbb{R}^{N}$ with the $i$ -th element $v_{i}$ , its maximum norm is

\|v\|_{\infty}\coloneqq\max\{|v_{1}|,\dots,|v_{N}|\},

and the corresponding induced norm of $A\in\mathbb{R}^{M\times N}$ with the $(i,j)$ -th element $A_{ij}$ is given by

\|A\|_{\infty}=\max\left\{\sum_{j=1}^{N}|A_{ij}|:1\leq i\leq M\right\}.

When the eigenvalues $\lambda_{1},\lambda_{2},\cdots,\lambda_{N}\in\mathbb{R}$ of a symmetric matrix $P\in\mathbb{R}^{N\times N}$ with $N\geq 2$ satisfy $\lambda_{1}\leq\lambda_{2}\leq\cdots\leq\lambda_{N}$ , we write $\lambda_{2}(P)\coloneqq\lambda_{2}$ . We define

\mathbf{1}\coloneqq\begin{bmatrix}1&1&\cdots&1\end{bmatrix}^{\top}\in\mathbb{R}^{N},\qquad\bar{\mathbf{1}}\coloneqq\frac{1}{N}\mathbf{1}^{\top}

and write $\mathrm{ave}(v)\coloneqq\bar{\mathbf{1}}v$ for $v\in\mathbb{R}^{N}$ . The graph Laplacian of an undirected graph $G$ is denoted by $L(G)$ . We denote the Lambert $W$ -function by $W(y)$ for $y\geq 0$ . In other words, $W(y)$ is the solution $x\geq 0$ of the transcendental equation $xe^{x}=y$ . Throughout this paper, we shall use the following fact frequently without comment: For $a,\omega>0$ and $c\in\mathbb{R}$ , the solution $x=x^{*}$ of the transcendental equation $a(x-c)=e^{-\omega x}$ can be written as

x^{*}=\frac{1}{\omega}W\left(\frac{\omega e^{-\omega c}}{a}\right)+c.

2. System Model

2.1. Multi-agent system

Let $N\in\mathbb{N}$ be $N\geq 2$ , and consider a multi-agent system with $N$ agents. Each agent has a label $i\in\mathcal{N}\coloneqq\{1,2,\dots,N\}$ . For every $i\in\mathcal{N}$ , the dynamics of agent $i$ is given by

(1)

\dot{x}_{i}(t)=u_{i}(t),\quad t\geq 0;\qquad x_{i}(0)=x_{i0}\in\mathbb{R},

where $x_{i}(t)\in\mathbb{R}$ and $u_{i}(t)\in\mathbb{R}$ are the state and the control input of agent $i$ , respectively. The network topology of the multi-agent system is given by a fixed undirected graph $G=(\mathcal{V},\mathcal{E})$ with vertex set $\mathcal{V}=\{v_{1},v_{2},\dots,v_{N}\}$ and edge set

\mathcal{E}\subseteq\{(v_{i},v_{j})\in\mathcal{V}\times\mathcal{V}:i\not=j\}.

If $(v_{i},v_{j})\in\mathcal{E}$ , then agent $j$ is called a neighbor of agent $i$ , and these two agents can measure the relative states and communicate with each other. For $i\in\mathcal{N}$ , we denote by $\mathcal{N}_{i}$ the set of all neighbors of agent $i$ and by $d_{i}$ the degree of the node $v_{i}$ , that is, the cardinality of the set $\mathcal{N}_{i}$ .

Consider the ideal case without quantization or self-triggered sampling, and set

(2)

u_{i}(t)=-\sum_{j\in\mathcal{N}_{i}}\big{(}x_{i}(t)-x_{j}(t)\big{)}

for $t\geq 0$ and $i\in\mathcal{N}$ . It is well known that the multi-agent system to which the control input (2) is applied achieves average consensus under the following assumption.

Assumption 2.1.

The undirected graph $G$ is connected.

In this paper, we place Assumption 2.1. Moreover, we make two assumptions, which are used to avoid the saturation of quantization schemes. These assumptions are relative-state analogues of the assumptions in the previous studies on quantized consensus based on absolute state measurements (see, e.g., Assumptions 3 and 4 of [44]).

Assumption 2.2.

A bound $E_{0}>0$ satisfying

\left|x_{i0}-\frac{1}{N}\sum_{j\in\mathcal{N}}x_{j0}\right|\leq E_{0}\qquad\text{for all~{}}i\in\mathcal{N}

is known by all agents.

Assumption 2.3.

A bound $\tilde{d}\in\mathbb{N}$ satisfying

d_{i}\leq\tilde{d}\qquad\text{for all~{}}i\in\mathcal{N}

is known by all agents.

We make an assumption on the number $R$ of quantization levels.

Assumption 2.4.

The number $R$ of quantization levels is an odd number, i.e., $R=2R_{0}+1$ for some $R_{0}\in\mathbb{N}_{0}$ .

In this paper, we study the following notion of consensus of multi-agent systems under Assumption 2.2.

Definition 2.5.

The multi-agent system achieves consensus exponentially with decay rate $\omega>0$ under Assumption 2.2 if there exists a constant $\Omega>0$ , independent of $E_{0}$ , such that

(3)

|x_{i}(t)-x_{j}(t)|\leq\Omega E_{0}e^{-\omega t}

for all $t\geq 0$ and $i,j\in\mathcal{N}$ .

2.2. Quantization scheme

Let $E>0$ be a quantization range and let $R\in\mathbb{N}$ be the number of quantization levels satisfying Assumption 2.4. We assume that $E$ and $R$ are shared among all agents. We apply uniform quantization to the interval $[-E,E]$ . Namely, a quantization function $Q_{E,R}$ is defined by

Q_{E,R}[z]\coloneqq\begin{cases}\dfrac{2pE}{R}&\text{if $\dfrac{(2p-1)E}{R}<z\leq\dfrac{(2p+1)E}{R}$}\vspace{8pt}\\ 0&\text{if $-\dfrac{E}{R}\leq z\leq\dfrac{E}{R}$}\vspace{8pt}\\ -Q_{E,R}[-z]&\text{if $z<-\dfrac{E}{R}$}\end{cases}

for $z\in[-E,E]$ , where $p\in\mathbb{N}$ and $p\leq R_{0}$ . By construction,

\big{|}z-Q_{E,R}[z]\big{|}\leq\frac{E}{R}

for all $z\in[-E,E]$ . The agents use a fixed $R$ but change $E$ in order to achieve consensus asymptotically. In other words, $E$ is the scaling parameter of the quantization scheme.

Let $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ be a strictly increasing sequence with $t_{0}^{i}\coloneqq 0$ , and $t_{k}^{i}$ is the $k$ -th sampling time of agent $i$ . To describe the quantized data used at time $t=t_{k}^{i}$ for $k\in\mathbb{N}_{0}$ , we assume for the moment that a certain function $E:[0,\infty)\to(0,\infty)$ satisfies the unsaturation condition

(4)

|x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})|\leq E(t_{k}^{i})\quad\text{for all $j\in\mathcal{N}_{i}$}.

Agent $i$ measures the relative state $x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})$ for each neighbor $j\in\mathcal{N}_{i}$ and obtains its quantized value

q_{ij}(t_{k}^{i})\coloneqq Q_{E(t_{k}^{i}),R}[x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})].

Then agent $i$ sends to each neighbor $j\in\mathcal{N}_{i}$ the sum

q_{i}(t_{k}^{i})\coloneqq\sum_{j\in\mathcal{N}_{i}}q_{ij}(t_{k}^{i}).

The neighbors use the sum $q_{i}(t_{k}^{i})$ to calculate the next sampling time, not the input. This data transmission implies that the agents use information not only about direct neighbors but also about two-hop neighbors as in the self-triggering mechanism developed in [14].

The sum $q_{i}(t_{k}^{i})$ consists of the quantized values, and therefore agent $i$ can transmit $q_{i}(t_{k}^{i})$ without errors even through finite-capacity channels. In fact, since $R$ is an odd number under Assumption 2.4, the sum $q_{i}(t_{k}^{i})$ belongs to the finite set

\left\{\frac{2pE(t_{k}^{i})}{R}:p\in\mathbb{Z}\text{~{}~{}~{}and~{}~{}}-\tilde{d}R_{0}\leq p\leq\tilde{d}R_{0}\right\},

where $\tilde{d}\in\mathbb{N}$ is as in Assumption 2.3. The encoder of agent $i$ assigns an index to each value $2pE/R$ and transmits the index corresponding to the sum $q_{i}(t_{k}^{i})$ to the decoder of each neighbor $j\in\mathcal{N}_{i}$ . Since the agents share $E$ , $R$ , and $\tilde{d}$ , the decoder can generate the sum $q_{i}(t_{k}^{i})$ from the received index.

2.3. Triggering mechanism

Let a strictly increasing sequence $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ with $t_{0}^{i}\coloneqq 0$ be the sampling times of agent $i\in\mathcal{N}$ as in Section 2.2, and let $k\in\mathbb{N}_{0}$ . As in the ideal case (2), the control input $u_{i}(t)$ of agent $i$ is given by the sum of the quantized relative state,

(5)

u_{i}(t)=-q_{i}(t_{k}^{i})=-\sum_{j\in\mathcal{N}_{i}}Q_{E(t_{k}^{i}),R}[x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})],

for $t_{k}^{i}\leq t<t_{k+1}^{i}$ when the unsaturation condition (4) is satisfied. Then the dynamics of agent $i$ can be written as

(6)

\displaystyle\dot{x}_{i}(t)=-\sum_{j\in\mathcal{N}_{i}}\big{(}x_{i}(t)-x_{j}(t)\big{)}+f_{i}(t)+g_{i}(t),

where $f_{i}(t)$ and $g_{i}(t)$ are, respectively, the errors due to sampling and quantization defined by

(7)		$\displaystyle f_{i}(t)$	$\displaystyle\coloneqq\sum_{j\in\mathcal{N}_{i}}\big{(}x_{i}(t)-x_{j}(t)\big{)}-\sum_{j\in\mathcal{N}_{i}}\big{(}x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})\big{)}$
(8)		$\displaystyle g_{i}(t)$	$\displaystyle\coloneqq\sum_{j\in\mathcal{N}_{i}}\big{(}x_{i}(t_{k}^{i})-x_{j}(t_{k}^{i})\big{)}-q_{i}(t_{k}^{i})$

for $t_{k}^{i}\leq t<t_{k+1}^{i}$ .

We make a triggering condition on the error $f_{i}$ due to sampling. From the dynamics (1) and the input (5) of each agent, we have that for all $t_{k}^{i}\leq t<t_{k+1}^{i}$ ,

(9)		$\displaystyle x_{i}(t)-x_{i}(t_{k}^{i})$	$\displaystyle=\int_{t_{k}^{i}}^{t}u_{i}(s)ds=-(t-t_{k}^{i})q_{i}(t_{k}^{i})$
(10)		$\displaystyle x_{j}(t)-x_{j}(t_{k}^{i})$	$\displaystyle=\int_{t_{k}^{i}}^{t}u_{j}(s)ds.$

Substituting (9) and (10) into (7) motivates us to consider the following function obtained only from the inputs:

	$\displaystyle f_{k}^{i}(\tau)$	$\displaystyle\coloneqq\sum_{j\in\mathcal{N}_{i}}\int_{t_{k}^{i}}^{t_{k}^{i}+\tau}\big{(}u_{i}(s)-u_{j}(s)\big{)}ds$
(11)			$\displaystyle=-\tau d_{i}q_{i}(t_{k}^{i})-\sum_{j\in\mathcal{N}_{i}}\int_{t_{k}^{i}}^{t_{k}^{i}+\tau}u_{j}(s)ds$

for $\tau\geq 0$ . Notice that

f_{i}(t_{k}^{i}+\tau)=f_{k}^{i}(\tau)

for all $\tau\in[0,t_{k+1}^{i}-t_{k}^{i})$ . Using the quantization range $E(t)$ , we define the $(k+1)$ -th sampling time $t_{k+1}^{i}$ of agent $i\in\mathcal{N}$ by

(12)

\left\{\begin{aligned} t_{k+1}^{i}&\coloneqq t_{k}^{i}+\min\{\tau_{k}^{i},\,\tau^{i}_{\max}\}\\ \tau_{k}^{i}&\coloneqq\inf\{\tau\geq\tau^{i}_{\min}:|f_{k}^{i}(\tau)|\geq\delta_{i}E(t_{k}^{i}+\tau)\},\end{aligned}\right.

where $\delta_{i}>0$ is a threshold and $\tau^{i}_{\max},\tau^{i}_{\min}>0$ are upper and lower bounds of inter-event times, respectively, i.e., $\tau^{i}_{\min}\leq\tau_{k}^{i}\leq\tau^{i}_{\max}$ .

The behaviors of the errors $f_{i}(t)$ and $g_{i}(t)$ can be roughly described as follows. Under the triggering mechanism (12), the error $|f_{i}(t)|$ due to sampling is upper-bounded by $\delta_{i}E(t)$ . The error $|g_{i}(t)|$ due to quantization is also bounded from above by a constant multiple of $E(t_{k}^{i})$ for $t_{k}^{i}\leq t<t_{k+1}^{i}$ when the quantizer is not saturated. Hence, if $E(t)$ decreases to zero as $t\to\infty$ , then both errors $f_{i}(t)$ and $g_{i}(t)$ also go to zero.

After some preliminaries in Section 3, Section 4 is devoted to finding a quantization range $E(t)$ , a threshold $\delta_{i}$ , and upper and lower bounds $\tau^{i}_{\max},\tau^{i}_{\min}$ of inter-event times such that consensus (3) as well as the unsaturation condition (4) are satisfied. In Section 5, we present a method for agent $i$ to compute the sampling times $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ in a self-triggered fashion.

We conclude this section by making two remarks on the triggering mechanism (12). First, the constraint $\tau_{k}^{i}\geq\tau_{\min}^{i}$ is made solely to simplify the consensus analysis, and agent $i$ can compute the sampling times $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ without using the lower bound $\tau^{i}_{\min}$ . Second, continuous communication with the neighbors is not required to compute the sampling times, although the inputs of the neighbors are used in the triggering mechanism (12). It is enough for agent $i$ to communicate with the neighbor $j\in\mathcal{N}_{i}$ at their sampling times $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ and $\{t_{k}^{j}\}_{k\in\mathbb{N}_{0}}$ . In fact, the inputs are piecewise-constant functions, and agent $i$ can know the input $u_{j}$ of the neighbor $j$ from the received data $q_{j}(t_{k}^{j})$ . Based on the updated information on $q_{j}(t_{k}^{j})$ , agent $i$ recalculates the next sampling time. We will discuss these issues in detail in Section 5.

3. Preliminaries

In this section, we introduce a semi-norm on $\mathbb{R}^{N}$ and basic properties of sampling times. The reader eager to pursue the consensus analysis of multi-agent systems might skip detailed proofs in this section and return to them when needed.

3.1. Semi-norm for consensus analysis

Inspired by the norm used in the theory of operator semigroups (see, e.g., the proof of Theorem 5.2 in Chapter 1 of [60]), we introduce a new semi-norm on $\mathbb{R}^{N}$ , which will lead to the semi-contractivity property [58, 59] of the matrix exponential of the negative Laplacian matrix.

Lemma 3.1.

Let $\|\cdot\|$ be an arbitrary norm on $\mathbb{R}^{N}$ , and let $L,F\in\mathbb{R}^{N\times N}$ . Assume that $\Gamma>0$ and $\gamma\in\mathbb{R}$ satisfy

(13)

\displaystyle\|e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|

\displaystyle\leq\Gamma e^{-\gamma t}\|Fv\|

for all $v\in\mathbb{R}^{N}$ and $t\geq 0$ . Then the function ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}\colon\mathbb{R}^{N}\to[0,\infty)$ defined by

\displaystyle{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}\coloneqq\sup_{t\geq 0}\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|,\quad v\in\mathbb{R}^{N},

satisfies the following properties:

a)

For all $v\in\mathbb{R}^{N}$ ,

$\|v-\mathrm{ave}(v)\mathbf{1}\|\leq{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}\leq\Gamma\|Fv\|.$
b)

For all $v\in\mathbb{R}^{N}$ , ${|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}=0$ if and only if $v=\mathrm{ave}(v)\mathbf{1}$ .

${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}$ is a semi-norm on $\mathbb{R}^{N}$ , i.e., for all $v,w\in\mathbb{R}^{N}$ and $\rho\in\mathbb{R}$ ,

{|\kern-1.07639pt|\kern-1.07639pt|\rho v|\kern-1.07639pt|\kern-1.07639pt|}=|\rho|~{}\!{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|},\quad{|\kern-1.07639pt|\kern-1.07639pt|v+w|\kern-1.07639pt|\kern-1.07639pt|}\leq{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}+{|\kern-1.07639pt|\kern-1.07639pt|w|\kern-1.07639pt|\kern-1.07639pt|}.

If $L$ satisfies $\bar{\mathbf{1}}L=0$ and $L\mathbf{1}=0$ , then

{|\kern-1.07639pt|\kern-1.07639pt|e^{-Lt}v|\kern-1.07639pt|\kern-1.07639pt|}\leq e^{-\gamma t}{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}

for all $v\in\mathbb{R}^{N}$ and $t\geq 0$ .

Proof.

Let $v,w\in\mathbb{R}^{N}$ and $\rho\in\mathbb{R}$ be given.

a) By definition, we have

\displaystyle{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}\geq\|e^{\gamma 0}e^{-L0}(v-\mathrm{ave}(v)\mathbf{1})\|=\|v-\mathrm{ave}(v)\mathbf{1}\|.

The inequality (13) yields

\displaystyle\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|

\displaystyle\leq\Gamma\|Fv\|

for all $t\geq 0$ . Hence, ${|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}\leq\Gamma\|Fv\|.$

b) This follows immediately from the definition of ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}$ .

c) We obtain

\displaystyle{|\kern-1.07639pt|\kern-1.07639pt|\rho v|\kern-1.07639pt|\kern-1.07639pt|}=|\rho|\sup_{t\geq 0}\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|=|\rho|~{}\!{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}.

Since $\mathrm{ave}(v+w)=\mathrm{ave}(v)+\mathrm{ave}(w),$ it follows from the triangle inequality for the norm $\|\cdot\|$ that

	$\displaystyle{\|\kern-1.07639pt\|\kern-1.07639pt\|v+w\|\kern-1.07639pt\|\kern-1.07639pt\|}$	$\displaystyle\leq\sup_{t\geq 0}\big{(}\\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|+\\|e^{\gamma t}e^{-Lt}(w-\mathrm{ave}(w)\mathbf{1})\\|\big{)}$
		$\displaystyle\leq\sup_{t\geq 0}\\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|+\sup_{t\geq 0}\\|e^{\gamma t}e^{-Lt}(w-\mathrm{ave}(w)\mathbf{1})\\|$
		$\displaystyle={\|\kern-1.07639pt\|\kern-1.07639pt\|v\|\kern-1.07639pt\|\kern-1.07639pt\|}+{\|\kern-1.07639pt\|\kern-1.07639pt\|w\|\kern-1.07639pt\|\kern-1.07639pt\|}.$

d) By assumption,

	$\displaystyle\mathrm{ave}(e^{-Lt}v)\mathbf{1}=(\bar{\mathbf{1}}e^{-Lt}v)\mathbf{1}=(\bar{\mathbf{1}}v)\mathbf{1}$
	$\displaystyle\quad=\mathrm{ave}(v)\mathbf{1}=\mathrm{ave}(v)(e^{-Lt}\mathbf{1})=e^{-Lt}(\mathrm{ave}(v)\mathbf{1}).$

This yields

	$\displaystyle{\|\kern-1.07639pt\|\kern-1.07639pt\|e^{-Lt}v\|\kern-1.07639pt\|\kern-1.07639pt\|}$	$\displaystyle=\sup_{s\geq 0}\\|e^{\gamma s}e^{-L(s+t)}(v-\mathrm{ave}(v)\mathbf{1})\\|$
		$\displaystyle\leq e^{-\gamma t}\sup_{s\geq 0}\\|e^{\gamma s}e^{-Ls}(v-\mathrm{ave}(v)\mathbf{1})\\|$
		$\displaystyle=e^{-\gamma t}{\|\kern-1.07639pt\|\kern-1.07639pt\|v\|\kern-1.07639pt\|\kern-1.07639pt\|}$

for all $t\geq 0$ . ∎

Remark 3.2.

If the inequality in Lemma 3.1.d) is satisfied for some $\gamma>0$ , then $e^{-Lt}$ is a semi-contraction with respect to the semi-norm ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}$ for all $t>0$ . In Lemma 9 of [58], a more general method is presented for constructing such semi-norms. The tuning parameter of this method is a matrix whose kernel coincides with the span $\{\alpha\mathbf{1}:\alpha\in\mathbb{R}\}$ . Since the constants $\Gamma$ and $\gamma$ in (13) are easier to tune for the joint design of a quantizer and a self-triggering mechanism, we will use Lemma 3.1 in the consensus analysis.

3.2. Basic properties of sampling times

Let $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ be a strictly increasing sequence of real numbers with $t_{0}^{i}\coloneqq 0$ for $i\in\mathcal{N}=\{1,2,\dots,N\}$ . Set $t_{0}\coloneqq 0$ and $k_{i}(0)\coloneqq 0$ for $i\in\mathcal{N}$ . Define

	$\displaystyle t_{\ell+1}$	$\displaystyle\coloneqq\min_{i\in\mathcal{N}}t^{i}_{k_{i}(\ell)+1}$
	$\displaystyle k_{i}(\ell+1)$	$\displaystyle\coloneqq\max\big{\{}k\in\mathbb{N}_{0}:k\leq k_{i}(\ell)+1\text{~{}~{}and~{}~{}}t_{k}^{i}\in\{t_{0},t_{1},\dots,t_{\ell+1}\}\big{\}}$

for $\ell\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ . Roughly speaking, in the context of the multi-agent system, $\{t_{\ell}\}_{\ell\in\mathbb{N}_{0}}$ are all sampling times of the agents without duplication, and $k_{i}(\ell)$ is the number of times agent $i$ has measured the relative states on the interval $(0,t_{\ell}]$ . Hence $t^{i}_{k_{i}(\ell)}$ is the latest sampling time of agent $i$ at time $t=t_{\ell}$ . Define $\mathcal{I}(0)\coloneqq\mathcal{N}$ and

\mathcal{I}(\ell+1)\coloneqq\{i\in\mathcal{N}:t_{\ell+1}=t_{k_{i}(\ell)+1}^{i}\}

for $\ell\in\mathbb{N}_{0}$ . In our multi-agent setting, $\mathcal{I}(\ell)$ represents the set of agents measuring the relative states at $t=t_{\ell}$ .

Proposition 3.3.

Let $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ be a strictly increasing sequence of real numbers with $t_{0}^{i}\coloneqq 0$ for $i\in\mathcal{N}=\{1,2,\dots,N\}$ . The sequences $\{t_{\ell}\}_{\ell\in\mathbb{N}_{0}}$ and $\{k_{i}(\ell)\}_{\ell\in\mathbb{N}_{0}}$ defined as above have the following properties for all $\ell\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ :

a)

$k_{i}(\ell)\leq k_{i}(\ell+1)\leq k_{i}(\ell)+1$ .
b)

$k_{i}(\ell+1)=k_{i}(\ell)+1$ if and only if $i\in\mathcal{I}(\ell+1)$ . In this case,

$t_{\ell+1}=t_{k_{i}(\ell+1)}^{i}.$
c)

$t^{i}_{k_{i}(\ell)}\leq t_{\ell}<t_{\ell+1}$ .
d)

If $t_{k}^{i}\leq t_{\ell_{1}}$ for some $k,\ell_{1}\in\mathbb{N}_{0}$ , then there exists $\ell_{0}\in\mathbb{N}_{0}$ with $\ell_{0}\leq\ell_{1}$ such that $t_{k}^{i}=t_{\ell_{0}}$ .
e)

If $t^{i}_{k+1}-t^{i}_{k}\leq\tau^{i}_{\max}$ for all $k\in\mathbb{N}_{0}$ , then

$t_{\ell+1}\leq t^{i}_{k_{i}(\ell)}+\tau^{i}_{\max}.$
f)

If for all $i\in\mathcal{N}$ , there exists $\tau_{\min}^{i}>0$ such that

$t_{k+1}^{i}-t_{k}^{i}\geq\tau_{\min}^{i},$

then $t_{\ell}\to\infty$ as $\ell\to\infty$ .

Proof.

a) The inequality

k_{i}(\ell+1)\leq k_{i}(\ell)+1

follows immediately from the definition of $k_{i}(\ell+1)$ . Since $k_{i}(0)=0\leq k_{i}(1)$ , the inequality

(14)

k_{i}(\ell)\leq k_{i}(\ell+1)

holds for $\ell=0$ . Suppose that the inequality (14) holds for some $\ell\in\mathbb{N}_{0}$ . Then

	$\displaystyle\big{\{}k\in\mathbb{N}_{0}:k\leq k_{i}(\ell)+1\text{~{}~{}and~{}~{}}t_{k}^{i}\in\{t_{0},t_{1},\dots,t_{\ell+1}\}\big{\}}$
	$\displaystyle\hskip 3.0pt\subseteq\big{\{}k\in\mathbb{N}_{0}:k\leq k_{i}(\ell+1)+1\text{~{}~{}and~{}~{}}t_{k}^{i}\in\{t_{0},t_{1},\dots,t_{\ell+2}\}\big{\}},$

which yields $k_{i}(\ell+1)\leq k_{i}(\ell+2)$ . Therefore, the inequality (14) holds for all $\ell\in\mathbb{N}_{0}$ by induction.

b) Assume that $k_{i}(\ell+1)=k_{i}(\ell)+1$ . By the definition of $t_{\ell+1}$ , we obtain $t_{\ell+1}\leq t^{i}_{k_{i}(\ell)+1}$ . On the other hand, $t^{i}_{k_{i}(\ell+1)}\in\{t_{0},\dots,t_{\ell+1}\}$ by the definition of $k_{i}(\ell+1)$ . Since $\{t_{\ell}\}_{\ell\in\mathbb{N}_{0}}$ is a nondecreasing sequence by a), it follows that

t^{i}_{k_{i}(\ell)+1}=t^{i}_{k_{i}(\ell+1)}\leq t_{\ell+1}.

Hence

t_{\ell+1}=t^{i}_{k_{i}(\ell)+1}=t^{i}_{k_{i}(\ell+1)}.

Conversely, assume that $t_{\ell+1}=t^{i}_{k_{i}(\ell)+1}$ . Then

t^{i}_{k_{i}(\ell)+1}\in\{t_{0},t_{1},\dots,t_{\ell+1}\}.

By the definition of $k_{i}(\ell+1)$ , we obtain $k_{i}(\ell+1)=k_{i}(\ell)+1$ .

c) The definition of $k_{i}(\ell)$ directly yields

t^{i}_{k_{i}(\ell)}\leq t_{\ell}.

It remains to show that

t_{\ell}<t_{\ell+1}.

By construction, $\mathcal{I}(\ell)\not=\emptyset$ holds for all $\ell\in\mathbb{N}_{0}$ . First, we consider the case

\mathcal{I}(\ell)\cap\mathcal{I}(\ell+1)=\emptyset.

Since $\mathcal{I}(0)=\mathcal{N}$ by definition, we obtain $\ell\geq 1$ . Let $i\in\mathcal{I}(\ell+1)$ . Then $t_{\ell+1}=t^{i}_{k_{i}(\ell)+1}$ . On the other hand, $i\not\in\mathcal{I}(\ell)$ and hence

t_{\ell}<t^{i}_{k_{i}(\ell-1)+1}.

Since $k_{i}(\ell-1)=k_{i}(\ell)$ by a) and b), we obtain

t_{\ell}<t^{i}_{k_{i}(\ell-1)+1}=t^{i}_{k_{i}(\ell)+1}=t_{\ell+1}.

Next, assume that

\mathcal{I}(\ell)\cap\mathcal{I}(\ell+1)\not=\emptyset.

Let

i\in\mathcal{I}(\ell)\cap\mathcal{I}(\ell+1).

Then $t_{\ell+1}=t^{i}_{k_{i}(\ell)+1}$ from $i\in\mathcal{I}(\ell+1)$ . If $\ell=0$ , then

t_{\ell}=t_{0}=0=t^{i}_{k_{i}(0)}=t^{i}_{k_{i}(\ell)}.

If $\ell\geq 1$ , then we have from $i\in\mathcal{I}(\ell)$ and b) that

t_{\ell}=t^{i}_{k_{i}(\ell)}.

Since $t^{i}_{k_{i}(\ell)}<t^{i}_{k_{i}(\ell)+1}$ , it follows that $t_{\ell}<t_{\ell+1}$ .

d) We have from c) that

t_{\ell_{1}}<t_{\ell_{1}+1}\leq t^{i}_{k_{i}(\ell_{1})+1}.

This and the assumption $t_{k}^{i}\leq t_{\ell_{1}}$ yield $t_{k}^{i}<t^{i}_{k_{i}(\ell_{1})+1}$ , and therefore $k\leq k_{i}(\ell_{1})$ . Let

\ell_{0}\coloneqq\min\{\ell\in\mathbb{N}_{0}:\ell\leq\ell_{1}\text{~{}~{}and~{}~{}}k=k_{i}(\ell)\}.

If $\ell_{0}=0$ , then we obtain

t_{k}^{i}=t_{0}^{i}=0=t_{0}=t_{\ell_{0}}.

Assume that $\ell_{0}\not=0$ . Then $k=k_{i}(\ell_{0})\geq 1$ and

k_{i}(\ell_{0})=k_{i}(\ell_{0}-1)+1.

This and b) yield

t^{i}_{k}=t_{k_{i}(\ell_{0})}^{i}=t_{\ell_{0}}.

e) Since $t_{\ell+1}\leq t^{i}_{k_{i}(\ell)+1}$ by the definition of $t_{\ell+1}$ , it follows that

t_{\ell+1}-t^{i}_{k_{i}(\ell)}\leq t^{i}_{k_{i}(\ell)+1}-t^{i}_{k_{i}(\ell)}\leq\tau^{i}_{\max}.

f) For all $\ell\in\mathbb{N}_{0}$ , there exists $i\in\mathcal{N}$ such that $t_{\ell}\in\{t^{i}_{k}\}_{k\in\mathbb{N}_{0}}$ . We have from c) that $t_{\ell}\not=t_{\ell+1}$ . Since $\mathcal{N}$ is a set with finite elements, there exist $i\in\mathcal{N}$ and a subsequence $\{t_{\ell(p)}\}_{p\in\mathbb{N}_{0}}$ of $\{t_{\ell}\}_{\ell\in\mathbb{N}_{0}}$ such that

t_{\ell(p)}\in\{t^{i}_{k}\}_{k\in\mathbb{N}_{0}}

for all $p\in\mathbb{N}_{0}$ . For each $p\in\mathbb{N}_{0}$ , let $k(p)\in\mathbb{N}_{0}$ satisfy

t_{\ell(p)}=t^{i}_{k(p)}.

Assume, to get a contradiction, that $\sup_{\ell\in\mathbb{N}_{0}}t_{\ell}<\infty$ . Take

0<\varepsilon<\tau_{\min}^{i}.

There exists $p_{0}\in\mathbb{N}_{0}$ such that

t_{\ell(p+1)}-t_{\ell(p)}<\varepsilon

for all $p\geq p_{0}$ .

Choose $p\geq p_{0}$ arbitrarily. We obtain

t_{\ell(p)}=t^{i}_{k(p)}<t^{i}_{k(p)+1}\leq t^{i}_{k(p+1)}=t_{\ell(p+1)}.

Hence

(15)

t^{i}_{k(p)+1}-t^{i}_{k(p)}\leq t_{\ell(p+1)}-t_{\ell(p)}<\varepsilon.

By assumption,

t^{i}_{k(p)+1}-t^{i}_{k(p)}\geq\tau_{\min}^{i}>\varepsilon,

which contradicts (15). ∎

4. Consensus Analysis

In this section, first we define a semi-norm based on the maximum norm. Next, we obtain a bound of the state with respect to the semi-norm for the design of the quantization range. After these preparations, we give a sufficient condition for consensus in the main theorem. Finally, we find bounds of the constant $\Gamma$ in (13) corresponding to our multi-agent setting.

Throughout this and the next sections, we consider the quantized self-triggered multi-agent system presented in Section 2. Let $\{t_{k}^{i}\}_{k\in\mathbb{N}_{0}}$ with $t_{0}^{i}\coloneqq 0$ be the sampling times of agent $i\in\mathcal{N}$ , which are given in (12). Define $\{t_{\ell}\}_{\ell\in\mathbb{N}_{0}}$ and $\{k_{i}(\ell)\}_{\ell\in\mathbb{N}_{0}}$ as in Section 3.2. We let $L\coloneqq L(G)$ , where $G$ is the undirected graph of the multi-agent system.

Define

	$\displaystyle x(t)$	$\displaystyle\coloneqq\begin{bmatrix}x_{1}(t)&x_{2}(t)&\cdots&x_{n}(t)\end{bmatrix}^{\top}$
	$\displaystyle x_{0}$	$\displaystyle\coloneqq\begin{bmatrix}x_{10}&x_{20}&\cdots&x_{n0}\end{bmatrix}^{\top}$
	$\displaystyle f(t)$	$\displaystyle\coloneqq\begin{bmatrix}f_{1}(t)&f_{2}(t)&\cdots&f_{n}(t)\end{bmatrix}^{\top}$
	$\displaystyle g(t)$	$\displaystyle\coloneqq\begin{bmatrix}g_{1}(t)&g_{2}(t)&\cdots&g_{n}(t)\end{bmatrix}^{\top}$

for $t\geq 0$ . Then we have from the dynamics (6) of individual agents that

\Sigma_{\mathrm{MAS}}\quad\begin{cases}\dot{x}(t)=-Lx(t)+f(t)+g(t),\quad t\geq 0;\\ x(0)=x_{0}.\end{cases}

4.1. Semi-norm based on the maximum norm

We start by showing the following simple result.

Lemma 4.1.

Let $N\in\mathbb{N}$ satisfy $N\geq 2$ and let $L$ be the Laplacian matrix of a connected undirected graph with $N$ vertices. Let $\|\cdot\|$ be an arbitrary norm on $\mathbb{R}^{N}$ and the corresponding induced norm on $\mathbb{R}^{N\times N}$ . Fix $\gamma\leq\lambda_{2}(L)$ , and define

\Gamma\coloneqq\sup_{t\geq 0}\|e^{\gamma t}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})\|.

Then $\Gamma<\infty$ and the inequalities

(16)		$\displaystyle\\|e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|$	$\displaystyle\leq\Gamma e^{-\gamma t}\\|v-\mathrm{ave}(v)\mathbf{1}\\|$
(17)		$\displaystyle\\|e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|$	$\displaystyle\leq\Gamma e^{-\gamma t}\\|v\\|$

hold for all $v\in\mathbb{R}^{N}$ and $t\geq 0$ .

Proof.

Let $\lambda_{1},\lambda_{2},\lambda_{3},\dots,\lambda_{N}$ be the eigenvalues of $L$ . Since the undirected graph corresponding to $L$ is connected, we have that $0$ is an eigenvalue of $L$ with algebraic multiplicity $1$ . Let $\lambda_{1}\coloneqq 0$ and define

	$\displaystyle\Lambda_{0}$	$\displaystyle\coloneqq\mathrm{diag}\big{(}0,\,\lambda_{2},\,\lambda_{3},\,\cdots,\,\lambda_{N}\big{)}$
	$\displaystyle\Lambda$	$\displaystyle\coloneqq\mathrm{diag}\big{(}\lambda_{2}\,,\lambda_{3}\,,\cdots,\,\lambda_{N}\big{)}.$

There exists an orthogonal matrix $V_{0}\in\mathbb{R}^{N\times N}$ such that

L=V_{0}\Lambda_{0}V_{0}^{\top}.

Since $\mathbf{1}$ is the eigenvector corresponding to the eigenvalue $\lambda_{1}=0$ , one can decompose $V_{0}$ into

V_{0}=\begin{bmatrix}\dfrac{\mathbf{1}}{\sqrt{N}}&V\end{bmatrix}

for some $V\in\mathbb{R}^{N\times(N-1)}$ .

Let $v\in\mathbb{R}^{N}$ and $t\geq 0$ . Noting that

\frac{\mathbf{1}}{\sqrt{N}}\left(\dfrac{\mathbf{1}^{\top}}{\sqrt{N}}v\right)=\mathrm{ave}(v)\mathbf{1},

we obtain

(18)

\displaystyle e^{-Lt}v

\displaystyle=V_{0}e^{-\Lambda_{0}t}V_{0}^{\top}v=\mathrm{ave}(v)\mathbf{1}+Ve^{-\Lambda t}V^{\top}v.

Since

\mathrm{ave}\big{(}(\mathrm{ave}(v)\mathbf{1})\big{)}\mathbf{1}=\mathrm{ave}(v)\mathbf{1},

it follows that

(19)

\displaystyle e^{-Lt}(\mathrm{ave}(v)\mathbf{1})=\mathrm{ave}(v)\mathbf{1}+Ve^{-\Lambda t}V^{\top}(\mathrm{ave}(v)\mathbf{1}).

By (18) and (19),

(20)

e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})=Ve^{-\Lambda t}V^{\top}(v-\mathrm{ave}(v)\mathbf{1}).

On the other hand, using $e^{-Lt}\mathbf{1}=\mathbf{1}$ , we obtain

(21)

e^{-Lt}(\mathrm{ave}(v)\mathbf{1})=\mathrm{ave}(v)\mathbf{1}.

By (18) and (21),

(22)

e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})=Ve^{-\Lambda t}V^{\top}v.

Since $\lambda_{i}\geq\lambda_{2}(L)\geq\gamma$ for all $i=2,3,\dots,N$ , it follows that

C\coloneqq\sup_{t\geq 0}\|e^{\gamma t}e^{-\Lambda t}\|<\infty.

Moreover, (21) gives

(23)

e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})=(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})v.

Using (22) and (23), we have

(24)

\Gamma=\sup_{t\geq 0}\|Ve^{\gamma t}e^{-\Lambda t}V^{\top}\|\leq C\|V\|~{}\!\|V^{\top}\|<\infty.

The inequalities (16) and (17) follow from (20) and (22), respectively. ∎

Fix a constant $0<\gamma\leq\lambda_{2}(L)$ . Here we apply Lemmas 3.1 and 4.1 in the case $\|\cdot\|=\|\cdot\|_{\infty}$ . By Lemma 4.1,

(25)

\Gamma_{\infty}\coloneqq\Gamma_{\infty}(\gamma)\coloneqq\sup_{t\geq 0}\|e^{\gamma t}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})\|_{\infty}<\infty.

It is immediate that

(26)

\Gamma_{\infty}\geq\|e^{\gamma 0}(e^{-L0}-\mathbf{1}\bar{\mathbf{1}})\|_{\infty}=\|I-\mathbf{1}\bar{\mathbf{1}}\|_{\infty}=2-\frac{2}{N}\geq 1

for all $N\geq 2$ . We also have

\|e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|_{\infty}\leq\Gamma_{\infty}e^{-\gamma t}\|Fv\|_{\infty},

where $F=I-\mathbf{1}\bar{\mathbf{1}}$ from (16) and $F=I$ from (17). Define

(27)

{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\coloneqq\sup_{t\geq 0}\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\|_{\infty},\quad v\in\mathbb{R}^{N}.

Then ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}$ is a semi-norm on $\mathbb{R}^{N}$ and satisfies the properties in Lemma 3.1. The next lemma motivates us to investigate the semi-norm of the state $x$ of $\Sigma_{\mathrm{MAS}}$ .

Lemma 4.2.

Define the semi-norm ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}$ as in (27). Let $v_{i}\in\mathbb{R}$ be the $i$ -th element of $v\in\mathbb{R}^{N}$ for $i=1,\dots,N$ . Then

(28)

|v_{i}-v_{j}|\leq 2{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}

for all $i,j=1,\dots,N$ .

Proof.

For all $i,j=1,\dots,N$ ,

|v_{i}-v_{j}|\leq\left|v_{i}-\mathrm{ave}(v)\right|+\left|v_{j}-\mathrm{ave}(v)\right|\leq 2\|v-\mathrm{ave}(v)\mathbf{1}\|_{\infty}.

By Lemma 3.1.a), we obtain

\|v-\mathrm{ave}(v)\mathbf{1}\|_{\infty}\leq{|\kern-1.07639pt|\kern-1.07639pt|v|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}.

Hence the desired inequality (28) holds for all $i,j=1,\dots,N$ . ∎

4.2. Design of quantization ranges

For a given $\omega>0$ , the quantization range $E(t)$ is defined by

(29)

\displaystyle E(t)\coloneqq 2\Gamma_{\infty}E_{0}e^{-\omega t},\quad t\geq 0.

We also set

\displaystyle\kappa(\omega)

\displaystyle\coloneqq\max\left\{\delta_{i}+\frac{d_{i}e^{\omega\tau^{i}_{\max}}}{R}:i\in\mathcal{N}\right\}

and

(30)		$\displaystyle\tilde{\tau}_{\min}^{i}$	$\displaystyle\coloneqq\min\left\{\tau>0:\tau\left(d_{i}^{2}+\sum_{j\in\mathcal{N}_{i}}d_{j}e^{\omega\tau_{\max}^{j}}\right)=\delta_{i}e^{-\omega\tau}\right\}$
(31)			$\displaystyle=\frac{1}{\omega}W\left(\frac{\omega\delta_{i}}{d_{i}^{2}+\sum_{j\in\mathcal{N}_{i}}d_{j}e^{\omega\tau_{\max}^{j}}}\right).$

The following lemma shows that ${|\kern-1.07639pt|\kern-1.07639pt|x(t)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}$ is bounded by $E(t)/2$ for a suitable decay parameter $\omega$ .

Lemma 4.3.

Suppose that Assumptions 2.1–2.4 hold. For each $i\in\mathcal{N}$ , let the lower bound $\tau_{\min}^{i}$ of inter-event times satisfy

0<\tau_{\min}^{i}\leq\min\{\tilde{\tau}_{\min}^{i},\,\tau_{\max}^{i}\}.

Assume that

(32)

0<\omega\leq\gamma-2\Gamma_{\infty}\kappa(\omega),

and define the quantization range $E(t)$ by (29). Then the state $x$ of $\Sigma_{\mathrm{MAS}}$ satisfies

{|\kern-1.07639pt|\kern-1.07639pt|x(t)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq\frac{E(t)}{2}

for all $t\geq 0$ , where the semi-norm ${|\kern-1.07639pt|\kern-1.07639pt|\cdot|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}$ is defined by (27).

Proof.

Since $t_{\ell}\to\infty$ as $\ell\to\infty$ by Proposition 3.3.f), it suffices to prove that

(33)

{|\kern-1.07639pt|\kern-1.07639pt|x(t)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq\frac{E(t)}{2},\quad 0\leq t\leq t_{\ell}

for all $\ell\in\mathbb{N}_{0}$ . Lemma 3.1.a) with $F=I-\mathbf{1}\bar{\mathbf{1}}$ gives

{|\kern-1.07639pt|\kern-1.07639pt|x(0)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq\Gamma_{\infty}\big{\|}x(0)-\mathrm{ave}\big{(}x(0)\big{)}\mathbf{1}\big{\|}_{\infty}.

By Assumption 2.2, we obtain

\big{\|}x(0)-\mathrm{ave}\big{(}x(0)\big{)}\mathbf{1}\big{\|}_{\infty}\leq E_{0}.

Since $E(0)=2\Gamma_{\infty}E_{0}$ by definition, it follows that

{|\kern-1.07639pt|\kern-1.07639pt|x(0)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq\frac{E(0)}{2}.

Therefore, (33) holds in the case $\ell=0$ .

We now proceed by induction and assume the inequality (33) to be true for some $\ell\in\mathbb{N}_{0}$ . Since

t_{k_{i}(p)}^{i}\leq t_{\ell}

for all $p=0,1,\dots,\ell$ and $i\in\mathcal{N}$ , Lemma 4.2 yields

\displaystyle|x_{i}(t_{k_{i}(p)}^{i})-x_{j}(t_{k_{i}(p)}^{i})|

\displaystyle\leq E(t_{k_{i}(p)}^{i})

for all $p=0,1,\dots,\ell$ and $i,j\in\mathcal{N}$ . In other words, the unsaturation condition (4) is satisfied for all $i\in\mathcal{N}$ until $t=t_{\ell}$ .

Fix $i\in\mathcal{N}$ . Recall that the dynamics of agent $i$ is given by (6). First we show that the error $f_{i}$ due to sampling, which is defined by (7), satisfies

(34)

|f_{i}(t)|<\delta_{i}E(t)

for all $t\in[t_{\ell},t_{\ell+1})$ . Suppose that $t\in[t_{\ell},t_{\ell+1})$ satisfies

t\geq t_{k_{i}(\ell)}^{i}+\tau_{\min}^{i}.

Since $t_{k_{i}(\ell)}^{i}\leq t_{\ell}$ and $t_{\ell+1}\leq t_{k_{i}(\ell)+1}^{i}$ by definition, it follows that

f_{i}(t)=f^{i}_{k_{i}(\ell)}(t-t_{k_{i}(\ell)}^{i}),

where $f^{i}_{k}$ is defined by (2.3). The triggering mechanism (12) guarantees that

|f^{i}_{k_{i}(\ell)}(t-t_{k_{i}(\ell)}^{i})|<\delta_{i}E(t),

and hence (34) holds when $t\geq t_{k_{i}(\ell)}^{i}+\tau_{\min}^{i}$ .

Let us consider the case where $t\in[t_{\ell},t_{\ell+1})$ satisfies

t<t_{k_{i}(\ell)}^{i}+\tau_{\min}^{i}.

By definition, $t_{k_{i}(\ell)}^{i}\leq t_{\ell}$ . Therefore, Proposition 3.3.d) yields

t_{k_{i}(\ell)}^{i}=t_{\ell_{0}}

for some $\ell_{0}\in\mathbb{N}_{0}$ with $\ell_{0}\leq\ell$ . Since the unsaturation condition (4) is satisfied until $t=t_{\ell}$ , the equations (9) and (10) yield

(35)

\displaystyle f_{i}(t)=-(t-t_{\ell_{0}})d_{i}q_{i}(t_{\ell_{0}})+(t-t_{\ell})\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell)})+\sum_{p=0}^{\ell-\ell_{0}-1}(t_{\ell_{0}+p+1}-t_{\ell_{0}+p})\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{0}+p)}).

By definition,

(36)

|q_{i}(t_{\ell_{0}})|\leq d_{i}E(t_{\ell_{0}}).

For each $p=0,1,\dots,\ell-\ell_{0}$ and $j\in\mathcal{N}_{i}$ , Proposition 3.3.a), c), and e) give

t_{\ell_{0}}-\tau_{\max}^{j}\stackrel{{\scriptstyle\textrm{c)}}}{{<}}t_{\ell_{0}+1}-\tau_{\max}^{j}\stackrel{{\scriptstyle\textrm{e)}}}{{\leq}}t^{j}_{k_{j}(\ell_{0})}\stackrel{{\scriptstyle\textrm{a)}}}{{\leq}}t^{j}_{k_{j}(\ell_{0}+p)}

and hence

(37)

|q_{j}(t^{j}_{k_{j}(\ell_{0}+p)})|\leq d_{j}E(t^{j}_{k_{j}(\ell_{0}+p)})\leq d_{j}e^{\omega\tau_{\max}^{j}}E(t_{\ell_{0}}).

Combining (35) with the inequalities (36) and (37), we obtain

\displaystyle|f_{i}(t)|\leq(t-t_{\ell_{0}})\left(d_{i}^{2}+\sum_{j\in\mathcal{N}_{i}}d_{j}e^{\omega\tau_{\max}^{j}}\right)E(t_{\ell_{0}}).

Since $t-t_{\ell_{0}}<\tilde{\tau}_{\min}^{i}$ , we see from the definition (30) of $\tilde{\tau}_{\min}^{i}$ that

\displaystyle(t-t_{\ell_{0}})\left(d_{i}^{2}+\sum_{j\in\mathcal{N}_{i}}d_{j}e^{\omega\tau_{\max}^{j}}\right)E(t_{\ell_{0}})<\delta_{i}e^{-\omega(t-t_{\ell_{0}})}E(t_{\ell_{0}})=\delta_{i}E(t).

Hence, the inequality (34) holds also when $t<t_{k_{i}(\ell)}^{i}+\tau_{\min}^{i}$ .

Next we study $|g_{i}(t)|$ for $t_{\ell}\leq t<t_{\ell+1}$ , where $g_{i}$ is defined as in (8) and is the error due to quantization. Since the unsaturation condition (4) is satisfied until $t=t_{\ell}$ , we have that

\big{|}\big{(}x_{i}(t_{k_{i}(\ell)}^{i})-x_{j}(t_{k_{i}(\ell)}^{i})\big{)}-q_{ij}(t_{k_{i}(\ell)}^{i})\big{|}\leq\frac{E(t_{k_{i}(\ell)}^{i})}{R}

for all $j\in\mathcal{N}_{i}$ . Proposition 3.3.e) shows that $t_{\ell+1}-t_{k_{i}(\ell)}^{i}\leq\tau_{\max}^{i}$ , which gives

\frac{E(t_{k_{i}(\ell)}^{i})}{R}=\frac{e^{\omega(t-t_{k_{i}(\ell)}^{i})}E(t)}{R}\leq\frac{e^{\omega\tau_{\max}^{i}}}{R}E(t)

for all $t\in[t_{\ell},t_{\ell+1})$ . Hence

(38)

\displaystyle|g_{i}(t)|\leq\sum_{j\in\mathcal{N}_{i}}\big{|}\big{(}x_{i}(t_{k_{i}(\ell)}^{i})-x_{j}(t_{k_{i}(\ell)}^{i})\big{)}-q_{ij}(t_{k_{i}(\ell)}^{i})\big{|}\leq\frac{d_{i}e^{\omega\tau_{\max}^{i}}}{R}E(t)

for all $t\in[t_{\ell},t_{\ell+1})$ .

From the inequalities (34) and (38), we obtain

\displaystyle|f_{i}(t)+g_{i}(t)|\leq\left(\delta_{i}+\frac{d_{i}e^{\omega\tau_{\max}^{i}}}{R}\right)E(t)\leq\kappa(\omega)E(t)

for all $t\in[t_{\ell},t_{\ell+1})$ and $i\in\mathcal{N}$ . This and Lemma 3.1.a) with $F=I$ give

{|\kern-1.07639pt|\kern-1.07639pt|f(t)+g(t)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq\Gamma_{\infty}\|f(t)+g(t)\|_{\infty}\leq\Gamma_{\infty}\kappa(\omega)E(t)

for all $t\in[t_{\ell},t_{\ell+1})$ . Therefore, we have from Lemma 3.1.c) and d) that

	$\displaystyle{\|\kern-1.07639pt\|\kern-1.07639pt\|x(t_{\ell}+\tau)\|\kern-1.07639pt\|\kern-1.07639pt\|}_{\infty}$	$\displaystyle\leq e^{-\gamma\tau}{\|\kern-1.07639pt\|\kern-1.07639pt\|x(t_{\ell})\|\kern-1.07639pt\|\kern-1.07639pt\|}_{\infty}+\Gamma_{\infty}\kappa(\omega)\int^{\tau}_{0}e^{-\gamma(\tau-s)}E(t_{\ell}+s)ds$
		$\displaystyle\leq\left(e^{-\gamma\tau}+2\Gamma_{\infty}\kappa(\omega)\int^{\tau}_{0}e^{-\gamma(\tau-s)}e^{-\omega s}ds\right)\frac{E(t_{\ell})}{2}$
(39)			$\displaystyle=\left(\left(1-\frac{2\Gamma_{\infty}\kappa(\omega)}{\gamma-\omega}\right)e^{-\gamma\tau}+\frac{2\Gamma_{\infty}\kappa(\omega)}{\gamma-\omega}e^{-\omega\tau}\right)\frac{E(t_{\ell})}{2}$

for all $\tau\in[0,t_{\ell+1}-t_{\ell}]$ . Since the condition (32) on $\omega$ yields

0<\frac{2\Gamma_{\infty}\kappa(\omega)}{\gamma-\omega}\leq 1,

it follows that

(40)

\left(1-\frac{2\Gamma_{\infty}\kappa(\omega)}{\gamma-\omega}\right)e^{-\gamma\tau}+\frac{2\Gamma_{\infty}\kappa(\omega)}{\gamma-\omega}e^{-\omega\tau}\leq e^{-\omega\tau}.

Combining the inequalities (39) and (40), we obtain

{|\kern-1.07639pt|\kern-1.07639pt|x(t_{\ell}+\tau)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq e^{-\omega\tau}\frac{E(t_{\ell})}{2}=\frac{E(t_{\ell}+\tau)}{2}

for all $\tau\in[0,t_{\ell+1}-t_{\ell}]$ . Thus ${|\kern-1.07639pt|\kern-1.07639pt|x(t)|\kern-1.07639pt|\kern-1.07639pt|}_{\infty}\leq E(t)/2$ for all $t\in[0,t_{\ell+1}]$ . ∎

The condition $0<\omega\leq\gamma-2\Gamma_{\infty}\kappa(\omega)$ obtained in Lemma 4.3 is in implicit form with respect to the decay parameter $\omega$ . We rewrite this condition in explicit form by using the Lambert $W$ -function. To this end, we define

(41)

\tilde{\omega}\coloneqq\min\left\{\eta_{i}-\frac{W(\xi_{i}\tau_{\max}^{i}e^{\eta_{i}\tau_{\max}^{i}})}{\tau_{\max}^{i}}:i\in\mathcal{N}\right\},

where

\displaystyle\xi_{i}\coloneqq\frac{2\Gamma_{\infty}d_{i}}{R},\quad\eta_{i}\coloneqq\gamma-2\Gamma_{\infty}\delta_{i}

for $i\in\mathcal{N}$ . Note also that

\gamma-2\Gamma_{\infty}\kappa(\omega)\leq\gamma-2\Gamma_{\infty}\left(\delta_{i}+\frac{d_{i}}{R}\right)

for all $i\in\mathcal{N}$ . Therefore, if the inequality $0<\gamma-2\Gamma_{\infty}\kappa(\omega)$ holds, then one has

(42)

\delta_{i}+\frac{d_{i}}{R}<\frac{\gamma}{2\Gamma_{\infty}}

for all $i\in\mathcal{N}$ .

Lemma 4.4.

Assume that the threshold $\delta_{i}>0$ and the number $R\in\mathbb{N}$ of quantization levels satisfy the inequality (42) for all $i\in\mathcal{N}$ . Then $\tilde{\omega}$ defined by (41) satisfies $\tilde{\omega}>0$ . Moreover, the decay parameter $\omega$ satisfies the condition (32) if and only if $0<\omega\leq\tilde{\omega}$ .

Proof.

Let $i\in\mathcal{N}$ . The inequality (42) is equivalent to

\gamma-2\Gamma_{\infty}\left(\delta_{i}+\frac{d_{i}}{R}\right)>0.

Since

\eta_{i}-\xi_{i}e^{\omega\tau_{\max}^{i}}=\gamma-2\Gamma_{\infty}\left(\delta_{i}+\frac{d_{i}e^{\omega\tau_{\max}^{i}}}{R}\right),

it follows that for all sufficiently small $\omega>0$ , the inequality

(43)

\omega\leq\eta_{i}-\xi_{i}e^{\omega\tau_{\max}^{i}}

holds. The inequality (43) is equivalent to

\xi_{i}\tau_{\max}^{i}e^{\eta_{i}\tau_{\max}^{i}}\leq(\eta_{i}-\omega)\tau_{\max}^{i}e^{(\eta_{i}-\omega)\tau_{\max}^{i}}.

Therefore, using the Lambert $W$ -function, one can write the inequality (43) as

\omega\leq\eta_{i}-\frac{W(\xi_{i}\tau_{\max}^{i}e^{\eta_{i}\tau_{\max}^{i}})}{\tau_{\max}^{i}}.

Since (43) holds for all sufficiently small $\omega>0$ , we obtain $\tilde{\omega}>0$ .

By definition,

\gamma-2\Gamma_{\infty}\kappa(\omega)=\min\{\eta_{i}-\xi_{i}e^{\omega\tau_{\max}^{i}}:i\in\mathcal{N}\}.

From this, it follows that $\omega\leq\gamma-2\Gamma_{\infty}\kappa(\omega)$ if and only if (43) holds for all $i\in\mathcal{N}$ . We have shown that (43) holds for all $i\in\mathcal{N}$ if and only if $\omega\leq\tilde{\omega}$ . Thus, the condition (32) is equivalent to $0<\omega\leq\tilde{\omega}$ . ∎

4.3. Main result

Before stating the main result of this section, we summarize the assumption on the parameters of the quantization scheme and the triggering mechanism.

Assumption 4.5.

Let upper bounds $\tau^{i}_{\max}>0$ be given for all $i\in\mathcal{N}$ . The following three conditions are satisfied:

a)

The threshold $\delta_{i}>0$ and the number $R\in\mathbb{N}$ of quantization levels satisfy the inequality (42) for all $i\in\mathcal{N}$ .
b)

For all $i\in\mathcal{N}$ , the lower bound $\tau_{\min}^{i}$ satisfies

$0<\tau_{\min}^{i}\leq\min\{\tilde{\tau}_{\min}^{i},\,\tau_{\max}^{i}\},$

where $\tilde{\tau}_{\min}^{i}$ is as in (31).
c)

The decay parameter $\omega$ of the quantization range $E(t)$ defined by (29) satisfies $0<\omega\leq\tilde{\omega}$ , where $\tilde{\omega}$ is as in (41).

Theorem 4.6.

Suppose that Assumptions 2.1–2.4 and 4.5 hold. Then the unsaturation condition (4) is satisfied for all $k\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ . Moreover, $\Sigma_{\mathrm{MAS}}$ achieves consensus exponentially with decay rate $\omega$ .

Proof.

Since $0<\omega\leq\tilde{\omega}$ , Lemma 4.4 shows that the condition (32) on $\omega$ is satisfied. By Lemmas 4.2 and 4.3, we obtain

(44)

|x_{i}(t)-x_{j}(t)|\leq E(t)

for all $t\geq 0$ and $i,j\in\mathcal{N}$ . Therefore, the unsaturation condition (4) is satisfied for all $k\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ . The inequality (44) and the definition (29) of $E(t)$ give

|x_{i}(t)-x_{j}(t)|\leq 2\Gamma_{\infty}E_{0}e^{-\omega t}

for all $t\geq 0$ and $i,j\in\mathcal{N}$ . Thus, $\Sigma_{\mathrm{MAS}}$ achieves consensus exponentially with decay rate $\omega$ . ∎

Recall that the maximum decay parameter $\tilde{\omega}$ is the minimum of

\eta_{i}-\frac{W(\xi_{i}e^{\eta_{i}\tau_{\max}^{i}})}{\tau_{\max}^{i}},\quad i\in\mathcal{N},

which is the solution of the equation $\omega=\eta_{i}-\xi_{i}e^{\omega\tau_{\max}^{i}};$ see the proof of Lemma 4.4. Moreover, $\xi_{i}$ becomes smaller as $d_{i}/R$ decreases, and $\eta_{i}$ becomes larger as $\delta_{i}$ decreases. Therefore, $\tilde{\omega}$ becomes larger as $d_{i}$ , $\delta_{i}$ , and $\tau_{\max}^{i}$ decreases and as $R$ increases. This also means that if agent $i$ has a large $d_{i}$ , i.e., many neighbors, then we need to use small $\delta_{i}$ and $\tau_{\max}^{i}$ in order to achieve fast consensus of the multi-agent system.

Remark 4.7.

The condition on the lower bound $\tau_{\min}^{i}$ in Assumption 4.5.b) is not used when each agent computes the next sampling time; see Section 5 for details. Therefore, Theorem 4.6 essentially shows that asymptotic consensus is achieved if (42) holds for each $i\in\mathcal{N}$ and if $0<\omega\leq\tilde{\omega}$ for given upper bounds $\tau^{1}_{\max},\dots,\tau^{N}_{\max}$ of inter-event times.

Remark 4.8.

To check the conditions obtained in Theorem 4.6, the global network parameters, $\lambda_{2}(L)$ and $\Gamma_{\infty}$ , are needed. In addition, the quantization range $E(t)$ is common to all agents as the scaling parameter of finite-level dynamic quantizers studied, e.g., in the previous works [40, 41]. These are drawbacks of the proposed method.

Remark 4.9.

Although the proposed method is inspired by the self-triggered consensus algorithm presented in [14], the approach to consensus analysis differs. In [14], a Lyapunov function and LaSalle’s invariance principle have been employed. In contrast, we develop a trajectory-based approach, where the semi-contractivity property of $e^{-Lt}$ plays a key role. Moreover, we discuss the convergence speed of consensus, by using the global parameters mentioned in Remark 4.8 above. The utilization of the global parameters also enables us to investigate the minimum inter-event time in a way different from that of [14].

4.4. Bounds of $\Gamma_{\infty}$

We use the constant $\Gamma_{\infty}$ in the definition (29) of $E(t)$ and the conditions for consensus given in Assumption 4.5. To apply the proposed method, we have to compute $\Gamma_{\infty}$ numerically by (25) or replace $\Gamma_{\infty}$ with an available upper bound of $\Gamma_{\infty}$ . In the next proposition, we provide bounds of $\Gamma_{\infty}$ by using the network size. The proof can be found in Appendix A.

Proposition 4.10.

Let $N\in\mathbb{N}$ satisfy $N\geq 2$ and let $G$ be a connected undirected graph with $N$ vertices. Define $L\coloneqq L(G)$ . Then the following statements hold for $\Gamma_{\infty}(\gamma)$ defined as in (25):

a)

For all $0<\gamma\leq\lambda_{2}(L)$ ,

$2-\frac{2}{N}\leq\Gamma_{\infty}(\gamma)\leq N-1.$
b)

If $G$ is a complete graph, then

$\Gamma_{\infty}(\gamma)=2-\frac{2}{N}$

for all $0<\gamma\leq\lambda_{2}(L)=N$ .

We conclude this section by using Proposition 4.10.b) to examine the relationship between the network size of complete graphs and the design parameters for quantization and self-triggered sampling. For real-valued functions $\Phi,\Psi$ on $\mathbb{N}$ , we write

\Phi(N)=\Theta\big{(}\Psi(N)\big{)}\quad\text{as $N\to\infty$}

if there are $C_{1},C_{2}>0$ and $N_{0}\in\mathbb{N}$ such that for all $N\geq N_{0}$ ,

C_{1}\Psi(N)\leq\Phi(N)\leq C_{2}\Psi(N).

Example 4.11.

Let $G$ be a complete graph with $N$ vertices.

Sensing accuracy: By Proposition 4.10.b), one can set

\gamma=N\text{~{}~{}and~{}~{}}\Gamma_{\infty}=2-\frac{2}{N}.

We see from the condition (42) that if the number $R$ of the quantization levels satisfies

(45)

R>\frac{2d_{i}\Gamma_{\infty}}{\gamma}=\frac{4(N-1)^{2}}{N^{2}},

then the quantized self-triggered multi-agent system achieves consensus exponentially for some threshold $\delta_{i}$ . Hence, the required sensing accuracy for asymptotic consensus is $\Theta(1)$ as $N\to\infty$ .

Number of indices for data transmission: Recall that the agents send the sum of relative state measurements to all neighbors for the computation of sampling times. The number of indices used for this communication is

2\tilde{d}R_{0}+1,

where $R_{0}\in\mathbb{N}_{0}$ and $\tilde{d}\in\mathbb{N}$ satisfy $R=2R_{0}+1$ and

d_{i}=N-1\leq\tilde{d}

for all $i\in\mathcal{N}$ , respectively. Hence, the required number of indices for asymptotic consensus is $\Theta(N)$ as $N\to\infty$ .

Threshold for sampling: We see from the condition (42) that the threshold $\delta_{i}$ of the triggering mechanism (12) of agent $i$ has to satisfy

\delta_{i}<\frac{\gamma}{2\Gamma_{\infty}}-\frac{d_{i}}{R}=\frac{N^{2}}{2(N-1)}-\frac{N-1}{R}.

Combining this inequality with (45), we have that the required threshold for asymptotic consensus is $\Theta(N)$ as $N\to\infty$ .

5. Computation of Sampling Times

In this section, we describe how the agents compute sampling times in a self-triggered fashion. We discuss an initial candidate of the next sampling time and then the first update of the candidate, followed by the $p$ -th update. Finally, we present a joint algorithm for quantization and self-triggering sampling.

Let $i\in\mathcal{N}$ and $k\in\mathbb{N}_{0}$ . Define $\tilde{\tau}_{\min}^{i}$ by (30). By Proposition 3.3.d) and f), there exists $\ell_{0}\in\mathbb{N}_{0}$ such that $t_{k}^{i}=t_{\ell_{0}}$ .

5.1. Initial candidate of the next sampling time

First, agent $i$ updates $q_{i}$ at time $t=t_{\ell_{0}}$ . If the neighbor $j$ also updates $q_{j}$ at time $t=t_{\ell_{0}}$ , then agent $i$ receives $q_{j}$ . Next, agent $i$ computes a candidate of the inter-event time,

\tau_{k,0}^{i}\coloneqq\min\{\tilde{\tau}_{k,0}^{i},\,\tau_{\max}^{i}\},

where

\displaystyle\tilde{\tau}_{k,0}^{i}\coloneqq\inf\Bigg{\{}\tau>0:\Bigg{|}\tau d_{i}q_{i}(t_{k}^{i})-\tau\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{0})})\Bigg{|}\geq\delta_{i}e^{-\omega\tau}E(t_{\ell_{0}})\Bigg{\}}.

By (36) and (37), $\tilde{\tau}_{k,0}^{i}\geq\tilde{\tau}_{\min}^{i}$ . Agent $i$ takes $t_{k}^{i}+\tau_{k,0}^{i}$ as an initial candidate of the next sampling time. If agent $i$ does not receive an updated $q_{j}$ from any neighbors $j$ on the interval $(t_{k}^{i},t_{k}^{i}+\tau_{k,0}^{i})$ , then $t_{k}^{i}+\tau_{k,0}^{i}$ is the next sampling time, that is, agent $i$ updates $q_{i}$ at $t=t_{k}^{i}+\tau_{k,0}^{i}$ .

Using the Lambert $W$ -function, one can write $\tau_{k,0}^{i}$ more explicitly. To see this, we first note that the solution $\tau=\tau^{*}$ of the equation

a\tau+c=be^{-\omega\tau},\quad a,b>0,\,c\in\mathbb{R}

is written as

\tau^{*}=\dfrac{1}{\omega}W\left(\dfrac{\omega b}{a}e^{\omega c/a}\right)-\dfrac{c}{a}.

Define the function $\phi_{0}$ by

\phi_{0}(a,b,c)\coloneqq\begin{cases}\dfrac{1}{\omega}W\left(\dfrac{\omega b}{|a|}e^{\omega c/a}\right)-\dfrac{c}{a}&\text{if $a\not=0$}\vspace{6pt}\\ \dfrac{1}{\omega}\log\dfrac{b}{|c|}&\text{if $a=0$ and $c\not=0$}\vspace{4pt}\\ \infty&\text{if $a=0$ and $c=0$}\end{cases}

for $a,c\in\mathbb{R}$ and $b>0$ . We also set

	$\displaystyle a_{k,0}^{i}$	$\displaystyle\coloneqq d_{i}q_{i}(t_{k}^{i})-\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{0})})$
(46)		$\displaystyle b_{k,0}^{i}$	$\displaystyle\coloneqq\delta_{i}E(t_{\ell_{0}})$
	$\displaystyle c_{k,0}^{i}$	$\displaystyle\coloneqq 0.$

Since

\displaystyle\tilde{\tau}_{k,0}^{i}=\inf\big{\{}

\displaystyle\tau>0:|a_{k,0}^{i}|\tau+c_{k,0}^{i}\geq b_{k,0}^{i}e^{-\omega\tau}\big{\}},

we have $\tilde{\tau}_{k,0}^{i}=\phi_{0}(a_{k,0}^{i},b_{k,0}^{i},c_{k,0}^{i})$ . Hence

(47)

\tau_{k,0}^{i}=\min\{\phi_{0}(a_{k,0}^{i},b_{k,0}^{i},c_{k,0}^{i}),\,\tau_{\max}^{i}\}.

5.2. First update

If agent $i$ receives an updated $q_{j}$ from some neighbor $j$ by $t=t_{k}^{i}+\tau_{k,0}^{i}$ , then agent $i$ must recalculate a candidate of the next sampling time as in the self-triggered method proposed in [14]. We will now consider this scenario, i.e., the case

\{\ell\in\mathbb{N}:t_{k}^{i}<t_{\ell}<t_{k}^{i}+\tau_{k,0}^{i}\text{~{}~{}and~{}~{}}\mathcal{I}(\ell)\cap\mathcal{N}_{i}\not=\emptyset\}\not=\emptyset,

where $\mathcal{I}(\ell)$ is defined as in Section 3.2. Let $t_{\ell_{1}}\in(t_{k}^{i},t_{k}^{i}+\tau_{k,0}^{i})$ be the first instant at which agent $i$ receives updated data after $t=t_{k}^{i}$ . Since $t_{k}^{i}=t_{\ell_{0}}$ , one can write $\ell_{1}$ as

\ell_{1}=\min\{\ell\in\mathbb{N}:\ell>\ell_{0}\text{~{}~{}and~{}~{}}\mathcal{I}(\ell)\cap\mathcal{N}_{i}\not=\emptyset\}.

Note that agent $i$ may receive updated data from several neighbors at time $t=t_{\ell_{1}}$ .

By using the new data, agent $i$ computes the following inter-event time at time $t=t_{\ell_{1}}$ :

\tau_{k,1}^{i}\coloneqq\min\{\tilde{\tau}_{k,1}^{i}+(t_{\ell_{1}}-t_{\ell_{0}}),\,\tau_{\max}^{i}\},

where

\displaystyle\tilde{\tau}_{k,1}^{i}\coloneqq\inf\Bigg{\{}\tau>0:\Bigg{|}\tau d_{i}q_{i}(t_{k}^{i})-\tau\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{1})})+(t_{\ell_{1}}-t_{\ell_{0}})a_{k,0}^{i}\Bigg{|}\geq\delta_{i}e^{-\omega\tau}E(t_{\ell_{1}})\Bigg{\}}.

Then $t_{k}^{i}+\tau_{k,1}^{i}$ is a new candidate of the next sampling time. By (36) and (37), we obtain

\tilde{\tau}_{k,1}^{i}+(t_{\ell_{1}}-t_{\ell_{0}})\geq\tilde{\tau}_{\min}^{i}.

As in the initial case, if agent $i$ does not receive an updated $q_{j}$ from any neighbors $j$ on the interval $(t_{\ell_{1}},t_{k}^{i}+\tau_{k,1}^{i})$ , then $t_{k}^{i}+\tau_{k,1}^{i}$ is the next sampling time. Otherwise, agent $i$ computes the next sampling time again in the same way.

One can rewrite $\tilde{\tau}_{k,1}^{i}$ by using the Lambert $W$ -function. To see this, we define

	$\displaystyle a_{k,1}^{i}$	$\displaystyle\coloneqq d_{i}q_{i}(t_{k}^{i})-\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{1})})$
	$\displaystyle b_{k,1}^{i}$	$\displaystyle\coloneqq\delta_{i}E(t_{\ell_{1}})$
	$\displaystyle c_{k,1}^{i}$	$\displaystyle\coloneqq(t_{\ell_{1}}-t_{\ell_{0}})a_{k,0}^{i}.$

Then

\displaystyle\tilde{\tau}_{k,1}^{i}=\inf\big{\{}

\displaystyle\tau>0:\big{|}a_{k,1}^{i}\tau+c_{k,1}^{i}\big{|}\geq b_{k,1}^{i}e^{-\omega\tau}\big{\}}.

From the definition of $\tilde{\tau}_{k,0}^{i}$ and $t_{\ell_{1}}-t_{\ell_{0}}<\tilde{\tau}_{k,0}^{i}$ , we obtain

|c_{k,1}^{i}|<b_{k,1}^{i}.

If the product $a_{k,1}^{i}c_{k,1}^{i}$ satisfies $a_{k,1}^{i}c_{k,1}^{i}\geq 0$ , then the condition

(48)

\big{|}a_{k,1}^{i}\tau+c_{k,1}^{i}\big{|}\geq b_{k,1}^{i}e^{-\omega\tau}

can be written as

|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau},

and hence $\tilde{\tau}_{k,1}^{i}=\phi_{0}(a_{k,1}^{i},b_{k,1}^{i},c_{k,1}^{i})$ .

Next we consider the case $a_{k,1}^{i}c_{k,1}^{i}<0$ . In this case, the condition (48) is equivalent to

\begin{cases}-|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}&\text{for $\displaystyle\tau\leq-c_{k,1}^{i}/a_{k,1}^{i}$}\vspace{3pt}\\ |a_{k,1}^{i}|\tau-|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}&\text{for $\tau>-c_{k,1}^{i}/a_{k,1}^{i}$}.\end{cases}

For the latter inequality, we have that

	$\displaystyle\inf\{\tau>-c_{k,1}^{i}/a_{k,1}^{i}:\|a_{k,1}^{i}\|\tau-\|c_{k,1}^{i}\|\geq b_{k,1}^{i}e^{-\omega\tau}\}$	$\displaystyle=\inf\{\tau>0:\|a_{k,1}^{i}\|\tau-\|c_{k,1}^{i}\|\geq b_{k,1}^{i}e^{-\omega\tau}\}$
		$\displaystyle=\phi_{0}(a_{k,1}^{i},b_{k,1}^{i},c_{k,1}^{i}).$

It may also occur that

\{0<\tau\leq-c_{k,1}^{i}/a_{k,1}^{i}:-|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}\}\not=\emptyset.

To see this, we first observe that

(49)

\displaystyle\{0<\tau\leq-c_{k,1}^{i}/a_{k,1}^{i}:-|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}\}=\{\tau>0:-|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}\}.

Let $W_{-1}$ be the secondary branch of the Lambert $W$ -function, i.e., $W_{-1}(y)$ is the solution $x\leq-1$ of the equation $xe^{x}=y$ for $y\in[-e^{-1},0)$ . We obtain the infimum of the set in (49) from the following proposition, whose proof is given in Appendix B.

Proposition 5.1.

Let $0<c<b$ . Then

\displaystyle\inf\{\tau>0:-\tau+c\geq be^{-\tau}\}=\begin{cases}W_{-1}(-be^{-c})+c&\text{if $1<b\leq e^{-1+c}$}\\ \infty&\text{otherwise}.\end{cases}

To apply Proposition 5.1, note that

-|a_{k,1}^{i}|\tau+|c_{k,1}^{i}|\geq b_{k,1}^{i}e^{-\omega\tau}

if and only if

-\hat{\tau}-\frac{\omega c_{k,1}^{i}}{a_{k,1}^{i}}\geq\frac{\omega b_{k,1}^{i}}{|a_{k,1}^{i}|}e^{-\hat{\tau}},\quad\text{where $\hat{\tau}\coloneqq\omega\tau$}.

Define the function $\phi$ by

\phi(a,b,c)\coloneqq\begin{cases}\dfrac{1}{\omega}W_{-1}\left(-\dfrac{\omega b}{|a|}e^{\omega c/a}\right)-\dfrac{c}{a}&\text{if $(a,b,c)\in\Upsilon_{\omega}$}\vspace{4pt}\\ \phi_{0}(a,b,c)&\text{if $(a,b,c)\not\in\Upsilon_{\omega}$}\end{cases}

for $a,c,\in\mathbb{R}$ and $b>0$ , where the set $\Upsilon_{\omega}$ is given by

\Upsilon_{\omega}\coloneqq\left\{(a,b,c):ac<0\text{~{}~{}and~{}~{}}1<\frac{\omega b}{|a|}\leq e^{-1-\omega c/a}\right\}.

From Proposition 5.1, we conclude that

\tilde{\tau}_{k,1}^{i}=\phi(a_{k,1}^{i},b_{k,1}^{i},c_{k,1}^{i})

in both cases $a_{k,1}^{i}c_{k,1}^{i}\geq 0$ and $a_{k,1}^{i}c_{k,1}^{i}<0$ .

5.3. $p$ -th update

Let $p\in\mathbb{N}$ and let

t_{\ell_{0}}<t_{\ell_{1}}<\dots<t_{\ell_{p}}<t_{\ell_{0}}+\tau_{\max}^{i}.

We consider the case where agent $i$ receives new data from its neighbors at times $t=t_{\ell_{1}},\dots,t_{\ell_{p}}$ before the next candidate sampling times.

At time $t=t_{\ell_{p}}$ , agent $i$ computes

(50)

\displaystyle\tau_{k,p}^{i}\coloneqq\min\{\phi(a_{k,p}^{i},b_{k,p}^{i},c_{k,p}^{i})+(t_{\ell_{p}}-t_{\ell_{0}}),\,\tau_{\max}^{i}\},

where

	$\displaystyle a_{k,p}^{i}$	$\displaystyle\coloneqq d_{i}q_{i}(t_{k}^{i})-\sum_{j\in\mathcal{N}_{i}}q_{j}(t^{j}_{k_{j}(\ell_{p})})$
(51)		$\displaystyle b_{k,p}^{i}$	$\displaystyle\coloneqq\delta_{i}E(t_{\ell_{p}})$
	$\displaystyle c_{k,p}^{i}$	$\displaystyle\coloneqq c_{k,p-1}^{i}+(t_{\ell_{p}}-t_{\ell_{p-1}})a_{k,p-1}^{i},$

and takes $t_{k}^{i}+\tau_{k,p}^{i}$ as a new candidate of the next sampling time. We have

(52)

\phi(a_{k,p}^{i},b_{k,p}^{i},c_{k,p}^{i})+(t_{\ell_{p}}-t_{\ell_{0}})\geq\tilde{\tau}_{\min}^{i}

as in the first update explained above. Since $\tau_{k,p}^{i}$ satisfies

\tilde{\tau}_{\min}^{i}\leq\tau_{k,p}^{i}\leq\tau_{\max}^{i},

only a finite number of data transmissions from neighbors occur until the next sampling time.

The next theorem shows that when the neighbors do not update the measurements on the interval $(t_{\ell_{p}},t_{k}^{i}+\tau_{k,p}^{i})$ , the candidate $t_{k}^{i}+\tau_{k,p}^{i}$ of the next sampling times constructed as above coincides with the next sampling time $t_{k+1}^{i}$ computed from the triggering mechanism (12).

Theorem 5.2.

Let $i\in\mathcal{N}$ and $k,p\in\mathbb{N}_{0}$ . Let $t_{\ell_{0}},\dots,t_{\ell_{p}}$ and $\tau_{k,p}^{i}$ be as above, and assume that agent $i$ does not receive any measurements from its neighbors on the interval $(t_{\ell_{p}},t_{k}^{i}+\tau_{k,p}^{i})$ . Then

(53)

t_{k}^{i}+\tau_{k,p}^{i}=t_{k+1}^{i},

where $t_{k+1}^{i}$ is defined by (12) with $0<\tau_{\min}^{i}\leq\min\{\tilde{\tau}_{\min}^{i},\,\tau_{\max}^{i}\}.$

Proof.

By the definition of $t_{\ell_{p}}$ , we obtain

|f_{k}^{i}(\tau)|<\delta_{i}E(t_{\ell_{0}}+\tau)

for all $\tau\in[0,t_{\ell_{p}}-t_{\ell_{0}}]$ . Moreover, the arguments given in Sections 5.1 and 5.2 show that

\displaystyle\phi(a_{k,p}^{i},b_{k,p}^{i},c_{k,p}^{i})=\inf\{\tau>0:|f_{k}^{i}(t_{\ell_{p}}-t_{\ell_{0}}+\tau)|\geq\delta_{i}E(t_{\ell_{p}}+\tau)\}.

From these facts, it follows that

	$\displaystyle\phi(a_{k,p}^{i},b_{k,p}^{i},c_{k,p}^{i})+(t_{\ell_{p}}-t_{\ell_{0}})$	$\displaystyle=\inf\{\tau>t_{\ell_{p}}-t_{\ell_{0}}:\|f_{k}^{i}(\tau)\|\geq\delta_{i}E(t_{\ell_{0}}+\tau)\}$
		$\displaystyle=\inf\{\tau>0:\|f_{k}^{i}(\tau)\|\geq\delta_{i}E(t_{\ell_{0}}+\tau)\}.$

Combining this with the inequality (52), we obtain

\displaystyle\phi(a_{k,p}^{i},b_{k,p}^{i},c_{k,p}^{i})+(t_{\ell_{p}}-t_{\ell_{0}})=\inf\{\tau\geq\tau^{i}_{\min}:|f_{k}^{i}(\tau)|\geq\delta_{i}E(t_{k}^{i}+\tau)\}=\tau_{k}^{i}

for all $0<\tau_{\min}^{i}\leq\min\{\tilde{\tau}_{\min}^{i},\,\tau_{\max}^{i}\}$ , where $\tau_{k}^{i}$ is defined as in (12). Thus, we obtain the desired result (53). ∎

5.4. Algorithm for quantization and self-triggered sampling

We are now ready to present a joint algorithm for finite-level dynamic quantization and self-triggered sampling. Under this algorithm, the unsaturation condition (4) is satisfied for all $k\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ , and the multi-agent system achieves consensus exponentially with decay rate $\omega$ ; see Theorems 4.6 and 5.2. Moreover, the inter-event times $t_{k+1}^{i}-t_{k}^{i}$ are bounded from below by the constant $\tilde{\tau}_{\min}^{i}>0$ for all $k\in\mathbb{N}_{0}$ and $i\in\mathcal{N}$ .

Algorithm 5.3 (Action of agent $i$ on the sampling interval $t_{k}^{i}\leq t<t_{k+1}^{i}$ ).

Step 0. Choose the threshold $\delta_{i}>0$ and the number $R=2R_{0}+1$ , $R_{0}\in\mathbb{N}_{0}$ , of quantization levels such that the inequality (42) holds for all $i\in\mathcal{N}$ . Choose the upper bounds $\tau^{1}_{\max},\dots,\tau^{N}_{\max}>0$ of inter-event times and the decay parameter $\omega$ of the quantization range $E(t)$ such that $0<\omega\leq\tilde{\omega}$ , where $\tilde{\omega}$ is defined as in (41).

Step 1. At time $t=t_{k}^{i}\eqqcolon t_{\ell_{0}}$ , agent $i$ performs the following actions i)–v).

i)

Measure the quantized relative state $q_{ij}(t_{k}^{i})$ for all $j\in\mathcal{N}_{i}$ and deactivate the sensor.
ii)

Encode the sum $q_{i}(t_{k}^{i})$ of the quantized measurements to an index in a finite set with cardinality $2\tilde{d}R_{0}+1$ and transmit the index to each neighbor $j\in\mathcal{N}_{i}$ .
iii)

If an index is received from a neighbor at time $t=t_{\ell_{0}}$ , then decode the index and update the sum of the relative state measurements of the neighbor.
iv)

Compute $\tau_{k,0}^{i}$ by (47), where $a_{k,0}^{i}$ , $b_{k,0}^{i}$ , and $c_{k,0}^{i}$ are defined as in (46).
v)

Set $p=0$ .

Step 2. Agent $i$ plans to activate the sensor at time $t=t_{k}^{i}+\tau_{k,p}^{i}$ .

Step 3-a. If agent $i$ receives an index from some neighbor on the interval $(t_{\ell_{p}},t_{k}^{i}+\tau_{k,p}^{i})$ , then agent $i$ performs the following actions i)–iii). Then go back to Step 2.

i)

Set $p$ to $p+1$ and store the time $t_{\ell_{p}}$ at which the index is received.
ii)

Decode the index and update the sum of the relative state measurements of the neighbor. If several indices are received at time $t=t_{\ell_{p}}$ , then this action is applied to all indices.
iii)

Compute $\tau_{k,p}^{i}$ by (50), where $a_{k,p}^{i}$ , $b_{k,p}^{i}$ , and $c_{k,p}^{i}$ are defined as in (51).

Step 3-b. If agent $i$ does not receive any indices on the interval $(t_{\ell_{p}},t_{k}^{i}+\tau_{k,p}^{i})$ , then agent $i$ sets $t_{k+1}^{i}\coloneqq t_{k}^{i}+\tau_{k,p}^{i}$ .

Step 4. Agent $i$ sets $k$ to $k+1$ . Then go back to Step 1.

Remark 5.4.

The proposed method takes advantage of the simplicity of the first-order dynamics in the following way. Assume that the dynamics of agent $i$ is given by

\dot{x}_{i}(t)=Ax_{i}(t)+Bu_{i}(t),

where $A\in\mathbb{R}^{n\times n}$ and $B\in\mathbb{R}^{n\times m}$ . Then the error $x_{i}(t_{k}^{i}+\tau)-x_{i}(t_{k}^{i})$ due to sampling is written as

\displaystyle x_{i}(t_{k}^{i}+\tau)-x_{i}(t_{k}^{i})=(e^{A\tau}-I)x_{i}(t_{k}^{i})+\int^{\tau}_{0}e^{A(\tau-s)}Bu_{i}(t_{k}^{i}+s)ds

for $\tau\geq 0$ . Since $e^{A\tau}-I\not=0$ in general, the absolute state $x_{i}(t_{k}^{i})$ is required to describe the error $x_{i}(t_{k}^{i}+\tau)-x_{i}(t_{k}^{i})$ . However, one has $e^{A\tau}-I=0$ in the first-order case $A=0$ , and hence the absolute state $x_{i}(t_{k}^{i})$ needs not be measured in the proposed algorithm. Moreover, since the input $u_{i}$ is constant on the sampling interval, the integral term is a linear function with respect to $\tau$ in the first-order case $A=0$ . This enables us to use the Lambert $W$ -function for the computation of sampling times.

6. Numerical simulation

In this section, we consider the connected network shown in Figure 1, where the number $N$ of agents is $N=6$ .

Figure 1. Network topology.

For each $i\in\mathcal{N}=\{1,2,\dots,6\}$ , the initial state $x_{i0}$ is given by $x_{i0}=\sin(i)$ . Since

\max_{i\in\mathcal{N}}\left|x_{i0}-\frac{1}{N}\sum_{j\in\mathcal{N}}x_{j0}\right|\leq 0.95,

a bound $E_{0}$ in Assumption 2.2 is chosen as $E_{0}=1$ . We set

\gamma=\lambda_{2}(L)=1

and then numerically compute $\Gamma_{\infty}=5/3$ , where $\Gamma_{\infty}$ is defined by (25).

The threshold $\delta_{i}$ and the upper bound $\tau_{\max}^{i}$ of inter-event times for the triggering mechanism (12) are given by

\displaystyle\delta_{i}=\begin{cases}0.04&\text{if $i=1,6$}\\ 0.09&\text{otherwise},\end{cases}\qquad\tau_{\max}^{i}=\begin{cases}1&\text{if $i=1,6$}\\ 1.5&\text{otherwise},\end{cases}

respectively. The reason why agents $1$ and $6$ have smaller thresholds and upper bounds of inter-event times is that these agents have more neighbors than others. For these thresholds, the minimum odd number $R$ satisfying the condition (42) for all $i\in\mathcal{N}$ is $13$ . By Theorem 4.6, if the number $R$ of quantization levels is odd and satisfies $R\geq 13$ , then the multi-agent system achieves consensus exponentially for a suitable decay parameter $\omega$ of the quantization range $E(t)$ . We use $R=19$ for the simulation below. Then $R_{0}\in\mathbb{N}_{0}$ with $R=2R_{0}+1$ is given by $R_{0}=9$ . When each agent knows

\tilde{d}=3

as a bound of the number of neighbors, as stated in Assumption 2.3, the number of quantization levels for the transmission of the sum of the relative states is

2\tilde{d}R_{0}+1=55,

which can be represented by $6$ bits. Under this setting of the parameters $\gamma$ , $\delta_{i}$ , $\tau_{\max}^{i}$ , and $R$ , the maximum decay parameter $\tilde{\omega}$ , which is defined as in (41), is given by

\tilde{\omega}=0.2145.

In the simulation, we set $\omega=\tilde{\omega}$ .

Using the Lambert $W$ -function, we can compute a lower bound $\tilde{\tau}_{\min}^{i}$ of inter-event times by (31):

\displaystyle\tilde{\tau}_{\min}^{i}=\begin{cases}2.192\times 10^{-3}&\text{if $i=1,6$}\\ 8.574\times 10^{-3}&\text{otherwise}.\end{cases}

Note, however, that these lower bounds are not used for the real-time computation of inter-event times, because all candidates of the inter-event times computed by the agents are greater than or equal to these lower bounds as shown in Section 5.

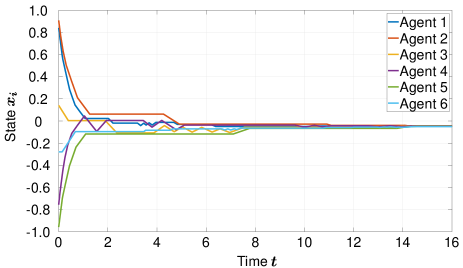
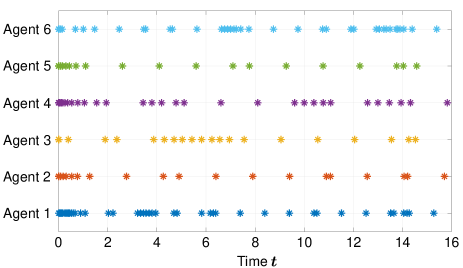
The state trajectory and the corresponding sampling times of each agent are shown in Figures 2 and 3, respectively, where the simulation time is $16$ and the time step is $10^{-4}$ . From Figure 2, we see that the deviation of each state from the average state converges to zero. Figure 3 shows that sampling occurs frequently on the interval $[0,1]$ but less frequently on the interval $[1,16]$ . Agent $3$ measures relative states more frequently on the interval $[4,7]$ than on other intervals. This is because the state of agent $3$ oscillates due to coarse quantization. Such oscillations can be observed also for other agents, e.g., agent $1$ on the interval $[3,4]$ . Moreover, we find in Figure 2 that the states of agents $2$ and $5$ do not change on the intervals $[2,4]$ and $[2,7]$ , respectively. This is also caused by coarse quantization. In fact, the quantized values of their relative state measurements are zero on these intervals. However, the proposed algorithm ensures that the quantization errors exponentially converge to zero, and hence the multi-agent system achieves asymptotic consensus.

Refer to caption — Figure 2. State trajectories.

7. Conclusion

We have proposed a joint design method of a finite-level dynamic quantizer and a self-triggering mechanism for asymptotic consensus by relative state information. The inter-event times are bounded from below by a strictly positive constant, and the sampling times can be computed efficiently by using the Lambert $W$ -function. The quantizer has been designed so that saturation is avoided and quantization errors exponentially converge to zero. The new semi-norm introduced for the consensus analysis is constructed based on the maximum norm, and the matrix exponential of the negative Laplacian matrix has the semi-contractivity property with respect to the semi-norm. Future work will focus on extending the proposed method to the case of directed graphs and agents with high-order dynamics.

8. Acknowledgments

This work was supported by JSPS KAKENHI Grant Number JP20K14362.

References

[1] Fax, J.A., Murray, R.M.: ‘Information flow and cooperative control of vehicle formations’, IEEE Trans Automat Control, 2004, 49, pp. 1465–1476
[2] Olfati.Saber, R., Shamma, J.S. ‘Consensus filters for sensor networks and distributed sensor fusion’. In: Proc. 44th IEEE Conf. Decis. Control, 2005. pp. 6698–6703
[3] Olfati-Saber, R., Murray, R.M.: ‘Consensus problems in networks of agents with switching topology and time-delays’, IEEE Trans Automat Control, 2004, 49, pp. 1520–1533
[4] Olfati-Saber, R., Fax, J.A., Murray, R.M.: ‘Consensus and cooperation in networked multi-agent systems’, Proc IEEE, 2007, 95, pp. 215–233
[5] Chen, F., Ren, W.: ‘On the control of multi-agent systems: A survey’, Found Trends Syst Control, 2019, 6, pp. 339–499
[6] Årzén, K.E. ‘A simple event-based PID controller’. In: Proc. 14th IFAC World Congress. vol. 18, 1999. pp. 423–428
[7] Tabuada, P.: ‘Event-triggered real-time scheduling of stabilizing control tasks’, IEEE Trans Automat Control, 2007, 52, pp. 1680–1685
[8] Heemels, W.P.M.H., Sandee, J., van den Bosch, P.: ‘Analysis of event-driven controllers for linear systems’, Int J Control, 2008, 81, pp. 571–590
[9] Velasco, M., Fuertes, J., Marti, P. ‘The self triggered task model for real-time control systems’. In: Proc. 24th IEEE Real-Time Syst. Symp, 2003. pp. 67–70
[10] Wang, X., Lemmon, M.D.: ‘Self-triggered feedback control systems with finite-gain $\mathcal{L}_{2}$ stability’, IEEE Trans Automat Control, 2009, 54, pp. 452–467
[11] Anta, A., Tabuada, P.: ‘To sample or not to sample: Self-triggered control for nonlinear systems’, IEEE Trans Automat Control, 2010, 55, pp. 2030–2042
[12] Dimarogonas, D.V., Frazzoli, E., Johansson, K.H.: ‘Distributed event-triggered control for multi-agent systems’, IEEE Trans Automat Control, 2012, 57, pp. 1291–1297
[13] Seyboth, G.S., Dimarogonas, D.V., Johansson, K.H.: ‘Event-based broadcasting for multi-agent average consensus’, Automatica, 2013, 49, pp. 245–252
[14] Fan, Y., Liu, L., Feng, G., Wang, Y.: ‘Self-triggered consensus for multi-agent systems with Zeno-free triggers’, IEEE Trans Automat Control, 2015, 60, pp. 2779–2784
[15] Yi, X., Liu, K., Dimarogonas, D.V., Johansson, K.H.: ‘Dynamic event-triggered and self-triggered control for multi-agent systems’, IEEE Trans Automat Control, 2019, 64, pp. 3300–3307
[16] Liu, K., Ji, Z.: ‘Dynamic event-triggered consensus of general linear multi-agent systems with adaptive strategy’, IEEE Trans Circuits Syst II, Exp Briefs, 2022, 69, pp. 3440–3444
[17] Ding, L., Han, Q.L., Ge, X., Zhang, X.M.: ‘An overview of recent advances in event-triggered consensus of multiagent systems’, IEEE Trans Cybern, 2018, 48, pp. 1110–1123
[18] Nowzari, C., Garcia, E., Cortés, J.: ‘Event-triggered communication and control of networked systems for multi-agent consensus’, Automatica, 2019, 105, pp. 1–27
[19] Dimarogonas, D.V., Johansson, K.H.: ‘Stability analysis for multi-agent systems using the incidence matrix: Quantized communication and formation control’, Automatica, 2010, 46, pp. 695–700
[20] Ceragioli, F., De Persis, C., Frasca, P.: ‘Discontinuities and hysteresis in quantized average consensus’, Automatica, 2011, 47, pp. 1916–1928
[21] Liu, S., Li, T., Xie, L., Fu, M., Zhang, J.F.: ‘Continuous-time and sampled-data-based average consensus with logarithmic quantizers’, Automatica, 2013, 49, pp. 3329–3336
[22] Guo, M., Dimarogonas, D.V.: ‘Consensus with quantized relative state measurements’, Automatica, 2013, 49, pp. 2531–2537
[23] Wu, Y., Wang, L.: ‘Average consensus of continuous-time multi-agent systems with quantized communication’, Int J Robust Nonlinear Control, 2014, 24, pp. 3345–3371
[24] Li, J., Ho, D.W.C., Li, J.: ‘Adaptive consensus of multi-agent systems under quantized measurements via the edge Laplacian’, Automatica, 2018, 92, pp. 217–224
[25] Xu, T., Duan, Z., Sun, Z., Chen, G.: ‘A unified control method for consensus with various quantizers’, Automatica, 2022, 136, Art. no. 110090
[26] Garcia, E., Cao, Y., Yu, H., Antsaklis, P., Casbeer, D.: ‘Decentralised event-triggered cooperative control with limited communication’, Int J Control, 2013, 86, pp. 1479–1488
[27] Zhang, Z., Zhang, L., Hao, F., Wang, L.: ‘Distributed event-triggered consensus for multi-agent systems with quantisation’, Int J Control, 2015, 88, pp. 1112–1122
[28] Zhang, Z., Zhang, L., Hao, F., Wang, L.: ‘Periodic event-triggered consensus with quantization’, IEEE Trans Circuits Syst II, Expr Briefs, 2016, 63, pp. 406–410
[29] Yi, X., Wei, J., Johansson, K.H. ‘Self-triggered control for multi-agent systems with quantized communication or sensing’. In: Proc. 55th IEEE Conf. Decis. Control, 2016. pp. 2227–2232
[30] Liu, Q., Qin, J., Yu, C. ‘Event-based multi-agent cooperative control with quantized relative state measurements’. In: Proc. 55th IEEE Conf. Decis. Control, 2016. pp. 2233–2239
[31] Wu, Z.G., Xu, Y., Pan, Y.J., Su, H., Tang, Y.: ‘Event-triggered control for consensus problem in multi-agent systems with quantized relative state measurements and external disturbance’, IEEE Trans Circuits Syst I, Reg Papers, 2018, 65, pp. 2232–2242
[32] Dai, M.Z., Xiao, F., Wei, B.: ‘Event-triggered and quantized self-triggered control for multi-agent systems based on relative state measurements’, J Frankl Inst, 2019, 356, pp. 3711–3732
[33] Li, K., Liu, Q., Zeng, Z.: ‘Quantized event-triggered communication based multi-agent system for distributed resource allocation optimization’, Inf Sci, 2021, 577, pp. 336–352
[34] Dai, M.Z., Fu, W., Zhao, D.J., Zhang, C. ‘Distributed self-triggered control with quantized edge state sampling and time delays’. In: Advances in Guidance, Navigation and Control. (Singapore: Springer, 2022. pp. 883–894
[35] Wang, F., Li, N., Yang, Y.: ‘Quantized-observer based consensus for fractional order multi-agent systems under distributed event-triggered mechanism’, Math Comput Simul, 2023, 204, pp. 679–694
[36] De Persis, C., Frasca, P.: ‘Robust self-triggered coordination with ternary controllers’, IEEE Trans Automat Control, 2013, 58, pp. 3024–3038
[37] Matsume, H., Wang, Y., Ishii, H.: ‘Resilient self/event-triggered consensus based on ternary control’, Nonlinear Anal: Hybrid Systems, 2021, 42, Art. no. 101091
[38] Golestani, F., Tavazoei, M.S.: ‘Event-based consensus control of Lipschitz nonlinea rmulti-agent systems with unknown input delay and quantization constraints’, Eur Phys J Spec Top, 2022, 231, pp. 3977–3985
[39] Carli, R., Bullo, F., Zampieri, S.: ‘Quantized average consensus via dynamic coding/decoding schemes’, Int J Robust Nonlinear Control, 2010, 20, pp. 156–175
[40] Li, T., Fu, M., Xie, L., Zhang, J.F.: ‘Distributed consensus with limited communication data rate’, IEEE Trans Automat Control, 2011, 56, pp. 279–292
[41] You, K., Xie, L.: ‘Network topology and communication data rate for consensusability of discrete-time multi-agent systems’, IEEE Trans Automat Control, 2011, 56, pp. 2262–2275
[42] Li, D., Liu, Q., Wang, X., Yin, Z.: ‘Quantized consensus over directed networks with switching topologies’, Syst Control Lett, 2014, 65, pp. 13–22
[43] Qiu, Z., Xie, L., Hong, Y.: ‘Quantized leaderless and leader-following consensus of high-order multi-agent systems with limited data rate’, IEEE Trans Automat Control, 2016, 61, pp. 2432–2447
[44] Ma, J., Ji, H., Sun, D., Feng, G.: ‘An approach to quantized consensus of continuous-time linear multi-agent systems’, Automatica, 2018, 91, pp. 98–104
[45] Chen, X., Liao, X., Gao, L., Yang, S., Wang, H., Li, H.: ‘Event-triggered consensus for multi-agent networks with switching topology under quantized communication’, Neurocomputing, 2017, 230, pp. 294–301
[46] Ma, J., Liu, L., Ji, H., Feng, G.: ‘Quantized consensus of multiagent systems by event-triggered control’, IEEE Trans Syst, Man, Cybern: Syst, 2018, 50, pp. 3231–3242
[47] Yu, P., Dimarogonas, D.V.: ‘Explicit computation of sampling period in periodic event-triggered multiagent control under limited data rate’, IEEE Trans Control Netw Syst, 2019, 6, pp. 1366–1378
[48] Lin, N., Ling, Q.: ‘Bit-rate conditions for the consensus of quantized multiagent systems based on event triggering’, IEEE Trans Cybern, 2022, 52, pp. 116–127
[49] Lin, N., Ling, Q.: ‘An event-triggered consensus protocol for quantized second-order multi-agent systems with network delay and process noise’, ISA Trans, 2022, 125, pp. 31–41
[50] Feng, S., Ishii, H.: ‘Dynamic quantized consensus of general linear multi-agent systems under denial-of-service attacks’, IEEE Trans Control Network Systems, 2022, 9, pp. 562–574
[51] Rikos, A.I., Hadjicostis, C.N.: ‘Event-triggered quantized average consensus via ratios of accumulated values’, IEEE Trans Automat Control, 2021, 66, pp. 1293–1300
[52] Rikos, A.I., Charalambous, T., Johansson, K.H., Hadjicostis, C.N.: ‘Distributed event-triggered algorithms for finite-time privacy-preserving quantized average consensus’, IEEE Trans Control Network Systems, 2023, 10, pp. 38–50
[53] Horaud, R., Hansard, M., Evangelidis, G., Ménier, C.: ‘An overview of depth cameras and range scanners based on time-of-flight technologies’, Mach Vis Appl, 2016, 27, pp. 1005–1020
[54] Spong, M.W., Hutchinson, S., Vidyasagar, M.: ‘Robot Modeling and Control’. 2nd ed. (Hoboken, NJ, USA: Wiley, 2020)
[55] Corless, R.M., Gonnet, G.H., Hare, D.E., Jeffrey, D.J., Knuth, D.E.: ‘On the Lambert $W$ function’, Adv Comput Math, 1996, 5, pp. 329–359
[56] Brockett, R.W., Liberzon, D.: ‘Quantized feedback stabilization of linear systems’, IEEE Trans Automat Control, 2000, 45, pp. 1279–1289
[57] Liberzon, D.: ‘Hybrid feedback stabilization of systems with quantized signals’, Automatica, 2003, 39, pp. 1543–1554
[58] Jafarpour, S., Cisneros.Velarde, P., Bullo, F.: ‘Weak and semi-contraction for network systems and diffusively coupled oscillators’, IEEE Trans Automat Control, 2022, 67, pp. 1285–1300
[59] De Pasquale, G., Smith, K.D., Bullo, F., Valcher, M.E. ‘Dual seminorms, ergodic coefficients and semicontraction theory’, to appear in IEEE Trans Automat Control 2023
[60] Pazy, A.: ‘Semigroups of Linear Operators and Applications to Partial Differential Equations’. (New York: Springer, 1983)

Appendix A: Proof of Proposition 4.10

Let $0<\gamma\leq\lambda_{2}(L)$ , and let $\Lambda_{0}$ , $\Lambda$ , $V_{0}$ , and $V$ be as in the proof of Lemma 4.1.

a) The inequality

2-\frac{2}{N}\leq\Gamma_{\infty}(\gamma)

has already been proved in (26). It remains to show that

\Gamma_{\infty}(\gamma)\leq N-1.

Since $V_{0}\in\mathbb{R}^{N\times N}$ is orthogonal, we have $\|V_{0}\|_{\infty}\leq\sqrt{N}$ . Hence,

\|V\|_{\infty}=\|V_{0}\|_{\infty}-\frac{1}{\sqrt{N}}\leq\sqrt{N}-\frac{1}{\sqrt{N}}.

Moreover, $\|V^{\top}\|_{\infty}\leq\|V_{0}^{\top}\|_{\infty}=\sqrt{N}$ and

C\coloneqq\sup_{t\geq 0}\|e^{\gamma t}e^{-\Lambda t}\|_{\infty}\leq 1.

Therefore, the inequality (24) yields

\Gamma_{\infty}(\gamma)\leq C\|V\|_{\infty}\|V^{\top}\|_{\infty}\leq\left(\sqrt{N}-\frac{1}{\sqrt{N}}\right)\sqrt{N}=N-1.

b) Suppose that $G$ is a complete graph. Then

\Lambda_{0}=\mathrm{diag}(0,\,N,\,\cdots,\,N).

If $0<\gamma\leq\lambda_{2}(L)=N$ , then

\|e^{\gamma t}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})\|_{\infty}\leq\|e^{Nt}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})\|_{\infty}

for all $t\geq 0$ . Hence, it suffices by a) to show that

(A1)

\sup_{t\geq 0}\|e^{Nt}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})\|_{\infty}=2-\frac{2}{N}.

Using $L=V_{0}\Lambda_{0}V_{0}^{\top}$ and

(A2)

\mathbf{1}\bar{\mathbf{1}}=V_{0}\,\mathrm{diag}(1,\,0,\,\cdots,\,0)\,V_{0}^{\top},

we obtain

	$\displaystyle e^{Nt}(e^{-Lt}-\mathbf{1}\bar{\mathbf{1}})$	$\displaystyle=V_{0}\left(e^{Nt}e^{-\Lambda_{0}t}-\mathrm{diag}(e^{Nt},\,0,\,\cdots,\,0)\right)V_{0}^{\top}$
		$\displaystyle=V_{0}\,\mathrm{diag}(0,\,1,\,\cdots,\,1)\,V_{0}^{\top}$

for all $t\geq 0$ . Moreover, (A2) yields

	$\displaystyle V_{0}\,\mathrm{diag}(0,\,1,\,\cdots,\,1)\,V_{0}^{\top}$	$\displaystyle=V_{0}V_{0}^{\top}-V_{0}\,\mathrm{diag}(1,\,0,\,\cdots,\,0)\,V_{0}^{\top}$
		$\displaystyle=I-\mathbf{1}\bar{\mathbf{1}}.$

Thus, (A1) holds by $\|I-\mathbf{1}\bar{\mathbf{1}}\|_{\infty}=2-2/N$ . ∎

Appendix B: Proof of Proposition 5.1

Define the function $H$ by

H(\tau)\coloneqq\tau+be^{-\tau}-c,\quad\tau\in\mathbb{R}.

Then

-\tau+c\geq b{e^{-\tau}}\quad\Leftrightarrow\quad H(\tau)\leq 0.

Since

H^{\prime}(\tau)=1-be^{-\tau},

it follows that $H^{\prime}(\tau)=0$ holds at $\tau=\log b$ . From the assumption $c<b$ , we have $H(0)>0$ . Therefore, there exists $\tau>0$ such that $H(\tau)\leq 0$ if and only if

(B1)

\log b>0\quad\text{and}\quad H(\log b)\leq 0.

Since

H(\log b)=\log b+1-c,

it follows that (B1) is equivalent to

(B2)

1<b\leq e^{-1+c}.

Hence,

\inf\{\tau>0:-\tau+c\geq be^{-\omega\tau}\}=\infty

if (B2) does not hold.

The inequality $-\tau+c\geq be^{-\tau}$ can be written as

(B3)

(\tau-c)e^{\tau-c}\leq-be^{-c}.

Let $W_{0}$ and $W_{-1}$ be the primary and secondary branch of the Lambert $W$ -function, respectively. In other words, $W_{0}(y)$ and $W_{-1}(y)$ are the solutions $x=x_{0}\in[-1,0)$ and $x=x_{-1}\in(-\infty,-1]$ of the equation $xe^{x}=y$ for $y\in[-e^{-1},0)$ , respectively. For each $y\in[-e^{-1},0)$ ,

(B4)

xe^{x}\leq y\quad\Leftrightarrow\quad W_{-1}(y)\leq x\leq W_{0}(y);

see, e.g., [55].

Suppose that the condition (B2) holds. The expression (B3) and the equivalence (B4) show that $-\tau+c\geq be^{-\tau}$ if and only if

W_{-1}(-be^{-c})+c\leq\tau\leq W_{0}(-be^{-c})+c.

Note that $W_{-1}(-be^{-c})+c$ and $W_{0}(-be^{-c})+c$ are the solutions of the equation $H(\tau)=0$ . Since $H(0)>0$ , both solutions are positive. Thus,

\inf\{\tau>0:-\tau+c\geq be^{-\tau}\}=W_{-1}(-be^{-c})+c

is obtained. ∎

	$\displaystyle{\|\kern-1.07639pt\|\kern-1.07639pt\|v+w\|\kern-1.07639pt\|\kern-1.07639pt\|}$	$\displaystyle\leq\sup_{t\geq 0}\big{(}\\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|+\\|e^{\gamma t}e^{-Lt}(w-\mathrm{ave}(w)\mathbf{1})\\|\big{)}$
		$\displaystyle\leq\sup_{t\geq 0}\\|e^{\gamma t}e^{-Lt}(v-\mathrm{ave}(v)\mathbf{1})\\|+\sup_{t\geq 0}\\|e^{\gamma t}e^{-Lt}(w-\mathrm{ave}(w)\mathbf{1})\\|$
		$\displaystyle={\|\kern-1.07639pt\|\kern-1.07639pt\|v\|\kern-1.07639pt\|\kern-1.07639pt\|}+{\|\kern-1.07639pt\|\kern-1.07639pt\|w\|\kern-1.07639pt\|\kern-1.07639pt\|}.$

	$\displaystyle{\|\kern-1.07639pt\|\kern-1.07639pt\|e^{-Lt}v\|\kern-1.07639pt\|\kern-1.07639pt\|}$	$\displaystyle=\sup_{s\geq 0}\\|e^{\gamma s}e^{-L(s+t)}(v-\mathrm{ave}(v)\mathbf{1})\\|$
		$\displaystyle\leq e^{-\gamma t}\sup_{s\geq 0}\\|e^{\gamma s}e^{-Ls}(v-\mathrm{ave}(v)\mathbf{1})\\|$
		$\displaystyle=e^{-\gamma t}{\|\kern-1.07639pt\|\kern-1.07639pt\|v\|\kern-1.07639pt\|\kern-1.07639pt\|}$

Self-triggered Consensus of Multi-agent Systems with Quantized Relative State Measurements

Abstract.

1. Introduction

2. System Model

2.1. Multi-agent system

Assumption 2.1.

Assumption 2.2.

Assumption 2.3.

Assumption 2.4.

Definition 2.5.

2.2. Quantization scheme

2.3. Triggering mechanism

3. Preliminaries

3.1. Semi-norm for consensus analysis

Lemma 3.1.

Proof.

Remark 3.2.

3.2. Basic properties of sampling times

Proposition 3.3.

Proof.

4. Consensus Analysis

4.1. Semi-norm based on the maximum norm

Lemma 4.1.

Proof.

Lemma 4.2.

Proof.

4.2. Design of quantization ranges

Lemma 4.3.

Proof.

Lemma 4.4.

Proof.

4.3. Main result

Assumption 4.5.

Theorem 4.6.

Proof.

Remark 4.7.

Remark 4.8.

Remark 4.9.

4.4. Bounds of Γ∞\Gamma_{\infty}

Proposition 4.10.

Example 4.11.

5. Computation of Sampling Times

5.1. Initial candidate of the next sampling time

5.2. First update

Proposition 5.1.

5.3. pp-th update

Theorem 5.2.

Proof.

5.4. Algorithm for quantization and self-triggered sampling

Algorithm 5.3 (Action of agent ii on the sampling interval tki≤t<tk+1it_{k}^{i}\leq t<t_{k+1}^{i}).

Remark 5.4.

6. Numerical simulation

7. Conclusion

8. Acknowledgments

References

Appendix A: Proof of Proposition 4.10

Appendix B: Proof of Proposition 5.1

4.4. Bounds of $\Gamma_{\infty}$

5.3. $p$ -th update

Algorithm 5.3 (Action of agent $i$ on the sampling interval $t_{k}^{i}\leq t<t_{k+1}^{i}$ ).