Semantic Recovery for Open-Set Domain Adaptation: Discover Unseen Categories in the Target Domain
Abstract
Semantic Recovery for unseen targets samples with help of attributes.
1 Introduction
Domain adaptation - require same label space
openset - lack of unknown set detailed categories
zero-shot - cannot manage domain shift, and convention ZSL already assumed test set from unseen categories.
Generalized ZSL - require knowledge of unseen categories and attributes, or word vector graphs.
Ours - truly explore unseen categories based on seen data. With help of attributes, to recover semantic characteristics and meaningful representations.
2 Related Works
Openset
ZSL - generalized ZSL and transductive ZSL
3 The Proposed Method
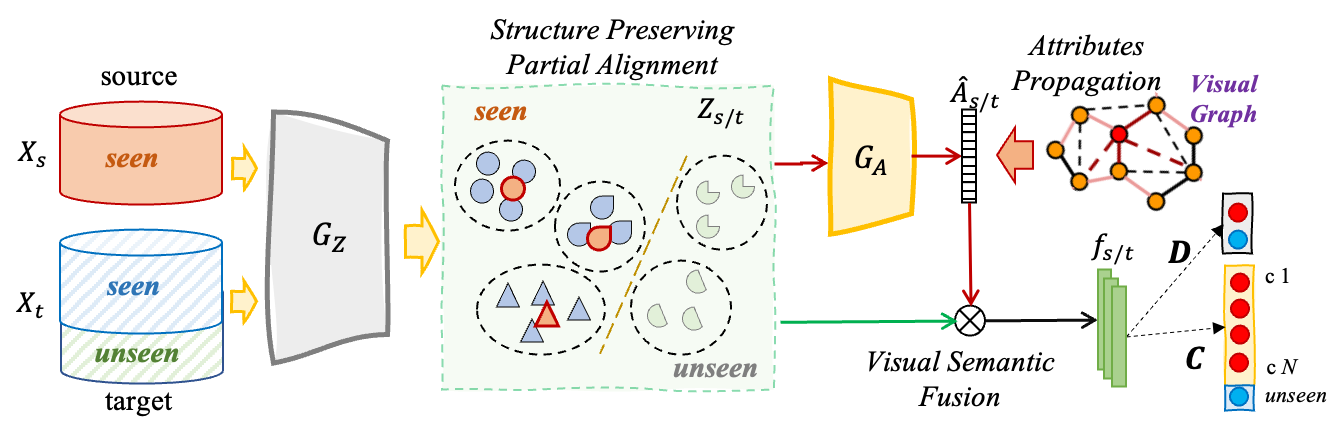
3.1 Problem Definition
Given the unlabeled target domain includes images belonging to categories drawn from the distribution . We seek help from another auxiliary source domain consisting of samples from categories and drawn from the distribution , where . In reality, cannot promise always cover the whole target domain label space, leading to the Open-Set problem where categories existing in the target domain but are unseen in the source domain. However, we are not satisfied with simply filtering out those unknown categories as most existing Open-Set domain adaptation solutions did, we would also like to explore target samples from unseen categories and discover them in a more meaningful way. Thus, we introduce the semantic description of those seen categories in the source domain, denoted as , to learn enriched knowledge and representations for the visual images. The semantic descriptions describe the characteristics of each category, so they are class-level descriptions, instead of sample-level. In other words, for source samples belonging to the same category , their semantic descriptions , are the same.
ZD: We should merge with the overall framework Moreover, we denote as the source/target features extracted by the pre-trained convolutional feature extractor, and denotes the source domain label set. It is noteworthy that, different from some generalized zero-shot learning tasks, we don’t expect the knowledge of the target domain unseen categories, no matter unseen classes numbers nor corresponding semantic descriptions. The goal of our work are recognizing the unlabeled target domain data into either seen categories as the source domain label space or the unseen set, and further explore the semantic descriptions of the all the target domain data especially for the samples from the target domain unseen set.
3.2 Framework
We illustrate the proposed framework of this paper as Fig. 1. Specifically, the framework consists of a Convolutional Neural Network as the feature extractor for both source and target domain, which extracts visual features from raw images. is a network mapping the source and target domain data into a shared feature space, from which the output is denoted as , . is used to mapping each sample from the visual feature space to the semantic feature space, and the predicted semantic description is denoted as for each instance. is a binary classifier to recognize if the target domain data is from the seen categories or the unseen categories. is a classifier with output dimension as , which can recognize the input sample is from which specific one of seen category or "unseen" set, and the predicted label is denoted as .
3.2.1 Towards Seen-Unseen Separation
ZD: This is initialization stage?
The prototypical classifier has been explored in transfer learning tasks. Specifically, for each input sample , prototypical classifier predicts the input sample into the label space of known prototypes, producing the probability distribution , where is the number of categories in the labels as well as the number of prototypes we have, because only the source domain has labels from categories. Specifically, for each class the predicted probability is:
| (1) |
where is to measure the distance between the input sample and the specific class prototype . For each sample , the predicted label with the highest probability is accepted as the pseudo label with confidence .
The prototypical classification measures the similarity between the input samples to each corresponding class prototype in the feature space, which means the more the input sample similar to one specific prototype, the more probable the input sample does belong to the specific category. So based on the prototypical classification results, we can separate the whole target domain set into High Confidence and Low Confidence subsets, denoted as and , respectively. Specifically, we accept the mean of the probability prediction on the whole target domain, i.e., , as the threshold to decide if the prediction to each sample is confident or not:
| (2) |
Unfortunately, due to the lack of the target domain labels, we cannot have the class prototypes of the target domain, so we have to initialize the prototypes based on the labeled source domain data. However, because of the domain shift across the source and target domain, such prototypes based on the source domain data cannot recognize the target domain data accurately. So we accept the target domain samples from the High Confidence set to adaptively refine the categories prototypes as:
| (3) |
where denotes a subset of the High Confidence set , consisting of samples predicted as , and is the weight to control the progress of refining the prototypes. In some cases there are no samples predicted as class in the High Confidence set, the corresponding prototype are just not updated and keep the same as the existing one.
For the Low Confidence set , consisting of samples predicted as far from the known categories prototypes, we also appreciate their characteristics and structure information, because they may include the knowledge of data from unseen categories. So we apply K-means clustering algorithm to cluster samples in into clusters, and the cluster centers are put together with the prototypes of seen categories building up the refined prototypes .
The refined prototypes are used to apply the prototypical classification to all target domain data again and obtain new pseudo labels . For all samples predicted as one of the seen categories, i.e., , are recognized as new High Confidence set . On the contrary, all samples predicted as more similar to the cluster centers, i.e., , making up the new Low Confidence set .
After iteratively applying the operations illustrated, prototypical classification Recognize High/Low Confidence sets Refine prototypes, we can get pseudo labels for all target domain data, where for \textigHigh Confidence set , describes each specific target sample is distributed closer to one of the seen categories prototypes, while for the Low Confidence set instances, the pseudo labels describes how similar they are to the one of the unseen subset cluster centers. We treat the target domain High Confidence set as the set consisting of target samples from the seen categories, while the Low Confidence set as the collection of samples from the unseen categories. Although there must be some samples with wrong pseudo labels and are recognized in the wrong set, after several rounds of prototypes refining, such recognition results still represent the target domain data structure knowledge with high confidence.
3.3 Aggregate structural knowledge by semantic propagation
The most challenging and practical task we focus in this work is to reveal meaningful semantic descriptions for the target domain data no matter they are from the seen categories as the source domain or from the unseen categories only existing in the target domain. So we expect a projector to map the data from visual feature space into the semantic feature space.
However, because only the knowledge of labels and semantic descriptions from seen categories are available, both the source domain and the target domain High Confidence set ignore the information and structure of those target samples from the unseen categories. Unfortunately, training the feature extractor and the semantic projector only on and makes things worse because of overfitting to the seen categories, although we seek to explore the characteristics of data from unseen categories. So we explore the mechanism of semantic propagation to aggregate the visual features structural knowledge into the semantic description projection.
Specifically, for samples in a training batch drawn from the source or target domain, the adjacency matrix is calculated as , where , and is the distance of two features . is a scaling factor and we accept as [rodriguez2020embedding] to stabilize training. Then we calculate the Laplacian of the adjacency matrix . Then, we have the semantic propagator matrix following the idea described in [zhou2004learning], and is a scaling factor, and is the identity matrix. Finally, the semantic descriptions projected from the visual features are obtained as:
| (4) |
After the semantic propagation, the projected semantic description is refined as a weighted combination of the semantic representation of its neighbors guided by the visual features graph structure. Such strategy aggregates the visual features similarity graph knowledge into the semantic description projection, preventing the risks of overfitting to the seen categories during training, and has the effect of removing undesired noise from the visual and semantic features vectors [rodriguez2020embedding].
Then for each source domain sample , the ground-truth label is known, so does the semantic description , where is obtained from by class label . We construct the semantic projection loss on the source domain as:
| (5) |
where is the binary cross-entropy loss. For each sample , each dimension value of the semantic description represent one specific semantic characteristic, so each dimension of the output measures the predicted probability that the input sample has such specific characteristic.
For the target domain, although the ground-truth labels and semantic descriptions are not available, fortunately we have already obtained confident pseudo labels and pseudo semantic descriptions after the operations in Section 3.2.1. So for each target domain sample from the High Confidence set, we accept its pseudo labels to get the pseudo semantic descriptions , as the samples in all have pseudo labels from the seen categories shared between the source and target domain. Then similarly, we construct the semantic projection loss on the target domain as:
| (6) |
where is the number of samples in .
Combining them together, we have the semantic description projection objective as:
| (7) |
3.4 Joint Representation From Visual and Semantic Perspectives
As the visual features and semantic descriptions explain the data from different perspectives in various modalities, we explore the joint distribution of both visual and semantic descriptions for each data simultaneously. Inspired by [long2017conditional], for each sample , we convey the semantic discriminative information into the visual features by construct the joint representation as:
| (8) |
where is the concatenation operation to combine the visual and semantic features and to construct a joint distribution , which will be used to do the classification optimization and cross-domain alignment.
It is noteworthy that we have already introduced several different semantic descriptions for each sample from different subsets, thus we will obtain various joint representations for the data as:
| (9) |
pecifically, for the source domain data , we can construct with the ground-truth semantic description , and is with the projected semantic description . Similarly, for the target domain High Confidence data , pseudo semantic feature can be obtained by pseudo label , together with the semantic representation prediction , we can construct two kind of joint representation as , and . Finally, for all data , the only semantic description we have is the prediction projected by , and we can construct the joint representation as . All the joint representations are input to the classifier and to optimize the framework.
3.5 Classification Supervision Optimization
Domain adaptation assumes that with the help of labeled source domain data, we can train a model to transferable to the unlabeled target domain data. A lot of existing domain adaptation works have proven the reasonableness and effectiveness of such strategy. So maintaining the ability of the model on the source domain data is crucial for transferring the model to the target domain tasks. For each source domain sample , the ground-truth label is known. We construct the classification loss on the source domain as:
| (10) |
where is the cross-entropy loss.
Moreover, we have already obtained confident pseudo labels for the target domain data, which are also accepted to optimize the model to the target domain. It is noteworthy that is an extended classifier recognizing the input instance into classes, which includes seen categories shared across domains plus the additional "unseen" class. Specifically, for samples from the High Confidence set , the model is optimized to recognize them as the corresponding pseudo labels in . For the samples from the Low Confidence set , the classifier recognize them as the "unseen" class. Thus we have the loss term on the target domain as:
| (11) | ||||
where if , if , and denotes the number of samples in . Then we have our classification supervision objective on both source and target domain as:
| (12) |
3.6 Fine-grained Seen/Unseen Subsets Separation
To more accurately recognize the target domain data into seen and unseen subsets, we further train a binary classifier to finely separate the seen and unseen classes. With the help of the joint representations of the target domain as input and the pseudo labels and pseudo semantic descriptions available, the fine-grained binary classifier can be optimized by:
| (13) | ||||
in which indicate if the target sample if from the seen categories (), or from the unseen categories ().
3.7 Structure Preserving Partial Cross-Domain Alignment
A lot of previous domain adaptation efforts focus on exploring a domain invariant feature space across domains. However, due to the mismatch of the source and target domains label space in our task, simply matching the feature distribution across domains becomes destructive. Moreover, the distribution structural information has been proven important for the label space mismatch tasks like conventional open-set domain adaptation [pan2020exploring]. Considering our goal of uncovering the unseen categories in the target domain, preserving the structural knowledge of the target domain data becomes even more crucial. Thanks to the refined prototypes and the pseudo labels for target domain data we already obtained in Section 3.2.1, we can get the prototype on the embedding features with the help of pseudo labels in the similar way. Specifically, for each pseudo label , the corresponding prototype can be calculated as . The prototypes of the target domain features describe the structural graph knowledge in the target domain, thus we propose the loss function to enforce the target domain data closer to their corresponding prototypes based on the pseudo labels as:
| (14) | ||||
where denotes the prototype with label , is the total number of prototypes in , and is the distance measurement between two features. Such loss function pushes the embedding feature of the target sample close to the corresponding prototype with pseudo label , while further away from other prototypes where .
Moreover, for the source domain data, we seek to map the source domain data into the target domain feature space, to preserve the target domain distribution structure, instead of mapping both source and target domain into a shared feature space as such strategy may break the original structural knowledge in the target domain. Then we propose the loss function on the source domain as:
| (15) | ||||
It is noteworthy that, these two loss functions simultaneously achieve the cross-domain partial alignment and enhancing the discriminative characteristics in the embedding feature space while preserving the target domain data structure. Thus we get our structure preserving partial cross-domain alignment loss as:
| (16) |
3.8 Overall Objective
Overall, we propose our final optimization objective as:
| (17) |
3.9 Training and Optimization Strategy
4 Experiments
4.1 Datasets
I2AwA is proposed by [zhuo2019unsupervised] consisting of 50 animal classes, split into 40 seen categories and 10 unseen categories as [xian2017zero]. The source domain includes 2,970 images from the seen categories collected via Google image search engine, while the target domain is the AwA2 dataset proposed in [xian2017zero] for zero-shot learning which contains all 50 classes with 37,322 images. We use the attributes feature of AwA2 as the semantic description, and only the seen categories attributes are available for training.
D2AwA is constructed from the DomainNet dataset [peng2019moment] and AwA2[xian2017zero]. Specifically, we choose the shared 17 classes between the DomainNet and AwA2 as the total dataset, and select the alphabetically first 10 classes as the seen categories, leaving the rest 7 classes as unseen. The corresponding attributes features in AwA2 are used as the semantic description. It is noteworkty that, DomainNet contains 6 different domains, while some of them are far from the semantic characteristics described by the attributes of AwA2, e.g., quick draw. So we only take the "real image" (R) and "painting" (P) domains into account, together with the AwA2 (A) data building up 6 source-target pair tasks as RA, RP, PA, PR, AR, AP.
4.2 Evaluation Metrics
We evaluate our method in two ways, open-set and semantic recovery. For open-set is same as the conventional open-set domain adaptation works did, recognizing the whole target domain data into the seen categories shared between the source and target domain, or 1 unseen category. We report the results of the classifier with the performance only on the seen categories (OS∗), unseen categories (OS⋄), and overall accuracy (OS) on the whole target data [panareda2017open]. For the semantic recovery task, we evaluate the predicted semantic description projected by by applying the prototypical classification with the ground-truth semantic attributes from all classes to get the classification accuracy on the whole target domain label space. We report the performances on the seen categories and unseen categories as and , respectively, and calculate the harmonic mean , defined as , to evaluate the performance on both seen and unseen categories. It is noteworthy that all results we reported are the average of class-wise top-1 accuracy, to eliminate the influence of imbalance of data distribution across classes. Furthermore, we will show the explored semantic attributes for some target samples from the unseen categories to intuitively evaluate the performance of discovering unseen classes only exist in the target domain.
4.3 Baselines
Open-Set Domain Adaptation
PGL (2020 ICML) [luo2020progressive]
TIM (2020 CVPR) [kundu2020towards]
AOD (2019 ICCV) [feng2019attract]
SAT (2019 CVPR) [liu2019separate]
USBP (2018 ECCV) [saito2018open]
ANMC (2020 IEEE TMM) [shermin2020adversarial]
Zero-Shot Learning
(ZSL)
(GZSL)
TF-CLSGAN (2020 ECCV) [narayan2020latent]
FFT (2019 ICCV) [zhu2019learning]
CADA-VAE (2019 CVPR) [schonfeld2019generalized]
GDAN (2019 CVPR) [Huang_2019_CVPR]
LisGAN (2019 CVPR) [Li19Leveraging]
Cycle-WGAN (2018 ECCV) [felix2018multi]
(Transductive Generalized Zero-Shot Learning)
4.4 Implementation
We use the binary attributes of AwA2 from corresponding classes as the semantic descriptions. ImageNet pre-trained ResNet-50 is accepted as the backbone, and we take the output before the last fully connected layer as the features [deng2009imagenet, he2016deep]. is two-layer fully connected neural networks with hidden layer output dimension as 1024, and the output feature dimension is 512. and are both two-layer fully connected layer neural network classifier with hidden layer output dimension as 256, and the output dimension of is , while output as two classes. is two-layer neural networks with hidden layer output dimension as 256 followed by ReLU activation, and the final output dimension is the same as the semantic attributes dimension followed by Sigmoid function. We accept the cosine distance for the prototypical classification, while all other distances used in the paper are Euclidean distance.