Semileptonic $D$ Meson Decays $D\to P/V/S\ell^{+}\nu_{\ell}$ with the SU(3) Flavor Symmetry/Breaking

Ru-Min Wang^1,†, Yue-Xin Liu¹, Chong Hua¹, Jin-Huan Sheng^2,§, Yuan-Guo Xu^1,♯
¹College of Physics and Communication Electronics, Jiangxi Normal University, Nanchang, Jiangxi 330022, China
²School of Physics and Engineering, Henan University of Science and Technology, Luoyang, Henan 471000, China
^†ruminwang@sina.com ^§jinhuanwuli@126.com ^♯yuanguoxu@jxnu.edu.cn

Abstract

Many exclusive $c\to d/s\ell^{+}\nu_{\ell}\leavevmode\nobreak\ (\ell=e,\mu,\tau)$ transitions have been well measured, and they can be used to test the theoretical calculations. Motivated by this, we study the $D\to P/V/S\ell^{+}\nu_{\ell}$ decays induced by the $c\to d/s\ell^{+}\nu_{\ell}$ transitions with the SU(3) flavor symmetry approach, where $P$ denotes the pseudoscalar meson, $V$ denotes the vector meson, and $S$ denotes the scalar meson with a mass below $1$ $GeV$ . The different decay amplitudes of the $D\to P\ell^{+}\nu_{\ell}$ , $D\to V\ell^{+}\nu_{\ell}$ or $D\to S\ell^{+}\nu_{\ell}$ decays can be related by using the SU(3) flavor symmetry and by considering the SU(3) flavor breaking. Using the present data of $D\to P/V/S\ell^{+}\nu_{\ell}$ , we predict the not yet measured or not yet well measured processes in the $D\to P/V/S\ell^{+}\nu_{\ell}$ decays. We find that the SU(3) flavor symmetry approach works well in the semileptonic $D\to P/V\ell^{+}\nu_{\ell}$ decays. For the $D\to S\ell^{+}\nu_{\ell}$ decays, only the decay $D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e}$ has been measured, the branching ratios of the $D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e}$ and $D\to S(S\to P_{1}P_{2})\ell^{+}\nu_{\ell}$ decays are used to constrain the nonperturbative parameters and then predict not yet measured $D\to S\ell^{+}\nu_{\ell}$ decays, in addition, the two quark and the four quark scenarios for the light scalar mesons are analyzed. The SU(3) flavor symmetry predictions of the $D\to S\ell^{+}\nu_{\ell}$ decays need to be further tested, and our predictions of the $D\to S\ell^{+}\nu_{\ell}$ decays are useful for probing the structure of light scalar mesons. Our results in this work could be used to test the SU(3) flavor symmetry approach in the semileptonic $D$ decays by the future experiments at BESIII, LHCb and BelleII.

I Introduction

Semileptonic heavy meson decays dominated by tree-level exchange of $W$ -bosons in the standard model have attracted a lot of attention in testing the stand model and in searching for the new physics beyond the stand model. Many semileptonic $D\to P/V\ell^{+}\nu_{\ell}$ decays and one $D\to S\ell^{+}\nu_{\ell}$ decay have been observed PDG2022 , and present experimental measurements give us an opportunity to additionally test theoretical approaches.

In theory, the description of semileptonic decays are relatively simple, and the weak and strong dynamics can be separated in these processes since leptons do not participate in the strong interaction. All the strong dynamics in the initial and final hadrons is included in the hadronic form factors, which are important for testing the theoretical calculations of the involved strong interaction. The form factors of the $D$ decays have been calculated, for examples, by quark model Melikhov:2000yu ; Cheng:2017pcq ; Soni:2018adu ; Faustov:2019mqr ; Chang:2020wvs ; Chang:2018zjq , QCD sum rules Ball:1993tp , light-cone sum rules Bhattacharyya:2017wxk ; Fu:2018yin ; Fu:2020vqd , covariant light-front quark models Grach:1996nz ; Cheng:2003sm ; Chang:2019mmh , and lattice QCD Lubicz:2018rfs ; Lubicz:2017syv .

The SU(3) flavor symmetry approach is independent of the detailed dynamics offering us an opportunity to relate different decay modes, nevertheless, it cannot determine the sizes of the amplitudes or the form factors by itself. However, if experimental data are enough, one may use the data to extract the amplitudes or the form factors, which can be viewed as predictions based on symmetry, has a smaller dependency on estimated form factors, and can provide some very useful information about the decays. The SU(3) flavor symmetry works well in the $b$ -hadron decays He:1998rq ; He:2000ys ; Fu:2003fy ; Hsiao:2015iiu ; He:2015fwa ; He:2015fsa ; Deshpande:1994ii ; Gronau:1994rj ; Gronau:1995hm ; Shivashankara:2015cta ; Zhou:2016jkv ; Cheng:2014rfa ; Wang:2021uzi ; Wang:2020wxn , and the $c$ -hadron decays Wang:2021uzi ; Wang:2020wxn ; Grossman:2012ry ; Pirtskhalava:2011va ; Cheng:2012xb ; Savage:1989qr ; Savage:1991wu ; Altarelli:1975ye ; Lu:2016ogy ; Geng:2017esc ; Geng:2018plk ; Geng:2017mxn ; Geng:2019bfz ; Wang:2017azm ; Wang:2019dls ; Wang:2017gxe ; Muller:2015lua .

Semileptonic decays of $D$ mesons have been studied extensively in the standard model and its various extensions, for instance, in Refs. Cheng:2017pcq ; Ivanov:2019nqd ; Barranco:2014bva ; Barranco:2013tba ; Akeroyd:2009tn ; Dobrescu:2008er ; Akeroyd:2007eh ; Fajfer:2006uy ; Fajfer:2005ug ; Fajfer:2004mv ; Akeroyd:2003jb ; Akeroyd:2002pi . In this work, we will systematically study the $D\to P/V/S\ell^{+}\nu_{\ell}$ decays with the SU(3) flavor symmetry. We will firstly construct the amplitude relations between different decay modes of $D\to P\ell^{+}\nu_{\ell}$ , $D\to V\ell^{+}\nu_{\ell}$ or $D\to S\ell^{+}\nu_{\ell}$ decays by the SU(3) flavor symmetry and the SU(3) flavor breaking. We use the available data to extract the SU(3) flavor symmetry/breaking amplitudes and the form factors, and then predict the not yet measured modes for further tests in experiments. The forward-backward asymmetries $A^{\ell}_{FB}$ , the lepton-side convexity parameters $C^{\ell}_{F}$ , the longitudinal polarizations of the final charged lepton $P^{\ell}_{L}$ , the transverse polarizations of the final charged lepton $P^{\ell}_{T}$ , the lepton spin asymmetries $A_{\lambda}$ and the longitudinal polarization fractions $F_{L}$ of the final vector mesons with two ways of integration have also been predicted in the $D\to P/V\ell^{+}\nu_{\ell}$ decays. In addition, the $q^{2}$ dependence of some differential observables for the $D\to P/V\ell^{+}\nu_{\ell}$ decays are shown in figures.

This paper will be organized as follows. In Sec. II, the theoretical framework in this work is presented, including the effective hamiltonian, the hadronic helicity amplitude relations, the observables and the form factors. The numerical results of the $D\to P/V/S\ell^{+}\nu_{\ell}$ semileptonic decays will be given in Sec. III. Finally, we give the summary and conclusion in Sec. IV.

II Theoretical Frame

II.1 The effective Hamiltonian

In the standard model, the four-fermion charged-current effective Hamiltonian below the electroweak scale for the decays $D\rightarrow M\ell^{+}\nu_{\ell}\leavevmode\nobreak\ (M=P,V,S)$ can be written as

\displaystyle\mathcal{H}_{eff}(c\rightarrow q\ell^{+}\nu_{\ell})

\displaystyle=

\displaystyle\frac{G_{F}}{\sqrt{2}}V^{*}_{cq}\bar{q}\gamma^{\mu}(1-\gamma_{5})c\leavevmode\nobreak\ \bar{\nu_{\ell}}\gamma_{\mu}(1-\gamma_{5})\ell,

(1)

with $q=s,d$ .

The helicity amplitudes of the decays $D\rightarrow M\ell^{+}\nu_{\ell}$ can be written as

\displaystyle\mathcal{M}(D\rightarrow M\ell^{+}\nu_{\ell})

\displaystyle=

\displaystyle\frac{G_{F}}{\sqrt{2}}V_{cb}\sum_{mm^{\prime}}g_{mm^{\prime}}L^{\lambda_{\ell}\lambda_{\nu}}_{m}H^{\lambda_{M}}_{m^{\prime}},

(2)

with

	$\displaystyle L^{\lambda_{\ell}\lambda_{\nu}}_{m}$	$\displaystyle=$	$\displaystyle\epsilon_{\alpha}(m)\bar{\nu_{\ell}}\gamma^{\alpha}(1-\gamma_{5})\ell,$		(3)
	$\displaystyle H^{\lambda_{M}}_{m^{\prime}}$	$\displaystyle=$	$\displaystyle\left\{\begin{array}[]{l}\epsilon{{}^{}_{\beta}}(m^{\prime})\langle{P/S}(p_{P/S})\|\bar{q}\gamma^{\beta}(1-\gamma_{5})c\|D(p_{D})\rangle\\ \epsilon^{}_{\beta}(m^{\prime})\langle{V}(p_{V},\epsilon^{*})\|\bar{q}\gamma^{\beta}(1-\gamma_{5})c\|D(p_{D})\rangle\end{array}\right.,\$		(6)

where the particle helicities $\lambda_{M}=0$ for $M=P/S$ , $\lambda_{M}=0,\pm 1$ for $M=V,\lambda_{\ell}=\pm\frac{1}{2}$ and $\lambda_{\nu}=+\frac{1}{2}$ , as well as $\epsilon_{\mu}(m)$ is the polarization vectors of the virtual $W$ with $m=0,t,\pm 1$ .

The form factors of the $D\to P$ , $D\to S$ and $D\to V$ transitions are given by Melikhov:2000yu ; Cheng:2017pcq ; Cheng:2003sm

$\displaystyle\left<P(p)\left\|\bar{d}_{k}\gamma_{\mu}c\right\|D(p_{D})\right>$	$\displaystyle=$	$\displaystyle f^{P}_{+}(q^{2})(p+p_{D})_{\mu}+\left[f^{P}_{0}(q^{2})-f^{P}_{+}(q^{2})\right]\frac{m^{2}_{D}-m^{2}_{P}}{q^{2}}q_{\mu},$	(7)
$\displaystyle\left<S(p)\left\|\bar{d}_{k}\gamma_{\mu}\gamma_{5}c\right\|D(p_{D})\right>$	$\displaystyle=$	$\displaystyle-i\Big{(}f^{S}_{+}(q^{2})(p+p_{D})_{\mu}+\left[f^{S}_{0}(q^{2})-f^{S}_{+}(q^{2})\right]\frac{m^{2}_{D}-m^{2}_{S}}{q^{2}}q_{\mu}\Big{)},$	(8)
$\displaystyle\left<V(p,\varepsilon^{*})\left\|\bar{d}_{k}\gamma_{\mu}(1-\gamma_{5})c\right\|D(p_{D})\right>$	$\displaystyle=$	$\displaystyle\frac{2V^{V}(q^{2})}{m_{D}+m_{V}}\epsilon_{\mu\nu\alpha\beta}\varepsilon^{*\nu}p^{\alpha}_{D}p^{\beta}$	(9)
		$\displaystyle-i\left[\varepsilon^{}_{\mu}(m_{D}+m_{V})A^{V}_{1}(q^{2})-(p_{D}+p)_{\mu}(\varepsilon^{}.p_{D})\frac{A^{V}_{2}(q^{2})}{m_{D}+m_{V}}\right]$
		$\displaystyle+iq_{\mu}(\varepsilon^{*}.p_{D})\frac{2m_{V}}{q^{2}}[A^{V}_{3}(q^{2})-A^{V}_{0}(q^{2})],$

where $s=q^{2}$ ( $q=p_{D}-p_{M}$ ), and $\varepsilon^{*}$ is the polarization of vector meson. The hadronic helicity amplitudes can be written as

$\displaystyle H_{\pm}$	$\displaystyle=$	$\displaystyle 0,$	(10)
$\displaystyle H_{0}$	$\displaystyle=$	$\displaystyle\frac{2m_{D_{q}}\|\vec{p}_{P}\|}{\sqrt{q^{2}}}f^{P}_{+}(q^{2}),$	(11)
$\displaystyle H_{t}$	$\displaystyle=$	$\displaystyle\frac{m_{D_{q}}^{2}-m_{P}^{2}}{\sqrt{q^{2}}}f^{P}_{0}(q^{2}),$	(12)

for $D\to P\ell^{+}\nu_{\ell}$ decays,

$\displaystyle H_{\pm}$	$\displaystyle=$	$\displaystyle 0,$	(13)
$\displaystyle H_{0}$	$\displaystyle=$	$\displaystyle\frac{i2m_{D_{q}}\|\vec{p}_{S}\|}{\sqrt{q^{2}}}f^{S}_{+}(q^{2}),$	(14)
$\displaystyle H_{t}$	$\displaystyle=$	$\displaystyle\frac{im_{D_{q}}^{2}-m_{S}^{2}}{\sqrt{q^{2}}}f^{S}_{0}(q^{2}),$	(15)

for $D\to S\ell^{+}\nu_{\ell}$ decays, and

$\displaystyle H_{\pm}$	$\displaystyle=$	$\displaystyle(m_{D_{q}}+m_{V})A_{1}(q^{2})\mp\frac{2m_{D_{q}}\|\vec{p}_{V}\|}{(m_{D_{q}}+m_{V})}V(q^{2}),$	(16)
$\displaystyle H_{0}$	$\displaystyle=$	$\displaystyle\frac{1}{2m_{V}\sqrt{q^{2}}}\left[(m_{D_{q}}^{2}-m_{V}^{2}-q^{2})(m_{D_{q}}+m_{V})A_{1}(q^{2})-\frac{4m_{D_{q}}^{2}\|\vec{p}_{V}\|^{2}}{m_{D_{q}}+m_{V}}A_{2}(q^{2})\right],$	(17)
$\displaystyle H_{t}$	$\displaystyle=$	$\displaystyle\frac{2m_{D_{q}}\|\vec{p}_{V}\|}{\sqrt{q^{2}}}A_{0}(q^{2}),$	(18)

for $D\to V\ell^{+}\nu_{\ell}$ decays, where $|\vec{p}_{M}|\equiv\sqrt{\lambda(m_{D_{q}}^{2},m_{M}^{2},q^{2})}/2m_{D_{q}}$ with $\lambda(a,b,c)=a^{2}+b^{2}+c^{2}-2ab-2ac-2bc$ .

II.2 Hadronic helicity amplitude relations by the SU(3) flavor symmetry

Charmed mesons containing one heavy $c$ quark are flavor SU(3) anti-triplets

\displaystyle D_{i}=\Big{(}D^{0}(c\bar{u}),\leavevmode\nobreak\ D^{+}(c\bar{d}),\leavevmode\nobreak\ D^{+}_{s}(c\bar{s})\Big{)}.

(19)

Light pseudoscalar $P$ and vector $V$ meson octets and singlets under the $SU(3)$ flavor symmetry of $u,d,s$ quarks are He:2018joe

	$\displaystyle P$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{ccc}\frac{\pi^{0}}{\sqrt{2}}+\frac{\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}&\pi^{+}&K^{+}\\ \pi^{-}&-\frac{\pi^{0}}{\sqrt{2}}+\frac{\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}&K^{0}\\ K^{-}&\overline{K}^{0}&-\frac{2\eta_{8}}{\sqrt{6}}+\frac{\eta_{1}}{\sqrt{3}}\end{array}\right)\,,$		(23)
	$\displaystyle V$	$\displaystyle=$	$\displaystyle\left(\begin{array}[]{ccc}\frac{\rho^{0}}{\sqrt{2}}+\frac{\omega_{8}}{\sqrt{6}}+\frac{\omega_{1}}{\sqrt{3}}&\rho^{+}&K^{+}\\ \rho^{-}&-\frac{\rho^{0}}{\sqrt{2}}+\frac{\omega_{8}}{\sqrt{6}}+\frac{\omega_{1}}{\sqrt{3}}&K^{0}\\ K^{-}&\overline{K}^{0}&-\frac{2\omega_{8}}{\sqrt{6}}+\frac{\omega_{1}}{\sqrt{3}}\end{array}\right)\,,$		(27)

where $\omega$ and $\phi$ mix in an ideal form, and the $\eta$ and $\eta^{\prime}$ ( $\omega$ and $\phi$ ) are mixtures of $\eta_{1}(\omega_{1})=\frac{u\bar{u}+d\bar{d}+s\bar{s}}{\sqrt{3}}$ and $\eta_{8}(\omega_{8})=\frac{u\bar{u}+d\bar{d}-2s\bar{s}}{\sqrt{6}}$ with the mixing angle $\theta_{P}$ ( $\theta_{V}$ ). $\eta$ and $\eta^{\prime}$ ( $\omega$ and $\phi$ ) are given by

\displaystyle\left(\begin{array}[]{c}\eta\\ \eta^{\prime}\end{array}\right)\,=\left(\begin{array}[]{cc}cos\theta_{P}&-sin\theta_{P}\\ sin\theta_{P}&cos\theta_{P}\end{array}\right)\,\left(\begin{array}[]{c}\eta_{8}\\ \eta_{1}\end{array}\right),\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \left(\begin{array}[]{c}\phi\\ \omega\end{array}\right)\,=\left(\begin{array}[]{cc}cos\theta_{V}&-sin\theta_{V}\\ sin\theta_{V}&cos\theta_{V}\end{array}\right)\,\left(\begin{array}[]{c}\omega_{8}\\ \omega_{1}\end{array}\right),

(40)

where $\theta_{P}=[-20^{\circ},-10^{\circ}]$ and $\theta_{V}=36.4^{\circ}$ from Particle Data Group (PDG) PDG2022 will be used in our numerical analysis.

The structures of the light scalar mesons are not fully understood yet. Many suggestions are discussed, such as ordinary two quark states, four quark states, meson-meson bound states, molecular states, glueball states or hybrid states, for examples, in Refs. Dai:2018fmx ; Maiani:2004uc ; tHooft:2008rus ; Pelaez:2003dy ; Sun:2010nv ; Oller:1997ti ; Baru:2003qq ; Cheng:2005nb ; Achasov:1996ei . In this work, we will consider the two quark and the four quark scenarios for the scalar mesons below or near 1 $GeV$ . In the two quark picture, the light scalar mesons can be written as Momeni:2022gqb

\displaystyle S

\displaystyle=

\displaystyle\left(\begin{array}[]{ccc}\frac{a^{0}_{0}}{\sqrt{2}}+\frac{\sigma}{\sqrt{2}}&a^{+}_{0}&K^{+}_{0}\\ a_{0}^{-}&-\frac{a_{0}^{0}}{\sqrt{2}}+\frac{\sigma}{\sqrt{2}}&K^{0}_{0}\\ K^{-}_{0}&\overline{K}^{0}_{0}&f_{0}\end{array}\right)\,.

(44)

The two isoscalars $f_{0}(980)$ and $f_{0}(500)$ are obtained by the mixing of $\sigma=\frac{u\bar{u}+d\bar{d}}{\sqrt{2}}$ and $f_{0}=s\bar{s}$

\displaystyle\left(\begin{array}[]{c}f_{0}(980)\\ f_{0}(500)\end{array}\right)\,=\left(\begin{array}[]{cc}\mbox{cos}\theta_{S}&\mbox{sin}\theta_{S}\\ -\mbox{sin}\theta_{S}&\mbox{cos}\theta_{S}\end{array}\right)\,\left(\begin{array}[]{c}f_{0}\\ \sigma\end{array}\right)\,,

(51)

where the three possible ranges of the mixing angle, $25^{\circ}<\theta_{S}<40^{\circ}$ , $140^{\circ}<\theta_{S}<165^{\circ}$ and $\leavevmode\nobreak\ -30^{\circ}<\theta_{S}<30^{\circ}$ Cheng:2005nb ; LHCb:2013dkk will be analyzed in our numerical results. In the four quark picture, the light scalar mesons are given as Jaffe:1976ig ; PDG2022

	$\displaystyle\sigma=u\bar{u}d\bar{d},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ f_{0}=(u\bar{u}+d\bar{d})s\bar{s}/\sqrt{2},$
	$\displaystyle a^{0}_{0}=(u\bar{u}-d\bar{d})s\bar{s}/\sqrt{2},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ a^{+}_{0}=u\bar{d}s\bar{s},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ a^{-}_{0}=d\bar{u}s\bar{s},$
	$\displaystyle K^{+}_{0}=u\bar{s}d\bar{d},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ K^{0}_{0}=d\bar{s}u\bar{u},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \bar{K}^{0}_{0}=s\bar{d}u\bar{u},\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ K^{+}_{0}=s\bar{u}d\bar{d},$		(52)

and the two isoscalars are expressed as

\displaystyle\left(\begin{array}[]{c}f_{0}(980)\\ f_{0}(500)\end{array}\right)\,=\left(\begin{array}[]{cc}\mbox{cos}\phi_{S}&\mbox{sin}\phi_{S}\\ -\mbox{sin}\phi_{S}&\mbox{cos}\phi_{S}\end{array}\right)\,\left(\begin{array}[]{c}f_{0}\\ \sigma\end{array}\right)\,,

(59)

where the constrained mixing angle $\phi_{S}=(174.6^{+3.4}_{-3.2})^{\circ}$ Maiani:2004uc .

In terms of the SU(3) flavor symmetry, meson states and quark operators can be parameterized into SU(3) tensor forms, while the leptonic helicity amplitudes $L^{\lambda_{\ell},\lambda_{\nu}}_{m}$ are invariant under the SU(3) flavor symmetry. And the hadronic helicity amplitude relations of the $D\rightarrow M\ell^{+}\nu_{\ell}(M=P,V,S)$ decays can be parameterized as

\displaystyle H(D\rightarrow M\ell^{+}\nu_{\ell})=c_{0}^{M}D_{i}M^{i}_{j}H^{j},

(60)

where $H^{2}\equiv V^{*}_{cd}$ and $H^{3}\equiv V^{*}_{cs}$ are the CKM matrix elements, and $c_{0}^{M}$ are the nonperturbative coefficients of the $D\rightarrow M\ell^{+}\nu_{\ell}$ decays under the SU(3) flavor symmetry. Noted that the hadronic helicity amplitudes for the $D\rightarrow S\ell^{+}\nu_{\ell}$ decays in Eq. (60) are given in the two quark picture of the light scalar mesons, and ones in the four quark picture of the light scalar mesons will be given later.

The SU(3) flavor breaking effects mainly come from different masses of $u$ , $d$ and $s$ quarks. Following Ref. Xu:2013dta , the SU(3) breaking amplitudes of the $D\rightarrow M\ell^{+}\nu_{\ell}$ decays can be give as

\displaystyle\Delta H(D\rightarrow M\ell^{+}\nu_{\ell})=c_{1}^{M}D_{a}W^{a}_{i}M^{i}_{j}H^{j}+c_{2}^{M}D_{i}M^{i}_{a}W^{a}_{j}H^{j},

(61)

with

\displaystyle W=\big{(}W^{i}_{j}\big{)}=\left(\begin{array}[]{ccc}1&0&0\\ 0&1&0\\ 0&0&-2\end{array}\right),

(65)

where $c_{1,2}^{M}$ are the nonperturbative SU(3) flavor breaking coefficients.

In the four quark picture of the light scalar mesons, the hadronic helicity amplitudes of the $D\rightarrow S\ell^{+}\nu_{\ell}$ decays under the SU(3) flavor symmetry are

\displaystyle H(D\rightarrow S\ell^{+}\nu_{\ell})^{4q}=c^{\prime S}_{0}D_{i}S^{im}_{jm}H^{j}.

(66)

And the corresponding SU(3) flavor breaking amplitudes of the $D\rightarrow S\ell^{+}\nu_{\ell}$ decays are

\displaystyle\Delta H(D\rightarrow S\ell^{+}\nu_{\ell})^{4q}=c^{\prime S}_{1}D_{a}W^{a}_{i}S^{im}_{jm}H^{j}+c^{\prime S}_{2}D_{i}S^{im}_{am}W^{a}_{j}H^{j}+c^{\prime S}_{1}D_{i}S^{im}_{ja}W^{a}_{m}H^{j}.

(67)

In terms of the SU(3) flavor symmetry, the hadronic helicity amplitude relations for the $D\rightarrow P\ell^{+}\nu_{\ell}$ , $D\rightarrow V\ell^{+}\nu_{\ell}$ and $D\rightarrow S\ell^{+}\nu_{\ell}$ decays are summarized in later Tab. 1, Tab. 4 and Tab. 8, respectively.

II.3 Observables for the $D\to M\ell^{+}\nu_{\ell}$ decays

The double differential branching ratios of the $D\to M\ell^{+}\nu_{\ell}$ decays are Ivanov:2019nqd

	$\displaystyle\frac{d\mathcal{B}(D\to M\ell^{+}\nu_{\ell})}{dq^{2}d(\cos\theta)}$	$\displaystyle=$	$\displaystyle\frac{\tau_{D}G_{F}^{2}\|V_{cq}\|^{2}\lambda^{1/2}(q^{2}-m_{\ell}^{2})^{2}}{64(2\pi)^{3}M_{D_{(s)}}^{3}q^{2}}\Biggl{[}(1+\cos^{2}\theta){\cal H}_{U}+2\sin^{2}\theta{\cal H}_{L}+2\cos\theta{\cal H}_{P}$		(69)
			$\displaystyle+\frac{m_{\ell}^{2}}{q^{2}}(\sin^{2}\theta{\cal H}_{U}+2\cos^{2}\theta{\cal H}_{L}+2{\cal H}_{S}-4\cos\theta{\cal H}_{SL})\Bigr{]},$		(69)

where $\lambda\equiv\lambda(m_{D_{q}}^{2},m_{M}^{2},q^{2})$ , $m_{\ell}^{2}\leq q^{2}\leq(m_{D_{q}}-m_{M})^{2}$ , and

{\cal H}_{U}=|H_{+}|^{2}+|H_{-}|^{2},\quad{\cal H}_{L}=|H_{0}|^{2},\quad{\cal H}_{P}=|H_{+}|^{2}-|H_{-}|^{2},\quad{\cal H}_{S}=|H_{t}|^{2},\quad{\cal H}_{SL}=\Re(H_{0}H_{t}^{\dagger}).

(70)

The differential branching ratios integrated over $\cos\theta$ are Ivanov:2019nqd

\frac{d\mathcal{B}(D_{(s)}\to M\ell^{+}\nu_{\ell})}{dq^{2}}=\frac{\tau_{D}G_{F}^{2}|V_{cq}|^{2}\lambda^{1/2}(q^{2}-m_{\ell}^{2})^{2}}{24(2\pi)^{3}M_{D_{(s)}}^{3}q^{2}}{\cal H}_{\rm total},

(71)

with

{\cal H}_{\rm total}\equiv({\cal H}_{U}+{\cal H}_{L})\left(1+\frac{m_{\ell}^{2}}{2q^{2}}\right)+\frac{3m_{\ell}^{2}}{2q^{2}}{\cal H}_{S}.

(72)

The lepton flavor universality in $D_{(s)}\to M\ell^{+}\nu_{\ell}$ is defined in a manner identical $R^{\mu/e}$ as

\displaystyle R^{\mu/e}=\frac{\int^{q_{max}}_{q_{min}}d\mathcal{B}(D_{(s)}\to M\mu^{+}\nu_{\mu})/dq^{2}}{\int^{q_{max}}_{q_{min}}d\mathcal{B}(D_{(s)}\to Me^{+}\nu_{e})/dq^{2}}.

(73)

The forward-backward asymmetries are defined as Ivanov:2019nqd

	$\displaystyle A_{FB}^{\ell}(q^{2})$	$\displaystyle=$	$\displaystyle\frac{\int^{0}_{-1}d\mbox{cos}\theta_{\ell}\leavevmode\nobreak\ \frac{d\mathcal{B}(D\to M\ell\nu)}{dq^{2}d\mbox{cos}\theta_{\ell}}-\int^{1}_{0}d\mbox{cos}\theta_{\ell}\frac{d\mathcal{B}(D\to M\ell\nu)}{dq^{2}d\mbox{cos}\theta_{\ell}}}{\int^{0}_{-1}d\mbox{cos}\theta_{\ell}\leavevmode\nobreak\ \frac{d\mathcal{B}(D\to M\ell\nu)}{dq^{2}d\mbox{cos}\theta_{\ell}}+\int^{1}_{0}d\mbox{cos}\theta_{\ell}\frac{d\mathcal{B}(D\to M\ell\nu)}{dq^{2}d\mbox{cos}\theta_{\ell}}}$		(74)
		$\displaystyle=$	$\displaystyle\frac{3}{4}\frac{{\cal H}_{P}-\frac{2m_{\ell}^{2}}{q^{2}}{\cal H}_{SL}}{{\cal H}_{\rm total}}.$		(75)

The lepton-side convexity parameters are given by Ivanov:2019nqd

C^{\ell}_{F}(q^{2})=\frac{3}{4}\left(1-\frac{m_{\ell}^{2}}{q^{2}}\right)\frac{{\cal H}_{U}-2{\cal H}_{L}}{{\cal H}_{\rm total}}.

(76)

The longitudinal polarizations of the final charged lepton $\ell$ are defined by Ivanov:2019nqd

P_{L}^{\ell}(q^{2})=\frac{({\cal H}_{U}+{\cal H}_{L})\left(1-\frac{m_{\ell}^{2}}{2q^{2}}\right)-\frac{3m_{\ell}^{2}}{2q^{2}}{\cal H}_{S}}{{\cal H}_{\rm total}},

(77)

and its transverse polarizations are

P_{T}^{\ell}(q^{2})=-\frac{3\pi m_{\ell}}{8\sqrt{q^{2}}}\frac{{\cal H}_{P}+2{\cal H}_{SL}}{{\cal H}_{\rm total}}.

(78)

The lepton spin asymmetry in the $\ell-\bar{\nu}_{\ell}$ center of mass frame is defined by Fajfer:2012vx ; Tanaka:1994ay ; Celis:2012dk ; Tanaka:2010se

	$\displaystyle A_{\lambda}(q^{2})$	$\displaystyle=$	$\displaystyle\frac{d\mathcal{B}(D\to M\ell^{+}\nu_{\ell})[\lambda_{\ell}=-\frac{1}{2}]/dq^{2}-d\mathcal{B}(D\to M\ell^{+}\nu_{\ell})[\lambda_{\ell}=+\frac{1}{2}]/dq^{2}}{d\mathcal{B}(D\to M\ell^{+}\nu_{\ell})[\lambda_{\ell}=-\frac{1}{2}]/dq^{2}+d\mathcal{B}(D\to M\ell^{+}\nu_{\ell})[\lambda_{\ell}=+\frac{1}{2}]/dq^{2}}$		(79)
		$\displaystyle=$	$\displaystyle\frac{{\cal H}_{\rm total}-\frac{6m_{\ell}^{2}}{2q^{2}}{\cal H}_{\rm S}}{{\cal H}_{\rm total}}.$		(80)

For the $D\to V\ell^{+}\nu_{\ell}$ decays, the longitudinal polarization fractions of the final vector mesons are given by Ivanov:2019nqd

F_{L}(q^{2})=\frac{{\cal H}_{L}\left(1+\frac{m_{\ell}^{2}}{2q^{2}}\right)+\frac{3m_{\ell}^{2}}{2q^{2}}{\cal H}_{S}}{{\cal H}_{\rm total}},

(81)

then its transverse polarization fraction $F_{T}(q^{2})=1-F_{L}(q^{2})$ .

Noted that, for $q^{2}$ -integration of $X(q^{2})=A^{\ell}_{FB},\leavevmode\nobreak\ C^{\ell}_{F},\leavevmode\nobreak\ P^{\ell}_{L},\leavevmode\nobreak\ P^{\ell}_{T},\leavevmode\nobreak\ A_{\lambda}$ and $F_{L}$ , following Ref. Bobeth:2010wg , two ways of integration are considered. The normalized $q^{2}$ -integrated observables $\langle X\rangle$ are calculated by separately integrating the numerators and denominators with the same $q^{2}$ bins. The “naively integrated” observables are obtained by

\displaystyle\overline{X}=\frac{1}{q^{2}_{max}-q^{2}_{min}}\int^{q^{2}_{max}}_{q^{2}_{min}}dq^{2}X(q^{2}).

(82)

II.4 Form factors

In order to obtain more precise observables, one also need considering the $q^{2}$ dependence of the form factors for the $D\to P\ell^{+}\nu_{\ell}$ , $D\to V\ell^{+}\nu_{\ell}$ and $D\to S\ell^{+}\nu_{\ell}$ decays. The following cases will be considered in our analysis of $D\to P/V\ell^{+}\nu_{\ell}$ decays.

$C_{1}$ :

All form factors are treated as constants without the hadronic momentum-transfer $q^{2}$ dependence, and different form factors are related by the SU(3) flavor symmetry, $i.e.$ , the SU(3) flavor breaking terms such as $c^{M}_{1,2}$ and $c^{\prime S}_{1,2,3}$ in later Tabs. 1, 4 and 8 are ignored.

C_{2}

With the SU(3) flavor symmetry, the modified pole model for the $q^{2}$ -dependence of $F_{i}(q^{2})$ is used Li:2020ylu

\displaystyle F_{i}(q^{2})=\frac{F_{i}(0)}{\left(1-\frac{q^{2}}{m^{2}_{pole}}\right)\left(1-\alpha_{i}\frac{q^{4}}{m^{4}_{pole}}\right)},

(83)

where $m_{pole}=m_{D^{*+}}$ for $c\to d\ell^{+}\nu_{\ell}$ transitions and $m_{pole}=m_{D^{*+}_{s}}$ for $c\to s\ell^{+}\nu_{\ell}$ transitions, and $\alpha_{i}$ are free parameters and are different for $f^{P}_{+}(q^{2})$ , $f^{P}_{0}(q^{2})$ , $V(q^{2})$ , $A_{1}(q^{2})$ and $A_{2}(q^{2})$ , we will take $\alpha_{i}\in[-1,1]$ in our analysis.

C_{3}

With the SU(3) flavor symmetry, following Ref. Melikhov:2000yu

	$\displaystyle F_{i}(q^{2})$	$\displaystyle=$	$\displaystyle\frac{F_{i}(0)}{\left(1-\frac{q^{2}}{m^{2}_{pole}}\right)\left(1-\sigma_{1i}\frac{q^{2}}{m^{2}_{pole}}+\sigma_{2i}\frac{q^{4}}{m^{4}_{pole}}\right)}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{for $f^{P}_{+}(q^{2})$ and $V(q^{2})$},$		(84)
	$\displaystyle F_{i}(q^{2})$	$\displaystyle=$	$\displaystyle\frac{F_{i}(0)}{\left(1-\sigma_{1i}\frac{q^{2}}{m^{2}_{pole}}+\sigma_{2i}\frac{q^{4}}{m^{4}_{pole}}\right)}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{for $f^{P}_{0}(q^{2})$, $A_{1}(q^{2})$ and $A_{2}(q^{2})$},$		(85)

where $\sigma_{1,2}$ for the $D\to\pi$ and $D\to K^{*}$ transitions from Ref. Melikhov:2000yu will be used in our results.

$C_{4}$ :

Considering the SU(3) flavor breaking terms such as $c^{M}_{1,2}$ and $c^{\prime S}_{1,2,3}$ in later Tabs. 1, 4 and 8, the form factors in $C_{3}$ case are used.

As for the form factors of the $D\to S\ell^{+}\nu_{\ell}$ decays, we find that the vector dominance model Achasov:2012kk and the double pole model Soni:2020sgn give the similar SU(3) flavor symmetry predictions for the branching ratios of the $D\to S\ell^{+}\nu_{\ell}$ decays. The following form factors from the vector dominance model will be used in the numerical results,

\displaystyle F_{i}(q^{2})=\frac{F_{i}(0)}{\left(1-q^{2}/m^{2}_{pole}\right)}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{ for $f^{S}_{+}(q^{2})$ and $f^{S}_{0}(q^{2})$}.

(86)

After considering above $q^{2}$ dependence, we only need to focus on the $F_{i}(0)$ . Since these form factors $F_{i}(0)$ also preserve the SU(3) flavor symmetry, the same relations in Tabs. 1, 4 and 8 will be used for $F_{i}(0)$ . If considering the form factors ratios $f_{+}(0)/f_{0}(0)=1$ for $D\to P/S\ell^{+}\nu_{\ell}$ decays, $r_{V}\equiv V(0)/A_{1}(0)=1.46\pm 0.07$ , $r_{2}\equiv A_{2}(0)/A_{1}(0)=0.68\pm 0.06$ in $D^{0}\to K^{*-}\ell^{+}\nu_{\ell}$ decays from PDG PDG2022 and the SU(3) flavor symmetry, there is only one free form factor $f^{P,S}_{+}(0)$ and $A_{1}(0)$ for the $D\to P/S\ell^{+}\nu_{\ell}$ and $D\to V\ell^{+}\nu_{\ell}$ decays, respectively. As a result, the branching ratios only depend on one form factor $f^{P}_{+}(0)$ , $f^{S}_{+}(0)$ or $A_{1}(0)$ and the CKM matrix element $V_{cq}$ .

III Numerical results

The theoretical input parameters and the experimental data within the $2\sigma$ errors from PDG PDG2022 will be used in our numerical results.

III.1 $D\to P\ell^{+}\nu_{\ell}$ decays

Considering both the SU(3) flavor symmetry and the SU(3) flavor breaking contributions, the hadronic helicity amplitudes for the $D\rightarrow P\ell^{+}\nu_{\ell}$ decays are given in Tab. 1, in which we keep the CKM matrix element $V_{cs}$ and $V_{cd}$ information for comparing conveniently. In addition, $H(D^{+}_{s}\to\pi^{0}\ell^{+}\nu_{\ell})$ are obtained by neutral meson mixing with $\delta^{2}=(5.18\pm 0.71)\times 10^{-4}$ in Ref. Li:2020ylu . From Tab. 1, we can easily see the hadronic helicity amplitude relations of the $D\rightarrow P\ell^{+}\nu_{\ell}$ decays. There are four nonperturbative parameters $A_{1,2,3,4}$ in the $D\rightarrow P\ell^{+}\nu_{\ell}$ decays with $A_{1}\equiv c^{P}_{0}+c^{P}_{1}-2c^{P}_{2}$ , $A_{2}\equiv c^{P}_{0}-2c^{P}_{1}-2c^{P}_{2}$ , $A_{3}\equiv c^{P}_{0}+c^{P}_{1}+c^{P}_{2}$ and $A_{4}\equiv c^{P}_{0}-2c^{P}_{1}+c^{P}_{2}$ . If neglecting the SU(3) flavor breaking $c^{P}_{1}$ and $c^{P}_{2}$ terms, $A_{1}=A_{2}=A_{3}=A_{4}=c^{P}_{0}$ , and then all hadronic helicity amplitudes are related by only one parameter $c^{P}_{0}$ .

Table 1: The hadronic helicity amplitudes for the

D\to P\ell^{+}\nu

decays including both the SU(3) flavor symmetry and the SU(3) flavor breaking contributions.

A_{1}\equiv c^{P}_{0}+c^{P}_{1}-2c^{P}_{2}

A_{2}\equiv c^{P}_{0}-2c^{P}_{1}-2c^{P}_{2}

A_{3}\equiv c^{P}_{0}+c^{P}_{1}+c^{P}_{2}

A_{4}\equiv c^{P}_{0}-2c^{P}_{1}+c^{P}_{2}

A_{1}=A_{2}=A_{3}=A_{4}=c^{P}_{0}

if neglecting the SU(3) flavor breaking

c^{P}_{1}

and

c^{P}_{2}

terms.

Hadronic helicity amplitudes	SU(3) flavor amplitudes
$H(D^{0}\to K^{-}\ell^{+}\nu_{\ell})$	$A_{1}V^{*}_{cs}$
$H(D^{+}\to\overline{K}^{0}\ell^{+}\nu_{\ell})$	$A_{1}V^{*}_{cs}$
$H(D^{+}_{s}\to\eta\ell^{+}\nu_{\ell})$	$\big{(}-cos\theta_{P}\sqrt{2/3}-sin\theta_{P}/\sqrt{3}\big{)}A_{2}V^{*}_{cs}$
$H(D^{+}_{s}\to\eta^{\prime}\ell^{+}\nu_{\ell})$	$\big{(}-sin\theta_{P}\sqrt{2/3}+cos\theta_{P}/\sqrt{3}\big{)}A_{2}V^{*}_{cs}$
$H(D^{+}_{s}\to\pi^{0}\ell^{+}\nu_{\ell})$	$-\delta\big{(}-cos\theta_{P}\sqrt{2/3}-sin\theta_{P}/\sqrt{3}\big{)}A_{2}V^{*}_{cs}$
$H(D^{0}\to\pi^{-}\ell^{+}\nu_{\ell})$	$A_{3}V^{*}_{cd}$
$H(D^{+}\to\pi^{0}\ell^{+}\nu_{\ell})$	$-\frac{1}{\sqrt{2}}A_{3}V^{*}_{cd}$
$H(D^{+}\to\eta\ell^{+}\nu_{\ell})$	$\big{(}cos\theta_{P}/\sqrt{6}-sin\theta_{P}/\sqrt{3}\big{)}A_{3}V^{*}_{cd}$
$H(D^{+}\to\eta^{\prime}\ell^{+}\nu_{\ell})$	$\big{(}sin\theta_{P}/\sqrt{6}+cos\theta_{P}/\sqrt{3}\big{)}A_{3}V^{*}_{cd}$
$H(D^{+}_{s}\to K^{0}\ell^{+}\nu_{\ell})$	$A_{4}V^{*}_{cd}$

Many decay modes of the $D\rightarrow Pe^{+}\nu_{e},P\mu^{+}\nu_{\mu}$ decays have been measured, and the experimental data with $2\sigma$ errors are listed in the second column of Tab. 2. One can constrain the parameters $A_{i}$ by the present experimental data within $2\sigma$ errors and then predict other not yet measured branching ratios. Four cases $C_{1,2,3,4}$ will be considered in our analysis. The numerical results of $\mathcal{B}(D\to P\ell^{+}\nu_{\ell})$ in the $C_{1}$ , $C_{2}$ , $C_{3}$ and $C_{4}$ cases are given in the third, forth, fifth and sixth columns of Tab. 2, respectively. And our comments on the results are as follows.

Table 2: Branching ratios of the

D\to P\ell^{+}\nu

decays. ^†Denotes that the corresponding experimental data from PDG PDG2022 are not used to constrain

A_{i}

in this case.

Branching ratios	Exp. data	Ones in $C_{1}$	Ones in $C_{2}$	Ones in $C_{3}$	Ones in $C_{4}$	Previous ones
$\mathcal{B}(D^{+}\to\overline{K}^{0}e^{+}\nu_{e})(\times 10^{-2})$	$8.72\pm 0.18$	$8.84\pm 0.06$	$8.83\pm 0.07$	$8.84\pm 0.06$	$8.83\pm 0.07$
$\mathcal{B}(D^{+}\to\pi^{0}e^{+}\nu_{e})(\times 10^{-3})$	$3.72\pm 0.34$	$3.75\pm 0.05$	$5.40\pm 1.33^{\dagger}$	$5.04\pm 0.12^{\dagger}$	$3.70\pm 0.11$
$\mathcal{B}(D^{+}\to\eta e^{+}\nu_{e})(\times 10^{-3})$	$1.11\pm 0.14$	$1.15\pm 0.05$	$1.20\pm 0.05$	$1.20\pm 0.05$	$0.92\pm 0.08$
$\mathcal{B}(D^{+}\to\eta^{\prime}e^{+}\nu_{e})(\times 10^{-4})$	$2.0\pm 0.8$	$2.59\pm 0.14$	$2.22\pm 0.34$	$2.09\pm 0.14$	$1.50\pm 0.20$
$\mathcal{B}(D^{0}\to K^{-}e^{+}\nu_{e})(\times 10^{-2})$	$3.549\pm 0.052$	$3.52\pm 0.02$	$3.52\pm 0.03$	$3.52\pm 0.03$	$3.52\pm 0.02$
$\mathcal{B}(D^{0}\to\pi^{-}e^{+}\nu_{e})(\times 10^{-3})$	$2.91\pm 0.08$	$2.95\pm 0.03$	$4.23\pm 1.03^{\dagger}$	$3.97\pm 0.09^{\dagger}$	$2.89\pm 0.06$
$\mathcal{B}(D^{+}_{s}\to\eta e^{+}\nu_{e})(\times 10^{-2})$	$2.32\pm 0.16$	$2.37\pm 0.11$	$2.34\pm 0.14$	$2.36\pm 0.12$	$2.32\pm 0.16$
$\mathcal{B}(D^{+}_{s}\to\eta^{\prime}e^{+}\nu_{e})(\times 10^{-3})$	$8.0\pm 1.4$	$9.05\pm 0.04$	$8.25\pm 1.13$	$8.04\pm 0.43$	$8.02\pm 1.38$
$\mathcal{B}(D^{+}_{s}\to K^{0}e^{+}\nu_{e})(\times 10^{-3})$	$3.4\pm 0.8$	$3.10\pm 0.08$	$3.56\pm 0.39$	$3.54\pm 0.12$	$3.40\pm 0.80$
$\mathcal{B}(D^{+}_{s}\to\pi^{0}e^{+}\nu_{e})(\times 10^{-5})$	$\cdots$	$1.51\pm 0.07$	$2.10\pm 0.56$	$1.96\pm 0.10$	$1.92\pm 0.13$	$2.65\pm 0.38$ Li:2020ylu
$\mathcal{B}(D^{+}\to\overline{K}^{0}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$8.76\pm 0.38$	$8.56\pm 0.06$	$8.69\pm 0.15$	$8.61\pm 0.06$	$8.61\pm 0.06$
$\mathcal{B}(D^{+}\to\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$3.50\pm 0.30$	$3.67\pm 0.05$	$5.32\pm 1.31^{\dagger}$	$4.96\pm 0.12^{\dagger}$	$3.64\pm 0.10$
$\mathcal{B}(D^{+}\to\eta\mu^{+}\nu_{\mu})(\times 10^{-3})$	$1.04\pm 0.22$	$1.11\pm 0.05$	$1.18\pm 0.07$	$1.17\pm 0.05$	$0.90\pm 0.08$	${}^{1.21\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Faustov:2019mqr}{\@@citephrase{(}}{\@@citephrase{)}}}}}_{0.75\pm 0.15\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Leng:2020fei}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu})(\times 10^{-4})$	$\cdots$	$2.42\pm 0.13$	$2.10\pm 0.33$	$1.96\pm 0.13$	$1.41\pm 0.19$	${}^{2.11\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Faustov:2019mqr}{\@@citephrase{(}}{\@@citephrase{)}}}}}_{1.06\pm 0.20\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Leng:2020fei}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{0}\to K^{-}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$3.41\pm 0.08$	$3.41\pm 0.02$	$3.44\pm 0.05$	$3.43\pm 0.02$	$3.43\pm 0.02$
$\mathcal{B}(D^{0}\to\pi^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$2.67\pm 0.24$	$2.89\pm 0.02$	$4.17\pm 1.01^{\dagger}$	$3.90\pm 0.09^{\dagger}$	$2.85\pm 0.06$
$\mathcal{B}(D^{+}_{s}\to\eta\mu^{+}\nu_{\mu})(\times 10^{-2})$	$2.4\pm 1.0$	$2.30\pm 0.10$	$2.30\pm 0.17$	$2.31\pm 0.12$	$2.26\pm 0.16$
$\mathcal{B}(D^{+}_{s}\to\eta^{\prime}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$1.1\pm 1.0$	$0.86\pm 0.03$	$0.79\pm 0.11$	$0.77\pm 0.04$	$0.76\pm 0.13$
$\mathcal{B}(D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$\cdots$	$3.01\pm 0.08$	$3.51\pm 0.38$	$3.46\pm 0.11$	$3.33\pm 0.78$	${}^{3.9\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Faustov:2019mqr}{\@@citephrase{(}}{\@@citephrase{)}}}}}_{3.85\pm 0.76\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Leng:2020fei}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$\cdots$	$1.48\pm 0.07$	$2.09\pm 0.53$	$1.93\pm 0.10$	$1.89\pm 0.13$
$\mathcal{B}(D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau})(\times 10^{-10})$	$\cdots$	$3.45\pm 0.21$	$160.34\pm 149.53$	$4.20\pm 0.26$	$4.08\pm 0.34$	$(27\sim 36)\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Li:2020ylu}{\@@citephrase{(}}{\@@citephrase{)}}}}$
$R^{\mu/e}(D^{+}\to\overline{K}^{0}\ell^{+}\nu_{\ell})$		$0.969$	$0.984\pm 0.013$	$0.974$	$0.974$
$R^{\mu/e}(D^{+}\to\pi^{0}\ell^{+}\nu_{\ell})$		$0.977$	$1.009\pm 0.026$	$0.984$	$0.984$
$R^{\mu/e}(D^{+}\to\eta\ell^{+}\nu_{\ell})$		$0.967$	$0.984\pm 0.014$	$0.973$	$0.973$
$R^{\mu/e}(D^{+}\to\eta^{\prime}\ell^{+}\nu_{\ell})$		$0.935$	$0.948\pm 0.012$	$0.940$	$0.940$
$R^{\mu/e}(D^{0}\to K^{-}\ell^{+}\nu_{\ell})$		$0.969$	$0.984\pm 0.013$	$0.974$	$0.974$
$R^{\mu/e}(D^{0}\to\pi^{-}\ell^{+}\nu_{\ell})$		$0.977$	$1.008\pm 0.026$	$0.984$	$0.984$
$R^{\mu/e}(D^{+}_{s}\to\eta\ell^{+}\nu_{\ell})$		$0.971$	$0.987\pm 0.013$	$0.976$	$0.976$
$R^{\mu/e}(D^{+}_{s}\to\eta^{\prime}\ell^{+}\nu_{\ell})$		$0.946$	$0.958\pm 0.011$	$0.952$	$0.952$
$R^{\mu/e}(D^{+}_{s}\to K^{0}\ell^{+}\nu_{\ell})$		$0.973$	$0.992\pm 0.016$	$0.978$	$0.978$
$R^{\mu/e}(D^{+}_{s}\to\pi^{0}\ell^{+}\nu_{\ell})$		$0.980$	$1.010\pm 0.025$	$0.985$	$0.985$

•

Results in $C_{1}$ case: From the third column of Tab. 2, one can see that the SU(3) flavor symmetry predictions of $\mathcal{B}(D\to P\ell^{+}\nu_{\ell})$ in the $C_{1}$ case are entirely consistent with all present experiential data. The not yet measured branching ratios of the $D^{+}_{s}\to\pi^{0}e^{+}\nu_{e}$ , $D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu}$ , $D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu}$ and $D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}$ decays are predicted on the order of $\mathcal{O}(10^{-3}-10^{-5})$ , nevertheless, $\mathcal{B}(D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau})$ is predicted on the order of $\mathcal{O}(10^{-10})$ due to its narrow phase space and $(q^{2}-m_{\tau}^{2})^{2}$ suppression of the differential branching ratios in Eq. (71).
•

Results in $C_{2,3}$ cases: The numerical results in $C_{2,3}$ cases are similar. The experimental upper limits of $\mathcal{B}(D^{+}\to\pi^{0}\ell^{+}\nu_{\ell})$ and $\mathcal{B}(D^{0}\to\pi^{-}\ell^{+}\nu_{\ell})$ have not been used to constrain the predictions of $\mathcal{B}(D\to P\ell^{+}\nu_{\ell})$ , since the upper limits of the predictions of $\mathcal{B}(D^{+}\to\pi^{0}\ell^{+}\nu_{\ell})$ and $\mathcal{B}(D^{0}\to\pi^{-}\ell^{+}\nu_{\ell})$ by the SU(3) flavor symmetry in $C_{2,3}$ cases are slightly larger than their experimental data. Other SU(3) flavor symmetry predictions are consistent with their experimental data within $2\sigma$ errors.
•

Results in $C_{4}$ case: As given in the sixth column of Tab. 2, if considering both the hadronic momentum-transfer $q^{2}$ dependence of the form factors and the SU(3) flavor breaking contributions, all SU(3) flavor symmetry predictions are consistent with their experimental data within $2\sigma$ errors. For some decays, the errors of the theoretical predictions are much smaller than ones of their experimental data.
•

The previous predictions for the not yet measured branching ratios are listed in the last column of Tab. 2, our predictions are in the same order of magnitude as previous ones for the $D\to Pe^{+}\nu_{e},P\mu^{+}\nu_{\mu}$ decays. And our prediction of $\mathcal{B}(D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau})$ is one order smaller than previous one in Ref. Li:2020ylu .
•

In addition, the lepton flavor universality parameters $R^{\mu/e}(D\to P\ell^{+}\nu_{\ell})$ are also given in Tab. 2, since many terms are canceled in the ratios, these predictions are quite accurate, and all processes have similar results.

For the $q^{2}$ dependence of the differential branching ratios of the $D\to P\ell^{+}\nu_{\ell}$ decays with present experimental bounds, we only show the not yet measured processes $D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu}$ and $D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau}$ in Fig. 1.

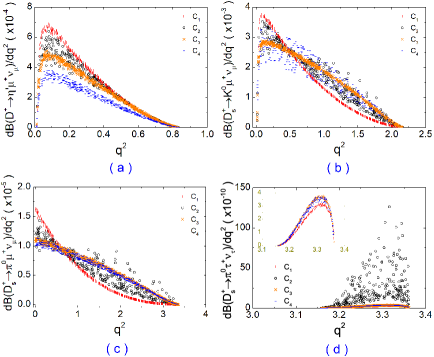
Refer to caption — Figure 1: The $q^{2}$ dependence of the differential branching ratios for some $D\to P\ell^{+}\nu_{\ell}$ with present experimental bounds.

We do not show $d\mathcal{B}(D^{+}_{s}\to\pi^{0}e^{+}\nu_{e})/dq^{2}$ , since it is similar to $d\mathcal{B}(D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu})/dq^{2}$ in Fig. 1 (c). From Fig. 1, one can see that present experimental measurements give quite strong bounds on the differential branching ratios of $D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu}$ and $D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau}$ decays in the $C_{1}$ , $C_{3}$ and $C_{4}$ cases as well as $D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}$ decays in the $C_{1}$ and $C_{3}$ cases, and all predictions of the four differential branching ratios in the $C_{2}$ case have large error due to the form factor choice. Comparing with $d\mathcal{B}(D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu})/dq^{2}$ in Fig. 1 (c), as shown in Fig. 1 (d), $d\mathcal{B}(D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau})/dq^{2}$ is suppressed about the order of $\mathcal{O}(10^{-4})$ by $m_{\tau}$ .

The forward-backward asymmetries $A^{\ell}_{FB}$ , the lepton-side convexity parameters $C^{\ell}_{F}$ , the longitudinal polarizations of the final charged leptons $P^{\ell}_{L}$ and the transverse polarizations of the final charged leptons $P^{\ell}_{T}$ with two ways of integration for the $D\to P\ell^{+}\nu_{\ell}$ decays could also be obtained. These predictions are very accurate, and they are similar to each other in the four $C_{1,2,3,4}$ cases. So we only give the predictions within the $C_{3}$ case in Tab. 3 for examples. From Tab. 3, one can see that the predictions are obviously different between two ways of $q^{2}$ integration, and the slight difference in the same way of $q^{2}$ integration is due to the different decay phase spaces. For displaying the differences between the $D\to Pe^{+}\nu_{e}$ and $D\to P\mu^{+}\nu_{\mu}$ decays, we take $D^{+}_{s}\to K^{0}e^{+}\nu_{e}$ and $D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}$ as examples. The differential forward-backward asymmetries, the differential lepton-side convexity parameters, the differential longitudinal lepton polarizations and the differential transverse lepton polarizations of $D^{+}_{s}\to K^{0}e^{+}\nu_{e}$ and $D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}$ decays within the $C_{3}$ case are displayed in Fig. 2. And one can see that differential observables between $\ell=e$ and $\ell=\mu$ are obviously different, specially in the low and high $q^{2}$ ranges.

Table 3: Quantities

\langle X\rangle

and

\overline{X}

of the

D\to P\ell^{+}\nu

C_{3}

case.

Decay modes	$\langle A^{\ell}_{FB}\rangle$	${}^{\overline{A^{e}_{FB}}(\times 10^{-6})}_{\overline{A^{\mu,\tau}_{FB}}(\times 10^{-2})}$	$\langle C^{\ell}_{F}\rangle$	$\overline{C^{\ell}_{F}}$	$\langle P^{\ell}_{L}\rangle$	$\overline{P^{\ell}_{L}}$	$\langle P^{\ell}_{T}\rangle$	${}^{\overline{P^{e}_{T}}(\times 10^{-3})}_{\overline{P^{\mu,\tau}_{T}}}$
$D^{+}\to\overline{K}^{0}e^{+}\nu_{e}$	$-0.087$	$-3.254\pm 0.001$	$-1.239$	$-1.500$	$0.768$	$1.000$	$-0.273$	$-2.442\pm 0.001$
$D^{+}\to\pi^{0}e^{+}\nu_{e}$	$-0.083$	$-2.054\pm 0.000$	$-1.252$	$-1.500$	$0.780$	$1.000$	$-0.260$	$-1.730\pm 0.000$
$D^{+}\to\eta e^{+}\nu_{e}$	$-0.087$	$-3.476\pm 0.001$	$-1.239$	$-1.500$	$0.768$	$1.000$	$-0.273$	$-2.490\pm 0.000$
$D^{+}\to\eta^{\prime}e^{+}\nu_{e}$	$-0.093$	$-7.075\pm 0.003$	$-1.222$	$-1.500$	$0.753$	$1.000$	$-0.290$	$-3.890\pm 0.001$
$D^{0}\to K^{-}e^{+}\nu_{e}$	$-0.087$	$-3.259\pm 0.001$	$-1.239$	$-1.500$	$0.768$	$1.000$	$-0.273$	$-2.446\pm 0.001$
$D^{0}\to\pi^{-}e^{+}\nu_{e}$	$-0.083$	$-2.077\pm 0.000$	$-1.252$	$-1.500$	$0.779$	$1.000$	$-0.260$	$-1.751\pm 0.000$
$D^{+}_{s}\to\eta e^{+}\nu_{e}$	$-0.086$	$-3.033\pm 0.001$	$-1.242$	$-1.500$	$0.770$	$1.000$	$-0.270$	$-2.300\pm 0.001$
$D^{+}_{s}\to\eta^{\prime}e^{+}\nu_{e}$	$-0.091$	$-5.829\pm 0.003$	$-1.226$	$-1.500$	$0.757$	$1.000$	$-0.286$	$-3.484\pm 0.001$
$D^{+}_{s}\to K^{0}e^{+}\nu_{e}$	$-0.085$	$-2.814\pm 0.001$	$-1.245$	$-1.500$	$0.773$	$1.000$	$-0.267$	$-2.118\pm 0.000$
$D^{+}_{s}\to\pi^{0}e^{+}\nu_{e}$	$-0.082$	$-1.850\pm 0.001$	$-1.254$	$-1.500$	$0.781$	$1.000$	$-0.258$	$-1.634\pm 0.001$
$D^{+}\to\overline{K}^{0}\mu^{+}\nu_{\mu}$	$-0.226$	$-4.278\pm 0.001$	$-0.822$	$-1.352$	$0.394$	$0.851$	$-0.655$	$-0.414$
$D^{+}\to\pi^{0}\mu^{+}\nu_{\mu}$	$-0.201$	$-2.810\pm 0.000$	$-0.897$	$-1.405$	$0.462$	$0.907$	$-0.602$	$-0.310$
$D^{+}\to\eta\mu^{+}\nu_{\mu}$	$-0.227$	$-4.490\pm 0.001$	$-0.819$	$-1.347$	$0.391$	$0.846$	$-0.657$	$-0.419$
$D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu}$	$-0.263$	$-8.097\pm 0.003$	$-0.708$	$-1.213$	$0.287$	$0.703$	$-0.725$	$-0.581$
$D^{0}\to K^{-}\mu^{+}\nu_{\mu}$	$-0.226$	$-4.285\pm 0.001$	$-0.822$	$-1.352$	$0.393$	$0.850$	$-0.656$	$-0.414$
$D^{0}\to\pi^{-}\mu^{+}\nu_{\mu}$	$-0.201$	$-2.844\pm 0.001$	$-0.895$	$-1.407$	$0.461$	$0.910$	$-0.603$	$-0.313$
$D^{+}_{s}\to\eta\mu^{+}\nu_{\mu}$	$-0.221$	$-4.001\pm 0.001$	$-0.836$	$-1.364$	$0.406$	$0.864$	$-0.646$	$-0.394$
$D^{+}_{s}\to\eta^{\prime}\mu^{+}\nu_{\mu}$	$-0.254$	$-6.952\pm 0.003$	$-0.736$	$-1.254$	$0.314$	$0.747$	$-0.709$	$-0.540$
$D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}$	$-0.215$	$-3.701\pm 0.001$	$-0.856$	$-1.377$	$0.425$	$0.879$	$-0.632$	$-0.367$
$D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu}$	$-0.197$	$-2.571\pm 0.001$	$-0.907$	$-1.417$	$0.472$	$0.920$	$-0.594$	$-0.295$
$D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau}$	$-0.281$	$-27.429\pm 0.105$	$-0.211\pm 0.003$	$-0.212\pm 0.003$	$-0.868\pm 0.001$	$-0.873\pm 0.001$	$-0.447\pm 0.002$	$-0.437\pm 0.002$

III.2 $D\to V\ell^{+}\nu_{\ell}$ decays

The hadronic helicity amplitudes for the $D\rightarrow V\ell^{+}\nu_{\ell}$ decays are given in Tab. 4. There are four nonperturbative parameters $B_{1,2,3,4}$ in the $D\rightarrow V\ell^{+}\nu_{\ell}$ decay modes. If neglecting the SU(3) flavor breaking $c^{V}_{1}$ and $c^{V}_{2}$ terms, $B_{1}=B_{2}=B_{3}=B_{4}=c^{V}_{0}$ , and then all hadronic helicity amplitudes of $D\rightarrow V\ell^{+}\nu_{\ell}$ are related by only one parameter $c^{V}_{0}$ .

Table 4: The hadronic helicity amplitudes for

D\to V\ell^{+}\nu

decays including both the SU(3) flavor symmetry and the SU(3) flavor breaking contributions.

B_{1}=c^{V}_{0}+c^{V}_{1}-2c^{V}_{2}

B_{2}=c^{V}_{0}-2c^{V}_{1}-2c^{V}_{2}

B_{3}=c^{V}_{0}+c^{V}_{1}+c^{V}_{2}

B_{4}=c^{V}_{0}-2c^{V}_{1}+c^{V}_{2}

. If neglecting the SU(3) flavor breaking

c^{V}_{1}

and

c^{V}_{2}

terms,

B_{1}=B_{2}=B_{3}=B_{4}=c^{V}_{0}

Hadronic helicity amplitudes	SU(3) IRA amplitudes
$H(D^{0}\to K^{*-}\ell^{+}\nu_{\ell})$	$B_{1}V^{*}_{cs}$
$H(D^{+}\to\overline{K}^{*0}\ell^{+}\nu_{\ell})$	$B_{1}V^{*}_{cs}$
$H(D^{+}_{s}\to\phi\ell^{+}\nu_{\ell})$	$\big{(}-cos\theta_{V}\sqrt{2/3}-sin\theta_{V}/\sqrt{3}\big{)}B_{2}V^{*}_{cs}$
$H(D^{+}_{s}\to\omega\ell^{+}\nu_{\ell})$	$\big{(}-sin\theta_{V}\sqrt{2/3}+cos\theta_{V}/\sqrt{3}\big{)}B_{2}V^{*}_{cs}$
$H(D^{0}\to\rho^{-}\ell^{+}\nu_{\ell})$	$B_{3}V^{*}_{cd}$
$H(D^{+}\to\rho^{0}\ell^{+}\nu_{\ell})$	$-\frac{1}{\sqrt{2}}B_{3}V^{*}_{cd}$
$H(D^{+}\to\phi\ell^{+}\nu_{\ell})$	$\big{(}cos\theta_{V}/\sqrt{6}-sin\theta_{V}/\sqrt{3}\big{)}B_{3}V^{*}_{cd}$
$H(D^{+}\to\omega\ell^{+}\nu_{\ell})$	$\big{(}sin\theta_{V}/\sqrt{6}+cos\theta_{V}/\sqrt{3}\big{)}B_{3}V^{*}_{cd}$
$H(D^{+}_{s}\to K^{*0}\ell^{+}\nu_{\ell})$	$B_{4}V^{*}_{cd}$

Among the $D\rightarrow V\ell^{+}\nu_{\ell}$ decay modes, 13 branching ratios have been measured, and 2 branching ratios have been upper limited by the experiments. The experimental data with $2\sigma$ errors are listed in the second column of Tab. 5. Now we use the listed experimental data to constrain the parameters $B_{i}$ and then predict other not yet measured and not yet well measured branching ratios. The numerical results of $\mathcal{B}(D\to V\ell^{+}\nu_{\ell})$ in the $C_{1}$ , $C_{2}$ , $C_{3}$ and $C_{4}$ cases are given in the third, forth, fifth and sixth columns of Tab. 5, respectively.

Table 5: Branching ratios of the

D\to V\ell^{+}\nu

within

2\sigma

errors. ^†The experimental data of

\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e})

and

\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu})

from PDG PDG2022 are not used in the

C_{1,2,3}

cases.

Branching ratios	Exp. data	Ones in $C_{1}$	Ones in $C_{2}$	Ones in $C_{3}$	Ones in $C_{4}$
$\mathcal{B}(D^{+}\to\overline{K}^{*0}e^{+}\nu_{e})(\times 10^{-2})$	$5.40\pm 0.20$	$5.44\pm 0.15$	$5.42\pm 0.18$	$5.36\pm 0.08$	$5.44\pm 0.16$
$\mathcal{B}(D^{+}\to\rho^{0}e^{+}\nu_{e})(\times 10^{-3})$	$2.18^{+0.34}_{-0.50}$	$2.31\pm 0.07$	$2.39\pm 0.13$	$2.33\pm 0.05$	$1.83\pm 0.15$
$\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e})(\times 10^{-3})$	$1.69\pm 0.22$	$2.24\pm 0.07^{\dagger}$	$2.33\pm 0.12^{\dagger}$	$2.26\pm 0.04^{\dagger}$	$1.77\pm 0.14$
$\mathcal{B}(D^{+}\to\phi e^{+}\nu_{e})(\times 10^{-7})$	$<130$	$3.13\pm 0.12$	$3.11\pm 0.19$	$3.07\pm 0.07$	$2.38\pm 0.23$
$\mathcal{B}(D^{0}\to K^{*-}e^{+}\nu_{e})(\times 10^{-2})$	$2.15\pm 0.32$	$2.12\pm 0.09$	$2.13\pm 0.10$	$2.08\pm 0.06$	$2.13\pm 0.10$
$\mathcal{B}(D^{0}\to\rho^{-}e^{+}\nu_{e})(\times 10^{-3})$	$1.50\pm 0.24$	$1.79\pm 0.08$	$1.86\pm 0.11$	$1.80\pm 0.06$	$1.41\pm 0.13$
$\mathcal{B}(D^{+}_{s}\to\phi e^{+}\nu_{e})(\times 10^{-2})$	$2.39\pm 0.32$	$2.46\pm 0.12$	$2.43\pm 0.14$	$2.40\pm 0.10$	$2.39\pm 0.32$
$\mathcal{B}(D^{+}_{s}\to\omega e^{+}\nu_{e})(\times 10^{-5})$	$<200$	$2.45\pm 0.13$	$2.56\pm 0.20$	$2.47\pm 0.10$	$2.49\pm 0.38$
$\mathcal{B}(D^{+}_{s}\to K^{*0}e^{+}\nu_{e})(\times 10^{-3})$	$2.15\pm 0.56$	$2.17\pm 0.10$	$2.25\pm 0.13$	$2.17\pm 0.08$	$2.15\pm 0.56$
$\mathcal{B}(D^{+}\to\overline{K}^{*0}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$5.27\pm 0.30$	$5.12\pm 0.15$	$5.13\pm 0.16$	$5.05\pm 0.08$	$5.12\pm 0.15$
$\mathcal{B}(D^{+}\to\rho^{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$2.4\pm 0.8$	$2.19\pm 0.07$	$2.29\pm 0.13$	$2.22\pm 0.04$	$1.74\pm 0.14$
$\mathcal{B}(D^{+}\to\omega\mu^{+}\nu_{\mu})(\times 10^{-3})$	$1.77\pm 0.42$	$2.13\pm 0.06$	$2.23\pm 0.12$	$2.15\pm 0.04$	$1.68\pm 0.13$
$\mathcal{B}(D^{+}\to\phi\mu^{+}\nu_{\mu})(\times 10^{-7})$	$\cdots$	$2.89\pm 0.11$	$2.89\pm 0.17$	$2.84\pm 0.07$	$2.20\pm 0.21$
$\mathcal{B}(D^{0}\to K^{*-}\mu^{+}\nu_{\mu})(\times 10^{-2})$	$1.89\pm 0.48$	$1.99\pm 0.09$	$2.01\pm 0.09$	$1.96\pm 0.06$	$2.01\pm 0.10$
$\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$1.35\pm 0.26$	$1.70\pm 0.07^{\dagger}$	$1.78\pm 0.11^{\dagger}$	$1.72\pm 0.06^{\dagger}$	$1.34\pm 0.13$
$\mathcal{B}(D^{+}_{s}\to\phi\mu^{+}\nu_{\mu})(\times 10^{-2})$	$1.9\pm 1.0$	$2.30\pm 0.12$	$2.29\pm 0.12$	$2.25\pm 0.09$	$2.24\pm 0.30$
$\mathcal{B}(D^{+}_{s}\to\omega\mu^{+}\nu_{\mu})(\times 10^{-5})$	$\cdots$	$2.34\pm 0.12$	$2.47\pm 0.19$	$2.37\pm 0.09$	$2.38\pm 0.36$
$\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$\cdots$	$2.06\pm 0.10$	$2.15\pm 0.13$	$2.07\pm 0.08$	$2.05\pm 0.53$
$R^{\mu/e}(D^{+}\to\overline{K}^{*0}\ell^{+}\nu_{\ell})$		$0.939\pm 0.001$	$0.944\pm 0.004$	$0.941\pm 0.001$	$0.941\pm 0.001$
$R^{\mu/e}(D^{+}\to\rho^{0}\ell^{+}\nu_{\ell})$		$0.950\pm 0.001$	$0.956\pm 0.005$	$0.952\pm 0.001$	$0.952\pm 0.001$
$R^{\mu/e}(D^{+}\to\omega\ell^{+}\nu_{\ell})$		$0.950\pm 0.001$	$0.956\pm 0.005$	$0.952\pm 0.001$	$0.952\pm 0.001$
$R^{\mu/e}(D^{+}\to\phi\ell^{+}\nu_{\ell})$		$0.923\pm 0.001$	$0.928\pm 0.005$	$0.925\pm 0.001$	$0.925\pm 0.001$
$R^{\mu/e}(D^{0}\to K^{*-}\ell^{+}\nu_{\ell})$		$0.939\pm 0.001$	$0.944\pm 0.004$	$0.941\pm 0.001$	$0.941\pm 0.001$
$R^{\mu/e}(D^{0}\to\rho^{-}\ell^{+}\nu_{\ell})$		$0.950\pm 0.001$	$0.956\pm 0.005$	$0.952\pm 0.001$	$0.952\pm 0.001$
$R^{\mu/e}(D^{+}_{s}\to\phi\ell^{+}\nu_{\ell})$		$0.937\pm 0.001$	$0.942\pm 0.004$	$0.939\pm 0.001$	$0.939\pm 0.001$
$R^{\mu/e}(D^{+}_{s}\to\omega\ell^{+}\nu_{\ell})$		$0.957\pm 0.001$	$0.963\pm 0.004$	$0.959\pm 0.001$	$0.959\pm 0.001$
$R^{\mu/e}(D^{+}_{s}\to K^{*0}\ell^{+}\nu_{\ell})$		$0.949\pm 0.001$	$0.955\pm 0.005$	$0.951\pm 0.001$	$0.951\pm 0.001$

The results in the $C_{1}$ , $C_{2}$ and $C_{3}$ cases are very similar. Since the SU(3) flavor symmetry predictions of $\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e})$ and $\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu})$ are slightly larger than their experimental data within $2\sigma$ errors in the three cases, we do not use them to constrain the nonperturbative parameter $c^{V}_{0}$ . One can see that the prediction of $\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu})$ is agree with its experimental data within $3\sigma$ errors, nevertheless, the prediction of $\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e})$ still slightly larger than experimental data within $3\sigma$ errors. $\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})$ and $\mathcal{B}(D^{+}_{s}\to\omega e^{+}\nu_{e},\omega\mu^{+}\nu_{\mu})$ are predicted on the order of $\mathcal{O}(10^{-3})$ and $\mathcal{O}(10^{-5})$ , respectively. And they could be measured in BESIII, LHCb and BelleII experiments. In the $C_{4}$ case, as given in the sixth column of Tab. 5, after considering both the hadronic momentum-transfer $q^{2}$ dependence of the form factors and the SU(3) flavor breaking contributions, all SU(3) flavor symmetry predictions are consistent with their experimental data within $2\sigma$ errors. Among relevant not yet measured decays, $\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})$ is calculated in the SM using light-cone sum rules Leng:2020fei and in the relativistic quark model Faustov:2019mqr , $\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})=(2.23\pm 0.32)\times 10^{-3}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Leng:2020fei}{\@@citephrase{(}}{\@@citephrase{)}}}}\leavevmode\nobreak\ \mbox{and}\leavevmode\nobreak\ 2.0\times 10^{-3}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Faustov:2019mqr}{\@@citephrase{(}}{\@@citephrase{)}}}}$ , and our predictions of $\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})$ in the $C_{1}$ , $C_{2}$ , $C_{3}$ and $C_{4}$ cases are coincident with previous ones in Refs. Leng:2020fei ; Faustov:2019mqr . In addition, the lepton flavor universality parameters $R^{\mu/e}(D\to V\ell^{+}\nu_{\ell})$ are also given in Tab. 5. Since many terms are canceled in the ratios, these predictions of the lepton flavor universality parameters are quite accurate, and our predictions in all four cases are similar to each other.

For the $q^{2}$ dependence of the differential branching ratios of the $D\to V\ell^{+}\nu_{\ell}$ decays with present experimental bounds, we only show the not yet measured processes $D^{+}\to\phi\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to\omega\mu^{+}\nu_{\mu}$ and $D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu}$ in Fig. 4. The differential branching ratios of $D^{+}\to\phi e^{+}\nu_{e}\leavevmode\nobreak\ (D^{+}_{s}\to\omega e^{+}\nu_{e})$ is similar to $D^{+}\to\phi\mu^{+}\nu_{\mu}\leavevmode\nobreak\ (D^{+}_{s}\to\omega\mu^{+}\nu_{\mu})$ , so we do not shown them in Fig. 4. From Fig. 4, one can see that present experiment data give quite strong bounds on all differential branching ratios of $D^{+}\to\phi\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to\omega\mu^{+}\nu_{\mu}$ and $D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu}$ decays in the $C_{1}$ , $C_{2}$ and $C_{3}$ cases. The prediction of $d\mathcal{B}(D^{+}\to\phi\mu^{+}\nu_{\mu})/dq^{2}$ in the $C_{4}$ case could be distinguished from ones in the $C_{1,2,3}$ cases within the middle range of $q^{2}$ . And the error of $d\mathcal{B}(D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu})/dq^{2}$ in the $C_{4}$ case is obviously larger than ones in $C_{1,2,3}$ cases.

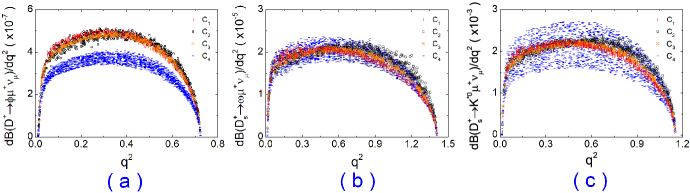
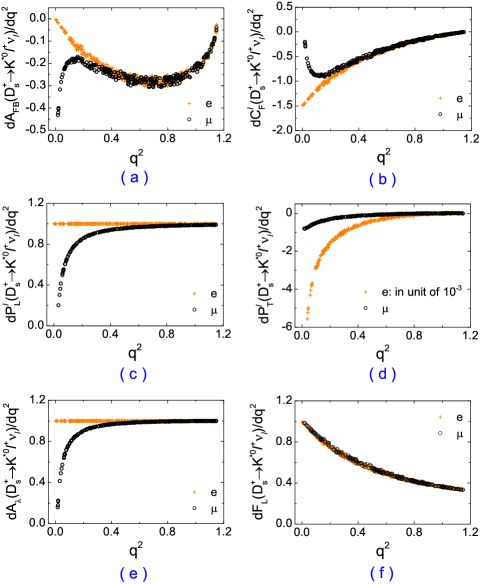
The forward-backward asymmetries $A^{\ell}_{FB}$ , the lepton-side convexity parameters $C^{\ell}_{F}$ , the longitudinal polarizations $P^{\ell}_{L}$ , the transverse polarizations $P^{\ell}_{T}$ , the lepton spin asymmetries $A_{\lambda}$ and the longitudinal polarization fractions of the final vector mesons $F_{L}$ with two ways of integration have also been predicted in the four cases. Since many theoretical uncertainties are canceled in the ratios, these predictions are very accurate. These predictions are similar to each other in the four cases, and we only list the results in the $C_{3}$ case in Tabs. 7-7 for examples. One can see that the predictions are obviously different between two ways of $q^{2}$ integration, and they are also quite different between $D\to Ve^{+}\nu_{e}$ and $D\to V\mu^{+}\nu_{\mu}$ decays.

Table 6: The forward-backward asymmetries

A^{\ell}_{FB}

, the lepton-side convexity parameters

C^{\ell}_{F}

, the longitudinal polarizations

P^{\ell}_{L}

of the

D\to V\ell^{+}\nu

decays in the

C_{3}

case.

Decay modes	$\langle A^{\ell}_{FB}\rangle$	$\overline{A^{\ell}_{FB}}$	$\langle C^{\ell}_{F}\rangle$	$\overline{C^{\ell}_{F}}$	$\langle P^{\ell}_{L}\rangle$	$\overline{P^{\ell}_{L}}$
$D^{+}\to\overline{K}^{*0}e^{+}\nu_{e}$	$-0.125\pm 0.006$	$-0.190\pm 0.020$	$-1.046\pm 0.019$	$-0.500\pm 0.032$	$0.786\pm 0.004$	$1.000$
$D^{+}\to\rho^{0}e^{+}\nu_{e}$	$-0.130\pm 0.008$	$-0.222\pm 0.024$	$-1.052\pm 0.023$	$-0.496\pm 0.041$	$0.789\pm 0.004$	$1.000$
$D^{+}\to\omega e^{+}\nu_{e}$	$-0.130\pm 0.008$	$-0.220\pm 0.024$	$-1.052\pm 0.023$	$-0.497\pm 0.041$	$0.789\pm 0.004$	$1.000$
$D^{+}\to\phi e^{+}\nu_{e}$	$-0.121\pm 0.005$	$-0.164\pm 0.017$	$-1.037\pm 0.015$	$-0.500\pm 0.025$	$0.784\pm 0.003$	$1.000$
$D^{0}\to K^{*-}e^{+}\nu_{e}$	$-0.125\pm 0.006$	$-0.191\pm 0.020$	$-1.046\pm 0.019$	$-0.500\pm 0.032$	$0.786\pm 0.004$	$1.000$
$D^{0}\to\rho^{-}e^{+}\nu_{e}$	$-0.130\pm 0.008$	$-0.221\pm 0.024$	$-1.052\pm 0.023$	$-0.497\pm 0.041$	$0.789\pm 0.004$	$1.000$
$D^{+}_{s}\to\phi e^{+}\nu_{e}$	$-0.122\pm 0.006$	$-0.176\pm 0.018$	$-1.043\pm 0.016$	$-0.500\pm 0.028$	$0.786\pm 0.003$	$1.000$
$D^{+}_{s}\to\omega e^{+}\nu_{e}$	$-0.130\pm 0.008$	$-0.229\pm 0.025$	$-1.057\pm 0.025$	$-0.496\pm 0.044$	$0.790\pm 0.004$	$1.000$
$D^{+}_{s}\to K^{*0}e^{+}\nu_{e}$	$-0.128\pm 0.007$	$-0.207\pm 0.022$	$-1.049\pm 0.021$	$-0.495\pm 0.036$	$0.789\pm 0.004$	$1.000$
$D^{+}\to\overline{K}^{*0}\mu^{+}\nu_{\mu}$	$-0.284\pm 0.009$	$-0.226\pm 0.019$	$-0.466\pm 0.021$	$-0.395\pm 0.028$	$0.514\pm 0.017$	$0.886\pm 0.002$
$D^{+}\to\rho^{0}\mu^{+}\nu_{\mu}$	$-0.292\pm 0.011$	$-0.252\pm 0.023$	$-0.491\pm 0.027$	$-0.405\pm 0.037$	$0.524\pm 0.020$	$0.903\pm 0.002$
$D^{+}\to\omega\mu^{+}\nu_{\mu}$	$-0.292\pm 0.011$	$-0.251\pm 0.022$	$-0.490\pm 0.027$	$-0.405\pm 0.037$	$0.524\pm 0.020$	$0.902\pm 0.002$
$D^{+}\to\phi\mu^{+}\nu_{\mu}$	$-0.277\pm 0.008$	$-0.206\pm 0.016$	$-0.433\pm 0.016$	$-0.376\pm 0.021$	$0.503\pm 0.014$	$0.864\pm 0.002$
$D^{0}\to K^{*-}\mu^{+}\nu_{\mu}$	$-0.284\pm 0.009$	$-0.226\pm 0.019$	$-0.466\pm 0.021$	$-0.395\pm 0.029$	$0.514\pm 0.017$	$0.886\pm 0.002$
$D^{0}\to\rho^{-}\mu^{+}\nu_{\mu}$	$-0.292\pm 0.011$	$-0.252\pm 0.023$	$-0.490\pm 0.027$	$-0.405\pm 0.037$	$0.524\pm 0.020$	$0.902\pm 0.002$
$D^{+}_{s}\to\phi\mu^{+}\nu_{\mu}$	$-0.277\pm 0.008$	$-0.213\pm 0.017$	$-0.459\pm 0.018$	$-0.391\pm 0.024$	$0.514\pm 0.015$	$0.882\pm 0.002$
$D^{+}_{s}\to\omega\mu^{+}\nu_{\mu}$	$-0.291\pm 0.012$	$-0.257\pm 0.024$	$-0.509\pm 0.029$	$-0.414\pm 0.041$	$0.531\pm 0.021$	$0.913\pm 0.002$
$D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu}$	$-0.286\pm 0.010$	$-0.239\pm 0.021$	$-0.485\pm 0.024$	$-0.402\pm 0.033$	$0.525\pm 0.018$	$0.900\pm 0.002$

Table 7: The transverse polarizations

P^{\ell}_{T}

, the lepton spin asymmetries

A_{\lambda}

and the longitudinal polarization fractions of the final vector mesons

F_{L}

of the

D\to V\ell^{+}\nu

decays in the

C_{3}

case.

Decay modes	$\langle P^{\ell}_{T}\rangle$	${}^{\overline{P^{e}_{T}}(\times 10^{-3})}_{\overline{P^{\mu}_{T}}}$	$\langle A_{\lambda}\rangle$	$\overline{A_{\lambda}}$	$\langle F_{L}\rangle$	$\overline{F_{L}}$
$D^{+}\to\overline{K}^{*0}e^{+}\nu_{e}$	$-0.251\pm 0.004$	$-1.205\pm 0.066$	$1.000$	$1.000$	$0.905\pm 0.010$	$0.556\pm 0.014$
$D^{+}\to\rho^{0}e^{+}\nu_{e}$	$-0.249\pm 0.005$	$-1.040\pm 0.072$	$1.000$	$1.000$	$0.907\pm 0.012$	$0.554\pm 0.018$
$D^{+}\to\omega e^{+}\nu_{e}$	$-0.249\pm 0.005$	$-1.049\pm 0.073$	$1.000$	$1.000$	$0.907\pm 0.012$	$0.554\pm 0.018$
$D^{+}\to\phi e^{+}\nu_{e}$	$-0.254\pm 0.003$	$-1.417\pm 0.061$	$1.000$	$1.000$	$0.902\pm 0.008$	$0.556\pm 0.011$
$D^{0}\to K^{*-}e^{+}\nu_{e}$	$-0.251\pm 0.004$	$-1.206\pm 0.067$	$1.000$	$1.000$	$0.905\pm 0.010$	$0.556\pm 0.014$
$D^{0}\to\rho^{-}e^{+}\nu_{e}$	$-0.249\pm 0.005$	$-1.045\pm 0.073$	$1.000$	$1.000$	$0.907\pm 0.012$	$0.554\pm 0.018$
$D^{+}_{s}\to\phi e^{+}\nu_{e}$	$-0.251\pm 0.004$	$-1.255\pm 0.060$	$1.000$	$1.000$	$0.904\pm 0.009$	$0.555\pm 0.012$
$D^{+}_{s}\to\omega e^{+}\nu_{e}$	$-0.247\pm 0.005$	$-0.953\pm 0.071$	$1.000$	$1.000$	$0.908\pm 0.013$	$0.554\pm 0.020$
$D^{+}_{s}\to K^{*0}e^{+}\nu_{e}$	$-0.248\pm 0.004$	$-1.075\pm 0.066$	$1.000$	$1.000$	$0.905\pm 0.011$	$0.553\pm 0.016$
$D^{+}\to\overline{K}^{*0}\mu^{+}\nu_{\mu}$	$-0.454\pm 0.022$	$-0.156\pm 0.012$	$0.935\pm 0.005$	$0.928\pm 0.002$	$0.775\pm 0.019$	$0.557\pm 0.014$
$D^{+}\to\rho^{0}\mu^{+}\nu_{\mu}$	$-0.452\pm 0.026$	$-0.139\pm 0.014$	$0.944\pm 0.006$	$0.937\pm 0.002$	$0.782\pm 0.023$	$0.555\pm 0.018$
$D^{+}\to\omega\mu^{+}\nu_{\mu}$	$-0.452\pm 0.026$	$-0.140\pm 0.014$	$0.944\pm 0.006$	$0.937\pm 0.002$	$0.782\pm 0.023$	$0.555\pm 0.018$
$D^{+}\to\phi\mu^{+}\nu_{\mu}$	$-0.455\pm 0.018$	$-0.175\pm 0.011$	$0.924\pm 0.005$	$0.915\pm 0.002$	$0.763\pm 0.015$	$0.557\pm 0.011$
$D^{0}\to K^{*-}\mu^{+}\nu_{\mu}$	$-0.454\pm 0.022$	$-0.156\pm 0.012$	$0.935\pm 0.005$	$0.927\pm 0.002$	$0.775\pm 0.019$	$0.557\pm 0.014$
$D^{0}\to\rho^{-}\mu^{+}\nu_{\mu}$	$-0.452\pm 0.026$	$-0.140\pm 0.014$	$0.944\pm 0.006$	$0.937\pm 0.002$	$0.782\pm 0.023$	$0.555\pm 0.018$
$D^{+}_{s}\to\phi\mu^{+}\nu_{\mu}$	$-0.454\pm 0.019$	$-0.162\pm 0.011$	$0.934\pm 0.005$	$0.925\pm 0.002$	$0.771\pm 0.016$	$0.557\pm 0.012$
$D^{+}_{s}\to\omega\mu^{+}\nu_{\mu}$	$-0.452\pm 0.027$	$-0.131\pm 0.014$	$0.950\pm 0.005$	$0.943\pm 0.002$	$0.788\pm 0.024$	$0.555\pm 0.019$
$D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu}$	$-0.451\pm 0.023$	$-0.143\pm 0.012$	$0.943\pm 0.005$	$0.936\pm 0.002$	$0.779\pm 0.021$	$0.555\pm 0.016$

The differential observables of $D^{+}_{s}\to K^{*0}\ell^{+}\nu_{\ell}$ decays in the $C_{3}$ case are displayed in Fig. 4. One can see that, in the low $q^{2}$ ranges, the differential observables expect $dF_{L}(D^{+}_{s}\to K^{*0}\ell^{+}\nu_{\ell})/dq^{2}$ are obviously different between decays with $\ell=e$ and $\ell=\mu$ .

III.3 $D\to S\ell^{+}\nu_{\ell}$ decays

For $D\to S\ell^{+}\nu_{\ell}$ decays, the two quark and the four quark scenarios for the scalar mesons below or near 1 $GeV$ are considered. The hadronic helicity amplitudes for the $D\rightarrow S\ell^{+}\nu_{\ell}$ decays are given in Tab. 8, in which the CKM matrix element $V_{cs}$ and $V_{cd}$ information are kept for comparing conveniently. There are four (five) nonperturbative parameters $E_{1,2,3,4}$ ( $E^{\prime}_{1,2,3,4,5}$ ) in the two quark (four quark) picture. After ignoring the SU(3) flavor breaking contributions, only one nonperturbative parameter $E_{1}=E_{2}=E_{3}=E_{4}=c^{S}_{0}$ or $E^{\prime}_{1}=E^{\prime}_{2}=E^{\prime}_{3}=E^{\prime}_{4}=E^{\prime}_{5}=c^{\prime S}_{0}$ relates all decay amplitudes in the two quark or the four quark picture, respectively.

Table 8: The hadronic helicity amplitudes for

D\to S\ell^{+}\nu

decays including both the SU(3) flavor symmetry and the SU(3) flavor breaking contributions. In the two quark picture of the scalar mesons,

E_{1}\equiv c^{S}_{0}+c^{S}_{1}-2c^{S}_{2}

E_{2}\equiv c^{S}_{0}-2c^{S}_{1}-2c^{S}_{2}

E_{3}\equiv c^{S}_{0}+c^{S}_{1}+c^{S}_{2}

E_{4}\equiv c^{S}_{0}-2c^{S}_{1}+c^{S}_{2}

E_{1}=E_{2}=E_{3}=E_{4}=c^{S}_{0}

if neglecting the SU(3) flavor breaking

c^{S}_{1}

and

c^{S}_{2}

terms. In the four quark picture of the scalar mesons,

E^{\prime}_{1}\equiv c^{\prime S}_{0}+c^{\prime S}_{1}-2c^{\prime S}_{2}+c^{\prime S}_{3}

E^{\prime}_{2}\equiv c^{\prime S}_{0}-2c^{\prime S}_{1}-2c^{\prime S}_{2}+c^{\prime S}_{3}

E^{\prime}_{3}\equiv c^{\prime S}_{0}+c^{\prime S}_{1}+c^{\prime S}_{2}-2c^{\prime S}_{3}

E^{\prime}_{4}\equiv c^{\prime S}_{0}+c^{\prime S}_{1}+c^{\prime S}_{2}+c^{\prime S}_{3}

E^{\prime}_{5}\equiv c^{\prime S}_{0}-2c^{\prime S}_{1}+c^{\prime S}_{2}+c^{\prime S}_{3}

E^{\prime}_{1}=E^{\prime}_{2}=E^{\prime}_{3}=E^{\prime}_{4}=E^{\prime}_{5}=c^{\prime S}_{0}

if neglecting the SU(3) flavor breaking

c^{\prime S}_{1}

c^{\prime S}_{2}

and

c^{\prime S}_{3}

terms.

Hadronic helicity amplitudes	ones for two-quark scenario	ones for four-quark scenario
$H(D^{0}\to K^{-}_{0}\ell^{+}\nu_{\ell})$	$E_{1}V^{*}_{cs}$	$E^{\prime}_{1}V^{*}_{cs}$
$H(D^{+}\to\overline{K}_{0}^{0}\ell^{+}\nu_{\ell})$	$E_{1}V^{*}_{cs}$	$E^{\prime}_{1}V^{*}_{cs}$
$H(D^{+}_{s}\to f_{0}\ell^{+}\nu_{\ell})$	$E_{2}V^{*}_{cs}$	$\sqrt{2}E^{\prime}_{2}V^{*}_{cs}$
$H(D^{+}_{s}\to f_{0}(980)\ell^{+}\nu_{\ell})$	$cos\theta_{S}\leavevmode\nobreak\ E_{2}V^{*}_{cs}$	$\sqrt{2}cos\phi_{S}\leavevmode\nobreak\ E^{\prime}_{2}V^{*}_{cs}$
$H(D^{+}_{s}\to f_{0}(500)\ell^{+}\nu_{\ell})$	$-sin\theta_{S}\leavevmode\nobreak\ E_{2}V^{*}_{cs}$	$-\sqrt{2}sin\phi_{S}\leavevmode\nobreak\ E^{\prime}_{2}V^{*}_{cs}$
$H(D^{0}\to a^{-}_{0}\ell^{+}\nu_{\ell})$	$E_{3}V^{*}_{cd}$	$E^{\prime}_{3}V^{*}_{cd}$
$H(D^{+}\to a^{0}_{0}\ell^{+}\nu_{\ell})$	$-\frac{1}{\sqrt{2}}E_{3}V^{*}_{cd}$	$-\frac{1}{\sqrt{2}}E^{\prime}_{3}V^{*}_{cd}$
$H(D^{+}\to f_{0}\ell^{+}\nu_{\ell})$	$0$	$\frac{1}{\sqrt{2}}E^{\prime}_{3}V^{*}_{cd}$
$H(D^{+}\to\sigma\ell^{+}\nu_{\ell})$	$\frac{1}{\sqrt{2}}E_{3}V^{*}_{cd}$	$E^{\prime}_{4}V^{*}_{cd}$
$H(D^{+}\to f_{0}(980)\ell^{+}\nu_{\ell})$	$\frac{1}{\sqrt{2}}sin\theta_{S}\leavevmode\nobreak\ E_{3}V^{*}_{cd}$	$(\frac{1}{\sqrt{2}}E^{\prime}_{3}cos\phi_{S}+E^{\prime}_{4}sin\phi_{S})V^{*}_{cd}$
$H(D^{+}\to f_{0}(500)\ell^{+}\nu_{\ell})$	$\frac{1}{\sqrt{2}}cos\theta_{S}\leavevmode\nobreak\ E_{3}V^{*}_{cd}$	$(-\frac{1}{\sqrt{2}}E^{\prime}_{3}sin\phi_{S}+E^{\prime}_{4}cos\phi_{S})V^{*}_{cd}$
$H(D^{+}_{s}\to K^{0}_{0}\ell^{+}\nu_{\ell})$	$E_{4}V^{*}_{cd}$	$E^{\prime}_{5}V^{*}_{cd}$

Unlike many measured decay modes in the $D\rightarrow P\ell^{+}\nu_{\ell}$ and $D\rightarrow V\ell^{+}\nu_{\ell}$ decays, among these $D\rightarrow S\ell^{+}\nu_{\ell}$ decays, only $D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e}$ decay has been measured, and its branching ratio with $2\sigma$ errors is PDG2022

\displaystyle\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})=(2.3\pm 0.8)\times 10^{-3}.

(87)

In addition, the branching ratios of the $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ decays with the light scalar resonances can be obtained by using $\mathcal{B}(D\to S\ell^{+}\nu_{\ell})$ and $\mathcal{B}(S\to P_{1}P_{2})$ , and the detail analysis can been found in Ref. wang:2022ourwork . Five branching ratios and two upper limits of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ have been measured, and the data within $2\sigma$ errors are

	$\displaystyle\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})=(1.30\pm 0.63)\times 10^{-3}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Hietala:2015jqa}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{0}\pi^{0})=(7.9\pm 2.9)\times 10^{-4}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{BESIII:2021pdt}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{0}\to a_{0}(980)^{-}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{-}\to\eta\pi^{-})=(1.33^{+0.68}_{-0.60})\times 10^{-4}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{ \cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{PDG2022}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{+}\to a_{0}(980)^{0}e^{+}\nu_{e},\leavevmode\nobreak\ a_{0}(980)^{0}\to\eta\pi^{0})=(1.7^{+1.6}_{-1.4})\times 10^{-4}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{ \cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{PDG2022}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{+}\pi^{-})=(6.3\pm 1.0)\times 10^{-4}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{ \cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{PDG2022}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(980)\to\pi^{+}\pi^{-})<2.8\times 10^{-5}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{ \cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{BESIII:2018qmf}{\@@citephrase{(}}{\@@citephrase{)}}}},$
	$\displaystyle\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e},\leavevmode\nobreak\ f_{0}(500)\to\pi^{0}\pi^{0})<6.4\times 10^{-4}\leavevmode\nobreak\ \leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{BESIII:2021pdt}{\@@citephrase{(}}{\@@citephrase{)}}}}.$		(88)

Two cases $S_{1}$ and $S_{2}$ will be considered in the $D\rightarrow S\ell^{+}\nu_{\ell}$ decays. In $S_{1}$ case, only experimental datum of $\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})$ is used to constrain one parameter $c^{S}_{0}$ or $c^{\prime S}_{0}$ and then predict other not yet measured branching ratios. The numerical results of $\mathcal{B}(D\to S\ell^{+}\nu)$ in $S_{1}$ case are given in the 2-4th and 8th columns of Tab. 9. In the $S_{2}$ case, the experimental data of both $\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})$ in Eq. (87) and $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ in Eq. (88) will be used to constrain the parameter $c^{S}_{0}$ or $c^{\prime S}_{0}$ . The predictions of $\mathcal{B}(D\to S\ell^{+}\nu)$ in $S_{2}$ case are listed in the 5-7th and 9th columns of Tab. 9. Our comments on the results in the $S_{1,2}$ cases are as follows.

•

Results in the two quark picture: In the two quark picture, the three possible ranges of the mixing angle, $25^{\circ}<\theta_{S}<40^{\circ}$ , $140^{\circ}<\theta_{S}<165^{\circ}$ and $-30^{\circ}<\theta_{S}<30^{\circ}$ Cheng:2005nb ; LHCb:2013dkk have been analyzed. In $S_{1}$ case, using the data of $\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})$ , many predictions of $\mathcal{B}(D\to S\ell^{+}\nu)$ are obtained. As given in the 2-4th columns of Tab. 9, one can see that the predictions with $25^{\circ}<\theta_{S}<40^{\circ}$ are similar to ones with $140^{\circ}<\theta_{S}<165^{\circ}$ , the predictions with $-30^{\circ}<\theta_{S}<30^{\circ}$ are slightly different from the first two, and the errors of predictions are quite large. After adding the experimental bounds of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ , as given in the 5-7th columns of Tab. 9, the three possible ranges of the mixing angle $\theta_{S}$ are obviously constrained, and they reduce to $25^{\circ}<\theta_{S}<35^{\circ}$ , $144^{\circ}<\theta_{S}<158^{\circ}$ and $22^{\circ}\leq|\theta_{S}|\leq 30^{\circ}$ , respectively. In addition, the error of every prediction become smaller by adding the experimental bounds of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ .
•

Results in the four quark picture: The predictions in the four quark picture are listed in the 8-9th columns of Tab. 9. The majority of predictions in four quark picture are smaller than corresponding ones in two quark picture. Strong coupling constants $g^{\prime}_{4}$ and $g_{4}$ are appeared in $S\to P_{1}P_{2}$ decays with the four quark picture of light scalar mesons. At present, we only can determine $\big{|}\frac{g^{\prime}_{4}}{g_{4}}\big{|}$ from the $S\to P_{1}P_{2}$ decays. The results of involved decays with both $\frac{g^{\prime}_{4}}{g_{4}}>0$ and $\frac{g^{\prime}_{4}}{g_{4}}<0$ are given in the 9th column of Tab. 9, and one can see that, except $\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e})$ and $\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu})$ , the other involved branching ratios are not obviously affected by the choice of $\frac{g^{\prime}_{4}}{g_{4}}>0$ or $\frac{g^{\prime}_{4}}{g_{4}}<0$ . The errors of the branching ratio predictions are obviously reduced by the experimental bounds of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ .
•

Comparing with previous predictions: Previous predictions are listed in the last column of Tab. 9. $\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e})$ , $\mathcal{B}(D^{+}_{s}\to f_{0}(500)\mu^{+}\nu_{\mu})$ and $\mathcal{B}(D^{+}\to f_{0}(500)\mu^{+}\nu_{\mu})$ are predicted for the first time. Our predictions of $\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu})$ , $\mathcal{B}(D^{+}\to a^{0}_{0}e^{+}\nu_{e})$ , $\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e})$ , $\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e})$ and $\mathcal{B}(D^{+}\to a^{0}_{0}\mu^{+}\nu_{\mu})$ are consistent with previous predictions in Refs. Soni:2020sgn ; Colangelo:2010bg ; Wang:2009azc . Our other predictions are about one order smaller or one order larger than previous ones in Refs. Momeni:2022gqb ; Cheng:2017fkw .

Table 9: Branching ratios of

D\to S\ell^{+}\nu

decays within

2\sigma

errors. As given in Ref. wang:2022ourwork ,

g^{\prime}_{4}

and

g_{4}

are strong coupling constants obtained by the SU(3) flavor symmetry in

S\to P_{1}P_{2}

decays, ^adenotes the results with

\frac{g^{\prime}_{4}}{g_{4}}>0

, and ^bdenotes ones with

\frac{g^{\prime}_{4}}{g_{4}}<0

{\dagger}

denotes the results with two quark picture, and

{\ddagger}

denotes the results with four quark picture.

Branching ratios	ones for $2q$ state in $S_{1}$			ones for $2q$ state in $S_{2}$			ones for $4q$	ones for $4q$	Previous ones
	$[25^{\circ},40^{\circ}]$	$[140^{\circ},165^{\circ}]$	$[-30^{\circ},30^{\circ}]$	$[25^{\circ},35^{\circ}]$	$[144^{\circ},158^{\circ}]$	$22^{\circ}\leq\|\theta_{S}\|\leq 30^{\circ}$	state in $S_{1}$	state in $S_{2}$
$\mathcal{B}(D^{0}\to K^{-}_{0}e^{+}\nu_{e})(\times 10^{-3})$	$3.38\pm 2.12$	$3.18\pm 2.05$	$2.57\pm 1.58$	$3.02\pm 1.11$	$3.00\pm 1.10$	$2.98\pm 1.05$	$1.11\pm 0.63$	$1.25\pm 0.45$	$0.103\pm 0.115^{\dagger}$ Momeni:2022gqb
$\mathcal{B}(D^{+}\to\overline{K}_{0}^{0}e^{+}\nu_{e})(\times 10^{-3})$	$8.66\pm 5.55$	$7.99\pm 5.02$	$7.02\pm 4.48$	$7.74\pm 2.88$	$7.78\pm 2.77$	$7.68\pm 2.78$	$2.85\pm 1.65$	$3.36\pm 1.25$	$38.8\pm 5.6^{\dagger}$ Momeni:2022gqb
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})(\times 10^{-3})$	$2.30\pm 0.80$	$2.30\pm 0.80$	$2.30\pm 0.80$	$2.58\pm 0.52$	$2.57\pm 0.53$	$2.71\pm 0.39$	$2.30\pm 0.80$	${}^{2.49\pm 0.61^{a}}_{2.54\pm 0.56^{b}}$	$2.1\pm 0.2^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Soni:2020sgn}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 2^{+0.5{\dagger}}_{-0.4}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Colangelo:2010bg}{\@@citephrase{(}}{\@@citephrase{)}}}}$
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)e^{+}\nu_{e})(\times 10^{-3})$	$6.73\pm 6.11$	$5.98\pm 5.75$	$3.25\pm 3.25$	$1.49\pm 0.43$	$1.45\pm 0.46$	$1.42\pm 0.50$	$0.37\pm 0.37$	${}^{0.31\pm 0.31^{a}}_{0.17\pm 0.17^{b}}$
$\mathcal{B}(D^{0}\to K^{-}_{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$2.90\pm 1.84$	$2.73\pm 1.77$	$2.20\pm 1.36$	$2.59\pm 0.97$	$2.57\pm 0.96$	$2.56\pm 0.92$	$0.95\pm 0.54$	$1.09\pm 0.39$	$0.103\pm 0.115^{\dagger}$ Momeni:2022gqb
$\mathcal{B}(D^{+}\to\overline{K}_{0}^{0}\mu^{+}\nu_{\mu})(\times 10^{-3})$	$7.46\pm 4.81$	$6.87\pm 4.33$	$6.04\pm 3.88$	$6.65\pm 2.52$	$6.69\pm 2.43$	$6.59\pm 2.43$	$2.45\pm 1.43$	$2.89\pm 1.09$	$38.8\pm 5.6^{\dagger}$ Momeni:2022gqb
$\mathcal{B}(D^{+}_{s}\to f_{0}(980)\mu^{+}\nu_{\mu})(\times 10^{-3})$	$1.95\pm 0.70$	$1.95\pm 0.70$	$1.95\pm 0.69$	$2.20\pm 0.45$	$2.20\pm 0.45$	$2.32\pm 0.33$	$1.95\pm 0.70$	${}^{2.12\pm 0.54^{a}}_{2.16\pm 0.49^{b}}$	$2.1\pm 0.2^{\dagger}$ Soni:2020sgn
$\mathcal{B}(D^{+}_{s}\to f_{0}(500)\mu^{+}\nu_{\mu})(\times 10^{-3})$	$6.21\pm 5.66$	$5.53\pm 5.32$	$3.01\pm 3.01$	$1.33\pm 0.39$	$1.31\pm 0.43$	$1.28\pm 0.46$	$0.34\pm 0.34$	${}^{0.29\pm 0.29^{a}}_{0.16\pm 0.16^{b}}$
$\mathcal{B}(D^{0}\to a^{-}_{0}e^{+}\nu_{e})(\times 10^{-5})$	$9.99\pm 6.54$	$9.56\pm 6.50$	$8.34\pm 5.67$	$9.22\pm 3.98$	$9.09\pm 3.65$	$9.17\pm 3.58$	$3.42\pm 2.06$	$4.32\pm 1.17$	${}^{16.8\pm 1.5^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Soni:2020sgn}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 40.8^{+13.7{\dagger}}_{-12.2}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Cheng:2017fkw}{\@@citephrase{(}}{\@@citephrase{)}}}},}_{24.4\pm 3.0^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Momeni:2022gqb}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{+}\to a^{0}_{0}e^{+}\nu_{e})(\times 10^{-5})$	$13.09\pm 8.62$	$12.62\pm 8.67$	$10.89\pm 7.35$	$12.09\pm 5.19$	$11.81\pm 4.71$	$11.97\pm 4.66$	$4.49\pm 2.71$	$5.68\pm 1.52$	${}^{21.8\pm 3.8^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Soni:2020sgn}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 54.0^{+17.8{\dagger}}_{-15.9}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Cheng:2017fkw}{\@@citephrase{(}}{\@@citephrase{)}}}}}_{6\sim 8^{{\dagger}}\mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Wang:2009azc}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 5\sim 5.4^{{\ddagger}}\mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Wang:2009azc}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{+}\to f_{0}(980)e^{+}\nu_{e})(\times 10^{-5})$	$3.92\pm 2.92$	$3.48\pm 3.13$	$1.59\pm 1.59$	$2.62\pm 0.82$	$2.52\pm 0.94$	$2.40\pm 0.80$	$3.14\pm 1.98$	${}^{3.35\pm 1.80^{a}}_{3.89\pm 1.35^{b}}$	${}^{7.78\pm 0.68^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Soni:2020sgn}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 5.7\pm 1.3^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Ke:2009ed}{\@@citephrase{(}}{\@@citephrase{)}}}}}_{0.4\sim 3.5^{\dagger}\mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Wang:2009azc}{\@@citephrase{(}}{\@@citephrase{)}}}},\leavevmode\nobreak\ 1.9\sim 6.3^{\ddagger}\mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Wang:2009azc}{\@@citephrase{(}}{\@@citephrase{)}}}}}$
$\mathcal{B}(D^{+}\to f_{0}(500)e^{+}\nu_{e})(\times 10^{-4})$	$4.05\pm 3.20$	$4.08\pm 3.10$	$4.21\pm 3.28$	$2.16\pm 0.96$	$2.59\pm 1.38$	$2.70\pm 1.28$	$4.97\pm 4.13$	${}^{4.97\pm 3.34^{a}}_{4.95\pm 3.36^{b}}$	$0.4\sim 0.6^{\dagger}$ Wang:2009azc , $\leavevmode\nobreak\ 0.88\sim 1.4^{\ddagger}$ Wang:2009azc
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}e^{+}\nu_{e})(\times 10^{-4})$	$3.73\pm 2.37$	$3.41\pm 2.13$	$2.99\pm 1.88$	$3.35\pm 1.21$	$3.32\pm 1.20$	$3.35\pm 1.15$	$1.25\pm 0.71$	$1.43\pm 0.51$	$26.5\pm 2.8^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Momeni:2022gqb}{\@@citephrase{(}}{\@@citephrase{)}}}}$
$\mathcal{B}(D^{0}\to a^{-}_{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$8.25\pm 5.45$	$7.89\pm 5.42$	$6.91\pm 4.75$	$7.61\pm 3.37$	$7.51\pm 3.10$	$7.57\pm 3.04$	$2.83\pm 1.72$	$3.57\pm 0.99$	$16.3\pm 1.4^{\dagger}$ Soni:2020sgn , $24.4\pm 3.0^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Momeni:2022gqb}{\@@citephrase{(}}{\@@citephrase{)}}}}$
$\mathcal{B}(D^{+}\to a^{0}_{0}\mu^{+}\nu_{\mu})(\times 10^{-5})$	$10.83\pm 7.19$	$10.44\pm 7.23$	$9.04\pm 6.16$	$10.00\pm 4.41$	$9.76\pm 4.00$	$9.89\pm 3.97$	$3.73\pm 2.28$	$4.69\pm 1.30$	$21.2\pm 3.7^{\dagger}$ Soni:2020sgn
$\mathcal{B}(D^{+}\to f_{0}(980)\mu^{+}\nu_{\mu})(\times 10^{-5})$	$3.23\pm 2.41$	$2.88\pm 2.60$	$1.32\pm 1.32$	$2.15\pm 0.70$	$2.09\pm 0.78$	$1.99\pm 0.66$	$2.56\pm 1.62$	${}^{2.74\pm 1.49^{a}}_{3.20\pm 1.14^{b}}$	$7.87\pm 0.67^{\dagger}$ Soni:2020sgn
$\mathcal{B}(D^{+}\to f_{0}(500)\mu^{+}\nu_{\mu})(\times 10^{-4})$	$3.69\pm 2.96$	$3.71\pm 2.86$	$3.84\pm 3.04$	$1.92\pm 0.88$	$2.32\pm 1.27$	$2.42\pm 1.19$	$4.54\pm 3.81$	${}^{4.52\pm 3.10^{a}}_{4.49\pm 3.12^{b}}$
$\mathcal{B}(D^{+}_{s}\to K^{0}_{0}\mu^{+}\nu_{\mu})(\times 10^{-4})$	$3.28\pm 2.10$	$3.00\pm 1.88$	$2.62\pm 1.66$	$2.94\pm 1.08$	$2.91\pm 1.06$	$2.94\pm 1.02$	$1.10\pm 0.63$	$1.26\pm 0.45$	$26.5\pm 2.8^{\dagger}\leavevmode\nobreak\ \mbox{\cite[cite]{\@@bibref{Authors Phrase1YearPhrase2}{Momeni:2022gqb}{\@@citephrase{(}}{\@@citephrase{)}}}}$

IV Summary

Many semileptonic $D\to P/V/S\ell^{+}\nu_{\ell}$ decays have been measured, and these processes could be used to test the SU(3) flavor symmetry approach. In terms of the SU(3) flavor symmetry and the SU(3) flavor breaking, the amplitude relations have been obtained. Then using the present data of $\mathcal{B}(D\to P/V/S\ell^{+}\nu_{\ell})$ , we have presented a theoretical analysis of the $D\to P/V/S\ell^{+}\nu_{\ell}$ decays. Our main results can be summarized as follows.

•

$D\to P\ell^{+}\nu_{\ell}$ decays: Our predictions with the SU(3) flavor symmetry in the $C_{1}$ case and the predictions after adding SU(3) flavor breaking contributions in the $C_{4}$ case are quite consistent with all present experimental data of $\mathcal{B}(D\to P\ell^{+}\nu_{\ell})$ within $2\sigma$ errors. In the $C_{2}$ and $C_{3}$ cases, our SU(3) flavor symmetry predictions are consistent with all present experimental data except $\mathcal{B}(D^{+}\to\pi^{0}\ell^{+}\nu_{\ell})$ and $\mathcal{B}(D^{0}\to\pi^{-}\ell^{+}\nu_{\ell})$ , which are slight larger than their experiential upper limits. The not yet measured $\mathcal{B}(D^{+}_{s}\to\pi^{0}e^{+}\nu_{e}),\leavevmode\nobreak\ \mathcal{B}(D^{+}\to\eta^{\prime}\mu^{+}\nu_{\mu}),\leavevmode\nobreak\ \mathcal{B}(D^{+}_{s}\to K^{0}\mu^{+}\nu_{\mu}),\leavevmode\nobreak\ \mathcal{B}(D^{+}_{s}\to\pi^{0}\mu^{+}\nu_{\mu}),\leavevmode\nobreak\ \mathcal{B}(D^{+}_{s}\to\pi^{0}\tau^{+}\nu_{\tau})$ and the lepton flavor universality parameters have been obtained. Moreover, the forward-backward asymmetries, the lepton-side convexity parameters, the longitudinal (transverse) polarizations of the final charged leptons with two ways of integration for the $D\to P\ell^{+}\nu_{\ell}$ decays have been predicted. The $q^{2}$ dependence of corresponding differential quantities of the $D\to P\ell^{+}\nu_{\ell}$ decays in the $C_{3}$ case have been displayed.
•

$D\to V\ell^{+}\nu_{\ell}$ decays: As given in the $C_{1}$ , $C_{2}$ and $C_{3}$ cases, our SU(3) flavor symmetry predictions of $\mathcal{B}(D^{+}\to\omega e^{+}\nu_{e})$ and $\mathcal{B}(D^{0}\to\rho^{-}\mu^{+}\nu_{\mu})$ are slightly larger than its experimental upper limits, and other SU(3) flavor symmetry predictions are consistent with present data. After considering the SU(3) flavor breaking effects, as given in the $C_{4}$ case, all predictions are consistent with present data. The not yet measured or not yet well measured branching ratios of $D^{+}\to\phi e^{+}\nu_{e},\leavevmode\nobreak\ D^{+}_{s}\to\omega e^{+}\nu_{e},\leavevmode\nobreak\ D^{+}\to\phi\mu^{+}\nu_{\mu},\leavevmode\nobreak\ D^{+}_{s}\to\omega\mu^{+}\nu_{\mu},$ and $D^{+}_{s}\to K^{*0}\mu^{+}\nu_{\mu}$ have been predicted. The $q^{2}$ dependence of corresponding differential quantities of the $D\to V\ell^{+}\nu_{\ell}$ decays in the $C_{3}$ case have also been displayed.
•

$D\to S\ell^{+}\nu_{\ell}$ decays: Among 18 $D\to S\ell^{+}\nu_{\ell}$ decay modes, only $\mathcal{B}(D^{+}_{s}\to f_{0}(980)e^{+}\nu_{e})$ has been measured, and this experimental datum has been used to constrain the SU(3) flavor symmetry parameter and then predict other not yet measured branching ratios. Furthermore, the relevant experimental bounds of $\mathcal{B}(D\to S\ell^{+}\nu_{\ell},\leavevmode\nobreak\ S\to P_{1}P_{2})$ have also been added. The two quark and the four quark scenarios for the light scalar mesons are considered, and the three possible ranges of the mixing angle $\theta_{S}$ in the two quark picture have been analyzed.

The SU(3) flavor symmetry is approximate approach, and it can still provide very useful information. We have found that the SU(3) flavor symmetry approach works well in the semileptonic $D\to P/V\ell^{+}\nu_{\ell}$ decays, and the SU(3) flavor symmetry predictions of the $D\to S\ell^{+}\nu_{\ell}$ decays need to be further tested, and our predictions of the $D\to S\ell^{+}\nu_{\ell}$ decays are useful for probing the structure of light scalar mesons. According to our predictions, some decay modes could be observed at BESIII, LHCb or BelleII in near future experiments.

ACKNOWLEDGEMENTS

The work was supported by the National Natural Science Foundation of China (12175088).

References

(1) R. L. Workman et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022, 083C01 (2022).
(2) D. Melikhov and B. Stech, Phys. Rev. D 62 (2000), 014006 [arXiv:hep-ph/0001113 [hep-ph]].
(3) H. Y. Cheng and X. W. Kang, Eur. Phys. J. C 77 (2017) no.9, 587 [erratum: Eur. Phys. J. C 77 (2017) no.12, 863] [arXiv:1707.02851 [hep-ph]].
(4) N. R. Soni, M. A. Ivanov, J. G. Körner, J. N. Pandya, P. Santorelli and C. T. Tran, Phys. Rev. D 98 (2018) no.11, 114031 [arXiv:1810.11907 [hep-ph]].
(5) Q. Chang, X. N. Li, X. Q. Li, F. Su and Y. D. Yang, Phys. Rev. D 98 (2018) no.11, 114018 [arXiv:1810.00296 [hep-ph]].
(6) Q. Chang, X. L. Wang and L. T. Wang, Chin. Phys. C 44 (2020) no.8, 083105 [arXiv:2003.10833 [hep-ph]].
(7) R. N. Faustov, V. O. Galkin and X. W. Kang, Phys. Rev. D 101 (2020) no.1, 013004 [arXiv:1911.08209 [hep-ph]].
(8) P. Ball, Phys. Rev. D 48 (1993), 3190-3203 [arXiv:hep-ph/9305267 [hep-ph]].
(9) S. Bhattacharyya, M. Haiduc, A. Tania Neagu and E. Firu, Eur. Phys. J. Plus 134 (2019) no.1, 37 [arXiv:1709.00882 [nucl-ex]].
(10) H. B. Fu, L. Zeng, R. Lü, W. Cheng and X. G. Wu, Eur. Phys. J. C 80 (2020) no.3, 194 [arXiv:1808.06412 [hep-ph]].
(11) H. B. Fu, W. Cheng, L. Zeng, D. D. Hu and T. Zhong, Phys. Rev. Res. 2 (2020) no.4, 043129 [arXiv:2003.07626 [hep-ph]].
(12) I. L. Grach, I. M. Narodetsky and S. Simula, Phys. Lett. B 385 (1996), 317-323 [arXiv:hep-ph/9605349 [hep-ph]].
(13) H. Y. Cheng, C. K. Chua and C. W. Hwang, Phys. Rev. D 69 (2004), 074025 [arXiv:hep-ph/0310359 [hep-ph]].
(14) Q. Chang, X. N. Li and L. T. Wang, Eur. Phys. J. C 79 (2019) no.5, 422 [arXiv:1905.05098 [hep-ph]].
(15) V. Lubicz et al. [ETM], Phys. Rev. D 98 (2018) no.1, 014516 [arXiv:1803.04807 [hep-lat]].
(16) V. Lubicz et al. [ETM], Phys. Rev. D 96 (2017) no.5, 054514 [erratum: Phys. Rev. D 99 (2019) no.9, 099902; erratum: Phys. Rev. D 100 (2019) no.7, 079901] [arXiv:1706.03017 [hep-lat]].
(17) X. G. He, Eur. Phys. J. C 9, 443 (1999) [hep-ph/9810397].
(18) X. G. He, Y. K. Hsiao, J. Q. Shi, Y. L. Wu and Y. F. Zhou, Phys. Rev. D 64, 034002 (2001) [hep-ph/0011337].
(19) H. K. Fu, X. G. He and Y. K. Hsiao, Phys. Rev. D 69, 074002 (2004) [hep-ph/0304242].
(20) Y. K. Hsiao, C. F. Chang and X. G. He, Phys. Rev. D 93, no. 11, 114002 (2016) [arXiv:1512.09223 [hep-ph]].
(21) X. G. He and G. N. Li, Phys. Lett. B 750, 82 (2015) [arXiv:1501.00646 [hep-ph]].
(22) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 50, 4529 (1994) [hep-ph/9404283].
(23) M. Gronau, O. F. Hernandez, D. London and J. L. Rosner, Phys. Rev. D 52, 6356 (1995) [hep-ph/9504326].
(24) S. H. Zhou, Q. A. Zhang, W. R. Lyu and C. D. Lü, Eur. Phys. J. C 77, no. 2, 125 (2017) [arXiv:1608.02819 [hep-ph]].
(25) H. Y. Cheng, C. W. Chiang and A. L. Kuo, Phys. Rev. D 91, no. 1, 014011 (2015) [arXiv:1409.5026 [hep-ph]].
(26) M. He, X. G. He and G. N. Li, Phys. Rev. D 92, no. 3, 036010 (2015) [arXiv:1507.07990 [hep-ph]].
(27) N. G. Deshpande and X. G. He, Phys. Rev. Lett. 75, 1703 (1995) [hep-ph/9412393].
(28) S. Shivashankara, W. Wu and A. Datta, Phys. Rev. D 91, 115003 (2015) [arXiv:1502.07230 [hep-ph]].
(29) R. M. Wang, Y. G. Xu, C. Hua and X. D. Cheng, Phys. Rev. D 103 (2021) no.1, 013007 [arXiv:2101.02421 [hep-ph]].
(30) R. M. Wang, X. D. Cheng, Y. Y. Fan, J. L. Zhang and Y. G. Xu, J. Phys. G 48 (2021) no.8, 085001 [arXiv:2008.06624 [hep-ph]].
(31) Y. Grossman and D. J. Robinson, JHEP 1304, 067 (2013) [arXiv:1211.3361 [hep-ph]].
(32) D. Pirtskhalava and P. Uttayarat, Phys. Lett. B 712, 81 (2012) [arXiv:1112.5451 [hep-ph]].
(33) H. Y. Cheng and C. W. Chiang, Phys. Rev. D 86, 014014 (2012) [arXiv:1205.0580 [hep-ph]].
(34) M. J. Savage and R. P. Springer, Phys. Rev. D 42, 1527 (1990).
(35) M. J. Savage, Phys. Lett. B 257, 414 (1991).
(36) G. Altarelli, N. Cabibbo and L. Maiani, Phys. Lett. 57B, 277 (1975).
(37) C. D. Lü, W. Wang and F. S. Yu, Phys. Rev. D 93, no. 5, 056008 (2016) [arXiv:1601.04241 [hep-ph]].
(38) C. Q. Geng, Y. K. Hsiao, Y. H. Lin and L. L. Liu, Phys. Lett. B 776, 265 (2018) [arXiv:1708.02460 [hep-ph]].
(39) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, Phys. Rev. D 97, no. 7, 073006 (2018) [arXiv:1801.03276 [hep-ph]].
(40) C. Q. Geng, Y. K. Hsiao, C. W. Liu and T. H. Tsai, JHEP 1711, 147 (2017) [arXiv:1709.00808 [hep-ph]].
(41) C. Q. Geng, C. W. Liu, T. H. Tsai and S. W. Yeh, arXiv:1901.05610 [hep-ph].
(42) W. Wang, Z. P. Xing and J. Xu, Eur. Phys. J. C 77, no. 11, 800 (2017) [arXiv:1707.06570 [hep-ph]].
(43) D. Wang, arXiv:1901.01776 [hep-ph].
(44) D. Wang, P. F. Guo, W. H. Long and F. S. Yu, JHEP 1803, 066 (2018) [arXiv:1709.09873 [hep-ph]].
(45) S. Müller, U. Nierste and S. Schacht, Phys. Rev. D 92, no. 1, 014004 (2015) [arXiv:1503.06759 [hep-ph]].
(46) J. Barranco, D. Delepine, V. Gonzalez Macias and L. Lopez-Lozano, arXiv:1404.0454 [hep-ph].
(47) J. Barranco, D. Delepine, V. Gonzalez Macias and L. Lopez-Lozano, Phys. Lett. B 731, 36 (2014) [arXiv:1303.3896 [hep-ph]].
(48) A. G. Akeroyd and F. Mahmoudi, JHEP 0904, 121 (2009) [arXiv:0902.2393 [hep-ph]].
(49) B. A. Dobrescu and A. S. Kronfeld, Phys. Rev. Lett. 100, 241802 (2008) [arXiv:0803.0512 [hep-ph]].
(50) A. G. Akeroyd and C. H. Chen, Phys. Rev. D 75, 075004 (2007) [hep-ph/0701078].
(51) S. Fajfer and J. F. Kamenik, Phys. Rev. D 73, 057503 (2006) [hep-ph/0601028].
(52) S. Fajfer and J. F. Kamenik, Phys. Rev. D 72, 034029 (2005) [hep-ph/0506051].
(53) S. Fajfer and J. F. Kamenik, Phys. Rev. D 71, 014020 (2005) [hep-ph/0412140].
(54) A. G. Akeroyd, Prog. Theor. Phys. 111, 295 (2004) [hep-ph/0308260].
(55) A. G. Akeroyd and S. Recksiegel, Phys. Lett. B 554, 38 (2003) [hep-ph/0210376].
(56) M. A. Ivanov, J. G. Körner, J. N. Pandya, P. Santorelli, N. R. Soni and C. T. Tran, Front. Phys. (Beijing) 14 (2019) no.6, 64401 [arXiv:1904.07740 [hep-ph]].
(57) X. G. He, Y. J. Shi and W. Wang, Eur. Phys. J. C 80, no.5, 359 (2020) [arXiv:1811.03480 [hep-ph]].
(58) H. Y. Cheng, C. K. Chua and K. C. Yang, Phys. Rev. D 73 (2006), 014017 [arXiv:hep-ph/0508104 [hep-ph]].
(59) L. Maiani, F. Piccinini, A. D. Polosa and V. Riquer, Phys. Rev. Lett. 93 (2004), 212002 [arXiv:hep-ph/0407017 [hep-ph]].
(60) L. Y. Dai, X. W. Kang and U. G. Meißner, Phys. Rev. D 98 (2018) no.7, 074033 [arXiv:1808.05057 [hep-ph]].
(61) G. ’t Hooft, G. Isidori, L. Maiani, A. D. Polosa and V. Riquer, Phys. Lett. B 662 (2008), 424-430 [arXiv:0801.2288 [hep-ph]].
(62) J. R. Pelaez, Phys. Rev. Lett. 92 (2004), 102001 [arXiv:hep-ph/0309292 [hep-ph]].
(63) Y. J. Sun, Z. H. Li and T. Huang, Phys. Rev. D 83 (2011), 025024 [arXiv:1011.3901 [hep-ph]].
(64) J. A. Oller and E. Oset, Nucl. Phys. A 620 (1997), 438-456 [erratum: Nucl. Phys. A 652 (1999), 407-409] [arXiv:hep-ph/9702314 [hep-ph]].
(65) V. Baru, J. Haidenbauer, C. Hanhart, Y. Kalashnikova and A. E. Kudryavtsev, Phys. Lett. B 586 (2004), 53-61 [arXiv:hep-ph/0308129 [hep-ph]].
(66) N. N. Achasov, V. V. Gubin and V. I. Shevchenko, Phys. Rev. D 56 (1997), 203-211 [arXiv:hep-ph/9605245 [hep-ph]].
(67) S. Momeni and M. Saghebfar, Eur. Phys. J. C 82 (2022) no.5, 473
(68) R. Aaij et al. [LHCb], Phys. Rev. D 87 (2013) no.5, 052001 [arXiv:1301.5347 [hep-ex]].
(69) R. L. Jaffe, Phys. Rev. D 15 (1977), 267
(70) D. Xu, G. N. Li and X. G. He, Int. J. Mod. Phys. A 29 (2014), 1450011 [arXiv:1307.7186 [hep-ph]].
(71) M. Tanaka and R. Watanabe, Phys. Rev. D 82, 034027 (2010) [arXiv:1005.4306 [hep-ph]].
(72) M. Tanaka, Z. Phys. C 67, 321 (1995) [hep-ph/9411405].
(73) S. Fajfer, J. F. Kamenik and I. Nisandzic, Phys. Rev. D 85, 094025 (2012) [arXiv:1203.2654 [hep-ph]].
(74) A. Celis, M. Jung, X. Q. Li and A. Pich, JHEP 1301, 054 (2013) [arXiv:1210.8443 [hep-ph]].
(75) C. Bobeth, G. Hiller and D. van Dyk, JHEP 1007, 098 (2010) [arXiv:1006.5013 [hep-ph]].
(76) H. B. Li and M. Z. Yang, Phys. Lett. B 811 (2020), 135879 [arXiv:2006.15798 [hep-ph]].
(77) N. N. Achasov and A. V. Kiselev, Phys. Rev. D 86 (2012), 114010 [arXiv:1206.5500 [hep-ph]].
(78) N. R. Soni, A. N. Gadaria, J. J. Patel and J. N. Pandya, Phys. Rev. D 102 (2020) no.1, 016013 [arXiv:2001.10195 [hep-ph]].
(79) X. Leng, X. L. Mu, Z. T. Zou and Y. Li, Chin. Phys. C 45 (2021) no.6, 063107 [arXiv:2011.01061 [hep-ph]].
(80) Ru-Min Wang, Yi-Jie Zhang, Yi Qiao, Xiao-Dong Cheng and Yuan-Guo Xu, Four-body Semileptonic Charm Decays $D\to P_{1}P_{2}\ell^{+}\nu_{\ell}$ with the SU(3) Flavor Symmetry, in preparation.
(81) J. Hietala, D. Cronin-Hennessy, T. Pedlar and I. Shipsey, Phys. Rev. D 92 (2015) no.1, 012009 [arXiv:1505.04205 [hep-ex]].
(82) M. Ablikim et al. [BESIII], [arXiv:2110.13994 [hep-ex]].
(83) M. Ablikim et al. [BESIII], Phys. Rev. Lett. 122 (2019) no.6, 062001 [arXiv:1809.06496 [hep-ex]].
(84) P. Colangelo, F. De Fazio and W. Wang, Phys. Rev. D 81 (2010), 074001 [arXiv:1002.2880 [hep-ph]].
(85) W. Wang and C. D. Lü, Phys. Rev. D 82 (2010), 034016 [arXiv:0910.0613 [hep-ph]].
(86) X. D. Cheng, H. B. Li, B. Wei, Y. G. Xu and M. Z. Yang, Phys. Rev. D 96 (2017) no.3, 033002 [arXiv:1706.01019 [hep-ph]].
(87) H. W. Ke, X. Q. Li and Z. T. Wei, Phys. Rev. D 80 (2009), 074030 [arXiv:0907.5465 [hep-ph]].

Semileptonic DD Meson Decays D→P/V/S​ℓ+​νℓD\to P/V/S\ell^{+}\nu_{\ell} with the SU(3) Flavor Symmetry/Breaking

Abstract

I Introduction

II Theoretical Frame

II.1 The effective Hamiltonian

II.2 Hadronic helicity amplitude relations by the SU(3) flavor symmetry

II.3 Observables for the D→M​ℓ+​νℓD\to M\ell^{+}\nu_{\ell} decays

II.4 Form factors

III Numerical results

III.1 D→P​ℓ+​νℓD\to P\ell^{+}\nu_{\ell} decays

III.2 D→V​ℓ+​νℓD\to V\ell^{+}\nu_{\ell} decays

III.3 D→S​ℓ+​νℓD\to S\ell^{+}\nu_{\ell} decays

IV Summary

ACKNOWLEDGEMENTS

References

References

Semileptonic $D$ Meson Decays $D\to P/V/S\ell^{+}\nu_{\ell}$ with the SU(3) Flavor Symmetry/Breaking

II.3 Observables for the $D\to M\ell^{+}\nu_{\ell}$ decays

III.1 $D\to P\ell^{+}\nu_{\ell}$ decays

III.2 $D\to V\ell^{+}\nu_{\ell}$ decays

III.3 $D\to S\ell^{+}\nu_{\ell}$ decays