Sending classical information through relativistic quantum channels
Abstract
We investigate how special relativity influences the transmission of classical information through quantum channels by evaluating the Holevo bound when the sender and the receiver are in (relativistic) relative motion. By using the spin degrees of freedom of spin- fermions to encode the classical information we show that, for some configurations, the accessible information in the receiver can be increased when the spin detector moves fast enough. This is possible by allowing the momentum wave packet of one of the particles to be wide enough while the momentum wave packets of other particles are kept relatively narrow. In this way, one can take advantage of the fact that boosts entangle the spin and momentum degrees of freedom of spin- fermions to increase the accessible information in the former. We close the paper with a discussion of how this relativistic quantum channel cannot in general be described by completely positive quantum maps.
pacs:
03.67.Hk, 03.65.Ta, 03.65.Ud, 03.30.+pI Introduction
Remarkable effects are found in information processing when communication channels are allowed to be quantum mechanical. Examples of these are fast quantum algorithms fastquantalg , quantum teleportation tele1 , quantum cryptography cripto1 ; cripto2 ; cripto3 , dense coding densecoding1 and quantum error correction errorcorrection . Quantum information theory nielsen&chuang commonly deals only with nonrelativistic systems. However, a relativistic treatment is relevant not only to the logical completeness of the theory but also to the disclosure of new physical effects and bounds that arise in information transfer and processing when there is relative motion between the parts that trade information Peres&Terno2003 ; Peres&Terno2004 . Moreover, a better understanding of the relativistic extension of quantum information theory may shed light on several important conceptual issues, for instance, the black hole information “paradox” Hawking1976 ; Wald2001 . For the aforementioned reasons, a great deal of attention has been paid to quantum information theory in the context of special relativity PST02 ; GA02 , the Unruh effect Fetal ; FKMB11 ; LM09b ; CLMS10 , and black holes PJ08 ; HBK12 ; ML10 . Recently, an experimental setup in which a relativistic formulation of quantum information theory may be important was proposed. It consists in using free-space transmission of photons between ground stations and satellites in order to test quantum mechanics for large space distances and, eventually, to implement quantum information protocols in global scales satellite1 ; satellite2 ; satellite3 ; satellite4 . In previous works, we have studied how special relativity affects the correlations between an entangled pair of both fermions LM2009 and photons LMT2010 by examining the Clauser-Horne-Shimony-Holt Bell inequality CHSH1969 when the detectors are moving. Here, we adopt a rather information-theoretic approach and analyze the classical capacity of a relativistic quantum channel in comparison to that of a nonrelativistic one.
One of the keystones of quantum information is the indistinguishability of arbitrary quantum states: given two non-orthogonal quantum states, one cannot distinguish between them with full reliability by making any measurement, a result that is easily shown to be equivalent to the no-cloning theorem nocloning1 ; nocloning2 ; nielsen&chuang . More precisely, let be an index that indicates each of the states from the set , and suppose that these states are prepared according to a probability distribution . An experimentalist performs a measurement described by the positive operator-valued measure (POVM) and is supposed to infer the state that was prepared from the measurement outcome . A good measure of how much information the experimentalist can gain about the state through this procedure is given by the mutual information , which can be defined as
| (1) |
Here, and are the Shannon entropies associated with the probability distribution of the preparation procedure and the probability distribution of the measurement outcomes, where , respectively, and is their joint entropy. It is well known that and that one can infer from if and only if . The closer gets to , the more accurately it is possible to infer from . Of course the mutual information depends on what measurement the experimentalist decides to perform, that is, on the POVM chosen. To avoid this indeterminacy, we define the accessible information to be the maximum of the mutual information over all possible measurement schemes. Although no general method for calculating the accessible information is known, it is possible to prove a very important upper bound known as the Holevo bound Holevo1973 . It states that, for any measurement the experimentalist may do, the inequality below holds:
| (2) |
where is the von Neumann entropy of the quantum state . It is easy to show nielsen&chuang that and, therefore, inequality (2) implies that one qubit contains at most one bit of information. The Holevo bound is especially relevant due to the Holevo-Schumacher-Westmoreland (HSW) theorem, independently proved by Schumacher and Westmoreland Schumacher&Westmorland1997 and by Holevo Holevo1998 , according to which the rate is asymptotically achievable and thus can be used to obtain an expression for the classical (product state) capacity of a quantum channel. Hence, in order to study the transmission of classical information through relativistic quantum channels, it is interesting to analyze the Holevo bound in a typical relativistic quantum communication setup. Here this is done by setting the detector in relative motion with respect to the preparation apparatus.
The indistinguishability of non-orthogonal quantum states mentioned above together with fact that any attempt to distinguish them ends up only imparting a disturbance to the states is what motivates their use in cryptographic protocols. This however is not the only setup in which non-orthogonal states play a relevant role. As it was first shown in fucs97 there are some noisy quantum channels in which the channel capacity is only achieved by the use of non-orthogonal states. In the present paper we will show that when the parts that trade information are in relative motion (and there is not any external noise afflicting the states), there is a certain class of non-orthogonal states for which the Holevo bound increases when compared to its value when the sender and the receiver are at rest relative to each other. This suggests that the relative motion may actually help to increase the capacity of some noisy quantum channels.
The paper is organized as follows. In Sec. II we analyze the transmission of two and four classical bits through nonrelativistic quantum communication channels. In Sec. III we study how relativity influences the previous quantum communication process. This is done by setting the receiver, Bob, in relative motion with respect to the sender, Alice. In this context we analyze how to optimize the accessible information on the receiver. In Sec. IV we define quantum maps that describe the quantum channels analyzed in the previous sections and show that there are cases in which they fail to be completely positive. Sec. V is dedicated to our final remarks. We adopt natural units unless stated otherwise.
II Nonrelativistic quantum communication setup
II.1 Two classical bits
Let us assume that Alice has a classical information source that produces symbols according to the probability distribution , . Depending on the value she obtains for , she prepares a pure quantum state , chosen from a fixed set , of a spin- particle with mass and then sends it to Bob. He then makes a spin measurement of his choice on that state and has to identify based on the outcome . We assume that (see, e.g., Ref. Bogolubov1975 for the two-spinor notation used below)
| (5) | |||||
| (10) |
where
| (11) |
Here, the parameters and , , give the particle’s momentum dispersion and the average momentum, respectively. Note that can be written as
making manifest its direct product structure.
First we summarize what happens when Bob is at rest relative to Alice, which is the typical quantum information scenario. All spin measurement results can be predicted through the reduced spin density operator, obtained by tracing out the momenta,
| (12) |
where
| (13) |
is the complete density operator of the system. We thus obtain
| (14) |
Note that, due to the linearity of the trace, we can write , where
| (15) |
and
| (16) |
As can be easily seen from Eq. (14), is just a statistical mixture of the pure spin states and
| (17) |
where and are the eigenvectors of with eigenvalues and , respectively. Note that is an eigenstate of where , , and is the Pauli vector. Thus, we can say that the momentum degrees of freedom play absolutely no role in this case. As and correspond to pure states, we have , so that
| (18) |
where are the eigenvalues of , namely,
| (19) |
Note that has periodicity with respect to . It is straightforward to verify that the Holevo bound reaches its maximum value when , corresponding to orthogonal spin states (see Fig. 1). At this point, and only at this point, it is possible for Bob to determine with certainty which state Alice has prepared, which he does simply by measuring . This is actually a general property of orthogonal states, which can always be completely distinguished by appropriate measurements. By contrast, the minimum is attained at and , which means that the states and are identical (up to a phase) when it comes solely to spin and, therefore, they cannot be distinguished at all.
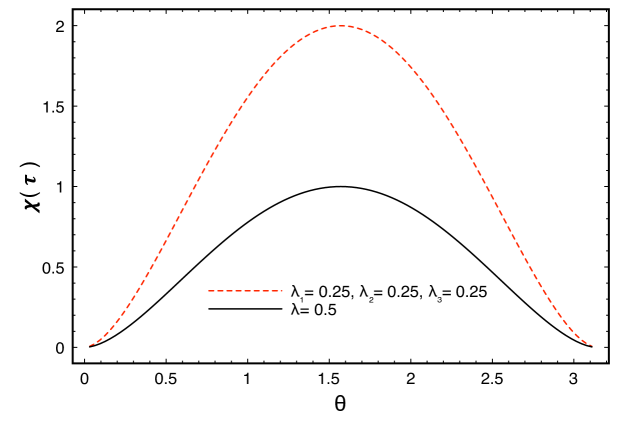
II.2 Four classical bits
Now, let us see how the above results generalize to the case where more classical bits are sent through the quantum communication channel. For this purpose, let us suppose now that Alice has a classical information source that produces symbols according to the probability distribution , , . As in the previous case, Alice can choose pure quantum states from the set , where and are given by Eqs. (5) and (10), respectively. Therefore, depending on the value of , Alice prepares one of the four product states
and sends it to Bob. He then makes a spin measurement of his choice on that state and has to identify based on the outcome . The total density operator of the system is given by
| (21) |
If the momentum degrees of freedom are traced out in Eq. (21), we obtain the reduced spin density operator
| (22) |
which can be written as
and from which all spin measurement results can be predicted. The density operators and are given in Eqs. (15) and (16), respectively. Now, by using that for any density matrices and and that we can write as
| (23) |
where are the eigenvalues of In Fig 1, is plotted when . We can see that, as in the case of two bits, its maximum value is attained when
III Relativistic Quantum Communication Optimization
Now we turn our attention to the relativistic case, in which Bob moves with three-velocity relative to Alice.
III.1 Two classical bits
Let us suppose first that Alice wants to transmit two bits of classical information. Thus, as explained in Section II.1, she prepares the state given in Eq. (13) and sends it to Bob. Due to his motion, Bob sees the state prepared by Alice unitarily transformed in his proper frame as
| (24) |
where Halpern1968 ; Weinberg1996
| (25) |
with
| (26) |
, and denoting the spatial part of the four-vector . The Wigner rotation is given by
| (27) | |||||
where , is the identity matrix, and gives the direction of the boost, which in our case is , so that
| (28) |
By using Eq. (27) in Eq. (26) with given in Eqs. (5) and (10), we obtain
| (29) |
and
| (30) |
where the momentum wave packets are given by
with
By tracing out the momentum degrees of freedom we obtain the reduced spin operator in Bob’s frame
| (31) |
where
| (32) |
| (33) |
and is given in Eq (24). Explicitly, we have
| (36) | |||||
| (39) |
where
| (40) | |||||
| (41) |
with and being given by
| (42) |
and
| (43) |
respectively. In the above equations, we have used the fact that is a relativistic invariant and performed the change of variables . Using Eqs. (36) and (39) in Eq (31), we can cast as
| (44) |
Note that, contrary to and , and are not pure states, so that and are both non-zero. The Holevo bound in Bob’s frame is given by
| (45) |
By using Eqs. (36), (39) and (44), the above equation can be rewritten as
| (46) | |||||
where, for , , , and are the eigenvalues of , , and , respectively. These can be easily calculated as functions of the integrals and . In this paper, we proceed a numerical analysis of Eq. (46) to examine various aspects of the transmission of classical information through relativistic quantum channels. In order to do that, we rewrite Eqs. (42) and (43) as
| (47) |
and
| (48) |
respectively, where we have used Eq. (11) and cylindrical coordinates with as the symmetry axis, and introduced
| (49) |
In addition, we have defined the normalized non-dimensional variables , , , and .
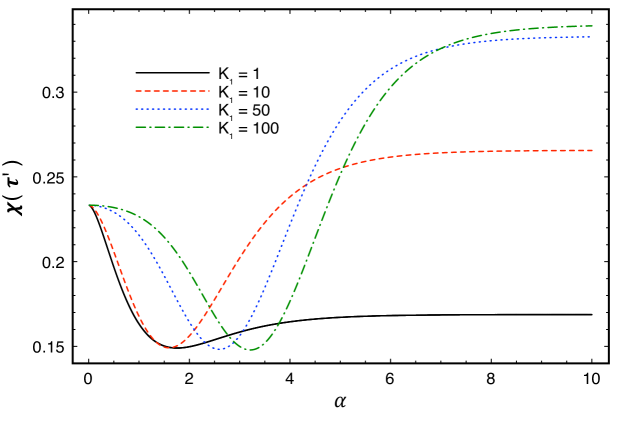
Let us first analyze the behavior of Eq (45) [or, equivalently, Eq (46)] as a function of the rapidity where we recall that is the relative velocity between Bob and Alice. First, it should be noted that if both and were much smaller than the unity, the effects of Bob’s velocity would be negligible and, for any value of , would have, approximately, its value for (since in this case, and would be almost momentum eigenstates). However, if we allow to be much larger than the situation changes considerably, as can be seen in Fig. 2. There, is plotted as a function of the rapidity , for different values of the normalized mean momentum of , when , , , , and . We can see that although initially decreases with , it begins to increase for larger values of the rapidity, eventually overcoming the value for when is large enough. Thus, for some codifications, i.e., for some values of , the (relativistic) velocity of the receiver can actually increase his accessible information. This is possible because, when is large, even though , the states and are almost orthogonal (despite of the fact that their spin parts, and , are not), as can be easily checked. When Bob is moving, the momentum and spin degrees of freedom of the original state prepared by Alice are mixed up by the Wigner rotation. As a consequence, Bob can obtain some extra information in the spin degrees of freedom due to the fact that the states and prepared by Alice are more clearly distinguishable in momentum than in spin.
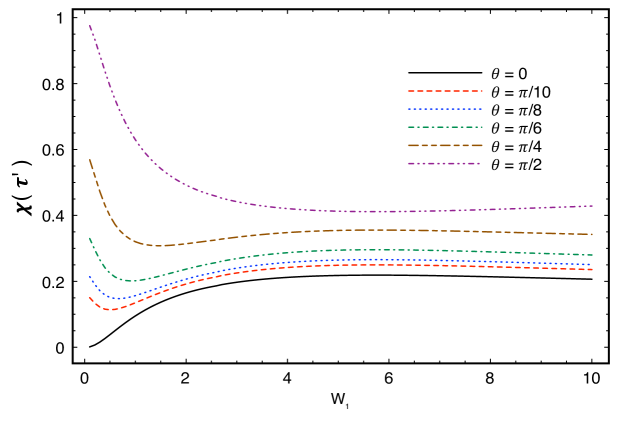
In view of the above results, let us study now how the width of the wave packet of the second state influences the accessible information in different codification schemes. In Fig. 3, is plotted as a function of , in the limit , for different values of . We have fixed , and . We can see that when is small and is large enough, the accessible information always increase when Bob moves with relativistic velocities with respect to Alice. When is larger (in particular, when it is close to ), the increase in always leads to a decrease in and therefore in the accessible information. This is so because the spin parts, and of the states and prepared by Alice are already quite distinguishable and thus the entanglement between the spin and momentum degrees of freedom caused by Bob’s movement ends up only making the spin degrees of freedom less distinguishable. It is interesting to note that Alice can codify the information in states and using . This makes the states completely indistinguishable in spin in her frame. Yet, Bob can have a non zero value of , as can be seen from Fig. 3. Thus, Alice can use the fact that spin and momentum are mixed up in Bob’s frame to “hide” the information in the momentum degrees of freedom in her frame, and let Bob movement make this information available to him in spin. This may be useful when considering noisy quantum channels in the spin degrees of freedom.
III.2 Four Classical Bits
We will analyze now if the above results still apply when Alice sends more classical bits through the quantum channel. For the sake of simplicity, we will describe here what happens when she tries to transmit four bits of classical information to Bob. Thus, as explained in Section II.2, Alice prepares the state given in Eq. (21) and sends it to Bob. As Bob is moving with respect to her, he sees the state prepared by Alice unitarily transformed in his proper frame as
| (50) |
where , , and and are given in Eqs. (29) and (30), respectively. If we trace out the momentum degrees of freedom in we obtain the density operator
| (51) |
which can be written as
| (52) | |||||
and from which all spin measurement results can be predicted. We recall that and are given in Eqs. (36) and (39), respectively.
Now, using again the identity , which is valid for any density matrices and , we can write the Holevo bound
| (53) | |||||
as
| (54) | |||||
where are the eigenvalues of .
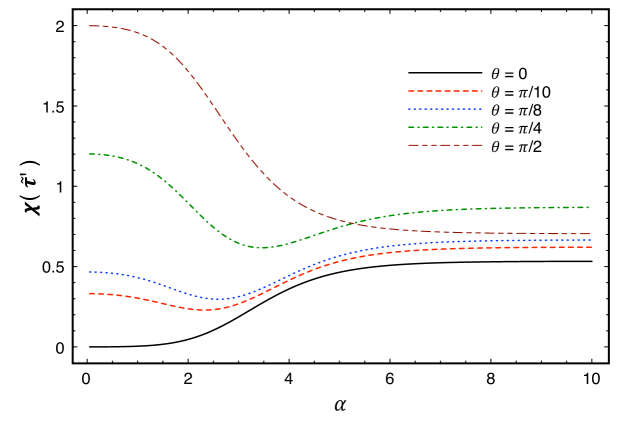
In Fig. 4 we plot as a function of the rapidity for different values of the angle . We have verified that the behavior of the Holevo bound for as a function of for different values of is very similar to that of , which is shown in Fig. 2. Similarly, the behavior , when , as a function of looks very close to the behavior of described in Fig. 3. Therefore, in order to analyze the Holevo bound for different choices of the angle of , we have fixed and much larger than and , respectively. Explicitly, we have chosen , , , , and As can be seen from Fig. 4, initially decreases as increases. However, for small angles (for instance, , and ), the Holevo bound begins to increase as gets larger and, eventually, overcomes its value for (where Bob is at rest with respect to Alice). Thus, for some codifications of the classical bits, the (relativistic) velocity of the receiver can increase his accessible information. For angles closer to Bob’s movement only makes the Holevo bound smaller compared to the case where Alice and Bob do not have a relative motion. In particular, we can see from the graph that, when is large enough, the use of orthogonal states, is not even the best strategy anymore [i.e. orthogonal states do not maximize ]. Thus, for larger angles, it is better to use both and much smaller than so that and are “almost” momentum eigenstates and therefore, the effects of the motion of the receiver on the accessible information are negligible.
It is interesting to note that, as in the case where two bits are being sent through the quantum channel, Alice can “hide” the information on the momentum degrees of freedom by using states , with (which are completely indistinguishable in spin), and let Bob’s movement make the information available to him in the spin degrees of freedom. As we have already pointed out in Section III.1, this might be useful to protect the communication against possible noises in the spin degrees of freedom.
IV Relativistic Quantum Map
Let us now define linear and trace-preserving maps that describe the relativistic quantum channels for both the transmission of two and four classical bits. For this purpose, we fix the values of , and , and define the convex sets
| (55) |
and
| (56) | |||||
where and are given in Eqs. (15) and (16), respectively. If denotes the set of (bounded) operators over a Hilbert space , the maps and are defined as
It is interesting to note that when and , the total state prepared by Alice, for the two-bit case and for the four-bit case, not only presents correlations between the spin and momentum degrees of freedom but also have non-vanishing quantum discord (with respect to measurements made on the spin degrees of freedom). For the sake of simplicity, let us prove this statement for the state . However, a complete analogous calculation also shows the non-vanishing of the quantum discord in the four-bits case. We first note that
| (59) |
where is the identity in the momentum space,
and, in the momentum representation, i.e., they are the reduced momentum density operator associated with . Now, we can see from Eq. (59) that whenever (which is the case when and ) the above commutator does not vanish and thus, as shown in facca10 , the state has non-vanishing quantum discord. Although it is not a sufficient condition, an initial state with non-vanishing discord indicates that the reduced spin dynamics ( and ) may not be completely positive (CP) bdmrr12 ; mbcpv12 ; sl09 .
Before we proceed to investigate this possibility, it is important to remark that one must be careful in defining an effective dynamics when there are some prior correlations between the system of interest and its environment, which in our case are the spin and momentum degrees of freedom of spin fermions, respectively. For example, even if the map describing the effective dynamics is linear and trace preserving, it may fail to be positive. Thus, to define a physically reasonable dynamics, one must restrict the domain of the map to a set in which it takes positive operators into positive operators mbcpv12 ; jss04 ; ctz08 ; mra12 ; rmg10 .
The maps and , given in Eqs. (57) and (58), describe the relativistic quantum channels for transmitting two and four bits of classical information, respectively. It is easy to see that they are convex-linear, trace preserving (and can be extended, in a non-unique way, to linear and trace preserving maps acting on all linear operators), and positive. Thus, at least on and , the maps and are well defined and describe the effective spin dynamics (which is enough for our purposes). It is well know that for any quantum map, i.e., any linear, trace-preserving, and CP operator , where is a Hilbert space, the Holevo bound satisfies nielsen&chuang
| (60) |
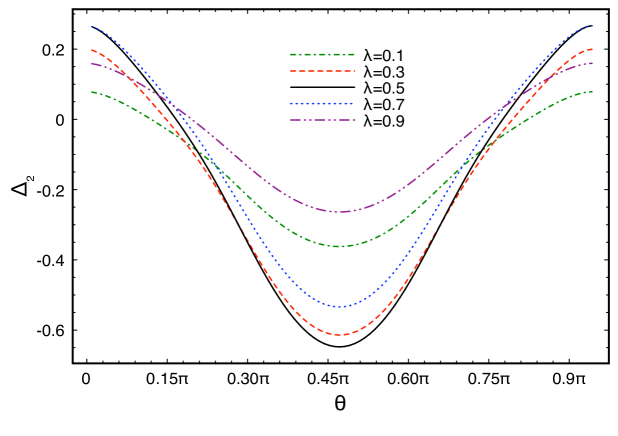
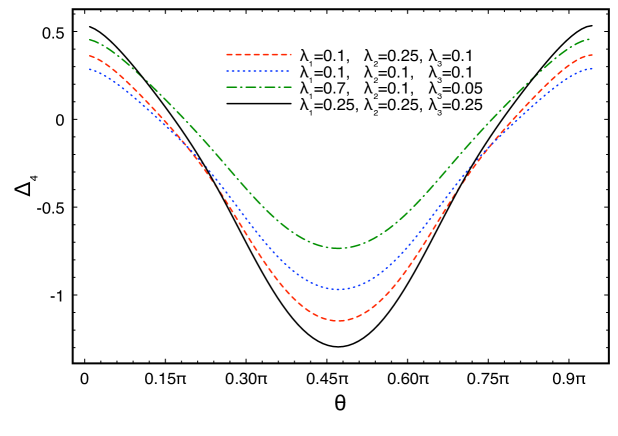
where is any density operator defined on Thus, quantum maps cannot increase the accessible information on the receiver. In Figs. 5 and 6 we plot
| (61) |
and
| (62) |
as functions of for different probability distributions and , respectively. In both figures we have fixed and . We can see from the plots that there are cases in which
| (63) |
and
| (64) |
Therefore, in the relativistic case, if one wants to always maximize the accessible information on the receiver, there will be quantum channels that cannot be described by quantum maps, i.e. linear, trace-preserving, and CP operators (the impossibility to describe quantum channels by CP maps in relativistic setups using photons as information carriers was noticed in PT02 ). This will be the case when the classical information is encoded in states with the angle characterizing the state being smaller (larger) than some angle (), with the value of depending on the number of bits and on their probability distribution, as can be seen from Figs. 5 and 6.
For angles closer to however, as we have already pointed out, the best strategy is to keep both and small to minimize the effects of the boost on the states. In the particular case where , , and , it is easy to see that both and are maps with Krauss decompositions
| (65) |
| (66) |
respectively, where the Krauss operators are given by
with being the identity operator and being given in Eq. (47).
Even in the CP regime, when one is dealing with quantum process tomography the initial correlations between the system of interest and its environment must be treated carefully. In such cases the preparation procedure plays a crucial role and the tomographically reconstructed quantum map may differ from the dynamical quantum map kmrs07 ; bgtw11 . It would be very interesting to investigate such issues in these relativistic scenarios.
V Final Remarks
In the present paper, we have used the Holevo bound to analyze how the relative motion between the sender and the receiver influences the capacity of a quantum communication channel to convey classical information. To this end, we have assumed that the sender, Alice, encodes the classical information in the spin degrees of freedom of spin- fermions of mass and sends the state prepared to the receiver, Bob, who is moving with velocity with respect to her. Bob then makes a spin measurement on the state and has to identify the message sent by Alice based on its measurement outcome.
First it was analyzed the case where Alice has a classical information source that produces symbols according to the probability distribution . Depending on the value of , Alice prepares the spin- particle in a pure quantum state and sends it to Bob. The spin part of and were assumed to be eigenstates, with eigenvalue , of and , with , respectively. It was shown that when is “close” to , Bob’s movement always reduces the Holevo bound and thus, the best strategy in this case is to use very narrow wave packets in the momentum degrees of freedom. This way, the states and are almost momentum eigenstates and therefore the effects of the boost on them are negligible. For small angles however, if Alice chooses and large enough, and Bob moves sufficiently fast, the Holevo bound overcomes , the Holevo bound in the case where Bob is at rest relative to Alice.
We have also analyzed how the above results generalize to the case where more classical bits are sent through the quantum channel. We have shown explicitly in the case where Alice has an information source that produces four bits according to the probability distribution and codifies each bit in one of the product states that the conclusions reached in the two bit case can be extended to this one.
The use of non-orthogonal quantum states to convey classical information is important not only due to cryptographic purposes but also due to the fact that there are noisy quantum channels in which the optimal rate of information transmission is achieved only by using non-orthogonal states fucs97 . Our results seem to indicate that when the classical information is conveyed through such noisy quantum channels and the sender and receiver are in relativistic relative motion, one might actually increase the channel capacity by carefully preparing the momentum degrees of freedom of the states. As we have shown, this is possible because, relativistically, boosts entangle the spin and momentum degrees of freedom of a spin- particle. Therefore, owing to his motion, the receiver can obtain some extra information in the spin degrees of freedom due to the fact that the states prepared by the sender are more distinguishable in momentum than in spin.
Acknowledgements.
The authors are indebted to George Matsas for useful discussions and for reading the manuscript. We also thank Roberto Serra for his useful comments and for pointing out Ref. [40] to us. A.L. and A.T. acknowledge partial and full support from the Brazilian National Institute for Science and Technology of Quantum Information (INCT-IQ) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) respectivelly.References
- (1) P. W. Shor, SIAM J. Sci. Stat. Comput. 26, 1484 (1997).
- (2) C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, Phys. Rev. Lett. 70, 1895 (1993).
- (3) S. Wiesner, SIGACT News 15, 78 (1983).
- (4) C. H. Bennett and G. Brassard, in Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, 1984 (IEEE, New York, 1984), p. 175.
- (5) A. K. Ekert, Phys. Rev. Lett. 67, 661 (1991).
- (6) C. H. Bennett and S. J. Wiesner, Phys. Rev. Lett. 69, 2881 (1992).
- (7) P. W. Shor, Phys. Rev. A 52, R2493 (1995).
- (8) M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2000).
- (9) A. Peres and D. R. Terno, Int. J. Quant. Info. 1, 225 (2003).
- (10) A. Peres and D. R. Terno, Rev. Mod. Phys. 76, 93 (2004).
- (11) S. W. Hawking, Phys. Rev. D 14, 2460 (1976).
- (12) R. M. Wald, Living Rev. Rel. 4, 6 (2001).
- (13) A. Peres, P. F. Scudo, and D. R. Terno, Phys. Rev. Lett. 88, 230402 (2002).
- (14) R. M. Gingrich and C. Adami, Phys. Rev. Lett. 89, 270402 (2002).
- (15) I. Fuentes-Schuller and R. B. Mann, Phys. Rev. Lett. 95, 120404 (2005) E. Martín-Martínez and I. Fuentes, Phys. Rev. A 83, 052306 (2011). G. Adesso, I. Fuentes-Schuller, and M. Ericsson, Phys. Rev. A 76, 062112 (2007).
- (16) N. Friis, P. Kohler, E. Martín-Martínez, and R. A. Bertlmann, Phys. Rev. A 84, 062111 (2011).
- (17) A. G. S. Landulfo and G. E. A. Matsas, Phys. Rev. A 80, 032315 (2009).
- (18) L. C. Céleri, A. G. S. Landulfo, R. M. Serra and G. E. A. Matsas, Phys. Rev. A 81, 062130 (2010).
- (19) Q. Pan and J. Jing, Phys. Rev. D 78, 065015 (2008).
- (20) E. Martín-Martínez and J. Leon, Phys. Rev. A 81, 032320 (2010).
- (21) D. Hosler, C. van de Bruck, and P. Kok, Phys. Rev. A 85, 042312 (2012).
- (22) M. Aspelmeyer, T. Jennewein, M. Pfennigbauer, W. Leeb, and A. Zeilinger, Selected Topics in Quantum Electronics, IEEE Journal of 9, 1541 (2003).
- (23) P. Villoresi et al., New J. Phys. 10, 033038 (2008).
- (24) R. Ursin et al., Space-QUEST: Experiments with quantum entanglement in space. IAC Proc. A2.1.3 (2008). arXiv: quant-ph/0806.0945v1.
- (25) C. Bonato, A. Tomaello, V. Da Deppo, G. Naletto, and P. Villoresi, New J. Phys. 11, 045017 (2009).
- (26) A. G. S. Landulfo and G. E. A. Matsas, Phys. Rev. A 79, 044103 (2009).
- (27) A. G. S. Landulfo, G. E. A. Matsas, and A. C. Torres, Phys. Rev. A 81, 044103 (2010).
- (28) J. F. Clauser, M. A. Horne, A. Shimony, and R. A. Holt, Phys. Rev. Lett. 23, 880 (1969).
- (29) W. K. Wootters and W. H. Zurek, Nature 299, 802 (1982).
- (30) V. Scarani, S. Iblisdir, and N. Gisin, Rev. Mod. Phys. 77, 1225 (2005).
- (31) A. S. Holevo, in Proceedings of the Second Japan-USSR Symposium on Probability Theory, edited by G. Maruyama and J. V. Prokhorov (Springer-Verlag, Berlin, 1973), p. 104.
- (32) B. Schumacher and M. D. Westmoreland, Phys. Rev. A 56, 131 (1997).
- (33) A. S. Holevo, IEEE Trans. Inf. Theory 44, 269 (1998).
- (34) C. A. Fuchs, Phys. Rev. Lett. 79, 1162 (1997).
- (35) N. N. Bogolubov, A. A. Logunov and I. T. Todorov, Introduction to Axiomatic Quantum Field Theory (W. A. Benjamin, Massachusetts, 1975).
- (36) F. R. Halpern, Special Relativity and Quantum Mechanics, (Prentice-Hall, Englewood Cliffs, NJ, 1968).
- (37) S. Weinberg, The Quantum Theory of Fields (Cambridge University Press, Cambridge, 1996), Vol. I.
- (38) E. P. Wigner, Ann. Math. 40, 149 (1939).
- (39) A. Ferraro, L. Aolita, D. Cavalcanti, F. M. Cucchietti, and A. Acín, Phys. Rev. A 81, 052318 (2010).
- (40) A. Brodutch, A. Datta, K. Modi, Ángel Rivas, and C. A. Rodríguez-Rosário, Phys. Rev. A 87, 042301 (2013).
- (41) K. Modi, A. Brodutch, H. Cable, T. Paterek, and V. Vedral, Rev. Mod. Phys. 84, 1655 (2012).
- (42) A. Shabani and D. A. Lidar, Phys. Rev. Lett 102, 100402 (2009).
- (43) T. F. Jordan, A. Shaji, and E. C. G. Sudarshan, Phys. Rev. A 70, 052110 (2004).
- (44) H. A. Carteret, D. R. Terno, and Karol Życzkowski, Phys. Rev. A 77, 042113 (2008).
- (45) C. A. Rodríguez-Rosário, K. Modi, and A. Aspuru-Guzik, Phys. Rev. A 81, 012313 (2010).
- (46) F. Masillo, G. Scolarici, and L. Solombrino, J. Math. Phys. 52, 012101 (2011).
- (47) A. Peres and D. R. Terno, J. Mod. Optics 50, 1165 (2003).
- (48) A. M. Kuah, K. Modi, C. A. Rodríguez-Rosário, and E. C. G. Sudarshan, Phys. Rev. A 76, 042113 (2007).
- (49) A. Brodutch, A. Gilchrist, D. R. Terno, and C. J. Wood, J. Phys.: Conf. Ser. 306, 012030 (2011).