Sequential Monte Carlo algorithms for agent-based models of disease transmission
Abstract
Agent-based models of disease transmission involve stochastic rules that specify how a number of individuals would infect one another, recover or be removed from the population. Common yet stringent assumptions stipulate interchangeability of agents and that all pairwise contact are equally likely. Under these assumptions, the population can be summarized by counting the number of susceptible and infected individuals, which greatly facilitates statistical inference. We consider the task of inference without such simplifying assumptions, in which case, the population cannot be summarized by low-dimensional counts. We design improved particle filters, where each particle corresponds to a specific configuration of the population of agents, that take either the next or all future observations into account when proposing population configurations. Using simulated data sets, we illustrate that orders of magnitude improvements are possible over bootstrap particle filters. We also provide theoretical support for the approximations employed to make the algorithms practical.
1 Introduction
1.1 Statistical inference for agent-based models
Agent-based models also called individual-based models are used in many fields, such as social sciences (Epstein, 2006), demographics (Hooten et al., 2020), ecology (DeAngelis and Gross, 2018) and macroeconomics (Turrell, 2016). These models describe the time evolution of a population according to a Markov process. The population comprises of agents who interact with one another through a probabilistic mechanism. The popularity of these models could be attributed to the ease of model building and interpretation, while allowing the representation of complex phenomena. Specialized software is available to facilitate their simulation and the visualization of their output (e.g. Tisue and Wilensky, 2004).
The primary use of these models seems to involve “forward simulations” using various parameters corresponding to hypothetical scenarios. In comparison, relatively fewer works have tackled the question of statistical inference for such models, i.e. the estimation of model parameters given available observations, also known as model calibration. Broad articles on the question of fitting agent-based models include Grazzini et al. (2017); Hooten et al. (2020); Hazelbag et al. (2020) and this is a very active research area. The question of estimation is well-posed: by viewing agent-based models as a subclass of hidden Markov models, we can define the associated likelihood function, from which maximum likelihood and Bayesian procedures can be envisioned.
Gibbs sampling or “data augmentation” Markov chain Monte Carlo (MCMC) methods, that alternate between parameter and latent agent states updates are generically applicable, see Fintzi et al. (2017); Bu et al. (2020) in the context of disease transmission. However, the mixing properties of these chains can be problematic, as we illustrate in Appendix C. Likelihood-based inference that avoid the use of data augmentation requires one to marginalize out the latent population process. This is computationally challenging as the number of possible configurations of the population of agents grows exponentially in . Our contribution is to design improved particle filters to estimate the likelihood function of agent-based models, which can then be used for parameter inference procedures such as simulated maximum likelihood and particle MCMC (Andrieu et al., 2010). Particle MCMC methods, based on more standard particle filters, have been used for agent-based models before, see e.g. Kattwinkel and Reichert (2017). For indirect inference and approximate Bayesian computation applied to agent-based models we refer to (Platt, 2020; van der Vaart et al., 2016; Chen et al., 2017; Sirén et al., 2018).
1.2 Statistical inference for agent-based models of disease transmission
We limit the scope of this article to some agent-based models of disease transmission. We next introduce a specific model which will be used to draw clear connections between agent-based models and more tractable but restrictive formulations of disease outbreak models.
The state of agent at time , denoted by , takes the value or , corresponding to a “susceptible” or “infected” status in the context of disease transmission. We consider a closed population of size , time steps and a stepsize of . Initial agent states follow independent Bernoulli distributions, i.e.
| (1) |
for , where we assume for the time being that each agent has the same probability of being infected. The state of the population evolves according to a Markov process that depends on the interactions between the agents. The Markov transition specifies that, given the previous states , the next agent states are conditionally independent Bernoulli variables with probabilities given by
| (2) |
Here and represent infection and recovery rate parameters respectively. An uninfected agent becomes infected with probability proportional to and to the proportion of infected individuals. An infected agent recovers with probability proportional to . The ratio is known as the basic reproductive number, which characterizes the transmission potential of a disease (Lipsitch et al., 2003; Britton, 2010). The latent population process can be related to aggregated observations of the entire population. For example, the number of infections reported at each time could be modelled as a Binomial distribution, i.e.
| (3) |
where counts the number of infected individuals and represents a reporting rate. Equations (1), (2) and (3) define a susceptible-infected-susceptible (SIS) hidden Markov model.
As the latent state space has cardinality , evaluating the likelihood function with the forward algorithm would be impractical. Statistical inference is still feasible as the latent process admits low-dimensional summaries. Since (2) assumes that all agents are interchangeable and all pairwise contact are equally likely, the dynamics depends only on the number of infected individuals and susceptible individuals . More precisely, the Markov transition for each can be summarized as
| (4) |
where and denote the number of new recoveries and infections, respectively. The initialization in (1) corresponds to having and . The process is a Markov chain on the lower-dimensional state space , and not in . When combined with (3), the resulting hidden Markov model can be estimated using particle filtering strategies; see e.g. Ionides et al. (2006); Endo et al. (2019); Whiteley and Rimella (2020).
For large population sizes , one can exploit the asymptotic properties of the dynamics (4) to further simplify inference procedures. As , the finite population proportions and admit deterministic limits and , defined by the recursion
| (5) |
with initial condition . If fine time resolutions are desired, one can also consider the limit , in which case converges to a deterministic continuous-time process , defined by the following system of ordinary differential equations
| (6) |
with . We refer to Allen and Burgin (2000) and Allen et al. (2008, Chapter 3) for formal links between stochastic and deterministic SIS models, in the form of limit theorems as . The dynamics in (5) or (6) combined with an observation model such as (3) leads again to a fairly tractable statistical model, which can be estimated by maximum likelihood or in the Bayesian framework (e.g. Osthus et al., 2019).
The tractability in (4) and its limits (5)-(6) hinges critically on the assumption that all agents are interchangeable and equally likely to be in contact. These assumptions are strong as it would be desirable to let the infection and recovery rates depend on individual characteristics or features, and the structure of interactions be specified by an undirected network. Adopting any one of these generalizations would result in an agent-based model that cannot be summarized by low-dimensional counts. This article is concerned with the task of inference when these assumptions are relaxed. Our approach is to return to the hidden Markov model formulation with latent space , and seek novel sampling algorithms that have polynomial rather than exponential costs in . The guiding principle of our contribution is that we can improve the performance of Monte Carlo algorithms, sometimes dramatically, by tailoring them to the models at hand, and by using available observations.
The rest of this article is organized as follows. In Section 2, we consider a “static” case with a single time step to illustrate some of the challenges and proposed solutions in a simple setting. We describe how the cost of likelihood evaluation and sampling the posterior of agent states given observations can be reduced from exponential to polynomial in . In Section 3, we consider the dynamic setting with multiple time steps and design auxiliary particle filters and controlled SMC algorithms tailored to heterogeneous SIS agent-based models. We also provide theoretical support for the approximations employed to make the algorithms practical. We extend our methodology to susceptible-infected-recovered (SIR) models in Section 4 and highlight the associated difficulties. Section 5 summarizes our findings and open questions. This manuscript represents preliminary work and further numerical experiments will be added in a later version. The code is available at https://github.com/nianqiaoju/agents. The proofs and more details are in appendices.
2 Static agent-based model
For simplicity we begin with the static model independently for , and allow each agent to be unique by modeling , where are parameters and are the covariates of agent . This allows individual factors to account for the probability of infection . Given an observation modelled as (3), our inferential objective might include estimating the unknown parameters and/or the latent states . The complete data likelihood is , where
| (7) |
Here and denote the corresponding probability mass functions (PMF). Marginalizing over the latent states yields the likelihood . The agent states given the observation and a parameter follow the posterior distribution . In Sections 2.1 and 2.2, we examine the cost of exactly computing and sampling from , respectively, and describe cheaper approximations. The gains are assessed numerically in Section 2.3.
2.1 Marginal likelihood computations
A naive approach to compute the marginal likelihood is to sum over all possible population configurations
| (8) |
This requires operations. A simple Monte Carlo approach involves sampling independently for , which represents possible configurations of the population, and return the Monte Carlo estimator that weights each configuration according to the observation density. The estimator is unbiased and only costs to compute, but its variance might be prohibitively large for practical values of , depending on the observation model . Another issue with this estimator is that it can collapse to zero whenever for all . Following Del Moral et al. (2015), this can be circumvented by repeatedly drawing samples independently until there are configurations that satisfy , and return the estimator , where denotes the number of repetitions needed. The resulting estimator can be shown to be unbiased and has a random cost of , that depends on the value of . An obvious shortcoming of the above estimators is that the agents are sampled from without using the available observation .
We can in fact reduce the cost of computing (8) without resorting to Monte Carlo approximations. The starting observation is that under is the sum of independent Bernoulli random variables with non-identical success probabilities, and follows a distribution called “Poisson Binomial”. We will refer to this distribution as PoiBin() and write its PMF as
| (9) |
Exact evaluation of (9) has been considered in Barlow and Heidtmann (1984); Chen et al. (1994); Chen and Liu (1997); Hong (2013) using different approaches. Defining for and , we will employ the following recursion
| (10) |
with initial conditions for , and for . The desired PMF for can thus be computed in operations; see Appendix A.1 for a derivation of (10).
Using the above observation, we can rewrite the marginal likelihood as
| (11) |
which costs to compute. Using a thinning argument detailed in Appendix A.2, the above sum is in fact equal to . Although the marginal likelihood will not admit such tractability in the general setup considered in Section 3, the preceding observations will guide our choice of approximations.
One can also rely on approximations of the Poisson Binomial distribution to further reduce the cost of computing (11) to . Choices include the Poisson approximation (Hodges and Le Cam, 1960; Barbour and Hall, 1984; Wang, 1993), the Normal approximation (Volkova, 1996) and the translated Poisson approximation (Barbour and Xia, 1999; Cekanavicius and Vaitkus, 2001; Barbour and Ćekanavićius, 2002). We will focus on the translated Poisson approximation which exactly matches the mean and approximately the variance of a Poisson Binomial distribution. Let denote a Poisson distribution with rate and write the mean and variance of PoiBin() as and , respectively. The translated Poisson approximation of (9) is given by
| (12) |
where and denote the floor and fractional part of , respectively. Since and can be computed in operations, the translated Poisson approximation (12) and the resulting approximation of (11) only require operations. Hence this can be appealing in the setting of large population sizes at the expense of an approximation error that is well-studied. Indeed results in Cekanavicius and Vaitkus (2001, Theorem 2.1 & Corollary 2.1) and Barbour and Ćekanavićius (2002, Theorem 3.1) imply that the error, measured in the total variation distance, decay at the rate of as .
2.2 Posterior sampling of agent states
Sampling from the posterior distribution by naively enumerating over all configurations is computationally impractical. A key observation is that the observation density in (7) depends on the high dimensional latent state only through the one-dimensional summary . This prompts the inclusion of as an auxiliary variable. Thus the joint posterior distribution can be decomposed as
| (13) |
The dominant cost of sampling the posterior distribution of the summary
| (14) |
is the evaluation of the Poisson Binomial PMF (9). Recall from Section 2.1 that this can be done exactly in , and in using a translated Poisson approximation. The conditional distribution of the latent state given the summary
| (15) |
is known as a conditional Bernoulli distribution, which we will write as . Various sampling schemes have been proposed (Fan et al., 1962; Chen et al., 1994); see Chen and Liu (1997, Section 4) for an overview. We will rely on the sequential decomposition
| (16) | ||||
where and for . A derivation of (16) can be found in Appendix A of Heng et al. (2020b). The values of for needed in (16) can be precomputed using the same recursion as (10) in cost. This precomputation is not necessary if these values are stored when computing Poisson Binomial probabilities.
To reduce the cost we can employ a Markov chain Monte Carlo (MCMC) method to sample from the conditional Bernoulli distribution . This incurs a cost of per iteration and converges in iterations, under some mild assumptions on , as shown in Heng et al. (2020b). On a related note, we can design MCMC algorithms to target . These might for example update the state of a few agents by sampling from their conditional distributions given every other variables, and alternately propose to swap zeros and ones in the vector . Each of these steps can be done with a cost independent of , but the number of iterations for the algorithm to converge is expected to grow at least linearly with .
2.3 Numerical illustration
We set up numerical experiments as follows. We generate covariates from for individuals independently, where denotes a Normal distribution with mean and variance . Individual specific infection probabilities are computed as using . We then simulate independently for all , and sample , with . We adopt a Bayesian approach and assign an independent prior of on and on . We focus on the task of sampling from the posterior distribution of given and the covariates .
We consider random walk Metropolis–Hastings with exact likelihood calculation (“MH-exact”), associated with a quadratic cost in . We also consider the same algorithm with a likelihood approximated by a translated Poisson (“MH-tp”), with a cost linear in . Finally we consider a pseudo-marginal approach (Andrieu and Roberts, 2009; Andrieu et al., 2010) with likelihood estimated with particles sampled from (“PMMH”). Note that samples resulted in a variance of the log-likelihood estimates of approximately at the data generating parameters (DGP). These samplers employ the same random walk, based on Normal proposals, independently on and with standard deviation of . As a baseline we also consider a Gibbs sampler that alternates between the updates of given , employing the same proposal as above, and updates of given . These employ an equally weighted mixture of kernels, performing either random swap updates, or a systematic Gibbs scan of the components of ; thus the cost per iteration is linear in .
We first run “MH-exact” with MCMC iterations (after a burn-in of iterations), to obtain estimates of the posterior means of and . Using these posterior estimates as ground truth, we compute the mean squared error (MSE) of the posterior approximations obtained using each method with MCMC iterations (excluding a burn-in of ) and 50 independent repetitions. Table 1 displays the MSE, as well as the relative wall-clock time to obtain each estimate. Comparing the results of MH-exact and MH-tp shows that it is possible to save considerable efforts at the expense of small differences in the parameter estimates using a translated Poisson approximation. The appeal of the PMMH approach compared to exact likelihood calculations is also clear. On the other hand, Gibbs samplers that alternate between the updates of and do not seem to be competitive in this example.
| Method | Relative cost | ||||
|---|---|---|---|---|---|
| Bias2 | Variance | Bias2 | Variance | ||
| MH-exact | 25 | 93.3 | 0.74 | 6.39 | 128 |
| MH-tp | 22 | 52.3 | 0.32 | 2.83 | 1 |
| PMMH | 18 | 79.2 | 0.50 | 4.67 | 8 |
| Gibbs | 1040 | 113 | 91.1 | 2.85 | 42 |
3 Susceptible-Infected-Susceptible model
We now extend the agent-based SIS model in Section 1.2. To allow for individual-specific attributes, for agent , we model her initial infection probability , infection rate and recovery rate as
| (17) |
Here are parameters and are the covariates of agent . The interactions between agents is assumed to be known and specified by an undirected network; inference of the network structure and extension to the time-varying case could be considered in future work. We will write and to denote the degree and neighbours of agent .
For ease of presentation, we consider time steps of size . The time evolution of the population is given by
| (18) |
The initial distribution corresponds to the static model in Section 2 with infection probabilities . The Markov transition has conditional probabilities given by
| (19) |
for . We will assume that the cost of evaluating is . We refer readers to McVinish and Pollett (2012) for the asymptotic behaviour of this process as , in the case of a fully connected network. In (19) we see the proportion of infected neighbours appearing in the infection probability at each time step. As an individual can have covariates that include measures of contact frequency, which would affect via , it is possible for an individual with many neighbours (large ) to have low infection probability if the frequency of contact is low.
Equations (17)-(19) and the observation model in (3) define a hidden Markov model on , with unknown parameters ; see Figure 1 for a graphical model representation in the case of a fully connected network. Given an observation sequence , the complete data likelihood is given by
| (20) |
Parameter inference will require marginalizing over the latent process to obtain the marginal likelihood and estimation of agent states will involve sampling from the smoothing distribution . Exact computation of the marginal likelihood and marginals of the smoothing distribution using the forward algorithm and forward-backward algorithm, respectively, both require operations. As this is computationally prohibitive for large , we will rely on sequential Monte Carlo (SMC) approximations.
In Section 3.1, we describe how SMC methods can be used to approximate the marginal likelihood and the smoothing distribution. Like many Monte Carlo schemes, the efficiency of SMC crucially relies on the choice of proposal distributions. The bootstrap particle filter (BPF) (Gordon et al., 1993), which corresponds to having the joint distribution of the latent process (18) as proposal, can often give poor performance in practice when the observations are informative. By building on the insights from Section 2, we will show how the fully adapted auxiliary particle filter (APF) (Pitt and Shephard, 1999; Carpenter et al., 1999) can be implemented. As the APF constructs a proposal transition at each time step that takes the next observation in account, it often performs better than the BPF, although not always (Johansen and Doucet, 2008). In Section 3.2, we adapt the ideas in Guarniero et al. (2017); Heng et al. (2020a) to our setting and present a novel controlled SMC (cSMC) method that can significantly outperform the APF. Central to our approach is to take the entire observation sequence into account by constructing proposal distributions that approximate the smoothing distribution . Using a simulated dataset, in Section 3.3 we show that cSMC provides orders of magnitude improvements over BPF and APF in terms of estimating the marginal likelihood. In Section 3.4, we illustrate the behaviour of marginal likelihood as the number of observations increases, and perform parameter inference and predictions. We consider MCMC strategies as alternatives to SMC-based methods in Appendix C.
3.1 Sequential Monte Carlo
SMC methods (Liu and Chen, 1998; Doucet et al., 2001), also known as particle filters, provide approximations of and by simulating an interacting particle system of size . In the following, we give a generic description of SMC to include several algorithms in a common framework.
At the initial time, one samples configurations of the population from a proposal distribution on , i.e. independently for . Each possible configuration is then assigned a weight that is normalized to sum to one. To focus our computation on the more likely configurations, we perform an operation known as resampling that discards some configurations and duplicates others according to their weights. Each resampling scheme involves sampling ancestor indexes from a distribution on . The simplest scheme is multinomial resampling (Gordon et al., 1993), which samples independently from the categorical distribution on with probabilities ; other lower variance and adaptive resampling schemes can also be employed (Fearnhead and Clifford, 2003; Gerber et al., 2019). Subsequently, for time step , one propagates each resampled configuration according to a proposal transition on , i.e. independently for . As before, we weight each new configuration according to , and for , resample by drawing the ancestor indexes . For notational simplicity, we suppress notational dependence of the weight functions on the parameter . To approximate the desired quantities and , these weight functions have to satisfy
| (21) |
Given the output of the above simulation, an unbiased estimator of the marginal likelihood is
| (22) |
and a particle approximation of the smoothing distribution is given by
| (23) |
In the latter approximation, each trajectory is formed by tracing the ancestral lineage of , i.e. with and for . Convergence properties of these approximations as the size of the particle system are well-studied; see for example Del Moral (2004). However, the quality of these approximations depends crucially on the choice of proposals and the corresponding weight functions that satisfy (21).
The BPF of Gordon et al. (1993) can be recovered by employing the proposals for and the weight functions for . Although the BPF only costs to implement and has convergence guarantees as , the variance of its marginal likelihood estimator can be too large to deploy within particle MCMC schemes for practical values of (see Section 3.3). Another issue with its marginal likelihood estimator, for this particular choice of observation equation, is that it can collapse to zero if all proposed configurations have less infections than the observed value, i.e. there exists such that for all . With increased cost, this issue can be circumvented using the alive particle filter of Del Moral et al. (2015), by repeatedly drawing samples at each time step until there are configurations with infections that are larger than or equal to the observed value.
Alternatively, one can construct better proposals with supports that respect these observational constraints. One such option is the fully adapted APF (Pitt and Shephard, 1999; Carpenter et al., 1999) that corresponds to having the proposals for and the weight functions and for . At the initial time, computing the marginal likelihood and sampling from the posterior of agent states can be done exactly (or approximately) as described in Sections 2.1 and 2.2 respectively for the static model. More precisely, we compute
| (24) |
and sample from
| (25) |
which admits as its marginal distribution. For time step , by conditioning on the previous configuration , the same ideas can be used to compute the predictive likelihood and sample from the transition , i.e. we compute
| (26) |
and sample from
| (27) | ||||
which admits as its marginal transition.
An algorithmic description of the resulting APF is detailed in Algorithm 1, where the notation refers to the categorical distribution on with probabilities . As the weights in the fully adapted APF at time only depend on the configuration at time , note that we have interchanged the order of sampling and resampling to promote sample diversity. The cost of running APF exactly is . To reduce the computational cost to one can approximate the above Poisson binomial PMFs with the translated Poisson approximation (12), and employ MCMC to sample from the above conditioned Bernoulli distributions.
3.2 Controlled sequential Monte Carlo
To obtain better performance than APF, we can construct proposals that take not just the next but all future observations into account. We can sequentially decompose the smoothing distribution as
| (28) |
and it follows that the optimal proposal is and for , as this gives exact samples from the smoothing distribution. The resulting SMC marginal likelihood estimator in (22) would have zero variance for any choice of weight functions satisfying (21). To design approximations of the optimal proposal, it will be instructive to rewrite it as
| (29) |
where for , denotes the expectation of with respect to and denotes the conditional expectation of under . Equation (29) shows how the latent process (18), defined by and , should be modified to obtain the optimal proposal. The functions , known as the backward information filter (BIF) (Bresler, 1986; Briers et al., 2010), can be defined using the backward recursion
| (30) |
which shows how information from future observations are propagated backwards over time. As the cost of computing and storing the BIF using the recursion (30) are and , respectively, approximations are necessary when is large. In contrast to Guarniero et al. (2017); Heng et al. (2020a) that rely on regression techniques to approximate the BIF, our approach is based on dimensionality reduction by coarse-graining the agent-based model.
At the terminal time , the function only depends on the agent states through the one-dimensional summary . Therefore it suffices to compute and store for all . Note that should be seen as a function of the agent states. To iterate the backward recursion (30), we have to compute the conditional expectation for all . By a thinning argument (Appendix A.2), this is equal to . Hence it is clear that all possible configurations of the population have to be considered to iterate the recursion, and an approximation of is necessary at this point.
To reduce dimension, we consider
| (31) |
This amounts to approximating the proportion of infected neighbours of each agent by the population proportion of infections, and replacing individual infection and recovery rates in (19) by their population averages, i.e. and . Writing as the Markov transition associated to (31), we approximate the conditional expectation by
| (32) |
where denotes the distribution of a sum of two independent and random variables. This follows as a Poisson binomial distribution with homogeneous probabilities (31) reduces to the SumBin distribution in (32), which is not analytically tractable but can be computed exactly in cost using a naive implementation of the convolution111 for .. In the large regime, we advocate approximating the SumBin distribution with the translated Poisson (12), which reduces the cost to at the price of an approximation error. Moreover, the latter bias only affects the quality of our proposal distributions, and not the consistency properties of SMC approximations. The resulting approximation of can be computed using
| (33) |
for all . This costs if convolutions are implemented naively and if translated Poisson approximations of (32) are employed. We then continue in the same manner to approximate the recursion (30) until the initial time. Algorithm 2 summarizes our approximation of the BIF , which costs or to compute and in storage.
Our corresponding approximation of the optimal proposal (29) is
| (34) |
To employ these proposals within SMC, the appropriate weight functions (Scharth and Kohn, 2016) satisfying (21) are
| (35) |
and . To evaluate the weights, note that expectations can be computed as
| (36) |
Sampling from the proposals in (34) can be performed in a similar manner as the APF. To initialize, we sample from
| (37) |
which admits as its marginal distribution, and for time
| (38) | ||||
which admits as its marginal transition. Algorithm 3 gives an algorithmic summary of the resulting SMC method, which we shall refer to as controlled SMC (cSMC), following the terminology of Heng et al. (2020a). This has the same cost as the APF, and one can also employ translated Poisson approximations (12) and MCMC to reduce the computational cost.
To study the performance of cSMC, we consider the Kullback–Leibler (KL) divergence from our proposal distribution to the smoothing distribution , denoted as , which characterizes the quality of our importance proposal (Chatterjee and Diaconis, 2018). The following result provides a decomposition of this KL divergence in terms of logarithmic differences between the BIF and our approximation under the marginal distributions of the smoothing distribution and our proposal distribution, denoted as and respectively for each time . Given a function , we will write and to denote expectations under these marginal distributions, and its corresponding -norms as and .
Proposition 3.1.
The Kullback–Leibler divergence from to satisfies
| (39) |
where and for .
The proof is given in Appendix B.1. We show in Appendix B.2 that the constants are finite by upper bounding the weight functions in (35). The next result characterizes the error of our BIF approximation measured in terms of the KL upper bound in (39).
Proposition 3.2.
For each time , the BIF approximation in Algorithm 2 satisfies:
| (40) | |||
| (41) |
with constants
for , functions ,
| (42) |
for , and the convention that for .
The proof of Proposition 3.2 in Appendix B.3 derives recursive bounds of the approximation errors. The crux of our arguments is to upper bound the error of taking conditional expectations under the homogeneous probabilities (31). This relies on an upper bound of the Kullback–Leibler divergence between two Poisson binomial distributions that is established in Appendix A.3, which may be of independent interest. If conditional expectations are further approximated using the translated Poisson approximations, one can also employ the results by Cekanavicius and Vaitkus (2001); Barbour and Ćekanavićius (2002) to incorporate these errors in our analysis. The error bounds in (40) and (41) show how the accuracy of the BIF approximation depend on our approximation of the success probability via the term . If we decompose , where
| (43) |
we see the effect of coarse-graining the agent-based model in (31). In Appendix B.4, we discuss how to reduce the errors and . By adopting a more fine-grained approximation based on clustering of the infection and recovery rates, one can obtain more accurate approximations at the expense of increased computational cost.
3.3 Numerical illustration of sequential Monte Carlo methods
We now illustrate the behaviour of the above SMC methods on simulated data. We consider a population of agents that are fully connected for time steps. The agent covariates are taken as and sampled from independently for . Given these covariates, we simulate data from model (17)-(19) and (3) with the parameters , , and .
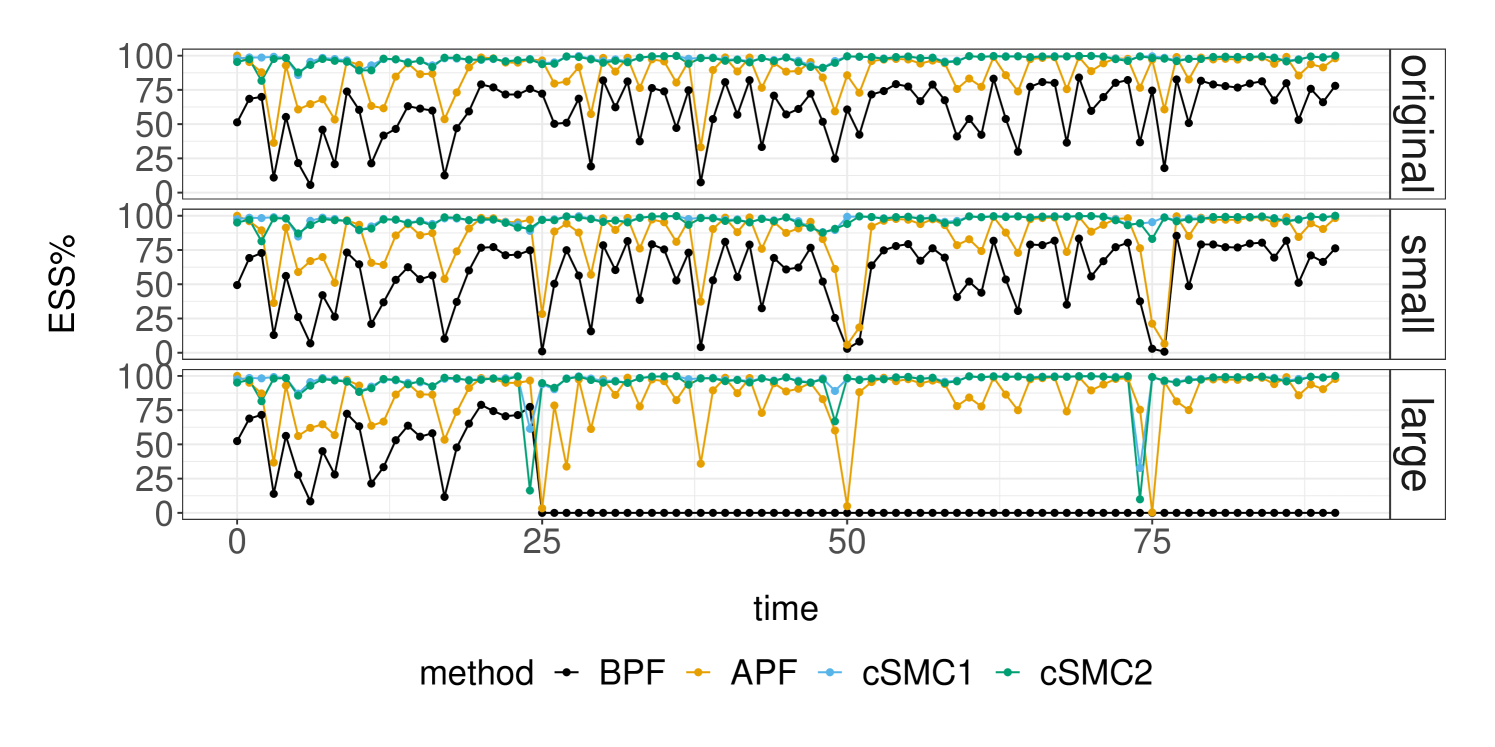
The top panel of Figure 2 illustrates the performance of these SMC methods at the data-generating parameter (DGP), measured in terms of the effective sample size (ESS) criterion (Kong et al., 1994). The ESS at time , defined in terms of the normalized weights as , measures the adequacy of the importance sampling approximation at each step. We consider two implementations of the controlled SMC in Algorithm 3: cSMC1 employs proposal distributions that are defined by the BIF approximation in Algorithm 2, while cSMC2 relies on translated Poisson approximations of the SumBin distributions in Algorithm 2 to lower the computational cost. This lowers the run-time of the BIF approximation from to second, which are insignificant relative to the cost of cSMC for a population size of . As expected, the APF performs better than the BPF by taking the next observation into account, and cSMC does better than APF by incorporating information from the entire observation sequence. Furthermore, the faster BIF approximation does not result in a noticeable loss of cSMC performance due to the accuracy of the translated Poisson approximations with agents. Although the performance of BPF seems adequate in this simulated data setting, the middle and bottom panels of Figure 2 reveal that its particle approximation can collapse whenever there are smaller or larger observation counts. In contrast, the performance of APF and cSMC appear to be more robust to such informative observations.
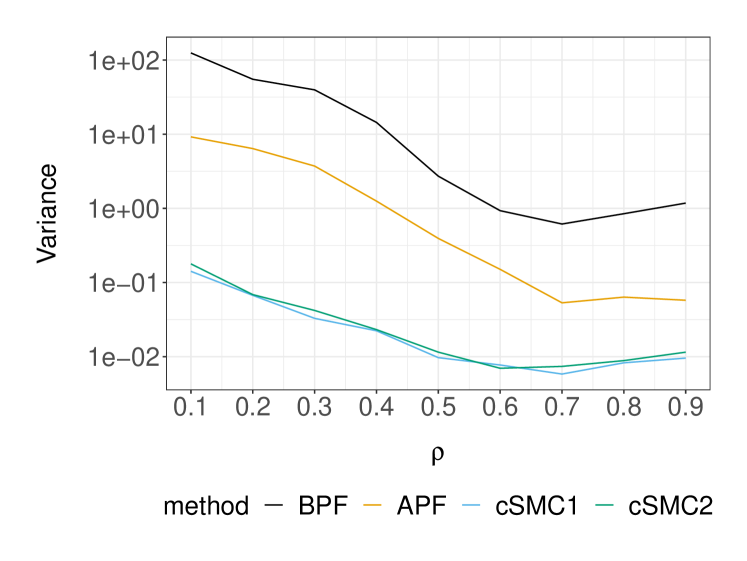
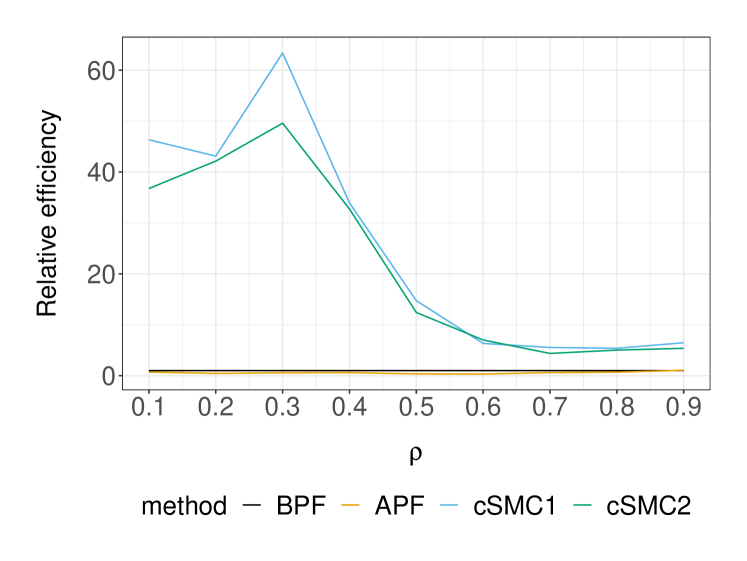
Next we examine the performance of these SMC methods in terms of marginal likelihood estimation. Table 2 displays the variance of the log-marginal likelihood estimator at two parameter sets, and its average cost measured as run-time that were estimated using independent repetitions of each method. At the DGP, it is apparent that the cSMC estimators achieve the asymptotic regime of earlier than BPF and APF, which seem to require at least particles. Based on the largest value of that we considered, the asymptotic variance of APF, cSMC1 and cSMC2 was found to be , and times smaller relative to BPF, respectively. As the cost of APF and cSMC was approximately times more expensive than BPF in our implementation, we see that APF, cSMC1 and cSMC2 are respectively , and times more efficient than BPF at the DGP. We can expect these efficiency gains to be more significant as we move away from the DGP. To illustrate this, we consider another parameter set which has and keeps all other parameters at the DGP. Although this is a less likely set of parameters as the log-marginal likelihood is approximately lower than the DGP, adequate marginal likelihood estimation is crucial when employing SMC methods within particle MCMC algorithms for parameter inference. In this case, we found that the BPF marginal likelihood estimates could collapse to zero for the values of that are considered in Table 2. In contrast, APF and cSMC would not suffer from this issue by construction. By increasing the number of BPF particles to and comparing its performance to APF, cSMC1 and cSMC2 with particles, we find that BPF is respectively , and times less efficient at this parameter set. Lastly, Figure 3 illustrates the comparison of SMC methods as the parameter varies and all other parameters fixed at the DGP.
| BPF | APF | cSMC1 | cSMC2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DGP | Cost | DGP | Non-DGP | Cost | DGP | Non-DGP | DGP | Non-DGP | Cost | |
| Var | (sec) | Var | Var | (sec) | Var | Var | Var | Var | (sec) | |
| 64 | 4.32 | 0.09 | 0.281 | 71.88 | 1.49 | 0.0696 | 13.52 | 0.0779 | 18.44 | 1.46 |
| 128 | 2.39 | 0.17 | 0.154 | 39.52 | 2.95 | 0.0285 | 8.62 | 0.0382 | 8.48 | 2.88 |
| 256 | 1.67 | 0.33 | 0.110 | 26.86 | 5.85 | 0.0164 | 4.11 | 0.0190 | 6.88 | 5.72 |
| 512 | 0.88 | 0.63 | 0.056 | 18.98 | 11.72 | 0.0087 | 3.57 | 0.0105 | 5.03 | 11.41 |
| 1024 | 0.55 | 1.25 | 0.026 | 13.38 | 23.46 | 0.0049 | 2.05 | 0.0046 | 3.41 | 22.83 |
| 2048 | 0.31 | 2.49 | 0.011 | 9.93 | 47.48 | 0.0020 | 1.15 | 0.0027 | 2.07 | 45.97 |
3.4 Parameter and state inference
We first concern ourselves with the behaviour of the marginal likelihood and the maximum likelihood estimator (MLE) as the number of observations . This is illustrated with our running simulated dataset from Section 3.3. Figure 4 plots the log-likelihood as a function of or with the other parameters fixed at their data generating values, estimated using cSMC with particles. These plots reveal the complex behavior of the likelihood functions induced by agent-based SIS models. Furthermore, we see that the likelihood concentrates more around the DGP as increases, and that the MLE can recover the DGP when is sufficiently large.
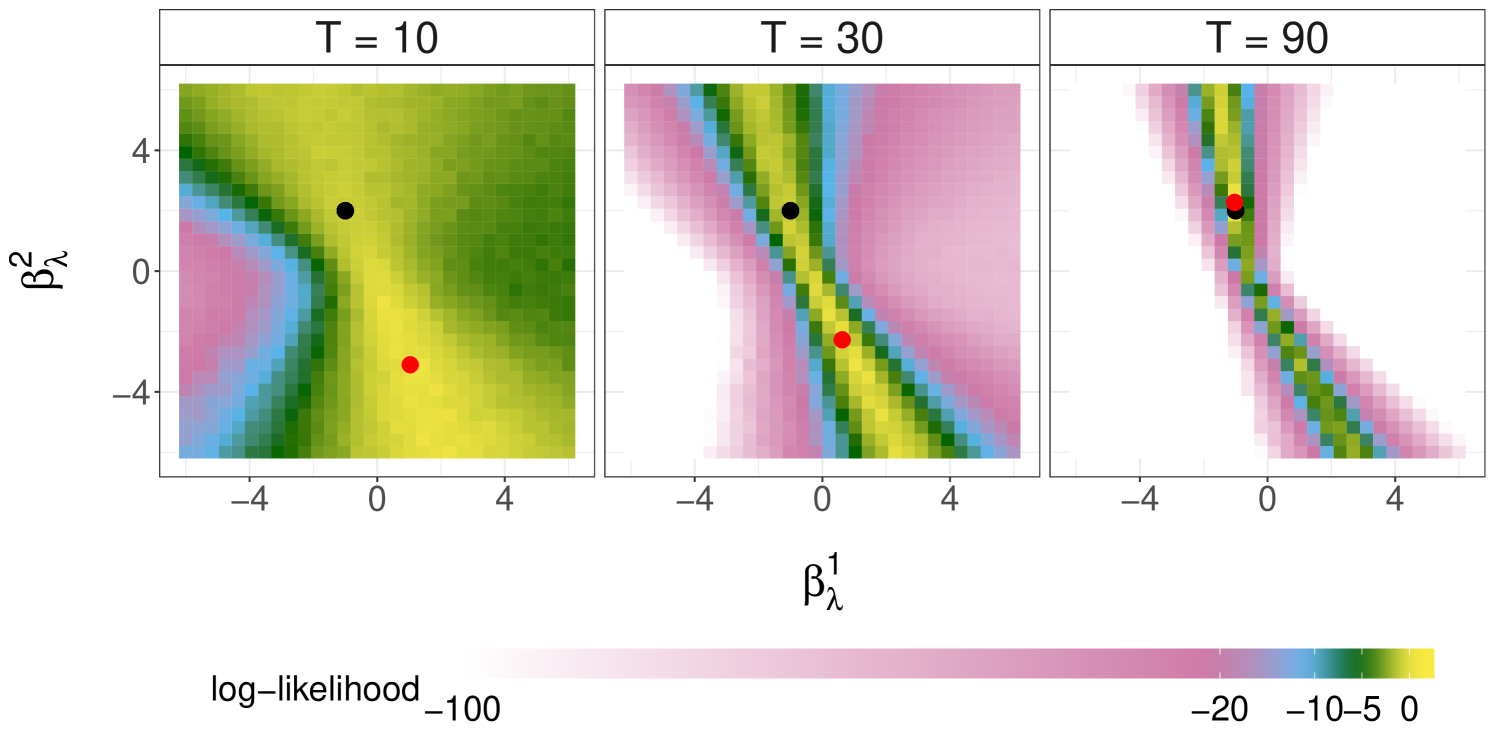
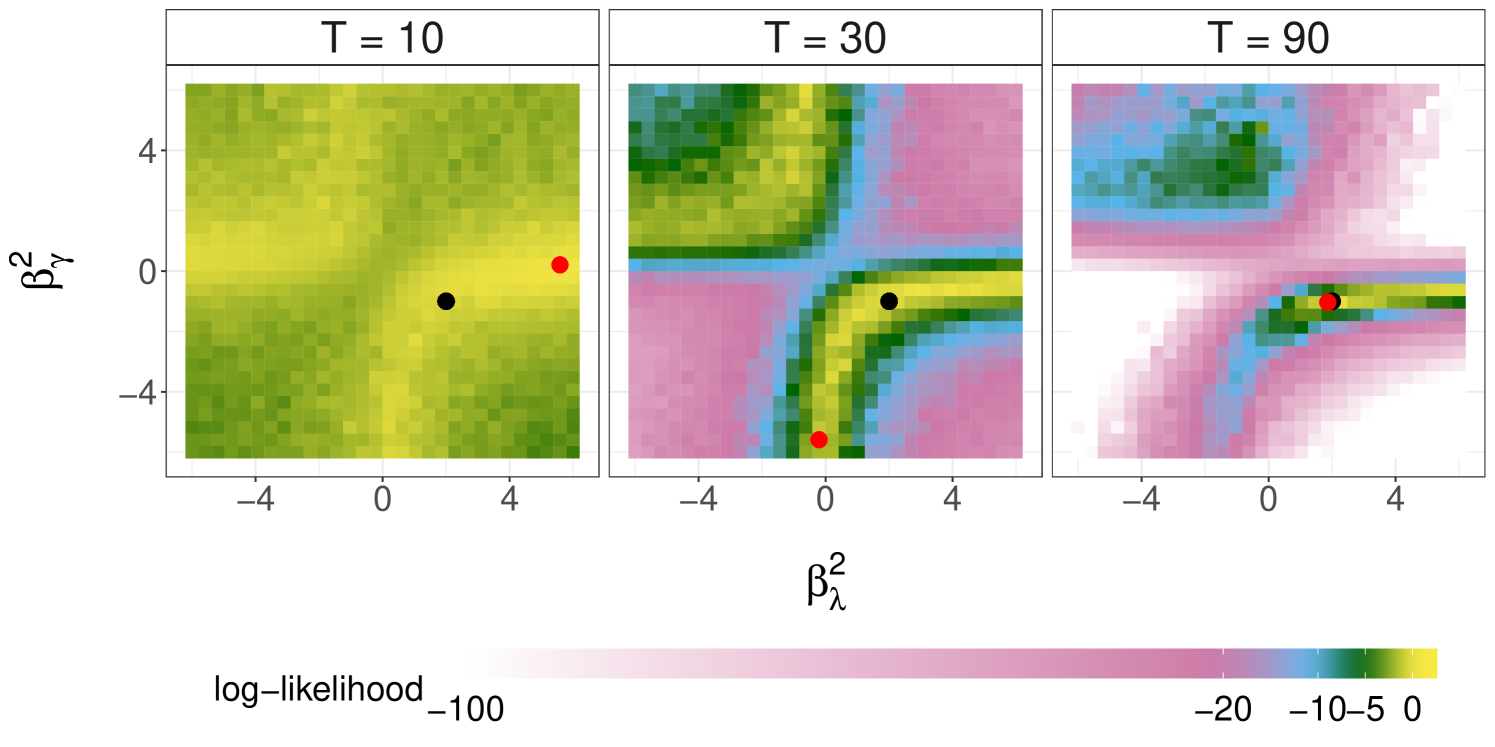
By building on the SMC methods in Sections 3.1 and 3.2, one can construct a stochastic gradient ascent scheme or an expectation-maximization algorithm to approximate the MLE. We refer readers to Kantas et al. (2015) for a comprehensive review of such approaches. In the Bayesian framework, our interest is on the posterior distribution
| (44) |
where is a given prior distribution on the parameter space . We employ particle marginal Metropolis–Hastings (PMMH) to sample from the posterior distribution. Following the discussion in Section 3.3, we will choose cSMC to construct a more efficient PMMH chain.
We now illustrate our inference method on the simulated data setup of Section 3.3. We adopt a prior distribution that assumes the parameters are independent with and . All MH parameter updates employ a Normal random walk proposal transition on the -space, with a standard deviation of to achieve suitable acceptance probabilities. We use particles in the cSMC algorithm within PMMH and we run the PMMH algorithm for iterations after a burn in of iterations. Using these posterior samples, we infer the ratios , which can be understood as the reproductive number of agent . In the left panel of Figure 5, we display the estimated posterior medians and credible sets, as well as the data generating values. Although the posterior median estimates are similar across agents, there is large posterior uncertainty for agents with small or large data generated ratios. To visualize how is distributed in the population, we estimate histograms that take parameter uncertainty into account, illustrate the results in the right panel of Figure 5. The posterior median estimates yields a histogram that is more concentrated than its data generating counterpart.
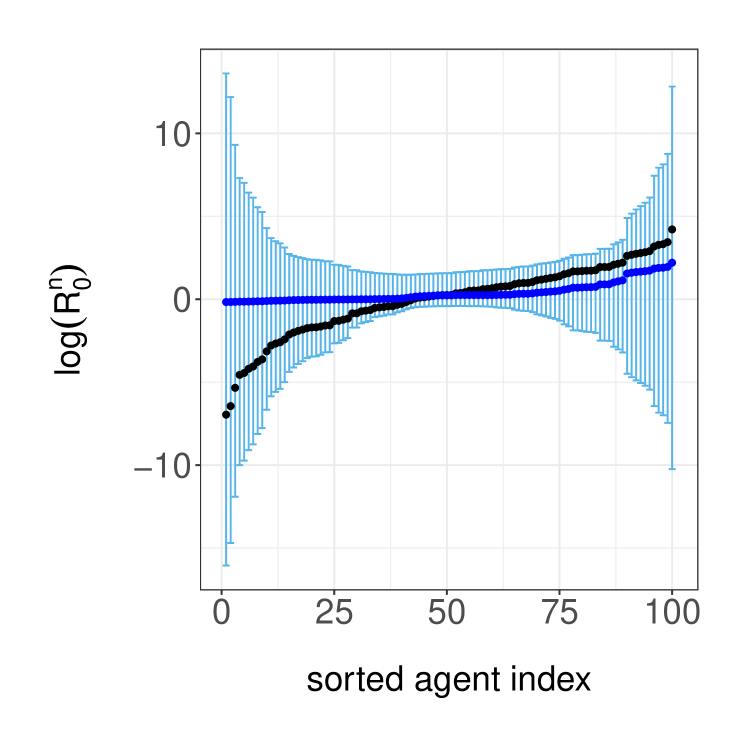
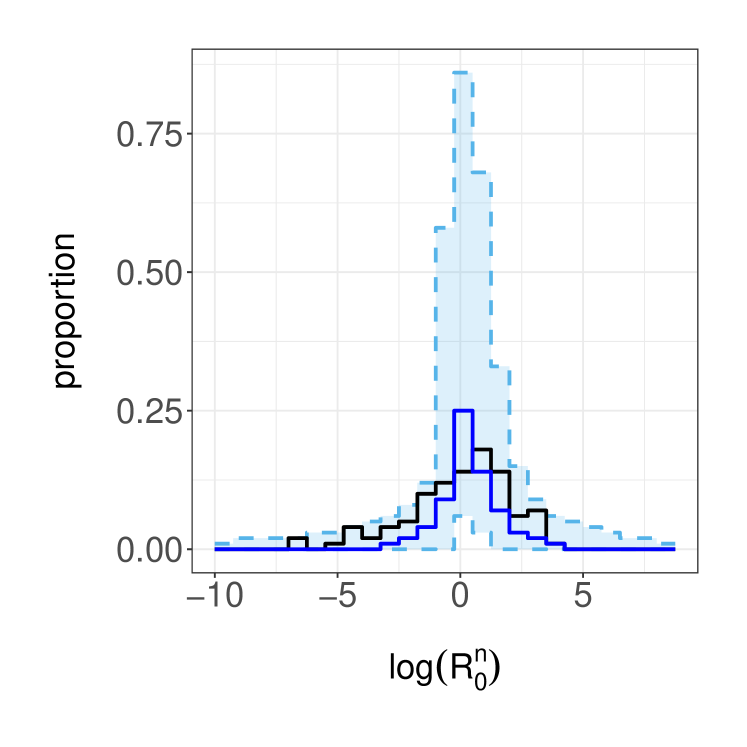
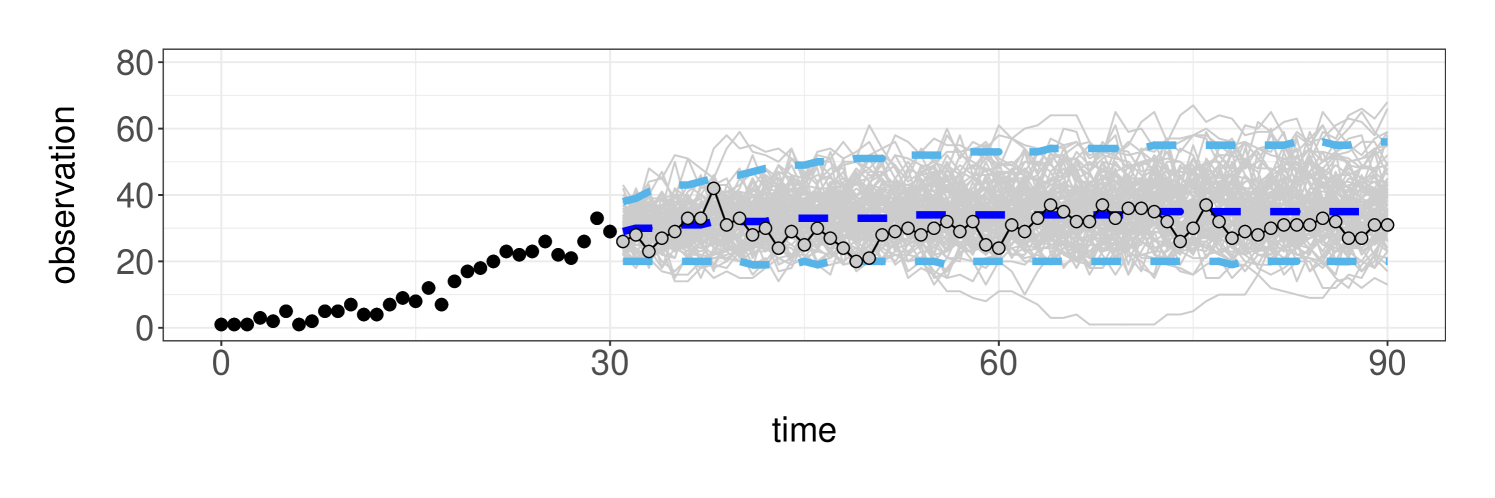
Lastly, we examine the predictive performance of the model when relatively few observations are available. As illustrated in Figure 6, we assume access to the first observations (black dots) and predict the rest of the time series up to time (grey dots) using the posterior predictive distribution . By simulating trajectories from the posterior predictive (grey lines), we obtain the model predictions and uncertainty estimates in Figure 6.
4 Susceptible-Infected-Recovered model
We consider a susceptible-infected-recovered (SIR) model, where agents become immune to a pathogen after they recover from an infection. The “recovered” status of an agent shall be encoded by a state of . Given a population configuration , we will write , , to indicate the status of agent , and , , to count the number of agents in each state. Under the assumption of a closed population, we have .
The time evolution of the population is now modelled by a Markov chain on , i.e. the specification in (18) with
| (45) |
The above probabilities are given by and where
| (46) | ||||
which satisfies . Note that if , which reflects the above-mentioned immunity. Just like the SIS model, the agents’ initial infection probabilities, infection and recovery rates are specified with (17), and the observation model for the number of infections reported over time is (3).
We consider again SMC approximations of the marginal likelihood and smoothing distribution of the resulting hidden Markov model on . The BPF can be readily implemented in cost, but suffers from the difficulties discussed in Section 3.1. To obtain better performance, we discuss how to implement the fully adapted APF in Section 4.1 and adapt our cSMC construction in Section 4.2. Alternative MCMC approaches such as those detailed in Appendix C could also be considered.
4.1 Auxiliary particle filter
We recall that implementing the fully adapted APF requires one to sample from proposals for , and evaluate the weight functions and for . At the initial time, we compute the marginal likelihood as
| (47) |
where , and sample from
| (48) | ||||
with , which admits the posterior of agent states as its marginal distribution. Similarly, for time step , we compute the predictive likelihood as
| (49) |
where , and sample from
| (50) | ||||
with , which admits as its marginal transition.
By augmenting the infection status of the agents , the first two steps in (48) and (50) are analogous to (25) and (27) for the SIS model, and the last step is to identify an agent’s state given her augmented current infection status and previous state. We point out that These expressions for and exploit the following facts: () susceptible agents either remain susceptible or become infected; () infected agents either remain infected or recover; () agents who have recovered enjoy immunity. Algorithm 4 provides an algorithmic description of the resulting APF, which has the same cost as APF for the SIS model.
4.2 Controlled sequential Monte Carlo
We now consider approximation of the BIF (30) to construct a proposal distribution approximating (29). At the terminal time , it suffices to compute for all to represent the function . As before, the next iterate requires an approximation of the conditional expectation . Following the arguments in (31), we approximate by
defined as
| (51) | ||||
which satisfies . Writing the corresponding Markov transition as , we approximate the conditional expectation by
| (52) |
Although (52) is analogous to (32) for the SIS model, the number of susceptible agents cannot be determined by just knowing the number of infections in the SIR model. Therefore it is necessary to account for both and in our approximation, i.e. we compute
| (53) |
for all . Since the number of agents in the population is fixed, it is also possible to work with the variables and instead. Subsequently for , we approximate (30) by
| (54) |
where ,
| (55) |
for , and zero otherwise. The above expression follows from the SIR model structure under homogeneous probabilities (4.2). Algorithm 5 summarizes our approximation of the BIF , which costs to compute and in storage.
We can define our proposal distribution and SMC weight functions in the same manner as (34) and (35), respectively. Expectations appearing in these SMC weights can be computed as
| (56) |
for and , where
| (57) |
for , and zero otherwise. The above expression should be understood as the analogue of (55) under the heterogeneous probabilities (4). Sampling from the proposals can be done in a similar manner as the APF in Section 4.1. At the initial time, we sample from
| (58) | |||
which admits as its marginal distribution. For time , we sample from
| (59) | |||
and
| (60) | |||
which admits as its marginal transition for all . Algorithm 6 details the resulting cSMC method, which costs the same as cSMC for the SIS model.
Our proposal distribution also satisfies the Kullback–Leibler upper bound in Proposition 3.1, with appropriate notational extensions to the state space . The following result is analogous to Proposition 3.2 for the SIS model.
Proposition 4.1.
For each time , the BIF approximation in Algorithm 5 satisfies:
| (61) | |||
| (62) |
for . The constants are , for , and the functions are , ,
| (63) | |||
| (64) |
for .
The arguments in the proof of Proposition 4.1 in Appendix B.3 are similar to Proposition 3.2, with some modifications tailored to the SIR model. This result shows the dependence of the BIF approximation error on our approximation of the transition probability via the terms and . As before, we can decompose and into the elements defined in (43). One can also obtain more fine-grained approximations using clustering in the spirit of Appendix B.4.
5 Discussion
Although agent-based models have been widely used as a simulation paradigm, statistical inference for these models has not received as much attention, due in part to the computational challenges involved. We have focused on agent-based models of disease transmission, and presented new SMC methods that can estimate their likelihood more efficiently than the standard BPF.
Our proposed methodology can be extended in various directions. Instead of the binomial model in (3), other observation models such as a negative binomial distribution could be considered. We could also adapt the controlled SMC methodology to handle the case where observations are only available at a collection of time instances, and we can expect further relative gains in such settings. Future work could consider settings where the difference in infection counts between successive time steps is observed.
We view our contribution as a step towards inference for larger classes of agent-based models, and that some of our contributions might be useful beyond the models considered here. We hope to motivate further work on alleviating the computational burden of inference in agent-based models, and that the removal of some of the computational bottlenecks might encourage further investigation on the statistical properties of these models.
Acknowledgments
This work was funded by CY Initiative of Excellence (grant “Investissements d’Avenir” ANR-16-IDEX-0008). Pierre E. Jacob gratefully acknowledges support by the National Science Foundation through grants DMS-1712872 and DMS-1844695.
References
- Allen and Burgin [2000] Linda JS Allen and Amy M Burgin. Comparison of deterministic and stochastic SIS and SIR models in discrete time. Mathematical biosciences, 163(1):1–33, 2000.
- Allen et al. [2008] Linda JS Allen, Fred Brauer, Pauline Van den Driessche, and Jianhong Wu. Mathematical epidemiology, volume 1945. Springer, 2008.
- Andrieu and Roberts [2009] Christophe Andrieu and Gareth O Roberts. The pseudo-marginal approach for efficient Monte Carlo computations. The Annals of Statistics, 37(2):697–725, 2009.
- Andrieu et al. [2010] Christophe Andrieu, Arnaud Doucet, and Roman Holenstein. Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72(3):269–342, 2010.
- Barbour and Ćekanavićius [2002] Andrew D Barbour and V Ćekanavićius. Total variation asymptotics for sums of independent integer random variables. The Annals of Probability, 30(2):509–545, 2002.
- Barbour and Hall [1984] Andrew D Barbour and Peter Hall. On the rate of Poisson convergence. In Mathematical Proceedings of the Cambridge Philosophical Society, volume 95, pages 473–480. Cambridge University Press, 1984.
- Barbour and Xia [1999] Andrew D Barbour and Aihua Xia. Poisson perturbations. ESAIM: Probability and Statistics, 3:131–150, 1999.
- Barlow and Heidtmann [1984] Richard E Barlow and Klaus D Heidtmann. Computing k-out-of-n system reliability. IEEE Transactions on Reliability, 33(4):322–323, 1984.
- Bresler [1986] Yoram Bresler. Two-filter formulae for discrete-time non-linear Bayesian smoothing. International Journal of Control, 43(2):629–641, 1986.
- Briers et al. [2010] Mark Briers, Arnaud Doucet, and Simon Maskell. Smoothing algorithms for state–space models. Annals of the Institute of Statistical Mathematics, 62(1):61, 2010.
- Britton [2010] Tom Britton. Stochastic epidemic models: A survey. Mathematical biosciences, 225(1):24–35, 2010.
- Bu et al. [2020] Fan Bu, Allison E Aiello, Jason Xu, and Alexander Volfovsky. Likelihood-based inference for partially observed epidemics on dynamic networks. Journal of the American Statistical Association, pages 1–17, 2020.
- Carpenter et al. [1999] James Carpenter, Peter Clifford, and Paul Fearnhead. Improved particle filter for nonlinear problems. IEE Proceedings-Radar, Sonar and Navigation, 146(1):2–7, 1999.
- Cekanavicius and Vaitkus [2001] V Cekanavicius and P Vaitkus. Centered Poisson approximation via Stein’s method. Lithuanian Mathematical Journal, 41(4):319–329, 2001.
- Chatterjee and Diaconis [2018] Sourav Chatterjee and Persi Diaconis. The sample size required in importance sampling. The Annals of Applied Probability, 28(2):1099–1135, 2018.
- Chen et al. [2017] CC-M Chen, Christopher C Drovandi, Jonathan M Keith, Ken Anthony, M Julian Caley, and KL Mengersen. Bayesian semi-individual based model with approximate bayesian computation for parameters calibration: Modelling crown-of-thorns populations on the Great Barrier Reef. Ecological Modelling, 364:113–123, 2017.
- Chen and Liu [1997] Sean X Chen and Jun S Liu. Statistical applications of the Poisson-Binomial and conditional Bernoulli distributions. Statistica Sinica, pages 875–892, 1997.
- Chen et al. [1994] Xiang-Hui Chen, Arthur P Dempster, and Jun S Liu. Weighted finite population sampling to maximize entropy. Biometrika, 81(3):457–469, 1994.
- DeAngelis and Gross [2018] Donald Lee DeAngelis and Louis J Gross. Individual-based models and approaches in ecology: Populations, communities and ecosystems. CRC Press, 2018.
- Del Moral [2004] Pierre Del Moral. Feynman-kac formulae: Genealogical and Interacting Particle Systems with Applications. Springer-Verlag New York, 2004.
- Del Moral et al. [2015] Pierre Del Moral, Ajay Jasra, Anthony Lee, Christopher Yau, and Xiaole Zhang. The alive particle filter and its use in particle Markov chain Monte Carlo. Stochastic Analysis and Applications, 33(6):943–974, 2015.
- Doucet et al. [2001] Arnaud Doucet, Nando De Freitas, and Neil Gordon. An introduction to sequential Monte Carlo methods. In Sequential Monte Carlo methods in practice, pages 3–14. Springer, 2001.
- Endo et al. [2019] Akira Endo, Edwin van Leeuwen, and Marc Baguelin. Introduction to particle Markov chain Monte Carlo for disease dynamics modellers. Epidemics, 29:100363, 2019.
- Epstein [2006] Joshua M Epstein. Generative social science: Studies in agent-based computational modeling, volume 13. Princeton University Press, 2006.
- Fan et al. [1962] CT Fan, Mervin E Muller, and Ivan Rezucha. Development of sampling plans by using sequential (item by item) selection techniques and digital computers. Journal of the American Statistical Association, 57(298):387–402, 1962.
- Fearnhead and Clifford [2003] Paul Fearnhead and Peter Clifford. On-line inference for hidden Markov models via particle filters. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 65(4):887–899, 2003.
- Fintzi et al. [2017] Jonathan Fintzi, Xiang Cui, Jon Wakefield, and Vladimir N Minin. Efficient data augmentation for fitting stochastic epidemic models to prevalence data. Journal of Computational and Graphical Statistics, 26(4):918–929, 2017.
- Gerber et al. [2019] Mathieu Gerber, Nicolas Chopin, and Nick Whiteley. Negative association, ordering and convergence of resampling methods. Annals of Statistics, 47(4):2236–2260, 2019.
- Ghahramani and Jordan [1996] Zoubin Ghahramani and Michael I Jordan. Factorial hidden Markov models. In Advances in Neural Information Processing Systems, pages 472–478, 1996.
- Gordon et al. [1993] Neil J Gordon, David J Salmond, and Adrian FM Smith. Novel approach to nonlinear/non-gaussian Bayesian state estimation. In IEE proceedings F (radar and signal processing), volume 140, pages 107–113. IET, 1993.
- Grazzini et al. [2017] Jakob Grazzini, Matteo G Richiardi, and Mike Tsionas. Bayesian estimation of agent-based models. Journal of Economic Dynamics and Control, 77:26–47, 2017.
- Guarniero et al. [2017] Pieralberto Guarniero, Adam M Johansen, and Anthony Lee. The iterated auxiliary particle filter. Journal of the American Statistical Association, 112(520):1636–1647, 2017.
- Hazelbag et al. [2020] C Marijn Hazelbag, Jonathan Dushoff, Emanuel M Dominic, Zinhle E Mthombothi, and Wim Delva. Calibration of individual-based models to epidemiological data: A systematic review. PLoS computational biology, 16(5):e1007893, 2020.
- Heng et al. [2020a] Jeremy Heng, Adrian N Bishop, George Deligiannidis, and Arnaud Doucet. Controlled sequential Monte Carlo. Annals of Statistics, 48(5):2904–2929, 2020a.
- Heng et al. [2020b] Jeremy Heng, Pierre E. Jacob, and Nianqiao Ju. A simple Markov chain for independent Bernoulli variables conditioned on their sum. arXiv preprint arXiv:2012.03103, 2020b.
- Hodges and Le Cam [1960] Joseph L Hodges and Lucien Le Cam. The Poisson approximation to the Poisson binomial distribution. The Annals of Mathematical Statistics, 31(3):737–740, 1960.
- Hong [2013] Yili Hong. On computing the distribution function for the Poisson binomial distribution. Computational Statistics & Data Analysis, 59:41–51, 2013.
- Hooten et al. [2020] Mevin Hooten, Christopher Wikle, and Michael Schwob. Statistical implementations of agent-based demographic models. International Statistical Review, 88(2):441–461, 2020.
- Ionides et al. [2006] Edward L Ionides, Carles Bretó, and Aaron A King. Inference for nonlinear dynamical systems. Proceedings of the National Academy of Sciences, 103(49):18438–18443, 2006.
- Johansen and Doucet [2008] Adam M Johansen and Arnaud Doucet. A note on auxiliary particle filters. Statistics & Probability Letters, 78(12):1498–1504, 2008.
- Kantas et al. [2015] Nikolas Kantas, Arnaud Doucet, Sumeetpal S Singh, Jan Maciejowski, and Nicolas Chopin. On particle methods for parameter estimation in state-space models. Statistical science, 30(3):328–351, 2015.
- Kattwinkel and Reichert [2017] Mira Kattwinkel and Peter Reichert. Bayesian parameter inference for individual-based models using a Particle Markov Chain Monte Carlo method. Environmental Modelling & Software, 87:110–119, 2017.
- Kong et al. [1994] Augustine Kong, Jun S Liu, and Wing Hung Wong. Sequential imputations and Bayesian missing data problems. Journal of the American statistical association, 89(425):278–288, 1994.
- Lipsitch et al. [2003] Marc Lipsitch, Ted Cohen, Ben Cooper, James M Robins, Stefan Ma, Lyn James, Gowri Gopalakrishna, Suok Kai Chew, Chorh Chuan Tan, Matthew H Samore, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science, 300(5627):1966–1970, 2003.
- Liu and Chen [1998] Jun S Liu and Rong Chen. Sequential Monte Carlo methods for dynamic systems. Journal of the American statistical association, 93(443):1032–1044, 1998.
- McVinish and Pollett [2012] R. McVinish and P. K. Pollett. A central limit theorem for a discrete-time SIS model with individual variation. Journal of Applied Probability, 49(2):521–530, 2012. doi: 10.1239/jap/1339878802.
- Osthus et al. [2019] Dave Osthus, James Gattiker, Reid Priedhorsky, and Sara Y Del Valle. Dynamic Bayesian influenza forecasting in the United States with hierarchical discrepancy (with discussion). Bayesian Analysis, 14(1):261–312, 2019.
- Pitt and Shephard [1999] Michael K Pitt and Neil Shephard. Filtering via simulation: Auxiliary particle filters. Journal of the American statistical association, 94(446):590–599, 1999.
- Platt [2020] Donovan Platt. A comparison of economic agent-based model calibration methods. Journal of Economic Dynamics and Control, 113:103859, 2020.
- Scharth and Kohn [2016] Marcel Scharth and Robert Kohn. Particle efficient importance sampling. Journal of Econometrics, 190(1):133–147, 2016.
- Sirén et al. [2018] Jukka Sirén, Luc Lens, Laurence Cousseau, and Otso Ovaskainen. Assessing the dynamics of natural populations by fitting individual-based models with approximate Bayesian computation. Methods in Ecology and Evolution, 9(5):1286–1295, 2018.
- Tisue and Wilensky [2004] Seth Tisue and Uri Wilensky. Netlogo: A simple environment for modeling complexity. In International conference on complex systems, volume 21, pages 16–21. Boston, MA, 2004.
- Turrell [2016] Arthur Turrell. Agent-based models: Understanding the economy from the bottom up. Bank of England Quarterly Bulletin, page Q4, 2016.
- van der Vaart et al. [2016] Elske van der Vaart, Alice SA Johnston, and Richard M Sibly. Predicting how many animals will be where: How to build, calibrate and evaluate individual-based models. Ecological modelling, 326:113–123, 2016.
- Volkova [1996] A Yu Volkova. A refinement of the central limit theorem for sums of independent random indicators. Theory of Probability & Its Applications, 40(4):791–794, 1996.
- Wang [1993] Yuan H Wang. On the number of successes in independent trials. Statistica Sinica, pages 295–312, 1993.
- Whiteley and Rimella [2020] Nick Whiteley and Lorenzo Rimella. Inference in stochastic epidemic models via multinomial approximations. arXiv preprint arXiv:2006.13700, 2020.
Appendix A Poisson binomial distributions
A.1 Recursive definition of Poisson binomial probabilities
The following provides a derivation of the recursion (10) for the function with independently. The recursion allows the computation of Poisson binomial probabilities in operations. Under independently for , the initial conditions are given by
| (65) |
in the case of no success, where the sum reduces to a single Bernoulli variable, and for because a sum of Bernoulli variables cannot be larger than , in particular for all . For and , by conditioning on the value of , the law of total probability gives (10):
| (66) | ||||
A.2 A thinning result
We show that under the static model independently for and the observation model , we have marginally. We first note that the characteristic function of is given by
| (67) |
for . Consider the representation where independently. Note that the characteristic function of each Bernoulli random variable with success probability is . By the law of iterated expectations, the characteristic function of is
| (68) | ||||
for . By comparing this characteristic function with (67), we can conclude that .
A.3 Comparing two Poisson binomial distributions
The following result will be of use in Appendix B.
Lemma A.1.
Let and denote two Poisson binomial distributions with probabilities and , respectively. The -norm between these PMFs satisfies
| (69) |
The Kullback–Leibler divergence from to , defined as
is upper bounded by
| (70) |
Proof.
To bound the -norm between two Poisson binomial PMFs, we rely on Parseval’s identity
| (71) |
where
| (72) |
denote the characteristic functions of and , respectively (as in (67)). Noting that each term of the products in (72) is at most one, by repeated applications of triangle inequality on the decomposition
| (73) | |||
(with the convention for ), we have
Hence (69) follows by squaring both sides and applying the identity in (71).
To bound the Kullback–Leibler divergence, we apply the inequality for and the Cauchy–Schwarz inequality
| (74) |
∎
Appendix B Controlled sequential Monte Carlo
B.1 Performance of controlled sequential Monte Carlo
Proof of Proposition 3.1.
Using the form of the smoothing distribution in (28) and (29), and the definition of the proposal distribution in (34), we have
| (75) |
By the log-sum inequality
| (76) |
and
| (77) |
Using the expression in (75) and the inequalities (76)-(B.1), the Kullback–Leibler divergence from to satisfies
| (78) | |||
Equation (39) follows by employing the upper bound and noting that
| (79) |
∎
B.2 Marginal distributions of smoothing distribution and proposal distribution
To show that the constants in Proposition 3.1 are finite for all , it suffices to upper bound the ratio by a constant for all . Under the requirement (21), we have
| (80) |
hence we will argue that each of the above weight functions can be upper bounded by some constant. From (35), the weight functions can be rewritten as and for . Noting that the ratio when for all and , we do not have to consider this case.
By induction, the BIF approximation are upper bounded by one, hence and for all and . It remains to show that is lower bounded by some strictly positive constant. We notice that the conditional expectation in (32) can be lower bounded by
| (81) |
Define the constant . At the terminal time, we have . By iterating the backward recursion, we have
| (82) |
for each . By induction, we have for all and . Combining the above observations allows us to conclude.
B.3 Backward information filter approximation
Proof of Proposition 3.2.
We will establish (40); the proof of (41) follows using similar arguments. Define for each time . At the terminal time , we have . For time , we consider the decomposition
| (83) |
where
| (84) |
Using the log-sum inequality and the decomposition of the smoothing distribution given in (28) and (29), the first term of (83) is bounded by
| (85) |
By the log-sum inequality, the second term of (83) is bounded by
| (86) |
The above repeatedly uses the fact that in the case of zero infections, i.e. for all , we have for all . The constant can be shown to be finite using the arguments in Appendix B.2. The last inequality also uses the fact that , which follows by induction. Applying (70) of Lemma A.1 and Cauchy–Schwarz inequality gives
| (87) |
By combining (B.3) and (87), we obtain the following recursion
| (88) |
The claim in (40) follows by induction. ∎
Proof of Proposition 4.1.
The arguments are similar to Proposition 3.2 with some modifications that we will outline below. Like before, we consider the quantity for in (61) as (62) follows using similar arguments. By the same arguments in (B.3)
| (89) |
Instead of (B.3), we have
| (90) |
The Kullback–Leibler divergence from to can be decomposed as
| (91) | |||
Applying (70) of Lemma A.1 gives
| (92) |
Hence by Cauchy–Schwarz inequality, we have
| (93) |
∎
B.4 Finer-grained approximations
We discuss finer approximations of the BIF and provide algorithmic details of the resulting cSMC. Instead of simply approximating individual infection and recovery rates by their population averages, we consider a clustering of agents based on their infection and recovery rates, and approximate these rates by their within-cluster average. More precisely, if denote the desired number of clusters, denote a partition of that represents our clustering and denotes the number of agents in cluster , we approximate and . For each state of the population , we define the summary , which counts the number of infected agents in cluster . We will write and . Note that . The corresponding approximation of is given by
| (94) |
where maps agent labels to cluster membership. We will write associated Markov transition as . The approximation in (94) recovers (31) in the case of cluster, in which case . Larger values of can be seen as finer-grained approximations at the expense of increased dimensionality of . Having clusters offers no dimensionality reduction as .
At the terminal time , since we have , it suffices to compute for all . To approximate the backward recursion (30) for , we proceed inductively by assuming an approximation of the form at time . By plugging in the approximation , we consider the iterate
| (95) |
to form an approximation of . We approximate the conditional expectation by
| (96) |
The resulting approximation of is computed using
| (97) |
for all in cost. Hence our overall approximation of the BIF costs to compute and in storage. It is straightforward to extend Proposition 3.2 to characterize the error of (97); we omit this for the sake of brevity.
The corresponding approximation of the optimal proposal (29) is
| (98) |
Analogous to (35), the appropriate SMC weight functions are
| (99) |
and . The above expectations are computed as
| (100) | ||||
| (101) |
where and . Sampling from the proposals (98) involves initializing from
| (102) |
which admits as its marginal distribution, and for time sampling from
| (103) | ||||
which admits as its marginal transition. The overall cost of implementing cSMC is
| (104) |
or
| (105) |
if one employs translated Poisson approximations (12) and the MCMC in Heng et al. [2020b] to sample from conditioned Bernoulli distributions. As alluded earlier, the choice of the number of clusters allows one to trade-off the quality of our proposal for computation complexity.
Appendix C Posterior sampling of agent states using MCMC
We now describe various MCMC algorithms that can be used to sample from the smoothing distribution of the agent-based SIS model in Section 3. These Gibbs sampling strategies can be seen as alternatives to the SMC approach in Sections 3.1 and 3.2. The same ideas can also be applied to the SIR model in Section 4 with some modifications.
A simple option is a single-site update that samples the state of an agent at a specific time from the full conditional distribution , where , for and that can be chosen deterministically or randomly with uniform probabilities using a systematic or random Gibbs scan. Using the conditional independence structure of the model, for , this full conditional is a Bernoulli distribution with success probability that is proportional to
| (106) |
where with . This expression also holds for the case by replacing with , and by removing the last product. As each update costs , the overall cost of a Gibbs scan is .
As discussed in Ghahramani and Jordan [1996] for a related class of models, one can consider block updates that jointly sample the trajectory of a few agents. For a subset of size , this Gibbs update involves sampling from , where and . This can be done using the forward-backward algorithm in cost. Hence the overall cost of a systematic Gibbs scan over the entire population is . As the latter is computationally prohibitive for large , one has to consider reasonably small block sizes.
We can also employ a swap update that leaves the full conditional distribution invariant for each (with ). Let denote the current state of the population at time . We will choose and uniformly from the sets and respectively. The proposed state is such that , and for . For , the MH acceptance probability is
| (107) |
The case can be accommodated by replacing with , and by removing the ratios of Bernoulli PMFs. The cost of each swap update ranges between and , depending on the structure of the network. As swap updates on their own do not change the number of infected agents, we propose to employ them within a mixture kernel that also relies on the above-mentioned forward-backward scans.
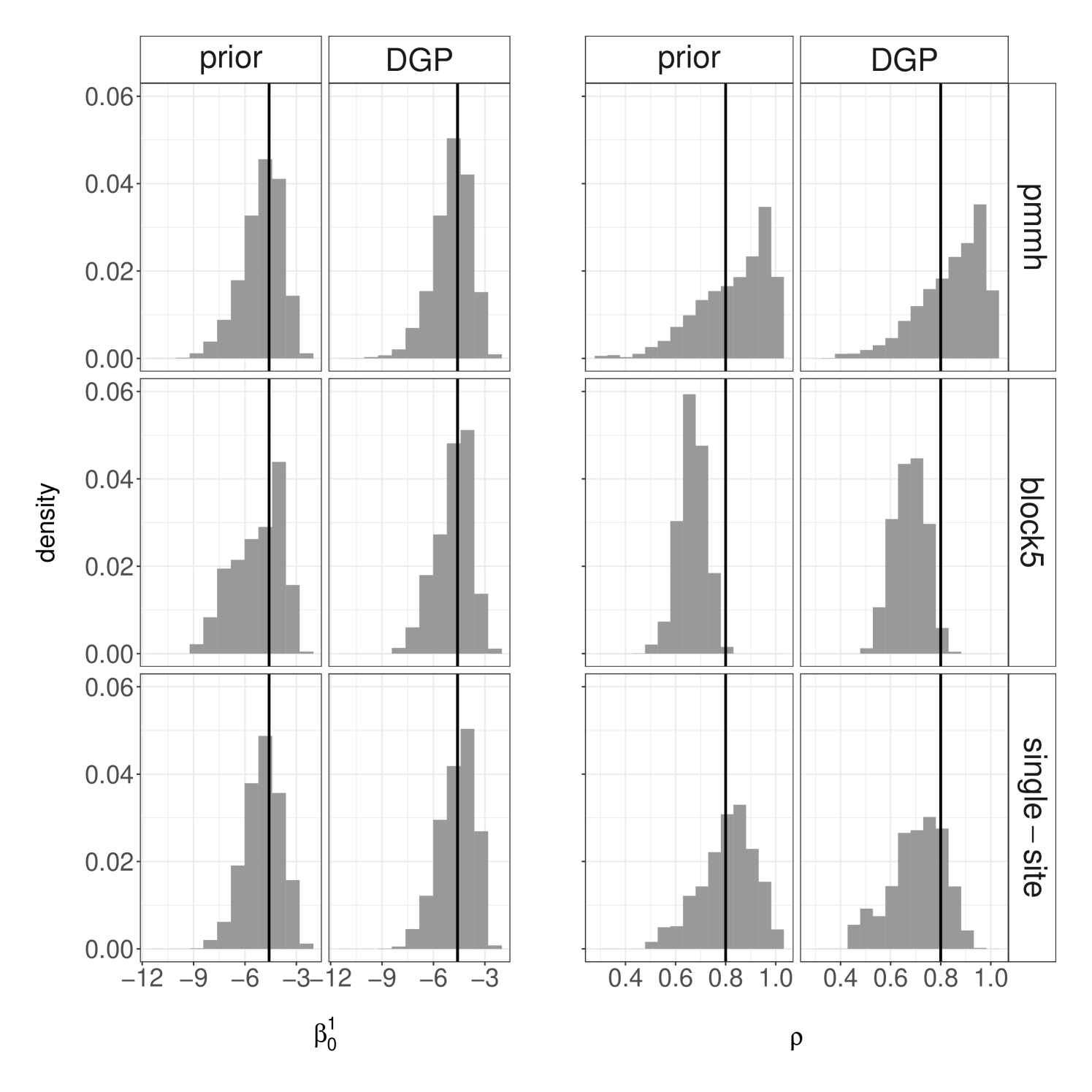
As alternatives to PMMH, we can consider Gibbs samplers that alternate between sampling the parameters from using a MH algorithm, and the agent states from using the above MCMC algorithms. In particular, we employ an equally weighted mixture of kernels, performing either random swap updates for each time step, or systematic Gibbs scan with single-site updates (“single-site”) or block updates for agents (“block5”). We compare these Gibbs samplers to PMMH on the simulated dataset of Section 3.3. We set the MH Normal proposal standard deviation within Gibbs samplers as to achieve suitable acceptance probabilities. We initialize the parameters from either the DGP or the prior distribution, and run all algorithms for the same number of iterations. Figure 7 displays the resulting approximations of the marginal posterior distribution of two parameters. Compared to the Gibbs samplers, the PMMH approximations seem to be more stable between runs with different initializations. These plots also suggest that the Gibbs samplers provide a poorer exploration of the tails of the posterior distribution, which may be attributed to the dependence between the agent states and parameters in this setting.