Shadowed triplet pairings in Hund’s metals with spin-orbit coupling
Abstract
Hund’s coupling in multiorbital systems allows for the possibility of even-parity orbital-antisymmetric spin-triplet pairing, which can be stabilized by spin-orbit coupling (SOC). While this pairing expressed in the orbital basis is uniform and spin-triplet, it appears in the band basis as a pseudospin-singlet, with the momentum dependence determined by the SOC and the underlying triplet character remaining in the form of interband pairing active away from the Fermi energy. Here, we examine the role of momentum-dependent SOC in generating nontrivial pairing symmetries, as well as the hidden triplet nature associated with this interorbital pairing, which we dub a “shadowed triplet”. Applying this concept to Sr2RuO4, we first derive several forms of SOC with -wave form-factors from a microscopic model, and subsequently we show that for a range of SOC parameters, a pairing state with symmetry can be stabilized. Such a pairing state is distinct from pure spin-singlet and -triplet pairings due to its unique character of pseudospin-energy locking. We discuss experimental probes to differentiate the shadowed triplet pairing from conventional pseudospin-triplet and -singlet pairings.
I Introduction
A key feature of superconductivity (SC) is the antisymmetric-wavefunction of the Cooper pair under the exchange of two electrons. This has limited the focus to even-parity spin-singlet and odd-parity spin-triplet pairings in a single Fermi surface (FS) system. In multiorbital systems, additional possibilities arise due to the orbital degree of freedom, such as even-parity spin-triplet, or odd-parity spin-singlet pairings. For example, it was shown earlier that Hund’s coupling in multiorbital systems allows for an even-parity spin-triplet pairing that is orbitally antisymmetric between two orbitals [1, 2, 3, 4, 5, 6, 7]. The Hund’s coupling, significant in transition metal systems, acts as an attractive pairing interaction [1]. Similar to the attractive Hubbard model, the Hund’s coupling allows a strong local Cooper pair to form between two orbitals with spin-triplet character.
However, when the electron motion is introduced, i.e., the kinetic term in the Hamiltonian, the pairing is drastically weakened, because the electrons comprising the Cooper pair with momenta and in different orbitals have different energies, due to the different electronic dispersions of the orbitals. Thus, to stabilize such an orbital antisymmetric pairing, significant orbital degeneracy is required throughout momentum space near the FS [1, 2]. Furthermore, hybridization between different orbitals can further weaken interorbital pairings, by splitting the degeneracy where it occurs.
The story becomes more interesting when spin-orbit coupling (SOC) is introduced. Note that with SOC, purely spin-singlet and -triplet pairings are no longer well-defined, since the spin and orbital degrees of freedom are coupled. Thus one defines Cooper pairs in the total angular momentum (pseudospin) basis. When the SOC is strong, this forms the basis for SC in the heavy fermion superconductors, such as UPt3, leading to odd-parity pseudospin-triplet SC [8, 9]. When the SOC is intermediate, i.e., comparable to the orbital degeneracy splitting terms, spin and orbital characters vary continuously, and one can define the pairing in either the orbital or band basis. Spin-orbital mixing then helps to stabilize the interorbital pairing. It was shown that SOC indeed enhances even-parity orbital-antisymmetric spin-triplet pairing [3]. The SOC not only supports the orbital-antisymmetric spin-triplet pairing, but it also transforms pure spin-triplet pairing into “both” pseudospin-singlet and -triplet pairings in the band basis.
Furthermore, the form of the SOC is not limited to atomic SOC, i.e., , where is the site index, and the precise form can determine the momentum dependence of the superconducting state. For example, -wave SC proximate to a topological insulator or strong Rashba SOC with broken inversion symmetry leads to an effective SC, which is odd-parity and a spinless triplet [10, 11, 12]. For materials with inversion symmetry, there is still the possibility of even-parity momentum-dependent SOC [13] (k-SOC), which has been discussed in the context of the unconventional superconductor, Sr2RuO4 [14, 15, 16, 17, 18, 19, 20]. Similar to a Rashba-SOC generated SC, the inclusion of k-SOC in a microscopic model with -wave pairing is reflected in an intraband pairing with the same momentum character as the SOC.
Here we study a microscopic route to k-SOC and how SOC transforms even-parity interorbital spin-triplet SC into pseudospin-singlet and -triplet SC in a Hund’s metal, where the multiorbital nature and strong Hund’s coupling are crucial. We also illustrate how pseudospin-triplet interband pairing remains, dubbed a “shadowed triplet” away from the Fermi energy. While this SC behaves like a singlet in response to low-energy excitations, its hidden identity shows up at finite magnetic fields, and it can be tested when the field strength reaches an appreciable percentage of the superconducting gap size [21]. Applying the concept to Sr2RuO4, we show that pairing is stabilized in the orbitals.
The paper is organized as follows. We first introduce the generic Hamiltonian that we will be concerned with throughout in Sec. II. We then consider a simple but general two-orbital model to show how even-parity spin-triplet pairing arises in Sec. III. This includes the stability conditions and how SOC transforms this pairing into a pseudospin-singlet and -triplet in the Bloch band basis. The SOC in the shadowed triplet not only plays an essential role in enhancing the pairing, but it also determines the pairing symmetry. In Sec. IV we investigate microscopic routes to several k-SOC terms with -wave symmetry, which can lead to various -wave pairing symmetries on the FS. In Sec. V, we apply the shadowed triplet pairing scenario to the prominent unconventional superconductor, Sr2RuO4 [14, 15, 16, 17], for which the SOC has been shown to be important [22, 23, 24, 3, 25, 26], and we discuss the leading instability towards pairing within a three-orbital model for a range of SOC parameters.
II General Microscopic Hamiltonian
We first introduce the generic Hamiltonian that we will be considering throughout. The Hamiltonian consists of three terms. The kinetic term, , denotes a tight-binding (TB) model, for which we will discuss the precise form in the subsequent sections. The SOC Hamiltonian, , refers to the atomic SOC written in the basis of orbitals and various momentum-dependent terms, also specified later. The interaction, , has the form of the Kanamori interactions,
| (1) | ||||
where and are the intra- and interorbital Hubbard repulsions, is the Hund’s coupling and is an electron operator creating an electron at site in orbital with spin . Decoupling these interaction terms into even-parity zero-momentum spin-singlet and spin-triplet order parameters[3, 7, 20, 21] gives,
| (2) | ||||
where is the number of sites, and the spin-triplet and -singlet order parameters are defined as
| (3) | ||||
and represents a sum over the unique pairs of orbital indices. An attractive interorbital spin-triplet, , channel is present when , which will be our focus. While this corresponds to a Hund’s coupling larger than the typical value of for Sr2RuO4 [26, 27], this type of pairing instability has also been found in several studies beyond mean field (MF) theory without such a requirement[4, 5, 6]. Furthermore, we note that the interorbital, , and intraorbital, , spin-singlet order parameters appear with repulsive interactions, but they can be induced by the spin-triplet order parameters through the SOC. Indeed, calculating the spin-singlet order parameters within a MF spin-triplet pairing state shows that they are generally one order of magnitude smaller than the spin-triplet order parameters.
III Two-orbital model
To illustrate how the shadowed triplet pairing occurs, we first consider a two-orbital MF Hamiltonian, , consisting of a generic TB model with a specific SOC and an even-parity spin-triplet pairing term. The following model allows for a systematic study of the microscopic components relevant to such pairing in multiorbital systems and is generalized to systems with three orbitals. We use , where indicates time-reversal and consists of electron operators creating an electron in one of the two orbitals with spin . We also introduce the Pauli matrices plus identity matrix, , in the particle-hole, spin and orbital spaces respectively, where the direct product between them is implied. is given by,
| (4) | ||||
where the TB contribution is given by the sum of the two orbital dispersions, , and the difference between them, , which are defined by , as well as the orbital hybridization of the two orbitals, . Here we consider , with the form , to illustrate the effects of the SOC. Later, we derive several possible k-SOC from a microscopic perspective in Sec. IV, which differ from the form included here. The pairing Hamiltonian is obtained through a MF decoupling of and favors the even-parity interorbital spin-triplet order parameter via , with the -vector aligned along the -direction, and thus is given by
| (5) |
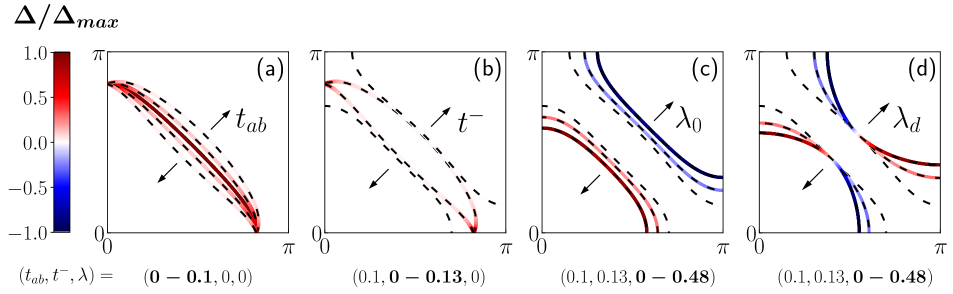
To understand the stability of the SC state, we consider the relationship between the various components of our model and their effects on the quasi-particle (QP) dispersion. The gap on the FS is shown in Fig. 1 for various cases of , and . Here, , and for we take . The orbitals are coupled through the SOC, for which we take two cases: the atomic SOC denoted by , and a -wave SOC given by , as well as the orbital hybridization, which we take as . With these dispersions, , where and all parameters are given in units of . The gap over the FS is shown for four cases: (a) , , as is increased from zero to ; (b) keeping , with as is increased by tuning from zero to ; (c) both and are kept the same as is increased from zero to 0.48; and (d) the same as (c) but with the -wave SOC, instead of , increased by tuning from zero to 0.48.
When the orbital dispersions are completely degenerate, we see that the gap is non-zero everywhere over the two identical bands, as shown by the middle contour in Fig. 1(a). As the strength of the hybridization, , is increased from zero, the energy separation of the two orbital dispersions increases wherever and the gap arising from interband pairing disappears on the FS, except where vanishes along the lines, where the two orbital dispersions remain degenerate. Starting from there with zero interband pairing over most of the FS, Fig. 1(b) demonstrates the effect of in further reducing the interband pairing to zero everywhere on the FS, due to the absence of phase space for zero-momentum pairing. Keeping the same parameters used in (b), Fig. 1(c) reveals how the SOC revives the SC state by allowing for an intraband pairing on the FS. As the SOC is increased from zero, the intraband gap becomes non-zero over the entire FS. Additionally, the sign of the gap function is opposite on the two bands, matching the dependence, which we will show below in Eq. (10) and Eq. (11), but uniform on each band due to the lack of momentum dependence of the atomic SOC. In contrast, Fig. 1(d) displays the -wave dependence of the gap arising from the -wave SOC. Thus with the introduction of , and , the pairing on the FS is transformed from an interband spin-triplet to a purely intraband pseudospin-singlet with the same momentum dependence as the associated SOC, while the pseudospin-triplet is active away from the Fermi energy.
The above results can also be understood via the commutation relations between the order parameter and other terms. The pair-breaking effects are revealed by the commuting behavior with the pairing term [28, 29, 30]. Conversely, the SOC anti-commutes with the pairing term and generally enhances the pairing state. The anti-commutators are given by
| (6) | ||||
These effects are reflected in the QP dispersion, given by
| (7) | ||||
The general equation of the FS is , from which it can be seen that if and , and the orbitals are degenerate, i.e., , we recover the conventional BCS result for the gap energy on the FS: . In the general case where these terms are non-zero, assuming is small, the QP gap is
| (8) |
From this, it is clear that increasing and decreases the overall gap size. The detrimental effects on the gap size, signified by the commuting nature of both and with the pairing Hamiltonian, are a result of shifting apart in energy the bands being paired, resulting in the gap moving away from the FS. However, turning on the SOC significantly enhances the gap size [3], as shown in Fig. 1(c), and as the SOC strength becomes larger than and , the gap can be restored to the order of . Furthermore, if has a -wave form factor such as (, the gap reflects the exact same -wave symmetry, as shown in Fig. 1(d). The enhancement of the SC state is accomplished by providing a non-zero intraband pseudospin-singlet pairing on the FS, as we show below in the band basis.
With the aim to further understand the nature of the SC state, we study how the pairing transforms to the Bloch band basis, labeled by band indices and pseudospin . The transformation is given by
| (9) |
where for and . The coefficients of the transformation are given by and , where is chosen to be complex with the same phase as , is real, and . Applying this transformation on results in the pairing in the band basis, where we have also defined the Pauli matrices in the Nambu, pseudospin, and band spaces with the basis and . We obtain,
| (10) | ||||
where and denote pseudospin-singlet intraband and interband pairings respectively, and is a pseudospin-triplet interband pairing. The intraband and interband nature of these pairings becomes more apparent from the operator form,
| (11) | ||||
The above equation shows the sign change in the intraband pairing between the two bands, as displayed in Fig. 1(c) and 1(d). This relative sign between the bands is similar to the gap structure [7], although it should be noted that here for simplicity we have ignored the SOC-induced intraorbital singlets [3, 7, 21, 31] that would add to the gap on each band. For small they are small compared to and they do not affect the conclusions of this section. The pairings in the band basis have the following form:
| (12) | ||||
While the orbital order parameter is -wave and contains no explicit momentum dependence, transforming to the band basis generates potentially complex momentum dependence from SOC and orbital hybridization. The orbital spin-triplet order parameter carries over to the interband pseudospin-triplet, which, in the limit of zero SOC, becomes equal to , while both the intraband and interband pseudospin-singlets vanish. The interband pseudospin-singlet pairing also vanishes for . However, an important feature for is the presence of the intraband pseudospin-singlet pairing, , which acquires the same symmetry dependence as a function of momentum as , as shown in Fig. 1(d). While the interband pseudospin-triplet is a signature of the fundamental interorbital spin-triplet order parameter, it is the intraband pseudospin-singlet that leads to a weak-coupling instability. This is because the interband pairing contribution to the gap will generally be negligible on the FS, such that the gap is given by . Considering the QP dispersion in terms of the band pairings,
| (13) | ||||
and evaluating this on either the or FS, for only intraband pairing, we obtain the gap energy . For either only or interband pairing, a gap of or forms where . This corresponds to an energy gap on the FS only where , which is not a generic feature but rather requires fine-tuning to achieve, otherwise the gap formed will be away from the Fermi energy.
While the model introduced in this section is simple, its generality gives insight into the role of the orbital degeneracy, hybridization, and SOC for multiorbital systems in dictating the stability of the even-parity spin-triplet SC state. It is straightforward to extend to three-orbital descriptions. Furthermore, we have seen that in the band basis, the intraband pairing on the FS takes on the momentum dependence of the SOC, allowing for a rich collection of pairing symmetries unexpected from the original -wave order parameter and in contrast to other forms of momentum-dependent SC that arise from nonlocal interactions. However, the possible pairing symmetries will depend on the forms of k-SOC that can be obtained from microscopic considerations. Therefore, we now turn to a study of how various forms of k-SOC can arise microscopically.
IV Microscopic route to momentum-dependent SOC
Here, we take as a specific microscopic example the layered perovskite Sr2RuO4, which has the tetragonal space group I4/mmm and point group , for which the Ru 4 orbitals are the relevant low-energy degrees of freedom. With this, we study how the various forms of k-SOC with different -wave form factors such as (a) an in-plane SOC in the B2g representation, (b) in-plane SOC in the B1g representation, and (c) interlayer SOC in the Eg representation can arise microscopically, going beyond a purely symmetry-based analysis.
IV.1 In-plane B2g
We begin by discussing the in-plane k-SOC in the B2g representation, which contains () momentum dependence. This SOC is important since based on symmetry, there will already be a finite in the presence of the orbital hybridization and atomic SOC. Since the orbital hybridization for the system considered here will appear between the and orbitals as , and transforms under the B2g representation, there is a cubic coupling term in the free energy between the atomic SOC (), transforming as A1g, orbital hybridization and B2g SOC. This symmetry-allowed coupling , where denotes the atomic SOC, ensures the presence of a non-zero B2g SOC in the presence of both orbital hybridization and atomic SOC.
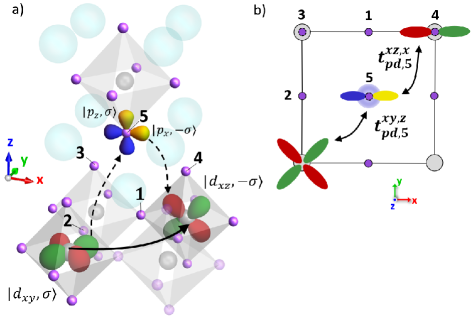
Furthermore, the in-plane k-SOC in the B2g representation arises through several hopping channels, all utilizing intermediate -orbitals, but different oxygen sites denoted by 1-5 in Fig. 2, including only nearby sites. As most of these channels occur in a single layer of Ru-O octahedra, this SOC should be expected to be the leading contribution beyond the atomic SOC, since we will see that the other two k-SOC always require hopping to additional layers. Such an in-plane k-SOC can be obtained through perturbation theory by considering hopping between next-nearest neighbor Ru atoms through the various channels, via the oxygen sites as intermediate states, and including the oxygen -orbitals’ atomic SOC. This hopping process results in an electron hopping from the orbital with spin to either a or orbital with spin , where the former case is shown in Fig. 2 by the black solid line. The contributing channels are indicated by the numbering of the intermediate oxygen sites, and only path 5 is shown explicitly for clarity. The effective SOC Hamiltonian involving the next-nearest neighbor Ru sites is obtained by
| (14) |
where denotes the hopping Hamiltonian involving both and orbitals. The sum runs over the intermediate oxygen states for all channels, which are eigenstates of the oxygen SOC , with the position of the oxygen site, and we consider up to the 2nd order of the perturbation theory for this process.
For instance, considering a hopping process between a state with spin- and a spin- state via the apical oxygen site shown, we have and . The energy denominator is given for and by and respectively, where is the difference in the on-site atomic potentials, and is the oxygen SOC constant. Considering the hopping amplitude between the orbital with spin at site R denoted by and the opposite spin state of the orbital at site , , we obtain,
| (15) | ||||
where the sum is over the contributing channels involving the different oxygen sites indicated in Fig. 2 and refer to the orbitals in the intermediate hopping amplitudes. All of these channels contain the hopping amplitudes between either the and , or and orbitals. From Fig. 2 it can be seen that the overall sign dependence of the hopping channel will match that of the orbital, since and change sign identically under the and mirror planes, while is even under them, leading to the dependence. Furthermore, the presence of in Eq. (15) gives rise to spin-dependence.
Taking into account the equivalent process between the and orbitals, which is related by a rotation, we obtain
| (16) | ||||
where and indicates the different -orbital sites involved in Fig. 2.
Quantifying the value of in Sr2RuO4 will require further studies to accurately include the additional effects of the coupling between other microscopic parameters such as the Ru on-site SOC and orbital hybridization, as discussed above. Correlation effects have also been shown to be crucial for the size of SOC, which is enhanced from the local-density approximation SOC values [26]. The current work is to show a microscopic route to generating k-SOC within a perturbation theory approach, beyond a purely symmetry-based perspective. These considerations also apply to the other k-SOC processes, to which we now turn.
IV.2 In-plane B1g
We now consider a microscopic route to obtaining an in-plane k-SOC in the B1g representation, which has a form factor. This requires a different layer of Ru-O octahedra, but the same procedure. An example of this process is shown in Fig. 3(a), for which the hopping between the orbital with a spin state and the opposite spin state of the orbital is indicated, where the overlap of the orbital with both the and orbitals is shown. The hopping amplitudes are represented schematically in Fig. 3(b) for both the or directions, where the lobe closest to the plane containing the effective hopping is shown, and the / orbitals are in separate squares for clarity. The numbering in Fig. 3(b) indicates whether the orbital is on the apical oxygen site (2) or the bottom (1) layer. We denote the hopping between the orbital and () as , with both having magnitude due to the rotational symmetry. The hopping between either of the orbitals and is denoted by , where the two are also of equal magnitude.
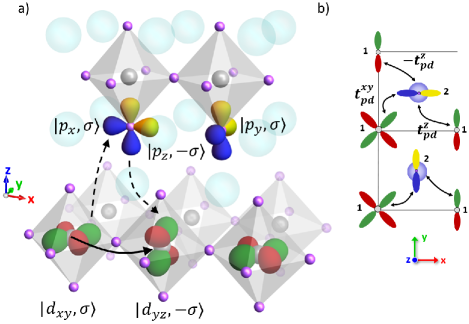
Evaluating the sum over the possible intermediate states for a given apical oxygen site, we obtain
| (17) | ||||
Due to the mirror symmetry about the plane, where the apical oxygen above the plane in the direction is shown in Fig. 3, the imaginary term cancels after summing over the two oxygen sites at , since , while the real term is invariant. Summing over both - and -direction paths, we have,
| (18) | ||||
where and it can be noted that this Hamiltonian is similar to , but with replaced with a form factor.
IV.3 Interlayer Eg
Here we consider an interlayer k-SOC as well as interlayer hopping between the and either of the orbitals. The k-SOC is the spin-dependent part of this process that occurs between states with the same spin in adjacent layers, via the apical oxygen sites as shown in Fig. 4(a), which displays the hopping process for the case.
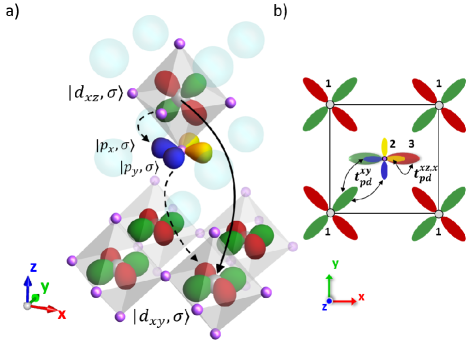
A schematic illustration of the relevant hopping amplitudes is represented in Fig. 4(b), where () is the hopping amplitude between the and () orbitals in different layers with equal magnitudes, . The hopping amplitude occurring purely in the direction between the orbital and the at the apical oxygen site is .
We have for the matrix element represented by Fig. 4,
| (19) | ||||
from which we see that the real part gives a spin-independent hopping between the orbitals and the imaginary part gives a spin-dependent hopping. Both real and imaginary parts are odd in since is odd with respect to reflection about the plane. Furthermore, since the real and imaginary parts are proportional to and respectively, the real part will be even (odd) in with the opposite signs for the imaginary part. A rotation yields the equivalent result involving , but with an opposite even/odd sign dependence with respect to the directions. The result is an effective interlayer hopping,
| (20) | ||||
as well as the effective SOC,
| (21) | ||||
where the effective hopping amplitudes are
| (22) | ||||
In summary, we have shown how three different k-SOC terms with distinct symmetries can be generated within a model consisting of the orbitals and oxygen -orbitals with associated on-site SOC. A fit to the density-functional theory (DFT) results of Ref. [25] was carried out within a TB model including k-SOC in Ref. [20], for which the size of the various k-SOC parameters were all determined to be . However, as discussed in Ref. [20], through comparison to angle-resolved photoemission spectroscopy (ARPES) measurements [26], it can be seen that the DFT parameters do not accurately account for the size of the SOC, which is enhanced through correlation effects [26]. Thus, as mentioned previously, quantifying the values of k-SOC in Sr2RuO4 requires future studies.
With a microscopic understanding of the origin of these three forms of k-SOC, we next turn to incorporating them into a three-orbital model and study the pairing instabilities that arise in Sr2RuO4 when the on-site interactions are included.
V Application to Sr2RuO4
We apply the shadowed triplet pairing scenario to the unconventional superconductor Sr2RuO4 [14, 15, 16, 17] by performing numerical calculations within MF theory for three orbitals. This includes 18 spin-triplet order parameters, described in Eq. (3), which are solved self-consistently at zero temperature. Let us take a Hamiltonian, , where the kinetic term, , is given by
| (23) |
with the orbital index and orbital dispersions, , and . The TB parameters, introduced in Ref. [21], are (, , , , , , , ) = (0.45, 0.05, 0.5, 0.2, 0.0025, 0.025, 0.54, 0.64), where all parameters are in units of 2. The SOC Hamiltonian is
| (24) |
where the atomic SOC in the basis of orbitals is , and is the completely anti-symmetric tensor with representing the orbitals. The resulting TB model is capable of reproducing the experimental FS of Sr2RuO4 [32, 33, 34, 26] and the pairing term, , consists of the attractive channel expressed in terms of the interorbital spin-triplet order parameters in Eq. (2).
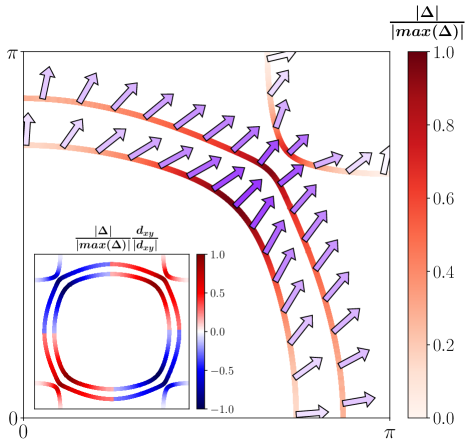
The MF results are obtained with and the atomic SOC fixed to . With , we obtain a purely -wave solution with , as shown in Ref. [3]. As reaches an appreciable percentage of , the component becomes non-zero, with orbital MFs . Also, there is a relative phase of compared to the -component of pairing. This solution is of the form in the band basis and has underlying triplet character with a predominantly in-plane -vector involving pairing mostly between the and as well as and orbitals. For , the and components are approximately equal in magnitude. The QP gap is found to be maximum along the line, with and . The pairing state exists for a range of and values around this. Increasing will eventually lead to a state with only the component. We note that while we have derived through a perturbative process and is therefore expected to be smaller than the SOC of oxygen, 20meV [35], there should be additional enhancement of the B2g SOC through the coupling to the atomic SOC and orbital hybridization, as well as correlations, which we discussed earlier. We therefore treat as an effective parameter taking these effects into account, while yielding a FS in agreement with ARPES.
We show the gap on the FS in Fig. 5, along with arrows indicating the nature of the shadowed triplet at select k points away from the Fermi energy. The SC gap is smallest on the band along the BZ boundaries, on the order of of the maximum gap or eV), using meV [36, 37], and can be even smaller as the MF gap is generally overestimated. Furthermore, these deep minima in the gap are robust to changes in the SOC parameters within the region where the solution is stabilized. The direction of the arrows indicates the in-plane direction of the -vector, with the length indicating the magnitude of the in-plane component; the shorter the arrow, the bigger the -axis component. Due to the component vanishing along the - and - axis, the pairing solution is composed of along the -axis and along the -axis, leading to a -vector that is parallel to the respective axis. The vanishing of the component of the pairing along the directions is illustrated in the inset of Fig. 5.
Within a microscopic theory including Kanamori interactions, the atomic SOC and the B2g and Eg k-SOCs derived in Sec. IV, it is possible to stabilize both order parameters of the or type at the FS, depending on the relative size of the Eg, B2g and atomic SOC strengths. As discussed in Sec. III, these order parameters will appear as intraband pseudospin-singlets on the FS, but with underlying interorbital triplet character originating from the orbital order parameters, . The atomic SOC will stabilize MFs of the form [3, 21, 18, 20]. The B2g SOC, which is given by Eq. (16), will favor an order parameter that appears with symmetry and underlying and triplet character. The Eg SOC, given by Eq. (21), will favor a multicomponent order parameter that appears as [18, 20] and have underlying and character. By including both the atomic and B2g SOCs, a multicomponent order parameter with symmetry can be stabilized, where the relative size of the and components is determined by the relative sizes of and . By comparing the ground-state energies, we find that the solution becomes favorable over the purely -wave solution when and . However, including the B2g SOC by fixing , the critical value at which the state is stabilized remains approximately the same. Given that the only contribution to the Eg SOC involves hopping between different layers, it is reasonable that is larger than , leading to a dominant pairing state over .
There has been a growing body of evidence suggesting that any viable order parameter must be a time-reversal symmetry breaking (TRSB) multicomponent order parameter [38, 39, 40, 41], with an appropriate symmetry that will lead to a jump in the elastic modulus at [42, 43], and lead to a substantial reduction of the nuclear magnetic resonance (NMR) Knight shift for an in-plane field [44, 45]. Two even parity proposals are the multicomponent order parameter in the two-dimensional Eg representation [46, 20] and the order parameter which relies on an accidental degeneracy with components from both the B1g and A2g representations [47]. The state proposed here is a combination of the A1g and B2g representations and generates a sudden change in the shear elastic modulus but not , consistent with the ultrasound data. This is in contrast to an order parameter in the Eg representation, leading to a jump also in the elastic modulus, which has not been observed experimentally [42, 43]. Since other pairing solutions such as are also found as local minima in MF theory, further experiments and theoretical studies to pin down different order parameters are left for the future.
VI Summary and Discussion
In summary, we have studied the microscopic mechanisms of k-SOC and its importance for even-parity spin-triplet pairing in Hund’s metals. By taking a simple two-orbital model, we show how a purely interorbital -wave triplet pairing in the orbital basis becomes an intraband pseudospin-singlet pairing with nontrivial momentum dependence near the FS, as well as pseudospin-singlet and -triplet interband pairings which also contain momentum dependence. In the process, we have illustrated the effects of orbital hybridization and SOC on the interorbital spin-triplet pairing state. Applying the idea to Sr2RuO4, we have derived several forms of -wave k-SOC in the B1g, B2g and Eg representations, by including the SOC of the oxygen sites within a model consisting of the orbitals and oxygen orbitals. While determining the precise size of the various k-SOC parameters in Sr2RuO4 will require future study, the perturbative approach taken here is an important step in understanding the microscopic origins of these terms in Sr2RuO4 and other materials. For instance, based on this analysis it is reasonable to expect that the dominant form of k-SOC will likely be from the next-nearest-neighbor in-plane B2g SOC, which will generate a pairing component in addition to the -wave pairing stabilized by the atomic SOC. Subsequently, we have demonstrated the viability of the multicomponent solution by including the atomic SOC, B2g and Eg SOCs with orbitals. For a range of the three SOC parameters, the existence of the state with a predominantly in-plane -vector is generic and independent of details, while competition with other shadowed triplet pairing symmetries depends on the microscopic parameters. The concept we have presented is also applicable to other correlated Hund’s metals with significant SOC.
While the pairing solution we have found manifests as a pseudospin-singlet on the FS, the shadowed triplet nature with a predominantly in-plane -vector will be apparent in the presence of finite fields [48]. As discussed previously in Ref. [21], these properties can be confirmed by NMR under uniaxial strain, with an in-plane field applied along both the direction of the strain and perpendicular to it. The state we have presented here has essentially the same property that near the directions, where there is mostly and orbital character, the -vector is parallel to the crystal axes due to the -wave component of pairing and the fact that the component vanishes along those directions. Therefore, under uniaxial strain, there should be a rotation of the average -vector, leading to an anisotropic Knight shift between the and directions when the field is a significant fraction of the gap size. Interestingly, the low field behavior is governed by the pairing near the FS, leading to a more isotropic response consistent with the Knight shift of NMR [21].
Going beyond the purely -wave case, an pairing naturally explains experiments suggesting a multicomponent order parameter with TRSB and the observed jump in the elastic modulus but not the modulus [38, 39, 40, 41, 42, 43]. While matches the jump in , the lack of an observed jump in is in favor of the pairing state over the state. These two pairing states can also be distinguished due to their different triplet character. The leading order parameter for the solution corresponds to an out-of-plane -vector, which would yield no rotation under uniaxial strain in contrast to the behavior of the state, as discussed above. Such an experiment could provide a test of the order parameter arising from the combination of local interactions and k-SOC in light of the lack of many other viable multicomponent alternatives.
In general, two order parameters from different representations with broken time-reversal symmetry implies the presence of two transition temperatures. However, currently there are conflicting experimental data under uniaxial strain regarding this issue: specific heat measurements show no signs of a second transition [49], while muon spin relaxation measurements do indicate a splitting of and the onset of TRSB [41]. Therefore, future experiments under strain will be an important test for a TRSB pairing state. Beyond the experiments under uniaxial strain, it will be important going forward for future experiments to clarify whether the putative gap nodes [50, 51, 52, 53, 54, 55] are indeed nodes or deep gap minima, which arise naturally in the pairing solution considered here, as well as the precise location in k-space of these nodes.
Acknowledgements.
We thank Y.-B. Kim for useful discussions. This work was supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grant No. 06089-2016, the Center for Quantum Materials at the University of Toronto, the Canadian Institute for Advanced Research, and the Canada Research Chairs Program. Computations were performed on the Niagara supercomputer at the SciNet HPC Consortium. SciNet is funded by: the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; Ontario Research Fund - Research Excellence; and the University of Toronto.References
- Klejnberg and Spalek [1999] A. Klejnberg and J. Spalek, Hund’s rule coupling as the microscopic origin of the spin-triplet pairing in a correlated and degenerate band system, J. Phys.: Condens. Matter 11, 6553 (1999).
- Dai et al. [2008] X. Dai, Z. Fang, Y. Zhou, and F.-C. Zhang, Even Parity, Orbital Singlet, and Spin Triplet Pairing for Superconducting , Phys. Rev. Lett. 101, 057008 (2008).
- Puetter and Kee [2012] C. M. Puetter and H.-Y. Kee, Identifying spin-triplet pairing in spin-orbit coupled multi-band superconductors, EPL (Europhysics Letters) 98, 27010 (2012).
- Hoshino and Werner [2015] S. Hoshino and P. Werner, Superconductivity from Emerging Magnetic Moments, Phys. Rev. Lett. 115, 247001 (2015).
- Hoshino and Werner [2016] S. Hoshino and P. Werner, Electronic orders in multiorbital Hubbard models with lifted orbital degeneracy, Phys. Rev. B 93, 155161 (2016).
- Gingras et al. [2019] O. Gingras, R. Nourafkan, A.-M. S. Tremblay, and M. Côté, Superconducting Symmetries of from First-Principles Electronic Structure, Phys. Rev. Lett. 123, 217005 (2019).
- Vafek and Chubukov [2017] O. Vafek and A. V. Chubukov, Hund Interaction, Spin-Orbit Coupling, and the Mechanism of Superconductivity in Strongly Hole-Doped Iron Pnictides, Phys. Rev. Lett. 118, 087003 (2017).
- Joynt and Taillefer [2002] R. Joynt and L. Taillefer, The superconducting phases of , Rev. Mod. Phys. 74, 235 (2002).
- Kallin and Berlinsky [2016] C. Kallin and J. Berlinsky, Chiral superconductors, Rep. Prog. Phys. 79, 054502 (2016).
- Fu and Kane [2008] L. Fu and C. L. Kane, Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator, Phys. Rev. Lett. 100, 096407 (2008).
- Fujimoto [2008] S. Fujimoto, Topological order and non-Abelian statistics in noncentrosymmetric -wave superconductors, Phys. Rev. B 77, 220501(R) (2008).
- Fu and Kane [2009] L. Fu and C. L. Kane, Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction, Phys. Rev. B 79, 161408(R) (2009).
- Chen and Kee [2014] Y. Chen and H.-Y. Kee, Topological phases in iridium oxide superlattices: Quantized anomalous charge or valley Hall insulators, Phys. Rev. B 90, 195145 (2014).
- Maeno et al. [1994] Y. Maeno, H. Hashimoto, K. Yoshida, S. Nishizaki, T. Fujita, J. G. Bednorz, and F. Lichtenberg, Superconductivity in a layered perovskite without copper, Nature (London) 372, 532 (1994).
- Mackenzie and Maeno [2003] A. P. Mackenzie and Y. Maeno, The superconductivity of and the physics of spin-triplet pairing, Rev. Mod. Phys. 75, 657 (2003).
- Kallin [2012] C. Kallin, Chiral p-wave order in Sr2RuO4, Rep. Prog. Phys. 75, 042501 (2012).
- Mackenzie et al. [2017] A. P. Mackenzie, T. Scaffidi, C. W. Hicks, and Y. Maeno, Even odder after twenty-three years: the superconducting order parameter puzzle of , npj Quantum Mater. 2, 40 (2017).
- Cheung and Agterberg [2019] A. K. C. Cheung and D. F. Agterberg, Superconductivity in the presence of spin-orbit interactions stabilized by Hund coupling, Phys. Rev. B 99, 024516 (2019).
- Ramires and Sigrist [2019] A. Ramires and M. Sigrist, Superconducting order parameter of : A microscopic perspective, Phys. Rev. B 100, 104501 (2019).
- Suh et al. [2020] H. G. Suh, H. Menke, P. M. R. Brydon, C. Timm, A. Ramires, and D. F. Agterberg, Stabilizing even-parity chiral superconductivity in , Phys. Rev. Res. 2, 032023 (2020).
- Lindquist and Kee [2020] A. W. Lindquist and H.-Y. Kee, Distinct reduction of Knight shift in superconducting state of under uniaxial strain, Phys. Rev. Res. 2, 032055 (2020).
- Pavarini and Mazin [2006] E. Pavarini and I. I. Mazin, First-principles study of spin-orbit effects and NMR in , Phys. Rev. B 74, 035115 (2006).
- Haverkort et al. [2008] M. W. Haverkort, I. S. Elfimov, L. H. Tjeng, G. A. Sawatzky, and A. Damascelli, Strong Spin-Orbit Coupling Effects on the Fermi Surface of and , Phys. Rev. Lett. 101, 026406 (2008).
- Rozbicki et al. [2011] E. J. Rozbicki, J. F. Annett, J.-R. Souquet, and A. P. Mackenzie, Spin–orbit coupling and k-dependent Zeeman splitting in strontium ruthenate, J. Phys.: Condens. Matter 23, 094201 (2011).
- Veenstra et al. [2014] C. N. Veenstra, Z.-H. Zhu, M. Raichle, B. M. Ludbrook, A. Nicolaou, B. Slomski, G. Landolt, S. Kittaka, Y. Maeno, J. H. Dil, I. S. Elfimov, M. W. Haverkort, and A. Damascelli, Spin-Orbital Entanglement and the Breakdown of Singlets and Triplets in Revealed by Spin- and Angle-Resolved Photoemission Spectroscopy, Phys. Rev. Lett. 112, 127002 (2014).
- Tamai et al. [2019] A. Tamai, M. Zingl, E. Rozbicki, E. Cappelli, S. Riccò, A. de la Torre, S. McKeown Walker, F. Y. Bruno, P. D. C. King, W. Meevasana, M. Shi, M. Radović, N. C. Plumb, A. S. Gibbs, A. P. Mackenzie, C. Berthod, H. U. R. Strand, M. Kim, A. Georges, and F. Baumberger, High-Resolution Photoemission on Reveals Correlation-Enhanced Effective Spin-Orbit Coupling and Dominantly Local Self-Energies, Phys. Rev. X 9, 021048 (2019).
- Mravlje et al. [2011] J. Mravlje, M. Aichhorn, T. Miyake, K. Haule, G. Kotliar, and A. Georges, Coherence-Incoherence Crossover and the Mass-Renormalization Puzzles in , Phys. Rev. Lett. 106, 096401 (2011).
- Fischer [2013] M. H. Fischer, Gap symmetry and stability analysis in the multi-orbital Fe-based superconductors, New J. Phys. 15, 073006 (2013).
- Ramires and Sigrist [2016] A. Ramires and M. Sigrist, Identifying detrimental effects for multiorbital superconductivity: Application to , Phys. Rev. B 94, 104501 (2016).
- Ramires et al. [2018] A. Ramires, D. F. Agterberg, and M. Sigrist, Tailoring by symmetry principles: The concept of superconducting fitness, Phys. Rev. B 98, 024501 (2018).
- Huang et al. [2019] W. Huang, Y. Zhou, and H. Yao, Exotic Cooper pairing in multiorbital models of , Phys. Rev. B 100, 134506 (2019).
- Mackenzie et al. [1996] A. P. Mackenzie, S. R. Julian, A. J. Diver, G. J. McMullan, M. P. Ray, G. G. Lonzarich, Y. Maeno, S. Nishizaki, and T. Fujita, Quantum Oscillations in the Layered Perovskite Superconductor SRu, Phys. Rev. Lett. 76, 3786 (1996).
- Bergemann et al. [2000] C. Bergemann, S. R. Julian, A. P. Mackenzie, S. NishiZaki, and Y. Maeno, Detailed Topography of the Fermi Surface of , Phys. Rev. Lett. 84, 2662 (2000).
- Damascelli et al. [2000] A. Damascelli, D. H. Lu, K. M. Shen, N. P. Armitage, F. Ronning, D. L. Feng, C. Kim, Z.-X. Shen, T. Kimura, Y. Tokura, Z. Q. Mao, and Y. Maeno, Fermi Surface, Surface States, and Surface Reconstruction in , Phys. Rev. Lett. 85, 5194 (2000).
- Oguchi [1995] T. Oguchi, Electronic band structure of the superconductor , Phys. Rev. B 51, 1385 (1995).
- Kim et al. [2018] M. Kim, J. Mravlje, M. Ferrero, O. Parcollet, and A. Georges, Spin-Orbit Coupling and Electronic Correlations in , Phys. Rev. Lett. 120, 126401 (2018).
- Røising et al. [2019] H. S. Røising, T. Scaffidi, F. Flicker, G. F. Lange, and S. H. Simon, Superconducting order of from a three-dimensional microscopic model, Phys. Rev. Res. 1, 033108 (2019).
- Luke et al. [1998] G. M. Luke, Y. Fudamoto, K. M. Kojima, M. I. Larkin, J. Merrin, B. Nachumi, Y. J. Uemura, Y. Maeno, Z. Q. Mao, Y. Mori, H. Nakamura, and M. Sigrist, Time-reversal symmetry-breaking superconductivity in , Nature (London) 394, 558 (1998).
- Xia et al. [2006] J. Xia, Y. Maeno, P. T. Beyersdorf, M. M. Fejer, and A. Kapitulnik, High Resolution Polar Kerr Effect Measurements of : Evidence for Broken Time-Reversal Symmetry in the Superconducting State, Phys. Rev. Lett. 97, 167002 (2006).
- Kidwingira et al. [2006] F. Kidwingira, J. D. Strand, D. J. Van Harlingen, and Y. Maeno, Dynamical superconducting order parameter domains in , Science 314, 1267 (2006).
- [41] V. Grinenko, S. Ghosh, R. Sarkar, J.-C. Orain, A. Nikitin, M. Elender, D. Das, Z. Guguchia, F. Brückner, M. E. Barber, J. Park, N. Kikugawa, D. A. Sokolov, J. S. Bobowski, T. Miyoshi, Y. Maeno, A. P. Mackenzie, H. Luetkens, C. W. Hicks, and H.-H. Klauss, Split superconducting and time-reversal symmetry-breaking transitions, and magnetic order in under uniaxial stress, arXiv:2001.08152 [cond-mat.supr-con] .
- Ghosh et al. [2020] S. Ghosh, A. Shekhter, F. Jerzembeck, N. Kikugawa, D. A. Sokolov, M. Brando, A. P. Mackenzie, C. W. Hicks, and B. J. Ramshaw, Thermodynamic evidence for a two-component superconducting order parameter in , Nat. Phys. (2020), doi: 10.1038/s41567-020-1032-4.
- Benhabib et al. [2020] S. Benhabib, C. Lupien, I. Paul, L. Berges, M. Dion, M. Nardone, A. Zitouni, Z. Q. Mao, Y. Maeno, A. Georges, et al., Ultrasound evidence for a two-component superconducting order parameter in , Nat. Phys. (2020), doi: 10.1038/s41567-020-01090-2.
- Pustogow et al. [2019] A. Pustogow, Y. Luo, A. Chronister, Y.-S. Su, D. A. Sokolov, F. Jerzembeck, A. P. Mackenzie, C. W. Hicks, N. Kikugawa, S. Raghu, et al., Constraints on the superconducting order parameter in from oxygen-17 nuclear magnetic resonance, Nature (London) 574, 72 (2019).
- Ishida et al. [2020] K. Ishida, M. Manago, K. Kinjo, and Y. Maeno, Reduction of the 17O Knight shift in the superconducting state and the heat-up effect by NMR pulses on , J. Phys. Soc. Jpn. 89, 034712 (2020).
- Žutić and Mazin [2005] I. Žutić and I. Mazin, Phase-Sensitive Tests of the Pairing State Symmetry in , Phys. Rev. Lett. 95, 217004 (2005).
- Kivelson et al. [2020] S. A. Kivelson, A. C. Yuan, B. Ramshaw, and R. Thomale, A proposal for reconciling diverse experiments on the superconducting state in , npj Quantum Mater. 5, 43 (2020).
- Yu et al. [2018] Y. Yu, A. K. C. Cheung, S. Raghu, and D. F. Agterberg, Residual spin susceptibility in the spin-triplet orbital-singlet model, Phys. Rev. B 98, 184507 (2018).
- [49] Y. S. Li, N. Kikugawa, D. A. Sokolov, F. Jerzembeck, A. S. Gibbs, Y. Maeno, C. W. Hicks, M. Nicklas, and A. P. Mackenzie, High sensitivity heat capacity measurements on under uniaxial pressure, arXiv:1906.07597 [cond-mat.supr-con] .
- NishiZaki et al. [2000] S. NishiZaki, Y. Maeno, and Z. Mao, Changes in the superconducting state of under magnetic fields probed by specific heat, J. Phys. Soc. Jpn. 69, 572 (2000).
- Bonalde et al. [2000] I. Bonalde, B. D. Yanoff, M. B. Salamon, D. J. Van Harlingen, E. M. E. Chia, Z. Q. Mao, and Y. Maeno, Temperature Dependence of the Penetration Depth in : Evidence for Nodes in the Gap Function, Phys. Rev. Lett. 85, 4775 (2000).
- Lupien et al. [2001] C. Lupien, W. A. MacFarlane, C. Proust, L. Taillefer, Z. Q. Mao, and Y. Maeno, Ultrasound Attenuation in : An Angle-Resolved Study of the Superconducting Gap Function, Phys. Rev. Lett. 86, 5986 (2001).
- Firmo et al. [2013] I. A. Firmo, S. Lederer, C. Lupien, A. P. Mackenzie, J. C. Davis, and S. A. Kivelson, Evidence from tunneling spectroscopy for a quasi-one-dimensional origin of superconductivity in , Phys. Rev. B 88, 134521 (2013).
- Hassinger et al. [2017] E. Hassinger, P. Bourgeois-Hope, H. Taniguchi, S. René de Cotret, G. Grissonnanche, M. S. Anwar, Y. Maeno, N. Doiron-Leyraud, and L. Taillefer, Vertical Line Nodes in the Superconducting Gap Structure of , Phys. Rev. X 7, 011032 (2017).
- Sharma et al. [2020] R. Sharma, S. D. Edkins, Z. Wang, A. Kostin, C. Sow, Y. Maeno, A. P. Mackenzie, J. S. Davis, and V. Madhavan, Momentum-resolved superconducting energy gaps of from quasiparticle interference imaging, Proc. Natl. Acad. Sci. (USA) 117, 5222 (2020).