csymbol=c \dottedcontentssection[4em]2.9em0.7pc \dottedcontentssubsection[0em]3.3em1pc
SHARP THRESHOLD FOR THE BALLISTICITY OF THE RANDOM WALK ON THE EXCLUSION PROCESS
Abstract
We study a non-reversible random walk advected by the symmetric simple exclusion process, so that the walk has a local drift of opposite sign when sitting atop an occupied or an empty site. We prove that the back-tracking probability of the walk exhibits a sharp transition as the density of particles in the underlying exclusion process varies across a critical density . Our results imply that the speed of the walk is a strictly monotone function and that the zero-speed regime is either absent or collapses to a single point, , thus solving a conjecture of [40]. The proof proceeds by exhibiting a quantitative monotonicity result for the speed of a truncated model, in which the environment is renewed after a finite time horizon . The truncation parameter is subsequently pitted against the density to carry estimates over to the full model. Our strategy is somewhat reminiscent of certain techniques recently used to prove sharpness results in percolation problems. A key instrument is a combination of renormalisation arguments with refined couplings of environments at slightly different densities, which we develop in this article. Our results hold in fact in greater generality and apply to a class of environments with possibly egregious features, outside perturbative regimes.
Guillaume Conchon-Kerjan1, Daniel Kious2 and Pierre-François Rodriguez3
September 2024
1King’s College London
Department of Mathematics
London WC2R 2LS
United Kingdom
guillaume.conchon-kerjan@kcl.ac.uk
2University of Bath
Department of Mathematical Sciences
Bath BA2 7AY
United Kingdom
3Imperial College London
Department of Mathematics
London SW7 2AZ
United Kingdom
1 Introduction
Transport in random media has been an active field of research for over fifty years but many basic questions remain mathematically very challenging unless the medium satisfies specific (and often rather restrictive) structural assumptions; see for instance [48, 72, 77] and references therein. In this article we consider the problem of ballistic behavior in a benchmark setting that is both i) non-reversible, and ii) non-perturbative (in the parameters of the model). To get a sense of the difficulty these combined features entail, general results in case i) are already hard to come by in perturbative regimes, see, e.g., [24, 75] regarding the problem of diffusive behavior.
Our focus is on a certain random walk in dynamic random environment, which lies outside of the well-studied ‘classes’ and has attracted increasing attention in the last decade, see for instance [40, 43, 44] and references below. The interest in this model stems in no small part from the nature of the environment, which is driven by a particle system (e.g. the exclusion process) that is typically conservative and exhibits slow mixing. Even in the (1+1)-dimensional case, unless one restricts its parameters to perturbative regimes, the features of the model preclude the use of virtually all classical techniques: owing to the dynamics of the environment, the model is genuinely non-reversible, and its properties make the search for an invariant measure of the environment as seen by the walker (in the spirit of [49, 62, 47]) inaccessible by current methods; see Section 1.2 for a more thorough discussion of these and related matters.
The model we study depends on a parameter governing the density of particles in the environment, which in turn affects the walk, whose transition probabilities depend on whether the walk sits on top of a particle (advection occurs) or not. This may (or not) induce ballistic behaviour. Our aim in this article is to prove that ballisticity is a property of the walk undergoing a ‘sharp transition’ as varies, which is an inherently non-perturbative result. Our results answer a number of conjectures of the past fifteen years, and stand in stark contrast with (i.i.d.) static environments [46, 69], where the zero-speed regime is typically extended. The sharpness terminology is borrowed from critical phenomena, and the analogy runs deep, as will become apparent. Drawing inspiration from it is one of the cornerstones of the present work.
1.1. Main results
We present our main results with minimal formalism in the model case where the environment is the (simple) symmetric exclusion process, abbreviated (S)SEP in the sequel, and refer to Sections 2 and 6 for full definitions. We will in fact prove more general versions of these results, see Theorem 3.1, which hold under rather broad assumptions on the environment, satisfied for instance by the SEP. Another environment of interest that fulfils these conditions is discussed in Appendix B, and is built using a Poisson system of particles performing independent simple random walks (PCRW, short for Poisson Cloud of Random Walks).
The SEP is the continuous-time Markov process taking values in and describing the simultaneous evolution of continuous-time simple random walks subject to the exclusion rule. That is, for a given realization of , one puts a particle at those sites such that . Each particle then attempts to move at a given rate , independently of its previous moves and of the other particles, to one of its two neighbours chosen with equal probability. The move happens if and only if the target site is currently unoccupied; see Section 6.1 for precise definitions. For the purposes of this article, one could simply set . We have kept the dependence on explicit in anticipation of future applications, for which one may wish to slow down/speed up the environment over time.
On top of the SEP , a random walk starting from moves randomly as follows. Fixing two parameters such that , the process moves at integer times to a neighbouring site, the right site being chosen with probability , resp. , depending on whether is currently located on an occupied or empty site. Formally, given a realization of the SEP, and for all ,
| (1.1) |
(notice that the transition probabilities depend on since by assumption). For we denote by the annealed (i.e. averaged over all sources of randomness; see Section 2.3 for details) law of whereby is sampled according to a product Bernoulli measure , with a Dirac measure at , which is an invariant measure for the SEP, see Lemma 6.1. Incidentally, one can check that except for the trivial cases , none of the invariant measures for the SEP (cf. [51, Chap. III, Cor. 1.11]) is invariant for the environment viewed from the walker (to see this, one can for instance consider the probability that the origin and one of its neighbours are both occupied). In writing , we leave the dependence on and implicit, which are regarded as fixed, and we will focus on the dependence of quantities on , the main parameter of interest. For a mental picture, the reader is invited to think of as evolving in a half-plane, with space being horizontal and time running upwards. All figures below will follow this convention.
We now describe our main results, using a language that will make analogies to critical phenomena apparent. Our first main result is simplest to formulate in terms of the fast-tracking probability, defined for and as
| (1.2) |
where . In words is the probability that visits before . Analogous results can be proved for a corresponding back-tracking probability, involving the event instead; see the end of Section 1.1 for more on this. The events in (1.2) being decreasing in , the following limit
| (1.3) |
is well-defined and constitutes an order parameter (in the parlance of statistical physics) for the model. Indeed, it is not difficult to see from (1.1) and monotonicity properties of the environment (see (P.3) in Section 2.2 and Lemma 2.2), that the functions , , and hence are non-decreasing, i.e. that whenever . One thus naturally associates to the function a corresponding critical threshold
| (1.4) |
The transition from the subcritical () to the supercritical () regime corresponds to the onset of a phase where the walk has a positive chance to escape to the right. In fact it will do so at linear speed, as will follow from our second main result. To begin with, in view of (1.4) one naturally aims to quantify the behavior of for large . Our first theorem exhibits a sharp transition for its decay.
Theorem 1.1.
For all , there exist constants depending on such that, with as in (1.4) and for all ,
-
(i)
, if ;
-
(ii)
, if .
The proof of Theorem 1.1 appears at the end of Section 3.2. Since , item (ii) is an immediate consequence of (1.4). The crux of Theorem 1.1 is therefore to exhibit the rapid decay of item (i) in the full subcritical regime, and not just perturbatively in , which is the status quo, cf. Section 1.2. In the context of critical phenomena, this is the famed question of (subcritical) sharpness, see for instance [53, 1, 36, 76] for sample results of this kind in the context of Ising and Bernoulli percolation models. Plausibly, the true order of decay in item (i) is in fact exponential in (for instance, a more intricate renormalisation following [40] should already provide a stretched-exponential bound in ). We will not delve further into this question in the present article.
Our approach to proving Theorem 1.1 is loosely inspired by the recent sharpness results [31] and [33, 34, 32] concerning percolation of the Gaussian free field and the vacant set of random interlacements, respectively, which both exhibit long-range dependence (somewhat akin to the SEP). Our model is nonetheless very different, and our proof strategy, outlined below in Section 1.3, vastly differs from these works. In particular, it does not rely on differential formulas (in ), nor does it involve the OSSS inequality or sharp threshold techniques, which have all proved useful in the context of percolation, see e.g. [35, 38, 17, 23]. One similarity with [33], and to some extent also with [76] (in the present context though, stochastic domination results may well be too much to ask for), is our extensive use of couplings. Developing these couplings represents one of the most challenging technical aspects of our work; we return to this in Section 1.3. It is also interesting to note that, as with statistical physics models, the regime near and at the critical density encompasses a host of very natural (and mostly open) questions that seem difficult to answer and point towards interesting phenomena; see Section 1.2 and Corollary 1.3 for more on this.
Our second main result concerns the asymptotic speed of the random walk, and addresses an open problem of [40] which inspired our work. In [40], the authors prove the existence of a deterministic non-decreasing function such that, for all ,
| (1.5) |
where
| (1.6) |
leaving open whether or not, and with it the possible existence of an extended (critical) zero-speed regime. Our second main result yields the strict monotonicity of and provides the answer to this question. Recall that our results hold for any choice of the parameters and .
Theorem 1.2.
The proof of Theorem 1.2 is given in Section 3.2 below. It will follow from a more general result, Theorem 3.1, which applies to a class of environments satisfying certain natural conditions. These will be shown to hold when is the SEP.
Let us now briefly relate Theorems 1.1 and 1.2. Loosely speaking, Theorem 1.1 indicates that whenever , whence in view of (1.6), which is morally half of Theorem 1.2. One can in fact derive a result akin to Theorem 1.1, but concerning the order parameter associated to the back-tracking probability instead. Defining in the same way as (1.4) but with in place of , our results imply that and that the transition for the back-tracking probability has similar sharpness features as in Theorem 1.1, but in opposite directions – the sub-critical regime is now for . Intuitively, this corresponds to the other inequality , which together with , yields (1.7).
Finally, Theorem 1.2 implies that whenever . Determining whether a law of large number holds at holds or not, let alone whether the limiting speed vanishes when , is in general a difficult question, to which we hope to return elsewhere; we discuss this and related matters in more detail below in Section 1.2.
One noticeable exception occurs in the presence of additional symmetry, as we now explain. In [40] the authors could prove that, at the ‘self-dual’ point (for any given value of ), one has and the law of large numbers holds with limit speed , but they could not prove that was non-zero for , or equivalently that . Notice that the value is special, since in this case (cf. (1.1)) has the same law under as under , and in particular when . In the result below, which is an easy consequence of Theorem 1.2 and the results of [40], we summarize the situation in the symmetric case. We include the (short) proof here. The following statement is of course reminiscent of a celebrated result of Kesten concerning percolation on the square lattice [45]; see also [23, 17, 58] in related contexts.
Corollary 1.3.
If , then
| (1.9) |
Moreover, under , is recurrent, and the law of large numbers (1.5) holds with vanishing limiting speed .
Proof.
From the proof of [40, Theorem 2.2] (and display (3.26) therein), one knows that and that the law of large numbers holds at . By Theorem 1.2, see (1.6) and (1.7), is negative on and positive on , which implies that . As for the recurrence of under , it follows from the ergodic argument of [61] (Corollary 2.2, see also Theorem 3.2 therein; these results are stated for a random walk jumping at exponential times but are easily adapted to our case). Since in view of (1.3), recurrence implies that , and (1.9) follows. ∎
1.2. Discussion
We now place the above results in broader context and contrast our findings with existing results. We then discuss a few open questions in relation with Theorems 1.1 and 1.2.
1.2.1. Related works
Random walks in dynamic random environments have attracted increasing attention in the past two decades, both in statistical physics - as a way to model a particle advected by a fluid [29, 59, 16, 42], and in probability theory - where they provide a counterpart to the more classically studied random walks in static environments [9, 22, 26, 40, 44, 66].
On , the static setting already features a remarkably rich phenomenology, such as transience with zero speed [71], owing to traps that delay the random walk, and anomalous fluctuations [46] - which can be as small as polylogarithmic in the recurrent case [69]. On for , some fundamental questions are still open in spite of decades of efforts, for instance the conjectures around Sznitman’s Condition (T) and related effective ballisticity criteria [72, 18], and the possibility that, for a uniformly elliptic environment, directional transience is equivalent to ballisticity. If true, these conjectures would have profound structural consequences, in essentially ascertaining that the above trapping phenomena can only be witnessed in dimension one. As with the model studied in this article, a circumstance that seriously hinders progress is the truly non-reversible character of these problems. This severely limits the tools available to tackle them.
New challenges arise when the environment is dynamic, requiring new techniques to handle the fact that correlations between transition probabilities are affected by time. In particular, the trapping mechanisms identified in the static case do not hold anymore and it is difficult to understand if they simply dissolve or if they are replaced by different, possibly more complex, trapping mechanisms. As of today, how the static and dynamic worlds relate is still far from understood. Under some specific conditions however, laws of large numbers (and sometimes central limit theorems) have been proved in dynamic contexts: when the environment has sufficiently good mixing properties [9, 22, 66], a spectral gap [7], or when one can show the existence of an invariant measure for the environment as seen by the walk ([19], again under some specific mixing conditions). One notable instance of such an environment is the supercritical contact process (see [25, 56], or [3] for a recent generalization). We also refer to [5, 57, 20, 6, 27] for recent results in the time-dependent reversible case, for which the assumptions on the environment can be substantially weakened.
The environments we consider are archetypal examples that do not satisfy any of the above conditions. In the model case of the environment driven by the SEP, the mixing time over a closed segment or a circle is super-linear (even slightly super-quadratic [55]), creating a number of difficulties, e.g. barring the option of directly building a renewal structure without having to make further assumptions (see [13] in the simpler non-nestling case). The fact that the systems may be conservative (as is the case for the SEP) further hampers their mixing properties. As such, they have been the subject of much attention in the past decade, see [10, 11, 12, 22, 28, 40, 41, 43, 44, 52] among many others. All of these results are of two types: either they require particular assumptions, or they apply to some perturbative regime of parameters, e.g. high density of particles [21, 26], strong drift, or high/low activity rate of the environment [43, 68].
Recently, building on this series of work, a relatively comprehensive result on the Law of Large Numbers (LLN) in dimension 1+1 has been proved in [40], see (1.5) above, opening an avenue to some fundamental questions that had previously remained out of reach, such as the possible existence of transient regime with zero speed. Indeed, cf. (1.5) and (1.6), the results of [40] leave open the possibility of having an extended ‘critical’ interval of ’s for which , which is now precluded as part of our main results, see (1.7). We seek the opportunity to stress that our strategy, outlined below in Section 1.3, is completely new and rather robust, and we believe a similar approach will lead to progress on related questions for other models.
1.2.2. Open questions
1) Existence and value of . Returning to Theorems 1.1 and 1.2, let us start by mentioning that , defined by (1.4) and equivalently characterized via (1.6)-(1.7), may in fact be degenerate (i.e. equal to or ) if stays of constant sign. It is plausible that if and only if , which corresponds to the (more challenging) nestling case, in which the walk has a drift of opposite signs depending on whether it sits on top of a particle or an empty site. Moreover, the function , as given by [40, Theorem 3.4], is well-defined for all values of (this includes a candidate velocity at ), but whether a LLN holds at with speed or the value of the latter is unknown in general, except in cases where one knows that by other means (e.g. symmetry), in which case a LLN can be proved, see [40, Theorem 3.5]. When is non-degenerate, given Theorem 1.2, it is natural to expect that , but this is not obvious as we do not presently know if is continuous at . It is relatively easy to believe that continuity on , when the speed is non-zero, can be obtained through an adaptation of the regeneration structure defined in [43], but continuity at (even in the symmetric case) seems to be more challenging.
Suppose now that one can prove that a law of large numbers holds with vanishing speed at , then one can ask whether is recurrent or transient at . A case in point where one knows the answer is the ‘self-dual’ point where the critical density equals and the walk is recurrent. In particular, this result and Theorem 1.2 imply that is zero if and only if , and thus there exists no transient regime with zero-speed in the symmetric case. This also answers positively the conjecture in [8] (end of Section 1.4), which states that in the symmetric case, the only density with zero speed is in fact recurrent.
2) Regularity of near and fluctuations at .
In cases where is proved, one may further wonder about the regularity of around (and similarly of as ). Is it continuous, and if yes, is it Hölder-continous, or even differentiable? This could be linked to the fluctuations of the random walk when , in the spirit of Einstein’s relation, see for instance [37] in the context of reversible dynamics. Whether the fluctuations of under are actually diffusive, super-diffusive or sub-diffusive is a particularly difficult question. It has so far been the subject of various conjectures, both for the RWdRE (e.g. Conjecture 3.5 in [14]) and very closely related models in statistical physics (e.g. [42], [39], [60]). One aspect making predictions especially difficult is that the answer may well depend on all parameters involved, i.e. , and . At present, any rigorous upper or lower bound on the fluctuations at would be a significant advance.
3) Comparison with the static setting. In the past decade, there have been many questions as to which features of a static environment (when , so that the particles do not move) are common to the dynamic environment, and which are different. In particular, it is well-known that in the static case, there exists a non-trivial interval of densities for which the random walker has zero speed, due to mesoscopic traps that the random walker has to cross on its way to infinity (see for instance [63, Example 1], and above references). It was conjectured that if is small enough, there could be such an interval in the dynamic set-up, see [14, (3.8)]. Theorem 1.2 thus disproves this conjecture.
Combined with the CLT from [40, Theorem 2.1], which is valid outside of , hence for all by Theorem 1.2, this also rules out the possibility of non-diffusive fluctuations for any , which were conjectured in [14, Section 3.5]. In light of this, one may naturally wonder how much one has to slow down the environment with time (one would have to choose a suitably decreasing function of the time ) in order to start seeing effects from the static world. We plan to investigate this in future work.
1.3. Overview of the proof
We give here a relatively thorough overview of the proof, intended to help the reader navigate the upcoming sections. For concreteness, we focus on Theorem 1.2 (see below its statement as to how Theorem 1.1 relates to it), and specifically on the equalities (1.7), in the case of SEP (although our results are more general; see Section 3). The assertion (1.7) is somewhat reminiscent of the chain of equalities associated to the phase transition of random interlacements that was recently proved in [34, 32, 33], and draws loose inspiration from the interpolation technique of [2], see also [30]. Similarly to [32] in the context of interlacements, and as is seemingly often the case in situations lacking key structural features (in the present case, a notion of reversibility or more generally self-adjointness, cf. [24, 75]), our methods rely extensively on the use of couplings.
The proof essentially consists of two parts, which we detail individually below. In the first part, we compare our model with a finite-range version, in which we fully re-sample the environment at times multiple of some large integer parameter (see e.g. [32] for a similar truncation to tame the long-range dependence). One obtains easily that for any and any density , the random walk in this environment satisfies a strong Law of Large Numbers with some speed (Lemma 3.2), and we show that in fact,
| (1.10) |
for some that are quantitative and satisfy as (see Proposition 3.3).
In the second part, we show that for any fixed , we have
| (1.11) |
for large enough (Proposition 3.4). Together, (1.10) and (1.11) readily imply that , and (1.7) follows. Let us now give more details.
First part: from infinite to finite range. For a density the environment of the range- model is the SEP starting from during the time interval . Then for every integer , at time we sample again as , independently from the past, and let it evolve as the SEP during the interval . The random walk on this environment is still defined formally as in (1.1), and we denote the associated annealed probability measure. Clearly, the increments are i.i.d. (and bounded), so that by the strong LLN, , a.s. as .
Now, to relate this to our original ’infinite-range’ () model, the main idea is to compare the range- with the range-, and more generally the range- with the range- model for all via successive couplings. The key is to prove a chain of inequalities of the kind
| (1.12) |
where the sequences of and are increasing, with and . In other words, we manage to pass from a scale to a larger scale , at the expense of losing a bit of speed , and using a little sprinkling in the density , with . From (1.12) (and a converse inequality proved in a similar way), standard arguments allow us to deduce (1.10). Let us mention that such a renormalization scheme, which trades scaling against sprinkling in one or several parameters, is by now a standard tool in percolation theory, see for instance [73, 67, 30].
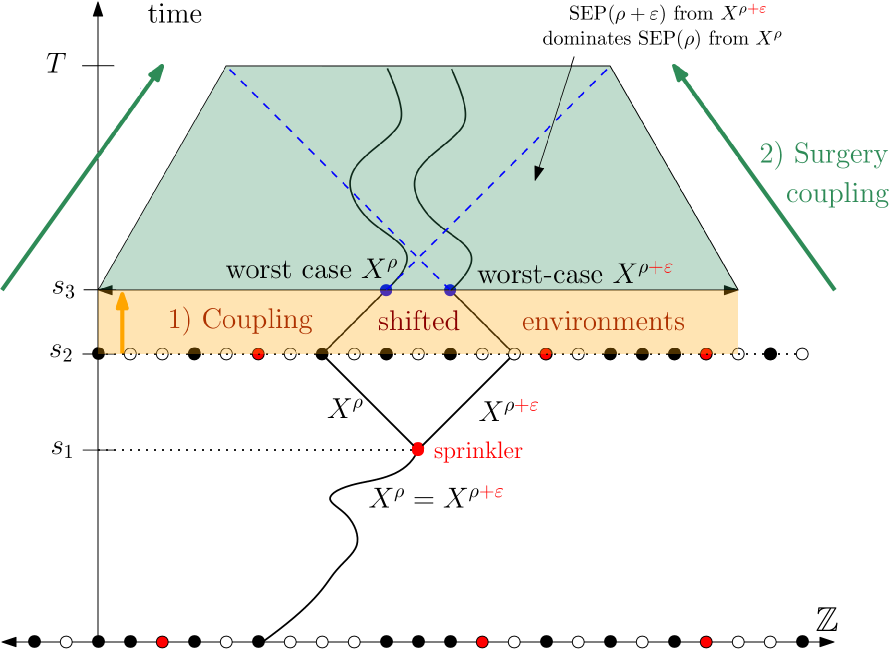
We now describe how we couple the range- and the range- models in order to obtain the first inequality, the other couplings being identical up to a scaling factor. We do this in detail in Lemma 4.1, where for technical purposes, we need in fact more refined estimates than only the first moment, but they follow from this same coupling. The coupling works roughly as follows (cf. Fig. 1). We consider two random walks and coupled via their respective environments and such that we retain good control (in a sense explained below) on the relative positions of their respective particles during the time interval , except during a short time interval after time after renewing the particles of . In some sense, we want to dominate by ‘as much as possible’, and use it in combination with the following monotonicity property of the walk: since , cannot be overtaken by if covers (cf. (1.1); see also Lemma 2.2 for a precise formulation). Roughly speaking, we will use this strategy from time to , then lose control for short time before recovering a domination and using the same argument but with a lateral shift (in space), as illustrated in Figure 1. The key for recovering a domination in as little time as possible is a property of the following flavour.
| (1.13) |
Roughly, for poly-logarithmic in the right-hand side of (1.13) will be as close to 1 as we need. We do not give precise requirements on the scales (nor a definition of empirical density), except that they must satisfy some minimal power ratio due to the diffusivity of the particles. We will formalize this statement in Section 3.1, see in particular condition (C.2.2), with exponents and constants that are likely not optimal but sufficient for our purposes. Even if the environment were to mix in super-quadratic (but still polynomial) time, our methods would still apply, up to changing the exponents in our conditions (C.1)-(C.3).
The only statistic we control is the empirical density, i.e. the number of particles over intervals of a given length. The relevant control is formalised in Condition (C.1). In particular, our environment couplings have to hold with a quenched initial data, and previous annealed couplings in the literature (see e.g. [15]) are not sufficient for this purpose (even after applying the usual annealed-to-quenched tricks), essentially due to the difficulty of controlling the environment around the walker in the second part of the proof, as we explain in Remark 5.5; cf. also [64, 4, 65] for related issues in other contexts.

Let us now track the coupling a bit more precisely to witness the quantitative speed loss incurred by (1.13). We start by sampling and such that a.s., for all , which is possible by stochastic domination. In plain terms, wherever there is a particle of , there is one of . Then, we can let and evolve during such that this domination is deterministically preserved over time (this feature is common to numerous particle systems, including both SSEP and the PCRW). As mentioned above, conditionally on such a realization of the environments, one can then couple and such that for all . The intuition for this is that ’at worst’, and sit on the same spot, where might see a particle and an empty site (hence giving a chance for to jump to the right, and for to the left), but not the other way around (recall to this effect that ).
At time , we have to renew the particles of , hence losing track of the domination of by . We intend to recover this domination within a time by coupling the particles of with those of using (1.13) (at least over a space interval , that neither nor can leave during ). Since during that time, could at worst drift of steps to the right (and make steps to the left), we couple de facto the shifted configurations with . Hence, we obtain that for all with high probability as given by (1.13). As a result, all the particles of are covered by particles of , when observed from the worst-case positions of and respectively.
Finally, during we proceed similarly as we did during , coupling with so as to preserve the domination, and two random walks starting respectively from the rightmost possible position for , and the leftmost possible one for . The gap between and thus cannot increase, and we get that , except on a set of very small probability where (1.13) fails. Dividing by and taking expectations, we get
| (1.14) |
for suitable . The exponent is somewhat arbitrary, but importantly, owing to the coupling time of the two processes (and the diffusivity of the SEP particles), this method could not work with a value of smaller than . In particular, the exponent of the logarithm must be larger than one, and this prevents potentially simpler solutions for the second part.
Second part: quantitative speed increase at finite range. We now sketch the proof of (1.11), which is a quantitative estimate on the monotonicity of , equivalently stating that for and ,
| (1.15) |
with explicit and supplied by the first part. This is the most difficult part of the proof, as we have to show that a denser environment actually yields a positive gain for the displacement of the random walk, and not just to limit the loss as in the first part. The main issue when adding an extra density of particles is that whenever is on top of one such particle, and supposedly makes a step to the right instead of one to the left, it could soon after be on top of an empty site that would drive it to the left, and cancel its previous gain.
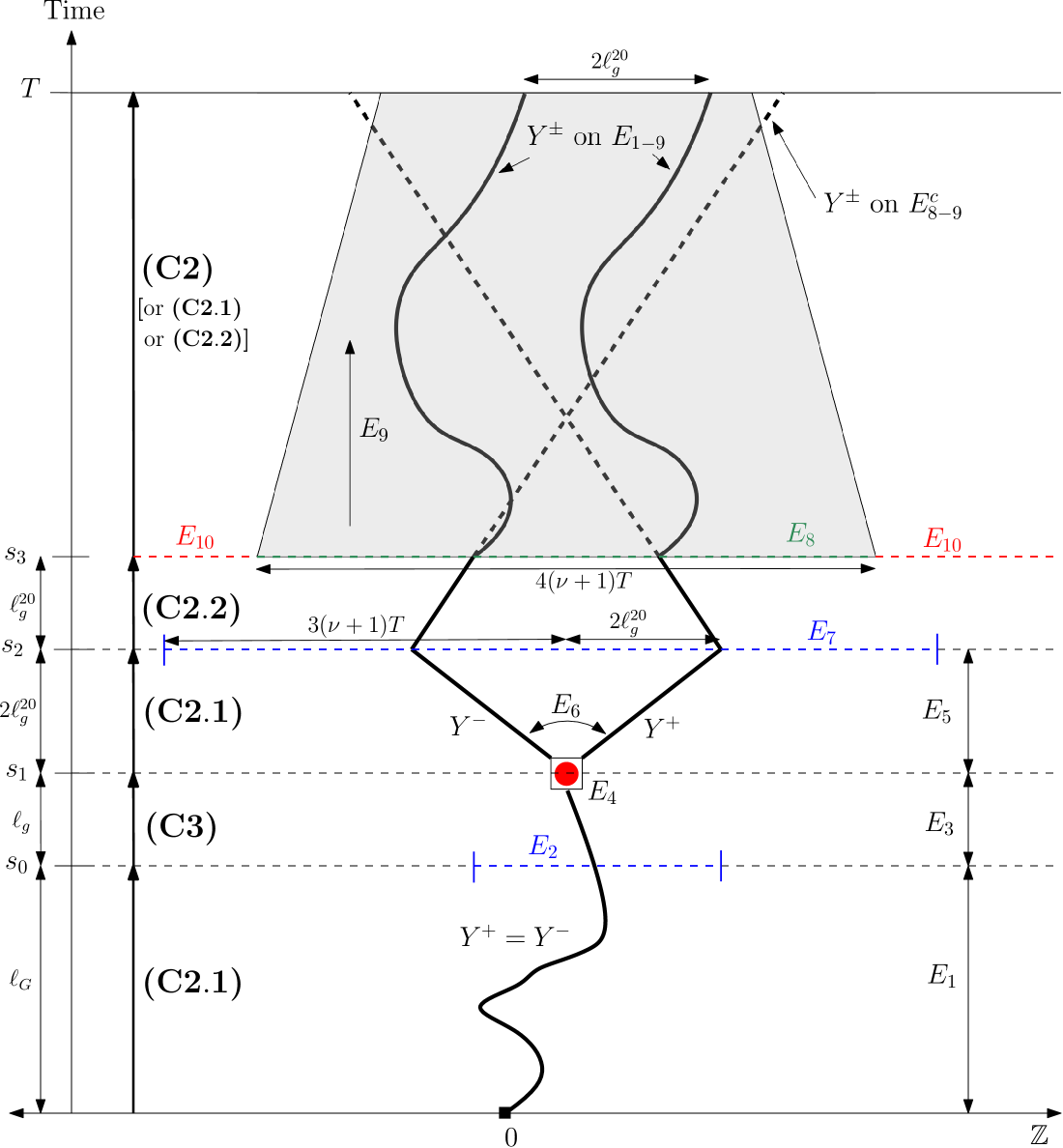
We design a strategy to get around this and preserve gaps, illustrated in Figure 2 (cf. also Figure 5 for the full picture, which is more involved). When coupling two walks , with respective environments , our strategy is to spot times when i) sees an extra particle (that we call sprinkler) and jumps to the right, while sees an empty site and jumps to the left, and ii) this gap is extended with then drifting to the left and drifting to the right, for some time that must necessarily satisfy – so that this has a chance of happening often during the time interval .
Once such a gap is created, on a time interval say with , we attempt to recouple the environments around the respective positions of their walker, so that the local environment seen from again dominates the environment seen from , which then allows us to preserve the gap previously created, up to some time which is a polynomial in . As we will explain shortly, this gap arises with not too small a probability, so that repeating the same procedure between times and (for ) will provide us with the discrepancy needed.
The re-coupling of the environments mentioned in the previous paragraph must happen in time less than (in fact less than ), in order to preserve the gap previously created. This leads to two difficulties:
-
•
in such a short time, we cannot possibly recouple the two environments over a space interval of size comparable to ( the space horizon the walk can explore during ), and
-
•
the coupling will have a probability to fail, hence with high probability, this will actually happen during ! In this case, we lose track of the domination of the environments completely, hence it could even be possible that overtakes .
We handle the first of these difficulties with a two-step surgery coupling:
-
1)
(Small coupling). We perform a first coupling of and on an interval of stretched exponential width (think for instance) during a time (cf. the orange region in Fig. 2), so as to preserve at least half of the gap created. We call this coupling “small” because is small (compared to ). If that coupling is successful, now sees an environment that strictly covers the one seen by , on a spatial interval of width . Due to the length of , this domination extends in time, on an interval of duration say (it could even be extended to timescales ): it could only be broken by SEP particles of lying outside of , who travel all the distance to meet the two walkers, but there is a large deviation control on the drift of SEP particles. The space-time zone in which the environment as seen from dominates that from is the green trapezoid depicted in Figure 2.
-
2)
(Surgery coupling). When the coupling in 1) is successful, we use the time interval to recouple the environments and on the two outer sides of the trapezoid, on a width of length say, so that dominates on the entire width, all the while preserving the fact that dominates inside the trapezoid at all times (for simplicity and by monotonicity, we can suppose assume that is exactly equal to , as pictured in Figure 2). This step is quite technical, and formulated precisely as Condition (C.2) in Section 3.1. It requires that different couplings can be performed on disjoint contiguous intervals and glued in a ‘coherent’ fashion, whence the name surgery coupling. Again, we will prove this specifically for the SEP in a dedicated section, see Lemma 6.9. Since this second coupling operates on a much longer time interval, we can now ensure its success with overwhelming probability, say .
We still need to address the difficulty described in the second bullet point above, which corresponds to the situation where the small coupling described at 1) fails. As argued, will happen a number of times within [0,L] because is small. If this occurs, we lose control of the domination of the environments seen by the two walkers. This leads to:
-
3)
(Parachute coupling). If the coupling in 1) is unsuccessful, instead of the surgery coupling, we perform a (parachute) coupling of and in so that covers , as we did in the first part of the proof. This again happens with extremely good probability . The price to pay is that on this event, the two walks may have drifted linearly in the wrong direction during (see the dashed blue trajectories in Figure 2), but we ensure at least that , and we have now re-coupled the environments seen from the walkers, hence we are ready to start a new such step during the interval , etc. This last point is crucial, as we need to iterate to ensure an expected gain that is large enough, cf. (1.15).
We now sketch a back-of-the-envelope calculation to argue that this scheme indeed generates the necessary discrepancy between and . During an interval of the form for (we take in the subsequent discussion for simplicity), with probability , we do not have the first separating event (around time ) between and , and we simply end up with , which is a nonnegative expected gain.
Else, with probability we have the first separation happening during . On this event, the coupling in 1) (and the subsequent impermeability of the green trapezoid) succeeds with probability , and we end up with , resulting in an expected gain of order . If the first coupling fails, and we resort to the parachute coupling, we have a (negative) expected gain . Multiplying by the probability of the first separation, we obtain a net expected gain .
Finally, we evaluate the possibility that the surgery coupling (in step 2) above) or the parachute coupling 3) fails, preventing us to restore the domination of by at time , and we do not control anymore the coupling of the walks. This has probability , and in the worst case we have deterministically , so the expected loss is .
Putting it all together, we get, for large enough by choosing e.g. and (it turns out that our couplings work with this choice of scales), that
| (1.16) |
As long as the surgery coupling or the parachute succeed, we can repeat this coupling for up to times during , thus obtaining
| (1.17) |
which establishes (1.15), with a sizeable margin.
1.4. Organization of the paper
In Section 2, we give rigorous definitions of general environments with a minimal set of properties (P.1)-(2.2), and of the random walk . In Section 3, we impose the mild coupling conditions (C.1)-(C.3) on the environments, state our general result, Theorem 3.1, and deduce Theorems 1.1 and 1.2 from it. We then define the finite-range models and give a skeleton of the proof. In Section 4, we proceed to the first part of the proof, and in Section 5, we proceed to the second part (cf. Section 1.3 reagrding the two parts). In Section 6, we define rigorously the SEP and show that it satisfies all the conditions mentioned above. The (short) Appendix A contains a few tail estimates in use throughout this article. In Appendix B, we introduce the PCRW environment and show that it equally satisfies the above conditions, which entails that our results also apply to this environment. Throughout this article all quantities may implicitly depend on the two parameters that are assumed to satisfy , cf. above (1.1) (and also Section 2.3).
2 Setup and useful facts
In this section, after introducing a small amount of notation (Section 2.1), we proceed to define in Section 2.2 a class of (dynamic) random environments of interest, driven by a Markov process characterized by properties (P.1)–(2.2) below. We will primarily be interested in environments driven by the exclusion process, which is introduced in Section 6 and shown to satisfy these properties. The framework developed in Section 2.2 and further in Section 3 will allow our results to apply directly to a second environment of interest, considered in Appendix B. We conclude by introducing in Section 2.3 the relevant walk in random environment along with its associated quenched and annealed laws and collect a few basic features of this setup.
2.1. Notation
We write , resp. , for the set of nonnegative integers, resp. real numbers. We use the letter exclusively to denote space-time points , and typically for spatial coordinates and for time coordinates. We usually use for non-negative integers. With a slight abuse of notation, for two integers , we will denote by the set of integers and declare that the length of is . Throughout, and denote generic constants in which are purely numerical and can change from place to place. Numbered constants are fixed upon first appearance.
2.2. A class of dynamic random environments
We will consider stationary Markov (jump) processes with values in . The state space carries a natural partial order: for two configurations , we write (or ) if, for all , . More generally, for , (or ) means that for all . For a finite subset , we use the notation . We will denote and the usual stochastic dominations for probability measures. Let be a (fixed) non-empty open interval of . An environment is specified in terms of two families of probability measures governing the process and , where is a measure on , which are required satisfy the following conditions:
| (P.1) | (Markov property and invariance). For every , the process defined under is a time-homogeneous Markov process, such that for all and , the process has law ; moreover, the process exhibits ‘axial symmetry’ in the sense that has law . |
| (P.2) | (Stationary measure). The initial distribution is a stationary distribution for the Markov process . More precisely, letting the -law of is identical to the -law of for all and . In particular, the marginal law of under is for all . | ||
| (P.3) | (Monotonicity). The following stochastic dominations hold: i) (quenched) For all , one has that , i.e. there exists a coupling of and such that for all . ii) (annealed) For all , one has that . Together with i), this implies that . |
2.3. Random walk
We now introduce the random walk in dynamic environment (RWdRE) that will be the main object of interest in this article. To this effect, we fix two constants such that and an environment configuration with (, see Section 2.2). Given this data, the random walk evolving on top of the environment is conveniently defined in terms of a family of i.i.d. uniform random variables on , as follows. For an initial space-time position , let be the law of the discrete-time Markov chain such that and for all integer ,
| (2.1) |
Let us call an occupied site of if , and empty otherwise. With this terminology, (2.1) implies for instance that when , started at a point , is on an occupied (resp. empty) site of , it jumps to its right neighbour with probability (resp. ) and to its left neighbour with probability (resp. . We call the quenched law of the walk started at and abbreviate ; here quenched refers to the fact that the environment is deterministic.
We now discuss annealed measures, i.e. including averages over the dynamics of the environment . We assume from here on that satisfies the assumptions of Section 2.2. Recall that denotes the law of starting from the configuration and that is declared in (P.2). Correspondingly, one introduces the following two annealed measures for the walk
| (2.2) | |||
| (2.3) |
for arbitrary . Whereas the latter averages over the dynamics of for a fixed initial configuration , the former includes , which is sampled from the stationary distribution for . Observe that . For , write for , for all , and write simply for .
We introduce a joint construction for the walk when started at different space-time points. This involves a graphical representation using arrows similar to that used in [40, Section 3], but simpler, which will be sufficient for our purposes. For a point , we let and denote the projection onto the first (spatial) and second (temporal) coordinate. We consider the discrete lattice
| (2.4) |
Note that the process evolves on the lattice defined by (2.4) when is started at under any of and the measures in (2.2)-(2.3).
We proceed to define a family of processes , such that almost surely and has the same law as under . Furthermore, and have the property that they coalesce whenever they intersect, that is if for some and , then for all .
Let be a collection of i.i.d. uniform random variables on . Given the environment , we define a field of arrows (see Figure 3), measurably in as follows:
| (2.5) |
For any , we then set and, for all integer , we define recursively
| (2.6) |

This defines the coupled family , and we note that trajectories the process , where , are embedded in (i.e. subsets of) . In view of (2.1) and (2.5)-(2.6), it follows plainly that the law of when averaging over while keeping fixed is the same as that of under .
We now discuss a variation of the construction specified around (2.5)-(2.6), which will be practical in Section 5.2.
Lemma 2.1.
Proof.
We show by induction over integer that for all such , the pair has the same law under both and (which, for the duration of the proof, we extend here to denote the joint distribution of , by a slight abuse of notation). The initialisation at is immediate, since and is deterministic.
As for the induction step, assume the induction hypothesis for some , and condition on the - algebra . We first let evolve between times and . Under both and and conditionally on , we have that is distributed as under , given the marginal distribution of and by the Markov property (P.1). Therefore, has the same law under both and . Now, conditioning on as defined in (2.8), and noticing that , (hence also ) are all -measurable (for this follows from (2.5)-(2.6)), we obtain that
| (2.11) |
Now, by (2.8), and using that is -measurable, we can evaluate the conditional probabilities in (2.11) to find that
| (2.14) |
where the second equality comes from the independence of and under , see (2.1) and (2.3). Integrating both sides of (2.14) under and , respectively, against a suitable (-measurable) test function of , it follows that have the same distribution under and . This concludes the proof of the induction step. ∎
We conclude this section by collecting a useful monotonicity property for the collection of random walks defined above, similar to [40, Proposition 3.1]. Its proof hinges on the fact that the trajectories considered cannot cross without first meeting at a vertex, after which they merge. In the sequel, for a given environment configuration , we refer to the process defined as in (2.6) but with in place of entering the definition of the arrows in (2.5). We will be interested in the case where and are such that
| (2.15) |
for some . The following result is already interesting for the choice , in which case below.
Lemma 2.2.
If and are such that (2.15) holds, then for every with and ,and for every such that for all , one has that
| (2.16) |
Proof.
We only treat the case to lighten the argument. The adaptation to a general is straightforward, as all possible trajectories considered for and lie in by assumption. The proof proceeds by a straightforward induction argument. Indeed, since and , one has that by assumption. To carry out the induction step, one notes that is even for any with increments ranging in , or , and combines this with the following observation: if , then
where the second equality follows using that (along with ) and the inequality is due to (2.15) and the fact that is increasing for any , which is straightforward from (2.5). ∎
3 Main results
In this section, we start by formulating in Section 3.1 precise coupling conditions that we require from the environments, and which are of independent interest. These are given by conditions (C.1)-(C.3) below (a flavor of the second of these was given in (1.13) in the introduction). Our main result, Theorem 3.1, appears in Section 3.2. It concerns the generic random walk in random environment defined in Section 2.2-2.3, subject to the conditions of Section 3.1. Our standing assumptions will thus be that all of properties (P.1)-(2.2) and the conditions (C.1)-(C.3) hold. We will verify separately in Section 6 that all of these conditions hold for SEP. From Theorem 3.1 we then readily deduce Theorems 1.1and 1.2 at the end of Section 3.2.
Towards the proof of Theorem 3.1, and following the outline of Section 1.3, we proceed to introduce in Section 3.3 a finite-range approximation of the model, in which the environment is renewed after time steps and gather its essential features that will be useful for us. We then state two key intermediate results, Propositions 3.3 and 3.4, which correspond to the first and second parts from the discussion in Section 1.3; cf. also (1.10) and (1.11). From these, we deduce Theorem 3.1 in Section 3.4. The proofs of the two propositions appear in forthcoming sections.
3.1. Coupling conditions on the environment
Recall the framework of Section 2.2-2.3, which we now amend with three further conditions. These involve an additional parameter which quantifies the activity of the environment (in practice it will correspond to the rate parameter appearing in (6.1) in the case of SEP). We keep the dependence on explicit in the following conditions for possible future applications, for which one may wish to tamper with the speed of the environment (for instance, by slowing it down). For the purposes of the present article however, one could simply set in what follows.
The first two conditions (C.1) and (C.2) below regard the environment alone, which, following the setup of Section 2.2, is assumed to be specified in terms of the measures and that satisfy (P.1)-(2.2). The first condition, (C.1), concerns the empirical density of the environment. Roughly speaking, it gives a quantitative control on how (2.2) is conserved over time. The second condition, (C.2), is more technical. In a nutshell, it states that if one environment covers another environment on a finite interval at a given time, and if has a larger empirical density than outside at the same time, the evolutions of and can be coupled in a way that covers on a larger interval after some time.
We proceed to formalize these two properties:
-
(C.1)
(Conservation of density). There exists constants such that for all and (with ), and for all satisfying and , the following two inequalities hold. Let be such that on every interval of length included , one has (resp. ). Then
-
(C.2)
(Couplings). There exists such that the following holds. Let , (with ), and be integers such that , and . Let be such that and such that for every interval of length , we have and . Then there exists a coupling of two environments with respective marginals such that
(3.4) and
(3.5)
For later reference, we record the following two particular instances of (C.2), which correspond to the cases where and , respectively. For convenience, we state them with better constants and exponents than in (C.2). In fact, when verifying condition (C.2) for the SEP in Section 6.2, we will first prove that these two conditions hold, and use them to prove (C.2).
-
(C.2.1)
(No particle drifting in from the side). Let and be integers, and let be such that . There exists a coupling of environments with respective marginals and such that
(3.6) Informally, with high probability no particle of outside of can drift into (when for instance) before time to perturb the domination of by .
-
(C.2.2)
(Covering by ). There exists such that for all and (with ), the following holds. If satisfy , and , then for all such that on each interval of length , where , and , there exists a coupling of with marginals so that
(3.7) In words, the coupling achieves order between and at time under suitable regularity assumptions on the empirical density of their initial configurations and .
The third and last property ensures that if an environment covers another environment and has at least one extra particle at distance of the origin (which typically happens if has higher density than ), then with probability at least exponentially small in , by time , this particle can reach the origin which will be empty for , while preserving the domination of by . We will combine this property with the uniform ellipticity of the random walk on top of the environment to show that the walker has at least an exponentially small probability to reach a position where has a particle but not , which in turn yields a probability bounded away from zero that a walker on steps to the right while a walker on steps to the left (under the coupling mentioned in Section 1.3), hence creating the desired initial gap that we will then exploit in our constructions.
-
(C.3)
(Sprinkler). For all , for all integers with and , the following holds. If satisfy for all , and , then there is a coupling of under and under such that, with
(3.8) for and with ,
(3.9)
3.2. Main result
Following is our main theorem.
Theorem 3.1 (Sharpness of ).
With Theorem 3.1 at hand, we first give the proofs of Theorems 1.1 and 1.2. We start with the latter.
Proof of Theorem 1.2.
Theorem 1.2 concerns the particular case where refers to the walk of Section 2.3 evolving on top of the exclusion process started from product Bernoulli distribution, for . The properties (P.1)-(2.2) and (C.1)-(C.3) are indeed all satisfied in this case, as is proved separately in Section 6 below, see Lemma 6.1 and Proposition 6.3.
In the notation of (1.6), we now separately consider the intervals , where , and . The fact that the law of large numbers (3.10) holds for any choice of is the content of [40, Theorem 1.1]. Thus Theorem 3.1 is in force, and is strictly increasing on for any . Since by direct application of (P.3) and Lemma 2.2, is already non-decreasing on , it must be (strictly) increasing on altogether, and (1.8) follows. In view of (1.6), the first equality in (1.7) is an immediate consequence of (3.11) with .
As to the second equality in (1.7), recalling the definition of from (1.4), we first argue that . If , then by (1.5)-(1.6), -a.s. and thus in particular (in fact it equals but we will not need this). On the other hand, , and the latter has probability tending to as under . It follows that in view of (1.3), whence , and thus upon letting .
Since , in order to complete the proof it is enough to show that . Let . We aim to show that . Using the fact that and (1.5), one first picks such that for any with (the worst case is , the other cases follow from the case using invariance under suitable space-time translations). Now, observe that for all , under ,
| (3.14) |
for, on the event on the right-hand side, one has that and the walk can in the worst case travel steps to the left during the time interval , whence in fact for all , and since . Combining (3.14), the fact that the last event on the RHS has full probability due to (1.5)-(1.6), the fact that on account of (2.5)-(2.6) and the Markov property of the quenched law at time , one finds that
where the second inequality follows by choice of . Thus, (see (1.3)), i.e. . Letting one deduces that , and this completes the verification of (1.7). ∎
Proof of Theorem 1.1.
Only item (i) requires an explanation. This is an easy consequence of [40, Proposition 3.6], e.g. with the choice for a given , and Theorem 1.2 (see (1.7)), as we now explain. Indeed one has that under as soon as is large enough (depending on ); to see the inclusion of events recall that on account of (1.7), which has already been proved, and therefore . The conclusion of item (i) now readily follows using the second estimate in [40, (3.27)]. ∎
3.3. The finite-range model
Following the strategy outlined in Section 1.3, we will aim at comparing the random walk in dynamic random environment, which has infinite-range correlations, to a finite-range model, which enjoys regeneration properties, and which we now introduce.
For a density (recall that is an open interval of ) and an integer , we define a finite-range version of the environment, that is, a probability measure on (see Section 2.2 for notation) such that the following holds. At every time multiple of , is sampled under according to (recall (P.2)), independently of and, given , the process has the same distribution under as under , cf. Section 2.2 regarding the latter. We denote the expectation corresponding to . It readily follows that is a homogenous Markov process under , and that inherits all of Properties (P.1)-(2.2) from . In particular is still an invariant measure for the time-evolution of this environment. Note that is well-defined and .
Recalling the quenched law of the walk in environment started at from Section 2.3, we extend the annealed law of the walk from (2.2) by setting so that corresponds to the annealed law defined in (2.2). We also abbreviate .
We now collect the key properties of finite-range models that will be used in the sequel. A straightforward consequence of the above definitions is that
| (3.17) |
Moreover, by direct inspection one sees that inherits the properties listed in (3.1) from ; that is, whenever does,
| (3.18) | satisfies (C.1), (C.2), (C.2.1), (C.2.2) (all for ) and (C.3) (for ). |
(more precisely, all of these conditions hold with in place of everywhere, where refers to the evolution under with initial condition ). The next result provides a well-defined monotonic speed for the finite-range model. This is an easy fact to check. A much more refined quantitative monotonicity result will follow shortly in Proposition 3.3 below (implying in particular strict monotonicity of ).
Lemma 3.2 (Existence of the finite-range speed ).
For and an integer , let
| (3.19) |
Then
| (3.20) |
Moreover, for any fixed , we have that
| (3.21) | the map is non-decreasing on . |
3.4. Key propositions and proof of Theorem 3.1
In this section, we provide two key intermediate results, stated as Propositions 3.3 and 3.4, which roughly correspond to the two parts of the proof outline in Section 1.3. Theorem 3.1 will readily follow from these results, and the proof appears at the end of this section. As explained in the introduction, the general strategy draws inspiration from recent interpolation techniques used in the context of sharpness results for percolation models with slow correlation decay, see in particular [31, 33], but the proofs of the two results stated below are vastly different.
Our first result is proved in Section 4 and allows us to compare the limiting speed of the full-range model to the speed of the easier finite-range model with a slightly different density. Note that, even though both and are monotonic, there is a priori no clear link between and .
Proposition 3.3 (Approximation of by ).
Under the assumptions of Theorem 3.1, there exists such that for all and such that ,
| (3.22) |
With Proposition 3.3 above, we now have a chance to deduce the strict monotonicity of from that of . Proposition 3.4 below, proved in Section 5, provides a quantitative strict monotonicity for the finite-range speed . Note however that it is not easy to obtain such a statement, even for the finite-range model: indeed, from the definition of in (3.19), one can see that trying to directly compute the expectation in (3.19) for any boils down to working with the difficult full range model. One of the main difficulties is that the environment mixes slowly and creates strong space-time correlations. Nonetheless, using sprinkling methods, it turns out that one can speed-up the mixing dramatically by increasing the density of the environment. This is the main tool we use in order to obtain the result below.
Proposition 3.4 (Quantitative monotonicity of ).
Assume (3.18) holds and let . For all such that , there exists such that, for all ,
| (3.23) |
4 Finite-range approximation of
In this section, we prove Proposition 3.3, which allows us to compare the speed of the full-range model to the speed (see (3.19)) of the finite-range model introduced in §3.3. The proof uses a dyadic renormalisation scheme. By virtue of the law(s) of large numbers, see (3.10) and (3.20), and for and fixed, the speed ought to be close to the speed , for some large integer . Hence, if one manages to control the discrepancies between and for all and prove that their sum is small, then the desired proximity between and follows. This is roughly the strategy we follow except that at each step, we slightly increase or decrease the density (depending on which bound we want to prove), in order to weaken the (strong) correlations in the model. This is why we only compare and for slightly different densities at the end. This decorrelation method is usually referred to as sprinkling; see e.g. [67, 74] for similar ideas in other contexts.
As a first step towards proving Proposition 3.3, we establish in the following lemma a one-step version of the renormalization, with a flexible scaling of the sprinkling ( below) in anticipation of possible future applications. For , let denote the negative part of . Throughout the remainder of this section, we are always tacitly working under the assumptions of Theorem 3.1.
Lemma 4.1.
There exists such that for all , all and all such that , the following holds: there exists a coupling of , , such that , with , and
| (4.1) |
Consequently,
| (4.2) |
and
| (4.3) |
The same conclusions hold with marginals and instead.
Proof.
Towards showing (4.1), let us first assume that
| (4.4) |
where, setting , the ‘good’ event is defined as
| (4.7) |
Given the above, we now extend the coupling to the random walks and , defined as in Section 2.3, up to time . To do that, we only need to specify how we couple the collections of independent uniform random variables and (recall that denotes space-time, see (2.4)) used to determine the steps of each random walk; the walks , , up to time are then specified in terms of as in (2.5)-(2.6). Under , we let be i.i.d. uniform random variable on and define, for ,
(for definiteness let when ). Clearly are i.i.d. uniform variables, hence also has the desired marginal law. Now, we will explain why, on this coupling, (4.1) holds, and refer to Figure 4 for illustration. We will only consider what happens on the event defined in (4.7).
On , by Lemma 2.2 with , we have that for all . This implies that owing to (2.18). Let , define by and . Let and be random walks evolving on top of and respectively, and both using the collection of uniform random variables . Then, conditionally on , and , and on the event , has the law of and has the law of the position at time of a random walk started at and evolving on top of , using the collection . In particular, it evolves on the same environment as and starts on the left of , so that (by Lemma 2.2 applied with and ). On , using the second event in the intersection on the right-hand side of (4.7), we can again apply Lemma 2.2, now at time , with and as described and . We obtain that for all . Thus, subtracting on both sides and using the previous facts, we have on that , for all . All in all, we have proved that
and therefore (4.1) follows from our assumption (4.4). The fact that (4.2) and (4.3) hold is a simple consequence of (4.1) and a straightforward computation using the deterministic inequality valid for all and the fact that (note that for large enough, we have for all ).
It remains to show that (4.4) holds, which brings into play several of the properties gathered in §3.1 and which hold by assumption. Let be such that for every and any choice of , with we have that and
| (4.8) |
where as defined above (4.7).
We will provide a step-by-step construction of , in four steps. First, note that by (P.3)-ii), there exists a coupling of environments and such that under , on the time interval , on the time interval and such that -a.s., for all and . We then extend to time for by sampling , independently of and . In particular the above already yields that the inequalities required as part of the event in (4.7) which involve actually hold -a.s.
Second, letting , we define to be the event that for every interval of length , the inequalities and hold (see the beginning of §2.2 for notation). By (2.2) and a union bound over the choices of such intervals , we get that
| (4.9) |
At time and on , extend to the time interval by letting and follow their dynamics and independently of each other (using (P.1)).
Third, we continue the construction of the coupling on by applying (C.2.2) with , and , checking the assumptions using (4.8) (note indeed that we have since , and then that ). This implies that, given and , on , there exists an extension of the coupling on the time interval such that, defining
| (4.10) |
we have
| (4.11) |
At time and on , we extend on the time interval by letting and follow their dynamics and independently of each other.
Fourth, we continue the construction of the coupling on by applying (C.2.1) with and , , and in (C.2.1) equal to . This implies that, given and , on , there exists an extension of the coupling on the time interval such that, defining
| (4.12) |
we have
| (4.13) |
Finally, note that , so that (4.4) is a straightforward consequence of (4.9), (4.11) and (4.13) provided that is chosen large enough, depending only on (as well as , and ). Note in particular that with our choices of , above (4.8) and , we have that . All in all (4.4) follows. The case and can be treated in the same way, by means of an obvious analogue of (4.4). The remainder of the coupling (once the environments are coupled) remains the same. ∎
We are now ready to prove Proposition 3.3. The proof combines the law of large numbers for the speed together with Lemma 4.1 applied inductively over increasing scales. The rough strategy is as follows. We aim to compare the speed of the full-range model to the speed of the finite-range model for some possibly large, but finite , and prove that these two are close. For , we know that the probability for the finite-range model to go slower than speed goes to on account of Lemma 3.2. Thus, in a large box of size , the -range model will most likely be faster than as soon as is large enough. Lemma 4.1 is used over dyadic scales to control the discrepancies between the -range model and the -range model for all from to , and to prove that they are small. It will be seen to imply that with high probability, in a box of size , the -range model will be faster than . Now, we only need to observe that when observed in a box of size , the -range model is equivalent to the full-range model. As Lemma 4.1 already hints at, this is but a simplified picture and the actual argument entails additional complications. This is because each increase in the range (obtained by application of Lemma 4.1) comes not only at the cost of slightly ‘losing speed,’ but also requires a compensation in the form of a slight increase in the density , and so the accumulation of these various effects have to be tracked and controlled jointly.
Proof of Proposition 3.3.
We only show the first inequality in Proposition 3.3, i.e. for and such that , abbreviating , one has
| (4.14) |
The first inequality in (3.22) then follows for all by suitably choosing the constant since . The second inequality of (3.22) is obtained by straightforward adaptation of the arguments below, using the last sentence of Lemma 4.1.
For , define for . As we now explain, the conclusion (4.14) holds as soon as for and as above, we show that
| (4.15) |
Indeed under the assumptions of Proposition 3.3, the law of large numbers (1.5) holds, and therefore in particular, for all , we have that tends to as . Together with (4.15) this is readily seen to imply (4.14).
We will prove (4.15) for , where the latter is chosen such that the conclusions of Lemma 4.1 hold for , and moreover such that
| (4.16) |
For such we define, for all integer , all and all , recalling the finite-range annealed measures from §3.3,
| (4.17) |
(observe that the notation is consistent with §3.3, i.e. ). In this language (4.15) requires that vanishes in the limit for a certain value of . We start by gathering a few properties of the quantities in (4.17). For all , the following hold:
| (4.18) | ||||
| (4.19) | ||||
| (4.20) |
As explained atop the start of the proof, owing to the form of Lemma 4.1 we will need to simultaneously sprinkle the density and the speed we consider in order to be able to compare the range- model to the range- model. To this effect, let
| (4.21) |
as well as
| (4.22) |
A straightforward computation, bounding the sum below for by the integral , yields that
| (4.23) |
Another straightforward computation yields that
| (4.26) |
In particular, since is increasing in , (4.23) implies that for all , we have , and (4.26) yields in view of (4.22) that , with as above (4.14). Using this, it follows that, for all ,
| (4.29) |
As the left-hand side in (4.29) is precisely equal to the probability appearing in (4.15), it is enough to argue that the right-hand side of (4.29) tends to as in order to conclude the proof. By recalling that from (4.22) and using (4.18), we see that , which takes care of the first term on the right of (4.29).
We now aim to show that the sum over in (4.29) vanishes in the limit , which will conclude the proof. Lemma 4.1 now comes into play. Indeed recalling the definition (4.17), the difference for fixed value of involves walks with range and , and Lemma 4.1 supplies a coupling allowing good control on the negative part of this difference (when expressed under the coupling). Specifically, for a given and , let and . Note that for , one has the rewrite
Therefore, due to the regenerative structure of the finite-range model, explicated in (3.17), it follows that, for , under ,
| (4.30) |
where , , is a collection of independent copies of under . Now recall the coupling measure provided by Lemma 4.1 with and let us denote by the product measure induced by this couplingfor the choices and in Lemma 4.1, so that supports the i.i.d. family of pairs , , each sampled under . In particular, under , for all , and have law and , respectively. Now, one can write, for any and , with the sum over ranging over below, that
Now, using Chebyshev’s inequality together with Lemma 4.1 (recall that ), it follows that for and ,
| (4.33) |
where the second line is obtained by considering the cases when or separately, together with straightforward computations. The bound (4.33) implies in turn that
which concludes the proof. ∎
5 Quantitative monotonicity for the finite-range model
The goal of this section is to prove Proposition 3.4. For this purpose, recall that is an open interval, and fix and such that . Morever, in view of (3.21), we can assume that . The dependence of quantities on and will be explicit in our notation. As explained above Proposition 3.4, even if we are dealing with the finite-range model, the current question is about estimating the expectation in (3.19), which is actually equivalent to working on the full-range model. Thus, we retain much of the difficulty, including the fact that the environment mixes slowly. The upshot is that the speed gain to be achieved is quantified, and rather small, cf. the right-hand side of (3.23).
The general idea of the proof is as follows. First, recall that we want to prove that at time , the expected position of (where denotes equality in law in the sequel) is larger than the expected position of by . The main conceptual input is to couple and in such a way that, after a well-chosen time , we create a positive discrepancy between them with a not-so-small probability, and that this discrepancy is negative with negligible probability, allowing us to control its expectation. We will also couple these walks in order to make sure that the environment seen from is dominated by the environment seen from , even if these walks are not in the same position, and we further aim for these environments to be ‘typical’. The last two items will allow us to repeat the coupling argument several times in a row and obtain a sizeable gap between and . In more quantitative terms, we choose below and create an expected discrepancy of at time . Repeating this procedure times provides us with an expected discrepancy at time larger than (and in fact larger than ). We refer to the second part of Section 1.3 for a more extensive discussion of how the expected gap size comes about.
We split the proof of Proposition 3.4 into two parts. The main part (Section 5.1) consists of constructing a coupling along the above lines. In Section 5.3, we prove Proposition 3.4.
5.1. The trajectories
In this section, we define two discrete-time processes and , , for some time horizon , see (5.2) below, which are functions of two deterministic environments and and an array (see Section 2 for notation) of numbers in . This construction will lead to a deterministic estimate of the difference , stated in Lemma 5.1. In the next section, see Lemma 5.2, we will prove that there exists a measure on such that under , dominates stochastically the law of a random walk (see below (2.3) for notation), is stochastically dominated by the law of a random walk , and we have a lower bound on , thus yielding a lower bound on .
The construction of the two processes will depend on whether some events are realized for and . We will denote these events, which will occur (or not) successively in time. We introduce the convenient notation
| (5.1) |
and write for the complement of . We refer to Figure 5 (which is a refined version of Figure 2) for visual aid for the following construction of , and to the discussion in Section 1.3 for intuition. Let us give a brief outlook on what follows. The outcome of the construction will depend on whether a sequence of events - happens or not: when all of these events occur, which we call a success, then and have a positive discrepancy and we retain a good control on the environments at time , namely dominates (or, more precisely, shifted by ). When at least one of these nine events does not happen, this can either result in a neutral event, where the trajectories end up at the same position and we still have control on the environments, or it could result in a bad event, where we can have (but we will show in Lemma 5.2 that we keep control on the environments with overwhelming probability, owing to the parachute coupling evoked at the end of Section 1.3). Whenever we observe a neutral or a bad event, we will exit the construction and define the trajectories at once from the time of observation all the way up to time . Finally, we note that the walks and are actually not Markovian. This is however not a problem as we use them later to have bounds on the expected displacements of the actual walks and .
We now proceed to make this precise. For , define
| (5.2) | , and , |
as well as
| (5.3) |
Let , which will parametrize the spatial length of a space-time box in which the entire construction takes place, and let . The definition of depends on the values of and , but we choose not to emphasize it in the notation. Given processes
| (5.4) |
on a state space such that the first two coordinates take values in and the last one in , we will define the events below measurably in and similarly with values in the set of discrete-time trajectories starting at . Unlike the sample paths of , the trajectories of may perform jumps that are not to nearest neighbors. Probability will not enter the picture until Lemma 5.2 below, see in particular (5.51), which specifies the law of . We now properly define the aforementioned three scenarii of success, neutral events and bad events, which will be mutually exclusive, and we specify in all cases.
Below and always denote integer times. Define the event (see Section 2.2 regarding the notation )
| (5.5) |
The event guarantees the domination of the environment by and is necessary for a success, while will be part of the bad event. On , for all , let recursively
| (5.6) |
where was defined in (2.5), so that we let the walks evolve together up to time . On the bad event , we exit the construction by defining
| (5.7) |
Next, define the events
| (5.8) | ||||
| (5.9) |
The event again ensures the domination of by on a suitable spatial interval while creates favourable conditions at time to possibly see a sprinkler at time . On the event (recall (5.1) for notation), for all , let recursively
| (5.10) |
so that the walks, from time , continue to evolve together up to time and, in particular, we have that
| (5.11) |
In order to deal with the case where or fail, we will distinguish two mutually exclusive cases, that will later contribute to an overall neutral and bad event, respectively; cf. (5.42) and (5.46). To this end, we introduce
| (5.12) |
On , which will be a neutral event, we exit the construction by letting the walk evolve together up to time , that is, we define
| (5.13) |
On the bad event , we exit the construction by defining
| (5.14) |
In the above, and may take a non-nearest neighbour jump at time , which is fine for our purpose. Next, define
| (5.15) | ||||
| (5.16) |
where states that the walkers see a sprinkler at time and guarantees domination of the environments from time to . We will first define what happens on the neutral and the bad events. For this purpose, define
| (5.17) |
Recall that on , we have defined up to time . On the neutral event , we define
| (5.18) |
On the bad event , we exit the construction by defining
| (5.19) |
On the event , because of the sprinkler, the walkers have a chance to split apart hence, for , we let
| (5.20) |
Above, and evolve on top of their respective environments and from time to time . To be able to continue the construction from time to , we define two events and concerning the environments from times to . If we are on , between times and we will require that and drift away, regardless of the states of and , using only the information provided by . For this purpose, define
| (5.21) |
where we set
| (5.22) |
On , steps to the left and steps to the right from their common position, thus creating a gap at time . Then for all , as long as and to happen, and are at distinct positions and allows to take one more step to the left and one more step to the right. Hence, using what we have constructed so far on , we have that
| (5.23) |
and we still have the domination of by at time , cf. (5.16).
Since and are no longer at the same position, we are going to momentarily allow to lose this domination in order to recreate it at time but in a suitably shifted manner, namely, achieve that for a suitable interval , see (5.33). To do so, we first need favourable conditions at time encapsulated by the event
| (5.26) |
The above requires good empirical densities at time on an interval of length of order centred around the common position of the walkers at time . On , we do not precisely control the position of the walkers from time to and define, for all ,
| (5.27) |
which corresponds to the worst case scenario assuming nearest-neighbour jumps. In particular, using (5.27), (5.23) and (5.3), we have that
| (5.28) |
We now need to consider the case where fails, and we will again distinguish two types of failure. For this purpose, define
| (5.29) |
and, on the neutral event , we merge with at time and then let them walk together, by defining
| (5.30) | ||||
| (5.31) |
(above one line would be sufficient but we single out (5.30) because the merging will typically occasion a jump for ). On the remaining bad event , we exit the construction in the now usual way by defining
| (5.32) |
It remains to define from time to on the event . The good event will require
| (5.33) |
that is, we want that the environment seen from covers seen from on an interval of length of order , which will enable us to let the walkers move in parallel (i.e. taking the same steps at the same time), even if they are at different positions. Moreover, we want this domination to persist from time to time , hence we require
| (5.34) |
On the good event , we let, for ,
| (5.35) |
Note that above, we choose to shift spatially the collection by spatially for , which corresponds to the difference between and . Therefore, both walks are using the same to determine their next step. Using (5.35), (5.28) and (5.34), one thus proves recursively that
| (5.36) |
Finally, on the bad event , we finish the construction by defining
| (5.37) |
This ends the definition of the trajectories and . Let us emphasize once more that these trajectories are not nearest-neighbour and not Markovian w.r.t. the canonical filtration associated to , but that this will not prevent us from obtaining the desired bounds.
Below, we proceed to define our three key events and summarise in Lemma 5.1 some of the important (deterministic) properties we will use.
- •
- •
- •
5.2. The coupling
We now aim to compare to and , and to integrate over the dynamics of the environments when started from a typical initial configuration. We will derive from this a bound on the expected discrepancy between and , and thus on the one between and . The main result of this section is Lemma 5.2, which entails a coupling with these features. Lemma 5.2 is the key ingredient in the proof of Proposition 3.4, which appears in the next subsection.
We will require the environments and to have a typical initial configuration under and in the following sense. Recall that and have been fixed at the start of this section, and that . For , we say that (recall that from Section 2.2) is -balanced if all of the following occur:
-
(i)
for all ,
-
(ii)
for all ,
-
(iii)
for all .
Lemma 5.2.
There exists such that for all , the following holds. For all and for every -balanced choice of , there exists a coupling of with the following properties:
| (5.51) | , and are i.i.d. uniform variables on ; | |||
| (5.52) | There exist such that and -a.s., the inequalities and hold, with as in Section 5.1; | |||
| (5.53) | ||||
| (5.54) | ||||
Proof.
Let to be chosen later, and . Fix , and let be -balanced. We construct the coupling below. We will then define and such that (5.52) is satisfied. To prove the main estimate (5.53), we will control the probabilities of the events , and emerging from the construction of , and use Lemma 5.1. Finally, proving (5.54) will require to bound the probability of losing the synchronisation of and by time .
Part I: Construction of .
We will denote the natural filtration generated by the triplet by
| (5.55) |
Under , we first let be a collection of i.i.d. uniform random variables on . We now define the coupling of and under in such a way that given , the evolution of has the right marginal (up to time one), cf. (P.1). Moreover, throughout the construction of , i.e. from (5.57) to (5.73) below, we will in fact ensure that for all integer , under ,
| (5.56) |
We now proceed to specify under , and refer again to Figure 5 for visual aid. On the time-interval , we
| (5.57) | couple as in (C.2.1) with , , , and ; |
in particular, the domination required by (C.2.1) is ensured by the fact that is -balanced; see item (i) in the corresponding definition above Lemma 5.2. Since by (5.5) and (5.55), we can observe at time whether occurred. Conditionally on and on , during , we
| (5.58) | let and evolve independently with respective marginals and . |
Recalling the definition (5.8), we have that . Conditionally on and on , we couple during the interval as
| (5.59) | in (C.2.1) with , , , and . |
On , note that . Hence, as we now explain, during the time-interval , conditionally on and on , we can
| (5.60) |
Note indeed that by (5.3) and (5.2), for large enough and for all , as required in (C.3). Together with the definition of in (5.8), this allows us to apply the coupling of (C.3).
So far we have specified for all of on and up to time on . As we now briefly elaborate, it is also plain from the construction above that the independence property postulated in (5.56) holds for all . This is a trivial matter for in view of (5.57), which does not involve at all. For , the only dependence on arises through via and (5.60). However, on account of (5.6), (5.7), (5.10), (5.13) and (5.14), only relies on variables in with time label at most , whence the claim. In the sequel (more precisely, up to (5.73)), considerations along similar lines allow to extend (5.56) to larger times . These will not be made explicit.
Returning to the construction of , it remains to specify after time on the event . Recall that by (5.9) and (5.15), both and are in . Over the time interval , conditionally on and on , we choose to
| (5.61) | let and evolve independently with respective marginals and . |
On the other hand, conditionally on and on , during , we
| (5.62) |
Conditionally on and on , during the time-interval , we
| (5.63) |
Note that in (5.63) by (5.3) and since by assumption (upon possibly enlarging ). Moreover, note that the conditions on the environments at time needed for (C.2.1) to apply in both (5.62) and (5.63) are met owing to the occurrence of , see (5.9).
We still have to specify from time onwards on the event . By definition (5.16), we have that . Hence, conditionally on and on , during , we
| (5.64) | let and evolve independently with respective marginals and . |
Using the definitions (5.21) and (5.26), we have that both and are in . During , conditionally on and on , observing that the defining features of (see (5.16)) allow to apply (C.2.1), we
| (5.65) |
Conditionally on and on , during , as we now explain, we
| (5.66) |
Indeed, one checks that the conditions needed for (C.2.2) to apply are all satisfied on the event whenever is large enough. First, by choice of and for all , one readily ensures (recall (5.2)-(5.3)) that all of , and hold. Moreover, the conditions on the empirical densities of and appearing above (3.7) hold by definition of at (5.26), since by (5.3). Note that the relevant intervals in the context of (C.2.2), which have length with , may in practice be much larger than those appearing in the definition of , but they can be paved by disjoint contiguous intervals as entering . The required controls on the corresponding empirical densities and are thus inherited from those defining . Similar considerations also apply below (whenever either of (C.2.2) or (C.2) are used).
It remains to specify on the event for the time interval . We now define an additional event whose realisation will allow us to couple on the whole window of width order at time , regardless of whether the coupling at (5.66) succeeds or not; here, by “succeed” we mean that the (high-probability) event appearing in (3.7) is realized. The following will play a key role when establishing (5.54). We set
| (5.69) |
The event above and defined in (5.33) are both -measurable. Conditionally on and on , during , we couple
| (5.70) |
To this effect, we verify that for large enough, by (5.3), (5.2) and since , we indeed have that , and Also, the domination on and the empirical density condition are respectively guaranteed by definition of at (5.33) and at (5.69).
If does not occur (hence we temporarily lose the domination of by ) but does, we proceed to what was referred to as the parachute coupling in Section 1.3, in order to recover this domination by time . Precisely, conditionally on and on , we
| (5.71) |
One checks indeed that the conditions of (C.2.2) hold, since for large enough (recalling (5.3) and (5.2)) we have that ,, and , so that on the condition on the empirical density holds.
The remaining cases are straightforward to specify. Conditionally on , on , we
| (5.72) |
Finally, conditionally on and on , during , we
| (5.73) | let and evolve independently with respective marginals and . |
We have now fully defined the measure and with it the triplet (in the time interval ). The task is now to verify that with these choices, all of (5.51)-(5.54) hold. For concreteness we extend all three processes independently at times , using the Markov property at time for . These extensions will de facto play no role because all of (5.52)-(5.54) only concern matters up to time
Part II: Proof of (5.51).
The fact that has the desired law is immediate, see below (5.55). We proceed to show that . Since the construction of only consists of successive couplings at times and where the marginals have the desired distributions (recall (C.2), (C.2.1), (C.2.2) and (C.3)), by virtue of the Markov property (P.1), it is enough to check that the events deciding which coupling to apply at time are -measurable for , which we already did at (5.58)-(5.66), (5.70), (5.71), (5.72) and (5.73). Therefore, . In the same way we deduce that .
Part III: Proof of (5.52).
We now use to construct explicit functions and with the correct marginal laws . The case of is easily dispensed with: we define as in (2.5) and (2.6) with instead of . Since we have already established that as part of (5.51), it follows using (5.56) and Lemma 2.1 that .
As for , we also define it via (2.5) and (2.6) using the construction specified around (2.7), replacing by where is defined as follows: for all with , , and for all with ,
| (5.74) |
Recalling that , and hence is independent of , it follows that again by combining the established fact that and (5.56). The rationale behind (5.74) will become clear momentarily.
We show that as defined above satisfy and -a.s. To this end, note first that on and by (5.47), and , hence -a.s. on we have using the trivial bounds that and .
Second, on and by (5.44), under , the process simply follows the environment as per (2.5) and (2.6), and so does by above definition of . Hence . Moreover, since by (5.42), the process follows the environment by (5.74). By Lemma 2.2 applied with , and , recalling (5.45), we get that . Using (5.43), we finally obtain -a.s. on .
Third, on , the process follows the environment by (5.6), (5.10) and (5.20), as is the case of , so that . Then by (5.27) we have that which guarantees that . From time to time , and follow the same environment by (5.35) and thus, by Lemma 2.2 with , and , we have that .
Similarly for and , on , during the process follows the environment while follows by (5.6), (5.10). By (5.40) we can apply Lemma 2.2 with , and to deduce that . Then during , both and follow (recall (5.20), and that ). Thus Lemma 2.2 with , and ensures that -a.s. on . Next, (5.27), which holds on , implies that , given that only takes nearest-neighbour steps. Finally, since , from time to , both and follow the environment , where is as in (5.74) (recall (5.35); this explains the choice in (5.74)). Applying Lemma 2.2 with , and therefore yields on . This concludes the proof of (5.52).
Part IV: Proof of (5.53).
By Lemma 5.1, we have that
| (5.75) |
Recalling the definitions of and from (5.38) and (5.46), as well as (5.2) and (5.3), it is thus enough to show that
| (5.76) |
and
| (5.79) |
Proof of (5.76). Recall from (5.5). By (5.57) and (3.6), which is in force, we get
| (5.80) |
the last inequality being true for large enough by (5.3) and (5.2). Next, recalling (5.8), that by (5.3) and that , and using that , we note that
| (5.81) |
We note in passing that we cannot locate precisely without (possibly heavily) conditioning the evolution of on . By (C.1) applied with either or , both times with and ranging from to we have by a union bound on and :
| (5.82) |
the last inequality holding for large enough by (5.2) and (5.3). Note that we can indeed apply (C.1) since is -balanced (see items (ii) and (iii) above Lemma 5.2), and and for large enough.
Next, we aim to derive a suitable deterministic lower bound on , on the event , which is -measurable. We aim to apply (C.3), cf. (5.60), and dealing with is straightforward, see (3.9), but requires a small amount of work, cf. (3.8) and (5.15). To this effect, we first observe that under , with as defined in (5.60), one has the inclusions
| (5.85) |
where and on account of (5.60) and (5.3). Now recalling that the evolution of on the time interval follows (5.10) on , and in view of (2.5), one readily deduces that the event is implied by the event , where refers to the joint occurrence of for even integer satisfying and for odd integer satisfying . (Observe indeed that, if is odd, whence , there will be one more step to the right than to the left in the resulting trajectory for ). Feeding this into (5.85), applying a union bound, using (3.9) and (3.8) (which are in force on account of (5.60)), it follows that on ,
(see above (C.3) regarding and ); in the penultimate step above, we have also used that, conditionally on , the events and are independent. Combining this with (5.80) and (5.82), we deduce that for large enough, using (5.2),
| (5.86) |
Next, recalling the definition (5.16) of and that , by (5.63) and the bound given in (C.2.1), we have that, -a.s. on ,
| (5.87) |
for all large enough by (5.3).
We will return to momentarily and first consider . To compute the probability of , we take a union bound over such that , use the definition (5.26) and the fact that is -balanced in order to apply (C.1) twice, once for and once for , choosing in both cases and, for , with and, for , with . Note that for large enough by (5.3) and (5.2), we have indeed and , as required in (C.1). We thus obtain that
| (5.88) |
where the last inequality holds for large enough (depending on , and ). Putting (5.86), (5.87) and (5.88) together and taking (hence ) large enough, it follows that
| (5.89) |
Concerning , we first observe that under , the field is independent from the -algebra generated by and ; this can be seen by direct inspection of the coupling construction until time , paying particular attention (with regards to the evolution of during ) to (5.61), (5.62), (5.63) (and (5.58)), which all involve only either i) trivial couplings or ii) couplings relying on (C.2.1). In particular these couplings do not involve at all. Using the previous observation and recalling (5.21)-(5.22), it follows that -a.s.,
| (5.90) |
Next, observe that and are measurable with respect to the -algebra generated by and owing to (5.5), (5.8), (5.9), (5.15), (5.16) and (5.26). Combining this with (5.89), and recalling the value of from (C.3), we obtain that
| (5.91) |
where, in the last two inequalities, we took (hence ) large enough.
Recalling from (5.33) along with the coupling defined in (5.66) and using that , we can apply (C.2.2), and obtain that, -a.s. on , for large enough (owing to (5.3) and (5.2)),
which implies that
| (5.92) |
Next, we control the probability of defined at (5.69). To do so, we take a union bound over and, using that is -balanced, we apply (C.1) twice for any fixed in this interval: once with , once with and both times with . Note once again that for large enough by (5.3) and (5.2), we have and , as required for (C.1) to apply. This yields, applying a union bound over the values of , that for large enough (recalling that ),
| (5.93) |
Finally, recalling the coupling (5.70) (together with (5.33), (5.34) and (5.69)), we have by (C.2), more precisely by (3.4), for large enough ,
| (5.94) |
Putting together (5.91), (5.92), (5.93) and (5.94), we obtain (5.76), as desired.
Proof of (5.79). We bound individually the six terms comprising on the left-hand side of (5.79). The first of these is already controlled by (5.80). Recall the coupling defined in (5.59) together with the definitions of , and in (5.5), (5.8) and (5.12). Observe that by (5.59) and (C.2.1), we have -a.s. on that Hence for large enough , by (5.3) and (5.2), this yields
| (5.95) |
Recall now the coupling (5.60) and the definition (5.9) of . By (3.9) which is in force, we have
| (5.96) |
for large enough due to (5.3) and (5.2). Next, remark that
| (5.97) |
On one hand, by (5.63) and (C.2.1) (recalling (5.16)) we have
| (5.98) |
On the other hand, by (5.62) and (C.2.1) (recalling (5.17)), we have
| (5.99) |
Together, (5.97), (5.98) and (5.99) yield that
| (5.100) |
for large enough, again via (5.3) and (5.2). Similarly, by (5.65), (C.2.1) and (5.29), for large enough we have that
| (5.101) |
In view of (5.79), putting together (5.80), (5.95), (5.96), (5.100) and (5.101) yields that
| (5.102) |
By (5.76), which has been already established, we know that for large enough by (5.2). Hence, in order to conclude the proof, it is enough to show that , or equivalently that
| (5.103) |
Indeed,
by virtue of (5.92), (5.94), (5.93) and (5.76) in the last line. For large enough (recalling (5.3) and (5.2)), this readily yields (5.103) and concludes the proof of (5.79).
Part V: Proof of (5.54).
Recall the event from (5.54). The proof of (5.54) is relatively straightforward at this point, we just need to keep careful track of those events in the above construction that can force us out of the event ; this is key to get the rapid decay in (5.54). First note that by (5.42), so that by (5.12), (5.17), (5.29) and (5.49) (and using that along with (5.2)), holds on for large enough (tacitly assumed in the sequel), hence can only happen on . As we now explain, looking at the decomposition of and at (5.38) and (5.46), and inspecting closely the construction (and ), especially in Part I of the proof, starting with the paragraph of (5.69) until (5.73), one notices that can in fact only happen:
-
(i)
on all but the last event (i.e. all but ) defining at (5.46), or
-
(ii)
on (see (5.69)), or
- (iii)
-
(iv)
on , or
- (v)
We now detail how the cases (i)-(v) arise. First note that, since as established above, and since by definition (see (5.38)), after discarding item (i) from the above list it only remains to investigate matters on the event , and the cases considered in items (ii)-(v) indeed form a partition of this event, save for the additional specifications (“if the coupling…”) in items (iii) and (v), which we now discuss. For item (iii), note indeed that if holds (see (5.46)) then by Lemma 5.1, and that since , if in addition holds then so does in view of (5.54). Similarly, regarding item (v), we have by (5.38) that so that if holds, by Lemma 5.1. Since , if in addition occurs then occurs as well.
Combining items (i)-(v) above and recalling (5.46) in the context of item (i), by a union bound we have that
By (5.80), (5.93), (5.94), (5.95), (5.96), (5.100) and (5.101), for large enough we obtain that
| (5.112) |
As to the last two terms in (5.112), using the coupling defined in (5.71) and (C.2.2), we get
| (5.115) |
where we used (5.2)-(5.3), the fact that and took large enough. Similarly, using the coupling defined in (5.70) and (C.2) (more precisely (3.5)), we obtain that
| (5.116) |
Finally, putting (5.112), (5.115) and (5.116) together, and using (5.2) with large enough, leads to . This concludes the proof of (5.54) and thus of Lemma 5.2, taking large enough so that (5.60)-(5.116) (which represent a finite number of constraints) hold. ∎
Remark 5.3.
In the coupling constructed in Lemma 5.2, is a priori not independent from ; for instance a synchronous evolution of and after could indicate that , which depends on during , has happened.
5.3. Proof of Proposition 3.4
Let be an integer satisfying , where is given by Lemma 5.2. Let , with as defined in (5.2). We start with a brief overview of the proof. To deduce (3.23), we will couple two walks and on the time interval , , recursively in . The processes will be specified in terms of associated environments , , and an i.i.d. array using Lemma 5.2 repeatedly, cf. (5.51)-(5.52). We will denote the associated coupling measure defined below, which will also comprise associated auxiliary walks that will be defined using the construction of in Section 5.1, iterated over and allow to keep control on the gap between and via a combination of (5.52)-(5.53). The very possibility of iteration is guaranteed by the high-probability event in (5.54).
We now proceed to make the above precise. For later reference we set , for . We further recall the filtration defined in (5.55) and write below when adding hats to all processes involved. Finally, for all , let
| (5.117) |
(see items (i)-(iii) above Lemma 5.2 for notation).
By successive extensions of , we will construct a coupling such that the following hold for all (as supplied by Lemma 5.2) and :
-
(-1)
The processes , (absent when ) and are defined under with the correct marginal laws. That is, , and has the same law as (the restriction to ) of under . Moreover, are i.i.d. uniform variables on , and given , is -measurable and has the law of (the restriction to of) under .
-
(-2)
The processes are -measurable and and hold -a.s.
-
(-3)
, and if , with as in (5.117),
(5.118) -
(-4)
and if , .
For we simply couple under two configurations and such that a.s. for all , which we can do with probability one by (P.3). We set . Thus (-1) and (-2) are satisfied, and (-3) is trivial. Finally since are in particular -balanced, whence (-4) holds.
Assume by induction that for some , we have constructed a coupling with the above properties. We now proceed to extend so as to have (-1)-(-4) with in place of . We first specify matters on the event . Conditionally on , if occurs, we let and evolve independently for according to and respectively, and independently of this, we choose as uniform random variables on in an i.i.d. manner, for such that . On , we further let and , for all and evolve as in (2.5) and (2.6) with instead of . With these choices it is clear that the inequalities in (-2) hold on , since for instance -a.s., using the induction hypothesis and the fact that increments of are bounded from below by . The inequality is derived similarly.
We now turn to the case that occurs, which brings into play Lemma 5.2. Conditionally on and on the event , we couple and for and , as well as following the coupling of provided by Lemma 5.2, with the choice . The requirement of -balancedness of the initial condition needed for Lemma 5.2 to apply is precisely provided by , cf. (5.117).
Combining (5.51), the Markov property (P.1) applied at time , and in view of the choices made on , it readily follows that the processes , thereby defined have the marginal laws prescribed in (-1). Moreover, by above application of Lemma 5.2, the processes and satisfying all of (5.52)-(5.54) are declared. Thus, setting
| (5.119) |
it readily follows, combining (5.119) and the induction assumption on the law of , , combined with the Markov property (P.1) and that of the quenched law, that declared by (5.119) has the desired marginal law, thus completing the verification of (-1) with in place of . Next, we show (-3) and (-4), before returning to (-2). Since by (5.119), the inequality (5.118) with in place of is an immediate consequence of (5.53). Hence (-3) holds. Finally, by construction of the coupling extension on the event , which uses Lemma 5.2, and in view of (5.119) and (5.117), the failure of on the event amounts to the failure of in (5.54), from which (-4) follows with in place of .
It remains to show that (-2) holds with in place of . To this effect, we introduce two auxiliary processes , defined as
| (5.120) |
Combining the induction assumption (-2), the definition of and in (5.119) and (5.120) (the latter implying in particular that ), one readily deduces from property (5.52) the -almost sure inequalities
| (5.121) |
To deduce from this the analogous inequalities with in place of , we apply Lemma 2.2, with , (whence (2.15) plainly holds), , , and to deduce that holds -a.s. Note that the condition necessary for Lemma 2.2 to apply is in force by induction hypothesis in (-2). Together with (5.121), this yields one of the desired inequalities in (-2) with in place of . The other one is obtained in a similar way using Lemma 2.2. This completes the proof of the induction step.
We now use the coupling , which satisfies (-1)-(-4) for all (and ), to complete the proof of (3.23). To this end, we first extend the laws of to all using the Markov property, by sampling independently conditionally on In particular, recalling that , this implies that is declared under . We thus proceed to derive a suitable lower bound on , which is well-defined, and from which (3.23) will follow.
Using that for any , we obtain (with ) that
| (5.125) |
for large enough , where, in the second inequality of the second line, we have used that , see (-3), and in the last line, we have first used that the difference of increments is deterministically bounded from below by (see (5.119) and Lemma 5.1), and for the last inequality that the events are increasing in , cf. (5.117). We also used in various places that .
It remains to suitably estimate the probability appearing in the last line of (5.125), for which we use (-4) and a straightforward induction argument to bound
using also in the penultimate step that . Feeding this into (5.125) yields that
| (5.126) |
as soon as is large enough (recall from (5.2)). Dividing by and applying (3.19) whilst observing that has the same law under as under and has the same law under as under , (5.126) implies that
| (5.127) |
which concludes the proof of Proposition 3.4. ∎
Remark 5.4.
As mentioned at (1.17), we prove in fact a much stronger statement than Proposition 3.4, owing to (5.126), namely that
| (5.128) |
where the denotes a negative quantity that goes to 0 as . This is however insufficient to imply directly Theorem 3.1, and the renormalisation in Section 4 is still essential to improve (5.128) to a right-hand side bounded away from 0 as .
Remark 5.5 (Necessity for couplings with quenched initial condition).
We explain here the main reason why we need quenched conditions for our couplings. In short, this is due to the lack of an invariant measure (or reasonable proxy thereof) from the point of view of the walk.
More precisely, abbreviating , the only a-priori lower bound we have for the probability that and drift away linearly from each other during (corresponding to at (5.90)) is for some large constant by uniform ellipticity – we are in fact precisely trying to derive a better bound in this section.
But this gap is necessary to create a difference between on a time interval of length . Hence, to accrue a significant gain in expectation between , we need to repeat this at least times. Thus, during that time, and could straddle an interval of width at least . The main issue is that we have no a priori information on their local environment (which would not be the case if we had access to an invariant measure and could estimate the speed of convergence to it). Hence if the coupling (C.2.2), that we use between and on a interval much narrower than , was only valid under the annealed product Bernoulli initial condition (which is a priori not what the walk sees), we could resort to the annealed-to-quenched trick (via Markov’s inequality) and a union bound over intervals to control the probability that the coupling fails. However, the failure probability at (C.2.2) is , hence we cannot obtain any non-trivial bound this way. Note that this does not depend on the choice of . Furthermore due to the diffusivity of the environment particles and large deviation considerations, it seems unlikely that one could improve the bound of (C.2.2) beyond .
This is why we resort to some quenched control, cf. items (i)-(iii) above Lemma 5.2, and also (5.117). The empirical density was the most accessible and relevant statistic (in particular if the environment is conservative, as is the case of SEP). For similar reasons, we had to establish (C.1) in a quenched setting, to ensure that whatever the distribution of the environment around the walker at time for some (as long as it is balanced), there is still a uniformly low probability not to have the required empirical density at time (see (5.88)) to perform the coupling of (C.2.2). Of course the necessity for quenched couplings encapsulated in (C.1) and in particular (C.2), means that we have (more) work to do in order to verify this in specific instances, as we do for SEP in the next section.
6 Exclusion process and couplings
We start by giving in §6.1 a formal definition of the main environment of interest in this article, the symmetric simple exclusion process (SEP), and first check that it fits the setup of §2.2, in particular, that the basic properties (P.1)–(2.2) listed in §2.2 hold. The main result of this section, proved in §6.2, is to show that the SEP satisfies the conditions (C.1)-(C.3) stated in §3.1; see Proposition 6.3 below. This implies that our main result, Theorem 3.1, applies in this case; cf. also Theorem 1.2 and its proof in §3.2. We refer to Appendix B for another environment of interest which fits this framework.
6.1. Definition of SEP and basic properties
We fix a parameter , which will be constant throughout this section and often implicit in our notation. The (rate ) symmetric simple exclusion process (SEP) is the Markov process on the state space (tacitly viewed as a subset of , cf. §2.2) with (pre-)generator
| (6.1) |
for and in the domain of , where is the configuration obtained from by exchanging the states of and , i.e. such that , and for all ; see [51, Chap. VIII]. We denote its canonical law with initial configuration and drop the subscript SEP whenever there is no risk of confusion. In words, (6.1) entails that the vertices such that , which can be seen as the locations of particles evolve like continuous-time symmetric simple random walks on with rate that obey the exclusion rule; that is, particles are only allowed to jump onto empty locations.
It will often be useful to consider the interchange process on , with generator defined as in (6.1) but omitting the exclusion constraint , which interchanges the state of neighbors and independently at rate . We will use the following specific construction of this process. Let denote the set of edges on and be a probability governing independent Poisson counting processes of intensity on attached to every edge . For any given , one defines under by exchanging the states of at and every time the ‘clock rings’ for , where . This is well-defined up to a set of measure zero. Then for every ,
| (6.2) |
This follows upon observing that the states of neighboring sites suffering the exclusion constraint can also be exchanged. For our purpose, these two processes are equivalent, but note that they differ when one distinguishes the particles of the system (for instance studying the motion of a tagged particle).
A useful feature of this alternative description is the following. A particle trajectory of the interchange process is obtained by following the trajectory of a state such that (a particle) under . We won’t define this formally but roughly speaking, if and are the two edges incident on , one waits until the minimum of the first arrival times of these two processes (which is an exponential variable with parameter ) and jumps across the corresponding edge. Then one repeats this procedure. In particular, it immediately follows that
| (6.3) | for each such that , the particle trajectory of under follows the law of a continuous time simple random walk with jump rate . |
Recalling the properties (P.1)–(2.2) from §2.2, we first record the following fact.
Proof.
Property (P.1) is classical, see [51, Chap. I, Thm. 3.9, p.27] along with Example 3.1(d), p.21 of the same reference. So is (P.2), i.e. the stationarity of the measure in (6.4), see [51, Chap. VIII, Thm. 1.12, p.369]. The required coupling (for two given initial configurations ) needed to verify the quenched monotonicity asserted in (P.3),i) is simply obtained by realizing the process under the auxiliary measure and using the same Poisson processes . In particular this measure yields a coupling over all possible initial distributions, including and , and this coupling is seen to preserve the partial order for all . The monotonicity in (P.3),ii) is classical. Lastly, upon observing that is a binomial random variable with parameters and under , property (2.2) is obtained by combining (A.3) and (A.4), which are well-known large deviation estimates. ∎
In anticipation of §6.2, we now collect a simple lemma to bound the linear deviations of an SEP particle, which we will routinely use in our couplings below.
Lemma 6.2.
Let denote a simple random walk on with jump rate , starting from at time , with law denoted by . For all and :
| (6.7) |
Proof.
The first inequality is immediate since only performs nearest-neighbor jumps. As for the second one, remark that the number of jumps performed by during is a Poisson random variable with parameter . Hence by (A.1) applied with and , we obtain that
| (6.8) |
and the conclusion follows. ∎
6.2. Conditions (C.1)–(C.3) for SEP
We now proceed to verify that the conditions introduced in §3.1 all hold for the exclusion process introduced in §6.1, as summarized in the next proposition. Its proof occupies the bulk of this section. These properties (above all, (C.1) and (C.2)) are of independent interest.
Proposition 6.3.
We now proceed to investigate each of the relevant conditions separately. Throughout the remainder of this section, we work implicitly under the assumptions of Proposition 6.3. In particular, in stating that some property ‘holds for SEP,’ we mean precisely that is verified for the choice with for all , and with the rate parameter underlying the construction of SEP.
Lemma 6.4.
The condition (C.1) holds for SEP, with no restriction on the choice of .
We give a brief overview of the proof. A key idea is to exploit the fact that SEP particles, although not independent, are in fact ‘more regularly’ spread out than a bunch of independent random walks (starting from the same initial positions), which is due to the inherent negative association of the SEP. This fact is implicit in the bound (6.10) below, which is borrowed from [43] (itself inspired from [70]), the proof of which uses in a crucial way an inequality due to Liggett, see [51, Chap. VIII, Prop. 1.7, p. 366], encapsulating this property. With this observation, it is enough to argue that after time (where is the precision mesh of the empirical density of the initial configuration, as in (C.1)), random walks have diffused enough to forget their initial positions and average their density, which follows from classical heat kernel estimates.
Proof.
We focus on proving the upper inequality (i.e. when each ), and comment where necessary on the minor adjustments needed to derive the other inequality in the course of the proof. Let , and be such that the conditions of (C.1) hold. We will in fact show (C.1) for an arbitrary value of although the restriction to is sufficient for later purposes (note that the statement is empty if ). Thus, let and denote the set of intervals of length included in , and define
| (6.9) |
the average number of occupied sites of after time . Note that . By Lemma 2.3 of [43] (see also Lemma 5.4 of [70]) one knows that for all and suitable ,
| (6.10) |
(in fact the bound (6.10) holds for any initial configuration ). Thus, if
| (6.11) |
under our assumptions on and , then (6.10), a union bound over , and the upper bound on the maximum in (6.11) yield that
| (6.12) |
A companion inequality to (6.10) can be deduced in a similar way using the lower bound on the minimum in (6.11) and exploiting symmetry, i.e. rewriting where , while observing that has law , cf. (6.1). The conclusion (C.1) then follows.
Therefore, we are left with showing (6.11). In view of (6.9), it is enough to prove that for every , and under our assumptions on and ,
| (6.13) |
Let denote a continuous-time symmetric simple random walk on with jump rate , defined under an auxiliary probability , and let , for and denote its transition probabilities, which are symmetric in and . Writing as the disjoint (due to the exclusion constraint) union over of the event that and the particle starting at is located at at time , it follows using (6.3) that for all ,
| (6.14) |
where and we used reversibility in the last step. Using the rewrite (6.14), we first show the upper bound in (6.13). Let us define , where the constant will be chosen below. Recalling that , we cover the sites of using intervals all contained in this interval and each containing sites, with . We may assume that all but the last interval are disjoint. For later reference, we note that for all by assumption on . By (6.14), we have that
| (6.15) |
We will look at the two terms on the right-hand side separately. Using (A.1)), one knows that with denoting the number of jumps of a continuous time random walk with jump rate until time , one has with . Combining this with the deviation estimate (A.3) yields that
| (6.19) |
where we choose , use that , thus choosing large enough, and use the conditions from (C.1) for the last inequality.
Next, we want to deal with the points in the interval . Recall that a continuous-time simple random walk with rate at time has the same law as a rate continuous-time simple random walk at time . Hence, by [50, Theorem 2.5.6], for all such that and , using that for large enough, with changing from line to line,
| (6.22) |
where we used that and , from (C.1), and chose large enough. Using [50, Theorem 2.5.6] again, we also have that, as soon as is large enough, using the conditions from (C.1),
| (6.23) |
Now, recalling that the intervals are disjoint for and that they all have cardinality , using (6.22) and (6.23), we have that
| (6.27) |
Putting together (6.15), (6.19) and (6.27), and using that , we obtain
| (6.28) |
This yields the upper bound in (6.13), and the upper inequality in (C.1) follows.
Lemma 6.5.
The condition (C.2.1) holds for SEP.
Proof.
Recall the construction in (6.2) of the SEP using . Setting , this yields a natural coupling of and with marginal laws and , respectively, for any choice of initial distribution and . In words, the coupling identifies and as interchange processes and uses the same Poisson processes on the edges of . Now if , then under , we claim that
| (6.29) |
where is the event that the particle at enters the interval before time . By (6.7) with , we have
| (6.30) |
Applying a union bound to (6.29) and feeding (6.30) thus yields that the probability of the complement of the event appearing on the left-hand side of (3.6) is bounded from above by
∎
Remark 6.6 (Locality in (C.2.1)).
For later reference, we record the following locality property of the coupling constructed in the course of proving Lemma 6.5. Let denote the edges having both endpoints in . Then the above argument continues to work for any specification of clock processes , for for and , respectively, so long as and end up having the correct law. This observation will be important when several couplings are ‘concatenated,’ as in the proof of Lemma 6.9 below (see also Figure 7).
Lemma 6.7.
The condition (C.2.2) holds for SEP.
We first give a brief overview of the argument. Lemma 6.7 corresponds to a quenched version of [15, Lemma 3.2] by Baldasso and Teixeira, in which and are sampled under and respectively. We mostly follow their argument. Since fixing the initial environments induces some changes, and because we will use a variation of this proof to show (C.2) for the SEP (Lemma 6.9), we detail below the coupling of and , seen as interchange processes. In doing so we also clarify an essential aspect of this coupling; see in particular (6.33)-(6.34) below.
In a nutshell, the idea is to pair injectively each particle of with one of at a relatively small distance (of order ), during a relatively long time (of order ), so that they perform independent random walks until they meet (which has a large probability to happen since ), after which they coalesce, i.e. follow the same evolution. To make such a matching possible, we ensure that with large probability, has more particles than on each interval of length roughly . Within the present quenched framework, this property is now obtained by means of (C.1), which has already been proved; see Lemma 6.4. Since the probability that at least one particle of does not get paired, i.e. does not meet its match, is relatively high (polynomially small in ), we repeat this coupling; see also Figure 6.
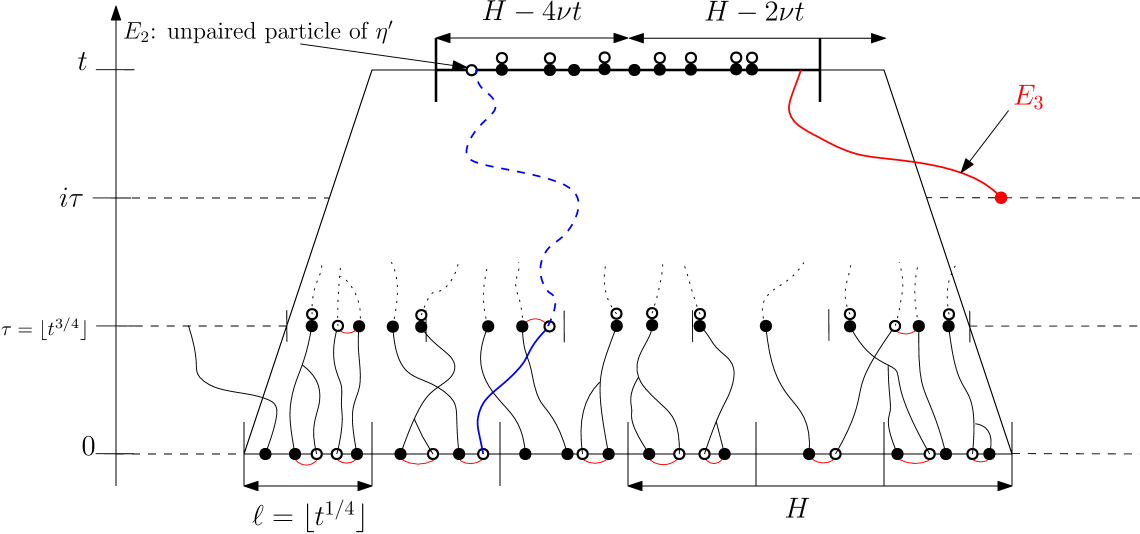
Proof of Lemma 6.7.
Let , , and and satisfy the conditions appearing in (C.2.2). Recall that
We abbreviate for in the sequel.
Let , where is a copy of , with , governing the independent processes , , respectively, cf. above (6.2). We will define a coupling of under (to be precise, a suitable extension of carrying additional independent randomness), inductively in over the time interval , for . Suppose have been declared under for some , with the correct marginal laws for and (the case of this induction assumption holds trivially). We start by controlling the empirical densities of and at time , which are already defined under . The original proof of [15] uses the stationarity of and and (2.2), while we resort to (C.1) (cf. (6.39) below). Let
| (6.31) |
Observe that is automatically satisfied by assumption on and .
We proceed to define and under . If does not occur, we sample (and in fact for all ) in a manner as in (6.2) using the processes after time , and similarly for using instead. Thus in this case evolves independently from from time on.
If on the other hand occurs, we proceed as follows. Let denote the set
| (6.32) |
so that is measurable relative to . We refer to as the set of paired particles (at time ). Let and . Observe that . Our goal is to reduce the size of their difference as for and eventually achieve equality when .
To this effect, we first define a matching, i.e. an injective map , still measurable relative to , as follows. The map acts as identity map on , a subset of both and , cf. (6.32). For each , is a point in at distance at most from . As we now briefly explain, owing to the occurrence of , this can be achieved in such a way that is injective. To see this, first note that one can write as disjoint union of intervals of length ranging in , as follows. One covers with contiguous intervals of length starting at one boundary, leaving a remaining interval at the other boundary of length less than . If has length at least , one simply adds it, else unless is empty one cuts the penultimate interval into two halves of length at least each and merges with the last of them. By construction any of the disjoint intervals thereby obtained has length as required, and thus on the event , see (6.31), one knows that . Since the ’s are disjoint and their union is , it follows that we can pair injectively each particle of with a particle of within the same interval. We now fix any such matching and call any two particles matched. We note that by construction.
The evolution for and under (and on ) is now prescribed as follows. Both and will be realized as interchange processes as in (6.2), thus it is sufficient to specify the relevant (Poisson) clock processes attached to each edge of . Let denote the set of edges of having both endpoints in . For , and simply use the clocks of and , respectively, where denotes the canonical time-shift of the process by . It remains to specify the clock processes for . Let . All clock processes attached to edges will be defined via suitable thinning of .
First, one orders chronologically all arrivals for the processes as varies (there are countably many such times and they are a.s. different so this is well-defined on a set of full measure). Let and etc. denote the chronologically ordered times thereby obtained. By suitable extension, is assumed to carry a family of i.i.d. Bernoulli variables with . We regard as the label attached to . Let be the thinned process obtained from by only retaining arrivals with label . Then,
| (6.33) | uses the clock process for each (and for each ). |
By elementary properties of Poisson processes and applying (6.2), it follows that has the correct conditional law given ; indeed by construction to each edge of one has associated independent Poisson processes having the correct intensity.
The definition of is analogous to (6.33), and the clock process for underlying the definition of is specified as follows. For a particle (resp. ), let (resp. ) denote its evolution under (resp. ). Proceeding chronologically starting at , one chooses whether the clock is retained or not according to the following rule. With denoting the edge of ,
| (6.34) |
here we think of right-continuous trajectories so is the position of the particle after the -th jump; in fact one could replace each occurrence of in (6.34) by an arbitrary time with , since there is no jump between those times. In words, at time , one inspects if at least one endpoint of contains (the evolution to time of) two matched particles, in which case the clock is retained if it has label only. If no endpoint of contains matched particles the clock is retained if it has label . The process then simply uses the clocks on edges that are retained according to (6.34) and such that . We will now argue that
| (6.35) | given , the process has law under . |
To see this, one simply notes using a straightforward induction argument that the conditional law of given , , and is that of a Bernoulli- random variable. From this and the thinning property for Poisson processes it readily follows that has the right law.
Overall we have now defined a coupling of until time . In case we simply use the same process to define the evolution of both and in the remaining time interval . The Markov property (P.1), (6.33) and (6.35) ensure that indeed have the desired marginals during . In view of (6.32), this immediately yields that
| (6.36) |
The key of the above construction is that the latter event forces one of three possible unlikely scenarios. Namely, as we explain below, one has that
| (6.37) |
where ,
| (6.38) |
here refers to the evolution of particle under and with , one sets . In words follows the evolution of the difference between , which is not paired at time since , and its match , which is well-defined on the event . Thus refers to the event that some particle is found in at time for all and never meets its match during the time interval .
We now explain (6.37). To this effect we first observe that (6.33) and (6.34) ensure that two matched particles at some stage follow the same evolution once they meet (and thus belong to for all later times ) as long as they stay in . Therefore, on the event , on which (due to occurrence of ) no unpaired -particle at time can arise by drifting in from the side, meaning that such a particle cannot be seen in at any time , the set being non-empty requires at least one particle from to never meet its match at any of the stages (matching happens at all stages due to occurrence of ). That is, occurs, and (6.37) follows.
To finish the proof, we now bound the (bad) events appearing in (6.37) separately. In view of (6.31), we apply (C.1) (which now holds on account of Lemma 6.4) to (resp. ) at time , with (resp. ) instead of , with instead of and with ranging from to , which fulfils the conditions of (C.1) if is large enough so that and
Recalling that and summing over the possible values of , this gives that
| (6.39) |
We deal with by applying (C.2.1), which is in force on account of Lemma 6.5. Noticing that the event indexed by entering the definition of in (6.38) implies that at least one particle of ends up in before time , we get using (3.6) with , , and playing the role of that
| (6.43) |
Finally, owing to our coupling in (6.33), (6.34), conditionally on , , the process is a one-dimensional continuous-time random walk with rate started at a point in (owing to the separation of and its match ) with absorption at . If is such a random walk and denotes the probability for this walk starting at , we have by invariance by translation and the reflection principle:
| (6.44) |
Using again [50, Theorem 2.5.6] and taking large enough (so that in particular for any ), we have thus for some universal constant (changing from one expression to the next):
| (6.45) |
Recalling that and taking a union bound over , the previous estimate applied with the Markov property for yields that, as long as is large enough:
| (6.46) |
Putting together (6.36), (6.37), (6.39), (6.43) and (6.46), we obtain that
which is larger than as required by (3.7) provided and are chosen large enough. ∎
Remark 6.8 (Locality in (C.2.2)).
Similarly as in Remark 6.6, which exhibits an analogous property for the coupling inherent to (C.2.1), the coupling yielding property (C.2.2) constructed in the proof of Lemma 6.7 can be performed for any specification of clock processes used to define , so long as the marginal laws of and , are that of independent Poisson processes of intensity . This can be seen by inspection of the proof: the only ‘non-trivial’ joint distribution concerns , which are obtained by suitable thinning from , see in particular the discussion around (6.33) and (6.34).
Combining the couplings supplied by Lemmas 6.5 and 6.7 multiple times, which will be permitted owing to Remarks 6.6 and 6.8, yields the following result.
Lemma 6.9.
The condition (C.2) holds for SEP.
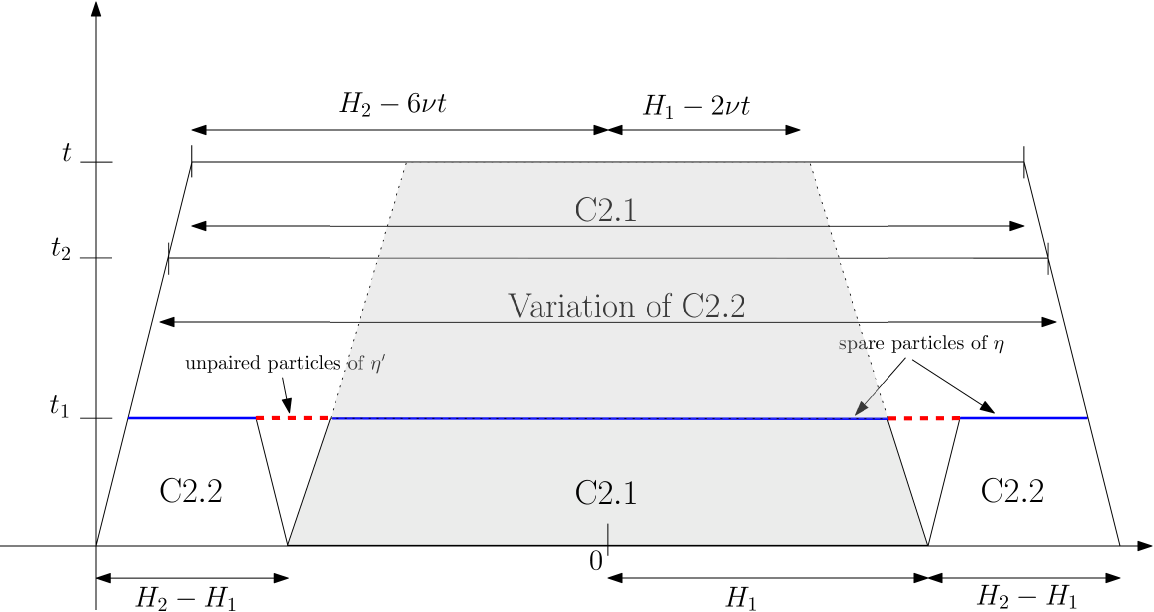
Proof.
Let , and be such that the assumptions of (C.2) hold. In particular, note that these entail that . Define
| (6.49) |
We proceed in two steps and refer to Figure 7 for visual aid. In the first step, we apply simultaneously the couplings of Lemma 6.5 on and of Lemma 6.7 on , in the time-interval (in doing so we shall explain how this preserves the marginals of and ). As a result, we get that for all , except possibly around two intervals around and , of width .
In the second step, we couple the particles of on these intervals with "additional" particles of on (using that the empirical density of is slightly larger than that of on by (C.1)), in a manner similar to that used in the proof of Lemma 6.7. This ensures that with large enough probability, all these particles of get covered by particles of within time , without affecting the coupling of the previous step on account of the Markov property. Finally, during the time interval we use again the natural coupling of Lemma 6.5, and conclude by showing (3.4) and (3.5). We now proceed to make this precise. Step 1: we construct a coupling of the evolutions of and during the time-interval such that if we define the (good) events
then
| (6.50) |
The coupling is defined as follows. Let be a family of i.i.d. Poisson processes on of intensity . These processes are used to describe the exchange times for (seen as an interchange process as in (6.2)), during the time-interval . We now define the exchange times to be used for during as follows. For an edge having at least one endpoint outside or at least one endpoint inside , set . It remains to specify for with both endpoints in but outside . This set splits into two disjoint intervals , which are both dealt with separately and in exactly the same manner. Thus restricting our attention to , one couples and in exactly the same manner as in the proof of Lemma 6.7, with the interval , defined as the set of all endpoints of edges in , playing the role of . The fact that Lemma 6.7 applies even though the processes and have been specified for certain edges is owed to Remark 6.8. Define similarly and perform the same coupling of and .
Since the sets of edges , and are disjoint, it readily follows that is an i.i.d. family of Poisson processes on of intensity . This ensures that under , and .
Now, by our assumptions on and , the above construction of together with Remark 6.6 ensure that Lemma 6.5 applies on the interval with and (recall to this effect that the relevant coupling for which (C.2.1) is shown to hold is simply , see above (6.29), and that this coupling is also local in the sense of Remark 6.6). This yields that
| (6.51) |
Second, our assumptions (taking ) and the above construction of also allow us to apply Lemma 6.7 on and on instead of , with the same values of and , and with (in particular, ). We obtain that
| (6.52) |
Combining (6.51) and (6.52) yields (6.50), since if is chosen large enough. This concludes Step 1.
Step 2: We now extend to a coupling up to time , using a slight variation of the coupling in the proof of Lemma 6.7 in the time-interval . For definiteness of , on the complement of , use for the exchange times of both and during the time . Focusing now on the case where occurs, the aim of the step is to show that we can have
| (6.53) |
Fix any realization of such that holds. Define (cf. (6.32)) as the set of vertices in containing both a particle of and of , and think of these particles as being paired. Let (resp. ) be the set of unpaired particles of (resp. ) in . By definition of and , the particles of must be in when the event occurs; cf. Figure 7. Hence, on we have that
| (6.54) |
Denote the event that on every interval of length between and included in , has at least unmatched particles (recall that by assumption). On , use as exchange time process to define both and during (cf. the discussion leading to (6.2)).
Henceforth, assume that occurs. Following the line of argument in the paragraph after (6.32), one matches injectively each particle of with a particle of at distance at most . In the present context this is possible owing to (6.54) and occurrence of . Then one couples the evolutions of and , first during as done in the proof of Lemma 6.7 during the time interval . Then iteratively at times for , one performs on the same coupling at times on the event that for any interval of length ranging between and , one has . On , use for the exchange times of both and during the time interval .
Overall, this yields a coupling of with the correct marginal law (as in the proof of Lemma 6.7). Finally one extends this coupling during on the event by using the same exchange times for and . It follows that and under .
In much the same way as in (6.36), it follows from the above construction that the complement of the event on the left-hand side of (6.53) implies that at least one particle of in the interval is unpaired at time , which in turn (cf. (6.37)-(6.38)) implies the occurrence of
where
We now mimic (6.39), (6.43) and (6.46) to handle , and respectively. In detail, for the first term, we apply (C.1) with for , and ranging from to , noting that
| (6.55) |
For the third inequality, remark that (taking ), hence it is enough to show that . But (since for ). Taking large enough so that and thus is large enough (recall that ), we have as desired. For the second term , we use (C.2.1), and for the third term , we note that a continuous-time random walk with rate started in will hit before time with probability at least (note that if we take ). We obtain that
Let . It remains to establish (3.4) and (3.5). Owing to the way the coupling is defined during the intervals and , has the following property: in , any particle of that is covered at some time by a particle of will be covered by this particle until time , or until it leaves . Moreover, by assumption every particle of is covered by a particle of . Therefore,
| (6.56) |
By Lemma 6.2 applied with for every and if , a union bound over all particles appearing in the event on the right-hand side of (6.56) leads to the bound on the -probability of the left-hand side by and (3.4) follows.
As for (3.5), first note that by (6.50) and (6.53), and for large enough, we have that
| (6.57) |
Since we use, during , the same natural coupling as in the proof of Lemma 6.5, letting denote the event that a particle of ends up in in time at most , we obtain, provided is large enough and abbreviating , that
This shows (3.5) (recalling that by (6.49)), and concludes the proof. ∎
The final result which feeds into the proof of Proposition 6.3 is the following.
Lemma 6.10.
The condition (C.3) holds for SEP.
Proof.
Let , and be such that the conditions of (C.3) hold. In particular, these imply the existence of such that and . Let as above (6.2), by which are coupled as interchange processes using the same exchange times . As observed in (6.3), under the particle of starting at moves like a simple random walk with jump rate , and we have for all by construction of . Hence, and therefore, in order to deduce (3.8) it is enough to argue that
| (6.60) |
Indeed, let (resp. ) denote the number of jumps of to the left (resp. right) during the time interval . These two variables are independent and distributed as , which entails that, for , and ,
using that in the third step. Since and , (6.60) follows for all (and ), and it is easy to see that the bound remains true in the remaining case, i.e. when (now forcing and instead, which by symmetry of and yields the same bound as when ). Overall this yields (3.8). Finally, since the marginal of the coupling for is that of Lemma 6.5, we get the first inequality of (3.9) from (C.2.1) with . The second inequality follows from our condition on (using that ). ∎
Appendix A Concentration estimates
We collect here a few classical facts on concentration of Poisson and binomial distributions, that are repeatedly use to control the probability that the environment could have an abnormal empirical density. The PCRW case corresponds to Poisson distributions, and the SSEP to binomial distributions).
Lemma A.1.
Let , and . Then
| (A.1) |
If , then
| (A.2) |
Let and . Then for all , we have
| (A.3) |
and for all :
| (A.4) |
Proof.
We get (A.3) (resp. (A.4)) from Theorem 4.4 (resp. Theorem 4.5) of [54] with and in both cases. We now turn to (A.1). By a classical application (and optimization) of Chernoff’s bound (see Theorem 5.4 of [54]), one shows that
Hence for (A.1), it remains to show that
Setting and multiplying both sides by this amounts to show that the map defined by
remains non-negative. Indeed, and . One checks that for all (with equality iff ) so that is nonnegative on , and this concludes the proof of (A.1). One proves (A.2) via the same method. ∎
Appendix B The PCRW environment
In this Appendix, we consider another environment, the Poisson Cloud of Random Walks (PCRW) previously considered in [41, 40] among others; we refer to the introduction for a more complete list of references. For this environment, the parameter governs the intensity of walks entering the picture. We show below, see Lemma B.1 and Proposition B.2, that the PCRW also fits the setup of §2.2 and satisfies (C.1)-(C.3). Hence, this environment yields another example to which the conclusions of our main result, Theorem 3.1, apply. The proof is virtually the same as that of Theorem 1.2 given in §3.2, upon noting that the relevant law of large numbers (3.10) in this context was also shown in [40], yielding the existence of the speed at all but at most two values (as for SEP). The PCRW is defined below using random walks evolving in discrete time, following the practice of [40] and other previous works, but the following results could easily be adapted to random walks in continuous time (with exponential holding times of mean one).
B.1. Definition of the PCRW
The PCRW is a stochastic process with state space defined as follows: for any given initial configuration and every , place particles at . Then, let all the particles follow independent discrete-time lazy simple random walks, i.e. at each integer time, any given particle stays put with probability , or jumps to its left or right neighbour with the same probability . For and , let be the number of particles located at . We denote by the canonical law of this environment with initial state , and frequently abbreviate below.
B.2. Properties of the PCRW
We proceed to show that the PCRW environment has the desired features, i.e. that the properties (P.1)-(2.2) listed in §2.2 as well as the conditions (C.1)-(C.2) appearing in §3.1 all hold. The parameter indexing the stationary measures will naturally vary in . We will in practice always consider a bounded open interval for arbitrary below. The constants appearing as part of the conditions we aim to verify will henceforth be allowed to tacitly depend on . Note that this is inconsequential for the purposes of deriving monotonicity of on (cf. (3.11)) since this is a local property: to check monotonicity at one simply picks large enough such that .
For the remainder of this appendix, let be arbitrary and . We start by verifying properties (P.1)-(2.2).
Proof.
Fix . Property (P.1) is classical, and follows readily from the time-homogeneity, translation invariance and axial symmetry of the lazy simple random walk. Property (P.2) is also standard: if , by suitably thinning the Poisson process one can realize by decomposing for all , where (resp. , ) is the number of particles starting from that make their first move to the left (resp. stay put, and make their first move to the right), with , and the family of variables is independent. From this one infers that , as for all , and the variables are independent as varies.
As for property (P.3), it holds with the following natural coupling (which straightforwardly yields the correct marginal laws for and ): if for all , then one matches injectively each particle of to a particle of located at the same position. The coupling imposes that matched particles follow the same trajectory, and the remaining particles of (if any) follow independent lazy simple random walks, independently of the matched particles. Finally, Property (2.2) is a consequence of the fact that under , for every finite interval and every time , , and combining with the tail estimates (A.1)-(A.2). ∎
The proof of Proposition B.2 is given in §B.3 below. We start with a coupling result (which for instance readily implies (C.1) as shall be seen), similar in spirit to Lemma B.3 of [41], stating that the evolution of the PCRW with a sufficiently regular deterministic initial condition can be approximated by a product of independent Poisson variables. This is of independent interest (and lurks in the background of various more elaborate coupling constructions employed in §B.3).
Proposition B.3.
There exist positive and finite constants , and such that the following holds. Let , and be such that and . There exists a coupling of with (and sampled under ) such that, if is such that for any interval with ,
| (B.2) |
then with (resp. ),
| (B.3) |
Moreover, the coupling is local in the sense that depends on the initial condition through , , alone.
We now prepare the ground for the proof of Proposition B.3. Let us abbreviate . We use the framework of soft local times from Appendix A of [41] (the latter following Section 4 of [64]), which we extend to fit our needs. We define a coupling as follows. Let (defined under ) be a Poisson point process on with intensity where stands for the counting measure and is the Lebesgue measure on . For each , set
| (B.4) |
For , let independently . This indeed yields the correct marginal distributions in view of (B.1).
As for , given any initial configuration let denote an arbitrary ordering of the positions of the (finitely many) particles of (counted with multiplicity, hence the sequence is not necessarily injective). Define for and with denoting the discrete-time heat kernel for the lazy simple random walk. Let and for , define recursively
| (B.5) |
see Figure 5 of [41]. Note that since each has a finite support (included in ), the ’s are well-defined. In fact by Propositions A.1-A.2 of [41], the variables are i.i.d. Exp(1). For all , we define the soft local time
| (B.6) |
with as in (B.5). With these definitions, it follows, denoting
| (B.7) |
that the family is distributed as , defined as the restriction of under restricted to the particles of . To see this, note that is such that, if is the -coordinate of the particle of seen when determining at (B.5), then the particle of moves to by time . Remark indeed that by (B.5) and the spatial Markov property for Poisson point processes, the choice of is proportional to and independent of what happened in the first steps. In particular, is distributed as , since all the particles of perform at most one step per unit of time, and must have been in at time . Finally, independently of all this, let all particles of follow independent lazy random walks.
Overall indeed defines a coupling of with the required marginal law, and the desired locality (see below (B.3)) follows immediately from the previous construction. Moreover, (B.4) and (B.7) imply that under , for all and ,
| (B.8) |
It is now clear from (B.8) that the desired high-probability domination in (B.3) hinges on a suitable control of the soft local time defined by (B.6). To this effect we first isolate the following first moment estimate.
Lemma B.4.
Under the assumptions of Proposition B.3, there exists such that for all ,
| (B.9) |
Proof.
Let and fix . Cover by a family of intervals of length , all disjoint except possibly and . We focus on the upper bound on in (B.9) (the lower bound is derived in a similar fashion). By assumption in (B.2), we have that for all , hence, recalling that in (B.5) has unit mean,
| (B.11) |
We start by dealing with the last term above. By Azuma’s inequality, we have that
| (B.12) |
for some constant , depending on . Let us now handle the first term in the right-hand side of (B.11). We start by noting that
| (B.15) |
By [50, Proposition 2.4.4], we have that
| (B.16) |
Recalling that at most and may overlap, the above implies that
| (B.17) |
It remains to deal with the last term in (B.15). By standard heat kernel estimates (see for instance [50, Proposition 2.5.3] and [50, Corollary 2.5.4]) and a computation similar to (6.22), combined with a large deviation estimate on the number of non-zero steps performed by the lazy random walk up to time (using Azuma’s inequality for instance), for all with and first assuming that both and are even, leaving be a universal constant changing from line to line, we have that
| (B.18) |
where we have to choose (and hence ) large enough in the assumptions of Proposition B.3 The case where both and are odd is treated similarly, considering instead of . If is even and is odd, note that for all such that ,
where a corresponding lower bound holds in order to treat the case where is odd and is even. Hence the result in (B.18) holds regardless of the parity of and . Using (B.18), we obtain that
| (B.21) |
where we used (B.16) and the fact that , chose (and hence ) large enough, and let the value of change from one line to the next. Substituting (B.17) and (B.21) into (B.15) and feeding the resulting estimate together with (B.12), into (B.11) yields that
and the conclusion follows. ∎
We are now ready to give the short proof of Proposition B.3, which combines the above ingredients.
Proof of Proposition B.3.
We use the coupling defined atop Lemma B.4 and show that concentrates in order to exploit (B.8). To this end, first note that for all ,
| (B.22) |
Observe that only a finite number of factors may differ from (which requires , hence ). By (B.8), the probability with is thus bounded from above by
| (B.25) |
using (B.22), the exponential Markov inequality and the inequality for in the second step and optimizing over in the third, and abbreviating . Using (B.16) and then (B.9), we have
| (B.28) |
where we used the assumptions of Proposition B.3, chose small enough (depending on ), and let the value of change in the last inequality (depending on ). Moreover,
| (B.29) |
provided that is small enough (depending on ). Substituting the two displays above into (B.25) provides the asserted upper bound on in (B.3). For the other choice of in (B.3), we bound, using that for all ,
| (B.32) |
optimizing again over in the last step. We conclude in the same way as for the upper bound. ∎
B.3. Proof of Proposition B.2
The proof of Proposition B.2 follows immediately by combining Lemmas B.5-B.9 below, each of which focuses on one specific property among (C.1), (C.2), (C.2.1), (C.2.2) and (C.3), which are proved in this order. Recall that for some and that constants may implicitly depend on .
Lemma B.5.
Condition (C.1) (with ) holds for PCRW.
Proof.
Let and be such that the conditions of (C.1) hold. It is straightforward to check that these imply the conditions for applying Proposition B.3 with instead of , provided that is large enough w.r.t. , and . Hence, we can now use Proposition B.3 with to show (C.1).
Let . By (B.3) (with an appropriate coupling under which and , and translating to by means of (P.1)), we have that
| (B.35) |
where
By (2.2) (which holds on account of Lemma B.1) and a union bound over all intervals of length , we have that Combining this and (B.35), noting that if we choose small enough w.r.t. and , yields (C.1). ∎
Lemma B.6.
For every , and all such that , there exists a coupling of with respective marginals and such that
| (B.36) |
Therefore, condition (C.2.1) holds for PCRW with .
Proof.
Clearly, (B.36) implies (C.2.1), up to changing to and translating to (using (P.1), as established in Lemma B.1). We now show (B.36).
Let and be as above. Couple and by matching injectively each particle of to a particle of , for all , and by imposing that matched particles follow the same trajectory (and by letting all other particles follow independent lazy random walks). Since particles can make at most one move (to a neighbouring position) per unit of time due to the discrete-time nature of the walks, no particle of outside of can land in before or at time . Thus the event in (B.36) holds with probability 1. ∎
Lemma B.7.
Let , , and be such that and . Let be such that for every interval of length , we have and . Then there exists a coupling of and such that
| (B.37) |
Consequently, (C.2.2) with holds for PCRW. Moreover, is local in that depends on the initial conditions through , , alone.
Proof.
We first show how (B.37) implies (C.2.2). Let and satisfy the assumptions of (C.2.2) (in particular, ). Then they also satisfy the assumptions of Lemma B.7 (with instead of ), upon taking large enough in (C.2.2). By (B.37) applied to instead of (again using translation invariance, see (P.1), established in Lemma B.1), (3.7) holds with since .
We now proceed to the proof of (B.37). Let and satisfy the assumptions of Lemma B.7. Then we can apply Proposition B.3 to with instead of , and the same values of . Similarly, we can apply it to with instead of . This entails the existence of two couplings of and of , where , such that, abbreviating ,
| (B.38) |
Applying [32, Lemma 2.4] with and , one can ‘chain’ and , i.e. one obtains a coupling of such that the pair has the same (marginal) law as under and has the same law as under ; explicitly, a possible choice is
with ranging over point measures on . On account of [32, Remark 2.5,2)] applied with the choices and , has the property that . In view of (B.38), (B.37) follows. The asserted locality of is inherited from , , due to Proposition B.3 (used to define ). ∎
Lemma B.8.
Condition (C.2) with holds for PCRW.
Proof.
Let , , and be such that the conditions of (C.2) hold. We proceed by a two-step coupling similar to the one in Lemma 6.9 and first give a short overview of both steps; cf. also Fig. 7. In the first step, we couple and during the time interval , with , using the coupling of Lemma B.7 on and the coupling given in Lemma B.6, making sure that these couplings can be simultaneously performed on disjoint intervals. As a result, we get that for all , except possibly within two intervals around and , of width .
In the second step, during the time interval , we couple the particles of on these intervals with "additional" particles of on (using that the empirical density of is slightly larger than that of on by (C.1)), using Lemma B.7. This ensures that with large enough probability, all these particles of get covered by particles of within time , without affecting the coupling of the previous step by the Markov property. Step 1: choosing large enough (in a manner depending on and ), as we now briefly explain, the conditions of Lemma B.7 hold for , with up to translating in either of the intervals or . Indeed, the choice and the assumptions in (C.2) yield that
where we choose large enough depending on and .
During the time interval , we apply Lemma B.7, which we now know is in force, simultaneously on and . This is possible owing to the locality property stated as part of Lemma B.7 (see below (B.37)), since the couplings involved rely independently on the particles of and , and those of and respectively. Moreover, by suitable extension of this coupling we can also couple, during the interval , the particles of and in the following way: match injectively each particle of to a particle of , for all , and impose that matched particles follow the same trajectory (note that this is precisely the coupling underlying the statement of Lemma B.6).
From the construction in the previous paragraph, the four groups of particles , , and evolve independently under , and within each group the particles themselves follow independent lazy simple random walks. Hence under , during , we have indeed , and by a similar argument that .
Now consider the events and declared under . By Lemmas B.6 and B.7, respectively, we have that
| (B.41) |
Then, define (still under ) two further events
We apply condition (C.1), which holds by Lemma B.5 to with , and to with . A straightforward computation proves that the necessary conditions are implied by the assumptions in (C.2). This yields
| (B.42) |
Step 2: since holds with full -measure, we can, as in Lemma B.6, pair injectively each particle of to one of on the same site, and impose by suitable extension of that paired particles follow the same trajectory during , all pairs being together independent. We obtain in this way that
| (B.43) |
To complete the construction of it remains to describe the trajectory of the particles of and , and those of that were not paired. On , let all these particles follow independent lazy simple random walks during , independently from the particles paired at (B.43). On , note that for all , where
We pair injectively each particle of to one of on the same site, and impose by suitable extension of that paired particles follow the same trajectory during , all pairs being together independent.
For convenience, we introduce
| (B.44) |
which denote the number of particles of and at position whose trajectory has not yet been described. It thus remains to cover the particles of by those of by time . Let us first explain the reasoning to establish this covering. Note that the two intervals making up escape to our couplings during , so that we can only guarantee that the empirical density of is lower than , see . Fortunately, and ensure that the empirical density of is at least on , which is much wider than . We thus apply Lemma B.7 with a mesh much larger than in order to ’dilute’ the particles of . By making this coupling independent of the other particles of previously paired, we will ensure that both and have the correct PCRW marginals. We now formalise this coupling. By choosing large enough, one can check, via a straightforward computation, that the assumptions in (C.2) imply the necessary conditions to apply Lemma B.7 for and of on with . Hence by Lemma B.7, we can extend such that
| (B.45) |
and such that (using that ), on the event ,
| (B.48) |
Let us check that Step 2 yields the marginals and during (we have already seen in Step 1 that and during so that the Markov property (P.1) will ensure that and during ). Remark that the events , are measurable w.r.t. the evolution of and until time . On , by (B.43) and the paragraph below (B.44), it is clear that all particles of follow independent lazy simple random walks, and that the same is true for . On , (B.45) and Lemma B.7 ensure that this is also the case. Therefore, we have indeed that and .
Finally, we explain how to derive (C.2) from our construction. Note that (3.4) immediately follows from (B.43) (with full -probability). As for (3.5), we have
| (B.51) |
by (B.43) and (B.44). Thus, by combining (B.41), (B.42), (B.48) and (B.51), we get
choosing and large enough (w.r.t. , and ). This yields (3.5) and concludes the proof, since (3.4) is implied by Lemma B.6. ∎
Lemma B.9.
Condition (C.3) (with ) holds for PCRW, the constraint on with the pre-factor now replaced by .
Remark B.10.
Proof.
We adapt the proof of Lemma 6.10. Let , and be such that the conditions of (C.3) hold. We can thus pair injectively each particle of to one particle of located at the same position. Moreover, y assumption there is at least one particle of that is not paired. For , denote the position of this particle at time .
Let be a coupling of and during such that paired particles perform the same lazy simple random walk (independently from all other pairs), and all other particles of and follow independent lazy simple random walks (which yields the marginals and ). As in Lemma B.6, we get that
| (B.54) |
and (3.9) follows.
It remains to show (3.8). Assume for convenience that is even (the case odd being treated in essentially the same way). Similarly as in the proof of Lemma 6.10, we get that
| (B.55) |
for . Note that by our construction, the two events and are independent. Clearly, we have that for both ,
| (B.56) |
Note that there is no parity issue in (B.56) because performs a lazy random walk. Moreover, since by assumption and since no particle outside can reach by time , it follows that at time , there are at most particles of in , and each of them has probability at least not to be at at time . Hence
| (B.57) |
Putting together (B.55), (B.56) and (B.57), we get that the probability on the left of (B.55) is bonded from below by , whence (3.8). ∎
References
- [1] M. Aizenman and D. J. Barsky. Sharpness of the phase transition in percolation models. Comm. Math. Phys., 108(3):489–526, 1987.
- [2] M. Aizenman and G. Grimmett. Strict monotonicity for critical points in percolation and ferromagnetic models. Journal of Statistical Physics, 63(5):817–835, 1991.
- [3] J. Allasia. Law of large numbers for a finite-range random walk in a dynamic random environment with nonuniform mixing, 2024.
- [4] C. Alves and S. Popov. Conditional decoupling of random interlacements. ALEA, Lat. Am. J. Probab. Math. Stat., 15(2):1027–1063, 2018.
- [5] S. Andres, A. Chiarini, J.-D. Deuschel, and M. Slowik. Quenched invariance principle for random walks with time-dependent ergodic degenerate weights. Ann. Probab., 46(1):302–336, 2018.
- [6] S. Andres, A. Chiarini, and M. Slowik. Quenched local limit theorem for random walks among time-dependent ergodic degenerate weights. Probab. Theory Relat. Fields, 179(3-4):1145–1181, 2021.
- [7] L. Avena, O. Blondel, and A. Faggionato. A class of random walks in reversible dynamic environments: Antisymmetry and applications to the east model. Journal of Statistical Physics, 165(1):1–23, Oct 2016.
- [8] L. Avena, F. den Hollander, and F. Redig. Large Deviation Principle for One-Dimensional Random Walk in Dynamic Random Environment: Attractive Spin-Flips and Simple Symmetric Exclusion. Markov Processes and Related Fields, 16(Issue 1):139 – 168, 2010.
- [9] L. Avena, F. den Hollander, and F. Redig. Law of Large Numbers for a Class of Random Walks in Dynamic Random Environments. Electronic Journal of Probability, 16(none):587 – 617, 2011.
- [10] L. Avena, R. S. dos Santos, and F. Völlering. Transient random walk in symmetric exclusion: limit theorems and an Einstein relation. ALEA, X(3):693 – 709, 2013.
- [11] L. Avena, T. Franco, M. Jara, and F. Völlering. Symmetric exclusion as a random environment: Hydrodynamic limits. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, 51(3):901 – 916, 2015.
- [12] L. Avena, M. Jara, and F. Völlering. Explicit ldp for a slowed rw driven by a symmetric exclusion process. Probability Theory and Related Fields, 171(3):865–915, Aug 2018.
- [13] L. Avena, R. Santos, and F. Völlering. Transient random walk in symmetric exclusion: limit theorems and an einstein relation. Latin American journal of probability and mathematical statistics, 10, 02 2011.
- [14] L. Avena and P. Thomann. Continuity and anomalous fluctuations in random walks in dynamic random environments: Numerics, phase diagrams and conjectures. Journal of Statistical Physics, 147(6):1041–1067, Jul 2012.
- [15] R. Baldasso and A. Teixeira. How can a clairvoyant particle escape the exclusion process? Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, 54(4):2177 – 2202, 2018.
- [16] U. Basu and C. Maes. Mobility transition in a dynamic environment. Journal of Physics A: Mathematical and Theoretical, 47(25):255003, jun 2014.
- [17] V. Beffara and H. Duminil-Copin. The self-dual point of the two-dimensional random-cluster model is critical for . Probab. Theory Related Fields, 153(3-4):511–542, 2012.
- [18] N. Berger, A. Drewitz, and A. F. Ramírez. Effective polynomial ballisticity conditions for random walk in random environment. Commun. Pure Appl. Math., 67(12):1947–1973, 2014.
- [19] S. A. Bethuelsen and F. Völlering. Absolute continuity and weak uniform mixing of random walk in dynamic random environment. Electronic Journal of Probability, 21(none):1 – 32, 2016.
- [20] M. Biskup and P.-F. Rodriguez. Limit theory for random walks in degenerate time-dependent random environments. J. Funct. Anal., 274(4):985–1046, 2018.
- [21] O. Blondel, M. R. Hilario, R. Soares dos Santos, V. Sidoravicius, and A. Teixeira. Random walk on random walks: higher dimensions. arXiv e-prints, page arXiv:1709.01253, Sept. 2017.
- [22] O. Blondel, M. R. Hilário, and A. Teixeira. Random walks on dynamical random environments with nonuniform mixing. The Annals of Probability, 48(4):2014 – 2051, 2020.
- [23] B. Bollobás and O. Riordan. The critical probability for random Voronoi percolation in the plane is 1/2. Probab. Theory Relat. Fields, 136(3):417–468, 2006.
- [24] J. Bricmont and A. Kupiainen. Random walks in asymmetric random environments. Commun. Math. Phys., 142(2):345–420, 1991.
- [25] F. den Hollander and R. S. dos Santos. Scaling of a random walk on a supercritical contact process. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, 50(4):1276 – 1300, 2014.
- [26] F. den Hollander, H. Kesten, and V. Sidoravicius. Random walk in a high density dynamic random environment. Indagationes Mathematicae, 25(4):785–799, 2014. Probability and Numbers.
- [27] J.-D. Deuschel, T. Kumagai, and M. Slowik. Gradient estimates of the heat kernel for random walks among time-dependent random conductances. Preprint, arXiv:2309.09675, 2023.
- [28] R. S. dos Santos. Non-trivial linear bounds for a random walk driven by a simple symmetric exclusion process. Electronic Journal of Probability, 19(none):1 – 18, 2014.
- [29] B. Drossel and M. Kardar. Passive sliders on growing surfaces and advection in burger’s flows. Phys. Rev. B, 66:195414, Nov 2002.
- [30] H. Duminil-Copin, S. Goswami, A. Raoufi, F. Severo, and A. Yadin. Existence of phase transition for percolation using the Gaussian free field. Duke Math. J., 169(18):3539 – 3563, 2020.
- [31] H. Duminil-Copin, S. Goswami, P.-F. Rodriguez, and F. Severo. Equality of critical parameters for percolation of Gaussian free field level sets. Duke Math. J., 172(5):839 – 913, 2023.
- [32] H. Duminil-Copin, S. Goswami, P.-F. Rodriguez, F. Severo, and A. Teixeira. Finite range interlacements and couplings. Ann. Probab. (to appear), available at arXiv:2308.07303, 2023.
- [33] H. Duminil-Copin, S. Goswami, P.-F. Rodriguez, F. Severo, and A. Teixeira. Phase transition for the vacant set of random walk and random interlacements. Preprint, arXiv:2308.07919, 2023.
- [34] H. Duminil-Copin, S. Goswami, P.-F. Rodriguez, F. Severo, and A. Teixeira. A characterization of strong percolation via disconnection. Proc. Lond. Math. Soc., 129(2):Paper No. e12622, 1–49, 2024.
- [35] H. Duminil-Copin, A. Raoufi, and V. Tassion. Sharp phase transition for the random-cluster and potts models via decision trees. Ann. of Math. (2), 189(1):75–99, 2019.
- [36] H. Duminil-Copin and V. Tassion. A new proof of the sharpness of the phase transition for Bernoulli percolation and the Ising model. Comm. Math. Phys, 343(2):725–745, 2016.
- [37] N. Gantert, X. Guo, and J. Nagel. Einstein relation and steady states for the random conductance model. Ann. Probab., 45(4):2533–2567, 2017.
- [38] C. Garban and J. E. Steif. Noise sensitivity of Boolean functions and percolation, volume 5 of IMS Textb. Cambridge: Cambridge University Press, 2015.
- [39] M. Gopalakrishnan. Dynamics of a passive sliding particle on a randomly fluctuating surface. Phys. Rev. E, 69(1):011105, Jan. 2004.
- [40] M. R. Hilário, D. Kious, and A. Teixeira. Random walk on the simple symmetric exclusion process. Commun. Math. Phys., 379(1):61–101, 2020.
- [41] M. Hilário, F. den Hollander, V. Sidoravicius, R. S. dos Santos, and A. Teixeira. Random walk on random walks. Electronic Journal of Probability, 20(none):1 – 35, 2015.
- [42] F. Huveneers. Response to a small external force and fluctuations of a passive particle in a one-dimensional diffusive environment. Phys. Rev. E, 97:042116, Apr 2018.
- [43] F. Huveneers and F. Simenhaus. Random walk driven by simple exclusion process. Electron. J. Probab., 20(none):1–42, 2015.
- [44] M. Jara and O. Menezes. Symmetric exclusion as a random environment: Invariance principle. The Annals of Probability, 48(6):3124 – 3149, 2020.
- [45] H. Kesten. The critical probability of bond percolation on the square lattice equals 1/2. Commun. Math. Phys., 74:41–59, 1980.
- [46] H. Kesten, M. V. Kozlov, and F. Spitzer. A limit law for random walk in a random environment. International Journal of Computer Mathematics, 1975.
- [47] C. Kipnis and S. R. S. Varadhan. Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Commun. Math. Phys., 104:1–19, 1986.
- [48] T. Komorowski, C. Landim, and S. Olla. Fluctuations in Markov processes. Time symmetry and martingale approximation., volume 345 of Grundlehren Math. Wiss. Berlin: Springer, 2012.
- [49] S. M. Kozlov. Averaging method and random walks in inhomogeneous environment. Usp. Mat. Nauk, 40(2(242)):61–120, 1985.
- [50] G. F. Lawler and V. Limic. Random walk: A modern introduction, volume 123 of Camb. Stud. Adv. Math. Cambridge: Cambridge University Press, 2010.
- [51] T. M. Liggett. Interacting particle systems, volume 276 of Grundlehren der mathematischen Wissenschaften. Springer-Verlag, New York, 1985.
- [52] O. Menezes, J. Peterson, and Y. Xie. Variable speed symmetric random walk driven by the simple symmetric exclusion process. Electron. J. Probab., 27:Paper No. 6, 14, 2022.
- [53] M. V. Menshikov. Coincidence of critical points in percolation problems. Dokl. Akad. Nauk SSSR, 288(6):1308–1311, 1986.
- [54] M. Mitzenmacher and E. Upfal. Probability and Computing : Randomized Algorithms and Probabilistic Analysis, volume 75. 01 2005.
- [55] B. Morris. The mixing time for simple exclusion. The Annals of Applied Probability, 16(2):615 – 635, 2006.
- [56] T. Mountford and M. E. Vares. Random walks generated by equilibrium contact processes. Electronic Journal of Probability, 20(none):1 – 17, 2015.
- [57] J.-C. Mourrat and F. Otto. Anchored Nash inequalities and heat kernel bounds for static and dynamic degenerate environments. J. Funct. Anal., 270(1):201–228, 2016.
- [58] S. Muirhead and H. Vanneuville. The sharp phase transition for level set percolation of smooth planar Gaussian fields. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques, 56(2):1358 – 1390, 2020.
- [59] A. Nagar, S. N. Majumdar, and M. Barma. Strong clustering of noninteracting, sliding passive scalars driven by fluctuating surfaces. Physical review. E, Statistical, nonlinear, and soft matter physics, 74(2 Pt 1):021124, August 2006.
- [60] A. Nagar, S. N. Majumdar, and M. Barma. Strong clustering of noninteracting, sliding passive scalars driven by fluctuating surfaces. Phys. Rev. E, 74:021124, Aug 2006.
- [61] T. Orenshtein and R. S. dos Santos. Zero-one law for directional transience of one-dimensional random walks in dynamic random environments. Electronic Communications in Probability, 21(none):1 – 11, 2016.
- [62] G. C. Papanicolaou and S. R. S. Varadhan. Diffusions with random coefficients. In Collected papers. Volume II: PDE, SDE, diffusions, random media. Edited by Rajendra Bhatia, Abhay Bhatt and K. R. Parthasarathy, pages 533–538. Berlin: Springer; New Dehli: Hindustan Book Agency, 2012.
- [63] J. Peterson. Lecture notes on random walks in random environments. Notes from a minicourse at IMPA, https://api.semanticscholar.org/CorpusID:124439870, 2013.
- [64] S. Popov and A. Teixeira. Soft local times and decoupling of random interlacements. J. Eur. Math. Soc., 17:2545–2593, 2015. No 10.
- [65] A. Prévost, P.-F. Rodriguez, and P. Sousi. Phase transition for the late points of random walk. Preprint, arXiv:2309.03192, 2023.
- [66] F. Redig and F. Völlering. Random walks in dynamic random environments: A transference principle. The Annals of Probability, 41(5):3157 – 3180, 2013.
- [67] P.-F. Rodriguez and A.-S. Sznitman. Phase transition and level-set percolation for the Gaussian free field. Comm. Math. Phys., 320(2):571–601, 2013.
- [68] M. Salvi and F. Simenhaus. Random Walk on a Perturbation of the Infinitely-Fast Mixing Interchange Process. Journal of Statistical Physics, 171:656 – 678, 2018.
- [69] Y. G. Sinai. The limiting behavior of a one-dimensional random walk in a random medium. Theory of Probability & Its Applications, 27(2):256–268, 1983.
- [70] R. Soares dos Santos. Non-trivial linear bounds for a random walk driven by a simple symmetric exclusion process. Electron. J. Probab., 19:1–18, 2014. Id/No 49.
- [71] F. Solomon. Random Walks in a Random Environment. The Annals of Probability, 3(1):1 – 31, 1975.
- [72] A.-S. Sznitman. Topics in random walks in random environment. School and Conference on Probability Theory, ICTP Lecture Notes, 17:203–266, 2004.
- [73] A.-S. Sznitman. Vacant set of random interlacements and percolation. Annals of Mathematics, 171(3):2039–2087, 2010.
- [74] A.-S. Sznitman. Decoupling inequalities and interlacement percolation on . Invent. Math., 187(3):645–706, 2012.
- [75] A.-S. Sznitman and O. Zeitouni. An invariance principle for isotropic diffusions in random environment. Invent. Math., 164(3):455–567, 2006.
- [76] H. Vanneuville. Sharpness of Bernoulli percolation via couplings. Preprint, arXiv:2201.08223, 2023.
- [77] O. Zeitouni. Random walks in random environment. In Lectures on probability theory and statistics. Ecole d’Eté de probabilités de Saint-Flour XXXI, pages 191–312. Berlin: Springer, 2004.