Simple and high-precision Hamiltonian simulation by compensating Trotter error with linear combination of unitary operations
Abstract
Trotter and linear-combination-of-unitary (LCU) are two popular Hamiltonian simulation methods. The Trotter method is easy to implement and enjoys good system-size dependence endowed by commutator scaling, while the LCU method admits high accuracy simulation with a smaller gate cost. We propose Hamiltonian simulation algorithms using LCU to compensate Trotter error, which enjoy both of their advantages. By adding few gates after the th-order Trotter formula, we realize a better time scaling than 2th-order Trotter. Our first algorithm exponentially improves the accuracy scaling of the th-order Trotter formula. For a generic Hamiltonian, the estimated gate counts of the first algorithm can be 2 orders of magnitude smaller than the best analytical bound of fourth-order Trotter formula. In the second algorithm, we consider the detailed structure of Hamiltonians and construct LCU for Trotter errors with commutator scaling. Consequently, for lattice Hamiltonians, the algorithm enjoys almost linear system-size dependence and quadratically improves the accuracy of the th-order Trotter. For the lattice system, the second algorithm can achieve 3 to 4 orders of magnitude higher accuracy with the same gate costs as the optimal Trotter algorithm. These algorithms provide an easy-to-implement approach to achieve a low-cost and high-precision Hamiltonian simulation.
I INTRODUCTION
Hamiltonian simulation, i.e., to simulate the real-time evolution of a physical Hamiltonian , is considered to be a natural and powerful application of quantum computing Feynman (1982). It can also be used as an important subroutine in many other quantum algorithms like ground-state preparation Abrams and Lloyd (1999); Aspuru-Guzik et al. (2005), optimization problems Farhi et al. (2014); Zhou et al. (2020), and quantum linear solvers Harrow et al. (2009). To pursue real-world applications of Hamiltonian simulation with near-term quantum devices, we need to design feasible algorithms with small space complexity (i.e., qubit number) and time complexity (i.e., circuit depth and gate number).
One of the most natural Hamiltonian simulation methods is based on Trotter formulas Lloyd (1996); Suzuki (1990, 1991); Berry et al. (2007); Campbell (2019); Childs et al. (2019); Childs and Su (2019); Endo et al. (2019); Heyl et al. (2019); Chen et al. (2021); Şahinoğlu and Somma (2021); Su et al. (2021); Tran et al. (2020); Childs et al. (2021); Layden (2021); Zhao et al. (2022), which approximate the real-time evolution of by the product of the simple evolution of its summands . Besides its prominent advantage of simple realization without ancillas, Trotter methods are recently rigorously shown to enjoy commutator scaling Childs and Su (2019); Childs et al. (2021), i.e., the Trotter error is only related to the nested commutators of the Hamiltonian summands . This is very helpful for the Hamiltonians with strong locality constraints. For example, when we consider -qubit lattice Hamiltonians, the gate cost of high-order Trotter methods is almost linear to the system size , which is nearly optimal Childs and Su (2019). The major drawback of the Trotter methods is its polynomial gate cost to the inversed accuracy , . This is unfavorable in many applications where high-precision simulation is demanded to obtain practical advantages over the existing classical algorithms Reiher et al. (2017).
In recent years, we have seen the developments of “post-Trotter” algorithms with exponentially improved accuracy dependence Berry et al. (2014, 2015, 2015); Low and Chuang (2019, 2017); Low (2019). Due to the smart choice of the expansion formulas (i.e., Taylor series Berry et al. (2015) or Jacobi-Anger expansion Low and Chuang (2017)), these post-Trotter methods are able to catch the dominant terms in the time evolution operator with polynomially increasing gate resources, leading to a logarithmic gate-number dependence on the accuracy requirement . Unlike Trotter methods, these advanced algorithms are not able to utilize the specific structure of Hamiltonians due to the lack of commutator-based error form. Consequently, for instance, for -qubit lattice Hamiltonians, their gate complexities are , which is worse than those in Trotter algorithms . Furthermore, these post-Trotter algorithms require the implementation of linear combination of unitary (LCU) formulas Childs and Wiebe (2012); Long (2011) or block encoding of Hamiltonians Low and Chuang (2019) which often costs many ancillary qubits and multicontrolled Toffoli gates. This is still experimentally challenging in a near-term or early fault-tolerant quantum computer Lin and Tong (2022). To reduce the hardware requirement of compiling the LCU formulas, recent studies focus on a random-sampling implementation of a LCU formula Childs and Wiebe (2012); Yang et al. (2021); Wan et al. (2022); Faehrmann et al. (2022), where the elementary unitaries are sampled to realize the LCU formula statistically. In this case, the Hamiltonian simulation is not performed by coherently implementing the unitary , but is instead realized through random sampling. This method remains effective for common applications, such as estimating the properties of the final state. Similar ideas have also been studied in the ground-state preparation algorithms Lin and Tong (2020); Zeng et al. (2021); Zhang et al. (2022).
Here, we propose composite algorithms that combine the inherent advantages of Trotter and LCU methods—easy implementation, high precision, and commutator scaling—by performing the Trotter method and then compensating the Trotter error with the LCU formulas we construct. We primarily focus on the random-sampling implementation of the LCU formula Childs and Wiebe (2012); Yang et al. (2021); Wan et al. (2022); Faehrmann et al. (2022), with the goal of estimating the properties of the target state after real-time evolution. We demonstrate that optimal performance can be achieved by allowing the Trotter circuit to handle the majority of the simulation, with the LCU method completing the remainder.
In Sec. II, we provide a summary of our construction and results, aimed at a general audience. We explain the key ideas behind the constructions with intuitive examples. For readers interested in the technical aspects, we introduce the necessary preliminary knowledge of Hamiltonian simulation in Sec. III to facilitate understanding of the technical results. Next, in Sec. IV and Sec. V, we present a detailed construction and gate complexity analysis of the two Trotter-LCU algorithms. Finally, in Sec. VI, we conclude our discussion and outline possible future directions.
II SUMMARY of RESULTS
II.1 General idea
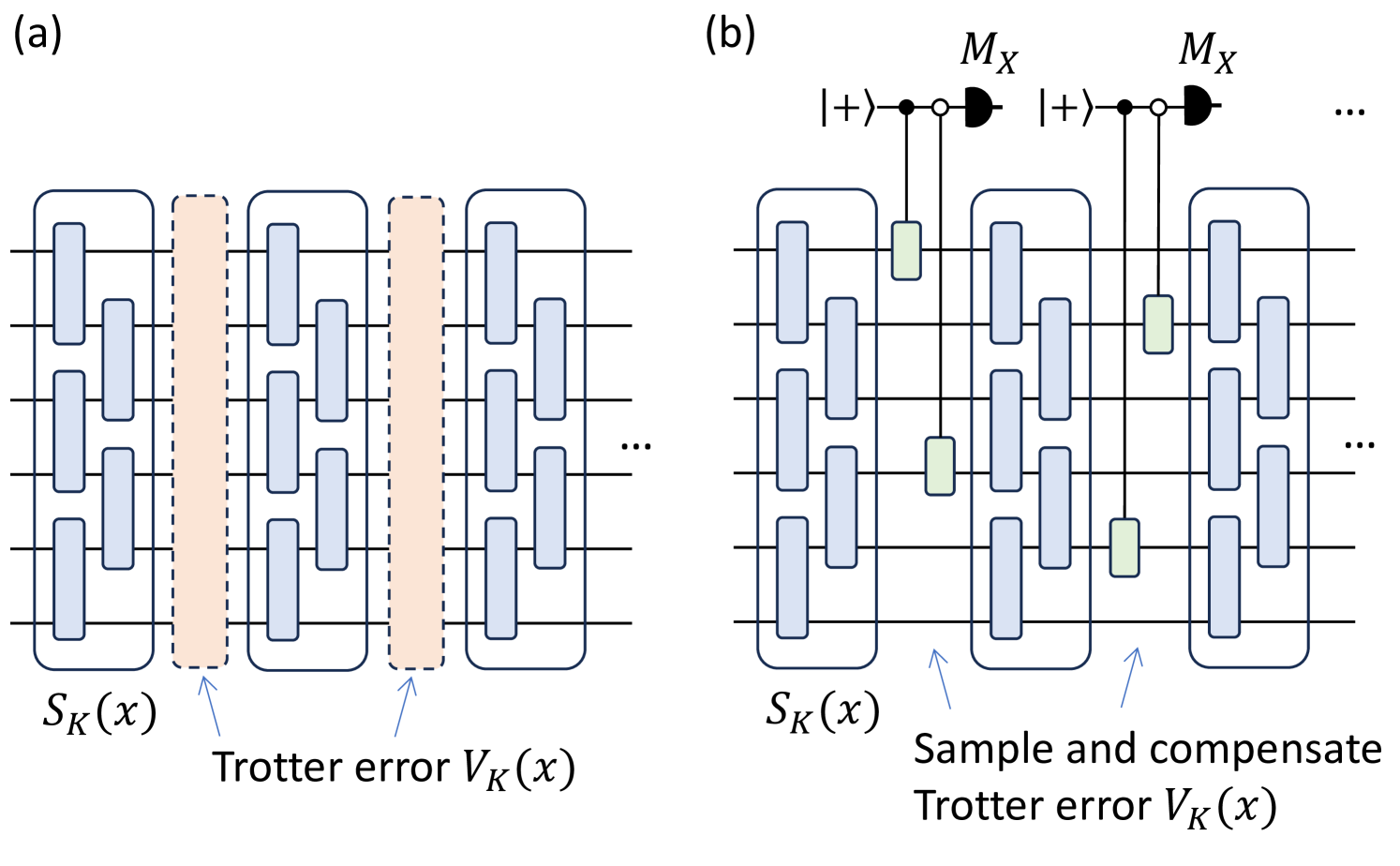
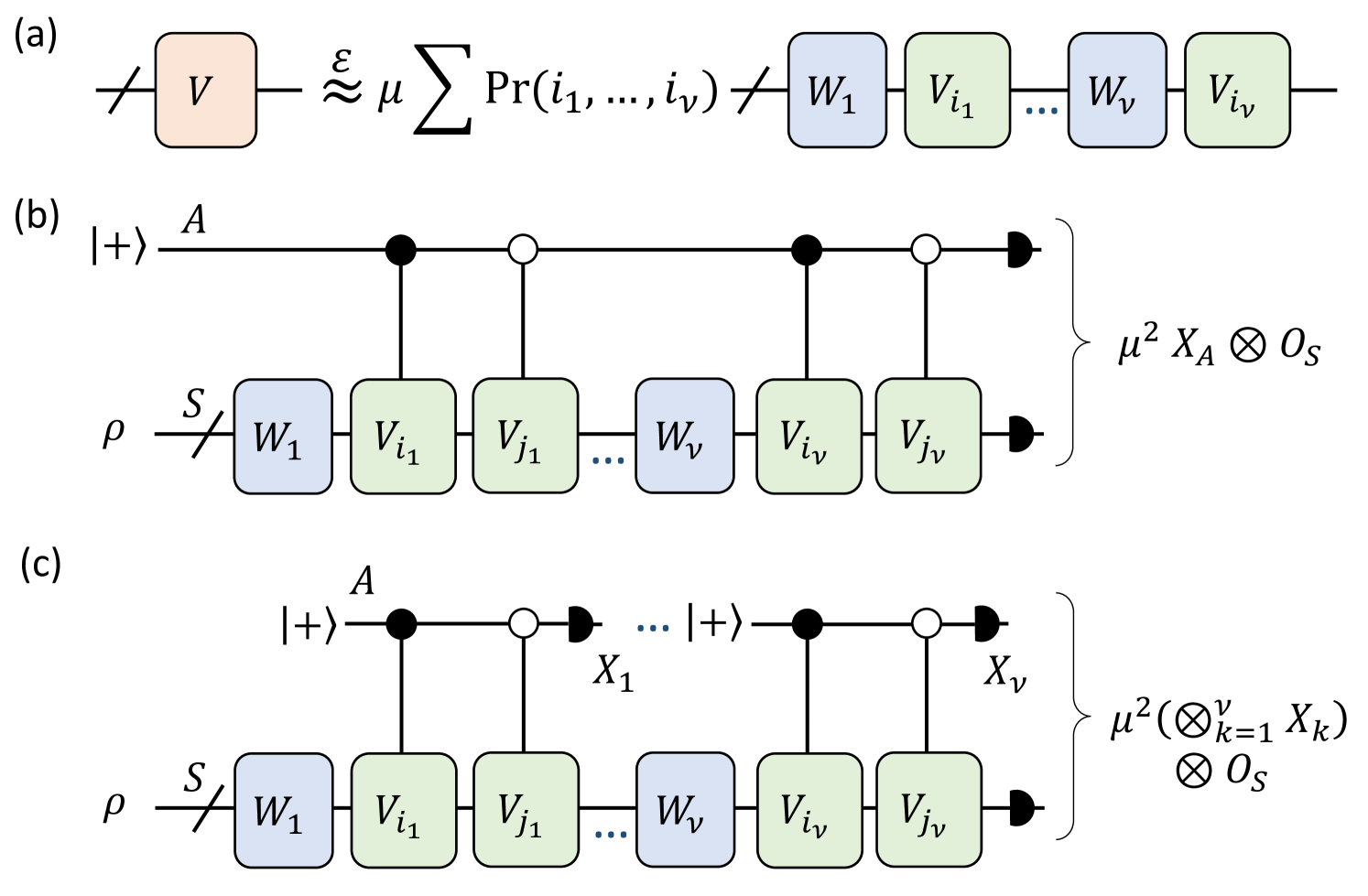
The major idea of the proposed Trotter-LCU algorithm is illustrated in Fig. 1. In a normal th-order Trotter circuit, we decompose the time evolution to segments, each with a small evolution time . For consistency, we denote the th-order Trotter formula as . After we perform the th-order Trotter formula , there will be a remaining Trotter error , which affects the simulation accuracy. To address this problem, we introduce a random LCU formula to compensate the Trotter error using one ancilla and simple gates, which achieves a high-precision Hamiltonian simulation with low cost.
Consider the following LCU formula of an operator ,
| (1) |
such that the spectral norm distance . Here, is the -norm (i.e., -norm) of the coefficient vector, is a probability distribution over different unitaries , and is a set of unitaries. There are usually two ways to implement the LCU formula: the coherent implementation Berry et al. (2014, 2015) and the random-sampling implementation Yang et al. (2021); Wan et al. (2022); Faehrmann et al. (2022). Our major focus is on the random-sampling implementation, where we can estimate the properties of the target state with only one ancillary qubit. In Appendix H, we discuss the potential use of the coherent implementation of our algorithm. In the random-sampling implementation, we can use Eq. 1 to estimate an arbitrary observable value on ,
| (2) |
As is shown in Fig. 2(b), since the estimation of can be implemented using Hadamard-test-type circuits Kitaev (1995), we only need to sample and based on the LCU formula in Eq. 1 to estimate with accuracy using sampling resource, which owns an extra overhead compared to the normal Hamiltonian simulation algorithms Faehrmann et al. (2022). To make the algorithm efficient, we need to set to be a constant. We also provide a variant in Fig. 2(c) where the ancillary qubit is measured and reset in each segment, which is equivalent to Fig. 2(b) for the observable estimation. In this case, the expectation value of provides an unbiased estimation of where is the multiplication of all the ancillary measurement values. This variant reduces the need to store the ancilla qubit, simplifying the implementation on a fault-tolerant quantum computer.
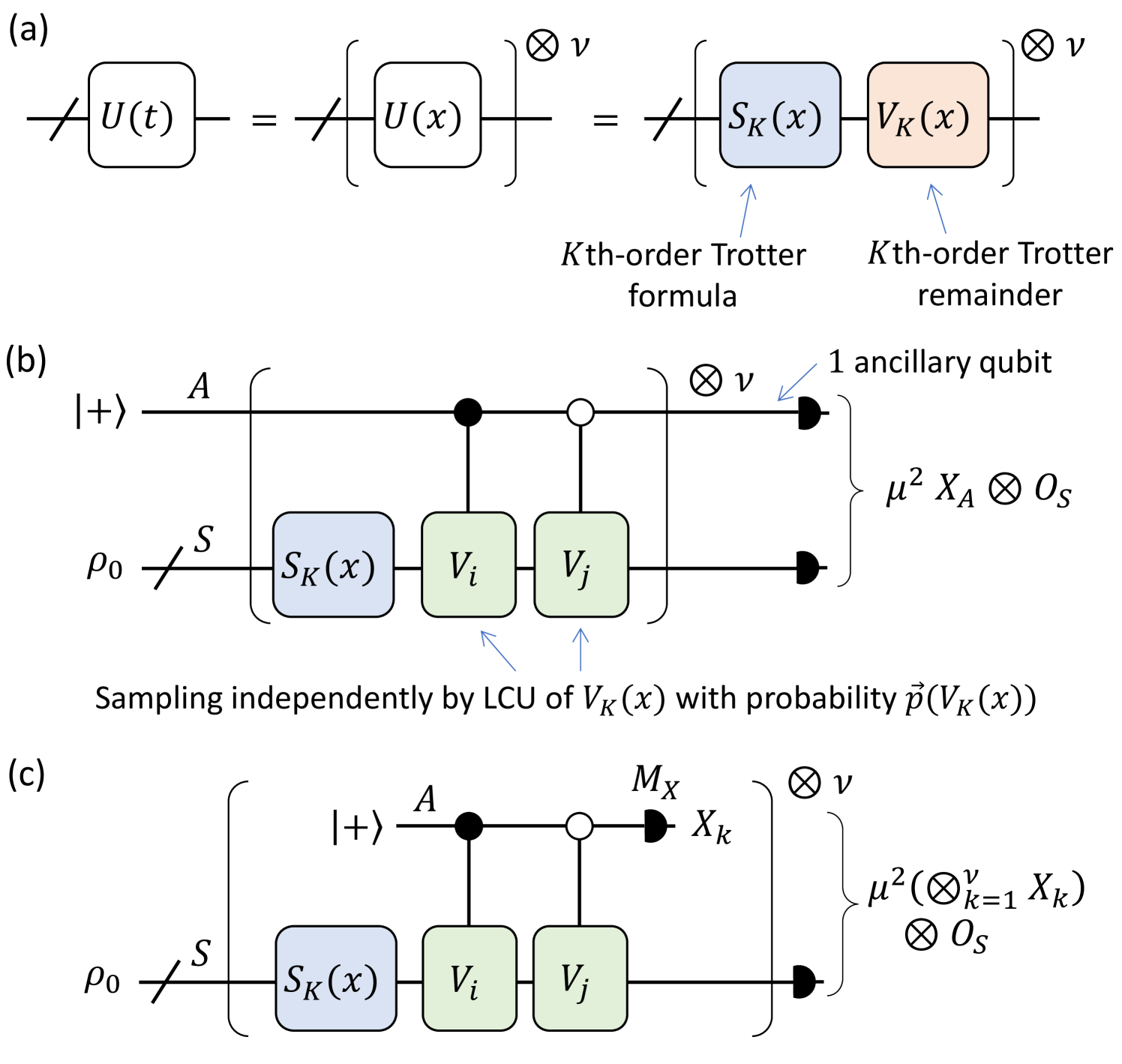
The construction of an appropriate LCU formula for the th-order Trotter remainder, , is crucial for developing an efficient Hamiltonian simulation algorithm. In the following subsections, we briefly introduce two approaches for constructing the LCU formula for . The resulting composite Trotter-LCU algorithms are referred to as paired Taylor-series compensation (PTSC) and nested-commutator compensation (NCC), respectively. Detailed analysis and performance proofs for these two algorithms can be found in Sec. IV and Sec. V.
II.2 Paired Taylor-series compensation: overview
Without loss of generality, we focus on the case of an -qubit Hamiltonian , which can be written as
| (3) |
where are different -qubit Pauli operators. We set all the coefficients to be positive and absorb the signs into Pauli operators . is the -norm of the Hamiltonian coefficient vector. We consider the Hamiltonians where increases polynomially with respect to .
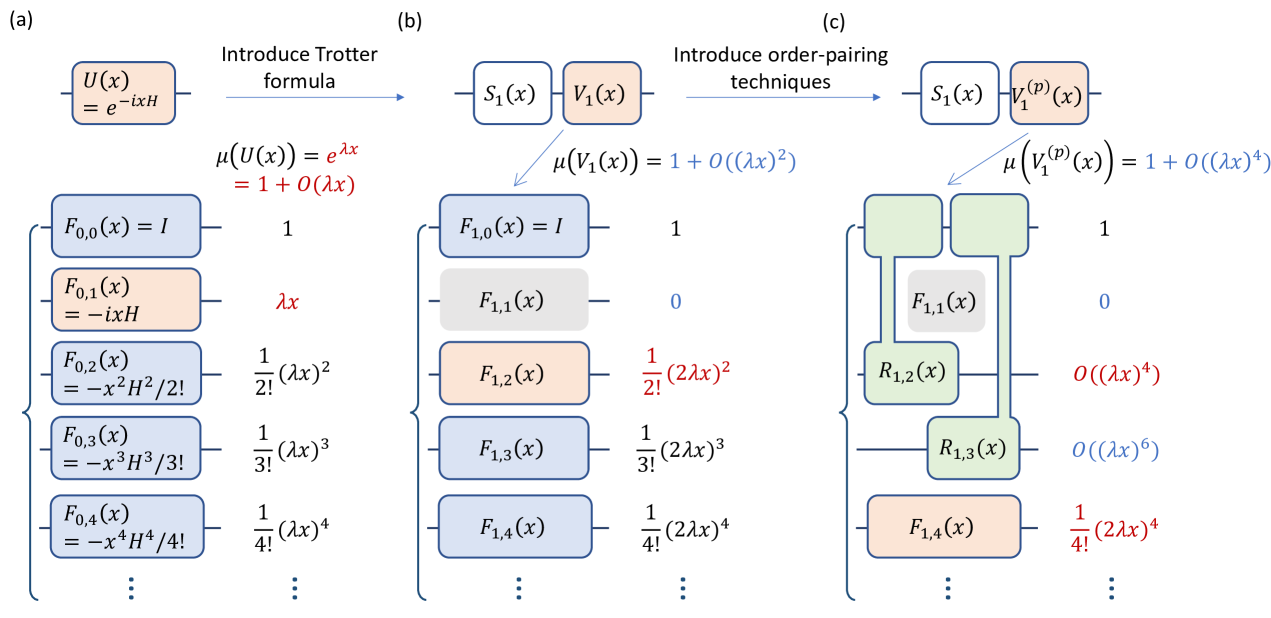
We first consider to construct the LCU formulas for from Taylor-series expansion Berry et al. (2015). In the th-order case, when no Trotter formula is introduced, the Trotter remainder is the short-time evolution itself, which can be expanded as
| (4) | ||||
Here, is the Poisson distribution. denotes the -order expansion term. Eq. 4 illustrated in Fig. 3(a) is a LCU formula of with -norm . The -norm of the overall evolution is then , which, unfortunately, grows exponentially with respect to regardless of how much we increase the segment number . This implies that the direct random-sampling implementation of the LCU formula in Eq. 4 is not feasible. In Ref. Berry et al. (2015), the authors discuss the coherent implementation of instead and find that one can achieve good time and accuracy dependence in that scenario.
When focusing on the random-sampling implementation, we need to suppress the -norm of each segment. To this end, we first consider the usage of the Trotter formula. For example, if we apply first-order Trotter formula in each segment, the first-order remainder can be expanded as
| (5) | ||||
where denotes expansion variables related to the Trotter formula and . denotes the -order expansion term of . The -norm of in Eq. 5 is , which seems to be even larger than the th-order case. However, since denotes the (multiplicative) Trotter error, we have . Using this condition, we can rewrite as
| (6) |
as illustrated in Fig. 3. From the Taylor-series expansion, we can bound the -norm of the new LCU formula in Eq. 6 by . In this way, we reduce from to . The -norm of the overall time evolution becomes . As a result, by increasing the segment number — or equivalently reducing the unit evolution time — we can decrease the 1-norm , leading to a lower sampling cost. If we choose the segment number as , will remain constant.
From the above discussion, it is clear that, to reduce the 1-norm of the overall LCU formula for , our main objective is to suppress the leading-order term of the -norm remainder for each segment, which determines the number of segments and hence circuit depth when is set to be a constant.
We can further reduce the -norm of by taking advantage of the structure of Trotter errors. For an anti-Hermian Pauli operator where , we have the following Euler’s formula,
| (7) |
Here, and we suppose . The 1-norm of the left-hand side of Eq. 7 is , while the 1-norm of the right-hand side is . As a result, the exponent of is effectively doubled. In subsection IV.2, we prove that the expansion terms and in the LCU formula Eq. 5 are anti-Hermitian. As a result, we can further suppress by pairing the terms in with using Euler’s formula in Eq. 7. When , the paired formula as a summation of Pauli rotation unitaries owns the -norm of , whose dependence is doubled, as illustrated inFig. 3(c).
To generalize the discussion, for the th-order Trotter error (, ), we have Suzuki (1990); Childs et al. (2021). Moreover, we can show that , ,…, are anti-Hermitian. We call the term with to the leading-order terms. The algorithm utilizing th-order Trotter formula and the paired idea in the LCU construction is called the th-order PTSC algorithm. We provide the detailed algorithm description and gate-complexity analysis in Sec. IV.
The PTSC algorithm is generic for the -sparse Hamiltonian with and are Pauli matrices. It can be implemented using a simple and universal classical random-sampling procedure: first, we sample the order from the Taylor-series expansion, and then we sample a Pauli string based on the Hamiltonian coefficients. With the random-sampling implementation, we prove that by appending few gates after the th-order Trotter formula with only one ancillary qubit, one can improve the time scaling from to and exponentially improves the accuracy scaling of the th-order Trotter formula compared to the th-order Trotter. We have the following theorem.
Theorem 1 (Informal, see Theorem 1 in Sec. IV) In a th-order paired Taylor-series compensation algorithm ( or , ), the gate complexity in a single round is , where , when or , otherwise.
From Theorem 1, we observe that setting , i.e., not using Trotter formulas, still yields a valid PTSC algorithm by pairing with . In this case, the gate complexity is independent of the sparsity but quadratically dependent on , similar to the algorithm in Ref. Wan et al. (2022). Conversely, when using a th-order Trotter formula, the PTSC algorithm becomes dependent with an almost linear dependence on . In both cases, the PTSC algorithms achieve high simulation accuracy . We expect the th-order algorithm to be particularly useful for quantum chemistry Hamiltonians with large , while higher-order algorithms are better suited for generic -sparse Hamiltonians with long simulation times .
II.3 Nested-commutator compensation: overview
The PTSC algorithms above are generic and applicable to any Hamiltonian. When we consider the detailed structure of Hamiltonians, we could make the compensation algorithms more efficient by taking advantage of the commutation relationship of the terms in the Hamiltonians, which was formerly also studied in the Trotter algorithms Childs et al. (2021).
We will take the first-order Trotter remainder as an illustrative example. Following the Taylor-series expansion in Eq. 5, the second-order term in can be written as
| (8) |
Since is anti-Hermitian, all the Hermitian expansion terms in Eq. 8 will cancel out. We can then simplify as,
| (9) | ||||
which is a summation of commutators. Since the commutators of Hermitian operators are always anti-Hermitian, this implies that the nested-commutator expansion of in Eq. 9 is compact enough since there is no Hermitian expansion terms in it.
For a common physical Hamiltonian with locality constraints, we can take advantage of the commutator-form expression like Eq. 9. For example, for an -qubit lattice Hamiltonian with the form,
| (10) |
where the summand acts on the th and th vertices. We can split the Hamiltonian to two components where , so that the summands commute with each other in each component. We denote the norm of each Hamiltonian summand as
| (11) |
Now, suppose we estimate the -norm of of the lattice Hamiltonian based on Eq. 9, we can see that there are only nonzero terms: for any given Hamiltonian component , only and do not commute with it. Then, the norm of is bounded by
| (12) |
Comparing with the original bound in Eq. 62, , we improve the system-size-related factor . The improved system-size dependence of the 1-norm suggests a corresponding improvement in the system-size dependence of the gate complexity for the nested commutator algorithm.
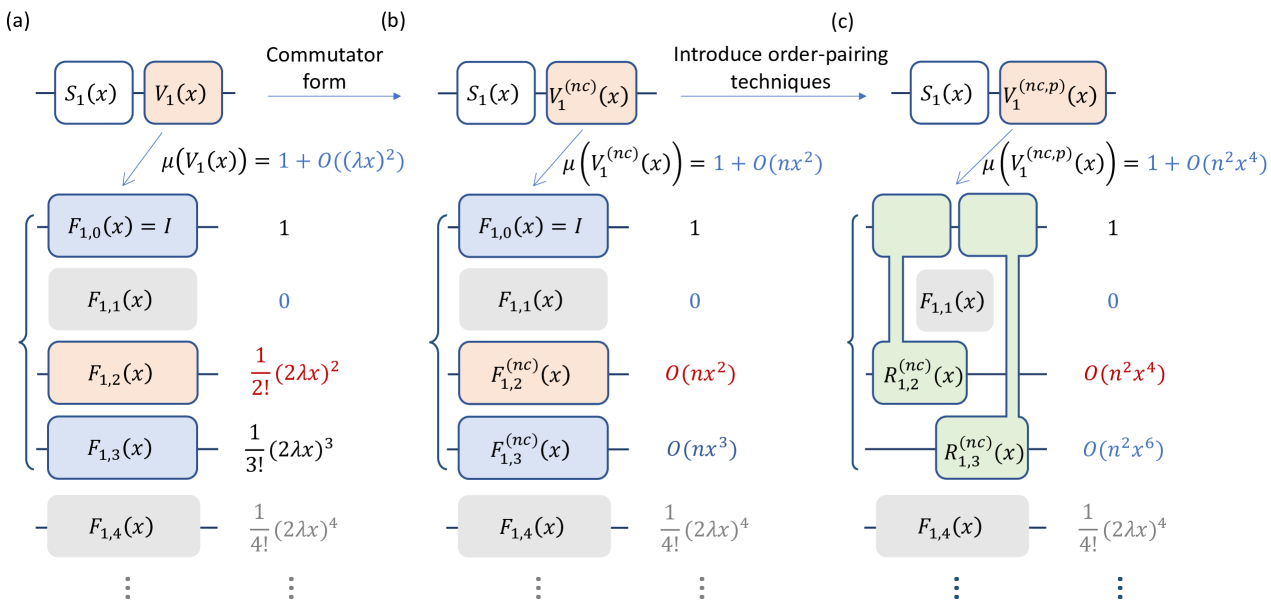
Now, we are going to generalize the idea above. In Sec. V, we show how to expand the second- and third-order terms of as a summation of nested commutators,
| (13) | ||||
where is defined to be
| (14) |
We also use the adjoint notation . It is easy to check that the form of ( or ) in Eq. 13 is anti-Hermitian, which is consistent with the discussion in the paired Taylor-series algorithm in the previous section. We can also generalize the method to the case of th-order Trotter remainder, that is, to express the expansion terms of the th-order Trotter remainder based on the nested commutators.
Based on the nested-commutator expansion, we propose the th-order nested-commutator compensation (NCC) algorithm. As is illustrated in Fig. 4, in the construction of NCC, we first utilize the nested-commutator forms of Trotter error terms from to order, i.e., the leading-order terms; then we apply the order-pairing techniques similar to PTSC in Fig. 3(c) to further suppress the -norm of . A key difference between NCC and PTSC algorithms is that in PTSC algorithms, we compensate the Trotter error up to arbitrary order; while in NCC algorithms, we only compensate for leading-order terms, which shrinks the error from to in one slice with the sampling cost . The gate complexity estimation is then converted to the calculation of the -norm of the commutator . For instance, if we consider the -qubit lattice Hamiltonian models in Eq. 10, then we can prove that . We can then provide the following performance guarantee for the NCC algorithms.
Theorem 2 (Informal, see Theorem 2 in Sec. V) In a th-order nested-commutator compensation (NCC) algorithm ( or ) with -qubit lattice Hamiltonians, the gate complexity in a single round is .
Compared to the performance of th-order Trotter algorithm Childs and Su (2019), we achieve - and -dependence better than th-order Trotter using only th-order Trotter formula with simple compensation gates of Pauli-rotation operators. To generalize the result in Theorem 2, we also study the performance of Nested Commutator (NCC) algorithms when applied to a general Hamiltonian in subsection V.3.
II.4 Efficient random-sampling implementation
A simple implementation of the Trotter-LCU algorithm in Fig. 2(b) or Fig. 2(c) requires not only an easy-to-implement quantum circuit but also efficient classical random sampling of Pauli operators from the Trotter remainder . We now briefly discuss how to realize an efficient classical random sampling in PTSC and NCC algorithms, that is, with a space resource of and time resource of where is the sparsity of the Hamiltonian.
A key idea for achieving efficient sampling is to use a multistage hierarchical sampling algorithm. Rather than fully expanding the Trotter remainder into a direct summation of Pauli operators, we structure the LCU formula into multiple layers. This allowss us to decompose the overall Pauli operator sampling process into a series of simpler, more manageable sampling tasks.
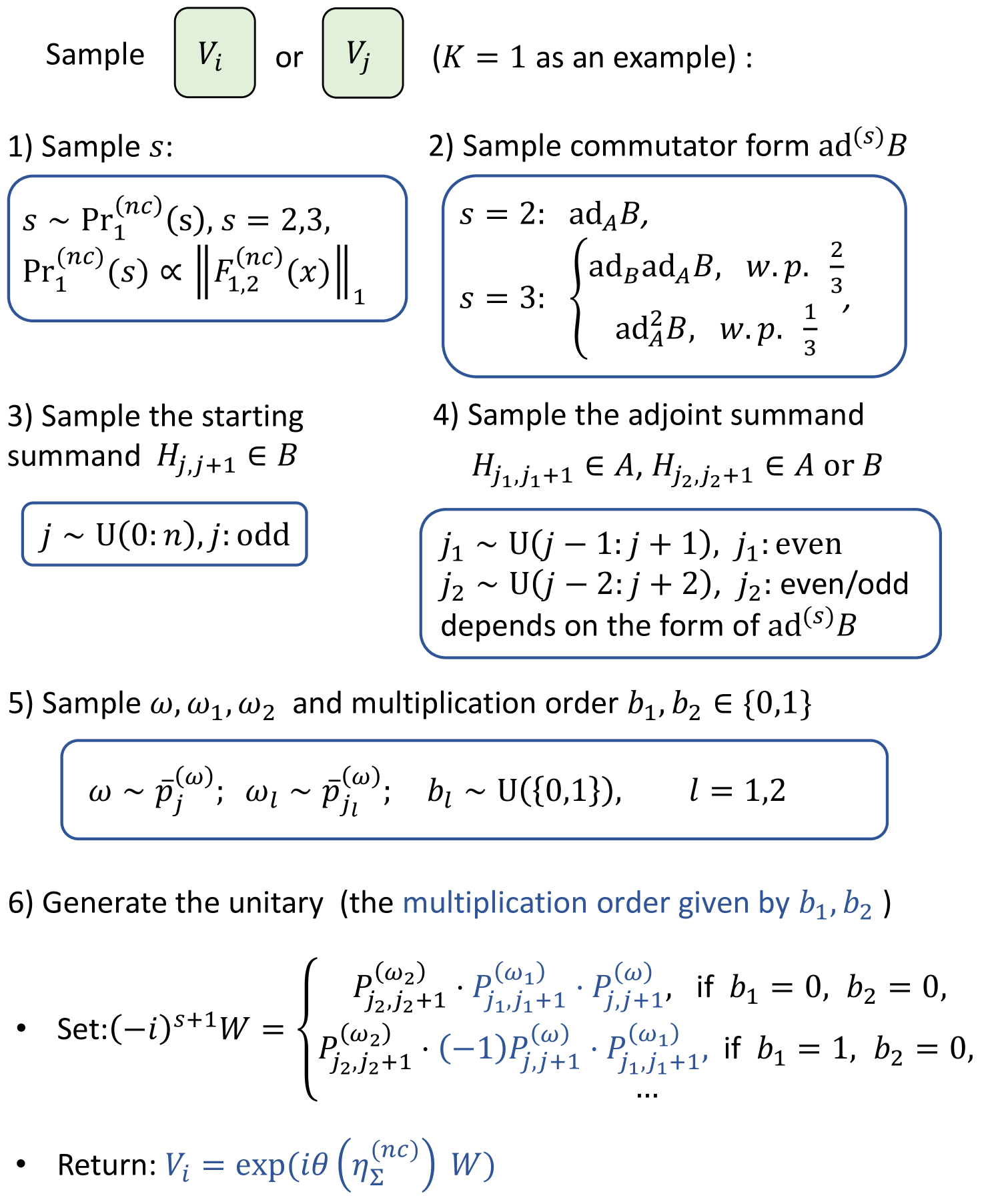
In the PTSC algorithm, the Trotter remainder in Eq. 5 is derived by expanding the time-evolution and each Hamiltonian summand term by Taylor series independently. As a result, the sampling can be done by first sampling the overall expansion order , then sample the individual expansion order of Hamiltonian or the expansion order of the summands . The sampling of and , following the analysis in Sec. IV, can be done based on a multinomial distribution where denotes the normalized coefficient factor of defined in Eq. 3. For the sampled Hamiltonian , we further sample the summands inside based on . We summarize the sampling algorithm in Fig. 5.

In the NCC algorithm, the Trotter remainder is expanded based on the adjoint operators. For example, for the lattice Hamiltonian in Eq. 10, we can write the second- and third-order Trotter remainder of as,
| (15) | ||||
We can first sample the expansion order or . If , we then sample the specific commutator, i.e., or . For the given commutator, for example, , we first randomly sample a summand for the rightmost as the starting point of the adjoint operator. The action of the subsequent and will enlarge the support of , but within a “light-cone” region shown in Fig. 6. We then sample the Hamiltonian summand and for the adjoint operators and , but within the light-cone region. This will ensure our sampling to be efficient and with nested-commutator scaling.
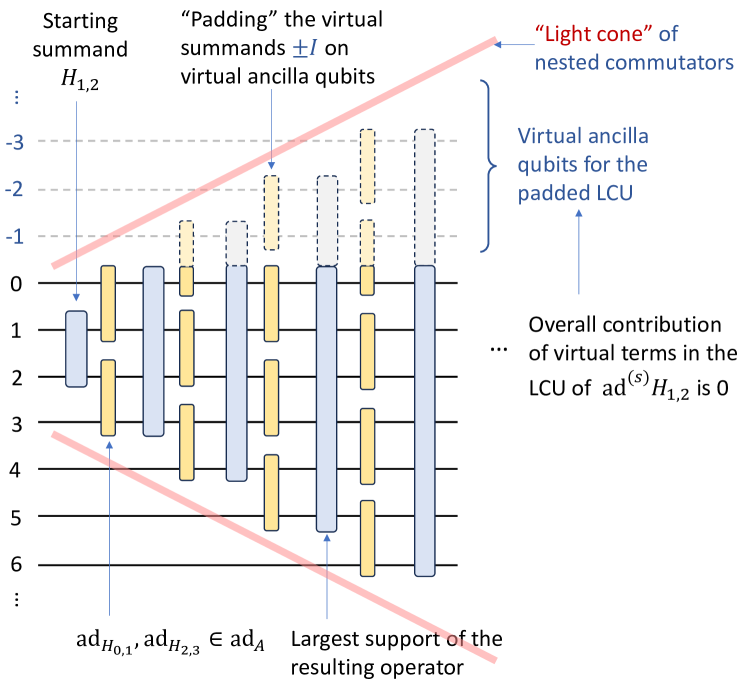
A problem of sampling the Hamiltonian summands in the commutator is that, since the Hamiltonian may be nonhomogeneous, the -norm of with different may be different. This will complicate the sampling algorithm, since we need to first calculate the -norm of all the elementary commutators with the form of
| (16) |
for all and . When the Trotter order and the expansion order gets larger, the number of elementary adjoint operators will increase exponentially. Consequently, we cannot estimate the -norm of all the elementary commutator.
To solve this problem but still keep the advantage of the NCC algorithm, we introduce the following Hamiltonian “padding” technique to ensure all the elementary nested commutator own the same -norm. Consider a Hamiltonian summand , which can be expanded to some Pauli operators,
| (17) |
where is a positive number and is a normalized Pauli operator whose support is on qubit and . Recall that and . When is smaller than , we add extra trivial terms in the Pauli decomposition of ,
| (18) | ||||
where . Eq. 18 holds naturally, but now with a manually predetermined -norm value . Similarly, we can pad all the elementary commutators with the form
| (19) |
so that their -norms are all . In this way, we ignore the commutator relationship between and as long as they are in the light-cone region.
After the padding procedure described above, all elementary nested commutators of the same order will have the same -norm. This property allows us to uniformly sample these commutators: the starting summand is sampled uniformly from those in , and the subsequent and are sampled uniformly within the light-cone region. However, when the starting summand is near the boundary, applying a few adjoint operators may cause it to touch the boundary. This reduces the number of possible elementary nested commutators compared to those starting from the center, resulting in different -norms for depending on . This complicates the sampling of the starting summand . To resolve this issue and ensure uniform sampling of , we introduce virtual qubits at the boundary, as illustrated in Fig. 6, and pad the virtual qubits with -summed terms. Since we only perform operation on the virtual qubits, we do not need to introduce it in the real experiments.
We remark that, our padding method preserve the locality structure. As a result, the performance guarantee in Theorem 2 still holds. We summarize the sampling algorithm in Fig. 7. If we consider the Heisenberg Hamiltonian
| (20) |
as an example, where is the vector of Pauli operators on the th qubit, we can define the summand to be
| (21) |
In this case, . The probability distribution in Fig. 7 is to uniformly sample the , , and term. As a demonstration, we explicitly present the algorithm to sample the Pauli-rotation operator in the first-order NCC algortihm for the Heisenberg Hamiltonian in Eq. 20 in Algorithm 1.
As a final remark, the sampling procedure in both PTSC and NCC algorithms are independent of the implementation of the quantum circuit and the measurement outcome. Thanks to this property, we can perform the classical sampling during the quantum circuit implementation or even generate the sampled Pauli matrices before the implementation of the quantum circuits.
II.5 Performance comparison
In Table 1, we compare the implementation complexity and the gate complexity in a single round of experiment of the th-order PTSC, th-order PTSC, and th-order NCC algorithms to previous Hamiltonian simulation algorithms. For a fair comparison, we set the 1-norm of all LCU formulas to be constant. In this case, the sample complexity of PTSC and NCC algorithms incurs a overhead compared to standard sampling from the th-order Trotter or post-Trotter algorithms.
We show that by inserting a few randomly sampled Pauli-rotation gates after each Trotter segment, as illustrated in Fig. 1, both PTSC and NCC achieve improved accuracy and time dependence. The gate counts for PTSC exhibit logarithmic dependence on accuracy, , while the NCC gate counts show improved system-size dependence.
| Algorithm | Implementation hardness | Accuracy | Size scaling (lattice Hamiltonian) | Time dependence |
| th-order Trotter Suzuki (1990) | Easy | |||
| Post-Trotter Berry et al. (2015); Low and Chuang (2019) | Hard | |||
| th-order PTSC | Easy | |||
| th-order PTSC | Easy | |||
| th-order NCC | Easy |
To demonstrate how the Trotter-LCU algorithms can help reduce gate costs in practical scenarios, we estimate the single-shot gate count of random-sampling Trotter-LCU algorithms and compare it with the state-of-the-art Trotter algorithm, i.e., fourth-order Trotter Suzuki (1991); Childs et al. (2019, 2021). To ensure a fair comparison, we set -norm of the LCU formula to be . Based on Proposition 1, this implies that the random-sampling Trotter-LCU algorithm will require an additional factor of in the sample number to estimate the properties of the target state where to a given precision compared to the normal Trotter or coherent implementation of LCU algorithms.
We compile their quantum circuits to gates, single-qubit Clifford gates, and single-qubit -axis rotation gates . Here, we mainly compare the number of gates since they are the most resource-consuming part on a fault-tolerant quantum computer Litinski (2019). The gate-number comparison results can be found in Appendix G, which is similar to the gate comparison. We also compare the gate counts of the Trotter-LCU algorithms to the coherent-implementation of LCU Berry et al. (2014, 2015) and QSP Low and Chuang (2017, 2019) in Appendix G.
In the first comparison, we consider the simulation of generic Hamiltonians without the usage of commutator information, for which we choose the -local Hamiltonian, where and are the Pauli matrices on the th qubit. Fig. 8(a,b) show the gate counts for the fourth-order Trotter formula and the PTSC Trotter-LCU algorithms with different orders with an increasing time and increasing system size , respectively. The gate counting method for fourth-order Trotter with random permutation is based on the analytical bounds in Ref. Childs et al. (2019).
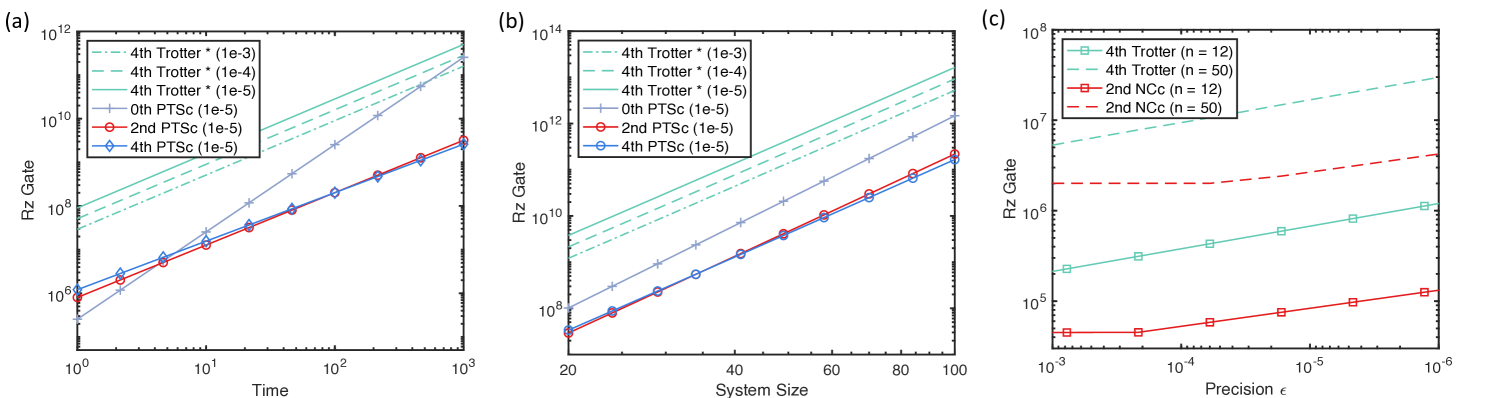
From Fig. 8(a,b), we can clearly see the advantage of composition of Trotter and LCU formulas: if we do not use LCU and merely apply Trotter formulas, the gate resource of fourth-order Trotter suffers from a large overhead that is 2 orders of magnitudes larger than the PTSC algorithms. Moreover, if we increase from to , we can see a clear increase of the gate resources for the Trotter algorithm. For the PTSC algorithms, however, the gate number is almost not affected by since they enjoy a logarithmic -dependence.
On the other hand, if we do not use Trotter formula, the th-order PTSC algorithm owns a quadratically worse -dependence () than the fourth-order Trotter (), second-order PTSC () and fourth-order PTSC () algorithms in Fig. 8(a). For a short-time evolution , the system-size dependence of second- or fourth-order PTSC in Fig. 8(b) outperforms th-order PTSC algorithm. In the case when long-time Hamiltonian simulation is required, for example, should be set to for the phase estimation Campbell (2019), the advantage of nd or fourth-order PTSC to th-order PTSC will be more obvious. The composition of Trotter and LCU formulas enables nd or fourth-order PTSC to enjoy good and dependence and small gate-resource overhead simultaneously.
Next, we compare the gate count when simulating the lattice models, where the commutator analysis will help remarkably reduce the gate count. We consider the Heisenberg Hamiltonian using the nested-commutator bounds. In Fig. 8(c), we choose and and show the gate number with respect to the accuracy requirement . The fourth-order Trotter error analysis is based on the nested-commutator bound (Proposition M.1 in Ref. Childs et al. (2021)), which is currently the tightest Trotter error analysis. The performance of our second-order NCC algorithm is based on the analytical bound in Sec. H in the Appendix. We mainly present results for the second-order NCC algorithm due to its simplicity and leave precise higher-order NCC gate count analysis for future study.
From Fig. 8(c), we can see that, while enjoying near-optimal system-size scaling similar to the fourth-order Trotter algorithm which is currently the best one for lattice Hamiltonians Childs et al. (2021); Childs and Su (2019), the second-order NCC algorithm shows better accuracy dependence than fourth-order Trotter algorithm. Particularly, using the same gate number as the fourth-order Trotter, we are able to achieve a 3 to 4 orders of magnitudes higher accuracy .
III PRELIMINARIES
In this section, we review the Hamiltonian simulation algorithms based on Trotter and LCU formulas.
In all the Hamiltonian simulation algorithms discussed in this work, we divide the real-time evolution into segments,
| (22) |
with , and consider the construction of each small segment . Without loss of generality, we assume .
III.1 Trotter formulas
The most natural way to approximate is to apply the Lie-Trotter-Suzuki formulas Suzuki (1990, 1991). Hereafter, we refer to them as Trotter formulas. The first-order Trotter formula is
| (23) |
Here, . In Eq. 23, we simplify the notation of the sequential products from to with the same form, using the arrow to denote the ascending direction of the dummy index . The Hermitian conjugation of can similarly be written as .
The second-order Trotter formula is
| (24) | ||||
where . We have .
The general th-order Trotter formula is Suzuki (1991)
| (25) | ||||
with for . The operator is defined recursively,
| (26) |
We also denote the zeroth-order Trotter formula to be for consistency. We denote the multiplicative remainder of the Trotter formulas as
| (27) |
for . In what follows, we name this Trotter error term as the th-order Trotter remainder to avoid ambiguity to other error effects such as truncation error.
In Ref. Suzuki (1990), Suzuki proves the following order condition for the Trotter formulas,
| (28) |
for or even positive . As a result, the remainder will only contain the terms of with . We will use the following order condition of Trotter formulas in the later discussion.
Lemma 1 (Order condition of Trotter formulas, Theorem 4 in Childs et al. (2021)).
III.2 LCU formulas
Instead of decomposing as a product of elementary unitaries, another way is to decompose to a summation of elementary unitaries. We now provide a formal definition of a LCU formula.
Definition 1 (Childs and Wiebe (2012)).
A (LCU) formula of an operator is defined to be
| (29) |
such that the spectral norm distance . Here, is the -norm of the coefficient vector, is a probability distribution over different unitaries , and is a set of unitaries. Here, we assume for all and absorb the phase into the unitaries . We call the -norm of this -LCU formula.
In what follows, we define the -norm of an operator to be its smallest -norm over all possible -LCU formulas for . Note that, for any unitary . One can easily check the validity of this norm definition.
We may consider two ways to implement the LCU formula of the operator . In the first way, we coherently implement the LCU formula by introducing an ancillary system with the dimension which costs qubits. For the LCU lemma defined in Eq. 29, we define the amplitude-encoding unitary and the select gate to be,
| (30) | ||||
Then, the following controlled-gate acting on ancillary and system defines a way to realize LCU coherently when we prepare on and measure it on computational basis to get ,
| (31) |
More precisely, if we set the initial state on to be , then we have
| (32) |
where is a state whose ancillary state is supported in the subspace orthogonal to .
If we perform computation-basis measurement directly on , the successful probability to obtain is . To boost the successful probability to nearly deterministic, we can introduce the amplitude amplification techniques Berry et al. (2014). To this end, we consider the following isometry
| (33) |
Here, is a reflection over on the system ,
| (34) |
Consider the case of and is small for the LCU formula. If is a unitary, then we have . For a general , we can verify the resulting operator
| (35) |
is close to with the spectral norm distance bound . Also, the successful probability to project the ancilla to is larger than .
In the second way to implement the LCU formula, we randomly sample the terms in Eq. 29 based on the probability Childs and Wiebe (2012). This way saves the ancillary qubit number and the cost to implement the multiqubit Toffoli gates in and in Eq. 30, which is more suitable to implement in the near-term devices. Instead of implementing the operator directly, we now focus on the task to estimate the properties of the target state where is the initial state of the Hamiltonian simulation task. Suppose we want to estimate expectation value of a given observable on , we can then embed the task to Hadamard test Kitaev (1995) shown in Fig. 9.
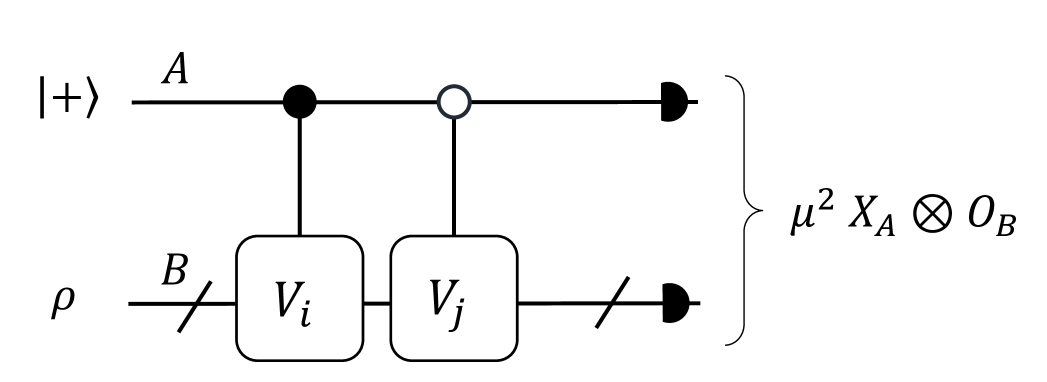
We first prepare a state on a single ancillary qubit. After that, we implement two controlled operations and where and are sampled independently from the LCU formula in Eq. 29. The measured expectation value of is then a nearly unbiased estimation of . We will use the following performance guarantee for the observable estimation.
Proposition 1 (Performance of the random-sampling LCU implementation, Theorem 2 from Faehrmann et al. (2022)).
For a target operator and its -LCU formula defined in Definition 1, if we estimate the value with an initial state and observable using the circuit in Fig. 9 for times, then the distance between the mean estimator value and the true value is bounded by
| (36) |
with successful probability . Here, , is the spectral norm of .
From Proposition 1 we can see that, the -norm of the LCU formula affects the sample complexity while the accuracy factor introduces extra bias in the observable estimation. To estimate using Hadamard-test-type circuits with accuracy, we need sampling resource, which owns an extra overhead compared to the normal Hamiltonian simulation algorithms Faehrmann et al. (2022). To make the algorithm efficient, we need to set to be a constant.
In the later discussion, we will construct new LCU formulas from the product of LCU formulas. We will use following proposition.
Proposition 2 (Product of LCU formulas).
Suppose we have a -LCU formula for an operator with the form of Eq. 29. Then the product formula
| (37) |
is a -LCU formula for with
| (38) |
Proof.
The -norm is obvious. We now bound the distance between and .
| (39) | ||||
∎
We remark that, when there are common unitary components for all in the LCU formula Eq. 29, we can simplify the circuit in Fig. 9 by removing the ancillary control on the common unitary components. Suppose we have the following LCU formula for an operator ,
| (40) |
such that , where are some fixed unitaries. Then according to Definition 1, Eq. 40 is a -LCU formula of with the elementary unitaries to be for . Instead of naively apply the Hadamard test circuit in Fig. 9, we can introduce an equivalent circuit implementation shown in Fig. 10(b). The performance guarantee in Proposition 1 also holds for the improved implementation.
Furthermore, we notice that can be written as,
| (41) |
where and for . As a result, we can implement each channel by a unitary and each map by a Hadamard-test-type circuit. This leads to a variant circuit shown in Fig. 10(c), where the ancillary qubit is measured and reset for every segment. While this circuit owns the same gate complexity as Fig. 10(b), it is beneficial in a fault-tolerant quantum computer since we do not need to store the ancillary qubit for a long time-the ancillary qubit is activated only in the compensation stage and is quickly measured.
IV Trotter-LCU algorithms with paired Taylor-series compensation
In this section, we construct a -LCU formula for the remainder of the -th order Trotter formula based on the idea to perform Taylor-series (TS) expansion on all the exponential terms in . Although TS expansion is naturally a LCU formula of , it usually owns poor performance. To further suppress the -norm of the expansion, we will modify the introduce a “pairing” idea to combine the terms that correspond to different TS expansion orders. We first consider a simple case without Trotter formula in subsection IV.1 to illustrate the major idea to construct TS-based LCU formula. Then we take the construction of LCU for the first-order Trotter formula as an example in subsection IV.2. Finally, in subsection IV.3, we discuss the random-sampling implementation of the algorithm and analyze its sample and gate complexity.
IV.1 Zeroth-order case
We begin our discussion from the case where the Trotter formula is trivial, i.e., for each segment. In this case, the Trotter remainder is . To construct LCU formula, we expand by Taylor series Berry et al. (2015),
| (42) | ||||
where
| (43) |
The -norm of is
| (44) |
That is, the -norm of is exponentially large with respect to . Suppose we use directly for the random-sampling implementation of LCU following Fig. 2(b), the composite LCU formula for is the product of . Based on Proposition 2, the -norm of the product formula is , which increases exponentially with the simulation time . Based on Proposition 1, this implies an exponentially increasing sample cost . To make the TS expansion practical for the random-sampling implementation, we need to reduce -norm of .
When is a small value, the major contribution to comes from the low-order terms of . Note that the first-order term is anti-Hermitian. This allows us to utilize the following Euler’s formula on Pauli operators: for a Pauli matrix and ,
| (45) |
where .
To suppress , we rewrite as follows:
| (46) | ||||
Then, we can apply Eq. 45 on Eq. 46 to convert the first-order term to Pauli rotation unitaries
| (47) |
where . We call the formula in Eq. 47 the th-order PTS formula.
In practice, to avoid the sampling in the infinitely large space, we introduce a truncation to the expansion order of . After this truncation, the approximated LCU formula of is
| (48) | ||||
where
| (49) | ||||
After “pairing” the terms with and , we obtain Eq. 48 which is a new LCU formula with the -norm . We have the following proposition to characterize the LCU formula in Eq. 48.
Proposition 3 (0th-order Trotter-LCU formula by paired Taylor-series compensation).
For and , in Eq. 48 is a -LCU formula of with
| (50) |
Proof.
For the normalization factor, we have
| (51) | |||
The fourth inequality is due to for .
From Proposition 3 we see that, the -norm of the LCU formula in Eq. 47 is , whose leading term is quadratically smaller than the one of when . We will later see that provides us an efficient random-sampling implementation of the Trotter-LCU algorithm.
IV.2 First-order case
Following similar ideas in subsection IV.1, we now study the PTS compensation of the Trotter remainder . We will take first-order case as an example. The Trotter remainder is
| (55) |
From Eq. 23 and Eq. 42 we have
| (56) | ||||
Here, we adopt the vector notations introduced in subsection III.1 to simplify the expressions. In Eq. 56, we also extend the notation of Poisson distribution,
| (57) |
Based on Eq. 56, we then write the Taylor-series expansion of first-order remainder as follows:
| (58) | ||||
which is a LCU formula with -norm . Here, and are two groups of independent variables.
Now, we utilize the order condition of the Trotter formula in Lemma 1 to reduce -norm of Eq. 58. To this end, we first rewrite Eq. 58 by classifying the terms based on the power of , which is determined by the value ,
| (59) |
Here, is the -norm of the -order expansion formula . denotes the normalized LCU formula for the -order terms. We have
| (60) | ||||
In the expression of , we use . The conditional probability indicates the probability to sample and when their summation is given,
| (61) | ||||
which is a multinomial distribution with trials and outcomes. In each trial, the outcomes occur with the corresponding probability . Recall that is the normalized Hamiltonian coefficients defined in Eq. 3.
We first estimate the normalization cost for different orders,
| (62) | ||||
In the second inequality, we use the following equation
| (63) |
We denote , which will be frequently used in the following discussion.
From Eq. 62 we can see that, similar to the expansion of , the -norm of the expansion terms with different orders of in follow the Possion distribution. This motivates us to eliminate the low-order terms such as . Based on Lemma 1, we have
| (64) |
As a result, we can directly remove the term in Eq. 59. The resulting formula is,
| (65) |
After the elimination of the first-order term, we now introduce Euler’s formula to suppress higher-order terms in and . For the convenience of later discussion, we simplify the notation of in Eq. 60 as follows:
| (66) |
where is used to denote all the expansion variables besides . and are then defined to be
| (67) | ||||
To apply Euler’s formula in Eq. 45 to Eq. 65, we need to make sure that the Pauli operator is Hermitian. To this end, we classify the Pauli terms of in Eq. 66 into Hermitian and anti-Hermitian types,
| (68) | ||||
where and , respectively, indicates the set of such that is Hermitian and anti-Hermitian. When , the corresponding Pauli operator owns a real coefficient, which cannot be paired with based on Euler’s formula.
It seems that we cannot eliminate the Hermitian terms in Eq. 68 by Euler’s formula. However, by taking advantage of the properties of Trotter remainder , we can show that and are actually anti-Hermitian. Recall that we can write the exponential form of by applying the BCH formula on the definition of in Eq. 27,
| (69) |
where are some Hermitian operators determined by the BCH formula. The first order term vanishes due to the order condition in Lemma 2.
Lemma 2 (Lemma 1 in Childs and Su (2019)).
Let be an operator-valued function that is infinitely differentiable. Let be a non-negative integer. The following two conditions are equivalent.
-
1.
Asymptotic scaling: .
-
2.
Derivative condition: .
Comparing Eq. 68 and Eq. 70, we can see that
| (71) |
This is because and are anti-Hermitian from Eq. 70.
We can then modify the form of ( or ) in Eq. 68 as follows:
| (72) | ||||
In Eq. 72, we intentionally add an extra phase on the Hermitian terms, which has no effect on as they own zero summation value. In this way, all the Pauli expansion terms in and are with imaginary coefficient, which can be paired with using Euler’s formula in Eq. 45. We call the second- and third-order terms the leading TS expansion orders of . The major reason to the Hermitian terms with zero summation value is to simplify the sampling procedure of , which will be clarified later.
Now, we are going to eliminate the leading-order terms in ,
| (73) | ||||
Here, the Pauli operator for the leading-order term is always with a real coefficient. We can then pair with the Pauli operators in and ,
| (74) | ||||
Here, . The third line of Eq. 74 is the final LCU formula used for the first-order PTSC algorithm. In the third line, we apply the following pairing procedure,
| (75) | ||||
In practice, we introduce a truncation on the expansion formula in Eq. 74. For the convenience of analysis, we set . The truncated LCU formula for is then
| (76) |
with the -norm and probabilities to sample the -order term
| (77) | ||||
Combined with the deterministic first-order Trotter formula, the overall LCU formula for is
| (78) |
The following proposition gives the performance characterization of in Eq. 78 to approximate .
Proposition 4 (first-order Trotter-LCU formula by paired Taylor-series compensation).
Proof.
We first bound the normalization factor . When we have
| (80) | |||
From Proposition 4 we have shown that, by introducing first-order Trotter formula, we can further suppress the 1-norm of the LCU formula to where is a constant. In Appendix A, we discuss the generalized LCU formula construction of higher-order Trotter remainder with . Under such constructions, we have,
| (82) |
In subsection IV.3 we will see how this can help us to improve the time scaling of the whole simulation algorithm.
IV.3 Random-sampling implementation and performance
We have now derived the LCU formulas for Trotter remainders and hence the small time evolution based on the idea to utilize the Trotter order condition and pair the leading-order terms in to suppress the normalization factors. We now discuss the practical random-sampling implementation of them, taking the first-order case as an example.
Suppose we want to perform Hamiltonian evolution on an initial state . As is illustrated in Fig. 2, in each segment, we first implement the Trotter circuit and then compensate the remainder by LCU. In the random-sampling implementation of LCU, we embed the LCU sampling into a modified Hadamard test. In Fig. 5, we show the detailed sampling procedure of and . In stage 1), we sample the Taylor-expansion order from a finite probability distribution . Afterwards, in stage 2) and 3), we randomly sample Pauli string indices and based on the LCU formula of . The variables obey a multinomial distribution defined in Eq. 61 while are sampled identically and independently from normalized Hamiltonian coefficients defined in Eq. 3. Finally, in stage 4), depending on whether is the leading-order ( for ) or not, we determine the sampled unitary to be a Pauli-rotation unitary or just Pauli operators .
For the gate complexity of the random-sampling implementation, we have the following theorem.
Theorem 1 (Gate complexity of the th-order random-sampling Trotter-LCU algorithm by paired Taylor-series compensation).
To realize a (probabilistic) Hamiltonian simulation of with accuracy , the gate complexity of random-sampling th-order Trotter-LCU algorithm ( or ) based on paired Taylor-series compensation is
| (83) |
Here, if or , or if .
Proof.
Without loss of generality, we focus on the case when . The case of and can be analyzed similarly following Proposition 3 and Proposition 10, respectively.
For the random-sampling implementation, the overall LCU formula for is to repeat the sampling of for times, . Using Proposition 2 and Proposition 4, when and , we conclude that is a -LCU formula of with
| (84) | ||||
Here, .
To realize a -LCU formula for , we only need to set the segment number and the truncation order to satisfy
| (85) | ||||
we can then realize a -LCU formula for based on segments of in Eq. 78. Here, . is the principle branch of the Lambert function whose scaling is approximately according to the tight bound in Lemma 7 in Appendix F. To derive the bound for in the second line of Eq. 85, we use Lemma 6 in Appendix F.
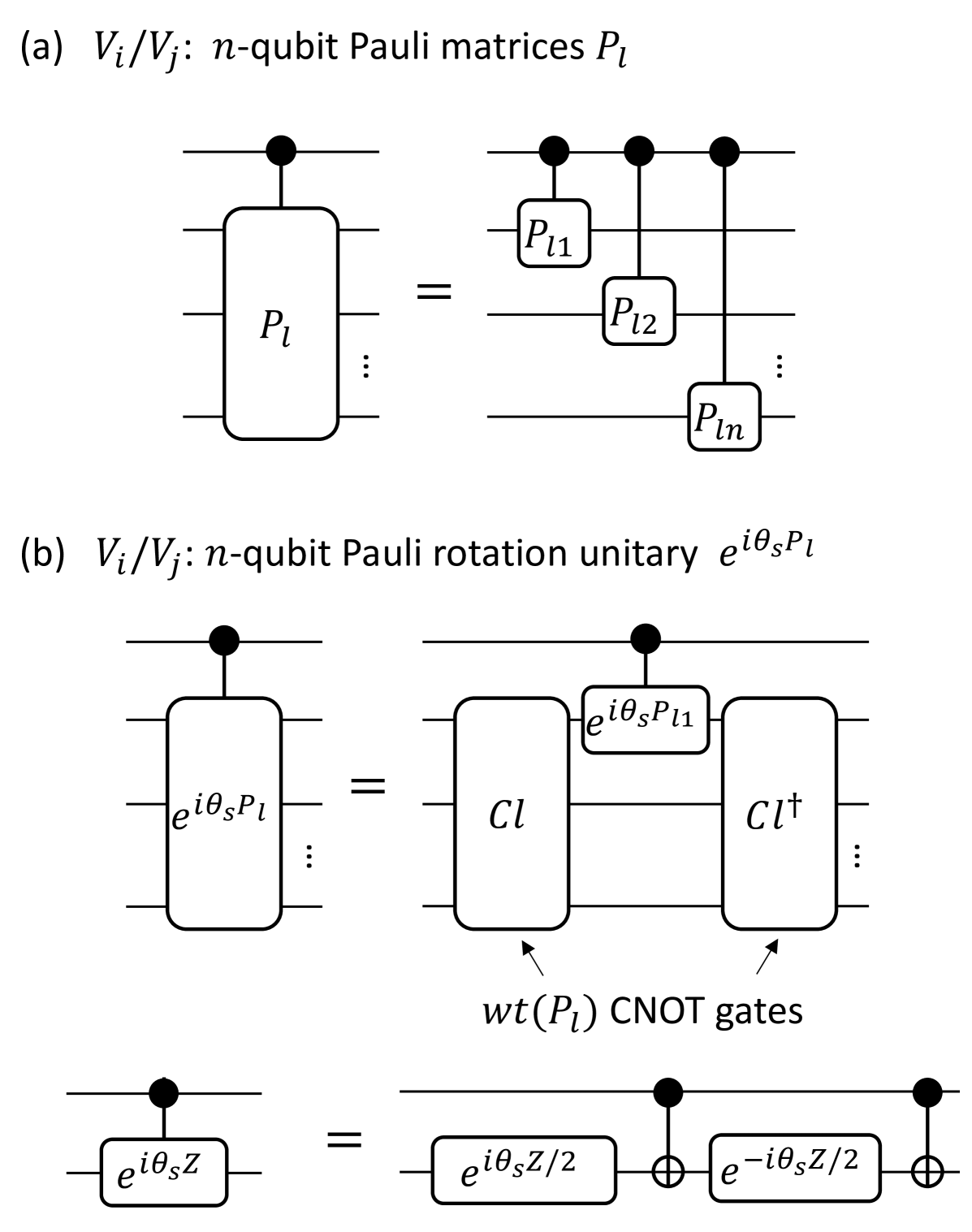
The gate complexity of the random-sampling implementation of the Trotter-LCU algorithm is determined by the segment number , Trotter order and the gate complexity of each elementary gate in the LCU formula. As shown in Fig. 5, to construct controlled-, we split it to segments. In each segment, we need to implement th-order Trotter circuits and LCU circuits. The gate complexity of each elementary gate in the LCU circuit is determined by the truncation order of the Taylor-series compensation. Specifically, we consider the compilation of the controlled-Pauli gate and controlled-Pauli rotation gate, as shown in Fig. 11. The number of gates is determined by the weight of the sampled Pauli matrices , which is upper bounded by .
Therefore, the gate complexity of the overall algorithm using th Trotter formula () is given by
| (86) |
where
| (87) |
Based on Eq. 86, the gate complexity of the th-order Trotter-LCU algorithm is then
| (88) |
Here, is the stage number of the Trotter formula. When , . When , . ∎
From Theorem 1 we can see that, by introducing the LCU compensation, the time scaling of the th-order Trotter-LCU algorithm improve the bare th-order Trotter time scaling from to . Moreover, the accuracy scaling is exponentially improved. This allowss us to achieve optimal gate complexity with lower-order Trotter implementation. For example, the time dependence of using first-order (respectively, second-order) Trotter formula can be improved from (respectively, ) to (respectively, ) by adding LCU compensation.
V TROTTER-LCU FORMULA WITH NESTED-COMMUTATOR COMPENSATION
In this section, we provide detailed construction of the nested-commutator compensation Trotter-LCU algorithms and the gate complexity analysis. We first sketch the procedure to derive the nested-commutator form LCU formula in subsection V.1. Then we construct the LCU formula of of the first-order Trotter remainder of the lattice Hamiltonians in subsection V.2 as an example. In subsection V.3, we describe the random-sampling implementation of the nested-commutator compensation algorithm and analyze its gate complexity.
V.1 Derivation of the nested-commutator formula
Our aim is to expand the LCU formula for the th-order Trotter remainder ( or , ) in the following form:
| (89) |
where the leading-order terms are written as a summation of nested commutators. We will use the following lemma of the operator-valued differential equation.
Lemma 3 ((Lemma A.1 in Childs et al. (2021)).
Let , be continuous operator-valued functions defined for . Then, the first-order differential equation
| (90) |
has a unique solution given by
| (91) | ||||
Here, is the time-ordering operator.
In Eq. 90, if we set to be the real-time evolution , we can find that and . Therefore, reflects the derivation of from the exponential function. We are going to apply Lemma 3 to , i.e., we set and . The deviation of from is characterized by the following function,
| (92) |
Applying Lemma 3, we have
| (93) |
The Trotter remainder can then be expressed as
| (94) | ||||
where
| (95) |
Eq. 94 provides a recurrence formula to solve the expansion terms in . To be more explicit, if we expand and based on the operator-valued Taylor series,
| (96) |
where and denotes the respective -order term, then we have
| (97) | ||||
since Eq. 94 holds for all . This is a recurrence formula which can be used to solve all the expansion terms of the remainder from the expansion terms of .
To solve the explicit form of , we need to study the form of expansion terms for the function . We will use the following proposition derived from Lemma 2.
Proposition 5 (Order condition).
Proof.
First, we note that , , and by applying Lemma 2 and setting to be , , and , respectively. So we only need to prove and .
We first prove . From we also have for . Based on Eq. 92 and Eq. 95, the derivatives of and are
| (98) | ||||
Based on we have for . Hence for .
For the reverse direction, we notice that . This implies
| (99) |
If we have for , then for . Then, from Eq. 98 we have for , which is equivalent to .
Now, we prove . Based on Eq. 89 we have
| (100) |
From we have
| (101) |
for . The reverse direction can be proven similarly based on the derivative of the formula . ∎
From Proposition 5, we have the following order condition for the th-order Trotter formula and remainders,
| (102) | ||||
Compare the recurrence formula in Eq. 94 and the order condition in Eq. 102, we will obtain the following relationship for the Taylor-series expansion terms and for and , respectively,
| (103) | ||||
Based on Eq. 103, we are going to expand based on the operator-valued Taylor-series expansion with integral remainders,
| (104) |
where
| (105) | ||||
Here, denotes the leading-order terms in . Then, from Eq. 94 and Eq. 103, the th-order Trotter remainder can be expressed as
| (106) | ||||
Here, .
From Eq. 106 we can see that, the leading-order expansion terms of with owns a simple expression related to . Later we will show that, can be simply written as a summation of nested commutators with the form,
| (107) |
where , are different summands in . Furthermore, we will show that are all anti-Hermitian. As a result, the expansion-order-pairing based on Euler’s formula introduced in Sec. IV can also be applied here. Since are anti-Hermitian, we can expand them by the Pauli operators as follows:
| (108) |
where are Hermitian Pauli operators with coefficients or . denotes the -norm of this expansion. The leading-order expansion term can then be expressed as
| (109) | ||||
Here, is the -norm of the LCU formula of in Eq. 109. is the normalized LCU formula.
The residue term in Eq. 106, however, is complicated and hard to be expressed simply using nested commutators. Due to the hardness to compensate , we will remove it in the truncated Trotter remainder formula,
| (110) | ||||
Here, . In the fourth line, we apply the following pairing procedure based on Euler’s formula, similar to Eq. 75,
| (111) | ||||
for . Recall that .
in Eq. 110 is the final LCU formula for the nested-commutator compensation of . In what follows, we estimate the -norm and distance of this LCU formula,
| (112) | ||||
Proposition 6 (Bound the 1-norm and error of nested-commutator expansion formula).
Proof.
The value of is derived based on Eq. 109 and Eq. 110. To calculate , we will use the following bound,
| (115) | ||||
In the second equality, we use the fact that is a unitary. To bound , we have
| (116) |
Finally, to bound in Eq. 115, we have
| (118) | ||||
In the first line, we use the definition of and the recurrence formula in Eq. 94. In the second line, we use the property that is a unitary. In the third line, we use the order condition in Proposition 5. In the final line, we apply the operator-valued Taylor-series expansion on and set the truncation order .
∎
From Proposition 6 we can see that, to study the performance of the truncated LCU formula in Eq. 110, we only need to study the property of the derivatives of , including . In the following section, we are going to derive the explicit formula of , taking the lattice Hamiltonian with first-order Trotter formulas as an example.
V.2 Example: first-order lattice Hamiltonian
Now, we focus on the lattice Hamiltonians with the form in Eq. 10. For the lattice Hamiltonian, the first-order Trotter formula is . Here, we assume that the time-evolution of each two-qubit component is easy to be implement on the quantum computer.
To derive the explicit form of the LCU formula in Eq. 110, we first derive defined in Eq. 95 and its derivatives . From Eq. 92 and Eq. 95 we have
| (119) | ||||
Applying the general Libniz formula to we have,
| (120) |
If we set the truncation of to be and apply the following operator Taylor-series expansion formula,
| (121) |
we can expand as
| (122) |
where
| (123) | ||||
We can see that, can be written as the summation of nested commutators with concise form . Note that, with is always anti-Hermitian when and are Hermitian. On the other hand, these nested commutators are all with the nice property that their spectral norm and -norm is linear to the system size . To be more specific, we have the following norm bound.
Proposition 7.
Consider a lattice Hamiltonian with the form in Eq. 10. Suppose the spectral norm and -norm of its components are upper bounded by and . Then for the nested commutators appearing in Eq. 123, we have the following bound
| (124) |
where are non-negative integers satisfying . As a result, we can bound the spectral norm of as . The -norm upper bound is to simply replace by .
Proof.
We first focus on one Hamiltonian term contained in and bound the norm,
| (125) |
To do this, we are going to decompose commutator to the elementary nested commutators in the following form:
| (126) | ||||
where are the possible vertice’s indices. For each elementary nested commutator, the spectral norm can be easily bounded by by simply expanding all the commutators and applying triangle inequality. Here, we use the property that the spectral norm of all the exponential operators with anti-Hermitian exponent is .
Now, we count the number of the possible elementary commutators with the form in Eq. 126. We will check the action of each adjoint operator or from the right to the left. For the first location, if we expand , there will be only two possible elementary nonzero components, and . If the next is still , the support will still be on the four qubits: , and . As a result, there will still be only two possible components, and . Similarly, the exponential operator will not enlarge the support since one can expand it to the power of . The support will be enlarged when comes. In this layer, the support of the operator will be expanded to six qubits, and there will be three elementary components. The number of possible elementary commutators is then
| (127) |
Combining the number of elementary nested commutators and the norm bound for each commutator and applying triangle inequality, we will obtain Eq. 125. Finally, in the operator , there are possible summands. This finishes the proof of Eq. 124.
Now, we apply Eq. 124 to bound the norm of . From Eq. 120 we have
| (128) | ||||
In the third line, we apply the binomial theorem.
Since -norm can be estimated based on the same logic by counting the number of elementary nested commutators and the -norm of each nest commutator, the derivation for the -norm is similar by replacing to . ∎
As introduced in subsection V.1, when , we set with to be the leading-order terms and set the truncation order . That is, we only compensate the second- and third-order error using LCU methods. While we are not able to achieve the logarithmic accuracy similar to PTSC algorithms, we can achieve a high accuracy of , which is cubicly improved comparing to the bare first-order Trotter result .
Based on Eq. 110, the truncated nested-commutator LCU formula for can be written as
| (129) | ||||
Here, . The explicit form of can be obtained by the definitions in Eq. 109, Eq. 111 and the Pauli operator decomposition based on the nested-commutator form in Eq. 123.
Combined with the deterministic first-order Trotter formula, the overall LCU formula for is
| (130) |
Following Proposition 6 and Proposition 7, we can bound the -norm and error of the LCU formula in Eq. 129 and Eq. 130 as follows.
Proposition 8 (first-order Trotter-LCU formula by nested-commutator compensation for lattice Hamiltonians).
Proof.
We start from bounding the -norm . From Proposition 6 we have
| (132) | ||||
In the third line, we use the fact that and Proposition 7. In the fourth line, we use the assumption that .
Now, we bound the spectral norm distance . From Proposition 6 we know that we only need to bound , , and based on Eq. 114. For , from Proposition 7 we have
| (133) |
For and , from Eq. 114 and Proposition 7 we have
| (134) | ||||
Based on Eq. 133, Eq. 134 and Proposition 6,
| (135) | ||||
In the fourth line, we use the assumption that . ∎
V.3 General construction and performance
We can easily extend the first-order analysis above to the higher-order case. In Appendix B, we provide an explicit construction for second-order nested-commutator expansion, which will be used for the later numerical results. For the general LCU formula for the th-order Trotter remainder, we have the following proposition to characterize the LCU formulas in Eq. 110.
Proposition 9 (Trotter-LCU formula by nested-commutator compensation for lattice Hamiltonians).
Consider a lattice Hamiltonian with the form in Eq. 10. We set where is the stage number of the th-order Trotter formula ( or ). For , in Eq. 110 is a -LCU formula of with
| (136) | ||||
As a result, in Eq. 110 is a -LCU formula of . Here, and are, respectively, the largest spectral norm and -norm of the lattice Hamiltonian components defined in Eq. 11.
The proof of Proposition 9 is in Appendix C.
The circuit of random-sampling implementation of the NCC algorithm is similar to the PTSC algorithm, which is illustrated in Fig. 7. The only difference is that we sample the Pauli operators based on the nested-commutator expansion formula. In Appendix D, we generalize our random-sampling algorithm to the th-order situation to demonstrate its scalability. Specifically, the space and time cost of the sampling algorithm are and , respectively. In practice, we need to expand the leading-order terms to a summation of different adjoint operators based on the methods in subsection V.1 first, and then calculate the corresponding sampling probability . We have the following theorem to characterize the gate complexity of the th-order NCC algorithm with random-sampling implementation.
Theorem 2 (Gate complexity of the th-order random-sampling Trotter-LCU algorithm by nested-commutator compensation for lattice Hamiltonians).
In a th-order Trotter-LCU algorithm ( or ) based on nested-commutator compensation, if the segment number satisfy all the requirements below,
| (137) | ||||
we can then realize a -LCU formula for based on segments of in Eq. 110. As a result, the gate complexity of random-sampling th-order Trotter-LCU algorithm based on nested-commutator compensation for the lattice Hamiltonian is
| (138) |
Here, where is the stage number of the Trotter formula. and are, respectively, the largest spectral norm and -norm of the lattice Hamiltonian components defined in Eq. 11.
Proof.
For the random-sampling implementation, the overall LCU formula for is to repeat the sampling of for times, . Using Proposition 2 and 9, when , we conclude that is a -LCU formula of with
| (139) | ||||
To realize a -LCU formula for , we only need the segment number satisfy all the requirements in Eq. 137. It suffices to choice
| (140) |
Based on Eq. 86, the gate complexity of the th-order Trotter-LCU algorithm is then
| (141) |
Here we use the fact that and for lattice Hamiltonians. ∎
So far, we have restricted our construction of the nested-commutator expansion to lattice Hamiltonians. In practice, various physical Hamiltonians, including those for the electronic structure of quantum materials Babbush et al. (2018a), quantum chemistry Hamiltonians Lee et al. (2021); Berry et al. (2019); von Burg et al. (2021) and power-law interaction Hamiltonians Childs et al. (2021), also possess sparse properties. As a result, the methods for the nested-commutator expansion of the Trotter remainder introduced in subsection V.1 can also be applied to a general Hamiltonian .
In Appendix E, we discuss how to perform the nested-commutator expansion of for general Hamiltonians, and discuss the performance of the resulting LCU formula in Proposition 13. We find that the -norm of the LCU formula based on nested-commutator expansion is closely related to the following nested commutator norm of the Hamiltonian ,
| (142) |
is originally defined in Ref. Childs et al. (2021) to analyze the performance of Trotter methods. In Ref. Childs et al. (2021), the authors estimate the values of for typical Hamiltonian models like plane-wave-basis quantum chemistry models, -local Hamiltonian, and Hamiltonians with power-law interactions. Following similar estimation methods, we can also calculate for different models and consider their explicit nested-commutator expansions. We will leave the explicit evaluation of other typical Hamiltonians for a future work.
VI CONCLUSION AND OUTLOOK
We study the Hamiltonian simulation algorithms based on the composition of Trotter and LCU algorithms. In both theoretical and numerical studies, we show that the th-order paired Taylor-series compensation (PTSC) algorithm, th-order PTSC algorithm and the th-order nested-commutator compensation (NCC) algorithm enjoy different advantages and will be useful in different scenarios. Taking the -qubit lattice Hamiltonian as an example: the th-order PTSC algorithm performs the best when is small compared with and ; the th-order PTSC algorithm performs the best when is small compared with and ; while the th-order NC algorithm performs the best when is small compared with and . In practice, with finite system size , simulation time and inverse accuracy , we can think about a hybrid implementation of different algorithms. For example, when the sparsity of a given Hamiltonian is large, we can first split the Hamiltonian to two parts,
| (143) |
where the summands in are the few dominant terms with large coefficients. We can then perform second-order Trotter only for , and use PTS to expand the remainder
| (144) |
If the number of dominant terms is small, we can then reduce the dependence of the algorithm similar to th-order PTSC algorithm while keep the good -dependence of second-order PTSC algorithm. As another example, we can hybridize second-order PTSC and NCC algorithms: we apply the nested-commutator compensation for the leading-order terms (i.e., the terms with , and ), and normal Taylor-series compensation for higher-order terms. In this case, we can find an optimal truncation location which fulfills the high simulation accuracy requirement and keeps the nested-commutator scaling for the leading-order compensation terms.
The design of Trotter-LCU algorithms is based on a series connection of Trotter and LCU algorithms. A similar composition method can also be exploited for other Hamiltonian simulation algorithms Hagan and Wiebe (2023). For example, we may replace the deterministic Trotter with the ones with random permutation Childs et al. (2019). Recently, Cho et al. Cho et al. (2024) consider similar idea to compensate the Trotter error using randomized unitary operators. Using anticommutative cancellation Zhao and Yuan (2021), we can further reduce the compensation terms.
Acknowledgements.
We thank Xiaoming Zhang, Xiao Yuan, Min-Hsiu Hsieh, Yuan Su, Kaiwen Gui, Ming Yuan, Senrui Chen, and Ying Li for helpful discussion and suggestions. We would like to especially thank Wenjun Yu for highlighting the validity of the variant where the ancillary qubit is measured and reset for each segment. P. Z. and L. J. acknowledge support from the ARO MURI (W911NF-21-1-0325), AFOSR MURI (FA9550-19-1-0399, FA9550-21-1-0209), AFRL (FA8649-21-P-0781), NSF (OMA-1936118, ERC-1941583, OMA-2137642), NTT Research, and the Packard Foundation (2020-71479). J.S. would like to thank support from the Innovate UK (Project No.10075020) and support through Schmidt Sciences, LLC. Q. Z. acknowledges HKU Seed Fund for Basic Research for New Staff via Project No. 2201100596, Guangdong Natural Science Fund via Project No. 2023A1515012185, National Natural Science Foundation of China (NSFC) via Projects No. 12305030 and No. 12347104, Hong Kong Research Grant Council (RGC) via No. 27300823, No. N_HKU718/23, and No. R6010-23, Guangdong Provincial Quantum Science Strategic Initiative GDZX2200001.Appendix A PAIRED TAYLOR-SERIES COMPENSATION WITH HIGHER-ORDER TROTTER FORMULAS
Following the same idea in subsection IV.2, we now generalize it to the case with th-order Trotter formula. Expanding the th-order Trotter remainder, we have
| (145) |
where
| (146) | ||||
Here, we use to denote all the expansion variables besides .
We ignore the derivation and provide the general form of the LCU formula for ,
| (147) | ||||
where
| (148) | ||||
The Pauli rotation unitary where and .
Combined with the deterministic Trotter formula, the overall LCU formula for is
| (149) |
The following proposition gives the performance characterization of to approximate .
Proposition 10 (th-order Trotter-LCU formula by paired Taylor-series compensation).
Appendix B TIGHT NESTED-COMMUTATOR ANALYSIS FOR SECOND-ORDER TROTTER-LCU ALGORITHM
We can easily extend the methods for the first-order analysis in subsection V.2 to the higher-order case. Taking the second-order case as an example, the second-order Trotter formula of the lattice Hamiltonian is .
To derive the explicit LCU formula in Eq. 110, we first derive defined in Eq. 95 and its derivatives . From Eq. 92 and Eq. 95 we have
| (153) | ||||
Following the approach in subsection V.1, we expand and by
| (154) |
then based on Proposition 5 and the recurrence formula Eq. 94 we have,
| (155) | |||
Combining Eq. 153 and Eq. 155, we can show that
| (156) |
Therefore, the first three nontrivial terms . These terms will be set as the leading-order terms.
Based on Eq. 155, we are going to expand based on the operator-valued Taylor-series expansion with integral remainders,
| (157) |
where
| (158) | ||||
denotes the leading-order terms in . Then, from Eq. 94 and Eq. 155, the second-order Trotter remainder can be expressed as
| (159) | ||||
We put the explicit nested-commutator expressions of the leading-order terms (, or ) in Sec. B.
In practice, we truncate the formula with the order . Based on Eq. 110, the truncated nested-commutator LCU formula for can be written as
| (160) | ||||
Here, . The explicit form of can be obtained by the definitions in Eq. 109, Eq. 111 and the Pauli operator decomposition based on the nested-commutator form in Eq. 164.
For a tight numerical estimation, we seek for a tighter bound of the -norm and spectral norm accuracy for the LCU formula in Eq. 160.
B.1 Bound the 1-norm of recurrence function
Hereafter, we define and to simplify the notation. We have
| (161) | ||||
Apply the Libniz rule to and , we have
| (162) | ||||
Then,
| (163) | ||||
We can solve the explicit form of the leading-order terms with , and ,
| (164) | ||||
We can then expand the operators and to Pauli operators and solve the -norm of , and under the Pauli decomposition based on Eq. 164. The -norm of is given by
| (165) |
We summarize the procedure to estimate the segment number of second-order Trotter-LCU under nested-commutator compensation as follows.
-
1.
For a specific lattice Hamiltonian, get the explicit Pauli expansion form of , , by Eq. 164.
-
2.
Get the expression of the -norm by Eq. 165. Calculate based on .
-
3.
Solve the following residue operator,
(166) calculate its spectral norm numerically. Check either the following requirement are satisfied:
(167) where is a preset accuracy requirement. If not, we search the largest value in the region by dichotomy which makes Eq. 167 satisfied.
-
4.
The number of segments is given by . We then calculate the number of gates based on methods in Appendix B.2.
We have a tighter count bound for the norm of and ,
Proposition 11.
Consider a lattice Hamiltonian with the form in Eq. 10. Suppose the spectral norm and -norm of its components are bounded by and . Then for the recurrence function , we have the following norm bound for its derivatives,
| (168) | ||||
Proof.
From Eq. 162 we have,
| (169) | ||||
To bound the norm of nested commutators, we use the same methods in Proposition 7. We have
| (170) | ||||
Here, the first bracket of each bound corresponds to possible nest commutators, while the second bracket of each bound indicates the norm enlargement of each nested commutator.
The -norm bound can be derived in the same way. ∎
B.2 Estimating the gate counts
To estimate the performance, i.e., gate complexity of the Trotter-LCU algorithm based on nested-commutator compensation, we need to first estimate the number of segments in the algorithm. This is determined by the following three constraints,
| (177) | ||||
After we solve the required segment number by Eq. 177, we can estimate the gate number accordingly. Here, we introduce the method to estimate the gate number of the LCU part. The gate number in the implementation of second-order Trotter formula can be evaluated following the methods in Ref. Childs et al. (2018). In the worst-case scenario, the Pauli weight of the gate is determined by the weight of Pauli operators contained in in Eq. 164. The largest Pauli weight is . As a result, a controlled-Pauli gate will cost at most six gates and no non-Clifford gate.
If we consider the paired algorithm, when we sample the third-order term, it will be a Pauli rotation unitary on four qubits. In this case, it will cost eight gates and two single-qubit Pauli rotation gates .
We summarize the whole procedure to estimate the gate complexity.
-
1.
Input: Hamiltonian parameters: , , , . Normalization requirements , accuracy requirements , time requirements .
- 2.
-
3.
Accuracy estimation.
-
(a)
Analytical way (scalable). Using Eq. 175 to get the function .
-
(b)
Numerical way (unscalable). Calculate numerically. Solve its largest singular value, which is an upper bound of .
-
(a)
-
4.
Based on the constraints in Eq. 177, calculate the segment number .
-
5.
Analyze the and gate number.
Appendix C EXPLICIT NESTED-COMMUTATOR COMPENSATION FOR HIGHER-ORDER TROTTER REMAINDERS
In this section, we provide detailed results for the nested-commutator compensation for higher-order Trotter remainders introduced in Sec. V. Here, we will focus on the lattice model Hamiltonians in Eq. 10. The results for general Hamiltonians will be presented in Appendix E.
As introduced in Sec. V.1, for the (asymmetric) multiplicative remainder , our aim is to construct a LCU formula with the following form
| (178) |
where denotes the term with -order . In practice, we will use the truncated LCU formula with paired leading-order terms, derived in Eq. 110,
| (179) | ||||
where .
We are going to finish the following tasks,
-
1.
(Sec. C.1) Derive the explicit formulas for the leading-order expansion terms with .
- 2.
C.1 Derivation of LCU formula with nested-commutator form
We first introduce the canonical expression of the th-order Trotter formula,
| (180) |
where
| (181) |
is the th stage of the Trotter formula. is the stage number. We have for and when . The stage lengths and are determined based on Eq. 24 and Eq. 25. We have
| (182) | ||||
For example, for the second-order Trotter formula , we set the stage number with .
The Hermitian conjugate of is
| (183) |
As is discussed in Sec. V.1, to derive the nested-commutator form of , we first solve defined in Eq. 95. We have
| (184) | ||||
From Proposition 5, we can write the th-Trotter remainder and as the following form:
| (185) | ||||
where and are the higher-order remaining terms to be analyzed later. We also denote
| (186) | ||||
as the leading-orders whose explicit forms will be calculated in this section. We will show that contains term where is the lattice size.
Now, we are going to solve the exact form of for the leading-orders. We first try to solve the succinct form of based on its definition in Eq. 184. Taking the derivative for each Trotter stage, we have
| (187) | ||||
Here we assume . When (or ), the value of the product (or ) will be regarded as . Recall that . We further expand and merge the two terms together,
| (188) | ||||
Here, we assume . Now, we simplify the commutator by splitting the product and then change the summation order,
| (189) | ||||
where
| (190) |
We also set .
Based on Eq. 189, we now derive the succinct form of ,
| (191) |
We expand each stage of the Trotter formula in the formula,
| (192) | ||||
Finally, we apply the following operator-valued Taylor expansion formula with integral form of the remainder:
| (193) |
By the general Libniz formula, we obtain the derivatives of as follows:
| (194) | ||||
We can then expand around as follows:
| (195) |
Here, we use the order condition in Proposition 5 so that the terms with expansion order from to are all zeros. The th-order term and the th-order residue can then be expressed as
| (196) | ||||
C.2 Norm bounds for LCU formula
In Sec. C.1 we have derived the explicit form of the LCU formula for the th-order Trotter remainder . Based on Eq. 192, Eq. 194, Eq. 196 and Proposition 6, we are going to prove the -norm bound and error bound in Proposition 9.
First of all, we need to estimate the norms of . We have the following results.
Proposition 12 (Upper bound of the norm of nested commutators).
Consider a lattice Hamiltonian with the form in Eq. 10. Suppose the spectral norm and -norm of its components are bounded by and . Then for the nested commutators appearing in Eq. 196, we have the following bound
| (197) | ||||
where are non-negative integers satisfying . is the stage number determined by the Trotter formula in Eq. 180. are defined by the Trotter formula in Eq. 181. are defined in Eq. 190. As a result, we can bound the norm of defined in Eq. 194 as follows:
| (198) |
The -norm upper bound for is to simply replace by .
Proof.
To begin with, we now focus on one Hamiltonian term in and bound the norm
| (199) | ||||
To this end, we decompose operator to the elementary nested commutators with the form,
| (200) | ||||
where are the possible vertex indices. For each elementary nested commutator, the spectral norm can be bounded by
| (201) |
This can he done by expand all the commutators and apply triangle inequality. Here, we use the property that the spectral norm of all the exponential operator with anti-Hermitian exponent is 1.
Now, we count the number of the possible elementary commutators with the form in Eq. 200. We will check the action of the adjoint operators from right to left. For the first location, we know that . For simplicity, we keep the term in the counting of elementary commutators. If the next is still , the support will still be on the two qubits and . As a result, there will be one possible elementary term left. Similarly, the exponential operator will not enlarge the support since one can expand it to the power of . The support will be enlarged when comes into play. In this layer, the support of the operator will be expanded to four qubits: , and . We can decompose to nonzero elementary elements, and . If the next operator is still or , it will not enlarge the support. Following this logic, we can see that the number of possible elementary commutators is bounded by
| (202) | ||||
We remark that, the elementary nested commutators with is actually . Here, we keep these commutators for the simplicity of counting.
Combining the number of elementary nested commutators and the norm bound for each commutator and applying triangle inequality, we will obtain Eq. 199.
Similarly, we can check one Hamiltonian term in and bound the norm with
| (203) | ||||
The counting logic is similar to the case for in . The only difference is that when counting the number of elementary nested commutators, the action of the first will enlarge the operator space to four qubits.
Now, we apply Eq. 197 to bound the norm of in Eq. 194. We have
| (204) | |||
In the third line, we use multinomial theorem. In the fourth line, we use the fact that and . The fifth line is due to for all . In the sixth line, we use the following bound:
| (205) | ||||
Here, is any real number.
Since -norm can be estimated based on the same logic by counting the number of nested commutators and the -norm of each nest commutator, the derivation for the -norm is similar by replacing to .
∎
Now, we prove the -norm bound of . From Proposition 6 we have
| (206) | |||
Here, we set . In the third line, we use Proposition 12. In the fourth line, we use the assumption that .
Then, we prove the distance bound . From Proposition 6 we know that we only need to bound , , and based on Eq. 114.
We start from . From Proposition 7 we have
| (207) | ||||
Appendix D EFFICIENT SAMPLING FOR THE HIGHER-ORDER NESTED-COMMUTATOR COMPENSATION ALGORITHM
Following the analysis in Appendix C, we now design a general sampling method for the general th-order Trotter remainder . We consider the general th-order Trotter formula in the canonical form in Eq. 180.
The truncated Trotter remainder can be expanded as
| (211) | ||||
Based on Eq. 194, we have shown that can be written as
| (212) |
where ,
| (213) | ||||
The values and are defined in Eq. 190.
We now construct efficient random sampling of and Eq. 213 based on LCU formulas with the -norm of
| (214) | ||||
respectively. Here,
| (215) | ||||
There are summands in . We now focus on a generic summand in and check the action of the adjoint operators on it,
| (216) | ||||
Recall that .
We would like to follow that construction in Proposition 12, where we first decompose the adjoint operator in Eq. 216 into the elementary operators with the form,
| (217) |
For each elementary nested commutator, the -norm is
| (218) |
Here, we have assumed that all the summands in or have been padded similar to Eq. 18 so that their -norms are all .
Now, we count the number of elementary nested commutators with the form of Eq. 217 in the adjoint operator in Eq. 216. In the proof of Proposition 12, we show the number of possible elementary nested commutator is upper bounded by
| (219) | ||||
We now discuss how to achieve this bound by “padding” zero-valued elementary nested commutators into the decomposition of . We notice that, after the sequential action of , the support, i.e., the index of the qubit where the operators act nontrivially, of the resulting operator is given by the “light cone” of , as illustrated inFig. 6. We keep track of the largest possible support of the resulting adjoint operators and pad the LCU formula in the following situations:
-
1.
(Padding small summands) When the -norm of the summand is smaller than , we add extra terms in the LCU formula of to make its -norm to , similar to Eq. 18.
-
2.
(Padding -valued commutators) Many nested commutators with the form of Eq. 217 may be 0 due to the commutation relationship, for example , since the support of is on qubits and which commutes with . However, we keep all these -valued terms as long as the support of the nested commutator is in the “light-cone” range of the operator.
-
3.
(Padding boundary terms) For the summands which are close to the boundary, after a few action of the adjoint operators, the “light cone” will touch the boundary of the system. In this case, we introduce virtual padding ancillary qubits and extra padding nested commutators on it:
-
(a)
For the summand or which own only one-qubit support on the boundary, we redefine the Pauli terms in the LCU of them. For example, if , we then redefined it to .
-
(b)
We define the “virtual” summand where qubits are all virtual qubits as
(220)
Since all the operations on the virtual qubits are , we do not need to introduce these qubits in the real implementation.
-
(a)
After these padding, we have now construct the LCU formula of with the following form:
| (221) | ||||
where are indices in the light-cone region. Recall that all the elementary operators with the form Eq. 217 are with the same -norm of , irrelevant of the qubit index and the rank number . Therefore, the -norm of is
| (222) |
which is irrelevant of the qubit index .
Now, based on Eq. 221, we can write in Eq. 213 as
| (223) | ||||
where
| (224) |
for and denotes a multinomial distribution where we sample the variable value based on the probability distribution for times. Based on Eq. 222 and Eq. 223, we can easily check that the -norm of is given by in Eq. 214. More importantly, since the -norm of is independent of and , the sampling of from all odd qubits and from the light-cone region follows uniform distribution.
Similarly, we can decompose and pad extra terms in to construct LCU with the following form:
| (225) | ||||
for , so that the -norm of is given by in Eq. 214. Again, the -norm of the operator is , independent of and . Therefore, the -norm of in Eq. 212 is
| (226) |
and the -norm of is
| (227) |
Based on the above analysis, we summarize the overall sampling procedure in Fig. 12 and Algorithm 2. We consider a multistage sampling: first, we sample the expansion order based on ; second, for a given expansion order , we sample the terms or in the nested commutator based on Eq. 212 and Eq. 214; third, we sample the power of the adjoint operators and based on the multinomial distribution in Eq. 223 and Eq. 225; fourth, we uniformly sample the specific Hamiltonian summands and uniformly sample the adjoint Hamiltonian summands , each from the light-cone region; finally, if there are multiple terms in the Hamiltonian summands, we then uniformly sample the specific Pauli terms in the summands.
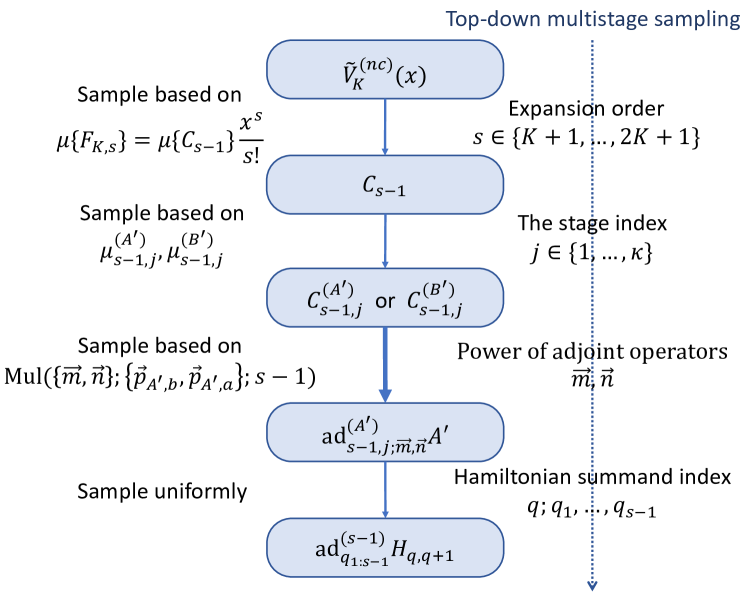
Now, we analyze the space and time cost of the whole sampling algorithm in Algorithm 2. The calculation of the -norms of and its components and requires spacetime resources. Consider a parallel calculation, we need spatial resources and time resources. We store all the above -norm coefficients in the memory with the size . The sampling of from discrete values requires steps Bringmann and Panagiotou (2012). For a given nested commutator , the sampling of and from discrete values requires steps. The multinomial sampling of the power of adjoint operators and requires steps. Finally, the uniform sampling of the Hamiltonian summands from the light-cone region requires steps. To summarize, the space and time cost of Algorithm 2 are and , respectively.
Appendix E NESTED COMMUTATOR COMPENSATION FOR TROTTER FORMULAS OF GENERAL HAMILTONIANS
We now extend the methods to analyze the lattice model Hamiltonian to a general Hamiltonian. Consider a -sparse Hamiltonian with the form . The th-order Trotter formula ( or , ) for can be written as
| (228) |
Here, is the number of stages in the Trotter formula, that is, how many times each Hamiltonian component is repeated in the implementation. We have for and when . The stage length coefficients are determined based on Eq. 24 and Eq. 25. The permutation indicates the ordering of the summands within the th stage in the Trotter formula. In Suzuki’s constructions Suzuki (1990) of Trotter formulas considered in this work, we alternately reverse the ordering of summands between neighboring stages.
In what follows, we omit the subscript in for simplicity. To further simplify the notation, we introduce the lexicographical order Childs et al. (2021) for the pair of tuples in Eq. 228. For two pairs of tuples and , we have
-
1.
if , or if and .
-
2.
if and .
We can also define and in the same way. We denote the number of different tuples in as , which is usually equal to . We can then express and in the following way:
| (229) |
Similar to the case of lattice Hamiltonians, based on Eq. 94 and Eq. 111, we can expand the Trotter remainder to the following form:
| (230) |
where
| (231) | ||||
Here, indicates the leading-order terms to be compensated by LCU formula, is the high-order part. In practice, we remove the high-order part with order and implement only the leading-order terms
| (232) | ||||
where . The explicit form of can be obtained by the definitions in Eq. 109, Eq. 111 and the Pauli operator decomposition based on the nested-commutator form in Eq. 164.
We are going to finish the following tasks:
-
1.
(App. E.1) Derive the explicit formulas for the leading-order expansion terms with .
- 2.
E.1 Derivation of nested-commutator form for general Hamiltonians
Based on the Trotter formulas in Eq. 229, we expand in Eq. 92 as follows:
| (233) | ||||
in Eq. 95 can then be written as,
| (234) | ||||
The derivative of is
| (235) | ||||
Using the operator-valued Taylor-series expansion in Eq. 121, we have
| (236) | ||||
which is the nested-commutator form. Here, are a group of integers whose summation is . Their corresponding multinomial coefficient is given by
| (237) |
E.2 Norm bounds for the nested-commutator expansion
Now, we are going to bound the -norm and distance of the truncated LCU formula in Eq. 110 for a general Hamiltonian. We will use the following formula in the derivation.
Lemma 4 (Theorem 5 in Childs et al. (2021)).
Let , …, and be operators. Then, the conjugation has the expansion,
| (240) | ||||
Here, are operators independent of . The operator-valued function is given by
| (241) | ||||
Furthermore, we have the spectral-norm bound,
| (242) |
for general operators and
| (243) |
when are anti-Hermitian. is defined in Eq. 245.
We have the following proposition.
Proposition 13 (Trotter-LCU formula by nested-commutator compensation for general Hamiltonians).
For , in Eq. 232 is a -LCU formula of th-order Trotter remainder with
| (244) | ||||
Here, we define the nested-commutator norms to be
| (245) | ||||
where indicates a sequence of summands with the lexicographical order given by the th-order Trotter formula in Eq. 229. is defined similarly by replacing the spectral norm to -norm in Eq. 245.
Proof.
From Eq. 239 we can bound the -norm and spectral norm of by
| (246) | ||||
Now, we are going to bound and . From Eq. 234 and using Lemma 4 we have
| (247) | ||||
In the second line, we use Lemma 4 to expand all the conjugate matrix exponentials to the following form:
| (248) | ||||
The low-order terms with in Eq. 247 cancel out due to the order condition in Proposition 5. Therefore, we have
| (249) | ||||
Following the same way, we can bound and in Eq. 246 as
| (250) | ||||
Now, we are going to bound . Similar to Eq. 247, we expand all the conjugate matrix exponentials to th-order,
| (251) | ||||
in the second line, we use the expansion of in Eq. 104. Based on Eq. 249 we then have
| (252) | ||||
We omit the derivation to the second line since it is the same as the one in Eq. 249.
Then we can bound by
| (253) |
From Proposition 13 we can see that, to characterize the performance of the Trotter-LCU algorithm, we only need to estimate the values of and for a given Hamiltonian. We can further simplify the form of by the following upper bound Childs et al. (2021),
| (256) | ||||
which is because the commutator terms in the left-hand side must be of the form on the right. Moreover, if we fix one term on the right-hand side, we can find at most times of this term on the left-hand side.
Appendix F SOME USEFUL FORMULAS IN THE PROOF
Lemma 5 (Tail bound for the Poisson distribution (Theorem 1 in Canonne (2016))).
Suppose is a random variable with Poisson distribution so that , where is the expectation value. Then, for any , we have,
| (257) |
and, for any ,
| (258) |
Here, for .
From Lemma 5 we have the following corollaries.
Corollary 1.
For and positive integer such that , we have
| (259) |
Corollary 2.
For and positive integer such that , we have
| (262) |
Lemma 6 (Proposition 9 in Wan et al. (2022)).
For any , , we have , for all . Here, is the principle branch of the Lambert function.
Lemma 7 (Theorem 2.7 in Hoorfar and Hassani (2008)).
When we have
| (264) | ||||
Appendix G ADDITIONAL NUMERICAL RESULTS
In this section, we provide more numerical results by comparing the gate costs of Trotter-LCU algorithms with other typical algorithms, especially the Trotter algorithm and “post-Trotter” algorithm with best performance, i.e., the fourth-order Trotter algorithm and the quantum signal processing (QSP) algorithm. We will mainly consider two different scenarios—generic -sparse Hamiltonians and lattice Hamiltonians. In the former case, the previously known best result is given by the QSP algorithm Low and Chuang (2017); in the latter case, since we can take advantage of the spacial locality and commutator information, the fourth-order Trotter algorithm is known to have the best performance Childs et al. (2018); Childs and Su (2019).
For the Trotter algorithms and Trotter-LCU algorithms, we first compile the circuit to gates, single-qubit Clifford gates and non-Clifford -axis rotation gate . On the other hand, the circuit compilation for the QSP algorithm is more complicated: we need to decompose the state-preparation oracles and the select- gates. We follow the qROM design in Ref. Babbush et al. (2018b) based on a sawtooth structure. The detailed gate resource analysis can be found in a companion work Sun et al. (2024). Based on the qROM design, we decompose all the state preparation oracles and the select- gates to Toffoli gates, which can be further decomposed to gates, single-qubit Clifford gates and gates.
For a fair comparison between the gate costs of Trotter, Trotter-LCU and QSP algorithms, we need to further compile the -axis rotation gate to gate. We follow the gate compilation work in Ref. Bocharov et al. (2015), where the expected -gate number to compile with random is about
| (265) |
where is the compilation accuracy. We set the accuracy in the later resource estimation. In this case, .
G.1 Generic -sparse Hamiltonians
For the generic -sparse Hamiltonian, we choose the -local Hamiltonian
| (266) |
with as an example, in which case we ignore the commutator information between different Hamiltonian summands. This simple model works as a representative of many generic Hamiltonians where the commutator information is not helpful or too complicated to count on, e.g., quantum chemistry Hamiltonian for the molecules. Without the commutator information, the former best Hamiltonian simulation algorithm is QSP Low and Chuang (2017).
In Fig. 13 and Fig. 14, we estimate and compare the and gate counts for the PTSC algorithms, QSP and fourth-order Trotter algorithm with respect to the evolution time. We choose fourth-order Trotter algorithm with random permutation since it performs the best over all the Trotter algorithms. The gate counting method for fourth-order Trotter with random permutation is based on the analytical bounds in Ref. Childs et al. (2019). For the QSP algorithm, we estimate the gate count based on the QROM construction in Ref. Babbush et al. (2018b). Only the high-accuracy results for our method and quantum signal processing are presented since our method and quantum signal processing has a logarithmic dependence and hence are less prone to the accuracy while the Trotter formulae has polynomial dependence on the accuracy.
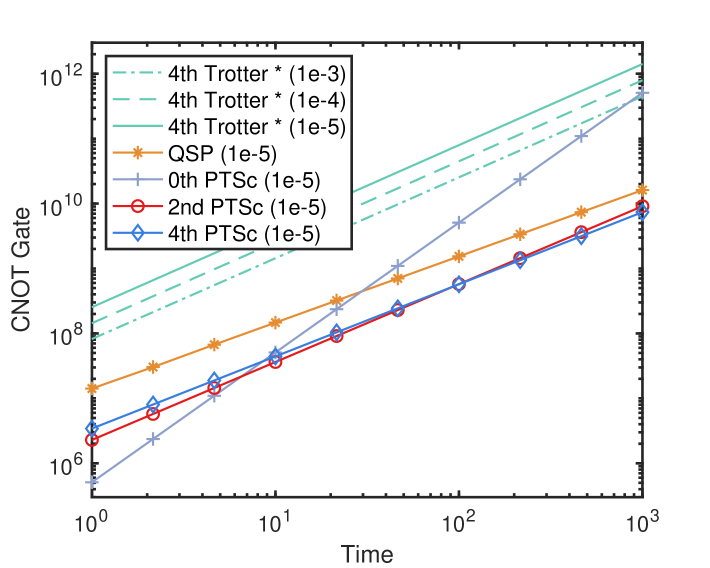
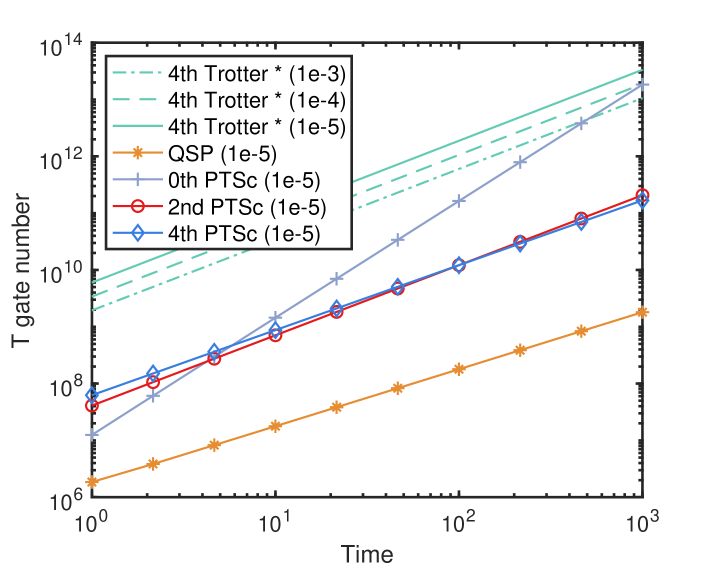
From Fig. 13 and Fig. 14 we can see that, the PTSC algorithm owns a lower gate cost than the QSP algorithm because it does not need the qROM for classical data loading. On the other hand, the PTSC algorithms have a larger T-gate cost than QSP algorithm. This is mainly due to the compilation cost of arbitrary -axis rotation gate to gates: for each gate with a random phase , we need gates on average to compile it to the accuracy of . In the Trotter or Trotter-LCU algorithms, the non-Clifford gate cost mainly originates from the gates: in each segment, there are roughly gates, leading to about compiled gates. As a comparison, there are only few gates in QSP algorithm used for the phase iteraction procedure to realize the Jacobi-Anger polynomials. The major non-Clifford gate cost lies in the compilation of state-preparation oracles and the select- gates, each of which can be realized by about gates based on the qROM design in Ref. Babbush et al. (2018b).
In Fig. 15 we compare the qubit number required to implement the QSP and the PTSC algorithms, based on the -local Hamiltonian model. We can see a clear advantage of the spacial resource cost of PTSC to QSP algorithm.
G.2 Lattice Hamiltonians
Now, we consider the case of lattice Hamiltonians. We consider the Heisenberg model, , where is the vector of Pauli operators on the th qubit and .
We compare the and gate number of the second-order NCC algorithm, QSP and fourth-order Trotter algorithm in Fig. 16 and Fig. 17, respectively. The fourth-order Trotter error analysis is based on the nested-commutator bound (Proposition M.1 in Ref. Childs et al. (2021)), which is currently the tightest Trotter error bound. The performance of our second-order NCC algorithm is analyzed based on the detailed analysis in Section B. We explicitly calculate the -norm of the LCU formula and use the analytical bound for the accuracy analysis. Here, we do not introduce the empirical analysis for a fair comparison. Since the explicit evaluation of our fourth-order NCC algorithm is complicated, we mainly present the results for our second-order algorithm.
As addressed in Childs et al. (2021); Childs and Su (2019), fourth-order Trotter formula shows a near-optimal scaling with respect to the system size for the lattice model, which is clearly shown in Fig. 16. From Fig. 16 we can see that, our second-order NCC algorithm shows an advantage over the fourth-order Trotter algorithm. Furthermore, the and scaling of our second-order NCC algorithm is similar to the fourth-order Trotter algorithm, which is near optimal.
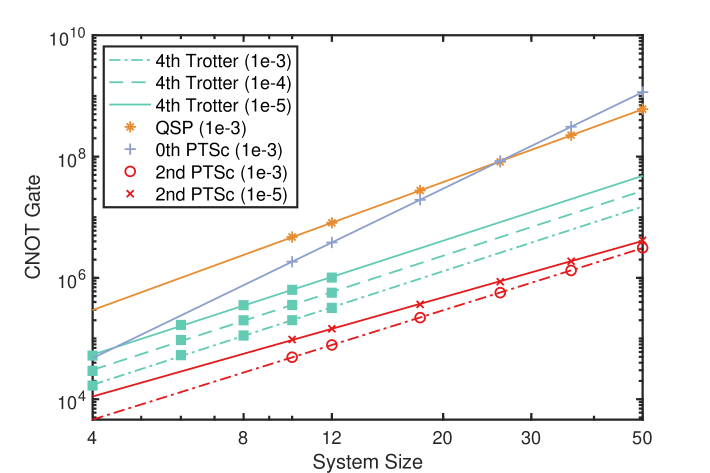
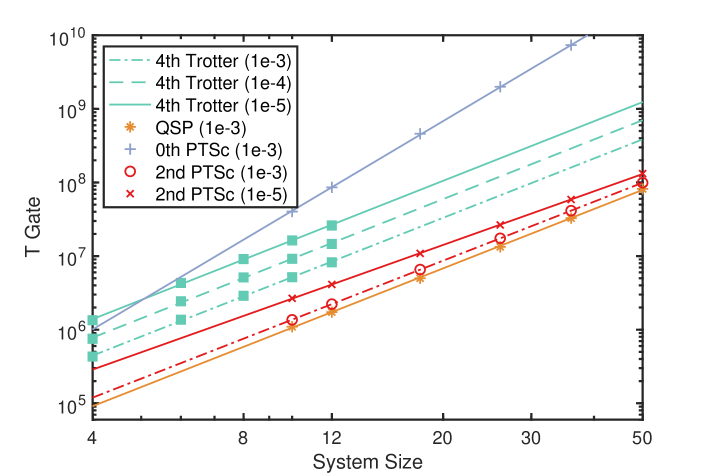
Appendix H COHERENT IMPLEMENTATION
In the main text, we primarily focus on the random-sampling implementation of the Trotter-LCU algorithms due to its simplicity. When the block encoding of an LCU formula of is feasible on a fault-tolerant quantum computer, we can also consider the coherent implementation of the Trotter-LCU algorithms.
The gate complexity of the coherent implementation of the Trotter-LCU algorithm is determined by the segment number , the Trotter order , the number of elementary unitaries and the gate complexity of each elementary unitary in the LCU formula. The value is related to the specific compensation method we use, which is usually proportional to and the truncation order . The gate complexity is
| (267) |
To estimate the segment number , we first find a proper evolution time such that the -norm . The segment number is then .
For the PTSC formula, based on the -norm bound in Theorem 1, we find that to ensure , it is sufficient to set . As a result, the number of segment . From Eq. 267, the overall gate complexity of the algorithm is
| (268) |
which is the same as the case when no Trotter formula is applied Berry et al. (2015).
For the NCC formula, based on the -norm bound in Theorem 2, we find that to ensure , we need to set . To achieve an overall simulation accuracy , we need
| (269) |
Therefore, it suffice to choose to be
| (270) |
In each segment, we need to implement th-order Trotter formula and the th- to th-order LCU formula. The number of elementary unitaries is . Therefore, the overall gate complexity is
| (271) |
Although it does not achieve the logarithmic accuracy dependence seen in standard post-Trotter algorithms Berry et al. (2015); Low and Chuang (2019), it has the unique advantage of a system-size dependence of , which could be advantageous in large-scale coherent Hamiltonian simulations.
References
- Feynman (1982) R. P. Feynman, International Journal of Theoretical Physics 21, 467 (1982), ISSN 1572-9575, URL https://doi.org/10.1007/BF02650179.
- Abrams and Lloyd (1999) D. S. Abrams and S. Lloyd, Phys. Rev. Lett. 83, 5162 (1999), URL https://link.aps.org/doi/10.1103/PhysRevLett.83.5162.
- Aspuru-Guzik et al. (2005) A. Aspuru-Guzik, A. D. Dutoi, P. J. Love, and M. Head-Gordon, Science 309, 1704 (2005), eprint https://www.science.org/doi/pdf/10.1126/science.1113479, URL https://www.science.org/doi/abs/10.1126/science.1113479.
- Farhi et al. (2014) E. Farhi, J. Goldstone, and S. Gutmann, A quantum approximate optimization algorithm (2014), URL https://arxiv.org/abs/1411.4028.
- Zhou et al. (2020) L. Zhou, S.-T. Wang, S. Choi, H. Pichler, and M. D. Lukin, Phys. Rev. X 10, 021067 (2020), URL https://link.aps.org/doi/10.1103/PhysRevX.10.021067.
- Harrow et al. (2009) A. W. Harrow, A. Hassidim, and S. Lloyd, Phys. Rev. Lett. 103, 150502 (2009), URL https://link.aps.org/doi/10.1103/PhysRevLett.103.150502.
- Lloyd (1996) S. Lloyd, Science 273, 1073 (1996), eprint https://www.science.org/doi/pdf/10.1126/science.273.5278.1073, URL https://www.science.org/doi/abs/10.1126/science.273.5278.1073.
- Suzuki (1990) M. Suzuki, Physics Letters A 146, 319 (1990), ISSN 0375-9601, URL https://www.sciencedirect.com/science/article/pii/037596019090962N.
- Suzuki (1991) M. Suzuki, Journal of Mathematical Physics 32, 400 (1991), URL https://aip.scitation.org/doi/10.1063/1.529425.
- Berry et al. (2007) D. W. Berry, G. Ahokas, R. Cleve, and B. C. Sanders, Communications in Mathematical Physics 270, 359 (2007), URL https://doi.org/10.1007/s00220-006-0150-x.
- Campbell (2019) E. Campbell, Phys. Rev. Lett. 123, 070503 (2019), URL https://link.aps.org/doi/10.1103/PhysRevLett.123.070503.
- Childs et al. (2019) A. M. Childs, A. Ostrander, and Y. Su, Quantum 3, 182 (2019), ISSN 2521-327X, URL https://doi.org/10.22331/q-2019-09-02-182.
- Childs and Su (2019) A. M. Childs and Y. Su, Phys. Rev. Lett. 123, 050503 (2019), URL https://link.aps.org/doi/10.1103/PhysRevLett.123.050503.
- Endo et al. (2019) S. Endo, Q. Zhao, Y. Li, S. Benjamin, and X. Yuan, Phys. Rev. A 99, 012334 (2019), URL https://link.aps.org/doi/10.1103/PhysRevA.99.012334.
- Heyl et al. (2019) M. Heyl, P. Hauke, and P. Zoller, Science Advances 5, eaau8342 (2019).
- Chen et al. (2021) C.-F. Chen, H.-Y. Huang, R. Kueng, and J. A. Tropp, PRX Quantum 2, 040305 (2021), URL https://link.aps.org/doi/10.1103/PRXQuantum.2.040305.
- Şahinoğlu and Somma (2021) B. Şahinoğlu and R. D. Somma, npj Quantum Information 7, 1 (2021), URL https://www.nature.com/articles/s41534-021-00451-w.
- Su et al. (2021) Y. Su, H.-Y. Huang, and E. T. Campbell, Quantum 5, 495 (2021), URL https://quantum-journal.org/papers/q-2021-07-05-495/.
- Tran et al. (2020) M. C. Tran, S.-K. Chu, Y. Su, A. M. Childs, and A. V. Gorshkov, Phys. Rev. Lett. 124, 220502 (2020), URL https://link.aps.org/doi/10.1103/PhysRevLett.124.220502.
- Childs et al. (2021) A. M. Childs, Y. Su, M. C. Tran, N. Wiebe, and S. Zhu, Phys. Rev. X 11, 011020 (2021), URL https://link.aps.org/doi/10.1103/PhysRevX.11.011020.
- Layden (2021) D. Layden, arXiv preprint arXiv:2107.08032 (2021).
- Zhao et al. (2022) Q. Zhao, Y. Zhou, A. F. Shaw, T. Li, and A. M. Childs, Phys. Rev. Lett. 129, 270502 (2022), URL https://link.aps.org/doi/10.1103/PhysRevLett.129.270502.
- Reiher et al. (2017) M. Reiher, N. Wiebe, K. M. Svore, D. Wecker, and M. Troyer, Proceedings of the National Academy of Sciences 114, 7555 (2017), eprint https://www.pnas.org/doi/pdf/10.1073/pnas.1619152114, URL https://www.pnas.org/doi/abs/10.1073/pnas.1619152114.
- Berry et al. (2014) D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma, in Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing (Association for Computing Machinery, New York, NY, USA, 2014), STOC ’14, p. 283–292, ISBN 9781450327107, URL https://doi.org/10.1145/2591796.2591854.
- Berry et al. (2015) D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma, Phys. Rev. Lett. 114, 090502 (2015), URL https://link.aps.org/doi/10.1103/PhysRevLett.114.090502.
- Berry et al. (2015) D. W. Berry, A. M. Childs, and R. Kothari, in 56th Annual IEEE Symposium on Foundations of Computer Science (2015), pp. 792–809, URL https://ieeexplore.ieee.org/abstract/document/7354428.
- Low and Chuang (2019) G. H. Low and I. L. Chuang, Quantum 3, 163 (2019), ISSN 2521-327X, URL https://doi.org/10.22331/q-2019-07-12-163.
- Low and Chuang (2017) G. H. Low and I. L. Chuang, Phys. Rev. Lett. 118, 010501 (2017), URL https://link.aps.org/doi/10.1103/PhysRevLett.118.010501.
- Low (2019) G. H. Low, in 51st Annual ACM Symposium on Theory of Computing (2019), pp. 491–502, ISBN 9781450367059, URL https://doi.org/10.1145/3313276.3316386.
- Childs and Wiebe (2012) A. M. Childs and N. Wiebe, Quantum Information and Computation 12, 0901 (2012), ISSN 1533-7146, URL http://dx.doi.org/10.26421/QIC12.11-12.
- Long (2011) G. L. Long, International Journal of Theoretical Physics 50, 1305 (2011), ISSN 1572-9575, URL https://doi.org/10.1007/s10773-010-0603-z.
- Lin and Tong (2022) L. Lin and Y. Tong, PRX Quantum 3, 010318 (2022), URL https://link.aps.org/doi/10.1103/PRXQuantum.3.010318.
- Yang et al. (2021) Y. Yang, B.-N. Lu, and Y. Li, PRX Quantum 2, 040361 (2021), URL https://link.aps.org/doi/10.1103/PRXQuantum.2.040361.
- Wan et al. (2022) K. Wan, M. Berta, and E. T. Campbell, Phys. Rev. Lett. 129, 030503 (2022), URL https://link.aps.org/doi/10.1103/PhysRevLett.129.030503.
- Faehrmann et al. (2022) P. K. Faehrmann, M. Steudtner, R. Kueng, M. Kieferova, and J. Eisert, Quantum 6, 806 (2022), ISSN 2521-327X, URL https://doi.org/10.22331/q-2022-09-19-806.
- Lin and Tong (2020) L. Lin and Y. Tong, Quantum 4, 372 (2020), ISSN 2521-327X, URL https://doi.org/10.22331/q-2020-12-14-372.
- Zeng et al. (2021) P. Zeng, J. Sun, and X. Yuan, Universal quantum algorithmic cooling on a quantum computer (2021), URL https://arxiv.org/abs/2109.15304.
- Zhang et al. (2022) R. Zhang, G. Wang, and P. Johnson, Quantum 6, 761 (2022), ISSN 2521-327X, URL https://doi.org/10.22331/q-2022-07-11-761.
- Kitaev (1995) A. Y. Kitaev, Quantum measurements and the abelian stabilizer problem (1995), URL https://arxiv.org/abs/quant-ph/9511026.
- Litinski (2019) D. Litinski, Quantum 3, 128 (2019), ISSN 2521-327X, URL https://doi.org/10.22331/q-2019-03-05-128.
- Canonne (2016) C. Canonne, A short note on poisson tail bounds (2016), URL http://www.cs.columbia.edu/~ccanonne/files/misc/2017-poissonconcentration.pdf.
- Babbush et al. (2018a) R. Babbush, N. Wiebe, J. McClean, J. McClain, H. Neven, and G. K.-L. Chan, Phys. Rev. X 8, 011044 (2018a), URL https://link.aps.org/doi/10.1103/PhysRevX.8.011044.
- Lee et al. (2021) J. Lee, D. W. Berry, C. Gidney, W. J. Huggins, J. R. McClean, N. Wiebe, and R. Babbush, PRX Quantum 2, 030305 (2021), URL https://link.aps.org/doi/10.1103/PRXQuantum.2.030305.
- Berry et al. (2019) D. W. Berry, C. Gidney, M. Motta, J. R. McClean, and R. Babbush, Quantum 3, 208 (2019), ISSN 2521-327X, URL https://doi.org/10.22331/q-2019-12-02-208.
- von Burg et al. (2021) V. von Burg, G. H. Low, T. Häner, D. S. Steiger, M. Reiher, M. Roetteler, and M. Troyer, Phys. Rev. Res. 3, 033055 (2021), URL https://link.aps.org/doi/10.1103/PhysRevResearch.3.033055.
- Hagan and Wiebe (2023) M. Hagan and N. Wiebe, Quantum 7, 1181 (2023), ISSN 2521-327X, URL https://doi.org/10.22331/q-2023-11-14-1181.
- Cho et al. (2024) C.-H. Cho, D. W. Berry, and M.-H. Hsieh, Phys. Rev. A 109, 062431 (2024), URL https://link.aps.org/doi/10.1103/PhysRevA.109.062431.
- Zhao and Yuan (2021) Q. Zhao and X. Yuan, Quantum 5, 534 (2021), ISSN 2521-327X, URL https://doi.org/10.22331/q-2021-08-31-534.
- Childs et al. (2018) A. M. Childs, D. Maslov, Y. Nam, N. J. Ross, and Y. Su, Proceedings of the National Academy of Sciences 115, 9456 (2018), URL https://www.pnas.org/content/115/38/9456.
- Bringmann and Panagiotou (2012) K. Bringmann and K. Panagiotou, in Automata, Languages, and Programming, edited by A. Czumaj, K. Mehlhorn, A. Pitts, and R. Wattenhofer (Springer Berlin Heidelberg, Berlin, Heidelberg, 2012), pp. 133–144, ISBN 978-3-642-31594-7.
- Hoorfar and Hassani (2008) A. Hoorfar and M. Hassani, J. Inequal. Pure and Appl. Math 9, 5 (2008), URL https://www.emis.de/journals/JIPAM/article983.html?sid=983.
- Babbush et al. (2018b) R. Babbush, C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler, and H. Neven, Phys. Rev. X 8, 041015 (2018b), URL https://link.aps.org/doi/10.1103/PhysRevX.8.041015.
- Sun et al. (2024) J. Sun, P. Zeng, T. Gur, and M. Kim, arXiv preprint arXiv:2406.04307 (2024).
- Bocharov et al. (2015) A. Bocharov, M. Roetteler, and K. M. Svore, Phys. Rev. Lett. 114, 080502 (2015), URL https://link.aps.org/doi/10.1103/PhysRevLett.114.080502.