Singlet, Triplet and Pair Density Wave Superconductivity in the Doped Triangular-Lattice Moiré System
Abstract
Recent experimental progress has established the twisted bilayer transition metal dichalcogenide (TMD) as a highly tunable platform for studying many-body physics. Particularly, the homobilayer TMDs under displacement field are believed to be described by a generalized triangular-lattice Hubbard model with a spin-dependent hopping phase . To explore the effects of on the system, we perform density matrix renormalization group calculations for the relevant triangular lattice t-J model. By changing at small hole doping, we obtain a region of quasi-long-range superconducting order coexisting with charge and spin density wave within . The superconductivity is composed of a dominant spin singlet -wave and a subdominant triplet -wave pairing. Intriguingly, the triplet pairing components feature pair density waves. In addition, we find a region of triplet superconductivity coexisting with charge density wave and ferromagnetism within , which is related to the former phase at smaller by a combined operation of spin-flip and gauge transformation. Our findings provide insights and directions for experimental search for exotic superconductivity in twisted TMD systems.
Introduction.—Moiré bilayer systems have attracted great attention over the last few years due to their high tunability and capacity to host a wealth of exotic states of matter Andrei et al. (2021); Balents et al. (2020); Kennes et al. (2021). Since the discovery of superconductivity (SC) and Mott insulating phase in magic-angle twisted bilayer graphene (TBG) Cao et al. (2018a, b), other Moiré systems have been realized and are under active studies Liu et al. (2020); Chen et al. (2019), including twisted bilayer transition metal dichalcogenides (TMDs) Zhang et al. (2020a); Shabani et al. (2021); Weston et al. (2020); Devakul et al. (2021); An et al. (2020); Naik and Jain (2018); Zhang et al. (2021); Regan et al. (2020); Schrade and Fu (2019); Zhang et al. (2020b). Compared to TBG, twisted bilayer TMDs have the advantages of accommodating flat Moiré bands over a much wider range of twist angles and fewer low-energy degrees of freedom, allowing for a simpler lattice model description Wu et al. (2018, 2019); Pan et al. (2020). Strong correlation effects such as correlated insulating phase Wang et al. (2020), metal-insulator transition Li et al. (2021a); Ghiotto et al. (2021), stripe phase Jin et al. (2021) and quantum anomalous Hall effect Li et al. (2021b) have recently been observed in these systems.
Twisted TMD bilayers can be classified into hetero- and homo-bilayers according to whether the two layers are made of the same or different materials. The low-energy electronic degrees of freedom in the former are believed to be described by a generalized triangular-lattice Hubbard model with pseudo-spin SU(2) rotation symmetry Wu et al. (2018); Tang et al. (2020), whereas in the latter the spin SU(2) symmetry is broken into U(1) by a vertical displacement field due to spin-valley locking and inversion symmetry breaking, and consequently the electron hopping acquires a spin-dependent phase Wu et al. (2019); Pan et al. (2020); Schrade and Fu (2019); Wang et al. (2023). Note that the standard Hubbard and t-J models on triangular lattices, i.e. , have exhibited a rich phenomenology enhanced by further-neighbor couplings due to the complex interplay between geometric frustration, quantum fluctuations and hole dynamics Raghu et al. (2010); Jiang (2021); Zhu and Chen (2023); Huang et al. (2023); Wang et al. (2004); Baskaran (2003); Motrunich and Lee (2004); Kumar and Shastry (2003); Chen et al. (2013); Venderley and Kim (2019a); Gannot et al. (2020); Peng et al. (2021). The hopping phase is shown to be widely tunable by the displacement field and thus may serve as a novel control knob of the many-body ground states of twisted TMD homobilayers. The magnetic and superconducting phases under the variation of both carrier density and of the U(1) Hubbard model and/or its closely related t-J model (for strong Hubbard U limit) at/near half-filling have been explored through mean-field calculations, renormalization group analysis, quantum cluster methods and Gutzwiller approximation Zang et al. (2021, 2022); Pan et al. (2020); Zhou and Zhang (2023); Wu et al. (2023a); Bélanger et al. (2022); Zegrodnik and Biborski (2023). However, these methods generally are not accurate in treating the strong electronic correlations present in the model Qin et al. (2022). Here we implement density matrix renormalization group (DMRG) White (1992) to accurately capture the ground states on quasi-1D few-leg cylinders, and thus reveal the different ordering tendencies at play and gain some insights into the physics at the 2D limit Stoudenmire and White (2012); Arovas et al. (2022). Particularly, DMRG has been applied onto a three-leg cylindrical Moiré Hubbard model but only weak SC correlations were observed Wietek et al. (2022). The effective spin-model derived at strong U and half-filling limit was also considered for exploring quantum spin liquid Kiese et al. (2022).
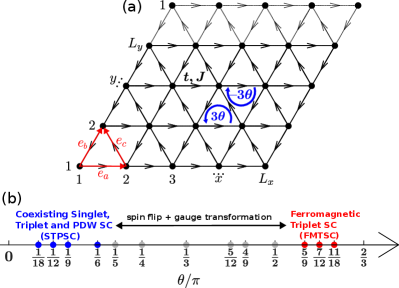
In this work we study SC of the lightly doped triangular lattice U(1) Moiré t-J model on a four-leg cylinder through DMRG calculations. By varying in the region of , we identify two conjugated superconducting phases as shown in Fig. 1(b): (i) Mixed spin singlet -wave and triplet -wave SC coexisting with spin, charge and pair density waves (PDW); (ii) Ferromagnetic triplet -wave SC coexisting with charge density wave (CDW). These two phases are related by a combined operation of spin flip and local gauge transformation, up to a change of the boundary condition. Their pairing correlations decay algebraically with the Luttinger exponents smaller or around two, demonstrating a robust quasi-long-range SC order Gong et al. (2021); Jiang and Kivelson (2021). Particularly, distinct from other SC phases on the triangular-lattice t-J model Jiang (2021); Huang et al. (2023); Zhu and Chen (2022), PDW is a novel SC state where Cooper pairs carry finite center-of-mass momentum Agterberg et al. (2020), which are not commonly realized in microscopic models Berg et al. (2010); Wu et al. (2023b, c); Huang et al. (2022); Jaefari and Fradkin (2012); Cho et al. (2012); Lee (2014); Soto-Garrido and Fradkin (2014); Venderley and Kim (2019b); Shaffer and Santos (2023). The plethora of interesting phases found in our calculations could motivate future experimental endeavour in search of novel SC in twisted TMD homobilayers.
Model and Method.— The Moiré t-J model is defined as
| (1) |
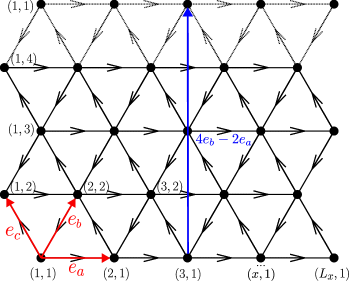
where represents spin up/down, and are the creation and annihilation operators for the electron with spin at the site , denote nearest neighbors whose locations satisfy (see Fig. 1(a)), are the spin- component, raising and lowering operators at site respectively, and is the electron number operator. Double occupancy is prohibited. The hopping phase produces a flux of at each triangular plaquette, and a gauge transformation connects two models differing in the fluxes by . We therefore focus on the region of . In the present study, we set the hole doping level , and choose and , corresponding to a realistic situation of Pan et al. (2020).
To obtain the ground state, we employ DMRG simulation with U(1)U(1) symmetry corresponding to charge and spin conservation on a cylindrical system with periodic boundary condition (PBC) along the circumferential ( or -) direction and open boundary condition along the axial ( or -) direction. The number of lattice sites is given by , where and are the number of sites along - and -direction respectively and are set as and in the main text. The corresponding geometry is called YC Yan et al. (2011). The doping level is defined by and we consider the zero total spin-z sector: , which hosts the ground state as verified in Sec. A of the supplemental materials (SM) SM . In DMRG, the number of Schmidt states kept for representing the reduced density matrix on either side of the system under bipartition is called “bond dimension” White (1992). The calculations improve with the increase of and become exact for a sufficiently large .
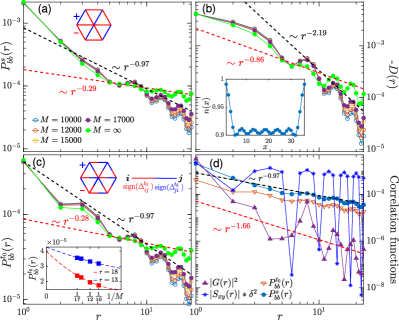
Coexisting Singlet, Triplet and PDW SC (STPSC).—The SC order is examined by the spin-singlet and triplet pairing correlation functions and defined by
| (2) |
where the reference point and the pairing operators and are defined on the bond along () at site :
| (3) |
Here corresponds to the triplet pairing with total spin-z .
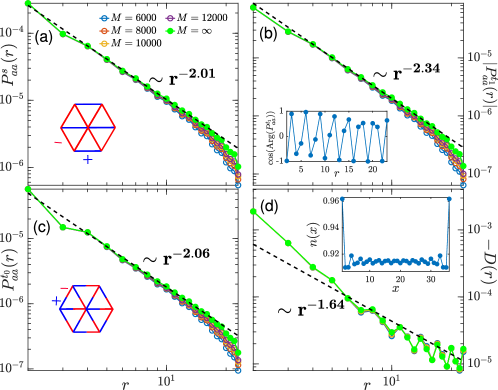
Fig. 2(a) and (c) show two dominant pairing components: -bond singlet pairing and opposite-spin-z () triplet pairing for in the STPSC phase. Both exhibit power-law decay with the Luttinger exponents , suggesting strongly diverging SC susceptibilities as the temperature Arrigoni et al. (2004). Note also that slow power-law decays are already exhibited by the largest- results with exponents around 0.97. The singlet pairing component is larger in amplitude than the triplet one, and they exhibit -wave and -wave symmetry respectively Raghu et al. (2010); Hsu et al. (2017); Venderley and Kim (2019a). The mixing of singlet and triplet pairings are permitted by the absence of the inversion and spin SU(2) symmetry Yip (2014). In particular, the absence of inversion center allows the mixing of parity-odd -wave and parity-even -wave basis functions in the irreducible representation of the symmetry group of the system Hsu et al. (2017). The charge density correlation function in Fig. 2(b) decays algebraically with a relatively larger exponent (around 0.86), suggesting weaker charge density modulations coexisting with stronger SC. Correspondingly we observe a charge stripe order with two holes per stripe in the inset. For comparison, Fig. 2(d) presents also the in-plane spin-spin correlations defined by
and the Green’s function . The in-plane spin correlation is the strongest among all correlations, characterizing a robust spin density wave order inherited from the 2D in-plane Néel order at half filling based on the spin structure factor calculations Wu et al. (2019); Zang et al. (2021); SM . The Green’s function squared is much weaker than the main pairing correlations, confirming the dominance of two-electron pairing over single-electron tunnelings.
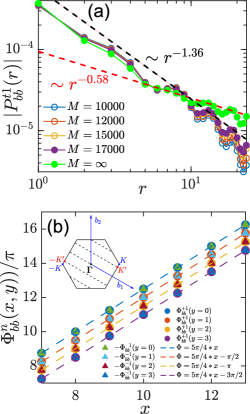
Moreover, in the triplet pairing components, we observe quasi-long-range PDW orders with a Luttinger exponent around 0.58 in Fig. 3(a). The PDW wavevector can be determined by the variation of the phase of the pairing correlation under displacement along both and . Specifically,
| (4) |
characterizes spatial variation of the phase of the -bond triplet pairing order parameters. In Fig. 3(b), is determined to be , which are the nearest accessible wavevectors to the Brillouin zone corners in the YC4 geometry. The same PDW wavevectors are identified for - and -bond. Note that a PDW ground state with was also predicted for the Moiré Hubbard model at by perturbative renormalization group analysis in the weak coupling regime Wu et al. (2023a, b).
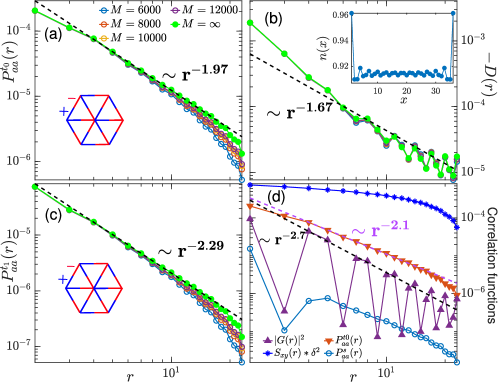
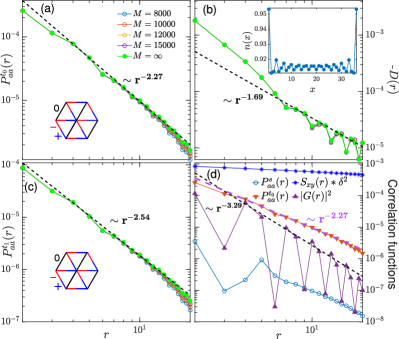
Ferromagnetic Triplet SC (FMTSC).—In the FMTSC phase, we find the dominant pairing channel to be a -wave spin triplet. In Fig. 4(a) and (c), both and are non-oscillatory, in accordance with uniform SC order in the bulk of the system, and decay algebraically with exponents slightly larger than 2. An accompanying CDW order is confirmed in Fig. 4(c) by both the quasi-long-range density correlation () and charge stripes in the electron density profile (one hole per stripe). In Fig. 4(d), a robust in-plane ferromagnetic spin correlation is observed in reminiscence of the parent ferromagnetic order Wu et al. (2019); Zang et al. (2021), with the total spin . The singlet paring is shown much weaker than the triplet ones as the triplet pairing is favored by ferromagnetism. The opposite-spin-z triplet pairing correlation has stronger amplitude and slower decay rate than those of the same-spin-z component because the ferromagnetic order is in-plane.
Discussion and Summary—The FMTSC and STPSC phases are related by a spin-flip operation followed by a local gauge transformation Zhou and Zhang (2023) as demonstrated in the SM. Particularly, the uniform z-spin-polarized triplet pairing order at in the FMTSC region is conjugated to the PDW order with at in the STPSC region:
| (5) |
with , where are the reciprocal wavevectors conjugated to and respectively. This is consistent with our observations at (Fig. 4(c)) and its conjugated partner (Fig. 3), albeit with a different flux (y-boundary phase) into the 4-leg cylinder. Moreover,
| (6) |
which means that the singlet and opposite-spin triplet pairing components are superposed to produce their counterparts in the conjugated phase. Since the singlet pairing component at is found negligible compared to the triplet components, and () or (), one has according to Eq. 6, which explains the larger magnitude of the spin singlet pairing than that of the triplet and the same power-law exponents in Fig. 2 (a) and (c).
However, the pairing correlations at has much stronger magnitude (over one order of magnitude larger) and slower decay rate compared to those at ( vs. ). This in addition to the difference in charge distributions (two vs. one holes per stripe) is caused by the change of the boundary condition: the periodic boundary condition at
| (7) |
turns into a twisted boundary condition Gannot and Kivelson (2023) at
| (8) |
after the gauge transformation, corresponding to inserting a magnetic flux of through the interior of the cylinder for electrons. The spin structure factor of the Néel order for is peaked at , which are not resolved in the 4-leg cylinder under PBC, whereas for the system is ferromagnetic with the peak at the system-supported momentum . Therefore, the former regime is more frustrated than the latter in the YC4 geometry and this might result in stronger SC. The sensitivity of SC to boundary conditions reveal finite-size effects in our four-leg system, so we also study a different cylinder geometry XC4 Szasz et al. (2020) (Sec. H in SM) as well as a YC3 system with (Sec. F in SM). Both systems preserve the PBC under local gauge transformation and support and in the Brillouin zone, therefore introducing no frustration. In the XC4 geometry, we again obtain the STPSC and FMTSC phases and their SC correlations now have similar amplitudes and decay with close exponents (), consistent with Eq. 6. In the YC3 cylinder at , the Luttinger exponents for SC () is nearly identical to that of the YC4 cylinder (). The observation of quasi-long-range SC order at different boundary conditions, cylinder geometries and sizes is positive evidence for the existence of SC in the 2D limit Szasz et al. (2020).
In contrast with the topological SC phases reported in the mean field and perturbative renormalization group studies of the doped TMD homobilayer Zhou and Zhang (2023); Wu et al. (2023a) or monolayer Hsu et al. (2017); Yuan et al. (2014), both the - and -wave SC phases found here are topologically trivial as the nearest-neighbor pairings acquire a phase of either 0 or after a rotation, instead of the nontrivial phases of and for and -wave topological SC phases Huang and Sheng (2022); Jiang and Jiang (2020); Huang et al. (2023). Furthermore, the SC phase here is distinct from the Ising SC found in electron-doped TMD monolayers Zhou et al. (2016); Lu et al. (2015); Xi et al. (2016); Saito et al. (2016) in that the former arises from hole doping the parent in-plane magnetic Mott insulator at strong electronic couplings whereas the latter the pinning of the electron spins in the Cooper pairs to the out-of-plane directions by the Ising spin-orbit interaction at weak electronic couplings. Finally, the case was also studied in Ref. Wietek et al. (2022), but a rather large power-law decay exponent () was found, so only weak SC was claimed there. Consistently we find that is located at the boundary of the SC region in Fig. 1, and its conjugated pair exhibits no clear signature of SC possibly because of less frustration.
In summary, we perform large-scale DMRG simulations of the Moiré t-J model on four-leg cylinders at small hole doping. By varying the spin-dependent hopping phase induced by the out-of-plane electric field, we identify two conjugated SC phases, one of which is characterized by the coexistence of singlet -wave, triplet -wave SC and PDW, and the other ferromagnetic triplet SC. Our study supports twisted TMDs as a highly tunable platform for realizing exotic SC phases.
Data Availability.— The ITensor DMRG code and the data for all the figures in the main text and SM can be accessed by https://github.com/cfengno1/Moire-t-J-Model.
Acknowledgments.— We thank Yuchi He for useful comments. This work was supported by the U.S. Department of Energy, Office of Basic Energy Sciences under Grant No. DE-FG02-06ER46305. ITensor library Fishman et al. (2022) is used in this work for all DMRG calculations.
References
- Andrei et al. (2021) E. Y. Andrei, D. K. Efetov, P. Jarillo-Herrero, A. H. MacDonald, K. F. Mak, T. Senthil, E. Tutuc, A. Yazdani, and A. F. Young, Nat Rev Mater 6, 201 (2021), number: 3 Publisher: Nature Publishing Group.
- Balents et al. (2020) L. Balents, C. R. Dean, D. K. Efetov, and A. F. Young, Nat. Phys. 16, 725 (2020), number: 7 Publisher: Nature Publishing Group.
- Kennes et al. (2021) D. M. Kennes, M. Claassen, L. Xian, A. Georges, A. J. Millis, J. Hone, C. R. Dean, D. N. Basov, A. N. Pasupathy, and A. Rubio, Nat. Phys. 17, 155 (2021), number: 2 Publisher: Nature Publishing Group.
- Cao et al. (2018a) Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori, and P. Jarillo-Herrero, Nature 556, 80 (2018a), number: 7699 Publisher: Nature Publishing Group.
- Cao et al. (2018b) Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Nature 556, 43 (2018b), number: 7699 Publisher: Nature Publishing Group.
- Liu et al. (2020) X. Liu, Z. Hao, E. Khalaf, J. Y. Lee, Y. Ronen, H. Yoo, D. Haei Najafabadi, K. Watanabe, T. Taniguchi, A. Vishwanath, and P. Kim, Nature 583, 221 (2020), number: 7815 Publisher: Nature Publishing Group.
- Chen et al. (2019) G. Chen, A. L. Sharpe, P. Gallagher, I. T. Rosen, E. J. Fox, L. Jiang, B. Lyu, H. Li, K. Watanabe, T. Taniguchi, J. Jung, Z. Shi, D. Goldhaber-Gordon, Y. Zhang, and F. Wang, Nature 572, 215 (2019), number: 7768 Publisher: Nature Publishing Group.
- Zhang et al. (2020a) Z. Zhang, Y. Wang, K. Watanabe, T. Taniguchi, K. Ueno, E. Tutuc, and B. J. LeRoy, Nat. Phys. 16, 1093 (2020a), number: 11 Publisher: Nature Publishing Group.
- Shabani et al. (2021) S. Shabani, D. Halbertal, W. Wu, M. Chen, S. Liu, J. Hone, W. Yao, D. N. Basov, X. Zhu, and A. N. Pasupathy, Nat. Phys. 17, 720 (2021), number: 6 Publisher: Nature Publishing Group.
- Weston et al. (2020) A. Weston, Y. Zou, V. Enaldiev, A. Summerfield, N. Clark, V. Zólyomi, A. Graham, C. Yelgel, S. Magorrian, M. Zhou, J. Zultak, D. Hopkinson, A. Barinov, T. H. Bointon, A. Kretinin, N. R. Wilson, P. H. Beton, V. I. Fal’ko, S. J. Haigh, and R. Gorbachev, Nat. Nanotechnol. 15, 592 (2020), number: 7 Publisher: Nature Publishing Group.
- Devakul et al. (2021) T. Devakul, V. Crépel, Y. Zhang, and L. Fu, Nat Commun 12, 6730 (2021), number: 1 Publisher: Nature Publishing Group.
- An et al. (2020) L. An, X. Cai, D. Pei, M. Huang, Z. Wu, Z. Zhou, J. Lin, Z. Ying, Z. Ye, X. Feng, R. Gao, C. Cacho, M. Watson, Y. Chen, and N. Wang, Nanoscale Horiz. 5, 1309 (2020), publisher: The Royal Society of Chemistry.
- Naik and Jain (2018) M. H. Naik and M. Jain, Phys. Rev. Lett. 121, 266401 (2018), publisher: American Physical Society.
- Zhang et al. (2021) Y.-H. Zhang, D. N. Sheng, and A. Vishwanath, Phys. Rev. Lett. 127, 247701 (2021).
- Regan et al. (2020) E. C. Regan, D. Wang, C. Jin, M. I. Bakti Utama, B. Gao, X. Wei, S. Zhao, W. Zhao, Z. Zhang, K. Yumigeta, M. Blei, J. D. Carlström, K. Watanabe, T. Taniguchi, S. Tongay, M. Crommie, A. Zettl, and F. Wang, Nature 579, 359 (2020), number: 7799 Publisher: Nature Publishing Group.
- Schrade and Fu (2019) C. Schrade and L. Fu, Phys. Rev. B 100, 035413 (2019), publisher: American Physical Society.
- Zhang et al. (2020b) Y. Zhang, N. F. Q. Yuan, and L. Fu, Phys. Rev. B 102, 201115(R) (2020b), publisher: American Physical Society.
- Wu et al. (2018) F. Wu, T. Lovorn, E. Tutuc, and A. H. MacDonald, Phys. Rev. Lett. 121, 026402 (2018), publisher: American Physical Society.
- Wu et al. (2019) F. Wu, T. Lovorn, E. Tutuc, I. Martin, and A. H. MacDonald, Phys. Rev. Lett. 122, 086402 (2019), publisher: American Physical Society.
- Pan et al. (2020) H. Pan, F. Wu, and S. Das Sarma, Phys. Rev. Res. 2, 033087 (2020), publisher: American Physical Society.
- Wang et al. (2020) L. Wang, E.-M. Shih, A. Ghiotto, L. Xian, D. A. Rhodes, C. Tan, M. Claassen, D. M. Kennes, Y. Bai, B. Kim, K. Watanabe, T. Taniguchi, X. Zhu, J. Hone, A. Rubio, A. N. Pasupathy, and C. R. Dean, Nat. Mater. 19, 861 (2020), number: 8 Publisher: Nature Publishing Group.
- Li et al. (2021a) T. Li, S. Jiang, L. Li, Y. Zhang, K. Kang, J. Zhu, K. Watanabe, T. Taniguchi, D. Chowdhury, L. Fu, J. Shan, and K. F. Mak, Nature 597, 350 (2021a), number: 7876 Publisher: Nature Publishing Group.
- Ghiotto et al. (2021) A. Ghiotto, E.-M. Shih, G. S. S. G. Pereira, D. A. Rhodes, B. Kim, J. Zang, A. J. Millis, K. Watanabe, T. Taniguchi, J. C. Hone, L. Wang, C. R. Dean, and A. N. Pasupathy, Nature 597, 345 (2021), number: 7876 Publisher: Nature Publishing Group.
- Jin et al. (2021) C. Jin, Z. Tao, T. Li, Y. Xu, Y. Tang, J. Zhu, S. Liu, K. Watanabe, T. Taniguchi, J. C. Hone, L. Fu, J. Shan, and K. F. Mak, Nat. Mater. 20, 940 (2021), number: 7 Publisher: Nature Publishing Group.
- Li et al. (2021b) T. Li, S. Jiang, B. Shen, Y. Zhang, L. Li, Z. Tao, T. Devakul, K. Watanabe, T. Taniguchi, L. Fu, J. Shan, and K. F. Mak, Nature 600, 641 (2021b), number: 7890 Publisher: Nature Publishing Group.
- Tang et al. (2020) Y. Tang, L. Li, T. Li, Y. Xu, S. Liu, K. Barmak, K. Watanabe, T. Taniguchi, A. H. MacDonald, J. Shan, and K. F. Mak, Nature 579, 353 (2020), number: 7799 Publisher: Nature Publishing Group.
- Wang et al. (2023) J. Wang, J. Zang, J. Cano, and A. J. Millis, Phys. Rev. Research 5, L012005 (2023).
- Raghu et al. (2010) S. Raghu, S. A. Kivelson, and D. J. Scalapino, Phys. Rev. B 81, 224505 (2010), publisher: American Physical Society.
- Jiang (2021) H.-C. Jiang, npj Quantum Mater. 6, 1 (2021), number: 1 Publisher: Nature Publishing Group.
- Zhu and Chen (2023) Z. Zhu and Q. Chen, Phys. Rev. B 107, L220502 (2023), publisher: American Physical Society.
- Huang et al. (2023) Y. Huang, S.-S. Gong, and D. N. Sheng, Phys. Rev. Lett. 130, 136003 (2023), publisher: American Physical Society.
- Wang et al. (2004) Q.-H. Wang, D.-H. Lee, and P. A. Lee, Phys. Rev. B 69, 092504 (2004), publisher: American Physical Society.
- Baskaran (2003) G. Baskaran, Phys. Rev. Lett. 91, 097003 (2003), publisher: American Physical Society.
- Motrunich and Lee (2004) O. I. Motrunich and P. A. Lee, Phys. Rev. B 69, 214516 (2004), publisher: American Physical Society.
- Kumar and Shastry (2003) B. Kumar and B. S. Shastry, Phys. Rev. B 68, 104508 (2003), publisher: American Physical Society.
- Chen et al. (2013) K. S. Chen, Z. Y. Meng, U. Yu, S. Yang, M. Jarrell, and J. Moreno, Phys. Rev. B 88, 041103(R) (2013), publisher: American Physical Society.
- Venderley and Kim (2019a) J. Venderley and E.-A. Kim, Phys. Rev. B 100, 060506(R) (2019a), publisher: American Physical Society.
- Gannot et al. (2020) Y. Gannot, Y.-F. Jiang, and S. A. Kivelson, Phys. Rev. B 102, 115136 (2020), publisher: American Physical Society.
- Peng et al. (2021) C. Peng, Y.-F. Jiang, Y. Wang, and H.-C. Jiang, New J. Phys. 23, 123004 (2021), publisher: IOP Publishing.
- Zang et al. (2021) J. Zang, J. Wang, J. Cano, and A. J. Millis, Phys. Rev. B 104, 075150 (2021), publisher: American Physical Society.
- Zang et al. (2022) J. Zang, J. Wang, J. Cano, A. Georges, and A. J. Millis, Phys. Rev. X 12, 021064 (2022), publisher: American Physical Society.
- Zhou and Zhang (2023) B. Zhou and Y.-H. Zhang, Phys. Rev. B 108, 155111 (2023).
- Wu et al. (2023a) Y.-M. Wu, Z. Wu, and H. Yao, Phys. Rev. Lett. 130, 126001 (2023a), publisher: American Physical Society.
- Bélanger et al. (2022) M. Bélanger, J. Fournier, and D. Sénéchal, Phys. Rev. B 106, 235135 (2022).
- Zegrodnik and Biborski (2023) M. Zegrodnik and A. Biborski, Phys. Rev. B 108, 064506 (2023).
- Qin et al. (2022) M. Qin, T. Schäfer, S. Andergassen, P. Corboz, and E. Gull, Annual Review of Condensed Matter Physics 13, 275 (2022), _eprint: https://doi.org/10.1146/annurev-conmatphys-090921-033948.
- White (1992) S. R. White, Phys. Rev. Lett. 69, 2863 (1992), publisher: American Physical Society.
- Stoudenmire and White (2012) E. Stoudenmire and S. R. White, Annual Review of Condensed Matter Physics 3, 111 (2012), _eprint: https://doi.org/10.1146/annurev-conmatphys-020911-125018.
- Arovas et al. (2022) D. P. Arovas, E. Berg, S. A. Kivelson, and S. Raghu, Annual Review of Condensed Matter Physics 13, 239 (2022), _eprint: https://doi.org/10.1146/annurev-conmatphys-031620-102024.
- Wietek et al. (2022) A. Wietek, J. Wang, J. Zang, J. Cano, A. Georges, and A. Millis, Phys. Rev. Res. 4, 043048 (2022), publisher: American Physical Society.
- Kiese et al. (2022) D. Kiese, Y. He, C. Hickey, A. Rubio, and D. M. Kennes, APL Materials 10, 031113 (2022), publisher: American Institute of Physics.
- Gong et al. (2021) S. Gong, W. Zhu, and D. N. Sheng, Phys. Rev. Lett. 127, 097003 (2021), publisher: American Physical Society.
- Jiang and Kivelson (2021) H.-C. Jiang and S. A. Kivelson, Phys. Rev. Lett. 127, 097002 (2021).
- Zhu and Chen (2022) Z. Zhu and Q. Chen, “Superconductivity in doped triangular mott insulators: the roles of parent spin backgrounds and charge kinetic energy,” (2022).
- Agterberg et al. (2020) D. F. Agterberg, J. S. Davis, S. D. Edkins, E. Fradkin, D. J. Van Harlingen, S. A. Kivelson, P. A. Lee, L. Radzihovsky, J. M. Tranquada, and Y. Wang, Annual Review of Condensed Matter Physics 11, 231 (2020), _eprint: https://doi.org/10.1146/annurev-conmatphys-031119-050711.
- Berg et al. (2010) E. Berg, E. Fradkin, and S. A. Kivelson, Phys. Rev. Lett. 105, 146403 (2010), publisher: American Physical Society.
- Wu et al. (2023b) Z. Wu, Y.-M. Wu, and F. Wu, Phys. Rev. B 107, 045122 (2023b).
- Wu et al. (2023c) Y.-M. Wu, P. A. Nosov, A. A. Patel, and S. Raghu, Phys. Rev. Lett. 130, 026001 (2023c), publisher: American Physical Society.
- Huang et al. (2022) K. S. Huang, Z. Han, S. A. Kivelson, and H. Yao, npj Quantum Mater. 7, 1 (2022), number: 1 Publisher: Nature Publishing Group.
- Jaefari and Fradkin (2012) A. Jaefari and E. Fradkin, Phys. Rev. B 85, 035104 (2012), publisher: American Physical Society.
- Cho et al. (2012) G. Y. Cho, J. H. Bardarson, Y.-M. Lu, and J. E. Moore, Phys. Rev. B 86, 214514 (2012), publisher: American Physical Society.
- Lee (2014) P. A. Lee, Phys. Rev. X 4, 031017 (2014), publisher: American Physical Society.
- Soto-Garrido and Fradkin (2014) R. Soto-Garrido and E. Fradkin, Phys. Rev. B 89, 165126 (2014), publisher: American Physical Society.
- Venderley and Kim (2019b) J. Venderley and E.-A. Kim, Science Advances 5, eaat4698 (2019b), publisher: American Association for the Advancement of Science.
- Shaffer and Santos (2023) D. Shaffer and L. H. Santos, Phys. Rev. B 108, 035135 (2023).
- (66) See Supplemental Material at http://link.aps.org/ supplemental/ for supporting results.
- Yan et al. (2011) S. Yan, D. A. Huse, and S. R. White, Science 332, 1173 (2011), publisher: American Association for the Advancement of Science.
- Arrigoni et al. (2004) E. Arrigoni, E. Fradkin, and S. A. Kivelson, Phys. Rev. B 69, 214519 (2004), publisher: American Physical Society.
- Hsu et al. (2017) Y.-T. Hsu, A. Vaezi, M. H. Fischer, and E.-A. Kim, Nat Commun 8, 14985 (2017), number: 1 Publisher: Nature Publishing Group.
- Yip (2014) S. Yip, Annual Review of Condensed Matter Physics 5, 15 (2014), _eprint: https://doi.org/10.1146/annurev-conmatphys-031113-133912.
- Gannot and Kivelson (2023) Y. Gannot and S. A. Kivelson, Phys. Rev. B 107, 075127 (2023), publisher: American Physical Society.
- Szasz et al. (2020) A. Szasz, J. Motruk, M. P. Zaletel, and J. E. Moore, Phys. Rev. X 10, 021042 (2020), publisher: American Physical Society.
- Yuan et al. (2014) N. F. Q. Yuan, K. F. Mak, and K. T. Law, Phys. Rev. Lett. 113, 097001 (2014), publisher: American Physical Society.
- Huang and Sheng (2022) Y. Huang and D. N. Sheng, Phys. Rev. X 12, 031009 (2022), publisher: American Physical Society.
- Jiang and Jiang (2020) Y.-F. Jiang and H.-C. Jiang, Phys. Rev. Lett. 125, 157002 (2020), publisher: American Physical Society.
- Zhou et al. (2016) B. T. Zhou, N. F. Q. Yuan, H.-L. Jiang, and K. T. Law, Phys. Rev. B 93, 180501(R) (2016), publisher: American Physical Society.
- Lu et al. (2015) J. M. Lu, O. Zheliuk, I. Leermakers, N. F. Q. Yuan, U. Zeitler, K. T. Law, and J. T. Ye, Science 350, 1353 (2015), publisher: American Association for the Advancement of Science.
- Xi et al. (2016) X. Xi, Z. Wang, W. Zhao, J.-H. Park, K. T. Law, H. Berger, L. Forró, J. Shan, and K. F. Mak, Nature Phys 12, 139 (2016), number: 2 Publisher: Nature Publishing Group.
- Saito et al. (2016) Y. Saito, Y. Nakamura, M. S. Bahramy, Y. Kohama, J. Ye, Y. Kasahara, Y. Nakagawa, M. Onga, M. Tokunaga, T. Nojima, Y. Yanase, and Y. Iwasa, Nature Phys 12, 144 (2016), number: 2 Publisher: Nature Publishing Group.
- Fishman et al. (2022) M. Fishman, S. White, and E. Stoudenmire, SciPost Phys. Codebases , 4 (2022).
Supplemental Materials
In the Supplemental Materials, we provide additional results to support the claims made in the main text. In Sec. .1, we verify that the ground state satisfies . In Sec. .2, we present the relative signs for pairings along different bonds, from which one can deduce the pairing symmetries. In Sec. .3, the spin structure factors for and are given to show the underlying in-plane Néel and ferromagnetic orders respectively. In Sec. .4, the Green’s functions are fitted by exponential decay. Sec. .5 shows the transformation between the STPSC and FMTSC phases. Sec. .6 shows the power-law decay of the pairing and CDW correlations on a width-3 cylinder. Sec. .7 shows the power-law fittings for the pairing correlations in the gray area (non-SC regime) of the phase diagram Fig. 1 in the main text, where large Luttinger exponents are found. Finally, in Sec. .8 the spin structure factors and different correlation functions of the XC4 cylinder are shown, exhibiting the same phases as those in the YC4 cylinder.
.1 Verification of in the ground state
To verify that the ground state satisfies , we run DMRG calculates for systemS imposing only the particle number conservation and find in the ground state.
.2 Sign structure of the pairing orders
We demonstrate the relative sign between pairings along two nearest-neighbor bonds and by the sign of their correlation . Specifically, for the STPSC phase represented by in Fig. S1(a), we deduce sign()=sign()=sign() and sign()=sign()=sign(), corresponding to ordinary -wave and -wave symmetry respectively. For the FMTSC phase represented by in Fig. S1(b), we deduce from the very weak -bond triplet pairing correlations . Besides, we find sign()=-sign(), therefore -wave symmetry is identified.
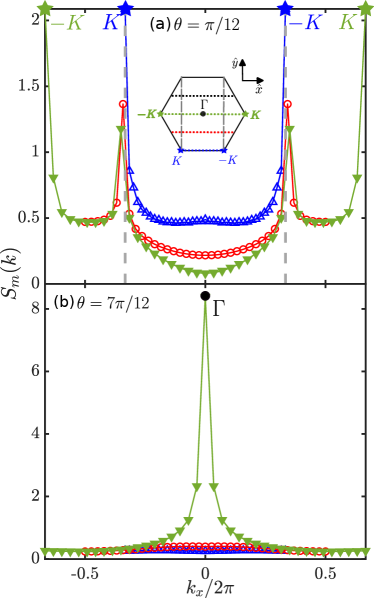
.3 Spin structure factors for and in the YC4 geometry
The spin structure factor is defined as
| (S1) |
For the geometry in Fig. 1 of the main text, the wavevector are quantized according to
| (S2) |
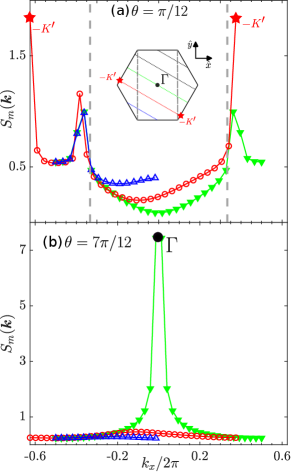
The undoped parent state has a in-plane Néel order charaterized by peaks at Brillouin zone corners Zang et al. (2021). Fig. S2(a) shows a dominant peak at when , and since are the nearest resolved wavevectors to the zone corners, we conclude that spin density wave order at is inherited from the parent state Néel order. In contrast, the structure factor is peaked at the Brillouin zone center when , indicating a ferromagnetic order, which is also host by the undoped system Zang et al. (2021).
.4 Exponential fits for at and in the YC4 geometry
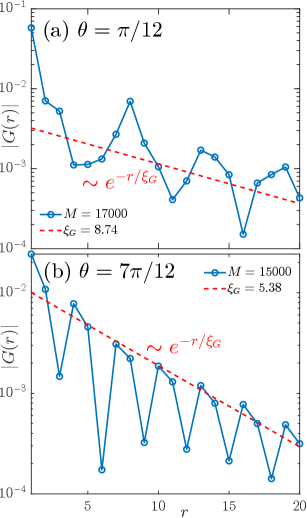
The Green’s functions in the main text are fitted by power-law decays with relatively larger exponents than the pairing correlations, but here we show in Fig. S3 that they can be equally well fitted by exponential decays.
.5 Transformation between STPSC and FMTSC phases
We show in this section how to transform between the FMTSC and STPSC phase by a spin-flip operation followed by a gauge transformation. First, the spin flip is tantamount to reversing in the Hamiltonian:
| (S3) |
Second, and are gauge equivalent as the flux through each triangle differs by in them and the gauge transformation Zhou and Zhang (2023) acts as:
| (S4) |
where are the reciprocal wavevectors conjugated to and respectively. Combining these two operations then gives
| (S5) |
Now suppose there is uniform pairing order parameter at :
where is the ground state for . Since , we have for :
| (S6) |
which gives rise to Eq. 5 and 6 in the main text.
.6 SC and CDW orders for
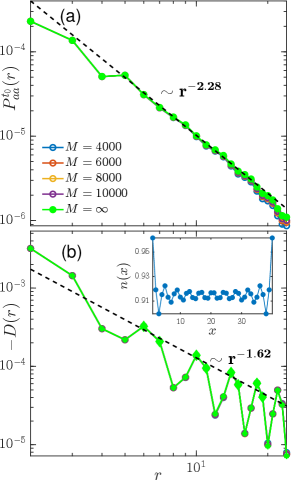
To study the width dependence of the SC and CDW order, we also calculate a YC3 system at (see Fig. S4) and find that the Luttinger exponents for pairing and charge density correlations are close to those of the YC4 system. Similarly, a charge stripe order with one hole per stripe is observed.
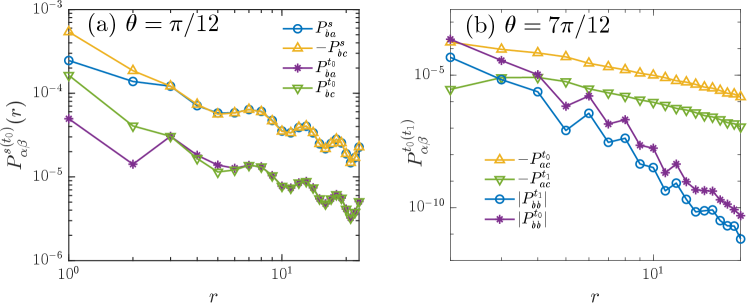
.7 SC correlation of non-SC (gray-dot) regime in the phase diagram
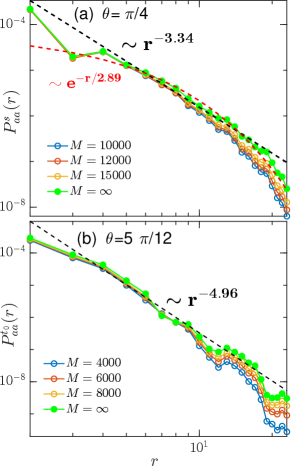
We show in Fig. S5 the dominant SC correlations for two representative points in the middle regime of the phase diagram Fig. 1(b) in the main text. The Luttinger exponents are significantly larger than 2 and the exponential fit gives a SC correlation length smaller than the system width. Therefore a clear signature of SC order is lacking.
.8 Results for the XC4 geometry
To complement the YC4 geometry in the main text, here we also study another geometry called XC4 Szasz et al. (2020) shown in Fig. S6. The wavevector s are quantized according to
| (S7) |
and the resolved s are denoted as dotted line in the inset of Fig. S7(a). The PBC
| (S8) |
is unchanged under gauge transformation.
The spin structure factors for and in Fig. S7 shows main peaks at and respectively, confirming the Néel and ferromagnetic orders inherited from the parent states.
Similar to the YC4 geometry, we also find the STPSC phase at (Fig. S8) and FMTSC phase at (Fig. S9) in the XC4 geometry with SC Luttinger exponents around 2. Note that the Luttinger exponents satisfy . This is expected due to the linear relation in Eq. 5 in the main text and the near absence of singlet pairing at in Fig. S9(d). Likewise , in agreement with the relation in Eq. S6.