Present address: ]Department of Physics, Shizuoka University, Shizuoka, 422-8529, Japan
Site-selective observation of spin dynamics of a Tomonaga-Luttinger liquid in frustrated Heisenberg chains
Abstract
Low-energy spin dynamics is investigated by 35 Cl NMR measurements in a frustrated antiferromagnet Ca3ReO5Cl2. The local spin susceptibility measured with the Knight shift behaves as a one-dimensional Heisenberg antiferromagnet and remains constant down to low temperatures, as expected in a gapless Tomonaga-Luttinger liquid. The nuclear spin-lattice relaxation rate demonstrates a slowing down of atomic motions and a power-law evolution of spin correlation. The Luttinger parameter is enhanced in a site-selective manner depending on the form factor of dynamical spin susceptibility. The strong anisotropy of reflects the strong spin-orbit coupling through Dzyaloshinskii-Moriya interaction. The ground state exhibits an incommensurate antiferromagnetic ordering with low-lying magnon excitations.
I Introduction
A Tomonaga-Luttinger liquid (TLL) is characterized by fractional gapless excitations and bosonic collective modes in one-dimensional (1D) localized spin chains [1, 2, 3]. The spin correlation function of TLL follows a universal power law. One of the observables is the nuclear spin-lattice relaxation rate , which measures the dynamical spin susceptibility summed over the wave vector space in a low-energy limit. It approximately obeys the power-law temperature dependence [4, 5, 6, 7, 8, 9]:
| (1) |
where is one of the TLL parameters. A spin-1/2 Heisenberg chain yields , in which becomes -invariant [10, 11, 12, 13]. depends on the Ising anisotropy and the magnetic field strength respectively acting as the interaction and chemical potential of spinless fermions [2]. As three-dimensional (3D) coupling between the chains sets in, the system heads toward long-range magnetic ordering with the effectively enhanced above the transition temperature [14, 15]. On the spin-1/2 ladder and spin-1 chain exhibiting a nonmagnetic ground state, the spin correlation measured with sensitively depends on the magnetic field [16, 17, 18, 19, 20, 21, 22, 23].
The anisotropic triangular antiferromagnet connects 1D TLL to two-dimensional (2D) quantum spin liquid as a function of the ratio of the interchain interaction and the intrachain interaction [2, 24, 25, 26, 27]. Geometrical frustration reduces the interchain correlation and hence the system dimensionality [28, 29]. The TLL phase is stabilized up to the exchange anisotropy for the interchain exchange coupling and the intrachain coupling [28, 25, 30, 29, 26, 27]. A spiral magnetic order occurs for - on the triangular lattice. The quantum spin liquid, if any, near the isotropic point may involve a tiny spin gap and topological order [10, 31], which is distinct from the renormalized 1D liquid phase.
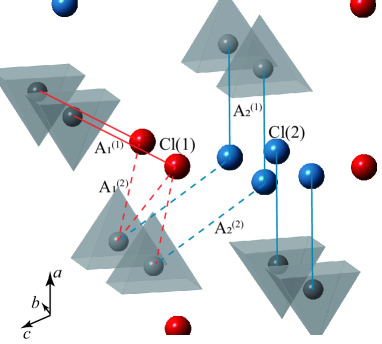
An example of the spin-1/2 anisotropic triangular antiferromagnets, Cs2CuCl4 (), exhibits magnetic orders and TLL behavior with bound spinons, depending on the magnetic field strength and direction, as observed by NMR and inelastic neutron-scattering measurements [32, 33, 34, 30, 35, 36, 37]. A transition-metal oxychloride Ca3ReO5Cl2 (CROC) is served as another example of the spin-1/2 quasi-1D antiferromagnet with the anisotropic triangular lattice, as shown in Fig. 1 [38, 39, 40]. CROC forms an orthorhombic lattice, where the ReO5 square-pyramid with the orbital forms a chain along the axis. Despite the strong spin-orbit coupling of Re ions, the orbital moment is quenched under the asymmetric ligand field and perturbatively contributes to the ground state through the Dzyaloshinskii-Moriya (DM) interaction , where is parallel to the axis in the mirror plane. The interchain coupling within the plane constructs an anisotropic triangular lattice, as shown in Fig. 1. The anisotropy of the triangular lattice has been evaluated as / = 0.25 from the high-field magnetization [41], consistent with that of the calculation of density functional theory (DFT) (/ = 0.295) [39, 42]. At low temperatures, behaves as a spin-1/2 1D antiferromagnetic Heisenberg model with = 41 K [39, 43], which implies a reduction of the dimensionality. The ground state eventually exhibits a long-range magnetic order below = 1.13 K. Thus, one can investigate the spin correlation of the TLL state featured by in an extensive temperature range of . Below , magnon excitation may coexist with bound spinons in the high-energy dispersion observed by the inelastic neutron scattering [44].
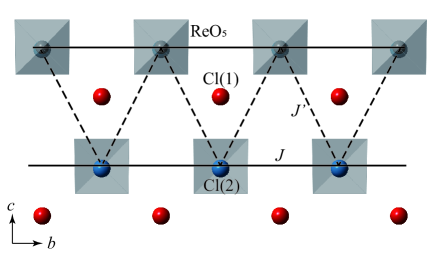
Here we investigate the spin excitation and structure on the quasi-1D CROC with site-selective Cl NMR spectroscopy. We determine the Knight shift and electric field gradient (EFG) tensors for two Cl sites and then compare the result with the calculation. and measurements respectively uncover static and dynamic spin susceptibilities of CROC in the TLL regime at low temperatures. We show remarkable anisotropy and site dependence of , which are discussed in terms of the DM interaction and the wave-vector dependence of the form factor of the anisotropic dynamical spin susceptibility.
II Method
The single crystals of CROC were grown by a flux method with a mixture of CaO, ReO3, and CaCl2 in a quartz ampule [38]. The typical dimensions of the crystal were 0.5 5 2 mm3. We performed 35Cl and 37Cl (nuclear spins ) NMR measurements on a single crystal of CROC under the steady magnetic field . We utilized a dual-axis rotator for the angular dependence measurement above 1.5 K and a single-axis one in a 3He cryostat below 1.5 K. Frequency-swept NMR spectra were obtained from spin-echo signals taken by a 0.3 MHz step using a pulse sequence with = 1.5–2.0 and = 50–100 s. The Knight shift was evaluated from the central resonance frequency by subtracting the higher-order quadrupole contribution with the exact diagonalization of the nuclear-spin Hamiltonian in Appendix A. The spin-lattice relaxation rate was measured with a saturation recovery method, in which nuclear magnetization obeys The spin-echo decay rate was obtained from for two Cl sites.
The nuclear quadrupole frequency was calculated with FPLO version 22 [45] for the standard basis (S), the extended basis (D), and the extended basis with additional (D4f) basis sets. The values presented in the manuscript were calculated using the D4f basis, which provides the highest accuracy, on a mesh of points. Relativistic effects were neglected full-relativistic calculations on sparser meshes yielded nearly identical (differing by less than 4%) quadrupole frequencies. Since there are many heavy atoms in the structure, we use the local density approximation (LDA) functional [46].
III Experimental results
III.1 Local spin susceptibility and magnetic order
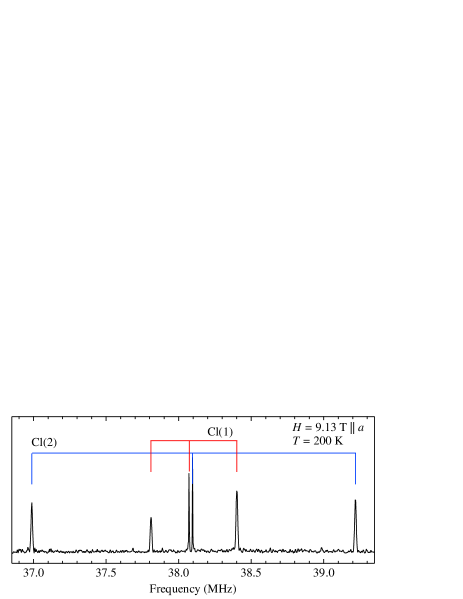
The 35Cl NMR spectrum of CROC consists of extremely sharp resonance lines coming from two Cl sites, Cl(1) and Cl(2), under magnetic field along the axis, as shown in Fig. 2. For , the spectrum from each Cl site splits into three due to the electric-quadrupole interaction between the nuclear quadrupole moment and the EFG at the Cl site. The number of resonance lines doubles as the inversion symmetry is broken away from the and planes, which allows us the accurate field alignment along the crystal axes within . The quadrupole splitting and the central frequency are plotted in Fig. 8 of Appendix A. The angular dependence is compared with the LDA calculation based on the crystal structure of CROC, leading to the unambiguous site assignment of the resonance lines into Cl(1) and Cl(2), as shown in Fig. 2.
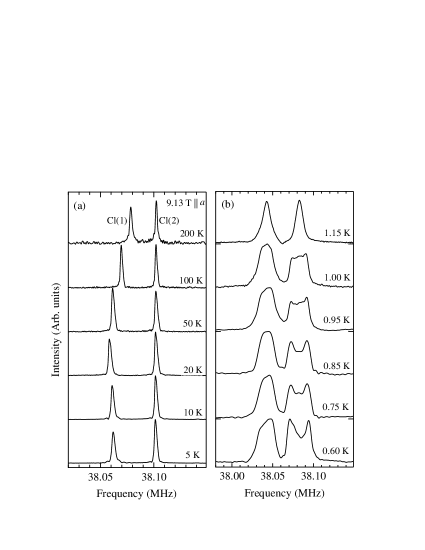
The NMR spectrum displays a site-dependent shift upon cooling, as shown in Fig. 3(a). The low-frequency spectrum from Cl(1) exhibits a downward shift, while the higher one from Cl(2) stays at nearly the same position. Since exhibits Curie-Weiss paramagnetic behavior at high temperatures, the downward shift indicates the negative hyperfine coupling constant for Cl(1). Surprisingly, the linewidth remains sharp down to low temperatures, indicating a high-quality crystal free from the magnetic inhomogeneity arond free spins.
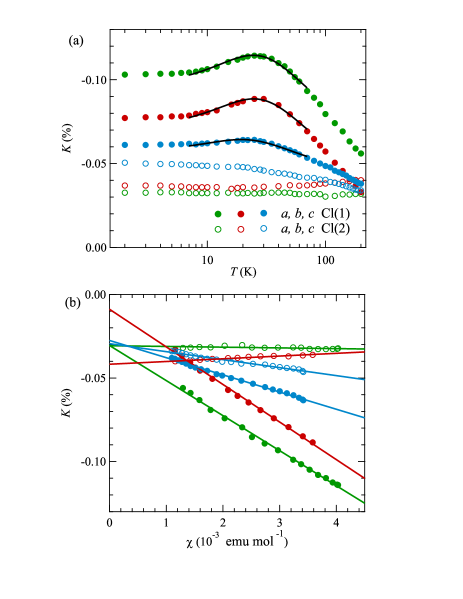
The Knight shift obtained from the central resonance line scales to the local spin susceptibility along the crystal axis; (), where is the diagonal hyperfine coupling, the Avogadro number, and the Bohr magneton. Figure 4 shows the dependence of for Cl(1) and Cl(2), denoted as and , respectively. increases upon cooling, showing a broad peak around 28 K. It becomes nearly constant at low temperatures. The temperature dependence of for each crystal axis fits to the Bonner-Fisher model with = 38 K ( K) [47] in agreement with the result of ( K) [39]. In contrast with the bulk , the local spin susceptibility obtained from excludes an impurity contribution and extracts the intrinsic residual spin susceptibility down to low temperatures ( emu/mol), which corroborates the gapless TLL state. The spin susceptibility of TLL is expressed as using the spin velocity at [48, 49]. Using the -linear term of the specific heat, mJ/(K mol) [39], the Wilson ratio is obtained as 2.46. It is compared with expected for TLL spin chains [49]. Using for Cl(1) from as described below (Table. 1), we can independently obtain –3.48, consistent with the Knight shift.
Since is nearly isotropic [39], the anisotropy of comes from the anisotropic hyperfine coupling constant governed by transfer or dipole interactions. linearly scales to above 28 K, as seen in the plot [Fig. 4(b)]. The components of the hyperfine coupling tensor are evaluated from the linearity as (, , , ) = (, , , 0.13)T/ for Cl(1). Here, is evaluated from the angular dependence of Knight shifts. The diagonalization yields the principal components of the hyperfine coupling (, , ) = (0.04, , )T/ for Cl(1). The anisotropy is not explained by the dipolar interaction (), and hence comes from the transferred hyperfine interaction. In contrast, along the and axes very weakly depends on , indicating the tiny hyperfine coupling constants. We obtained (, , , ) = (, 0.01, , 0.14)T/ and (, , ) = (0.12, 0.01, )T/ for Cl(2). The remarkable site dependence reflects the transferred hyperfine paths originating the anisotropic Re orbital, as discussed in Appendixes.
Below = 1.1 K, the NMR spectrum broadens and changes to a double horn shape, as shown in Fig. 3(b). It shows an emergence of the spontaneous local field below . One can exclude a possible collinear magnetic ordering that involves a discrete splitting of the NMR spectrum by the staggered hyperfine field. Despite a hyperfine coupling constant of Cl(1) greater than Cl(2), the splitting amplitude is smaller for Cl(1) along the axis. This means that the local fields at Cl sites are generated through the off-diagonal hyperfine coupling from the Re magnetic moments oriented perpendicular to the axis. The double horn shape is typically observed in incommensurate magnetic orders such as corn and spiral orders [35, 50]. In the present case with strong 1D anisotropy, weakly incommensurate modulation of the wave vector can be induced by DM interactions due to the lack of inversion symmetry along the chain [44, 41]. For the -vector parallel to the axis, the DM interaction forces the magnetic moments to align perpendicular to D. Therefore, we conclude that the moment direction should be close to the axis.
III.2 Critical slowing-down of spin and atomic fluctuations
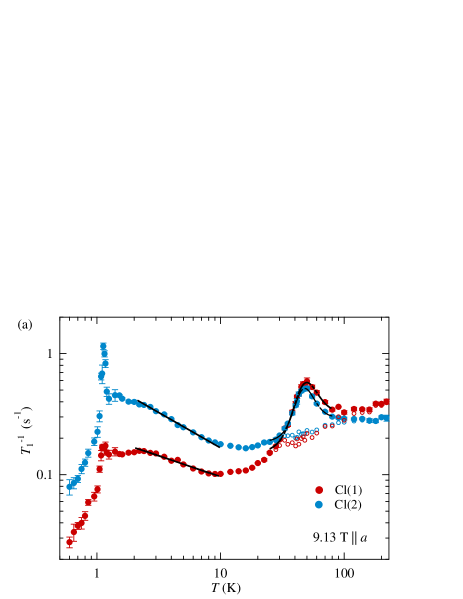
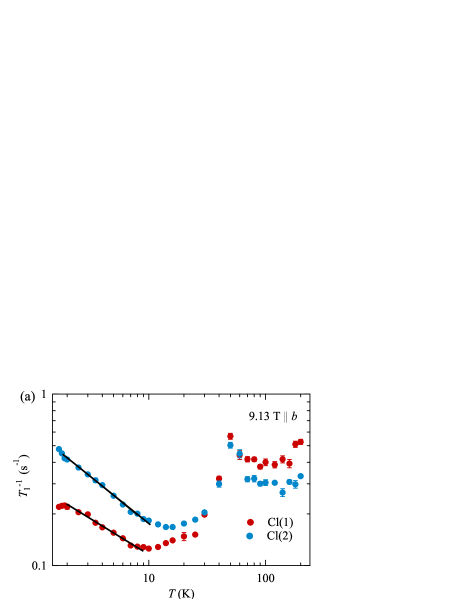
The nuclear spin-lattice relaxation rate measures low-energy excitations in the NMR frequency window through magnetic and electric hyperfine interactions. As shown in Fig. 5(a), exhibits sharp and broad peaks around 1.1 and 50 K, respectively, for = 9.13 T along the axis. The sharp peak manifests the critical slowing-down of spin fluctuations toward long-range magnetic ordering at = 1.1 K. drops steeply () below where the excitation is dominated by gapless magnons.
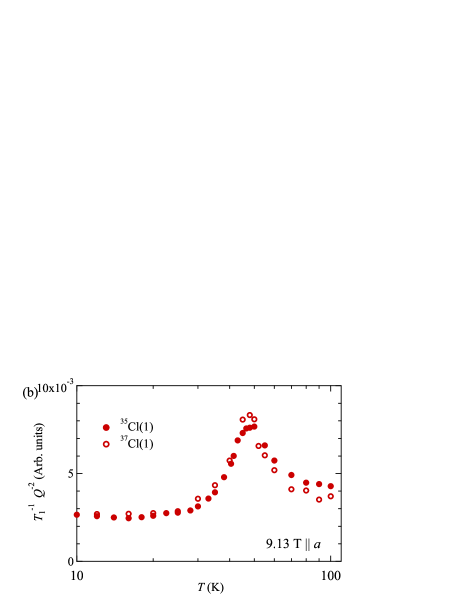
The broad peak around 50 K can be attributed to structural fluctuations such as atomic motions instead of phase transition, since there is no signature of symmetry breaking in the NMR spectrum (Fig. 3) and specific heat [39]. For confirmation, we measured of two isotopes 35Cl and 37Cl having distinct nuclear quadrupole moments and , respectively. As shown in Fig. 5(b), approximately scales to around 50 K, consistent with the predominant EFG fluctuations [51].
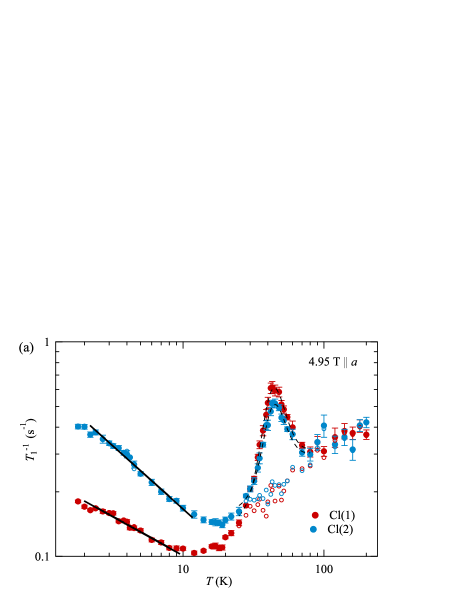
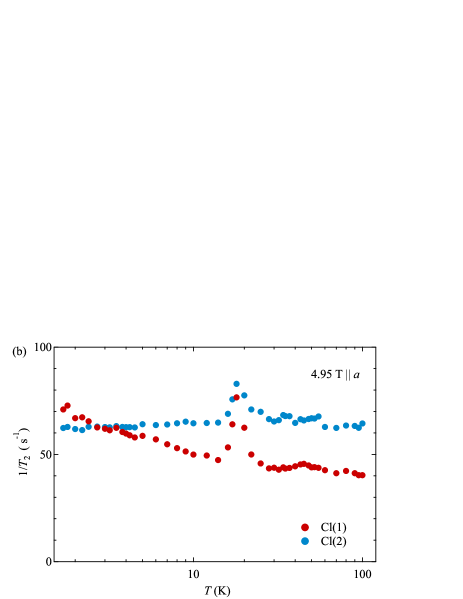
As the resonance frequency decreases from 38 MHz at 9.13 T to 20 MHz at 4.95 T, the peak shifts to 43 K, as shown in Fig. 6(a). Further low frequency ( kHz) fluctuations can be observed through , where the spin-echo intensity decays exponentially with the pulse interval time s. As seen from the sharp resonance line, is extremely long, despite a paramagnetic Mott insulator, and reaches ms for Cl(1). As shown in Fig. 6(b), is independent of above 30 K and exhibits a sharp peak at = 18 K, indicating the freezing of atomic motions. Upon cooling, remains constant for Cl(2), while it gradually increases for Cl(1) toward the magnetic order.
From a structural point of view, the x-ray diffraction measurement on CROC shows a large thermal structure factor of Cl sites at room temperature [38]. Although the structural data of CROC are absent at low temperatures, the metastable atomic positions may induce a persistent structural instability due to the large open space. Interestingly, the structural freezing coincides with the onset of antiferromagnetic correlation, as manifested in the peak at 20 K.
The system crossovers from a quantum TLL regime () into a classical diffusive regime () with increasing temperature. In an intermediate temperature range of , spin dynamics of 1D chains is expected to obey the superdiffusive Kardar-Parisi-Zhang (KPZ) universality with characteristic spin correlation [52, 53]. To extract the spin dynamics of the crossover regime, we subtract the structural contribution from by assuming the Lorentzian correlation function in the Bloembergen-Purcell-Pound (BPP) model [54]:
| (2) |
where is the correlation time, , with the activation energy and the constant . The experimental result is well fitted by Eq. (2) at the measured frequency (38 and 20 MHz at 9.13 and 4.95 T, respectively), as shown in Figs. 5 and 6, which yields 300 K. The fitting extracts a power law term with the exponent in the temperature range above 20 K. It differs from those of the local spin fluctuations () [55] and the KPZ universality () [52, 53]. The exponent is rather close to that expected in the spin-drag relaxation of the spin-diffusion regime [56].
III.3 Spin dynamics in the critical TLL regime
At low temperatures (), would be dominated by spin fluctuations along the chain, where structural fluctuations are exponentially suppressed. According to the fluctuation-dissipation theorem, the imaginary part of dynamical spin susceptibility relates to the dynamical spin structure factor . is expressed as [55, 57, 50, 58]
where () is the form factor at the wave vector q and defined by using the Fourier transformed hyperfine coupling . and are the imaginary part of the dynamical spin susceptibility perpendicular and parallel to the magnetic field. Here, the axis is taken along the applied magnetic field direction. In 1D Mott insulators the low-energy is dominated by specific wave vectors close to = (0, , 0) [2, 4, 10]. A shift from by the magnetic field would be negligible when the Zeeman energy is much lower than the exchange interaction . Instead, the DM interaction induces a small splitting of the spinon dispersion by [44], which is also omitted in the following analysis for simplicity.
In a TLL regime, obeys a power law in an anisotropic manner, and [4, 7]. For an isotropic case, both transverse and longitudinal components of are independent of temperature (), as expected for the antiferromagnetic Heisenberg chain [10, 4]. They become anisotropic as the Ising anisotropy of the model deviates from unity. For , the transverse component is enhanced at low temperatures, whereas the parallel component vanishes and thus becomes negligible. Furthermore, as seen from Eq. (3), contributes to only through the off-diagonal hyperfine coupling. Therefore, would be dominated by , as shown in Eq.(1).
Below 10 K, increases with a power law , as shown in Fig. 5. The fitting yields for Cl(1) and for Cl(2) in a magnetic field of 9.13 T along the axis. Applying the relation in Eq. (1), we obtained = 0.79 and 1.21 for Cl(1) and Cl(2), respectively. Since the dynamical spin susceptibility is carried by Re spins, should be independent of the probe nuclear spins. Therefore, the observed Cl site dependence comes from the form factor dependence that filters antiferromagnetic fluctuations at the specific wave vector, as typically observed in tetragonal cuprate and pnictide superconductors [11, 58].
Referring to the crystal structure of CROC in Figs. 1 and 9, Cl(1) is located between neighboring Re atoms, while Cl(2) is on the Re atom along the axis. Here we consider antiferromagnetic spin fluctuations at the wave vector = (0, , 0) along the chain. The staggered hyperfine fields from the second-neighbor Re sites are canceled out at Cl(1), as shown by the site-symmetry analysis in Appendix B. Then, the antiferromagnetic correlation at = is filtered through the form factor at Cl(1), while it remains at Cl(2). Therefore, measured at Cl(1) is strongly suppressed in contrast to that of Cl(2), despite the uniform hyperfine coupling of Cl(1) greater than that of Cl(2). is indeed reversed between Cl(1) and Cl(2) at high temperatures above 50 K, where the uniform mode becomes dominant.
In the TLL regime, the external magnetic field works as chemical potential and enhances magnetization or , as observed in the spin-1/2 ladder system with the spin gap [15]. We have investigated the field dependence of for the Cl sites at = 4.95 T, as shown in Fig. 6. There is no significant field effect on , consistent with the negligible effect of the Zeeman energy in the gapless TLL, as listed in Table 1. Instead, the energy scale of the DM interaction is comparable to the magnetic field and thus impacts on the anisotropy.
III.4 Anisotropy of
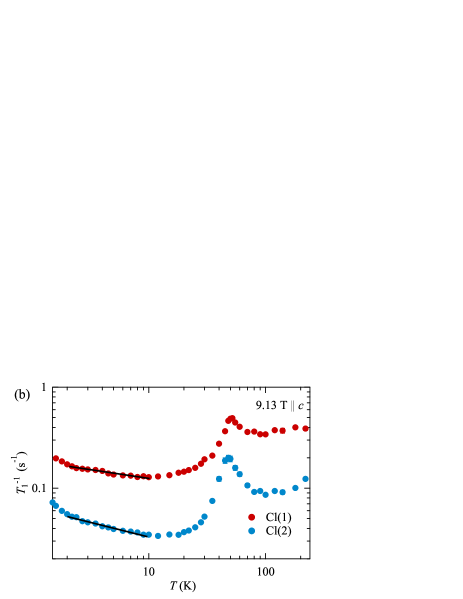
Finally, we investigate the anisotropy of by applying the magnetic field = 9.13 T along the and axes, as shown in Fig. 7. The result along the axis is similar to that for the axis in Figs. 5(a) and 6, where is dominated by atomic fluctuations at high temperatures and then by electric spin fluctuations below 20 K. At low temperatures, we obtain and 1.13 for Cl(1) and Cl(2), respectively, as listed in Table 1. In contrast, the anisotropy of for the axis is not reversed at low temperatures, suggesting that the mode is less dominant in for Cl(1) and Cl(2). Interestingly, remains anisotropic in the intermediate temperature range where exhibits the broad peak. It may indicate significant spin-lattice coupling through the DM interaction. In the TLL regime below 20 K, we obtained , 0.61 for Cl(1) and 0.70 for Cl(2), which is much lower than those in the other directions. The reason can be attributed to the anisotropy of dynamical spin susceptibility, as discussed below.
IV Discussion
The enhancement of might be interpreted as the repulsive interaction of spinless fermions based on the model. In the present system showing isotropic spin susceptibility, the effective spin Hamiltonian would be close to the Heisenberg model with . Therefore, the large for Cl(2) will originate in the antiferromagnetic correlation toward , which is not taken into account within the simple TLL theory.
In the critical regime, the transverse component of is expected to follow the power law against reduced temperature, , within the dynamical scaling hypothesis [59, 14], where is the correlation length exponent, the dynamical exponent, the dimensionality, and the anomalous exponent. The exponents depend on the universality: e.g. a mean field and a 2D model yield and , respectively. Approaching , the system exhibits a crossover from 1D to 3D regime, leading to the nominal enhancement of .
The effect of critical spin fluctuations on can be calculated from the random phase approximation (RPA) below 10 K [14, 15]. A fitting into our experimental result reduces , as listed in Table 1. The value is still close to unity for Cl(2). The result implies that critical spin fluctuations can be reproduced beyond the mean-field approximation near .
The anisotropy of can be explained in terms of spinon dynamics under the DM interaction . In CROC, the DM vector is directed along the axis within the mirror plane. Spinon dispersion splits by = 310 GHz at or along the chain, as observed by the EPR measurement [41]. The excitation branches split with increasing the magnetic field strength along the axis, whereas they monotonically increase with magnetic field along the and axes. The DM interaction induces the magnetic order with the moments directed within the plane. As a result, antiferromagnetic fluctuations are enhanced when the magnetic field is applied to the plane, while they are suppressed under the field along the axis where the effect of DM interaction is minimized. Therefore, the critical spin fluctuations are largely suppressed for the axis, which extracts the intrinsic of the TLL regime.
The field dependence of differs from that of the spin-ladder system with the gapped ground state [15, 19, 18]. The magnetic field induces the paramagnetic or long-range order phase where the effect of the DM interaction may not be negligible. However, detailed angular dependence measurements of spin fluctuations are absent. Our determination of the TLL parameter through the anisotropy measurement will promote further theoretical studies on the anisotropic hydrodynamics of quasi-1D quantum liquids.
V Conclusion
We have investigated the magnetic ground state and the anisotropic low-energy excitation through the 35Cl NMR measurement on the quasi-one-dimensional antiferromagnet Ca3ReO5Cl2 with the DM interaction. We determined the nuclear quadrupole splitting and Knight shift tensors by the angular dependence of the 35Cl NMR spectrum in agreement with the LDA calculation. The nuclear spin-lattice and spin-spin relaxation rates show slow atomic dynamics in the intermediate temperature range. We observed a power-law devolution of spin correlation, characteristic of one-dimensional quantum liquid. The site and angular dependence of the Luttinger parameter comes from the form-factor filtering of the antiferromagnetic correlation induced by the DM interaction. The incommensurate magnetic order occurs below 1 K with the low-lying magnon excitation.
Acknowledgements
We thank a technical support from T. Jinno and useful discussion with H. Yoshioka, S. Capponi, and N. Shannon. We acknowledge the financial support from Grant-in-aid in scientific research by JSPS (No.19H05824, 22H05256, 23H04025, 24H00954, 20H05150, 22H01178, 22H04462).
Appendix A Nuclear quadrupole splitting
In this section, we show a complete set of the angular dependence of nuclear quadrupole splitting , which is compared with the DFT calculation.
The nuclear spin Hamiltonian is expressed as a sum of the magnetic Zeeman interaction and the electric quadrupole interaction :
| (4) |
where the Zeeman term is given by
| (5) |
The hyperfine field is given by with the Knight shift tensor . The nuclear quadrupole interaction is given by
| (6) |
where the nuclear quadrupole splitting is defined by
| (7) |
with the electric field gradient (EFG) and the nuclear quadrupole moment . Under an intense magnetic field, the 35Cl () NMR spectrum splits into three by the interval frequency .
The second-order electric quadrupole interaction gives a frequency shift of the central transition in the order of . The satellite lines from the and transitions shift equally by the second-order effect. We obtain by subtracting the lowest satellite frequency from the highest one.
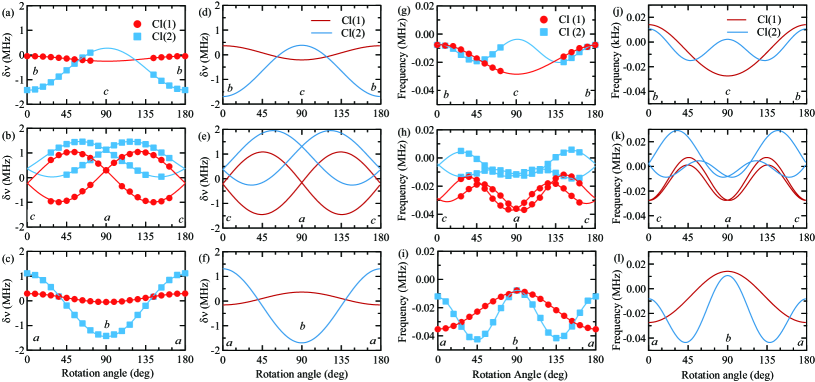
We measured the angular dependence of about three crystal axes at 20 K and 9.13 T, as shown in Fig. 8. Without detailed analysis below, the profiles of the experimental result in Figs. 8(a,b,c) agree well with those of the LDA calculation in Figs. 8(d,e,f). Thus, we can successfully assign the 35Cl NMR spectra to two Cl sites with different local environment.
Since both Cl sites are located on the mirror plane normal to the axis, the axis must be one of the principal axes of the EFG tensor [60, 61]. Thus, there is only one set of the spectrum from each Cl site, when we rotate the sample in the crystal plane including the axis. Then the off-diagonal terms vanish in the tensor: = 0, = .
The number of NMR lines doubles in the -plane rotation about the axis without the spatial inversion symmetry. The rotation about the axis is analyzed with the Volkoff formula [62, 63]. On the -plane rotation with the angle measured from the axis, is fitted by
| (8) |
where the fitting coefficients are given by
| (9) |
Thus, we obtained ( for each crystal axis and the off-diagonal element , as listed in Table 2. The diagonalization of the tensor yields the principal components ( = X, Y, Z) and the asymmetric factor , where , , and are defined by satisfying . The results are compared with the LDA calculation based on the electronic structure of CROC in Figs. 8(d-f) and Table. 3. Then We can obtain the quadrupole frequency :
| (10) |
where the principal component of the diagonalized electric field gradient tensor [51].
| Cl(1) | 0.29 | 0.98 | 0.05 | 0.99 | 0.90 | |||
| Cl(2) | 1.09 | 0.36 | 0.61 | 0.02 | 1.43 | 0.98 |
| Cl(1) | 0.47 | 0.05 | 1.27 | 0.05 | 1.34 | 0.92 | ||
| Cl(2) | 1.29 | 0.36 | 1.00 | 1.93 | 0.77 |
The angular dependence of the central resonance () frequency is shown in Figs. 8(g-i) and compared to the second-order nuclear quadrupole effect obtained from the LDA calculation in Figs. 8(k-l). The good agreement between the experimental result and the calculation allows the site assignment for the two Cl sites. Then we obtained the Knight shift tensor K after subtracting the second-order quadrupole contribution by the exact diagonalization of the nuclear spin Hamiltonian of Eq.(5).
We obtained the Knight shift tensor arising from the hyperfine interaction with Re electron spins at 200 K:
| , |
in % for Cl(1) and Cl(2), respectively. The diagonalization of the tensor yields for Cl(1) and for Cl(2), where is directed at and from the axis in the plane, respectively. We also calculated the magnetic dipole field at Cl sites from Re ions. However, the result disagrees with the experimental result, which indicates that the Knight shift is governed by the transferred hyperfine coupling through the oxygen and calcium ions. Therefore, the hyperfine coupling does not necessarily scale to the atomic distances but depends on the paths through the overlap between the wavefunctions. The following discussion for the form factor is independent of the numerical value of the hyperfine coupling.
Appendix B Form factors of dynamical spin susceptibility
To explain the site dependence of , we evaluated the form factor of the dynamical spin susceptibility using the symmetry operation in the crystal structure of CROC [38]. As shown in Fig. 1, Cl(1) and Cl(2) sites are located between Re ions and on the Re ion, respectively. Here we focus on the original Cl sites with the fractional coordinate of the position, , , and the surrounding Re sites (). Then we semi-quantitatively evaluate the hyperfine coupling based on the local symmetry.
For Cl(1), there are one first neighbor Re site (3.716Å), Re, two second ones (4.094Å), Re and Re, two third ones (4.892Å), Re and Re, and one fourth one (5.868Å) Re. The fractional coordinates of Re are given by Re = , Re, Re, Re, Re, and Re, where . The relative vectors of the Cl(1)-Re bonds are thus written as , , , , , and . Here Re and Re are connected via mirror reflection normal to the plane on Cl(1).
Thus the hyperfine coupling tensor can be expressed as
| (11) | |||||
| (12) |
, , and are written similar to , , and , respectively. The net hyperfine coupling tensor is expressed as a sum of the hyperfine paths, . Taking Fourier transformation
| (13) |
we obtain the uniform mode of the hyperfine coupling tensor for Cl(1)
where we omit the higher order terms for simplicity. The staggered mode along the axis with the specific wave vector is expected to dominate the low-energy spin correlation in the 1D chain. The hyperfine tensor at is calculated as
The second neighbor interactions remain for but vanished for in the diagonal components. Namely, antiferromagnetic spin fluctuations are partly filtered through the hyperfine form factor at Cl(1).
As for Cl(2) = , , there are one nearest neighbor (3.555Å) and one second neighbor (4.350Å) Re site. We omit the higher order terms with the distance exceeding 5 Å. Similar to Cl(1), the Cl(2)-Re vectors are expressed as and . Thus both the uniform and staggered mode of the hyperfine coupling tensor () is expressed as
The hyperfine form factor along the field direction, is calculated as . For , is greater than . Since the staggered spin fluctuations at are dominant at low temperatures, the reversed values of Cl(1) and Cl(2) can be attributed to the partial cancellation of the form factor at Cl(1) due to the antisymmetric spin fluctuations at the second neighbor Re spins.
References
- Haldane [1981] F. D. M. Haldane, J. Phys. C: Solid State Phys. 14, 2585 (1981).
- Giamarchi [2003] T. Giamarchi, Quantum physics in one dimension (Oxford Univ. Press, 2003).
- Sachdev [2011] S. Sachdev, Quantum Phase Transitions, 2nd ed. (Cambridge University Press, 2011).
- Chitra and Giamarchi [1997] R. Chitra and T. Giamarchi, Critical properties of gapped spin-chains and ladders in a magnetic field, Phys. Rev. B 55, 5816 (1997).
- Bocquet et al. [2001] M. Bocquet, F. H. L. Essler, A. M. Tsvelik, and A. O. Gogolin, Finite-temperature dynamical magnetic susceptibility of quasi-one-dimensional frustrated spin- Heisenberg antiferromagnets, Phys. Rev. B 64, 094425 (2001).
- Hikihara and Furusaki [2001] T. Hikihara and A. Furusaki, Spin correlations in the two-leg antiferromagnetic ladder in a magnetic field, Phys. Rev. B 63, 134438 (2001).
- Sato et al. [2009] M. Sato, T. Momoi, and A. Furusaki, NMR relaxation rate and dynamical structure factors in nematic and multipolar liquids of frustrated spin chains under magnetic fields, Phys. Rev. B 79, 060406 (2009).
- Sato et al. [2011] M. Sato, T. Hikihara, and T. Momoi, Field and temperature dependence of NMR relaxation rate in the magnetic quadrupolar liquid phase of spin- frustrated ferromagnetic chains, Phys. Rev. B 83, 064405 (2011).
- Coira et al. [2016] E. Coira, P. Barmettler, T. Giamarchi, and C. Kollath, Temperature dependence of the NMR spin-lattice relaxation rate for spin- chains, Phys. Rev. B 94, 144408 (2016).
- Sachdev [1994] S. Sachdev, NMR relaxation in half-integer antiferromagnetic spin chains, Phys. Rev. B 50, 13006 (1994).
- Takigawa et al. [1991] M. Takigawa, A. P. Reyes, P. C. Hammel, J. D. Thompson, R. H. Heffner, Z. Fisk, and K. C. Ott, Cu and O nmr studies of the magnetic properties of YBa2Cu3O6.63 (Tc=62 K), Phys. Rev. B 43, 247 (1991).
- Takigawa et al. [1996] M. Takigawa, N. Motoyama, H. Eisaki, and S. Uchida, Dynamics in the one-dimensional antiferromagnet Sr2CuO3 via 63Cu NMR, Phys. Rev. Lett. 76, 4612 (1996).
- Thurber et al. [2001] K. R. Thurber, A. W. Hunt, T. Imai, and F. C. Chou, 17O NMR study of spin excitations in a nearly ideal 1D Heisenberg antiferromagnet, Sr2CuO3, up to 800 K, Phys. Rev. Lett. 87, 247202 (2001).
- Dupont et al. [2018] M. Dupont, S. Capponi, N. Laflorencie, and E. Orignac, Dynamical response and dimensional crossover for spatially anisotropic antiferromagnets, Phys. Rev. B 98, 094403 (2018).
- Horvatić et al. [2020] M. Horvatić, M. Klanjšek, and E. Orignac, Direct determination of the Tomonaga-Luttinger parameter in quasi-one-dimensional spin systems, Phys. Rev. B 101, 220406 (2020).
- Giamarchi and Tsvelik [1999] T. Giamarchi and A. M. Tsvelik, Coupled ladders in a magnetic field, Phys. Rev. B 59, 11398 (1999).
- Thurber et al. [2000] K. R. Thurber, T. Imai, T. Saitoh, M. Azuma, M. Takano, and F. C. Chou, 63Cu NQR evidence of dimensional crossover to anisotropic 2D regime in three-leg ladder Sr2Cu3O5, Phys. Rev. Lett. 84, 558 (2000).
- Klanjšek et al. [2008] M. Klanjšek, H. Mayaffre, C. Berthier, M. Horvatić, B. Chiari, O. Piovesana, P. Bouillot, C. Kollath, E. Orignac, R. Citro, and T. Giamarchi, Controlling Luttinger liquid physics in spin ladders under a magnetic field, Phys. Rev. Lett. 101, 137207 (2008).
- Bouillot et al. [2011] P. Bouillot, C. Kollath, A. M. Läuchli, M. Zvonarev, B. Thielemann, C. Rüegg, E. Orignac, R. Citro, M. Klanjšek, C. Berthier, M. Horvatić, and T. Giamarchi, Statics and dynamics of weakly coupled antiferromagnetic spin- ladders in a magnetic field, Phys. Rev. B 83, 054407 (2011).
- Mukhopadhyay et al. [2012] S. Mukhopadhyay, M. Klanjšek, M. S. Grbić, R. Blinder, H. Mayaffre, C. Berthier, M. Horvatić, M. A. Continentino, A. Paduan-Filho, B. Chiari, and O. Piovesana, Quantum-critical spin dynamics in quasi-one-dimensional antiferromagnets, Phys. Rev. Lett. 109, 177206 (2012).
- Jeong et al. [2016] M. Jeong, D. Schmidiger, H. Mayaffre, M. Klanjšek, C. Berthier, W. Knafo, G. Ballon, B. Vignolle, S. Krämer, A. Zheludev, and M. Horvatić, Dichotomy between attractive and repulsive Tomonaga-Luttinger liquids in spin ladders, Phys. Rev. Lett. 117, 106402 (2016).
- Möller et al. [2017] J. S. Möller, T. Lancaster, S. J. Blundell, F. L. Pratt, P. J. Baker, F. Xiao, R. C. Williams, W. Hayes, M. M. Turnbull, and C. P. Landee, Quantum-critical spin dynamics in a Tomonaga-Luttinger liquid studied with muon-spin relaxation, Phys. Rev. B 95, 020402 (2017).
- Dupont et al. [2016] M. Dupont, S. Capponi, and N. Laflorencie, Temperature dependence of the NMR relaxation rate for quantum spin chains, Phys. Rev. B 94, 144409 (2016).
- Sachdev et al. [1994] S. Sachdev, T. Senthil, and R. Shankar, Finite-temperature properties of quantum antiferromagnets in a uniform magnetic field in one and two dimensions, Phys. Rev. B 50, 258 (1994).
- Yunoki and Sorella [2006] S. Yunoki and S. Sorella, Two spin liquid phases in the spatially anisotropic triangular Heisenberg model, Phys. Rev. B 74, 014408 (2006).
- Heidarian et al. [2009] D. Heidarian, S. Sorella, and F. Becca, Spin- Heisenberg model on the anisotropic triangular lattice: From magnetism to a one-dimensional spin liquid, Phys. Rev. B 80, 012404 (2009).
- Hauke [2013] P. Hauke, Quantum disorder in the spatially completely anisotropic triangular lattice, Phys. Rev. B 87, 014415 (2013).
- Weng et al. [2006] M. Q. Weng, D. N. Sheng, Z. Y. Weng, and R. J. Bursill, Spin-liquid phase in an anisotropic triangular-lattice heisenberg model: Exact diagonalization and density-matrix renormalization group calculations, Phys. Rev. B 74, 012407 (2006).
- Hayashi and Ogata [2007] Y. Hayashi and M. Ogata, Possibility of gapless spin liquid state by one-dimensionalization, J. Phys. Soc. Jpn. 76, 053705 (2007).
- Starykh and Balents [2007] O. A. Starykh and L. Balents, Ordering in spatially anisotropic triangular antiferromagnets, Phys. Rev. Lett. 98, 077205 (2007).
- Wen [2002] X.-G. Wen, Quantum orders and symmetric spin liquids, Phys. Rev. B 65, 165113 (2002).
- Coldea et al. [2001] R. Coldea, D. A. Tennant, A. M. Tsvelik, and Z. Tylczynski, Experimental realization of a 2D fractional quantum spin liquid, Phys. Rev. Lett. 86, 1335 (2001).
- Coldea et al. [2003] R. Coldea, D. A. Tennant, and Z. Tylczynski, Extended scattering continua characteristic of spin fractionalization in the two-dimensional frustrated quantum magnet Cs2CuCl4 observed by neutron scattering, Phys. Rev. B 68, 134424 (2003).
- Kohno et al. [2007] M. Kohno, O. Starykh, and L. Balents, Spinons and triplons in spatially anisotropic frustrated antiferromagnets., Nat. Phys. 3, 790 (2007).
- Starykh et al. [2010] O. A. Starykh, H. Katsura, and L. Balents, Extreme sensitivity of a frustrated quantum magnet: Cs2CuCl4, Phys. Rev. B 82, 014421 (2010).
- Vachon et al. [2006] M.-A. Vachon, W. Kundhikanjana, A. Straub, V. F. Mitrović, A. P. Reyes, P. Kuhns, R. Coldea, and Z. Tylczynski, 133Cs NMR investigation of 2D frustrated Heisenberg antiferromagnet, Cs2CuCl4, New J. Phys. 8, 222 (2006).
- Vachon et al. [2011] M.-A. Vachon, G. Koutroulakis, V. F. Mitrović, O. Ma, J. B. Marston, A. P. Reyes, P. Kuhns, R. Coldea, and Z. Tylczynski, The nature of the low-energy excitations in the short-range-ordered region of Cs2CuCl4 as revealed by 133Cs nuclear magnetic resonance, New J. Phys. 13, 093029 (2011).
- Hirai et al. [2017] D. Hirai, T. Yajima, D. Nishio-Hamane, C. Kim, H. Akiyama, M. Kawamura, T. Misawa, N. Abe, T. Arima, and Z. Hiroi, Visible orbital states in a pleochroic oxychloride, J. Am. Chem. Soc. 139, 10784 (2017).
- Hirai et al. [2019] D. Hirai, K. Nawa, M. Kawamura, T. Misawa, and Z. Hiroi, One-dimensionalization by geometrical frustration in the anisotropic triangular lattice of the quantum antiferromagnet Ca3ReO5Cl2, J. Phys. Soc. Jpn. 88, 044708 (2019).
- Hirai [2024] D. Hirai, Pinalites: Optical properties and quantum magnetism of heteroanionic O compounds, Inorganic Chemistry 63, 4001 (2024).
- Zvyagin et al. [2022] S. A. Zvyagin, A. N. Ponomaryov, J. Wosnitza, D. Hirai, Z. Hiroi, M. Gen, Y. Kohama, A. Matsuo, Y. H. Matsuda, and K. Kindo, Dimensional reduction and incommensurate dynamic correlations in the triangular-lattice antiferromagnet Ca3ReO5Cl2., Nat. Commun. 13, 6310 (2022).
- Choi et al. [2021] Y. Choi, S. Lee, J.-H. Lee, S. Lee, M.-J. Seong, and K.-Y. Choi, Bosonic spinons in anisotropic triangular antiferromagnets, Nat. Commun. 12, 6453 (2021).
- Zheng et al. [2005] W. Zheng, R. R. P. Singh, R. H. McKenzie, and R. Coldea, Temperature dependence of the magnetic susceptibility for triangular-lattice antiferromagnets with spatially anisotropic exchange constants, Phys. Rev. B 71, 134422 (2005).
- Nawa et al. [2020] K. Nawa, D. Hirai, M. Kofu, K. Nakajima, R. Murasaki, S. Kogane, M. Kimata, H. Nojiri, Z. Hiroi, and T. J. Sato, Bound spinon excitations in the spin- anisotropic triangular antiferromagnet Ca3ReO5Cl2, Phys. Rev. Research 2, 043121 (2020).
- Koepernik and Eschrig [1999] K. Koepernik and H. Eschrig, Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme, Phys. Rev. B 59, 1743 (1999).
- Perdew and Wang [1992] J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B 45, 13244 (1992).
- Bonner and Fisher [1964] J. C. Bonner and M. E. Fisher, Linear magnetic chains with anisotropic coupling, Phys. Rev. 135, A640 (1964).
- Eggert et al. [1994] S. Eggert, I. Affleck, and M. Takahashi, Susceptibility of the spin 1/2 Heisenberg antiferromagnetic chain, Phys. Rev. Lett. 73, 332 (1994).
- Ninios et al. [2012] K. Ninios, T. Hong, T. Manabe, C. Hotta, S. N. Herringer, M. M. Turnbull, C. P. Landee, Y. Takano, and H. B. Chan, Wilson ratio of a Tomonaga-Luttinger liquid in a spin- Heisenberg ladder, Phys. Rev. Lett. 108, 097201 (2012).
- Nawa et al. [2013] K. Nawa, M. Takigawa, M. Yoshida, and K. Yoshimura, Anisotropic spin fluctuations in the quasi one-dimensional frustrated magnet LiCuVO4, J. Phys. Soc. Jpn. 82, 094709 (2013).
- Abragam and Bleaney [1970] A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions (Oxford University Press, London, 1970).
- De Nardis et al. [2019] J. De Nardis, M. Medenjak, C. Karrasch, and E. Ilievski, Anomalous spin diffusion in one-dimensional antiferromagnets, Phys. Rev. Lett. 123, 186601 (2019).
- Dupont et al. [2021] M. Dupont, N. E. Sherman, and J. E. Moore, Spatiotemporal crossover between low- and high-temperature dynamical regimes in the quantum Heisenberg magnet, Phys. Rev. Lett. 127, 107201 (2021).
- Bloembergen et al. [1947] N. Bloembergen, E. Purcell, and R. Pound, Nuclear magnetic relaxation., Nature(London) 160, 475 (1947).
- Moriya [1956] T. Moriya, Nuclear magnetic relaxation in antiferromagnetics, Phys. Rev. 101, 1435 (1956).
- Polini and Vignale [2007] M. Polini and G. Vignale, Spin drag and spin-charge separation in cold fermi gases, Phys. Rev. Lett. 98, 266403 (2007).
- Berthier et al. [2017] C. Berthier, M. Horvatić, M.-H. Julien, H. Mayaffre, and S. Krämer, Nuclear magnetic resonance in high magnetic field: Application to condensed matter physics, Comptes Rendus. Physique 18, 331 (2017).
- Smerald and Shannon [2011] A. Smerald and N. Shannon, Angle-resolved NMR: Quantitative theory of 75As relaxation rate in BaFe2As2, Phys. Rev. B 84, 184437 (2011).
- Hohenberg and Halperin [1977] P. C. Hohenberg and B. I. Halperin, Theory of dynamic critical phenomena, Rev. Mod. Phys. 49, 435 (1977).
- Shimizu et al. [2015] Y. Shimizu, S. Aoyama, T. Jinno, M. Itoh, and Y. Ueda, Site-selective Mott transition in a quasi-one-dimensional vanadate V6O13, Phys. Rev. Lett. 114, 166403 (2015).
- Shimizu et al. [2020] Y. Shimizu, T. Jin-no, F. Iwase, M. Itoh, and Y. Ueda, Occupation switching of orbitals in vanadium dioxide probed via hyperfine interactions, Phys. Rev. B 101, 245123 (2020).
- Volkoff [1953] G. M. Volkoff, Second order nuclear quadrupole effects in single crystals: Part I. theoretical, Can. J. Phys. 31, 820 (1953).
- Slichter [1970] C. P. Slichter, Principles of magnetic resonance (Springer Berlin, Heidelberg, Berlin, 1970).