Slow Stable Self-bound Hybrid Star Can Relieve All Tensions
Abstract
Some recent pulsar observations cannot naturally fit into the conventional picture of neutron stars: the compact objects associated with HESS J1731-347 and XTE J1814-338 have too small radii at the low-mass regime, while the secondary component of GW190814 is too massive for neutron stars to be compatible with constraints from the GW170817 event. In this study, we demonstrate that all these anomalous observations and tensions, together with other conventional ones such as recent NICER observations of PSR J0740+6620, J0030+0451, and PSR J0437-4715, can be naturally explained simultaneously by a new general type of hybrid stars that are self-bound and radially stable in the slow phase transition context, and by some subsets even in the rapid phase transition context also. As a proof of concept, we use hybrid quark stars, inverted hybrid stars, and hybrid strangeon stars as benchmark examples to explicitly demonstrate the advantage and feasibility of slow stable self-bound hybrid stars in relieving all tensions related to compact stars’ masses, radii, and tidal deformabilities.
I Introduction
Phase transitions within compact stars are a long-studied possibility Dexheimer et al. (2018); Orsaria et al. (2019); Heiselberg and Hjorth-Jensen (1999); Glendenning (2001); Yang and Shen (2008); Reddy et al. (2000); Glendenning (1992); Burgio et al. (2002), which would provide a unique opportunity to understand the fundamental strong interaction between quarks, in both the perturbative and the non-perturbative regimes. More and more researches indicate that quark matter (QM), a state comprised of deconfined free-flowing quarks, can possibly exist inside the neutron star core from hadron-quark phase transitions, forming so-called hybrid stars (e.g., Alford et al., 2005, 2013).
It is possible that QM is absolutely stable (i.e., energy per baryon number MeV) even at zero pressure, either in the form of strange quark matter (SQM) Bodmer (1971); Witten (1984); Terazawa (1979); Farhi and Jaffe (1984) or up-down quark matter (QM) Holdom et al. (2018); Wang et al. (2021); Xia et al. (2022); Bai and Korwar (2025); Bai and Chen (2024). They can constitute the entire star Haensel et al. (1986); Alcock et al. (1986); Xu et al. (1999); Yang et al. (2023); Zhang (2020); Zhao et al. (2019); Ren and Zhang (2020); Cao et al. (2022); Yuan et al. (2022); Restrepo et al. (2023); Xia et al. (2020); Zhang and Mann (2021); Pretel and Zhang (2024); Zhou et al. (2024); Wang et al. (2024a); Xie and Xia (2025); Chen et al. (2025), forming the so-called quark star that is self-bound featuring a high-density surface. Possible phase transitions can also occur inside the quark stars, leading to self-bound hybrid stars such as hybrid quark stars (HybQSs) from a QM-QM (different QM phases) transition Yang et al. (2025a), or inverted hybrid stars (IHSs) from a speculated quark-hadron phase transition Zhang and Ren (2023); Zhang et al. (2024); Negreiros et al. (2025). Clustered SQM, or in another name Strangeon Matter (SM), like strange quark matter, comprises nearly equal numbers of quarks Xu (2003); Lai and Xu (2009, 2017) as favoured by the approximate SU(3) flavour symmetry, and could also be absolutely stable, forming a solid state with localized quark clusters (strangeons) due to their large mass and strong interaction. Strangeon stars Xu (2003); Lai and Xu (2017, 2009); Miao et al. (2022); Gao et al. (2021); Zhang et al. (2023a), composed of SM and thus self-bound, have a stiff equation of state (EOS) and high compactness that helps address various astrophysical observations Zhang et al. (2023a); Li et al. (2023, 2024); Wang et al. (2024b); Yuan et al. (2025). A transition from SM to SQM is possible Miao et al. (2022), forming the so-called Hybrid Strangeon Stars (HybSSs) with a strangeon crust and a SQM core Zhang et al. (2023b).
The stability of compact stars is generally determined by the fundamental () mode frequency of radial oscillations, whose squared eigenfrequencies’ () positive signs indicate the star’s stability against small adiabatic perturbations. Studies of radial pulsations in hybrid stars are typically categorized into two types: slow and rapid transitions, depending on the phase-transition timescale relative to the oscillation timescale. For rapid transitions, the region where coincides with the conventional stability condition (i.e., star mass increases with increasing center pressure ), implying that the zero fundamental eigenfrequency point coincides with the maximum mass point Glendenning (1997); Pereira et al. (2018); Pretel et al. (2024). However, this coincidence does not hold for the slow-transition case, where an extended region of stability develops after a sharp phase transition even with , corresponding to the so-called slow stable hybrid stars (SSHS) Pereira et al. (2018); Lugones and Grunfeld (2021); Lugones et al. (2023); Goncalves et al. (2022), which can be formed from early phase transitions triggered by quantum or thermal nucleations in realistic astrophysical scenarios such as protoneutron stars or the post-merger hot stars Lugones et al. (2023).
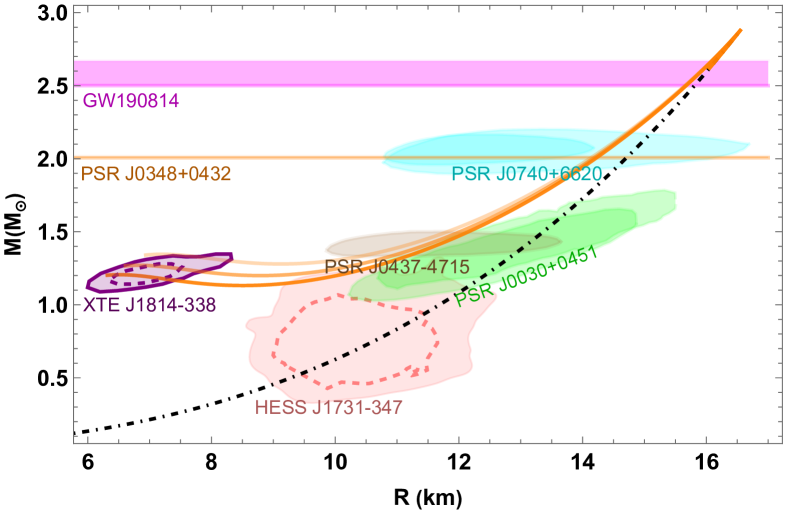
In 2022, Doroshenko et al. Doroshenko et al. (2022) reported puzzlingly low mass-radius values (, km at ) for the central compact object in the supernova remnant HESS J1731-347, which have prompted extensive studies proposing several explanations such as hybrid star model with early phase transition Tsaloukidis et al. (2023); Sagun et al. (2023); Laskos-Patkos et al. (2024, 2025); Mariani et al. (2024); Gao et al. (2024); Pal et al. (2025); Hong and Ren (2024a), strange quark star model Di Clemente et al. (2024); Horvath et al. (2023); Oikonomou and Moustakidis (2023); Rather et al. (2023); Gholami et al. (2025); Issifu et al. (2025); Kourmpetis et al. (2025), a soft nuclear EOS neutron star Brodie and Haber (2023); Huang et al. (2024); Li and Sedrakian (2023); Kubis et al. (2023), or mixed dark matter models Hong and Ren (2024b); Routaray et al. (2024). Recently, Kini et al. Kini et al. (2024) reported similarly puzzling ultracompact parameters for XTE J1814-338 (, at ), with proposed explanations including a hybrid star branch Laskos-Patkos and Moustakidis (2025); Zhou and Huang (2025), a bosonic star with nuclear core Pitz and Schaffner-Bielich (2025), a dark matter admixed neutron star Lopes and Issifu (2025) or a strange star admixed with dark matter Yang et al. (2025b); Lopes (2025). Nevertheless, it is very difficult to reconcile both puzzling objects at the same time Veselsky et al. (2025); Laskos-Patkos and Moustakidis (2025); Kourmpetis et al. (2025). Besides, a binary merger event GW190814 was reported Abbott et al. (2020), featuring a primary black hole with mass , and a secondary companion of , which is much larger than the upper bound of the maximum mass for a non-rotating neutron star, set by various analyses of GW170817 Margalit and Metzger (2017); Rezzolla et al. (2018); Ruiz et al. (2018); Shibata et al. (2019). To the best of our knowledge, no previous studies have managed to build models that could accommodate all these anomalous observations at the same time.
In the absence of a comprehensive model capable of describing all observational mass-radius and tidal deformability measurements, this work examines slow stable self-bound hybrid stars with quite promising results. The general finding that self-bound stars like strange stars can saturate HESS J1731-347 easily Doroshenko et al. (2022), and the slow stable hybrid stars benefit to meet XTE J1814-338 Laskos-Patkos and Moustakidis (2025), naturally motivates us to propose the slow stable self-bound hybrid stars that combine these two advantages. As we will explicitly show in the main text, the new branch that gives rise to the slow stable self-bound hybrid stars helps explain all these anomalous objects at the same time, while also fulfilling other astrophysical observations such as GW170817 Abbott et al. (2017), recent NICER analysis of PSR J0030+0451 Miller et al. (2019); Riley et al. (2019), PSR J0740+6620 Miller et al. (2021); Riley et al. (2021), and the more recent PSR J0437-4715 Choudhury et al. (2024); Rutherford et al. (2024).
This paper is organized as follows: first, we introduce models for the EOSs of three types of self-bound hybrid stars: HybQS, HybSS, and IHS. Then, we consider the mass-radius relations, radial oscillations, and tidal deformabilities with varying parameters, where we look for radially stable solutions that satisfy all the notable astrophysical constraints, particularly aiming to explain HESS J1731-347 and XTE J1814-338 at the same time. We employ the Maxwell construction for phase transitions and geometric units () throughout this paper.
II Model of Self-bound hybrid stars
To model the HybQS, we use the conventional MIT bag model EOS
| (1) |
for the quark matter composing the crust before the transition pressure , with the effective bag constant characterizing the QCD vacuum difference inside and outside the quark matter bag. We then adopt the constant-sound-speed (CSS) parametrization Alford et al. (2013) for the quark matter core with EOS
| (2) |
for the core quark matter after , with denoting the sound speed squared, denoting the energy density at , and as the energy density discontinuity of the phase transition interface. Therefore, we have four independent parameters (, , , ) for this HybQS construction.
To model HybSSs, the EOS of strangeon matter Xu (2003); Lai and Xu (2017) located at the outer layer () can be written into the following form Zhang et al. (2023a, b)
| (3) | ||||
where , is the average constituent quark mass, is the number density of strangeons with being the surface baryon number density. The normalized quantities and with describing the depth of the interaction potential between strangeons, and being the number of quarks in a strangeon. A larger will then indicate a larger repulsive force at short range and thus maps to a stiffer EOS. The CSS parameterization (Eq. 2) is then used to model the quark matter core (. Thus, we have five independent parameters (, , , , ) for this HybSS construction.
To model IHSs Zhang and Ren (2023); Zhang et al. (2024); Negreiros et al. (2025), we use the simple MIT bag model Eq. (1) for the quark matter crust like the hybrid quark star model, and with the -type polytrope EOS111Note that the polytope EOS can have different forms depending on whether the directly related variable is energy density (-type) or rest mass density (-type). For details, see discussions below Eq. (22) of Ref. Damour and Nagar (2009a). Damour and Nagar (2009a)
| (4) |
for the hadronic core. The constant pressure at the interface of the two matter phases yields
| (5) |
Therefore, in this IHS model we have four independent parameters (, , , ). Due to the uncertainties associated with hadronic EOS, one can piecewise the polytrope EOS of different parameter sets at different density regimes Hebeler et al. (2013); Huang and Sourav (2025).
III Stellar properties and stability
The static spherically symmetric background spacetime has the following line element
| (6) |
where , with being a mass function within the hybrid star. To obtain the configuration of relativistic stellar structure, we incorporate the combined EOS described above into the so-called Tolman-Oppenheimer-Volkov (TOV) equations Oppenheimer and Volkoff (1939); Tolman (1939)
| (7) |
with the boundary conditions where the star’s radius and mass are determined by the conditions and , respectively.
To investigate the radial stability of our hybrid stellar models, we assume that a fluid element is displaced from its equilibrium position to the perturbed position , where such a perturbation has a harmonic time dependence . The equations for solving infinitesimal radial oscillations and the corresponding pressure perturbations of a spherical object are Chanmugam (1977); Väth and Chanmugam (1992); Pereira et al. (2018); Gondek et al. (1997); Vásquez Flores and Lugones (2010); Pretel and da Silva (2020)
| (8) | |||||
| (9) |
with the coefficients given by
| (10) | ||||
where is the adiabatic index. The initial conditions are and . We obtain the squared eigenfrequencies by solving Eq. (8) and Eq. (9) using the shooting method, so that the boundary condition is satisfied at the surface. The fundamental zero mode that determines the radial stability is the lowest-lying one, the frequency of which is commonly denoted as . For rapid transitions, the matching conditions at the interface are and , where and primes on the variables denote the partial derivatives with respect to . In this context, the stable region determined from these radial oscillation calculations generally coincides with the simple criterion Glendenning (1997); Pereira et al. (2018). For slow transitions, in which we are most interested, the matching conditions across the interface of the two matter phases are and . The classical stability criterion generally fails in this context, and it is necessary to use the signs of squared eigenfrequencies to determine the stability Pereira et al. (2018); Lugones and Grunfeld (2021); Pretel et al. (2024); Goncalves et al. (2022).
For comparison with gravitational wave observations, the dimensionless tidal deformability can be computed, where is the compactness and is the Love number characterizing the stellar response to external perturbations Hinderer (2008); Hinderer et al. (2010); Postnikov et al. (2010). The Love number is determined by solving a differential equation for Postnikov et al. (2010) concurrently with the TOV equation Eq. (7), using the boundary condition . For self-bound hybrid stars, the matching condition must be applied at (i.e., at both the core radius where and the star surface ), where an energy density jump occurs Damour and Nagar (2009b); Takátsy and Kovács (2020).
IV RESULTS AND Discussions
We aim to explain the puzzling XTE J1814-338 and HESS J1731-347 together with other astrophysical observations utilizing the slow stable branch of self-bound hybrid stars. There are two possible scenarios:
-
•
Scenario 1: GW170817’s constraint needs to be met by the non-hybrid branch (i.e., for bare quark stars of HybQS and IHS cases, and for bare strangeon stars of HybSS case).
-
•
Scenario 2: GW170817’s constraint is only met by the hybrid branch (i.e., after ).
In all scenarios, the HESS J1731-347 constraint can be easily met by all the non-hybrid self-bound branches, while the XTE J1814-338 is conveniently met by the (slow stable) hybrid branches in a viable EOS parameter space.
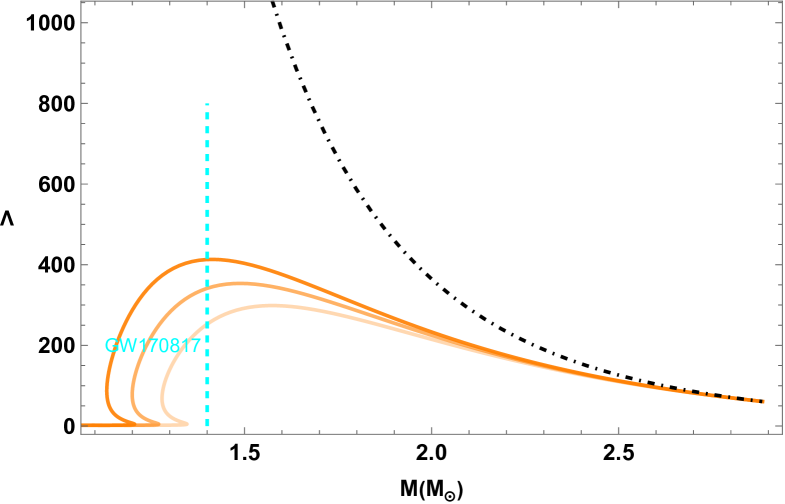
Studies Abbott et al. (2019a); Radice et al. (2018a); Most et al. (2018); De et al. (2018); Burgio et al. (2018); Shibata et al. (2019) have shown that GW170817’s tidal deformability constraints exclude very stiff EOSs and large radius around (), constraining possible maximum mass well below that of the massive object () observed in GW190814. Interestingly, Scenario 2 can relax and to large values, and reconcile the tension between the gravitational wave events GW170817 and GW190814 by leaving GW170817’s constraints satisfied only by the hybrid branch, as we will explicitly show later.
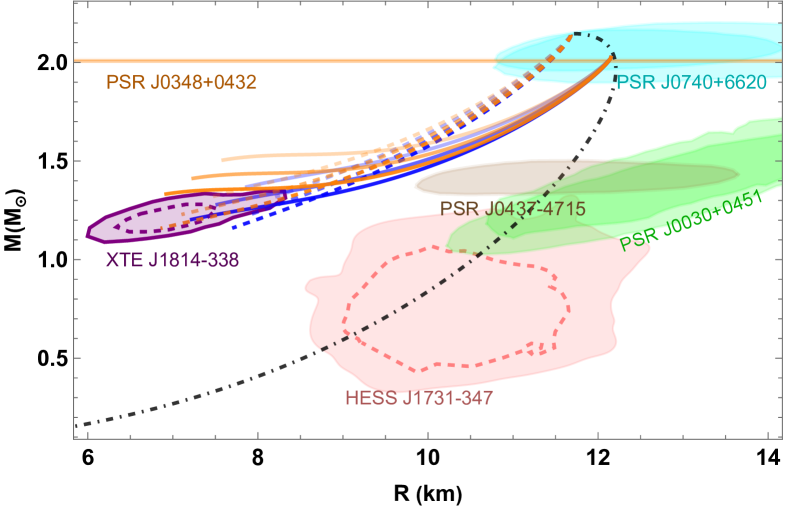
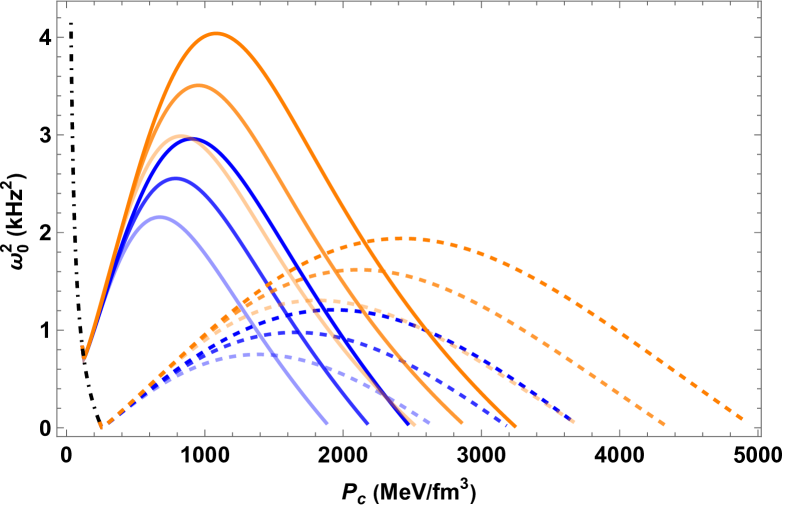
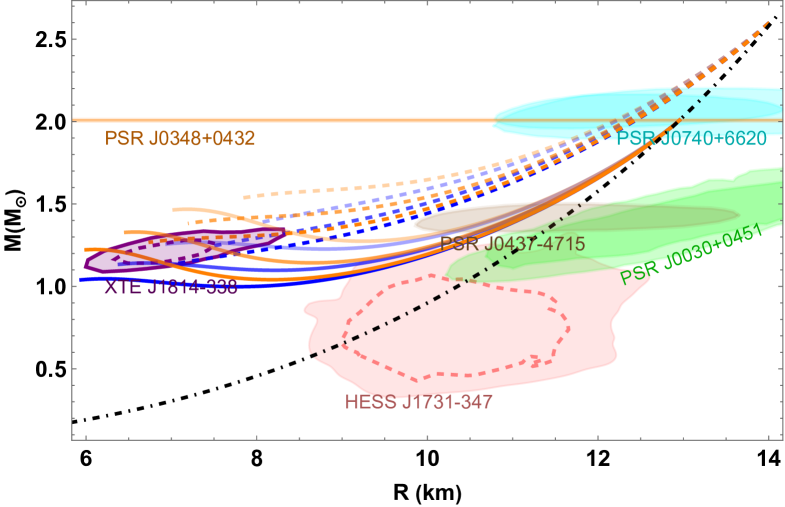
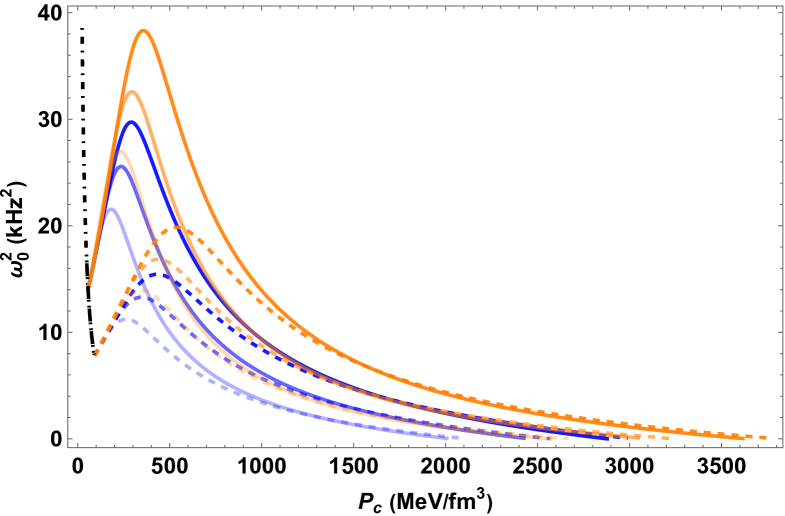
First, for Scenario 1, we choose the EOS parameters of the out-layer matter (i.e., bag constant of quark matter for HybQSs and IHSs, () of strangeon matter for HybSSs) so that GW170817’s bound222Note that other constraints from analyses of GW170817 commonly assumes neutron star EOS Abbott et al. (2018, 2019b); Radice et al. (2018b); Kiuchi et al. (2019), so that they do not apply to our study of self-bound stars. For details, see related discussions in Ref. Zhang (2020). is satisfied by the non-hybrid branch Zhang (2020); Zhang et al. (2023a) before the phase transition (i.e., ). We display the results of Scenario 1 in Fig. 1. The non-hybrid branch is naturally identified as the compact object associated with HESS J1731-347, GW170817, and all the NICER-related PSR J0030+0451, PSR J0740+6620 and the very recent PSR J0437-4715. At the more massive region above , a hybrid branch is developed from a sharp 1st-order phase transition, where the large densities discontinuities at the phase transition interface will render , however, still be radially stable in the context of slow phase transition even until the XTE J1814-338’s constrained - region. Note that for the case of inverted hybrid quark stars (second row of Fig. 1), some of the curves that are not terminated at zero frequency because they violate causality () earlier before reaching zero , due to a combined effect of their large polytrope index for the core EOS and the large center pressure extended.
We can see that all three types of self-bound stars can have viable parameter space for their slow stable branch (colored curves) to satisfy the constraints of XTE J1914-338, while the non-hybrid star branch (dot-dashed black curves) before the phase transition to meet all other constraints without the need for much fine-tuning. Besides, it can be seen that the slow stable branch of all hybrid star types manifests the following common features:
-
•
increases after the phase transition, with a larger slope and eigenfrequency peak for a smaller (dashed) or a larger (darker) or stiffer core EOS (orange).
-
•
a larger or a stiffer core EOS (i.e., larger for HybQS and HybSS, or larger for IHS) maps to a more extended slow stable branch.
We expect these features to also apply to conventional slow stable hybrid stars.
Besides, Fig. 1 also shows that HybSSs have some peculiar behaviour compared to other types: for cases of transition near (solid curves), they develop hybrid branches that cross the XTE J1914-338’s - region with , meaning that they are even stable in the rapid transition context. Furthermore, without invoking Scenario 2, they can already satisfy GW190814’s constraint, provided a late phase transition (dashed curves).
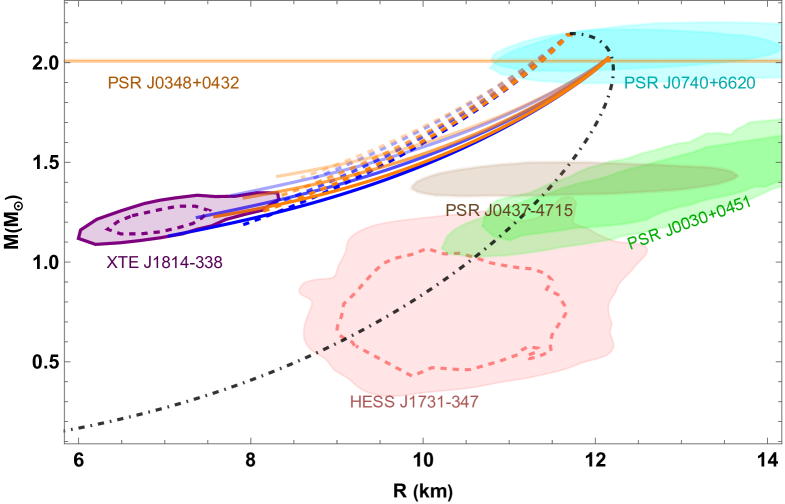
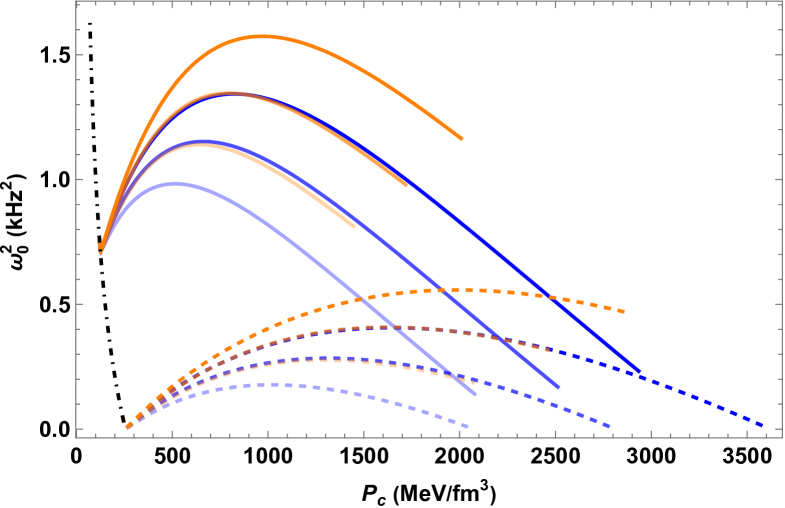
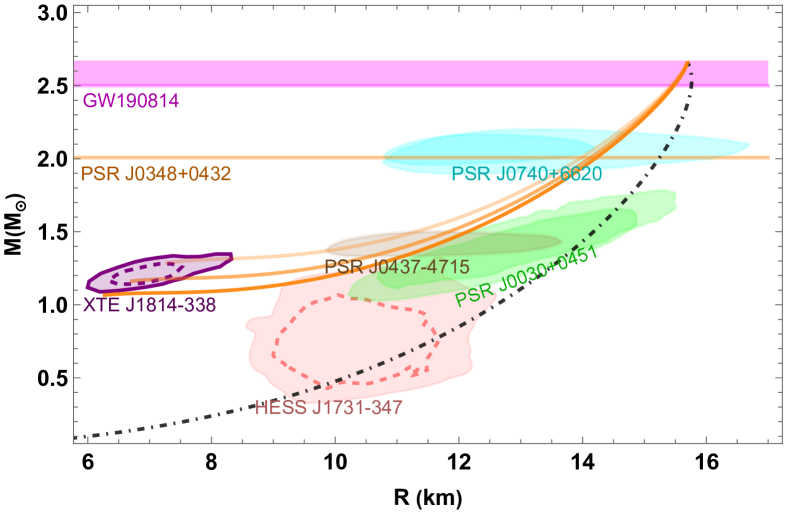
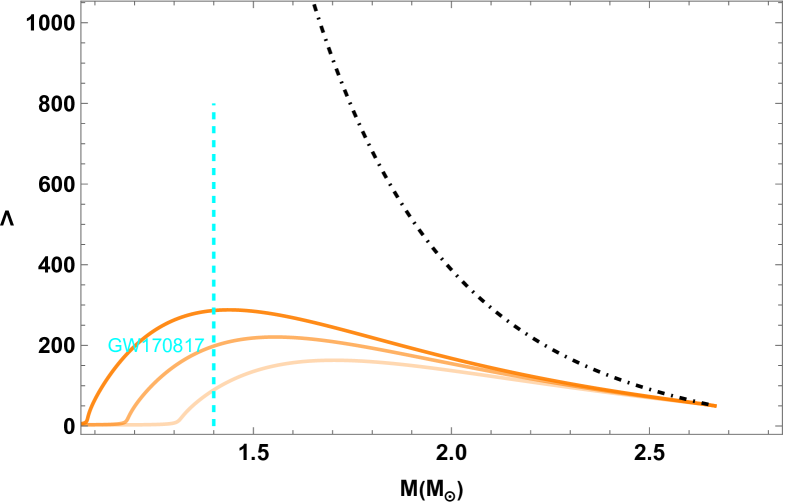
For Scenario 2 which addresses GW170817’s tidal deformability constraints only with the hybrid branch, we directly choose large , stiff EOS and large to get a more extended slow stable branch, saving us efforts of tuning parameters, benefited from the general features observed in Scenario 1 as discussed above. We display the results in Fig. 2, skipping showing the drawing of since they share a similar feature as Scenario 1, but instead put the results of tidal deformability to show the main difference. We can easily identify the viable solutions for HybQSs and HybSSs that satisfy all the constraints, even including the GW190814, benefited from a very stiff non-hybrid branch with a late sharp phase transition, leaving the extended hybrid branch satisfying the tidal deformability bounds of GW170817. Note that the HybSS examples cross the XTE J1914-338’s - region with , thus are even stable in the rapid transition context like Scenario 1. The very recent PSR J0437-4715 constraint is easily met by the slow stable branches of all star types. However, by varying the simple polytrope model and even its piecewised form (i.e., piecewise another one or two polytrope EOSs of different parameter set at higher densities) for the hadronic EOS, we find that the slow stable branches of IHSs that overlaps with GW190814’s large mass region can hardly reach the XTE J1814-338’s - region, mainly because the polytrope model of their core hadronic matter would easily violate causality () in order to make its EOS stiff enough to meet GW190814 while at even much higher center pressure have a long extended stable slow branch to reach XTE J1814-338’s - region. So we neglect this case in this figure.
V Summary and Outlook
Recent astrophysical observations challenge conventional neutron star models: Compact stars identified in HESS J1731-347 (, ) and XTE J1814-338 (, ) exhibit anomalously small radii, while GW190814’s secondary component () significantly exceeds typical neutron star masses without violating GW170817 constraints from various analyses. In this work, we resolve these tensions by proposing a novel class of self-bound hybrid stars featuring a sharp but slow first-order phase transition, i.e., a large but with phase transition timescales that exceed oscillation periods. A larger energy density jump () or stiffer core EOSs extend this slow stable branch to smaller radii, enabling explanations of ultracompact objects.
Our key findings demonstrate that self-bound hybrid stars such as hybrid quark stars (HybQSs), inverted hybrid stars (IHSs), and hybrid strangeon stars (HybSSs) all accommodate HESS J1731-347 and XTE J1814-338 together with other observational constraints via their slow stable branches, and even via the rapid stable branches for HybSSs. In general, the self-bound feature (i.e., mass grows with radius as center pressure increases at the small-mass regime) benefits saturating HESS J1731-347, while the extended stable hybrid branch benefits meeting XTE J1814-338. We also showed the advantage of slow stable self-bound hybrid stars in explaining GW190814’s anomalously massive object by allowing a very stiff EOS of the non-hybrid branch if leaving the slow stable hybrid branches to meet the GW170817 constraint, which turns out to be very feasible for HybQSs and HybSSs. Therefore, our work has demonstrated the first working example that reconciles all the astrophysical tensions related to compact stars’ masses, radii, and tidal deformabilities, revealing new intriguing possibilities for the behavior of matter and stars under extreme conditions.
While the IHS case turns out to have difficulties in meeting GW190814 and XTE J1814-338 at the same time using the simple -type polytrope model and its piecewised version for its core hadronic matter EOS, the chance is still open for other EOS constructions of hadronic matter, such as -type polytrope Read et al. (2009), more generalized polytope constructions O’Boyle et al. (2020), spectral representation Lindblom (2010), or the speed-of-sound parameterization Greif et al. (2019). It is also more exhaustive to explore a general Bayesian analysis of all parameter space on this new subject. We leave these for future studies.
There are potential distinct signatures of slow stable self-bound hybrid stars compared to other types of compact stars. The gravitational-wave asteroseismology of this new object may also exhibit interesting features Zhang et al. (2024), particularly their -mode of nonradial oscillations Sun et al. (2025); Guha et al. (2025); Zhao et al. (2025), which may have significantly large frequencies Tonetto and Lugones (2020). In addition, the unusually large density discontinuities at their phase transition interface will likely cause a large violation of neutron star universal relations Han and Steiner (2019); Hoyos et al. (2022); Annala et al. (2018); Ranea-Sandoval et al. (2022); Ranea et al. (2023). Moreover, the strong phase transition is accompanied by a release of energy from the changes of internal energy and gravitational potential energy, potentially sourcing supergiant glitches Ma and Xie (1996), core-quakes Bejger et al. (2005) and electromagnetic wave radiations such as gamma-ray burst Loeb (1998); Menezes et al. (2006) and fast radio burst Shen et al. (2023); Wang et al. (2024b), which may also originate from the self-bound star’s surface Geng et al. (2021); Xu et al. (2025).
Acknowledgements.
Acknowledgments
We thank Chun Huang and Zhi-qiang Miao for useful discussions. C. Zhang is supported by the Jockey Club Institute for Advanced Study at The Hong Kong University of Science and Technology. JMZP acknowledges support from “Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro” – FAPERJ, Process SEI-260003/000308/2024. R.-X Xu is supported by the National SKA Program of China (2020SKA0120100).
References
- Dexheimer et al. (2018) V. Dexheimer, L. T. T. Soethe, J. Roark, R. O. Gomes, S. O. Kepler, and S. Schramm, International Journal of Modern Physics E 27, 1830008 (2018).
- Orsaria et al. (2019) M. G. Orsaria, G. Malfatti, M. Mariani, I. F. Ranea, F. García, W. M. Spinella, G. A. Contrera, G. Lugones, and F. Weber, Journal of Physics G: Nuclear and Particle Physics 46, 073002 (2019).
- Heiselberg and Hjorth-Jensen (1999) H. Heiselberg and M. Hjorth-Jensen, The Astrophysical Journal 525, L45 (1999).
- Glendenning (2001) N. K. Glendenning, Physics Reports 342, 393 (2001).
- Yang and Shen (2008) F. Yang and H. Shen, Physical Review C 77, 025801 (2008).
- Reddy et al. (2000) S. Reddy, G. Bertsch, and M. Prakash, Physics Letters B 475, 1 (2000).
- Glendenning (1992) N. K. Glendenning, Physical Review D 46, 1274 (1992).
- Burgio et al. (2002) G. Burgio, M. Baldo, P. Sahu, and H.-J. Schulze, Physical Review C 66, 025802 (2002).
- Alford et al. (2005) M. Alford, M. Braby, M. W. Paris, and S. Reddy, Astrophys. J. 629, 969 (2005), arXiv:nucl-th/0411016 .
- Alford et al. (2013) M. G. Alford, S. Han, and M. Prakash, Phys. Rev. D 88, 083013 (2013), arXiv:1302.4732 [astro-ph.SR] .
- Bodmer (1971) A. R. Bodmer, Phys. Rev. D 4, 1601 (1971).
- Witten (1984) E. Witten, Phys. Rev. D 30, 272 (1984).
- Terazawa (1979) H. Terazawa, 2nd KEK Symposium on Radiation Dosimetry, Tsukuba, Japan, Mar 22-23, 1979, (1979).
- Farhi and Jaffe (1984) E. Farhi and R. L. Jaffe, Phys. Rev. D 30, 2379 (1984).
- Holdom et al. (2018) B. Holdom, J. Ren, and C. Zhang, Phys. Rev. Lett. 120, 222001 (2018), arXiv:1707.06610 [hep-ph] .
- Wang et al. (2021) L. Wang, J. Hu, C.-J. Xia, J.-F. Xu, G.-X. Peng, and R.-X. Xu, Galaxies 9, 70 (2021).
- Xia et al. (2022) C.-J. Xia, J.-F. Xu, G.-X. Peng, and R.-X. Xu, Phys. Rev. D 106, 034016 (2022), arXiv:2205.10610 [hep-ph] .
- Bai and Korwar (2025) Y. Bai and M. Korwar, JHEP 06, 059 (2025), arXiv:2409.16487 [hep-ph] .
- Bai and Chen (2024) Y. Bai and T.-K. Chen, (2024), arXiv:2410.19678 [hep-ph] .
- Haensel et al. (1986) P. Haensel, J. L. Zdunik, and R. Schaeffer, Astron. Astrophys. 160, 121 (1986).
- Alcock et al. (1986) C. Alcock, E. Farhi, and A. Olinto, Astrophys. J. 310, 261 (1986).
- Xu et al. (1999) R. X. Xu, G. J. Qiao, and B. Zhang, Astrophys. J. Lett. 522, L109 (1999), arXiv:astro-ph/9907132 .
- Yang et al. (2023) S.-H. Yang, C.-M. Pi, X.-P. Zheng, and F. Weber, Universe 9, 202 (2023), arXiv:2304.09614 [astro-ph.HE] .
- Zhang (2020) C. Zhang, Phys. Rev. D 101, 043003 (2020), arXiv:1908.10355 [astro-ph.HE] .
- Zhao et al. (2019) T. Zhao, W. Zheng, F. Wang, C.-M. Li, Y. Yan, Y.-F. Huang, and H.-S. Zong, Physical Review D 100, 043018 (2019).
- Ren and Zhang (2020) J. Ren and C. Zhang, Phys. Rev. D 102, 083003 (2020), arXiv:2006.09604 [hep-ph] .
- Cao et al. (2022) Z. Cao, L.-W. Chen, P.-C. Chu, and Y. Zhou, Phys. Rev. D 106, 083007 (2022), arXiv:2009.00942 [astro-ph.HE] .
- Yuan et al. (2022) W.-L. Yuan, A. Li, Z. Miao, B. Zuo, and Z. Bai, Phys. Rev. D 105, 123004 (2022), arXiv:2203.04798 [nucl-th] .
- Restrepo et al. (2023) T. E. Restrepo, C. Providência, and M. B. Pinto, Phys. Rev. D 107, 114015 (2023), arXiv:2212.11184 [hep-ph] .
- Xia et al. (2020) C.-J. Xia, S.-S. Xue, R.-X. Xu, and S.-G. Zhou, Phys. Rev. D 101, 103031 (2020), arXiv:2001.03531 [nucl-th] .
- Zhang and Mann (2021) C. Zhang and R. B. Mann, Phys. Rev. D 103, 063018 (2021), arXiv:2009.07182 [astro-ph.HE] .
- Pretel and Zhang (2024) J. M. Z. Pretel and C. Zhang, JCAP 10, 032 (2024), arXiv:2401.12519 [nucl-th] .
- Zhou et al. (2024) Y. Zhou, C. Zhang, J. Zhao, K. Kiuchi, S. Fujibayashi, and E. Zhou, Phys. Rev. D 110, 103012 (2024), arXiv:2407.08544 [astro-ph.HE] .
- Wang et al. (2024a) Z. Wang, Y. Gao, D. Liang, J. Zhao, and L. Shao, JCAP 11, 038 (2024a), arXiv:2409.11103 [astro-ph.HE] .
- Xie and Xia (2025) W.-J. Xie and C.-J. Xia, (2025), arXiv:2506.22781 [astro-ph.HE] .
- Chen et al. (2025) L.-F. Chen, J.-Y. Wu, H. Feng, T.-S. Chen, and K. Zhang, (2025), 10.3390/universe11070199, arXiv:2505.04477 [hep-ph] .
- Yang et al. (2025a) Z. Yang, T. Zeng, Y. Yan, W.-L. Yuan, C. Zhang, and E. Zhou, “Hybrid quark stars with quark-quark phase transitions,” (2025a), arXiv:2507.00776 [astro-ph.HE] .
- Zhang and Ren (2023) C. Zhang and J. Ren, Phys. Rev. D 108, 063012 (2023), arXiv:2211.12043 [astro-ph.HE] .
- Zhang et al. (2024) C. Zhang, Y. Luo, H.-b. Li, L. Shao, and R. Xu, Phys. Rev. D 109, 063020 (2024), arXiv:2306.08234 [astro-ph.HE] .
- Negreiros et al. (2025) R. Negreiros, C. Zhang, and R. Xu, Phys. Rev. D 111, 063026 (2025), arXiv:2407.06410 [astro-ph.HE] .
- Xu (2003) R.-X. Xu, Astrophys. J. Lett. 596, L59 (2003), arXiv:astro-ph/0302165 .
- Lai and Xu (2009) X. Y. Lai and R. X. Xu, Monthly Notices of the Royal Astronomical Society: Letters 398, L31 (2009).
- Lai and Xu (2017) X. Lai and R. Xu, J. Phys. Conf. Ser. 861, 012027 (2017), arXiv:1701.08463 [astro-ph.HE] .
- Miao et al. (2022) Z.-Q. Miao, C.-J. Xia, X.-Y. Lai, T. Maruyama, R.-X. Xu, and E.-P. Zhou, Int. J. Mod. Phys. E 31, 2250037 (2022), arXiv:2008.06932 [nucl-th] .
- Gao et al. (2021) Y. Gao, X.-Y. Lai, L. Shao, and R.-X. Xu, Mon. Not. Roy. Astron. Soc. 509, 2758 (2021), arXiv:2109.13234 [gr-qc] .
- Zhang et al. (2023a) C. Zhang, Y. Gao, C.-J. Xia, and R. Xu, Phys. Rev. D 108, 063002 (2023a), arXiv:2305.13323 [astro-ph.HE] .
- Li et al. (2023) H.-B. Li, Y. Kang, Z. Hu, L. Shao, C.-J. Xia, and R.-X. Xu, Mon. Not. Roy. Astron. Soc. 527, 855 (2023), arXiv:2309.09847 [astro-ph.HE] .
- Li et al. (2024) H.-B. Li, Y. Gao, L. Shao, and R.-X. Xu, Universe 10, 157 (2024).
- Wang et al. (2024b) W.-Y. Wang, C. Zhang, E. Zhou, X. Liu, J. Niu, Z. Zhou, H. Gao, J. Liu, R. Xu, and B. Zhang, Res. Astron. Astrophys. 24, 105012 (2024b), arXiv:2405.07152 [astro-ph.HE] .
- Yuan et al. (2025) W.-L. Yuan, C. Huang, C. Zhang, E. Zhou, and R. Xu, Phys. Rev. D 111, 063033 (2025), arXiv:2411.14938 [astro-ph.HE] .
- Zhang et al. (2023b) C. Zhang, Y. Gao, C.-J. Xia, and R. Xu, Phys. Rev. D 108, 123031 (2023b), arXiv:2309.14114 [nucl-th] .
- Glendenning (1997) N. K. Glendenning, Compact stars: Nuclear physics, particle physics, and general relativity (1997).
- Pereira et al. (2018) J. P. Pereira, C. V. Flores, and G. Lugones, Astrophys. J. 860, 12 (2018), arXiv:1706.09371 [gr-qc] .
- Pretel et al. (2024) J. M. Z. Pretel, M. Dutra, and S. B. Duarte, Phys. Rev. D 109, 023524 (2024).
- Lugones and Grunfeld (2021) G. Lugones and A. G. Grunfeld, Universe 7, 493 (2021).
- Lugones et al. (2023) G. Lugones, M. Mariani, and I. F. Ranea-Sandoval, JCAP 03, 028 (2023), arXiv:2106.10380 [nucl-th] .
- Goncalves et al. (2022) V. P. Goncalves, J. C. Jiménez, and L. Lazzari, Eur. Phys. J. C 82, 1117 (2022), arXiv:2206.10513 [nucl-th] .
- Doroshenko et al. (2022) V. Doroshenko, V. Suleimanov, G. Phlhofer, and A. Santangelo, Nat. Astron. 6, 1444 (2022).
- Tsaloukidis et al. (2023) L. Tsaloukidis, P. S. Koliogiannis, A. Kanakis-Pegios, and C. C. Moustakidis, Phys. Rev. D 107, 023012 (2023), arXiv:2210.15644 [astro-ph.HE] .
- Sagun et al. (2023) V. Sagun, E. Giangrandi, T. Dietrich, O. Ivanytskyi, R. Negreiros, and C. Providência, Astrophys. J. 958, 49 (2023), arXiv:2306.12326 [astro-ph.HE] .
- Laskos-Patkos et al. (2024) P. Laskos-Patkos, P. S. Koliogiannis, and C. C. Moustakidis, Phys. Rev. D 109, 063017 (2024), arXiv:2312.07113 [astro-ph.HE] .
- Laskos-Patkos et al. (2025) P. Laskos-Patkos, G. A. Lalazissis, S. Wang, J. Meng, P. Ring, and C. C. Moustakidis, Phys. Rev. C 111, 025801 (2025), arXiv:2408.15056 [astro-ph.HE] .
- Mariani et al. (2024) M. Mariani, I. F. Ranea, G. Lugones, and M. G. Orsaria, Phys. Rev. D 110, 043026 (2024).
- Gao et al. (2024) B. Gao, Y. Yan, and M. Harada, Phys. Rev. C 109, 065807 (2024), arXiv:2404.04786 [nucl-th] .
- Pal et al. (2025) S. Pal, S. Podder, and G. Chaudhuri, Astrophys. J. 983, 24 (2025), arXiv:2504.02945 [nucl-th] .
- Hong and Ren (2024a) B. Hong and Z. Ren, Phys. Rev. D 110, 023012 (2024a).
- Di Clemente et al. (2024) F. Di Clemente, A. Drago, and G. Pagliara, The Astrophysical Journal 967, 159 (2024).
- Horvath et al. (2023) J. E. Horvath, L. S. Rocha, L. M. de Sá, P. H. R. S. Moraes, L. G. Barão, M. G. B. de Avellar, A. Bernardo, and R. R. A. Bachega, Astron. Astrophys. 672, L11 (2023), arXiv:2303.10264 [astro-ph.HE] .
- Oikonomou and Moustakidis (2023) P. Oikonomou and C. Moustakidis, Physical Review D 108 (2023), 10.1103/physrevd.108.063010.
- Rather et al. (2023) I. A. Rather, G. Panotopoulos, and I. Lopes, Eur. Phys. J. C 83, 1065 (2023), arXiv:2307.03703 [astro-ph.HE] .
- Gholami et al. (2025) H. Gholami, I. A. Rather, M. Hofmann, M. Buballa, and J. Schaffner-Bielich, Phys. Rev. D 111, 103034 (2025), arXiv:2411.04064 [hep-ph] .
- Issifu et al. (2025) A. Issifu, F. M. da Silva, L. C. N. Santos, D. P. Menezes, and T. Frederico, Classical and Quantum Gravity 42, 125004 (2025).
- Kourmpetis et al. (2025) K. Kourmpetis, P. Laskos-Patkos, and C. C. Moustakidis, (2025), arXiv:2505.10329 [astro-ph.HE] .
- Brodie and Haber (2023) L. Brodie and A. Haber, Phys. Rev. C 108, 025806 (2023), arXiv:2302.02989 [nucl-th] .
- Huang et al. (2024) K. Huang, H. Shen, J. Hu, and Y. Zhang, Phys. Rev. D 109, 043036 (2024), arXiv:2306.04992 [nucl-th] .
- Li and Sedrakian (2023) J. J. Li and A. Sedrakian, Phys. Lett. B 844, 138062 (2023), arXiv:2306.14185 [nucl-th] .
- Kubis et al. (2023) S. Kubis, W. Wójcik, D. A. Castillo, and N. Zabari, Phys. Rev. C 108, 045803 (2023), arXiv:2307.02979 [nucl-th] .
- Hong and Ren (2024b) B. Hong and Z. Ren, Phys. Rev. D 109, 023002 (2024b).
- Routaray et al. (2024) P. Routaray, H. C. Das, J. A. Pattnaik, and B. Kumar, Int. J. Mod. Phys. E 33, 2450052 (2024), arXiv:2307.12748 [math.NA] .
- Kini et al. (2024) Y. Kini et al., Mon. Not. Roy. Astron. Soc. 535, 1507 (2024), arXiv:2405.10717 [astro-ph.HE] .
- Laskos-Patkos and Moustakidis (2025) P. Laskos-Patkos and C. C. Moustakidis, Phys. Rev. D 111, 063058 (2025), arXiv:2410.18498 [astro-ph.HE] .
- Zhou and Huang (2025) T. Zhou and C. Huang, (2025), arXiv:2504.08662 [astro-ph.HE] .
- Pitz and Schaffner-Bielich (2025) S. L. Pitz and J. Schaffner-Bielich, Phys. Rev. D 111, 043050 (2025), arXiv:2408.13157 [astro-ph.HE] .
- Lopes and Issifu (2025) L. L. Lopes and A. Issifu, Phys. Dark Univ. 48, 101922 (2025).
- Yang et al. (2025b) S.-H. Yang, C.-M. Pi, and F. Weber, Phys. Rev. D 111, 043037 (2025b), arXiv:2409.15969 [astro-ph.HE] .
- Lopes (2025) L. L. Lopes, (2025), arXiv:2501.06379 [astro-ph.HE] .
- Veselsky et al. (2025) M. Veselsky, V. Petousis, P. S. Koliogiannis, C. C. Moustakidis, and J. Leja, Phys. Rev. D 111, L061308 (2025), arXiv:2412.01426 [nucl-th] .
- Abbott et al. (2020) R. Abbott, T. Abbott, S. Abraham, F. Acernese, K. Ackley, C. Adams, R. X. Adhikari, V. Adya, C. Affeldt, M. Agathos, et al., The Astrophysical Journal Letters 896, L44 (2020).
- Margalit and Metzger (2017) B. Margalit and B. D. Metzger, The Astrophysical Journal Letters 850, L19 (2017).
- Rezzolla et al. (2018) L. Rezzolla, E. R. Most, and L. R. Weih, The Astrophysical Journal Letters 852, L25 (2018).
- Ruiz et al. (2018) M. Ruiz, S. L. Shapiro, and A. Tsokaros, Physical Review D 97, 021501 (2018).
- Shibata et al. (2019) M. Shibata, E. Zhou, K. Kiuchi, and S. Fujibayashi, Physical Review D 100, 023015 (2019).
- Abbott et al. (2017) B. P. Abbott et al. (LIGO Scientific, Virgo), Phys. Rev. Lett. 119, 161101 (2017), arXiv:1710.05832 [gr-qc] .
- Miller et al. (2019) M. C. Miller et al., Astrophys. J. Lett. 887, L24 (2019), arXiv:1912.05705 [astro-ph.HE] .
- Riley et al. (2019) T. E. Riley et al., Astrophys. J. Lett. 887, L21 (2019), arXiv:1912.05702 [astro-ph.HE] .
- Miller et al. (2021) M. C. Miller, F. Lamb, A. Dittmann, S. Bogdanov, Z. Arzoumanian, K. Gendreau, S. Guillot, W. Ho, J. Lattimer, M. Loewenstein, et al., The Astrophysical Journal Letters 918, L28 (2021).
- Riley et al. (2021) T. E. Riley, A. L. Watts, P. S. Ray, S. Bogdanov, S. Guillot, S. M. Morsink, A. V. Bilous, Z. Arzoumanian, D. Choudhury, J. S. Deneva, et al., The Astrophysical Journal Letters 918, L27 (2021).
- Choudhury et al. (2024) D. Choudhury, T. Salmi, S. Vinciguerra, T. E. Riley, Y. Kini, A. L. Watts, B. Dorsman, S. Bogdanov, S. Guillot, P. S. Ray, et al., The Astrophysical Journal Letters 971, L20 (2024).
- Rutherford et al. (2024) N. Rutherford, M. Mendes, I. Svensson, A. Schwenk, A. L. Watts, K. Hebeler, J. Keller, C. Prescod-Weinstein, D. Choudhury, G. Raaijmakers, et al., The Astrophysical Journal Letters 971, L19 (2024).
- Damour and Nagar (2009a) T. Damour and A. Nagar, Phys. Rev. D 80, 084035 (2009a), arXiv:0906.0096 [gr-qc] .
- Hebeler et al. (2013) K. Hebeler, J. Lattimer, C. J. Pethick, and A. Schwenk, The Astrophysical Journal 773, 11 (2013).
- Huang and Sourav (2025) C. Huang and S. Sourav, Astrophys. J. 983, 17 (2025), arXiv:2502.11976 [astro-ph.HE] .
- Oppenheimer and Volkoff (1939) J. R. Oppenheimer and G. M. Volkoff, Phys. Rev. 55, 374 (1939).
- Tolman (1939) R. C. Tolman, Phys. Rev. 55, 364 (1939).
- Chanmugam (1977) G. Chanmugam, Astrophys. J. 217, 799 (1977).
- Väth and Chanmugam (1992) H. M. Väth and G. Chanmugam, A&A 260, 250 (1992).
- Gondek et al. (1997) D. Gondek, P. Haensel, and J. L. Zdunik, A&A 325, 217 (1997).
- Vásquez Flores and Lugones (2010) C. Vásquez Flores and G. Lugones, Phys. Rev. D 82, 063006 (2010).
- Pretel and da Silva (2020) J. M. Z. Pretel and M. F. A. da Silva, MNRAS 495, 5027 (2020).
- Hinderer (2008) T. Hinderer, The Astrophysical Journal 677, 1216 (2008).
- Hinderer et al. (2010) T. Hinderer, B. D. Lackey, R. N. Lang, and J. S. Read, Physical Review D—Particles, Fields, Gravitation, and Cosmology 81, 123016 (2010).
- Postnikov et al. (2010) S. Postnikov, M. Prakash, and J. M. Lattimer, Physical Review D—Particles, Fields, Gravitation, and Cosmology 82, 024016 (2010).
- Damour and Nagar (2009b) T. Damour and A. Nagar, Physical Review D—Particles, Fields, Gravitation, and Cosmology 80, 084035 (2009b).
- Takátsy and Kovács (2020) J. Takátsy and P. Kovács, Physical Review D 102, 028501 (2020).
- Abbott et al. (2019a) B. P. Abbott et al. (LIGO Scientific, Virgo), Phys. Rev. X 9, 011001 (2019a), arXiv:1805.11579 [gr-qc] .
- Radice et al. (2018a) D. Radice, A. Perego, F. Zappa, and S. Bernuzzi, Astrophys. J. Lett. 852, L29 (2018a), arXiv:1711.03647 [astro-ph.HE] .
- Most et al. (2018) E. R. Most, L. R. Weih, L. Rezzolla, and J. Schaffner-Bielich, Phys. Rev. Lett. 120, 261103 (2018), arXiv:1803.00549 [gr-qc] .
- De et al. (2018) S. De, D. Finstad, J. M. Lattimer, D. A. Brown, E. Berger, and C. M. Biwer, Phys. Rev. Lett. 121, 091102 (2018), [Erratum: Phys.Rev.Lett. 121, 259902 (2018)], arXiv:1804.08583 [astro-ph.HE] .
- Burgio et al. (2018) G. F. Burgio, A. Drago, G. Pagliara, H. J. Schulze, and J. B. Wei, Astrophys. J. 860, 139 (2018), arXiv:1803.09696 [astro-ph.HE] .
- Abbott et al. (2018) B. P. Abbott et al. (LIGO Scientific, Virgo), Phys. Rev. Lett. 121, 161101 (2018), arXiv:1805.11581 [gr-qc] .
- Abbott et al. (2019b) B. Abbott, R. Abbott, T. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. Adhikari, V. Adya, et al., Physical Review X 9, 011001 (2019b).
- Radice et al. (2018b) D. Radice, A. Perego, F. Zappa, and S. Bernuzzi, The Astrophysical Journal Letters 852, L29 (2018b).
- Kiuchi et al. (2019) K. Kiuchi, K. Kyutoku, M. Shibata, and K. Taniguchi, The Astrophysical Journal Letters 876, L31 (2019).
- Read et al. (2009) J. S. Read, B. D. Lackey, B. J. Owen, and J. L. Friedman, Phys. Rev. D 79, 124032 (2009), arXiv:0812.2163 [astro-ph] .
- O’Boyle et al. (2020) M. F. O’Boyle, C. Markakis, N. Stergioulas, and J. S. Read, Phys. Rev. D 102, 083027 (2020), arXiv:2008.03342 [astro-ph.HE] .
- Lindblom (2010) L. Lindblom, Phys. Rev. D 82, 103011 (2010), arXiv:1009.0738 [astro-ph.HE] .
- Greif et al. (2019) S. K. Greif, G. Raaijmakers, K. Hebeler, A. Schwenk, and A. L. Watts, Mon. Not. Roy. Astron. Soc. 485, 5363 (2019), arXiv:1812.08188 [astro-ph.HE] .
- Sun et al. (2025) H. Sun, J.-X. Niu, H.-B. Li, C.-J. Xia, E. Zhou, Y. Ma, and Y.-X. Zhang, Phys. Rev. D 111, 103019 (2025), arXiv:2501.07188 [astro-ph.HE] .
- Guha et al. (2025) A. Guha, D. Sen, and C. H. Hyun, Eur. Phys. J. C 85, 442 (2025), arXiv:2412.18569 [hep-ph] .
- Zhao et al. (2025) T. Zhao, P. B. Rau, A. Haber, S. P. Harris, C. Constantinou, and S. Han, (2025), arXiv:2504.12230 [astro-ph.HE] .
- Tonetto and Lugones (2020) L. Tonetto and G. Lugones, Phys. Rev. D 101, 123029 (2020), arXiv:2003.01259 [astro-ph.HE] .
- Han and Steiner (2019) S. Han and A. W. Steiner, Physical Review D 99, 083014 (2019).
- Hoyos et al. (2022) C. Hoyos, N. Jokela, and A. Vuorinen, Progress in Particle and Nuclear Physics 126, 103972 (2022).
- Annala et al. (2018) E. Annala, C. Ecker, C. Hoyos, N. Jokela, D. R. Fernández, and A. Vuorinen, Journal of High Energy Physics 2018, 1 (2018).
- Ranea-Sandoval et al. (2022) I. F. Ranea-Sandoval, M. Mariani, G. Lugones, and O. M. Guilera, Mon. Not. Roy. Astron. Soc. 519, 3194 (2022), arXiv:2212.10514 [astro-ph.HE] .
- Ranea et al. (2023) I. F. Ranea, M. Mariani, M. O. Celi, M. C. Rodríguez, and L. Tonetto, Phys. Rev. D 107, 123028 (2023), arXiv:2306.02823 [astro-ph.HE] .
- Ma and Xie (1996) F. Ma and B.-r. Xie, Astrophys. J. Lett. 462, L63 (1996), arXiv:astro-ph/9603134 .
- Bejger et al. (2005) M. Bejger, P. Haensel, and J. L. Zdunik, Mon. Not. Roy. Astron. Soc. 359, 699 (2005), arXiv:astro-ph/0502348 .
- Loeb (1998) A. Loeb, The Astrophysical Journal 499, L111–L114 (1998).
- Menezes et al. (2006) D. P. Menezes, D. B. Melrose, C. Providencia, and K. Wu, Phys. Rev. C 73, 025806 (2006).
- Shen et al. (2023) J.-Y. Shen, Y.-C. Zou, S.-H. Yang, X.-P. Zheng, and K. Wang, The Astrophysical Journal 951, 3 (2023).
- Geng et al. (2021) J.-J. Geng, B. Li, and Y.-F. Huang, Innovation 2, 100152 (2021), arXiv:2103.04165 [astro-ph.HE] .
- Xu et al. (2025) Z.-H. Xu, W.-Y. Wang, and R.-X. Xu, (2025), arXiv:2506.12305 [astro-ph.HE] .