Small RNA driven feed-forward loop: critical role of sRNA in noise filtering

Swathi Tej^∗, Kumar Gaurav^∗∗ and Sutapa Mukherji^∗ ^∗Department of Protein Chemistry and Technology, CSIR - Central Food Technological Research Institute, Mysore 570 020, India
^∗∗ Department of Biosciences and Bioengineering, Indian Institute of Technology, Guwahati 781 039, India

(August 2, 2025)

Abstract

Gene regulatory networks are often partitioned into different types of recurring network motifs. A feed-forward loop (FFL) is a common motif in which an upstream regulator is a protein, typically a transcription factor, that regulates the expression of the target protein in two ways - first, directly by regulating the mRNA levels of the target protein and second, indirectly via an intermediate molecule that in turn regulates the target protein level. Investigations on two variants of FFL - purely transcriptional FFL (tFFL) and sRNA-mediated FFL (smFFL) reveal several advantages of using such motifs. Here, we study a distinct sRNA-driven FFL (sFFL) that was discovered recently in Salmonella enterica: The distinction being the upstream regulator here is not a protein but an sRNA that translationally activates the target protein expression directly; and also indirectly via regulation of the transcriptional activator of the target protein. This variant, i.e. sFFL has not been subjected to rigorous analysis. We, therefore, set out to understand two aspects. First is a quantitative comparison of the regulatory response of sFFL with tFFL and smFFL using a differential equation framework. Since the process of gene expression is inherently stochastic, the second objective is to find how noise in gene expression affects the functionality of the sFFL. We find that unlike for tFFL and smFFL, the response of sFFL is stronger and faster: the change in target protein concentration is rapid and depends critically on the initial concentration of sRNA. Further, our analysis based on generating function approach and stochastic simulations leads to a non-trivial prediction that an optimal noise filtration can be attained depending on the synthesis rate of the upstream sRNA and the degradation rate of the intermediate transcriptional activator. A comparison with a simpler process involving only translational activation by sRNA indicates that the design of sFFL is crucial for optimal noise filtration. These observations prompt us to conclude that sFFL has distinct advantages where the master regulator, sRNA, plays a critical role not only in driving a rapid and strong response, but also a reliable response that depends critically on its concentration.

1 Introduction

Small non-coding RNAs (small RNAs/micro RNAs) and proteins are two important regulators of gene expression at different levels. While a major role of protein regulators is to activate or repress gene expression at the transcriptional level by binding to DNA, the small RNAs (sRNA) often bind to their target mRNAs through sequence complementarity and regulate translation. Experimental studies indicate that sRNAs might regulate gene expression in different ways - by translational repression or activation, or by regulating the mRNA stability storz ; gottesman2 ; papenfort1 ; altuvia ; shimoni ; hwa ; bharat . Since sRNAs are small in size and do not further code for a protein, it is believed that sRNA-mediated regulation can lead to quick response with less energetic cost compared to protein-mediated regulation. Several recent studies show that the gene expression often involves dual strategies combining both protein- and sRNA-mediated regulation.shimoni ; bose2

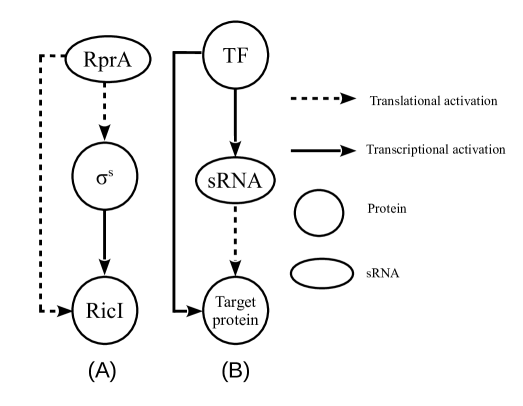
The process of gene regulation is, in general, non-linear and involves complex networks consisting of a number of genes, proteins, and sRNAs, which are themselves extensively regulated by proteins, sRNAs etc. Despite the complexity, it is possible to break down these complex regulatory networks into smaller sub-networks that function as basic building blocks of the bigger network. The sub-networks, typically known as network motifs, can then be analysed and based on the dynamics of individual motifs one may attempt to understand the dynamics of the entire complex network. The network motifs often have recurrent occurrences and typically certain specific types of network motifs, such as feed-back loops, feed-forward loops (FFL), are over-represented. It is believed that these frequently occurring sub-networks are naturally chosen over others as they provide distinct evolutionary advantages such as speeding up the response time, dampening of noise, etc.alon1 ; mangan ; shen . FFLs involving transcriptional regulators have been studied extensively in the past alon2 . In a transcriptional FFL (referred as tFFL from now on), a protein regulator X transcriptionally activates protein Z directly and also indirectly through the transcriptional activation of an intermediate protein regulator Y which in turn activates Z transcriptionally. An FFL where X positively (or negatively) regulates Z both directly and indirectly, is known as the coherent FFL. FFLs where the direct and indirect paths have opposite regulatory effects are referred as incoherent FFLs. Further, coherent (or incoherent) FFLs can be of different types depending on the nature of interactions (activating or inhibiting) in the individual paths mangan . FFLs involving purely transcriptional regulation are found, for example, in L-arabinose utilisation system schleif . In addition to tFFL, there are other types of FFLs where Y is an sRNA regulating the translation or the stability of the target mRNA (of Z). Such FFLs will be referred in the following as sRNA-mediated FFL (smFFL) from hereon. Another interesting variation is an FFL, wherein the upstream regulator (for example, X, as introduced above) is an sRNA that drives the entire FFL. sRNA, in general, may activate or repress translation or the stability of downstream mRNAs. We shall refer to such FFL in the following as sRNA-driven feed-forward loop (sFFL). The comparison between the two variants, sFFL and smFFL, is presented in figures (1A) and (1B), respectively. Through mathematical and computational modelling, a significant progress has been made in understanding the role of FFL in gene regulation. For example, mathematical modelling suggests that a coherent tFFL can reject transient activation in X and respond only to persistent activation of X mangan . Similar studies also elucidate diverse beneficial features of smFFL like a quick to response to sudden changes in the input signal which is advantageous under transient stress conditions shimoni , the ability to dampen the fluctuations under different contexts osella ; caselle ; caselle2 ; samsonov ; marinari etc.. In this work, using different types of modelling schemes, we study two different aspects of the sFFL; one associated with the response of the system under different types of input signal, the other associated with the noise characteristics of the network.

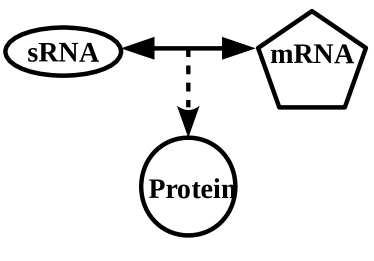
The sFFL of current interest has a significant role in horizontal gene transfer in Salmonella enterica papenfort2 . As figure (1A) and (1C) show, the FFL is driven by the sRNA, RprA, which is one of the three sRNAs (others being DsrA and ArcZ) that activate the translation of $\sigma^{s}$ mRNA that codes for the alternative sigma-factor, $\sigma^{s}$ gottesman3 ; gottesman4 . In this FFL, RprA sRNA drives the regulation in the synthesis of RicI protein through two parallel pathways, both involving translational activation by RprA. RprA binds to $\sigma^{s}$ mRNA through base-pairing and opens up a translation-inhibitory structure in the $5^{\prime}$ -untranslated region (5’-UTR) of the mRNA to facilitate ribosome binding and thereby promote $\sigma^{s}$ translation papenfort2 . $\sigma^{s}$ being a transcriptional activator for RicI mRNA up-regulates RicI mRNA synthesis. Finally, RprA, by opening the translation-inhibitory structure of its other target, RicI mRNA, leads to an increased synthesis of RicI protein. Thus, the FFL involves an AND gate mechanism where both $\sigma^{s}$ and RprA sRNA are essential for the up-regulation of RicI protein. Different types of stress conditions are expected to activate $\sigma^{s}$ production. The AND gate mechanism, through the involvement of both RprA and $\sigma^{s}$ , ensures that not every stress condition activating $\sigma^{s}$ synthesis leads to over-expression of RicI protein.

The inter-cellular transmission of plasmid through bacterial conjugation has an important role in microbial evolution and survival alberts . It is believed that this RprA driven FFL is crucial for regulation in the transfer of plasmid pSLT which encodes several virulence genes in Salmonella. Plasmid transfer via bacterial conjugation is a complex, energy-intensive process consisting of several proteins and RNAs functioning in concert. An important part of this process is the formation of pilus which establishes a contact between the donor and the receptor cells and enables the transfer of genetic material. Although such processes are found to be beneficial in terms of adaptation in the changing environment, due to significant fitness cost, such processes are usually tightly regulated inside the cells papenfort3 . It has been experimentally found that the synthesis of RicI protein is up-regulated in Salmonella treated with bile salt which is a bactericidal agent. Bile salt disrupts the bacterial cell membrane and under such membrane damaging activities, RicI protein interferes with transmembrane assembly that, under a normal condition, leads to pilus formation. Thus, RicI protein provides an extra protection to the bacterial cell by inhibiting energy expensive processes associated with pSLT transfer papenfort2 .

One of the major aims of mathematical modelling is to understand, in general, how a network processes or differentiates different types input signals such as sustained signal, transient signal or oscillatory signal. These studies reveal, for example, the response or shut down time scales of the network under different types of input signals mangan or sometimes more drastic response of the network depending on the details of the input signal lingchong . Such temporal behaviour can be found out by solving the differential equations that describe how the densities of various regulatory components change with time. The differential equation framework essentially captures the time variation of the average concentrations of various regulatory molecules. The gene expression is, however, inherently noisy due to the probabilistic nature of various biochemical processes involved and the noise may lead to significant fluctuations in concentrations of the regulatory molecules raj . These fluctuations are especially relevant when the number of regulatory molecules is small in which case the noise may cause significant deviations in the number of molecules from the respective average values. An important question in this case is that how, despite the inherent stochasticity, the network controls the target protein level reliably. Interestingly, it has been found that there are specific network motifs such as negative feed-back loop or coherent transcriptional FFL that can filter or dampen fluctuations in comparison to many other network motifs alon1 ; bose1 . In this context, one of the pertinent questions is how the gene expression noise contributes to the target protein fluctuation in sFFL.

The aim of the present work is two-fold. The first objective is to use the differential equation description to quantitatively understand how the response of sFFL differs from the other types of FFLs, such as tFFL or smFFL. Interestingly, we find that the response of sFFL to an input signal is, in general, strong and rapid compared to tFFL or smFFL. Furthermore, it is possible to find approximate mathematical solutions for various concentrations by solving a system of coupled, non-linear equations under specific types of input signals. We show that the mathematical solutions agree reasonably well with exact numerical solutions of the differential equations. Such mathematical solutions describe how the concentrations depend on various interactions, thereby reducing the need of further analysis on parameter variation. The second objective of the work is to explore the noise processing characteristics of the sFFL and identify interactions that might be crucial in minimizing fluctuations in the target protein concentration. We address this question by solving the stochastic model analytically using the master equation based generating function approach vankampen . This analysis leads to an interesting observation that the present loop can effectively filter the noise and this noise filtering ability depends crucially on the synthesis rate of the upstream sRNA regulator and the degradation rate of the transcriptional activator of the target protein. In particular, we find a range of values of these parameters over which the noise attenuation becomes optimal. We verify our predictions through stochastic simulations based on Gillespie algorithm (GA), which yields exact results on fluctuations in target protein concentration gillespie1 ; gillespie . The simulation results agree well with mathematical predictions. These observations prompt us to conclude that the master regulator sRNA, not only leads to strong and rapid response through target protein synthesis, but it also plays a significant role in minimizing fluctuations in target protein concentrations.

Refer to caption — Figure 1: (A) sRNA-driven coherent feed-forward loop (sFFL). Here the upstream, master regulator is an sRNA, RprA. (B) The sRNA-mediated coherent feed-forward loop (smFFL). Here the upstream, master regulator is a transcription factor (TF). The transcription factor activates the synthesis of the target protein mRNA directly and also activates sRNA synthesis which in turn activates the translation of the target protein. The ellipse and the circle represent sRNA and protein molecules, respectively. (C) A detailed diagram of sFFL with various processes such as synthesis, degradation, etc. shown explicitly. $k^{+}$ and $k^{-}$ , in general, represent the association and dissociation rates, respectively, of protein regulators or sRNAs with the respective target gene or the target mRNA.

2 Results and discussions

2.1 Model and the deterministic description

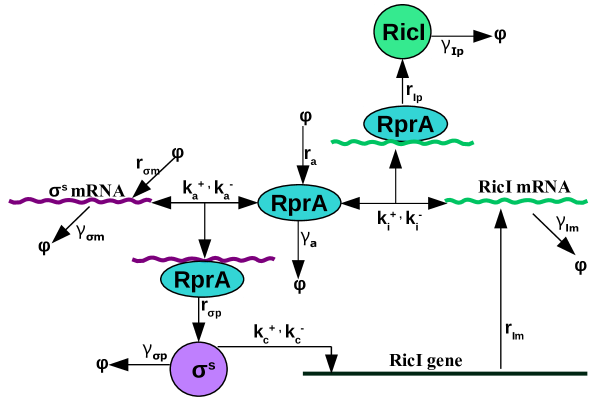
The sFFL of our interest is shown in figure (1A). This can be compared with the smFFL in figure (1B). The change in concentrations of various regulators such as proteins, mRNAs and sRNAs in sFFL with time is described through the following differential equations

	$\displaystyle\frac{d}{dt}[Ra]=r_{a}-\gamma_{a}[Ra],\ \ \frac{d}{dt}{[\sigma^{s}m]}=r_{\sigma m}-\gamma_{\sigma m}[\sigma^{s}m],\ \ \frac{d}{dt}[\sigma^{s}p]=r_{\sigma p}[Ra][\sigma^{s}m]-\gamma_{\sigma p}[\sigma^{s}p],$		(1)
	$\displaystyle\frac{d}{dt}[Rim]=f([\sigma^{s}p])-\gamma_{im}[Rim],\ \ \frac{d}{dt}[Rip]=r_{ip}[Ra][Rim]-\gamma_{ip}[Rip].$		(2)

The notations used for various concentrations in these equations are displayed in table 1. In general, the synthesis and degradation rates are denoted by $r$ and $\gamma$ , respectively. Here, $f([\sigma^{s}p])=\frac{r_{im}[\sigma^{s}p]}{1+k_{c}[\sigma^{s}p]}$ is the Hill function representing transcriptional activation in the synthesis of RicI mRNA by $\sigma^{s}$ protein and $k_{c}$ is the ratio of activation and deactivation rates of RicI gene. $1/k_{c}$ , also known as the activation threshold, corresponds to the special value of $\sigma^{s}$ protein concentration at which the transcription rate is the same as $1/2$ of its maximum value.

Table 1: Notations used in the text

Protein or mRNA or sRNA	Short form used in the text	Mathematical notation for concentrations
RprA sRNA	RprA	[Ra]
$\sigma^{s}$ mRNA	$\sigma^{s}m$	$[\sigma^{s}m]$
$\sigma^{s}$ protein	$\sigma^{s}p$	$[\sigma^{s}p]$
RicI mRNA	RicIm	$[Rim]$
RicI protein	RicIp	$[Rip]$

2.2 Approach to the steady state

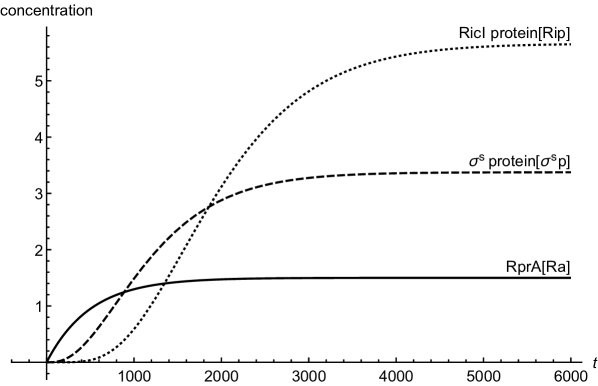
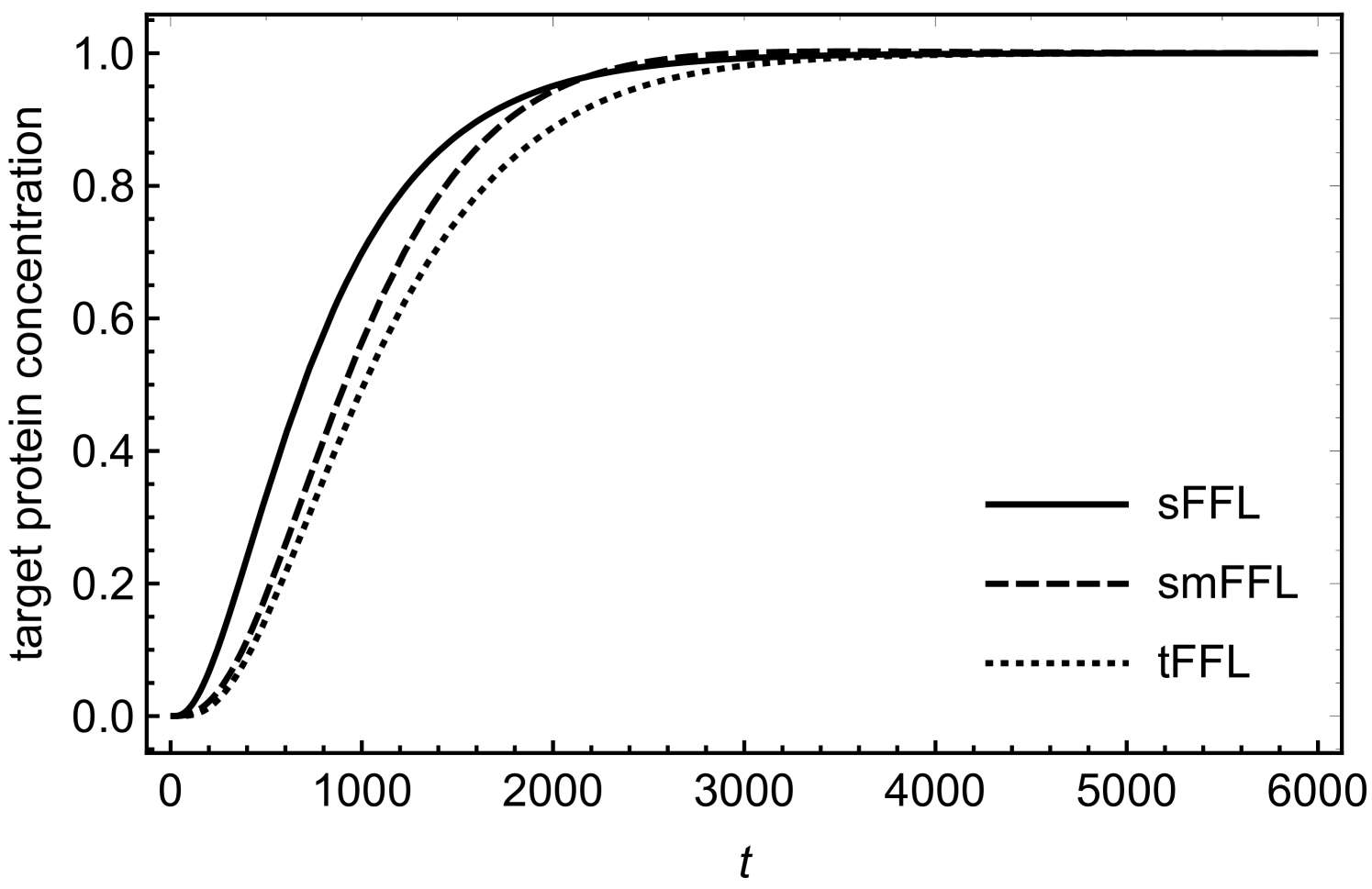
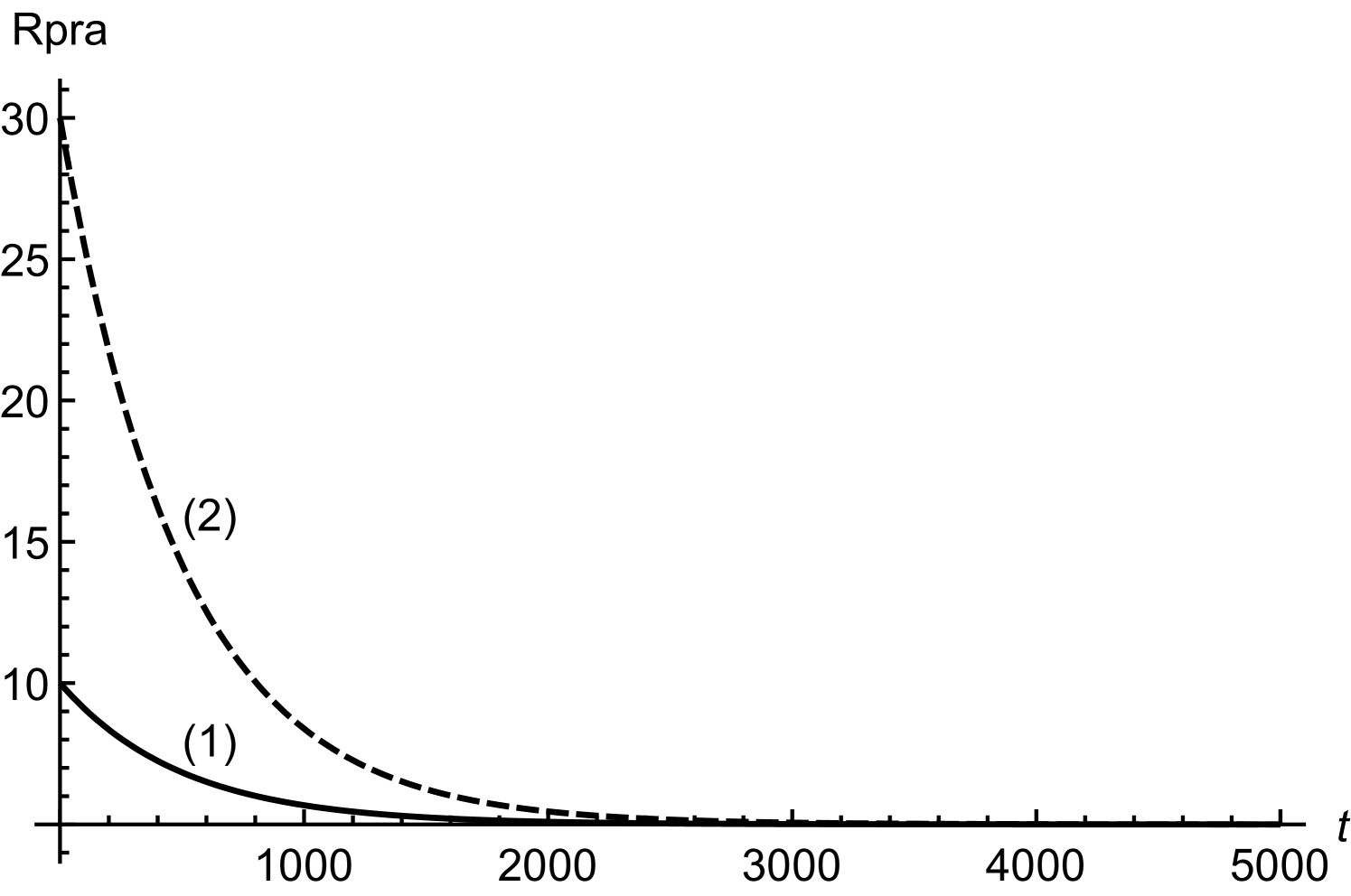
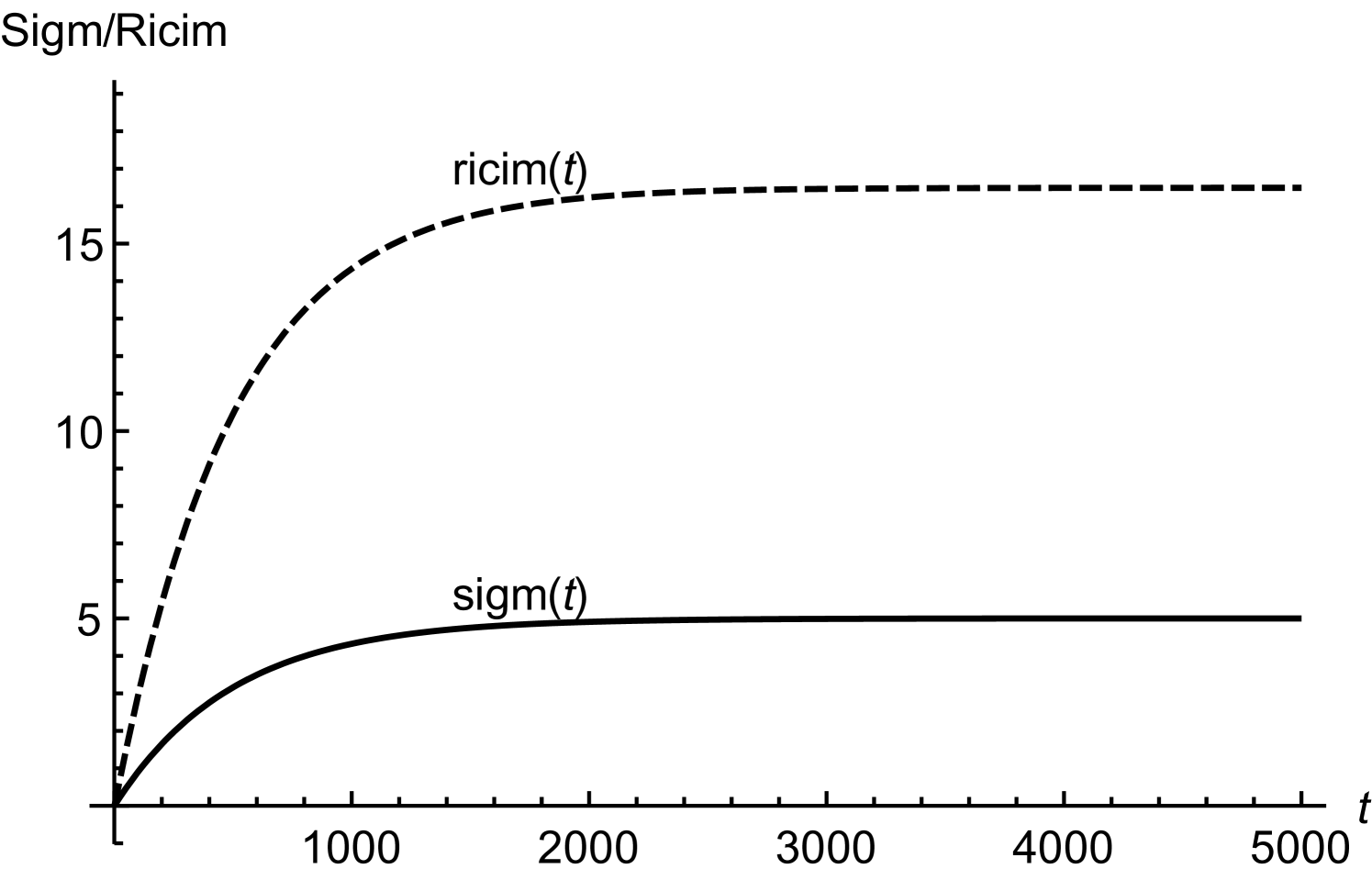
The steady-state concentrations of various regulators can be obtained by equating the time derivatives of various concentrations in equations (1) and (2) to zero and solving the resulting algebraic equations. Figure (2) shows a comparison as how different concentrations change with time as they approach the respective steady-state values. For enabling a meaningful comparison, we have chosen the same synthesis and degradation rates for all the regulatory components shen . Unless mentioned otherwise, for all the figures in the following, we assume negligible initial concentrations for all the regulators. As the figure shows, the increase in RicI protein concentration is slower compared to that of $\sigma^{s}$ protein initially (see also mangan ; papenfort2 ). This lag in RicI production is due to the fact that the transcriptional activation of RicI gene requires production of sufficient amount of transcriptional activator, $\sigma^{s}$ . The amount of delay in RicI production is, of course, strongly dependent on various biochemical parameters such as $k_{c}$ (the activation threshold for RicI mRNA transcription), degradation and synthesis rates of various regulatory components.

2.3 Temporal Solution

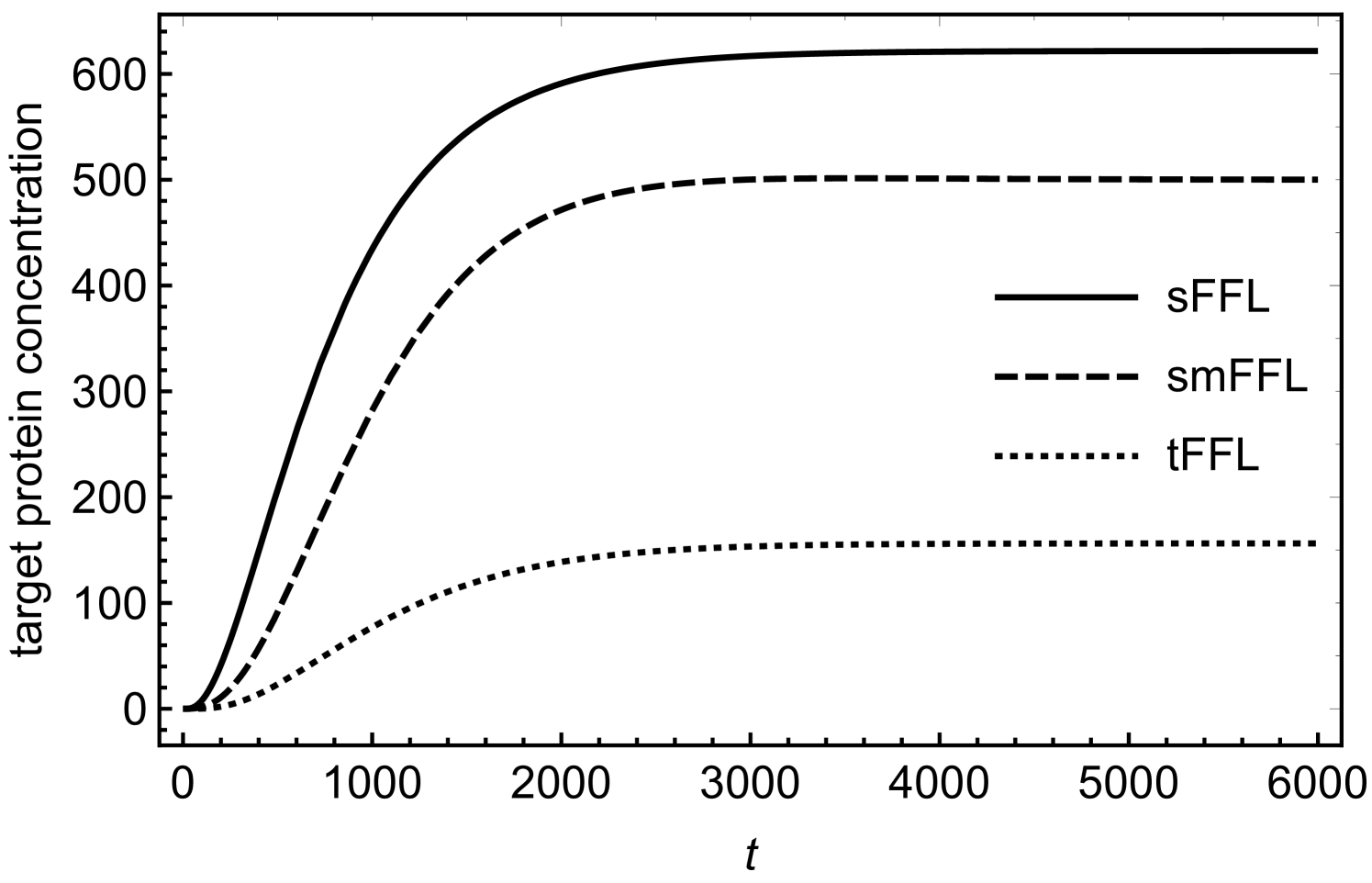
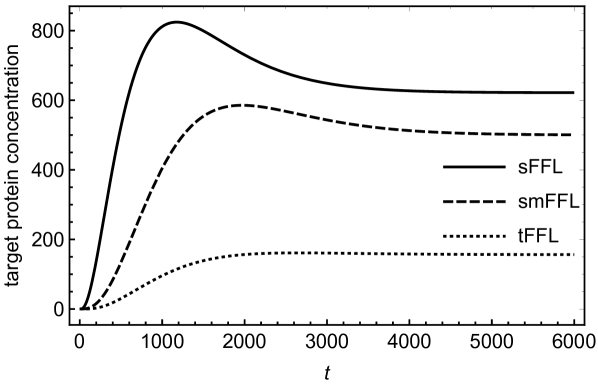
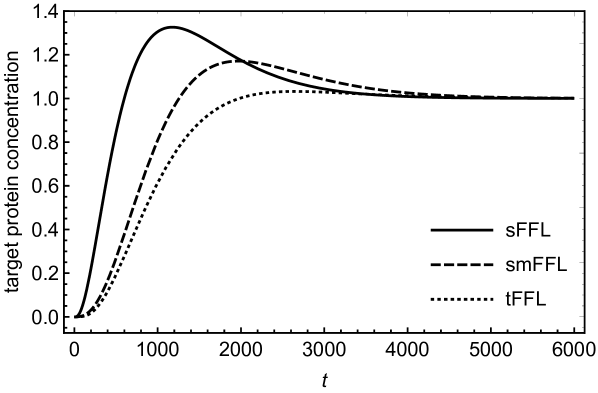
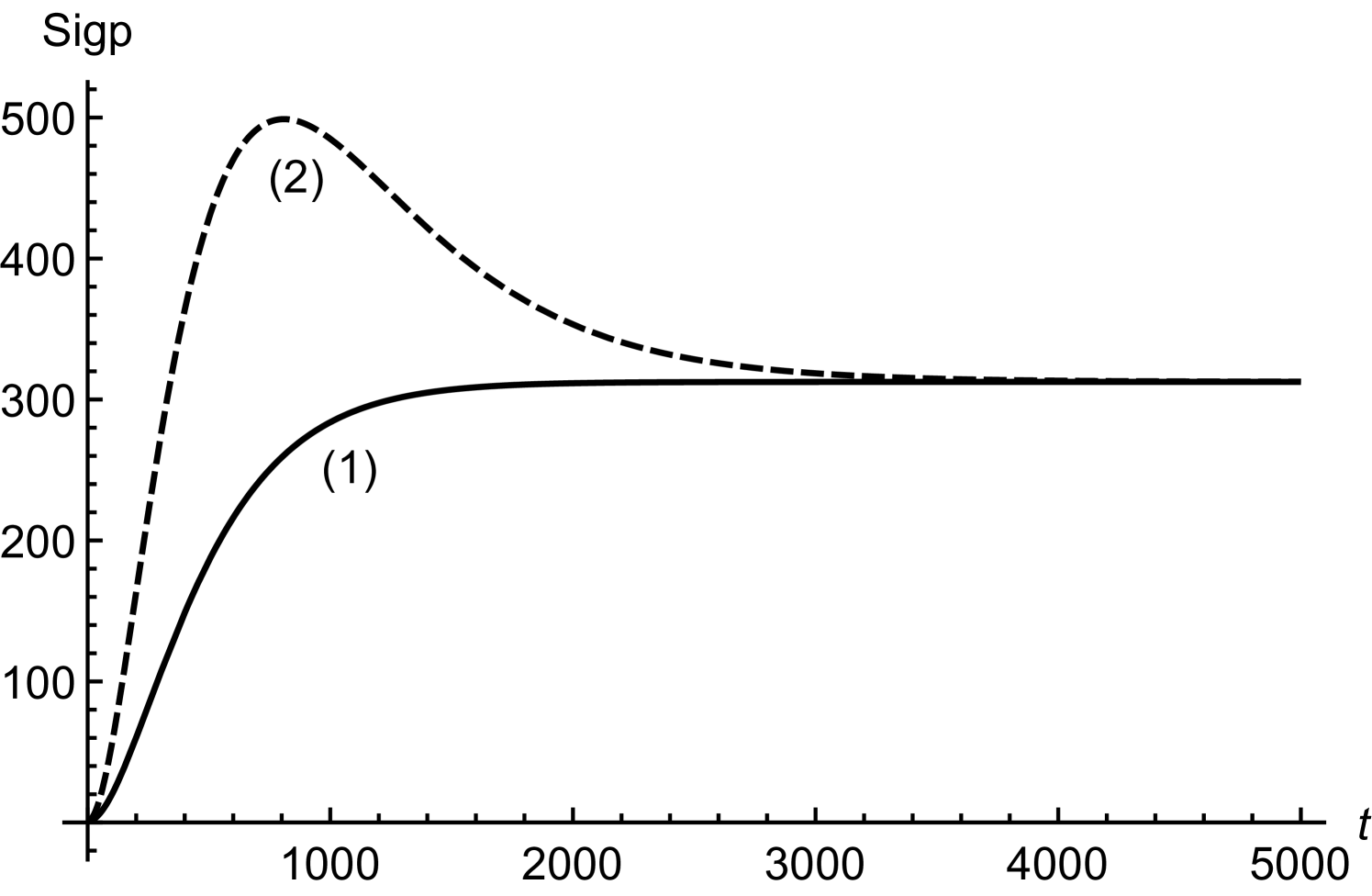
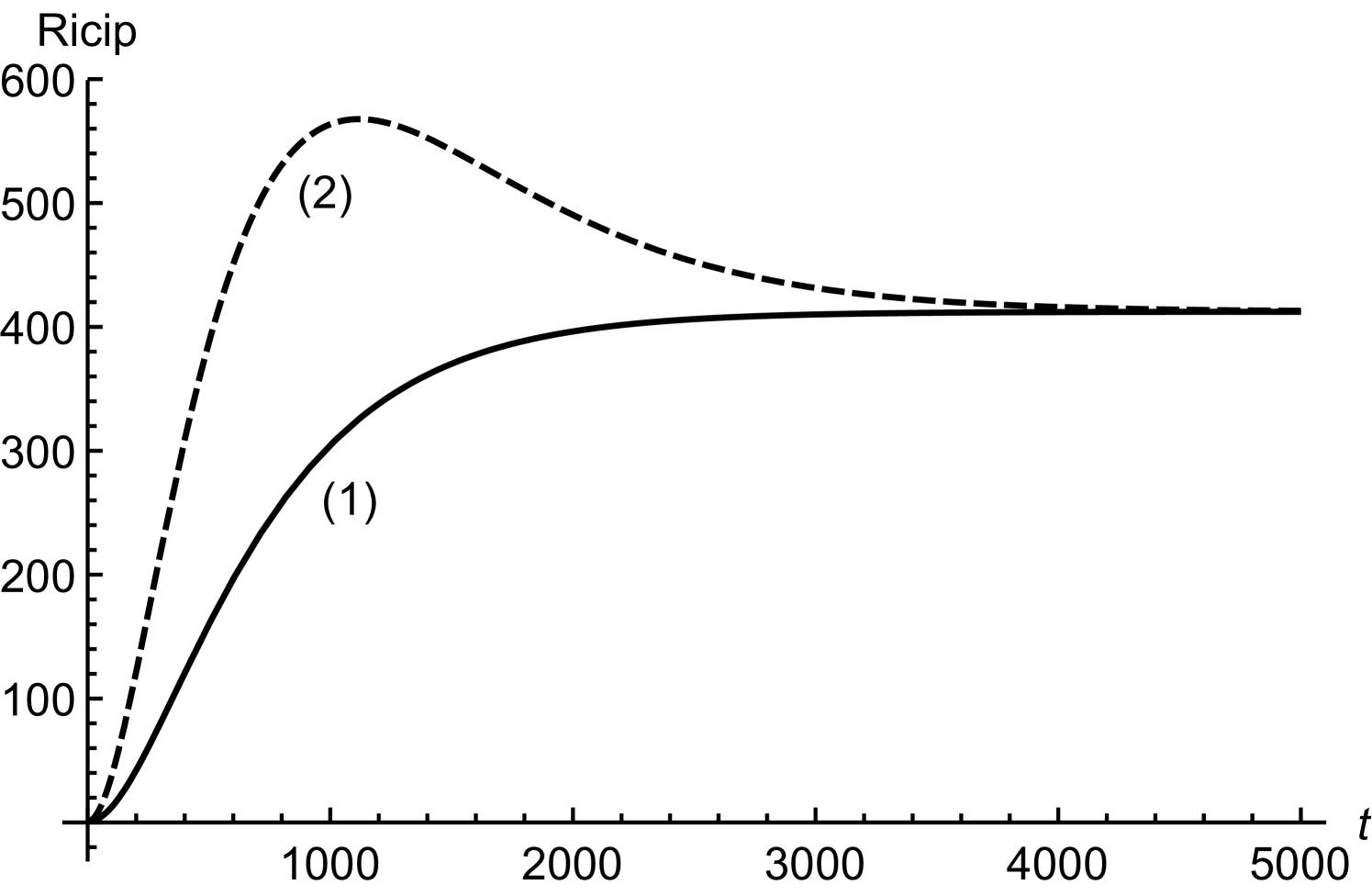
In order to understand the functionality of the present network motif in comparison with other motifs such as tFFL and smFFL, we solve the differential equations numerically for these three types of motifs. The differential equations describing the dynamics of the tFFL and smFFL are shown in appendix A. For sFFL, we consider differential equations in (1) and (2). Figures (3) and (4) show a comparison as how the target protein concentration approaches the steady state with time in three different cases. In order to have a meaningful comparison, we consider the same parameter values for all the three motifs. While for figure (3), the initial concentration of the upstream, master regulator is low, in case of figure (4) the initial concentration of the upstream regulator is relatively high. Irrespective of the initial condition, the response of the sFFL is the fastest among all the three motifs. The difference in the regulatory patterns seems to originate from the fundamental difference in the mechanism of transcritptional and translational activations. The transcriptional activation that happens through binding to the DNA is expected to cause a delayed response since sufficient concentration of transcriptional activator is required for crossing the activation threshold. In addition to this, due to the saturation kinetics, the transcriptional activation also reaches a saturation value that is independent of the concentration of the transcriptional activator. This results in a delayed response in tFFL that functions through transcriptional activation at three different stages. While in smFFL, the transcription interaction is required for activation of two different genes, in sFFL, only RicI gene is transcriptionally activated. It appears that the fast response of sFFL is linked to a reduced number of transcriptional activation steps associated with the loop. The difference due to the mode of regulation appears more prominently in figure (4) where an increased initial concentration in the upstream regulator leads to a faster and stronger response in sFFL as compared to other FFLs. The peak (non-monotonicity) in the response curve, present in case of smFFL, becomes more prominent in case of sFFL. It might be that for sFFL, the high initial concentration of RprA and the direct interaction between RprA and RicI mRNA lead to a significant translational up-regulation in RicI protein synthesis even when the initial RicI mRNA concentration is low. The sFFL is activated when the cell is exposed to stress due to membrane-damaging activities of bile-salt. RprA, along with $\sigma^{s}$ which activates RicI transcription, increases the expression of RicI protein. RicI protein localizes at the cytoplasmic membrane and, together with other proteins, blocks the conjugation machinery required for pSLT transfer thereby providing protection to the cell by inhibiting energy-expensive conjugation process. The rapid increase in RicI concentration especially when the initial RprA concentration is high, is possibly crucial for cell’s survival under stress due to bactericidal agents such as bile salt.

We have, further, obtained approximate mathematical solutions (see appendix B for details) for the target protein concentration in case of sFFL for two different cases; (i) with a constant pool of upstream sRNA regulators and (ii) with sRNA concentrations changing due to its synthesis and degradation processes. Mathematical solutions of such coupled, non-linear equations can be obtained only over restricted parameter space. We show that the mathematical solutions agree reasonably well with exact numerical solutions of the differential equations in (1) and (2) and display a rapid growth in the target protein concentrations for large initial concentration of the upstream sRNA regulator as seen in figure (4).

2.4 Noise processing characteristics

Here we focus on fluctuations in the target protein level in the sFFL of present interest. Using a general notation, we introduce $s$ , $m_{1}$ , $m_{2}$ , $p_{1}$ and $p_{2}$ as the number of sRNA (RprA), $\sigma^{s}$ mRNA, RicI mRNA, $\sigma^{s}$ protein and RicI protein molecules, respectively. This set of numbers represents a state of the system and $P_{s,m_{1},m_{2},p_{1},p_{2}}(t)$ denotes the probability that the system is in a given state specified by these numbers at time $t$ . Our fluctuation analysis is based on the master equation which is a differential equation that describes how this probability changes with time osella . The probability changes with time due to various processes such as transcription, translation and degradation of different types of molecules as per the details of the network. The master equation that takes into account all these processes is

$\displaystyle\frac{\partial}{\partial t}P_{s,m_{1},m_{2},p_{1},p_{2}}$	$\displaystyle=r_{s}(P_{{s-1},m_{1},p_{1},{m_{2}},p_{2}}-P_{s,m_{1},p_{1},{m_{2}},p_{2}})+\gamma_{s}((s+1)P_{s+1,m_{1},p_{1},{m_{2}},p_{2}}-sP_{s,m_{1},p_{1},{m_{2}},p_{2}})+$	(3)
	$\displaystyle\ r_{m_{1}}(P_{s,m_{1}-1,p_{1},{m_{2}},p_{2}}-P_{s,m_{1},p_{1},{m_{2}},p_{2}})+\gamma_{m_{1}}((m_{1}+1)P_{s,m_{1}+1,p_{1},{m_{2}},p_{2}}-m_{1}P_{s,m_{1},p_{1},{m_{2}},p_{2}})+$
	$\displaystyle\ r_{p_{1}}\ s\ m_{1}(P_{s,m_{1},p_{1}-1,{m_{2}},p_{2}}-P_{s,m_{1},p_{1},{m_{2}},p_{2}})+\gamma_{p_{1}}((p_{1}+1)P_{s,m_{1},p_{1}+1,{m_{2}},p_{2}}-p_{1}P_{s,m_{1},p_{1},{m_{2}},p_{2}})+$
	$\displaystyle\ r_{m_{2}}(p_{1})(P_{s,m_{1},p_{1},{m_{2}}-1,p_{2}}-P_{s,m_{1},p_{1},{m_{2}},p_{2}})+\gamma_{m_{2}}(({m_{2}}+1)P_{s,m_{1},p_{1},{m_{2}}+1,p_{2}}-{m_{2}}P_{s,m_{1},p_{1},{m_{2}},p_{2}})+$
	$\displaystyle\ r_{p_{2}}\ s\ {m_{2}}\ (P_{s,m_{1},p_{1},{m_{2}},p_{2}}-P_{s,m_{1},p_{1},{m_{2}},p_{2}})+\gamma_{p_{2}}((p_{2}+1)P_{s,m_{1},p_{1},{m_{2}},p_{2}+1}-p_{2}P_{s,m_{1},p_{1},{m_{2}},p_{2}})$

Here $r$ and $\gamma$ , in general, represent synthesis and degradation rates, respectively, of different types of molecules. $r_{m_{2}}(p_{1})$ denotes the transcription rate under transcriptional activation by $p_{1}$ and it is represented by the Hill function as $r_{m_{2}}(p_{1})=\frac{r_{m_{2}}k_{c}\ p_{1}}{1+k_{c}\ p_{1}}$ , where $1/k_{c}$ , as before, denotes the activation threshold. In order to proceed further, we approximate the Hill function about the average density $\langle p_{1}\rangle$ at the steady state. Under such approximation, we have

\displaystyle r_{m_{2}}(p_{1})=r_{m_{2}}^{0}+r_{m_{2}}^{1}p_{1},\ \ {\rm where}\ \ r_{m_{2}}^{0}=\frac{r_{m_{2}}k_{c}^{2}\left\langle p_{1}\right\rangle^{2}}{{(1+k_{c}\left\langle p_{1}\right\rangle)}^{2}}\qquad{\rm and}\qquad r_{m_{2}}^{1}=\frac{r_{m_{2}}k_{c}}{{(1+k_{c}\left\langle p_{1}\right\rangle)}^{2}}

(4)

Next, we introduce the moment generating function

\displaystyle G(z_{1},z_{2},z_{3},z_{4},z_{5})=\sum_{s,m_{1},p_{1},{m_{2}},p_{2}}z^{s}_{1}\ z^{m_{1}}_{2}\ z^{p_{1}}_{3}\ z^{m_{2}}_{4}\ z^{p_{2}}_{5}\ P_{s,m_{1},p_{1},{m_{2}},p_{2}}

(5)

with $G\mid_{\{z_{i}\}=1}=1$ . Various derivatives of the generating function are related to average quantities as $\frac{\partial}{\partial z_{i}}G(z_{1},z_{2},z_{3},z_{4},z_{5})\mid_{\{z_{i}\}=1}=\langle n_{i}\rangle$ and $\frac{\partial^{2}}{\partial z_{i}^{2}}G(z_{1},z_{2},z_{3},z_{4},z_{5})\mid_{\{z_{i}\}=1}=\langle n_{i}^{2}\rangle-\langle n_{i}\rangle$ where $\langle n_{i}\rangle$ denotes the mean number of molecules of the $i$ th species. Denoting $G_{ij}$ as $G_{ij}=\frac{\partial^{2}}{\partial z_{i}\partial z_{j}}G\mid_{\{z_{i}\}=1}$ , one may find the fluctuation in the target protein concentration as $G_{55}+G_{5}-G_{5}^{2}$ . Using (3), it can be seen that the moment generating function satisfies the following equation

	$\displaystyle\partial_{t}G=$		$\displaystyle r_{s}(z_{1}-1)G+\gamma_{s}(1-z_{1})\partial_{z_{1}}G+r_{m_{1}}(z_{2}-1)G+\gamma_{m_{1}}(1-z_{2})\partial_{z_{2}}G+r_{p_{1}}z_{1}z_{2}(z_{3}-1)\partial^{2}_{z_{1}z_{2}}G+\gamma_{p_{1}}(1-z_{3})\partial_{z_{3}}G$		(6)
			$\displaystyle+\ r_{m_{1}}^{0}(z_{4}-1)G+r_{m_{1}}^{1}z_{3}(z_{4}-1)\partial_{z_{3}}G+r_{p_{2}}z_{1}z_{4}(z_{5}-1)\partial^{2}_{z_{1}z_{4}}G+\gamma_{m_{2}}(1-z_{4})\partial_{4}G+\gamma_{p_{2}}(1-z_{5})\partial_{5}G,$		(6)

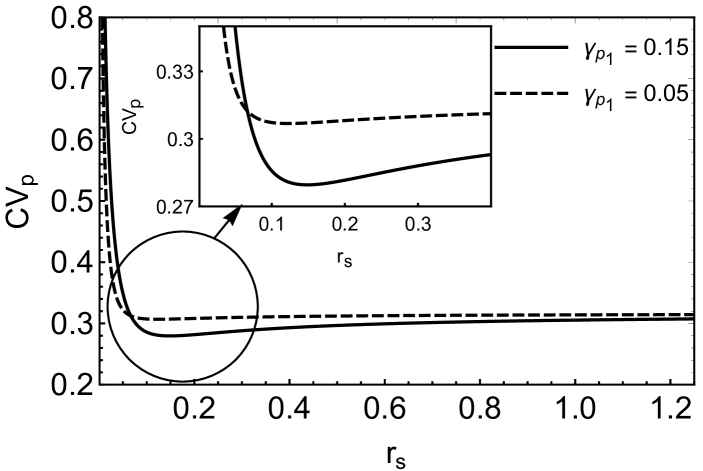
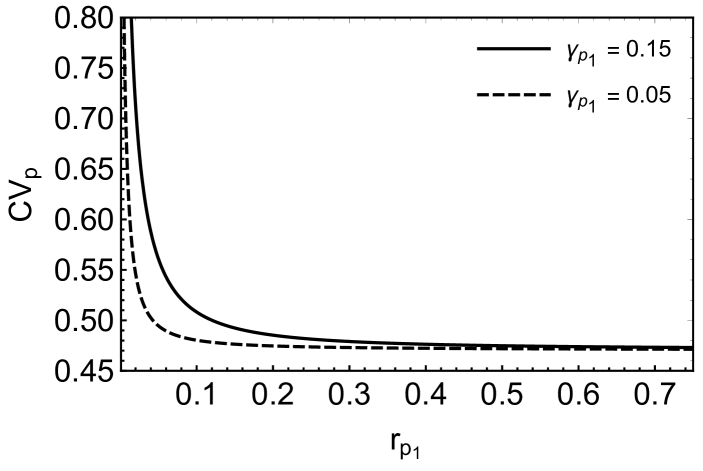
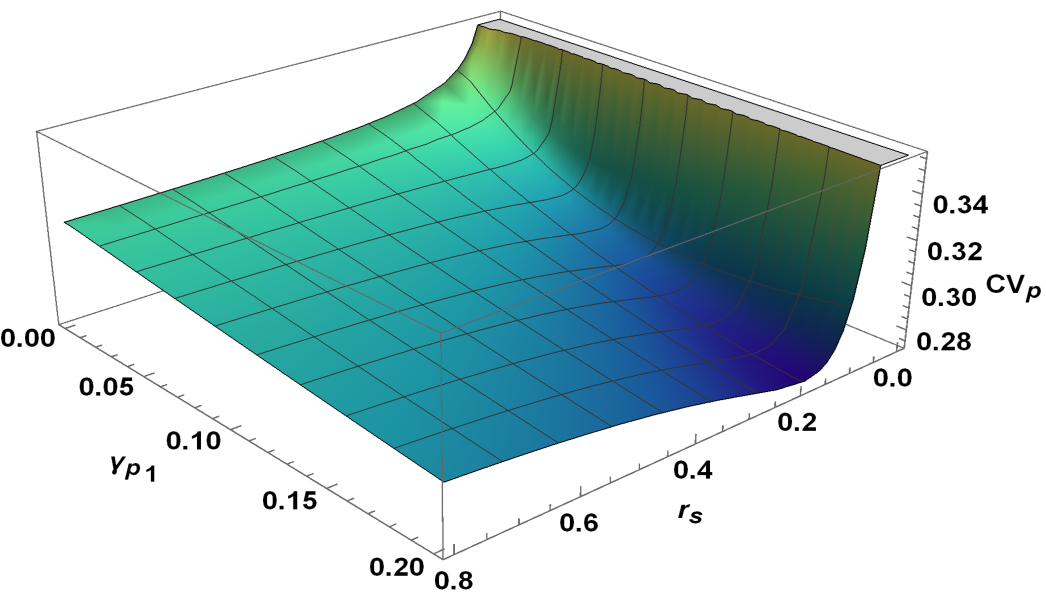
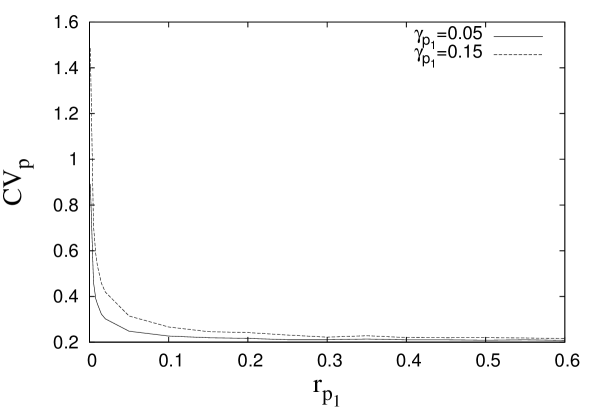
where $\partial_{x}G=\frac{\partial}{\partial x}G$ . In the steady state ( $\partial_{t}G=0$ ), one may obtain successive moments by taking successive derivatives of equation (6) and then substituting $\{z_{i}\}=1$ in the resulting equations. In order to obtain the target protein fluctuations, we need to find the first and second moments such as $G_{5}$ and $G_{55}$ . The evaluation of these moments becomes complex since an equation for a moment, in general, involves the higher order moments. In the present case, we are able to obtain the target protein fluctuation by evaluating up to fourth moment and ignoring the contributions of the higher order moments (see appendix C for details). The coefficient of variation for the target protein, $CV_{p}=({\langle p_{2}^{2}\rangle-\langle p_{2}\rangle^{2}})^{1/2}/{\langle p_{2}\rangle}$ , has been plotted in figure (5A). The figure shows a minimum indicating an optimal attenuation of fluctuations in the target protein level as $r_{s}$ is changed. Similar optimal noise filtration can also be seen with respect to $\gamma_{p_{1}}$ , the degradation rate of the transcriptional activator, $p_{1}$ . Figure (6) shows a 3-dimensional picture of optimum noise filtration as $r_{s}$ and $\gamma_{p_{1}}$ are changed. These figures show that an optimal noise attenuation is seen only over an intermediate range of values of $r_{s}$ and $\gamma_{p_{1}}$ and the minimum disappears as one increases the values of these parameters. Further, with similar parameter values, no optimal filtration of noise can be found with respect to the synthesis rates of $m_{1}$ and $p_{1}$ (see, for example, figure (5B)).

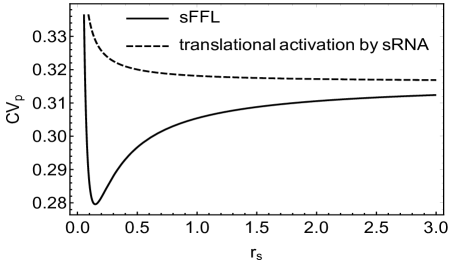
For understanding the rationale behind such noise processing characteristics of the sFFL, we compare these results with the case where gene regulation involves only translational activation by sRNAs (see figure (11A) in appendix (D)). This is equivalent to considering only the direct pathway in the sFFL through which RprA translationally activates RicI mRNA. This is also how RprA up-regulates $\sigma^{s}$ translation in the present sFFL while $\sigma^{s}$ transcripts are synthesized in the cell under various stress conditions. Various moments for such a minimal motif can be obtained in a straightforward way from the details presented in appendix C for the sFFL. The coefficients of variation for the target protein of such a minimal motif and the sFFL are shown in figure (11B) in appendix D. The figure clearly shows that the noise processing characteristics of the simple motif with only translational activation by sRNA are significantly different from that of sFFL considered here. In particular, no optimal noise filtration can be found in case of the minimal motif. Further, for the parameter values chosen here, near the region of optimal attenuation of noise, the coefficient of variation of sFFL becomes approximately $85\%$ of that of the simple case of gene regulation through translational activation. Despite having additional regulatory molecules and hence, associated fluctuations, the sFFL seems to be less noisy as compared to the simple sRNA regulation scheme discussed here. Further, it appears that the topology of the sFFL and the non-linear interactions play a crucial role in noise filtration characteristics.

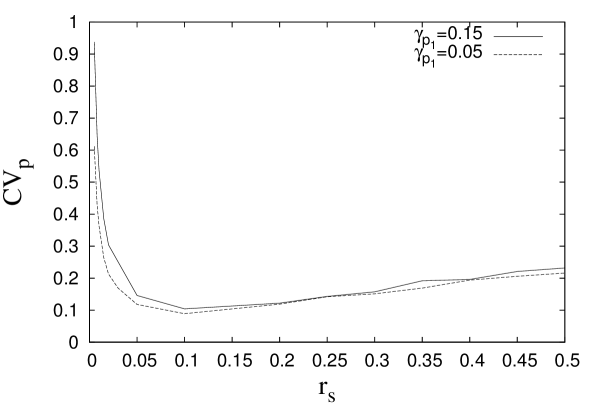
The results from the above mathematical analysis are supported by stochastic simulations discussed below. Stochastic simulations based on Gillespie algorithm (GA) is an exact method that allows us to incorporate the probabilistic features in the gene expression in a systematic way gillespie ; gillespie1 . In GA, we take into account different types of molecules such as protein, sRNA, mRNA molecules associated with the regulatory network and the relevant interactions between them. The number of each species of molecules at a given instant of time is denoted by $x_{i}(t)$ where $i=1,\ 2,\ 3,...N$ denotes a specific species of molecules given that there are totally $N$ different species of molecules. GA is based on two assumptions; (1) the time interval between two successive reactions is a random variable obeying Poisson Distribution and (2) the specific reaction that occurs at a given instant of time is selected randomly. In the simulation, this is executed by drawing two random numbers at each simulation step; one random number, $r_{1}$ , is used to decide the time interval between two successive reactions and the other random number, $r_{2}$ , is used to decide which reaction would occur in the next time step. Denoting a specific reaction by $\mu$ , where $\mu=1,2,3...$ , one may define a probability $a_{\mu}(t)dt$ which indicates the probability of occurrence of the $\mu$ th reaction in the time interval $t$ and $t+dt$ . Here $a_{\mu}(t)$ is expressed as the product of two factors; one is the reaction rate and the other factor is the number of possible $\mu$ type reactions. Thus at each simulation step, the time interval before the next reaction is determined and depending on the value of $r_{2}$ and the various reaction rates $a_{\mu}(t)$ , the next reaction is chosen. Subsequently, based on which reaction has occurred, the values of appropriate $x_{i}$ are updated. We allow the system to evolve over $5\times 10^{7}$ simulation steps and keep a record of the number of sRNA, mRNA, target protein number after every $500$ simulation steps leaving about $2\times 10^{4}$ initial steps. The details of the reactions considered and the corresponding rate constants are presented in appendix (E). The coefficients of variation for the target protein is shown in figures (7A) and (7B). Consistent with the mathematical analysis (figure (5A)), figure (7A) also shows an optimal noise attenuation with $r_{s}$ , the sRNA synthesis rate. As figure (5B), figure (7B) shows no minimum in the coefficient of variation as $r_{p_{1}}$ i.e. the synthesis rate of protein $p_{1}$ is changed.

The noise processing characteristics of different types of FFLs have been studied in the past. Using a Langevin description, it was shown that among various types of tFFLs, the coherent tFFL with all three activating regulatory interactions, was the least noisy among other kinds of coherent tFFL bose1 . In particular, it was shown that the activating nature of all regulatory interactions is responsible for such maximal noise reduction. Recently, noise processing characteristics have also been studied in detail for incoherent micro RNA (miRNA) mediated FFL osella ; caselle ; caselle2 ; marinari . Unlike Fig. 1B, in such miRNA mediated FFL, the miRNA represses the target protein synthesis by binding to the mRNA of the target protein and degrading it subsequently. Since sRNA/miRNA mediated target repression is a common scenario in gene regulation, there have been efforts in the past to understand the fundamental differences between the miRNA/sRNA mediated and TF mediated gene repression hwa . Currently, it is well established that, in general, sRNA-mediated repression reduces fluctuations in the target protein level as compared to TF mediated repression. Physically, this happens since in case of TF mediated repression, occasional transcriptional leakage is amplified due to translation causing large fluctuations in the protein concentration. In contrary to this, in case of sRNA-mediated repression of the target mRNA, the mRNAs are rarely translated leading to a relatively smooth gene expression. This feature of reducing fluctuations in the target protein level is also found in incoherent miRNA mediated FFL osella . Here, while the fluctuations in the top-tier transcription factor introduces similar variations in both miRNA and mRNA levels, the miRNA due to its repression activity reduces the target protein fluctuations against the transcription factor fluctuations. This leads to a significant noise attenuation in miRNA mediated FFL in comparison to gene expression regulated by transcription factor alone. Additionally, it was also shown in osella that the noise-filtration in incoherent miRNA mediated FFL becomes optimal over a range of miRNA mediated repression strength, miRNA concentration and the transcription factor concentration. In contrary to the earlier work, the sFFL considered here has all the regulatory interactions activating in nature. Interestingly, however, this motif also shows a significant noise attenuation at the target protein level as compared to a much simpler scenario where the gene regulation involves only translational activation by sRNA. From this comparison, it appears that such noise processing behavior of the sFFL is a result of a complex interplay of the non-linear interactions present in the two branches of the sFFL. It would be of considerable interest to explore if, in the realistic scenario, the parameter values are tuned in a specific way that leads to maximum noise attenuation in the target protein level. We believe that the mathematical results for the fluctuations determined here can be used for exploring such possibilities.

3 Conclusion

In this paper, we have studied an sRNA-driven feed-forward loop (sFFL) through mathematical and computational modelling. Here the upstream, master regulator is an sRNA, RprA, which activates the synthesis of the final, target protein, RicI, using two parallel pathways; one, directly through translational activation of the RicI mRNA and the other, via translational activation of $\sigma^{s}$ , which, in turn, functions as a transcriptional activator of RicI protein. Thus unlike other FFLs involving sRNAs as regulators at an intermediate level and proteins as the upstream regulator, here the upstream regulator is an sRNA while the intermediate regulator is a protein $\sigma^{s}$ . This kind of an FFL was found only recently; and it is believed that such an FFL plays an important role in horizontal gene transfer in S. enterica. During horizontal gene transfer, bacterial conjugation happens through pilus formation, which is an energy-expensive process. In the presence of bactericidal agents, the RicI interferes with pilus formation and thereby inhibits horizontal gene transfer. This is one way to protect the bacteria during stress. Hence, a quick response to stress necessitates a rapid increase in the levels of RicI. Our work presented here, allows us to rationalize how RprA driven FFL could be a productive strategy to achieve this control to rapidly interfere with pilus formation. In principle, this would be general to any sRNA-driven FFL.

While extensive studies to understand the general characteristics of FFLs, such as purely transcriptional FFL (tFFL) or sRNA-mediated feed-forward loop (smFFL) were carried out previously, FFL driven by sRNA as the top-tier regulator, being a new variant, has not been subject of extensive investigations. To the best of our knowledge, the present work is the first, detailed modelling-based analysis of an sFFL. A major finding of this analysis is that an sFFL is capable of producing a strong and rapid response in terms of enhancing target protein levels, compared to that by tFFL or by smFFL. By comparison, we believe, this would be a generic feature that is linked due to the number of transcriptional activation steps present in sFFL as against tFFL or smFFL. While sFFL involves transcriptional activation of only one gene, for tFFL and smFFl two or more genes are transcriptionally activated. The saturation kinetics and the delay in response due to the presence of the activation threshold appear to be the reasons for delayed and weak response in case of transcriptional activation. This difference in the mode of regulation is captured by the mathematical equations for the respective FFLs and such generic features can be compared meaningfully, when the same parameter values are used for all three cases. A high sensitivity to the initial concentration of the upstream regulator, i.e. sRNA, and therefore a rapid initial response in the target protein level is an additional characteristic of sFFL. We have obtained explicit mathematical solutions describing how the concentrations of various regulatory molecules change with time. These solutions clearly demonstrate the sensitivity of the target protein concentration to the initial conditions. This phenomenon may be rationalized as follows in the context of RprA driven inhibition of pilus formation in S. enterica. This sFFL is triggered during membrane-damaging activities of the bactericidal agent, bile salt, in order to arrest pilus formation by increasing RicI level rapidly. Hence, a sensitive and rapid response to the initial-conditions (concentration of sRNA) might be a necessary strategy for the cell to respond to stress. These insights can also be tested experimentally. A plasmid vector can be designed in a manner that the expression of RprA under the control of arabinose, can lead to the synthesis of $\sigma^{s}$ and RicI protein. In order to examine the levels of these proteins, reporter genes such as lacZ, GFP and RFP can be fused with the genes coding for $\sigma^{s}$ and RicI resulting in the synthesis of fluorescent labeled proteins. Such a design would allow a direct validation of the model proposed here.

Furthermore, the RprA driven FFL is expected to function reliably despite the presence of noise in gene expression. This implies that the FFL should ideally filter out the noise such that the target protein (RicI) concentration does not fluctuate significantly from the average concentration level. Keeping this in mind, we analysed the noise characteristics of the sFFL through master equation based modelling and stochastic simulations. We find that the network indeed filters out the noise and this aspect depends significantly on the synthesis rate of the upstream regulatory sRNA and the degradation rate of the transcriptional activator of the target protein. More specifically, an optimal attenuation of noise can be achieved by varying the synthesis rate of sRNA or by varying the degradation rate of the transcriptional activator. In order to have a quantitative comparison of the noise filtering ability of the present loop with a simple sRNA-driven mode of regulation, we consider gene expression regulated through translational activation by sRNAs alone. We find that, in this case, the coefficient of variation in the target protein number is significantly different from that of sFFL and, in particular, no optimal noise attenuation can be found. It appears that an optimal noise attenuation in sFFL is a result of a complex interplay of the non-linear interactions present in the two branches of sFFL. The results from this stochastic analysis can also be verified experimentally by extending the experimental design mentioned before suitably and quantitating the amount of mRNA and protein of RicI as a function of RprA concentration. Overall, the present work suggests that the function of sFFL is critically governed by the sRNA - not only in generating a speedy and strong response but also in producing a reliable response by regulating the gene expression noise. The prediction about the critical role of sRNA in noise filtering raises new questions, such as, how the concentration of the top-tier sRNA is regulated in the cell in order to achieve optimal noise filtration through the FFL. Besides, this being a general model, the insights obtained from the present study will be applicable to other sRNA-driven coherent FFLs that might be discovered in the future and also for designing artificial networks for optimal regulation.

Conflict of interest: Authors declare no conflict of interest.

Acknowledgement ST and SM thank DBT, India for financial support through grant no. BT/PR16861/BRB/10/1475/2016.

APPENDIX

Appendix A Purely transcriptional feed-forward loop and sRNA-mediated feed-forward loop

In figures (3) and (4) of the main text, we have shown how the target protein concentration changes with time for tFFL and smFFLs. In the following, we present the differential equations that describe the dynamics of the tFFL and smFFL. A schematic representation of the tFFL network is shown in figure (8). The parameters, $r$ and $\gamma$ , in general, represent the synthesis and degradation rates, respectively, of various regulatory molecules. Parameters denoted by $k$ in Hill functions are, in general, related to the activation threshold.

A.1 Transcriptional feed-forward loop (tFFL)

The following equations describe the tFFL.

$\displaystyle\frac{d}{dt}[x]$	$\displaystyle=$	$\displaystyle r_{x}-\gamma_{x}[x],$	(7)
$\displaystyle\frac{d}{dt}[y_{m}]$	$\displaystyle=$	$\displaystyle\frac{r_{y_{m}}[x]}{1+k_{xy}[x]}-\gamma_{y_{m}}[y_{m}],$	(8)
$\displaystyle\frac{d}{dt}[y_{p}]$	$\displaystyle=$	$\displaystyle r_{y_{p}}[y_{m}]-\gamma_{y_{p}}[y_{p}],$	(9)
$\displaystyle\frac{d}{dt}[z_{m}]$	$\displaystyle=$	$\displaystyle r_{z_{m}}\frac{[x]}{(1+k_{xz}[x])}\frac{[y_{p}]}{(1+k_{yz}[y_{p}])}-\gamma_{z_{m}}[z_{m}]\ \ \ {\rm and}$	(10)
$\displaystyle\frac{d}{dt}[z_{p}]$	$\displaystyle=$	$\displaystyle r_{z_{p}}[z_{m}]-\gamma_{z_{p}}[z_{p}].$	(11)

$[x]$ , $[y_{m}]$ , $[y_{p}]$ , $[z_{m}]$ , and $[z_{p}]$ represent the concentrations of the upstream transcriptional activator, $y$ -mRNA, $y$ -protein, $z$ -mRNA, and $z$ -protein, respectively. $x$ transcriptionally activates the synthesis of $y$ -mRNA; $x$ and $y$ are both required for transcriptional activation of $z$ .

A.2 sRNA-mediated feed-forward loop (smFFL)

Equations describing smFFL are

$\displaystyle\frac{d}{dt}[x]$	$\displaystyle=$	$\displaystyle r_{x}-\gamma_{x}[x],$	(12)
$\displaystyle\frac{d}{dt}[s]$	$\displaystyle=$	$\displaystyle\frac{r_{s}[x]}{1+k_{s}[x]}-\gamma_{s}[s],$	(13)
$\displaystyle\frac{d}{dt}[m]$	$\displaystyle=$	$\displaystyle\frac{r_{m}[x]}{1+k_{m}[x]}-\gamma_{m}[m],\ \ \ {\rm and}$	(14)
$\displaystyle\frac{d}{dt}[p]$	$\displaystyle=$	$\displaystyle r_{p}\ [m]\ [s]-\gamma_{p}[p].$	(15)

Here, [x], [s], [m], and [p] denote the concentrations of the upstream transcriptional activator, sRNA, target protein mRNA and target protein, respectively. $x$ translationally activates sRNA synthesis as well as the synthesis of the target protein transcripts. Finally, the sRNA translationally activates the synthesis of the target protein, $p$ .

Appendix B Details on Temporal Solutions

Here we find the response of the network under persistent or time-varying input signals. We assume two possible scenarios as a response to stress; (a) a constant pool of sRNA, RprA, (b) the concentration of sRNA, RprA, varies due to its synthesis and degradation. Under these conditions, we explicitly find the solutions of the differential equations that describe how the concentrations of various regulators change with time.

B.1 Under a constant pool of sRNA

Assuming a constant solution for RprA as $Ra(t)=R_{0}$ , and using a solution for $\sigma^{s}m(t)=c_{2S}e^{-\gamma_{\sigma m}t}+\frac{r_{\sigma m}}{\gamma_{\sigma m}}$ , we find

\displaystyle[\sigma^{s}_{p}](t)=\frac{\sigma_{1S}}{\gamma_{\sigma p}-\gamma_{\sigma m}}e^{-\gamma_{\sigma m}t}+\frac{\sigma_{2S}}{\gamma_{\sigma p}}+c_{3S}e^{-\gamma_{\sigma p}t},

(16)

where $c_{2S}$ and $c_{3S}$ are the integration constants. Considering negligible initial concentration of $\sigma^{s}$ mRNA and $\sigma^{s}$ protein, we find $c_{2S}=-\frac{r_{\sigma m}}{\gamma_{\sigma m}}$ and $c_{3S}=-\frac{\sigma_{1S}}{\gamma_{\sigma p}-\gamma_{\sigma m}}-\frac{\sigma_{2S}}{\gamma_{\sigma p}}$ . Here $\sigma_{1S}=r_{\sigma p}R_{0}c_{2S}$ and $\sigma_{2S}=\frac{r_{\sigma p}R_{0}r_{\sigma m}}{\gamma_{\sigma m}}$ . The concentration of RicI mRNA can be found in a similar way starting with $[Rim](t)=e^{-\gamma_{im}t}f_{2}(t)$ . The solution for $f_{2}(t)$ can be written as

\displaystyle f_{2}(t)=\frac{r_{im}}{k_{c}\gamma_{im}}e^{\gamma_{im}t}-\frac{r_{im}}{k_{c}\gamma_{im}}\int\frac{du}{A_{S}+B_{S}u^{-2}}+c_{4S},

(17)

where $c_{4S}$ is the integration constant, $A_{S}=1+\frac{k_{c}\sigma_{2S}}{\gamma_{\sigma p}}$ and $B_{S}=\frac{k_{c}\sigma_{1S}}{\gamma_{\sigma p}-\gamma_{\sigma m}}+k_{c}c_{3S}$ . For the integration, we have used $u=e^{\gamma_{im}t}$ . $B_{S}$ turns out to be negative upon substituting the expression for $c_{3S}$ in the definition of $B_{S}$ . While obtaining (17), we have assumed that the degradation constant of RicI mRNA, $\gamma_{im}$ is twice smaller than the degradation constants of $\sigma^{s}$ mRNA and $\sigma^{s}$ protein $\gamma_{\sigma m}$ and $\gamma_{\sigma p}$ , respectively and $\gamma_{\sigma p}\approx\gamma_{\sigma m}$ . The final solution for RicIm is

\displaystyle[Rim](t)=\frac{r_{im}}{k_{c}\gamma_{im}}\left[1-\frac{1}{A_{S}}-\frac{\mid B_{S}\mid^{1/2}}{2A_{S}^{3/2}}e^{-\gamma_{im}t}\log[(e^{\gamma_{im}t}-\sqrt{\mid B_{S}\mid/A_{S}})/(e^{\gamma_{im}t}+\sqrt{\mid B_{S}\mid/A_{S}})]\right]+c_{4S}e^{-\gamma_{im}t}.

(18)

Assuming RicIp has a solution of the form $[Rip](t)=f_{3}(t)e^{-\gamma_{ip}t}$ , we have the following differential equation satisfied by $f_{3}$

\displaystyle\frac{df_{3}}{dt}=C_{S}e^{\gamma_{ip}t}-D_{S}e^{(\gamma_{ip}-\gamma_{im})t}{\Big{(}}\log[e^{\gamma_{im}t}-(\mid B_{S}\mid/A_{S})^{1/2}]-\log[e^{\gamma_{im}t}+(\mid B_{S}\mid/A_{S})^{1/2}]{\Big{)}}+E_{S}e^{(\gamma_{ip}-\gamma_{im})t},

(19)

where $C_{S}=r_{ip}R_{0}\frac{r_{im}}{k_{c}\gamma_{im}}(1-1/A_{S})$ , $D_{S}=r_{ip}R_{0}\frac{r_{im}B_{S}^{1/2}}{2k_{c}\gamma_{im}A_{S}^{3/2}}$ and $E_{S}=r_{ip}R_{0}c_{4S}$ . Solving this equation, we finally find the solution for RicIp as

	$\displaystyle[Rip](t)=$		$\displaystyle\frac{C_{S}}{\gamma_{ip}}+E_{S}\frac{e^{-\gamma_{im}t}}{\gamma_{ip}-\gamma_{im}}+\frac{D_{S}}{\gamma_{im}}e^{-\gamma_{ip}t}{\Big{(}}(e^{\gamma_{im}t}+(\mid B_{S}\mid/A_{S})^{1/2})\log[e^{\gamma_{im}t}+(\mid B_{S}\mid/A_{S})^{1/2}]-$		(20)
			$\displaystyle(e^{\gamma_{im}t}-(\mid B_{S}\mid/A_{S})^{1/2})\log[e^{\gamma_{im}t}-(\mid B_{S}\mid/A_{S})^{1/2}]{\Big{)}}+(c_{5S}-\frac{2D_{S}}{\gamma_{im}}(\mid B_{S}\mid/A_{S})^{1/2})e^{-\gamma_{ip}t},$		(20)

where $c_{5S}$ is the integration constant.

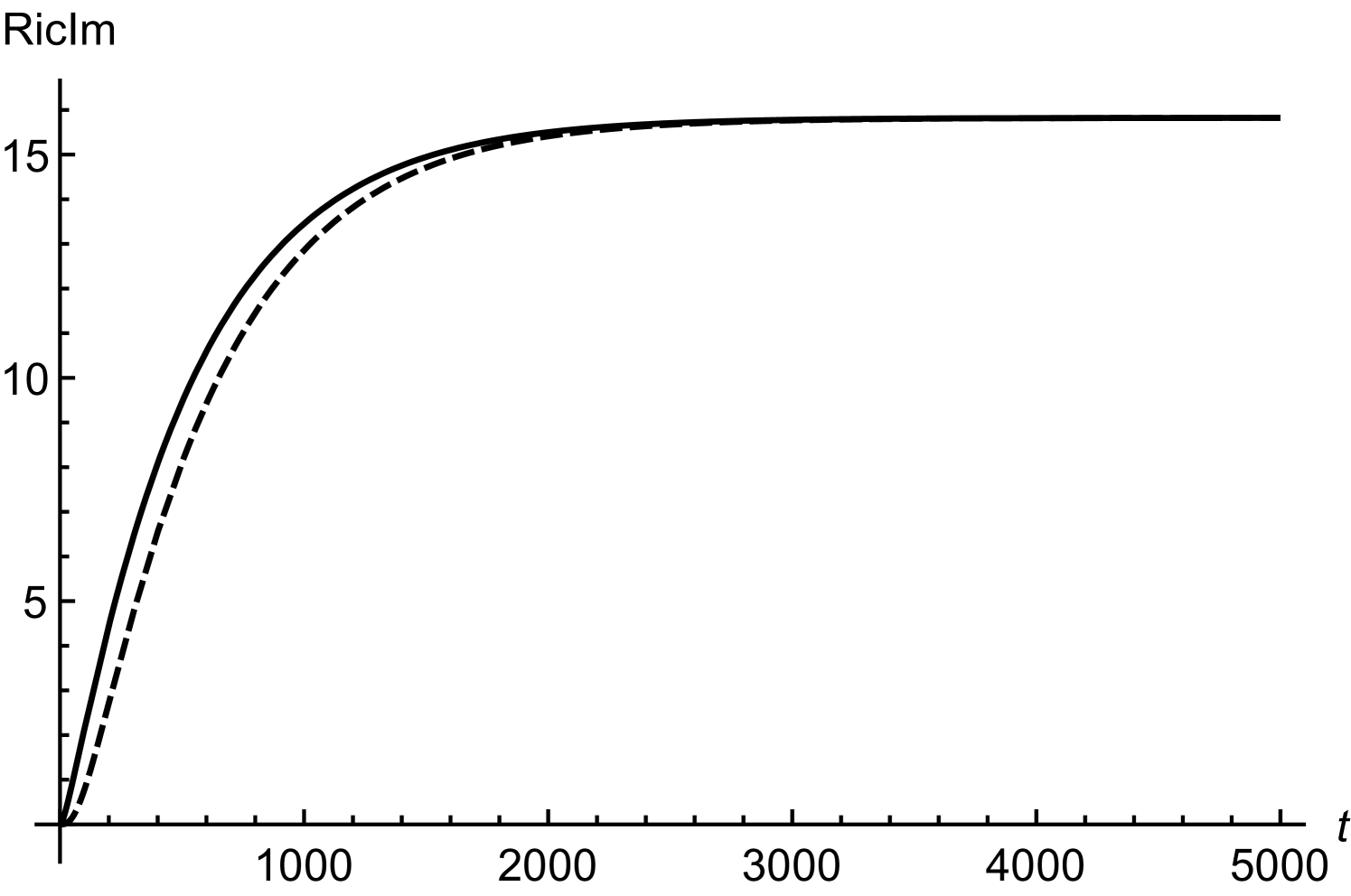
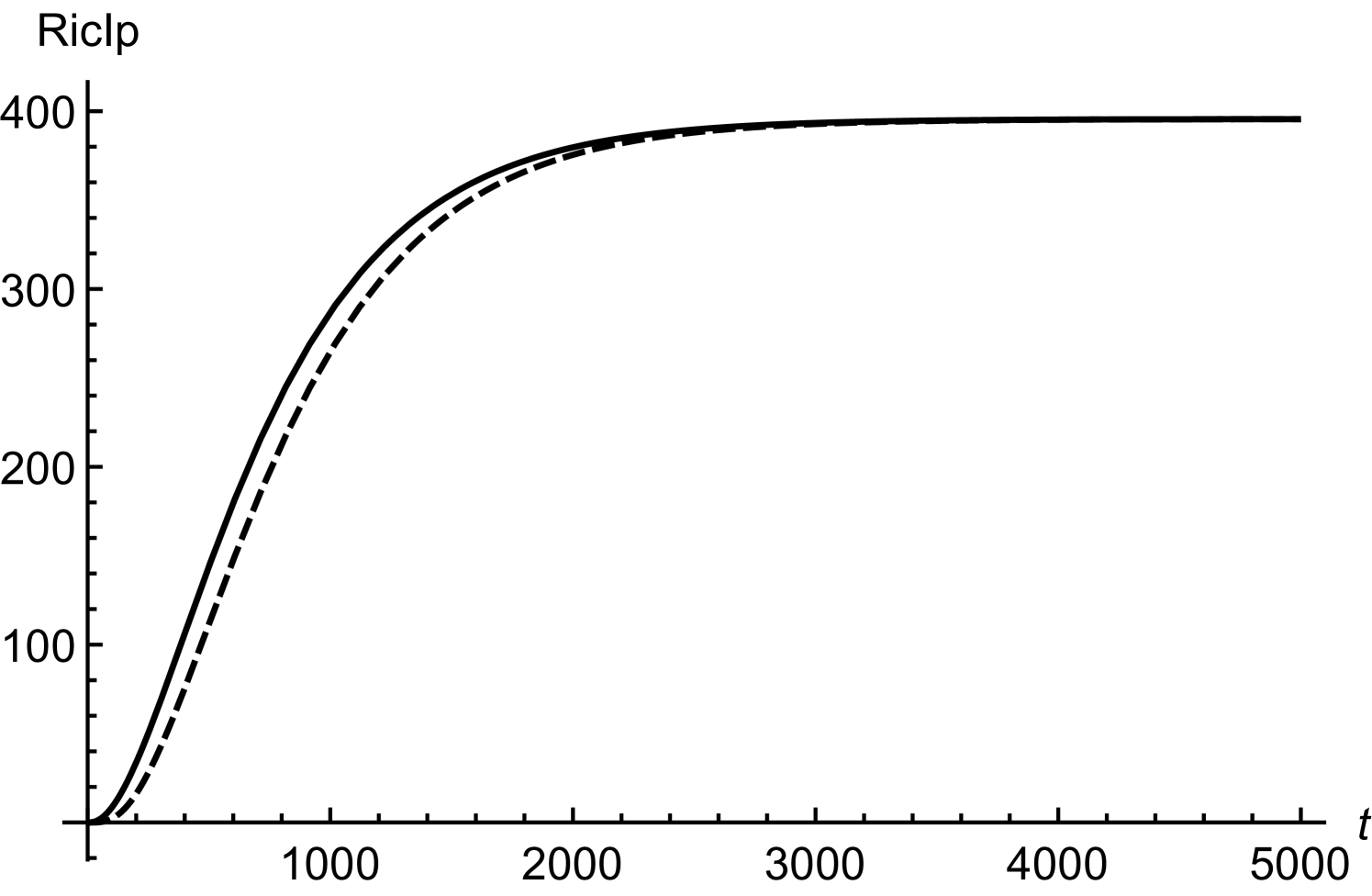
In order to obtain (20), we have assumed $\gamma_{im}$ twice smaller than $\gamma_{ip}$ . Considering initial concentrations of all the regulatory molecules to be negligible, we have compared numerical and mathematical solutions for RicIm and RicIp in figure (9). The numerical solutions provide an exact picture as how various concentrations vary with time. Based on $\gamma_{\sigma p}\approx\gamma_{\sigma m}$ and $\gamma_{im}$ is approximately twice smaller than $\gamma_{\sigma p}$ or $\gamma_{\sigma m}$ , we have obtained an approximate form of the integrand in equation (17). Due to this approximation, the mathematical solutions deviate slightly from the exact, numerical solutions. Since the deviations are small, we assume that (18) and (20) provide a reasonable quantitative description of time-variation in the target protein concentrations.

B.2 Under time-varying concentration of sRNA

Here, we find analytical solutions of the coupled, non-linear equations in (1) and (2) of the main text. Unlike the previous section, Rpra concentration is non-constant and it is governed by the equation

\displaystyle\frac{d}{dt}[Ra]=r_{a}-\gamma_{a}[Ra],\ \ \

(21)

The solutions for $[Ra](t)$ and $[\sigma^{s}m](t)$ are as follows.

\displaystyle[Ra](t)=c_{1}\ e^{-\gamma_{a}t}+\frac{r_{a}}{\gamma_{a}},\ \ {\rm and}\ \ [\sigma^{s}m](t)=c_{2}\ e^{-\gamma_{\sigma m}t}+\frac{r_{\sigma m}}{\gamma_{\sigma m}}.

(22)

With these equations, the equation for $\sigma^{s}$ protein is as follows

\displaystyle\frac{d}{dt}[\sigma^{s}p](t)=r_{\sigma p}\ (c_{1}\ e^{-\gamma_{a}t}+\frac{r_{a}}{\gamma_{a}})(c_{2}\ e^{-\gamma_{\sigma m}t}+\frac{r_{\sigma m}}{\gamma_{\sigma m}})-\gamma_{\sigma p}[\sigma^{s}p].

(23)

The solution for $[\sigma^{s}p](t)$ is

\displaystyle[\sigma^{s}p](t)=c_{3}\ e^{-\gamma_{\sigma p}t}+A+B\ e^{-\gamma_{a}t}+C\ e^{-\gamma_{\sigma m}t}+D\ e^{-\gamma_{a}t-\gamma_{\sigma m}t},

(24)

where various constants are as given below.

	$\displaystyle A=\frac{r_{\sigma p}}{\gamma_{\sigma p}}\frac{r_{a}}{\gamma_{a}}\frac{r_{\sigma m}}{\gamma_{\sigma m}},\ \ B=\frac{r_{\sigma p}}{(\gamma_{\sigma p}-\gamma_{a})}\frac{r_{\sigma m}}{\gamma_{\sigma m}}([Ra0]-\frac{r_{a}}{\gamma_{a}}),\ \ C=\frac{r_{a}}{\gamma_{a}}\frac{r_{\sigma p}}{(\gamma_{\sigma p}-\gamma_{\sigma m})}([\sigma^{s}m0]-\frac{r_{\sigma m}}{\gamma_{\sigma m}}),\ \ {\rm and}$		(25)
	$\displaystyle D=\frac{r_{\sigma p}}{\gamma_{\sigma p}-(\gamma_{a}+\gamma_{\sigma m})}\ ([Ra0]-\frac{r_{a}}{\gamma_{a}})\ ([\sigma^{s}m0]-\frac{r_{\sigma m}}{\gamma_{\sigma m}}),$		(26)

with $[\sigma^{s}m0]$ and $[Ra0]$ being the initial concentrations of Rpra and $\sigma^{s}m$ . The equation for RicIm can be solved by assuming a solution of the form $[Rim](t)=e^{-\gamma_{im}t}f_{2}(t)$ with $f_{2}(t)$ satisfying the equation

\displaystyle\frac{df_{2}(t)}{dt}=e^{\gamma_{im}t}\frac{r_{im}\sigma^{s}p}{1+k_{c}\sigma^{s}p}.

(27)

The solution for $f_{2}(t)$ is

	$\displaystyle f_{2}(t)$	$\displaystyle=$	$\displaystyle\frac{r_{im}}{k_{c}}\int dt\ e^{\gamma_{im}t}(1-\frac{1}{1+k_{c}\sigma^{s}p})$		(28)
		$\displaystyle=$	$\displaystyle\frac{r_{im}}{k_{c}}\frac{e^{\gamma_{im}t}}{\gamma_{im}}-\frac{r_{im}}{\gamma_{im}k_{c}}\int du\{1+k_{c}[c_{3}\ u^{\frac{-\gamma_{\sigma p}}{\gamma_{im}}}+A+B\ u^{-\frac{\gamma_{a}}{\gamma_{im}}}+C\ u^{\frac{-\gamma_{\sigma m}}{\gamma_{im}}}+Du^{-(\frac{\gamma_{a}+\gamma_{\sigma m}}{\gamma_{im}})}]\}^{-1},$		(28)

where $u=e^{\gamma_{im}t}$ .

In order to have explicit mathematical solutions for different concentrations, we assume $\gamma_{im}=\gamma_{a}=\gamma_{\sigma m}$ and $\gamma_{im}\approx\frac{1}{2}\gamma_{\sigma p}$ . Under these conditions, the integration for $f_{2}(t)$ can be done exactly. We find

$\displaystyle f_{2}(t)$	$\displaystyle=$	$\displaystyle\frac{r_{im}}{k_{c}\gamma_{im}}e^{\gamma_{im}t}-\frac{r_{im}}{\gamma_{im}k_{c}}\int du\frac{u^{2}}{(Ak_{c}+1)u^{2}+(B+C)k_{c}u+k_{c}(D+c_{3})}$	(29)
	$\displaystyle=$	$\displaystyle\frac{r_{im}}{k_{c}\gamma_{im}}e^{\gamma_{im}t}-\frac{r_{im}}{\gamma_{im}k_{c}}\Bigg{[}\frac{u}{(Ak_{c}+1)}-\frac{(B+C)k_{c}}{2(Ak_{c}+1)^{2}}\log[\mid(Ak_{c}+1)u^{2}+(B+C)k_{c}u+(D+c_{3})k_{c}\mid]$
	$\displaystyle+$	$\displaystyle\frac{1}{2(1+Ak_{c})^{2}}\frac{(-2k_{c}(D+c_{3})(Ak_{c}+1)+(B+C)^{2}k_{c}^{2})}{\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}\times$
		$\displaystyle\log{\bigg{\{}}\frac{2(Ak_{c}+1)u+(B+C)k_{c}-\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}{2(Ak_{c}+1)u+(B+C)k_{c}+\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}\bigg{\}}\Bigg{]}+c_{4},$

when $(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})>0$ . The solution for RicI mRNA is thus

$\displaystyle[Rim](t)$	$\displaystyle=$	$\displaystyle\frac{r_{im}}{k_{c}\gamma_{im}}-\frac{r_{im}}{\gamma_{im}k_{c}}\bigg{[}\frac{1}{(Ak_{c}+1)}-\frac{(B+C)k_{c}e^{-\gamma_{im}t}}{2(Ak_{c}+1)^{2}}\log[\mid(Ak_{c}+1)e^{2\gamma_{im}t}+(B+C)k_{c}e^{\gamma_{im}t}+(D+c_{3})k_{c}\mid]$	(30)
	$\displaystyle+$	$\displaystyle\frac{e^{-\gamma_{im}t}}{2(1+Ak_{c})^{2}}\frac{(-2k_{c}(D+c_{3})(Ak_{c}+1)+(B+C)^{2}k_{c}^{2})}{\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}\times$
		$\displaystyle\log{\bigg{\{}}\frac{2(Ak_{c}+1)e^{\gamma_{im}t}+(B+C)k_{c}-\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}{2(Ak_{c}+1)e^{\gamma_{im}t}+(B+C)k_{c}+\sqrt{(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})k_{c}}}\bigg{\}}\Bigg{]}+c_{4}e^{-\gamma_{im}t}$

for $(B+C)^{2}k_{c}^{2}-4(Ak_{c}+1)(D+c_{3})>0$ . To find $[Rip](t)$ , we numerically integrate the equation

\displaystyle\frac{d}{dt}[Rip](t)=r_{ip}(c_{1}\ e^{-\gamma_{a}t}+\frac{r_{a}}{\gamma_{a}})[Rim](t)-\gamma_{ip}[Rip](t)

(31)

using the mathematical solution for $[Rim](t)$ in (30). The change in various concentrations are shown in figure (10).

Appendix C Moments

In the following, we show our results for first, second, and third moments derived using the generating function formulation described in sub-section (2.4) of the main text.

$\displaystyle G_{1}$	$\displaystyle=$	$\displaystyle\frac{r_{s}}{\gamma_{s}}$	(32)
$\displaystyle G_{2}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{1}}}{\gamma_{m_{1}}}$	(33)
$\displaystyle G_{3}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{1}}G_{12}}{\gamma_{p_{1}}}$	(34)
$\displaystyle G_{4}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{2}}^{0}+r_{m_{2}}^{1}G_{3}}{\gamma_{m_{2}}}$	(35)
$\displaystyle G_{5}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{2}}G_{14}}{\gamma_{p_{2}}}$	(36)
$\displaystyle G_{11}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{1}}{\gamma_{s}}$	(37)
$\displaystyle G_{22}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{1}}G_{2}}{\gamma_{m_{1}}}$	(38)
$\displaystyle G_{33}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{1}}G_{123}}{\gamma_{p_{1}}}$	(39)
$\displaystyle G_{44}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{2}}^{0}G_{4}+r_{m_{2}}^{1}G_{34}}{\gamma_{m_{2}}}$	(40)
$\displaystyle G_{55}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{2}}G_{145}}{\gamma_{p_{2}}}$	(41)
$\displaystyle G_{12}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{2}+r_{m_{1}}G_{1}}{\gamma_{s}+\gamma_{m_{1}}}$	(42)
$\displaystyle G_{13}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{3}+r_{p_{1}}(G_{12}+G_{112})}{\gamma_{s}+\gamma_{p_{1}}}$	(43)
$\displaystyle G_{14}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{4}+r_{m_{2}}^{0}G_{1}+r_{m_{2}}^{1}G_{13}}{\gamma_{s}+\gamma_{m_{2}}}$	(44)
$\displaystyle G_{15}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{5}+r_{p_{2}}(G_{14}+G_{114})}{\gamma_{s}+\gamma_{p_{2}}}$	(45)
$\displaystyle G_{23}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{1}}G_{3}+r_{p_{1}}(G_{12}+G_{122})}{\gamma_{m_{1}}+\gamma_{p_{1}}}$	(46)
$\displaystyle G_{24}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{1}}G_{4}+r_{m_{2}}^{0}G_{2}+r_{m_{2}}^{1}G_{23}}{\gamma_{m_{1}}+\gamma_{m_{2}}}$	(47)

$\displaystyle G_{25}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{1}}G_{5}+r_{p_{2}}G_{124}}{\gamma_{m_{1}}+\gamma_{p_{2}}}$	(48)
$\displaystyle G_{34}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{1}}G_{124}+r_{m_{2}}^{0}G_{3}+r_{m_{2}}^{1}(G_{3}+G_{33})}{\gamma_{p_{1}}+\gamma_{m_{2}}}$	(49)
$\displaystyle G_{35}$	$\displaystyle=$	$\displaystyle\frac{r_{p_{1}}G_{125}+r_{p_{2}}G_{134}}{\gamma_{p_{1}}+\gamma_{p_{2}}}$	(50)
$\displaystyle G_{45}$	$\displaystyle=$	$\displaystyle\frac{r_{m_{2}}^{0}G_{5}+r_{m_{2}}^{1}G_{35}+r_{p_{2}}(G_{14}+G_{144})}{\gamma_{m_{2}}+\gamma_{p_{2}}}$	(51)
$\displaystyle G_{111}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{11}}{\gamma_{s}}$	(52)
$\displaystyle G_{112}$	$\displaystyle=$	$\displaystyle\frac{2r_{s}G_{12}+r_{m_{1}}G_{11}}{2\gamma_{s}+\gamma_{m_{1}}}$	(53)
$\displaystyle G_{113}$	$\displaystyle=$	$\displaystyle\frac{2r_{s}G_{13}+2r_{p_{1}}G_{112}+r_{p_{1}}G_{1112}}{2\gamma_{s}+\gamma_{p_{1}}}$	(54)
$\displaystyle G_{114}$	$\displaystyle=$	$\displaystyle\frac{2r_{s}G_{14}+r_{m_{2}}^{0}G_{11}+r_{m_{2}}^{1}G_{113}}{2\gamma_{s}+\gamma_{m_{2}}}$	(55)
$\displaystyle G_{115}$	$\displaystyle=$	$\displaystyle\frac{2r_{s}G_{15}+r_{p_{2}}(2G_{114}+G_{1114})}{2\gamma_{s}+\gamma_{p_{2}}}$	(56)
$\displaystyle G_{122}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{22}+2r_{m_{1}}G_{12}}{\gamma_{s}+2\gamma_{m_{1}}}$	(57)
$\displaystyle G_{123}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{23}+r_{m_{1}}G_{13}+r_{p_{1}}(G_{12}+G_{112}+G_{122}+G_{1122})}{\gamma_{s}+\gamma_{m_{1}}+\gamma_{p_{1}}}$	(58)
$\displaystyle G_{124}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{24}+r_{m_{1}}G_{14}+r_{m_{2}}^{0}G_{12}+r_{m_{2}}^{1}G_{123}}{\gamma_{s}+\gamma_{m_{1}}+\gamma_{m_{2}}}$	(59)
$\displaystyle G_{125}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{25}+r_{m_{1}}G_{15}+r_{p_{2}}(G_{124}+G_{1124})}{\gamma_{s}+\gamma_{m_{1}}+\gamma_{p_{2}}}$	(60)
$\displaystyle G_{133}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{33}+2r_{p_{1}}(G_{123}+G_{1123})}{\gamma_{s}+2\gamma_{p_{1}}}$	(61)
$\displaystyle G_{134}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{34}+r_{p_{1}}(G_{124}+G_{1124})+r_{m_{2}}^{0}G_{13}+r_{m_{2}}^{1}(G_{13}+G_{133})}{\gamma_{s}+\gamma_{p_{1}}+\gamma_{m_{2}}}$	(62)
$\displaystyle G_{135}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{35}+r_{p_{1}}(G_{125}+G_{1125})+r_{p_{2}}(G_{134}+G_{1134})}{\gamma_{s}+\gamma_{p_{1}}+\gamma_{p_{2}}}$	(63)
$\displaystyle G_{144}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{44}+2(r_{m_{2}}^{0}G_{14}+r_{m_{2}}^{1}G_{134})}{\gamma_{s}+2\gamma_{m_{2}}}$	(64)
$\displaystyle G_{145}$	$\displaystyle=$	$\displaystyle\frac{r_{s}G_{45}+r_{m_{2}}^{0}G_{15}+r_{m_{2}}^{1}G_{135}+r_{p_{2}}(G_{14}+G_{114}+G_{144}+G_{1144})}{\gamma_{s}+\gamma_{m_{2}}+\gamma_{p_{2}}}$	(65)

Appendix D Translational activation by an sRNA

Here we consider a simple mechanism where the gene expression only involves translational activation by sRNA. In other words, sRNAs bind to the mRNAs and activate translation (see Fig. (11A)). The differential equations describing variations of different concentrations with time are given below.

	$\displaystyle\frac{d}{dt}[s]=r_{s}-\gamma_{s}[s],$		(66)
	$\displaystyle\frac{d}{dt}{[m]}=r_{m}-\gamma_{m}[m],\ \text{and}$		(67)
	$\displaystyle\frac{d}{dt}[p]=r_{p}[s][m]-\gamma_{p}[p],$		(68)

where $[s]$ , $[m]$ , and $[p]$ denote concentrations of sRNA, mRNA, and protein, respectively. The stochastic analysis can be performed in a similar way as described in the main text. In this case, the number of moments required to find the coefficient of variation is smaller compared to that of sFFL and one requires the moments $G_{1}$ , $G_{2}$ , $G_{3}$ , $G_{11}$ , $G_{12}$ , $G_{13}$ , $G_{22}$ , $G_{23}$ , $G_{33}$ , $G_{112}$ , $G_{122}$ , $G_{123}$ and $G_{1122}$ to find the coefficient of variation. The coefficient of variation for the target protein has been plotted in figure (11B).

Appendix E Reaction Scheme

Here, we list different biochemical reactions considered in stochastic simulations. The values of various rate constants used for figure (7A) are mentioned inside the brackets.


			(70)
			(71)
			(72)
			(73)
			(74)
			(75)
			(76)
			(77)
			(78)
			(79)
			(80)
			(81)
			(82)
			(83)
			(84)

Here, $G_{I}$ and $G_{I}^{*}$ denote the inactivated and activated form of the gene synthesising $m_{2}$ . For figure (7B), we choose $r_{s}=0.01\ (\rm molecules.\ s^{-1})$ .

References

(1) Storz G, Altuvia S, Wassarman KM 2005 An abundance of RNA regulators. Annu. Rev. Biochem. 74 199-217
(2) Gottesman S 2005 Micros for microbes: non-coding regulatory RNAs in bacteria Trends Genet. 21 399-404
(3) Papenfort K and Vanderpool C K 2015 Target activation by regulatory RNAs in bacteria FEMS Microbiol. Rev. 39 362-78
(4) Altuvia S 2004 Regulatory Small RNAs: the Key to Coordinating Global Regulatory Circuits J. Bacteriol. 186 6679-80
(5) Shimoni Y, Friedlander G, Hetzroni G, Niv G, Altuvia S, Biham O and Margalit H 2007 Regulation of gene expression by small non-coding RNAs: a quantitative view Mol. Syst. Biol. 3 1-9
(6) Levine E, Zhang Z, Kuhlman T and Hwa T 2007 Quantitative Characteristics of Gene Regulation by Small RNA PLoS Biol. 6 e5
(7) Iyengar B R, Pillai B, Venkatesh K V and Gadgil C J 2017 Systematic comparison of the response properties of protein and RNA mediated gene regulatory motifs Mol. BioSyst. 13 1235-45
(8) M Pal, S Ghosh and I Bose 2016 Functional characteristics of gene expression motifs with single and dual strategies of regulation Biomed. Phys. Eng. Express 2 025009
(9) Alon U S 2006 An introduction to systems biology: design principles of biological circuits (London, UK: Chapman and Hall/CRC)
(10) Mangan S and Alon U 2003 Structure and function of the feed-forward loop network motif Proc. Natl. Acad. Sci. U S A. 100 11980-5
(11) Shen-Orr S S, Milo R, Mangan S and Alon U 2002 Network motifs in the transcriptional regulation network of Escherichia coli Nat. Genet. 31 64-8
(12) Alon U 2007 Network motifs: theory and experimental approaches Nat. Rev. Genet. 8 450-61
(13) Schleif R 2000 Regulation of the L-arabinose operon of Escherichia coli Trends Genet. 16 559-65
(14) Osella M, Bosia C, Cora D and Caselle M 2011 The Role of Incoherent MicroRNA-Mediated Feed-forward Loops in Noise Buffering PLoS Comput Biol. 7 e1001101
(15) Riba A, Bosia C, Baroudi M E, Ollino L, Caselle M 2014 A Combination of Transcriptional and MicroRNA Regulation Improves the Stability of the Relative Concentrations of Target Genes PLoS Comput Biol. 10 e1003490
(16) Cora D, Re A, Caselle M, and Bussolino F 2017 MicroRNA-mediated regulatory circuits: outlook and perspectives Phys. Biol. 14 045001-11
(17) Duk M, Samsonova M and Samsonov A 2014 Dynamics of miRNA driven feed-forward loop depends upon miRNA action mechanisms BMC Genomics. 15 S9
(18) Grigolon Silvia, Di Patti Francesca, De Martino Andrea and Marinari Enzo 2016 Noise Processing by MicroRNA-Mediated Circuits: the Incoherent Feed-Forward Loop, Revisited Heliyon 2 e00095 (revisited)
(19) Papenfort K, Espinosa E, Casadesus J and Vogel J 2015 Small RNA-based feed-forward loop with AND-gate logic regulates extrachromosomal DNA transfer in Salmonella Proc. Natl. Acad. Sci. U S A. 112 E4772-81
(20) Majdalani N, Hernandez D and Gottesman S 2002 Regulation and mode of action of the second small RNA activator of RpoS translation, RprA Mol. Microbiol. 46 813-26
(21) Majdalani N, Chen S, Murrow J, John K S and Gottesman S 2004 Regulation of RpoS by a novel small RNA: the characterization of RprAMol. Microbiol. 39 1382-94
(22) Alberts B, Johnson A, Lewis J, Raff M, Roberts K and Walter P 2008 Molecular biology of the cell (New York: Garland Science Taylor and Francis Group)
(23) Frohlich K S and Papenfort K 2016 Interplay of regulatory RNAs and mobile genetic elements in enteric pathogens Mol. Microbiol. 101 701-13
(24) Zhang C, Tsoi R, Wu F and You L 2016 Processong oscillatory signals by incoherent feedforward loops PLoS Comput Biol. 12 e1005101.
(25) Raj A and Oudenaarden A van 2008 Nature, nurture, or chance: Stochastic gene expression and its consequences Cell 135 216-26
(26) Ghosh B, Karmakar R and Bose I 2005 Noise characteristics of feed forward loops Phys. Biol. 2 36-45
(27) Kampen N G van 2007 Stochastic processes in physics and chemistry (Amsterdam: Elsevier)
(28) Gillespie D T 1976 A general method for numerically simulating the stochastic time evolution of coupled chemical reactions J. Comput. Phys. 22 403-34
(29) Gillespie D T 1977 Exact stochastic simulation of coupled chemical reactions J. Phys. Chem. 81 2340-61