Smooth and probabilistic PARAFAC model with auxiliary covariates
Abstract
In immunological and clinical studies, matrix-valued time-series data clustering is increasingly popular. Researchers are interested in finding low-dimensional embedding of subjects based on potentially high-dimensional longitudinal features and investigating relationships between static clinical covariates and the embedding. These studies are often challenging due to high dimensionality, as well as the sparse and irregular nature of sample collection along the time dimension. We propose a smoothed probabilistic PARAFAC model with covariates (SPACO) to tackle these two problems while utilizing auxiliary covariates of interest. We provide intensive simulations to test different aspects of SPACO and demonstrate its use on an immunological data set from patients with SARs-CoV-2 infection.
Keywords: Tensor decomposition; Time series; Missing data; Probabilistic model.
1 Introduction
Sparsely observed multivariate times serious data are now common in immunological studies. For each subject or participant i , we can collect multiple measurements on features over time, but often at different time stamps . For example, for each subject, immune profiles are measured for hundreds of markers at irregular sampling times in Lucas et al. (2020) and Rendeiro et al. (2020). Let be the longitudinal measurements for subject , we can collect for all subjects into a sparse three-way tensor , where is the number of distinct time stamps across all subjects. Since {} tend to be small in size and have low overlaps for different subject , may have a high missing rate along the time dimension.
In addition to , researchers often have a set of nontemporal covariates for subject such as medical conditions and demographics, which may account partially for the variation in the temporal measurements across subjects. Modeling such auxiliary covariates together with might help with the estimation quality and understanding for the cross-subject heterogeneity.
In this paper, we propose SPACO (smooth and probabilistic PARAFAC model with auxiliary covariates) to adapt to the sparsity long the time dimension in and utilize the auxiliary variables . SPACO assumes that is a noisy realization of some low-rank signal tensor whose time components are smooth and subject scores have a potential dependence on the auxiliary covariates :
Here, (1) describes the dependence of the expected subject score for subject on , and (2) , , are the subject score, trajectory value and feature loading for factor in the PARAFAC model and the observation indexed by where has a normal prior . We impose smoothness on time trajectories and sparsity on to deal with the irregular sampling along the time dimension and potentially high dimensionality in .
Alongside the model proposal, we will also discuss several issues related to SPACO, including model initialization, auto-tuning of smoothness and sparsity in and hypothesis testing on through cross-fit. Successfully addressing these issues is crucial to practitioners interested in applying SPACO to their analysis.
In the remaining of the article, we summarize some closely related work in section 1.1 and describe the SPACO model in Section 2 and model parameter estimation with fixed tuning parameters in Section 3. In Section 4, we discuss the aforementioned related issues that could be important in practice. We compare SPACO to several existing methods in Section 5. Finally, in Section 6, we apply SPACO to a highly sparse tensor data set on immunological measurements for SARS-COV-2 infected patients. We provide a python package SPACO for researchers interested in applying the proposed method.
1.1 Related work
In the study of multivariate longitudinal data in economics, researchers have combined tensor decomposition with auto-cross-covariance estimation and autoregressive models (Fan et al., 2008; Lam et al., 2011; Fan et al., 2011; Bai and Wang, 2016; Wang et al., 2019, 2021). These approaches do not work well with highly sparse data or do not scale well with the feature dimensions, which are important for working with medical data. Functional PCA (Besse and Ramsay, 1986; Yao et al., 2005) is often used for modeling sparse longitudinal data in the matrix-form. It utilizes the smoothness of time trajectories to handle sparsity in the longitudinal observations, and estimates the eigenvectors and factor scores under this smoothness assumption. Yokota et al. (2016) and Imaizumi and Hayashi (2017) introduced smoothness to tensor decomposition models, and estimated the model parameters by iteratively solving penalized regression problems. The methods above don’t consider the auxiliary covariates .
It has been previously discussed that including could potentially improve our estimation. Li et al. (2016) proposed SupSFPC (supervised sparse and functional principal component) and observed that the auxiliary covariates improve the signal estimation quality in the matrix setting for modeling multivariate longitudinal observations. Lock and Li (2018) proposed SupCP which performs supervised multiway factorization model with complete observation and employs a probabilistic tensor model (Tipping and Bishop, 1999; Mnih and Salakhutdinov, 2007; Hinrich and Mørup, 2019). Although an extension to sparse tensor is straightforward, SupCP does not model the smoothness and can be much more affected by severe missingness along the time dimension.
SPACO can be viewed as an extension of functional PCA and SupSFPC to the setting of three-way tensor decomposition (Acar and Yener, 2008; Sidiropoulos et al., 2017) using the parallel factor (PARAFAC) model (Harshman and Lundy, 1994; Carroll et al., 1980). It uses a probabilistic model and jointly models the smooth longitudinal data with potentially high-dimensional non-temporal covariates . We refer to the SPACO model as SPACO- when no auxiliary covariate is available. SPACO- itself is an attractive alternative to existing tensor decomposition implementations with probabilistic modeling, smoothness regularization, and automatic parameter tuning. In our simulations, we compare SPACO with SPACO to demonstrate the gain from utilizing .
2 SPACO Model
2.1 Notations
Let be a tensor for some sparse multivariate longitudinal observations, where is the number of subjects, is the number of features, and is the number of total unique time points. For any matrix , we let denote its row/column, and often write as for the column for convenience. Let , , be the matrix unfolding of in the subject/feature/time dimension respectively. We also define:
Tensor product : , , , then, with .
Kronecker product : , , then
Column-wise Khatri-Rao product : , , then with for .
Element-wise multiplication : , then with ; for , ; for , .
2.2 smooth and probabilistic PARAFAC model with covariates
We assume to be a noisy realization of an underlying signal array . We stack as the columns of , denote the rows of by , and their entries by . We let denote the -entry of . Then,
| (1) |
where is a diagonal covariance matrix. Even though is often of high rank, we consider the scenario where the rank of is small.
Without covariates, we set the prior mean parameter . If we are interested in explaining the heterogeneity in across subjects with auxiliary covariates , then we may model as a function of . Here, we consider a linear model . To avoid confusion, we will always call the “features”, and the “covariates” or “variables”.
We refer to as the subject scores, which characterize differences across subjects and are latent variables. We refer to as the feature loadings, which reveal the composition of the factors using the original features and could assist the downstream interpretation. Finally, is referred to as the time trajectories, which can be interpreted as function values sampled from some underlying smooth functions at a set of discrete-time points, e.g., .
Recalling that is the unfolding of in the subject direction, we write for the indices of observed values in the row of , and for the vector of these observed values. Each such observed value has noise variance , and we write to represent the diagonal covariance matrix with diagonal values being the corresponding variances for at indices in . Similarly, we define for the unfolding , and for the observed indices, the associated observed vector and diagonal covariance matrix for the row in . We set to denote all model parameters. Set and . If is observed, the complete data log-likelihood is
| (2) |
Set . The marginalized log likelihood integrating out the randomness in enjoys a closed form (Lock and Li, 2018):
| (3) |
Set . We can also equivalent express the marginal likelihood as below.
| (4) |
We use the form in eq. (4) to derive the updating formulas and criteria for rank selection since it does not involve the inverse of a large non-diagonal matrix.
Model parameters in eq. (3) or eq. (4) are not identifiable due to (1) parameters rescaling from to for any , and (2) reordering of different component for . More discussions of the model identifiability can be found in Lock and Li (2018). Hence, adopting similar rules from Lock and Li (2018), we require
-
(C.1)
, .
-
(C.2)
The latent components are in decreasing order based on their overall variances , and the first non-zero entries in and to be positive, e.g., and if they are non-zero.
To deal with the sparse sampling along the time dimension and take into consideration that features are often smooth over time in practice, we assume that the time component is sampled from a slowly varying trajectory function , and encourage smoothness of by directly penalizing the function values via a penalty term . This paper considers a Laplacian smoothing (Sorkine et al., 2004) with a weighted adjacency matrix . Let represent the associated time for . We define and as
Practitioners may choose other forms for . If practitioners want to have slowly varying derivatives, they can also use a penalty matrix that penalizes changes in gradients over time.
Further, when the number of covariates in is moderately large, we may wish to impose sparsity in the parameter. We encourage such sparsity by including a lasso penalty (Tibshirani, 2011) in the model. In summary, our goal is then to find parameters maximizing the expected penalized log-likelihood, or minimizing the penalized expected deviance loss, under norm constraints:
| (5) |
Only the identifiability constraint (C.1) has entered the objective. We can always guarantee (C.2) by changing the signs in , , and reordering the components afterward without changing the achieved objective value.
Eq. (2.2) describes a non-convex problem. We will find locally optimal solutions via an alternating update procedure: (1) fixing other parameters and updating via lasso regressions; (2) fixing and updating other model parameters using the EM algorithm. We give details of our iterative estimation procedure in Section 3.
3 Model parameter estimation
Given the model rank and penalty terms , , we alternately update parameters , , , and with a mixed EM procedure described in Algorithm 1. We briefly explain the updating steps here:
(1): Given other parameters, we find to to directly minimize the objective by solving a least-squares regression problem with lasso penalty.
(2): Fixing , we update the other parameters using an EM procedure. Denote the current parameters as . Our goal is to minimize the penalized expected negative log-likelihood
| (6) |
under the current posterior distribution . We adopt a block-wise parameter updating scheme where we update , , and sequentially.
Algorithm 1 describes the high level ideas of our updating schemes. In line 5 and 6, we guarantee the norm constraints on and by adding an additional quadratic term and set the coefficient to guarantee the norm requirements. Even though this is not a convex problem, the proposed approaches provide optimal solutions for sub-routines updating different parameter blocks, and the penalized (marginalized) deviance loss is non-increasing over the iterations.
Theorem 3.1
In Algorithm 1, let and are the estimated parameters at the beginning and end of the iteration of the outer while loop. We have .
Proof of Theorem 3.1 is given in Appendix B.1. In Algorithm 1, the posterior distribution of for each row in is Gaussian, with posterior covariance the same as defined earlier, and posterior mean given below.
| (7) |
Explicit formulas and steps for carrying out the subroutines at lines 4-7 and line 9 are deferred to Appendix A.1
4 Initialization, tuning and testing
4.1 Initialization
One initialization approach is to form a Tucker decomposition of using HOSVD/MLSVD (De Lathauwer et al., 2000) where is the core tensor and , , are unitary matrices multiplied with the core tensors along the subject, time and feature directions respectively ( is the smallest between and ), and then perform PARAFAC decomposition on the small core tensor (Bro and Andersson, 1998; Phan et al., 2013). We initialize SPACO with Algorithm 2, which combines the above approach with functional PCA (Yao et al., 2005) to work with sparse longitudinal data. Algorithm 2 consists of the following steps: (1) perform SVD on to get ; (2) project onto each column of and perform functional PCA to estimate ; (3) run a ridge-penalized regression of rows of on , and estimate and from the regression coefficients
In a noiseless model with and complete temporal observations, one may replace the functional PCA step of Algorithm 2 with standard PCA. Then becomes a PARAFAC decomposition of .
Lemma 4.1
4.2 Auto-selection of tuning parameters
Selection of regularizers and : One way to choose the tuning parameters and is to use cross-validation. However, this can be computationally expensive even if we tune each parameter sequentially. It is also difficult to determine a good set of candidate values for the parameters before running SPACO. Instead, we determine the tuning parameters via nested cross-validation, which has been shown to be empirically useful (Huang et al., 2008; Li et al., 2016). In nested cross-validation, the parameters are tuned within their corresponding subroutines:
(1) In the update for , perform column-wise leave-one-out cross-validation to select , where we leave out all observations from a single time point. (See Appendix A.3.)
(2) In the update for , perform K-fold cross-validation to select .
Rank selection: We can perform rank selection via cross-validation as suggested in SupCP (Lock and Li, 2018). To reduce the computational cost, we deploy two strategies. (1) Early stopping: we stop where the cross-validated marginal log-likelihood is no longer decreasing. (2) Warm start and short-run: we initialize the model parameters for each cross-validated model at the global solution and only run a small number of iterations. We found 5 or 10 iterations are usually sufficiently large in practice (the default maximum number of iterations is ).
4.3 Covariate importance
In our synthetic experiments in Section 5, we observe that the inclusion of can result in a better estimate of the subject scores when the true subject scores strongly depend on . A natural following-up question is if we can ascertain the importance of such covariates when they exist. Here, we consider the construction of approximated p-values from conditional independence/marginal independence tests between and :
Both questions are of practical interest.
Recap on randomization-based hypothesis testing: Before we proceed to our proposal, we review some basic results for hypothesis testing via randomization. Consider a linear regression problem where , with mean-zero noise . Randomization test is a procedure for constructing a valid p-value without assuming the correctness of the linear model of on .
Testing for marginal independent between and any covariate is straightforward. Let be a test statistic. Let and , where is a permutation of . Then, under the null hypothesis , are exchangeable with independent copies of . Hence, for any where is the -percentile of the empirical distribution formed by copies and .
Suppose that we have access to the conditional distribution of . Let be a test statistic. Let and , where is an independent copy generated from the conditional distribution and . Then, under the null hypothesis , and have the same law conditional on and . So , where is the -percentile of the conditional distribution of (Candès et al., 2018).
Oracle randomization test in SPACO: Let’s now go back to SPACO and consider the ideal setting where , , and are given. Lemma 4.2 forms the basis of our proposal.
Lemma 4.2
Given , and let be the true regression coefficients on the covariates for , . For any , we define
| (8) | |||
| (9) | |||
| (10) |
Then, set , can be expressed as
| (11) |
Proof of Lemma 4.2 is given in Appendix B.3. As a result, when the term , we can apply the traditional randomization tests with response and features for subject . Proposition 4.3 gives our construction of the observed and randomized test statistics .
Proposition 4.3
Set , . Replacing with the properly randomized to create and is the permutation of in and is independently generated from in . When , we have
| (12) | |||
| (13) |
In practice, for the other factors are also estimated from the data. When , we could have , which renders the randomization test invalid. Thus, we typically set . For convenience, we drop the argument when , e.g., . Algorithm 3 summarizes our proposal.
Remark 4.3.1
For , the test based on , , and trades off robustness against estimation errors in for possibly increased power. To see this, suppose that for and . The signal to noise ratio with can be calculated as
Thus, the signal-to-noise ratio is higher with if we have access to the true .
The conditional randomization test requires generating from the conditional distribution . We estimate the conditional distribution of via proper exponential family distribution . More details on the generations of are provided in Appendix A.4.
Approximated p-value construction with estimated model paramters: The true model parameters for , , and are of course unknown. We will substitute their empirical estimates in the above procedure. However, the substitutes from a full SPACO fit may suffer from fitting towards the empirical noise. To reduce the influence of over-fitting, we use from cross-validation as described for performing the rank selection. That is, for where is the index set for fold in cross-validation, we construct , where , are estimates using fold other than . is also estimated using , and cross-validated prior covariance . We refer it as cross-fit, where we estimate some model parameters using data from other folds and update the quantity of interest using them and the current fold. Since each fold is initialized at the global solution, this further encourages the comparability of the constructed and from different folds. We observe that the cross-fit offers better Type I error control than the naive plug-in of the full estimates.
5 Numerical studies with synthetic data
In this section, we evaluate SPACO with synthetic Gaussian data. We fix the variance at 1 for the noise and the number of true ranks . We consider simulated data with dimensions and , with the observed rate (missing rate) along the time dimension and observed time stamps chosen randomly for each subject. Given the dimension and the observed rate, we generate and for , and . Then, (1)we set , , with random parameters for , and (2) we set for for the first , and set otherwise. Each is standardized to be mean 0 and variance 1 after generation. This generates 54 different simulation setups in total.
5.1 Reconstruction quality evaluation
We compare SPACO, SPACO-, plain CP from python package tensorly, and a proxy to SupCP by setting as small fixed values in SPACO (the additional small penalties improve numerical stability to deal with large and high missing rate). Although this is not exactly SupCP, they are very similar. We refer to this special case of SPACO as SupCP and include it to evaluate the gain from smoothness regularization on the time trajectory. Note that we use the proposed initialization in SPACO, SPACO- and SupCP, which provide better and more stable results when the missing rate is high. A comparison between SupCP with random and proposed initialization is given in Appendix C.1. We use the true rank in all four methods in our estimation. Figure 1 shows the achieved correlation between the reconstructed tensors and the underlying signal tensors across different setups and 20 random repetitions. SNR1 represents , SNR2 represents , and each sub-plot represents different signal-to-noise ratios SNR1 and SNR2, as indicated by its row and column names. The y and x axes indicate the achieved correlation and different combinations of and observed rate, respectively. For example, x-axis label means the feature dimension is 10, and 10% of entries are observed. The “Raw” method indicates the results by correlating the true signal and the empirical observation on only the observed entries. It is not directly comparable to others with missing data, but we include it here to show the signal level of different simulation setups. We also compare the reconstruction quality on missing entries in Appendix C.2.
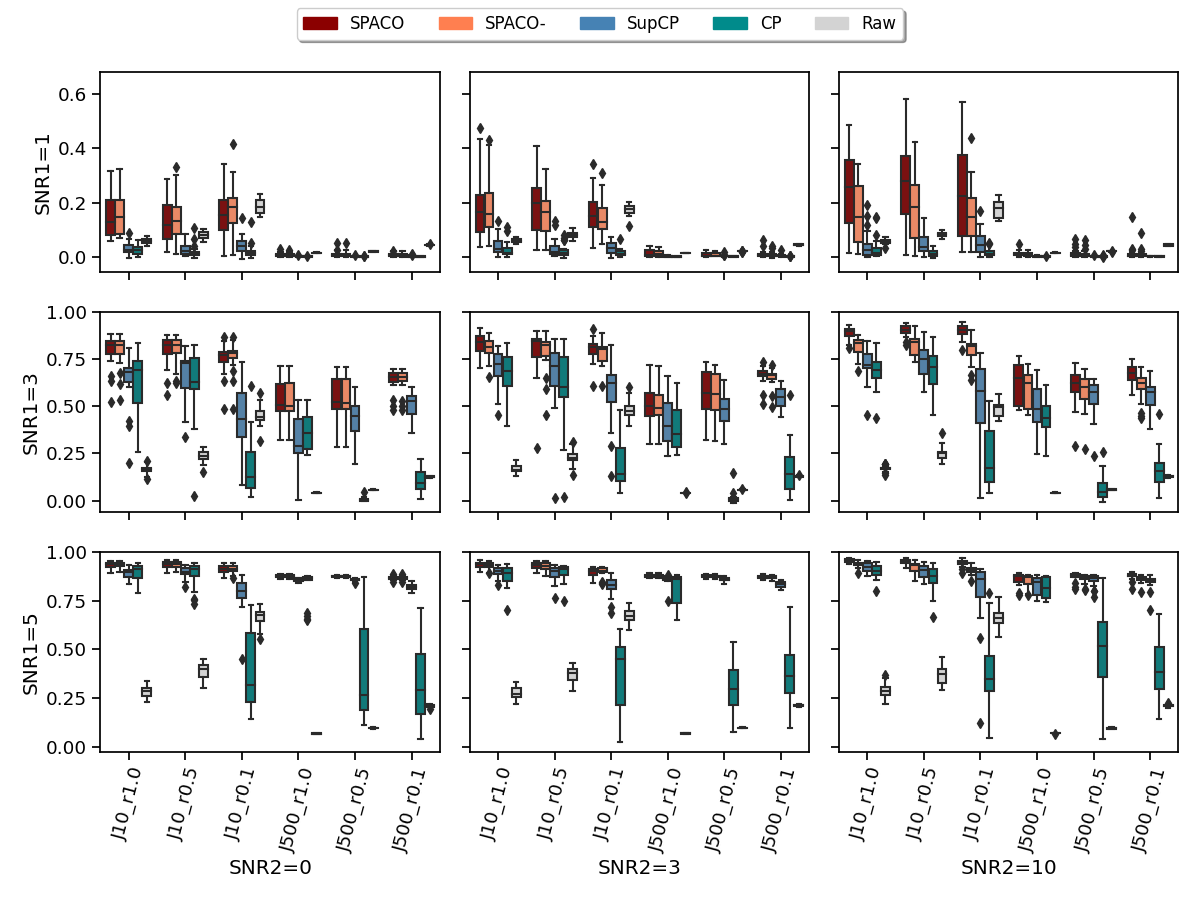
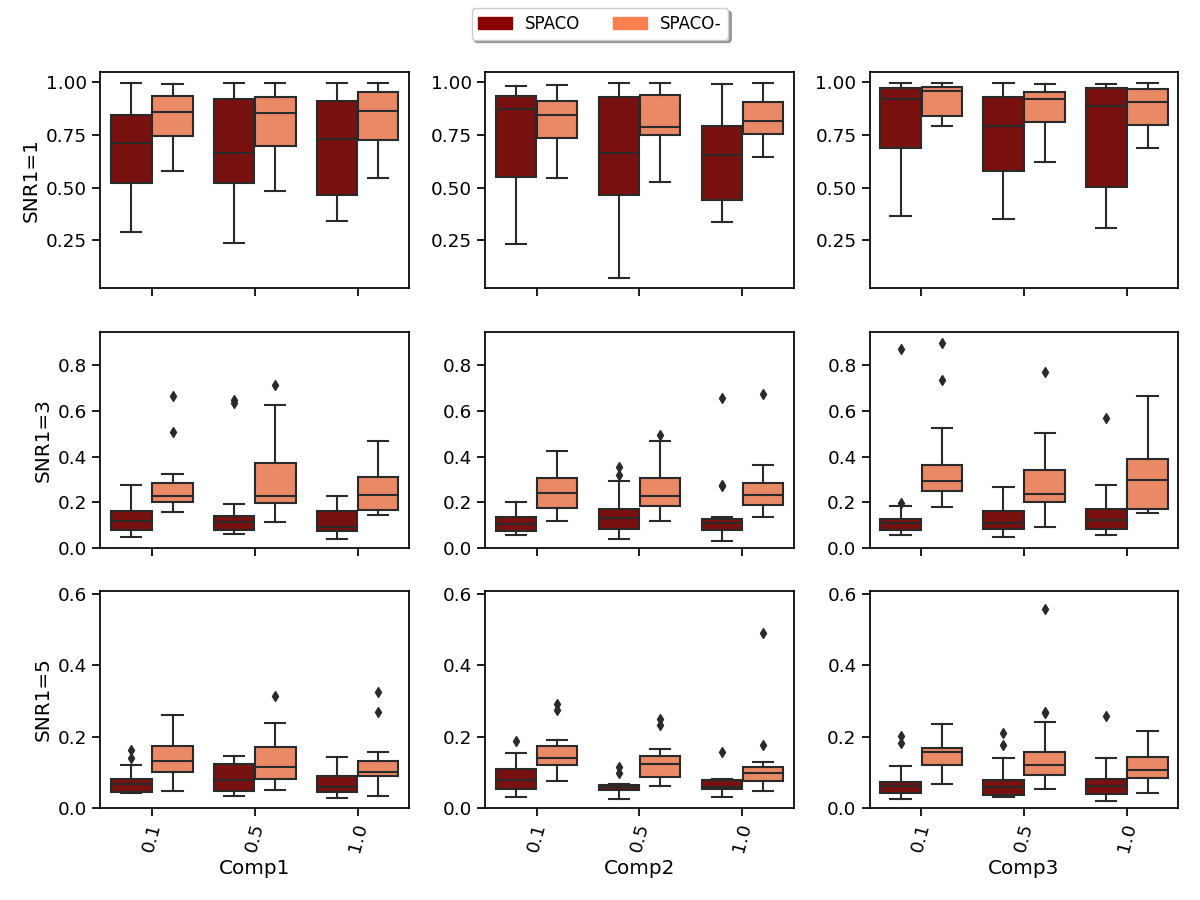
SPACO outperforms SPACO- when the subject score depends strongly on , which could result from a more accurate estimation of the subject scores. To confirm this, we evaluate the estimation quality of at and SNR2 and measure the estimation quality by (regressing the true subject scores on the estimated ones). In Figure 2, we shows the achieved for SPACO and SPACO- (smaller is better), where x-axis label represents the observing rate and column names represent the component, e.g., Comp1.
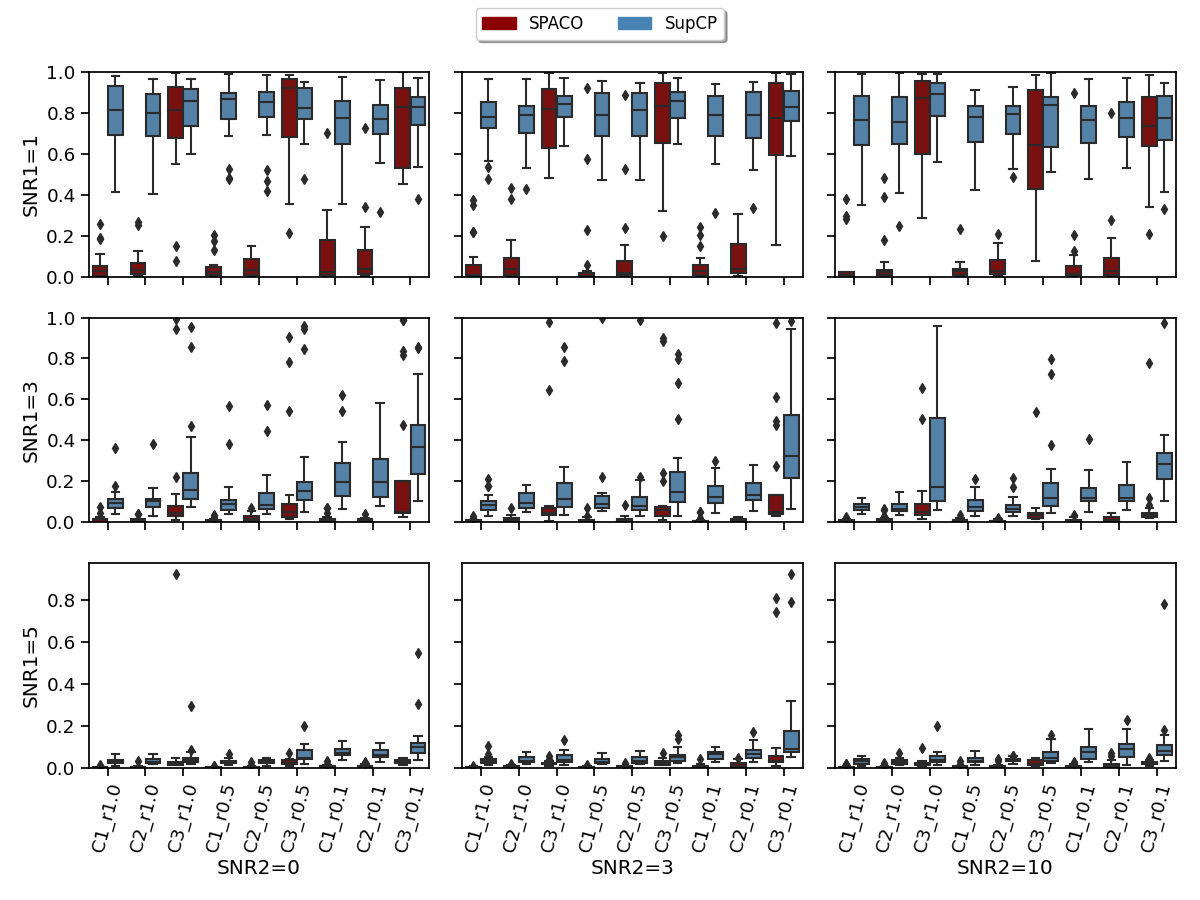
SPACO /SPACO- are both top performers for our smooth tensor decomposition problem and achieve significantly better performance than CP and SupCP when the signal is weak and when the missing rate is high by utilizing the smoothness of the time trajectory. To see this, we compared the estimation quality of the time trajectories using SPACO and SupCP. In Figure 3, we shows the achieved for SPACO and SupCP at . In the x-axis label represents different trajectory and observed rate, e.g., ( estimation of at observing rate ). When the signal is weak (SNR1=1), SPACO could approximate the constant trajectory component () and start to estimate other trajectories successfully as the signal increases. SPACO achieves significantly better estimation of the true underlying trajectories than SupCP for various signal-to-noise ratios.
5.2 Variable importance and hypothesis testing
We investigate the approximated p-values based on cross-fit for testing the partial and marginal associations of with under the same simulation set-ups. Since our variables in are generated independently, the two null hypotheses coincide in this setting. However, the two tests have different powers given the same p-value cut-off because the test statistics differ.
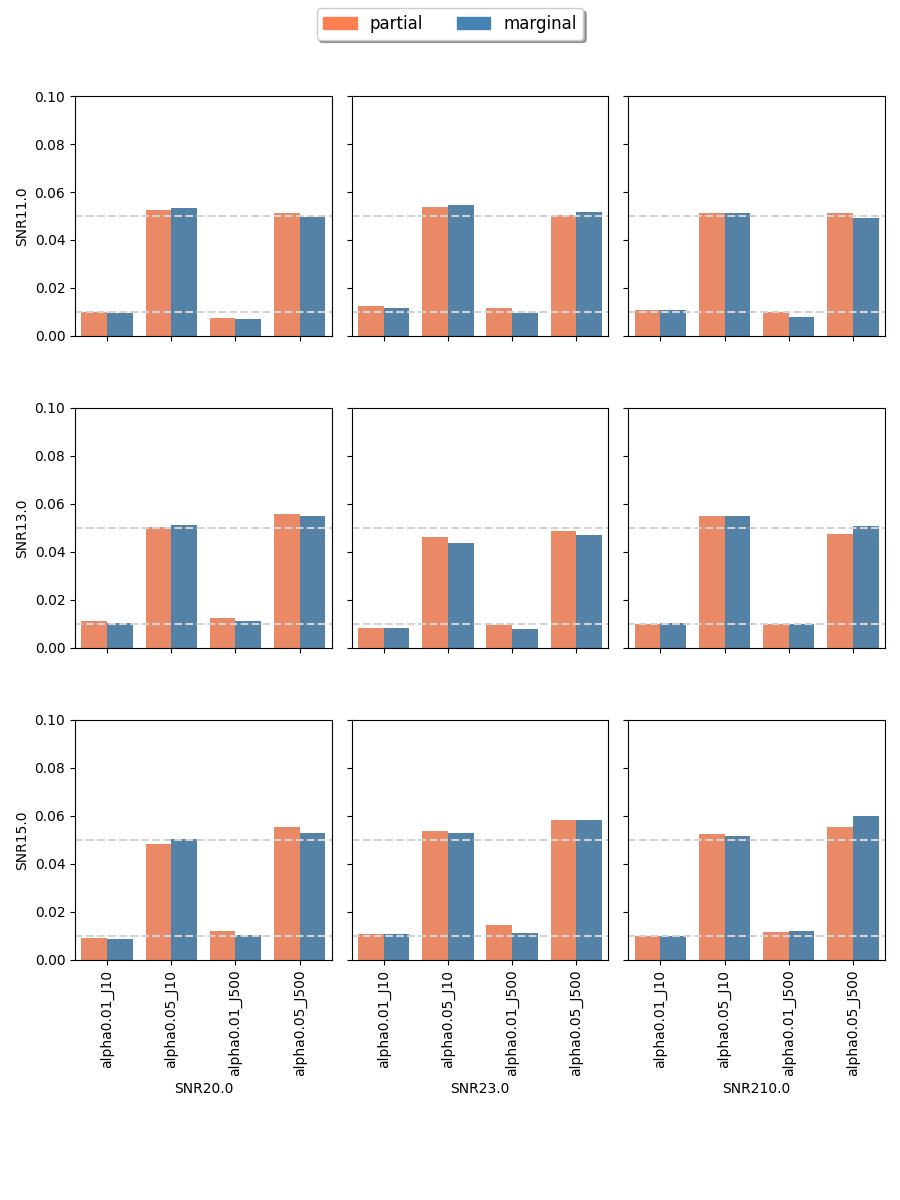
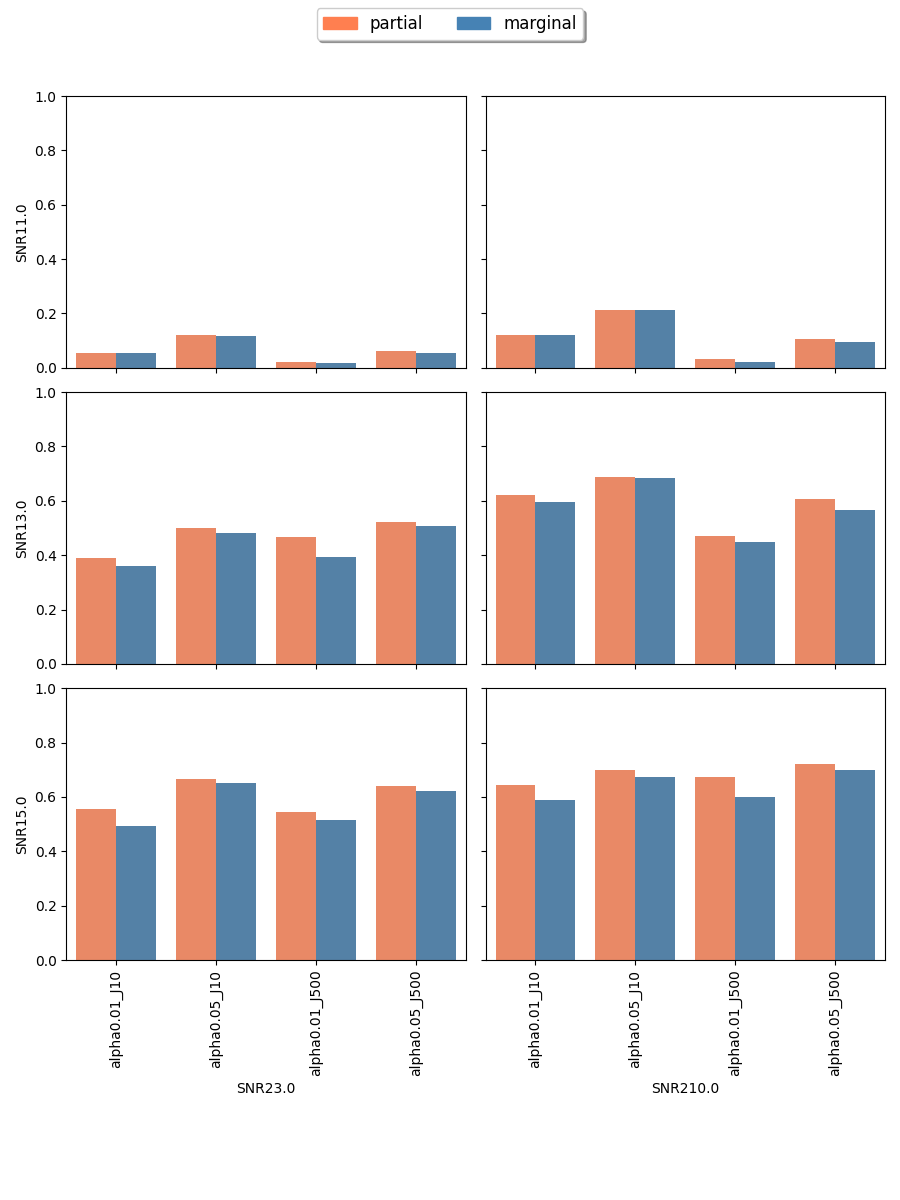
The proposed randomization tests for SPACO achieve reasonable Type I error controls. Cross-fit is important for a good Type I error control: In Appendix C.4, we present qq-plots comparing p-values using cross-fitted and and the naive construction. We observe noticeable deviations from the uniform distribution for the later construction when the signal-to-noise ratio is low. Fig.10 and Fig.5 show the the achieved Type I error and power with p-value cut-offs at and with observed rate . The type I errors are also well controlled for (Appendix C.3).
6 Case study
We now apply SPACO to a longitudinal immunological data set on COVID 19 from the IMPACT study (Lucas et al., 2020). Initially, the data contained 180 samples on 135 immunological features, collected from 98 participants with COVID-19 infection. We filter out features with more than missingness among collected samples and imputed the missing observations using MOFA (Argelaguet et al., 2018) for the remaining features. This leaves us with a complete matrix with 111 features and 180 samples, which is organized into a tensor of size where is the number of unique DFSO (days from symptom onsite) in this data set. This is a sparsely observed tensor, and the average observing rate is 1.84 along the time dimension. Apart from the immunological data, the data set also provides non-immunological covariates. We use eight static risk factors as our covariate (COVID_risk1 - COVID_risk5, age, sex, BMI), and four symptom measures as additional responses (ICU, Clinical score, LengthofStay, Coagulopathy).
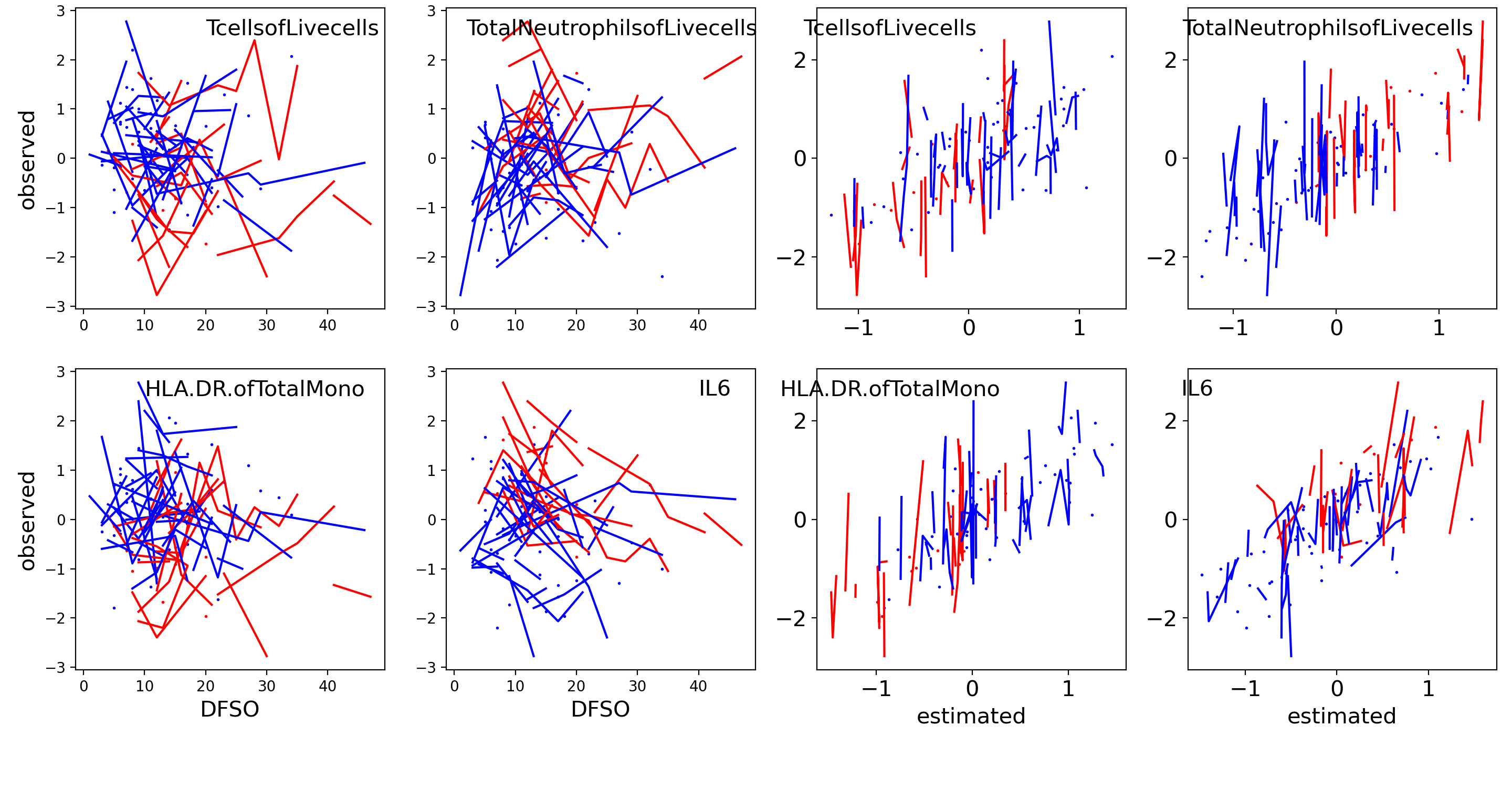
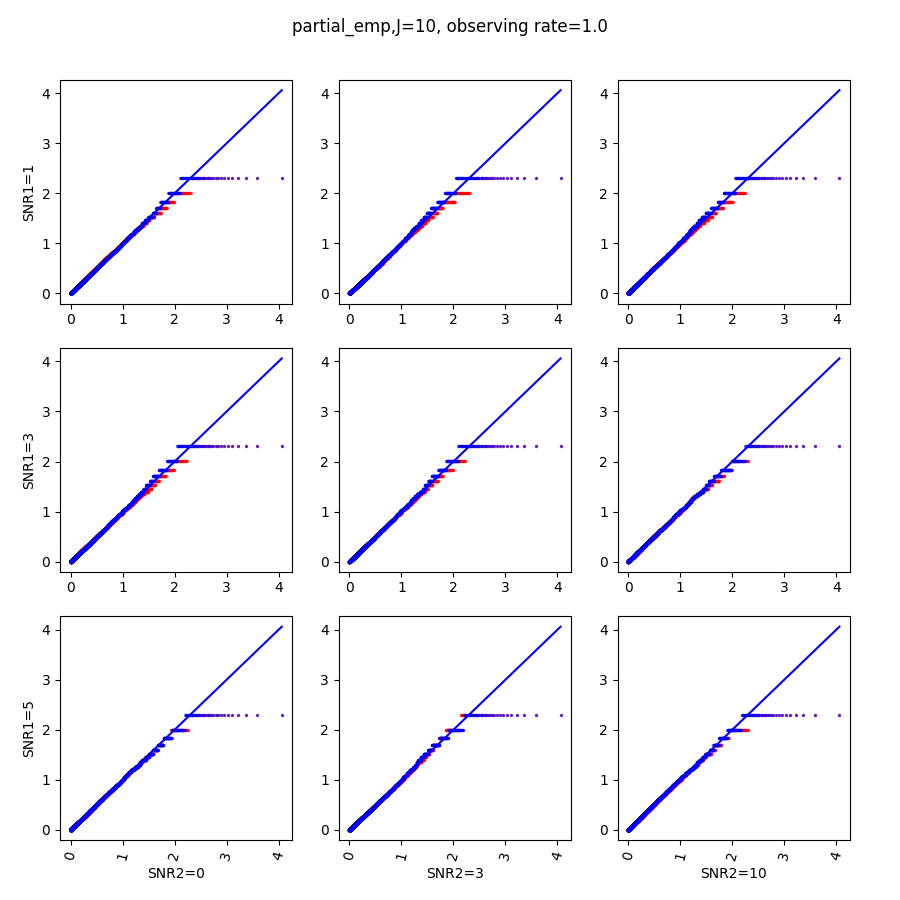
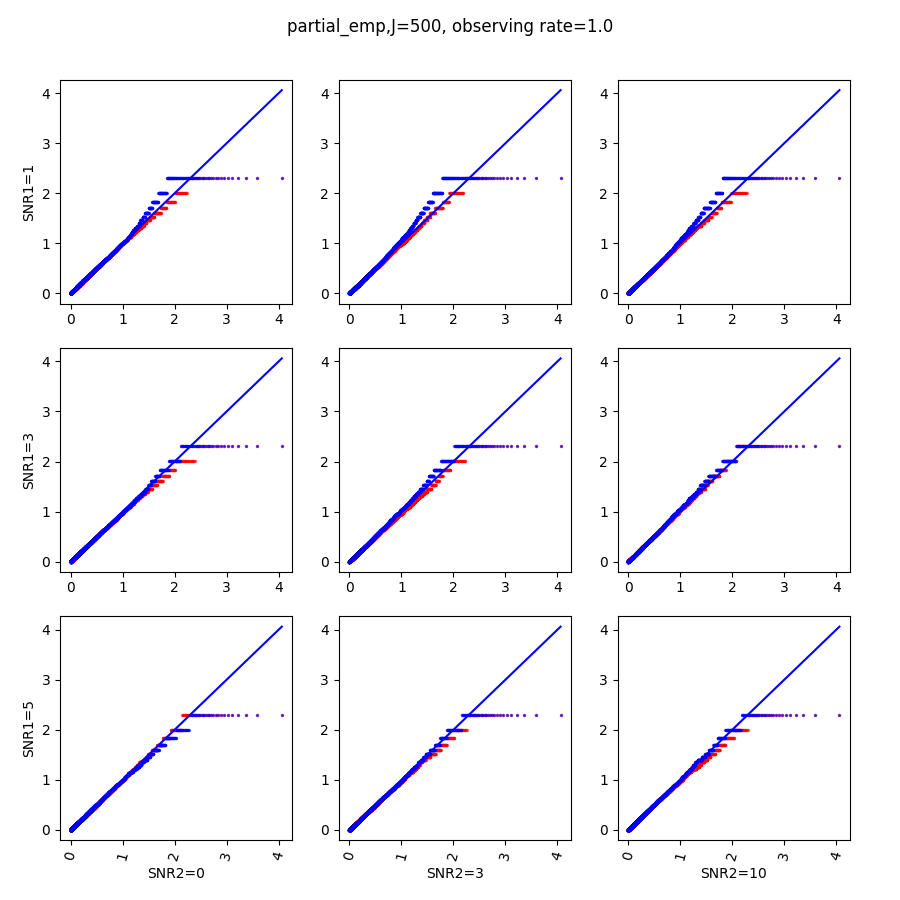
We run SPACO with processed , , and model rank , selected from finding the first maxima for the five-fold cross-validated marginal log-likelihood. Fig.6 shows example plots of raw observations against our reconstructions across all samples. We see a positive correlation between these observed and reconstructed values.
Combining static covariates with the longitudinal measurements can sometimes improve the estimation quality of subject scores compared to SPACO-, as we have illustrated in our synthetic data examples. We can not possibly get the true subject scores in the real data set. However, we could still compare the estimated subject scores are clinically relevant by comparing them to the responses. Here, we also run SPACO- with and examine if the resulting subject scores from SPACO associate better with the responses. Table 1 shows the spearman correlations and their p-values when comparing the estimated subject scores and each response. The top three components C1, C2, C3 are significantly associated with the responses. Among them, uniquely captures variability for the length of stay (in hospital), and only heavily depends on (the estimated coefficients are for both and ). C3 from SPACO achieved a better association with the clinical outcomes than SPACO.
C1cor C1pval C2cor C2pval C3cor C3pval C4cor C4pval SPACO ICU -0.20 4.9E-02 0.37 1.7E-04 0.28 5.4E-03 0.00 9.8E-01 Clinicalscore -0.32 1.2E-03 0.42 1.3E-05 0.44 6.4E-06 0.07 4.8E-01 LengthofStay -0.10 3.4E-01 0.28 5.2E-03 0.14 1.8E-01 0.11 2.9E-01 Coagulopathy -0.03 7.7E-01 0.22 3.1E-02 0.21 3.5E-02 0.03 7.9E-01 SPACO- ICU -0.20 5.1E-02 0.38 1.4E-04 0.25 1.5E-02 -0.00 9.6E-01 Clinicalscore -0.32 1.3E-03 0.43 1.0E-05 0.40 4.5E-05 0.07 4.9E-01 LengthofStay -0.09 3.9E-01 0.29 4.4E-03 0.10 3.5E-01 0.10 3.3E-01 Coagulopathy -0.03 8.0E-01 0.22 3.0E-02 0.19 5.9E-02 0.02 8.2E-01
Using the randomization test, we can also test for the contribution of each to C3. Table 2 shows the p-value and adjusted p-value from the partial dependence test and marginal dependence test, with the number of randomization . The top associate is COVIDRISK_3 (hypertension) with a p-value around 0.01 (adjusted p-value around 0.1). BMI is also weakly associated with C3, with p values for both tests. In this data set, we observe that the immunological measurements contain information strongly related to clinical responses of interest. Although some risk factors like hypertension and BMI contains relatively weaker signal, they may still improve the estimated subject scores like in the case of C3.
pval(partial) pval(marginal) padj(partial) padj(marginal) nonzero COVIDRISK_1 0.877 0.905 1.000 0.905 7 COVIDRISK_2 0.263 0.063 0.701 0.169 24 COVIDRISK_3 0.013 0.011 0.101 0.088 50 COVIDRISK_4 0.563 0.712 1.000 1.000 23 COVIDRISK_5 0.919 0.885 0.919 1.000 5 Age 0.584 0.423 0.935 0.846 – sex 0.715 0.727 0.953 0.970 47 BMI 0.029 0.041 0.117 0.166 –
7 Discussion
We propose SPACO to model sparse multivariate longitudinal data and auxiliary covariates jointly. The smoothness regularization may lead to a dramatic improvement in the estimation quality with high missing rates, and access to informative auxiliary covariates could improve the estimation of subject scores. We applied the proposed pipeline to COVID-19 data sets. Even though both data sets are highly sparse and of small size, SPACO identifies components whose subject scores are strongly associated with clinical outcomes of interest and identify static covariates that might contribute to the severe symptoms. A future direction is to extend SPACO to model multi-omics data. Different omics can be measured at different times and have distinct data types or scales. These motivate a tailored model’s more careful design rather than a naive approach of blindly pooling all omics data together.
SUPPLEMENTARY MATERIAL
- Python package for SPACO:
-
https://github.com/LeyingGuan/SPACO
- Python pipeline for reproducing results in the manuscript:
-
https://github.com/LeyingGuan/SPACOexperments
Appendix A Additional Algorithmic Details
A.1 Updating rules in Algorithm 1
Lemma A.1 provides exact parameter update rules used in Algorithm 1. We also define as the expectation of some quantity with respect to the posterior distribution of . Let with if time is observed for subject and otherwise.
Lemma A.1
The parameter update steps in Algorithm 1 take the following forms:
-
•
In line 4, , where
(14) (15) Here is the row of , and is this row with entry removed; is the sub matrix of with the column and row removed.
-
•
Set , and with and . In line 5, the update of considers the following problem:
where , and is the largest value such that the solution satisfies .
-
•
Set , and with and . In line 5, the update of considers the following problem:
where , and is the largest value such that the solution satisfies .
-
•
In lines 14 and 15,
and
A.2 Functional PCA for initializations
In Yao et al. (2005), the authors suggest a functional PCA analysis by performing eigenvalue decomposition of the smoothed matrix fitted with a local linear surface smoother. Here, we apply the suggested estimation approach on the total product matrix: Let be the empirical estimate of the total product matrix for subject , we first estimate via local surface smoother and then perform PCA on the estimated :
-
•
To fit a local linear surface smoother for the off-diagonal element of , we consider the following problem:
with , and is a standard two-dimensional Gaussian kernel.
-
•
For the diagonal element, we estimate it by local linear regression: for each :
where .
By default, we let .
A.3 Parameter tuning on
In this section, we provide more details on the leave-one-time-out cross-validation for tuning , . From eq. (19), the expected penalized deviance loss can be written as (keeping only terms relevant to ):
For a given , we define the diagonal matrix and the vector as
When we leave out a specific time point , we optimize for minimizing the following leave-one-out constrained loss,
We set as with the -entry zeroed out, and as with zeroed out. The leave-one-time cross-validation error is calculated based on the expected deviance loss (unpenalized) at the leave-out time point :
where is the leave-one-out estimate. To reduce the computational cost, we drop the norm constraint when picking , which enables us to adopt the following short-cut:
| (16) |
where is the unconstrained solution from using all time points. This follows from the arguments below:
-
1.
Drop the constraint, the original problem is equivalent to:
-
2.
Consider the augmented problem:
where , and and for . The augmented problem also has as its solution.
-
3.
Hence, without the constraint, we have and . Consequently:
-
4.
Finally, we obtain
Hence, we have
A.4 Generation of randomized covariates for testing
In the simulations and real data examples, we encounter two types of : Gaussian and binary. We model the conditional distribution of given with a (penalized) GLM. For Gaussian data, we consider a model where
We estimate and empirically from data. When , the dimension of , is large, we apply a lasso penalty on with penalty level selected with cross-validation. Let and be our estimates of the distribution parameters. We then generate new for subject from the estimated distribution , with independently generated from . For binary , we consider the model
Again, we estimate empirically, with cross-validated lasso penalty for large . We then generate independently from
To generate from the marginal distribution of , instead of estimating this distribution, we let be a random permutation of .
The randomization test requires generating from the conditional or marginal distribution of , and estimating the resulting distribution of . We will estimate the distribution of by fitting a skewed t-distribution as suggested in (Katsevich and Roeder, 2020). The use of the fitted instead of the naive empirical CDF can greatly reduce the computational cost: We may obtain accurate estimates of small p-values around using only 200 independent generations of and the fitted .
Appendix B Proofs
B.1 Proof of Theorem 3.1
The first step leads to non-decreasing marginal log-likelihood by definition, while the second step is a EM procedure. If we can show that the penalized marginal log-likelihood is non-decreasing at each subroutine of the EM procedure, we prove Theorem 3.1.
For simplicity, be the parameters that is being updated in some subroutine and parameters excluding . Let , . It is known that if a new is no worse compared with using the EM objective, it is no worse than when it comes to the (regularized) marginal MLE (Dempster et al., 1977). We include the short proof here for completeness.
Because the log of the posterior of can be decomposed into the difference between the log of the log complete likelihood and the log marginal likelihood, , we have (expectation with respect to posterior distribution of with parameters ):
As a result, when
the following inequality holds,
The last inequality is due to the fact that the mutual information is nonnegative. Now, we return to our subroutines for updating parameters :
-
•
For our subroutines of updating and , they are defined as the maximizers of .
-
•
From the proof to Lemma A.1 in deriving the explicit form for updating and (see section), we know that is a convex quadratic loss and for coefficients with explicit forms. If we can show that
is an minimizer to the problem , then updating to this new vector is valid and will not increase our loss. This is true by standard optimization arguments. Let . Let be such a value such that , and let be the solution at this . Then,
Hence, the proposed strategy at line 5 in Algorithm 1 solves the original problem. The same arguments hold for updating .
Hence, given the posterior distribution at the beginning of iteration , if we update the model parameters at proposed to acquire , we always have .
B.2 Proof of Lemma 4.1
Statement I: Suppose , and for some matrices , , . Then, there exists a rank-K core-array , such that , and form a PARAFAC decomposition of : Argument I: Statement I can be checked easily: since spans the row space of , we can find a matrix such that if we replace with , we still have a PARAFAC decomposition of . We can apply the same arguments to , and hence prove the statement at the beginning. As a result, we need to show that , and spans the column spaces of the three unfolding matrices and is the unfolding of such a core array along the subject dimension.
-
•
The proposed satisfies the requirement by construction. Hence, we need only to check that and spans the row space of and respectively.
-
•
The projection of onto results in , where . Hence, we have
where with . Notice that
Hence, is the top left singular vectors of . We set .
-
•
is estimated by regression on . Because both and are orthonormal, is also orthonormal:
Hence, we have
The row space spanned by is the same as the row space spanned by , thus, the space spanned by top left singular vectors of is the same by that of . As a result, also satisfies the requirement.
-
•
In particular, we also have
where is the unfolding of the core array in the subject dimension. Hence, we recover applying a rank-K PARAFAC decomposition on the arranged three-dimensional core array from as described in Algorithm 2.
B.3 Proof of Lemma 4.2
Let . Plug-in the expression of into the expression of :
where and
B.4 Proof of Lemma A.1
B.4.1 Update of :
B.4.2 Update of and :
We can rewrite the complete log-likelihood using the unfolding along the feature dimension and the time dimension. The relevant terms to and are:
Let if observation time index for subject is available, and let be the set of index where for subject i. By direct calculation, the expectation of the negative log-likelihood (keeping only terms relevant to and ) are given below:
| (18) | ||||
| (19) | ||||
Update : From eq. (18), update of considers the following problem
Here, and are defined below:
Hence, if we set , , as specified, we have and .
Update Updating is similar to updating apart from the inclusion of the smoothness regularizer. Set , and with
Then,
where and .
B.4.3 Update of and
Since the expected log likelihood related to is
Consequently, the solution for given other parameters is .
the expected log likelihood related to is
Consequently, the updating rule given other parameters is
Appendix C Additional numerical results
C.1 Comparison of two initialization strategies
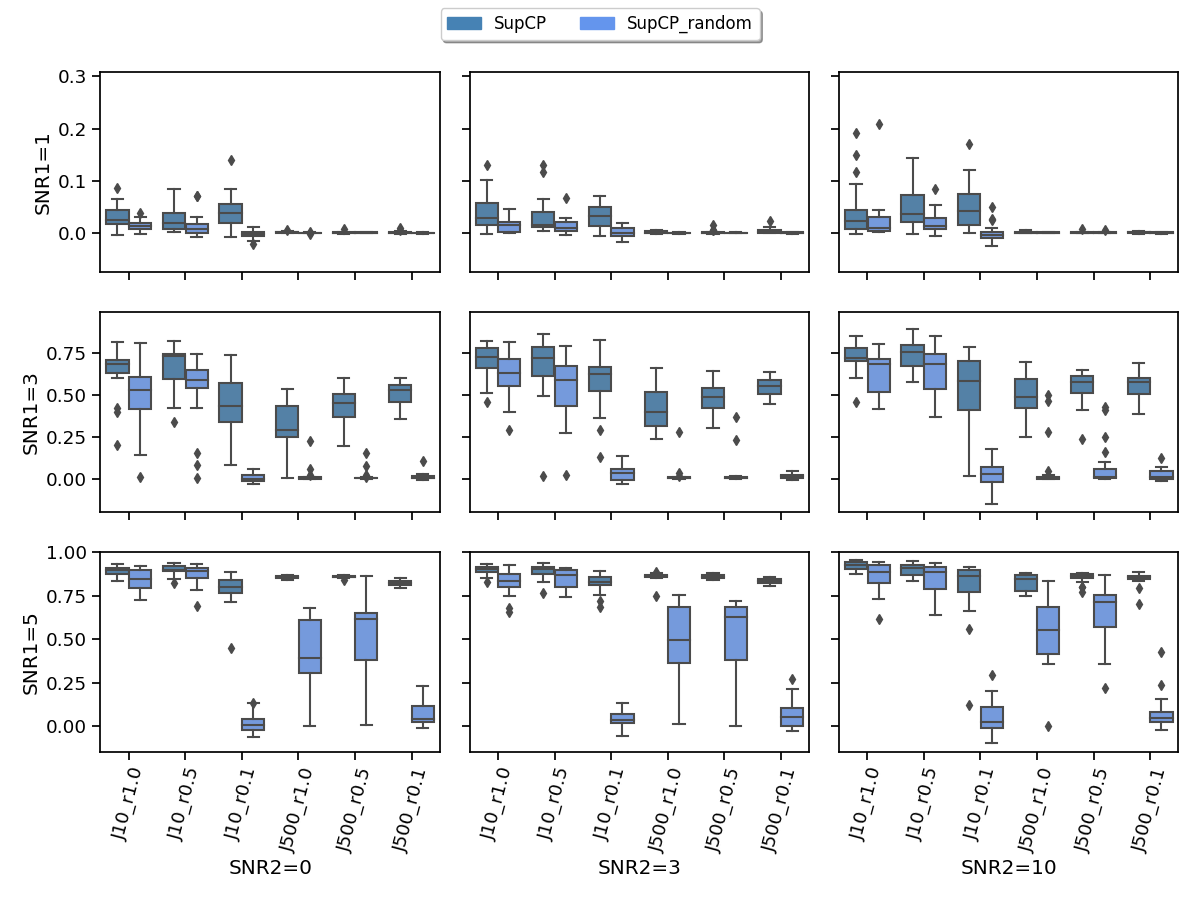
Fig.7 compares the achieved correlations with the signal tensor when SupCP are initialized using the proposed initialization method (referred to as SupCP) and the random initialization method (referred to as SupCP_random) (Lock and Li, 2018). The proposed strategy shows a clear gain in the setting of high missing rate or weak signal.
C.2 Signal reconstruction on missing entries
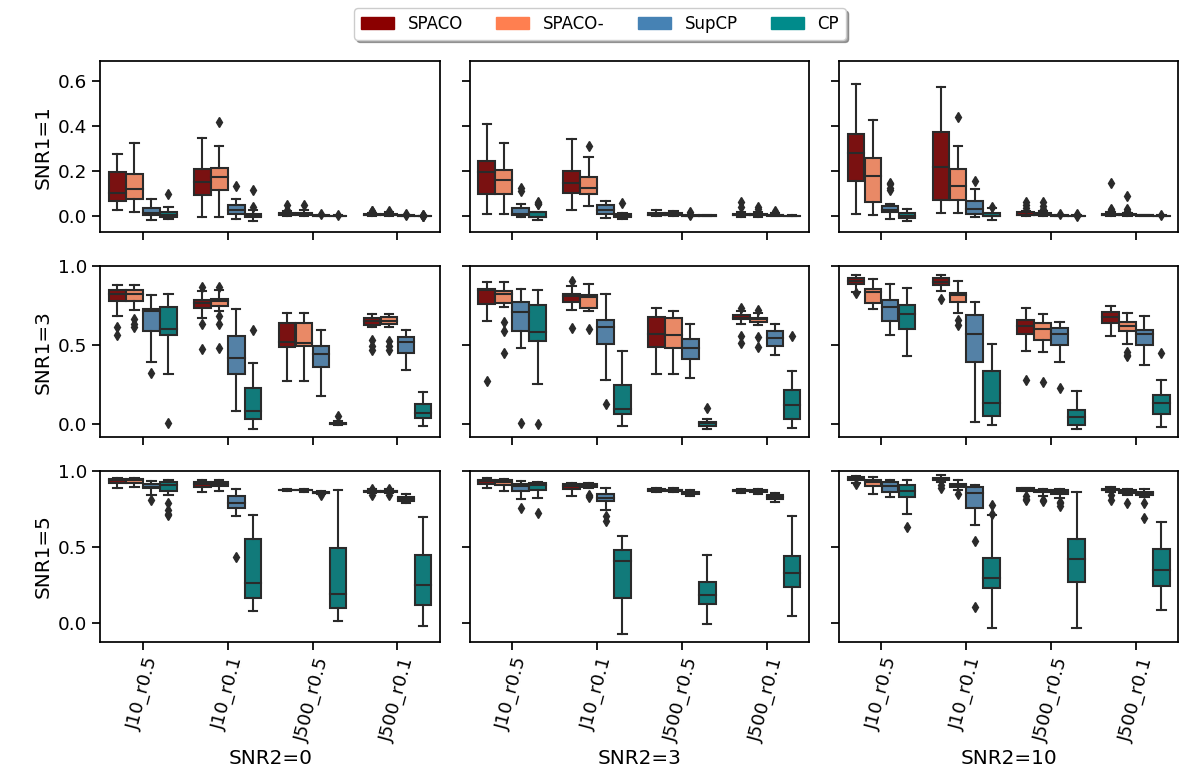
Fig.8 compares the achieved correlations with the signal tensor using different methods, but only on those missing entries. The proposed strategy shows a clear gain in the setting of high missing rate or weak signal. Consistent with Fig.1, SPACO improves over SPACO- with high SNR2, and is much better than SupCP or CP when the signal size SNR1 is weak (but still estimable using SPACO) or when the missing rate is high.
C.3 Type I error with observing rate
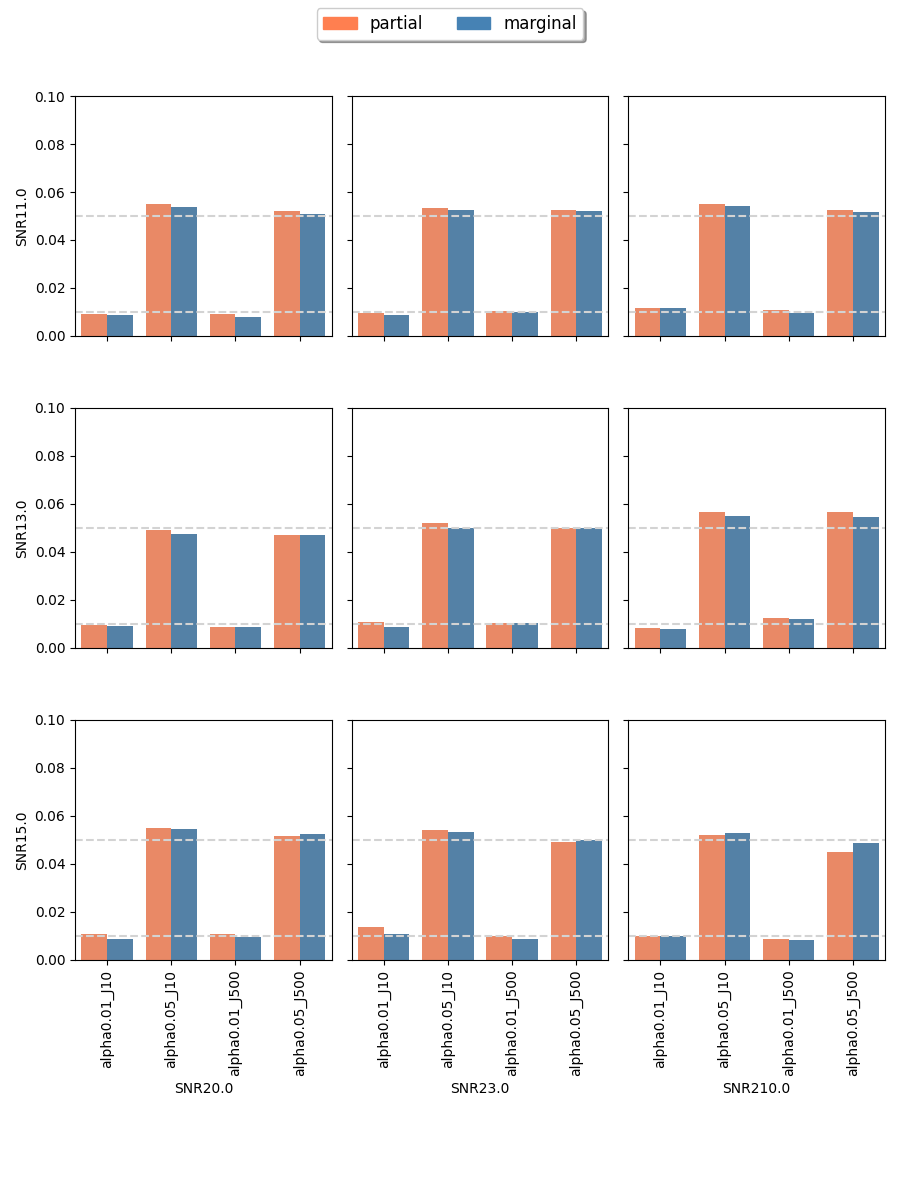
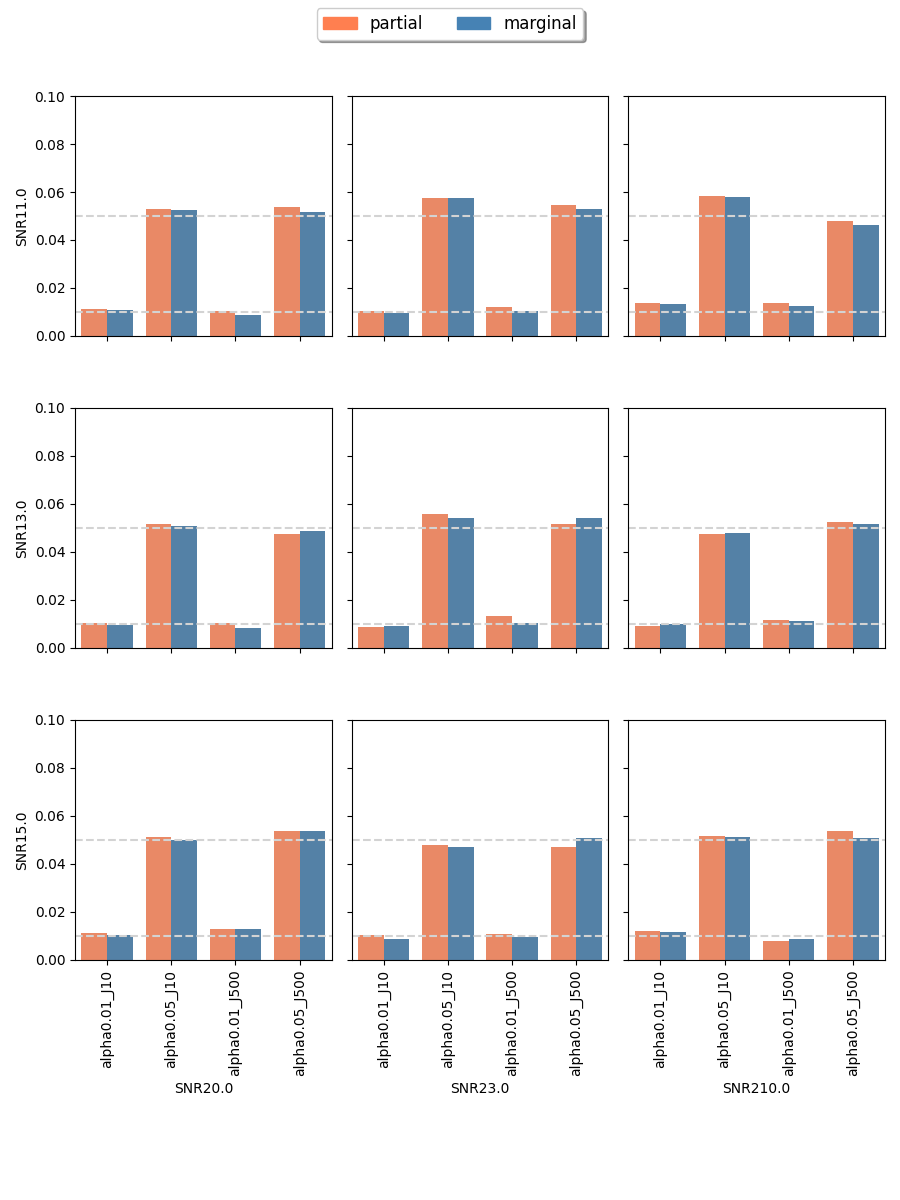
C.4 empirical p-value: cross-fit vs naive fit
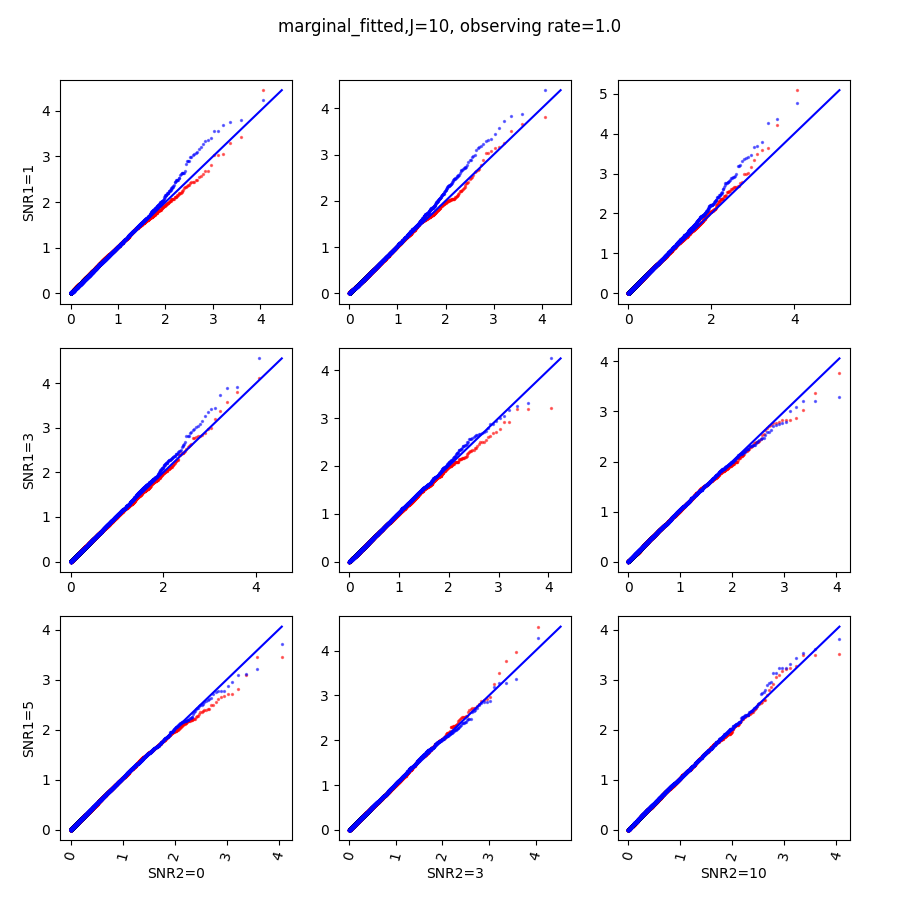
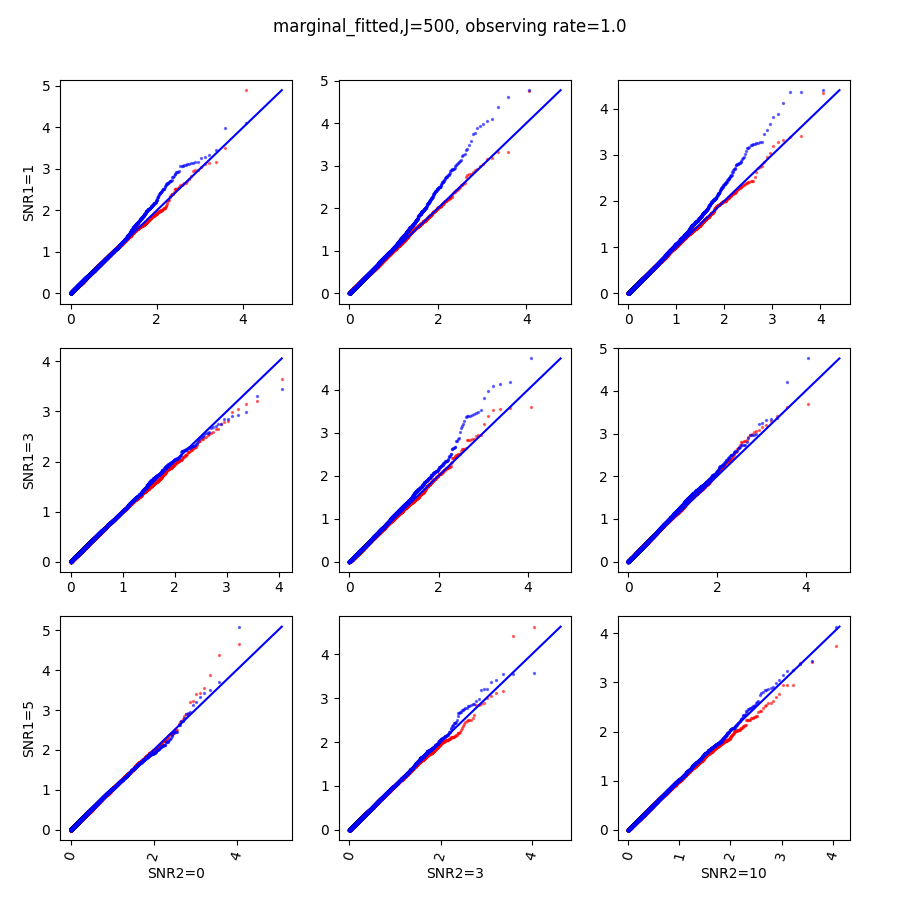
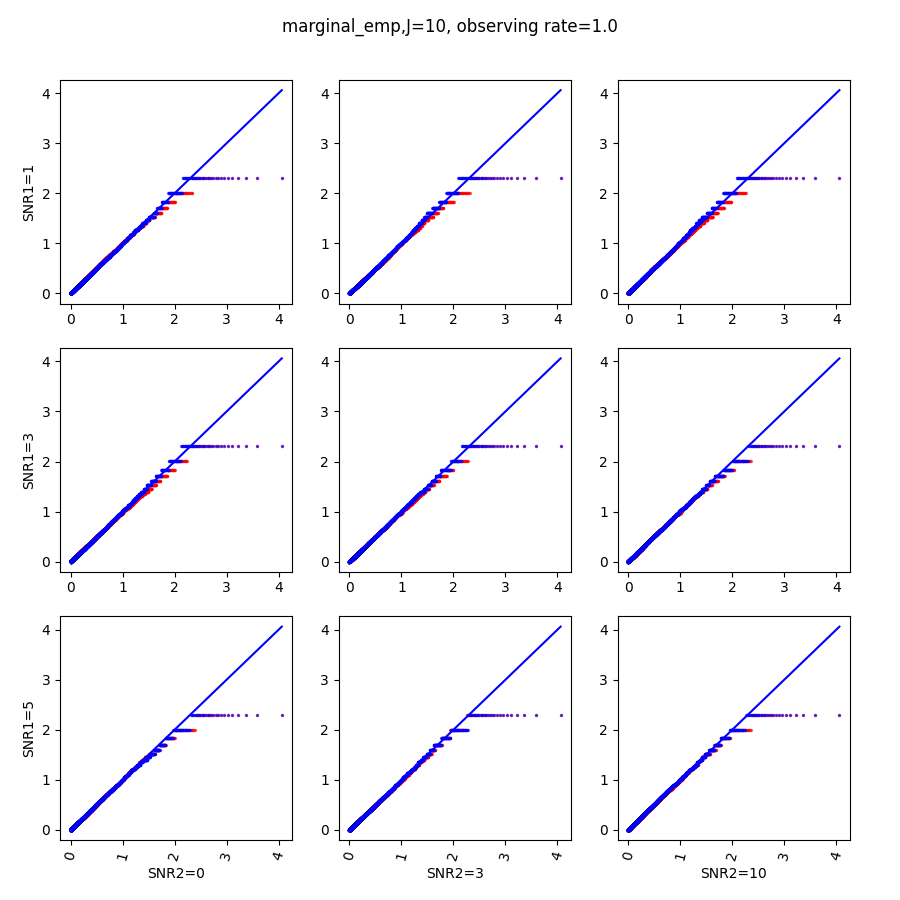
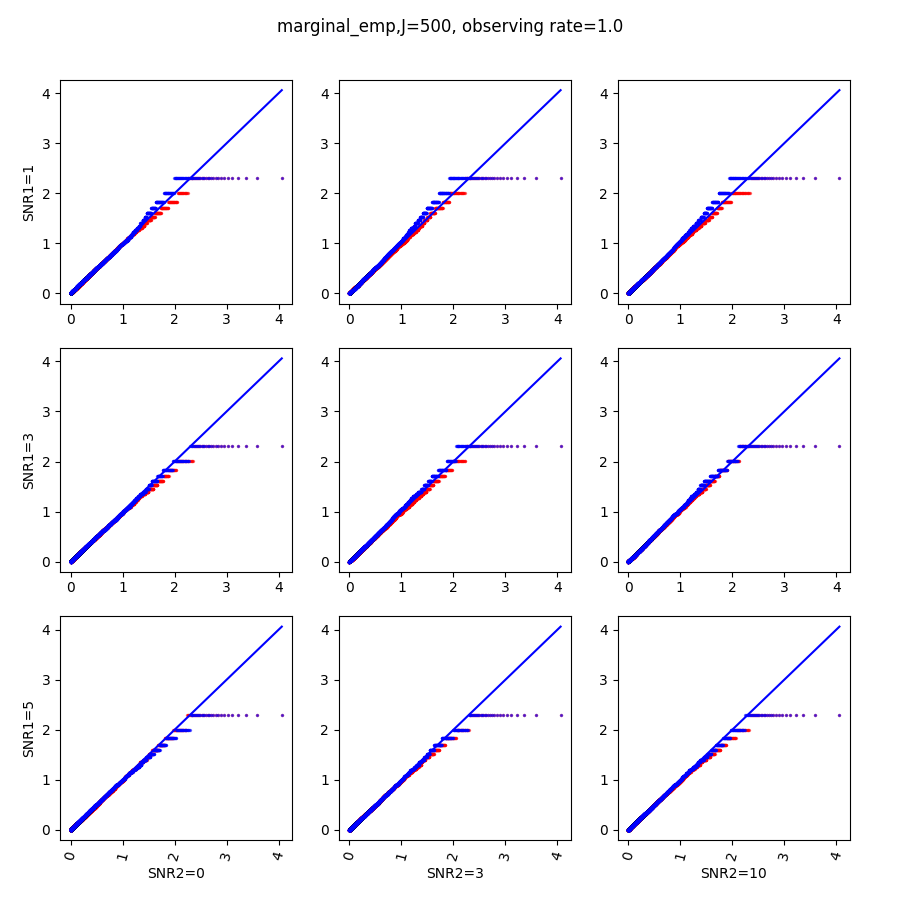
In this section, we show qq-plots of the negative from the null hypotheses against its theoretical values from the uniform distribution. In Fig.11-Fig.13, we show the results from observing rate respectively, and the red/blue points represent those from the cross fit and the full fit with blue diagonal representing the expected theoretical behavior. The sub-title indicates the dimensionality , observing rate and the type of estimate: partial_fitted means p values from partial independence test with p-value estimated using nct distribution and marginal_fitted means p values from marginal independence test with p-value estimated using nct distribution. The number of randomization used here is . We observe that direct plug-in of model parameters from full fit leads to poor performance when the signal-to-noise ratio is low. When SNR1, the log pvalue is severely inflated based on the full fit, the cross-fit provides much uniform null p-value distribution even with only a five-step update.
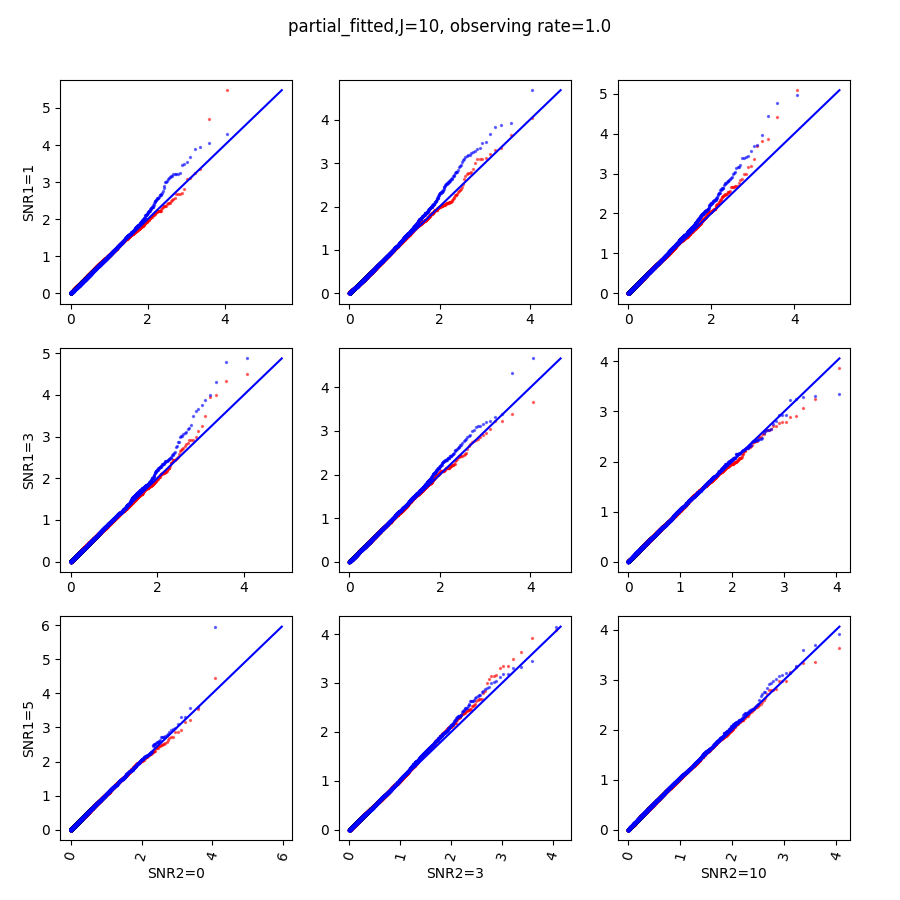
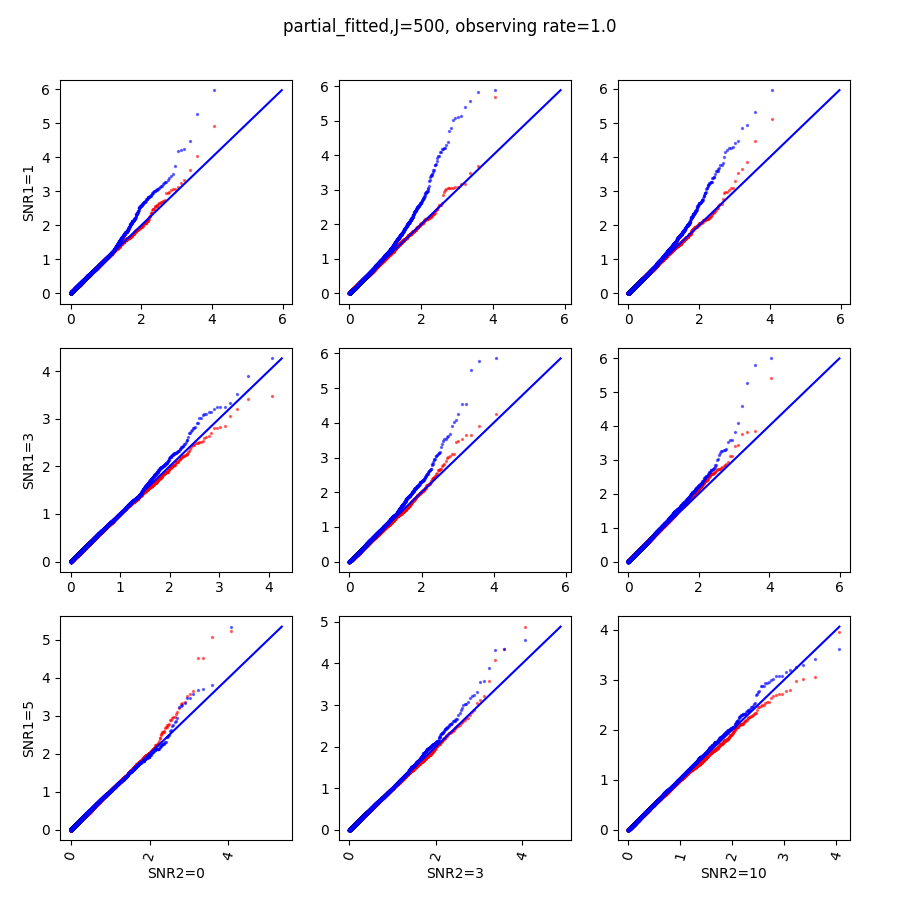
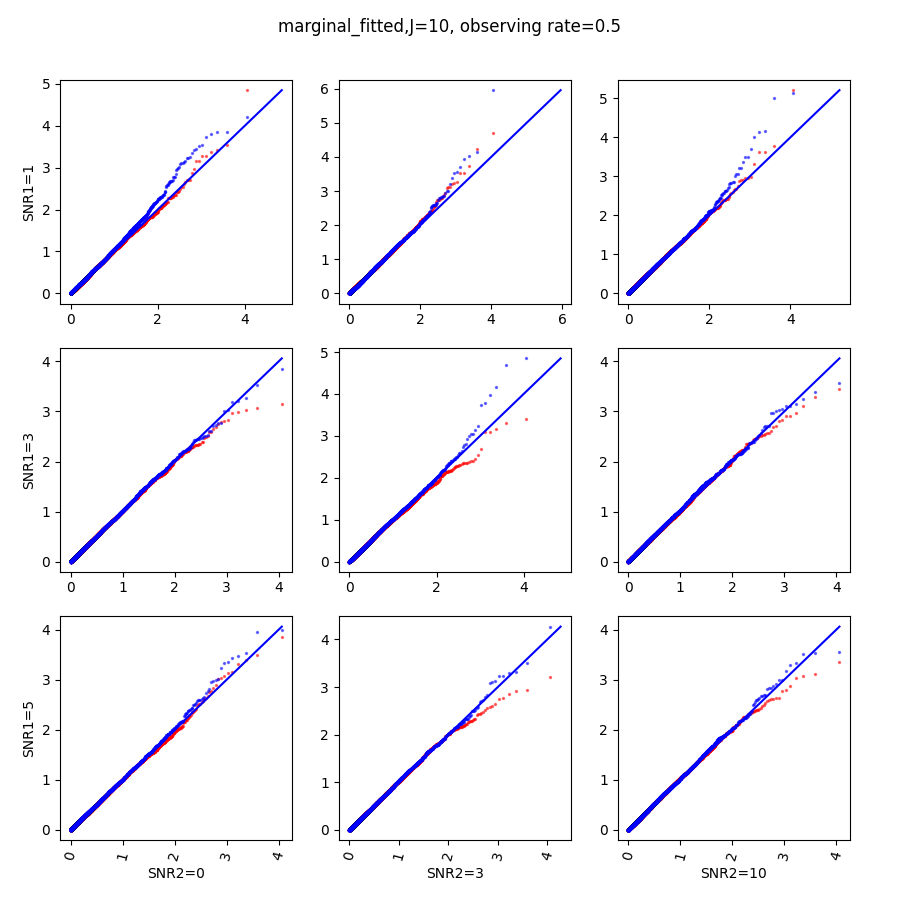
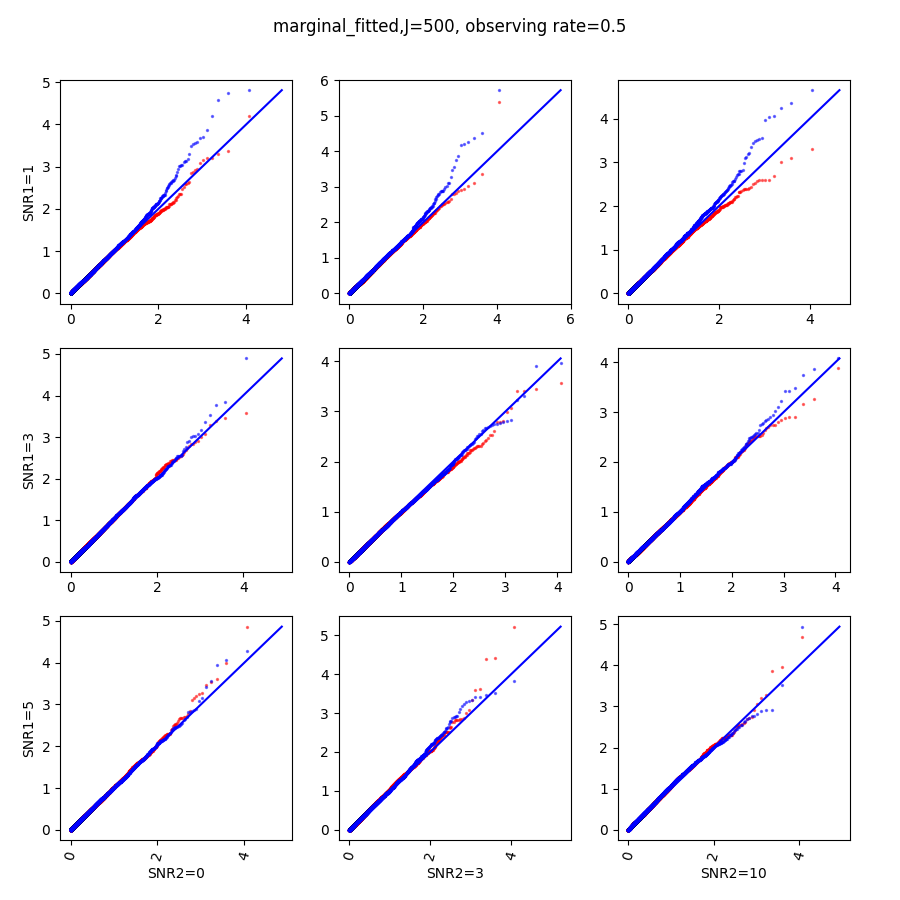
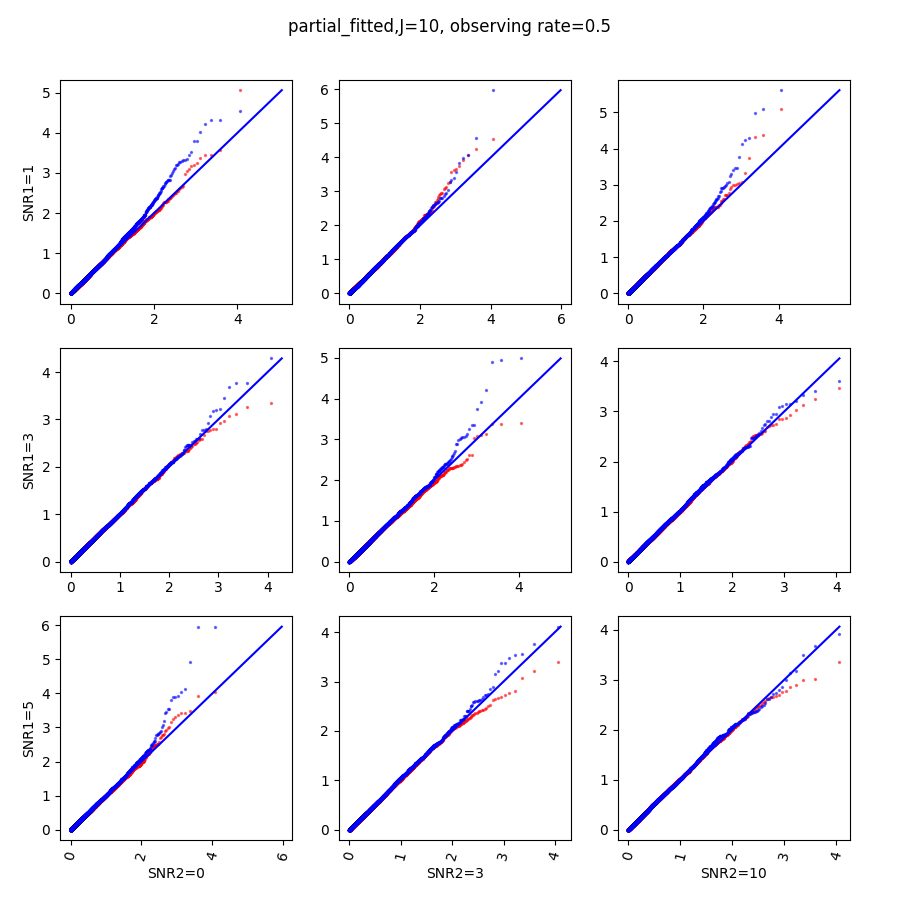
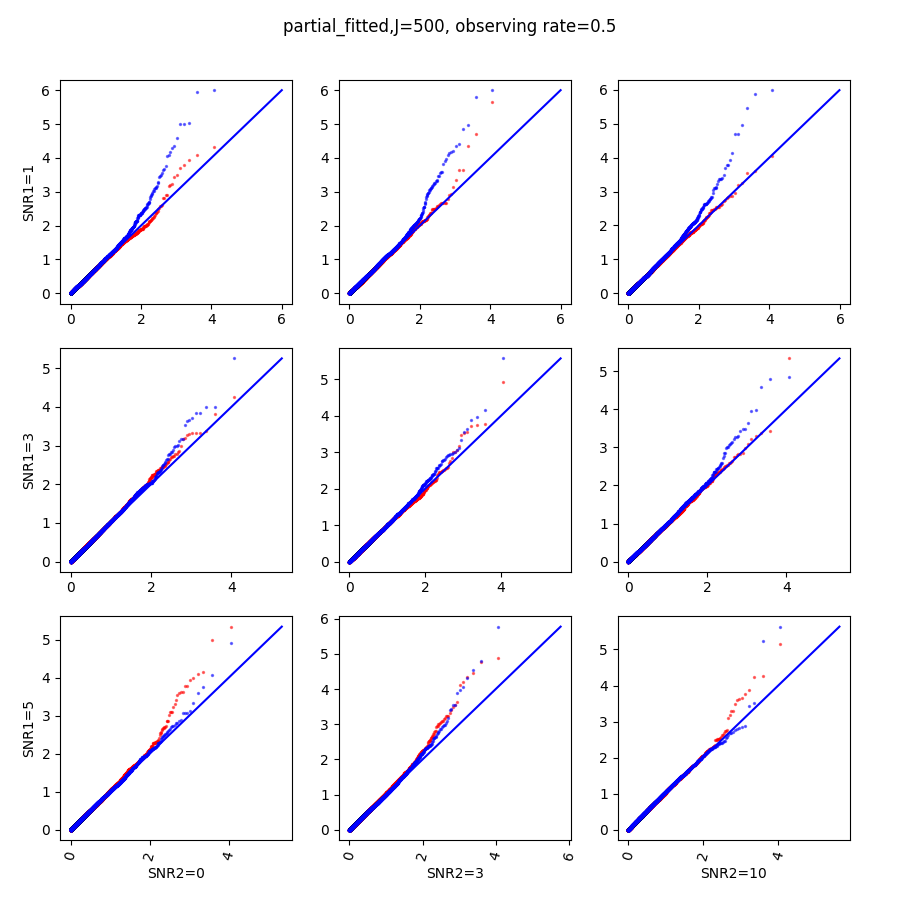
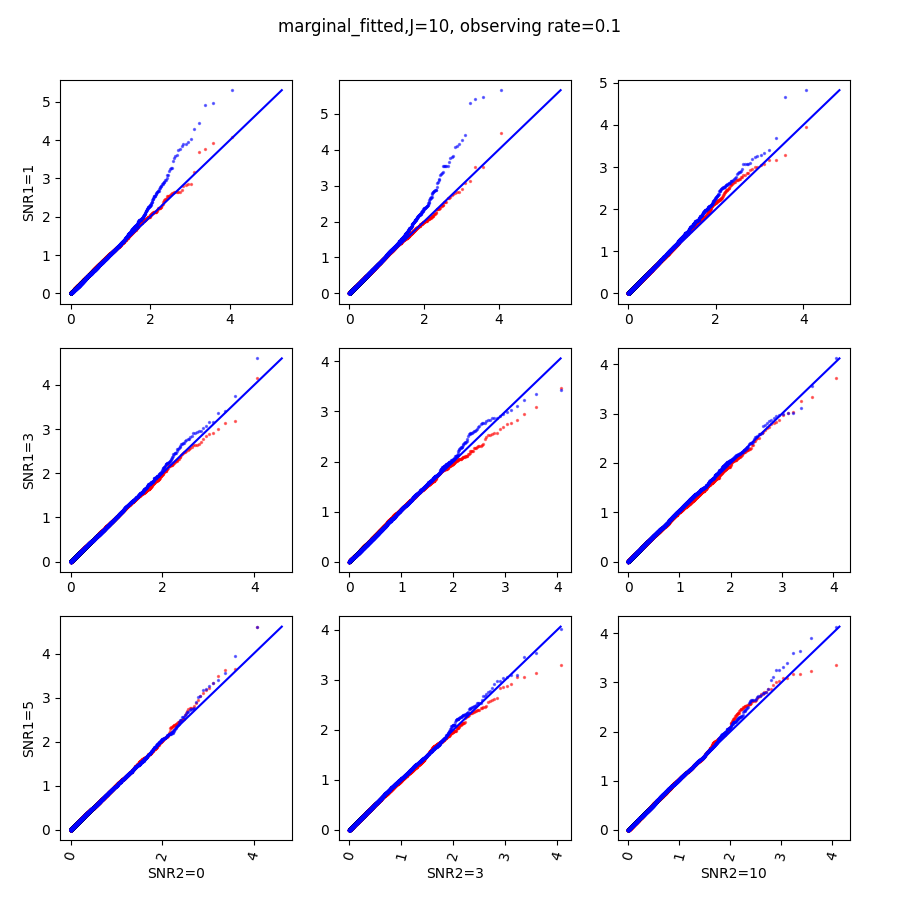
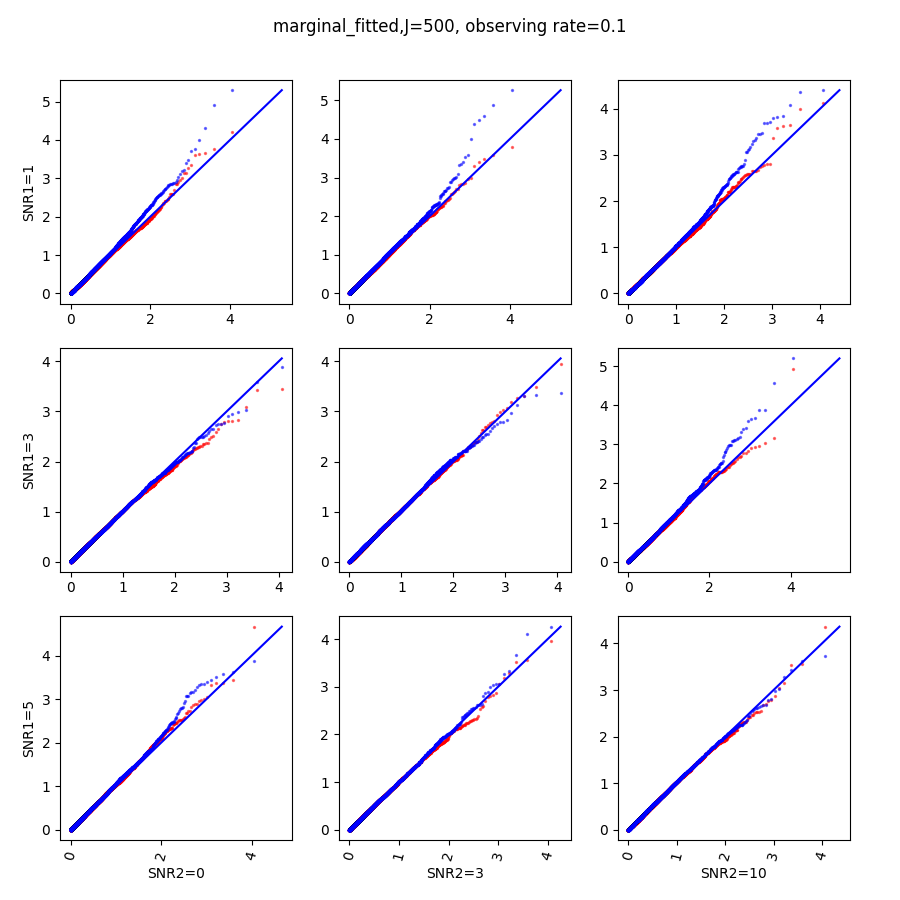
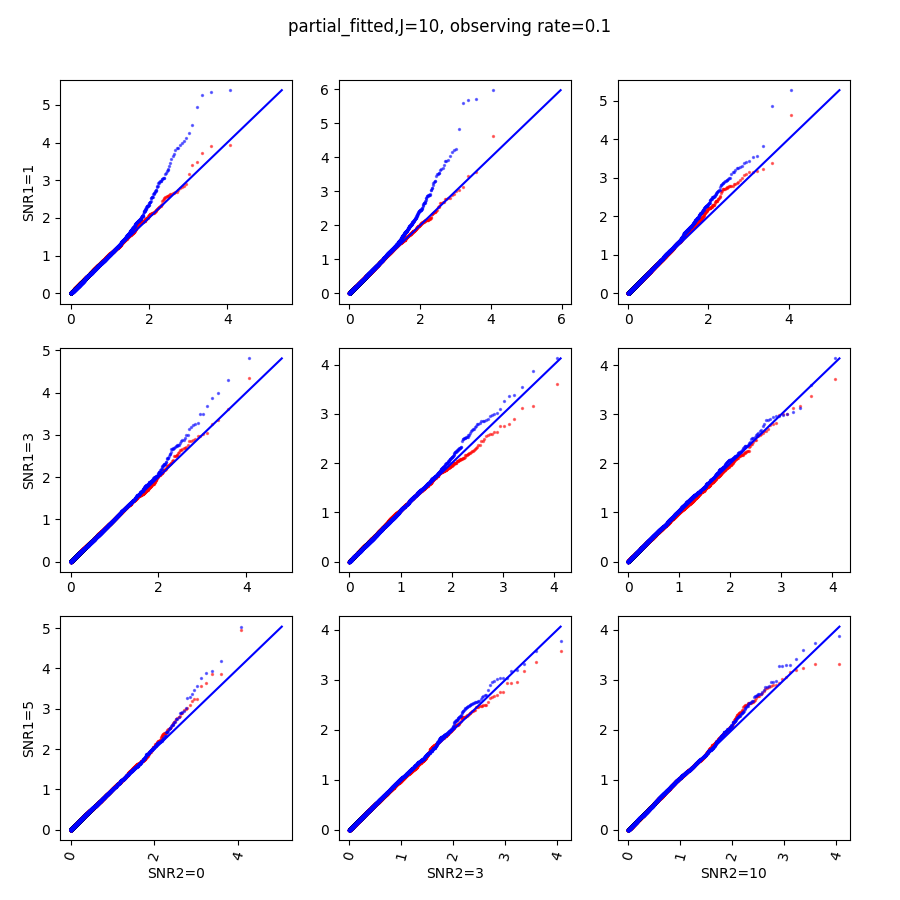
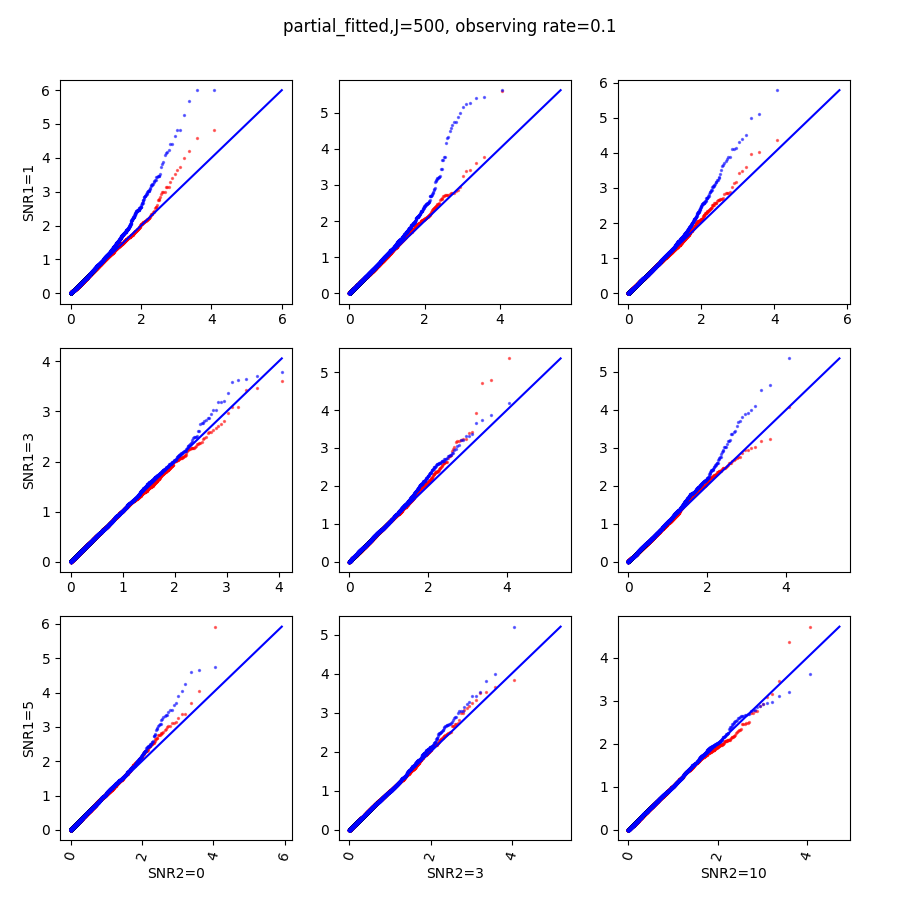
When , the non-parametric estimate of the p values has a lower bound of , but the nct-estimated p values do not have such a restriction. Fig.14 shows the non-parametric p value estimates at , we can easily show that the nct-estimated version provides more details for small p-values.
References
- Acar and Yener (2008) Acar, E. and B. Yener (2008). Unsupervised multiway data analysis: A literature survey. IEEE transactions on knowledge and data engineering 21(1), 6–20.
- Argelaguet et al. (2018) Argelaguet, R., B. Velten, D. Arnol, S. Dietrich, T. Zenz, J. C. Marioni, F. Buettner, W. Huber, and O. Stegle (2018). Multi-omics factor analysis—a framework for unsupervised integration of multi-omics data sets. Molecular systems biology 14(6), e8124.
- Bai and Wang (2016) Bai, J. and P. Wang (2016). Econometric analysis of large factor models. Annual Review of Economics 8, 53–80.
- Besse and Ramsay (1986) Besse, P. and J. O. Ramsay (1986). Principal components analysis of sampled functions. Psychometrika 51(2), 285–311.
- Bro and Andersson (1998) Bro, R. and C. A. Andersson (1998). Improving the speed of multiway algorithms: Part ii: Compression. Chemometrics and intelligent laboratory systems 42(1-2), 105–113.
- Candès et al. (2018) Candès, E., Y. Fan, L. Janson, and J. Lv (2018). Panning for gold:‘model-x’knockoffs for high dimensional controlled variable selection series b statistical methodology.
- Carroll et al. (1980) Carroll, J. D., S. Pruzansky, and J. B. Kruskal (1980). Candelinc: A general approach to multidimensional analysis of many-way arrays with linear constraints on parameters. Psychometrika 45(1), 3–24.
- De Lathauwer et al. (2000) De Lathauwer, L., B. De Moor, and J. Vandewalle (2000). A multilinear singular value decomposition. SIAM journal on Matrix Analysis and Applications 21(4), 1253–1278.
- Dempster et al. (1977) Dempster, A. P., N. M. Laird, and D. B. Rubin (1977). Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39(1), 1–22.
- Fan et al. (2008) Fan, J., Y. Fan, and J. Lv (2008). High dimensional covariance matrix estimation using a factor model. Journal of Econometrics 147(1), 186–197.
- Fan et al. (2011) Fan, J., Y. Liao, and M. Mincheva (2011). High dimensional covariance matrix estimation in approximate factor models. Annals of statistics 39(6), 3320.
- Harshman and Lundy (1994) Harshman, R. A. and M. E. Lundy (1994). Parafac: Parallel factor analysis. Computational Statistics & Data Analysis 18(1), 39–72.
- Hinrich and Mørup (2019) Hinrich, J. L. and M. Mørup (2019). Probabilistic tensor train decomposition. In 2019 27th European Signal Processing Conference (EUSIPCO), pp. 1–5. IEEE.
- Huang et al. (2008) Huang, J. Z., H. Shen, A. Buja, et al. (2008). Functional principal components analysis via penalized rank one approximation. Electronic Journal of Statistics 2, 678–695.
- Imaizumi and Hayashi (2017) Imaizumi, M. and K. Hayashi (2017). Tensor decomposition with smoothness. In International Conference on Machine Learning, pp. 1597–1606. PMLR.
- Katsevich and Roeder (2020) Katsevich, E. and K. Roeder (2020). Conditional resampling improves sensitivity and specificity of single cell crispr regulatory screens. bioRxiv.
- Lam et al. (2011) Lam, C., Q. Yao, and N. Bathia (2011). Estimation of latent factors for high-dimensional time series. Biometrika 98(4), 901–918.
- Li et al. (2016) Li, G., H. Shen, and J. Z. Huang (2016). Supervised sparse and functional principal component analysis. Journal of Computational and Graphical Statistics 25(3), 859–878.
- Lock and Li (2018) Lock, E. F. and G. Li (2018). Supervised multiway factorization. Electronic journal of statistics 12(1), 1150.
- Lucas et al. (2020) Lucas, C., P. Wong, J. Klein, T. B. Castro, J. Silva, M. Sundaram, M. K. Ellingson, T. Mao, J. E. Oh, B. Israelow, et al. (2020). Longitudinal analyses reveal immunological misfiring in severe covid-19. Nature 584(7821), 463–469.
- Mnih and Salakhutdinov (2007) Mnih, A. and R. R. Salakhutdinov (2007). Probabilistic matrix factorization. Advances in neural information processing systems 20, 1257–1264.
- Phan et al. (2013) Phan, A.-H., P. Tichavskỳ, and A. Cichocki (2013). Candecomp/parafac decomposition of high-order tensors through tensor reshaping. IEEE transactions on signal processing 61(19), 4847–4860.
- Rendeiro et al. (2020) Rendeiro, A. F., J. Casano, C. K. Vorkas, H. Singh, A. Morales, R. A. DeSimone, G. B. Ellsworth, R. Soave, S. N. Kapadia, K. Saito, et al. (2020). Longitudinal immune profiling of mild and severe covid-19 reveals innate and adaptive immune dysfunction and provides an early prediction tool for clinical progression. medRxiv.
- Sidiropoulos et al. (2017) Sidiropoulos, N. D., L. De Lathauwer, X. Fu, K. Huang, E. E. Papalexakis, and C. Faloutsos (2017). Tensor decomposition for signal processing and machine learning. IEEE Transactions on Signal Processing 65(13), 3551–3582.
- Sorkine et al. (2004) Sorkine, O., D. Cohen-Or, Y. Lipman, M. Alexa, C. Rössl, and H.-P. Seidel (2004). Laplacian surface editing. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, pp. 175–184.
- Tibshirani (2011) Tibshirani, R. (2011). Regression shrinkage and selection via the lasso: a retrospective. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73(3), 273–282.
- Tipping and Bishop (1999) Tipping, M. E. and C. M. Bishop (1999). Probabilistic principal component analysis. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 61(3), 611–622.
- Wang et al. (2019) Wang, D., X. Liu, and R. Chen (2019). Factor models for matrix-valued high-dimensional time series. Journal of econometrics 208(1), 231–248.
- Wang et al. (2021) Wang, D., Y. Zheng, H. Lian, and G. Li (2021). High-dimensional vector autoregressive time series modeling via tensor decomposition. Journal of the American Statistical Association, 1–19.
- Yao et al. (2005) Yao, F., H.-G. Müller, and J.-L. Wang (2005). Functional data analysis for sparse longitudinal data. Journal of the American statistical association 100(470), 577–590.
- Yokota et al. (2016) Yokota, T., Q. Zhao, and A. Cichocki (2016). Smooth parafac decomposition for tensor completion. IEEE Transactions on Signal Processing 64(20), 5423–5436.