$SO(10)$ SUSY GUTs with
mainly axion cold dark matter:
implications for cosmology and colliders

The idea of the Standard Model extended by weak scale broken supersymmetry (SUSY) is extremely attractive in that it stabilizes the weak scale against quantum corrections, and allows ultimately for an embedding in Grand Unified Theories (GUTs)dg . GUTs are also highly attractive in that they unify the disparate forces contained in the SM into (usually) a single gauge group. SUSY GUTs receive some well-known indirect support from experiment in that the three gauge couplings– when extrapolated up to $Q\sim 2\times 10^{16}$ GeV via the MSSM RGEsdrw – very nearly meet at a point!

The gauge group $SO(10)$ is especially compellingso10 . Not only does it unify the SM forces, but it also unifies the SM matter of each generation into the 16-dimensional spinor representation. This unification only works if there is in addition to the SM superfields, a gauge singlet $\hat{N}^{c}_{i}$, for generations $i=1-3$, which contains a right-hand neutrino state, as is required for see-saw neutrino massesseesaw . $SO(10)$ is naturally anomaly-free, thus explaining the otherwise ad-hoc anomaly cancellation in the SM or in $SU(5)$. In addition, $SO(10)$ provides a basis for $R$-parity conservation, in that only matter-matter-Higgs couplings are allowed, while the $R$-violating matter-Higgs or matter-matter-matter couplings are forbidden. If $SO(10)$ is broken properly, the $R$-parity survives as an exact symmetryspmartin . The simplest $SO(10)$ models also allow for Higgs unification, since both $H_{u}$ and $H_{d}$ live in the 10 of $SO(10)$. Finally, in the simplest models, we also expect $t-b-\tau$ third generation Yukawa coupling unification at $Q=M_{GUT}$. The above features have convinced many theorists that the main ideas behind $SO(10)$ SUSY GUTs are surely right (even while most or all explicit models in the literature are likely wrong).

Here, we will assume (motivated by gauge coupling unification) that the MSSM, or MSSM plus gauge singlets, is the correct effective field theory valid from $M_{weak}\sim 1$ TeV all the way up to $M_{GUT}\sim 2\times 10^{16}$ GeV. We will also require that the third generation $t-b-\tau$ Yukawa couplings should unify to reasonable ($\stackrel{{\scriptstyle<}}{{\sim}}5\%$) precision at $M_{GUT}$.

To test Yukawa unification, we scan over $SO(10)$-inspired SUSY parameter space:

Here, $m_{16}$ is the common matter-scalar mass at $M_{GUT}$, $m_{10}$ the common Higgs mass, $m_{1/2}$ the common gaugino mass and $A_{0}$ the common trilinear soft term. $M_{D}^{2}$ parametrizes the Higgs multiplet splittingmur , i.e. $m_{H_{u,d}}^{2}=m_{10}^{2}\mp 2M_{D}^{2}$ as is given by $D$-term mass contributions arising from the breaking of $SO(10)$. We will examine two cases: the “just-so” Higgs splitting (HS) model, where only the Higgs scalars split, and the DR3 model, where full scalar $D$-term splitting is invoked, along with right-hand neutrino contributions, and possible third generation scalar mass splitting (i.e. $m_{16}(3)\neq m_{16}(1,2)$ at $M_{GUT}$).

We use the Isajet/Isasugra sparticle mass spectrum calculatorisajet . This includes full two-loop RGEsmv , an RG-improved one-loop effective potential calculation (evaluated at an optimized scale to account for leading two-loop effects) and full 1-loop sparticle mass correctionspbmz . Especially important is including the weak scale $t$, $b$ and $\tau$ self energy corrections when transitioning from MSSM to SM effective theories; these depend on the entire superparticle mass spectrum, and are especially large for the $m_{b}$ correction at large $\tan\beta$hrs .

Exhaustive scans over parameter space reveal that $t-b-\tau$ Yukawa unification only occurs when the following conditions are metbf ; bdr ; us :

• •

  $A_{0}^{2}=2m_{10}^{2}=4m_{16}^{2}$, with

• •

  $m_{16}\sim 8-20$ TeV,

• •

  $m_{1/2}$ very small $\sim 20-100$ GeV),

• •

  $\tan\beta\sim 50$

• •

  $m_{D}^{2}>0$.

These conditions, derived earlier by Bagger et al.bfpz , yield a radiatively driven inverted scalar mass hierarchy (RIMH). The physical sparticle mass spectrum is then given by

• •

  first/second generation squarks and sleptons $\sim 8-20$ TeV,

• •

  third generation squarks, sleptons, $m_{A}$ and $\mu$: $\sim 1-2$ TeV,

• •

  light gauginos with $m_{\tilde{g}}\sim 300-500$ GeV, $m_{\tilde{\chi}^{\pm}_{1}}\sim 100-180$ GeV and $m_{\tilde{\chi}^{0}_{1}}\sim 50-80$ GeV.

The heavy first/second generation squarks and sleptons can act to suppress possible SUSY FCNC and $CP$ violating interactions, and proton decay. The much lighter third generation scalars meet the needs for technical naturalness. Note that Yukawa-unified SUSY provides a viable realization of the “effective SUSY” scenario put forth by Cohen, Kaplan and Nelsonckn , while maintaining the MSSM as the correct effective theory all the way up to $M_{GUT}$.

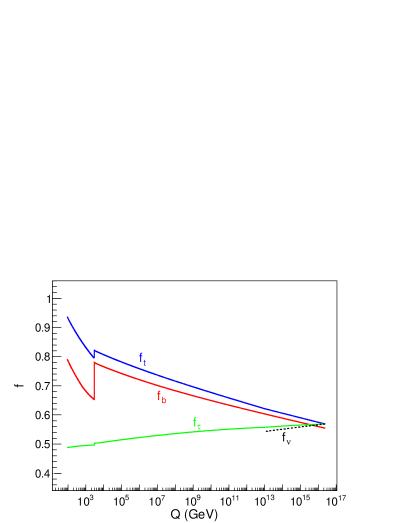
The HS model is found to give many cases with exact $t-b-\tau$ unificationbdr ; us (which is perhaps better than expected, given the theoretical uncertainties of the perturbative calculations). The DR3 modeldr3 , with full $D$-term splitting, can give Yukawa unification down to the 2% level, but only if neutrino Yukawa running is included down to $Q\sim 10^{13}$ GeV (as suggested by neutrino mass difference measurements), and there is a small first/third generation scalar splitting at $M_{GUT}$. An example case is shown in Fig. 1.

If SUSY is broken in gravity mediation, then one expects the scalar masses to be directly related to the gravitino mass. In this case, $m_{3/2}\sim 8-20$ TeV as well. This range of $m_{3/2}$ solves a major portion of the cosmological gravitino problem: such a heavy gravitino will have a lifetime less than 1 secondmoroi , so that it decays just before the onset of BBN. Thus, this model should be BBN safe, and should allow for a re-heat temperature $T_{R}\sim 10^{6}-10^{9}$ GeV. While this $T_{R}$ value is not enough to sustain thermal leptogenesis as a baryogenesis mechanism, it is enough to sustain non-thermal leptogenesis, wherein right hand neutrinos are produced via inflaton decay, or Affleck-Dine leptogenesis.

The above mass spectrum predicted by Yukawa-unified SUSY has many desirable features. However, if we calculate the thermally produced relic abundance of neutralinos (we use IsaReDisared ), we find $\Omega_{\tilde{\chi}^{0}_{1}}h^{2}\sim 10^{2}-10^{4}$, i.e. 3-5 orders of magnitude higher than the measured valuerelic !

At this point, we have totally neglected (at our peril!) the strong $CP$ problem. If we invoke the PQWWpqww solution to the strong CP problem with an “invisible” axioninvax , then we must include the axion/axino supermultiplet in the theory. The QCD axion has mass $m_{a}\sim 10^{-6}-10^{-3}$ eV according to astrophysical/cosmological constraints. The axino $\tilde{a}$ is $R$-parity odd, and can serve as the LSPrtw . Its mass is relatively unconstrained, and can span the keV$\rightarrow$ GeV range. If $m_{\tilde{a}}\sim$ MeV range, then $\tilde{\chi}^{0}_{1}\rightarrow\tilde{a}\gamma$ with a lifetime typically less than 1 second (BBN safe). Each thermally produced neutralino will decay to exactly one axino, and the (non-thermally produced) axino abundance will be $\Omega_{\tilde{a}}^{NTP}h^{2}=\frac{m_{\tilde{a}}}{m_{\tilde{\chi}^{0}_{1}}}\Omega_{\tilde{\chi}^{0}_{1}}h^{2}$ckkr : the ratio of masses yields a factor $\sim 10^{-3}-10^{-5}$, and can completely wipe out the neutralino overabundance. These decay-produced MeV-scale axinos would likely constitute warm dark matterjlm .

The axinos can also be produced thermally via scattering off quarks and gluons early on in the cosmic soup. The abundance depends on the axino mass, the PQ breaking scale $f_{a}$ and the re-heat temperature $T_{R}$ after inflationckkr ; bsteff . The thermally produced axinos will constitute cold dark matter so long as $m_{\tilde{a}}\stackrel{{\scriptstyle>}}{{\sim}}0.1$ MeV.

A third dark matter component comes as usual from vacuum misalignment production of cold axions, as shown by Sikivie and othersas . This contribution $\Omega_{a}h^{2}$ depends on the PQ scale $f_{a}$ (or alternatively the axion mass) and the initial mis-alignment angle $\theta_{i}$.

The total dark matter abundance in the PQMSSM model comes from three components:

We examined Yukawa-unified SUSY models with both low and high values of $f_{a}$ and $m_{\tilde{a}}$bhkss . By enforcing $\Omega_{DM}h^{2}=0.1$ as measured by WMAP, we can extract the required re-heat temperature. The values of $T_{R}$ can range easily between $10^{6}-10^{8}$ GeV, thus being in the range required by the gravitino problem, and also allowing for non-thermal or Affleck-Dine leptogenesis!

The Yukawa-unified SUSY model predicts a rather light gluino with $m_{\tilde{g}}\sim 300-500$ GeV. In standard SUSY models with gaugino mass unification, the LEP2 limit on $m_{\tilde{\chi}^{\pm}_{1}}>103.5$ GeV implies $m_{\tilde{g}}\stackrel{{\scriptstyle>}}{{\sim}}420$ GeV, which is somewhat beyond Tevatron reach. However, in Yukawa-unified SUSY, the huge $A_{0}\sim 20$ TeV parameter feeds into gaugino mass evolution via two-loop RGEs to suppress the gap between the $SU(2)$ and $SU(3)$ gaugino masses $M_{2}$ and $M_{3}$. Thus, in Yukawa-unified SUSY, $m_{\tilde{g}}$ can be as low as $\sim 300$ GeV while respecting the LEP2 chargino limit. Also, the huge first generation squark masses actually suppress negative interference in the $q\bar{q}\rightarrow\tilde{g}\tilde{g}$ production cross section, thus raising the $\tilde{g}\tilde{g}$ production cross section at the Tevatron by factors of 3-10 beyond standard calculations! Finally, the $\tilde{g}$ decays nearly 100% of the time via 3-body modes into $b$-quarks. Thus, four or more $b$-jets are expected in each final state. By requiring $n_{b}\geq 2$ or even $n_{b}\geq 3$, SM backgrounds are highly suppressed. Detailed calculations find a 5 fb^-1 reach of Tevatron to $m_{\tilde{g}}\sim 400$ GeVtev . This probes the most favored portion of Yukawa-unified parameter space, since Yukawa-unification worsens as $m_{\tilde{g}}$ increases. This search is strongly recommended for CDF and D0!

At the $\sqrt{s}=7$ TeV LHC, the $pp\rightarrow\tilde{g}\tilde{g}X$ cross section ranges between 2000-6000 fb, and occurs mainly via $gg$ annihilation. The events should again be characterized by high $b$-jet multiplicity. In addition, the decay $\tilde{g}\rightarrow b\bar{b}\tilde{\chi}^{0}_{2}$ followed by $\tilde{\chi}^{0}_{2}\rightarrow\tilde{\chi}^{0}_{1}\ell^{+}\ell^{-}$ can occur at a large rate. In this case, the $m(\ell^{+}\ell^{-})$ distribution for SF/OS dileptons should have a characteristic mass bump followed by an edge at $m_{\tilde{\chi}^{0}_{2}}-m_{\tilde{\chi}^{0}_{1}}$: see Fig. 2. Since this mass gap is typically bounded by about 90 GeV, the bump/edge should sit between the $\gamma$ and $Z$ peaks, and should be easily visible even with very low integrated luminosity $\sim 0.1$ fb^-1. An estimate of the $\sqrt{s}=7$ TeV LHC reach with just 0.1 fb^-1 of integrated luminosity, and not using $E_{T}^{\rm miss}$ cuts, is to $m_{\tilde{g}}\sim 400$ GeV. With 1 fb^-1 of integrated luminosity, which is now anticipated in LHC run 1, the reach using $E_{T}^{\rm miss}$ cuts is to $m_{\tilde{g}}\sim 630$ GeV. Thus, it is expected that LHC will be able to either discover or rule out Yukawa-unified SUSY during its first run at $\sqrt{s}=7$ TeV! This search is strongly recommended for Atlas and CMS!

Finally, since a large value of $f_{a}$ is favored cosmologically, we would expect the axion/axino abundance to be mainly mis-alignment produced axions. Thus, we can anticipate a possible axion discovery by ADMXadmx in the years to come, if Yukawa-unified SUSY is correct.

The Yukawa-unified SUSY scenario invokes IMO the four greatest ideas in physics beyond the SM: grand unification, supersymmetry, see-saw neutrino masses and the PQWW axion solution to the strong CP problem. Yukawa-unified SUSY with mixed axion/axino CDM also solves several cosmological problems, and is consistent with low energy realizations of the fifth greatest idea: string theoryraby . The immediate prediction is a rather light gluino with $m_{\tilde{g}}\sim 300-500$ GeV which decays via three-body modes into mainly $b$-quarks: it should be observable in the next year or two via Tevatron and LHC run 1 data. A positive signal would also be likely at the ADMX experiment.