Solar Wind Structures from the Gaussianity of Magnetic Magnitude
Abstract
One of the primary science objectives of Parker Solar Probe (PSP) is to determine the structures and dynamics of the plasma and magnetic fields at the sources of the solar wind. However, establishing the connection between in situ measurements and structures and dynamics in the solar atmosphere is challenging: most of the magnetic footpoint mapping techniques have significant uncertainties in the source localization of a plasma parcel observed in situ, and the PSP plasma measurements suffer from a limited field of view. Therefore it is of interest to investigate whether in situ measurements can be used on their own to identify streams originating from the same structures in the corona more finely than the well known fast wind-coronal hole, slow wind-elsewhere distinction. Here we develop a novel time series visualization method (time-frequency representation or TFR) named Gaussianity Scalogram. Utilizing this method, by analyzing the magnetic magnitude data from both PSP and Ulysses, we successfully identify in situ structures that are possible remnants of solar atmospheric and magnetic structures spanning more than seven orders of magnitude, from years to seconds, including polar and mid-latitude coronal holes, as well as structures compatible with super-granulation , “jetlets” and “picoflares”. Furthermore, computer simulations of Alfvénic turbulence successfully reproduce the Gaussianization of the magnetic magnitude for locally homogeneous structures. Building upon these discoveries, the Gaussianity Scalogram can help future studies to reveal the fractal-like fine structures in the solar wind time series from both PSP and decades-old data archive.
1 Introduction
The solar atmosphere is highly structured both spatially and temporally (Bale et al., 2019; Kasper et al., 2019). Recent studies have successfully established connections between PSP (Fox et al. (2016) and see Raouafi et al. (2023a) for a review for results of the first four years of the mission) in situ observations and solar atmospheric structures including mid-latitude coronal holes (Badman et al., 2023; Davis et al., 2023), pseudostreamers (Kasper et al., 2021), and supergranulation (Bale et al., 2021; Fargette et al., 2021; Bale et al., 2023), even though alternative explanations remain (Shi et al., 2022). Recent advances in remote sensing provide strong support for the minutes long small-scale jetting activity from magnetic reconnection (“jetlets”) as a major source of the solar wind (Raouafi et al., 2023b). In addition, EUV observations from Solar Orbiter (Müller et al., 2020) unveiled ubiquitous brightening termed “picoflare” (Chitta et al., 2023) with associated jets that last only a few tens of seconds, suggesting the solar wind source might be highly intermittent. However, magnetic footpoint mapping methods (Badman et al., 2020; Panasenco et al., 2020; Badman et al., 2023) use photospheric magnetic field observations over the whole visible disk that are refreshed at best once every six hours and lack, of course, any real temporal reliability for the far side. Therefore, such methods are hardly able to reliably contextualize and explain the boundaries of the highly structured solar wind in situ time series, except perhaps in a statistical sense.
Previous studies on the distribution of solar wind parameters primarily focused on the statistical properties of the solar wind magnetic field and plasma moments at 1 AU and beyond. For example, Whang (1977) and Padhye et al. (2001) found that the magnetic field components follow near-Gaussian distributions, and Bandyopadhyay et al. (2020) showed similar properties in Earth’s magnetosheath turbulence. For the magnetic field magnitude, Burlaga & Lazarus (2000) and Burlaga (2001) demonstrated that it generally follows a log-normal distribution. On the simulation side, Yamamoto & Kambe (1991) conducted a 3D hydrodynamic simulation and found that the velocity components follow a Gaussian distribution at small wave numbers and a long-tail distribution at larger wave numbers. It is hence empirically expected that the magnetic field components follow a Gaussian distribution, and thus the magnetic magnitude follows a or Maxwell-Boltzmann distribution. However, for the solar wind measured at PSP perihelion distances, the distributions of magnetic field components generally deviate significantly from Gaussian due to the presence of large amplitude spherically polarized Alfvén waves (i.e., switchbacks, see e.g., Bale et al. (2019); Larosa et al. (2021); Drake et al. (2021); Dudok de Wit et al. (2020); Shi et al. (2022); Bale et al. (2023)). Therefore, it is not expected from any of the previous studies that the magnetic magnitude should follow a Gaussian distribution or any known distributions.
Contrary to previous attempts, using a data mining approach, this study starts by reporting an unexpected property of the solar wind magnetic field. We find that the magnetic magnitude , once normalized by a power law fit with regard to the heliocentric distance, occasionally exhibits perfect Gaussian distributions. Based on this discovery, we introduce a novel time series visualization method (time-frequency representation or TFR) named Gaussianity Scalogram (GS) to visualize the spatial-scale (time-frequency) dependent Gaussianity of . Applying this method to data from PSP and Ulysses, we find that the Gaussian intervals successfully map to the in situ remnants of coronal holes (Badman et al., 2023; Davis et al., 2023) and switchback patches (Bale et al., 2021; Shi et al., 2022; Bale et al., 2023). On smaller scales, Gaussian intervals map to structures that are temporally compatible with small-scale jetting activity, including ”jetlets” and ”picoflares” (Raouafi et al., 2023b; Chitta et al., 2023). The rest of the paper is structured as follows: In the next section, we describe the helio-radial power law fit and the construction of GS; in Section 3, we present some applications of GS; in Section 4, we discuss the computer simulation of Gaussianization of in MHD turbulence and the major implications; in Section 5, we conclude and summarize our results.
2 Helioradial Dependence of and the Gaussianity Scalogram
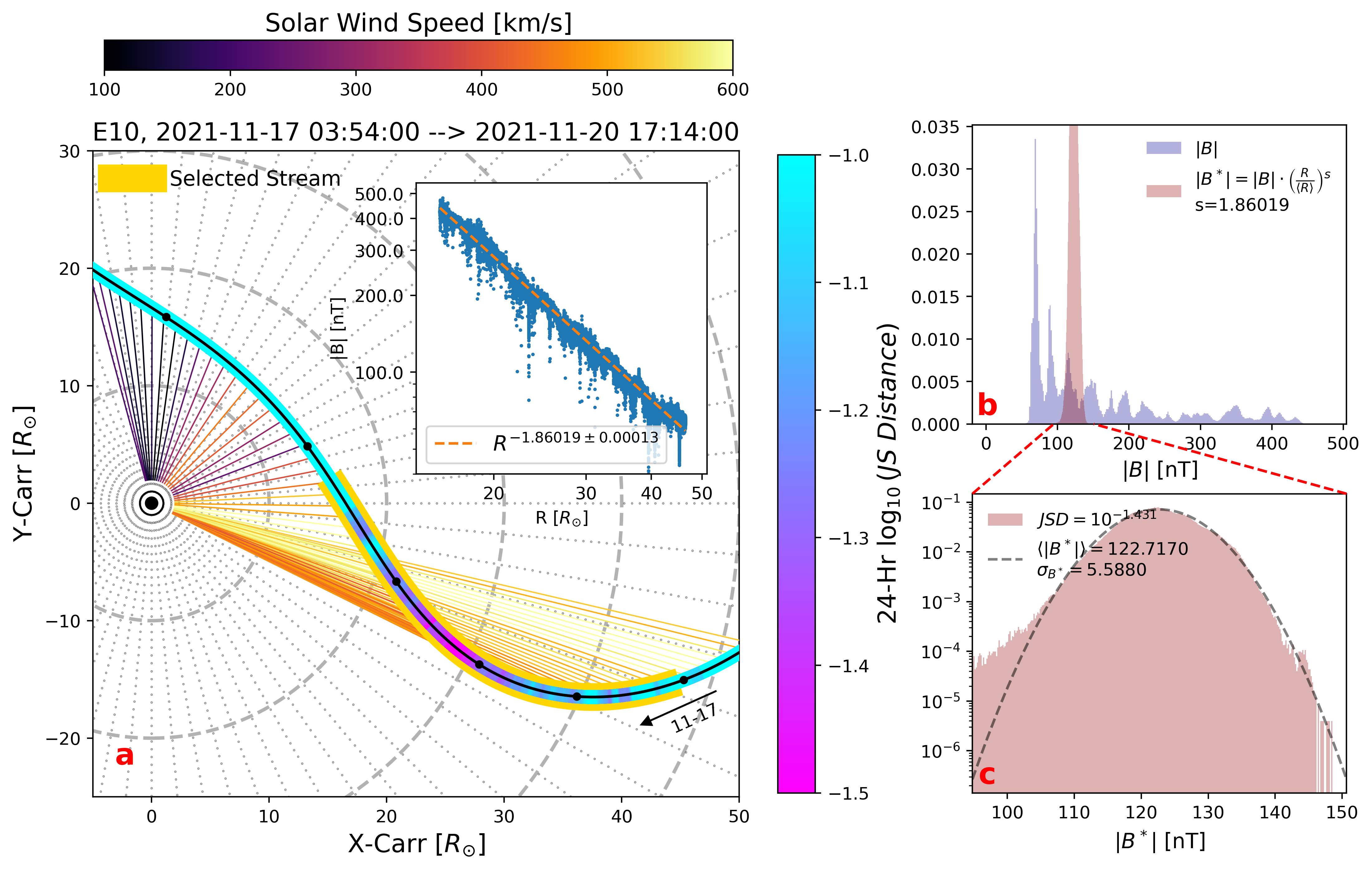
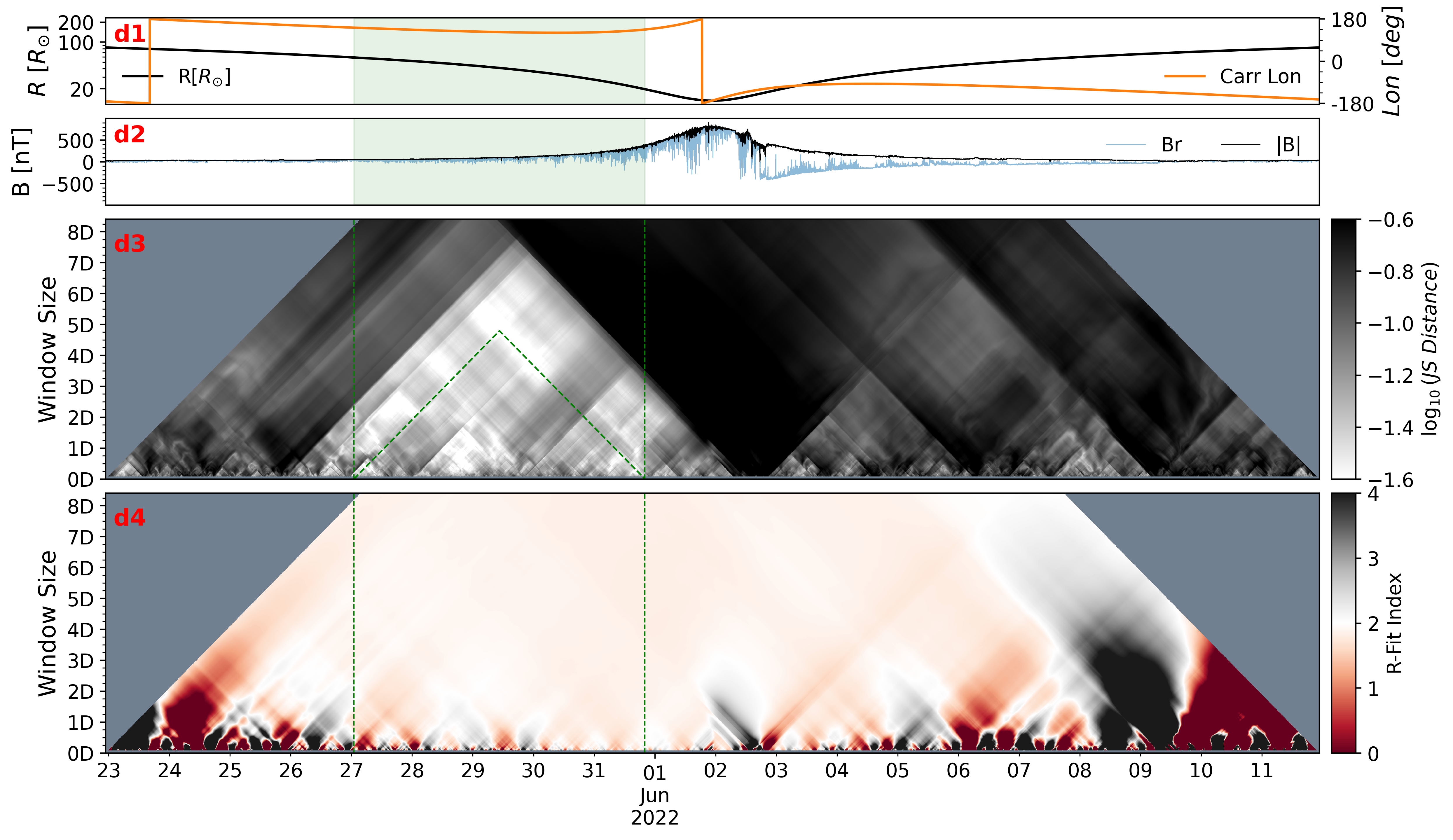
Two of the most interesting yet overlooked features of the time series of the solar wind magnetic field magnitude are that: 1. Sometimes displays a surprisingly stable power law dependence on the heliocentric distance ; 2. By applying a helio-radial power law fit between and , i.e. , the fit normalized magnetic magnitude sometimes displays a near-perfect Gaussian distribution. This is illustrated in Figure 1 (a-c), where the selected interval is highlighted with a golden bar in panel (a) and the helio-radial power law fit (fit index ) is shown in the inset figure. The histogram of is shown in blue in panel (b) and the normalized is shown in red. To illustrate the close proximity of the probability density function of () to a Gaussian distribution (), a standard Gaussian curve is overplotted in panel (c) (shifted with the mean value and scaled with the standard deviation ). The Jensen-Shannon Distance (JSD) of base (a statistical distance metric between probability density functions (Lin, 1991)) is calculated between and , and the value is , indicating considerable closeness between two distribution functions (for benchmark, see appendix). In addition, this highly Gaussian interval coincides with the radial solar wind speed profile which is visualized with radial colored lines in panel (a) and Figure 9 (c) (compiled with SPAN-ion from SWEAP suite Kasper et al. (2016)). From Nov-17 to Nov-20, the spacecraft was immersed in the high speed solar wind, indicating its coronal hole origin. The JSD produced by this process is represented as one pixel (tip of the green pyramid) in the Gaussianity Scalogram (GS) shown in panel (d3), and the scalogram for the corresponding helio-radial power law fit index is displayed in panel (d4).
Each pixel in the GS is characterized by a timestamp () and window size (), similar to wavelet scalogram. Uniquely in GS, the step size in (vertical axis) is chosen to be twice the step size in (horizontal axis), and thus the time range covered by one pixel corresponds to the same time range covered by three pixels in the following row, and so on towards the smallest scales. Therefore, if an interval and the nested sub-intervals possess similar characteristics (e.g. relatively small JSD regardless of and within the interval), a pyramidal structure is expected from the GS, and the base of the pyramid indicates the start and end time of the interval. One example is highlighted by the green dashed pyramid in panel (d3), where the tip of the pyramid is in fact selected a posteriori as the local minimum in the GS ( being closest to Gaussian among the surrounding time and scales). Ample information can be inferred from the GS: 1. A semi-crossing of the heliospheric current sheet (HCS) at noon of Nov-22 is visualized as an inverted black pyramid. This is because the rapid drop of during HCS crossing can significantly destroy its Gaussianity; 2. It has been confirmed recently by Badman et al. (2023) that the solar wind can be traced back to a single mid-latitude coronal hole from Nov-17 to the end of Nov-20, and from another coronal hole for the whole day of Nov-21 (see also Bale et al. (2023); Panasenco et al. (2020); Badman et al. (2020)). The coronal holes are naturally visualized here as two white pyramids (green and red dashed lines) separated by a dark region around the mid-night of Nov-20; 3. The helio-radial power law fit index is unexpectedly stable regardless of locations and scales and systematically deviates from () (see also Bale et al. (2019)).
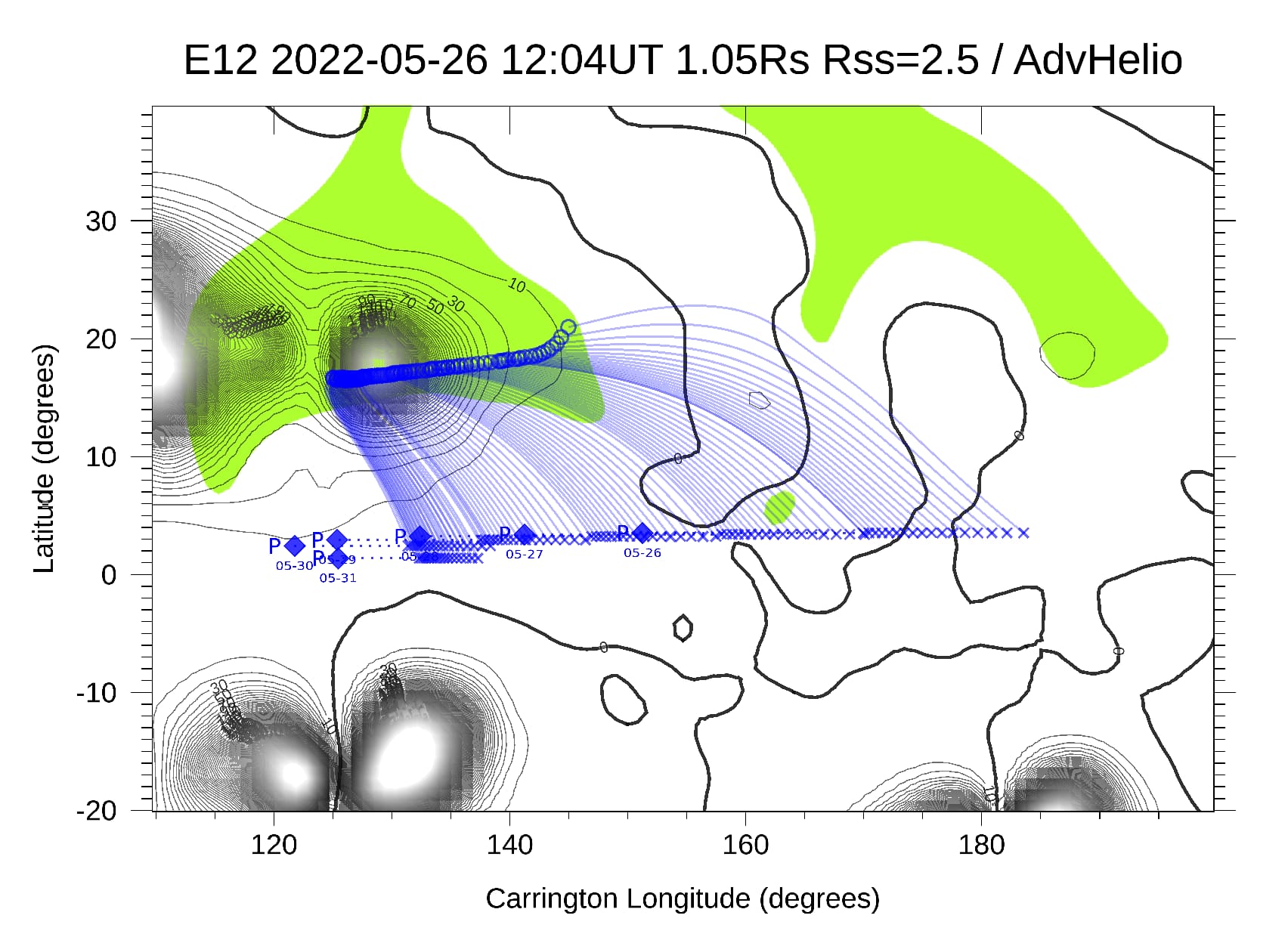
The clear correspondence between the white pyramid and coronal hole encourages us to predict intervals of solar wind originating from coronal holes with GS compiled from PSP data. Among the first 14 encounters (Nov-2018 to Dec-2022), we only identified one more (for a total of 2) long intervals ( 3 days) characterized by high Gaussianity in . A panoramic view of these two long intervals is shown in Figure 9. The newly found interval from the inbound of E12, shown in Figure 10 and Figure 9 (d), is characterized by a 5-day long highly Gaussian time series. For illustration purpose, the green pyramid in Figure 10 (d3) is selected as the deepest local minimum in GS for 3 days. The histogram of is remarkably concentrated (panel (b)) and aligns with Gaussian almost perfectly within 4 standard deviation (panel (c)). Similar to Figure 1 (c), the non-Gaussian part of has a systematic bias towards magnetic holes (weaker magnetic magnitudes, for recent studies using PSP data see e.g. Yu et al. (2021, 2022)), and the helio-radial power law fit index scalogram also shows a systematic deviation from , similarly . To validate this prediction, independent results from Potential Field Source Surface (PFSS) modeling is shown in Figure 2 (see Panasenco et al. (2020) for more details), which indicates that the selected interval is indeed magnetically connected to a mid-latitude coronal hole.

3 Fractal-Like Gaussian Structures in the Solar Wind
To substantiate the applications of GS, here we demonstrate several examples that visualize the fractal-like Gaussian structures in the solar wind (Due to the rapid movement of PSP around perihelia, the structures in the in situ time series can be categorized into two kinds. Spatial: longitudinal structures traversed by PSP; Temporal (radial): radial structures advected by the solar wind and/or propagation of Alfvén waves) based on Taylor Hypothesis (Perez et al., 2021). From the largest scales: Ulysses, years-long polar coronal hole (McComas et al., 2003), towards the smaller scales: hour-long switchback patches (Bale et al., 2021; Fargette et al., 2021; Shi et al., 2022; Bale et al., 2023); minutes-long structures compatible with “jetlets” Raouafi et al. (2023b); and second-long structures compatible with “picoflare” Chitta et al. (2023).
Figure 3 shows the GS of the first Ulysses orbit, and the colorbar in panel (b) is enhanced compared to Figure 1 (d3) for illustration purposes. The solar latitude and wind speed profile in panel (a) indicate that the spacecraft was in southern and northern polar coronal holes in the whole year of 1994, and from 1995 to 1997 (see also McComas et al. (2003)). The two large white pyramids in the GS clearly correspond to the two polar coronal holes. Notably, the boundary observed in panel (b) results from an artificial cut-off in the helio-radial power law fit, as shown in panel (c). The cut-off value is chosen to be , below which the spacecraft is considered stationary, and is not normalized to using helio-radial power law fit prior to the calculation of Gaussianity. However, the Gaussianity is much weaker in the polar coronal holes compared to the mid-latitude coronal holes observed by PSP at much smaller heliocentric distance, and the histograms of magnetic magnitude show much more significant fat tail towards the magnetic holes side (not shown here). This indicates that the Gaussianity of magnetic magnitudes decreases with increasing heliocentric distance, possibly due to the transition from low- to high- environment ( is the ratio between plasma thermal pressure and magnetic pressure ), and the plasma thermal pressure hence has a larger influence on the distribution of . Additionally this also indicates that magnetic holes are much more preferred than spikes in the solar wind plasma.
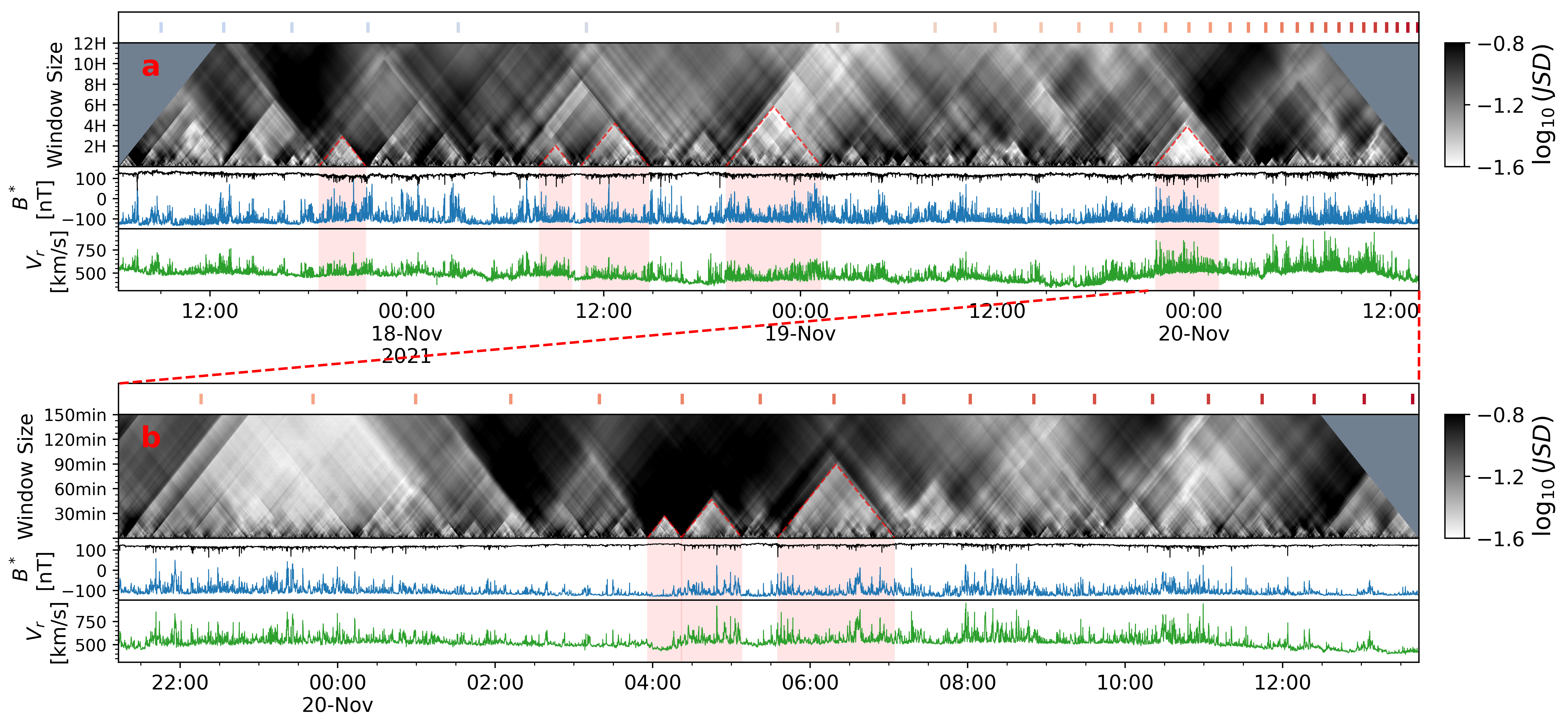
Figure 4 shows the hour-long switchback patches from a single mid-latitude coronal hole in PSP E10, which have been recently proposed to be the remnants of the supergranulations in the solar atmosphere (Bale et al., 2021; Fargette et al., 2021; Bale et al., 2023). To indicate the spacecraft movement, the Carrington longitude of PSP is plotted every one degree on the top bars of both panels (a) and (b), and the color indicates spacecraft angular velocity in the corotating frame (blue: prograde, red: retrograde, see also Figure 1 for PSP trajectory in the corotating frame at the same perihelion). The magnetic magnitude is normalized with a universal helio-radial power law fit index () and the GS is compiled with the high-resolution fluxgate magnetic data ( 292 Hz, see Bale et al. (2016); Bowen et al. (2020)). The red dashed pyramids in panel (a) and (b) are drawn to highlight the intervals with high level of Gaussianity. The selected intervals in panel (a) show that the GS effectively captures some of the switchback patches. When these are compared with the Carrington longitude, it becomes evident that some of the structures align with the size of supergranulation, as discussed in Bale et al. (2023). However, other structures, which are smaller in angular size and likely temporal in nature, could be more accurately attributed to the ’breathing’ phenomenon of the solar wind, as explained in Berger et al. (2017); Shi et al. (2022). After the “fast radial scan” phase on Nov-18, the spacecraft began to rapidly retrograde on Nov-19 and Nov-20 (see Figure 1 (a) for the spacecraft trajectory in the corotating frame). For better comparison, an expanded view is shown in panel (b). The second and third pyramids also show decent capability of capturing the switchback patches, whereas the first pyramid seems to capture a boundary between the patches. Starting from 7:00 on Nov-20, the remaining patches consistently exhibit a high level of Gaussianity across all scales and locations, resulting in indistinct boundaries between them.
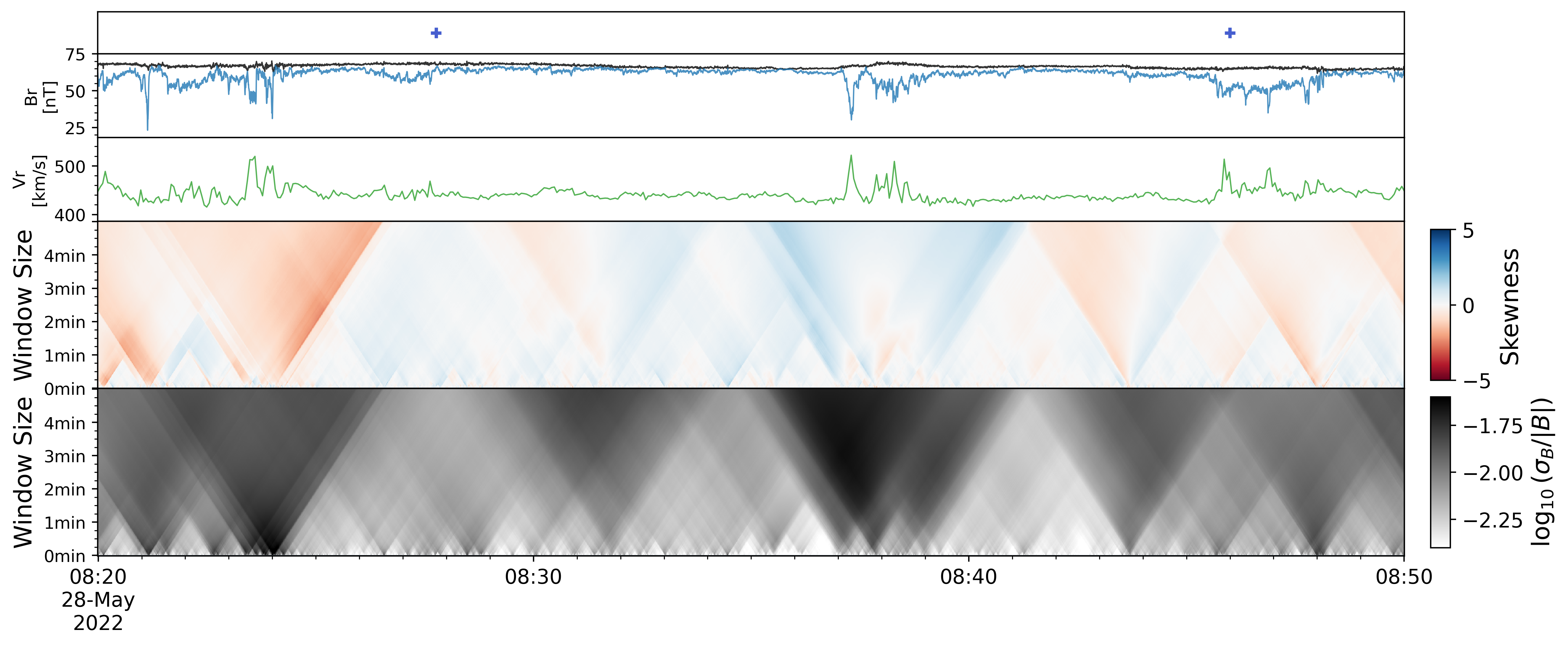
Figure 5 presents a hierarchic GS of the mid-latitude coronal hole from the inbound of PSP E12. In panels (d) and (e), focusing on the smallest scales resolvable by the JSD (approximately 1 minute, corresponding to around 20,000 data points for the shortest interval. For details on how the number of data points influences this analysis, see Appendix), we observe a surprising number of structures with distinct boundaries. In fact, these structures, typically lasting 1-10 minutes, are omnipresent in the Alfvénic solar wind for all PSP encounters. Notably, they are not limited to winds with a clear coronal hole origin, such as those in the outbound paths of E12 (for more details, see the video in the supplementary materials). These structures are typically separated (interrupted) by radial jets (i.e. individual switchbacks), and these separations are frequently accompanied by close to kinetic scale ( 5 seconds) fluctuations that are bursty and short-lived in all three components of magnetic field. For further illustration, refer to the skewness scalogram video in the supplementary materials. Unlike the spatial structures shown in panels (a), (b), and (c) (as well as in Figure 1 and Figure 3), the longitude change of the spacecraft for each structure in panel (d) and (e) is less than 0.1 degree, as indicated by the crosses plotted every 0.1 Carrington longitude in the top bar. Therefore, these structures are likely temporal, i.e. advected by the solar wind. All of these features are highly compatible with the “jetlets” observed in equatorial coronal holes (Raouafi et al., 2023b), and therefore could potentially be the “building blocks” of the solar wind. In fact, even finer structures can be found with the normalized standard deviation () scalogram and skewness scalogram shown in Figure 11. For example, the small white pyramid around 8:36 in Figure 5e has two 30-seconds long substructures nested beneath in Figure 11. These seconds-long structures are intervals with smaller standard deviation compared to the surroundings, and their interruptions are temporally compatible with the “picoflare” (Chitta et al., 2023).
4 Discussion
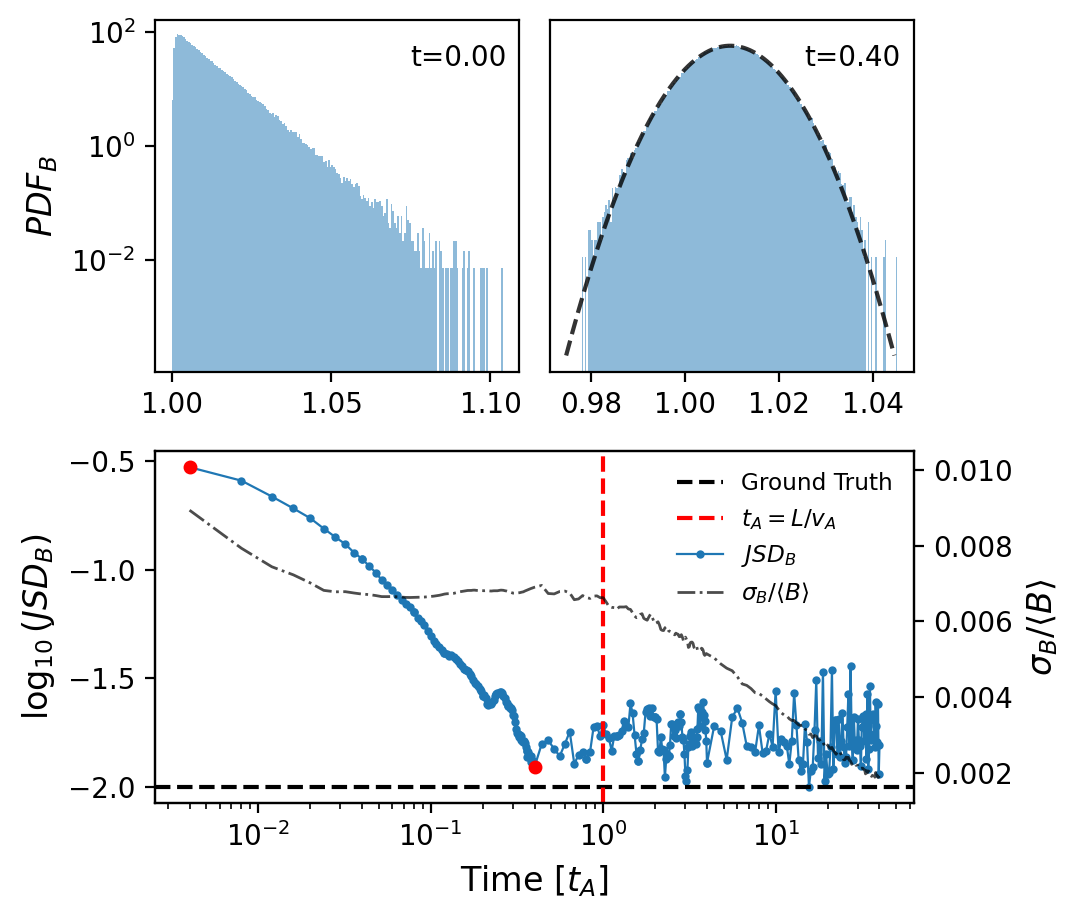
These observations indicate that the Alfvénic solar wind is permeated with highly Gaussian magnetic magnitude intervals that are often interrupted by radial jets (switchbacks) every 1-10 minutes. In addition, the magnetic fluctuations inside the intervals often resemble the small amplitude outward propagating linear Alfvén waves. It is therefore reasonable to model the system using small amplitude Alfvénic MHD turbulence. Figure 6 shows the temporal evolution of the of a 3D MHD small amplitude Alfvénic turbulence simulation (Shi et al., 2023). The simulation is run with periodic box, and is initialized with unidirectional small amplitude linearly polarized Alfvén waves with isotropic wave vector spectrum (see Methods section for more details). At (Alfvén crossing time , where is the simulation box size), deviates significantly from a Gaussian distribution due to the small amplitude shear Alfvén wave initialization (fluctuations in are positive definite). The corresponding JSD is highlighted as the first red dot in the lower panel and is much larger than 0. Surprisingly, within one Alfvén crossing time at , the distribution of rapidly relaxes to a near-perfect Gaussian distribution, and the JSD rapidly drops towards the ground truth value (see Benchmark in Methods). As the simulation evolves, the JSD remains considerably small and thus the distribution of remains very close to Gaussian. The simulation indicates that Gaussian is the natural relaxation state for magnetic magnitude in small amplitude Alfvénic turbulence, consistent with the ubiquitous 1-10 minutes Gaussian intervals found in the solar wind. However, a 3D analytical model of a switchback with constant magnetic magnitude and fully open field lines is not yet available (see Tenerani et al. (2020); Squire & Mallet (2022); Shi et al. (2024b); Matteini et al. (2024) for recent progress on switchback modeling). Therefore, our simulation can not reproduce the realistic physical condition of the solar wind turbulence in which large amplitude spherically polarized Alfvénic fluctuations dominate.
Nevertheless, the simulation suggests that information is fully exchanged within the system, as it propagates at Alfvén speed throughout the simulation box. This allows to relax to a Gaussian distribution, which occurs within about 0.5 , i.e. the time it takes for Alfvén waves to carry information from the center of the simulation box to its edges. This is indicative of a dynamic Gaussianization of in MHD turbulence, which requires MHD waves to facilitate this process due to causality in this physical system. However, for the hours and days long interval, the physical distance PSP and Ulysses trajectories covered are often degrees or tens of degrees apart in Carrington longitude (and latitude). Due to the lack of perpendicular information carrier, plasma that is degrees of Carrington longitude apart should not be considered as part of the same turbulent plasma parcel, and thus our simulation does not apply to such situation.
Therefore, alternative explanations are necessary for the observed hour-long (and longer) Gaussian structures. The simplest explanation for the Gaussian structures originating from coronal holes (mid-latitude coronal holes from E10 and E12, and polar coronal holes from Ulysses) is the pressure balance between the open coronal field lines. Close to the sun, the solar wind originating from the coronal holes is mostly magnetic dominant (plasma , see e.g. (Kasper et al., 2021)). To maintain pressure balance, the open field lines from the same coronal hole tend to evolve to a state in which the magnetic pressure is mostly uniform for a given cross section of the magnetic flux tube. In Figure 1, the helio-radial power law normalization of essentially maps the magnetic field line density, which is effectively the magnetic flux density due to the spherical polarization of the Alfvén waves, from various radial distances and transverse locations to a single cross-section of the flux tube (for more details of spherical polarization of Alfvén waves, see the appendix and Matteini et al. (2014, 2015)). As a support of this idea, from the PSP observations of E10 and E12 (Figure 1 and Figure 10), the helio-radial power law normalization of effectively collapses the histogram of into a delta-function-like histogram of . This is indicative of identical field line density within a single coronal hole due to the magnetic pressure balance. The detailed distribution of is hence the feature of the noise in magnetic magnitude within a single coronal hole, which can be considered as a one-dimensional random walk (continuous addition of small amplitude random fluctuations that can be considered as samples drawn from the same stochastic source throughout its passage from the base of the corona to the spacecraft). Therefore, the Gaussian distribution of can be easily explained as the result of the stopped random walk according to central limit theorem. Nevertheless, difficulties remain for the physical origin of the hour-long structures. They may be the manifestation of the denser field line density originating from a single supergranule based on its connection with switchback patches, but a more detailed discussion lies beyond the scope of this study.
Finally, the existence of a stable power law dependence of with regard to heliocentric distance itself already sheds light on the physics of the solar wind originating from coronal holes. As solar activities ramp up for solar cycle 25, 4 out of the 5 recent encounters (E10, E11, E12, E14) of PSP show systematic preference for a single helio-radial power law index, which consistently deviates from . However, the power law, expected only from the dominant radial component as a result of the Parker Spiral (conservation of magnetic flux in spherical expansion), is not strictly applicable to , especially for PSP, due to the ubiquitous switchbacks. Due to the relation between and the local magnetic flux density, this is indicative of a stable expansion rate for the magnetic flux tube in the magnetic dominant wind () close to the sun. Such an expansion rate is crucial for the estimation of the WKB evolution of the fluctuation quantities like the magnetic and velocity field (Hollweg, 1973; Heinemann & Olbert, 1980; Velli et al., 1991; Huang et al., 2022). It should be noted that the fit indices of coincide with the helio-radial dependence of the electron density compiled from Quasi Thermal Noise (Kruparova et al., 2023; Moncuquet et al., 2020), indicating that the deviation from could be the evidence of active acceleration of the solar wind.
5 Conclusion and Summary
Compiled from the almost featureless magnetic magnitude time series from the solar wind, the Gaussianity Scalogram (GS) unveils a striking number of fractal-like magnetic structures spanning across over seven orders of magnitude in time. These structures include spatial structures like polar coronal holes (McComas et al., 2003), mid-latitude coronal holes (Badman et al., 2023), and switchback patches (Bale et al., 2023). They also include temporal structures compatible with “jetlets” (Raouafi et al., 2023b) and “picoflare” (Chitta et al., 2023), which are often interrupted by the radial jets (switchbacks). In addition, three-dimensional MHD simulations have shown that Gaussian is the natural relaxation state for small amplitude unidirectional Alfvénic turbulence. The minute-long structures are hence likely to be the natural products of Alfvénic MHD turbulence. Thus, it is now clear that the Alfvénic solar wind is permeated with these intermittent Gaussian structures, which are self-similarly organized from seconds to years, and are possibly the remnants of the magnetic structures on the solar surface (Uritsky & Davila, 2012; Aschwanden, 2011; Aschwanden et al., 2016; Bale et al., 2023; Raouafi et al., 2023b; Chitta et al., 2023). This paper reveals just a fraction of the rich structures uncovered by the GS from the solar wind time series. The GS proves to be a versatile tool, essential not only for deciphering the structure and dynamics of plasma and magnetic fields, one of the key objectives of the PSP mission (Fox et al., 2016), but also for revitalizing decades-old solar wind data from missions like Helios, Ulysses, and WIND. These efforts unveil new physics previously hidden within these data sets. Additionally, the GS applicability may extend beyond solar wind analysis, potentially serving other kinds of high resolution stochastic time series data.
Acknowledgment
Z.H. thanks Jiace Sun, Benjamin Chandran, Anna Tenerani, Victor Réville for valuable discussions. C.S. is supported by NSF SHINE #2229566. C.S. acknowledges the support of Extreme Science and Engineering Discovery Environment (XSEDE) EXPANSE at SDSC through allocation No. TG-AST200031, which is funded by National Science Foundation grant number ACI-1548562 (J. Towns et al., 2014). C.S. also acknowledges the support of Derecho: HPE Cray EX System (https://doi.org/10.5065/qx9a-pg09) of Computational and Information Systems Laboratory (CISL), National Center for Atmospheric Research (NCAR) (allocation No. UCLA0063). This research was funded in part by the FIELDS experiment on the Parker Solar Probe spacecraft, designed and developed under NASA contract UCB #00010350/NASA NNN06AA01C, and the NASA Parker Solar Probe Observatory Scientist grant NASA NNX15AF34G, and NASA HTMS 80NSSC20K1275. M.V. acknowledges support from ISSI via the J. Geiss fellowship.
Data Availability
The PSP and Ulysses mission data used in this study are openly available at the NASA Space Physics Data Facility (https://nssdc.gsfc.nasa.gov) and were analyzed using the following open-source softwares: NumPy (Harris et al., 2020), SciPy (Virtanen et al., 2020), Matplotlib, SPEDAS (Angelopoulos et al., 2019), Numba (Lam et al., 2015).
Appendix A Jensen-Shannon Distance, Gaussianity scalogram and Benchmark

The Jensen-Shannon Distance is the square root of Jensen-Shannon Divergence (Lin, 1991) which is the symmetrized and smoothed version of Kullback–Leibler Divergence (Kullback & Leibler, 1951). Due to its symmetry and smoothness, Jensen-Shannon Distance is an ideal metric for the similarity between the observed magnetic magnitude distribution and the Gaussian distribution. For two discrete probability distribution functions and defined in the same space , the Jensen-Shannon Divergence is calculated as following:
| (A1) |
where is the mixture distribution of and , and is the Kullback–Leibler Divergence:
| (A2) |
In this study, we use scipy.spatial.distance.jensenshannon (Virtanen et al., 2020) to calculate the Jensen-Shannon Distance. This program uses natural base logarithm in Kullback–Leibler Divergence, and therefore the final Jensen-Shannon distance is bounded by . Note that kurtosis has been commonly used in past studies to quantify the Gaussianity of probability distribution functions (see e.g., Sioulas et al. (2022)). However, kurtosis is only a necessary condition for Gaussianity; for instance, a uniform distribution can have a kurtosis of 3. Therefore, in this study, we chose JSD for its simplicity and interpretability in quantifying Gaussianity. Nonetheless, recent studies have shown that Wasserstein distance (Xia et al., 2024a, b) has advantages over divergence methods, and we plan to investigate these methods in future work.
The Gaussianity scalogram (GS) is a map where the vertical axis is window size () and the horizontal axis is the central time of each interval (), together forming a scalogram of Jensen-Shannon distance between the normalized probability density function of a given interval and the standard Gaussian distribution , i.e. , or simply . To calculate from the ensemble of samples from a given interval, there are three controlling parameters: sample size , number of bins , and number of standard deviation considered . In addition, for benchmark purposes, it is necessary to calculate the JSD between some well-known symmetric distributions and standard Gaussian distribution. The summary of the influence of the controlling parameters and the comparison with well-known distributions are shown in Figure 7.
The JSD between Laplace and Logistic distributions and Gaussian distribution as a function of standard deviation range considered is shown in panel (a). The JSD value stablizes approximately at 5 , and therefore for all GS shown in this paper, the are all compiled for . To see how and control the JSD value, samples are repeated drawn from a true Logistic distribution to calculate . In panel (c), we see a much stablized region for large enough and not-too-large (The stable region is orange-ish because theoretical value at 5 is slightly smaller than the true value shown in panel (a) as dark red horizontal dashed line). Two purple dashed regions are highlighted in panel (c), where the right one indicates the parameter space used for low resolution GS shown in Figure 1 and 10, and the left one corresponds to the high resolution version shown in Figure 5 (c-e).
In addition, and also influence the ground truth value, i.e. the Jensen-Shannon distance between an ensemble statistically drawn from Gaussian generator and the real Gaussian PDF, which is not available in closed form (Nielsen, 2019). To obtain the ground truth value, the PDF is a histogram of equally spaced bins located within 5 compiled from independent samples drawn from a standard Gaussian source numpy.random.randn (Harris et al., 2020), and then the JSD is the averaged distance between the statistically calculated PDF() (repeated 30 times for each and ) and the true Gaussian PDF. The standard deviation is found to be small for a given tuple of and . The resulting - map is shown in panel (b), and the two parameter space considered are also shown as purple dashed regions. Even for the poorest case (), the ground truth value is still sufficiently away from JSD().
Finally, it should be pointed out that slightly similar multi-resolution visualization (scalogram) methods based on Jensen-Shannon divergence have been proposed in other fields. For example, Torres et al. (2007) use JSD to measure the divergence between wavelet coefficients of speech signals in consecutive time windows, focusing on enhancing speech recognition in noisy environments. Zhang et al. (2017) apply JSD to compare the probability distributions of EEG segments during awake and NREM sleep states to analyze EEG complexity. Both studies utilize JSD to compare distributions within their respective datasets, not against a Gaussian distribution. In contrast, our work applies JSD specifically to measure how closely the normalized magnetic magnitude data from the solar wind aligns with a Gaussian distribution. This unique approach allows us to identify and visualize various solar wind structures, such as coronal holes, across multiple temporal scales using the Gaussianity Scalogram. Our domain is solar physics, and by normalizing the magnetic field magnitude with a power law fit, we reveal fractal-like structures in the solar wind spanning seconds to years, offering new insights into their solar origins.
Appendix B Spherical Polarization of Alfvén Waves
Although the spherical (arc) polarization of observed Alfvén waves is well-known (Del Zanna, 2001; Riley et al., 1996; Vasquez & Hollweg, 1996; Tsurutani et al., 1994; Wang et al., 2012; Erofeev, 2019; Johnston et al., 2022; Hollweg, 1974; Squire & Mallet, 2022), we provide here a description here for spherically polarized Alfvén waves in a magnetically dominated plasma (plasma , typical for Alfvénic solar wind measured by PSP around perihelion (Kasper et al., 2021)). Similar to Matteini et al. (2014), this consider the background magnetic field to have the same constant magnetic magnitude , differently from Hollweg (1974) where is calculated as the spatial average , yielding a smaller field magnitude than the radius of the sphere .
For a fluctuation-free magnetic flux tube originating from a coronal hole, the magnetic field is pointing mostly radially in the high corona and solar wind close to the sun. The spherically polarized Alfvén waves can therefore be considered as a perturbation to this otherwise quiet system. To maintain the constant state observed in the solar wind, the additive magnetic perturbation has to “switchback” on top of the radial background field. This scenario is depicted in Figure 4 in Matteini et al. (2014). The constant magnetic magnitude is shown as the radius of the circle and the static radial field from coronal hole is . To maintain the constant state, the perturbation to the system is restricted to the semi-circle, and the resultant magnetic vector can thus fluctuate on a constant sphere of . Following this setup, the magnetically dominant () incompressible MHD equations can be rewritten as follows (, , , ):
| (B1) | |||
| (B2) |
where . Assuming the frame is co-moving with the bulk flow and the perturbations are Alfvénic, i.e. and , the equations can be further reduced into a wave equation:
| (B3) |
where . This equation is identical to the circularly polarized Alfvén wave equation, except that can be large but restricted to the sphere defined by and the Alfvén phase velocity is precisely defined (not defined with time-averaged field).
This model leads to some important implications: 1. The spherically polarized Alfvén wave is an exact solution and is mathematically identical to the small amplitude shear Alfvén mode; 2. If a radial jet is present in the system, i.e. , in accordance with the observed “switchbacks”, the spherically polarized Alfv́en waves can only be outward-propagating. This is because to maintain the constant state, the only possible polarization is ; 3. There exists a well-defined background field for the constant state, and hence the constant magnetic magnitude can be regarded as a good proxy for the local , i.e. the local magnetic flux density.
In fact, the reversal of the magnetic field line (switchback) does not increase the number of field lines (thus field line density) and the Alfvén wave, being a solenoidal mode, does not change the local magnetic flux density. This establishes a connection between the magnetic magnitude (magnetic field line density) and the local magnetic flux density within the magnetically dominated coronal holes close to the sun. The helio-radial normalization of in the main text can therefore be regarded as mapping the magnetic flux density measured at different radial distances and longitudinal locations back to a cross section of the magnetic flux tube originating from the coronal hole.
Appendix C PSP and Ulysses Data Analysis
The Gaussianity scalograms in this paper are compiled from magnetic magnitude time series of PSP and Ulysses. The fluxgate magnetometer of PSP (Bale et al., 2016; Bowen et al., 2020) offers two versions of level-2 data in RTN coordinates: mag_rtn_4_per_cyc and mag_rtn. The GS for intervals longer than one day are compiled with the low resolution (4 samples per 0.874 second) data product and the rest are compiled with the high resolution (256 samples per 0.874 second) mag_rtn. All magnetic magnitude data points for each interval are treated as independent samples drawn from a stochastic source and therefore the invalid (NaN) values are discarded and no interpolation is applied. The Ulysses magnetic field data is treated the same way.
Appendix D Three-Dimensional MHD Alfvénic Turbulence Simulation
The simulation is conducted using a 3D Fourier-transform based pseudo-spectral MHD code (Shi et al., 2020, 2024a). MHD equation set in conservation form is evolved with a third-order Runge-Kutta method. A detailed description of the simulation set-up and normalization units can be found in (Shi et al., 2023). Here we briefly summarize the key parameters.
The domain of the simulation is a rectangular box with the length of each side being . The number of grid points along each dimension is . To ensure numerical stability, explicit resistivity and viscosity are adopted besides a de-aliasing.
For the initial configuration, uniform density, magnetic field and pressure are added: , . The magnetic field has a small angle () with respect to -axis, and it is inside plane. On top of the background fields, we add correlated velocity and magnetic field fluctuations, i.e. the fluctuations are Alfvénic, with 3D isotropic power spectra. The reduced 1D spectra roughly follow . The strength of the fluctuations is where is the root-mean-square of the magnetic field fluctuation.
Appendix E Fluxgate Magnotometer Noise and Zeros-Drift
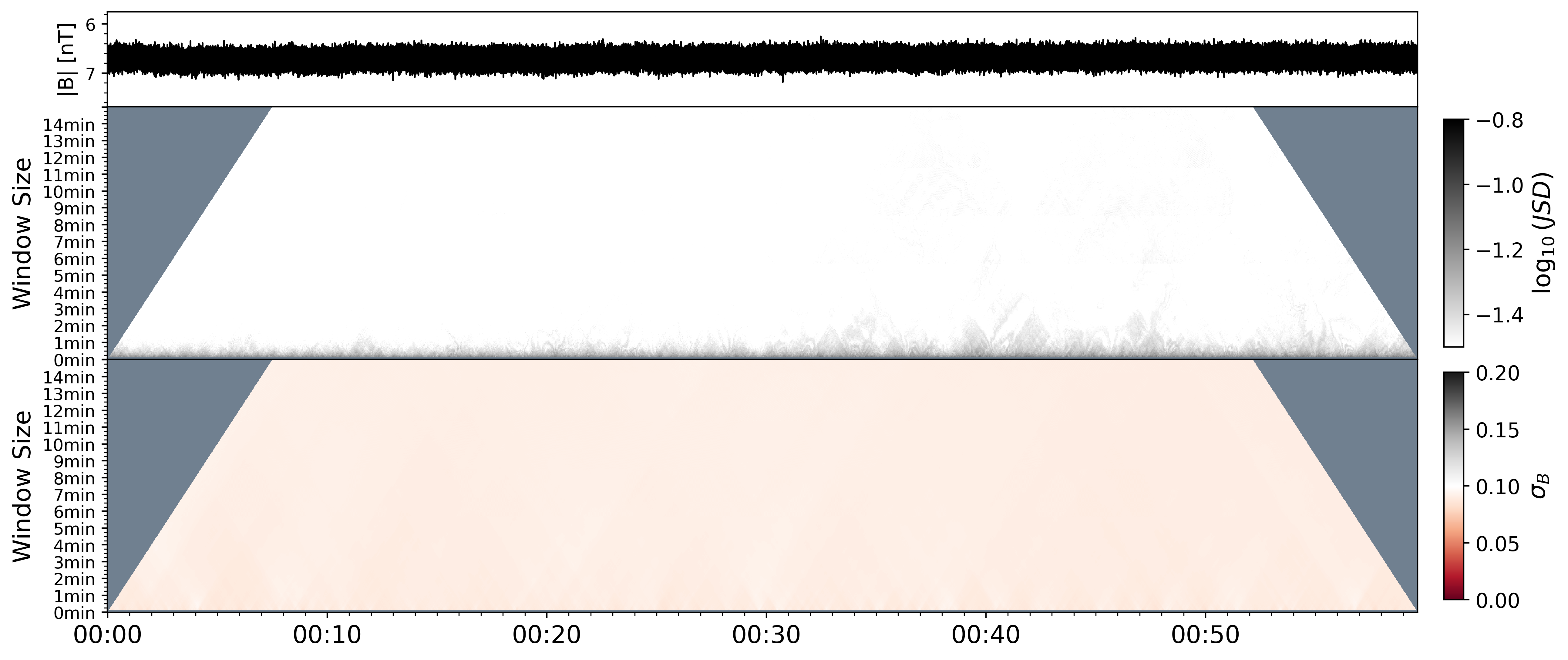
There are several sources of error in the PSP fluxgate magnetometer measurements Bale et al. (2016), including the instrumental noise as well as uncertainty in the zero offsets which drift in time Bowen et al. (2020). The instrumental noise of each vector component is approximated as Gaussian white noise with a standard deviation , and together produce a noise with a standard deviation of for the magnetic magnitude. is usually much smaller than the standard deviation of the in situ measured for all scales that we are interested in. Nevertheless, the GS of a ground measured one-hour magnetic field time series for calibration is shown in Figure 8. The distribution of the noise signal is universally Gaussian regardless of scales and location, and the standard deviations are unanimously small. Therefore, most of the Gaussian structures we show in the paper are real signals rather than instrument noise.
The error from drifting spacecraft offsets is a significantly larger contribution to the error as the approximated zero-offsets drift over time and are calibrated each day Bowen et al. (2020). The drift of the spacecraft offsets, which is thought to occur due to slowly varying currents on the spacecraft is not well constrained and varies over time. This error is not Gaussian in nature, but should introduce small offsets in the measured field from the real background magnetic field. Spacecraft rolls are used to determine zero-offsets in both the inbound and outbound phases of each orbit, and are updated daily through optimizing the measurements to ensuring that spherically polarized magnetic field intervals maintain a constant magnitude. Typical offset values drift about /day. Due to the continuous drift and non-Gaussian nature, the sub-day () structures are not strongly affected by the zeros-drift. And the days-long structures are also not affected because of the instrument calibration of the zeros-offset.
Appendix F Supplementary Materials
F.1 Supplementary Videos
This manuscript contains one supplementary video: gaussianity_skewness_scalogram_E12.mp4.
It shows the Gaussianity scalogram and normalized standard deviation scalogram of magnetic magnitude with window sized from 30 second to 15 minutes for the whole Parker Solar Probe E12. This video aims to show the self-similar magnetic structures revealed by GS and the corresponding sub-structures from the normalized standard deviation scalogram. For the first one minute, the GS looks different because of the low sampling rate of the fluxgate magnetometer. It also shows the Skewness scalogram and normalized standard deviation scalogram of magnetic magnitude with window sized from 1 second to 5 minutes for the whole Parker Solar Probe E12. This video aims to show the systematic tendency for magnetic holes in the magnetic magnitude distributions.
F.2 Supplementary Figures

References
- Angelopoulos et al. (2019) Angelopoulos, V., Cruce, P., Drozdov, A., et al. 2019, Space Science Reviews, 215, 9, doi: 10.1007/s11214-018-0576-4
- Aschwanden (2011) Aschwanden, M. 2011, Self-Organized Criticality in Astrophysics: The Statistics of Nonlinear Processes in the Universe (Berlin, Heidelberg: Springer Berlin Heidelberg), doi: 10.1007/978-3-642-15001-2
- Aschwanden et al. (2016) Aschwanden, M. J., Crosby, N. B., Dimitropoulou, M., et al. 2016, Space Science Review, 198, 47, doi: 10.1007/s11214-014-0054-6
- Badman et al. (2020) Badman, S. T., Bale, S. D., Oliveros, J. C. M., et al. 2020, The Astrophysical Journal Supplement Series, 246, 23, doi: 10.3847/1538-4365/ab4da7
- Badman et al. (2023) Badman, S. T., Riley, P., Jones, S. I., et al. 2023, Journal of Geophysical Research: Space Physics, 128, e2023JA031359, doi: 10.1029/2023JA031359
- Bale et al. (2016) Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, ßr, 204, 49, doi: 10.1007/s11214-016-0244-5
- Bale et al. (2019) Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 1, doi: 10.1038/s41586-019-1818-7
- Bale et al. (2021) Bale, S. D., Horbury, T. S., Velli, M., et al. 2021, The Astrophysical Journal, 923, 174, doi: 10.3847/1538-4357/ac2d8c
- Bale et al. (2023) Bale, S. D., Drake, J. F., McManus, M. D., et al. 2023, Nature, 618, 252, doi: 10.1038/s41586-023-05955-3
- Bandyopadhyay et al. (2020) Bandyopadhyay, R., Matthaeus, W. H., Parashar, T. N., et al. 2020, Physical Review Letters, 124, 255101, doi: 10.1103/PhysRevLett.124.255101
- Berger et al. (2017) Berger, T., Hillier, A., & Liu, W. 2017, The Astrophysical Journal, 850, 60, doi: 10.3847/1538-4357/aa95b6
- Bowen et al. (2020) Bowen, T. A., Bale, S. D., Bonnell, J. W., et al. 2020, Journal of Geophysical Research: Space Physics, 125, e2020JA027813, doi: 10.1029/2020JA027813
- Burlaga (2001) Burlaga, L. F. 2001, Journal of Geophysical Research: Space Physics, 106, 15917, doi: 10.1029/2000JA000107
- Burlaga & Lazarus (2000) Burlaga, L. F., & Lazarus, A. J. 2000, Journal of Geophysical Research: Space Physics, 105, 2357, doi: 10.1029/1999JA900442
- Chitta et al. (2023) Chitta, L. P., Zhukov, A. N., Berghmans, D., et al. 2023, Science, 381, 867, doi: 10.1126/science.ade5801
- Davis et al. (2023) Davis, N., Chandran, B. D. G., Bowen, T. A., et al. 2023, The Astrophysical Journal, 950, 154, doi: 10.3847/1538-4357/acd177
- Del Zanna (2001) Del Zanna, L. 2001, Geophysical Research Letters, 28, 2585, doi: 10.1029/2001GL012911
- Drake et al. (2021) Drake, J. F., Agapitov, O., Swisdak, M., et al. 2021, Astronomy & Astrophysics, 650, A2
- Dudok de Wit et al. (2020) Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., et al. 2020, The Astrophysical Journal Supplement Series, 246, 39, doi: 10.3847/1538-4365/ab5853
- Erofeev (2019) Erofeev, D. V. 2019, Geomagnetism and Aeronomy, 59, 1081, doi: 10.1134/S0016793219080061
- Fargette et al. (2021) Fargette, N., Lavraud, B., Rouillard, A. P., et al. 2021, The Astrophysical Journal, 919, 96, doi: 10.3847/1538-4357/ac1112
- Fox et al. (2016) Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Science Reviews, 204, 7, doi: 10.1007/s11214-015-0211-6
- Harris et al. (2020) Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357, doi: 10.1038/s41586-020-2649-2
- Heinemann & Olbert (1980) Heinemann, M., & Olbert, S. 1980, Journal of Geophysical Research: Space Physics, 85, 1311, doi: 10.1029/JA085iA03p01311
- Hollweg (1973) Hollweg, J. V. 1973, Journal of Geophysical Research (1896-1977), 78, 3643, doi: 10.1029/JA078i019p03643
- Hollweg (1974) —. 1974, Journal of Geophysical Research (1896-1977), 79, 1539, doi: 10.1029/JA079i010p01539
- Huang et al. (2022) Huang, Z., Shi, C., Sioulas, N., & Velli, M. 2022, The Astrophysical Journal, 935, 60, doi: 10.3847/1538-4357/ac74c5
- J. Towns et al. (2014) J. Towns, T. Cockerill, M. Dahan, et al. 2014, Computing in Science & Engineering, 16, 62, doi: 10.1109/MCSE.2014.80
- Johnston et al. (2022) Johnston, Z., Squire, J., Mallet, A., & Meyrand, R. 2022, Physics of Plasmas, 29, 072902, doi: 10.1063/5.0097983
- Kasper et al. (2016) Kasper, J. C., Abiad, R., Austin, G., et al. 2016, ßr, 204, 131, doi: 10.1007/s11214-015-0206-3
- Kasper et al. (2019) Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228
- Kasper et al. (2021) Kasper, J. C., Klein, K. G., Lichko, E., et al. 2021, Physical Review Letters, 127, 255101, doi: 10.1103/PhysRevLett.127.255101
- Kruparova et al. (2023) Kruparova, O., Krupar, V., Szabo, A., Pulupa, M., & Bale, S. D. 2023, The Astrophysical Journal, 957, 13, doi: 10.3847/1538-4357/acf572
- Kullback & Leibler (1951) Kullback, S., & Leibler, R. A. 1951, The Annals of Mathematical Statistics, 22, 79, doi: 10.1214/aoms/1177729694
- Lam et al. (2015) Lam, S. K., Pitrou, A., & Seibert, S. 2015, in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC (Austin Texas: ACM), 1–6, doi: 10.1145/2833157.2833162
- Larosa et al. (2021) Larosa, A., Krasnoselskikh, V., Wit, T. D. d., et al. 2021, Astronomy & Astrophysics, 650, A3, doi: 10.1051/0004-6361/202039442
- Lin (1991) Lin, J. 1991, IEEE Transactions on Information Theory, 37, 145, doi: 10.1109/18.61115
- Matteini et al. (2014) Matteini, L., Horbury, T. S., Neugebauer, M., & Goldstein, B. E. 2014, Geophysical Research Letters, 41, 259, doi: 10.1002/2013GL058482
- Matteini et al. (2015) Matteini, L., Horbury, T. S., Pantellini, F., Velli, M., & Schwartz, S. J. 2015, The Astrophysical Journal, 802, 11, doi: 10.1088/0004-637X/802/1/11
- Matteini et al. (2024) Matteini, L., Tenerani, A., Landi, S., et al. 2024, Physics of Plasmas, 31, 032901, doi: 10.1063/5.0177754
- McComas et al. (2003) McComas, D. J., Elliott, H. A., Schwadron, N. A., et al. 2003, Geophysical Research Letters, 30, doi: 10.1029/2003GL017136
- Moncuquet et al. (2020) Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, The Astrophysical Journal Supplement Series, 246, 44, doi: 10.3847/1538-4365/ab5a84
- Müller et al. (2020) Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, åp, 642, A1, doi: 10.1051/0004-6361/202038467
- Nielsen (2019) Nielsen, F. 2019, Entropy, 21, 485, doi: 10.3390/e21050485
- Padhye et al. (2001) Padhye, N. S., Smith, C. W., & Matthaeus, W. H. 2001, Journal of Geophysical Research, 106, 18635, doi: 10.1029/2000JA000293
- Panasenco et al. (2020) Panasenco, O., Velli, M., D’Amicis, R., et al. 2020, The Astrophysical Journal Supplement Series, 246, 54, doi: 10.3847/1538-4365/ab61f4
- Perez et al. (2021) Perez, J. C., Bourouaine, S., Chen, C. H. K., & Raouafi, N. E. 2021, Astronomy & Astrophysics, 650, A22, doi: 10.1051/0004-6361/202039879
- Raouafi et al. (2023a) Raouafi, N. E., Matteini, L., Squire, J., et al. 2023a, Space Science Reviews, 219, 8, doi: 10.1007/s11214-023-00952-4
- Raouafi et al. (2023b) Raouafi, N. E., Stenborg, G., Seaton, D. B., et al. 2023b, The Astrophysical Journal, 945, 28, doi: 10.3847/1538-4357/acaf6c
- Riley et al. (1996) Riley, P., Sonett, C. P., Tsurutani, B. T., et al. 1996, Journal of Geophysical Research: Space Physics, 101, 19987
- Shi et al. (2023) Shi, C., Sioulas, N., Huang, Z., et al. 2023, Evolution of MHD turbulence in the expanding solar wind: residual energy and intermittency, arXiv, doi: 10.48550/arXiv.2308.12376
- Shi et al. (2024a) Shi, C., Tenerani, A., Rappazzo, A. F., & Velli, M. 2024a, Frontiers in Astronomy and Space Sciences, 11, doi: 10.3389/fspas.2024.1412905
- Shi et al. (2020) Shi, C., Velli, M., Tenerani, A., Rappazzo, F., & Réville, V. 2020, The Astrophysical Journal, 888, 68, doi: si
- Shi et al. (2024b) Shi, C., Velli, M., Toth, G., et al. 2024b, The Astrophysical Journal Letters, 964, L28, doi: 10.3847/2041-8213/ad335a
- Shi et al. (2022) Shi, C., Panasenco, O., Velli, M., et al. 2022, The Astrophysical Journal, 934, 152, doi: 10.3847/1538-4357/ac7c11
- Sioulas et al. (2022) Sioulas, N., Huang, Z., Velli, M., et al. 2022, The Astrophysical Journal, 934, 143, doi: 10.3847/1538-4357/ac7aa2
- Squire & Mallet (2022) Squire, J., & Mallet, A. 2022, Journal of Plasma Physics, 88, 175880503, doi: 10.1017/S0022377822000848
- Tenerani et al. (2020) Tenerani, A., Velli, M., Matteini, L., et al. 2020, The Astrophysical Journal Supplement Series, 246, 32, doi: 10.3847/1538-4365/ab53e1
- Torres et al. (2007) Torres, M. E., Rufiner, H. L., Milone, D. H., & Cherniz, A. S. 2007, Physica A: Statistical Mechanics and its Applications, 385, 319, doi: 10.1016/j.physa.2007.06.031
- Tsurutani et al. (1994) Tsurutani, B. T., Ho, C. M., Smith, E. J., et al. 1994, Geophysical Research Letters, 21, 2267, doi: 10.1029/94GL02194
- Uritsky & Davila (2012) Uritsky, V. M., & Davila, J. M. 2012, Astrophys. J., 748, 60, doi: 10.1088/0004-637X/748/1/60
- Vasquez & Hollweg (1996) Vasquez, B. J., & Hollweg, J. V. 1996, Journal of Geophysical Research: Space Physics, 101, 13527, doi: 10.1029/96JA00612
- Velli et al. (1991) Velli, M., Grappin, R., & Mangeney, A. 1991, Geophysical & Astrophysical Fluid Dynamics, 62, 101, doi: 10.1080/03091929108229128
- Virtanen et al. (2020) Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261, doi: 10.1038/s41592-019-0686-2
- Wang et al. (2012) Wang, X., He, J., Tu, C., et al. 2012, The Astrophysical Journal, 746, 147, doi: 10.1088/0004-637X/746/2/147
- Whang (1977) Whang, Y. C. 1977, Solar Physics, 53, 507, doi: 10.1007/BF00160293
- Xia et al. (2024a) Xia, M., Li, X., Shen, Q., & Chou, T. 2024a, An efficient Wasserstein-distance approach for reconstructing jump-diffusion processes using parameterized neural networks, arXiv, doi: 10.48550/arXiv.2406.01653
- Xia et al. (2024b) —. 2024b, Squared Wasserstein-2 Distance for Efficient Reconstruction of Stochastic Differential Equations, arXiv, doi: 10.48550/arXiv.2401.11354
- Yamamoto & Kambe (1991) Yamamoto, K., & Kambe, T. 1991, Fluid Dynamics Research, 8, 65, doi: 10.1016/0169-5983(91)90031-D
- Yu et al. (2021) Yu, L., Huang, S. Y., Yuan, Z. G., et al. 2021, The Astrophysical Journal, 908, 56, doi: 10.3847/1538-4357/abb9a8
- Yu et al. (2022) —. 2022, Journal of Geophysical Research: Space Physics, 127, e2022JA030505, doi: 10.1029/2022JA030505
- Zhang et al. (2017) Zhang, Z., Wang, J., Dai, J., Li, J., & Hou, F. 2017, in 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), 1–5, doi: 10.1109/CISP-BMEI.2017.8302218