Solution to Banff 2 Challenge Based on Likelihood Ratio Test
Abstract
We describe our solution to the Banff 2 challenge problems as well as the outcomes.
1 Introduction
In July of 2010 a conference was held on the statistical issues relevant to significance of discovery claims at the LHC. The conference took place at the Banff International Research Station in Banff, Alberta, Canada. After many discussions it was decided to hold a competition to see which methods would perform best. One of the participants, Thomas Junk, would create a large number of data sets, some with a signal and some without. There were two main parts to the competition:
Problem 1 was essentially designed to see whether the methods could cope with the ”look-elsewhere” effect, the issue of searching through a mass spectrum for a possible signal.
Problem 2 was concerned with the problem that sometimes there are no known distributions for either the backgrounds or the signal and they have to be estimated via Monte Carlo.
For a detailed description of the problems as well as the data sets and a discussion of the results see Tom Junk’s CDF web page at http://www-cdf.fnal.gov/˜trj/. In this paper we will present a solution based on the likelihood ratio test, and discuss the performance of this method in the challenge.
2 The method
Our solution for both problems is based on the likelihood ratio test statistic
According to standard theorems in Statistics often has a distribution with the number of degrees of freedom the difference between the number of free parameters and the number of free parameters under the null hypothesis. This turns out to be true for problem 2 but not for problem 1, in which case the null distribution can be found via simulation.
2.1 Problem 1
Here we have:
|
Now is the log likelihood function evaluated at the maximum likelihood estimator and . Note that if any choice of E yields the same value of the likelihood function.
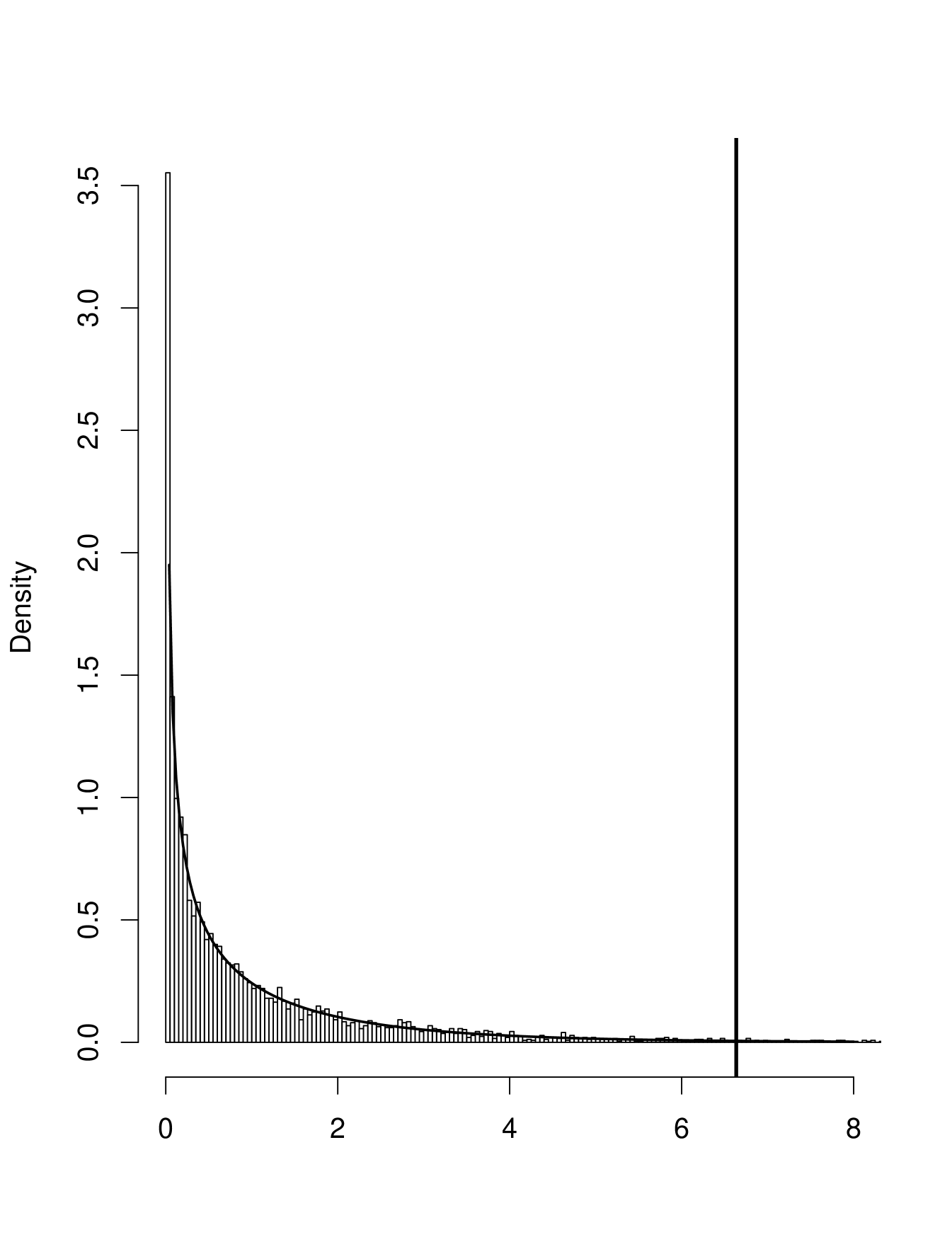
In the following figure we have the histogram of 100000 values of for a simulation with and together with the densities of the distribution with df’s from 1 to 5. Clearly non of these yields an acceptable fit. Instead we use the simulated data to find the 99% quantile and reject the null hypothesis if is larger than that, shown as the vertical line in the graph.
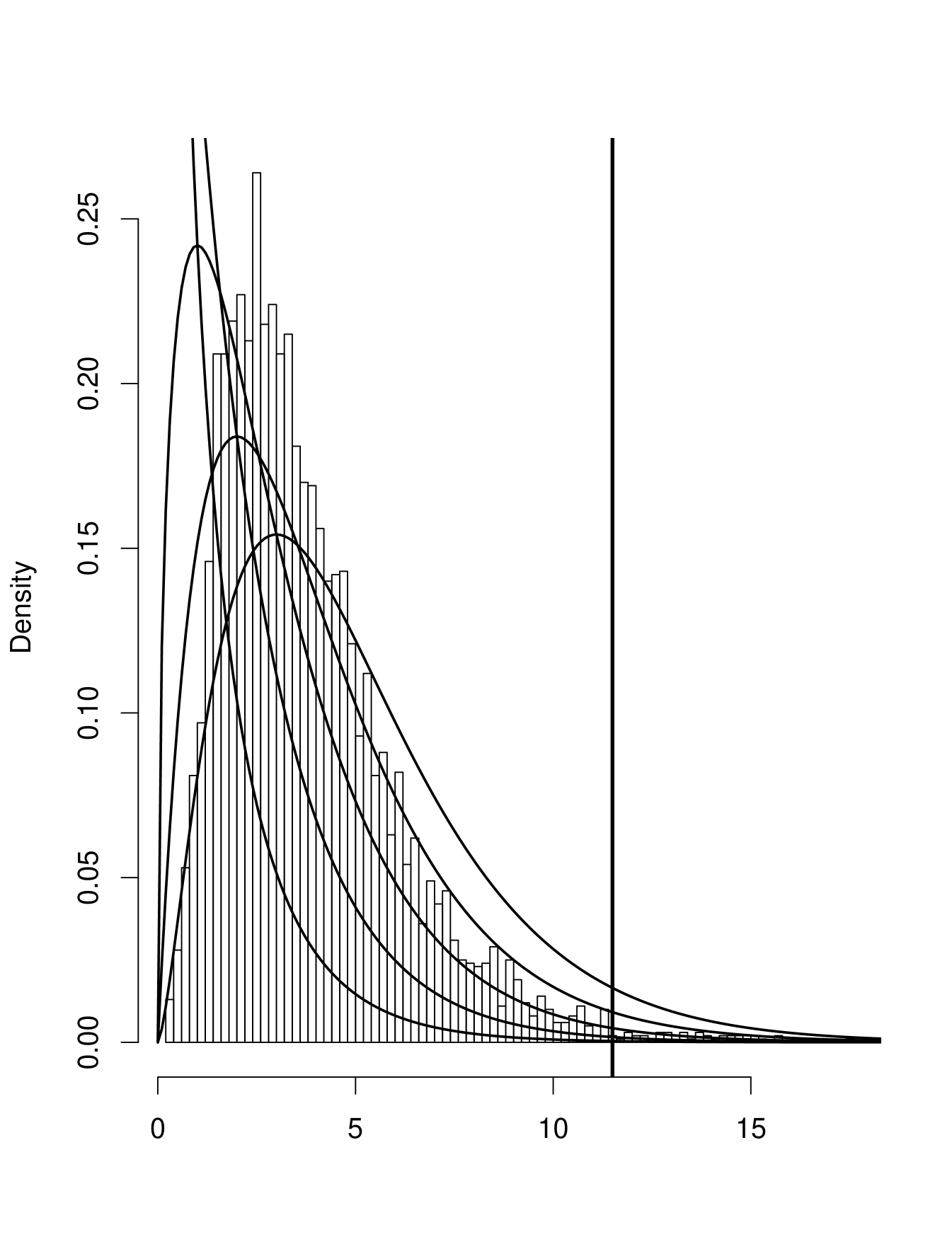
In general the critical value will depend on the sample size, but for those in the challenge () it is always about .
If it was decided to do discovery using the critical value can be found using importance sampling. Recently Eilam Gross and Ofer Vitells have developed an analytic upper bound for the tail probabilities of the null distribution, see ”Trial factors for the look elsewhere effect in high energy physics”, Eilam Gross, Ofer Vitells, Eur.Phys.J.C70:525-530,2010. Their result agrees with our simulations.
Finding the mle is a non-trivial exercise because there are many local minima. The next figure shows the log-likelihood as a function of with fixed at for 4 cases.
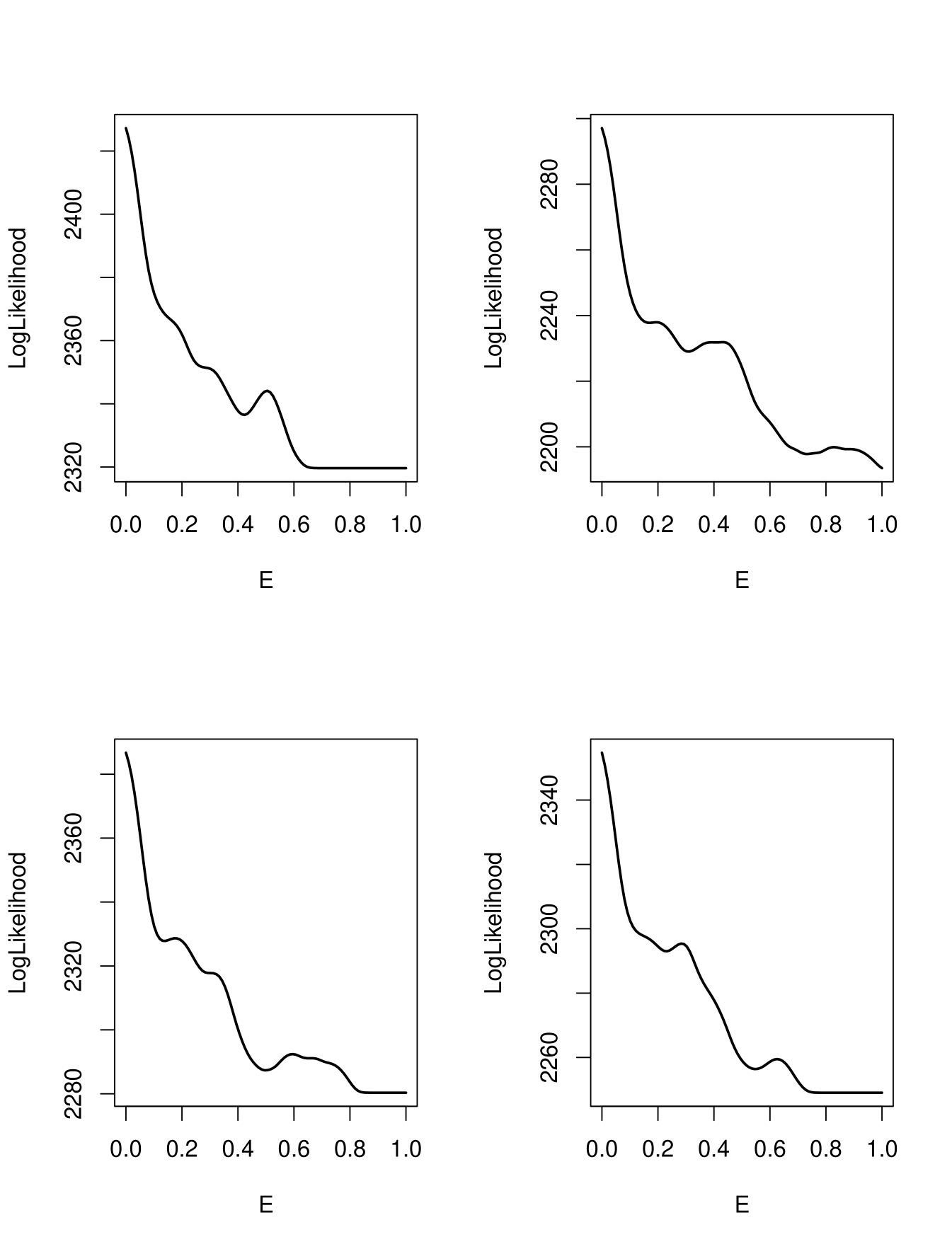
To find the mle we used a two-step procedure: first a fine grid search over values of from to in steps of . At each value of the corresponding value of that maximizes the log-likelihood is found. In a second step the procedure starts at the best point found above and uses Newton-Raphson to find the overall mle.
2.2 Problem 2
Again we want to use:
|
Now is the log likelihood function evaluated at the maximum likelihood estimator and .
The difficulty is of course that we don’t know , or . We have used three different ways to find them:
2.2.1 Parametric Fitting
Here one tries to find a parametric density that gives a reasonable fit to the data. For the data in the challenge this turns out to be very easy. In all three cases a Beta density gives a very good fit:
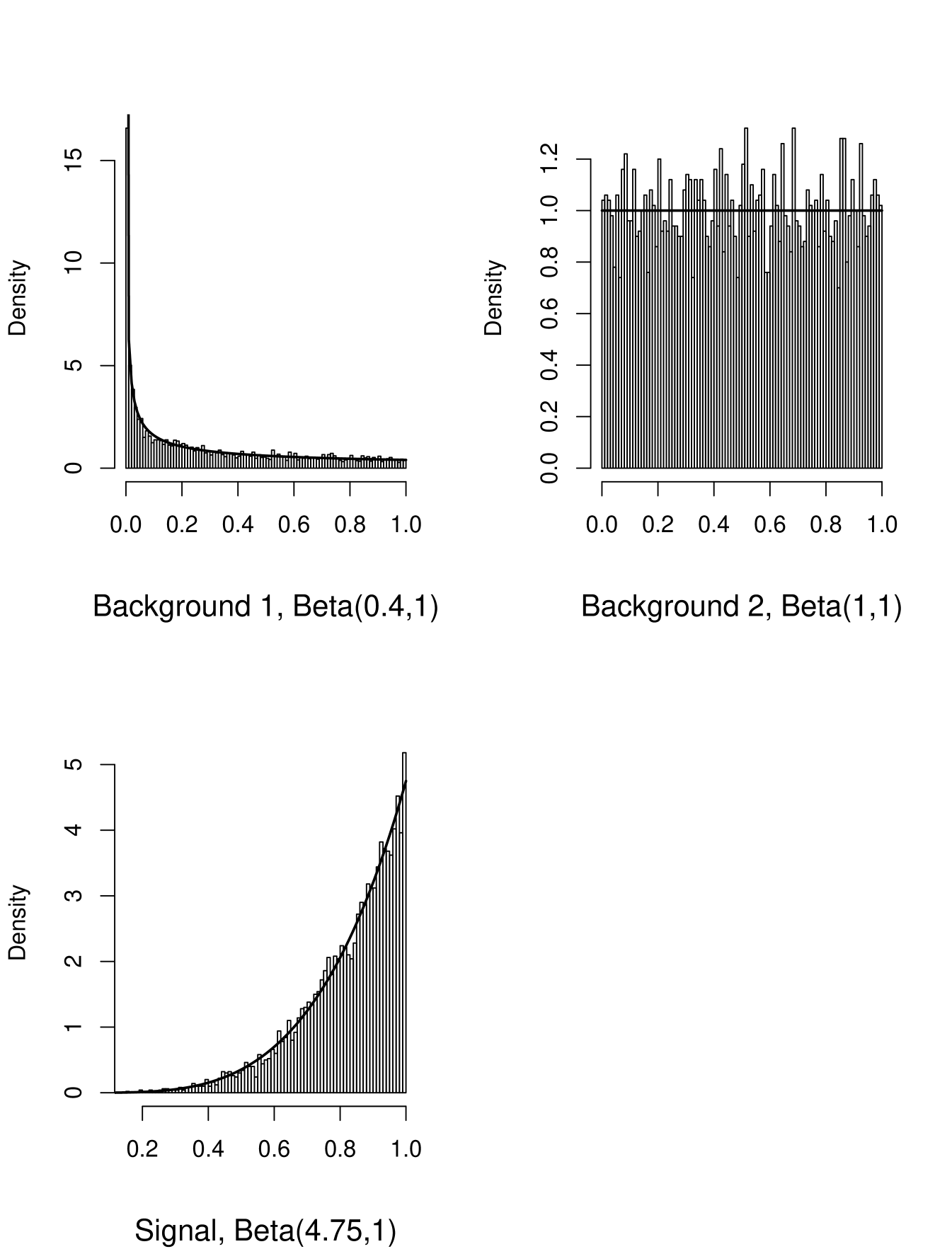
2.2.2 Nonparametric Fitting:
There are a variety of methods known in Statistics for non-parametric density estimation. The difficulty with the data in the challenge is that it is bounded on a finite interval, a very common feature in HEP data. Moreover the slope of the density of Background 1 at 0 is infinite. I checked a number of methods and eventually ended up using the following: for Background 2, the Signal and the right half of Background 1 i bin the data (250 bins) find the counts and scale them to integrate to unity. Then i use the non-parametric density estimator loess from R with the default span (smoothing parameter). This works well except on the left side of Background 1. There the infinite slope of the density would require a smoothing parameter that goes to 0. Instead i transform the data with . The resulting data has a density without boundary, which i estimate using the routine density from R, again with the default bandwidth. This is then back-transfomed to the 0-1 scale. This works well for the left side but not the right one, and so i ”splice” the two densities together in the middle. The resulting densities are shown here:
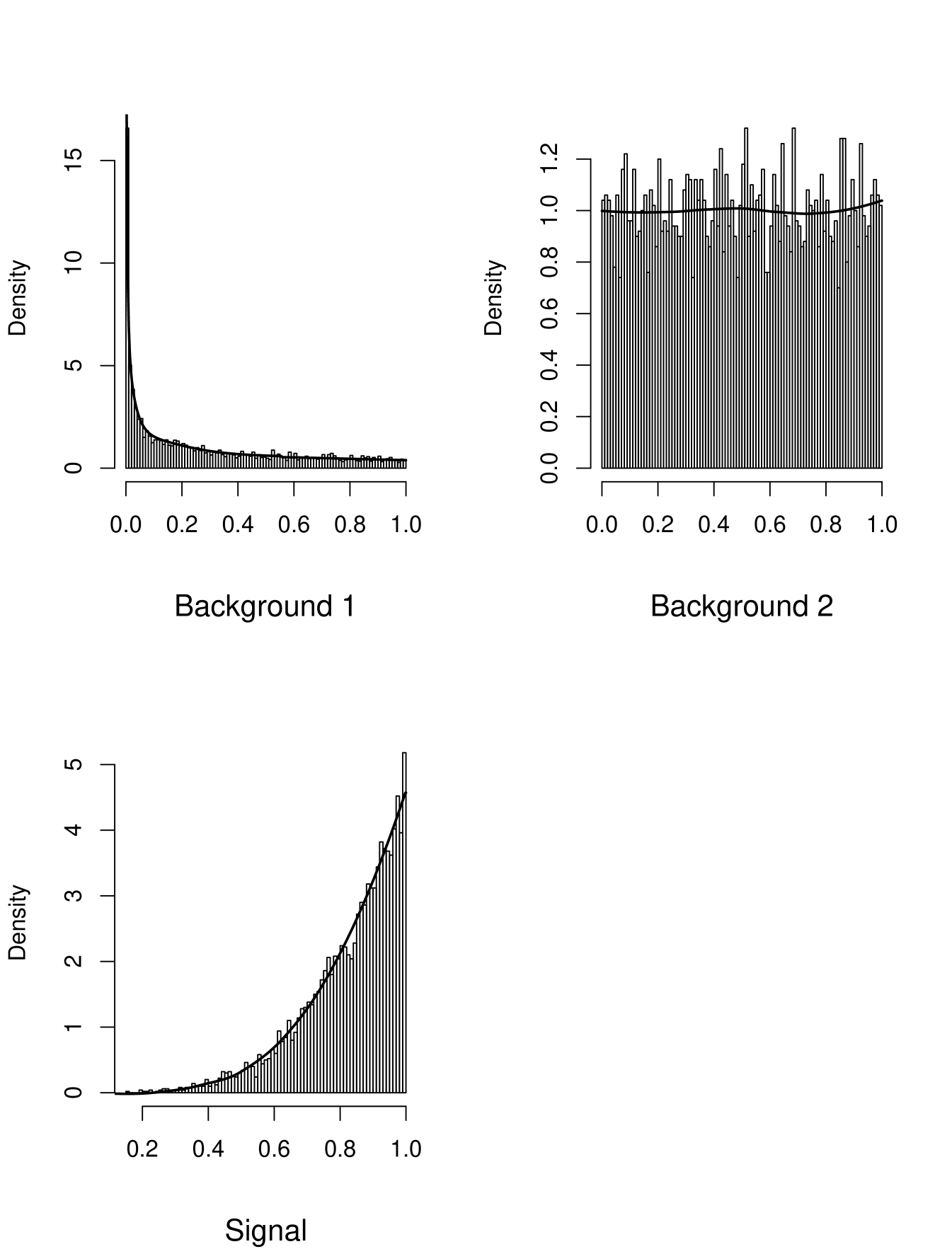
2.2.3 Semiparametric Fitting
It is possible to combine the two approaches above: fit some of the data parametrically and others non-parametrically, for example if the signal is known to have a Gaussian distribution but the background density is Monte Carlo data.
For the data in the challenge the three methods give very similar results, so i am submitting only the solution using the parametric fits.
2.2.4 Back to the Test
What is the null distribution of now? In the following figure we have the histogram of 5000 values of for a simulation with events from Background 1, events from Background 2 and no Signal events. together with the density of a distribution with df. The densities are fit parametrically.
Clearly this yield a very good fit, so we will reject the null hypothesis if , the percentile of a chi-square distribution with degree of freedom. The same result holds if the fitting was done non parametrically or semi parametrically.
2.3 Error Estimation
We have the following large sample theorem for maximum likelihood estimators: if we have a sample with density and is the mle for the parameter , then under some regularity conditions
where , the Fisher information number. This can be estimated using the observed Fisher information number
For problem 1 we find:
|
so the standard error of is estimated with and the standard error of is given by .
For problem 2 the errors are found similarly.
How good are these errors? As always with large sample theory, there is a question whether it works for a specific problem at the available sample sizes. Here is the result of a mini MC study: we generate events from the background of problem 1 and events from the signal with . This is repeated times. The histogram of estimates for the mixing ratio is shown here:
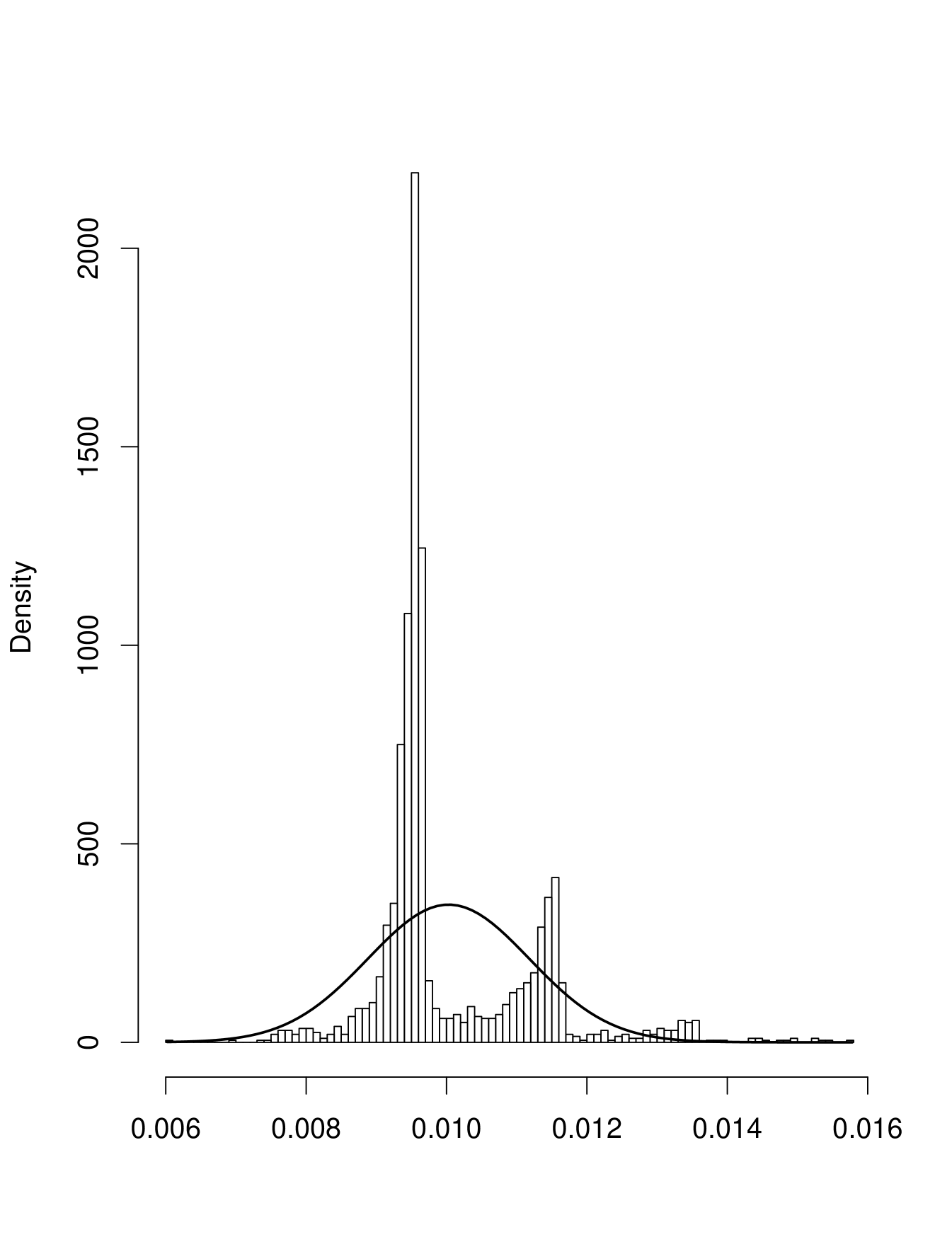
Clearly the distribution of the estimates is not Gaussian, and therefore the errors are wrong.
So we need a different method for finding the 68% intervals. This can be done via the statistical bootstrap. In our submission we will include intervals based on the bootstrap, specifically the and the percentile of a bootstrap sample of size . In a real live problem it would be easy to run a mini MC for a specific case and then decide which errors to use. Because we have to process data sets we can not do so for each individually, and therefore use of the bootstrap intervals.
2.4 Power Studies
Problem 1:
We used the following code to do the power study:
counter=0;
for(int k=0;k10000;++k) {
nsig=rpois(0.07519885*D,seed);
for (int i=0; insig; ++i) x[i]=rnorm(E,seed);
nback=rpois(1000,seed);
for (int i=0; inback; ++i) x[nsig+i]=rbackground(seed)
lrt=findLRT(x);
if(lrt11.5) ++counter;
}
power=counter/M;
The results are :
Problem 2:
We used the following code to do the power study:
counter=0;
for(int k=0;k10000;++k) {
n1=rnorm(1,900,90)
x1=sample(bc2p2b1mc,size=n1)
n2=max(rnorm(1,100,100),0)
x2=sample(bc2p2b2mc,size=n2)
n3=rpois(75,seed);
x3=sample(bc2p2sigmc,size=n3)
nback=rpois(1000,seed);
x=c(x1,x2,x3)
lrt=findLRT(x);
if(lrt6.635) ++counter;
}
power=counter/M;
The result is a power of .
3 Discussion of Results
For a detailed discussion of the performance of all the submitted methods see Tom Junk’s CDF web page at http://www-cdf.fnal.gov/˜trj . Here we will discuss only the results of our method.
3.1 Problem 1
True type I error probability
Missed signals:
So the method achieves the desired type I error probability of .
How about the errors? For the cases were a signal was claimed correctly the nominal CI included the true number of signal events of the time and the true signal location , somewhat lower than desired. This is unexpected because these errors were tested via simulation. For example, for one of the cases in the data set, and signal events, the true error rates are for the number of signal events and for the signal location. It turns out, though, that the error estimates are quite bad in cases were the signal rate is very low. For example for the case and signal events the true error rates are for the number of signal events and for the signal location.
We also checked the errors based on the Fisher Information as described above. Their performance was comparable to the bootstrap errors. The conclusion is that for cases were the signal is small error estimates are difficult.
3.2 Problem 2
True type I error probability
Missed signals:
So for this problem the type I error probability is too large. The reason turns out to be the parametric fit. We used Beta densities for all components, specifically for background 1, for background 2 and for the signal. These give excellent fits to the MC data provided. For example, generating random variates from a , running the Kolmogorov-Smirnoff test and repeating this procedure many times rejects the null hypothesis of equal distributions only about of the time, at a nominal rate. This problem was caused by the size of the MC samples. If instead of MC events there had been the same procedure as above would have rejected the null hypothesis of equal distributions of the time, and a better fitting density would have to be found. The real conclusion here is that a very good density estimate is required to make this test work.